- Department of Chemistry, Stanford University, Stanford, CA, United States
To control molecular scattering, we consider hydrogen molecules prepared in a coherent superposition of m states within a single rovibrational (v, j) energy eigenstate using Stark-induced adiabatic Raman passage (SARP). Specifically, SARP can prepare a bi-axial state of the HD molecule in which the HD bond axis exists simultaneously in two possible alignments at right angles to one another with a well-defined relative phase. We show that scattering from this biaxial state will interfere, resulting in a φ -dependent scattering intensity distribution, where φ is the azimuthal angle about the collision velocity direction. Using the scattering matrix extracted from our experiments on the rotationally inelastic collisions of quantum state prepared HD at low temperatures, we calculate the differential scattering cross-section dσ/dΩ, which shows an interference pattern as function of θ and φ in the image plane perpendicular to the collision velocity. The calculated scattering image shows that scattering from the bi-axial state directs molecules along well-defined angles, corresponding to interference maxima. Thus, the bi-axial state behaves like a double slit for molecular scattering. Moreover, by rotating the polarizations of the SARP preparation lasers, we can control the interference thereby altering the scattering angular distribution. This molecular interferometer, which experimentally measures the relative phases of the scattering matrix elements, allows a direct test of theoretical calculations on important, fundamental collision processes.
Introduction
Interference is a fundamental characteristic of the physical world that results from the intrinsic uncertainty in which multiple definite pathways connect the initial and final states of a system [1]. This uncertainty arises because, at the most fundamental level, a physical system is described by a quantum mechanical wavefunction that defines the state variables probabilistically. While interference plays an important role in controlling dynamics at the atomic scale, its effects are generally impossible to discern at the macroscopic level because the presence of many quantum states with randomly fluctuating phases either removes the interference or obscures its effects. Control over the quantum state of the system is therefore a necessary prerequisite for the interrogation of any interference effects in collision processes [2].
The progenitor of the quantum mechanical interference experiment is Young's double-slit experiment, where interference was observed as light passed through two different optical pathways. A long series of more modern experiments has successfully demonstrated interference of this type using collimated monoenergetic beams of electrons, atoms, and molecules [3–5]. In these experiments, constructive, and destructive interference of two coupled pathways connecting the impinging beam and the detector created positional maxima and minima of particle detection probability in much the same way as bright and dark optical fringes appeared in Young's experiment. Interference is only observed whenever the two slits are separated by nearly the De Broglie wavelength of the particles, meaning that finer and finer control is required as the mass of the system is increased.
Quantum interference that arises from the wave nature of matter contributes to the dynamics of many collision systems. Using advanced techniques to prepare the quantum states of isolated atomic and molecular systems, recent experiments have illustrated the effects of these interferences on the integral or differential cross section of the scattering process. In each of these instances the interference effects resulted because of the possibility of two or more pathways connecting the initial and final states of the matter system. One dramatic example exists in the photoionization of a diatomic molecule [6, 7]. Because the electron is delocalized over two atomic centers, the nuclei function analogously to a double slit in creating two distinct pathways for the excited electron to leave the molecule, thus generating an interference effect that has been measured in the angle-resolved double photoionization of H2 molecules. In addition to the photoionization half-reaction, signatures of interference are also present in two-body collision processes when the transformation involved is mediated by two separate pathways [8–10]. Interference effects of this type have been measured in the rotationally inelastic scattering of optically excited states of small molecular systems including Na2 and CO, where the interference occurred between the singlet and triplet pathways [11]. Similarly, such interferences have been observed in the reactive scattering of systems ranging from H + H2 to Li + NaLi [12–16]. However, in most of the prior experimental interrogations of scattering interferences, the multiple pathways were determined entirely by the material properties of the system, and therefore the interferences could not be controlled experimentally.
With even more precise ability to define the molecular quantum state, interference resulting from multiple quantum mechanical pathways can be exploited to control the outcome of a molecular collision [8, 10, 17–20]. This is achieved by preparing the atom-molecule collision system in a phase coherent superposition of quantum states. Because each state in the superposition provides a distinct pathway to the scattering output, control can be achieved by varying the amplitudes and phases of the superposed states. An experimental example can be found in the work of Nichols et al. who prepared NO in a coherent mixture of even and odd Λ-doublet states by the application of a DC field, to study how an inelastic scattering process is influenced by quantum interference between the coherently coupled initial states [8]. In this paper, we will consider the rotationally inelastic collision between a state-prepared H2 molecule and a ground state He atom. Prior to the collision event, the H2 has been placed in a specific target state that consists of a coherent superposition of m states belonging to a rovibrational (v, j) energy eigenstate. Here, the m quantum number defines the projection of the rotational angular momentum j on a suitable symmetry axis of the collision system. Following preparation, collision with the He atom will induce the Δj transition (v, j, m → v, jf, mf). The target state can be expressed as follows:
where the coefficients Cm are the complex numbers representing the time-independent amplitudes to find the target state in a specific m sublevel. When calculating the probability density of this state, gives the population of the various m sublevels, while the terms (m ≠ m′) are the off-diagonal elements of the density matrix describing the coherences between different m sublevels. As opposed to a rotational wavepacket [21–23], the superposition in Equation (1) evolves with a single frequency Ev, j/ℏ, and so the superposition is a temporally stationary state, which is most desirable in a collision experiment. Optical excitation can be used to prepare a degenerate superposition of m states, thereby injecting optical coherence into the molecular system. To prepare large atomic and molecular ensembles in a coherent superposition of the m sublevels, many coherent optical methods including stimulated Raman adiabatic passage (STIRAP) [24–27], and Stark-induced adiabatic Raman passage (SARP) [28–30] have been developed.
The inelastically scattered quantum state of the H2 molecule can be expressed as:
where Amf(v, jf, θ, φ) is the probability amplitude to find the scattered product (H2) in a rovibrational m eigenstate |v, jf, mf〉 within a unit solid angle along the direction |v, jf, mf〉 . The polar angle (θ, φ) is defined in the center of mass coordinate system with the Z axis oriented along the relative velocity of the colliding partners. Equation (2) is fully general in that it can describe a pure scattered state as well as one that is coherently generated as a superposition of degenerate m states. In this case, the collision process, be it reactive, inelastic, or elastic, has transferred coherence (information) from the target state defined by Equation (1) to the product state defined by Equation (2). The product state coherence is determined by the off-diagonal density matrix elements ρmfmf′ proportional to .
In this paper, we consider theoretically a state-resolved scattering experiment where the unpolarized differential scattering cross section is measured as a sum over all sublevels mf:
The scattering amplitude Amf(v, jf, θ, φ) may be expressed as:
where q(v, j, m, Ec → v, jf, mf) is the state-to-state reaction amplitude within a unit solid angle defined by in the center-of-mass frame. For scattering with well-defined initial momentum, the incoming orbital state is a plane wave described by a superposition of many partial waves. Each of these incoming orbitals is then scattered by the interaction potential to produce multiple orbitals in the outgoing channel. A scattering process can thus be regarded as the diffraction of the incoming matter wave by the colliding partner, where the diffraction efficiency is determined by the strength of the interaction forces. The scattering amplitudes q(v, j, m, Ec → v, jf, mf) are determined by the coherent sum over the contribution of all these outgoing waves. These individual contributions are given by the scattering matrix, which asymptotically connects the incoming and outgoing orbital states and contains information about the dynamics of the molecular interaction.
The measured state-resolved differential scattering cross-section (unpolarized) is given by
Here, Qmm′ contains the phase information of the state-to-state scattering amplitude q as follows:
The population-driven term in Equation (5) is defined as follows:
Equation (7) shows that without m state coherence, the collision cross-section measured in a scattering experiment is determined solely by the m state population of the target state. This is because without coherence each m state contributes independently to the differential cross-section. As a result, no information about the phase of the state-to-state scattering amplitude q can be determined.
The second term on the right-hand side of Equation (5) contains terms, and thus gives rise to the interference effects in the scattering angular distribution. Specifically, the terms Qmm′ defined in Equation (6) give the products of the state-to-state reaction amplitudes for two different initial target states and |v, j, m′〉 that scatter into the same final product state|v, jf, mf〉, thus describing interference between two coherently tied input channels. The interference thus results from the fact that each m state in the superposition provides a possible quantum mechanical pathway connecting an incoming orbital to an outgoing or scattered orbital. The m state superposition thus behaves much like a multi-slit interferometer where the number of slits, or the number of m states, and their separations, or their relative phase, can be varied experimentally. The maxima and minima of the resulting interference are determined by the amplitudes as well as the relative phases of the complex amplitudes Cm. However, if the molecules are not prepared in a phase coherent superposition of m states, the effect of these cross terms vanish, for m ≠ m′, where the angular bracket represents the ensemble average.
We show in this paper that the outcome of a collision experiment can be directly controlled using modulation of the superposition of the target state. Further, we demonstrate that the interference in the state-resolved differential scattering cross-section for molecular targets prepared in addressable quantum states is a useful probe for both the magnitude and the phase of the state-to-state reaction amplitudes q(v, j, m, Ec → v, jf, mf). To illustrate these points, we consider the molecular interferometer created by preparing specific superpositions of m states, including an entangled biaxial state, of the HD molecule and show the interference effects in the rotational relaxation of these state-prepared HD by collision with a ground-state He atom. Our work here parallels a recent theoretical study that investigated coherent control using m state superposition in the F + H2 reaction [31].
A Molecular Interferometer Illustrated by Preparing HD Molecules in a Superposition State
The molecular interferometer discussed in this work has been previously prepared using SARP [28, 32]. SARP accomplishes population transfer by manipulating the crossings of the optically dressed adiabatic states using a pair of partially overlapping nanosecond laser pulses of unequal intensities. The dynamic Stark shift from the intense laser pulse controls the crossing of resonance. A large population is adiabatically transferred to the target state in the presence of a strong two-photon Rabi frequency as the Stark-shifted detuning slowly passes through the Raman resonance. The molecular axis orientation is controlled by the polarization of the two laser pulses. A comprehensive description of SARP can be found elsewhere [29, 30, 33, 34]. Figure 1 describes the geometry of SARP excitation where the lasers propagate along the Y axis, while their polarizations are confined to the XZ plane. By rotating the pump and Stokes laser polarizations, various molecular axis orientations can be realized as shown in Figure 1B. Throughout this paper, we will consider the Z axis as the angular momentum quantization axis.
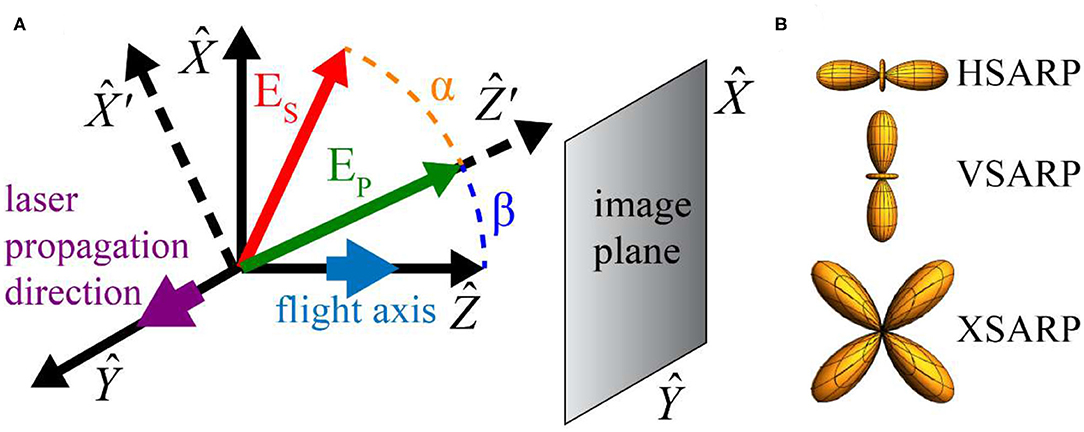
Figure 1. (A) The coordinate system used in this paper. The Z axis is the direction of the molecular beam, which defines the collision velocity, while the laser propagates along the Y axis. The polarization of the pump and Stokes lasers are in the XZ plane, and their directions are given by the angles β and α. The scattered particles are imaged in the XY plane. (B) Axis distributions for the three specific alignment states discussed in the paper shown with the plane of the page as the XZ plane.
We consider three specific axis alignments, shown in Figure 1B as well as the top panel of Figure 2 below. The simplest, called HSARP, is prepared when α = 0 and β = 0 and consists of only |m = 0〉. Because HSARP is a pure uniaxial state preferentially polarized along the collision velocity axis, the density matrix has only one element ρmm = 1 . Choosing both polarizations perpendicular to the Z axis (α = 0, β = π/2) creates the superposition state with non-zero off diagonal density matrix elements called VSARP. However, it is possible to diagonalize its density matrix by appropriate rotation of the coordinate system because VSARP is a uniaxial state preferentially polarized perpendicular to the collision velocity axis. Rotating only one polarization away from the Z axis (α = π/2, β = 0) produces the state called XSARP. The off-diagonal elements are ρmm′ = −1/2 for m ≠ m′, |m| = |m′| = 1. The XSARP state is a biaxial, and so there is no coordinate rotation that transforms it to a pure state. The presence of two simultaneous axis alignments provides two possibilities for the rotationally inelastic scattering. The two distinct pathways connecting the initial and the final scattering states will interfere, making XSARP the molecular scattering analog of an optical double-slit experiment.
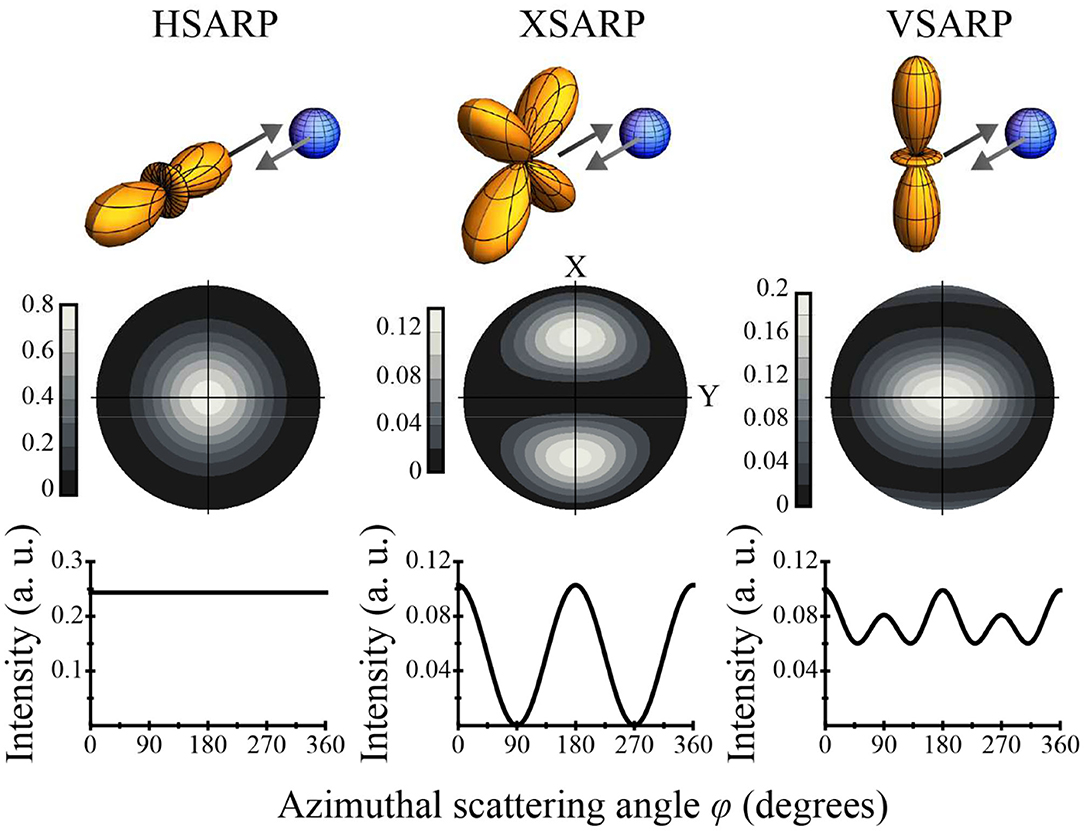
Figure 2. Controlling molecular collision using m state superposition of three orientations: (A) HSARP |m = 0〉 obtained with pump and Stokes polarizations given by α = 0, β = 0 in Figure 1. (B) XSARP: obtained with α = π/2, β = 0. (C) VSARP: . Here the plane of the page is the XY image plane shown in Figure 1A, which is perpendicular to the collision velocity along Z. The top panel gives the axis distributions and the collision geometry. The second panel shows the scattered images of rotationally relaxed HD (v = 1, jf = 0, mf = 0). The third panel shows the φ dependence of the scattering images.
To show the interference effects in molecular collisions produced by a superposition of m quantum states, we consider the specific example of cold, rotationally inelastic hydrogen-helium scattering. We have previously studied cold HD (v = 1, j = 2) → (v = 1, jf = 0) rotational relaxation via collision with a ground state He atom [35]. These collisions were confined within a single supersonic beam moving along the Z axis in Figure 1, thus precisely defining the collision geometry. Figure 2 shows the calculated differential scattering cross-section dσ(θ, φ)/dΩ given in Equation (5), which we also call the scattering image, in the X-Y plane. The scattering image is calculated using the experimentally determined scattering matrix from our earlier work. In this calculation, each of the scattering amplitudes q(v, j, m, Ec → v, jf, mf) is expanded in terms of the outgoing partial waves with complex amplitudes proportional to the scattering matrix element . Here, l and lf give the orbital angular momentum of the incoming and outgoing orbitals, respectively, and J gives the total angular momentum, which is conserved in the collision process. A detailed description of the scattering calculation can be found in our publications [32, 35, 36] and is briefly reproduced in the Supplementary Material. Although we have considered here a specific example of Δj =2 rotational relaxation with a single final state (jf = 0, mf = 0), our treatment will remain valid even if there are multiple final states. For example, in Δj = 1 transition with (jf = 1, mf = 0, ±1), the scattered intensity will be just the sum of the intensities for each individual mf state shown in Equation (5).
The second panel in Figure 2 shows the image of scattered HD (v = 1, jf = 0) for the HSARP, XSARP, and VSARP axis orientations. The cylindrical symmetry of HSARP about the collision velocity is readily reflected in the scattering image shown in Figure 2A. The cylindrical symmetry about the Z-axis is broken for the VSARP orientation as seen in Figure 2C. The scattering image for the XSARP orientation in Figure 2B differs drastically from the HSARP and VSARP images. For the XSARP scattering not only is the azimuthal symmetry about the collision velocity broken, two bright interference fringes separated by a dark region in the center of the image are created. The dark center corresponds to a complete absence of the intense forward and backward scattering present for the HSARP and VSARP orientations. We note that the XSARP axis orientation scatters particles in well-defined directions in space much like a grating interferometer for optical waves. The third panel of Figure 2 shows the φ dependence of the scattering images for the three axis distributions. The scattering intensity as a function of φ was calculated by integrating dσ(θ, φ)/dΩ over all polar angles θ . The characteristic interference pattern for the XSARP makes it clear that the scattering of this state acts like a classic double-slit interferometer for molecular scattering. Because of the symmetry about the collision velocity, HASRP does not produce any φ dependency. The VSARP orientation breaks the cylindrical symmetry about the collision velocity axis and modulates the scattering intensity as a function of φ. However, compared to XSARP, the φ dependence is much weaker because VSARP is still a uniaxial state and therefore does not act as a double-slit interferometer.
Figure 3 compares the scattering images for the XSARP and VSARP orientations calculated with and without the coherence terms. For the right-hand images with coherence turned off, the calculation is performed by setting the off-diagonal density matrix elements ρmm′ = CmCm′ for m ≠ m′ to zero. As described by Equation (7), in the absence of m state coherence the scattering angular distribution is determined by the m state populations. The cylindrically symmetric scattering angular distributions shown in Figure 3 prove that the symmetry about the collision velocity can be broken only by introducing m sublevel or Zeeman coherence.
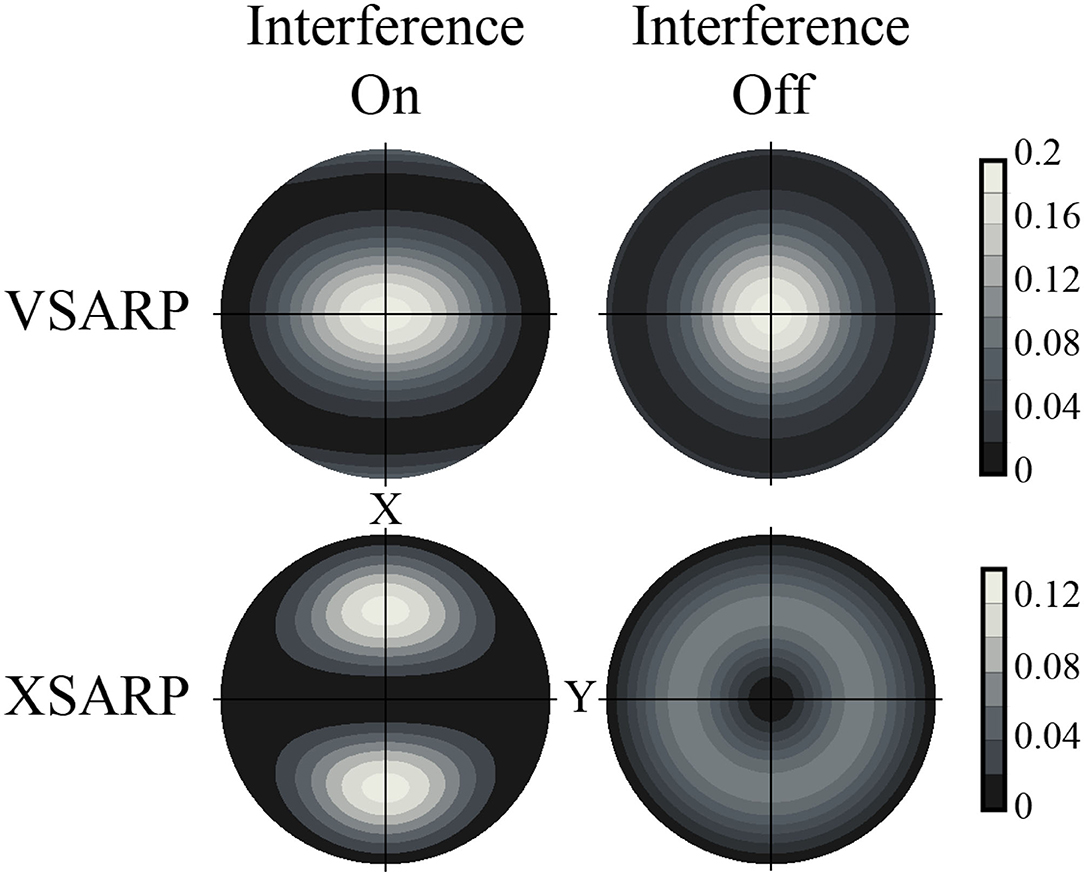
Figure 3. The effect of the coherent interfering terms given in Equation (6) on the scattering images of rotationally relaxed HD (v = 1, jf = 0, mf = 0) for the VSARP and XSARP axis orientations. The scattering images including the coherence terms are given on the left side, while those without are given on the right side. Clearly, the m state superposition breaks the φ symmetry.
Testing the S-Matrix Using the Molecular Double-Slit Interferometer
An optical interferometer measures the phase shift between two optical waves. Given the direct parallel between the XSARP state and an optical double slit, this molecular interferometer ought to be able to measure phase shift of the scattered waves. The scattering image is generated as the coherent sum of the many partial waves, whose complex amplitudes are determined by the scattering matrix elements. To calculate the images shown in Figure 4, the phase of one of the scattering matrix elements was varied from 0 to π. As the phase of the chosen scattering matrix element is changed by relatively small increments from 0.6 to 0.8π, the calculated image changes dramatically, demonstrating the power of the molecular interferometer as an experimental tool to interrogate the scattering matrix. This tool may be instrumental in resolving the many disagreements between experiment and theory that persist for even the simplest low temperature atom-diatom scattering. This is especially true for all-important scattering resonances, where the phase of the scattering matrix becomes more sensitive to the exact structure of the long-range potential.
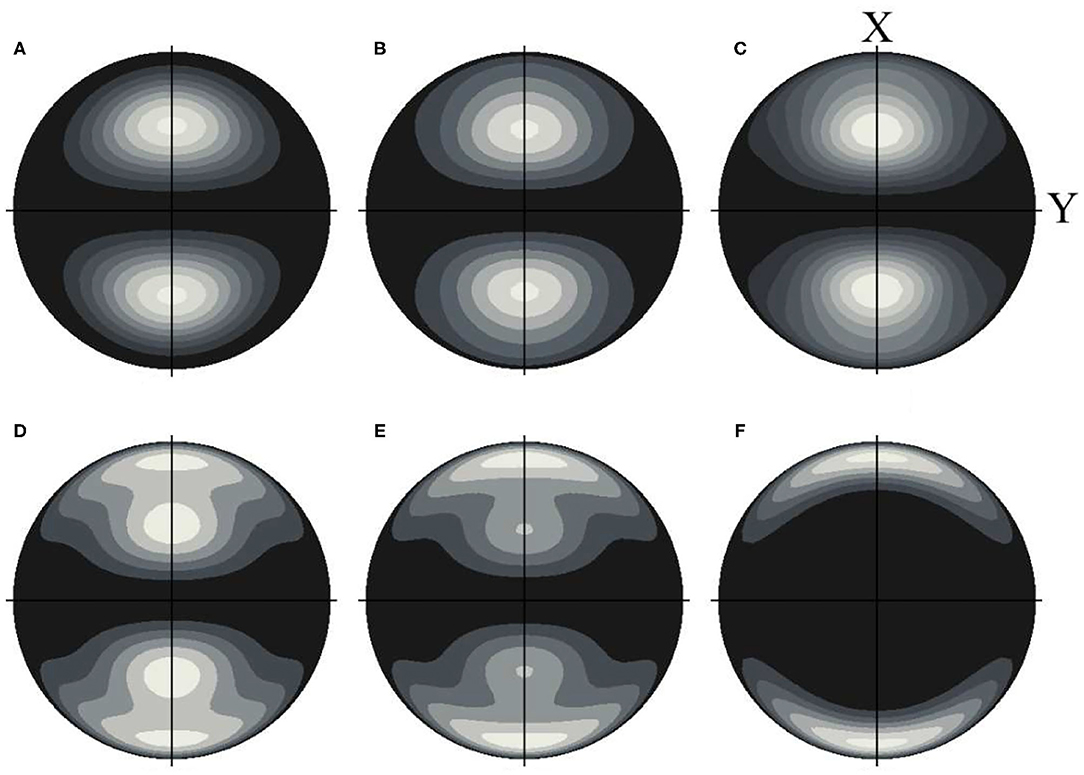
Figure 4. Scattering images of rotationally relaxed HD (v = 1, jf = 0, mf = 0) calculated by varying the phase of one of the scattering matrix element (see Supplementary Material). From (A)–(F), the six images are calculated using phases of 0, 0.6π, 0.65π, 0.75π, 0.8π, and π.
Control of Molecular Diffraction by Rotating the Polarization of the Preparation Laser
Figure 5 shows how the diffraction by the molecular grating can be controlled simply by rotating the polarization of one of the preparation lasers. In these examples the different axis distributions are generated by rotating the Stokes laser polarization angle (α) in the XZ plane, while the pump laser polarization is kept fixed parallel to the X axis corresponding to β = 90° (see Figure 1). The oriented rovibrational (v, j = 2) state can be expressed as:
In Equation (8) represents the Wigner rotation matrix for the j = 2 rotational state. Figure 5 illustrates the control of scattering using four specific axis distributions obtained by varying the Stokes polarization according to (a) α = 0, β = 90°, (b) α = 30°, β = 90°, (c) α = 60°, β = 90°, (d) α = 90°, β = 90°. Figure 5 shows that the three-dimensional scattering distribution changes in a spectacular way as the axis orientation changes from VSARP (a) to XSARP (d) with rotation of the angle α by 90°.
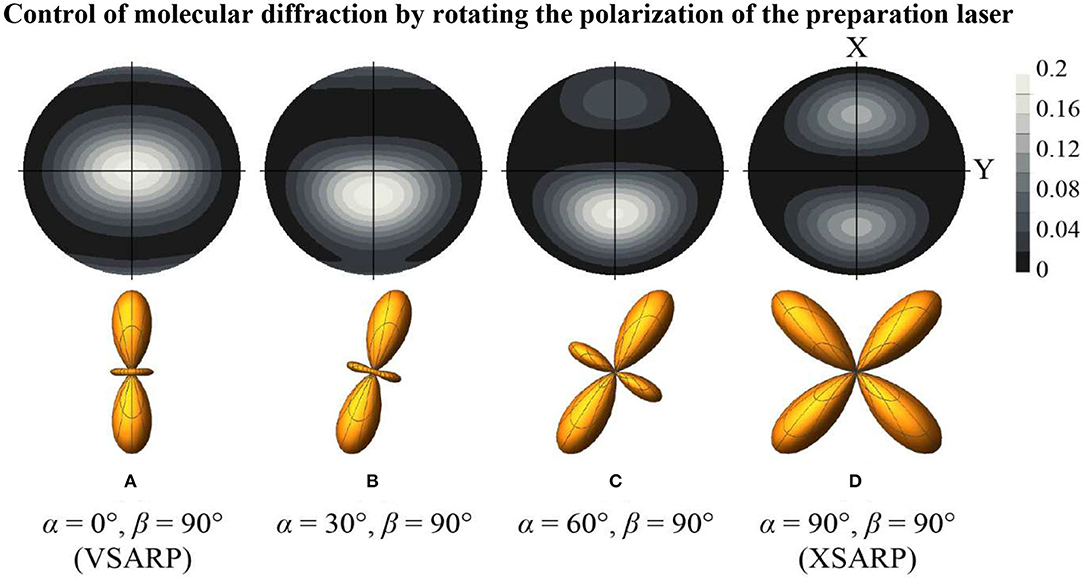
Figure 5. Control of molecular scattering by laser polarizations. Here, the pump laser polarization is kept fixed parallel to the X axis, corresponding to β = 90°, while the Stokes laser polarization is rotated from α= 0 (A), 30 (B), 60 (C), to 90° (D). The axis distributions shown in the bottom panel are given with the plane of the page as the XZ plane. The top panel shows the calculated scattering images of rotationally relaxed HD (v = 1, jf = 0, mf = 0), demonstrating that the maxima of the scattering can be directed at different positions.
Conclusion
We have shown that a coherent superposition of degenerate m states within a single rovibrational eigenstate behaves like a multi-slit interferometer for molecular scattering. To illustrate this idea, we considered the Δ j = 2 rotationally inelastic scattering of HD prepared in coherent superpositions of m states within a single (v = 1, j = 2) eigenstate using SARP. The m sublevel coherence breaks the symmetry about the collision velocity direction. Each m state in the superposition provides a quantum mechanical pathway connecting the initial and final state in the collision process that gives rise to the interference pattern in the azimuthal angle φ, the coordinate canonically connected to the Z component of the angular momentum. In particular, we showed that the coherently mixed m = ±1 biaxial state of HD behaves like an optical interferometer producing interference fringes for the scattered intensity as a function of φ. The two phase-locked orientations of the molecular axis create two distinct quantum mechanical pathways, and so this molecular interferometer provides a proof of fundamental quantum mechanical principles. The biaxial state has already been prepared and used in scattering experiments in our laboratory, and so demonstration of these interference effects is highly experimentally feasible. We further showed that the phase of the scattering matrix can be measured using such a molecular interferometer. We also demonstrated that the coherent superposition can be used to control molecular scattering by spatially directing the scattered molecules in much the same way a multi-slit grating interferometer diffracts optical waves. Because the polarization directions of the pump and Stokes laser pulses determine the m state superposition, they can be used to control the interference effects in the scattering process. Such control is not limited to inelastic scattering, the m state superposition can control elastic and reactive scattering processes as well [9, 37, 38].
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.
Author Contributions
All authors discussed and wrote this manuscript.
Funding
This work has been supported by the U.S. Army Research Office under ARO Grant Nos. W911NF-19-1-0163 and W911NF-19-1-0283.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.671997/full#supplementary-material
References
1. Feynman RP, Leighton RB, Sands ML. Feynman Lectures on Physics, Vol. 3. Boston, MAL Addison Wesley Publishing Co (1963).
2. Gong J, Brumer P. Indistinguishability and interference in the coherent control of atomic and molecular processes. J Chem Phys. (2010) 132:054306. doi: 10.1063/1.3304921
3. Tavabi AH, Boothroyd CB, Yücelen E, Frabboni S, Gazzadi GC, Dunin-Borkowski RE, et al. The young-feynman controlled double-slit electron interference experiment. Sci Rep. (2019) 9:2–9. doi: 10.1038/s41598-019-43323-2
4. Frabboni S, Gazzadi GC, Pozzi G. Young's double-slit interference experiment with electrons. Am J Phys. (2007) 75:1053–5. doi: 10.1119/1.2757621
5. Arndt M, Nairz O, Vos-Andreae J, Keller C, Van der Zouw G, Zeilinger A. Wave-particle duality of C60. Nature. (1999) 401:680–2. doi: 10.1038/44348
6. Canton SE, Plésiat E, Bozek JD, Rude BS, Decleva P, Martín F. Direct observation of young's double-slit interferences in vibrationally resolved photoionization of diatomic molecules. Proc Natl Acad Sci USA. (2011) 108:7302–6. doi: 10.1073/pnas.1018534108
7. Akoury D, Kreidi K, Jahnke T, Weber T, Staudte A, Schöffler M, et al. The simplest double slit : interference and entanglement in double photoionization of H2. Science. (2007) 318:949–52. doi: 10.1126/science.1144959
8. Nichols B, Chadwick H, Gordon SD, Eyles CJ, Hornung B, Brouard M, et al. Steric effects and quantum interference in the inelastic scattering of NO(X) + Ar. Chem Sci. (2015) 6:2202–10. doi: 10.1039/C4SC03842H
9. Sha G, He J, Jiang B, Zhang C. Evidence for quantum interference in collision-induced intramolecular energy transfer within CO singlet-triplet mixed states. J Chem Phys. (1995) 102:2772–9. doi: 10.1063/1.468653
10. Onvlee J, Gordon SD, Vogels SN, Auth T, Karman T, Nichols B, et al. Imaging quantum stereodynamics through fraunhofer scattering of NO radicals with rare-gas atoms. Nat Chem. (2017) 9:226–33. doi: 10.1038/nchem.2640
11. Chen XL, Chen HM, Li J, Liu YM, Dai XC, Sha GH, et al. Quantum interference effect on collisional energy transfer within singlet ~ triplet mixed states of Na2. Chem Phys Lett. (2000) 318:107–12. doi: 10.1016/S0009-2614(99)01432-3
12. Jambrina PG, Herráez-Aguilar D, Aoiz FJ, Sneha M, Jankunas J, Zare RN. Quantum interference between H + D 2 quasiclassical reaction mechanisms. Nat Chem. (2015) 7:661–7. doi: 10.1038/nchem.2295
13. Jambrina PG, Aldegunde J, Aoiz FJ, Sneha M, Zare RN. Effects of reagent rotation on interferences in the product angular distributions of chemical reactions. Chem Sci. (2016) 7:642–9. doi: 10.1039/C5SC03373J
14. Sneha M, Gao H, Zare RN, Jambrina PG, Menéndez M, Aoiz FJ. Multiple scattering mechanisms causing interference effects in the differential cross sections of H + D2 → HD(v ′ = 4, j ′) + D at 3.26 eV collision energy. J Chem Phys. (2016) 145:024308. doi: 10.1063/1.4955294
15. Xie Y, Zhao H, Wang Y, Huang Y, Wang T, Xu X, et al. Quantum interference in H + HD → H2 + D between direct abstraction and roaming insertion pathways. Science. (2020) 368:767–71. doi: 10.1126/science.abb1564
16. Kendrick BK, Li H, Li M, Kotochigova S, Croft JF, Balakrishnan N. Non-adiabatic quantum interference in the ultracold Li + LiNa → Li2 + Na reaction. Phys Chem Chem Phys. (2021) 23:5096–112. doi: 10.1088/1742-6596/1412/12/122016
17. Brumer P, Abrashkevich A, Shapiro M. Laboratory conditions in the coherent control of reactive scattering. Faraday Discuss. (1999) 113:291–302. doi: 10.1039/a902135c
18. Arango CA, Shapiro M, Brumer P. Coherent control of collision processes: penning versus associative ionization. J Chem Phys. (2006) 125:094315. doi: 10.1063/1.2336430
19. Král P, Thanopulos I, Shapiro M. Colloquium: coherently controlled adiabatic passage. Rev Mod Phys. (2007) 79:53–77. doi: 10.1103/RevModPhys.79.53
20. Krause JL, Shapiro M, Brumer P. Coherent control of bimolecular chemical reactions. J Chem Phys. (1990) 92:1126–31. doi: 10.1063/1.458174
21. Seideman T. Revival structure of aligned rotational wave packets. Phys Rev Lett. (1999) 83:4971–4. doi: 10.1103/PhysRevLett.83.4971
22. Dooley PW, Litvinyuk IV, Lee KF, Rayner DM, Spanner M, Villeneuve DM, et al. Direct imaging of rotational wave-packet dynamics of diatomic molecules. Phys Rev A. (2003) 68:023406. doi: 10.1103/PhysRevA.68.023406
23. Yang J, Guehr M, Vecchione T, Robinson MS, Li R, Hartmann N, et al. Diffractive imaging of a rotational wavepacket in nitrogen molecules with femtosecond megaelectronvolt electron pulses. Nat Commun. (2016) 7:11232. doi: 10.1038/ncomms11232
24. Bergmann K, Theuer H, Shore BW. Coherent population transfer among quantum states of atoms and molecules. Rev Mod Phys. (1998) 70:1003–25. doi: 10.1103/RevModPhys.70.1003
25. Vitanov NV, Rangelov AA, Shore BW, Bergmann K. Stimulated raman adiabatic passage in physics, chemistry, and beyond. Rev Mod Phys. (2017) 89:1–66. doi: 10.1103/RevModPhys.89.015006
26. Vitanov NV, Halfmann T, Shore BW, Bergmann K. Laser-Induced population transfer by adiabatic passage techniques. Annu Rev Phys Chem. (2001) 52:763–809. doi: 10.1146/annurev.physchem.52.1.763
27. Vewinger F, Heinz M, Garcia Fernandez R, Vitanov NV, Bergmann K. Creation and measurement of a coherent superposition of quantum states. Phys Rev Lett. (2003) 91:213001. doi: 10.1103/PhysRevLett.91.213001
28. Mukherjee N, Dong W, Zare RN. Coherent superposition of M-states in a single rovibrational level of H2 by Stark-induced adiabatic raman passage. J Chem Phys. (2014) 140:074201. doi: 10.1063/1.4865131
29. Mukherjee N, Zare RN. Stark-induced adiabatic Raman passage for preparing polarized molecules. J Chem Phys. (2011) 135:024201 doi: 10.1063/1.3599711
30. Mukherjee N, Perreault WE, Zare RN. Stark-Induced adiabatic passage processes to selectively prepare vibrationally excited single and superposition of quantum states. In: Jaan L, editor. Frontiers and Advances in Molecular Spectroscopy. Amsterdam: Elsevier Inc (2018). p. 1–46. doi: 10.1016/B978-0-12-811220-5.00001-0
31. Devolder A, Tscherbul T, Brumer P. Coherent control of reactive scattering at low temperatures: signatures of quantum interference in the differential cross sections for F+ H2 and F+ HD coherent control of reactive scattering at devolder, tscherbul, and brumer. Phys Rev A. (2020) 102:31303. doi: 10.1103/PhysRevA.102.031303
32. Perreault WE, Mukherjee N, Zare RN. Quantum control of molecular collisions at 1 Kelvin. Science. (2017) 358:356–9. doi: 10.1126/science.aao3116
33. Perreault WE, Mukherjee N, Zare RN. Stark-induced adiabatic Raman passage examined through the preparation of D2 (v = 2, j = 0) and D2 (v = 2, j = 2, m = 0). J Chem Phys. (2019) 150:234201. doi: 10.1063/1.5109261
34. Perreault WE, Zhou H, Mukherjee N, Zare RN. Harnessing the power of adiabatic curve crossing to populate the highly vibrationally excited H2 (v = 7, j = 0) level. Phys Rev Lett. (2020) 124:163202. doi: 10.1103/PhysRevLett.124.163202
35. Perreault WE, Mukherjee N, Zare RN. HD (v = 1, j = 2, m) orientation controls HD-He rotationally inelastic scattering near 1 K. J Chem Phys. (2019) 150:174301. doi: 10.1063/1.5096531
36. Perreault WE, Mukherjee N, Zare RN. Quantum controlled rotationally inelastic scattering of HD with H2 and D2 near 1 Kelvin reveals collisional partner reorientation. Nat Chem. (2018) 10:561–7. doi: 10.1038/s41557-018-0028-5
37. Gong J, Shapiro M, Brumer P. Entanglement-assisted coherent control in nonreactive diatom-diatom scattering. J Chem Phys. (2003) 118:2626–36. doi: 10.1063/1.1535428
Keywords: interference, biaxial spatial distribution, angular distribution, molecular scattering, coherence
Citation: Perreault WE, Zhou H, Mukherjee N and Zare RN (2021) A Bi-Axial Quantum State That Controls Molecular Collisions Like a Double-Slit Interferometer. Front. Phys. 9:671997. doi: 10.3389/fphy.2021.671997
Received: 24 February 2021; Accepted: 15 April 2021;
Published: 28 May 2021.
Edited by:
Tamar Seideman, Northwestern University, United StatesReviewed by:
David Parker, Radboud University Nijmegen, NetherlandsVitaly V. Kresin, University of Southern California, Los Angeles, United States
Copyright © 2021 Perreault, Zhou, Mukherjee and Zare. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nandini Mukherjee, bm11a2hlcmpAc3RhbmZvcmQuZWR1; Richard N. Zare, emFyZUBzdGFuZm9yZC5lZHU=
 William E. Perreault
William E. Perreault Haowen Zhou
Haowen Zhou Nandini Mukherjee
Nandini Mukherjee Richard N. Zare
Richard N. Zare