Introduction
Fluid flow past a stretching sheet has been discussed extensively due to its practical applications in science and engineering. The pioneering works of Sakiadis and Crane [1, 2] on the subjects of free stream velocity and sheet stretching remain some of the most fundamental papers. However, literature on this subject is extensive, particularly when it comes to the linear stretching of plane surface for Newtonian fluid. The tremendous practical importance of stretching sheets in the chemical, polymer, and manufacturing industry, such as in fiber spinning, casting and drawing of annealing wires, and glass fiber, and extrusion of polymer sheets instigated linear stretching for viscous flow over a plane surface. Later on, other forms of stretching are introduced and more meaningful in practice, but the mathematical concept in exploring the solution of Navier-Stokes’s equations remains the prime task. The physical significance underlying this concept gives rise to non-linear velocity for power-law, exponential, and quadratic stretching in the forms of , , and , respectively [3–15]. Non-Newtonian fluids are classified based on natural fluids, industrial fluids, and biological fluids. The study of these fluids becomes imperative without exception and due to the absence of a unified model that could exhibit all the intrinsic properties of non-Newtonian fluids. This observation encourages several rheological models to be developed in order to accommodate the physical features of these fluids through various distinctive complex constitutive equations. The magnetohydrodynamics of non-Newtonian fluids in the phase of uniform, variable, and radially varying magnetic fields has various applications: in the production of plastic film, manufacturing of sensors for aerospace engineering, metallurgy, purification of crude oil, nuclear fuel slurries, hydroelectric power plants, cancer research, melt spinning processes, nuclear reactor-power plant, etc. Malik et al. [16] investigated the boundary-layer flow of MHD Sisko fluid past a stretchable cylinder with the dissipating effect of viscosity. Heat transfer of MHD stagnation point flow of a melting Sisko liquid is presented by Hayat et al. [17]. The thermal analysis of an unsteady hydromagnetic nano-Erying Powell fluid due to a convective heated stretching sheet with viscous dissipation and radiation is documented by Mahanthesh et al. [18]. Hayat et al. [19] discussed the flow of hydromagnetic Jeffrey fluid past a nonlinear radially stretching sheet. Khalil et al. [20] examined the numerical solution of hydromagnetic Casson-nanofluid flow in a rigid rotating disk with Navier’s slip effect. For more relevant papers see [21–24]. The needs for heat and mass transfer in engineering, manufacturing, and geophysical applications cannot be over-exaggerated; examples include solar collector, drying of porous solids, hydrometallurgy, underground energy, transport, geothermal reservoirs, treatment of chemical vapor deposition on a surface freezing of ice (icing), packed bed catalytic reactors, thermal insulation, cooling of the skin of high-speed aero-velocity and turbine blades, and polymer melts. Moreover, the occurrence of chemical reactions in bulk fluid transport expedited the interest of several investigators to analyze some crucial aspects of fluid flow. Hammed et al. [25] used the Lie group to investigate the effects of convective boundary conditions over the flow, heat, and mass transfer. The hydromagnetic slip effect of MHD porous channel in the presence of entropy generation with the convective boundary condition was studied by Guillermo Ibanez [26]. Akhil et al. [27] presented micropolar ferrofluid in mixed convection flow subjected to convective Joule heating boundary conditions with dissipation effect. Reddy et al. [28] documented the flow of magnetohydrodynamic nanofluid with convective heat and mass transfer past a vertical cone. Mair et al. [29] studied with variable viscosity the nanofluid of the Casson model over a convective stretchable surface with heat and mass diffusion. Some non-Newtonian flow models are less descriptive and less generalized to accommodate certain essential features of non-Newtonian fluids. Power-law fluid is only credible for low shear rate; Ellis fluid can predict the behavior of shear thinning to a realistic degree of shear rates; Carreau fluid best fits for cases of low and high limiting; and Sisko fluid behaves like a shear-thinning fluid by varying its parameters. Cross [30] introduced a viscous rheology model that generalizes the power law and Sisko and Bingham fluid models and predicts the drawbacks of these fluids in which and are two curve fitting parameters. The Cross viscous model tends to predict flow behavior at very low and high shear rates. The model can reduce to various viscosity models under certain approximations. It yields a power-law model if and , Sisko model if and Bingham model if with slight parameter adjustment. This fluid consists of a time constant, which makes it predominantly useful in carrying out industrial calculations. Its importance includes changing to the Newtonian fluid in the limit for both low and high shear rates. The appearance of a time constant in the governing equation widens the range of its industrial solicitations. We observe these features, and few papers have addressed the consideration of Cross fluid on plane flows, which includes the numerical investigations of heat transfer stagnation point flow of MHD Cross fluid toward stretching sheet by Hayat et al. [31]. The mixed convection Cross fluid flow in the presence of thermal radiation with buoyancy effects is studied by Manzur et al. [32]. Khan et al. [33] investigated Cross fluid flow on axisymmetric past a radially stretching plate with heat transfer phenomena. The point-stagnation flow of MHD Cross fluid over the stretched plane surface with numerical simulation and heat transfer is analyzed by Ijaz et al. [34]. The problem of stretching on curved surfaces has attracted the attention of many researchers in the last couple of years. However, few articles have appeared for curved surfaces; nevertheless, curved structures are more realistic and can correspond to a wide range of flow situations. Sajid et al. [35] initiated viscous flow over a curved surface using the curvilinear coordinate to model linear stretching of viscous fluid. They observed that the pressure variations inside the boundary layer cannot be ignored compared to the plane-stretching sheet. Sanni et al. [36] presented a nonlinear power stretching of the curved surface, and unsteady flow of Micropolar fluid past a stretching/shrinking curved surface in the presence of permeability is examined by Saleh et al. [37]. Nadeem et al. [38] studied the variable viscosity of magneto nanofluid over a stretching curved surface with carbon nanotubes. Saba et al. [39] investigated the effects of internal heat generation in nanofluid flow past a curved stretching surface. The dual solutions of a hydromagnetic viscous fluid with shrinking effects over a curved plate were analyzed by Naveed et al. For further studies, readers can refer to [40–47]. In view of the above-cited literature, no investigation has been made on the stretching problem of non-Newtonian Cross fluid in curved geometry. The objective of this investigation is to envisage the fluid velocity, heat transport, and concentration developed in manufacturing and engineering processes under desirable flow conditions. It analytically explores another important way to control the velocity using curved structures and widened the scope to foresee the most realistic phenomenon. The curved mechanism has been extensively hailed in surgical procedures where the blood flow requires to be controlled and minimized. Results show that both velocity and temperature are decreased for small curvature in the stretching problem and nonlinear stretching power, whereas the velocity increases for large Lorentz force and fluid rheology parameter. On the other hand, the fluid concentration shows the opposite effects.
Governing Equations
The steady state of mass with linear momentum of an incompressible fluid flow is given by
In which is the velocity, is the density of the fluid, represents the pressure, and the body force. In this study, the modified Cross fluid viscous model (see reference [30]) is expressed as
where , , , , and are the low and high limit of shear rates, Cross material time constant, dimensionless Cross fluid index, and symmetry deformation rate taken as a function of second invariant strain rate tensor, respectively. is the first Rivlin-Erickson tensor.
Problem Modeling
Consider the 2D flow of an incompressible MHD Cross-fluid past a boundary driven curved sheet of radius . We introduce a curvilinear coordinate in which axis is normal to the flow and as the curvature for . A radially varying applied magnetic is acting transversely to the flow. The Lorentz force generated due to an electrically conducting Cross fluid is defined by , where the current density expresses as . In the absence of the electrical field, , the Lorentz force can now be described as
such that is the fluid conductivity, is the magnetic field strength, and and are the velocity components in radial and axial directions, respectively. The physical flow geometry is given in Figure 1.
denotes the velocity vector field, , with and being the unit vector in radial and axial direction, respectively. The governing equations for the continuity and momentum from Eqs. 1–4 are obtained as follows:
where the various stress components can be expressed as
Boundary conditions relevant for the velocity are
such that is constant and is the characteristic length. Consider the dimensionless variables given below.
Using Eq. 10 and dropping the bars, the boundary layer equations from Eqs. 5,8 take the form
It is worth mentioning that the existing model of a Newtonian fluid can be recovered by setting the Cross fluid parameter, from Eq. 12. For similarity investigation, the following variables are given:
in which represents the flow stream function. Using Eqs. 13,14 in Eqs. 5,11,12, one can get
remains identically satisfied and primes symbolize derivatives with respect to
. The Weissenberg number,
, gives dimensionless Cross-fluid parameter and
represents the Hartmann number. The limiting case (
and
) confirms the correctness of the present model, thus
Eq. 16 reduces to flow problem over a flat stretching sheet. The second tier induces the linear stretching (
),
The solution of Eq. 17 has been numerically given [31–34]. Moreover, the model governing power stretching for gives
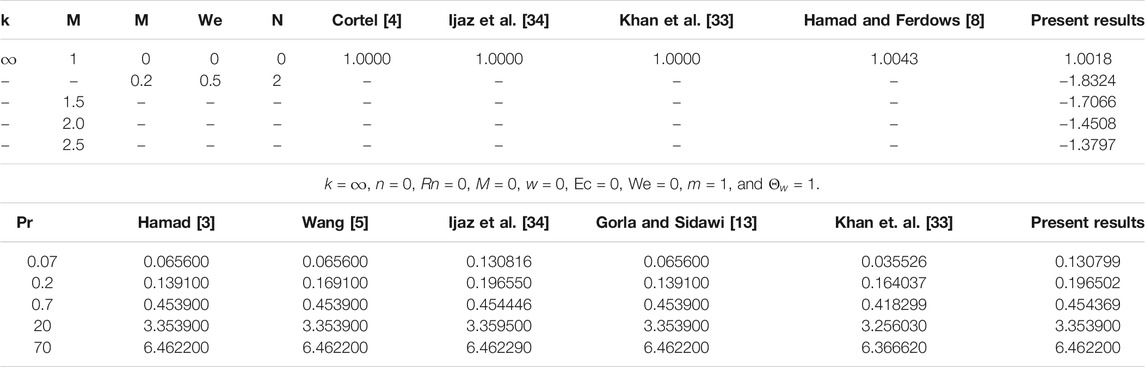
Here, numerical results of Eq. 18 for a large value of the dimensionless radius of curvature are provided (see Table 1).
Utilizing Eq. 15 in Eq. 16, the pressure term is eliminated and one can get
There exist corresponding boundary conditions to Eqs 9,10 in the dimensionless form.
Heat and Mass Transfer
The thermodynamics and Fick’s law for heat transport and concentration diffusion are given:
in which and denote viscous dissipation term and radiative heat flux, respectively. is the thermal conductivity, the specific heat capacity at constant pressure, the fluid concentration, the coefficient of chemical diffusion, the reaction rate of the first order, and the last term of Eq. 22 represents the Ohmic heating. After using Eqs. 3,22,23 in Eq. 21, we get
subjected to the boundary conditions;
is the surface temperature, the ambient temperature, and and are convective heat and mass transport, respectively.
By virtue of Rosseland approximation, the radiative heat flux can be written in the form
such that is Stefan-Boltzmann constant and the mean spectral absorption coefficient.
Using Eq. 28 in Eq. 24, we obtain
yields the thermal diffusivity and is the radiation parameter. If dimensionless similarity for the temperature and concentration take form
we can express . Utilizing this expression and Eq. 30 together with Eqs. 13,14, the dimensionless form of Eqs. 25,29 give the following:
In these equations, is the temperature parameter, Ec = the Eckert number, Pr = () the Prandtl number, the chemical reaction parameter, the Peclet number, the Schmidt number, and an Ohmic heating parameter. The linear radiation can be verified if , whereas corresponds to the nonlinear part.
Equations 26,27 yield
where and are the thermal and concentration Biot number, respectively.
Quantities like surface drag force, heat, and mass transfer rate are influential in fluid flow control and thermal regulation from an engineering and practical point of view. These physical quantities for the Cross fluid are calculated as follows:
where
After incorporating Eqs. 13,14,36 into Eq. 35, we arrive at
Numerical Solution
The transformed system of nonlinear ODEs gotten in Eqs. 19,31,32 together with the conditions given in Eqs. 20,33,34 are numerically solved using the Runge-Kutta (RK) fourth order with shooting technique. The higher-order ODEs (BVPs) are discretized into a system of initial value problems (IVPs) by swapping the characterized variables:
Invoking Eq. 40 in the required equations, a linearized first order is presented in block:
for
where , , , and are unknown conditions initially at infinity. These conditions are treated using Taylor’s series for , , , and about while and . The shooting technique assumed guesses for to and numerically integrate Eq. 40 to a given endpoint. The accuracy of these guesses is checked in comparison with the value of the dependent variable at that end point, and guesses are updated if differences exist via loops and the process is repeated until accurate guesses are obtained and then terminated. The algorithm is implemented through ode45 built-in MATLAB command with the step size of () and tolerance error of to obtain the numerical results.
Results and Discussion
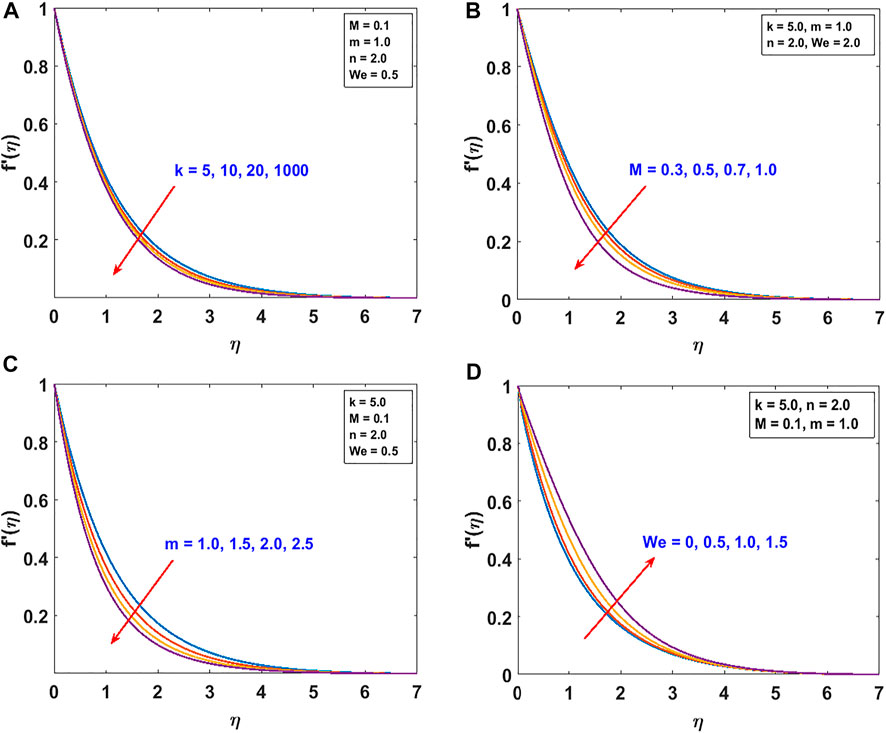
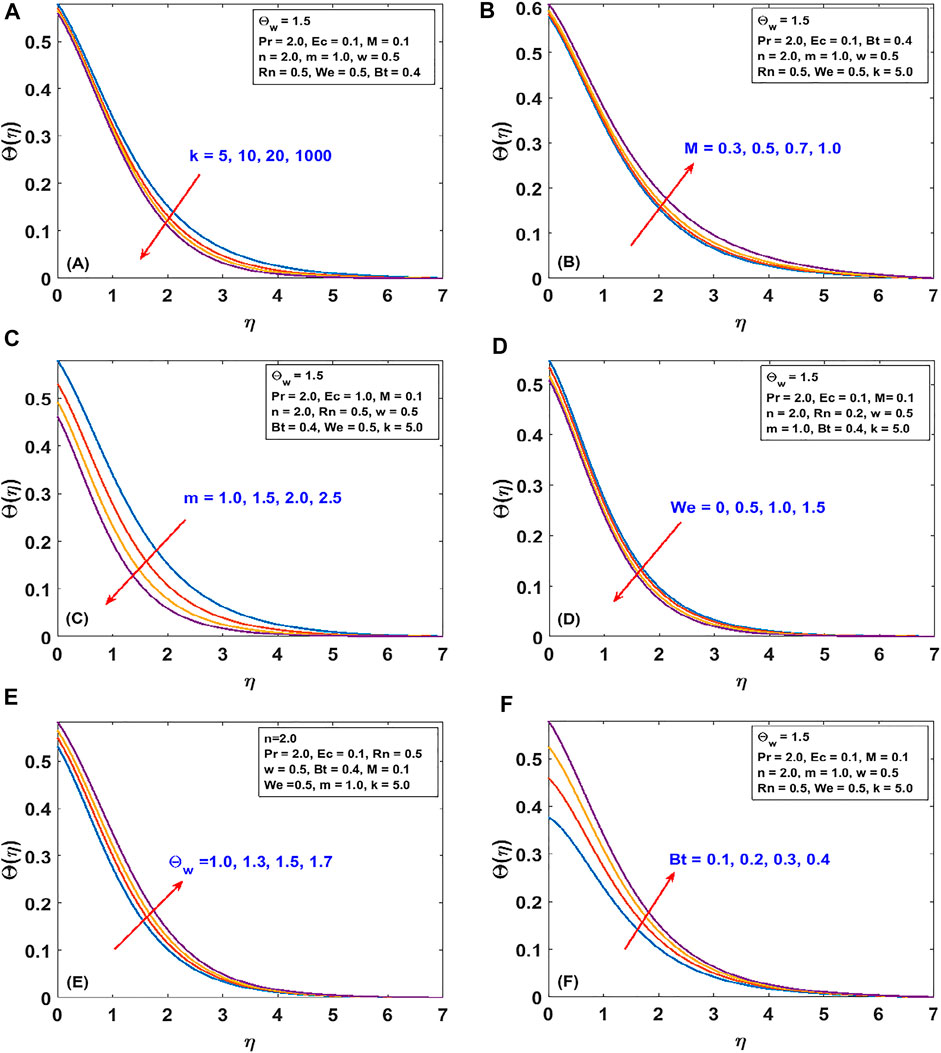
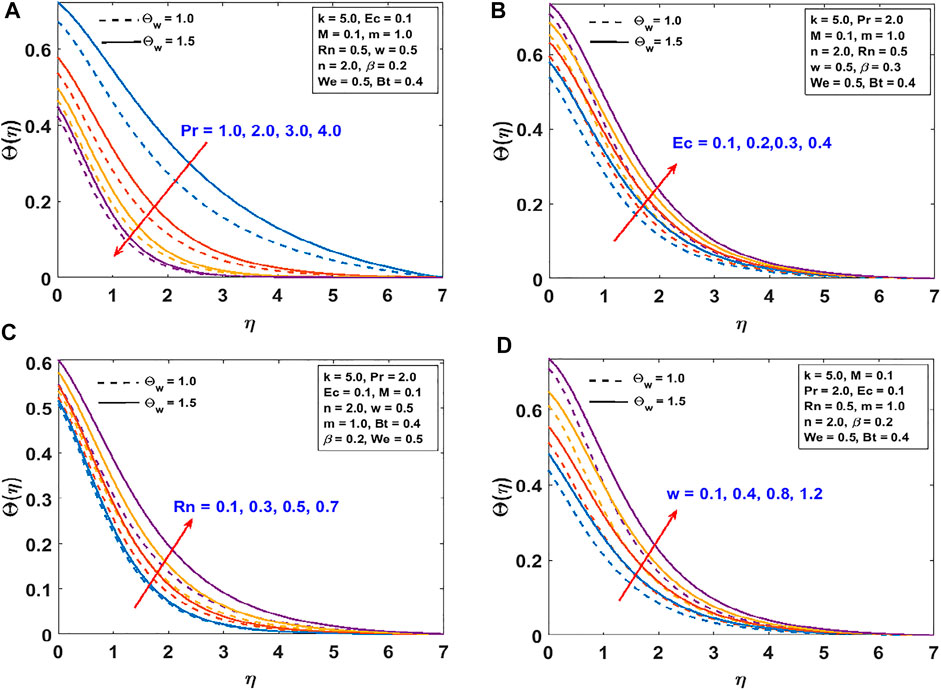
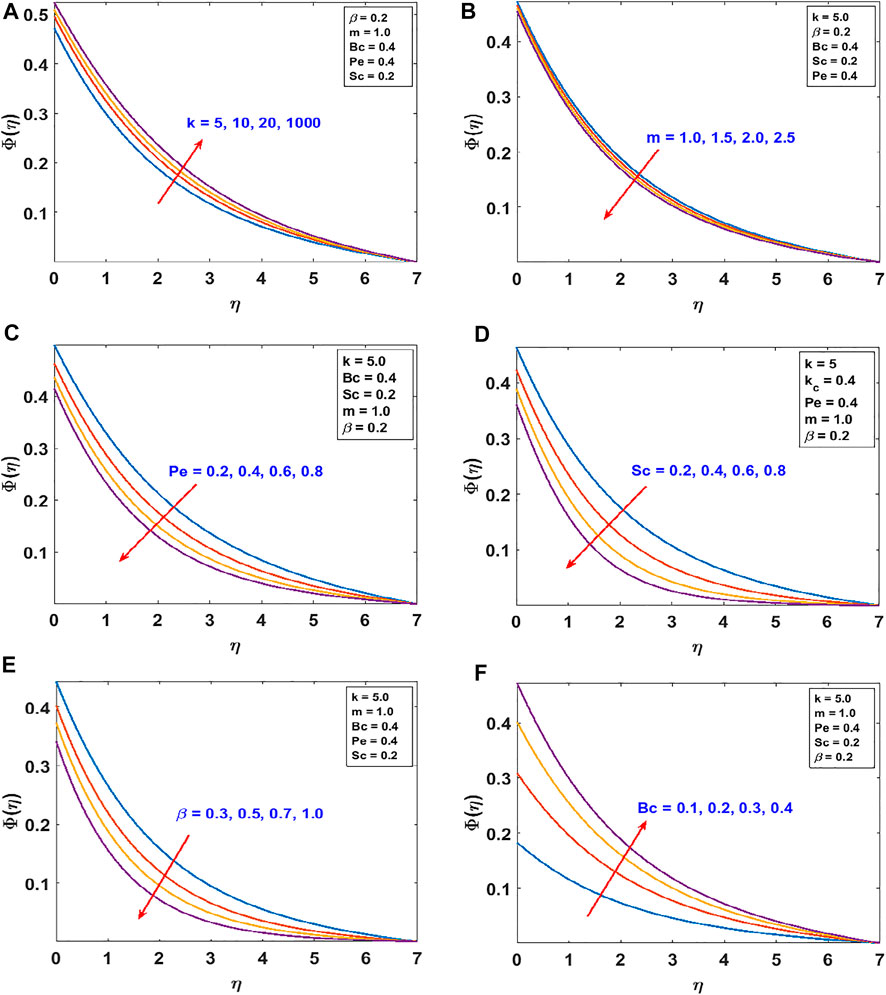
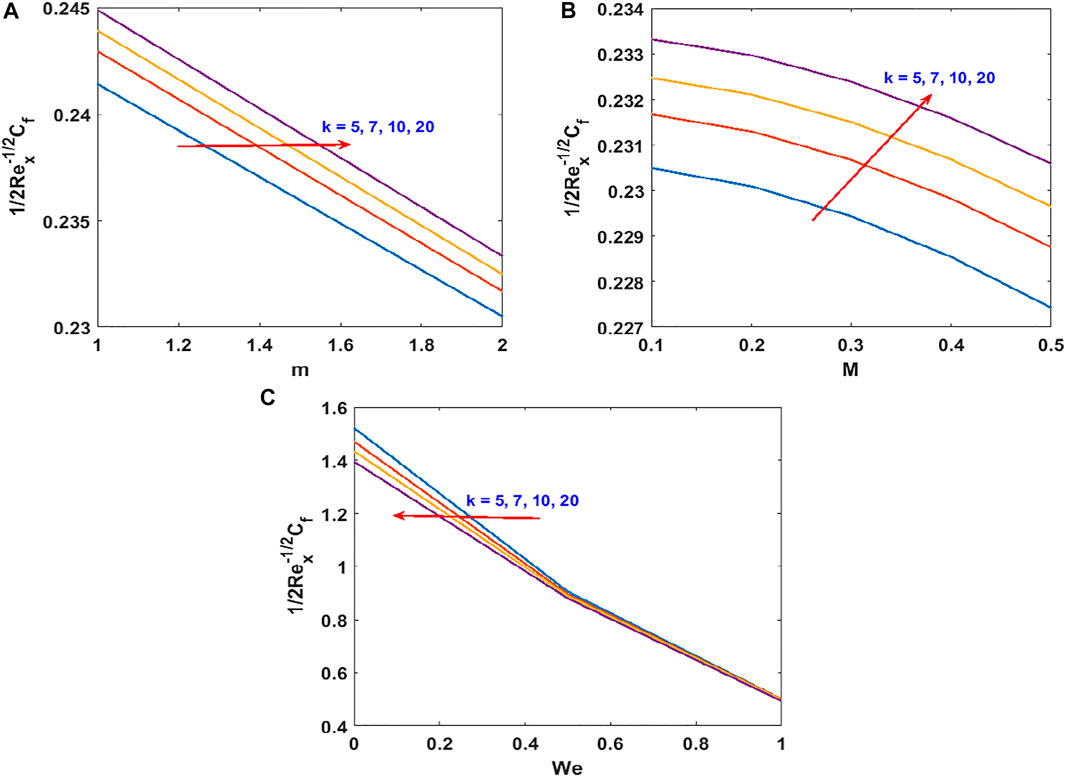
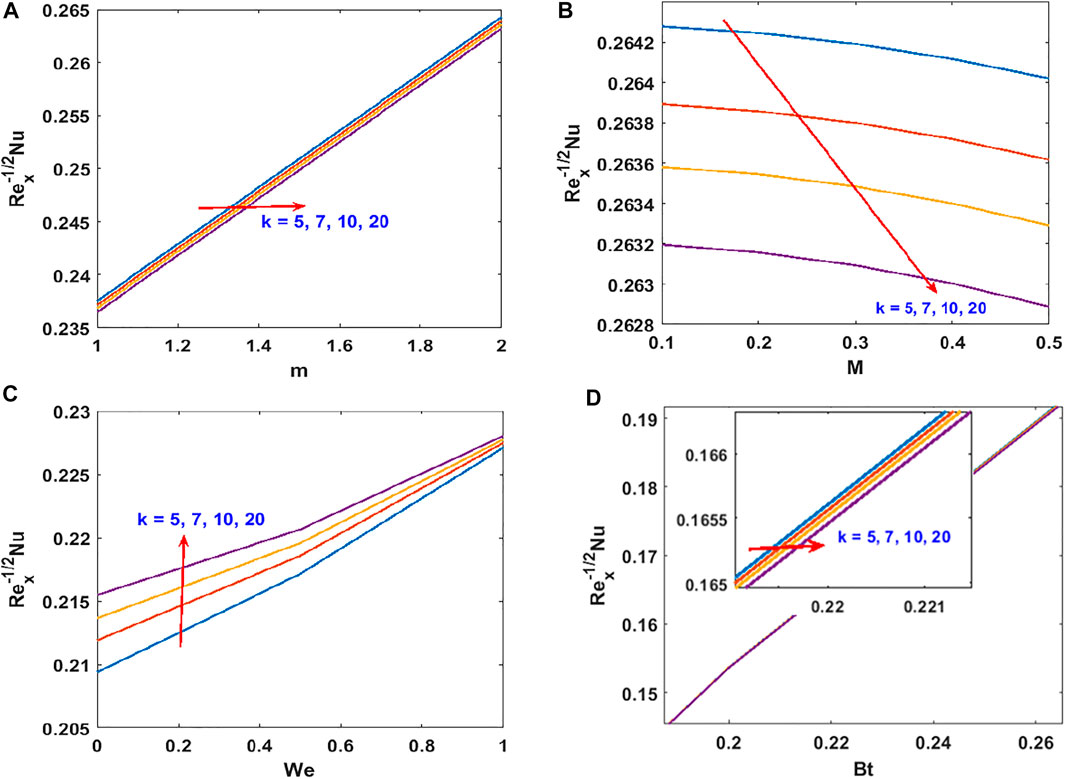
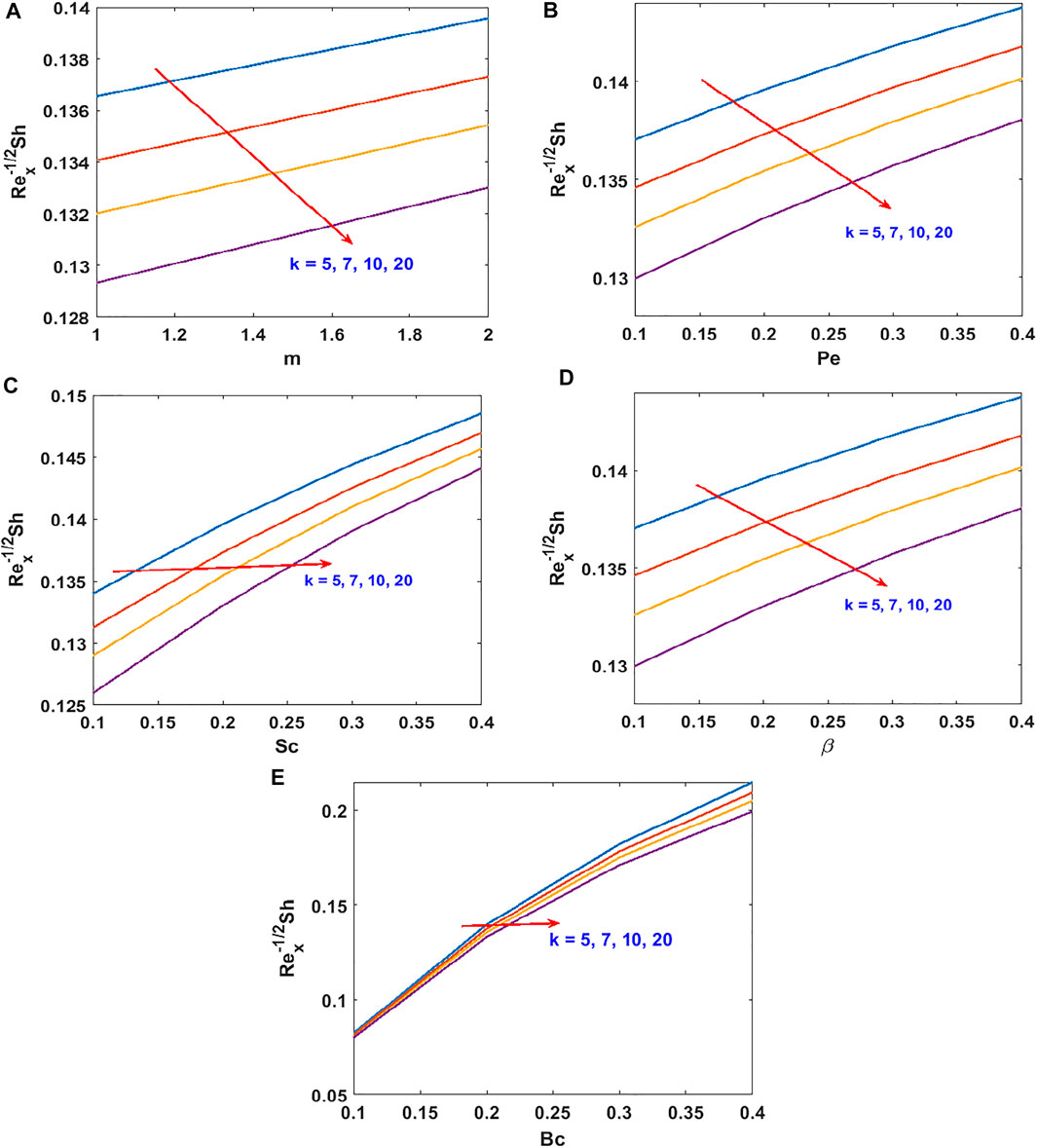
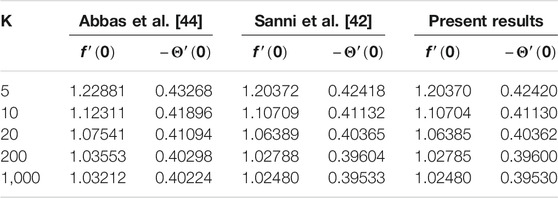
The responses of the curvature , Lorentz force , power law stretching index , and Cross fluid parameter on the stream function are presented in Figure 2. Figure 2A shows that the stream function decreases steadily with increasing radius of curvature (as the surface becomes flat). Figure 2B confirms the reduction of the flow lines due to the applied magnetic field , which produces the opposing Lorentz force. The flow trajectories are reduced by the stretching index as shown in Figure 2C. From these figures, we conclude that the flow trajectories can be controlled/regulated with the geometry parameter (radius of curvature), body force (magnetic field), and induced stretching index. This observation will aid the flow control system in polymer dynamics, manufacturing, and engineering industry. Figure 2D explains the rheology effect of We (Weissenberg number) on flow lines. It is observed that the stream lines increase for increasing We. Physically, the shear thinning (low viscosity) of the Cross fluid having less resistance increases the flow lines and enlarges the momentum boundary layer. The flow velocity accompanied by the boundary layer thickness that is developed on the curved surface can be portrayed in Figure 3. An increase in the flow parameters results in decreasing the velocity, , which in turn decreases the momentum boundary layer thickness. We recall that the velocity decreases with the radius of curvature, magnetic field, and power law index. Accordingly, the momentum boundary layer thickness will be controlled by these parameters (most revered phenomena in fluid dynamics). These observations are presented in Figures 3A–C. The rheology effect of We is presented in Figure 3D. That is, increasing the Weissenberg number (We) increases the velocity as well as momentum boundary layer thickness. In other words, this affirms that the flow field can be optimized for a higher shear-thinning parameter for the Cross fluid. The heat transport is investigated under the influence of non-linear Stefan-Boltzmann radiations against linear scenario. From Figure 4A, we observe that a large radius of curvature reduces the temperature and the thermal boundary layer region. In other words, heat kinematics can be minimized inside the boundary layer region by virtue of increasing/decreasing . The influence of the Lorentz force on the temperature is given in Figure 4B. The graph reveals an increasing trend in thermal profile with increasing magnetic field parameter, M. An important conclusion of the heat transfer analysis is that additional heat is generated by the application of Lorentz force and nonlinear radiation, which are the two additional features included in this study. Figures 4C,D present the effect of stretching velocity power index and Cross fluid parameter on the temperature field. In these graphs, both the temperature and thermal boundary layer region diminish for increasing and , respectively. This observation shows that the temperature and associated thermal boundary layer can be controlled by means of any of these parameters. Figures 4E,F illustrate the impacts of temperature parameters and thermal Biot number, Bt, on the temperature profile. In these plots, increasing, , enhances the temperature and widens the thermal boundary region. Thus, both the parameters play a substantial improvement to the heat flow and vital to this study. With much emphasis on the temperature difference to harness the linear and nonlinear radiative impact, a comparative illustration is given in Figure 5. However, the usual interpretations of the various physical parameters, Pr, Ec, Rn, and w, involved in this study are present with a striking difference between linear and non-linear radiation. Figure 5A shows a decaying temperature profile for large Pr. This observation is due to an increase in fluid conductivity. Figures 5B–D displayed an increasing temperature profile together with an accompanying thermal boundary layer. The reason being this is that the viscosity bond dissociates as the Eckert number increases (see Figure 5B). Moreover, the response of the nonlinear term is obviously intense in comparison with linear radiation . The effect of radiation on temperature profile is presented in Figure 5C. As radiation is a habitual source of heat, increasing increases the thermal boundary layer thickness and temperature profile. The effect of Ohmic heating on the temperature field experienced by the surface is shown in Figure 5D. In this figure, the thermal profile increases slightly for increasing owing to the additional heat generated at the surface and flows to the fluid. However, the nonlinear difference, , slightly optimizes the temperature and thermal boundary layer thickness. The influence of radius of curvature , stretching power , Peclet number Pe, Schmidt number Sc, reaction parameter , and concentration Biot number Bc on concentration profile are sketched in Figure 6. Figure 6A explains the impact of increasing on . We observe that the concentration profile increases as the surface curvature reduces. Figures 6B–E present consequences of , Pe, Sc, and on . Increasing stretching power-index decreases fluid concentration (see Figure 6B). Figures 6C,D elucidate reducing concentrations due to high Pe (low diffusivity) and Sc (low mass diffusion). Further, the effect of the rate of chemical reaction on is shown Figure 6E. This implies the higher the chemical reaction in the flow field, the lesser the fluid concentration. In fact, these observations are important in regulating the concentration profile and will be helpful in the chemical industry. Figure 6F lightens the influence of concentration Biot number on . It is seen that increase in Bc boosts the concentration profile inferring a remarkable consequence of depressing mass diffusivity. The variation in the physical quantities, surface drag force , heat transfer rate , and mass transfer rate are presented in Figures 7–9. Figure 7 presents the variation of the skin drag force for different k against stretching index, Lorenz force, and fluid rheology parameters, respectively. In Figure 8, variation in heat transfer against parameters examined in Figure 7 is presented in addition to the thermal Biot number. Figure 9 gives the variation of the mass transfer rate for different values of k against the stretching power-index, Peclet number, Schmidt number, reaction rate, and concentration Biot number. The upper part of Table 1 shows dual numerical results of the surface drag force in agreement with the published work and for the special case of Eq. 18. The rate of heat transfer computed shows a good agreement with the previous work (see the lower part of the table). Table 2 gives the present results in comparison with the existing literature on curved surfaces. These two tables show an excellent agreement and confirm the results in the literature as special cases of this present study. Appendix Table A1 presents the surface drag force and rate of heat and mass transfer of the present problem.
Conclusion
This study investigated the nonlinear radiative heat and mass transport of MHD fluid developed by non-linear stretching (power law index) of the curved surface. A non-Newtonian Cross fluid with a radially varying magnetic field is examined. The flow fields, velocity, temperature, and concentration are explained under the effect of viscous dissipation, Ohmic heating, and chemical reaction, respectively. The thermal and concentration appearances are good empirical proof, and the emerging parameters of the flow problem and main findings of this study are highlighted below.
• The velocity and associated momentum boundary layer decreases for small curvature (large radius of curvature), high Lorentz force, and nonlinear stretching power (m) whereas it increases for the high fluid rheology parameter (We). Thus, the flow field can be controlled/regulated through these parameters as a requirement of industrial, bio-mechanical, and engineering processes.
• The temperature profile decreases for an increase in the following: radius of curvature, , stretching power-index, , and the fluid rheology parameter, We. On the other hand, the heat flow region is enhanced by way of the impacts of the magnetic field M, nonlinear radiative temperature difference, , and thermal Biot number, Bt.
• The temperature profile is significantly improved for optimizing Eckert number, radiation, and Ohmic heating parameters (due to quantum heat produced by Lorentz force). The effect is substantial for the nonlinear radiation. A lower temperature profile is experienced for a higher Prandtl number. These observations have been widely discussed and accepted in their consequences.
• The concentration profile is increased for; small curvature (large radius of curvature) parameter, increasing the stretching power parameter, high Peclet and Schmidt numbers, and high rate of reaction. However, the opposite behavior is observed as the temperature profile enhances for an increasing concentration of the Biot number.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. 61673169).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Sakiadis BC. Boundary-layer Behavior on Continuous Solid Surfaces: I. Boundary-Layer Equations for Two-Dimensional and Axisymmetric Flow. Aiche J (1961) 7:26–8. doi:10.1002/aic.690070108
CrossRef Full Text | Google Scholar
3. Hamad MAA. Analytical Solution of Natural Convection Flow of a Nanofluid over a Linearly Stretching Sheet in the Presence of Magnetic Field. Int Commun Heat Mass Transfer (2011) 38(4):487–92. doi:10.1016/j.icheatmasstransfer.2010.12.042
CrossRef Full Text | Google Scholar
4. Cortell R. Viscous Flow and Heat Transfer over a Nonlinearly Stretching Sheet. Appl Math Comput (2007) 184(2):864–73. doi:10.1016/j.amc.2006.06.077
CrossRef Full Text | Google Scholar
5. Wang CY. Free Convection on a Vertical Stretching Surface. Z Angew Math Mech (1989) 69:418–20. doi:10.1002/zamm.19890691115
CrossRef Full Text | Google Scholar
6. Andersson HI, Bech KH, Dandapat BS. Magnetohydrodynamics Flow of a Power-Law Fluid over a Stretching Sheet. Int J Nonlinear Mech (2016) 27(6):929–36. doi:10.1016/0020-7462(92)90045-9
CrossRef Full Text | Google Scholar
7. Jalil M, Asghar S. Flow of Power-Law Fluid over a Stretching Surface: A Lie Group Analysis. Int J Non-Linear Mech (2013) 48:65–71. doi:10.1016/j.ijnonlinmec.2012.07.004
CrossRef Full Text | Google Scholar
8. Hamad MAA, Ferdows M. Similarity Solutions to Viscous Flow and Heat Transfer of Nanofluid over Nonlinearly Stretching Sheet. Appl Math Mech.-Engl Ed (2012) 33(7):923–30. doi:10.1007/s10483-012-1595-7
CrossRef Full Text | Google Scholar
9. MaboodKhan FWA, Khan WA, Ismail AIM. MHD Flow over Exponential Radiating Stretching Sheet Using Homotopy Analysis Method. J King Saud Univ - Eng Sci (2017) 29(1):68–74. doi:10.1016/j.jksues.2014.06.001
CrossRef Full Text | Google Scholar
10. Mustafa M, Khan JA, Hayat T, Alsaedi A. Simulations for Maxwell Fluid Flow Past a Convectively Heated Exponentially Stretching Sheet with Nanoparticles. AIP Adv (2015) 5(3):037133. doi:10.1063/1.4916364
CrossRef Full Text | Google Scholar
11. Kumaran V, Ramanaiah G. A Note on the Flow over a Stretching Sheet. Acta Mechanica (1996) 116:229–33. doi:10.1007/BF01171433
CrossRef Full Text | Google Scholar
12. Kumar SK, Sanjayanand E. Viscoelastic Boundary Layer MHD Flow through a Porous Medium over a Porous Quadratic Stretching Sheet. Arch Mech (2004) 56(3):191–204. am.ippt.pan.pl/index.php/am/article/view/158.
Google Scholar
13. Gorla RSR, Sidawi RI. Free Convection on a Vertical Stretching Surface with Suction and Blowing. Appl Sci Res (1994) 52:247–57. doi:10.1007/BF00853952
CrossRef Full Text | Google Scholar
14. Cortell R. Further Results on Nonlinearly Stretching Permeable Sheets: Analytic Solution for MHD Flow and Mass Transfer. Math Probl Eng (2012) 2012:1–18. doi:10.1155/2012/743130
CrossRef Full Text | Google Scholar
15. Shafiq A, Hammouch Z, Oztop HF. Radiative MHD Flow of Third-Grade Fluid towards a Stretched cylinder. In: International Conference on Comput. Math. Eng SciSpringer Cham (2019). p. 166–85.
Google Scholar
16. Ghalib MM, Zafar AA, Riaz MB, Hammouch Z, Shabbir K. Analytical Approach for the Steady MHD Conjugate Viscous Fluid Flow in a Porous Medium with Nonsingular Fractional Derivative. Physica A: Stat Mech its Appl (2020) 554:123941. doi:10.1016/j.physa.2019.123941
CrossRef Full Text | Google Scholar
17. Shafiq A, Hammouch Z, Turab A. Impact of Radiation in a Stagnation point Flow of Walters' B Fluid towards a Riga Plate. Therm Sci Eng Prog (2018) 6:27–33. doi:10.1016/j.tsep.2017.11.005
CrossRef Full Text | Google Scholar
18. MahantheshGireesha BBJ, Gireesha BJ, Gorla RSR. Unsteady Three-Dimensional MHD Flow of a Nano Eyring-Powell Fluid Past a Convectively Heated Stretching Sheet in the Presence of thermal Radiation, Viscous Dissipation and Joule Heating. J Assoc Arab Universities Basic Appl Sci (2017) 23:75–84. doi:10.1016/j.jaubas.2016.05.004
CrossRef Full Text | Google Scholar
19. Hayat T, Bashir G, Waqas M, Alsaedi A. MHD Flow of Jeffrey Liquid Due to a Nonlinear Radially Stretched Sheet in Presence of Newtonian Heating. Results Phys (2016) 6:817–23. doi:10.1016/j.rinp.2016.10.001
CrossRef Full Text | Google Scholar
20. Khalil R, Malik MY, Zahri M, Tahir M. Numerical Analysis of MHD Casson Navier’s Slip Nanofluid Flow Yield by Rigid Rotating Disk. Results Phys (2018) 8:744–51. doi:10.1016/j.rinp.2018.01.017
CrossRef Full Text | Google Scholar
21. Ellahi R, Riaz A. Analytical Solutions for MHD Flow in a Third-Grade Fluid with Variable Viscosity. Math Comp Model (2010) 52:1783–93. doi:10.1016/j.mcm.2010.07.005
CrossRef Full Text | Google Scholar
22. Azam M, Khan M, Alshomrani AS. Effects of Magnetic Field and Partial Slip on Unsteady Axisymmetric Flow of Carreau Nanofluid over a Radially Stretching Surface. Results Phys (2017) 7:2671–82. doi:10.1016/j.rinp.2017.07.025
CrossRef Full Text | Google Scholar
23. Zeeshan A, Majeed A. Heat Transfer Analysis of Jeffery Fluid Flow over a Stretching Sheet with Suction/injection and Magnetic Dipole Effect. Alexandria Eng J (2016) 55:2171–81. doi:10.1016/j.aej.2016.06.014
CrossRef Full Text | Google Scholar
24. Soid SK, Ishak A, Pop I. MHD Stagnation-point Flow over a Stretching/shrinking Sheet in a Micropolar Fluid with a Slip Boundary. Jsm (2018) 47(11):2907–16. core.ac.uk/download/pdf/188194323.pdf. doi:10.17576/jsm-2018-4711-34
CrossRef Full Text | Google Scholar
25. Hamad MAA, Uddin MJ, Ismail AIM. Investigation of Combined Heat and Mass Transfer by Lie Group Analysis with Variable Diffusivity Taking into Account Hydrodynamic Slip and thermal Convective Boundary Conditions. Int J Heat Mass Transfer (2012) 55:1355–62. doi:10.1016/j.ijheatmasstransfer.2011.08.043
CrossRef Full Text | Google Scholar
26. Ibáñez G. Entropy Generation in MHD Porous Channel with Hydrodynamic Slip and Convective Boundary Conditions. Int J Heat Mass Transfer (2015) 80:274–80. doi:10.1016/j.ijheatmasstransfer.2014.09.025
CrossRef Full Text | Google Scholar
27. Akhil SM, Harshad RP, Rakesh RD. Mixed Convective Micropolar Ferrofluid Flow with Viscous Dissipation, Joule Heating and Convective Boundary Conditions. Int Commun Heat Mass (2019) 108:104320. doi:10.1016/j.icheatmasstransfer.2019.104320
CrossRef Full Text | Google Scholar
28. Reddy PS, Sreedevi P, Chamkha AJ. Magnetohydrodynamic (MHD) Boundary Layer Heat and Mass Transfer Characteristics of Nanofluid over a Vertical Cone under Convective Boundary Condition. Propulsion Power Res (2018) 7(4):308–19. doi:10.1016/j.jppr.2018.11.004
CrossRef Full Text | Google Scholar
29. Mair K, Amna S, Salahuddin T, Malik MY, Mushtaq M. Heat and Mass Diffusion for Casson Nanofluid Flow over a Stretching Surface with Variable Viscosity and Convective Boundary Conditions. J Braz Soc Mech Sci Eng (2018) 40(533):3–10. doi:10.1007/s40430-018-1415-y
CrossRef Full Text | Google Scholar
30. Cross MM. Rheology of Non-newtonian Fluids: a New Flow Equation for Pseudoplastic Systems. J Colloid Sci (1965) 20(5):417–37. doi:10.1016/0095-8522(65)90022-X
CrossRef Full Text | Google Scholar
31. Hayat T, Khan MI, Tamoor M, Waqas M, Alsaedi A. Numerical Simulation of Heat Transfer in MHD Stagnation point Flow of Cross Fluid Model towards a Stretched Surface. Results Phys (2017) 7:1824–7. doi:10.1016/j.rinp.2017.05.022
CrossRef Full Text | Google Scholar
32. Manzur M, Khan M, Rahman Mu. Mixed Convection Heat Transfer to Cross Fluid with thermal Radiation: Effects of Buoyancy Assisting and Opposing Flows. Int J Mech Sci (2018) 138-139:515–23. doi:10.1016/j.ijmecsci.2018.02.010
CrossRef Full Text | Google Scholar
33. Khan M, Manzur M, ur Rahman M. On Axisymmetric Flow and Heat Transfer of Cross Fluid over a Radially Stretching Sheet. Results Phys (2017) 7:3767–72. doi:10.1016/j.rinp.2017.08.039
CrossRef Full Text | Google Scholar
34. Ijaz MK, Waqas W, Hayat T, Alsaedi A. Magneto-hydrodynamical Numerical Simulation of Heat Transfer in MHD Stagnation point Flow of Cross Fluid Model towards a Stretched Surface. Phys Chem Liq (2017) 56(5):584–95. doi:10.1016/j.rinp.2017.05.022
CrossRef Full Text | Google Scholar
35. Sajid M, Ali N, Javed T, Abbas Z. Stretching a Curved Surface in a Viscous Fluid. Chin Phys Lett (2010) 27:024703. doi:10.1088/0256-307X/27/2/024703/meta
CrossRef Full Text | Google Scholar
36. Sanni KM, Asghar S, Jalil M, Okechi NF. Flow of Viscous Fluid along a Nonlinearly Stretching Curved Surface. Results Phys (2017) 7:1–4. doi:10.1016/j.rinp.2016.11.058
CrossRef Full Text | Google Scholar
37. Saleh SHM, Arifin NM, Nazar R, Pop I. Unsteady Micropolar Fluid over a Permeable Curved Stretching Shrinking Surface. Math Probl Eng (2017) 2017:1–13. doi:10.1155/2017/3085249
CrossRef Full Text | Google Scholar
38. Nadeem S, Ahmed Z, Saleem S. Carbon Nanotubes Effects in Magneto Nanofluid Flow over a Curved Stretching Surface with Variable Viscosity. Microsyst Technol (2018) 25:2881–8. doi:10.1007/s00542-018-4232-4
CrossRef Full Text | Google Scholar
39. Saba F, Ahmed N, Hussain S, Khan U, Mohyud-Din S, Darus M. Thermal Analysis of Nanofluid Flow over a Curved Stretching Surface Suspended by Carbon Nanotubes with Internal Heat Generation. Appl Sci (2018) 8:395. doi:10.3390/app8030395
CrossRef Full Text | Google Scholar
40. Naveed M, Abbas Z, Sajid M, Hasnain J. Dual Solutions in Hydromagnetic Viscous Fluid Flow Past a Shrinking Curved Surface. Arab J Sci Eng (2018) 43:1189–94. doi:10.1007/s13369-017-2772-z
CrossRef Full Text | Google Scholar
41. Hayat T, Sajjad R, Ellahi R, Alsaedi A, Muhammad T. Homogeneous-heterogeneous Reactions in MHD Flow of Micropolar Fluid by a Curved Stretching Surface. J Mol Liquids (2017) 240:209–220. doi:10.1016/j.molliq.2017.05.054
CrossRef Full Text | Google Scholar
42. Sanni K. M., Hussain Q., Asghar S. Heat Transfer Analysis for Non-linear Boundary Driven Flow over a Curved Stretching Sheet with a Variable Magnetic Field. Front Phys (2020) 8:113. doi:10.3389/fphy.2020.00113
CrossRef Full Text | Google Scholar
43. Sanni KM, Hussain Q, Asghar S. Thermal Analysis of a Hydromagnetic Viscoelastic Fluid Flow over a Continuous Curved Stretching Surface in the Presence of Radiative Heat Flux. Arab J Sci Eng (2020) 46:631–44. doi:10.1007/s13369-020-04671-8
CrossRef Full Text | Google Scholar
44. Abbas Z, Naveed M, Sajid M. Heat Transfer Analysis for Stretching Flow over a Curved Surface with Magnetic Field. J Engin Thermophys (2013) 22:337–45. doi:10.1134/S1810232813040061
CrossRef Full Text | Google Scholar
45. Xia Y, Lin J, Ku X. Flow-induced Rotation of Circular cylinder in Poiseuille Flow of Power-Law Fluids. J Non-Newtonian Fluid Mech (2018) 260:120–32. doi:10.1016/j.jnnfm.2018.07.003
CrossRef Full Text | Google Scholar
46. Malik MY, Hussain A, Salahuddin T, Awais M. Effects of Viscous Dissipation on MHD Boundary Layer Flow of Sisko Fluid over a Stretching cylinder. AIP Adv (2016) 6:035009. doi:10.1063/1.4944347
CrossRef Full Text | Google Scholar
47. Hayat T, Ullah I, Alsaedi A, Asghar S. Magnetohydrodynamics Stagnation-Point Flow of Sisko Liquid with Melting Heat Transfer and Heat Generation/Absorption. J Therm Sci Eng Appl (2018) 10:1–8. doi:10.1115/1.4040032
CrossRef Full Text | Google Scholar
Appendix
The expressions for are given below:
 Kehinde Musodiq Sanni
Kehinde Musodiq Sanni Saleem Asghar1
Saleem Asghar1 Saima Rashid
Saima Rashid Yu-Ming Chu
Yu-Ming Chu