Brief Review of the Results Regarding the Possible Underlying Mechanisms Driving the Neutrinoless Double Beta Decay

Since the experimental discovery of neutrino oscillations, the search for the neutrinoless double beta (0νββ) decay has intensified greatly, as this particular decay mode, if experimentally discovered, could offer a testing ground for Beyond Standard Model (BSM) theories related to the yet hidden fundamental properties of neutrinos and the possibility of violating of some fundamental symmetries. In this work we make a brief review of the nuclear matrix elements and phase space factors calculations performed mainly by our group. Next, using these calculations and the most recent experimental half-life limits, we revise the constraints on the BSM parameters violating the lepton number corresponding to four mechanisms that could contribute to 0νββ decay. Finally, using the values obtained for the BSM parameters from one of the most sensitive double-beta decay experiments, we provide a comparison with the sensitivities of other experiments.

1. Introduction

Two decades ago, the successful experimental measurement of neutrino oscillations [1, 2] established that neutrinos have a mass different from zero. Although this discovery was a significant one, many of the neutrino properties still remain unknown to this day. Because in neutrino oscillation experiments only squared mass differences can be measured, we still have unanswered questions regarding their absolute masses, the mass hierarchy, the underlying mechanism that gives neutrinos mass, and even the very nature of the neutrinos (whether they are Dirac or Majorana particles). While there are many experimental and theoretical endeavors to bring clear answers to some of these questions, like high-precision calculations, measurements of different single-β decays, cosmological observations, the double-beta decay (DBD) and particularly the 0νββ decay mode are still considered the most appealing approaches to study the yet unknown properties of neutrinos. However, even if one 0νββ transition event would be experimentally observed, not all of the desired information about neutrinos would be immediately revealed. Recording such an event would demonstrate that the lepton number conservation is violated by two units, but cannot indicate the mechanism that dominates this process. Many large-scale experiments dedicated to the discovery of this lepton number violating (LNV) decay are already collecting data, with up-dates and new ones planned for the future, but so far there is no experimental proof of 0νββ transitions, only reports of lower limits for the corresponding half-lives. Experimentally, DBD of the isotopes ⁷⁶Ge and ¹³⁶Xe are currently the most accurately measured, but others like ⁴⁸Ca, ⁸²Se, and ¹³⁰Te are also investigated, with ¹²⁴Sn being considered for the future. There are advantages and disadvantages to studying each of these isotopes (costs, purity, Q-value, background signals, etc.), but the fact that different ones are being investigated is of great importance if an experimental confirmation is obtained for any of them. Theoretical studies of 0νββ involve the computation of nuclear matrix elements (NME) and phase space factors (PSF) appearing in the half-life expressions, whose precise calculation is essential for predicting the neutrino properties and interpretation of the DBD experimental data. Particularly, the NME computation is the subject of the largest uncertainties, so much effort is devoted to their accurate estimation. The most commonly used nuclear structure approaches for the NME calculation are proton-neutron Quasi Random Phase Approximation (pnQRPA) [3–11], Interacting Shell Model (ISM) [12–30], Interacting Boson Model (IBM-2) [31–35], Projected Hartree Fock Bogoliubov method (PHFB) [36], Energy Density Functional method (EDF) [37], and the Relativistic Energy Density Functional method (REDF) [38]. Each of these methods presents various advantages and disadvantages when compared to each other, especially when dealing with the nuclear structure of particular isotopes. Once experimentally confirmed, it is also important to establish the underlying mechanism(s) that may contribute to the 0νββ decay, as to properly extend the Standard Model. For the longest time, studies only addressed the so called “mass mechanism” that involves the exchange of light left-handed (LH) Majorana neutrinos. Presently, more scenarios are being considered and their investigation consists of calculating of the NME associated to each mechanism and the corresponding PSF. For example, possible contributions to 0νββ decay may come via the exchange of the right-handed (RH) heavy neutrinos [39]. Other contributions from possible RH components of the weak currents, through the so-called “λ” and “η” mechanisms could also be taken into account [40]. One of the most popular model that includes these mechanisms is the left-right symmetric model (LRSMM) [41–45]. In this work we consider several of these scenarios for 0νββ decay, following the prescriptions of [46]. We present and discuss the NME and PSF calculations that were recently published by our group. For the nuclear structure calculations our group and collaborators use Shell Model (ShM) techniques and codes [19–29]. For the PSF calculations we use our results from [47, 48] for the light neutrino and the heavy neutrino exchange mechanisms, and results from [49] for the other mechanisms. Using the latest experimental limits for the half-lives reported in literature, we up-date the constraints on the LNV parameters corresponding to each mechanism. Finally, we use the calculated values of the LNV parameters deduced with the half-life limits taken from the ⁷⁶Ge experiment [50], to evaluate the half-lives of the other four isotopes that should be achieved by their experiments to reach the sensitivity of the Ge experiment.

2. Brief Formalism of the 0νββ decay

For a long time, most of the 0νββ decay literature has focused its interest mainly on the mass mechanism, that assumes that this decay mode occurs via the exchange of light LH Majorana neutrinos between two nucleons inside the nucleus. The inclusion of contributions coming from RH components of the weak currents has also been discussed (for example in [40, 51]), but very few papers presented theoretical results considering these contributions. However, any mechanism/scenario that violates with two units the lepton number conservation may, in principle, contribute to the decay rate. Considering several mechanisms, the 0νββ decay half-life can be written in a factorized compact form, as a sum of products of PSF, NME, and the BSM parameters, corresponding to each mechanism [52], as follows:

$\begin{array}{ll}{\left[T_{1/2}^{0\nu }\right]}^{-1}=g_A^4\left[{\displaystyle \sum _i}|{{E}}_i{|}^2{{M}}_i^2+Re{\displaystyle \sum _{i\ne j}}{{E}}_i{{E}}_j{{M}}_{ij}\right].& (1)\end{array}$

Here, the ${{E}}_i$ contain the BSM parameters associated with the following mechanisms: ${{E}}_1={{E}}_{0\nu }=\sum _k^{light}{U}_{ek}^2\frac{m_k}{m_e}$ the exchange of light LH neutrinos, ${{E}}_2={{E}}_{\lambda }={\left(\frac{M_{WL}}{M_{WR}}\right)}^2\left|\sum _k^{light}{U}_{ek}{V}_{ek}\right|$ corresponds to the “λ mechanism” with RH leptonic and LH hadronic currents, ${{E}}_3={{E}}_{\eta }=\xi \left|\sum _k^{light}{U}_{ek}{V}_{ek}\right|$ is associated to the “η mechanism” with RH leptonic and RH hadronic currents, and ${{E}}_4={{E}}_{0N}={\left(\frac{M_{W_L}}{M_{W_R}}\right)}^4\sum _k^{heavy}{V}_{ek}^2\frac{m_p}{M_k}$ comes from the exchange of heavy RH neutrinos, with m_e being the electron mass and m_p the proton mass. M_WL and M_WR denote the masses of the LH and the RH W bosons, respectively. We assume that the neutrino mass eigenstates are separated as light, m_k(m_k ≪ 1 eV), and heavy, M_k(M_k ≫ 1 GeV). U_ek and V_ek are electron neutrino mixing matrices for the light LH and heavy RH neutrino, respectively [14, 44]. Following [4–6, 39, 46], ${{M}}_i^2$ are factors expressed in a standardized form as combinations of NME described in Equation (2) and integrated PSF denoted with G₀₁ − G₀₉. Values for the PSF used in this paper can be seen in Table 1, together with our ShM values for the individual NME M_α (with α= GTq, Fq, Tq, GTω, Fω, P, R, M_GTN, M_FN, and M_TN). Assuming that only one mechanism dominates the 0νββ transition, we can perform a so called "on-axis" analysis where the interference terms ${{E}}_i{{E}}_j{{M}}_{ij}$ are no longer taken into account.

TABLE 1

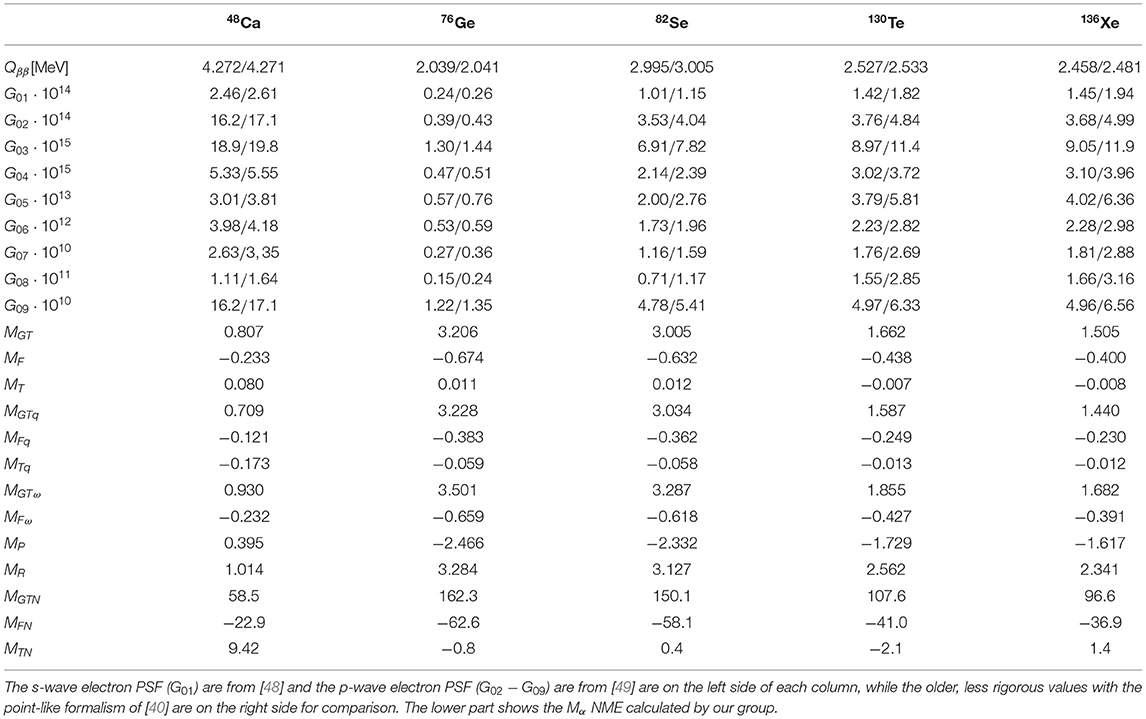
Table 1. In the upper part we present the Q_ββ values and the calculated PSF (G₀₁−G₀₉) in years⁻¹ for all five isotopes currently under investigation.

$\begin{array}{ll}\hfill {{M}}_{0\nu }^2=G_{01}{\left[M_{GT}-{\left(\frac{g_V}{g_A}\right)}^2{M}_F+M_T\right]}^2,& (\mathrm{2a})\end{array}$

$\begin{array}{ll}\hfill {{M}}_{0N}^2=G_{01}{\left[M_{GTN}-{\left(\frac{g_V}{g_A}\right)}^2{M}_{FN}+M_{TN}\right]}^2,& (\mathrm{2b})\end{array}$

$\begin{array}{l}{{M}}_{\lambda }^2=G_{02}{{M}}_{2+}^2-\frac{2}{9}{G}_{03}{{M}}_{1-}{{M}}_{2+}+\frac{1}{9}{G}_{04}{{M}}_{1-}^2\\ -G_{07}{M}_P{M}_R+G_{08}{M}_P^2+G_{09}{M}_R^2,& (\mathrm{2c})\end{array}$

$\begin{array}{ll}\hfill {{M}}_{\eta }^2=G_{02}{{M}}_{2-}^2-\frac{2}{9}{G}_{03}{{M}}_{1+}{{M}}_{2-}+\frac{1}{9}{G}_{04}{{M}}_{1+}^2,& (\mathrm{2d})\end{array}$

$\begin{array}{l}\hfill \text{with }{{M}}_{1\pm }=M_{GTq}\pm 3{\left(\frac{g_V}{g_A}\right)}^2{M}_{Fq}-6M_{Tq},\end{array}$

$\begin{array}{l}\hfill \text{and }{{M}}_{2\pm }=M_{GT\omega }\pm {\left(\frac{g_V}{g_A}\right)}^2{M}_{F\omega }-\frac{1}{9}{{M}}_{1\pm }.\end{array}$

Detailed equations of individual NME M_α can be found in the Appendix of [46], where they have been expressed in a consistent form. The expressions for the PSF can be found in [47, 49]. We note that Equations (2a, 2b) contain combinations of NME and PSF coming from contributions of only s-wave electron wave functions, while Equations (2c, 2d) present combinations of NME and PSF with contributions only from p-wave electron wavefunctions.

To use the expressions in Equation (2), we need accurate calculations of both the PSF that embed the distortion of the motion of outgoing electrons by the electric field of the daughter nucleus, and of the NME that depend on the nuclear structure of the parent and the daughter nuclei. Thus, the theoretical investigation of 0νββ transitions is a complex task that involves knowledge of physics at the atomic level for the PSF, nuclear level when calculating the NME, and at the fundamental particle level dealing with the LNV couplings.

2.1. Phase Space Factors

For a long time, PSF that enter the ββ half-life equations were considered to be calculated accurately enough [40, 53]. However, more recent reevaluations of their values using methods that use improved Fermi functions and more accurate integration routines have shown relevant differences in several cases, when compared to the previous results. Within these new methods of PSF calculation, the Fermi functions are constructed with "exact" electron wave functions (w.f.) obtained by solving the Dirac equation and consider finite nuclear size (FNS) and screening effects [47–49, 54]. In addition, in [47, 48] a Coulomb potential built from a realistic proton distribution in the daughter nucleus is used and the most recent Q-values [55] are taken into account.

In the upper part of Table 1, we present our choice of values for the nine PSF that enter Equation (2) for the five nuclei of interest. The PSF values obtained with s-electron w.f. (G₀₁) are taken from [48], while the PSF values obtained with the p-electron w.f. (G₀₂ − G₀₉) are from [49]. Both references provide consistently very similar values for the PSF needed in this study. Also, these current PSF values are compared to the previous calculations of [40] that relied on older Q_ββ values and where the proton distribution in the daughter nucleus, FNS, or electron screening effects were not considered. This comparison is meant to emphasize the need to use the results of newer calculations for more reliable analyzes.

2.2. Nuclear Matrix Elements

We choose our NME values from [46]. These were calculated using ShM techniques in the closure approximation with optimal closure energies ❬E❭ taken from [21, 23, 26]. These values were found to reproduce the NME results obtained in non-closure calculations. The Hamiltonians specific for each model space are chosen such that good agrements with experimental spectroscopic observables is achieved. The testing of these Hamiltonians can be found in [27, 28], where we performed calculations of 2νββ NME, the energy spectra for the first [0⁺ − 6⁺] states, B(E2)↑ transition probabilities, occupation probabilities and the Gamow-Teller strengths, which were compared to the experimental data available. For ⁴⁸Ca in the pf model space (0f_7/2, 1p_3/2, 0f_5/2, 1p_1/2) we use the GXPF1A [56] effective Hamiltonian and ❬E❭0.5 MeV, for ⁷⁶Ge and ⁸²Se in the jj44 model space (0f_5/2, 1p_3/2, 1p_1/2, 0g_9/2) we choose the JUN45 [57] effective Hamiltonian and ❬E❭3.4 MeV, and for ¹³⁰Te and ¹³⁶Xe in the jj55 model space (0g_7/2, 1d_5/2, 1d_3/2, 1s_1/2, 0h_11/2) we use the SVD [58] effective Hamiltonian and ❬E❭3.5 MeV. For the calculation of our two-body NME, we use finite size effects and higher order corrections of the nucleon current (with the vector and axial-vector form factors Λ_V = 850 MeV and Λ_A = 1086 MeV, respectively), and we include short-range correlations by multiplying the harmonic oscillator wave functions ψ_nl(lr) and the Jastrow correlation function ψ_nl(r) → [1+f(r)]ψ_nl(r) with the CD-Bonn parametrization (f(r) = −c·e^−ar2(1−br²), with a = 1.59, b = 1.45, and c = 0.46) [19, 27–29].

The lower part of Table 1 shows the ShM individual NME that enter Equation (2) which were calculated by our group using the effective Hamiltonians and ingredients listed above. In the values presented, the sign convention is that the Gamow-Teller NME M_GT is taken positive, with the other contributions having their sign listed as relative to that of M_GT.

3. Discussions

This brief review summarizes our recent calculations of the PSF and NME involved in 0νββ decay for four possible decay mechanisms, namely the light LH neutrino exchange, heavy RH neutrino exchange, λ−mechanism involving RH leptonic and RH hadronic currents, and the η−mechanism involving RH leptonic and LH hadronic currents. The PSF are calculated with Fermi functions built with exact electron w.f. solutions of the Dirac equation with a Coulomb-type potential obtained from a realistic distribution of protons in the daughter nucleus. FNS and screening effects were taken into account, as well. G₀₁ that include s-w.f. are taken from [48], while G_(02−09) that include p-w.f. are taken from [49]. Between the newer and the older PSF values, one can observe numerous differences in the range of 5–30%, with some rising of up to 90% (see G₀₈ of ¹³⁶Xe in Table 1). Such differences would impact the LNV values and the conclusions regarding the sensitivity of the experiments with various isotopes to the possible 0νββ mechanisms. In passing, we mention that in addition to the development of the new PSF codes, our group has also developed a very fast effective method [59] that is still based on the formalism of [40], but is fitted and tweaked to replicate the current results obtained with the most rigorous methods. Within reasonable precision, this method can be used for rapid PSF estimations and for plotting the un-integrated angular and energy electron distributions.

The NME are calculated within a ShM approach with the ingredients presented in section 2.2. ShM calculations are attractive because they consider all the correlations around the Fermi surface, respect all symmetries, and take into account consistently the effects of the missing single particle space via many-body perturbation theory (the effects were shown to be small, about 20%, for ⁸²Se [60]). In the case of closed-shell nuclei, ShM calculations using optimized Hamiltonians for nucleon-nucleon interactions are very reliable and compare well with the spectroscopic data available from experiments. Another advantage of this approach, important for reliable calculations, is that the calculated nucleon occupancies are close to the experimental ones. ShM calculations were successful in predicting the 2νββ decay half-life of ⁴⁸Ca [12] before experimental measurements. Calculations of different groups largely agree with each other without the need to adjust model parameters.

From Equation (2), using the NME and PSF in Table 1, we calculate the ${{M}}_i^2$ factors that enter the half-life in Equation (1). Using these factors and the most recent experimental half-life limits, we re-evaluate the LNV parameters corresponding to the four mechanisms. These results are presented in Table 2.

TABLE 2

Table 2. The first line shows the experimental lower half-life limits T_1/2 in years.

Table 2 first presents in the top section the experimental lower half-life limits T_1/2 in years. The next rows list the ${{M}}_i^2$ factors that contain combinations of PSF and NME for the five nuclei of current experimental interest, in the case of four possible 0νββ decay mechanisms described in Equation (2). In the middle section are found the values of the LNV parameters ${{E}}_i$ deduced from the experimental T_1/2 and the ${{M}}_i^2$ factors. For the mass mechanism, we also show the electron neutrino mass parameters ❬m_0ν❭ in units of eV that are obtained by the multiplication of ${{E}}_{0\nu }$ with the electron mass m_e. This extracted ❬m_0ν❭ is what is most commonly reported in the literature and is presented here for the convenience of the reader and an easier comparison with other references.

Lastly, we perform predictions of the half-lives for each isotope that would correspond to the LNV parameters extracted from one experiments of the highest sensitivity. Choosing the ${{E}}_i$ LNV deduced from the ⁷⁶Ge experiment [50], we estimate the half-lives of the other four isotopes. These values are displayed in the lower section of Table 2 and offer an indication about the relative sensitivity between DBD experiments.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This work has been supported by the grants of Romanian Ministry of Research Innovation and Digitalization through the projects No. PN19-030102-INCDFM and CNCS - UEFISCDI No. PN-III-P4-ID-PCE-2020-2374, within PNCDI III.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors thank Prof. Mihai Horoi for useful discussions and comments.

References

1. Fukuda Y, Hayakawa T, Ichihara E, Inoue K, Ishihara K, Ishino H, et al. Evidence for oscillation of atmospheric neutrinos. Phys Rev Lett. (1998) 81:1562–7. doi: 10.1103/PhysRevLett.81.1562

CrossRef Full Text | Google Scholar

2. Ahmad QR, Allen RC, Andersen TC, Anglin JD, Bühler G, Barton JC, et al. Measurement of the rate of ${\nu }_e+d\to p+p+e^{-}$ interactions produced by ⁸B solar neutrinos at the sudbury neutrino observatory. Phys Rev Lett. (2001) 87:071301. doi: 10.1103/PhysRevLett.87.071301

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Hirsch M, Klapdor-Kleingrothaus HV, Kovalenko SG. On the SUSY accompanied neutrino exchange mechanism of neutrinoless double beta decay. Phys Lett B. (1996) 372:181–6. doi: 10.1016/0370-2693(96)00050-0

CrossRef Full Text | Google Scholar

4. Pas H, Hirsch M, Klapdor-Kleingrothaus HV, Kovalenko SG. Towards a superformula for neutrinoless double beta decay. Phys Lett B. (1999) 453:194–8. doi: 10.1016/S0370-2693(99)00330-5

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Pas H, Hirsch M, Klapdor-Kleingrothaus HV, Kovalenko SG. A Superformula for neutrinoless double beta decay. 2. The Short range part. Phys Lett B. (2001) 498:35–9. doi: 10.1016/S0370-2693(00)01359-9

CrossRef Full Text | Google Scholar

6. Deppisch FF, Hirsch M, Pas H. Neutrinoless double-beta decay and physics beyond the standard model. J Phys G. (2012) 39:124007. doi: 10.1088/0954-3899/39/12/124007

CrossRef Full Text | Google Scholar

7. Simkovic F, Pantis G, Vergados JD, Faessler A. Additional nucleon current contributions to neutrinoless double-beta decay. Phys Rev C. (1999) 60:055502. doi: 10.1103/PhysRevC.60.055502

CrossRef Full Text | Google Scholar

8. Suhonen J, Civitarese O. Effects of orbital occupancies and spin-orbit partners on 0v beta beta-decay rates. Nucl Phys A. (2010) 847:207. doi: 10.1016/j.nuclphysa.2010.08.003

CrossRef Full Text | Google Scholar

9. Faessler A, Meroni A, Petcov ST, Simkovic F, Vergados J. Uncovering multiple CP-nonconserving mechanisms of (beta beta)(0v) decay. Phys Rev D. (2011) 83:113003. doi: 10.1103/PhysRevD.83.113003

CrossRef Full Text | Google Scholar

10. Mustonen MT, Engel J. Large-scale calculations of the double-beta decay of Ge-76, Te-130, Xe-136, and Nd-150 in the deformed self-consistent Skyrme quasiparticle random-phase approximation. Phys Rev C. (2013) 87:064302. doi: 10.1103/PhysRevC.87.064302

CrossRef Full Text | Google Scholar

11. Faessler A, Gonzalez M, Kovalenko S, Simkovic F. Arbitrary mass Majorana neutrinos in neutrinoless double beta decay. Phys Rev D. (2014) 90:096010. doi: 10.1103/PhysRevD.90.096010

CrossRef Full Text | Google Scholar

12. Retamosa J, Caurier E, Nowacki F. Neutrinoless double-beta decay of CA-48. Phys Rev C. (1995) 51:371. doi: 10.1103/PhysRevC.51.371

CrossRef Full Text | Google Scholar

13. Caurier E, Nowacki F, Poves A, Retamosa J. Shell model studies of the double beta decays of ⁷⁶Ge, ⁸²Se, and ¹³⁶Xe. Phys Rev Lett. (1996) 77:1954. doi: 10.1103/PhysRevLett.77.1954

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Horoi M. Shell model analysis of competing contributions to the double-beta decay of Ca-48. Phys Rev C. (2013) 87:014320. doi: 10.1103/PhysRevC.87.014320

CrossRef Full Text | Google Scholar

15. Neacsu A, Stoica S. Constraints on heavy neutrino and SUSY parameters derived from the study of neutrinoless double beta decay. Adv High Energy Phys. (2014) 2014:724315. doi: 10.1155/2014/724315

CrossRef Full Text | Google Scholar

16. Caurier E, Menendez J, Nowacki F, Poves A. Influence of pairing on the nuclear matrix elements of the neutrinoless beta beta decays. Phys Rev Lett. (2008) 100:052503. doi: 10.1103/PhysRevLett.100.052503

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Menendez J, Poves A, Caurier E, Nowacki F. Disassembling the nuclear matrix elements of the neutrinoless beta beta decay. Nucl Phys A. (2009) 818:139. doi: 10.1016/j.nuclphysa.2008.12.005

CrossRef Full Text | Google Scholar

18. Caurier E, Martinez-Pinedo G, Nowacki F, Poves A, Zuker AP. The shell model as a unified view of nuclear structure. Rev Mod Phys. (2005) 77:427. doi: 10.1103/RevModPhys.77.427

CrossRef Full Text | Google Scholar

19. Horoi M, Stoica S. Shell model analysis of the neutrinoless double-beta decay of Ca-48. Phys Rev C. (2010) 81:024321. doi: 10.1103/PhysRevC.81.024321

CrossRef Full Text | Google Scholar

20. Neacsu A, Stoica S, Horoi M. Fast, efficient calculations of the two-body matrix elements of the transition operators for neutrinoless double-beta decay. Phys Rev C. (2012) 86:067304. doi: 10.1103/PhysRevC.86.067304

CrossRef Full Text | Google Scholar

21. Sen'kov RA, Horoi M. Neutrinoless double-beta decay of Ca-48 in the shell model: closure versus nonclosure approximation. Phys Rev C. (2013) 88:064312. doi: 10.1103/PhysRevC.88.064312

CrossRef Full Text | Google Scholar

22. Horoi M, Brown BA. Shell-model analysis of the Xe-136 double Beta Decay Nuclear Matrix Elements. Phys Rev Lett. (2013) 110:222502. doi: 10.1103/PhysRevLett.110.222502

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Sen'kov RA, Horoi M, Brown BA. Neutrinoless double-beta decay of Se-82 in the shell model: Beyond the closure approximation. Phys Rev C. (2014) 89:054304. doi: 10.1103/PhysRevC.89.054304

CrossRef Full Text | Google Scholar

24. Brown BA, Horoi M, Sen'kov RA. Nuclear structure aspects of neutrinoless double-beta decay. Phys Rev Lett. (2014) 113:262501. doi: 10.1103/PhysRevLett.113.262501

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Neacsu A, Stoica S. Study of nuclear effects in the computation of the 0 nu beta beta decay matrix elements. J Phys G. (2014) 41:015201. doi: 10.1088/0954-3899/41/1/015201

CrossRef Full Text | Google Scholar

26. Sen'kov RA, Horoi M. Accurate shell-model nuclear matrix elements for neutrinoless double-beta decay. Phys Rev C. (2014) 90:051301(R). doi: 10.1103/PhysRevC.90.051301

CrossRef Full Text | Google Scholar

27. Neacsu A, Horoi M. Shell model studies of the ¹³⁰Te neutrinoless double-beta decay. Phys Rev C. (2015) 91:024309. doi: 10.1103/PhysRevC.91.024309

CrossRef Full Text | Google Scholar

28. Horoi M, Neacsu A. Shell model predictions for ¹²⁴Sn double-β decay. Phys Rev C. (2016) 93:024308. doi: 10.1103/PhysRevC.93.024308

CrossRef Full Text | Google Scholar

29. Horoi M, Stoica S, Brown BA. Shell-model calculations of two-neutrino double-beta decay rates of ⁴⁸Ca with the GXPF1A interaction. Phys Rev C. (2007) 75:034303. doi: 10.1103/PhysRevC.75.034303

CrossRef Full Text | Google Scholar

30. Blennow M, Fernandez-Martinez E, Lopez-Pavon J, Menendez J. Neutrinoless double-beta decay in seesaw models. JHEP. (2010) 07:096. doi: 10.1007/JHEP07(2010)096

CrossRef Full Text | Google Scholar

31. Barea J, Iachello F. Neutrinoless double-beta decay in the microscopic interacting boson model. Phys Rev C. (2009) 79:044301. doi: 10.1103/PhysRevC.79.044301

CrossRef Full Text | Google Scholar

32. Barea J, Kotila J, Iachello F. Limits on neutrino masses from neutrinoless double-beta decay. Phys Rev Lett. (2012) 109:042501. doi: 10.1103/PhysRevLett.109.042501

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Barea J, Kotila J, Iachello F. Nuclear matrix elements for double-beta decay. Phys Rev C. (2013) 87:014315. doi: 10.1103/PhysRevC.87.014315

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Barea J, Kotila J, Iachello F. 0νββ and 2νββ nuclear matrix elements in the interacting boson model with isospin restoration. Phys Rev C. (2015) 91:034304. doi: 10.1103/PhysRevC.91.034304

CrossRef Full Text | Google Scholar

35. Deppisch FF, Graf L, Iachello F, Kotila J. Analysis of light neutrino exchange and short-range mechanisms in 0νββ decay. Phys Rev D. (2020) 102:095016. doi: 10.1103/PhysRevD.102.095016

CrossRef Full Text | Google Scholar

36. Rath PK, Chandra R, Chaturvedi K, Lohani P, Raina PK, Hirsch JG. Neutrinoless beta beta decay transition matrix elements within mechanisms involving light Majorana neutrinos, classical Majorons, and sterile neutrinos. Phys Rev C. (2013) 88:064322. doi: 10.1103/PhysRevC.88.064322

CrossRef Full Text | Google Scholar

37. Rodriguez TR, Martinez-Pinedo G. Energy density functional study of nuclear matrix elements for neutrinoless beta beta decay. Phys Rev Lett. (2010) 105:252503. doi: 10.1103/PhysRevLett.105.252503

CrossRef Full Text | Google Scholar

38. Song LS, Yao JM, Ring P, Meng J. Relativistic description of nuclear matrix elements in neutrinoless double-beta decay. Phys Rev C. (2014) 90:054309. doi: 10.1103/PhysRevC.90.054309

CrossRef Full Text | Google Scholar

39. Vergados JD, Ejiri H, Simkovic F. Theory of neutrinoless double-beta decay. Rep Prog Phys. (2012) 75:106301. doi: 10.1088/0034-4885/75/10/106301

CrossRef Full Text | Google Scholar

40. Doi M, Kotani T, Takasugi E. Double-beta decay and Majorana neutrino. Prog Theor Phys Suppl. (1985) 83:1. doi: 10.1143/PTPS.83.1

CrossRef Full Text | Google Scholar

41. Pati JC, Salam A. Lepton number as the fourth color. Phys Rev D. (1974) 10:275.

Google Scholar

42. Keung WY, Senjanovic G. Majorana neutrinos and the production of the right-handed charged gauge boson. Phys Rev Lett. (1983) 50:1427.

Google Scholar

43. Rodejohann W. Neutrinoless double-beta decay and neutrino physics. J Phys G. (2012) 39:124008. doi: 10.1088/0954-3899/39/12/124008

CrossRef Full Text | Google Scholar

44. Barry J, Rodejohann W. Lepton number and flavor violation in TeV-scale left-right symmetric theories with large left-right mixing. J High Energy Phys. (2013) 9:153. doi: 10.1007/JHEP09(2013)153

CrossRef Full Text | Google Scholar

45. Bhupal Dev PS, Goswami S, Mitra M. TeV-scale left-right symmetry and large mixing effects in neutrinoless double beta decay. Phys Rev D. (2015) 91:113004. doi: 10.1103/PhysRevD.91.113004

CrossRef Full Text | Google Scholar

46. Horoi M, Neacsu A. Shell model study of using an effective field theory for disentangling several contributions to neutrinoless double-β decay. Phys Rev C. (2018) 98:035502. doi: 10.1103/PhysRevC.98.035502

CrossRef Full Text | Google Scholar

47. Stoica S, Mirea M. New calculations for phase space factors involved in double-beta decay. Phys Rev C. (2013) 88:037303. doi: 10.1103/PhysRevC.88.037303

CrossRef Full Text | Google Scholar

48. Mirea M, Pahomi T, Stoica S. Values of the phase space factors involved in double beta decay. Rom Rep Phys. (2015) 67:035503.

Google Scholar

49. Stefanik D, Dvornicky R, Simkovic F, Vogel P. Reexamining the light neutrino exchange mechanism of the 0νββ decay with left- and right-handed leptonic and hadronic currents. Phys Rev C. (2015) 92:055502. doi: 10.1103/PhysRevC.92.055502

CrossRef Full Text | Google Scholar

50. Agostini M, Araujo GR, Bakalyarov AM, Balata M, Barabanov I, Baudis L, et al. Final results of GERDA on the search for neutrinoless double-β decay. Phys Rev Lett. (2020) 125:252502. doi: 10.1103/PhysRevLett.125.252502

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Doi M, Kotani T, Nishiura H, Takasugi E. Double beta-decay. Progr Theor Exp Phys. (1983) 69:602. doi: 10.1143/PTP.69.602

CrossRef Full Text | Google Scholar

52. Horoi M, Neacsu A. Analysis of mechanisms that could contribute to neutrinoless double-beta decay. Phys Rev D. (2016) 93:113014. doi: 10.1103/PhysRevD.93.113014

CrossRef Full Text | Google Scholar

53. Suhonen J, Civitarese O. Weak-interaction and nuclear-structure aspects of nuclear double beta decay. Phys Rep. (1998) 300:123. doi: 10.1016/S0370-1573(97)00087-2

CrossRef Full Text | Google Scholar

54. Kotila J, Iachello F. Phase-space factors for double-beta decay. Phys Rev C. (2012) 85:034316. doi: 10.1103/PhysRevC.85.034316

CrossRef Full Text | Google Scholar

55. Kondev FG, Wang M, Audi G, Wapstra AH, MacCormick M, Xu X, et al. The AME2012 atomic mass evaluation: (II). Tables, graphs and references. Chinese Phys C. (2012) 36:12. doi: 10.1088/1674-1137/36/12/003

CrossRef Full Text | Google Scholar

56. Honma M, Otsuka T, Brown BA, Mizusaki T. New effective interaction for pf-shell nuclei and its implications for the stability of the N=Z=28 closed core. Phys Rev C. (2004) 69:034335. doi: 10.1103/PhysRevC.69.034335

CrossRef Full Text | Google Scholar

57. Honma M, Otsuka T, Mizusaki T, Hjorth-Jensen M. New effective interaction for f5pg9-shell nuclei. Phys Rev C. (2009) 80:064323. doi: 10.1103/PhysRevC.80.064323

CrossRef Full Text | Google Scholar

58. Qi C, Xu ZX. Monopole-optimized effective interaction for tin isotopes. Phys Rev C. (2012) 86:044323. doi: 10.1103/PhysRevC.86.044323

CrossRef Full Text | Google Scholar

59. Horoi M, Neacsu A. An effective method to accurately calculate the phase space factors for β⁻β⁻ decay. Adv High Energy Phys. (2016) 2016:7486712. doi: 10.1155/2016/7486712

CrossRef Full Text | Google Scholar

60. Holt JD, Engel J. Effective double-beta-decay operator for Ge-76 and Se-82. Phys Rev C. (2013) 87:064315. doi: 10.1103/PhysRevC.87.064315

CrossRef Full Text | Google Scholar

61. Arnold R, Augier C, Bakalyarov AM, Baker JD, Barabash AS, Basharina-Freshville A, et al. Measurement of the double-beta decay half-life and search for the neutrinoless double-beta decay of ⁴⁸Ca with the NEMO-3 detector. Phys Rev D. (2016) 93:112008. doi: 10.1103/PhysRevD.93.112008

CrossRef Full Text | Google Scholar

62. Latest Results From NEMO-3 Status of the SuperNEMO Experiment. (2016). Available online at: http://neutrino2016.iopconfs.org/IOP/media/uploaded/EVIOP/event_948/10.25__5__waters.pdf

Google Scholar

63. Alfonso K, Artusa DR, Avignone FT, Azzolini O, Balata M, Banks TI, et al. Search for neutrinoless double-beta decay of ¹³⁰Te with CUORE-0. Phys Rev Lett. (2015) 115:102502. doi: 10.1103/PhysRevLett.115.102502

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Gando A, Gando Y, Hachiya T, Hayashi A, Hayashida S, Ikeda H, et al. Search for majorana neutrinos near the inverted mass hierarchy region with KamLAND-Zen. Phys Rev Lett. (2016) 117:082503. doi: 10.1103/PhysRevLett.117.082503

PubMed Abstract | CrossRef Full Text | Google Scholar