- 1Institute for Theoretical Physics, University of Leipzig, Leipzig, Germany
- 2Department of Physics, Indian Institute of Science Education and Research, Mohali, India
- 3Department of Physics and Materials Science, University of Luxembourg, Luxembourg, Luxembourg
We investigate coarse-grained models of suspended self-thermophoretic microswimmers. Upon heating, the Janus spheres, with hemispheres made of different materials, induce a heterogeneous local solvent temperature that causes the self-phoretic particle propulsion. Starting from molecular dynamics simulations that schematically resolve the molecular composition of the solvent and the microswimmer, we verify the coarse-grained description of the fluid in terms of a local molecular temperature field, and its role for the particle’s thermophoretic self-propulsion and hot Brownian motion. The latter is governed by effective nonequilibrium temperatures, which are measured from simulations by confining the particle position and orientation. They are theoretically shown to remain relevant for any further spatial coarse-graining towards a hydrodynamic description of the entire suspension as a homogeneous complex fluid.
1 Introduction
Mesoscale phenomena are at the core of current research in hard and soft matter systems [1, 2]. The reason for this is at least twofold. Firstly, some of the most interesting states of matter are not properties of single atoms or elementary particles, but emerge from many-body interactions, at the mesoscale; e.g., the mechanical strength of many materials is determined by low-dimensional mesostructures. Secondly, these interesting mesoscale properties are often insensitive to molecular details and amenable to widely applicable coarse-grained models that provide both physical insight and efficient control [3]. Extensive atomistic computer simulations can therefore usually be bypassed either by much more efficient coarse-grained numerical techniques [4–6] or even by analytical methods [7, 8]. Both exploit the universality of the mesoscale physics to compute experimental observables without having to resolve the atomistic details. The price one pays for this efficiency is that fluctuations, which are increasingly important in biophysical and nanotechnological applications [9–13], may get renormalized or even inadvertently lost upon coarse graining. It is then not always obvious how they have to be properly re-introduced when need arises [14]. Systems with non-equilibrium mesoscale fluctuations, such as suspensions of self-propelled particles and other active fluids [15, 16], are of particular interest in this respect.
One might imagine an approach based on non-equilibrium thermodynamics, which, like hydrodynamics itself, is often valid down to the nanoscale, if judiciously applied [17]. But this theory’s starting point is a macroscopic deterministic one, without fluctuations, so that it is natively blind to the refinements we are after. The framework of stochastic thermodynamics would seem more appropriate, but, in its current formulations, temperature gradients, which are of particular interest to us, are explicitly excluded [18]. So the question that we address here, namely how nonisothermal and other non-homogeneous fluctuations scale under hydrodynamic coarse-graining, is not only of practical interest, but is also a profound theoretical problem that affects the construction of hydrodynamic theories, in general.
Our strategy is to start from a complete atomistic description of a well-defined model system that allows for analytical progress, yet provides the basis for simulating a number of innovative technologies [9, 11–13, 19]. The system is a solvent of Lennard–Jones atoms with embedded nanoparticles that are themselves made of Lennard–Jones atoms but maintained in a solid state by additional FENE attractions. The computer simulation of the model reveals that, even upon mesoscopic heating, nanoparticles and solvent admit a local-equilibrium description in which a (molecular) temperature field
The paper is organized as follows. Section 2 introduces the atomistic description of our model. The first coarse-graining step that admits the formulation of a local temperature field
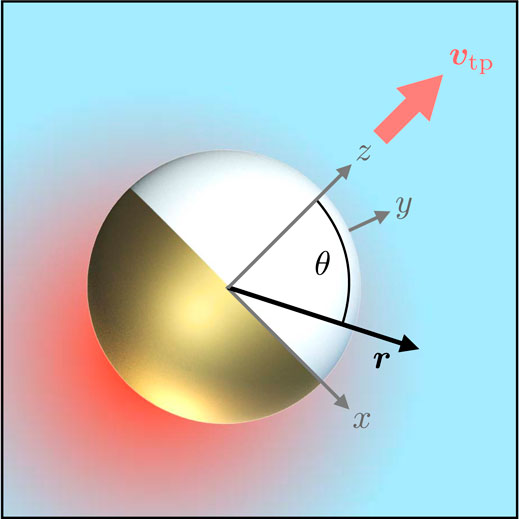
FIGURE 1. Sketch of a spherical Janus particle coated with a thin gold layer on one hemisphere. Upon heating (indicated by the schematic red color gradient), the particle induces an anisotropic temperature profile in the ambient fluid. The resulting thermo-osmotic interfacial flux gives rise to a net propulsion at swim speed
Not only does the symmetry breaking complicate the computation of its hot Brownian fluctuations compared to an isotropic particle, it also gives rise to a spontaneous anisotropic solvent flow in its vicinity [23, 24]. Such a particle therefore advances thermophoretically along its symmetry axis, under non-isothermal conditions [20, 21]. In the supplemental material pertaining to this article, we provide evidence that our simulation method indeed leads to a well-controlled, sizable net propulsion of the Janus particle, as was already reported in [22]. Finally, in Sec. 6 we address the largely open task of homogenizing a whole suspension of hot, active particles, before we close with a brief conclusion.
2 Atomistic Model of a Hot Janus Swimmer
Here, we briefly characterize the most salient features of our simulation setup. For additional technical details, the reader is referred to Refs. [22, 25–27]. We consider a heated metal-capped Janus sphere immersed in a fluid as depicted in Figure 1. In order to resolve microscopic details, such as the interfacial thermal resistance and the mechanism of thermophoresis [23], our simulation is based on a schematic molecular model, in which both the fluid and the Janus particle are atomistically resolved. All atomic interactions are modeled by a modified Lennard–Jones 12–6 potential
(truncated at
Colloidal thermophoresis has been studied extensively by means of mesoscopic theories and atomistic computer simulations. For example, thermal conductivity and thermodiffusion in nanofluids were studied in [35, 36] by means of nonequilibrium molecular dynamics simulations, whereas Refs. [22, 27, 37–39] focused on the realization of self-phoretic microswimmers and the study of their dynamical properties utilizing MPC and/or MD simulation methods. Moreover, molecular simulations were used to quantify thermo-osmotic forces and the associated thermo-osmotic slip [40–42], also employing MPC and MD methods. Thermal nonequilibrium transport in colloids and the role of hydrodynamic slip were theoretically studied in [43, 44], and a unified description of colloidal thermophoresis was suggested in [45] using a nonequilibrium-theromodynamics approach. Furthermore, different minimal models have been employed, e.g., to derive a force density from a gradient in a certain potential that is associated with the colloid [46–50]. The following paragraphs of the present contribution focus on a specific aspect, which has received relatively little attention so far, namely the enhanced thermal fluctuations experienced by a heated Brownian particle in its (self-created) nonisothermal environment. The swimmer’s so-called hot Brownian motion inevitably interferes with its self-propulsion randomizing particle position and orientation. In the following section, the crucial elementary notion for theories of hot Brownian motion, namely that of a molecular temperature field at which the Lennard–Jones fluid locally equilibrates, is properly introduced, analytically studied, and tested against simulation results.
3 Molecular Temperature Field
In order to justify the concept of a molecular temperature field
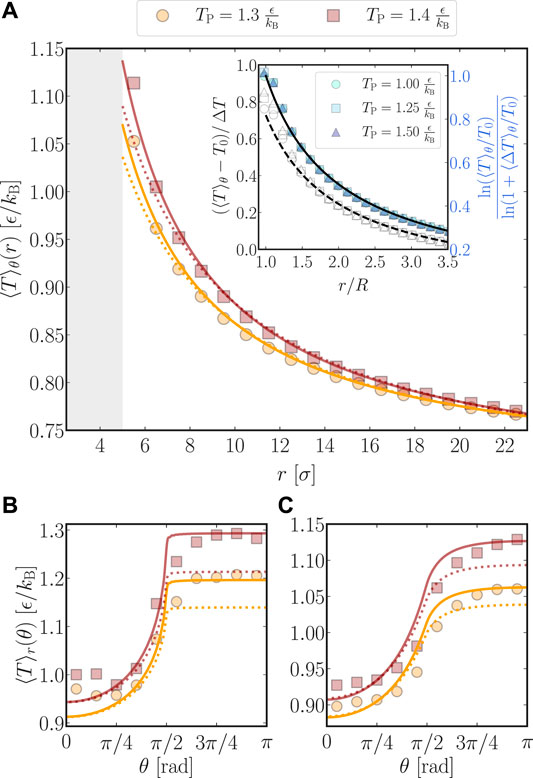
FIGURE 2. Mean fluid temperatures extracted from MD simulations (symbols) with wetting parameters
We start our quantitative discussion with the thermodynamic description of heat conduction. In steady state, the heat conduction equation for the temperature profile
where
along the uncoated part of the Janus sphere. Motivated by its very large heat conductivity, the gold cap of the Janus sphere is modelled as an isotherm kept at surface temperature
where
with the Legendre polynomials
Due to the orthogonality relations (
and with the short-hand notation
We infer from Eq. 11 that the actual and mean surface temperature increment are related via
Using the ambient fluid temperature
The described shortcomings of the theoretical temperature profile 6) can be improved by taking the temperature dependence of the heat conductivity
As detailed in the supplemental material, an analytic expression for the radially averaged temperature field
of an isotropic particle homogeneously heated up by
obtained by rearranging Eq. 14. In contrast, the collapse is violated close to the particle surface when the temperature profiles are simplified according to Eq. 11,
as can be inferred from the open symbols and dashed curve. This indicates that, close to the particle surface, the characteristic decay of
The measured temperature profiles in Figure 2B also show that for
Having justified the notion of a local molecular temperature, we next exploit the aforementioned Brownian time scale separation in order to calculate the effective nonequilibrium temperatures
4 Hot Brownian Motion
A hot nanoswimmer is inevitably subject to Brownian motion which randomizes the path of the particle in both position and orientation. In the classical Langevin picture of equilibrium Brownian motion, the Sutherland-Einstein relation
for the particle diffusivity D guarantees that the stochastic forces driving the Brownian particle balance the losses by the friction
are found to hold [54, 55]. Here,
with effective temperatures
The weight function
is the (excess) viscous dissipation function induced by the velocity fields
We stress the fact that the theory of hot Brownian motion connects the particle’s enhanced thermal fluctuations with the associated energy dissipation into the ambient fluid. Therefore, the dissipation function
In the following section, we use Eq. 21 to estimate effective temperatures characterizing the rotational and translational hot Brownian motion of a Janus sphere.
5 Estimating
Since a generally temperature dependent viscosity
•
•
The effective temperature
Note that superpositions of the motion types listed above generally sense yet different effective temperatures, e.g.,
The temperature field around a Janus sphere of radius R solves the heat conduction Eq. 3. Assuming constant viscosity and heat conductivity κ, the solution can be expanded in terms of Legendre polynomials
with the ambient fluid temperature
Since the coefficient
We now turn to the calculation of the effective temperature
where we introduced
with the constant coefficients
Therefore, only the coefficients
The denominator analogously gives
Hence, for translation along its symmetry axis, the Janus sphere’s hot Brownian motion is identical to that of a sphere homogeneously heated by
As anticipated on the same grounds and explicitly shown in the supplemental material, a similar calculation with a simple coordinate transformation leads to
for the particle’s translation perpendicular to its symmetry axis. Thus, also for transverse motion the corresponding effective temperatures are exactly given by those of a sphere homogeneously heated up by
We now turn to the particle’s rotational degrees of freedom starting with the calculation of
Using Eq. 29, the non-trivial part of the numerator of Eq. 23 evaluates to
and likewise the denominator to
Using
In contrast to our results for translation, Eq. 35, Eq. 36, we find that
A simple coordinate transformation (see supplemental material) and similar calculations as presented above yield
for rotation perpendicular to the particle’s symmetry axis. In this case, the correction term is only half in magnitude and has opposite sign as compared to the one in Eq. 42. This stems from the fact that the symmetry axis of the particle, and thus of the temperature profile, does not coincide with the rotation axis, thus leading to a distinct coupling between the temperature field and the dissipation function.
In order to test the theory, we measured the effective temperatures using MD computer simulations as described in Sec. 2. We therefor additionally confined the Janus sphere employing an external angular or spatial harmonic potential parallel or perpendicular to its symmetry axis [51] and measured its response. Figures 3A,B illustrate the respective distributions of the Janus particle’s position z and orientation θ relative to its symmetry axis for distinct heating temperatures.
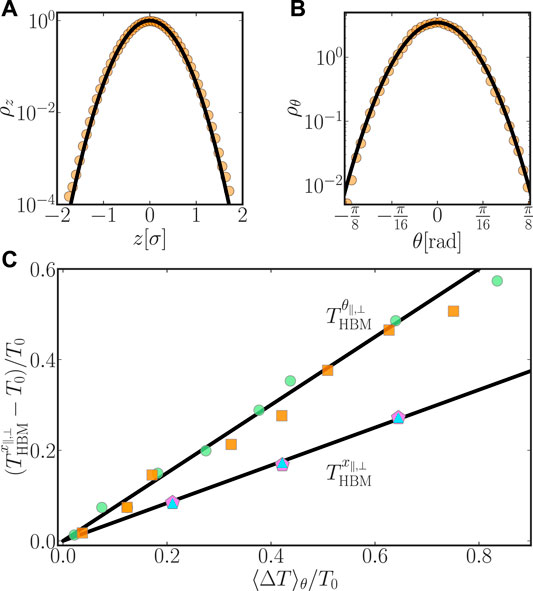
FIGURE 3. Upper panels: Histograms of harmonically confined position (A) and orientation (B) of the Janus particle heated to
From the variances of the effectively Gaussian distributions, we extracted the effective temperatures for translation and rotation, respectively [51]. The corresponding average surface temperature increments
Having seen that the coarse-grained non-equilibrium hydrodynamic description works well on the single-particle level, we now address the task of further coarse graining a suspension of hot microswimmers to an effective homogeneous complex fluid. Although for related microswimmer systems, scientists have developed powerful methods accounting for large numbers of individual swimmers [58–61], the task of homogenizing a whole suspension of hot, active particles and the role of effective nonequilibrium temperatures has received relatively little attention.
6 Complex Fluid Homogenisation
One is often interested in the collective (thermo) dynamical properties of an assembly of colloids and their embedding solvent, rather than in the motion of a single unit. Particle-based descriptions are impractical to inspect the behavior of such a complex fluid and one therefore often seeks a more versatile continuum approach, which allows one to leapfrog, in an efficient way, over the diverse time and length scales of its various constituents.
To this aim, we study non-isothermal fluctuating hydrodynamic equations of a fluid with suspended colloids, which are recast in terms of dynamical equations for coarse-grained volume elements. Surprisingly, a non-local frequency-dependent temperature appears due to the presence of the dispersed particles, which characterizes the intensity of their thermal fluctuations. Consider an incompressible solvent of density ϱ with velocity field
and N suspended colloids coupled to the fluid velocity via no-slip boundary conditions. Here,
The colloids are idealized as spheres with radius R and mass M, and their positions are denoted by
The coarse-graining procedure proceeds as follows:
1. We divide the system into mesoscopic volumes
2. We define the coarse-grained velocity of the complex fluid
3. In Eq. 46 the integration volume
where we have defined the local average velocity of the colloids
4. We take the time derivative of Eq. 47,
The first summand is rewritten, using Eq. 44
where
It is not hard to convince oneself that the random tensor
and the correlation function becomes
which is nonzero only if
where, we used
where we introduced the particle moment of inertia
and displays a tensorial frequency-dependent temperature—generally distinct from
whose zero-frequency limit should be compared with Eq. 21. The weight function
This analysis suggests that a non-trivial coarse-grained noise temperature arises through the presence of “slow” degrees of freedom. These are, in a hydrodynamic description, coupled to the fast ones via boundary conditions and thus are subjected to long-range forces, in contrast to the local, Markovian thermal stresses acting on the fluid elements.
7 Conclusion
We have performed microscopically resolved molecular dynamics simulations of a single hot Janus swimmer immersed in a Lennard-Jones fluid. We locally measured the inhomogeneous and anisotropic temperature profile induced in the solvent and compared it against analytic expressions basing on the heat conduction equation. We thereby verify the notion of a molecular temperature at which the surrounding medium locally equilibrates. We then exploited a large Brownian timescale separation in order to address the Janus particle’s overdamped hot Brownian motion. In a first-order approximation in the mean temperature increment
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
Author Contributions
The simulations were designed and performed by DC and RP. Both also analyzed the raw data. The theory was done by SA and GF. The manuscript was written by SA and KK.
Funding
We acknowledge funding by the Deutsche Forschungsgemeinschaft (DFG) through the priority program “Microswimmers” (SPP 1726, project 237143019), and Leipzig University within the program of Open Access Publishing. This work was supported by funding from the Science and Engineering Research Board (SERB), India, vide Grant No. SB/S2/CMP-113/2013 and by nVidia® corporation through its GPU Grant Program.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.655838/full#supplementary-material
References
1. Aharony A, Entin-Wohlman O. Perspectives of Mesoscopic Physics: Dedicated to Yoseph Imry’s 70th Birthday. London: World Scientific Publishing Company (2010).
2. Kroy K, Frey E. Focus on Soft Mesoscopics: Physics for Biology at a Mesoscopic Scale. New J Phys (2015) 17:110203. doi:10.1088/1367-2630/17/11/110203
3. Laughlin RB, Pines D. The Theory of Everything. Proc Natl Acad Sci (2000) 97:28–31. doi:10.1073/pnas.97.1.28
4. Gompper G, Ihle T, Kroll DM, Winkler RG. Multi-particle Collision Dynamics: A Particle-Based Mesoscale Simulation Approach to the Hydrodynamics of Complex Fluids. Adv Comp Simulation Approaches Soft Matter Sci (2009) III:1–87. doi:10.1007/978-3-540-87706-6_1
5. Carenza LN, Gonnella G, Lamura A, Negro G, Tiribocchi A. Lattice Boltzmann Methods and Active Fluids. Eur Phys J E (2019) 42:81. doi:10.1140/epje/i2019-11843-6
6. Shaebani MR, Wysocki A, Winkler RG, Gompper G, Rieger H. Computational Models for Active Matter. Nat Rev Phys (2020) 2:181–99. doi:10.1038/s42254-020-0152-1
7. Steffenoni S, Kroy K, Falasco G. Interacting Brownian Dynamics in a Nonequilibrium Particle bath. Phys Rev E (2016) 94:062139. doi:10.1103/PhysRevE.94.062139
8. Lämmel M, Kroy K. Analytical Mesoscale Modeling of Aeolian Sand Transport. Phys Rev E (2017) 96:052906. doi:10.1103/PhysRevE.96.052906
9. Bregulla AP, Yang H, Cichos F. Stochastic Localization of Microswimmers by Photon Nudging. ACS Nano (2014) 8:6542–50. doi:10.1021/nn501568e
10. Jikeli JF, Alvarez L, Friedrich BM, Wilson LG, Pascal R, Colin R, et al. Sperm Navigation along Helical Paths in 3d Chemoattractant Landscapes. Nat Commun (2015) 6:7985. doi:10.1038/ncomms8985
11. Qian B, Montiel D, Bregulla A, Cichos F, Yang H. Harnessing thermal Fluctuations for Purposeful Activities: the Manipulation of Single Micro-swimmers by Adaptive Photon Nudging. Chem Sci (2013) 4:1420–9. doi:10.1039/c2sc21263c
12. Selmke M, Khadka U, Bregulla AP, Cichos F, Yang H. Theory for Controlling Individual Self-Propelled Micro-swimmers by Photon Nudging I: Directed Transport. Phys Chem Chem Phys (2018) 20:10502–20. doi:10.1039/c7cp06559k
13. Selmke M, Khadka U, Bregulla AP, Cichos F, Yang H. Theory for Controlling Individual Self-Propelled Micro-swimmers by Photon Nudging II: Confinement. Phys Chem Chem Phys (2018) 20:10521–32. doi:10.1039/c7cp06560d
14. Adhikari R, Stratford K, Cates ME, Wagner AJ. Fluctuating Lattice Boltzmann. Europhys Lett (2005) 71:473–9. doi:10.1209/epl/i2004-10542-5
15. Menon GI. Active Matter. Rheology of Complex Fluids (2010) 1:193–218. doi:10.1007/978-1-4419-6494-6_9
16. Marchetti MC, Joanny JF, Ramaswamy S, Liverpool TB, Prost J, Rao M, et al. Hydrodynamics of Soft Active Matter. Rev Mod Phys (2013) 85:1143–89. doi:10.1103/revmodphys.85.1143
17. Celani A, Bo S, Eichhorn R, Aurell E. Anomalous Thermodynamics at the Microscale. Phys Rev Lett (2012) 109:260603. doi:10.1103/physrevlett.109.260603
18. Seifert U. Stochastic Thermodynamics, Fluctuation Theorems and Molecular Machines. Rep Prog Phys (2012) 75:126001. doi:10.1088/0034-4885/75/12/126001
19. Braun M, Cichos F. Optically Controlled Thermophoretic Trapping of Single Nano-Objects. ACS Nano (2013) 7:11200–8. doi:10.1021/nn404980k
20. Jiang H-R, Yoshinaga N, Sano M. Active Motion of a Janus Particle by Self-Thermophoresis in a Defocused Laser Beam. Phys Rev Lett (2010) 105:268302. doi:10.1103/physrevlett.105.268302
21. Bregulla AP, Cichos F. Size Dependent Efficiency of Photophoretic Swimmers. Faraday Discuss (2015) 184:381–91. doi:10.1039/c5fd00111k
22. Kroy K, Chakraborty D, Cichos F. Hot Microswimmers. Eur Phys J Spec Top (2016) 225:2207–25. doi:10.1140/epjst/e2016-60098-6
23. Anderson JL. Colloid Transport by Interfacial Forces. Annu Rev Fluid Mech (1989) 21:61–99. doi:10.1146/annurev.fl.21.010189.000425
24. Bickel T, Majee A, Würger A. Flow Pattern in the Vicinity of Self-Propelling Hot Janus Particles. Phys Rev E Stat Nonlin Soft Matter Phys (2013) 88:012301. doi:10.1103/PhysRevE.88.012301
25. Chakraborty D, Gnann MV, Rings D, Glaser J, Otto F, Cichos F, et al. Generalised Einstein Relation for Hot Brownian Motion. Epl (2011) 96:60009. doi:10.1209/0295-5075/96/60009
26. Falasco G, Pfaller R, Bregulla AP, Cichos F, Kroy K. Exact Symmetries in the Velocity Fluctuations of a Hot Brownian Swimmer. Phys Rev E (2016) 94:030602(R). doi:10.1103/PhysRevE.94.030602
27. Chakraborty D. Orientational Dynamics of a Heated Janus Particle. J Chem Phys (2018) 149:174907. doi:10.1063/1.5046059
28. Grest GS, Kremer K. Molecular Dynamics Simulation for Polymers in the Presence of a Heat bath. Phys Rev A (1986) 33:3628–31. doi:10.1103/physreva.33.3628
29. Barrat J-L, Bocquet Lr.. Influence of Wetting Properties on Hydrodynamic Boundary Conditions at a Fluid/solid Interface. Faraday Disc. (1999) 112:119–28. doi:10.1039/a809733j
30. Barrat J-L, Chiaruttini F. Kapitza Resistance at the Liquid-Solid Interface. Mol Phys (2003) 101:1605–10. doi:10.1080/0026897031000068578
31. Errington JR, Debenedetti PG, Torquato S. Quantification of Order in the Lennard-Jones System. J Chem Phys (2003) 118:2256–63. doi:10.1063/1.1532344
32. Potoff JJ, Panagiotopoulos AZ. Critical point and Phase Behavior of the Pure Fluid and a Lennard-jones Mixture. J Chem Phys (1998) 109:10914–20. doi:10.1063/1.477787
33. Fedosov DA, Sengupta A, Gompper G. Effect of Fluid-Colloid Interactions on the Mobility of a Thermophoretic Microswimmer in Non-ideal Fluids. Soft Matter (2015) 11:6703–15. doi:10.1039/c5sm01364j
34. Yang M, Ripoll M. Simulations of Thermophoretic Nanoswimmers. Phys Rev E Stat Nonlin Soft Matter Phys (2011) 84:061401. doi:10.1103/PhysRevE.84.061401
35. Vladkov M, Barrat J-L. Modeling Transient Absorption and thermal Conductivity in a Simple Nanofluid. Nano Lett (2006) 6:1224–8. doi:10.1021/nl060670o
36. Galliero G, Volz S. Thermodiffusion in Model Nanofluids by Molecular Dynamics Simulations. J Chem Phys (2008) 128:064505. doi:10.1063/1.2834545
37. Lüsebrink D, Yang M, Ripoll M. Thermophoresis of Colloids by Mesoscale Simulations. J Phys Condens Matter (2012) 24:284132. doi:10.1088/0953-8984/24/28/284132
38. Yang M, Wysocki A, Ripoll M. Hydrodynamic Simulations of Self-Phoretic Microswimmers. Soft Matter (2014) 10:6208–18. doi:10.1039/c4sm00621f
39. Olarte-Plata JD, Bresme F. Orientation of Janus Particles under thermal fields: The Role of Internal Mass Anisotropy. J Chem Phys (2020) 152:204902. doi:10.1063/5.0008237
40. Ganti R, Liu Y, Frenkel D. Molecular Simulation of Thermo-Osmotic Slip. Phys Rev Lett (2017) 119:038002. doi:10.1103/PhysRevLett.119.038002
41. Burelbach J, Brückner DB, Frenkel D, Eiser E. Thermophoretic Forces on a Mesoscopic Scale. Soft Matter (2018) 14:7446–54. doi:10.1039/c8sm01132j
42. Proesmans K, Frenkel D. Comparing Theory and Simulation for Thermo-Osmosis. J Chem Phys (2019) 151:124109. doi:10.1063/1.5123164
43. Würger A. Thermal Non-equilibrium Transport in Colloids. Rep Prog Phys (2010) 73:126601. doi:10.1088/0034-4885/73/12/126601
44. Morthomas J, Würger A. Thermophoresis at a Charged Surface: the Role of Hydrodynamic Slip. J Phys Condens Matter (2008) 21:035103. doi:10.1088/0953-8984/21/3/035103
45. Burelbach J, Frenkel D, Pagonabarraga I, Eiser E. A Unified Description of Colloidal Thermophoresis. Eur Phys J E Soft Matter (2018) 41:7. doi:10.1140/epje/i2018-11610-3
46. Dhont JKG. Thermodiffusion of Interacting Colloids. I. A Statistical Thermodynamics Approach. J Chem Phys (2004) 120:1632–41. doi:10.1063/1.1633546
47. Fayolle S, Bickel T, Le Boiteux S, Würger A. Thermodiffusion of Charged Micelles. Phys Rev Lett (2005) 95:208301. doi:10.1103/physrevlett.95.208301
48. Dhont JKG, Wiegand S, Duhr S, Braun D. Thermodiffusion of Charged Colloids: Single-Particle Diffusion. Langmuir (2007) 23:1674–83. doi:10.1021/la062184m
49. Würger A. Heat Capacity-Driven Inverse Soret Effect of Colloidal Nanoparticles. Europhys Lett (2006) 74:658–64. doi:10.1209/epl/i2005-10579-x
50. Bringuier E, Bourdon A. Colloid Transport in Nonuniform Temperature. Phys Rev E Stat Nonlin Soft Matter Phys (2003) 67:011404. doi:10.1103/PhysRevE.67.011404
51. Rings D, Chakraborty D, Kroy K. Rotational Hot Brownian Motion. New J Phys (2012) 14:053012. doi:10.1088/1367-2630/14/5/053012
52. Rings D, Selmke M, Cichos F, Kroy K. Theory of Hot Brownian Motion. Soft Matter (2011) 7:3441. doi:10.1039/c0sm00854k
53. Pitaevskii LP, Lifshitz E. Course of Theoretical Physics X – Physical Kinetics. Oxford: Butterworth-Heinemann (1981).
54. Falasco G, Kroy K. Nonisothermal Fluctuating Hydrodynamics and Brownian Motion. Phys Rev E (2016) 93:032150. doi:10.1103/PhysRevE.93.032150
55. Falasco G, Gnann MV, Rings D, Kroy K. Effective Temperatures of Hot Brownian Motion. Phys Rev E Stat Nonlin Soft Matter Phys (2014) 90:032131. doi:10.1103/PhysRevE.90.032131
56. Rings D, Schachoff R, Selmke M, Cichos F, Kroy K. Hot Brownian Motion. Phys Rev Lett (2010) 105:090604. doi:10.1103/PhysRevLett.105.090604
57. Selmke M, Schachoff R, Braun M, Cichos F. Twin-focus Photothermal Correlation Spectroscopy. RSC Adv (2013) 3:394–400. doi:10.1039/c2ra22061j
58. Thakur S, Kapral R. Collective Dynamics of Self-Propelled Sphere-Dimer Motors. Phys Rev E Stat Nonlin Soft Matter Phys (2012) 85:026121. doi:10.1103/PhysRevE.85.026121
59. Wagner M, Ripoll M. Hydrodynamic Front-like Swarming of Phoretically Active Dimeric Colloids. Epl (2017) 119:66007. doi:10.1209/0295-5075/119/66007
60. Wagner M, Roca-Bonet S, Ripoll M. Collective Behavior of Thermophoretic Dimeric Active Colloids in Three-Dimensional Bulk. The Eur Phys J E (2021) 44. doi:10.1140/epje/s10189-021-00043-8
Keywords: homogenisation, active particles, microswimmers, hot brownian motion, non-isothermal molecular dynamics simulations
Citation: Auschra S, Chakraborty D, Falasco G, Pfaller R and Kroy K (2021) Coarse Graining Nonisothermal Microswimmer Suspensions. Front. Phys. 9:655838. doi: 10.3389/fphy.2021.655838
Received: 19 January 2021; Accepted: 28 June 2021;
Published: 19 July 2021.
Edited by:
Ayan Banerjee, Indian Institute of Science Education and Research Kolkata, IndiaReviewed by:
Vasileios Basios, Université libre de Bruxelles, BelgiumMarisol Ripoll, Julich-Forschungszentrum, Helmholtz-Verband Deutscher Forschungszentren (HZ), Germany
Copyright © 2021 Auschra, Chakraborty, Falasco, Pfaller and Kroy. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sven Auschra, c3Zlbi5hdXNjaHJhQGdtYWlsLmNvbQ==; Klaus Kroy, a2xhdXMua3JveUB1bmktbGVpcHppZy5kZQ==
 Sven Auschra
Sven Auschra Dipanjan Chakraborty
Dipanjan Chakraborty Gianmaria Falasco
Gianmaria Falasco Richard Pfaller1
Richard Pfaller1 Klaus Kroy
Klaus Kroy