- 1Department of Mathematics, Faculty of Science, Jiangsu University, Zhenjiang, China
- 2Department of Mathematical and Physics, Nanjing Institute of Technology, Nanjing, China
- 3Department of Mathematics and Statistics, College of Science, Taif University, Taif, Saudi Arabia
- 4Department of Mathematics, Obour High Institute for Engineering and Technology, Cairo, Egypt
This study analyzes the exact solutions of the compliance fractional non-linear time–space telegraph (FNLTST) equation by Oliver Heaviside in 1880 via three non-applied analytical schemes. The solutions obtained to define the advanced or voltage spectrum of electrified transmission with day-to-day distance from electrical communication or the application of electromagnetic waves. Many new solutions are obtained, and three distinct styles of drawings are introduced (two-dimensional, three-dimensional, and density plots). Furthermore, stability characterization of the solutions is addressed using the properties of the Hamiltonian system. The originality of this study is shown by matching the solutions built with solutions produced previously using various analytical methods. Overall, the success of the three systems demonstrates their quality, intensity, and capacity to cope with several different types of non-linear evolutionary equations.
1. Introduction
The new generators of complicated systems, namely infectious disease epidemiology [1], neural network [2], genetics [3], fluid mechanic [4], community ecology [5], Solid-State Physics [6], plasma wave spread [7], thermodynamics [8], matter condensation [9], non-linear optimal [10], were employed. Formulating these phenomena through non-linear evolution equations relies on real testing to define parameters and to provide empirically unmistakable evidence that describes the intricate mechanisms of their physical and dynamic actions [11–13]. This implies that the key activity of these models is specified as functions, while the success factors for this behavior become [14] parameters. Many separate mathematicians and physicists also concentrate extensively on researching these mathematical models to understand more about their undiscovered properties [15, 16]. On the other hand, computational, analytical, and semi-analytical structures have been derived from fulfilling the same function [17–20].
Nowadays, fractional computation receives great attention in several science branches as it is able to discuss the non-local property of the mathematical models in detail [21, 22]. Thus, many fractional derivative operators have been derived to convert the non-linear partial differential equations into the ordinary differential equations, such as Riemann–Liouville, Caputo, the conformal fractional, and Atangana–Baleanu derivative operators [23–26]. These fractional operators have been employed for several non-linear evolution equations and have proved their effectiveness and powerfulness [27, 28].
This study handles a fundamental non-linear construction equation in electromagnetic waves, namely the compatible non-linear time-space equation. This equation model illustrates the advanced or voltage spectrum of an electrical transmission range with day-to-day distance from the electrical or wave application. This model is given mathematically by [29–31]
where b, d are arbitrary constants to be evaluated through the considered analytical schemes. Mixing between conformable fractional derivative and traveling wave transformation as following , where a, c are arbitrary constants, and using it along with Equation (1) converts the non-linear partial differential equation (NLPDE) into the next ordinary differential equation (ODE).
Using the homogeneous balance principle along the auxiliary equation of extended simplest equation method [32–35] , with n = 1, where n is the obtained value of homogeneous principle between the highest order derivative term and non-linear term in Equation (2), we get the following .
The section of the rest of the study are ordered as follows: in section 2, the above analytical schemes [32–35] are employed to achieve the solitary solution of the non-linear fractional time-space equation. Besides, the dynamical behavior of the solutions obtained is investigated through two-dimensional, three-dimensional, and density plots. The originality of the research is clarified in section 3. The conclusion of the entire study is presented in section 4.
2. Solitary Wave Solutions
In this section, the solitary wave solutions of fractional non-linear time–space telegraph (FNLTST) equation are investigated through the abovementioned computational schemes as following:
2.1. Extended Sech–Tanh Expansion Method's Solution
The general solution of the FNLTST equation is formulated by the suggested structure and measured balance value by
where a0, a1, and b1 are arbitrary constants to be determined later. Using the framework of the suggested method, produces the value of above-shown parameters is given as follows
Hence, the solutions of Equation (1) in the next form is
2.2. The Solutions of Extended sinh-Gordon Equation Expansion Method
The general solution of the FNLTST equation is formulated by the suggested structure and the measured balance value by
where A0, A1, and B1 are arbitrary constants to be evaluated later. Using the framework of the suggested method, the value of above shown parameters can be obtained as follows
Case 1. For w′(θ) = sinh(θ) and by substituting Equation (5) and its derivatives into Equation (2) in the framework of the suggested scheme, we obtained the following values of the abovementioned arbitrary constants:
Family I.
Hence, the solutions of Equation (1) take the next forms
Family II.
Thus, the solutions of Equation (1) are constructed by
Family III.
Therefore, the solutions of Equation (1) are given by
Case 2. For w′(θ) = cosh(θ) and by substituting Equation (5) and its derivatives into Equation (2) in the framework of the suggested scheme, we obtained the following values of the abovementioned arbitrary constants:
Family I.
Thus, the solutions of Equation (1) take the following formulas
Family II.
Hence, the solutions of Equation (1) are formulated in the following forms
Family III.
Hence, the solutions of Equation (1) are constructed by
2.3. Extended Simplest Equation Method's Solutions
The general solution of the FNLTST equation is formulated by the suggested structure and the measured balance value by
where a−1, a0, and a1 are arbitrary constants to be determined later, while Φ(Ξ) is the solution function of the next ODE
where α∗, λ, and μ are arbitrary constants to be calculated later. Using the framework of the suggested method, gets the value of above shown parameters as follows:
Family I.
Hence, the solitary solutions of Equation (1) take the following formulas
When λ = 0,
for α∗μ > 0, we obtain
for α∗μ < 0, we obtain
When α∗ = 0,
for λ > 0, we obtain
for λ < 0, we obtain
The general solutions has the next form:
When and μ > 0, we get
When and μ < 0, we get
Family II.
Hence, the solitary solutions of Equation (1) are constructed in the next forms
for λ > 0, as
for λ < 0, as
Family III.
Hence, the solitary solutions of Equation (1) are given,
for λ > 0, as
for λ < 0, as
Family IV.
Hence, the solitary solutions of Equation (1) are evaluated in the following formulas:
When λ = 0,
for α∗μ > 0, we obtain
for α∗μ < 0, we obtain
When α∗ = 0,
for λ > 0, we obtain
for λ < 0, we get
The general solutions has the next form:
For and μ > 0, we get
For and μ < 0, we get
Family V.
Therefore, the solitary solutions of Equation (1) are evaluated
for α∗μ > 0, as
for α∗μ < 0, as
3. Results and Discussion
This section studies the constructed traveling wave solutions of the FNLTST equation through the above applied schemes:
1. The obtained solution by using sech-tanh expansion method (4) is equal to the solution that obtained by using extended sinh-Gorden expansion method (6).
2. All other solutions are different. This shows the powerfulness and effectiveness of these three different techniques.
3. Comparing the constructed solutions with that which have been obtained by Ozkan Guner and Ahmet Bekir, who used the Exp-function method [36], shows the novelty and originality of the study, where all our solutions are completely different from their solutions.
4. Interpretation of figures:
We have explained some of the evaluated solutions through three different schemes (three-dimensional, two-dimensional, and density plots).
• Figure 1 shows kink wave of Equation (4) along with b = 4, d = 9.
• Figure 2 explains periodic wave of Equation (6) along with b = 2, d = −4.
• Figure 3 demonstrates solitary wave of Equation (7) along with b = 7, d = −3.
• Figure 4 figures out periodic wave of Equation (8) along with b = 4, d = −7.
• Figure 5 explains solitary wave of Equation (9) along with b = 5, d = −6.
• Figure 6 shows dark cone wave of Equation (22) along with a0 = 1, a = 2, α∗ = −1, c = 1, C = 3, μ = 4.
• Figure 7 explains bright cone wave of Equation (24) along with a0 = 3, a = 5, c = 2, C = 4, λ = 4.
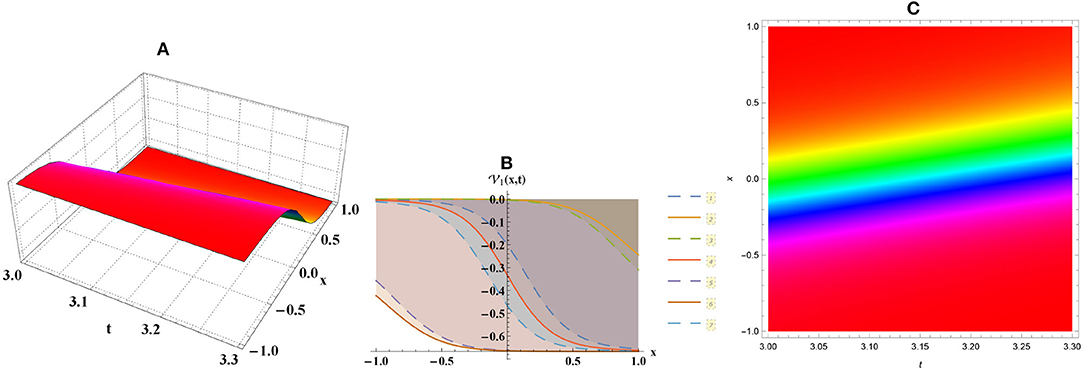
Figure 1. Kink numerical graph for Equation (4) through (A) three-dimensional, (B) two-dimensional, and (C) density plots.
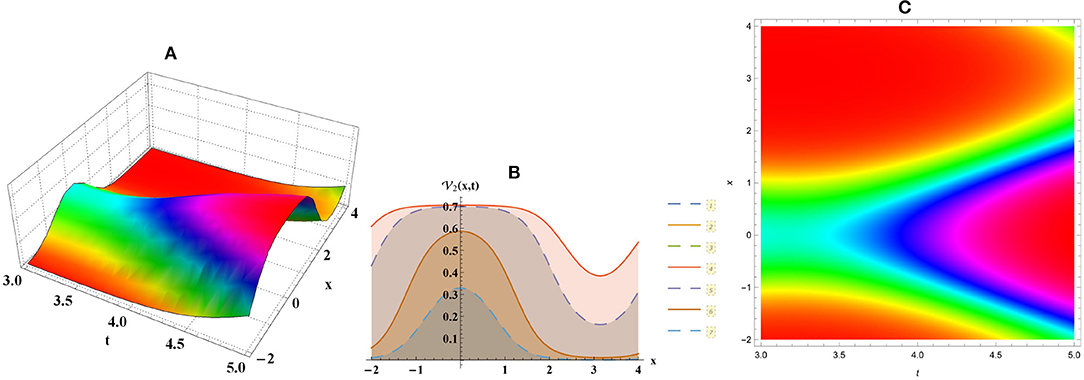
Figure 2. Periodic numerical graph for Equation (6) through (A) three-dimensional, (B) two-dimensional, and (C) density plots.
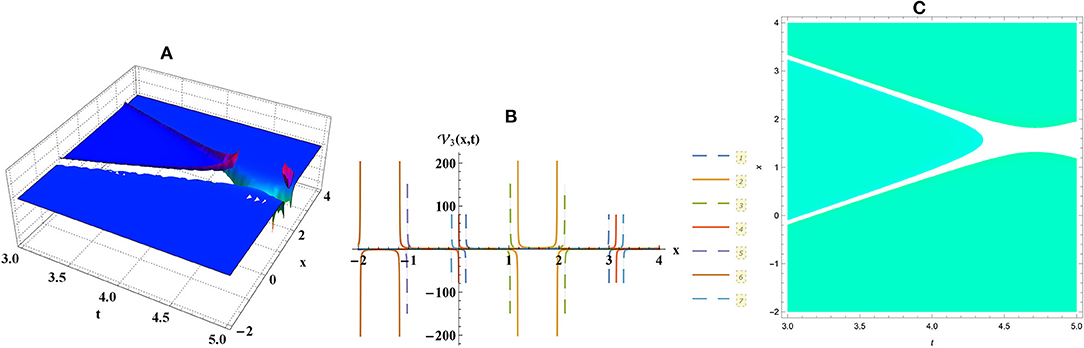
Figure 3. Solitary numerical graph for Equation (7) through (A) three-dimensional, (B) two-dimensional, and (C) density plots.
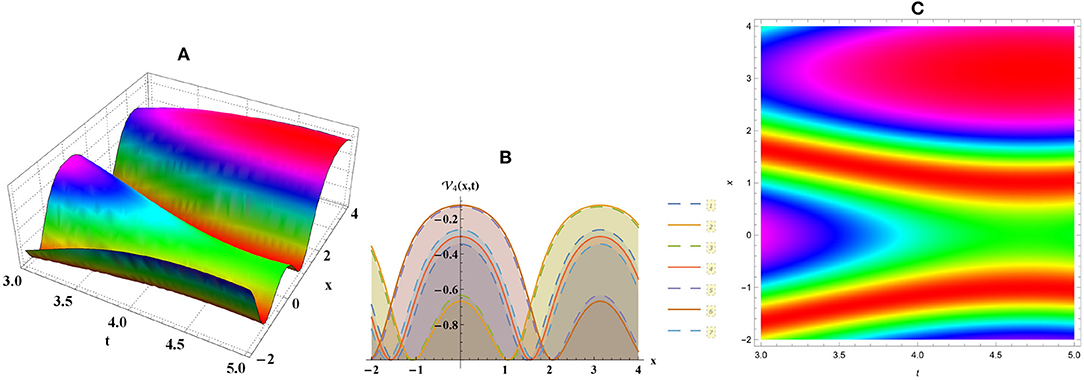
Figure 4. Periodic numerical graph for Equation (8) through (A) three-dimensional, (B) two-dimensional, and (C) density plots.
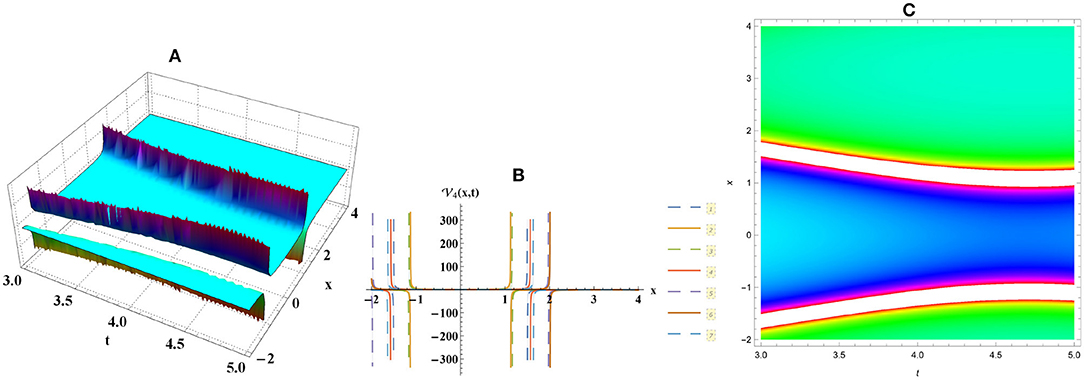
Figure 5. Solitary numerical graph for Equation (9) through (A) three-dimensional, (B) two-dimensional, and (C) density plots.
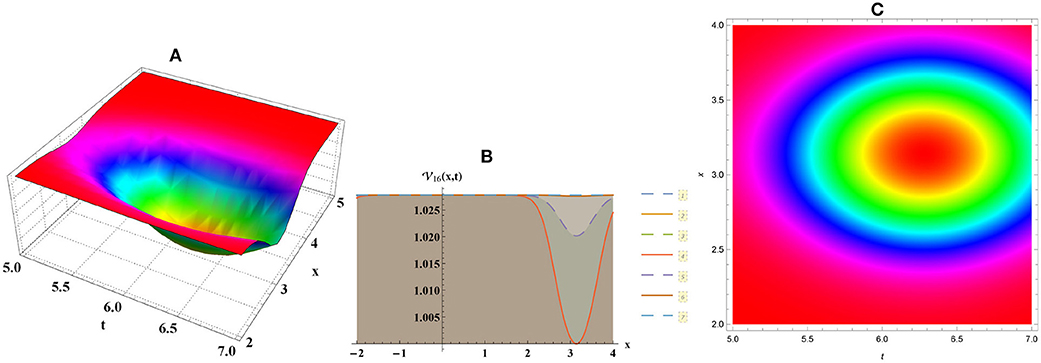
Figure 6. Dark cone numerical graph for Equation (22) through (A) three-dimensional, (B) two-dimensional, and (C) density plots.
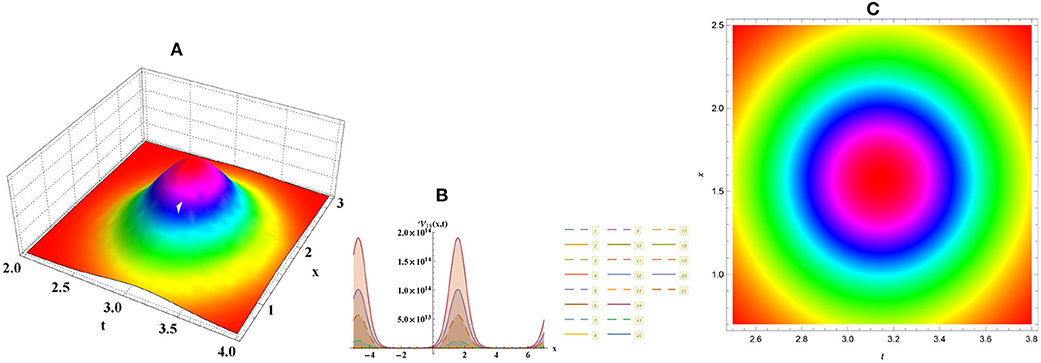
Figure 7. Bright cone numerical graph for Equation (24) through (A) three-dimensional, (B) two-dimensional, and (C) density plots.
4. Conclusion
This study effectively applied three non-applied methods to the FNLTST equation. The compatible fractional operator is used to transform the non-linear fractional partial differential equation into an ordinary differential equation of integer order. Various modern numerical options have been developed to illustrate the cutting-edge or voltage of an electrical transmission spectrum with a day yet distance across two-dimensional, three-dimensional, and density plots. The physical interpretation of these sketches have been explained in Equation (3) to show more novel properties of the considered model. The newness of this study is explored by contrasting the observations in the previous study.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research was supported by Taif University Researchers Supporting Project Number (TURSP-2020/48), Taif University, Taif, Saudi Arabia, and the Research Innovation Program for College Graduates of Jiangsu Province (Grant No. KYCX19_1609).
References
1. Khater MM, Inc M, Nisar K, Attia RA. Multi-solitons, lumps, and breath solutions of the water wave propagation with surface tension via four recent computational schemes. Ain Shams Eng J. (2021). doi: 10.1016/j.asej.2020.10.029
2. Khater MM, Mohamed MS, Attia RA. On semi analytical and numerical simulations for a mathematical biological model; the time-fractional nonlinear Kolmogorov-Petrovskii-Piskunov (KPP) equation. Chaos Solit Fract. (2021) 144:110676. doi: 10.1016/j.chaos.2021.110676
3. Khater MM, Ahmed AES, El-Shorbagy M. Abundant stable computational solutions of Atangana-Baleanu fractional nonlinear HIV-1 infection of CD4+ T-cells of immunodeficiency syndrome. Results Phys. (2021) 22:103890. doi: 10.1016/j.rinp.2021.103890
4. Khater MM, Nofal TA, Abu-Zinadah H, Lotayif MS, Lu D. Novel computational and accurate numerical solutions of the modified Benjamin-Bona-Mahony (BBM) equation arising in the optical illusions field. Alexandria Eng J. (2021) 60:1797–806. doi: 10.1016/j.aej.2020.11.028
5. Evans DJ, Bulut H. The numerical solution of the telegraph equation by the alternating group explicit (AGE) method. Int J Comput Math. (2003) 80:1289–97. doi: 10.1080/0020716031000112312
6. Khater MM, Anwar S, Tariq KU, Mohamed MS. Some optical soliton solutions to the perturbed nonlinear Schrödinger equation by modified Khater method. AIP Adv. (2021) 11:025130. doi: 10.1063/5.0038671
7. Khater MM. Novel explicit breath wave and numerical solutions of an Atangana conformable fractional Lotka-Volterra model. Alexandria Eng J. (2021) 60:4735–43. doi: 10.1016/j.aej.2021.03.051
8. Khater MM, Seadawy AR, Lu D. Dispersive optical soliton solutions for higher order nonlinear Sasa-Satsuma equation in mono mode fibers via new auxiliary equation method. Superlatt Microstruct. (2018) 113:346–58. doi: 10.1016/j.spmi.2017.11.011
9. Khater MM, Nisar KS, Mohamed MS. Numerical investigation for the fractional nonlinear space-time telegraph equation via the trigonometric Quintic B-spline scheme. Math Methods Appl Sci. (2021) 44:4598–606. doi: 10.1002/mma.7052
10. Alshahrani B, Yakout H, Khater MM, Abdel-Aty AH, Mahmoud EE, Baleanu D, et al. Accurate novel explicit complex wave solutions of the (2 + 1)-dimensional chiral nonlinear Schrödinger equation. Results Phys. (2021) 23:104019. doi: 10.1016/j.rinp.2021.104019
11. Khater MM, Mohamed MS, Elagan S. Diverse accurate computational solutions of the nonlinear Klein-Fock-Gordon equation. Results Phys. (2021) 23:104003. doi: 10.1016/j.rinp.2021.104003
12. Khater MM. Diverse solitary and Jacobian solutions in a continually laminated fluid with respect to shear flows through the Ostrovsky equation. Mod Phys Lett B. (2021) 35:2150220. doi: 10.1142/S0217984921502201
13. Chu Y, Khater MM, Hamed Y. Diverse novel analytical and semi-analytical wave solutions of the generalized (2 + 1)-dimensional shallow water waves model. AIP Adv. (2021) 11:015223. doi: 10.1063/5.0036261
14. Khater MM, Ahmed AES. Strong Langmuir turbulence dynamics through the trigonometric quintic and exponential B-spline schemes. AIMS Math. (2021) 6:5896–908. doi: 10.3934/math.2021349
15. Attia RA, Baleanu D, Lu D, Khater MM, Ahmed ES. Computational and numerical simulations for the deoxyribonucleic acid (DNA) model. Discrete Contin Dyn Syst. (2021) doi: 10.3934/dcdss.2021018
16. Sun GQ. Mathematical modeling of population dynamics with Allee effect. Nonlin Dyn. (2016) 85:1–12. doi: 10.1007/s11071-016-2671-y
17. Lopatiev A, Ivashchenko O, Khudolii O, Pjanylo Y, Chernenko S, Yermakova T. Systemic approach and mathematical modeling in physical education and sports. J Phys Educ Sport. (2017) 17:146–55. Available online at: http://repository.ldufk.edu.ua/handle/34606048/10563
18. Zhang P, Xiao X, Ma Z. A review of the composite phase change materials: fabrication, characterization, mathematical modeling and application to performance enhancement. Appl Energy. (2016) 165:472–510. doi: 10.1016/j.apenergy.2015.12.043
19. Attia RA, Lu D, Ak T, Khater MM. Optical wave solutions of the higher-order nonlinear Schrödinger equation with the non-Kerr nonlinear term via modified Khater method. Mod Phys Lett B. (2020) 34:2050044. doi: 10.1142/S021798492050044X
20. Ali AT, Khater MM, Attia RA, Abdel-Aty AH, Lu D. Abundant numerical and analytical solutions of the generalized formula of Hirota-Satsuma coupled KdV system. Chaos Solit Fract. (2020) 131:109473. doi: 10.1016/j.chaos.2019.109473
21. Khater MM, Attia RA, Abdel-Aty AH, Abdou M, Eleuch H, Lu D. Analytical and semi-analytical ample solutions of the higher-order nonlinear Schrödinger equation with the non-Kerr nonlinear term. Results Phys. (2020) 16:103000. doi: 10.1016/j.rinp.2020.103000
22. Khater MM, Park C, Abdel-Aty AH, Attia RA, Lu D. On new computational and numerical solutions of the modified Zakharov-Kuznetsov equation arising in electrical engineering. Alexandria Eng J. (2020) 59:1099–105. doi: 10.1016/j.aej.2019.12.043
23. Park C, Khater MM, Attia RA, Alharbi W, Alodhaibi SS. An explicit plethora of solution for the fractional nonlinear model of the low-pass electrical transmission lines via Atangana-Baleanu derivative operator. Alexandria Eng J. (2020) 59:1205–14. doi: 10.1016/j.aej.2020.01.044
24. Khater MM, Alzaidi J, Attia RA, Lu D, et al. Analytical and numerical solutions for the current and voltage model on an electrical transmission line with time and distance. Phys Scripta. (2020) 95:055206. doi: 10.1088/1402-4896/ab61dd
25. Khater MM, Attia RA, Baleanu D. Abundant new solutions of the transmission of nerve impulses of an excitable system. Eur Phys J Plus. (2020) 135:1–12. doi: 10.1140/epjp/s13360-020-00261-7
26. Li J, Attia RA, Khater MM, Lu D. The new structure of analytical and semi-analytical solutions of the longitudinal plasma wave equation in a magneto-electro-elastic circular rod. Mod Phys Lett B. (2020) 34:2050123. doi: 10.1142/S0217984920501237
27. Yue C, Khater MM, Attia RA, Lu D. The plethora of explicit solutions of the fractional KS equation through liquid-gas bubbles mix under the thermodynamic conditions via Atangana-Baleanu derivative operator. Adv Differ Equat. (2020) 2020:1–12. doi: 10.1186/s13662-020-2540-3
28. Khater MM, Park C, Lu D, Attia RA. Analytical, semi-analytical, and numerical solutions for the Cahn-Allen equation. Adv Differ Equat. (2020) 2020:1–12. doi: 10.1186/s13662-019-2475-8
29. Chen J, Liu F, Anh V. Analytical solution for the time-fractional telegraph equation by the method of separating variables. J Math Anal Appl. (2008) 338:1364–77. doi: 10.1016/j.jmaa.2007.06.023
30. Kumar S. A new analytical modelling for fractional telegraph equation via Laplace transform. Appl Math Model. (2014) 38:3154–63. doi: 10.1016/j.apm.2013.11.035
31. Orsingher E, Zhao X. The space-fractional telegraph equation and the related fractional telegraph process. Chin Ann Math. (2003) 24:12–45. doi: 10.1142/S0252959903000050
32. Guo M, Dong H, Liu J, Yang H. The time-fractional mZK equation for gravity solitary waves and solutions using sech-tanh and radial basic function method. Nonlin Anal Model Control. (2019) 24:1–19. doi: 10.15388/NA.2019.1.1
33. Ganji D, Abdollahzadeh M. Exact travelling solutions for the Lax's seventh-order KdV equation by sech method and rational exp-function method. Appl Math Comput. (2008) 206:438–44. doi: 10.1016/j.amc.2008.09.033
34. Wang G. A novel (3 + 1)-dimensional sine-Gorden and sinh-Gorden equation: derivation, symmetries and conservation laws. Appl Math Lett. (2020) 113:106768. doi: 10.1016/j.aml.2020.106768
35. Kudryashov NA, Loguinova NB. Extended simplest equation method for nonlinear differential equations. Appl Math Comput. (2008) 205:396–402. doi: 10.1016/j.amc.2008.08.019
Keywords: electrical transmission, electromagnetic waves, fractional non-linear time–space telegraph equation, computational simulation, conformable fractional derivative
AMS classification: 35Q55, 33F05, 65D07, 37K10, 35C08
Citation: Yue C, Wu L, Mousa AA, Lu D and Khater MMA (2021) Diverse Novel Stable Traveling Wave Solutions of the Advanced or Voltage Spectrum of Electrified Transmission Through Fractional Non-linear Model. Front. Phys. 9:654047. doi: 10.3389/fphy.2021.654047
Received: 15 January 2021; Accepted: 22 April 2021;
Published: 01 June 2021.
Edited by:
Jordan Yankov Hristov, University of Chemical Technology and Metallurgy, BulgariaReviewed by:
Haci Mehmet Baskonus, Harran University, TurkeyM. S. Osman, Cairo University, Egypt
Hasan Bulut, Firat University, Turkey
Abdullahi Yusuf, Federal University, Dutse, Nigeria
Sania Qureshi, Mehran University of Engineering and Technology, Pakistan
Ervin Kaminski Lenzi, Universidade Estadual de Ponta Grossa, Brazil
Copyright © 2021 Yue, Wu, Mousa, Lu and Khater. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mostafa M. A. Khater, bW9zdGFmYS5raGF0ZXIyMDI0QHlhaG9vLmNvbQ==
 Chen Yue1
Chen Yue1 Mostafa M. A. Khater
Mostafa M. A. Khater