Comparative Analysis of Nuclear Matrix Elements of 0νβ+β+ Decay and Muon Capture in 106Cd

Comparative analyses of the nuclear matrix elements (NMEs) related to the 0νβ⁺β⁺ decay of ¹⁰⁶Cd to the ground state of ¹⁰⁶Pd and the ordinary muon capture (OMC) in ¹⁰⁶Cd are performed. This is the first time the OMC NMEs are studied for a nucleus decaying via positron-emitting/electron-capture modes of double beta decay. All the present calculations are based on the proton-neutron quasiparticle random-phase approximation with large no-core single-particle bases and realistic two-nucleon interactions. The effect of the particle-particle interaction parameter g_pp of pnQRPA on the NMEs is discussed. In the case of the OMC, the effect of different bound-muon wave functions is studied.

1. Introduction

Neutrinoless double beta (0νββ) decay is a process in which a nucleus (A, Z), with mass number A and proton number Z, decays to a daughter nucleus with two more or two less protons. In the 0νβ⁻β⁻ mode the final nucleus is (A, Z + 2), and two electrons are emitted. In the case of the 0νβ⁺β⁺ mode the final nucleus is (A, Z − 2), and two positrons are emitted. In the latter case also the electron capture (EC) is possible through the mode 0νβ⁺EC. In this article we denote also this mode by the generic symbol 0νβ⁺β⁺. In the case of ¹⁰⁶Cd also the 0νECEC (neutrinoless double electron capture) [1] is possible, but it goes to an excited state, and thus is beyond the scope of the present work, as we analyze here only the ground-state-to-ground-state transition. In addition, it should be noted that the same nuclear matrix elements (NMEs) are involved in the 0νβ⁺β⁺ and 0νβ⁺EC modes. In any case, the neutrinoless double beta decay would immediately provide striking new-physics vistas beyond the standard model, since it not only violates lepton-number conservation, but also requires the neutrino to be of Majorana character. After the discovery of neutrino oscillations [2–4], this process has become even the more of vital interest because its discovery could potentially provide us with information on the yet-unknown absolute mass scale of neutrinos.

While neutrinoless double beta decay remains hypothetical, the two-neutrino decay mode (2νββ), which is allowed by the standard model, has been observed in several isotopes. Most of the observed decays are of two-neutrino double-beta minus (2νβ⁻β⁻) type, and there are only six isotopes capable of 2νβ⁺β⁺ decaying: ⁷⁸Kr, ⁹⁶Ru, ¹⁰⁶Cd, ¹²⁴Xe, ¹³⁰Ba, and ¹³⁶Ce. Naturally, these isotopes can also decay via the 2νβ⁺EC and 2νECEC (two-neutrino double electron capture) modes. Of these isotopes, ¹⁰⁶Cd is a particularly promising candidate for the 2νβ⁺β⁺-decay searches since it has the biggest decay energy, Q_ββ = 2775.39(10) keV, as well as other experimentally favorable features. At present, there are three running experiments searching for the β⁺β⁺ decay of ¹⁰⁶Cd, namely COBRA [5, 6], TGV-2 [7], and ¹⁰⁶CdWO₄ crystal scintillator [8].

Ordinary muon capture (OMC) on nuclei is a weak-interaction nuclear process, in which a negative muon μ⁻ is captured by a nucleus (A, Z) resulting in an atomic-number reduction by one and emission of a muon neutrino. It can significantly extend the kinematic region of ordinary beta decay, owing to the high energy release and large momentum transfer associated with the process. The energy release in the nuclear capture process is about 100 MeV, of which the largest fraction is donated to the neutrino, being the lightest particle in the process. Large mass of the captured muon allows highly-forbidden transitions and high excitation energies of the final states. These features make the OMC a particularly promising probe for the 0νββ decay. In fact, there are several completed, ongoing and planned experiments aiming to study OMC in double-beta-decay triplets. In [9], partial OMC rates to numerous excited states of intermediate nuclei of ββ-decay triplets, including the A = 106 triplet we are studying here, were extracted from γ-ray spectra. In [10], on the other hand, OMC strength function and the associated giant resonances in ¹⁰⁰Nb were studied for the first time. There is an ongoing joint program pursued at RCNP, J-PARC, and the Paul Scherrer Institute (PSI) aiming to extend these studies to a wide range of nuclei from sd-shell nuclei such as ²⁴Mg up to as heavy nuclei as ²⁴⁰Pu [11].

In the work of Kortelainen et al. [12] the OMC rates were compared against the 2νβ⁻β⁻-decay NMEs for light nuclei using the nuclear shell model. It was found that there was a clear correlation between the energy-distributed OMC rates to 1⁺ states and the energy-based decomposition of the NMEs for the 2νβ⁻β⁻ decays of the sd-shell nuclei ³⁶Ar, ⁴⁶Ca, and ⁴⁸Ca. In [13], we extended these studies to 0νβ⁻β⁻ decays of medium-heavy and heavy nuclei by computing the average matrix elements corresponding to the OMC transitions to the intermediate nuclei of 0νβ⁻β⁻ decays up to some 50 MeV using the pnQRPA formalism. We then compared these matrix elements with the energy-multipole decompositions of the NMEs of 0νβ⁻β⁻ decays computed using the same formalism and model spaces. We found that there are clear correspondencies between the 0νβ⁻β⁻-decay NMEs and the average OMC matrix elements, especially for the J^π = 3⁺, 3⁻, 4⁺, and 4⁻ states.

In [14], double beta decays of ¹⁰⁶Cd were studied in the pnQRPA framework using ⁴⁰Ca as the inert core. Here we extend those studies, for the ground-state-to-ground-state transition, by making a comparative analysis of the 0νβ⁺β⁺-decay and OMC NMEs of ¹⁰⁶Cd in the pnQRPA formalism with large no-core single-particle bases, in a manner pursued in [13]. The OMC on ¹⁰⁶Cd leads to excited states of ¹⁰⁶Ag which, on the other hand, act as virtual intermediate states of the β⁺β⁺ decay of ¹⁰⁶Cd (see Figure 1). Hence, we hope the comparison between OMC and 0νβ⁺β⁺-decay matrix elements will help improve the accuracy of the 0νβ⁺β⁺-decay NMEs by using the data of future muon-capture experiments. Particularly, in the case of ¹⁰⁶Cd, a measured OMC-strength spectrum would help pin down the value of the particle-particle parameter g_pp of pnQRPA, which in this case cannot be adjusted to 2νββ-decay data. We also study the effect of different bound-muon wave function on the OMC matrix elements. This is the first time when such calculations are being done on the positron-decay side of the nuclear chart.

FIGURE 1

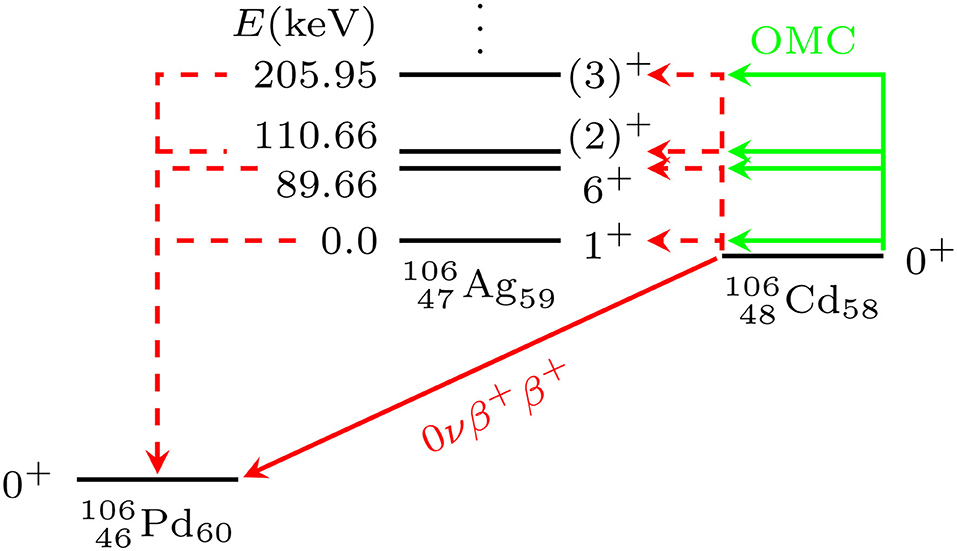
Figure 1. Level scheme of the A = 106 system. The solid red line indicates the 0νβ⁺β⁺-decay transition from the ground state of ¹⁰⁶Cd to the ground state of ¹⁰⁶Pd, and the dashed red lines refer to virtual transitions related to the 0νβ⁺β⁺ decay. The green lines correspond to OMC on the ground state of ¹⁰⁶Cd leading to different excited states of ¹⁰⁶Ag. The excitation energies of ¹⁰⁶Ag are shown in units of keV.

2. Two-Neutrino Double-Beta Decay

The half-life of a ground-state-to-ground-state two-neutrino double-beta decay can be written in the form

$\begin{array}{ll}{\left[t_{1/2}^{(2\nu )}(0_i^{+}\to 0_f^{+})\right]}^{-1}={(g_{\text{A}}^{\text{eff}})}^4{G}_{2\nu }{\left|M^{(2\nu )}\right|}^2,& (1)\end{array}$

where $g_{\text{A}}^{\text{eff}}$ is the effective value of the weak axial-vector coupling strength. The factor G_2ν is a leptonic phase-space factor (in units of inverse years) defined in [15, 16]. The ground states of the initial and final nuclei are denoted by $0_i^{+}$ and $0_f^{+}$, correspondingly.

The Gamow-Teller NME involved in Equation (1) can be written as

$\begin{array}{ll}{M}^{(2\nu )}={\displaystyle \sum _{m,n}}\frac{(0_f^{+}\parallel {\displaystyle {\sum }_k}{t}_k^{-}{\sigma }_k\parallel 1_m^{+})\langle 1_m^{+}|1_n^{+}\rangle (1_n^{+}\parallel {\displaystyle {\sum }_k}{t}_k^{-}{\sigma }_k\parallel 0_i^{+})}{D_m+1},& (2)\end{array}$

with the energy denominator

$\begin{array}{ll}{D}_m=(\frac{1}{2}\Delta +\frac{1}{2}\left[E(1_m^{+})+\tilde{E}(1_m^{+})\right]-M_i)/m_e,& (3)\end{array}$

where Δ is the nuclear mass difference between the initial and final 0⁺ ground states, M_i the mass of the initial nucleus, and m_e the electron rest mass. $\tilde{E}(1_m^{+})$ and $E(1_m^{+})$ are the (absolute) energies of the mth 1⁺ state in a pnQRPA calculation based on the left- and right-side ground states.

In principle, the expression in Equation (2) could also contain a Fermi NME. However, the ground states of the mother and daughter nuclei belong to different isospin multiplets, and due to the isospin symmetry, the Fermi contribution to the 2νββ-decay NME should vanish, leaving the Gamow-Teller NME in Equation (2) as the sole contributor to the 2νββ-decay rate.

In [16], the phase-space factors for the 2νβ⁺β⁺ decay, as well as for the competing modes 2νβ⁺EC and 2νECEC were computed. In [8], the experimentally extracted lower limits for half-lives of the different modes for ¹⁰⁶Cd were given. These values, together with the corresponding phase-space factors and resulting experimental matrix elements, are listed in Table 1.

TABLE 1

Table 1. Phase-space factors [16], half-lives [8], and the resulting experimental NMEs of different decay modes of ¹⁰⁶Cd.

3. Neutrinoless Double-Beta Decay

We assume that the 0νββ decay is dominated by the light-Majorana-neutrino-exchange mechanism, and exploit the formalism presented in [17]. Here we are only interested in the ground-state-to-ground-state transitions. The half-life for such a 0νββ transition can be written as

$\begin{array}{ll}{\left[t_{1/2}^{(0\nu )}(0_i^{+}\to 0_f^{+})\right]}^{-1}={(g_{\text{A}}^{\text{eff}})}^4{G}_{0\nu }{\left|M^{(0\nu )}\right|}^2{\left|\frac{\langle m_{\nu }\rangle }{m_e}\right|}^2,& (4)\end{array}$

where G_0ν is a phase-space factor for the final-state leptons in units of inverse years (see [15, 16]), defined here without including the axial-vector coupling g_A. The effective light-neutrino mass, 〈m_ν〉, of Equation (4) is defined as

$\begin{array}{ll}\langle m_{\nu }\rangle ={\displaystyle \sum _j}{(U_{ej})}^2{m}_j& (5)\end{array}$

with m_j being the mass eigenstates of light neutrinos. The amplitudes U_ej are the components of the electron row of the light-neutrino-mass mixing matrix.

The 0νββ-decay NME M^(0ν) in Equation (4) is defined as

$\begin{array}{ll}{M}^{(0\nu )}=M_{\text{GT}}^{(0\nu )}-{\left(\frac{g_{\text{V}}}{g_{\text{A}}^{\text{eff}}}\right)}^2{M}_{\text{F}}^{(0\nu )}+M_{\text{T}}^{(0\nu )},& (6)\end{array}$

where we adopt the CVC value g_V = 1.0 for the weak vector coupling strength. The definitions for the double Fermi, Gamow-Teller, and tensor NMEs $M_{\text{F}}^{(0\nu )}$, $M_{\text{GT}}^{(0\nu )}$, and $M_{\text{T}}^{(0\nu )}$ can be found e.g., in [17].

For the nucleon-nucleon short-range correlations (SRC) [18, 19], included in the NMEs, we use the CD-Bonn form [20] with the parametrization,

$\begin{array}{ll}{f}_{\text{CD}}(r)=1-0.46{\text{e}}^{-(1.52/{\text{fm}}^2)r^2}[1-(1.88/{\text{fm}}^2)r^2].& (7)\end{array}$

4. Muon Capture

Ordinary muon capture (OMC) is a semileptonic weak interaction process, quite like electron capture (EC). The OMC process we are interested in here can be written as

$\begin{array}{ll}{\mu }^{-}{+}_Z^A\text{X}(0^{+})\to {\nu }_{\mu }{+}_{Z-1}^A\text{Y}(J^{\pi }),& (8)\end{array}$

where the negatively charged muon (μ⁻) is captured by the 0⁺ ground state of the even-even nucleus X of mass number A and atomic number Z. The process leads to the J^π multipole states of Y, the odd-odd isobar of the mother nucleus, of atomic number Z−1; here J is the angular momentum and π the parity of the final state. At the same time a muon neutrino ν_μ is emitted.

4.1. Bound-Muon Wave Functions

The wave function of the muon bound on an atomic orbit of the initial nucleus can be written as an expansion in terms of the normalized spherical spinors χ_κμ

$\begin{array}{ll}{\psi }_{\mu }(\kappa ,\mu ;\text{r})={\psi }_{\kappa \mu }^{(\mu )}=\left[\begin{array}{c}-i{F}_{\kappa }{\chi }_{-\kappa \mu }\\ G_{\kappa }{\chi }_{\kappa \mu }\end{array}\right],& (9)\end{array}$

where G_κ and F_κ are the large and small radial components of the wave functions of the bound state [21]. Here κ denotes the atomic orbit in the following manner

$\begin{array}{ll}\{\begin{array}{c}l=\kappa \text{ and }j=l-\frac{1}{2},\text{ for }\kappa >0\hfill \\ l=-\kappa -1\text{ and }j=l+\frac{1}{2},\text{ for }\kappa <0.\hfill \end{array}\hfill & (10)\end{array}$

After being stopped in the outermost shell of an atom, the negatively charged muon undergoes a cascade of transitions to lower atomic orbitals, leaving it finally on the lowest, K atomic orbit. Hence, the captured muon can be assumed to be initially bound in the lowest state, 1s_1/2, corresponding to κ = −1 and $\mu =\pm \frac{1}{2}$. Making this assumption, we can estimate the bound-muon wave function by the Bethe-Salpeter point-like-nucleus approximation formulae [22]

$\begin{array}{l}{G}_{-1}={(2Z/a_0)}^{\frac{3}{2}}\sqrt{\frac{1+\gamma }{2\Gamma (2\gamma +1)}}{\left(\frac{2Zr}{a_0}\right)}^{\gamma -1}{e}^{-Zr/a_0},\\ F_{-1}=-\sqrt{\frac{1-\gamma }{1+\gamma }}{G}_{-1},& (11)\end{array}$

where γ is defined as

$\gamma =\sqrt{1-{(\alpha Z)}^2},$

where α is the fine-structure constant and Z the atomic number of the nucleus. The Bohr radius of the μ-mesonic atom is

$a_0=\frac{\hslash }{m_{\mu }^{\prime }c\alpha }=\frac{1}{m_{\mu }^{\prime }},$

where we have adopted the values ℏ = c = 1. The

$\begin{array}{ll}{m}_{\mu }^{\prime }=\frac{m_{\mu }}{1+\frac{m_{\mu }}{AM}}& (12)\end{array}$

is the reduced muon mass in the μ-mesonic atom. If we assume that αZ is very small, γ ≈ 1, and therefore

$\begin{array}{l}{G}_{-1}=2{(\alpha Z{m}_{\mu }^{\prime })}^{\frac{3}{2}}{e}^{-\alpha Z{m}_{\mu }^{\prime }r},\\ F_{-1}=0.& (13)\end{array}$

Alternatively, we can reconstruct a realistic bound-muon wave function by solving from the Dirac wave equations the large, G₋₁, and small, F₋₁, parts of the wave function (9) in the Coulomb field created by the nucleus. If we assume that the muon is in the lowest state 1s_1/2 (κ = −1), the components satisfy the coupled differential equations (see, e.g., [23], but note that they use different notations for the large and small parts)

$\begin{array}{ll}\{\begin{array}{c}\frac{\text{d}}{\text{d}r}{G}_{-1}+\frac{1}{r}{G}_{-1}=\frac{1}{\hslash c}(m{c}^2-E+V(r))F_{-1},\hfill \\ \frac{\text{d}}{\text{d}r}{F}_{-1}-\frac{1}{r}{F}_{-1}=\frac{1}{\hslash c}(m{c}^2+E-V(r))G_{-1}.\hfill \end{array}\hfill & (14)\end{array}$

Assuming finite nuclear size and uniform distribution of the nuclear charge within a charge radius $R_c=r_0{A}^{1/3}$ with r₀ = 1.2 fm, the potential energy V(r) in Equation (14) can be written in the form

$\begin{array}{ll}V(r)=\{\begin{array}{cc}\frac{(Z-1)e^2}{2R_c}\left[3-{\left(\frac{r}{R_c}\right)}^2\right],\hfill & \text{if }r\le R_c\hfill \\ \frac{(Z-1)e^2}{r},\hfill & \text{if }r>R_c,\hfill \end{array}\hfill & (15)\end{array}$

similarly as in [15, 16, 24] in the case of bound-electron wave functions in the context of double beta decay. Equation (14) can then be solved by means of the package RADIAL [25] by using a piecewise-exact power-series expansion of the radial functions, which then are summed up to a prescribed accuracy.

In Figure 2, we compare the large component, G₋₁, of the bound-muon wave function, computed using this method (blue line), with the approximate wave function (black line) of Equation (13). For the sake of comparison, we have also plotted the exact solution of the Dirac equation corresponding to point-like nucleus (red line). The exact solution for the point-like nucleus is notably close to the Bethe-Salpeter approximation, whereas the finite-size-nucleus solution differs significantly from the point-like-nucleus solution, especially at r ≤ 7 fm.

FIGURE 2

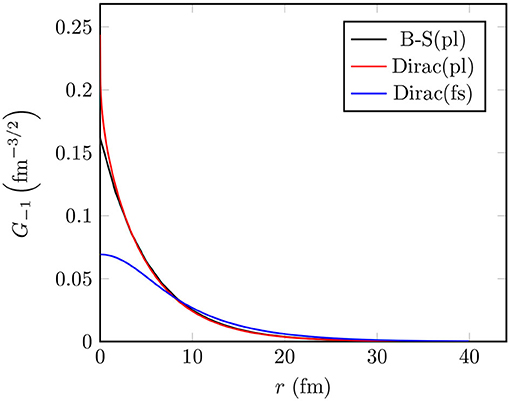
Figure 2. The large component, G₋₁, of the bound-muon wave function in ¹⁰⁶Cd. Here “B-S” refers to the Bethe-Salpeter approximation formula and “Dirac” to the wave function obtained by solving the Dirac equation. Furthermore, “pl” refers to a point-like nucleus and “fs” to a finite-size nucleus.

4.2. Muon-Capture Matrix Elements

We compute the OMC matrix elements using the formalism that was originally developed by Morita and Fujii [21]. This formalism takes into account both the genuine and induced vector and axial-vector weak nucleon currents. The OMC rate from a J_i initial state to a J_f final state can be written as

$\begin{array}{ll}W=2\pi {\langle |\text{M}.\text{E}.{|}^2\rangle }_{av}{q}^2\frac{dq}{d{E}_f},& (16)\end{array}$

where

$\begin{array}{ll}\frac{dq}{d{E}_f}=\left[1-\frac{q}{m_{\mu }+AM}\right]& (17)\end{array}$

and the Q-value of the OMC process can be computed from

$\begin{array}{ll}q=(m_{\mu }-W_0)\left(1-\frac{m_{\mu }-W_0}{2(M_f+m_{\mu })}\right),& (18)\end{array}$

where W₀ = M_f −M_i+m_e+E_X [21]. Here M_f (M_i) is the nuclear mass of the final (initial) nucleus, m_e the rest mass of an electron and E_X the excitation energy of the final J^π state. The expectation value in Equation (16) can be written as

$\begin{array}{l}{\langle |\text{M}.\text{E}.{|}^2\rangle }_{av}=\frac{2J_f+1}{(2j^{\prime }+1)(2J_i+1)}\\ \times {\displaystyle \sum _{ij}}{\displaystyle \sum _{\kappa u}}{\left[{\displaystyle \sum _{\nu }}{C}^{(i)}{{M}}_{\nu u}^{(i)}\right]}^{*}\left[{\displaystyle \sum _{{\nu }^{\prime }}}{C}^{(j)}{{M}}_{{\nu }^{\prime }u}^{(j)}\right],& (19)\end{array}$

where j′ is the angular momentum of the bound muon. The definitions of the matrix elements ${{M}}_{\nu u}^{(i)}$ and the corresponding coefficients C⁽ⁱ⁾ can be found in Table 5.1 of [26] (or in Table 1 of [21]). However, note that we use different notation for the coupling constants.

The factors C⁽ⁱ⁾ contain the usual weak vector and axial-vector couplings g_V ≡ g_V(q) and g_A ≡ g_A(q) at finite momentum transfer q > 0. The conserved vector current (CVC) and partially conserved axial-vector current (PCAC) hypotheses give the values g_V(0) = 1.00 and g_A(0) = 1.27 for a free nucleon at zero momentum transfer, and for finite momentum transfer we can use the dipole approximation [27]. For the induced pseudoscalar coupling g_P the Goldberger-Treiman PCAC relation [28] gives g_P/g_A = 7.0. However, at zero momentum transfer deviations from the CVC and PCAC values have been obtained in several analyses [29–32].

The matrix elements ${{M}}_{\nu u}^{(i)}$ in Equation (19) consist of radial integrals of different integrands containing spherical harmonics, geometric factors and components of neutrino and muon wave functions. The different terms are listed in Table 5.1 of [26]. We assume that the muon is bound on the κ = −1 orbit and that the small component of the bound muon wave function is negligible, which simplifies the expressions of the matrix elements notably [see Equation (5.26) and Table 5.2 of [26] for the Bethe-Salpeter approximation and Equation (5.37) and Table 5.3 for a general muon wave function].

Here we define an average OMC matrix element as

$\begin{array}{ll}|M^{(\mu )}{|}_{av}=\sqrt{{\langle |\text{M}.\text{E}.{|}^2\rangle }_{av}}& (20)\end{array}$

and compare this quantity, instead of OMC rate, with the 0νβ⁺β⁺-decay NME in order to reduce the phase-space effects.

In this work we choose the slightly quenched values of $g_{\text{A}}(0)=g_{\text{A}}^{\text{eff}}=1.0$ and g_P(0) = 7.0 and keep the CVC value g_V(0) = 1.0 for all the studied cases. In general, OMC serves as a probe of the effective values of these parameters at the momentum-exchange region g ≈ 100 MeV, which is particularly relevant for 0νββ decay. These parameter values could be constrained by the measured capture rates to individual excited nuclear states, especially in light nuclei which are well-described by shell-model and different ab initio methods. However, for the lack of the OMC data on the OMC in ¹⁰⁶Cd, this is not possible in the present study.

5. Spherical Proton-Neutron QRPA and Its Hamiltonian Parameters

The results reported in the present study are based on a spherical proton-neutron quasiparticle random-phase approximation (pnQRPA), which describes nuclear excitations in odd-odd nuclei (such as ¹⁰⁶Ag) as proton-neutron quasiparticle pairs. In order to reach wide region of excitation-energies up to 50 MeV, we use large no-core single-particle bases consisting of proton and neutron states from the 0s−0p−1s−0d−1p−0f−2s−1d−0g−2p−1f−0h−1g−0i oscillator shells. As a starting point, the single-particle energies were generated by a spherical Coulomb-corrected Woods-Saxon (WS) potential with the parametrization of [33]. This basis is denoted as “WS” in this study. Furthermore, we modified the WS energies in the same way as in [34] in order to better reproduce the spectra of the neighboring odd-A nuclei. This basis, in turn, is denoted by “Adj.”.

For the muon-capture calculations, we generate the pnQRPA excitations in ¹⁰⁶Ag starting from the even-even mother nucleus, ¹⁰⁶Cd. As for the 0νβ⁺β⁺ decay, we generate two sets of pnQRPA excitations for each J^π multipole—one based on the mother nucleus ¹⁰⁶Cd, and one based on the daughter nucleus ¹⁰⁶Pd. We call these sets the right- and left-hand pnQRPA sets, correspondingly. In the 0νβ⁺β⁺-decay calculations, we then use the average of the left- and right-hand-side excitation energies as the excitation energy of a given intermediate state. We also take into account the overlap of these two sets in the definition of the matrix element.

The quasiparticle spectra for protons and neutrons, needed in the pnQRPA diagonalization, are obtained by solving the BCS equations for protons and neutrons in the even-even reference nuclei. The calculated BCS pairing gaps are adjusted to the phenomenological proton and neutron pairing gaps in a way described in detail in [35].

The X and Y amplitudes in the pnQRPA equations are calculated by diagonalizing the pnQRPA matrix separately for each multipole J^π. We adopt as the two-body interaction the one derived from the Bonn-A one-boson-exchange potential, introduced in [36]. The particle-hole part was scaled by a common factor g_ph fixed by fitting the centroid of the Gamow-Teller giant resonance (GTGR) in the 1⁺ channel of the calculations.

As for the particle-particle parameter g_pp, we follow the partial isospin-restoration scheme introduced in [37], and multiply the isoscalar (T = 0) and isovector (T = 1) parts of the particle-particle G-matrix elements by factors $g_{\text{pp}}^{(T=0)}$ and $g_{\text{pp}}^{(T=1)}$, respectively. The isovector parameter $g_{\text{pp}}^{(T=1)}$ is adjusted such that the Fermi part of the corresponding two-neutrino double beta (2νβ⁺β⁺) NME vanishes, leading to partial isospin-symmetry restoration. Usually, for the 2νβ⁻β⁻ decays, the value of the isoscalar parameter $g_{\text{pp}}^{(T=0)}$ is determined by fitting the corresponding experimental half-life. Here we do not have a measured half-life and the corresponding experimental NME available (see Table 1) so that the value of $g_{\text{pp}}^{(T=0)}$ is a matter of choice. In this work we choose to adopt the rather wide range of values $g_{\text{pp}}^{(T=0)}=0.6-0.8$ for this parameter, where the upper limit is at a safe distance from the collapse point of the pnQRPA for both single-particle bases.

All the parameter values resulting from the above-described procedures are listed in Table 2.

TABLE 2

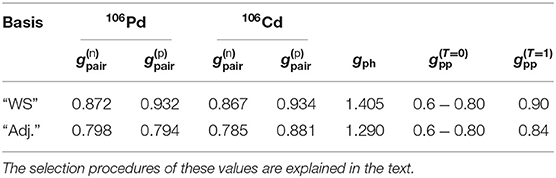
Table 2. Adopted values of the pairing parameters of the BCS and the particle-hole and particle-particle parameters of the pnQRPA.

6. Results

In order to investigate the possibility of using the OMC as a probe of 0νββ decay, we have studied the 0νβ⁺β⁺-decay matrix elements and the average OMC matrix elements of ¹⁰⁶Cd in the pnQRPA framework in detail. The results are presented in the following subsections. In order to make the comparison between the two processes meaningful, we need to adjust the excitation energies in ¹⁰⁶Ag (being the intermediate nucleus of 0νβ⁺β⁺ decay and the final nucleus of OMC) in a consistent manner. For muon capture, the excitation energy of the lowest pnQRPA excited state for each J^π multipole is adjusted to the measured excitation energy, when available. For the 0νβ⁺β⁺ decay we adjust the right-hand pnQRPA set of states in a similar manner. Hence, we can compare the two processes as a function of the excitation energy in ¹⁰⁶Ag in a consistent way.

6.1. Multipole Decompositions of the Total 0νββ-Decay and OMC Matrix Elements

In contrast to the 2νββ decay which has only the J^π = 1⁺ states active in the process, in the case of the 0νββ decay all the multipole states J^π of the intermediate nucleus are active. On the other hand, in the OMC the large mass of the captured muon allows highly forbidden transitions to all possible J^π final states up to highest excitation energy. Hence, by studying the OMC on relevant nuclei, one can access the intermediate states of 0νββ decay by complementary means. In this section we investigate the multipole decompositions of the 0νβ⁺β⁺-decay and OMC matrix elements.

In Figures 3, 4, we show the multipole decompositions of the total 0νβ⁺β⁺-decay NME and the average OMC matrix element of ¹⁰⁶Cd, respectively. The compositions correspond to the parameter value $g_{\text{pp}}^{(T=0)}=0.7$, which is at a safe distance from the pnQRPA breaking point. In the case of the 0νβ⁺β⁺ decay, the 1⁺ multipole plays a dominant role both for the bare Woods-Saxon basis and for the adjusted basis. This ensues from the dominating role of the Gamow-Teller type of transitions. The 1⁻ contribution is the second largest, whereas the 0⁺ and 0⁻ contributions are negligible. The contributions coming from the higher multipoles decrease rather smoothly as a function of J.

FIGURE 3

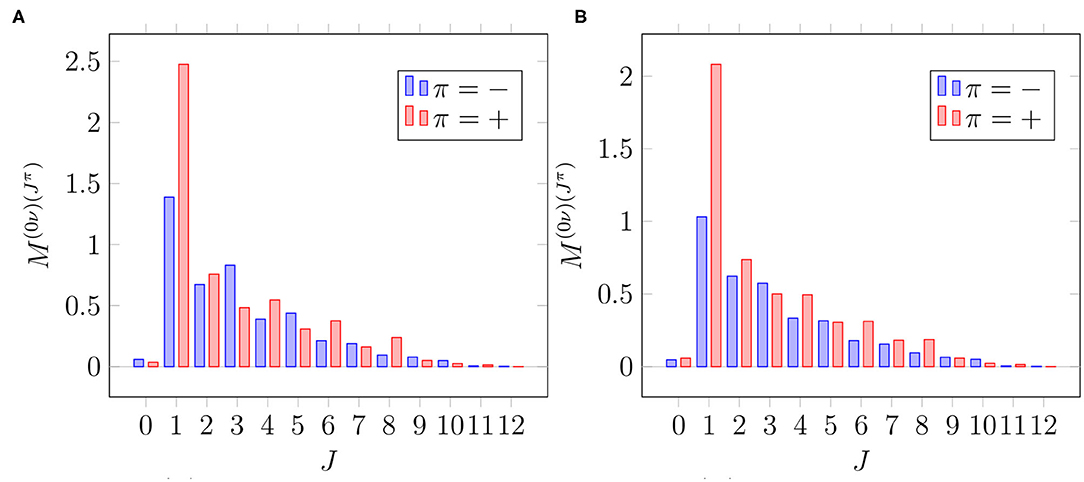
Figure 3. Multipole decomposition of the total 0νβ⁺β⁺-decay matrix element in different single-particle bases. The decompositions correspond to the parameter value $g_{\text{pp}}^{(T=0)}=0.7$. (A) Basis: “Adj.”. (B) Basis: “WS”.

FIGURE 4

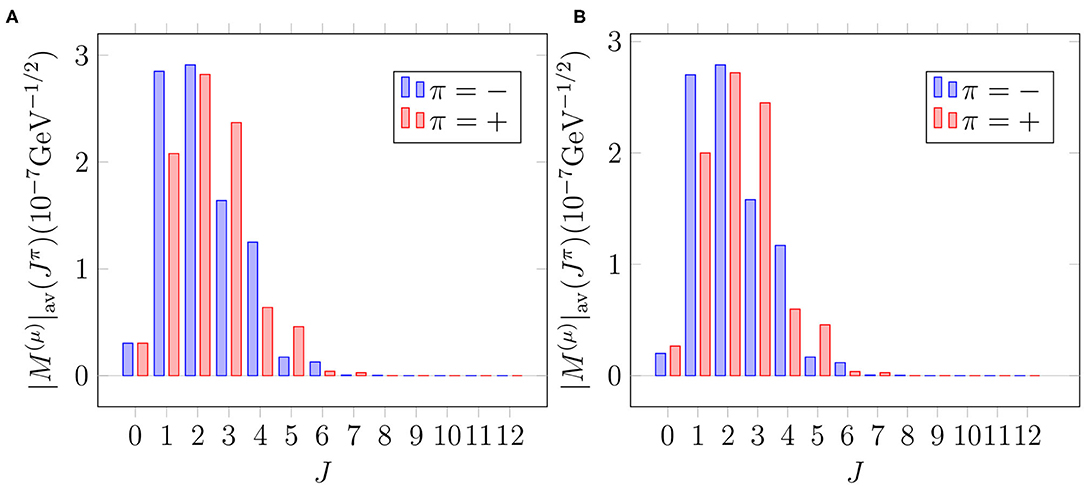
Figure 4. Multipole decomposition of the total OMC matrix element in different single-particle bases. Here we have used the bound muon wave function solved from the Dirac equation. The decompositions correspond to the parameter value $g_{\text{pp}}^{(T=0)}=0.7$. Note that the unit and scale of the matrix element comes from our definition of the average OMC matrix element (20). For more information, see the text and [26]. (A) Basis: “Adj.”. (B) Basis: “WS”.

As for the muon capture (see Figure 4), the major part of the average matrix element consists of transitions to the states with 1 ≤ J ≤ 4, the leading multipoles being those with J^π = 2⁻, 2⁺, 1⁻, and 3⁺. In contrast to 0νβ⁺β⁺ decay, the strength is more evenly distributed among the few leading multipoles. On the other hand, the multipoles with J ≥ 6 play a minor role compared with the 0νβ⁺β⁺ decay.

6.2. Dependence of the Matrix Elements on the Single-Particle Bases and g_pp

As mentioned in section 5, the particle-particle strength parameter g_pp strongly affects the ββ-decay rates. In the muon-capture studies of e.g., [38, 39] it was found that g_pp affects also the muon capture rates. Hence, in this section we study the effect of g_pp on both the 0νβ⁺β⁺-decay and OMC matrix elements of ¹⁰⁶Cd in detail. The exploration also paves the way for possible future adjustments of g_pp using, e.g., the shape of the OMC strength function.

The total 0νβ⁺β⁺-decay NME of ¹⁰⁶Cd is plotted as a function of the isoscalar part of the particle-particle parameter $g_{\text{pp}}^{(T=0)}$ in different single-particle bases in Figure 5. For the isovector part $g_{\text{pp}}^{(T=1)}$, we adopt the value that was adjusted so that the Fermi part of the 2νβ⁺β⁺-decay NME vanishes, as explained in section 5. It is evident from the plots that the value of M^(0ν) is sensitive to the value of $g_{\text{pp}}^{(T=0)}$: increasing $g_{\text{pp}}^{(T=0)}$ decreases the value of the matrix element. In both bases, varying g_pp from 0.6 to 0.8 reduces the value of M^(0ν) by some 25%. Hence, constraining the value of g_pp is of utmost importance in the 0νβ⁺β⁺-decay studies. In the absence of a measured 2νβ⁺β⁺-decay half-life, adjusting g_pp to OMC data, once measured, would help reduce the large uncertainty related to g_pp. It is seen that in the adjusted (“Adj.”) basis, the matrix element is consistently about 20% larger than in the bare Woods-Saxon (“WS”) basis. It is to be noted that soon after the $g_{\text{pp}}^{(T=0)}$ values shown in the x axis, between $g_{\text{pp}}^{(T=0)}0.82-0.84$, depending on the single-particle basis, the ground state of pnQRPA collapses and the value of M^(0ν) blows up: the value rapidly increases by some 10%. Since the values after the pnQRPA breaking point are not physically meaningful, they are not shown in the figure.

FIGURE 5

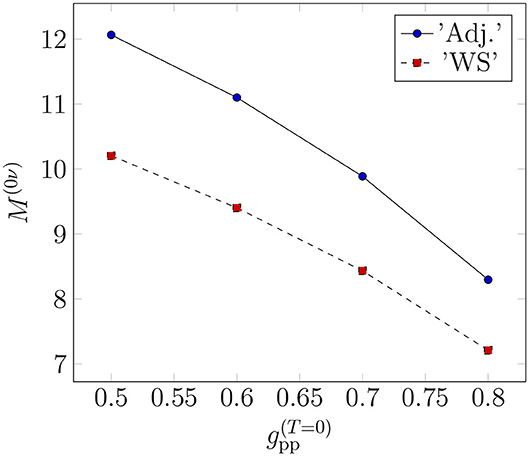
Figure 5. Dependence of the 0νβ⁺β⁺-decay NME on the isoscalar part of the particle-particle parameter g_pp in the two different single-particle bases.

In Figure 6, we plot the average OMC matrix element $|M^{(\mu )}{|}_{\text{av}}$ as a function of $g_{\text{pp}}^{(T=0)}$. Contrary to the 0νβ⁺β⁺-decay NME, the OMC matrix element is not sensitive to the small adjustments of the single-particle bases or to the value of the $g_{\text{pp}}^{(T=0)}$ between $g_{\text{pp}}^{(T=0)}=0.5-0.8$. Instead, after $g_{\text{pp}}^{(T=0)}=0.8$, close to the pnQRPA breaking point, the average OMC matrix element becomes unstable. On the other hand, the value of the average OMC matrix element is much more dependent on the bound-muon wave function: the use of the Bethe-Salpeter approximation results in about three times larger values than those obtained with the exact Dirac wave function.

FIGURE 6

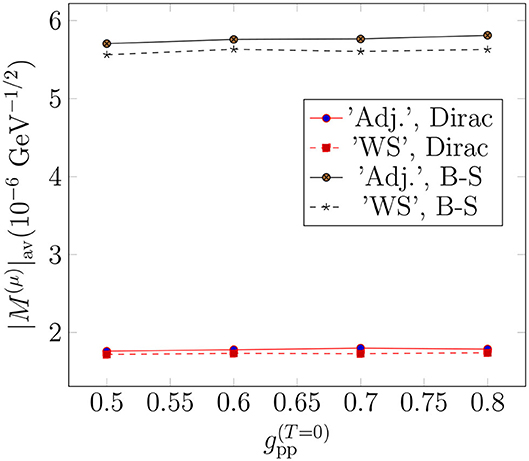
Figure 6. Dependence of the average OMC matrix element on the isoscalar part of the particle-particle parameter g_pp in the two different single-particle bases, and for the exact Dirac finite-nucleus and approximate Bethe-Salpeter point-like-nucleus bound-muon wave functions.

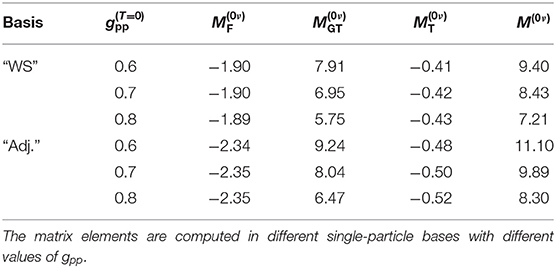
The different parts of the 0νβ⁺β⁺-decay NMEs in different single-particle bases in the adopted ranges of the parameter $g_{\text{pp}}^{(T=0)}$ (see Table 2) are listed in Table 3. In Table 4, we list the corresponding values obtained in [14] in a smaller single-particle basis, which corresponds to the “Adj.” basis in the present study. In [14], the NMEs were computed by the use of Jastrow [18] and UCOM [19] short-range correlations.

TABLE 3

Table 3. Nuclear matrix elements for 0νβ⁺β⁺ decay of ¹⁰⁶Cd corresponding to $g_{\text{A}}(0)=g_{\text{A}}^{\text{eff}}=1.0$.

TABLE 4

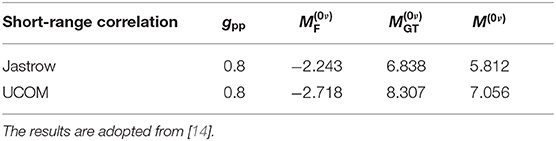
Table 4. Nuclear matrix elements for 0νβ⁺β⁺ decay of ¹⁰⁶Cd corresponding to $g_{\text{A}}(0)=g_{\text{A}}^{\text{eff}}=1.0$ in the single-particle bases used in [14], corresponding to the “Adj.” basis of the present study.

The total 0νβ⁺β⁺-decay NMEs computed in the present study (Table 3) are consistently larger than those computed in the smaller, core-based single-particle bases, used in [14]. The values computed with the UCOM short-range correlations are closer to the values computed in the present study, which is natural since the presently adopted short-range correlations are a parametrization of the UCOM correlator. The dependence of the NMEs on the size of the single-particle bases is in accordance with the findings of our previous work [40], where we noticed that the size of the single-particle bases affects the 0νβ⁻β⁻-decay NMEs much more than the different adjustment procedures of the particle-hole parameter g_ph of the pnQRPA. This is most likely due to the fact that in the smaller bases we cannot reach the highly-excited intermediate states which play a non-negligible role in the 0νββ-decay process.

According to Figures 3, 4 the multipoles J^π = 1⁺ and 2⁺ are among the leading ones for both the 0νβ⁺β⁺-decay and OMC matrix elements of ¹⁰⁶Cd. Hence, it is illuminating to study the effect of g_pp on these multipoles in more detail. In Figures 7, 8 we plot the total 0νβ⁺β⁺-decay NME on the positive y axis and the average OMC matrix element on the negative y axis in the cases of J^π = 1⁺ and 2⁺, respectively. We decompose the average OMC NME for the J^π = 1⁺, 2⁺ multipole states within MeV energy bins while for the 0νβ⁺β⁺ decay the energy-multipole decomposition entails division of the NMEs into multipoles J^π = 1⁺, 2⁺ and their energy distributions binned by MeV-energy intervals. We have chosen to plot only the absolute values of the matrix elements since they carry the essential information needed in the present comparison of the basic features of the OMC and 0νβ⁺β⁺ decay.

FIGURE 7

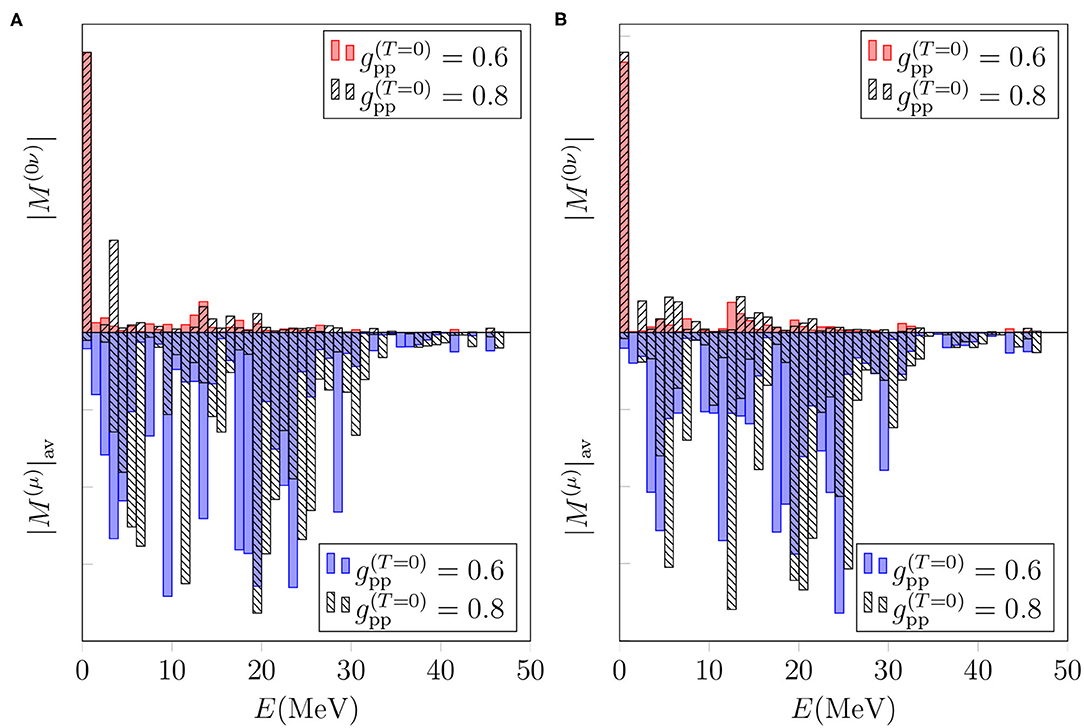
Figure 7. Dependence of the energy distributions of the 0νβ⁺β⁺-decay and OMC matrix elements for the J^π = 1⁺ multipole on the particle-particle parameter $g_{\text{pp}}^{(T=0)}$ in different bases. The OMC matrix elements are computed assuming the exact Dirac wave functions for a finite nucleus with uniform charge distribution. (A) Basis: “Adj.”. (B) Basis: “WS”.

FIGURE 8

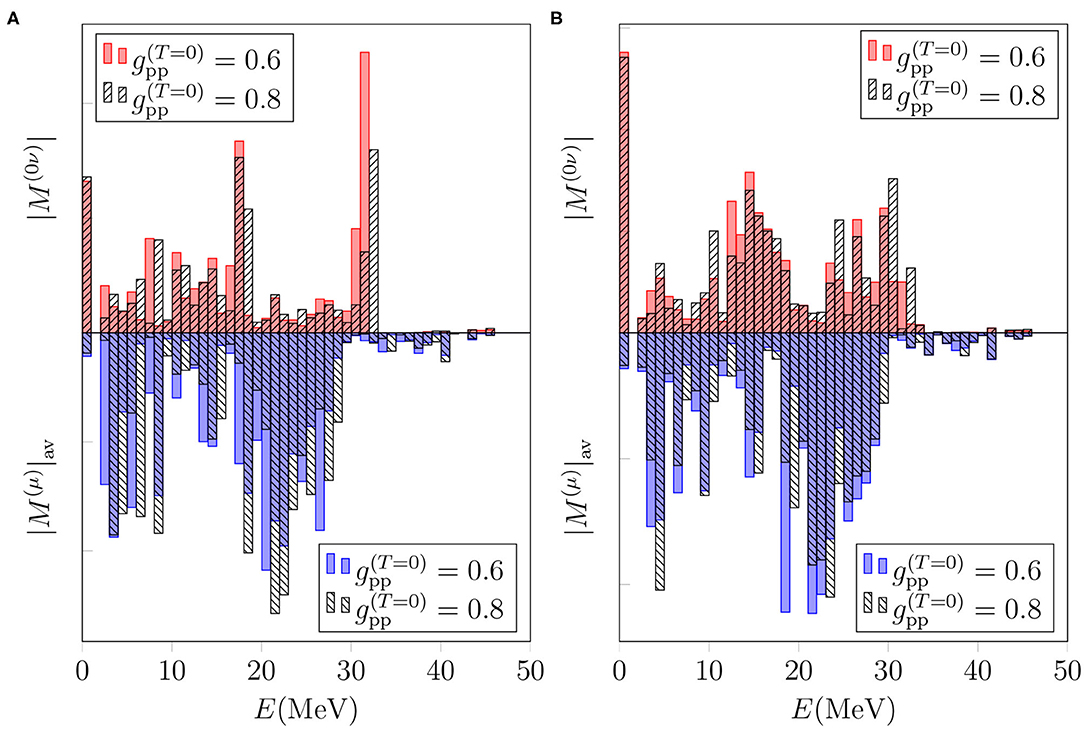
Figure 8. Dependence of the energy distributions of the 0νβ⁺β⁺-decay and OMC matrix elements for the J^π = 2⁺ multipole on the particle-particle parameter $g_{\text{pp}}^{(T=0)}$ in different bases. The OMC matrix elements are computed assuming the exact Dirac wave functions for a finite nucleus with uniform charge distribution. (A) Basis: “Adj.”. (B) Basis: “WS”.

Figures 7, 8 show similar behavior for both the multipoles J^π = 1⁺ and 2⁺: decreasing the value of $g_{\text{pp}}^{(T=0)}$ from 0.8 to 0.6 shifts the spectrum to lower energies for both the 0νβ⁺β⁺ decay and OMC. Note that the present comparison does not reflect the results of Figure 5, since here we are considering the absolute values of the 0νβ⁺β⁺-decay NME for each bin. However, these figures show that even though the average OMC matrix element is quite independent of the value of g_pp, the shape of the OMC spectrum depends on g_pp. This, in turn, raises interest of studying the possibility of adjusting g_pp to the locations of OMC giant resonances, once measured.

6.3. Dependence of the OMC Matrix Elements on the Bound-Muon Wave Function

As mentioned in section 4.1, the OMC matrix elements have usually been computed by approximating the bound-muon wave function by a point-like-nucleus approximation. In our previous works [13, 41, 42] we used the Bethe-Salpeter point-like-nucleus approximation formula for the muon wave function. Here we study the effect of the exact muon wave function, solved from the Dirac equation by taking into account the finite size of the nucleus with uniform charge distribution, on the OMC matrix elements. The effects of the two muon wave functions (see Figure 2) on the OMC matrix element are clearly seen in Figure 6, where the g_pp dependence of the OMC matrix element is displayed in the two different single-particle bases and for the exact Dirac finite-nucleus and approximate Bethe-Salpeter point-like-nucleus bound-muon wave functions. The difference between the matrix elements is considerable. However, one has to keep in mind that in the OMC-rate calculations this difference is to a major part compensated by the use of a phenomenological effective charge Z_eff (the so-called Primakoff approximation [43]) in the calculations using the Bethe-Salpeter approximation.

Next we study the effect of the different bound-muon wave functions on the multipole decomposition of the average OMC matrix elements in the cases of the multipoles J^π = 1⁺, 2⁺, which are among the leading ones for both the 0νβ⁺β⁺ decay and the OMC. In Figures 9, 10 we plot the energy-decompositions of the average OMC matrix element for the transitions to J^π = 1⁺ and 2⁺ states, respectively. In both figures, the Bethe-Salpeter point-like-nucleus approximation (blue bars) results in notably larger values of the average OMC matrix element than the Dirac wave function (black and white bars). All in all, the use of the Dirac wave function results in about 50–60% reduction of the matrix elements in all the energy bins. This makes sense, since looking at Figure 2, especially at r ≤ 7 fm, the behavior of the Dirac wave function, taking into account the finite size of the nucleus, differs significantly from the Bethe-Salpeter approximation. The finding is also in keeping with results for the total OMC matrix element, depicted in Figure 6.

FIGURE 9

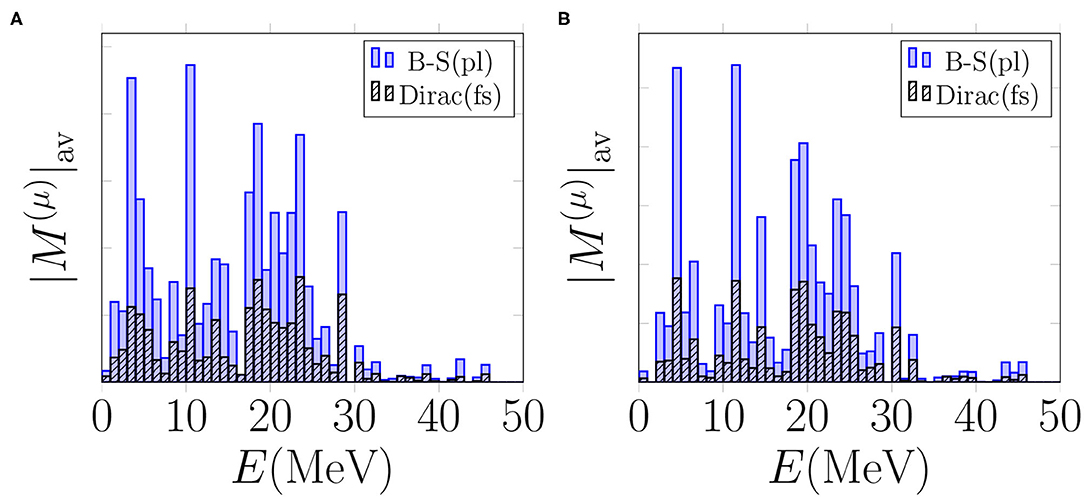
Figure 9. Average OMC matrix elements for the captures to J^π = 1⁺ states computed with different bound-muon wave functions. “B-S(pl)” denotes the Bethe-Salpeter point-like-nucleus approximation and “Dirac(fs)” the exact wave function solved from the Dirac equation taking into account the finite size of the nucleus. The value $g_{\text{pp}}^{(T=0)}=0.7$ is adopted for particle-particle interaction parameter. (A) Basis: “Adj.”. (B) Basis: “WS”.

FIGURE 10

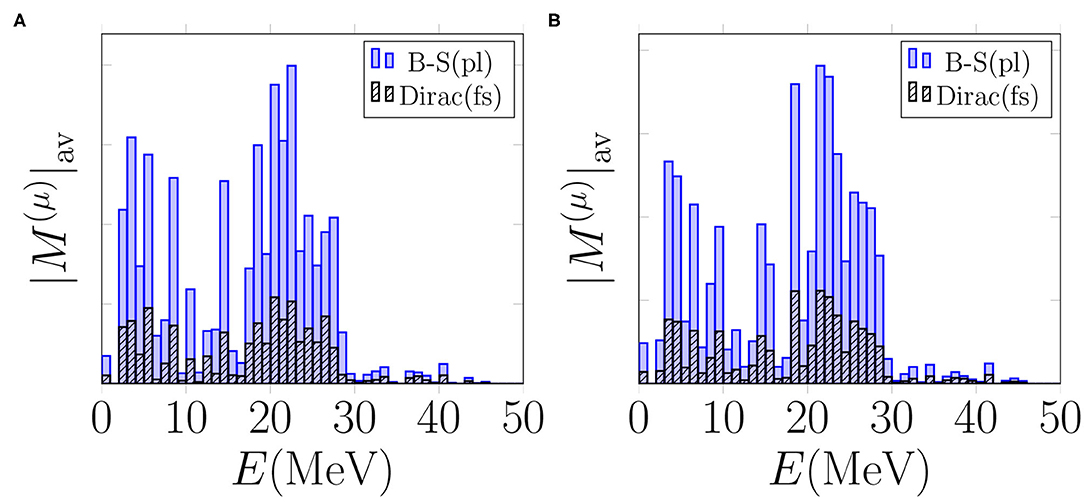
Figure 10. Average OMC matrix elements for the captures to J^π = 2⁺ states computed with different bound-muon wave functions. “B-S(pl)” denotes the Bethe-Salpeter point-like-nucleus approximation and “Dirac(fs)” the exact wave function solved from the Dirac equation taking into account the finite size of the nucleus. The value $g_{\text{pp}}^{(T=0)}=0.7$ is adopted for particle-particle interaction parameter. (A) Basis: “Adj.”. (B) Basis: “WS”.

6.4. Comparison of the 0νβ⁺β⁺ and OMC Matrix Elements

Here we finally compare the absolute values of the 0νβ⁺β⁺-decay and average OMC matrix elements in the same manner as in [13]. We analyze the summed absolute values of the matrix elements in the same way as we did in Figures 7, 8. We plot the summed absolute values of the 0νβ⁺β⁺-decay NMEs and the average OMC matrix elements for J^π = 0⁺, 1⁺, 2⁺, 3⁺, 4⁺, 1⁻, 2⁻, 3⁻, and 4⁻ in Figure 11. The matrix elements are computed in the adjusted Woods-Saxon basis (“Adj.”) with the parameter value $g_{\text{pp}}^{(T=0)}=0.7$. The OMC matrix elements are computed with the exact Dirac muon wave function.

FIGURE 11

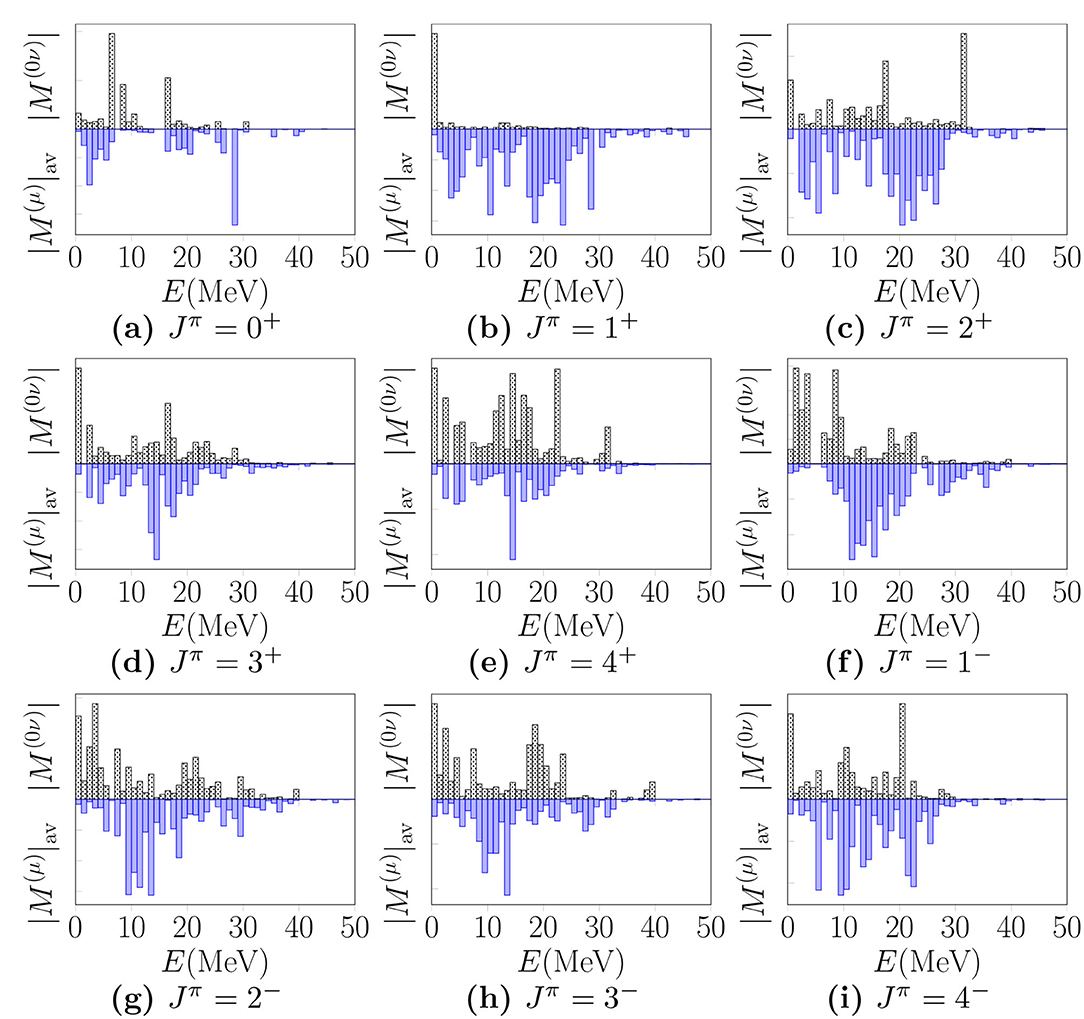
Figure 11. Multipole decompositions in terms of relative 0νβ⁺β⁺-decay matrix elements (positive y axes) and average matrix elements of the OMC (negative y axes) for ¹⁰⁶Cd as functions of the excitation energy E in the intermediate nucleus (¹⁰⁶Ag) of the 0νβ⁺β⁺ decay of ¹⁰⁶Cd. These matrix elements correspond the adjusted Woods-Saxon basis and $g_{\text{pp}}^{(T=0)}=0.7$. For the bound-muon wave function we have used the realistic exact wave function solved from the Dirac equation. Here J^π refer to the angular momenta and parities of the virtual states in ¹⁰⁶Ag and all quantities have been summed within 1 MeV energy bins. The subfigures represent different J^π values. The scale values of the y axes have been omitted, since they are not relevant for the current analysis. For more information see the text.

Looking at Figure 11, one can see clear correspondences between the 0νβ⁺β⁺-decay and OMC matrix elements, especially in the cases of J^π = 3⁺ (Figure 11D), J^π = 4⁺ (Figure 11E) and J^π = 4⁻ (Figure 11I). This observation is in accordance with our earlier study in the 0νβ⁻β⁻ side of double beta decays [13]. There are also notable similarities in the distributions corresponding to multipoles J^π = 2⁻ (Figure 11G) and J^π = 3⁻ (Figure 11H). For the rest of the multipoles, the correspondencies are not so well visible. Especially, in the case of J^π = 1⁺ (Figure 11B), the major part of the 0νβ⁺β⁺-decay NME is coming from the first energy bin E ≤ 1 MeV, while the OMC distribution is clearly more spread to higher energies. This is also the most notable difference between the present results and those of our earlier study [13], where the 1⁺ contributions to the 0νβ⁻β⁻-decay matrix elements were more evenly distributed to higher excitation energies.

7. Discussion

Double beta decay is one of the most intensively studied topics in neutrino, nuclear and particle physics. While the ordinary two-neutrino double beta decay mode has been observed in several isotopes, the neutrinoless decay mode remains hypothetical. Most of the observed decays are of β⁻β⁻ type, and there are only six isotopes known to be capable of β⁺β⁺ decaying. Here we have studied a particularly promising candidate: ¹⁰⁶Cd, for which currently only the lower limit of the 2νβ⁺β⁺-decay half-life has been extracted experimentally.

In the present work, we have made a comparative analysis of the 0νβ⁺β⁺-decay and average OMC matrix elements of ¹⁰⁶Cd in the pnQRPA framework using large no-core single-particle bases. This comparison is the first ever done on the positron-emission side of the nuclear chart, and could potentially help improve the accuracy of the 0νβ⁺β⁺-decay matrix elements once access to the data of future muon-capture experiments is gained. In particular, adjusting the g_pp parameter to future data on OMC giant resonances could help reducing the sizeable uncertainty related to the unknown value of g_pp.

Analysis of the multipole decompositions of the total 0νβ⁺β⁺-decay matrix element and the average OMC matrix element shows that the J^π = 1⁺ multipole has a dominating role in the 0νβ⁺β⁺-decay process, while the total OMC matrix element is more evenly distributed to a few leading multipoles. The multipoles J^π = 1⁺ and 2⁺ play a major role in both processes, hence we have studied the transitions involving those multipoles in more detail: we have studied the effect of different particle-particle parameter values on both the 0νβ⁺β⁺-decay and the OMC matrix elements, and the effect of different bound-muon wave functions on the OMC matrix elements in these cases.

Our studies indicate that the 0νβ⁺β⁺-decay matrix element of ¹⁰⁶Cd strongly depends on the value of the isovector part $g_{\text{pp}}^{(T=0)}$ of the particle-particle interaction parameter of pnQRPA. Contrary to this, the average value of the OMC matrix element is less dependent on the $g_{\text{pp}}^{(T=0)}$. However, near the pnQRPA breaking point the average OMC matrix element becomes unstable and grows fast in magnitude. Furthermore, when comparing the 0νβ⁺β⁺-decay matrix elements of the present work with those computed in (much) smaller single-particle bases in [14], we noticed that the matrix elements are sensitive to the size of the single-particle basis. This observation is in accordance with our earlier work on the β⁻β⁻ type of decays [13].

Finally, we compared the energy distributions of the multipole-decomposed 0νβ⁺β⁺-decay matrix elements and the average OMC matrix elements, computed in the adjusted Woods-Saxon single-particle basis. We identified a clear correspondence between the absolute values of the 0νβ⁺β⁺-decay and OMC multipole contributions, especially in the cases of the J^π = 3⁺, 4⁺, and 4⁻ multipoles. This finding is in accordance with our previous work [13], where we compared the energy distributions of the multipole-decomposed 0νβ⁻β⁻-decay and OMC matrix elements for several 0νβ⁻β⁻-decay triplets in a similar manner.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This work has been partially supported by the Academy of Finland under the Academy project no. 318043. JK has been supported by the Academy of Finland, Grant Nos. 314733 and 320062.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Blaum K, Eliseev S, Danevich FA, Tretyak VI, Kovalenko S, Krivoruchenko MI, et al. Neutrinoless double-electron capture. Rev Mod Phys. (2020) 92:045007. doi: 10.1103/RevModPhys.92.045007

CrossRef Full Text | Google Scholar

2. Aharmin B, Ahmed SN, Amsbaugh JF, Anthony AE, Banar J, Barros N, et al. Independent measurement of the total active 8B solar neutrino flux using an array of 3He proportional counters at the sudbury neutrino observatory. Phys Rev Lett. (2008) 101:111301. doi: 10.1103/PhysRevLett.101.111301

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Abe K, Haga Y, Hayato Y, Ikeda M, Iyogi K, Kameda J, et al. Solar neutrinomeasurements in Super-Kamiokande-IV. Phys Rev D. (2016) 94:052010. doi: 10.1103/PhysRevD.94.052010

CrossRef Full Text | Google Scholar

4. Abe K, Amey J, Andreopoulos C, Antonova M, Aoki S, Ariga A, et al. Combined analysis of neutrino and antineutrino oscillations at T2K. Phys Rev Lett. (2018) 118:151801. doi: 10.1103/PhysRevLett.118.151801

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Ebert J, Fritts M, Gling C, Gfert T, Gehre D, Hagner C, et al. Current status and future perspectives of the COBRA experiment. Adv High Energy Phys. (2013) 2013:703572. doi: 10.1155/2013/703572

CrossRef Full Text | Google Scholar

6. Ebert J, Fritts M, Gehre D, Gling C, Hagner C, Heidrich N, et al. Results of a search for neutrinoless double-β decay using the COBRA demonstrator. Phys Rev C. (2016) 94:024603. doi: 10.1103/PhysRevC.94.024603

CrossRef Full Text | Google Scholar

7. Rukhadze NI, Brianon C, Brudanin VB, ermk P, Egorov VG, Klimenko AA, et al. Experiment TGV-2-search for double beta decay of ¹⁰⁶Cd. Nucl Phys B. (2012) 229:232–478. doi: 10.1016/j.nuclphysbps.2012.09.115

CrossRef Full Text | Google Scholar

8. Belli P, Bernabei R, Brudanin VB, Cappella F, Caracciolo V, Cerulli R, et al. Search for double beta decay of ¹⁰⁶Cd with an enriched ¹⁰⁶CdWO₄ crystal scintillator in coincidence with CdWO₄ scintillation counters. Universe. (2020) 2020:182. doi: 10.3390/universe6100182

CrossRef Full Text | Google Scholar

9. Zinatulina D, Brudanin V, Egorov V, Petitjean C, Shirchenko M, Suhonen J, et al. Ordinary muon capture studies for the matrix elements in ββ decay. Phys Rev C. (2019) 99:024327. doi: 10.1103/PhysRevC.99.024327

CrossRef Full Text | Google Scholar

10. Hashim IH, Ejiri H, Shima T, Takahisa K, Sato A, Kuno Y, et al. Muon capture reaction on ¹⁰⁰Mo to study the nuclear response for double-β decay and neutrinos of astrophysics origin. Phys Rev C. (2018) 97:014617. doi: 10.1103/PhysRevC.97.014617

CrossRef Full Text | Google Scholar

11. Hashim IH, Ejiri H. New research project with muon beams for neutrino nuclear responses and nuclear isotopes production. AAPPS Bull. (2019) 29:21–6. doi: 10.22661/AAPPSBL.2019.29.3.21

CrossRef Full Text | Google Scholar

12. Kortelainen M, Suhonen J. Nuclear muon capture as a powerful probe of double-beta decays in light nuclei. J Phys G Nucl Part Phys. (2004) 30:2003–18. doi: 10.1088/0954-3899/30/12/017

CrossRef Full Text | Google Scholar

13. Jokiniemi L, Suhonen J. Comparative analysis of muon-capture and 0νββ-decay matrix elements. Phys Rev C. (2020) 102:024303. doi: 10.1103/PhysRevC.102.024303

CrossRef Full Text | Google Scholar

14. Suhonen J. Neutrinoless double beta decays of ¹⁰⁶Cd revisited. Phys Lett B. (2011) 701:490–5. doi: 10.1016/j.physletb.2011.06.016

CrossRef Full Text | Google Scholar

15. Kotila J, Iachello F. Phase-space factors for double-β decay. Phys Rev C. (2012) 85:034316. doi: 10.1103/PhysRevC.85.034316

CrossRef Full Text | Google Scholar

16. Kotila J, Iachello F. Phase space factors for β⁺β⁺ decay and competing modes of double-β decay. Phys Rev C. (2013) 87:024313. doi: 10.1103/PhysRevC.87.024313

CrossRef Full Text | Google Scholar

17. Hyvärinen J, Suhonen J. Nuclear matrix elements for 0νββ decays with light or heavy Majorana-neutrino exchange. Phys Rev C. (2015) 91:024613. doi: 10.1103/PhysRevC.91.024613

CrossRef Full Text | Google Scholar

18. Miller GA, Spencer JE. A survey of pion charge-exchange reactions with nuclei. Ann Phys. (1976) 100:562. doi: 10.1016/0003-4916(76)90073-7

CrossRef Full Text | Google Scholar

19. Kortelainen M, Civitarese O, Suhonen J, Toivanen J. Short-range correlations and neutrinoless double beta decay. Phys Lett B. (2007) 647:128. doi: 10.1016/j.physletb.2007.01.054

CrossRef Full Text | Google Scholar

20. Šimkovic F, Faessler A, Müther H, Rodin V, Stauf M. 0νββ-decay nuclear matrix elements with self-consistent short-range correlations. Phys Rev C. (2009) 79:055501. doi: 10.1103/PhysRevC.79.055501

CrossRef Full Text | Google Scholar

21. Morita M, Fujii A. Theory of allowed and forbidden transitions in Muon capture reactions. Phys Rev. (1960) 118:606–18. doi: 10.1103/PhysRev.118.606

CrossRef Full Text | Google Scholar

22. Bethe HA, Salpeter EE. Quantum Mechanics of One- and Two-Electron Atoms. New York, NY: Academic Press Inc. (1959).

Google Scholar

23. Tsoulos IG, Kosmas OT, Stavrou VN. DiracSolver: a tool for solving the Dirac Equation (2018). arXiv:1810.13042 [physics.comp-ph]. doi: 10.1016/j.cpc.2018.10.010

CrossRef Full Text | Google Scholar

24. Kotila J, Barea J, Iachello F. Neutrinoless double-electron capture. Phys Rev C. (2014) 89:064319. doi: 10.1103/PhysRevC.89.064319

CrossRef Full Text | Google Scholar

25. Salvat F, Fernández-Varea J, Williamson W Jr. Accurate numerical solution of the radial Schrödinger and Dirac wave equations. Comput Phys Commun. (1995) 90:151–68. doi: 10.1016/0010-4655(95)00039-I

CrossRef Full Text | Google Scholar

26. Jokiniemi L. Probing neutrinoless double-beta decay by charge-exchange reactions and muon capture (JYU Dissertations). University of Jyväskylä, Jyväskylä, Finland (2020).

Google Scholar

27. Ejiri H, Suhonen J, Zuber K. Neutrino-nuclear responses for astro-neutrinos, single beta decays and double beta decays. Phys Rep. (2019) 797:1–102. doi: 10.1016/j.physrep.2018.12.001

CrossRef Full Text | Google Scholar

28. Goldberger ML, Treiman SB. Form factors in β decay and μ capture. Phys Rev. (1958) 111:354. doi: 10.1103/PhysRev.111.354

CrossRef Full Text | Google Scholar

29. Ejiri H. Nuclear matrix elements for β and ββ decays and quenching of the weak coupling g_A in QRPA. Front Phys. (2019) 7:30. doi: 10.3389/fphy.2019.00030

CrossRef Full Text | Google Scholar

30. Suhonen JT. Value of the axial-vector coupling strength in β and ββ decays: a review. Front Phys. (2017) 5:55. doi: 10.3389/fphy.2017.00055

CrossRef Full Text | Google Scholar

31. Kolbe E, Langanke K, Vogel P. Muon capture, continuum random phase approximation, and in-medium renormalization of the axial-vector coupling constant. Phys Rev C. (1994) 50:2576. doi: 10.1103/PhysRevC.50.2576

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Johnson BL, Gorringe TP, Armstrong DS, Bauer J, Hasinoff MD, Kovash MA, et al. Observables in muon capture on ²³Na and the effective weak couplings ga and gp. Phys Rev C. (1996) 54:2714. doi: 10.1103/PhysRevC.54.2714

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Bohr A, Mottelson BR. Nuclear Structure. Vol. 1. New York, NY: Benjamin (1969). doi: 10.1063/1.3022342

CrossRef Full Text | Google Scholar

34. Suhonen J, Civitarese O. Theoretical results on the double positron decay of ¹⁰⁶Cd. Phys Lett B. (2001) 497:221–7. doi: 10.1016/S0370-2693(00)01324-1

CrossRef Full Text | Google Scholar

35. Jokiniemi L, Suhonen J. Isovector spin-multipole strength distributions in double-β-decay triplets. Phys Rev C. (2017) 96:034308. doi: 10.1103/PhysRevC.96.034308

CrossRef Full Text | Google Scholar

36. Holinde K. Two-nucleon forces and nuclear matter. Phys Rep. (1981) 68:121. doi: 10.1016/0370-1573(81)90188-5

CrossRef Full Text | Google Scholar

37. Šimkovic F, Rodin V, Faessler A, Vogel P. 0νββ and 2νββ nuclear matrix elements, quasiparticle random-phase approximation, and isospin symmetry restoration. Phys Rev C. (2013) 87:045501. doi: 10.1103/PhysRevC.87.045501

CrossRef Full Text | Google Scholar

38. Kortelainen M, Suhonen J. Ordinary muon capture as a probe of virtual transitions of ββ decay. Europhys Lett. (2002) 58:666–72. doi: 10.1209/epl/i2002-00401-5

CrossRef Full Text | Google Scholar

39. Šimkovic F, Dvornický R, Vogel P. Muon capture rates: evaluation within the quasiparticle random phase approximation. Phys Rev C. (2020) 102:034301. doi: 10.1103/PhysRevC.102.034301

CrossRef Full Text | Google Scholar

40. Jokiniemi L, Ejiri H, Frekers D, Suhonen J. Neutrinoless ββ nuclear matrix elements using isovector spin-dipole J^π = 2⁻ data. Phys Rev C. (2018) 98:024608. doi: 10.1103/PhysRevC.98.024608

CrossRef Full Text | Google Scholar

41. Jokiniemi L, Suhonen J, Ejiri H, Hashim IH. Pinning down the strength function for ordinary muon capture on ¹⁰⁰Mo. Phys Lett B. (2019) 794:143–7. doi: 10.1016/j.physletb.2019.05.037

CrossRef Full Text | Google Scholar

42. Jokiniemi L, Suhonen J. Muon-capture strength functions in intermediate nuclei of 0νββ decays. Phys Rev C. (2019) 100:014619. doi: 10.1103/PhysRevC.100.014619

CrossRef Full Text | Google Scholar

43. Primakoff H. Theory of muon capture. Rev Mod Phys. (1959) 31:802–22. doi: 10.1103/RevModPhys.31.802

CrossRef Full Text | Google Scholar