- 1Key Laboratory of Polar Materials and Devices (MOE), School of Physics and Electronic Science, East China Normal University, Shanghai, China
- 2Laboratory for Multiscale Materials Experiments, Paul Scherrer Institut, Villigen, Switzerland
- 3Laboratory for Muon-Spin Spectroscopy, Paul Scherrer Institut, Villigen, Switzerland
- 4Laboratorium für Festkörperphysik, ETH Zürich, Zürich, Switzerland
In the recent search for unconventional- and topological superconductivity, noncentrosymmetric superconductors (NCSCs) rank among the most promising candidate materials. Surprisingly, some of them—especially those containing rhenium—seem to exhibit also time-reversal symmetry (TRS) breaking in their superconducting state, while TRS is preserved in many other isostructural NCSCs. To date, a satisfactory explanation for such discrepant behavior, albeit crucial for understanding the unconventional superconductivity of these materials, is still missing. Here we review the most recent developments regarding the Re-based class, where the muon-spin relaxation (μSR) technique plays a key role due to its high sensitivity to the weak internal fields associated with the TRS breaking phenomenon. We discuss different cases of Re-containing superconductors, comprising both centrosymmetric- and noncentrosymmetric crystal structures, ranging from pure rhenium, to ReT (T = 3d-5d early transition metals), to the dilute-Re case of ReBe22. μSR results suggest that the rhenium presence and its amount are two key factors for the appearance and the extent of TRS breaking in Re-based superconductors. Besides summarizing the existing findings, we also put forward future research ideas regarding the exciting field of materials showing TRS breaking.
1 Introduction
The combination of intriguing fundamental physics with far-reaching potential applications has made unconventional superconductors one of the most studied classes of materials. Standing out among them are the noncentrosymmetric superconductors (NCSCs) [1], whose crystal structures lack the inversion symmetry. As a consequence, in NCSCs, the strict symmetry-imposed requirements are relaxed, allowing mixtures of spin-singlet and spin-triplet Copper pairing channels, thus setting the scene for a variety of exotic properties, as e.g., upper critical fields beyond the Pauli limit, nodes in the superconducting gaps, etc. (see Refs. [1, 2, 3] for an overview). The degree of mixing in such combined pairings is related to the strength of the antisymmetric spin-orbit coupling (ASOC) and to other microscopic parameters, still under investigation. Currently, NCSCs rank among the foremost categories of superconducting materials in which to look for topological superconductivity (SC) or to realize the Majorana fermions, pairs of the latter potentially acting as noise-resilient qubits in quantum computing [4–11].
In general, the various types of NCSCs can be classified into two classes. One consists of strongly correlated materials, as e.g., CePt3Si [12], or Ce(Rh,Ir)Si3 [13], which belong to the heavy-fermion compounds. Owing to the strong correlation and the interplay between d- and f-electrons, these materials often exhibit rich magnetic and superconducting properties. Since their superconductivity is most likely mediated by spin fluctuations, this implies an unconventional (i.e., non phonon-related) pairing mechanism. Conversely, the other class consists mainly of weakly correlated materials, which are free of “magnetic” f-electrons, as e.g., LaNiC2, La7Ir3, CaPtAs, or ReT (T = 3d-5d early transition metals) [14–20]. Obviously, their superconductivity is not mediated by the electrons’ spin fluctuations. Hence, they lead themselves as prototype parent systems where one can study the intrinsic pairing mechanisms in NCSCs.
Recently, superconductivity with broken time-reversal symmetry (TRS) has become a hot topic in NCSCs. The main reason for this is the discovery of TRS breaking in some weakly-correlated NCSCs using muon-spin relaxation (μSR). Surprisingly, the superconducting properties of the latter largely resemble those of conventional superconductors, i.e., their properties are clearly distinct from those of the above mentioned strongly-correlated NCSCs. To date, only a handful of NCSC families have been shown to exhibit TRS breaking in the superconducting state, including LaNiC2 [14], La7(Rh,Ir)3 [15, 21], Zr3Ir [22], CaPtAs [16], and ReT [14–20]. Except for the recently studied CaPtAs, where coexisting TRS breaking and superconducting gap nodes were observed below
In general, the causes behind the TRS breaking at the onset of superconductivity are mostly unknown. In particular, the α-Mn-type noncentrosymmetric ReT (T = Ti, Nb, Zr, and Hf) superconductors have been widely studied and demonstrated to show a superconducting state with broken TRS [17–20]. Yet, TRS seems to be preserved in the isostructural (but Re-free) Mg10Ir19B16 and Nb0.5Os0.5 [23, 24]. Further, depending on the synthesis protocol, Re3W is either a centro- (hcp-Mg-type) or a noncentrosymmetric (α-Mn-type) superconductor, yet neither is found to break TRS [25]. In case of binary Re-Mo alloys, depending on the Re/Mo ratio, the compounds can exhibit up to four different crystal structures, including both centrosymmetric and noncentrosymmetric cases. Most importantly, all these alloys become superconductors at low temperatures [26]. A comparative μSR study of Re-Mo alloys, covering all the different crystal structures, reveals that the spontaneous magnetic fields occurring below
This short review article focuses mostly on the experimental study of Re-based binary superconductors. In Section 2, we discuss the basic principles of our probe of choice, the μSR, here used to detect the TRS breaking and to characterize the superconducting properties. Section 3 describes the possible crystal structures and superconducting transition temperatures of ReT binary alloys. In Section 4, we focus on the upper critical fields and the order parameter in ReT superconductors. Section 5 discusses the TRS breaking in ReT superconductors and its possible origins. Finally, in the last section, we outline some possible future research directions.
2 Muon-Spin Relaxation and Rotation
Initially considered as an “exotic” technique, over the years muon-spin rotation, relaxation, and resonance (known as μSR), has become one of the most powerful methods to study the magnetic and superconducting properties of matter. This follows from a series of fortunate circumstances, related to the muon properties as a fundamental particle. Most notably, these include the 100% initial muon-spin polarization, following the two-body decay from pions, and the subsequent preservation of such information through the weak decay into positrons. In the search for unconventional superconductivity, as well as for TRS breaking effects, the very high sensitivity of the μSR technique to tiny magnetic fields is especially important [28]. Below we briefly outline the basics of the μSR technique and direct the reader to other references for more detailed information [29–31].
2.1 Principles of the μSR Technique
Central to the μSR method is the availability of polarized positive muon (
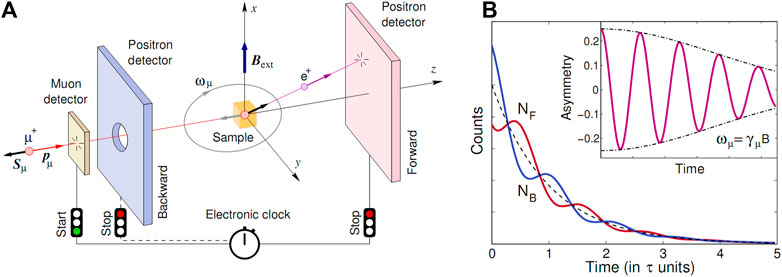
FIGURE 1. Principle of the time-differential μSR experiment. (A) An incoming polarized muon (with spin
A schematic diagram of a time-differential μSR experiment is shown in Figure 1A. The incoming muon triggers a clock that defines the starting time
Here, the exponential factor accounts for the radioactive muon decay,
2.2 Transverse-Field μSR
Depending on the reciprocal orientation of the external magnetic field
Although, in principle, the TF scheme shown in Figure 1A works fine, strong transverse fields perpendicular to the muon momentum (
Since muons are uniformly implanted in the sample, they can detect the coexistence of different domains, characterized by distinct
More in detail, in a TF-μSR experiment, the time evolution of the asymmetry can be modeled by:
Here
The first- and second moments of the field distribution in the sample can be calculated by:
where
To get further insights into the superconducting gap value and its symmetry, the temperature-dependent superfluid density
Here,
2.3 Zero-Field μSR
A particular case of LF, is that of zero-field (ZF) μSR, characterized by the absence of an external magnetic field. In this configuration the frequency of the μSR signal is exclusively proportional to the internal magnetic field, making it possible to determined the size of the ordered moments and, hence, the magnetic order parameter. Unlike various techniques, which require an external field to polarize the probe, μSR is unique in its capability of studying materials unperturbed by externally applied fields and in accessing their spontaneous magnetic fields. Due to the large muon magnetic moment (
If the amplitudes of the local fields reflect a Gaussian distribution with zero average (a rather common circumstance), the μSR signal consists of overlapping oscillations with different frequencies. While at short times the spin dephasing is limited, at long times it becomes relevant and gives rise to a so-called Kubo-Toyabe (KT) relaxation function [31, 38]. Two different models are frequently used to analyze the ZF-μSR data:
or
Equation 6 is also known as a combined Gaussian- and Lorentzian Kubo-Toyabe function, with the additional exponential relaxation describing the electronic contributions present in many real materials. In polycrystalline samples, the 1/3-non-relaxing and the 2/3-relaxing components of the asymmetry correspond to the powder average of the internal fields with respect to the initial muon-spin direction (statistically, with a 1/3 probability, the directions of the muon spin and of the local field coincide). Clearly, in the case of single crystals, such prefactors might be different. The
3 Re-Based Superconductors
In this section, we review the different phases of the binary ReT alloys. These are obtained when rhenium reacts with various early transition metals (see Figure 2A) and show rich crystal structures. Representative examples are shown in Figures 2C–F, including the hexagonal hcp-Mg- (
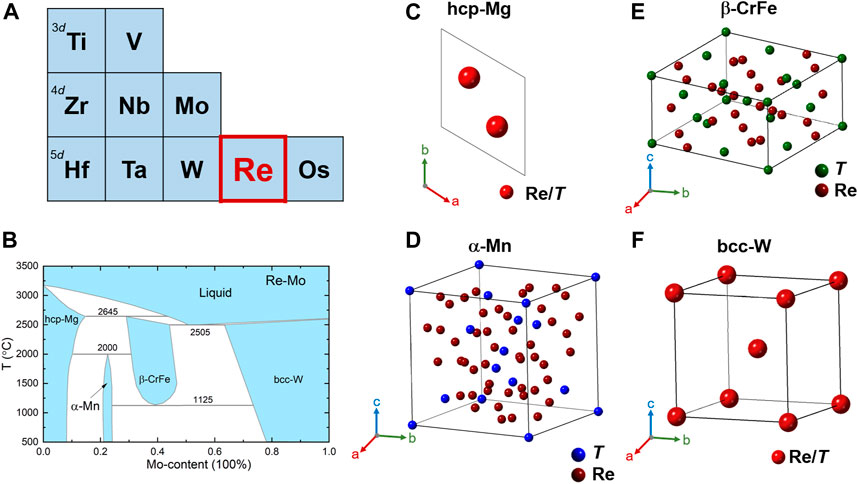
FIGURE 2. Crystal structures of rhenium transition-metal (ReT) superconductors. (A) List of 3d, 4d, and 5d early transition metals, which can react with rhenium to form different crystal structures. (B) Binary phase diagram for the typical case of Re-Mo alloys (data adopted from Ref. [39]). (C–F) Unit cells of four most representative crystal structures of ReT binary compounds. Among these the cubic α-Mn type (
For T = Ti 3d metal, the known binary compounds are Re24Ti5, Re6Ti, and ReTi [41, 42]. The former two adopt a noncentroysmmetric α-Mn-type structure and become superconductors below
For T = Zr 4d metal, the α-Mn-type Re24Zr5 (
For T = Hf 5d metal, the Re-Hf alloys show a similar phase diagram to Re-Zr. With only ∼3% Hf substitution,
4 Upper Critical Field and Nodeless Superconductivity
As mentioned in the introduction, due to the mixture of singlet- and triplet paring, some NCSCs may exhibit relatively high upper critical fields, often very close to or even exceeding the Pauli limit, as e.g., CePt3Si [12], Ce(Rh,Ir)Si3 [58, 59], and recently (Ta,Nb)Rh2B2 [60]. Therefore, the upper critical field can provide valuable clues about the nature of superconductivity. To investigate the temperature evolution of the upper critical field

FIGURE 3. Upper critical field and superconducting energy gap. (A) The upper critical field
Transverse-field μSR represents one of the most powerful techniques to investigate the superconductivity at a microscopic level. To illustrate this, in the inset of Figure 3C we show two typical TF-μSR spectra for bcc-W-type Re0.4Mo0.6 in the normal and the superconducting states. Below
Figure 3D summarizes the zero-temperature superconducting energy gap value for ReT and α-Mn-type NbOs2 and TaOs superconductors as a function of their critical temperatures. Most of them exhibit a Δ0/kBTc ratio larger than 1.76 (see dashed line in Figure 3D), the value expected for a weakly coupled BCS superconductor, which indicates a moderately strong coupling in these superconductors. In addition, the specific-heat discontinuity at
As discussed in the introduction, the lack of inversion symmetry in the NCSCs often induces an ASOC. This splits the Fermi surface by lifting the degeneracy of the conduction electrons, thus allowing admixtures of spin-singlet and spin-triplet pairing. In general, the strength of ASOC determines the degree of such an admixture and thus the superconducting properties of NCSCs [1, 2]. A fully-gapped superconductor (i.e., dominated by spin-singlet pairing) can be tuned into a nodal superconductor (dominated by spin-triplet pairing) by increasing the strength of ASOC. Such mechanism has been successfully demonstrated, e.g., in weakly-correlated Li2Pt3B (
5 Time-Reversal Symmetry Breaking
Owing to its very high sensitivity (see details in Section 2.3), ZF-μSR has been successfully used to search for spontaneous magnetic fields, reflecting the breaking of TRS in the superconducting states of different types of superconductors, as e.g., Sr2RuO4, UPt3, PrOs4Sb12, LaNiGa2, LaNiC2, La7(Rh,Ir)3, and α-Mn-ReT [14, 15, 17, 18, 19, 20, 21, 75, 76, 77, 78, 79, 80]. The latter three are typical examples of weakly-correlated NSCSs, to be contrasted with strongly-correlated NCSCs, where either the TRS is broken by a coexisting long-range magnetic order, or the tiny TRS-breaking signal is very difficult to detect due to the presence of strong magnetic fluctuations [28]. In the former case, the broken TRS is unrelated to the superconductivity, while in the later case, a genuine TRS breaking effect is masked by the much faster muon-spin relaxation caused by magnetic fluctuations. Therefore, in general, a TRS breaking effect is more easily (and reliably) detected in weakly-correlated- or non-magnetic superconductors using μSR techniques. Normally, in the absence of external fields, the onset of superconductivity does not imply changes in the ZF-μSR relaxation rate. However, in presence of a broken TRS, the onset of a tiny spontaneous polarization or of currents gives rise to associated (weak) magnetic fields, readily detected by ZF-μSR as an increase in the relaxation rate. Given the tiny size of such effects, the ZF-μSR measurements are usually performed in both the normal- and the superconducting state with a relatively high statistics, at least twice that of the TF-μSR spectra. As an example, Figure 4A plots the ZF-μSR spectra of α-Mn-type Re25Nb5, with the other ReT superconductors showing a similar behavior. The ZF-μSR spectra collected below- and above

FIGURE 4. ZF-μSR and evidence for TRS breaking. (A) ZF-μSR spectra for Re24Nb5 collected in the superconducting and normal states. Top: additional μSR data collected at 1.5 K in a 15-mT longitudinal field, are also shown. The solid lines are fits using Eq. 6. (B) Gaussian relaxation rate
Recently, the breaking of TRS and the presence of nodes in the SC gap, attributed to an admixture of singlet- and triplet paring, has been reported in the noncentrosymmetric CaPtAs superconductor [16]. In general, however, the breaking of TRS in the superconducting state and a lack of space-inversion symmetry in the crystal structure are independent events, not necessarily occurring together. For instance, the unconventional spin-triplet pairing is expected to break TRS below
If SOC can be ignored, an alternative mechanism, which can account for the TRS breaking in ReT superconductors in presence of a fully-opened superconducting gap, is the internally-antisymmetric nonunitary triplet (INT) pairing. The INT pairing was originally proposed to explain the TRS breaking and nodeless SC in centrosymmetric LaNiGa2 [3, 80, 89] and noncentrosymmetric LaNiC2 [14, 90], both exhibiting a relatively weak SOC. In case of INT pairing, the superconducting pairing function is antisymmetric with respect to the orbital degree of freedom, while remaining symmetric in the spin- and crystal-momentum channels [14, 80, 89, 90]. Since in ReT superconductors, too, the SOC interaction is relatively weak (∼30 meV, see Section 4) [72] and since neither TRS breaking nor the nodeless SC are related to the symmetry of ReT crystal structures, the effect of SOC to the observed TRS breaking is insignificant. This could, therefore, explain why a lack of inversion symmetry (essential to SOC) is not a precondition for TRS breaking in ReT superconductors. Moreover, the occurrence of an INT state relies on the availability of a local-pairing mechanism driven by Hund’s rules, e.g., by Ni 3d-electrons in LaNiC2 and LaNiGa2 [3, 14, 80, 89, 90]. Such local-pairing mechanism may also occur in ReT superconductors, since rhenium too can be magnetic [91, 92]. This consideration is also in good agreement with the observation that TRS breaking depends on Re content, but not on a noncentrosymmetric crystal structure.
6 Conclusion
In this short review we focused on recent experimental studies of ReT superconductors, where time-reversal symmetry breaking effects are often present and whose superconductivity can, therefore, be considered as unconventional. Due to its high sensitivity to the weak internal fields associated with TRS breaking, μSR represents one of the key techniques in the search for TRS-breaking effects in the superconducting state. Nonetheless, in certain cases, the amplitude of the spontaneous magnetic fields (the fingerprint of TRS breaking) may still be below the resolution of the μSR technique (
To date, as nearly all current studies have focused exclusively on α-Mn-type ReT superconductors (except for the Re-Mo series considered here), the superconducting properties of most other ReT alloys remain basically unexplored. Hence, the synthesis and characterization of non-α-Mn-type ReT alloys, including the study of their electrical, magnetic, and thermodynamic properties, is of clear interest. Similarly, systematic μSR measurements, crucial for detecting the presence of TRS breaking in Re-based superconductors, are in high demand. For instance, although both Re-Zr and Re-Nb alloys exhibit rich crystal structures and superconducting phase diagrams, only their α-Mn-type phase has been explored. In addition, most of the original measurements were performed only on polycrystalline samples. Hence, the synthesis of single crystals will be essential in the comprehensive search for possible superconducting nodes and, thus, for mixed singlet-triplet pairing. Finally, it would be of interest to extend the μSR studies on elementary rhenium from the bulk-to its thin-film form, where inversion symmetry is artificially broken. By checking if the TRS breaking is maintained or not, will help us to further clarify the rhenium conundrum.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work was supported by the start funding from East China Normal University (ECNU), the Swiss National Science Foundation (Grant No. 200021-169455) and the Sino-Swiss Science and Technology Cooperation (Grant No. IZLCZ2-170075).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank M. Shi for the fruitful discussion. We thank M. Medarde for the assistance during the electrical resistivity and magnetization measurements, and D. J. Gawryluk and E. Pomjakushina for synthesizing the materials. We acknowledge the allocation of beam time at the Swiss muon source (SμS) (Dolly, GPS, and LTF spectrometers).
References
1. Bauer E, Sigrist M., editors. Non-Centrosymmetric Superconductors, 847. Berlin: Springer-Verlag (2012).
2. Smidman M, Salamon MB, Yuan HQ, Agterberg DF. Superconductivity and Spin–Orbit Coupling in Non-centrosymmetric Materials: A Review. Rep Prog Phys (2017) 80:036501. doi:10.1088/1361-6633/80/3/036501
3. Ghosh SK, Smidman M, Shang T, Annett JF, Hillier AD, Quintanilla J, et al. Recent Progress on Superconductors with Time-Reversal Symmetry Breaking. J Phys Condens Matter (2021) 33:033001. doi:10.1088/1361-648x/abaa06
4. Kim H, Wang K, Nakajima Y, Hu R, Ziemak S, Syers P, et al. Beyond Triplet: Unconventional Superconductivity in a Spin-3/2 Topological Semimetal. Sci Adv (2018) 4. doi:10.1126/sciadv.aar796910.1126/sciadv.aao4513eaao4513
5. Sun Z, Enayat M, Maldonado A, Lithgow C, Yelland E, Peets DC, et al. Dirac Surface States and Nature of Superconductivity in Noncentrosymmetric BiPd. Nat Commun (2015) 6:6633. doi:10.1038/ncomms7633
6. Ali MN, Gibson QD, Klimczuk T, Cava RJ. Noncentrosymmetric Superconductor with a Bulk Three-Dimensional Dirac Cone Gapped by Strong Spin-Orbit Coupling. Phys Rev B (2014) 89:020505. doi:10.1103/PhysRevB.89.020505
7. Sato M, Fujimoto S. Topological Phases of Noncentrosymmetric Superconductors: Edge States, Majorana Fermions, and Non-abelian Statistics. Phys Rev B (2009) 79:094504. doi:10.1103/PhysRevB.79.094504
8. Tanaka Y, Mizuno Y, Yokoyama T, Yada K, Sato M. Anomalous Andreev Bound State in Noncentrosymmetric Superconductors. Phys Rev Lett (2010) 105:097002. doi:10.1103/PhysRevLett.105.097002
9. Sato M, Ando Y. Topological Superconductors: A Review. Rep Prog Phys (2017) 80:076501:076501. doi:10.1088/1361-6633/aa6ac7
10. Qi X-L, Zhang S-C. Topological Insulators and Superconductors. Rev Mod Phys (2011) 83:1057–110. doi:10.1103/RevModPhys.83.1057
11. Kallin C, Berlinsky J. Chiral Superconductors. Rep Prog Phys (2016) 79:054502:054502. doi:10.1088/0034-4885/79/5/054502
12. Bauer E, Hilscher G, Michor H, Paul C, Scheidt EW, Gribanov A, et al. Heavy Fermion Superconductivity and Magnetic Order in Noncentrosymmetric CePt3Si. Phys Rev Lett (2004) 92:027003. doi:10.1103/PhysRevLett.92.027003
13. Muro Y, Eom D, Takeda N, Ishikawa M. Contrasting Kondo-Lattice Behavior in CeTSi3 and CeTGe3 (T = Rh and Ir). J Phys Soc Jpn (1998) 67:3601–4. doi:10.1143/JPSJ.67.3601
14. Hillier AD, Quintanilla J, Cywinski R. Evidence for Time-Reversal Symmetry Breaking in the Noncentrosymmetric Superconductor LaNiC2. Phys Rev Lett (2009) 102:117007. doi:10.1103/PhysRevLett.102.117007
15. Barker JAT, Singh D, Thamizhavel A, Hillier AD, Lees MR, Balakrishnan G, et al. Unconventional Superconductivity in La7Ir3 Revealed by Muon Spin Relaxation: Introducing a New Family of Noncentrosymmetric Superconductor that Breaks Time-Reversal Symmetry. Phys Rev Lett (2015) 115:267001. doi:10.1103/PhysRevLett.115.267001
16. Shang T, Smidman M, Wang A, Chang L-J, Baines C, Lee MK, et al. Simultaneous Nodal Superconductivity and Time-Reversal Symmetry Breaking in the Noncentrosymmetric Superconductor CaPtAs. Phys Rev Lett (2020) 124:207001. doi:10.1103/PhysRevLett.124.207001
17. Singh RP, Hillier AD, Mazidian B, Quintanilla J, Annett JF, Paul DM, et al. Detection of Time-Reversal Symmetry Breaking in the Noncentrosymmetric Superconductor Re6Zr Using Muon-Spin Spectroscopy. Phys Rev Lett (2014) 112:107002. doi:10.1103/PhysRevLett.112.107002
18. Singh D, Barker JAT, Thamizhavel A, Paul DM, Hillier AD, Singh RP. Time-reversal Symmetry Breaking in the Noncentrosymmetric Superconductor Re6Hf : Further Evidence for Unconventional Behavior in the α-Mn Family of Materials. Phys Rev B (2017a) 96:180501. doi:10.1103/PhysRevB.96.180501
19. Shang T, Pang GM, Baines C, Jiang WB, Xie W, Wang A, et al. Nodeless Superconductivity and Time-Reversal Symmetry Breaking in the Noncentrosymmetric Superconductor Re24Ti5. Phys Rev B (2018) 97:020502. doi:10.1103/PhysRevB.97.020502
20. Shang T, Smidman M, Ghosh SK, Baines C, Chang LJ, Gawryluk DJ, et al. Time-reversal Symmetry Breaking in Re-based Superconductors. Phys Rev Lett (2018) 121:257002. doi:10.1103/PhysRevLett.121.257002
21. Singh D, Scheurer MS, Hillier AD, Adroja DT, Singh RP. Time-reversal-symmetry Breaking and Unconventional Pairing in the Noncentrosymmetric Superconductor La7Rh3. Phys Rev B (2020) 102:134511. doi:10.1103/PhysRevB.102.134511
22. Shang T, Ghosh SK, Zhao JZ, Chang L-J, Baines C, Lee MK, et al. Time-reversal Symmetry Breaking in the Noncentrosymmetric Zr3Ir superconductorIr Superconductor. Phys Rev B (2020) 102:020503. doi:10.1103/PhysRevB.102.020503
23. Aczel AA, Williams TJ, Goko T, Carlo JP, Yu W, Uemura YJ, et al. Muon Spin Rotation/relaxation Measurements of the Noncentrosymmetric Superconductor Mg10Ir19B16. Phys Rev B (2010) 82:024520. doi:10.1103/PhysRevB.82.024520
24. Singh D, Barker JAT, Thamizhavel A, Hillier AD, Paul DM, Singh RP. Superconducting Properties and μSR Study of the Noncentrosymmetric Superconductor Nb0.5Os0.5. J Phys Condens Matter (2018) 30:075601:075601. doi:10.1088/1361-648X/aaa376
25. Biswas PK, Hillier AD, Lees MR, Paul DM. Comparative Study of the Centrosymmetric and Noncentrosymmetric Superconducting Phases of Re3W Using Muon Spin Spectroscopy and Heat Capacity Measurements. Phys Rev B (2012) 85:134505. doi:10.1103/PhysRevB.85.134505
26. Shang T, Gawryluk DJ, Verezhak JAT, Pomjakushina E, Shi M, Medarde M, et al. Structure and Superconductivity in the Binary Re1−xMox Alloys. Phys Rev Mater (2019) 3:024801. doi:10.1103/PhysRevMaterials.3.024801
27. Shang T, Baines C, Chang L-J, Gawryluk DJ, Pomjakushina E, Shi M, et al. Re1−xMox as an Ideal Test Case of Time-Reversal Symmetry Breaking in Unconventional Superconductors. npj Quan Mater. (2020) 5:76. doi:10.1038/s41535-020-00279-1
28. Amato A. Heavy-fermion Systems Studied by μSR Technique. Rev Mod Phys (1997) 69:1119–80. doi:10.1103/RevModPhys.69.1119
29. Blundell SJ. Spin-polarized Muons in Condensed Matter Physics. Contemp Phys (1999) 40:175–92. doi:10.1080/001075199181521
30. Brewer JH. Muon Spin Rotation/relaxation/resonance. In: GL Trigg., editor. Digital Encyclopedia of Applied Physics. Weinheim: Wiley VCH eap258. (2003). doi:10.1002/3527600434.eap258
31. Yaouanc A, de Réotier PD. Muon Spin Rotation, Relaxation, and Resonance: Applications to Condensed Matter. Oxford: Oxford University Press (2011).
32. Sonier JE, Brewer JH, Kiefl RF. μSR Studies of the Vortex State in Type-II Superconductors. Rev Mod Phys (2000) 72:769–811. doi:10.1103/RevModPhys.72.769
33. Barford W, Gunn JMF. The Theory of the Measurement of the London Penetration Depth in Uniaxial Type II Superconductors by Muon Spin Rotation. Physica C: Superconductivity (1988) 156:515–22. doi:10.1016/0921-4534(88)90014-7
34. Brandt EH. Properties of the Ideal Ginzburg-Landau Vortex Lattice. Phys Rev B (2003) 68:054506. doi:10.1103/PhysRevB.68.054506
35. Maisuradze A, Khasanov R, Shengelaya A, Keller H. Comparison of Different Methods for Analyzing μSR Line Shapes in the Vortex State of Type-II Superconductors. J Phys Condens Matter 21, 075701 (2009) 075701. doi:10.1088/0953-8984/21/7/075701
37. Carrington A, Manzano F. Magnetic Penetration Depth of MgB2. Physica C: Superconductivity (2003) 385:205–14. doi:10.1016/S0921-4534(02)02319-5
38. Kubo R, Toyabe T. A Stochastic Model for Low-Field Resonance and Relaxation. In: R Blinc., editor. Magnetic Resonance and Relaxation. Proceedings of the XIVth Colloque Ampère. Amsterdam: North-Holland) (1967). p. 810–23.
39. Massalski TB, Okamoto H, Kacprzak L, Subramanian PR. Binary Alloy Phase Diagrams. 2 edn. Materials Park, OH: ASM International (1996).
40. Roberts BW. Survey of Superconductive Materials and Critical Evaluation of Selected Properties. J Phys Chem Reference Data (1976) 5:581–822. doi:10.1063/1.555540
41. Murray JL. The Re−Ti (Rhenium-Titanium) System. J Phase Equilib (1982) 2:462–6. doi:10.1007/BF02876164
42. Philip TV, Beck PA. CsCl-type Ordered Structures in Binary Alloys of Transition Elements. JOM J Min Met Mat S (1957) 9:1269–71. doi:10.1007/BF03398305
43. Singh D, K. P. S, Barker JAT, Paul DM, Hillier AD, Singh RP. Time-reversal Symmetry Breaking in the Noncentrosymmetric Superconductor Re6Ti. Phys Rev B (2018b) 97:100505. doi:10.1103/PhysRevB.97.100505
44. Jorda JL, Muller J. The Vanadium-Rhenium System: Phase Diagram and Superconductivity. J Less Common Met (1986) 119:337–45. doi:10.1016/0022-5088(86)90694-6
45. Eremenko VN, Velikanova T. Intrusion Phases Based on Metallides in Ternary Systems of Transition Metals with Carbon. Sov Prog Chem (1990) 56:21–8.
46. Matano K, Yatagai R, Maeda S, Zheng G-q. Full-gap Superconductivity in Noncentrosymmetric Re6Zr, Re27Zr5, and Re24Zr5. Phys Rev B (2016) 94:214513. doi:10.1103/PhysRevB.94.214513
47. Giorgi AL, Szklarz EG. Superconductivity and Lattice Parameters of the Dirhenides and Ditechnides of Thorium, Hafnium and Zirconium. J Less Common Met (1970) 22:246–8. doi:10.1016/0022-5088(70)90027-5
48. Cirillo C, Fittipaldi R, Smidman M, Carapella G, Attanasio C, Vecchione A, et al. Evidence of Double-Gap Superconductivity in Noncentrosymmetric Nb0.18Re0.82 Single Crystals. Phys Rev B (2015) 91:134508. doi:10.1103/PhysRevB.91.134508
49. Chen J, Jiao L, Zhang JL, Chen Y, Yang L, Nicklas M, et al. BCS-like Superconductivity in the Noncentrosymmetric Compounds NbxRe1−x(0.13≤x≤0.38). Phys Rev B (2013) 88:144510. doi:10.1103/PhysRevB.88.144510
50. Karki AB, Xiong YM, Haldolaarachchige N, Stadler S, Vekhter I, Adams PW, et al. Physical Properties of the Noncentrosymmetric Superconductor Nb0.18Re0.82. Phys Rev B (2011) 83:144525. doi:10.1103/PhysRevB.83.144525
51. Lue CS, Su TH, Liu HF, Young B-L. Evidence Fors-Wave Superconductivity in Noncentrosymmetric Re24Nb5 from 93Nb NMR Measurements. Phys Rev B (2011) 84:052509. doi:10.1103/PhysRevB.84.052509
52. Chen B, Guo Y, Wang H, Su Q, Mao Q, Du J, et al. Superconductivity in the Noncentrosymmetric Compound Re6Hf. Phys Rev B (2016) 94:024518. doi:10.1103/PhysRevB.94.024518
53. Singh D, Hillier AD, Thamizhavel A, Singh RP. Superconducting Properties of the Noncentrosymmetric Superconductor Re6Hf. Phys Rev B (2017) 96:064521. doi:10.1103/PhysRevB.96.06452110.1103/physrevb.96.180501
54. Barker JAT, Breen BD, Hanson R, Hillier AD, Lees MR, Balakrishnan G, et al. Superconducting and Normal-State Properties of the Noncentrosymmetric Superconductor Re3Ta. Phys Rev B (2018) 98:104506. doi:10.1103/PhysRevB.98.104506
55. Arushi SD, Singh D, Biswas PK, Hillier AD, Singh RP. Unconventional Superconducting Properties of Noncentrosymmetric Re5.5Ta. Phys Rev B (2020) 101:144508. doi:10.1103/PhysRevB.101.144508
56. Mamiya T, Nomura K, Masuda Y. Superconductivity of Tantalum-Rhenium Alloys. J Phys Soc Jpn (1970) 28:380–9. doi:10.1143/JPSJ.28.380
57. Biswas PK, Lees MR, Hillier AD, Smith RI, Marshall WG, Paul DM. Structure and Superconductivity of Two Different Phases of Re3W. Phys Rev B (2011) 84:184529. doi:10.1103/PhysRevB.84.184529
58. Kimura N, Ito K, Aoki H, Uji S, Terashima T. Extremely High Upper Critical Magnetic Field of the Noncentrosymmetric Heavy Fermion Superconductor CeRhSi3. Phys Rev Lett (2007) 98:197001. doi:10.1103/PhysRevLett.98.197001
59. Sugitani I, Okuda Y, Shishido H, Yamada T, Thamizhavel A, Yamamoto E, et al. Pressure-induced Heavy-Fermion Superconductivity in Antiferromagnet CeIrSi3 without Inversion Symmetry. J Phys Soc Jpn (2006) 75:043703. doi:10.1143/JPSJ.76.05100910.1143/jpsj.75.043703
60. Carnicom EM, Xie W, Klimczuk T, Lin J, Górnicka K, Sobczak Z, et al. TaRh2B2 and NbRh2B2: Superconductors with a Chiral Noncentrosymmetric Crystal Structure. Sci Adv (2018) 4:eaar7969:eaar7969. doi:10.1126/sciadv.aar7969
61. Singh D, K. P. S, Marik S, Hillier AD, Singh RP. Superconducting and Normal State Properties of the Noncentrosymmetric Superconductor NbOs2. Investigated by Muon Spin Relaxation and Rotation. Phys Rev B (2019) 99:014516. doi:10.1103/PhysRevB.99.014516
62. Singh D, Sajilesh KP, Marik S, Hillier AD, Singh RP. Superconducting Properties of the Noncentrosymmetric Superconductor TaOs. Supercond Sci Technol (2017) 30:125003. doi:10.1088/1361-6668/aa8f8e
63. Mayoh DA, Barker JAT, Singh RP, Balakrishnan G, Paul DM, Lees MR. Superconducting and Normal-State Properties of the Noncentrosymmetric Superconductor Re6Zr. Phys Rev B (2017) 96:064521. doi:10.1103/PhysRevB.96.064521
64. Pang GM, Nie ZY, Wang A, Singh D, Xie W, Jiang WB, et al. Fully Gapped Superconductivity in Single Crystals of Noncentrosymmetric Re6Zr with Broken Time-Reversal Symmetry. Phys Rev B (2018) 97:224506. doi:10.1103/PhysRevB.97.224506
65. Parab P, Singh D, Haram S, Singh RP, Bose S. Point Contact Andreev Reflection Studies of a Non-centro Symmetric Superconductor Re6Zr. Sci Rep (2019) 9:2498. doi:10.1038/s41598-019-39160-y
66. Yuan HQ, Agterberg DF, Hayashi N, Badica P, Vandervelde D, Togano K, et al. S-wave Spin-Triplet Order in Superconductors without Inversion Symmetry:Li2Pd3B and Li2Pt3B. Phys Rev Lett (2006) 97:017006. doi:10.1103/PhysRevLett.97.017006
67. Nishiyama M, Inada Y, Zheng G-q. Spin Triplet Superconducting State Due to Broken Inversion Symmetry in Li2Pt3B. Phys Rev Lett (2007) 98:047002. doi:10.1103/PhysRevLett.98.047002
68. Xie W, Zhang P, Shen B, Jiang W, Pang G, Shang T, et al. CaPtAs: a New Noncentrosymmetric Superconductor. Sci China Phys Mech Astron (2020) 63:237412. doi:10.1007/s11433-019-1488-5
69. Samokhin KV, Zijlstra ES, Bose SK. CePt3Si: An Unconventional Superconductor without Inversion Center. Phys Rev B (2004) 69:094514. doi:10.1103/PhysRevB.69.094514
70. Suetin DV, Ivanovskii AL. Comparative Study of Electronic Structure of Cubic and Hexagonal Phases of Re3W as Non-centrosymmetric and Centrosymmetric Low-Tc Superconductors. Intermetallics (2013) 34:101–5. doi:10.1016/j.intermet.2012.11.015
71. Winiarski MJ. Electronic Structure of Non-centrosymmetric Superconductors Re24(Nb;Ti)5 by Ab Initio Calculations. J Alloys Comp (2014) 616:1–4. doi:10.1016/j.jallcom.2014.07.081
72. Mojammel AK, Karki AB, Samanta T, Browne D, Stadler S, Vekhter I, et al. Complex Superconductivity in the Noncentrosymmetric Compound Re6Zr. Phys Rev B (2016) 94:144515. doi:10.1103/PhysRevB.94.144515
73. Shang T, Philippe J, Verezhak JAT, Guguchia Z, Zhao JZ, Chang L-J, et al. Nodeless Superconductivity and Preserved Time-Reversal Symmetry in the Noncentrosymmetric Mo3P Superconductor. Phys Rev B (2019) 99:184513. doi:10.1103/PhysRevB.99.184513
74. Yip S. Noncentrosymmetric Superconductors. Annu Rev Condens Matter Phys (2014) 5:15–33. doi:10.1146/annurev-conmatphys-031113-133912
75. Luke GM, Keren A, Le LP, Wu WD, Uemura YJ, Bonn DA, et al. Muon Spin Relaxation in UPt3. Phys Rev Lett (1993) 71:1466–9. doi:10.1103/PhysRevLett.71.1466
76. Luke GM, Fudamoto Y, Kojima KM, Larkin MI, Merrin J, Nachumi B, et al. Time-reversal Symmetry-Breaking Superconductivity in Sr2RuO4. Nature (1998) 394:558–61. doi:10.1038/29038
77. Xia J, Maeno Y, Beyersdorf PT, Fejer MM, Kapitulnik A. High Resolution Polar Kerr Effect Measurements of Sr2RuO4: Evidence for Broken Time-Reversal Symmetry in the Superconducting State. Phys Rev Lett (2006) 97:167002. doi:10.1103/PhysRevLett.97.167002
78. Aoki Y, Tsuchiya A, Kanayama T, Saha SR, Sugawara H, Sato H, et al. Time-Reversal Symmetry-Breaking Superconductivity in Heavy-fermion PrOs4Sb12 Detected by Muon-Spin Relaxation. Phys Rev Lett (2003) 91:067003. doi:10.1103/PhysRevLett.91.067003
79. Schemm ER, Gannon WJ, Wishne CM, Halperin WP, Kapitulnik A. Observation of Broken Time-Reversal Symmetry in the Heavy-Fermion Superconductor UPt3. Science (2014) 345:190–3. doi:10.1126/science.1248552
80. Hillier AD, Quintanilla J, Mazidian B, Annett JF, Cywinski R. Nonunitary Triplet Pairing in the Centrosymmetric Superconductor LaNiGa2. Phys Rev Lett (2012) 109:097001. doi:10.1103/PhysRevLett.109.097001
81. Ran S, Eckberg C, Ding Q-P, Furukawa Y, Metz T, Saha SR, et al. Nearly Ferromagnetic Spin-Triplet Superconductivity. Science (2019) 365:684–7. doi:10.1126/science.aav8645
82. Ishida K, Mukuda H, Kitaoka Y, Asayama K, Mao ZQ, Mori Y, et al. Spin-triplet Superconductivity in Sr2RuO4 Identified by 17O Knight Shift. Nature (1998) 396:658–60. doi:10.1038/25315
83. Tou H, Kitaoka Y, Ishida K, Asayama K, Kimura N, O¯nuki Y, et al. Nonunitary Spin-Triplet Superconductivity in UPt3: Evidence from 195Pt Knight Shift Study. Phys Rev Lett (1998) 80:3129–32. doi:10.1103/PhysRevLett.80.3129
84. Mackenzie AP, Maeno Y. The Superconductivity of Sr2RuO4 and the Physics of Spin-Triplet Pairing. Rev Mod Phys (2003) 75:657–712. doi:10.1103/RevModPhys.75.657
85. Joynt R, Taillefer L. The Superconducting Phases of UPt3. Rev Mod Phys (2002) 74:235–94. doi:10.1103/RevModPhys.74.235
86. Lee W-C, Zhang S-C, Wu C. Pairing State with a Time-Reversal Symmetry Breaking in FeAs-Based Superconductors. Phys Rev Lett (2009) 102:217002. doi:10.1103/PhysRevLett.102.217002
87. Sharma S, Motla K, Beare J, Nugent M, Pula M, Munsie T, et al. Fully Gapped Superconductivity in Centrosymmetric and Noncentrosymmetric Re-B Compounds Probed with μSR. Phys Rev B (2021) 103:104507. doi:10.1103/PhysRevB.103.104507
88. Shang T, Amon A, Kasinathan D, Xie W, Bobnar M, Chen Y, et al. Enhanced Tc and Multiband Superconductivity in the Fully-Gapped ReBe22 Superconductor. New J Phys (2019) 21:073034:073034. doi:10.1088/1367-2630/ab307b
89. Weng ZF, Zhang JL, Smidman M, Shang T, Quintanilla J, Annett JF, et al. Two-Gap Superconductivity in LaNiGa2 with Nonunitary Triplet Pairing and Even Parity Gap Symmetry. Phys Rev Lett (2016) 117:027001. doi:10.1103/PhysRevLett.117.027001
90. Quintanilla J, Hillier AD, Annett JF, Cywinski R. Relativistic Analysis of the Pairing Symmetry of the Noncentrosymmetric Superconductor LaNiC2. Phys Rev B (2010) 82:174511. doi:10.1103/PhysRevB.82.174511
91. Yang S, Wang C, Sahin H, Chen H, Li Y, Li S-S, et al. Tuning the Optical, Magnetic, and Electrical Properties of ReSe2 by Nanoscale Strain Engineering. Nano Lett (2015) 15:1660–6. doi:10.1021/nl504276u
92. Kochat V, Apte A, Hachtel JA, Kumazoe H, Krishnamoorthy A, Susarla S, et al. Re Doping in 2D Transition Metal Dichalcogenides as a New Route to Tailor Structural Phases and Induced Magnetism. Adv Mater (2017) 29:1703754. doi:10.1002/adma.201703754
Keywords: time-reversal symmetry breaking, noncentrosymmetric superconductors, unconventional superconductivity, muon-spin spectroscopy, rhenium compounds
Citation: Shang T and Shiroka T (2021) Time-Reversal Symmetry Breaking in Re-Based Superconductors: Recent Developments. Front. Phys. 9:651163. doi: 10.3389/fphy.2021.651163
Received: 08 January 2021; Accepted: 29 April 2021;
Published: 24 May 2021.
Edited by:
Yuji Muro, Toyama Prefectural University, JapanReviewed by:
Amitava Bhattacharyya, Ramakrishna Mission Vivekananda Educational and Research Institute, IndiaJess H. Brewer, University of British Columbia, Canada
Copyright © 2021 Shang and Shiroka. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tian Shang, dHNoYW5nQHBoeS5lY251LmVkdS5jbg==; Toni Shiroka, dHNoaXJva2FAcGh5cy5ldGh6LmNo
 Tian Shang
Tian Shang Toni Shiroka
Toni Shiroka