Algebraic Structure and Poisson Integral Method of Snake-Like Robot Systems

The algebraic structure and Poisson's integral of snake-like robot systems are studied. The generalized momentum, Hamiltonian function, generalized Hamilton canonical equations, and their contravariant algebraic forms are obtained for snake-like robot systems. The Lie-admissible algebra structures of the snake-like robot systems are proved and partial Poisson integral methods are applied to the snake-like robot systems. The first integral methods of the snake-like robot systems are given. An example is given to illustrate the results.

Introduction

The snake-like robot, which is based on the biological characteristics of snakes, constitutes an important branch of bionic robots [1]. Hirose developed the first snake robot in 1972 [2]. The snake robot is significantly different from a tracked robot, wheeled robot, and legged robot, being a mobile robot with high redundancy. Because of the multi-joint flexible structure design, a snake robot has the advantage of multi-gait motion and the ability to adapt to a complex unknown environment, and can be widely used in disaster rescue, underwater surveys, industrial testing, and other special environments that traditional robots or humans cannot enter; as a result, increasing attention is being paid to snake robots [3–6].

In 1946, Gray divided movement gaits into serpentine movement, rectilinear movement, concertina movement, and sidewinding movement in the study of the biological nature of snakes [7]. According to this study, there are two starting points to study the motion of the snake-like robot: One is to observe the movement rule of biological snakes from the perspective of bionics, and then apply the rule to the snake-like robot to verify its effectiveness and controllability; on the other hand, the physical models are established according to the actual physical systems, and based on the physical model a control law is proposed to make snake-like robots move in a serpentine motion. For example, Tang et al. [8] studied the control methods of snake-like robots in different environments. Hirose established a serpentine gait kinematics model with linkage structures based on the observation of biological snake movement processes and bone anatomy [2], Lilijeback et al. analyzed the position relationship between a snake robot and obstacles, proposed an obstacle assistant movement gait in planar motion, and built the kinematics and dynamics model for the snake robot [9, 10]. At present, the serpentine motion of many snake-like robots are realized on the passive wheel, while the passive wheel provides a non-holonomic constraint for the system of snake-like robots in dynamics, so it is necessary to analyze and discuss the constraint systems of snake-like robots. Ostrowski and Burdick [11] and Guo et al. [12] developed the kinematic model considering the constraint systems of snake-like robots.

It is well-known that algebraic structure and Poisson's theory for constrained mechanical systems have been developed to seek invariants of mechanical and physical systems [13, 14]. Mei and Shi [15] have extended this method to non-holonomic constrained mechanical systems. Fu et al. have studied the algebraic structure and Poisson's theory of the relativistic Birkhoffian system, rotational relativistic dynamical system, mechanico-electrical coupling system, and f (R) cosmology system [16–18]. In this paper, we make an effort in this direction and demonstrate the applications of the algebraic structure and Poisson's theory of dynamical systems to snake-like robot system. This paper gives the algebraic structure and the first integral methods of snake-like robots. Firstly, the kinematics of the snake-like robot is analyzed, and then the generalized Lagrange equations and generalized Hamilton canonical equations of the snake-like robot systems are given. Secondly, contravariant algebraic forms of snake-like robot systems are obtained. Thirdly the Lie-admissible algebraic structure of the snake-like robot is researched. Fourthly, the Poisson integral methods are applied to the snake-like robot systems. Finally, an example is studied for a snake-like robot.

Lagrangian of Snake-Like Robot Systems

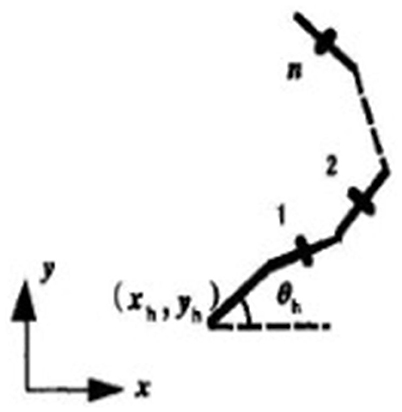
In order to facilitate the analysis, the snake-like robot systems are simplified as a link mechanism, each link rod represents a joint of the snake-like robot (mechanical structure of snake-like robot systems are depicted in Figure 1). Then, according to Figure 1, we can get the analysis as follows: let (x_i, y_i) denote the center of gravity of each joint (each coordinate is set in the middle of each link), φ_i is the angle between the link and the horizontal direction, (x_h, y_h) and the θ_h denote the position of the snake-like robot and the absolute angle of snake-head, respectively, and m_h denotes the weight of the head of the robot. Length 2l and weight m are the same for each link.

FIGURE 1

Figure 1. Mechanical structure of snake-like robot.

We choose q_i = φ_i, q_n+1 = x_h, q_n+2 = y_h, q_n+3 = θ_h, (i = 1, 2, ⋯ , n) as the generalized coordinates.

From Figure 1, the relationship between the center of gravity of each joint (x_i, y_i) and the position of the snake head (x_h, y_h) can be given by

$\begin{array}{l}{x}_i=q_{n+1}+2l\text{ cos }\left(q_{n+3}\right)+2l{\displaystyle \sum _{k=1}^{i-1}\text{ cos }\left(q_k\right)}+l\text{ cos }\left(q_i\right),\\ \left(i=1,\cdots ,n\right)\\ y_i=q_{n+2}+2l\text{ sin }\left(q_{n+3}\right)+2l{\displaystyle \sum _{k=1}^{i-1}\text{ sin }\left(q_k\right)}+l\text{ sin }\left(q_i\right),& (1)\end{array}$

so, the generalized velocities of snake-like systems can be given by

$\begin{array}{l}{ẋ}_i=7{\stackrel{.}{q}}_{n+1}-2lsin\left(q_{n+3}\right){\stackrel{.}{q}}_{n+3}-2l{\displaystyle \sum _{k=1}^{i-1}}sin\left(q_k\right){\stackrel{.}{q}}_k-lsin\left(q_i\right){\stackrel{.}{q}}_i,\\ {ẏ}_i={\stackrel{.}{q}}_{n+2}+2lcos\left(q_{n+3}\right){\stackrel{.}{q}}_{n+3}+2l{\displaystyle \sum _{k=1}^{i-1}}cos\left(q_k\right){\stackrel{.}{q}}_k+lcos\left(q_i\right){\stackrel{.}{q}}_i.& (2)\end{array}$

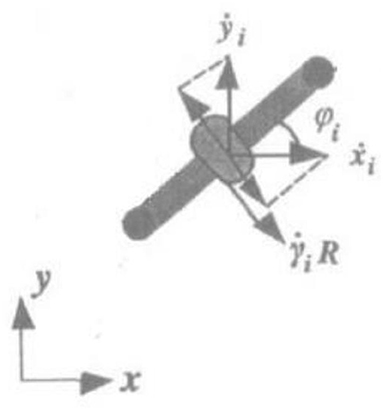
We give a simplified model of one unit of the snake-like robot system as shown in Figure 2.

FIGURE 2

Figure 2. A simplified model of one unit of the snake-like robot.

The constraint equations of the snake-like robot system are given by

$\begin{array}{ll}{ẋ}_{i}sin\left(q_i\right)-{ẏ}_{i}cos\left(q_i\right)={\stackrel{.}{q}}_{n+3+i}R,& (3)\end{array}$

where q_n+3+i = γ_i denotes the rotating angle of each unit's sideslip, R denotes the turning radius of the unit;

submitting constraints (2) into (3), we can derive

$\begin{array}{l}{f}_{\beta }\left(q,\stackrel{.}{q}\right)={\stackrel{.}{q}}_{n+1}sin\left(q_i\right)-{\stackrel{.}{q}}_{n+2}cos\left(q_i\right)-2lcos\left(q_{n+3}-q_i\right){\stackrel{.}{q}}_{n+3}\\ -2l{\displaystyle \sum _{k=1}^{i-1}}cos\left(q_i-q_k\right){\stackrel{.}{q}}_k-l{\stackrel{.}{q}}_i-{\stackrel{.}{q}}_{n+3+i}R=0.& (4)\end{array}$

The symbols cos and sin are written as C and S respectively, then the kinetic energy of the snake-like robot system is given by

$\begin{array}{l}T=\frac{1}{2}\left[m_h\left({\stackrel{.}{q}}_{n+1}^2+{\stackrel{.}{q}}_{n+2}^2\right)+J_h{\stackrel{.}{q}}_{n+3}^2\right]+\frac{1}{2}m{\displaystyle \sum _{i=1}^n[{\stackrel{.}{q}}_{n+1}^2+{\stackrel{.}{q}}_{n+2}^2}\\ +4l^2{\stackrel{.}{q}}_{n+3}^2+4l^2\left[{\left({\displaystyle \sum _{k=1}^{i-1}S\left(q_k\right)}{\stackrel{.}{q}}_k\right)}^{\text{2}}\text{+}{\left({\displaystyle \sum _{k=1}^{i-1}C\left(q_k\right)}{\stackrel{.}{q}}_k\right)}^{\text{2}}\right]\\ \text{+}{l}^2{\stackrel{.}{q}}_2^2+4l{\stackrel{.}{q}}_{n+3}\left({\stackrel{.}{q}}_{n+3}C\left(q_{n+3}\right)-{\stackrel{.}{q}}_{n+1}S\left(q_{n+3}\right)\right)\\ +4l{\stackrel{.}{q}}_{n+2}{\displaystyle \sum _{k\text{=}1}^{i-1}C\left(q_k\right)}{\stackrel{.}{q}}_k-4l{\stackrel{.}{q}}_{n+1}{\displaystyle \sum _{k=1}^{i-1}S\left(q_k\right)}{\stackrel{.}{q}}_k+2l{\stackrel{.}{q}}_{n+2}C\left(q_i\right){\stackrel{.}{q}}_i\\ -2l{\stackrel{.}{q}}_{n+1}S\left(q_i\right){\stackrel{.}{q}}_i+\text{8}{l}^2{\stackrel{.}{q}}_{n+3}S\left(q_{n+3}\right){\displaystyle \sum _{k=1}^{i-1}S\left(q_k\right)}{\stackrel{.}{q}}_k\text{+8}{l}^2{\stackrel{.}{q}}_{n+3}\\ C\left(q_{n+3}\right)C{\stackrel{.}{q}}_k+4l^2{\stackrel{.}{q}}_{n+3}{\stackrel{.}{q}}_{2}S\left(q_{n+3}\right)S\left(q_k\right)\\ \text{+}4l^2{\stackrel{.}{q}}_{n+3}{\stackrel{.}{q}}_{2}C\left(q_{n+3}\right)C\left(q_k\right)+4l^{2}S\left(q_i\right){\stackrel{.}{q}}_i{\displaystyle \sum _{k=1}^{i-1}S\left(q_k\right)}{\stackrel{.}{q}}_k\\ +4l^{2}C\left(q_i\right){\stackrel{.}{q}}_i{\displaystyle \sum _{k=1}^{i-1}C\left(q_k\right)}\stackrel{.}{q}]+\frac{1}{2}{\displaystyle \sum _{i=1}^n{J}_y{\stackrel{.}{q}}_i^2\text{+}{J}_{\gamma }{\stackrel{.}{q}}_{n+3+i}^2},\\ \left(i=1,\cdots ,n\right).& (5)\end{array}$

The potential energy of the snake-like robot system is assumed to be

$\begin{array}{ll}U=0.& (6)\end{array}$

The dissipative functions of the snake-like robot system are assumed to be given by

$\begin{array}{l}D=\frac{1}{2}{D}_{xy}{\displaystyle \sum _{i=1}^n[{\stackrel{.}{q}}_{n+1}^2+{\stackrel{.}{q}}_{n+2}^2+4l^2{\stackrel{.}{q}}_{n+3}^2}\\ +4l^2\left[{\left({\displaystyle \sum _{k=1}^{i-1}S\left(q_k\right)}{\stackrel{.}{q}}_k\right)}^{\text{2}}\text{+}{\left({\displaystyle \sum _{k=1}^{i-1}C\left(q_k\right)}{\stackrel{.}{q}}_k\right)}^{\text{2}}\right]\\ \text{+}{l}^2{\stackrel{.}{q}}_2^2+4l{\stackrel{.}{q}}_{n+3}\left({\stackrel{.}{q}}_{n+3}C\left(q_{n+3}\right)-{\stackrel{.}{q}}_{n+1}S\left(q_{n+3}\right)\right)\\ +4l{\stackrel{.}{q}}_{n+2}{\displaystyle \sum _{k=1}^{i-1}C\left(q_k\right)}{\stackrel{.}{q}}_k-4l{\stackrel{.}{q}}_{n+1}{\displaystyle \sum _{k=1}^{i-1}S\left(q_k\right)}{\stackrel{.}{q}}_k+2l{\stackrel{.}{q}}_{n+2}C\left(q_i\right){\stackrel{.}{q}}_i\\ -2l{\stackrel{.}{q}}_{n+1}S\left(q_i\right){\stackrel{.}{q}}_i+\text{8}{l}^2{\stackrel{.}{q}}_{n+3}S\left(q_{n+3}\right){\displaystyle \sum _{k=1}^{i-1}S\left(q_k\right)}{\stackrel{.}{q}}_k\text{+8}{l}^2{\stackrel{.}{q}}_{n+3}\\ C\left(q_{n+3}\right){\displaystyle \sum _{k=1}^{i-1}C\left(q_k\right)}{\stackrel{.}{q}}_k+4l^2{\stackrel{.}{q}}_{n+3}{\stackrel{.}{q}}_{2}S\left(q_{n+3}\right)S\left(q_k\right)\\ \text{+}4l^2{\stackrel{.}{q}}_{n+3}{\stackrel{.}{q}}_{2}C\left(q_{n+3}\right)C\left(q_k\right)+4l^{2}S\left(q_i\right){\stackrel{.}{q}}_i{\displaystyle \sum _{k=1}^{i-1}S\left(q_k\right)}{\stackrel{.}{q}}_k\\ +4l^{2}C\left(q_i\right){\stackrel{.}{q}}_i{\displaystyle \sum _{k=1}^{i-1}C\left(q_k\right)}{\stackrel{.}{q}}_k]+\frac{1}{2}{\displaystyle \sum _{i=1}^n{D}_y{\stackrel{.}{q}}_i^2}.& (7)\end{array}$

The Routh equation of the snake-like robot system can be given by

$\begin{array}{l}\frac{d}{dt}{\frac{\partial T}{\partial \stackrel{.}{q}}}_s-\frac{\partial T}{\partial q_s}={\text{Q}}_s+{\displaystyle \sum _{\beta =1}^n}{\lambda }_{\beta }\frac{\partial f_{\beta }}{\partial {\stackrel{.}{q}}_s}\\ (s=1,\cdots ,2n+3;\beta =1,\cdots ,n).& (8)\end{array}$

After derivation of the constraints of the snake-like robot system (4), we have

$\begin{array}{ll}{ḟ}_{\beta }(q,\stackrel{.}{q})=0.& (9)\end{array}$

From Equation (8) and (9), the Lagrange multiply λ can be calculated as

$\begin{array}{ll}\lambda =\left\{{\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n\right\}& (10)\end{array}$

Submitting (10) into (8), we can derive

$\begin{array}{ll}\frac{d}{dt}{\frac{\partial T}{\partial \stackrel{.}{q}}}_s-\frac{\partial T}{\partial q_s}=Q_s+{\Lambda }_s,(s=1,\cdots ,2n+3)& (11)\end{array}$

where ${\Lambda }_s={\displaystyle \sum _{\beta =1}^n}{\lambda }_{\beta }\frac{\partial f_{\beta }}{\partial {\stackrel{.}{q}}_s}.$

The motion equation (12) of the complete system corresponding to the snake-like robot system (4, 11) can be given as

$\begin{array}{ll}\frac{d}{dt}{\frac{\partial L}{\partial \stackrel{.}{q}}}_s-\frac{\partial L}{\partial q_s}={Q_s}^{\prime }+{\Lambda }_s,& (12)\end{array}$

where ${Q_s}^{\prime }=-\frac{\partial D_s}{\partial {\stackrel{.}{q}}_s}+\tau -\frac{\partial U}{\partial q_s}$ are the non-potential force, ${\Lambda }_s={\lambda }_{\beta }\frac{\partial f_{\beta }}{\partial {\stackrel{.}{q}}_s}$ the generalized nonholonomic constraint anti-forces, L = T − U the Lagrangian of the snake-like robot system.

Generalized Hamilton Canonical Equations of Snake-Like Robot Systems

Assume that the generalized momentums of snake-like robot systems are

$\begin{array}{l}{p}_1=\frac{\partial L}{\partial {\stackrel{.}{q}}_1}=\frac{1}{2}[(-4m(n-1\left)lS\right(q_{n+3})-2mlS(q_{n+3}+q_1\left)\right){\stackrel{.}{q}}_{n+1}\\ +\left(4m\right(n-1\left)lC\right(q_{n+3})+2mlC(q_{n+3}+q_1\left)\right){\stackrel{.}{q}}_{n+2}\\ +\left(2m\right(2+4(n-1)\left)l^2{C}_{h1}\right){\stackrel{.}{q}}_{n+3}\\ +\left(8m\right(n-1)l^2+2m{l}^2+2J_y){\stackrel{.}{q}}_1+\cdots +\left(4m{l}^2{C}_{1n}\right){\stackrel{.}{q}}_n],& (13)\end{array}$

$\begin{array}{l}{p}_2=\frac{\partial L}{\partial {\stackrel{.}{q}}_2}=\frac{1}{2}[(-4m(n-2\left)lS\right(q_{n+3})-2mlS(q_2\left)\right){\stackrel{.}{q}}_{n+1}\\ +\left(4m\right(n-2\left)lC\right(q_{n+3})+2mlC(q_{n+3}+q_1\left)\right){\stackrel{.}{q}}_{n+2}\\ +\left(2m\right(2+4(n-2)\left)l^2{C}_{h2}\right){\stackrel{.}{q}}_{n+3}\\ +\left(2m\right(2+4(n-2)\left)l^2{C}_{h12}\right){\stackrel{.}{q}}_1\left(8m\right(n-2)l^2+2m{l}^2+2J_y)\\ {\stackrel{.}{q}}_2+\cdots +\left(4m{l}^2{C}_{2n}\right){\stackrel{.}{q}}_n],& (14)\end{array}$

$\begin{array}{l}⋮⋮⋮\\ p_n=\frac{\partial L}{\partial {\stackrel{.}{q}}_n}=\frac{1}{2}[\left(-2mlS\left(q_{n+3}+{\displaystyle \sum _{k=1}^n{q}_k}\right)\right){\stackrel{.}{q}}_{n+1}\\ +\left(-2mlC\left(q_{n+3}+{\displaystyle \sum _{k=1}^n{q}_k}\right)\right){\stackrel{.}{q}}_{n+2}\\ +\left(4m{l}^2{C}_{h2}\right){\stackrel{.}{q}}_{n+3}+\left(4m{l}^2{C}_{1h}\right){\stackrel{.}{q}}_1+\cdots +\left(2m{l}^2+2J_y\right){\stackrel{.}{q}}_n],& (15)\end{array}$

$\begin{array}{l}{p}_{n+1}=\frac{\partial L}{\partial {\stackrel{.}{q}}_{n+1}}=\frac{1}{2}[(2m_h+2mn){\stackrel{.}{q}}_{n+1}+(0){\stackrel{.}{q}}_{n+2}\\ +(-4mnlS(q_{n+3}\left)\right){\stackrel{.}{q}}_{n+3}\\ +(-4m(n-1\left)lS\right(q_{n+3})+2mlS(q_{n+3}+q_1\left)\right){\stackrel{.}{q}}_1+\cdots +\\ \left(-2mlS\left(q_{n+3}+{\displaystyle \sum _{k=1}^n{q}_k}\right)\right){\stackrel{.}{q}}_n],& (16)\end{array}$

$\begin{array}{l}{p}_{n+2}=\frac{\partial L}{\partial {\stackrel{.}{q}}_{n+2}}=\frac{1}{2}[(0){\stackrel{.}{q}}_{n+1}+(0){\stackrel{.}{q}}_{n+2}+(4mnlC\left(q_{n+3}\right)){\stackrel{.}{q}}_{n+3}\\ +\left(4m\right(n-1\left)lC\right(q_{n+3})+2mlC(q_{n+3}+q_1\left)\right){\stackrel{.}{q}}_1+\cdots +\\ \left(-2mlC\left(q_{n+3}+{\displaystyle \sum _{k=1}^n{q}_k}\right)\right){\stackrel{.}{q}}_n],& (17)\end{array}$

$\begin{array}{l}{p}_{n+3}=\frac{\partial L}{\partial {\stackrel{.}{q}}_{n+3}}=\frac{1}{2}[(-4mnlS\left(q_{n+3}\right)){\stackrel{.}{q}}_{n+1}\\ +\left(4mnlC\right(q_{n+3}\left)\right){\stackrel{.}{q}}_{n+2}+(2m_h+2mn){\stackrel{.}{q}}_{n+3}& (18)\end{array}$

$\begin{array}{l}+\left(2m\right(2+4(n-1)\left)l^2{C}_{h1}\right){\dot{q}}_1+\cdots +\left(4m{l}^2{C}_{hn}\right){\stackrel{.}{q}}_n],\\ p_{n+4}=\frac{\partial L}{\partial {\stackrel{.}{q}}_{n+4}}=J_r{\stackrel{.}{q}}_{n+4},& (19)\end{array}$

$\begin{array}{l}⋮\\ p_{2n+3}=\frac{\partial L}{\partial {\stackrel{.}{q}}_{2n+3}}=J_r{\stackrel{.}{q}}_{2n+3}.& (20)\end{array}$

And introduce the Hamiltonian of the snake-like robot system as

$\begin{array}{l}H\left(t,q,\stackrel{.}{q}\right)=p_s{\stackrel{.}{q}}_s-L=p_s{\stackrel{.}{q}}_s\left(t,q,p\right)-L\left(t,q_s,{\stackrel{.}{q}}_s\left(t,q,p\right)\right)\\ =H\left(t,q,p\right),& (21)\end{array}$

where p = {p₁, p₂, ⋯ , p_2n+3} denotes generalized momentums, equation (16) can be partially regularized as

$\begin{array}{l}{\stackrel{.}{q}}_s=\frac{\partial H}{\partial p_s},{ṗ}_s=-\frac{\partial H}{\partial q_s}+{Q_s}^{\prime }+{\Lambda }_s|{\stackrel{.}{q}}_s={\stackrel{.}{q}}_s\left(t,q,p\right),\\ \left(s=1,\cdots ,2n+3\right)& (22)\end{array}$

which is called the generalized Hamilton canonical equation of snake-like robot systems.

Contravariant Algebraic Forms of Snake-Like Robot Systems

For snake-like robot systems, we can introduce contravariant vectors

$\begin{array}{ll}{a}^{\mu }=\{\begin{array}{c}{q}^{\mu }\\ p_{\mu -n}\end{array}\begin{array}{c}\left(\mu =1,\cdots ,2n+3\right),\\ \left(\mu =2n\text{+4,}\cdots \text{,4}n\text{+6}\right),\end{array}& (23)\end{array}$

then the Hamiltonian of snake-like robot systems will be written in the form

$\begin{array}{ll}H\left(t,q_s,p_s\right)=H\left(t,a^{\mu }\right).& (24)\end{array}$

For generalized Hamilton canonical equation (15) of snake-like robot systems, we let

$\begin{array}{l}\left({Q_s}^{\prime }+{\Lambda }_s\right)|q_s=q_s\left(t,q,p\right)={{\Lambda }^{\prime }}_s=-{\Omega }_{sk}\frac{\partial H}{\partial p_k}\\ \left(s,k=1,\cdots ,2n+3\right),& (25)\end{array}$

where

$\begin{array}{ll}{\Omega }_{sk}=\left(\begin{array}{cccc}{\Omega }_{11}& 0& \cdots & 0\\ 0& {\Omega }_{22}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & {\Omega }_{(2n+3)(2n+3)}\end{array}\right),& (26)\end{array}$

then Equation (15) can be expressed in the contravariant algebraic form

$\begin{array}{ll}{ȧ}^{\mu }-S^{\mu \nu }\frac{\partial H}{\partial a^{\nu }}=0,(\mu ,v=1,\cdots ,4n+6)& (27)\end{array}$

where

$\begin{array}{ll}{S}^{\mu \nu }={\omega }^{\mu \nu }+T^{\mu \nu }& (28)\end{array}$

$\begin{array}{ll}{\omega }^{\mu \nu }=\left(\begin{array}{cc}\begin{array}{c}{0}_{(2n+3)(2n+3)}\\ -I_{(2n+3)(2n+3)}\end{array}& \begin{array}{c}{I}_{(2n+3)(2n+3)}\\ 0_{(2n+3)(2n+3)}\end{array}\end{array}\right),& (29)\end{array}$

$\begin{array}{ll}{T}^{\mu \nu }=\left(\begin{array}{cc}{0}_{(2n+3)(2n+3)}& 0_{(2n+3)(2n+3)}\\ 0_{(2n+3)(2n+3)}& -{\Omega }_{kk}\\ \end{array}\right).& (30)\end{array}$

It is obvious that the tensor S^μν is composed of anti-symmetrical tensor ω^μν and symmetrical tensor T^μν.

Algebraic Structure of Snake-Like Robot Systems

Firstly, we study the algebraic structure of snake-like robot systems.

Performing the full derivative of function A(a) along Equation (27), and this derivative is defined as a product:

$\begin{array}{ll}Ȧ(a)=\frac{\partial A}{\partial a_{\mu }}{S}^{\mu \nu }\frac{\partial H}{\partial a^{\nu }}\stackrel{def}{=}A◦H,(\mu ,v=1,\cdots ,2n+3)& (31)\end{array}$

this product satisfies the right-hand assignment law, left-hand assignment law, and scalar law, so we can derive that the snake-like robot system possesses a compatible algebraic structure.

If the snake-like robot system in Equation (27) possesses the Lie algebraic structure, then Equation (31) satisfies the anti-symmetrical property

$\begin{array}{ll}A◦B+B◦A=0,& (32)\end{array}$

and Jacobi identical equation

$\begin{array}{ll}\left[A,\left[B,C\right]\right]+\left[B,\left[C,A\right]\right]+\left[C,\left[A,B\right]\right]=0.& (33)\end{array}$

When considering Equations (28)-(30), Equations (32) and (33) lead to a condition with respect to T^μν

$\begin{array}{ll}{T}^{\mu \nu }+T^{\nu \mu }=0& (34)\end{array}$

$\begin{array}{l}{T}^{\tau \rho }\frac{\partial T^{\mu \nu }}{\partial a^{\rho }}+T^{\mu \rho }\frac{\partial T^{\nu \tau }}{\partial a^{\rho }}+T^{\nu \rho }\frac{\partial T^{\tau \mu }}{\partial a^{\rho }}=0,\\ (\mu ,v,\tau ,\rho =1,\cdots ,4n+6).& (35)\end{array}$

Further, we have Ω_kk = 0, Q_s = 0,(s, k = 1, ⋯ , 2n + 3). Then Equation (27) has no Lie algebraic structure, and we have

Conclusion 1: The snake like-robot systems do not have Lie algebraic structure.

For Equation (31), we define a new product

$\begin{array}{ll}\left[A,B\right]\stackrel{def}{=}A◦B-B◦A,& (36)\end{array}$

we can prove that Equation (36) has anti-symmetrical property, and satisfies the Jacobi identical equation, namely, a new product with Lie algebraic structure, then Equation (27) has

Conclusion 2: The snake like-robot systems have Lie-admissible algebraic structure.

The Poisson's Integral Method of Snake-Like Robot Systems

The classical Poisson integral method includes setting up the Poisson condition of the first integral for the Hamilton system, the Poisson theorem of third integrals is generated from two known integrals by Poisson brackets. The theoretical foundation of this method includes equations of motion of systems with Lie algebraic structure. Because the snake-like robot system has no Lie algebraic structure, it possesses Lie-admissible algebraic structure. Therefore, part of the Poisson integral methods can be applied to snake-like robot systems. Then we have the following conclusions:

Proposition 1: The necessary and sufficient condition on which I(a^μ, t) = c is the first integral of snake-like robot systems (27) in that the I(a^μ, t) satisfies

$\begin{array}{ll}\frac{\partial I}{\partial t}+\left[I,H\right]=0,& (37)\end{array}$

Proposition 2: H = c is a first integral of snake-like robot systems (27), if the Hamiltonian of the system does not depend explicitly on time t, and for${{\Lambda }^{\prime }}_s\text{= 0}$.

Proposition 3: For snake-like robot systems (27), which possess a first integral I(a^μ, t) that contains t, but H and ${{\Lambda }^{\prime }}_s$do not depend explicitly on t, then

$\begin{array}{ll}\frac{\partial }{\partial t}\left(\frac{\partial I}{\partial t}\right)+\left[\frac{\partial I}{\partial t}H\right]+\frac{\partial {{\Lambda }^{\prime }}_s}{\partial t}\frac{\partial I}{\partial a^{\mu }}+\frac{\partial I}{\partial a_{\mu }}{S}^{\mu \nu }\frac{\partial }{\partial a^{\nu }}\left(\frac{\partial H}{\partial t}\right)=0& (38)\end{array}$

i.e.,

$\begin{array}{ll}\frac{\partial }{\partial t}\left(\frac{\partial I}{\partial t}\right)+\left[\frac{\partial I}{\partial t}H\right]=0.& (39)\end{array}$

Namely, $\frac{\partial I}{\partial t}$ is the first integral of the snake-like robot system (27), and $\frac{\partial I^2}{\partial t^2},\dots ,$ are also first integrals of the snake-like robot system.

Proposition 4: For snake-like robot systems (27), which possess a first integral I(a^μ, t) containing a^ρ, but H and ${{\Lambda }^{\prime }}_s$do not depend explicitly on a^ρ, $\frac{\partial I}{\partial a^{\rho }},\frac{\partial I^2}{\partial a^{{\rho }^2}},\cdots ,$ are also first integrals of the snake-like robot system.

Example

We set up a simple snake-like robot which only has one joint, and choose q₁ = φ₁, q₂ = x_h, q₃ = y_h, q₄ = θ_h, q₅ = γ₁ as generalized coordinates.

The relationship between the center of gravity of the first joint (x₁, y₁) and the position of the snake head (x_h, y_h) can be given by

$\begin{array}{l}{x}_1=q_2+2lc\left(q_4\right)+lc\left(q_1\right),\\ y_1=q_3+2ls\left(q_4\right)+ls\left(q_1\right),& (40)\end{array}$

so, the velocities of snake-like systems can be given by

$\begin{array}{l}{ẋ}_1={\stackrel{.}{q}}_2-2ls\left(q_4\right){\stackrel{.}{q}}_4-ls\left(q_1\right){\stackrel{.}{q}}_1,\\ {ẏ}_1={\stackrel{.}{q}}_3+2lc\left(q_4\right){\stackrel{.}{q}}_4+lc\left(q_1\right){\stackrel{.}{q}}_1.& (41)\end{array}$

The constraints of the snake-like robot system are given by

$\begin{array}{l}{f}_{\beta }\left(q,\stackrel{.}{q}\right)={\stackrel{.}{q}}_{2}s\left(q_1\right)-{\stackrel{.}{q}}_{3}c\left(q_1\right)-2lc\left(q_4-q_1\right){\stackrel{.}{q}}_4\\ -l{\stackrel{.}{q}}_1-{\stackrel{.}{q}}_{5}R=0.& (42)\end{array}$

We obtain the kinetic energy of the snake-like robot system

$\begin{array}{l}T=\frac{1}{2}\left(m+m_h\right)\left({\stackrel{.}{q}}_2^2+{\stackrel{.}{q}}_3^2\right)+\frac{1}{2}\left(J_h+2m{l}^2\right){\stackrel{.}{q}}_4^2+\frac{1}{2}\left(J_y+\frac{1}{2}m{l}^2\right)\\ {{\stackrel{.}{q}}^2}_1+2ml{\stackrel{.}{q}}_4\left({\stackrel{.}{q}}_{2}s\left(q_4\right)-{\stackrel{.}{q}}_{3}c\left(q_4\right)\right)\\ +ml{\stackrel{.}{q}}_1\left[{\stackrel{.}{q}}_{2}s\left(q_1\right)-{\stackrel{.}{q}}_{3}c\left(q_1\right)\right]+2m{l}^2{\stackrel{.}{q}}_4{\stackrel{.}{q}}_1\left({\stackrel{.}{q}}_4+{\stackrel{.}{q}}_1\right)\\ s\left(q_4+q_1\right)+\frac{1}{2}{J}_r{\stackrel{.}{q}}_5^2,& (43)\end{array}$

potential energy

$\begin{array}{ll}U=0,& (44)\end{array}$

and dissipative function

$\begin{array}{l}D=\frac{1}{2}{D}_y{\stackrel{.}{q}}_1^2+\frac{1}{2}{D}_{xy}[{\stackrel{.}{q}}_2^2+{\stackrel{.}{q}}_3^2+4l{\stackrel{.}{q}}_4^2+l^2{\stackrel{.}{q}}_1^2+4l{\stackrel{.}{q}}_1({\stackrel{.}{q}}_{2}s\left(q_4\right)\\ -{\stackrel{.}{q}}_{3}c\left(q_4\right))\\ +2l{\stackrel{.}{q}}_1\left({\stackrel{.}{q}}_{2}s\left(q_1\right)-{\stackrel{.}{q}}_{3}c\left(q_1\right)\right)+4l^2{\stackrel{.}{q}}_4{\stackrel{.}{q}}_{1}s\left(q_4+q_1\right)].& (45)\end{array}$

The Lagrange function of the system is written in the form

$\begin{array}{l}L=\frac{1}{2}\left(m+m_h\right)\left({\stackrel{.}{q}}_2^2+{\stackrel{.}{q}}_3^2\right)+\frac{1}{2}\left(J_h+2m{l}^2\right){\stackrel{.}{q}}_4^2+\frac{1}{2}\left(J_y+\frac{1}{2}m{l}^2\right)\\ {\stackrel{.}{q}}_1^2+2ml{\stackrel{.}{q}}_4\left({\stackrel{.}{q}}_{2}s\left(q_4\right)-{\stackrel{.}{q}}_{3}c\left(q_4\right)\right)\\ +ml{\stackrel{.}{q}}_1\left[{\stackrel{.}{q}}_{2}s\left(q_1\right)-{\stackrel{.}{q}}_{3}c\left(q_1\right)\right]+2m{l}^2{\stackrel{.}{q}}_4{\stackrel{.}{q}}_1\left({\stackrel{.}{q}}_4+{\stackrel{.}{q}}_1\right)\\ s\left(q_4+q_1\right)+\frac{1}{2}{J}_r{\stackrel{.}{q}}_5^2.& (46)\end{array}$

Taking the generalized momenta of snake-like robot systems

$\begin{array}{l}{p}_1=\left(J_y+m{l}^2\right){\stackrel{.}{q}}_1+ml\left({\stackrel{.}{q}}_{2}s\left(q_1\right)-{\stackrel{.}{q}}_{3}s\left(q_1\right)\right)+2m{l}^2{\stackrel{.}{q}}_4\\ s\left(q_4+q_1\right),\\ p_2=m_h{\stackrel{.}{q}}_2+2ml{\stackrel{.}{q}}_{4}s\left(q_4\right)+ml{\stackrel{.}{q}}_{1}s\left(q_1\right),\\ p_3=m_h{\stackrel{.}{q}}_3-2ml{\stackrel{.}{q}}_{4}s\left(q_4\right)-ml{\stackrel{.}{q}}_{1}c\left(q_1\right),\\ p_4=\left(J_h+4m{l}^2\right){\stackrel{.}{q}}_4+2ml\left({\stackrel{.}{q}}_{2}s\left(q_4\right)-{\stackrel{.}{q}}_{3}c\left(q_4\right)\right)+2m{l}^2{\stackrel{.}{q}}_1\\ s\left(q_4+q_1\right),\\ p_5=J_r{\stackrel{.}{q}}_5,& (47)\end{array}$

using Equation (47), we can obtain the generalized velocities in the form

$\begin{array}{l}{\stackrel{.}{q}}_1=\frac{mls\left(q_1\right)-\left(J_y+m{l}^2\right)mlc\left(q_1\right)}{\left(J_y+m{l}^2\right)mlc\left(q_1\right)}{p}_1,\\ {\stackrel{.}{q}}_2=\frac{2mlc\left(q_1\right)+mls\left(q_4+q_1\right)}{ml\left(J_h+4m{l}^{2}s\left(q_1\right)+ml\right)}{p}_2,\\ {\stackrel{.}{q}}_3=\frac{\left(J_y+m{l}^2\right)\left(J_y+m{l}^2\right)ml+2m{l}^{2}s\left(q_4+q_1\right)mlc\left(q_1\right)}{4ml\left(s\left(q_1\right)-s\left(q_1\right)\right)\left(J_y+m{l}^2\right)}{p}_3,\\ {\stackrel{.}{q}}_4=\frac{m_{h}mls\left(q_4\right)\left(s\left(q_1\right)-s\left(q_1\right)\right)}{2ml}{p}_4,\\ {\stackrel{.}{q}}_5=\frac{P_5}{J_r}.& (48)\end{array}$

The Hamiltonian of the snake-like robot system can be expressed as

$\begin{array}{l}H=\frac{1}{2}\frac{mls\left(q_1\right)-\left(J_y+m{l}^2\right)mlc\left(q_1\right)}{\left(J_y+m{l}^2\right)mlc\left(q_1\right)}{p}_1^2\\ +\frac{mlc\left(q_1\right)+mls\left(q_4+q_1\right)}{ml\left(J_h+4m{l}^{2}s\left(q_1\right)+ml\right)}{p}_2^2\\ +\frac{\left(J_y+m{l}^2\right)\left(J_y+m{l}^2\right)ml+2m{l}^{2}s\left(q_4+q_1\right)mlc\left(q_1\right)}{4ml\left(s\left(q_1\right)-s\left(q_1\right)\right)\left(J_y+m{l}^2\right)}{p}_3^2\\ +\frac{ml\left(J_y+m{l}^2\right)+\left(s\left(q_1\right)-s\left(q_1\right)\right)}{J_h+4m{l}^{2}s\left(q_1\right)}{p}_4^2+\frac{1}{2}\frac{{P_5}^2}{J_r}.& (49)\end{array}$

Using Equations (47)–(49), we can obtain

$\begin{array}{l}{ṗ}_1=\frac{1}{2}\frac{mlc\left(q_1\right)+\left(J_y+m{l}^2\right)}{\left(J_y+m{l}^2\right)ml{c}^2\left(q_1\right)}{p}_1^2\\ +\frac{mls\left(q_1\right)+mlc\left(q_4+q_1\right)}{ml\left(J_h+4m{l}^2{s}^2\left(q_1\right)c\left(q_1\right)+ml\right)}{p}_2^2+\\ \frac{2m{l}^{2}c\left(q_4+q_1\right)mlc\left(q_1\right)}{4ml\left(c\left(q_1\right)-s^2\left(q_1\right)\right)\left(J_y+m{l}^2\right)}{p}_3^2\\ +\frac{ml\left(J_y+m{l}^2\right)+\left(c\left(q_1\right)+s\left(q_1\right)\right)}{J_h+4m{l}^{2}c\left(q_1\right)}{p}_4^2\\ +\frac{1}{2}{D}_y{p}_{1}mlc\left(q_1\right)+D_{xy}{p}_3{p}_{4}s\left(q_4+q_1\right)+m{l}^2{p}_{1}c\left(q_1\right),\\ {ṗ}_2=+\frac{mlc\left(q_1\right)+mls\left(q_4+q_1\right)}{ml\left(J_h+4m{l}^{2}s\left(q_1\right)+ml\right)}{p}_2^2\\ +\frac{ml\left(J_y+m{l}^2\right)+\left(s\left(q_1\right)-s\left(q_1\right)\right)}{4m{l}^{2}s\left(q_1\right)}{p}_4^2\\ +D_{y}ml{p}_5{p}_{1}c\left(q_4\right)+D_{xy}{p}_3+ml{p}_{2}s\left(q_1\right)p_2,\\ {ṗ}_3=\frac{mls\left(q_1\right)-\left(J_y+m{l}^2\right)mlc\left(q_1\right)}{\left(J_y+m{l}^2\right)mlc\left(q_1\right)}\\ +\frac{\left(J_y+m{l}^2\right)\left(J_y+m{l}^2\right)ml+2m{l}^{2}s\left(q_4+q_1\right)mlc\left(q_1\right)}{4ml\left(s\left(q_1\right)-s\left(q_1\right)\right)\left(J_y+m{l}^2\right)}{p}_3^2\\ +D_{y}ml{p}_5{p}_{1}c\left(q_4\right)+D_{xy}{p}_3+J_h+4p_{2}m{l}^{2}s\left(q_1\right)+ml,\\ {ṗ}_4=\frac{mls\left(q_1\right)-mlc\left(q_4+q_1\right)}{ml\left(J_h+4m{l}^{2}s\left(q_1\right)+ml\right)}{p}_2^2\\ +\frac{\left(J_y+m{l}^2\right)\left(J_y+m{l}^2\right)ml+2m{l}^{2}c\left(q_4+q_1\right)mlc\left(q_1\right)}{4ml\left(s\left(q_1\right)-s\left(q_1\right)\right)\left(J_y+m{l}^2\right)}{p}_3^2\\ +D_{y}m{l}^2{p^{\prime }}_4{p}_{1}s\left(q_1+q_4\right)+2ml{D}_{xy}{p}_2+J_y+m{l}^2,\\ {ṗ}_5=J_r{p}_5+D_y{m}^2{l}^2{p}_2{p}_{1}c\left(q_4\right)+D_{xy}{p}_2{p}_4\\ +ml{p}_{2}s\left(q_1\right)p_2,& (50)\end{array}$

We call Equations (48) and (50) the generalized Hamilton canonical equations of the snake-like robot system.

In which

$\begin{array}{ll}\{\begin{array}{c}{{\Lambda }^{\prime }}_1=\frac{1}{2}{D}_y{p}_{1}mlc(q_1)+D_{xy}{p}_3{p}_4\text{s}(q_4+q_1)+m{l}^2{p}_{1}c(q_1),\\ {{\Lambda }^{\prime }}_2=D_{y}ml{p}_5{p}_{1}c(q_4)+D_{xy}{p}_3+ml{p}_{2}s(q_1)p_2,\\ {{\Lambda }^{\prime }}_3=D_{y}ml{p}_5{p}_{1}c(q_4)+D_{xy}{p}_3+J_h+4p_{2}m{l}^{2}s(q_1)+ml,\\ {{\Lambda }^{\prime }}_4=D_{y}m{l}^2{p^{\prime }}_4{p}_{1}s(q_1+q_4)+2ml{D}_{xy}{p}_2+J_y+m{l}^2,\\ {{\Lambda }^{\prime }}_5={\text{D}}_y{m}^2{l}^2{p}_2{p}_{1}c(q_4)+D_{xy}{p}_2{p}_4+ml{p}_{2}s(q_1)p_2.\end{array}& (51)\end{array}$

Let

$\begin{array}{l}{a}_1=q_1,a_2=q_2,a_3=q_3,a_4=q_4,a_5=q_5,\\ a_6=p_1,a_7=p_2,a_8=p_3,a_9=p_4,a_{10}=p_5,& (52)\end{array}$

then Equation (50) can be expressed in the contravariant algebraic form

$\begin{array}{ll}{ȧ}^{\mu }-S^{\mu v}\frac{\partial H}{\partial a^{\nu }}=0(\mu \nu \text{= 1}\cdots 5,)& (53)\end{array}$

where

$\begin{array}{l}{S}^{\mu v}={\omega }^{uv}+T^{uv}\\ {\omega }^{\mu \nu }=\left(\begin{array}{cc}\begin{array}{c}{0}_{5\times 5}\\ -I_{5\times 5}\end{array}& \begin{array}{c}{I}_{5\times 5}\\ 0_{5\times 5}\end{array}\end{array}\right),T^{\mu \nu }=\left(\begin{array}{cc}{0}_{5\times 5}& 0_{5\times 5}\\ 0_{5\times 5}& -{\Omega }_{k\times k}\end{array}\right)& (54)\end{array}$

using Equations (25) and (51), we have

$\begin{array}{ll}\{\begin{array}{c}-{\Omega }_{11}=\frac{1}{2}{D}_y{a}_{1}mlc(a_1)+D_{xy}{p}_3{p}_{4}s(a_4+a_1)+2s(a_4)m{l}^2{p}_{1}c(a_1)\\ -{\Omega }_{22}=D_{y}ml{p}_5{p}_{1}c(a_4)+D_{xy}{p}_1+ml{a}_{4}s(a_1)a_5\\ -{\Omega }_{33}=2D_{y}ml{p}_5{a}_{3}c(q_4)+D_{xy}{p}_1+J_h+4a_{4}m{l}^{2}s(a_1)+ml\\ -{\Omega }_{44}=D_{y}m{l}^2{p}_3{a}_{1}s(a_1+a_4)+2ml{D}_{xy}{p}_1+J_y+m{l}^2\\ -{\Omega }_{55}={\text{D}}_y{m}^2{l}^2{p}_3{p}_{1}c(a_4)+D_{xy}{p}_1{p}_4+ml{a}_{7}s(a_1)p_2.\end{array}& (55)\end{array}$

Substituting Equations (53) and (54) into Equation (27) leads to the contravariant algebraic form of snake-like robot systems

$\begin{array}{ll}\{\begin{array}{c}{ȧ}_1=\frac{mls(a_1)-(J_y+m{l}^2)mlc(a_1)}{(J_y+m{l}^2)mlc(a_1)}{p}_1+2m{l}^2\text{s}(a_4+a_1)mlc(a_1)p_2\\ {ȧ}_2=\frac{2mlc(a_1)+ml\text{s}(a_4+a_1)}{ml(J_h+4m{l}^{2}s(a_1)+ml)}{p}_1\\ {ȧ}_3=\frac{(J_y+m{l}^2)(J_y+m{l}^2)ml+2m{l}^{2}s(a_4+a_1)mlc(a_1)}{4ml(s(a_1)-s(a_1))(J_y+m{l}^2)}{p}_3,\\ {ȧ}_4=\frac{m_{h}mls(a_4)(s(a_1)-c(a_1))}{2ml}{p}_1,\\ {ȧ}_5=\frac{p_1}{J_r}+2m{l}^{2}c(a_4+a_1)mlc(a_1),\\ {ṗ}_1=\frac{1}{2}\frac{mlc(a_1)+(J_y+m{l}^2)}{(J_y+m{l}^2)ml{c}^2(a_1)}{p_1}^2+\frac{mls(a_1)+mlc(a_4+a_1)}{ml(J_h+4m{l}^2{s}^2(a_1)c(a_1)+ml)}{p_2}^2+\\ \frac{2m{l}^{2}c(a_4+a_1)mlc(a_1)}{4ml(c(a_1)-s^2(a_1))(J_y+m{l}^2)}{p_4}^2+\frac{1}{2}{D}_y{p}_{1}mlc(a_1)+D_{xy}{p}_4{p}_3\text{s}(a_4+a_1),\\ {ṗ}_2=\frac{mlc(a_1)+ml\text{s}(a_4+a_1)}{ml(J_h+4m{l}^{2}s(a_1)+ml)}{p_1}^2+\frac{ml(J_y+m{l}^2)+(s(a_1)-c(a_1))}{4m{l}^{2}s(a_1)}{p_4}^2\\ +D_{y}ml{p}_5{p}_{1}c(q_4)+D_{xy}{p}_3+ml{p}_{2}s(a_1)p_2,\\ {ṗ}_3=\frac{mls(a_1)-(J_y+m{l}^2)mlc(a_1)}{(J_y+m{l}^2)mlc(a_1)}+D_{y}ml{p}_5{p}_{1}c(a_4)+D_{xy}{p}_3+J_h\\ +4p_{2}m{l}^{2}s(a_1),\\ {ṗ}_4=\frac{mls(a_1)-mlc(a_4+a_1)}{ml(J_h+4m{l}^{2}s(a_1)+ml)}{p_2}^2+\frac{(J_y+m{l}^2)ml+2m{l}^{2}c(a_4+a_1)mlc{a}_1}{4ml(s(a_1)-s(a_1))(J_y+m{l}^2)}{p_4}^2,\\ {ṗ}_5=D_y{m}^2{l}^2{p}_2{p}_{1}c(a_4)+D_{xy}{p}_3{p}_4+ml{p}_{2}s(a_1)p_3\end{array}& (56)\end{array}$

From Proposition (2), the Hamiltonian of the system is written in the form

$\begin{array}{l}H=\frac{1}{2}\frac{mls\left(a_1\right)-\left(J_y+m{l}^2\right)mlc\left(a_1\right)}{\left(J_y+m{l}^2\right)mlc\left(a_1\right)}{p_1}^2\\ +\frac{mlc\left(a_1\right)+mls\left(a_4+a_1\right)}{ml\left(J_h+4m{l}^{2}s\left(a_1\right)+ml\right)}{p_2}^2+\\ \frac{\left(J_y+m{l}^2\right)\left(J_y+m{l}^2\right)ml+2m{l}^{2}s\left(a_4+a_1\right)mlc\left(a_1\right)}{4ml\left(s\left(a_1\right)-c\left(a_1\right)\right)\left(J_y+m{l}^2\right)}{p_3}^2\\ +\frac{ml\left(J_y+m{l}^2\right)+\left(s\left(a_1\right)-c\left(a_1\right)\right)}{J_h+4m{l}^{2}s\left(a_1\right)}{p_4}^2+\frac{1}{2}\frac{{p_5}^2}{J_r}={\text{C}}_1,& (57)\end{array}$

and is the first integral.

Using Proposition (1), we can obtain the following integrals:

$\begin{array}{l}{I}_1={\displaystyle \int }\frac{mls\left(a_1\right)-\left(J_y+m{l}^2\right)mlc\left(a_1\right)}{\left(J_y+m{l}^2\right)mlc\left(a_1\right)}dt\\ +4ml\left(s\left(a_1\right)-c\left(a_1\right)\right)\text{s}\left(a_4+a_1\right){p_2}^2={\text{C}}_2,& (58)\end{array}$

$\begin{array}{l}{I}_2={\displaystyle \int }2m{l}^2\text{s}\left(a_4+a_1\right)mlc\left(a_1\right)p_1+D_{y}4m{l}^{2}s\left(a_1\right)dt\\ +\frac{m{l}^2{D}_{xy}s\left(a_4\right)p_2{a}_5}{4m{l}^{2}s\left(a_1\right)c\left(a_4+a_1\right)}+2mls\left(a_1\right)a_5{p}_3=C_3,& (59)\end{array}$

$\begin{array}{l}{I}_3={\displaystyle \int }2D_{y}m{l}^2{p}_2\text{s}\left(a_4+a_1\right)mlc\left(a_1\right)dt\\ +ml{D}_{xy}\left(J_h+4m{l}^{2}s\left(a_1\right)+ml\right)=C_4.& (60)\end{array}$

The first integral I₂ includes a₅. Using Proposition (4), from I₂ we obtain a new integral.

$\begin{array}{ll}{I}_4=\frac{m{l}^2{D}_{xy}s\left(a_4\right)a_7}{4m{l}^{2}s\left(a_1\right)c\left(a_4+a_1\right)}+2mls\left(a_1\right)p_3=C_4.& (61)\end{array}$

Conclusion

In this paper, we have studied the algebraic structure and Poisson integral theory of snake-like robot systems. This method reduces the expression variables of the snake-like robot and makes the expression more concise. We can also obtain the algebraic structure and Poisson integral theory of other soft robots.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

FJ-L is responsible for the topic selection and research work of the paper. ML is responsible for the research work of the paper. XC participates in the research of the topic selection and the establishment of motion equation.

Funding

This work was Supported by National Natural Science Foundation of China: 11872335 750000RMB, 11472247 900000RMB.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors of this manuscript acknowledge support from the National Natural Science Foundation of China (Grant Nos. 11872335, 11472247).

References

1. Chen L, Wang YC, Li B. Persent state and future direction towards Snake-robot research. Robot. (2002) 24:559–63. doi: 10.1007/s11769-002-0038-4

CrossRef Full Text

2. Hirose S. Biologically Inspired Robots: Snake-Like Locomotors and Manipulators. Oxford: Oxford University Press (1993). p. 351–63.

Google Scholar

3. Liljebäck P, Pettersen KY, Stavdahl Ø, Gravdahl JT. A review on modelling, implementation, and control of snake robots. Rob Auton Syst. (2012) 60:29–40. doi: 10.1016/j.robot.2011.08.010

CrossRef Full Text | Google Scholar

4. Sanfilippo F, Azpiazu J. A review on perception-driven obstacle-aided locomotion for snake robots. Int Conf Control. (2017). doi: 10.1109/ICARCV.2016.7838565

CrossRef Full Text | Google Scholar

5. Li B. Research on snake-like robots and its application in disaster rescue. Rob Technol Appl. (2003). 3:22–6.

6. Wang GB, Chen DS, Chen KW, Zhang ZQ. The current research status and development strategy on biomimetic robot. J Mech Eng. (2015) 13:27–44. doi: 10.3901/JME.2015.13.027

CrossRef Full Text

7. Gray J. The mechanism of locomotion in snakes. J Exp Biol. (1946) 23:101–20. doi: 10.1242/jeb.23.2.101

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Tang CQ, Ma SG, Li B, Wang MH, Wang WC. The study of snake robots biomimetic control method with the environments adaptability. Chin Sci Inform Sci. (2014) 44:647–63. doi: 10.1360/112011-1341

CrossRef Full Text | Google Scholar

9. Liljeback P, Pettersen KY, Stavdahl O, Gravdahl JT. Compliant control of the body shape of snake robots. IEEE Int Conf Rob Autom. (2014) 31:4548–55. doi: 10.1109/ICRA.2014.6907523

CrossRef Full Text | Google Scholar

10. Liljeback P, Pettersen KY, Stavdahl O. Modelling and control of obstacle-aided snake robot locomotion based on jam resolution. IEEE Int Conf Rob Autom. (2009) 15:3807–14. doi: 10.1109/ROBOT.2009.5152273

CrossRef Full Text | Google Scholar

11. Ostrowski J, Burdick J. Gait kinematics for a serpentine robot. IEEE Int Conf Rob Autom. (1994) 2:1294–9. doi: 10.1109/ROBOT.1996.506885

CrossRef Full Text | Google Scholar

12. Guo X, Ma SG, Li BM, Wang H, Wang YC. Modeling and optimal torque control of a snake-like robot based on the fiber bundle theory. Sci China. (2015) 58:183–95. doi: 10.1007/s11432-014-5253-y

CrossRef Full Text | Google Scholar

13. Mei FX. Applications of Lie Groups and Lie Algebras to Constrained Mechanical Systems. Beijing: Science Press (1999). p. 1–167.

14. Mei FX. On the integration methods of non-holonomic dynamics. Int J Non Linear Mech. (2000) 35:229–38. doi: 10.1016/S0020-7462(99)00011-6

CrossRef Full Text | Google Scholar

15. Mei FX, Shi RC. The algebraic structure and the poisson integral method of the nonholonomic systems. J Beijing Inst Technol. (1996) 13:51–5.

16. Fu JL. The algebraic structure and poisson integral procedure of dynamic equation for relativistic Birkhoof's systems. Acta Math Sci. (2001)21:70–8.

Google Scholar

17. Fu JL, Chen XW, Luo SK. Algebraic structure and poisson integrals of relativistic dynamical equations for rotational systems. Appl Math Mech. (1999) 20:1266–74. doi: 10.1007/BF02463795

CrossRef Full Text | Google Scholar

18. Fu JL, Xie FP, Guo YX. Algebraic structure and Poisson's integral theoryof f (R), Cosmology. Int. J.Theor. Phys. (2012) 51:35–48. doi: 10.1007/s10773-011-0875-y

CrossRef Full Text | Google Scholar