- Section on Critical Brain Dynamics, National Institute of Mental Health, National Institutes of Health, Bethesda, MD, United States
Self-organized criticality (SOC) refers to the ability of complex systems to evolve toward a second-order phase transition at which interactions between system components lead to scale-invariant events that are beneficial for system performance. For the last two decades, considerable experimental evidence has accumulated that the mammalian cortex with its diversity in cell types, interconnectivity, and plasticity might exhibit SOC. Here, we review the experimental findings of isolated, layered cortex preparations to self-organize toward four dynamical motifs presently identified in the intact cortex in vivo: up-states, oscillations, neuronal avalanches, and coherence potentials. During up-states, the synchronization observed for nested theta/gamma oscillations embeds scale-invariant neuronal avalanches, which can be identified by robust power law scaling in avalanche sizes with a slope of −3/2 and a critical branching parameter of 1. This precise dynamical coordination, tracked in the negative transients of the local field potential (nLFP) and spiking activity of pyramidal neurons using two-photon imaging, emerges autonomously in superficial layers of organotypic cortex cultures and acute cortex slices, is homeostatically regulated, exhibits separation of time scales, and reveals unique size vs. quiet time dependencies. A subclass of avalanches, the coherence potentials, exhibits precise maintenance of the time course in propagated local synchrony. Avalanches emerge in superficial layers of the cortex under conditions of strong external drive. The balance of excitation and inhibition (E/I), as well as neuromodulators such as dopamine, establishes powerful control parameters for avalanche dynamics. This rich dynamical repertoire is not observed in dissociated cortex cultures, which lack the differentiation into cortical layers and exhibit a dynamical phenotype expected for a first-order phase transition. The precise interactions between up-states, nested oscillations, and avalanches in superficial layers of the cortex provide compelling evidence for SOC in the brain.
Introduction
Brains are inherently complex. Composed of a vast number of cell types, orders of magnitude larger number of connections, and a myriad of structural and functional networks that make up biochemical pathways affecting every spatial and temporal scale of brain organization, brains are deeply challenging to study. Yet, elaborate efforts to assemble the rich and detailed structural evidence on brain circuits have uncovered a rather small set of dynamical features. Highly detailed brain models comprised of thousands of neurons exhibit relatively simple neuronal activity patterns that range from irregular firing to synchronized or oscillatory activity similar to what is measured in real brains [1,2]. Importantly, the major aspect of brain dynamics that has been particularly difficult to understand thus far is how many neurons in the cortex selectively communicate over long distances with associated characteristic times and level of coherence.
The aspect of many interacting elements leading to relatively few dynamical motifs is also a major appeal of self-organized criticality (SOC) [3]. SOC will drive a system toward a second-order phase transition at which dynamics are dominated by universal properties (for review, see [4–10]). The universal property that is of particular interest to brain functions is scale invariance indicative of system-wide correlations that emerge in a system exhibiting SOC. Such scale invariance could be a hallmark of coordinated, yet adaptive, neuronal activity that incorporates large numbers of brain cells.
For the brain, and specifically the cortex, it is currently an intensive field of research whether certain aspects of brain dynamics are true aspects of SOC. Fortunately, numerous key features of SOC can be addressed experimentally in a number of advanced brain preparations [11]. For example, one would expect cortical tissue, developing autonomously in isolation, i.e., in the absence of any instructive sensory and motor inputs, to exhibit scale-invariant properties in the emergent dynamics. One would expect that the emergence of scale invariance is highly regulated as well. For example, it should be robust to slow driving (i.e., exhibiting a separation of time scales) and it should exhibit homeostatic regulation (i.e., returning to scale invariance after profound perturbations), with these regulations failing when essential circuit components are absent or suppressed.
This review summarizes the experimental findings on the emergent dynamics of immature and mature cortical networks when taken in isolation and, thus, disconnected from any external, structuring input or required outputs. These dynamics from cortical tissue in isolation, i.e., in vitro, will be compared to the corresponding dynamical findings in the intact brain, i.e., in vivo. It will be argued that the four dynamical motifs of up-states, nested oscillations, neuronal avalanches, and coherence potentials emerge in superficial layers of the cortex as major hallmarks of SOC in the brain.
Structural Motifs of Self-Organization: Cortical Layers, Pyramidal Neurons, Interneurons, and Glial Cells
Until now, the organotypic cortex culture to date represents the most complex in vitro model of the cortex. Typically taken from a newborn rodent and grown in isolation for up to several months (Figure 1), it captures several core features of cortical organization. First, it exhibits the major division of the mammalian cortex into superficial and deep cortical layers (Figures 1A,B) [12–15], which exhibit distinct functional properties [16,17]. Superficial layers 2/3, called the associative layers, are composed of pyramidal (excitatory) neurons with reduced branching of their apical dendrites that preferentially connect to other intralaminar pyramidal neurons (Figure 1C, top). In contrast, pyramidal neurons from deep layers 5/6 typically feature elaborate apical dendrites and, besides selectively connecting with superficial layers, communicate in vivo with brain regions outside the cortex (Figure 1C, bottom; [18]). In vivo, layer 4 receives sensory input via the thalamus, a brain structure that conveys sensory information to the cortex; this selective connectivity has been found as well for organotypic cocultures using the thalamus and cortex [19–21]. The second important hallmark in cortical organization is the presence of three major interneuron (inhibitory) classes identified as parvalbumin (PV), somatostatin (SST), and vasoactive intestinal peptide (VIP)–expressing neurons, which exhibit highly selective connectivity and specific firing patterns (for review, see [22,23]). Several of these classes, with their layer-specific distribution and electrophysiology, have been demonstrated in organotypic cortex cultures using various immunochemical markers (Figure 1B [14,24,25]). The third and often overlooked hallmark of the cortical microcircuit is the up to 10× higher presence of nonneuronal cells, or glial cells, compared to neurons. Of the three types of glial cells, cortical astrocytes exhibit brain-region–specific control over neuronal excitation and dynamics, among many other functions [26–28]. For organotypic cortex cultures, glial cells have been demonstrated to protect the neuronal tissue from mechanical damage [29,30]. Also, organotypic cortex cultures show clear differences compared to the in vivo cortex, such as an overall reduced connectivity due to a reduction in the third dimension when preparing the brain slice taken into culture [31] or a change in glial protein expression [32]. Organotypic cultures are typically prepared from newborn animals. Therefore, the cortical section of the postnatal brain, which is taken for culturing, is still immature, particularly with respect to the development of superficial layers. However, this immature cortex has benefited from structuring input during embryonic development, which has been shown to be important for somatotopic map formation, i.e., establishing a correspondence between body parts and brain regions [33]. Therefore, the organotypic cortex culture should be best thought of as an in vitro system that has experienced a robust structural organization during embryogenesis and contains the blueprint for the organization of layered, cortical columns in isolation. The next section will summarize how structural self-organization continues as the cortex further matures in isolation and gives rise to several dynamical motifs of neuronal population activity.
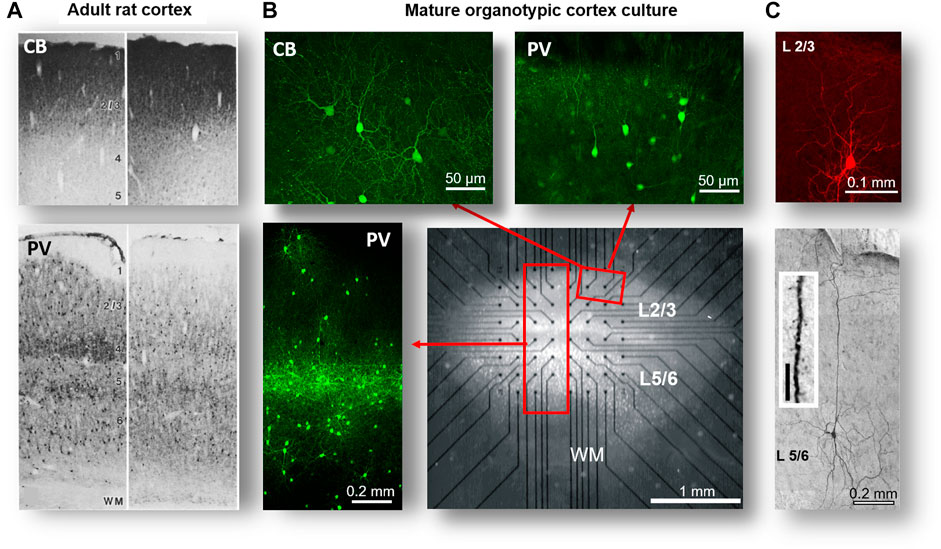
FIGURE 1. Structural motifs of self-organization: cortical layers, pyramidal neurons, and interneurons in organotypic cortex cultures. (A) Coronal sections from the brain in adult rats showing the somatosensory cortex (left) and motor cortex (right). Note high density of calbindin (CB)–positive interneuron stain typical for superficial layers (top) and the layer-dependent bands of parvalbumin (PV)–positive interneurons in deep layers (bottom). (B) Organotypic cortex culture after ∼4 weeks grown on a planar multielectrode array (MEA). Note transparent healthy neural tissue of ∼4 mm2 covering the array at a thickness of ∼100–200 µm and electrodes (black dots), conductors of the MEA. Composite images (red rectangles) indicating superficial layers (L2/3) that contain PV and CB-positive interneurons and deep layers (L5/6) with their intense band of PV-positive interneurons. WM: white matter region. (C) Typical cell body and dendritic morphology of pyramidal neurons from L2/3 and L5, the latter with their characteristically long and branched apical dendrite. Inset: spiny dendrite typical for pyramidal neurons (A reprinted with permission from [165], B modified with permission from [14], and C modified with permission from [18]; Copyright 1998 Society for Neuroscience).
The First and Second Dynamical Motifs of Self-Organization: Up-States and Nested θ/γ-Oscillations
The structural self-organization in organotypic cultures should parallel a self-organization of dynamical motifs found in the fully mature brain. One of these motifs, which is dominant in the electrocorticogram (ECoG) of humans in the awake state, is composed of transient, i.e., up to several seconds lasting, nested oscillations in the theta (θ: 8–12 Hz) and gamma (γ: >25 Hz) range capturing the emergence of population synchrony at many local sites (Figure 2A; [34]). The nesting of high-frequency γ-oscillations to each θ-cycle has been proposed to be essential for working memory [35,36] and information transfer from lower to higher cortical areas (e.g., [37,38]). In mature organotypic cortex cultures, detailed intracellular recordings demonstrated the presence of nested θ/γ-oscillations that arise during pronounced depolarizations that can last up to several seconds (Figures 2B,C; [25,39,40]). This depolarization establishes the well-known dynamical motif of an “up-state”, which is typically defined as a prolonged period of self-sustained network excitation lasting from hundreds of milliseconds to several seconds.
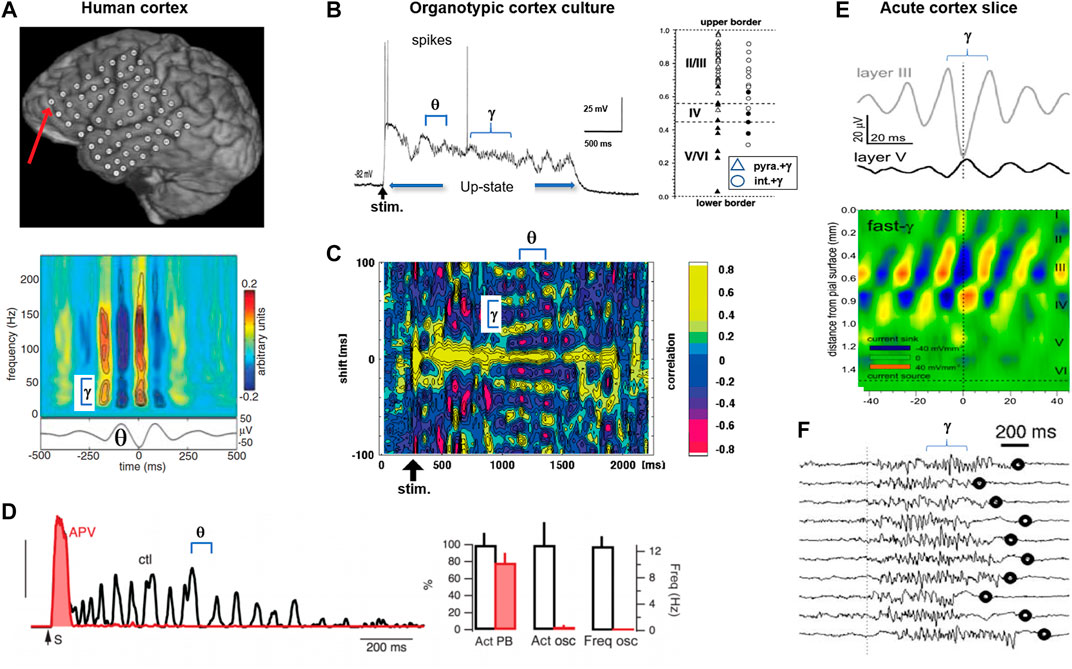
FIGURE 2. The first and second dynamical motif of dynamical self-organization: up-state and nested θ/γ-oscillations in organotypic cortex cultures and acute cortex slices. (A) The human brain displaying distinct periods of nested θ/γ-oscillations at rest and during behavior. Top: electrode array on the cortex surface (circles) recording the electrocorticogram. Bottom: corresponding power spectrum of fast γ-oscillations (>25 Hz; top) phase locked over several cycles of a θ-oscillation (bottom) (reprinted with permission from [34]). (B) In mature organotypic cortex cultures, neuronal activity self-organizes into up-states with nested θ/γ-oscillations in superficial layers. Left: time course of the intracellular membrane potential for a pyramidal neuron in response to a microsecond-lasting, electrical shock stimulation (stim; arrow). Note self-sustained up-state with nested θ/γ-oscillations and sparse occurrence of action potentials (spikes). Right: γ-oscillations are found in pyramidal neurons (triangles) and interneurons (circles) of superficial (open), but not deep layers (filled). (C) Cross correlation over time in the membrane potential of two pyramidal neurons in response to electrical shock stimulation (stim; arrow). Note maintained phase locking of nested θ/γ-oscillations during the up-state with drop in γ-frequency creating a fan-out pattern (subpanels B and C modified from [39]). (D) Self-sustained up-states with θ-oscillations require recurrent, excitatory network connections. Blocking the excitatory NMDA glutamate receptor with the antagonist APV only leaves an initial, short-lasting direct response (organotypic cortex culture) (red). Left: population activity time course to electric shock stimulation (S; arrow). ctl: control. Right: APV only slightly reduces the number of up-states (leftmost bars) but blocks the emergence of oscillations at θ-frequency (middle and rightmost bars). Act: control (reprinted with permission from [42]). (E) In the acute cortex slice, γ-oscillations emerge in superficial layers (CSD analysis) (reprinted with permission from [63]). (F) Acute cortex slice from adult ferret with spontaneous, self-sustained period of fast γ-oscillations in the LFP (reprinted with permission from [43]; Copyright 2008 Society for Neuroscience). Oscillation identifiers have been added to some subpanels for clarity.
The dominance of up-states supporting nested θ/γ-oscillations has several profound implications when studying SOC in isolated cortex preparations. First, it is well known that up-states, particularly prolonged ones (>0.2 s), require stimulation of both the fast-acting (<30 ms) AMPA-glutamate receptor and the slow-acting (>50 ms) NMDA-glutamate receptor (Figure 2D). The prolonged time course of the NMDA-glutamate receptor reduces the precision in action potential timing [41], suggesting that the scaffolding of precise spatiotemporal events requires alternative mechanisms, e.g., interneuron firing. Indeed, pyramidal neurons tend to fire sparsely during up-states, whereas interneurons fire reliably during almost every γ-cycle, a robust finding established in organotypic cortex cultures [25,39,42] and in acute cortex slices [43].
Second, the profound intracellular depolarization found in neurons during up-states indicates an overall increase in network activity. However, the up-state depolarization should not be equated with a higher excitability of individual neurons, which is implicitly assumed in neuronal models that do not take intracellular membrane conductance changes into account, i.e., due to synaptic inputs [44]. On the contrary, individual neurons significantly change in how they respond to additional input during up-states [42,45,46]; this change is effected by a rather expansive combination of a decrease in neuronal input resistance [47], a shortened synaptic integration window [44], transient changes in the balance of excitatory to inhibitory (E/I) synaptic transmission [48], active dendritic conductances [49], a critical slowing down of the threshold to action potential generation [50], and other mechanisms (for further reading, see [51]). Few neuronal simulations take these changes during the buildup of network activity into account [1,2], potentially limiting insights that can be gained into these dynamical motifs from less biophysically oriented modeling.
Third, nested θ/γ-oscillations during the up-state are not blocked by the gap junction blocker carbenoxolone [52] and the activity propagates relatively fast, with a velocity >50 mm/s [53]. These findings support the view that nested θ/γ-oscillations originate in superficial layers from synaptic interactions between local interneurons and pyramidal neurons [39]. These nested oscillations are, therefore, considered to differ from the so-called slow oscillations, which, in vivo, can be induced by deep but not superficial layer stimulation [54]. Slow oscillations were shown in vitro to originate in deep layers and to propagate significantly slower than θ/γ-oscillations locally, yet they were shown to contribute to up-state initiation in superficial layers [55–57].
The propensity of the isolated cortex to produce up-states and nested oscillations is demonstrated in the acute cortex slice as well, in which tissue is studied within hours after being taken from the adult brain. In the acute slice, synchronized nesting during up-states can be induced by an external, pharmacological stimulation that includes direct neuronal depolarization through excitatory glutamate receptors in combination with the neuromodulator acetylcholine (Figures 2E,F; [43,58,59]). Current-source density (CSD) analysis, which tracks the spatial location of neuronal current generation [60–62], demonstrates that nested θ/γ-oscillations originate in superficial layers 2/3 in both the acute cortex slice (Figure 2E; [63]) and the organotypic cortex culture (Figure 3). Developmentally, these dynamical motifs occur in organotypic cultures with a similar time course compared to in vivo, specifically when coculturing the cortex with midbrain regions, which provide the neuromodulator dopamine (Figure 3; [52]). In summary, isolated cortex preparations demonstrate the autonomous emergence of two dynamical motifs in superficial layers of the cortex: up-states and nested oscillations.
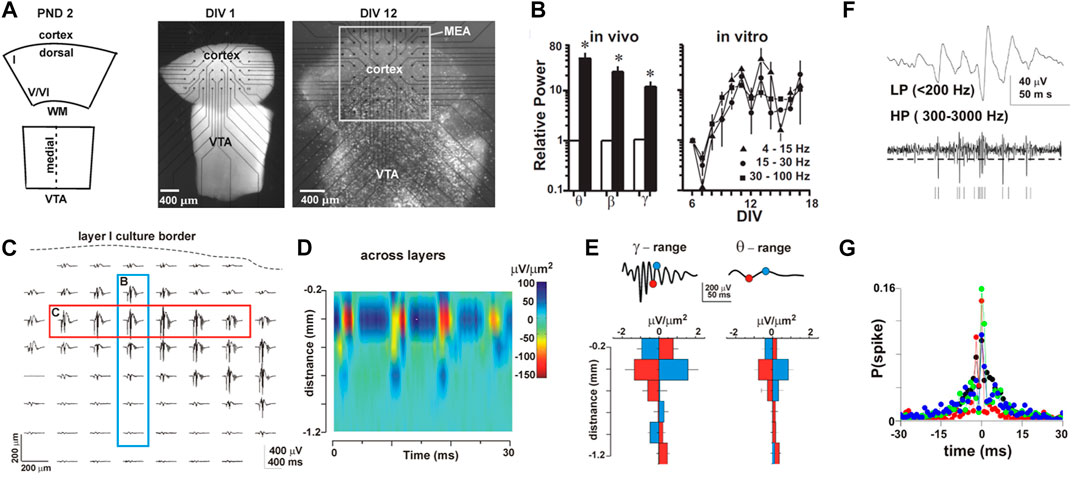
FIGURE 3. Self-organization into nested θ/γ-oscillations in organotypic cortex cultures during the second week postnatal when superficial layers mature. (A) Coronal sections of the cortex and ventral tegmental area (VTA) are combined and grown on the MEA over two weeks in culture. Left: sketch of the coronal cortex slice and midline crossing midbrain region containing the VTA at postnatal day (PND) 1–2, when taken into culture after 1 day in vitro (DIV 1; middle), and about 2 weeks later (DIV 12; right). Note flattening of the culture visible by the increased transparency and expansion of the dorsal tissue on the MEA as superficial layers develop (light microscopic image). (B) Nested oscillations increase in power from first (white) to second (black) postnatal week in vivo (left), a developmental time course mirrored in organotypic cortex-VTA cocultures (right). (C) Spontaneous nested θ/γ-oscillations distribute along the dorsal part of the cortex within superficial layers (red rectangle; single culture). (D) Corresponding CSD (across blue rectangle in C) demonstrates θ/γ-oscillations to originate from synaptic sources (sinks) within superficial layers; CSD density with distance from the upper culture border over time. (E) Summary of average CSD with distance from the dorsal border for 7 cultures separated into θ- and γ-oscillation activity. (F) Separating the broadband LFP into a spike-information–carrying high-frequency band (HP) and the population-activity–containing low-frequency band (LP) demonstrates local spiking (vertical bars) to be phase locked to γ-oscillations. (G) Spike probability is highest at the negative peak of the γ-cycle (nLFP) at t = 0 (color code shows 4 cultures) (reprinted with permission from [52]; Copyright 2008 National Academy of Sciences).
The Third Dynamical Motif of Self-Organization: Neuronal Avalanches
Until now, the two dynamical motifs of up-states and nested oscillations have been treated from the point of view of averages. In this view, an up-state is approximated as a binary transition between two network states that differ in overall activity and oscillations are treated to be spatiotemporally stationary. These views are ill-equipped to capture spatiotemporal propagation in synchronized cortical activity as well as the spatiotemporal variability encountered in spontaneous or evoked instantiation of synchronous activity.
In contrast, the third dynamical motif of self-organization, neuronal avalanches [53], emphasizes both spatiotemporal propagation and variability in cortical synchronization. In that respect, avalanches are related to the spatially compact, wave-like propagation of cortical activity [64–66] as well as the concept of “synfire chains,” spatiotemporally selective cascades of neuronal firing proposed by Abeles [67]. Neuronal avalanche dynamics introduces several major concepts with respect to propagation and variability in cortical synchronization. First, avalanche dynamics quantifies synchronization within a period of duration Δt and successive occurrences of synchronization in near future time periods. It, therefore, covers “instantaneous” and propagated synchrony (see Figure 4). Second, avalanche dynamics exhibits scale-invariance in space and time, which introduces power laws as the statistical measure of variability and the concept of critical branching (see Figures 4, 5). Third, avalanche dynamics allows for the decomposition of propagated synchrony into “coherence potentials,” a previously unknown concept in cortical dynamics for information transfer (Figure 6). Fourth, avalanche dynamics lifts the idea of one particular spatiotemporal pattern to that of “avalanches of avalanches,” which serves as a set of very specific predictions of how spatiotemporal synchronization events in the cortex are linked to each other in sizes and time (see Figure 11). Finally, avalanche dynamics introduces quantitative and absolute measures to study optimization in cortical networks (see Figure 12). We will elaborate on these major conceptual changes in studying cortical synchronization in the following sections.
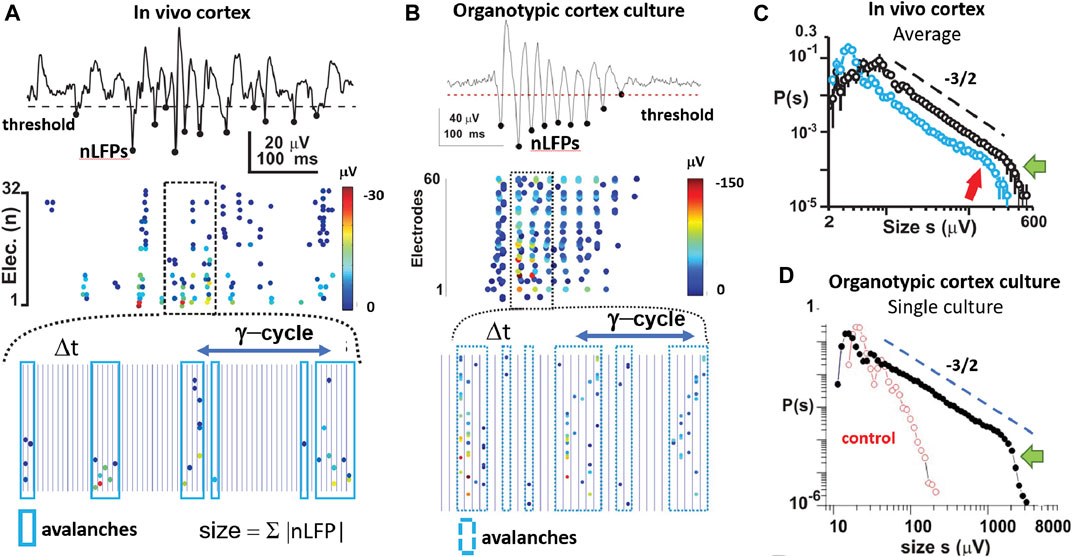
FIGURE 4. The third dynamical motif of self-organization: neuronal avalanches embedded in nested oscillations. (A) Nested θ/γ-oscillations in the superficial layer of a 2-week-old rat in vivo organize as neuronal avalanches that predominantly emerge at oscillation cycles. Top: single cortical electrode with continuous LFP from which negative peak deflections (nLFP; filled circles) are identified after threshold crossing. Middle: corresponding raster of nLFPs on the full 32-MEA exhibiting columnar, variable bouts of synchronization in space and time. nLFP peak amplitudes are color coded. Bottom: expanded view of identified avalanches (blue rectangles) during each γ-oscillation period plotted in discrete time steps of duration Δt (vertical lines). Size of an avalanche is defined as the sum of absolute nLFP amplitudes within each avalanche. (B) As in A but for a transient γ-oscillation in an organotypic culture. (C) At the end of the second week postnatal (black), avalanches distribute in size from 10 to 300 μV followed by a cutoff (green arrow; n = 7 animals). Broken line: slope of −3/2 as guide to the eye. Size distribution is slightly bimodal (red arrow) at the beginning of the second week postnatal (blue; n = 5 animals). (D) Power law in avalanche size distribution for a single culture and exponential size distribution obtained from time-shuffled controls in which spatial and temporal correlations among nLFPs are destroyed (reprinted with permission from [52]; Copyright 2008 National Academy of Sciences).
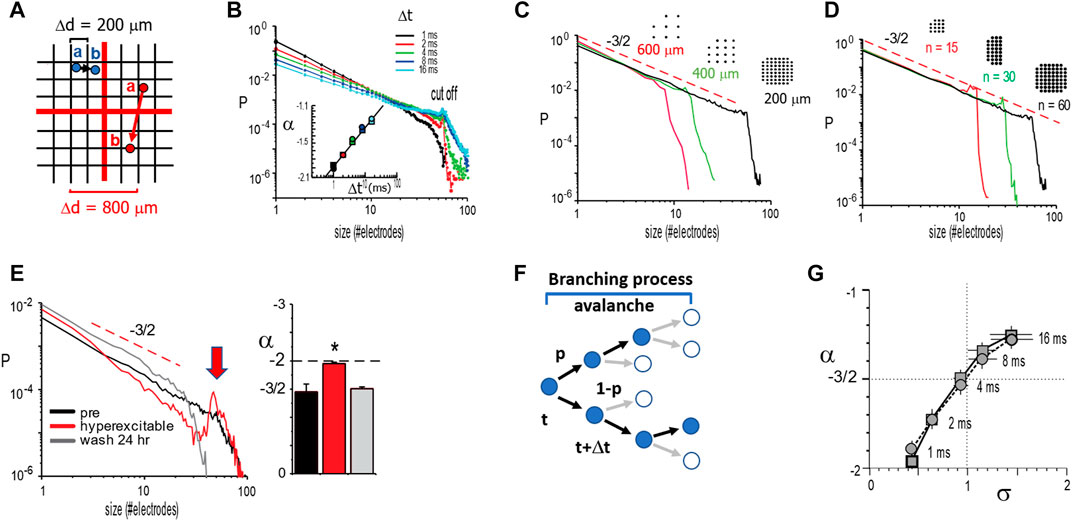
FIGURE 5. Temporal and spatial scaling links size distribution slope −3/2 to a critical branching parameter for neuronal avalanches. (A) When identifying spatial propagation of activity over time (a → b; blue and red circles), the distances between neighboring electrodes on a multielectrode array introduce a discrete spatial scale Δd. For different spatial scales (grids: black: 200 μm; red: 800 µm) and a finite propagation velocity <v>, the time Δt to wait in order to identify propagation toward an electrode is approximately Δt
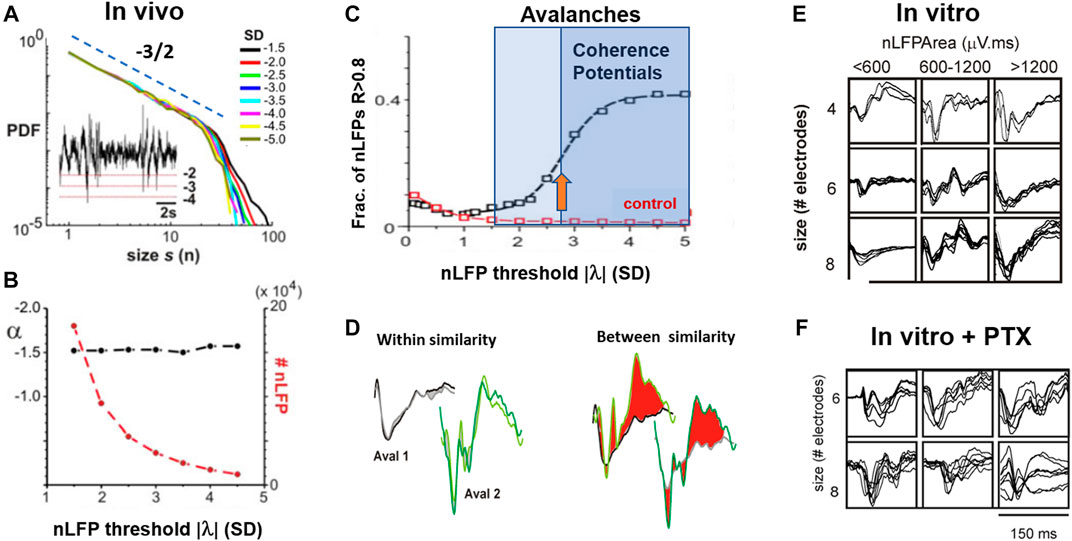
FIGURE 6. The fourth dynamical motif of self-organization: The coherence potential. (A) LFP avalanches from ongoing activity in nonhuman primate show a robust power law in sizes for a range in threshold λ at which nLFPs are detected. Inset: example LFP trace and nLFP detection for three different values of λ. SD: standard deviation. Broken line: slope of −3/2. (B) The number of nLFPs >λ drops several orders of magnitude with an increase in λ, while the power law in sizes remains robust with slope α close to −3/2. (C) The similarity in nLFP waveforms within avalanches rapidly increases for λ> ∼2.7 SD (orange arrow). This threshold-dependent sigmoidal increase in within-nLFP similarity identifies a relatively small number (∼20%) of nLFPs that constitute coherence potentials (cf. B). Control: expected change in similarity after random temporal shifts in the LFP. (D) Complex nLFP waveforms within a coherence potential are highly similar. Example comparison for two subsequent coherence potentials at two sites. Within similarity (gray/black; light/dark green) is high for each coherence potential (CP), whereas between similarity is very low with large waveform deviations highlighted in red for visual contrast. (E) Coherence potentials spontaneously form in vitro in organotypic cultures. Overplot matrix of waveform examples for coherence potentials of size four to eight for nLFP areas in three size categories. (F) Under disinhibited conditions (PTX), coherence potentials are absent (reproduced with permission from [11]).
We start with the basic definition of avalanches using the comparative in vivo and in vitro study on the developmental emergence of neuronal avalanches in superficial layers of the cortex (Figures 3, 4). Gireesh and Plenz [52] used multielectrode array (MEA) recordings to demonstrate the embedding of avalanches into ongoing nested oscillations. Using a simple threshold crossing approach, they extracted the time and amplitude of negative peak deflections in the LFP (nLFP) at each electrode in order to identify the location, time, and size of short-lasting, synchronized activity in a local group of neurons (Figures 3F,G; Figure 4A; [11, 74]). Contiguous time periods with nLFPs were defined as avalanches (Figure 4A, bottom), which resulted in a large variety of different patterns. The size of these patterns, here defined as the absolute sum of nLFPs distributed according to a power law up to a cutoff, serves as the hallmark of neuronal avalanches (Figure 4C). This power law was also found when defining avalanche size by the number of threshold crossing electrodes [52], which approximates the spatial extent of avalanches [68]. The embedding of avalanches in nested oscillations clearly emerges in cortex-VTA cocultures, with avalanche size distributions exhibiting a precise power law up to the cutoff (Figures 4C,D). These findings established that the complex developmental signature of avalanches and nested oscillations in vivo develops autonomously in organotypic cortex cultures with a similar developmental time course; i.e., it is established toward the end of the second week postnatal, in the absence of any structuring sensory input or motor output (Figures 4C,D). The precise match of the power law in avalanche sizes with a slope of −3/2 that emerges from the variability of nested θ/γ-oscillations is not a statistical coincidence. Besides both dynamical motifs being highly sensitive to fast inhibition via the GABAA receptor and slow excitation via the NMDA-glutamate receptor, this coexistence requires fine tuning via the dopamine D1 receptor. Specifically, when the dopamine D1- but not D2-receptor was blocked, nested oscillations continued to emerge, yet the resulting nLFP cascades now exhibited a much steeper size distribution [52]. This regulation of avalanche size distributions to a slope of −3/2 as a function of NMDA/D1 receptor costimulation has been confirmed for superficial layers in acute slices of the prefrontal cortex taken from two-month-old adult rats [69,70] (cf. Figure 11). Recent analysis in vivo in the prefrontal cortex of awake nonhuman primates further confirmed this precise relationship between avalanche dynamics and γ-oscillations [71].
We note that the definition of neuronal avalanches, originally introduced by Beggs and Plenz [53] using the LFP, requires that each local site exceeds a minimal activity threshold. Using a neuronal network model, Poil et al. [72] adopted a scheme in which the summed spiking activity within Δt of the finite-size network is required to exceed a population threshold. This latter definition is very similar to a threshold applied to the LFP, as will be argued in more detail below (cf. Figure 13). It potentially introduces linear terms in certain scaling relationships as pointed out by Villegas et al. [73]. As for statistical tests demonstrating the presence of a power law in avalanche size distributions, we refer to the work of Yu et al. [68] for a more detailed discussion.
To summarize, in vivo experiments in rodents and nonhuman primates, as well as developmentally well-controlled in vitro experiments using organotypic cortex cultures and acute cortex slices, demonstrate a precise regulation between up-states, nested oscillations, and neuronal avalanches that involves fast GABA-mediated inhibition, slow glutamate-mediated excitation, and the neuromodulator dopamine.
Temporal and Spatial Scaling Links Size Distribution Slope −3/2 to a Critical Branching Parameter for Neuronal Avalanches
The identification of avalanches and their implication for SOC has been a particular challenge from an experimental point of view. Besides the structural constraints of superficial layers and developmental period that must be considered, there are additional aspects specific to the emergence of neuronal avalanches themselves that are of importance. These points will be addressed in the following sections. The original identification of neuronal avalanches [53] involved numerous scaling controls to demonstrate that power laws identified in propagated neuronal activity were robust to obvious choices in the experimental setup. Specifically, tracking the spatiotemporal spreading of an avalanche using discrete, spatial sensors such as MEAs requires the appropriate choice of a discrete time interval Δt (Figure 5A). This choice of Δt is imposed by the average, finite propagation velocity <v> for neuronal activity in the system and the introduction of a discrete sampling distance of Δd by the MEA. Three observations laid the groundwork that established the power law in avalanche sizes with a slope α = −3/2. First, increasing Δt, while keeping Δd constant, led to a shallower slope α without change in power law shape. This dependency of α(Δt) itself is approximated by a power law, allowing for scaling collapse in vitro (Figures 5B,C) and in vivo [74]. Second, when changing Δd and accordingly adjusting Δt =<v> * Δd, a robust size exponent of α = −3/2 was obtained (Figure 5C). Third, the cutoff of the power law was simply a function of the finite MEA size and did not change α itself (Figure 5D). Importantly, when cultures were made more excitable, by reducing inhibition in the system using pharmacological means, avalanche size distribution changed from a power law to a bimodal distribution exhibiting an initial steep slope close to −2 and a pronounced system size peak indicative of all-or-none, system-wide population events (Figure 5E). This latter separation into local, nonpropagated events and large system-wide synchronization exhibits the phenotype of a first-order discontinuous phase transition. We will point out in detail in subsequent sections that these scaling operations are not robustly observed in dissociated culture experiments, where an increase in Δt typically steepens the initial slope and uncovers a bimodal cascade size distribution (see below for details; cf. Figure 13), which is more in line with a hyperexcitable system.
The original work by Beggs and Plenz [53] provided the first insights into a critical branching process as a proxy to understand avalanche dynamics in cortical networks as well. A memoryless branching process captures the probability of an initial event to spawn future events at new sites [75]. The corresponding branching parameter, σ, quantifies the average ratio of next generation to the currently active sites (Figure 5F). For random neighbors and σ = 1, the resulting size distribution from such an unbiased or critical branching process exhibits a power law with a slope of −3/2 and can be analytically linked to the self-organized critical sandpile [76]. In line with these basic expectations, it was found that σ is close to one and α = −3/2 for neuronal avalanches at Δt = <v>* Δd (Figure 5G). These findings introduced branching processes as a promising entry point to study avalanche generation.
These original scaling operations for avalanches involved >10 h of continuous recordings in vitro, which is difficult to achieve under standard experimental conditions. Recently, Miller et al. [71,77] extended this scaling analysis of LFP-based avalanches. They identified a scaling exponent of two for an avalanche waveform and a mean size vs. duration relationship in line with predictions for a critical branching process. We also note that LFP avalanches show nearest-neighbor propagation and typically involve no loops [68]. The precise identification of scaling exponents for neuronal avalanches and the conditions under which they are robust is currently an intense field of research. Several alternative processes, both critical and noncritical, have been suggested to produce size exponents close to −3/2 (for further reading, see, e.g., [78,79]). In the following sections, we will focus on additional dimensions of neuronal avalanche dynamics that go beyond these basic scaling relationships. Importantly, the presence of a power law in avalanche sizes and a critical branching parameter of one is linked to several distinct aspects in the emergence and propagation of neuronal activity.
The Fourth Dynamical Motif of Self-Organization: The Coherence Potential
In the previous section, the scaling relationship between the temporal and spatial resolution was reviewed. The third free parameter in assessing avalanche dynamics is the threshold, λ, at which a local site is considered to carry significant activity. For LFP-based avalanches, this threshold is typically chosen to be around three SD of the fluctuations in activity at each site and it has been shown in numerous studies that the presence of a power law is rather robust to the threshold chosen, assuming that it is reasonably outside of baseline noise [53,74,80]. Yet, when systematic evaluations of threshold effects were conducted within a regime of robust power law scaling, it was found that avalanche dynamics implicitly contains a local synchrony threshold that identifies a subclass of avalanches in vivo and in vitro: the coherence potential (Figure 6; [11,81]). Coherence potentials constitute avalanches with nLFPs above a minimal amplitude threshold, typically ∼3 SD, of the ongoing LFP fluctuations [82]. Both avalanches and coherence potentials form power laws in size distributions that are indistinguishable by simple thresholding (Figure 6A). Only when the waveform of nLFPs is explicitly taken into account is a sigmoidal function identified separating the high-fidelity activity propagation regime that constitutes the relatively small number of coherence potentials from that of all other avalanches (Figures 6B–D). The identity of an nLFP waveform correlates with the identity of local spike sequences across different cortical locations [81], suggesting that coherence potentials confer the exact temporal activity of local neuronal firing over wide distances of the cortex. In the human ECoG, coherence potentials were found to initiate finger tapping [83]. The emergence of coherence potentials in cortical networks with avalanche dynamics has been compared to the emergence of “gliders” in cellular automata and hypothesized to be a vehicle of information transfer within the cortex at the network level [11].
The waveform identity in coherence potentials could be expanded to area identity in vitro and in vivo. By grouping nLFPs in coherence potentials into different size categories, waveform similarity within these categories was established and shown to break down when the network was disinhibited (Figures 6E,F). This demonstrates that coherence potentials are actively regulated by the network through the E/I-balance. Coherence potentials were shown to demonstrate initial group size conservation as well. Specifically, it was demonstrated that the area of nLFPs, which participate in a single coherence potential, does not grow nor decay on average as the coherence potential unfolds, a finding that is independent of the size of the initiating nLFP (Figures 7A–C). This property of preserving the local group size initiating an avalanche was lost when the cortex was even mildly disinhibited, upon which propagated activity displayed a within-cascade explosive growth (Figure 7D). This particular approach extends the original identification of the critical branching parameter [53], which was estimated by the ratio between the number of nLFPs in the second (“descendants”) and first (“ancestors”) time bins of an avalanche. The analysis in Figure 7 is more complete by including an nLFP area and waveform and considers all avalanches in their full duration. The critical branching parameter is reflected in the finding that normalized distributions have a stable mode of 1, i.e., log(1) = 0, for up to 20 ms of propagation, which typically covers the full area of recording. The area of the nLFP correlates tightly with the number of neurons firing at the corresponding electrode in vivo and in vitro [11]. Therefore, the critical branching parameter established for coherence potentials demonstrates a conservation law, specifically in which the initiating group size determines all group sizes that emerge within the coherence potential. This complements the finding that spike sequences at different locations within a coherence potential are similar [11].
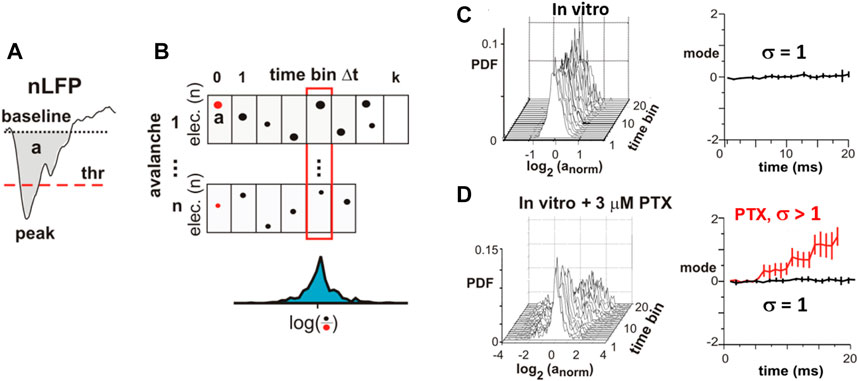
FIGURE 7. Critical branching parameter estimation for coherence potentials. (A) Area a and waveform of a local nLFP identified by threshold (thr) crossing. (B) nLFP areas normalized by the initial nLFP area (red dots) distribute around a median value (blue distribution) after n time bins of duration Δt. (C)In vitro avalanches reveal distribution around the log(1) = 0 mode demonstrating that, as an avalanche unfolds, nLFPs on average neither grow nor decay in the area in line with expectations for a critical branching process with σ = 1. (D) In organotypic cortex cultures that are made more excitable by slightly reducing inhibition (PTX), an expansion of the nLFP area with time from cascade initiation is found in line with the prediction for a supercritical branching process with σ> 1. These experiments demonstrate that a transition from a power law in sizes to a bimodal size distribution under reduced inhibition changes the system from critical to supercritical dynamics (reproduced with permission from [11]).
Oscillation-Synchronization Transition and Neuronal Avalanches: Simulations
Over the last decade, several models have explored these challenging relationships between oscillations, neuronal avalanches, coherence potentials, and critical dynamics. The group of Linkenkaer-Hansen [72,84] demonstrated the emergence of avalanches with
Developmental Self-Organization of Robust Avalanche Dynamics in Organotypic Cortex Cultures
The previous sections demonstrated the emergence of neuronal avalanches around the second week postnatally in culture and in adult slices when tested in isolation. It is well understood that cortical development in vivo involves intrinsically maturing cellular properties and microcircuits in a complex interplay with structuring sensory inputs and motor outputs [17]. Many of these intrinsic embryonic and neonatal dynamics are found to arise autonomously in isolated cortex preparations [16,93]. Yet, so far, only few studies have reliably covered the time course of avalanche emergence during development over prolonged periods. In a first study of postnatal maturation of avalanches in vitro, Stewart and Plenz [94] grew individual organotypic cortex cultures on a planar MEA in sterile chambers over many weeks (Figure 8A). Spontaneous LFP activity emerged toward the beginning of the second week postnatally with a typical bimodal distribution in cascade sizes (Figures 8B–D) indicating a bias toward system-wide population bursts before the time of superficial layer maturation. During the end of the second week, stable power laws in avalanche activity emerged, particularly in those cultures that reached a high level of spontaneous activity and intermittent synchronized activity (Figures 8B–F). Given the late development of superficial layers and the well-known preponderance of deep-layer gap–junctions during the first week postnatal [95], the initial bimodal distribution in cascade sizes might reflect system-wide deep-layer synchronization supported by extensive gap–junction coupling [96], in turn potentially facilitated by transient hyperconnectivity that reduces toward the end of the second postnatal week in vivo [97]. The ability of the young cortex to express neuronal avalanches toward the end of the second week postnatally was recently confirmed for superficial layers in young acute cortex slices [70].
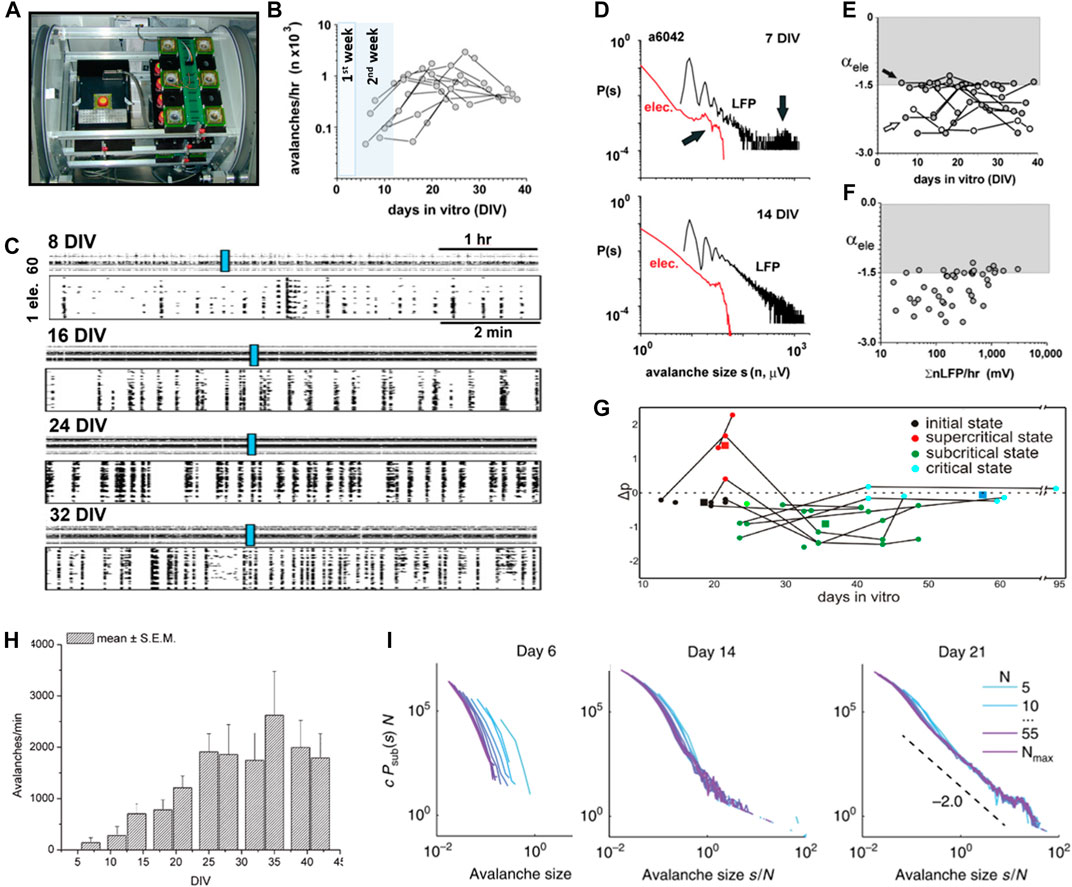
FIGURE 8. Developmental time course for the self-organization of neuronal avalanches in isolated cortex preparations. (A) Overview picture of a custom-made incubator for long-term recordings of individual organotypic cortex cultures on an MEA in a chronic, sterile chamber with head stage (left) and off-recording storage racks (right). For details, see [166]. (reproduced with permission from [167]). (B) In organotypic cortex cultures, avalanches are absent during the first postnatal week in vitro, but increase in rate during the second and third postnatal weeks in line with in vivo maturation of superficial layers. Highlighted periods: equivalent postnatal week in vivo when cultures are taken from pups at postnatal day 1–2. (C) Raster plots of spontaneous nLFP increase in complexity from the first to fifth week (rows) postnatally in vitro. Top of each row: 5 h raster. Bottom of each row: higher temporal resolution for periods indicated by the blue rectangle. (D) Example of early (7 DIV) bimodal size distribution (top) and second week power law size distribution (bottom) in a single organotypic cortex culture. Sizes are defined as the number of active electrodes (red) or summed nLFP (black). (E) Most organotypic cortex cultures achieved α = −3/2 within 2 - 3 weeks in vitro (arrow), except for one (open circle). Time course in avalanche size distribution slope α for individual organotypic cortex cultures. (F) The emergence of slope α = −3/2 correlates with a ∼10x increase in LFP activity. (B–F modified and reproduced with permission from [94]). (G) In dissociated cultures taken at PND 0 - 1, power laws tend to be reported after ∼4 weeks in culture (reproduced under CC-NY license from [98]). (H) Neuronal activity reaches a steady state in dissociated cortex cultures after ∼4 weeks in vitro (reproduced with permission from [107]). (I) Transition of avalanche size distributions from exponential to bimodal in dissociated cortex cultures (reproduced under CC-NY license from [99]).
A second developmental study followed avalanche emergence in dissociated cortex cultures grown on MEAs, starting with neonatal cortex tissue around postnatal day (PND) 0–1 [98]. This study described an initial bimodal size distribution as well, characterized as “supercritical,” followed by a pronounced “subcriticality” and, eventually, after more than 5 weeks in culture, a “critical” condition characterized by stable power laws in size distribution (Figure 8G). While both organotypic and dissociated cultures capture an initial bimodal activity state, the developmental time course in dissociated cultures appears to be delayed by more than three weeks with respect to the buildup of neuronal activity (Figure 8H) and power law formation when compared to in vivo [52]. Recently, Levina and Priesemann [99] showed that the bimodal distribution in avalanche sizes is maintained in dissociated cultures over long periods, questioning the robustness of power laws identified by previous studies for that system (Figure 8I; see also below).
These developmental studies of cortical tissue in isolation suggest distinct differences in neuronal avalanche emergence between organotypic and dissociated cortex cultures, with the latter demonstrating a delayed maturation time course compared to in vivo and a tendency of bimodal size distributions. In contrast, avalanche emergence in organotypic cortex cultures matches that of the in vivo development with respect to layer location and robust power law scaling.
Separation of Time Scales and Homeostatic Regulation of Neuronal Avalanches
A separation of time scales, in which the time course of driving the system is slow enough as to not interfere with the fast avalanching process itself, is of essence in some models of SOC (e.g., [8]). This concept was tested in organotypic cortex cultures grown individually in sterile, closed chambers, while the chamber is tilted periodically. This approach periodically submerges the culture in a liquid culture medium (“feeding”) followed by exposure to normal air (“breathing”) and slowly drives the system through concomitant, large changes in neuronal population activity (Figure 9A, top; [11]). The resulting avalanche size distributions were power law distributed despite strong common, external triggers from the change in environmental condition (Figure 9A, bottom). In a second series of experiments, the well-established effect of rebound activity and rebound bursts after prolonged periods of suppression in excitatory synaptic transmission (Figures 9B,C; [100,101]) was used to study the robustness of avalanche dynamics. Excitatory synaptic transmission was mildly reduced in organotypic cultures by adding a low amount of the fast glutamate receptor antagonist, DNQX, to the culture medium for 24 h. This reduction in excitatory transmission steepened the distribution in cascade sizes. Importantly, after removing the “brake” on excitatory transmission, cascade size distributions rapidly became bimodal with an initial steep slope close to −2, but autonomously recovered within 24 h toward the power law distribution with a slope of −3/2 observed prior to the perturbation (Figure 9D; [11]). These experiments demonstrate homeostatic regulation of avalanche dynamics from a supercritical to a critical state in the absence of any structuring external inputs. A recent study by Ma et al. [102] demonstrated recovery to power-law–distributed avalanches during monocular deprivation in vivo over the course of several days, suggesting that recovery can be initiated from the subcritical phase as well.
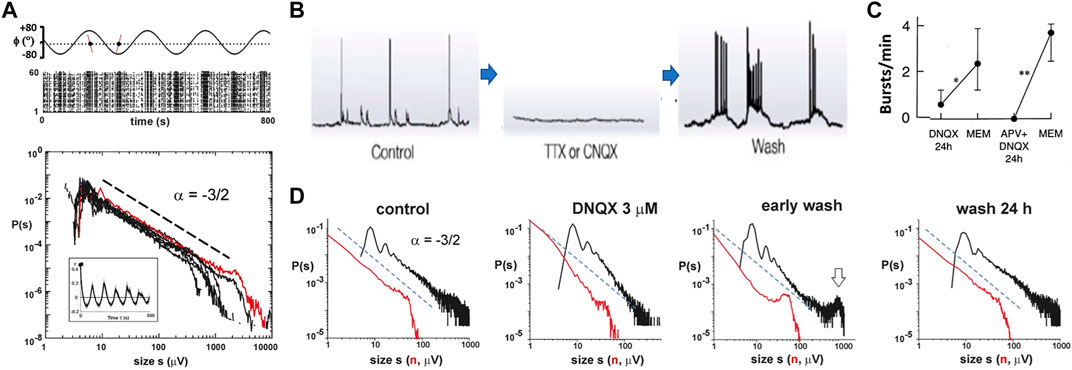
FIGURE 9. Separation of time scales and homeostatic regulation of neuronal avalanches in vitro. (A) Power law in avalanche sizes is preserved during externally induced slow changes in neuronal activity. Top: periodic tilting (ϕ) of the sealed, sterile chamber, which contains the organotypic culture grown on the MEA, alternates culture exposure to feeding medium or air. This slowly drives the network through the corresponding large changes in nLFP activity visualized in the corresponding raster plot. Bottom: power law in avalanche sizes for n = 7 cultures under conditions of periodic tilting. Red: distribution from single culture shown in the raster plot. Inset: average autocorrelation of population activity demonstrating strong correlations from periodic tilting. (B) Intracellular recording demonstrating rebound hyperactivity when neuronal activity is suppressed in dissociated cortex cultures (reproduced with permission from [101]). (C) Increase in rebound population bursts after 24 h of excitatory glutamate receptor suppression in organotypic cortex cultures (reproduced with permission from [100]). (D) Homeostatic regulation of avalanches in organotypic cortex cultures. Control: size distribution before manipulation. DNQX: size distribution during 24 h of reducing excitatory synaptic transmission. Early wash: bimodal size distribution demonstrating hyperexcitability after wash out of DNQX. Wash 24 h: homeostatic return to avalanche dynamics before pharmacological manipulation. Distributions are based on 1 h recordings each from a single culture (A, D reproduced with permission from [11]).
Size-Dependent Nesting in the Temporal Self-Organization of Neuronal Avalanches
Population activity that spontaneously forms in isolated cortex preparations has been typically described as intermittent bursts of variable length, as well as variable intensity, pauses in between (cf. Figure 8C). When analyzing the summed population activity of avalanche activity more closely, the picture of “avalanches within avalanches” readily emerges (Figures 10A,B), which dominates periodically driven cultures as well [11]. Based on the observation of an avalanche, the average time to wait before observing a future avalanche is known as the waiting time distribution and was found to reflect the characteristic time scales of θ/γ-oscillations and up-states (Figure 10C; [103]). This was true for avalanches independent of minimal size and with strong dependence on the E/I balance [104]. By calculating conditional probabilities, Lombardi et al. [105] obtained precise functions capturing the nesting of avalanches with respect to size and time to the next avalanche. It was generally found that there is a high probability that the next avalanche will be smaller than the currently observed avalanche. This finding was robust to a large range of sizes and time windows of observation as well for periodically driven activity (Figure 10D, left, middle). Importantly, this relationship reverses when reducing inhibition; more specifically, the network becomes hyperexcitable at which point future “avalanches” are likely to be larger than the currently observed activity (Figure 10D, right; cf. also Figure 7D). These experimental findings add an important dimension to the discussion of hyperexcitable network activity beyond the finding of bimodal size distributions.
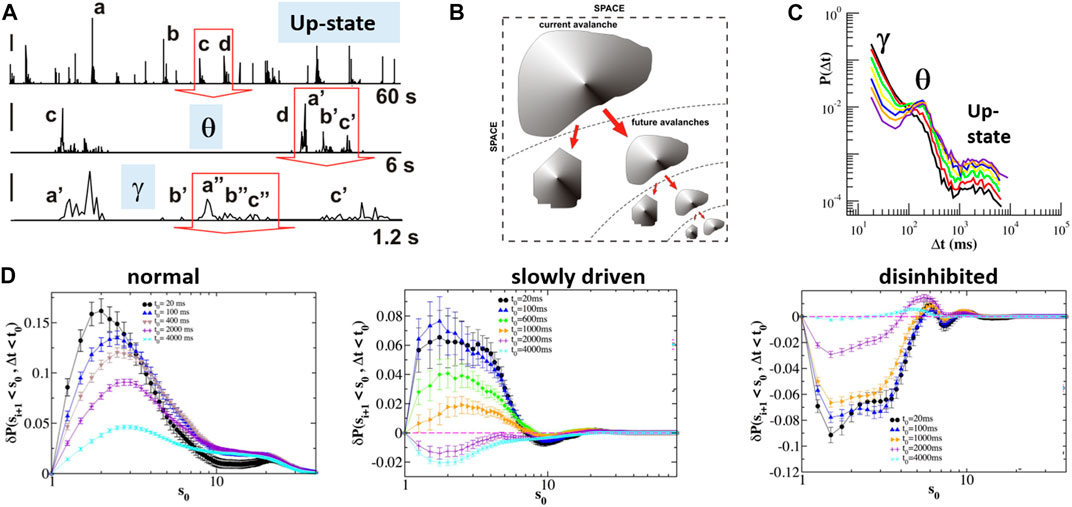
FIGURE 10. Size-dependent nesting in the temporal self-organization of neuronal avalanches. (A) Time course of integrated avalanche activity at three different resolutions. Note the presence of intermittent bursts of successively smaller size [e.g., (a, b, c, d)] that are recursively embedded at smaller time scales [e.g., d-> (a′, b′, c′); b′-> (a″, b″, c″)]. Red arrows indicate the zoomed-in period from larger time scale (single organotypic culture; slowly driven; cf. Figure 9A). Labels place each time scale within the corresponding up-state and nested oscillation regimes. (B) Sketch of size-dependent nesting of avalanches begetting future avalanches (A, B modified and reproduced with permission from [11]). (C) Quiet time distribution of avalanches revealing power law decay with θ-oscillation peak and indicated γ-oscillation and up-state regime (organotypic cortex cultures) (modified and reproduced under CC-BY license from [103]). (D) Quantification of the dependency in preavalanche size and successive quiet time. Avalanches beget future avalanches (left) absent driving and during periodic, slowly driven condition (middle). This relationship is reversed in disinhibited cultures (right). The Y-axis displays the probability that the next avalanche within observation window t0 is smaller given size s0 of the current avalanche (reproduced under CC-BY license from [105]).
Control Parameters Identified in the Regulation of Neuronal Avalanches
The core requirement for SOC is the ability for the system to adjust a control parameter, which allows the system to reside near the critical point [8,106]. Given the complexity of cortical microcircuits regarding neurotransmitter categories (excitatory and inhibitory), neuromodulators (e.g., dopamine, acetylcholine, and serotonin), and brain states (e.g., wakefulness, sleep, and attention), there could be many control parameters that are able to tune cortical networks toward or away from criticality, yet few have been experimentally examined so far. Of common focus, the E/I balance establishes an important control parameter, first demonstrated for avalanches in organotypic cortex cultures [53]. Specifically, reducing fast inhibitory synaptic transmission nonselectively by pharmacological means, rapidly destroys the power law in LFP-based avalanches and causes bimodal distributed cascade sizes (cf. Figure 5E). Similar results have been obtained in dissociated cultures, in which a power law distribution in avalanches changed to a bimodal distribution when inhibition was blocked (e.g., [107]). In more detailed follow-up studies, a reduction in fast synaptic inhibition or in fast and slow synaptic excitation changes the dynamics from avalanches to a “supercritical” or “subcritical”-like condition [108–111]. These studies, by quantifying the distance of bimodal or exponential distributions from a power law, demonstrated that numerous network parameters are maximized at the E/I balance at relatively low level of synchronizations, where avalanche dynamics reigns (Figure 11).
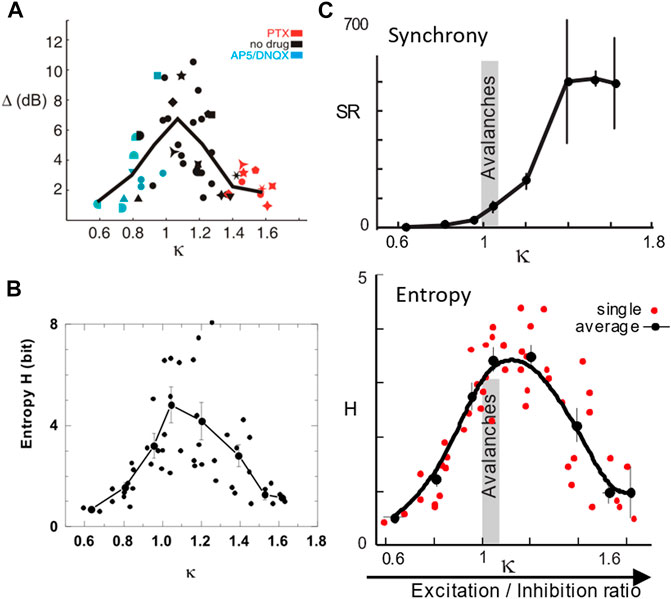
FIGURE 11. The E/I balance is a control parameter for the emergence of avalanches. (A) The dynamic range Δ is maximized when avalanche size distributions are closest to a power law. The parameter κ quantifies the Kolmogorov–Smirnov deviation at 10 equidistant steps of the actual cumulative size distribution from that of a power law [108,109]. When κ = 1, the distribution is a power law, whereas κ>1 for a bimodal distribution and κ< 1 for an exponential distribution. (B) Information capacity is maximized close to κ = 1. (C) Synchronization exhibits a phase transition at κ = 1 (top) where the entropy of synchronization is maximal (bottom) and total synchronization is still orders of magnitude lower than that of the hyperexcitable regime for κ> 1. A–C are derived from LFP avalanches measured in organotypic cortex cultures with κ changed pharmacologically as indicated in A (reproduced from [108–110], respectively; Copyright 2009, 2011, 2012 Society for Neuroscience).
The neuromodulator dopamine has been identified as a second control parameter for the regulation of neuronal avalanches in the prefrontal cortex (Figure 12). Dopamine is crucial for working memory performance, which in turn requires prefrontal cortex functioning [112,113]. Acute prefrontal cortex slices taken from adult rats, exposed to a moderate external excitatory drive, rapidly respond to the presence of dopamine with the emergence of avalanche activity in superficial cortex layers (Figures 12A,B; [69]). At intermediate levels, but not low or high levels of dopamine, nLFPs formed a power law in avalanche sizes with a slope of −3/2 (Figure 12C). The activity was selective for the dopamine D1 receptor and required NMDA-glutamate receptor stimulation, thus matching the pharmacological inverted-U profile reported for working memory performance in the prefrontal cortex [114]. Analysis of the intracellular membrane potential in individual pyramidal neurons in the acute slice, as well as extracellular single-unit analysis in vivo, demonstrated that even large LFP avalanches engage individual pyramidal neurons selectively and this selectivity breaks down when inhibition is reduced [70]. These results taken together suggest that the control parameter dopamine maximizes the spatial extent and occurrence frequency of system-wide avalanches formed by selective activation of distributed pyramidal neurons in the network.
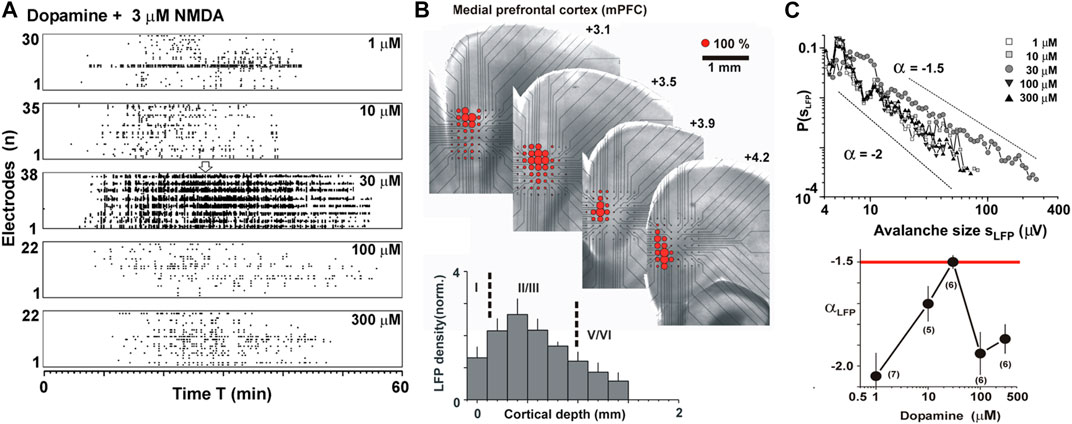
FIGURE 12. Dopamine is a control parameter for the emergence of neuronal avalanches in superficial layers of the cortex. (A) Externally driven acute cortex slice using weak excitatory drive (3 µM NMDA) maximizes avalanche activity at intermediate dopamine concentrations. Raster plots of nLFPs from different slices for increasing dopamine concentrations (top to bottom). (B) Externally driven neuronal avalanches emerge in superficial layers 2/3. Average nLFP density (red circle size) projected onto the light microscopic image of the MEA with the corresponding acute coronal slice from the medial prefrontal cortex. Lower left: nLFP density projected along cortical layers demonstrating that most avalanche activity is induced in L2/3. (C) Avalanche activity exhibits a power law slope of −3/2 at moderate dopamine concentration. Size distributions (top) and corresponding slopes (bottom) are a function of dopamine concentration (reprinted with permission from [69]; Copyright 2006 Society for Neuroscience).
The high sensitivity of the power law to the reported control parameters suggests that thresholding of the LFP is unlikely to play a major role in the origin of scale-invariant avalanches. The LFP is a continuous time-varying signal, for which avalanche processing requires a threshold operation to convert this signal into point process-like data. Such thresholding preserves essential avalanche information in a discretized spatiotemporal raster, e.g., as shown for human avalanches in the fMRI [80]. Yet, thresholding is a nonlinear operation and can affect scaling regimes, particularly, in the temporal domain [73,115]. On the other hand, if thresholding were the underlying cause to observe avalanches, one would expect power law characteristics in the observed dynamics to be robust to relatively mild pharmacological manipulation, which is not the case.
Changes in network connectivity based on local plasticity rules have been demonstrated to establish SOC in models [116], suggesting that plasticity could function as a control parameter (e.g., [117,118]). Since network connectivity was found to support avalanche dynamics in dissociated cultures, it could be considered a control parameter as well [119]. On the other hand, measurements in organotypic cortex cultures and in nonhuman primates in vivo demonstrate that avalanches establish integrative network architectures that are robust to certain plastic changes [77,120,121]. Of note, in vivo studies have shown avalanches to be exquisitely sensitive to the sleep/wakefulness transition [122–126], suggesting sleep [127,128] and sleep-arousal transitions [129] as a behavioral state control parameter.
Lack of Scale-Invariant LFP Avalanches in Deep Layers
The results summarized here were based on LFP recordings taken from high-density arrays oriented in a specific manner with respect to the underlying cortical column. The planar projection of the array was aligned in such a way where propagation of activity in all layers of the cortex can be monitored. Even under those carefully chosen projection conditions, deep-layer LFP activity was strikingly absent, e.g., during spontaneous avalanche emergence in organotypic cortex cultures (cf. Figure 3) or during external glutamate-mediated depolarization, which induces avalanche activity in superficial layers in the acute cortex slice (Figure 13). The absence of LFP-based avalanches in deep layers in vitro could have various causes. First, deep layers could mature incompletely in organotypic culture preparations, e.g., due to lack of subcortical inputs from the thalamus or lack of subcortical targets. However, this argument does not apply to the acute cortex slice. Second, deep layers might require the presence of neuromodulators such as acetylcholine and neurotensin, often provided by brain regions outside the cortex, which regulate the amount of bursting in deep-layer pyramidal neurons [130,131]. However, even in the awake nonhuman primate, the LFP activity in deep layers does not establish power laws even when avalanche activity propagates simultaneously in superficial layers (Fig. S4 of [74]). Third, avalanches in deep layers could be composed of spatially distributed neurons that are difficult to track in the LFP. However, local cortical connectivity favors connections between nearby pyramidal neurons [132] such that avalanche activity would be expected to sum in the LFP. Taken together, these arguments suggest that deep layers might not be able to support scale-invariant avalanche dynamics in general. Even advanced recording techniques in vivo in the awake rodent demonstrate the absence of avalanches in deep layers. Using two-photon imaging in vivo, power laws in spike-based avalanches were identified in cortical layer 2/3 and layer 4 [133], but seem to be absent in deep layers [134].
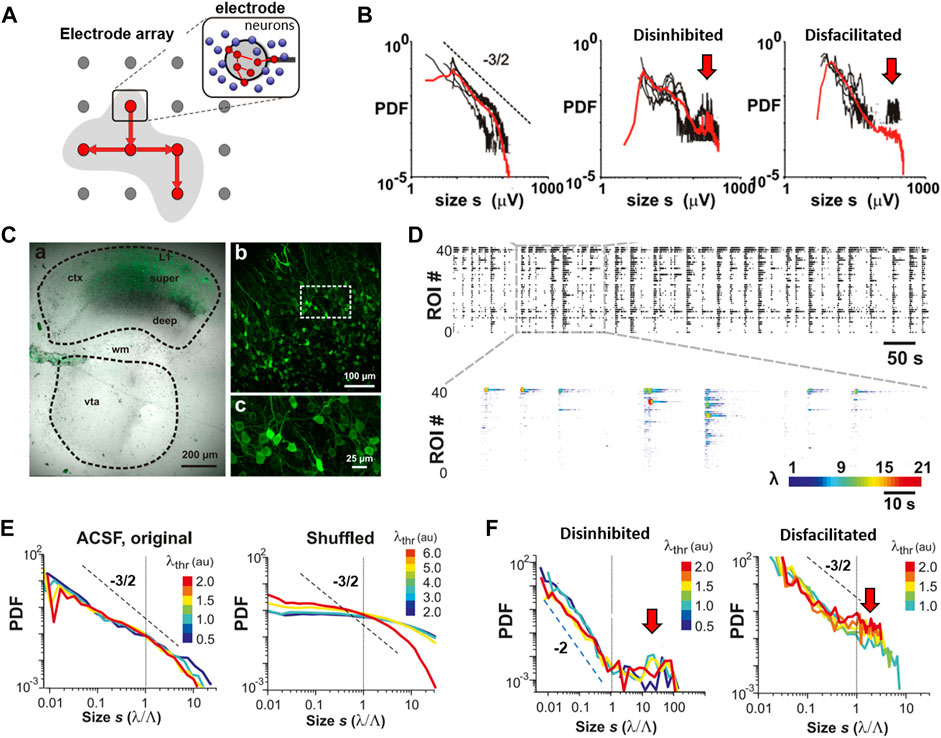
FIGURE 13. Experimental transition from single-nLFP avalanches to spike avalanches in organotypic cortex cultures using two-photon imaging (2PI). (A) Sketch of spatial transformation of propagated nLFPs on the electrode array to propagated spike activity in local neuronal groups (circles; red: spiking; blue: quiet) within the neighborhood of a single electrode (zoom). (B) Distribution of nLFP amplitudes at single electrodes (red: average; black: example single electrodes). Power-law–like distributions change into bimodal distributions when reducing inhibition (disinhibited) or excitation (disfacilitated) (reproduced with permission from [11]). (C)–(F) Reconstruction of spike avalanches in an organotypic cortex culture. (C) Single organotypic coculture of the cortex (ctx) and ventral tegmental area (VTA) after ∼3 weeks grown postnatal. Electroporation of the embryo at E16.5 leads to expression of the genetically encoded calcium indicator YC2.6 in pyramidal neurons from superficial cortex layers (b and c are successive zooms from a). Broken lines: tissue borders. wm: white matter. (D) Raster of spontaneous spike density monitored with 2PI and obtained through deconvolution (n = 40 pyramidal neurons). Top: binarized raster. Bottom: temporally expanded raster segmented with color coded spike intensity λ for each neuron. (E) Spontaneous neuronal activity reveals power laws in spike avalanches that are robust to the threshold λthr applied at the single neuron level (left). Temporal shuffling of spike activity abolishes the power law in avalanche sizes (right). (F) Mild disinhibition changes the power law to a bimodal distribution with an initial steep slope of −2 and system-wide population events (red arrow; cf. Figure 5E). System-wide events also become prominent when mildly reducing excitation (right). (modified for C and C–F reproduced under CC0 license from [124]).
The Negative Transients of the Local Field Potential is the Avalanche: A Local Reconstruction From Spike Avalanches Using Two-Photon Imaging
In the LFP, the structural and dynamical heterogeneity of the network is summed to form a local point source, which does not allow for the identification of the network elements contributing to the LFP [135]. While many experimental findings on avalanches have utilized spatially expansive MEAs, scale invariance predicts that avalanche dynamics should be observable even within the local neighborhood of a single electrode as the spatial resolution increases. This in turn should allow for a more detailed analysis of the underlying network components contributing to scale invariance. In this scenario, the nLFP amplitude should reflect the local neuronal group activity governed by avalanche dynamics (Figure 13A). Accordingly, it was found that the nLFP amplitude distribution at the single-electrode level approximates a power law with a slope of −3/2, which is destroyed when pharmacologically changing the E/I balance (Figure 13B; [11]).
The notion that locally summed the activity of neuronal group firing constitutes avalanche dynamics was first demonstrated directly with two-photon imaging using the genetically encoded calcium indicator (GECI) YC2.60, which exhibits single-spike sensitivity [124,136]. The indicator was selectively expressed in pyramidal neurons from superficial layers in organotypic cortex cultures by electroporation (Figure 13C; [124]). When the coordinated firing in groups of pyramidal neurons was studied, it was found that the highly irregular firing of pyramidal neurons during ongoing spontaneous activity exhibits clear avalanche signatures. We note that these power laws are robust at the temporal scale of Δt = 30 ms (i.e., at an imaging frame rate of 30 Hz) and their slope α is more shallow than −3/2 as predicted from LFP avalanche analysis (cf. Figures 5B,G). Importantly, the power law in avalanche sizes was transformed to a bimodal distribution only after pharmacologically reducing inhibition at which the typical hyperexcitable phenotype of an initial steep slope close to −2 and an overabundance of system-wide cascades robustly presents (Figures 13D–F). We note in passing that a hypersynchronized phenotype in the size distribution also emerges when mildly reducing excitatory transmission (cf. Figures 13B,F, right, “Disfacilitated”). Such a reduction increases spontaneous synchronization in the network due to an overall increase in synaptic transmission efficacy when the global rate of activity drops (e.g., [137]). Taken together, these results demonstrate that the nLFP reflects local avalanche activity and should not be equated to single spikes. In this context, the threshold, λ, applied to extract nLFPs is similar to the population threshold applied to summed spiking activity in identifying neuronal avalanches in network models (e.g., [72]). These findings identify pyramidal neuron activity in superficial cortex layers to carry signatures associated with the organization of avalanches, which, since then, has been confirmed in vivo [124,133,134,138]. The relationship between firing statistics of single neurons and critical exponents in avalanche dynamics has been a major research topic in neural network dynamics (e.g., [139–142]).
Not All Avalanches Are Self-Organized Criticality Avalanches: The Prevalence of Local and System-Wide Population Events in Dissociated Neuronal Cultures
Dissociated cultures [143] have been used for decades to study the autonomous development in structure and dynamics of cortical microcircuits. As a complementary approach to organotypic cultures [20], dissociated neuronal cultures are prepared from cortical tissue typically taken from an embryo at embryonic days 15–18 (that is, 3–6 days before birth). The tissue is then mechanically and enzymatically disintegrated, and the remaining neuronal cell bodies and precursor cells are reseeded on a glia-feeder layer and grown for up to several months in vitro [143]. Dissociated cultures appeal by focusing on the de novo formation of neuronal connections, yet they require careful attention to the design of glia-feeder layers and the culture medium composition. They lack cortical layers and a clear classification of pyramidal neurons and interneurons into functional subtypes, which, in contrast, are both well-established in vivo and organotypic cortex cultures during various developmental stages (see introductory sections). Synchronized bursting has been the hallmark of the developing population activity in dissociated cultures grown on MEAs [144]. Despite the apparent simplicity of this culture system, when systematically studied using a large number of cultures grown on MEAs over many weeks, highly variable outcomes in neuronal synchronization have been documented that depend on plating density, which affects the number of neurons per area and developmental trajectory [145]. Accordingly, the application of avalanche analysis to these synchronized bursts has yielded heterogenous outcomes across and within studies (Figure 14). Nevertheless, a consistent finding emerges from these studies, which deviates from results reported for LFP- and spike-based avalanches in organotypic cortex cultures, as detailed below.
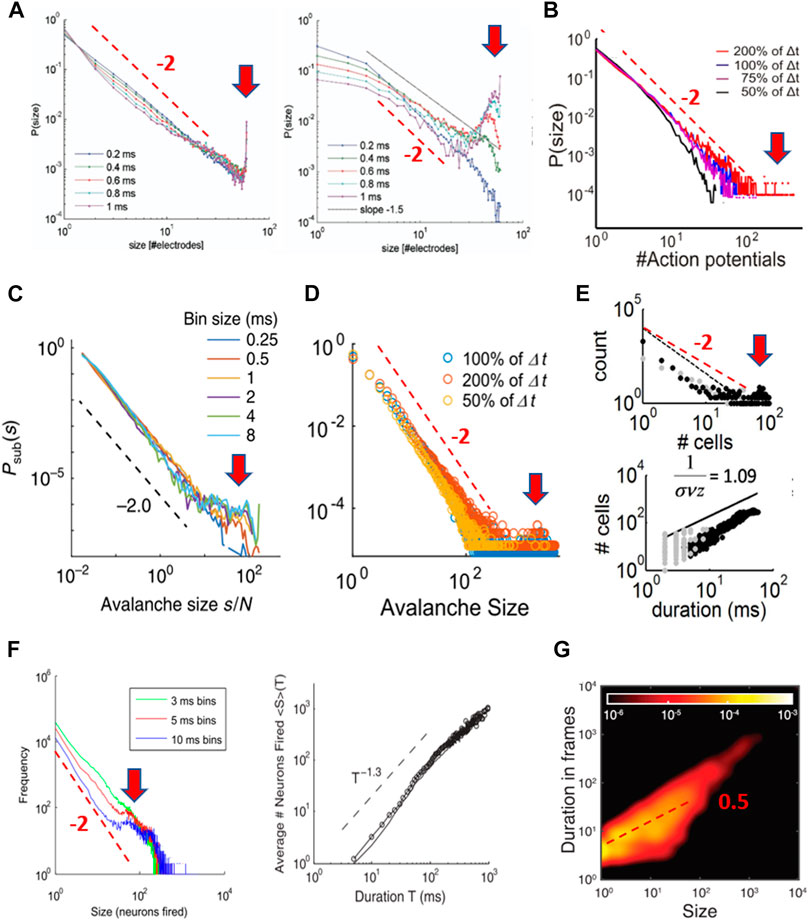
FIGURE 14. Spike “avalanches” in dissociated cultures display the scaling characteristic of hyperexcitable dynamics. (A) Spike avalanches in dissociated cultures exhibit a steeper initial slope and become more bimodal with an increase in Δt. Left: cultures; Right: model (reproduced with permission from [107]). (B) With an increase in Δt, spike avalanches in dissociated culture change from exponential to bimodal size distribution with steep initial slope close to −2 (reproduced under CC-NY license from [98]). (C) Initial slope of −2 and bimodality with an increase in Δt in mature dissociated cultures (reproduced under CC-NY license from [99]). (D) Bimodal size distributions in dissociated cultures around the mean interspike interval Δt exhibit an initial slope of −2. The mean interspike interval Δt has been used as a proxy at which the size distribution should show a power law with slope α = −3/2 (see Figure 5) (reproduced with permission from [146]). (E) Bimodal size distribution and linear mean-size-to-duration relation at Δt close to the mean interspike interval for dissociated cultures (reproduced under CC-NY license from [147]). (F) Spike avalanches of unknown layer origin in organotypic cortex cultures. Left: the bimodal size distribution and steepening initial slope with an increase in Δt suggest hyperexcitable culture condition. Right: near linear mean-size-vs.-duration scaling similar to spike avalanches from dissociated cultures in E suggests deviation from critical branching that predicts a slope of 2 (reproduced under CC-BY license from [157]). (G) Duration-to-mean-size slope close to 1/2 in dissociated cultures prepared from postnatal tissue in line with prediction for a critical branching process (reproduced under CC-BY license from [163]). Subpanels A–F have been modified by adding a red arrow emphasizing the bimodal feature in each size distribution and/or a broken red line with a slope of −2 as a guide to the eye. A broken red line with a slope of −0.5 was added to subpanel G.
Pasquale et al. [107] were the first to report spike avalanches in six dissociated cultures with size distribution of either exponential, bimodal, or power law form. Two out of six cultures displayed the power law in avalanche size, however, only at submillisecond temporal resolution Δt. In fact, increasing Δt to 1 ms steepened the initial slope and rapidly uncovered a bimodal distribution, explained in their model as explosive growth introduced by neuronal hubs (Figure 14A). Using neonatal tissue right after birth, Tetzlaff et al. [98] tracked spike avalanche distributions during development and found an initial slope close to −2 for mature cultures and an increase in bimodality with increasing bin size (Figure 14B). Similar findings were presented by Levina and Priesemann [99] using dissociated cultures prepared from E18 tissue and grown for ∼3 weeks. Spike avalanches revealed a size distribution with a steep slope close to −2 and a preference for large avalanches. Again, an increase in Δt steepened the initial slope further and disproportionately increased the probability for large activity events (Figure 14C). Even when examining only a small range of bin width, reported results for dissociated culture experiments are more in line with expectations for a hyperexcitable system. Yada et al. [146] tracked the development of spike avalanches in six cultures and reported a bimodal form and an initial steep slope close to −2 that was robust to modest changes in Δt (Figure 14D). Similarly, robust bimodality and initial steep slope were reported in [147] (Figure 14E).
These experimental findings are in contrast to what has been reported for sizes of LFP and spike avalanches in organotypic cultures, where an increase in Δt leads to a more shallow slope in the size distribution and bimodality only arises when the system is made hyperexcitable (cf. Figures 5, 13). The notion that dissociated cultures might be characterized better by hyperexcitable dynamics is in line with a recent finding that increasing inhibition by adding a GABA agonist reduces bimodal size distributions in dissociated cultures, bringing them closer to a power law [148]. It is striking that, in some dissociated cultures, power laws were found mainly at submillisecond Δt (e.g., [107]). Given that synaptic integration times between neurons are on the order of 2–3 ms, a submillisecond temporal integration window will prematurely terminate the tracking of propagated activity, thereby randomly partitioning synchronous activity and potentially creating heavy-tail statistics in cascade sizes. Accordingly, at temporal resolutions >3–4 ms, which overlap with synaptic integration times, a strongly bimodal population dynamics of local, nonpropagated activity and global, propagated activity is revealed in these systems. For comparison, temporal resolutions studied in organotypic cultures ranged up to 16 ms (LFP avalanches; Figures 5B,G) and 33 ms (spike avalanches; an imaging frame rate of 30 Hz; Figure 13). Despite these long integration windows, bimodal distributions were absent, unless the system was made hyperexcitable. These integration windows are about an order of magnitude longer than those at which dissociated cultures show clear bimodal dynamics.
We suggest that the bimodal size distribution in dissociated cultures reflects a predominance of local activity and system-wide propagated activity. Such heterogenous dynamics can arise from several scenarios. The bimodality could reflect different structural networks, potentially including different cell types, that mature in dissociated cultures. For example, Orlandi et al. [149] applied an avalanche algorithm to neuronal activity tracked with intracellular calcium imaging in dissociated cultures grown from embryos for up to three weeks. They separated functional networks of “background” avalanches that established a cascade size distribution steeper than −2 from system-wide avalanches. Alternatively, dissociated cultures could establish a homogenous neural network in which bimodality arises from a discontinuous, first-order phase transition. In this latter case, neuronal activity either remains local and small or, alternatively, propagated and system wide. Increasing Δt in such a system more robustly collects activity into system-wide events, concomitantly reducing smaller-sized events steepening the initial slope in size distributions as observed for dissociated cultures. In fact, the simulation of population activity in dissociated cultures using a first-order phase transition has a long tradition. These dynamics were captured in early models featuring a first-order phase transition of all-or-none propagation [150], as well as recently for up-state generation in deep layers of cortical slices (e.g., [57]). They have been recently revived within the framework of self-organized bistability [151–154] or quasicriticality as well [155].
We note that spatial subsampling of activity, by recording only from a small number of neurons from the full network, is a common technical challenge in avalanche analysis. Yet, this technical constraint cannot explain the uncovering of a bimodal distribution at large Δt. Spatial subsampling decorrelates activity, leading to exponential distributions in cascade sizes [156]. However, in the present cases, a power-law–like or exponential distribution is observed at the outset for spike avalanches at small Δt, which changes to a bimodal distribution with increasing Δt (Figures 14A–D). In fact, avalanche analysis under increased spatial sampling in dissociated cultures, e.g., using intracellular calcium imaging, established clear bimodal size distribution [149]. Further support that spike avalanches in dissociated cultures differ from LPF avalanches in vivo comes from the mean size vs. duration scaling exponent. This exponent was found to be 2, which is in line with expectations for a critical branching process [71], but ranges between 1–1.5 for spike-based avalanches with bimodal distributions even at large Δt [146,147]. This is more in line with expectations for a noise process wherein size simply grows more linearly with duration [73,79].
We note that, in a study by Friedman et al. [157], spike avalanche distributions were calculated from ten cortex slice cultures, and this study is often used as an introduction of scaling relationships for spike avalanches. Three of those cultures exhibited bimodal, four exponential, and two were reported as “critical,” i.e., power-law–like in their size distribution. However, similar to spike avalanches in dissociated cultures, power law distributions in their cultures considered “critical” steepened in initial slope and became bimodal when increasing Δt (Figure 14F, left). The loss of the power law at low temporal resolution supports the interpretation of this activity to be of a first-order phase transition either from preferentially recording spikes from deep layers or from networks that are hyperexcitable, i.e., “supercritical.” This interpretation is further supported by their report of a mean size vs. duration exponent close to 1 (Figure 14F, right; [157]).
Developmental Differences Between Organotypic Cultures and Dissociated Cultures of the Cortex
Organotypic cortex cultures that are grown from postnatal brains demonstrate up-states and nested θ/γ-oscillations in their superficial layers, which give rise to avalanche scaling (see Figures 2–7). The conspicuous absence of these dynamics in dissociated cultures suggests an incomplete maturation of superficial layer circuitry, which is supported by several arguments, with the most obvious one being that the standard protocol for dissociated cortex culture biases toward the formation of deep-layer circuits. Dissociated cultures are typically prepared from the cortex at embryonic day E18 [107], which is dominated by deep-layer neurons known to autonomously generate population burst activity, also called “delta” brushes [158]. In contrast, superficial precursor neurons develop relatively late [16,17] and at E15–16 are still migrating toward the cortex along the periventricular wall, a developmental feature that can be used to selectively transfect superficial cells at that developmental stage [124,159] (cf. Figure 13). In addition, late migrating interneurons will be absent in dissociated cultures prepared from the embryonic cortical mantle only. Without an endogenous neurotransmitter such as acetylcholine, which is lacking in vitro, deep-layer pyramidal neurons exhibit intrinsic bursting [130,160,161] that can result in network-wide events [55–57]. Importantly, organotypic cortex cultures are typically prepared from the cortex after birth between postnatal day P1 and 2, at which point most precursor neurons required for establishing superficial pyramidal and interneurons have already arrived in the cortex, allowing an autonomous assembly of superficial layers in the isolated local cortical culture (see above). This sensitivity to the developmental time point of neuronal harvest is further exemplified by cultures of the hippocampus, an evolutionary early part of cortex. Dissociated hippocampus cultures, when taken at E18, reveal an avalanche size distribution slope close to −2 and a supercritical branching parameter at 3 ms bin width [162]. In contrast, dissociated hippocampus cultures made from newborn pups reveal mean size vs. duration scaling exponents of 2, not found for supercritical dynamics (Figure 14G; [163]). Similarly, Tetzlaff et al. [98] prepared dissociated cultures from postnatal day P1–2 resulting in relatively mild bimodality with increasing bin width (Figure 14B). Preparing dissociated cultures from postnatal tissue, expansion toward three-dimensional scaffolding using microbeads, and coculturing with other brain regions, e.g., the hippocampus, might introduce structural heterogeneity that stabilizes avalanche dynamics in future analysis [119,164].
To summarize, most avalanche analyses in dissociated cortex cultures reveal power laws that change to a bimodal distribution with steepening initial slope at longer integration windows. This dependency on the integration time window seems to reflect a first-order phase transition commonly found for predominantly deep layer pyramidal networks. These findings suggest that the activity in dissociated cultures does not compare well with neuronal avalanche dynamics originally described in organotypic cortex cultures and acute cortex slices and further established in awake in vivo preparation that features neuronal activity localized to superficial layers of the cortex.
Summary and Conclusion
The experimental evidence for SOC in the brain points to the presence of at least four dynamical motifs, up-states, nested oscillations, neuronal avalanches, and coherence potentials. These motifs have been robustly reported for the intact brain and in the isolated mammalian cortex, with its layered structure and cell type diversity largely preserved, specifically for the organotypic cortex culture and in the acute cortex slice. The coemergence of scale-invariant neuronal avalanches with oscillations during up-states should encourage future work on SOC in the brain at a disorder-synchronization phase transition. Neuronal population activity measured in dissociated cortex cultures typically differs from that reported for layered cortex preparations and is more in line with supercritical dynamics. Identifying the precise structural and dynamical constraints responsible for these differences might provide important insights into the mechanisms supporting SOC in the brain.
Author Contributions
DP took the lead in writing the manuscript and in discussions with all other authors.
Funding
This research was supported by the Division of the Intramural Research Program of the National Institute of Mental Health (NIMH), United States, ZIAMH002797. This research utilized the computational resources of Biowulf (http://hpc.nih.gov) at the National Institutes of Health (NIH), United States.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Dante R. Chialvo and Patrick Kanold for comments and support during writing of this manuscript.
References
1. Markram H, Muller E, Ramaswamy S, Reimann MW, Abdellah M, Sanchez CA, et al. Reconstruction and Simulation of Neocortical Microcircuitry. Cell (2015) 163(2):456–92. doi:10.1016/j.cell.2015.09.029
2. Dura-Bernal S, Suter BA, Gleeson P, Cantarelli M, Quintana A, Rodriguez F, et al. NetPyNE, a Tool for Data-Driven Multiscale Modeling of Brain Circuits. eLife (2019) 8:e44494. doi:10.7554/eLife.44494
3. Bak P, Tang C, Wiesenfeld K. Self-organized Criticality: An Explanation of the 1/fnoise. Phys Rev Lett (1987) 59(4):381–4. doi:10.1103/PhysRevLett.59.381
4. Jensen HJ. Self-organized Criticality.Cambridge: Cambridge University Press (1998). doi:10.1017/cbo9780511622717
6. Mora T, Bialek W. Are Biological Systems Poised at Criticality?. J Stat Phys (2011) 144(2):268–302. doi:10.1007/s10955-011-0229-4
7. Pruessner G. Self-organised Criticality: Theory, Models and Characterisation. Cambridge: Cambridge University Press (2012). doi:10.1017/cbo9780511977671
8. Hesse J, Gross T. Self-organized Criticality as a Fundamental Property of Neural Systems. Front Syst Neurosci (2014) 8:11. doi:10.3389/fnsys.2014.00166
9. Marković D, Gros C. Power Laws and Self-Organized Criticality in Theory and Nature. Phys Rep (2014) 536(2):41–74. doi:10.1016/j.physrep.2013.11.002
10. Muñoz MA. Colloquium: Criticality and Dynamical Scaling in Living Systems. Rev Mod Phys (2018) 90(3):031001. doi:10.1103/RevModPhys.90.031001
11. Plenz D. Neuronal Avalanches and Coherence Potentials. Eur Phys J Spec Top (2012) 205(1):259–301. doi:10.1140/epjst/e2012-01575-5
12. Götz M, Bolz J. Formation and Preservation of Cortical Layers in Slice Cultures. J Neurobiol (1992) 23:783–802. doi:10.1002/neu.480230702
13. Plenz D, Aertsen A. Neural Dynamics in Cortex-Striatum Co-cultures-II. Spatiotemporal Characteristics of Neuronal Activity. Neuroscience (1996) 70:893–924. doi:10.1016/0306-4522(95)00405-X
14. Plenz D, Aertsen A. Neural Dynamics in Cortex-Striatum Co-cultures-I. Anatomy and Electrophysiology of Neuronal Cell Types. Neuroscience (1996) 70:861–91. doi:10.1016/0306-4522(95)00406-8
15. Gorba T, Klostermann O, Wahle P. Development of Neuronal Activity and Activity-dependent Expression of Brain-Derived Neurotrophic Factor mRNA in Organotypic Cultures of Rat Visual Cortex. Cereb Cortex (1999) 9(8):864–77. doi:10.1093/cercor/9.8.864
16. Luhmann HJ, Sinning A, Yang J-W, Reyes-Puerta V, Stüttgen MC, Kirischuk S, et al. Spontaneous Neuronal Activity in Developing Neocortical Networks: from Single Cells to Large-Scale Interactions. Front NeuralCircuits (2016) 10(40):29. doi:10.3389/fncir.2016.00040
17. Molnár Z, Luhmann HJ, Kanold PO. Transient Cortical Circuits Match Spontaneous and Sensory-Driven Activity during Development. Science (2020) 370(6514):eabb2153. doi:10.1126/science.abb2153
18. Plenz D, Kitai ST. Up and Down States in Striatal Medium Spiny Neurons Simultaneously Recorded with Spontaneous Activity in Fast-Spiking Interneurons Studied in Cortex-Striatum-Substantia Nigra Organotypic Cultures. J Neurosci (1998) 18:266–83. doi:10.1523/JNEUROSCI.18-01-00266.1998
19. Bolz J, Novak N, Götz M, Bonhoeffer T. Formation of Target-specific Neuronal Projections in Organotypic Slice Cultures from Rat Visual Cortex. Nature (1990) 346:359–62. doi:10.1038/346359a0
20. Gähwiler B, Capogna M, Debanne D, McKinney RA, Thompson SM. Organotypic Slice Cultures: a Technique Has Come of Age. Trends Neurosci (1997) 20(10):471–7. doi:10.1016/s0166-2236(97)01122-3
21. Humpel C. Organotypic Brain Slice Cultures: A Review. Neuroscience (2015) 305:86–98. doi:10.1016/j.neuroscience.2015.07.086
22. Tremblay R, Lee S, Rudy B. GABAergic Interneurons in the Neocortex: From Cellular Properties to Circuits. Neuron (2016) 91(2):260–92. doi:10.1016/j.neuron.2016.06.033
23. Lim L, Mi D, Llorca A, Marín O. Development and Functional Diversification of Cortical Interneurons. Neuron (2018) 100(2):294–313. doi:10.1016/j.neuron.2018.10.009
24. Götz M, Bolz J. Development of Vasoactive Intestinal Polypeptide (VIP)-containing Neurons in Organotypic Slice Cultures from Rat Visual Cortex. Neurosci Lett (1989) 107:6–11. doi:10.1016/0304-3940(89)90782-9
25. Klostermann O, Wahle P. Patterns of Spontaneous Activity and Morphology of Interneuron Types in Organotypic Cortex and Thalamus-Cortex Cultures. Neuroscience (1999) 92(4):1243–59. doi:10.1016/s0306-4522(99)00009-3
26. Halassa MM, Fellin T, Haydon PG. The Tripartite Synapse: Roles for Gliotransmission in Health and Disease. Trends Mol Med (2007) 13(2):54–63. doi:10.1016/j.molmed.2006.12.005
27. Fellin T, Halassa MM, Terunuma M, Succol F, Takano H, Frank M, et al. Endogenous Nonneuronal Modulators of Synaptic Transmission Control Cortical Slow Oscillations In Vivo. Proc Natl Acad Sci (2009) 106(35):15037–42. doi:10.1073/pnas.0906419106
28. Perea G, Sur M, Araque A. Neuron-glia Networks: Integral Gear of Brain Function. Front Cel Neurosci. (2014) 8:112. doi:10.3389/fncel.2014.00378
29. Schultz-Süchting F, Wolburg H. Astrocytes Alter Their Polarity in Organotypic Slice Cultures of Rat Visual Cortex. Cel Tissue Res (1994) 277(3):557–64. doi:10.1007/BF00300229
30. Schmidt-Kastner R, Humpel C. Nestin Expression Persists in Astrocytes of Organotypic Slice Cultures from Rat Cortex. Int J Dev Neurosci (2002) 20(1):29–38. doi:10.1016/S0736-5748(02)00003-5
31. Cäser M, Schüz A. Maturation of Neurons in Neocortical Slice Cultures. A Light and Electron Microscopic Study on In Situ and In Vitro Material. J für Hirnforschung (1992) 33:429–43.
32. Staal JA, Alexander SR, Liu Y, Dickson TD, Vickers JC. Characterization of Cortical Neuronal and Glial Alterations during Culture of Organotypic Whole Brain Slices from Neonatal and Mature Mice. PLoS One (2011) 6(7):e22040. doi:10.1371/journal.pone.0022040
33. Antón-Bolaños N, Sempere-Ferràndez A, Guillamón-Vivancos T, Martini FJ, Pérez-Saiz L, Gezelius H, et al. Prenatal Activity from Thalamic Neurons Governs the Emergence of Functional Cortical Maps in Mice. Science (2019) 364(6444):987–90. doi:10.1126/science.aav7617
34. Canolty RT, Edwards E, Dalal SS, Soltani M, Nagarajan SS, Kirsch HE, et al. High Gamma Power Is Phase-Locked to Theta Oscillations in Human Neocortex. Science (2006) 313(5793):1626–8. doi:10.1126/science.1128115
35. Lisman J, Idiart M. Storage of 7 +/- 2 Short-Term Memories in Oscillatory Subcycles. Science (1995) 267:1512–5. doi:10.1126/science.7878473
36. Lisman JE, Jensen O. The Theta-Gamma Neural Code. Neuron (2013) 77(6):1002–16. doi:10.1016/j.neuron.2013.03.007
37. André M, Vezoli J, Conrado R, Oostenveld R, Jarrod L, et al. Visual Areas Exert Feedforward and Feedback Influences through Distinct Frequency Channels. Neuron (2015) 85(2):390–401. doi:10.1016/j.neuron.2014.12.018
38. Lundqvist M, Rose J, Herman P, Brincat SL, Buschman TJ, Miller EK. Gamma and Beta Bursts Underlie Working Memory. Neuron (2016) 90(1):152–64. doi:10.1016/j.neuron.2016.02.028
39. Plenz D, Kitai ST. Generation of High-Frequency Oscillations in Local Circuits of Rat Somatosensory Cortex Cultures. J Neurophysiol (1996) 76(6):4180–4. doi:10.1152/jn.1996.76.6.4180
40. Johnson HA, Buonomano DV. Development and Plasticity of Spontaneous Activity and up States in Cortical Organotypic Slices. J Neurosci (2007) 27(22):5915–25. doi:10.1523/JNEUROSCI.0447-07.2007
41. Harsch A, Robinson HPC. Postsynaptic Variability of Firing in Rat Cortical Neurons: the Roles of Input Synchronization and Synaptic NMDA Receptor Conductance. J Neurosci (2000) 20(16):6181–92. doi:10.1523/jneurosci.20-16-06181.2000
42. Czarnecki A, Tscherter A, Streit J. Network Activity and Spike Discharge Oscillations in Cortical Slice Cultures from Neonatal Rat. Eur J Neurosci (2012) 35(3):375–88. doi:10.1111/j.1460-9568.2011.07966.x
43. Compte A, Reig R, Descalzo VF, Harvey MA, Puccini GD, Sanchez-Vives MV. Spontaneous High-Frequency (10-80 Hz) Oscillations during up States in the Cerebral Cortex In Vitro. J Neurosci (2008) 28(51):13828–44. doi:10.1523/jneurosci.2684-08.2008
44. Bernander O, Douglas RJ, Martin KA, Koch C. Synaptic Background Activity Influences Spatiotemporal Integration in Single Pyramidal Cells. Proc Natl Acad Sci (1991) 88:11569–73. doi:10.1073/pnas.88.24.11569
45. Petersen CCH, Hahn TTG, Mehta M, Grinvald A, Sakmann B. Interaction of Sensory Responses with Spontaneous Depolarization in Layer 2/3 Barrel Cortex. Proc Natl Acad Sci (2003) 100(23):13638–43. doi:10.1073/pnas.2235811100
46. Reig R, Zerlaut Y, Vergara R, Destexhe A, Sanchez-Vives MV. Gain Modulation of Synaptic Inputs by Network State in Auditory Cortex In Vivo. J Neurosci (2015) 35(6):2689–702. doi:10.1523/JNEUROSCI.2004-14.2015
47. Monier C, Fournier J, Frégnac Y. In Vitro and In Vivo Measures of Evoked Excitatory and Inhibitory Conductance Dynamics in Sensory Cortices. J Neurosci Methods (2008) 169(2):323–65. doi:10.1016/j.jneumeth.2007.11.008
48. Haider B, Duque A, Hasenstaub AR, McCormick DA. Neocortical Network Activity In Vivo Is Generated through a Dynamic Balance of Excitation and Inhibition. J Neurosci (2006) 26(17):4535–45. doi:10.1523/JNEUROSCI.5297-05.2006
49. Ness TV, Remme MWH, Einevoll GT. Active Subthreshold Dendritic Conductances Shape the Local Field Potential. J Physiol (2016) 594(13):3809–25. doi:10.1113/JP272022
50. Meisel C, Klaus A, Kuehn C, Plenz D. Critical Slowing Down Governs the Transition to Neuron Spiking. Plos Comput Biol (2015) 11(2):e1004097e1004097. doi:10.1371/journal.pcbi.1004097
51. Fregnac Y, Blatow M, Changeux J-P, DeFelipe J, Lansner A, Maass W, et al. UPs and DOWNs in Cortical Computation. In Dahlem Workshop on Microcircuits (2004). MIT Press. p. 393–433.
52. Gireesh ED, Plenz D. Neuronal Avalanches Organize as Nested Theta- and Beta/gamma-Oscillations during Development of Cortical Layer 2/3. Proc Natl Acad Sci (2008) 105:7576–81. doi:10.1073/pnas.0800537105
53. Beggs JM, Plenz D. Neuronal Avalanches in Neocortical Circuits. J Neurosci (2003) 23(35):11167–77. doi:10.1523/JNEUROSCI.23-35-11167.2003
54. Beltramo R, D'Urso G, Dal Maschio M, Farisello P, Bovetti S, Clovis Y, et al. Layer-specific Excitatory Circuits Differentially Control Recurrent Network Dynamics in the Neocortex. Nat Neurosci (2013) 16(2):227–34. doi:10.1038/nn.3306
55. Sanchez-Vives MV, McCormick DA. Cellular and Network Mechanisms of Rhythmic Recurrent Activity in Neocortex. Nat Neurosci (2000) 3:1027–34. doi:10.1038/79848
56. Wester JC, Contreras D. Columnar Interactions Determine Horizontal Propagation of Recurrent Network Activity in Neocortex. J Neurosci (2012) 32(16):5454–71. doi:10.1523/JNEUROSCI.5006-11.2012
57. Capone C, Rebollo B, Muñoz A, Illa X, Del Giudice P, Sanchez-Vives MV, et al. Slow Waves in Cortical Slices: How Spontaneous Activity Is Shaped by Laminar Structure. Cereb Cortex (2017) 29(1):319–35. doi:10.1093/cercor/bhx326
58. Buhl EH, Tamas G, Fisahn A. Cholinergic Activation and Tonic Excitation Induce Persistent Gamma Oscillations in Mouse Somatosensory Cortex In Vitro. J Physiol (1998) 513(Pt 1):117–26. doi:10.1111/j.1469-7793.1998.117by.x
59. Yamawaki N, Stanford IM, Hall SD, Woodhall GL. Pharmacologically Induced and Stimulus Evoked Rhythmic Neuronal Oscillatory Activity in the Primary Motor Cortex In Vitro. Neuroscience (2008) 151(2):386–95. doi:10.1016/j.neuroscience.2007.10.021
60. Nicholson C, Freeman JA. Theory of Current Source-Density Analysis and Determination of Conductivity Tensor for Anuran Cerebellum. J Neurophysiol (1975) 38:356–68. doi:10.1152/jn.1975.38.2.356
61. Mitzdorf U. Current Source-Density Method and Application in Cat Cerebral Cortex: Investigation of Evoked Potentials and EEG Phenomena. Physiol Rev (1985) 65:37–100. doi:10.1152/physrev.1985.65.1.37
62. Plenz D, Aertsen A. Current Source Density Profiles of Optical Recording Maps: a New Approach to the Analysis of Spatio-Temporal Neural Activity Patterns. Eur J Neurosci (1993) 5:437–48. doi:10.1111/j.1460-9568.1993.tb00510.x
63. Oke OO, Magony A, Anver H, Ward PD, Jiruska P, Jefferys JGR, et al. (2010). High-frequency Gamma Oscillations Coexist with Low-Frequency Gamma Oscillations in the Rat Visual Cortexin Vitro.Eur. J. Neurosci.31(8),1435–45. doi:10.1111/j.1460-9568.2010.07171.x
64. Ermentrout GB, Kleinfeld D. Traveling Electrical Waves in Cortex. Neuron (2001) 29(1):33–44. doi:10.1016/s0896-6273(01)00178-7
65. Rubino D, Robbins KA, Hatsopoulos NG. Propagating Waves Mediate Information Transfer in the Motor Cortex. Nat Neurosci (2006) 9(12):1549–57. doi:10.1038/nn1802
66. Takahashi K, Saleh M, Penn RD, Hatsopoulos NG. Propagating Waves in Human Motor Cortex. Front Hum.Neurosci (2011) 5:40. doi:10.3389/fnhum.2011.00040
67. Abeles M. Corticonics: Neural Circuits of the Cerebral Cortex. New York: Cambridge University Press (1991). doi:10.1017/cbo9780511574566
68. Yu S, Klaus A, Yang H, Plenz D. Scale-invariant Neuronal Avalanche Dynamics and the Cut-Off in Size Distributions. PLoS One (2014) 9(6):e99761. doi:10.1371/journal.pone.0099761
69. Stewart CV, Plenz D. Inverted-U Profile of Dopamine-NMDA-Mediated Spontaneous Avalanche Recurrence in Superficial Layers of Rat Prefrontal Cortex. J Neurosci (2006) 26(31):8148–59. doi:10.1523/JNEUROSCI.0723-06.2006
70. Bellay T, Shew WL, Yu S, Falco-Walter JJ, Plenz D. Selective Participation of Single Cortical Neurons in Neuronal Avalanches. Front NeuralCircuits (2021) 14(90):117.doi:10.3389/fncir.2020.620052
71. Miller SR, Yu S, Plenz D. The Scale-Invariant, Temporal Profile of Neuronal Avalanches in Relation to Cortical γ-oscillations. Scientific Rep (2019) 9:16403. doi:10.1101/757278
72. Poil S-S, Hardstone R, Mansvelder HD, Linkenkaer-Hansen K. Critical-state Dynamics of Avalanches and Oscillations Jointly Emerge from Balanced Excitation/inhibition in Neuronal Networks. J Neurosci (2012) 32(29):9817–23. doi:10.1523/jneurosci.5990-11.2012
73. Villegas P, Di Santo S, Burioni R, Muñoz MA. Time-series Thresholding and the Definition of Avalanche Size. Phys Rev E (2019) 100(1). doi:10.1103/PhysRevE.100.012133
74. Petermann T, Thiagarajan TC, Lebedev MA, Nicolelis MAL, Chialvo DR, Plenz D. Spontaneous Cortical Activity in Awake Monkeys Composed of Neuronal Avalanches. Pnas (2009) 106(37):15921–6. doi:10.1073/pnas.0904089106
75. Harris TE. The Theory of Branching Processes. Berlin: Springer-Verlag (1963). doi:10.1007/978-3-642-51866-9
76. Christensen K, Olami Z. Sandpile Models with and without an Underlying Spatial Structure. Phys Rev E (1993) 48(5):3361–72. doi:10.1103/physreve.48.3361
77. Miller SR, Yu S, Pajevic S, Plenz D. Long-term Stability of Avalanche Scaling and Integrative Network Organization in Prefrontal and Premotor Cortex. Netw Neurosci (2021). 13:155. doi:10.1101/2020.11.17.386615
78. Martinello M, Hidalgo J, Maritan A, di Santo S, Plenz D, Muñoz MA. Neutral Theory and Scale-free Neural Dynamics. Phys Rev X (2017) 7(4):041071. doi:10.1103/physrevx.7.041071
79. Touboul J, Destexhe A. Power-law Statistics and Universal Scaling in the Absence of Criticality. Phys Rev E (2017) 95:113.doi:10.1103/PhysRevE.95.012413
80. Tagliazucchi E, Balenzuela P, Fraiman D, Chialvo DR. Criticality in Large-Scale Brain fMRI Dynamics Unveiled by a Novel point Process Analysis. Front Physio (2012) 3(15):27. doi:10.3389/fphys.2012.00015
81. Thiagarajan TC, Lebedev MA, Nicolelis MA, Plenz D. Coherence Potentials: Loss-Less, All-Or-None Network Events in the Cortex. Plos Biol (2010) 8(1):e1000278. doi:10.1371/journal.pbio.1000278
82. Yu S, Yang H, Nakahara H, Santos GS, Nikolic D, Plenz D. Higher-order Interactions Characterized in Cortical Activity. J Neurosci (2011) 31(48):17514–26. doi:10.1523/JNEUROSCI.3127-11.2011
83. Parameshwaran D, Crone NE, Thiagarajan TC. Coherence Potentials Encode Simple Human Sensorimotor Behavior. PLoS One (2012) 7(2):e30514. doi:10.1371/journal.pone.0030514
84. Poil S-S, Van Ooyen A, Linkenkaer-Hansen K. Avalanche Dynamics of Human Brain Oscillations: Relation to Critical Branching Processes and Temporal Correlations. Hum Brain Mapp (2008) 29:770–7. doi:10.1002/hbm.20590
85. Dalla Porta L, Copelli M. Modeling Neuronal Avalanches and Long-Range Temporal Correlations at the Emergence of Collective Oscillations: Continuously Varying Exponents Mimic M/EEG Results. Plos Comput Biol (2019) 15(4):e1006924. doi:10.1371/journal.pcbi.1006924
86. Wang S-J, Ouyang G, Guang J, Zhang M, Wong KM, Zhou C. Stochastic Oscillation in Self-Organized Critical States of Small Systems: Sensitive Resting State in Neural Systems. Phys Rev Lett (2016) 116(1):133. doi:10.1103/physrevlett.116.018101
87. Yang D-P, Zhou H-J, Zhou C. Co-emergence of Multi-Scale Cortical Activities of Irregular Firing, Oscillations and Avalanches Achieves Cost-Efficient Information Capacity. Plos Comput Biol (2017) 13(2):e1005384. doi:10.1371/journal.pcbi.1005384
88. di Santo S, Villegas P, Burioni R, Muñoz MA. Landau–Ginzburg Theory of Cortex Dynamics: Scale-free Avalanches Emerge at the Edge of Synchronization. In: Proceedings of the National Academy of Sciences (2018). p. 201712989.
89. Pausch J, Garcia-Millan R, Pruessner G. Time-dependent Branching Processes: A Model of Oscillating Neuronal Avalanches. Berlin: Springer (2019).
90. Gong P, van Leeuwen C. Distributed Dynamical Computation in Neural Circuits with Propagating Coherent Activity Patterns. Plos Comput Biol (2009) 5(12):e1000611. doi:10.1371/journal.pcbi.1000611
91. Gong P, Robinson PA. Dynamic Pattern Formation and Collisions in Networks of Excitable Elements. Phys Rev E (2012) 85(5):055101. doi:10.1103/PhysRevE.85.055101
92. Chen G, Gong P. Computing by Modulating Spontaneous Cortical Activity Patterns as a Mechanism of Active Visual Processing. Nat Commun (2019) 10(1):4915. doi:10.1038/s41467-019-12918-8
93. Allene C, Cossart R. Early NMDA Receptor-Driven Waves of Activity in the Developing Neocortex: Physiological or Pathological Network Oscillations?. J Physiol (2010) 588(1):83–91. doi:10.1113/jphysiol.2009.178798
94. Stewart CV, Plenz D. Homeostasis of Neuronal Avalanches during Postnatal Cortex Development In Vitro. J Neurosci Meth (2007) 169:405–16.doi:10.1016/j.jneumeth.2007.10.021
95. Dupont E, Hanganu IL, Kilb W, Hirsch S, Luhmann HJ. Rapid Developmental Switch in the Mechanisms Driving Early Cortical Columnar Networks. Nature (2006) 439(7072):79–83. doi:10.1038/nature04264
96. Kandler K, Katz LC. Coordination of Neuronal Activity in Developing Visual Cortex by gap junction-mediated Biochemical Communication. J Neurosci (1998) 18(4):1419–27. doi:10.1523/JNEUROSCI.18-04-01419.1998
97. Meng X, Solarana K, Bowen Z, Liu J, Nagode DA, Sheikh A, et al. Transient Subgranular Hyperconnectivity to L2/3 and Enhanced Pairwise Correlations during the Critical Period in the Mouse Auditory Cortex. Cereb Cortex (2019) 30(3):1914–30. doi:10.1093/cercor/bhz213
98. Tetzlaff C, Okujeni S, Egert U, Wörgötter F, Butz M. Self-organized Criticality in Developing Neuronal Networks. Plos Comput Biol (2010) 6(12):e1001013. doi:10.1371/journal.pcbi.1001013
100. Corner MA, van Pelt J, Wolters PS, Baker RE, Nuytinck RH. Physiological Effects of Sustained Blockade of Excitatory Synaptic Transmission on Spontaneously Active Developing Neuronal Networks-An Inquiry into the Reciprocal Linkage between Intrinsic Biorhythms and Neuroplasticity in Early Ontogeny. Neurosci Biobehavioral Rev (2002) 26(2):127–85. doi:10.1016/S0149-7634(01)00062-8
101. Turrigiano GG, Nelson SB. Homeostatic Plasticity in the Developing Nervous System. Nat Rev Neurosci (2004) 5(2):97–107. doi:10.1038/nrn1327
102. Ma Z, Turrigiano GG, Wessel R, Hengen KB. Cortical Circuit Dynamics Are Homeostatically Tuned to Criticality In Vivo. Neuron (2019) 104:655–64. doi:10.1016/j.neuron.2019.08.031
103. Lombardi F, Herrmann HJ, Plenz D, de Arcangelis L. On the Temporal Organization of Neuronal Avalanches. Front Syst Neurosci (2014) 8:204. doi:10.3389/fnsys.2014.00204
104. Lombardi F, Herrmann HJ, Perrone-Capano C, Plenz D, de Arcangelis L. Balance between Excitation and Inhibition Controls the Temporal Organization of Neuronal Avalanches. Phys Rev Lett (2012) 108(22):228703. doi:10.1103/PhysRevLett.108.228703
105. Lombardi F, Herrmann HJ, Plenz D, de Arcangelis L. Temporal Correlations in Neuronal Avalanche Occurrence. Sci Rep (2016) 6:24690. doi:10.1038/srep24690
106. Chialvo DR, Cannas SA, Grigera TS, Martin DA, Plenz D. Controlling a Complex System Near its Critical point via Temporal Correlations. Sci Rep (2020) 10(1):12145. doi:10.1038/s41598-020-69154-0
107. Pasquale V, Massobrio P, Bologna LL, Chiappalone M, Martinoia S. Self-organization and Neuronal Avalanches in Networks of Dissociated Cortical Neurons. Neuroscience (2008) 153(4):1354–69. doi:10.1109/EMBC.2015.731945210.1016/j.neuroscience.2008.03.050
108. Shew WL, Yang H, Petermann T, Roy R, Plenz D. Neuronal Avalanches Imply Maximum Dynamic Range in Cortical Networks at Criticality. J Neurosci (2009) 29(49):15595–600. doi:10.1523/JNEUROSCI.3864-09.2009
109. Shew WL, Yang H, Yu S, Roy R, Plenz D. Information Capacity and Transmission Are Maximized in Balanced Cortical Networks with Neuronal Avalanches. J Neurosci (2011) 31:55–63. doi:10.1523/JNEUROSCI.4637-10.2011
110. Yang H, Shew WL, Roy R, Plenz D. Maximal Variability of Phase Synchrony in Cortical Networks with Neuronal Avalanches. J Neurosci (2012) 32(3):1061–72. doi:10.1523/JNEUROSCI.2771-11.2012
111. Shew WL, Plenz D. The Functional Benefits of Criticality in the Cortex. Neuroscientist (2013) 19(1):88–100. doi:10.1177/1073858412445487
112. Durstewitz D, Seamans JK. The Dual-State Theory of Prefrontal Cortex Dopamine Function with Relevance to Catechol-O-Methyltransferase Genotypes and Schizophrenia. Biol Psychiatry (2008) 64(9):739–49. doi:10.1016/j.biopsych.2008.05.015
113. Arnsten AFT. Catecholamine Influences on Dorsolateral Prefrontal Cortical Networks. Biol Psychiatry (2011) 69(12):e89–e99. doi:10.1016/j.biopsych.2011.01.027
114. Cai J, Arnsten A. Dose-dependent Effects of the Dopamine D1 Receptor Agonists A77636 or SKF81297 on Spatial Working Memory in Aged Monkeys. J Pharmacol Exp Ther (1997) 283(1):183–9.
115. Francesc F-C, Gunnar P, Nicholas RM, Anna D. The Perils of Thresholding. New J Phys (2015) 17(4):043066. doi:10.1088/1367-2630/17/4/043066
116. Bornholdt S, Rohlf T. Topological Evolution of Dynamical Networks: Global Criticality from Local Dynamics. Phys Rev Lett (2000) 84(26):6114–7. doi:10.1103/PhysRevLett.84.6114
117. de Arcangelis L, Herrmann HJ. Learning as a Phenomenon Occurring in a Critical State. Proc Natl Acad Sci (2010) 107(9):3977–81. doi:10.1073/pnas.0912289107
118. Michiels van Kessenich L, Luković M, de Arcangelis L, Herrmann HJ. Critical Neural Networks with Short- and Long-Term Plasticity. Phys Rev E (2018) 97(3):032312. doi:10.1103/PhysRevE.97.032312
119. Massobrio P, Pasquale V, Martinoia S. Self-organized Criticality in Cortical Assemblies Occurs in Concurrent Scale-free and Small-World Networks. Sci Rep (2015) 5(1):10578. doi:10.1038/srep10578
120. Pajevic S, Plenz D. Efficient Network Reconstruction from Dynamical Cascades Identifies Small-World Topology of Neuronal Avalanches. Plos Comput Biol (2009) 5(1):e1000271. doi:10.1371/journal.pcbi.1000271
121. Pajevic S, Plenz D. The Organization of strong Links in Complex Networks. Nat Phys (2012) 8(5):429–36. doi:10.1038/NPHYS2257
122. Ribeiro TL, Copelli M, Caixeta F, Belchior H, Chialvo DR, Nicolelis MAL, et al. Spike Avalanches Exhibit Universal Dynamics across the Sleep-Wake Cycle. PLoS One (2010) 5(11):e14129. doi:10.1371/journal.pone.0014129
123. Scott G, Fagerholm ED, Mutoh H, Leech R, Sharp DJ, Shew WL, et al. Voltage Imaging of Waking Mouse Cortex Reveals Emergence of Critical Neuronal Dynamics. J Neurosci(2014) 34(50):16611–20. doi:10.1523/JNEUROSCI.3474-14.2014
124. Bellay T, Klaus A, Seshadri S, Plenz D. Irregular Spiking of Pyramidal Neurons Organizes as Scale-Invariant Neuronal Avalanches in the Awake State. eLife (2015) 4:e07224. doi:10.7554/eLife.07224
125. Fagerholm ED, Scott G, Shew WL, Song C, Leech R, Knöpfel T, et al. Cortical Entropy, Mutual Information and Scale-free Dynamics in Waking Mice. Cereb Cortex (2016) 26:3945–52. doi:10.1093/cercor/bhw200
126. Ribeiro TL, Ribeiro S, Copelli M. Repertoires of Spike Avalanches Are Modulated by Behavior and novelty. Front NeuralCircuits (2016) 10:16. doi:10.3389/fncir.2016.00016
127. Meisel C, Olbrich E, Shriki O, Achermann P. Fading Signatures of Critical Brain Dynamics during Sustained Wakefulness in Humans. J Neurosci (2013) 33(44):17363–72. doi:10.1523/JNEUROSCI.1516-13.2013
128. Meisel C, Bailey K, Achermann P, Plenz D. Decline of Long-Range Temporal Correlations in the Human Brain during Sustained Wakefulness. Sci Rep (2017) 7(1):11825. doi:10.1038/s41598-017-12140-w
129. Lombardi F, Gómez-Extremera M, Bernaola-Galván P, Vetrivelan R, Saper CB, Scammell TE, et al. Critical Dynamics and Coupling in Bursts of Cortical Rhythms Indicate Non-homeostatic Mechanism for Sleep-Stage Transitions and Dual Role of Vlpo Neurons in Both Sleep and Wake. J Neurosci (2020) 40(1):171–90. doi:10.1523/jneurosci.1278-19.2019
130. McCormick DA, Prince DA. Mechanisms of Action of Acetylcholine in the guinea-pig Cerebral Cortex In Vitro. J Physiol (London) (1986) 375:169–94. doi:10.1113/jphysiol.1986.sp016112
131. Case L, Lyons DJ, Broberger C. Desynchronization of the Rat Cortical Network and Excitation of white Matter Neurons by Neurotensin. Cereb Cortex (2016) 27(4):bhw100–2685. doi:10.1093/cercor/bhw100
132. Braitenberg V, Schüz A. Anatomy of the Cortex: Statistics and Geometry. Berlin, Heidelberg, New York: Springer-Verlag (1991). doi:10.1007/978-3-662-02728-8
133. Bowen Z, Winkowski DE, Seshadri S, Plenz D, Kanold PO. Neuronal Avalanches in Input and Associative Layers of Auditory Cortex. Front Syst Neurosci (2019) 13, 137.doi:10.3389/fnsys.2019.00045
134. Ma Z, Liu H, Komiyama T, Wessel R. Stability of Motor Cortex Network States during Learning-Associated Neural Reorganizations. J Neurophysiol (2020) 124(5):1327–42. doi:10.1152/jn.00061.2020
135. Buzsáki G, Anastassiou CA, Koch C. The Origin of Extracellular fields and Currents - EEG, ECoG, LFP and Spikes. Nat Rev Neurosci (2012) 13(6):407–20. doi:10.1038/nrn3241
136. Yamada Y, Mikoshiba K, Hashimoto M, Horikawa K, Nagai T, Miyawaki A, et al. Quantitative Comparison of Novel GCaMP-type Genetically Encoded Ca2+ Indicators in Mammalian Neurons. Front Cel Neurosci. (2011) 6:18. doi:10.3389/fncel.2012.00041
137. O'Donovan MJ. The Origin of Spontaneous Activity in Developing Networks of the Vertebrate Nervous System. Curr Opin Neurobiol (1999) 9(1):94–104. doi:10.1016/s0959-4388(99)80012-9
138. Karimipanah Y, Ma Z, Miller J-e. K, Yuste R, Wessel R. Neocortical Activity Is Stimulus- and Scale-Invariant. PLoS One (2017) 12(5):e0177396e0177396. doi:10.1371/journal.pone.0177396
139. Buice MA, Cowan JD. Field-theoretic Approach to Fluctuation Effects in Neural Networks. Phys Rev.E.Stat.Nonlin.Soft.Matter Phys (2007) 75:051919. doi:10.1103/physreve.75.051919
140. Benayoun M, Cowan JD, van Drongelen W, Wallace E. Avalanches in a Stochastic Model of Spiking Neurons. Plos Comput Biol (2010) 6(7):e1000846. doi:10.1371/journal.pcbi.1000846
141. Buice MA, Cowan JD, Chow CC. Systematic Fluctuation Expansion for Neural Network Activity Equations. Neural Comput (2010) 22(2):377–426. doi:10.1162/neco.2009.02-09-960
142. Liang J, Zhou T, Zhou C. Hopf Bifurcation in Mean Field Explains Critical Avalanches in Excitation-Inhibition Balanced Neuronal Networks: A Mechanism for Multiscale Variability. Front Syst Neurosci (2020) 14(87):155.doi:10.3389/fnsys.2020.580011
143. Dichter MA. Rat Cortical Neurons in Cell Culture: Culture Methods, Cell Morphology, Electrophysiology, and Synapse Formation. Brain Res (1978) 149:279–93. doi:10.1016/0006-8993(78)90476-6
144. Maeda E, Robinson H, Kawana A. The Mechanisms of Generation and Propagation of Synchronized Bursting in Developing Networks of Cortical Neurons. J Neurosci (1995) 15:6834–45. doi:10.1523/JNEUROSCI.15-10-06834.1995
145. Wagenaar D, Pine J, Potter S. An Extremely Rich Repertoire of Bursting Patterns during the Development of Cortical Cultures. BMC Neurosci (2006) 7(1):11. doi:10.1186/1471-2202-7-11
146. Yada Y, Mita T, Sanada A, Yano R, Kanzaki R, Bakkum DJ, et al. Development of Neural Population Activity toward Self-Organized Criticality. Neuroscience (2017) 343:55–65. doi:10.1016/j.neuroscience.2016.11.031
147. Shaukat A, Thivierge J-P. Statistical Evaluation of Waveform Collapse Reveals Scale-free Properties of Neuronal Avalanches. Front Comput Neurosci (2016) 10:27.doi:10.3389/fncom.2016.00029
148. Heiney K, Ramstad OH, Sandvig I, Sandvig A, Nichele S. Assessment and Manipulation of the Computational Capacity of In VitroNeuronal Networks through Criticality in Neuronal Avalanches. In IEEE Symposium Series on Computational Intelligence (SSCI). IEEE (2019). p. 247–54.
149. Orlandi JG, Soriano J, Alvarez-Lacalle E, Teller S, Casademunt J. Noise Focusing and the Emergence of Coherent Activity in Neuronal Cultures. Nat Phys (2013) 9(9):582–90. doi:10.1038/nphys2686
150. Giugliano M, Darbon P, Arsiero M, Lüscher H-R, Streit J. Single-neuron Discharge Properties and Network Activity in Dissociated Cultures of Neocortex. J Neurophysiol (2004) 92(2):977–96. doi:10.1152/jn.00067.2004
151. Scarpetta S, de Candia A. Neural Avalanches at the Critical point between Replay and Non-replay of Spatiotemporal Patterns. PLoS One (2013) 8(6):e64162. doi:10.1371/journal.pone.0064162
152. di Santo S, Burioni R, Vezzani A, Muñoz MA. Self-organized Bistability Associated with First-Order Phase Transitions. Phys Rev Lett (2016) 116(24):240601. doi:10.1103/PhysRevLett.116.240601
153. Scarpetta S, Apicella I, Minati L, de Candia A. Hysteresis, Neural Avalanches, and Critical Behavior Near a First-Order Transition of a Spiking Neural Network. Phys Rev E (2018) 97(6):062305. doi:10.1103/PhysRevE.97.062305
154. Buendía V, di Santo S, Villegas P, Burioni R, Muñoz MA. Self-organized Bistability and its Possible Relevance for Brain Dynamics. Phys Rev Res (2020) 2(1):013318. doi:10.1103/PhysRevResearch.2.013318
155. Kinouchi O, Pazzini R, Copelli M. Mechanisms of Self-Organized Quasicriticality in Neuronal Network Models. Front Phys (2020) 8(530):113. doi:10.3389/fphy.2020.583213
156. Ribeiro TL, Ribeiro S, Belchior H, Caixeta F, Copelli M. Undersampled Critical Branching Processes on Small-World and Random Networks Fail to Reproduce the Statistics of Spike Avalanches. PLoS One (2014) 9(4):e94992. doi:10.1371/journal.pone.0094992
157. Friedman N, Ito S, Brinkman BAW, Shimono M, DeVille REL, Dahmen KA, et al. Universal Critical Dynamics in High Resolution Neuronal Avalanche Data. Phys Rev Lett (2012) 108(20):208102. doi:10.1103/physrevlett.108.208102
158. Khazipov R, Luhmann HJ. Early Patterns of Electrical Activity in the Developing Cerebral Cortex of Humans and Rodents. TrendsNeurosciences (2006) 29(7):414–8. doi:10.1016/j.tins.2006.05.007
159. Saito T. In Vivo electroporation in the Embryonic Mouse central Nervous System. Nat Protoc (2006) 1(3):1552–8. doi:10.1038/nprot.2006.276
160. Wang Z, McCormick D. Control of Firing Mode of Corticotectal and Corticopontine Layer V Burst-Generating Neurons by Norepinephrine, Acetylcholine, and 1S,3R- ACPD. J Neurosci (1993) 13:2199–216. doi:10.1523/JNEUROSCI.13-05-02199.1993
161. Compte A, Sanchez-Vives MV, McCormick DA, Wang X-J. Cellular and Network Mechanisms of Slow Oscillatory Activity (. J Neurophysiol (2003) 89(5):2707–25. doi:10.1152/jn.00845.2002
162. Pu J, Gong H, Li X, Luo Q. Developing Neuronal Networks: Self-Organized Criticality Predicts the Future. Sci Rep (2013) 3(1):1081. doi:10.1038/srep01081
163. Yaghoubi M, de Graaf T, Orlandi JG, Girotto F, Colicos MA, Davidsen J. Neuronal Avalanche Dynamics Indicates Different Universality Classes in Neuronal Cultures. Sci Rep (2018) 8(1):3417. doi:10.1038/s41598-018-21730-1
164. Brofiga M, Pisano M, Tedesco M, Raiteri R, Massobrio P. Three-dimensionality Shapes the Dynamics of Cortical Interconnected to Hippocampal Networks. J Neural Eng (2020) 17(5):056044056044. doi:10.1088/1741-2552/abc023
165. Van Brederode JFM, Helliesen MK, Hendrickson AE. Distribution of the Calcium-Binding Proteins Parvalbumin and Calbindin-D28k in the Sensorimotor Cortex of the Rat. Neuroscience (1991) 44:157–71. doi:10.1016/0306-4522(91)90258-p
166. Plenz D, Stewart CV, Shew W, Yang H, Klaus A, Bellay T. Multi-electrode Array Recordings of Neuronal Avalanches in Organotypic Cultures. JoVE (2011)11(54) e2949. doi:10.3791/2949
Keywords: organotypic cortex culture, acute cortex slice, dissociated cortex culture, neuronal avalanches, oscillations, up-state
Citation: Plenz D, Ribeiro TL, Miller SR, Kells PA, Vakili A and Capek EL (2021) Self-Organized Criticality in the Brain. Front. Phys. 9:639389. doi: 10.3389/fphy.2021.639389
Received: 08 December 2020; Accepted: 10 June 2021;
Published: 07 July 2021.
Edited by:
Alex Hansen, Norwegian University of Science and Technology, NorwayReviewed by:
Ernesto Altshuler, University of Havana, CubaChangsong Zhou, Hong Kong Baptist University, Hong Kong
Copyright © 2021 Plenz, Ribeiro, Miller, Kells, Vakili and Capek. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dietmar Plenz, cGxlbnpkQG1haWwubmloLmdvdg==
 Dietmar Plenz
Dietmar Plenz Tiago L. Ribeiro
Tiago L. Ribeiro Stephanie R. Miller
Stephanie R. Miller Patrick A. Kells
Patrick A. Kells