An Overview of Spintronic True Random Number Generator

A True Random Number Generator is an essential component in data encryption, hardware security, physical unclonable functions, and statistical analyses. Conventional CMOS devices usually exploit the thermal noise or jitter to generate randomness, which suffers from high energy consumption, slow bit generating rate, large area, and over-complicated circuit. In this mini review, we introduce the novel physical randomness generating mechanism based on the stochastic switching behavior of magnetic tunnel junctions. As compared to CMOS technologies, the random number generator based on spintronic devices can have many inherent advantages, such as simpler structure, compact area, higher throughput, and better energy-efficiency. Here, we review and compare various existing schemes at the device and circuit levels to achieve high performance magnetic tunnel junctions based on a True Random Number Generator. Future research trends and challenges are also discussed to stimulate more works in this area.

Introduction

Random numbers play a crucial role in modern information technology. Conventionally, random number arrays are used in encryption algorithms, from widely-used RSA encryption to basic digital signature, to generate uncrackable ciphertext [1]. Recently, the development of deep learning and neural networks has led to new scope in the application of random numbers: to initialize matrixes with random elements so that the network could converge efficiently. Similar stochastic behavior is also favored by the artificial neurons or synapses in a spiking neuron network, which are fundamental to building next generation brain-inspired computing platforms. Biological neurons in the human brain fire pulses stochastically, which is considered one of the key strategies in the low power computation of the brain. Noise or random numbers can also be used to control the behavior of artificial neurons or synapses and to reduce the computational power [2, 3]. Aside from the areas mentioned above, random numbers are also the basis for performing the Monte Carlo method in numerical simulations, which simulates a system with random variables.

The computer component that generates random numbers is called a Random Number Generator (RNG). The output numbers of an RNG are supposed to be uniformly distributed within the range required by users. One typical category of RNGs is Pseudo Random Number Generators (PRNGs). PRNG is not a hardware device, but a series of algorithms that output uniformly distributed numbers based on certain seeds (such as the system clock). Strictly speaking, PRNGs are not fundamentally random because their seemingly random outputs are still based on a fixed calculation process and/or the system parameters. In comparison, True Random Number Generators (TRNG) are thus defined as physical devices that output random numbers without the dependence of any algorithms or seeds. TRNGs output sequences of zeros (“0”s) and ones (“1”s) at an equal probability of 50% to form uniformly distributed binary numbers. The quality of a TRNG is usually assessed in the following four aspects: (i) throughput capability, i.e., the generation speed of random bits; (ii) energy efficiency, i.e., the energy consumption of harvesting one random bit; (iii) randomness, which is quantified by the pass rate of NIST Special Publication 800 Statistical Tests Suite (NIST-SP800); and (iv) simplicity and scalability of the design itself, which is indicated by the area of the core circuit.

Conventional CMOS-based TRNGs extract bits from classical random phenomena, such as thermal noise [4–6] or oscillator jitter [7, 8]. Although the designs can achieve sufficient randomness, noticeable drawbacks still exist in these relatively mature CMOS-based TNRGs. Some of the designs suffer from poor generation speed and energy inefficiency, e.g., 0.011 Mb/s and 181.81 nJ/bit [9]; while others need complicated assisting circuits to modify the output that yields a minimum size of hundreds or thousands μm² for the core circuit [10, 11]. A stable power supply for the oscillators is also often needed, which further limits the scalability of the device [12]. A recent state-of-art design by Intel gives a reference for the performance standard of CMOS-based TRNGs: 162.5 Mb/s, 9 pJ/bit, NIST pass rate over 99% with a circuit area of 1,088 μm² [13]. However, such performance is not able to fully meet the demands of emerging applications of neural networks, in particular the energy consumption of fJ for the artificial neuron or synapse devices [14].

To extend the fundamental limits of CMOS-based TRNGs, researchers have turned their attention to spintronic devices based on magnetic tunnel junction (MTJ). A typical MTJ has a sandwich structure, consisting of one non-magnetic middle tunneling layer (usually made of MgO) nipped by two ferromagnetic (FM, usually made of CoFeB) layers: i.e., the pinned and free layer (Figure 1A). If the magnetization of the two FM layers has the same orientation (parallel or P state), the resistance of the whole structure is low. On the contrary, if the magnetizations are staggered (anti-parallel or AP state), the junction shows a larger resistance. Conversely, the magnetization of the free FM layer can be orientated so that the MTJs are switched between parallel and anti-parallel states to encode information (Figure 1B). There are three main types of physical mechanisms that change the state of MTJ, namely the toggle switching by charge current induced Oersted field [15, 16], the spin transfer torque (STT) [17–21], or the spin orbit torque (SOT) by spin current mediated angular momentum transfer [22, 23]. Aside from these different switching mechanisms, the structure of MTJ itself also differs in different forms, such as the conventional in-plane magnetized MTJs [24], the perpendicular MTJs (p-MTJ) with magnetizations perpendicular to the film plane [25], and the orthogonal MTJs with in-plane free FM layer and perpendicular pinned FM layer [26]. Despite these differences, the MTJ with low thermal stability always tends to flip its free layer randomly at room temperature. This thermal instability causes trouble when MTJs are used in Magnetic Random Access Memory (MRAM) applications, but inspires researchers to create random numbers through inherent randomness.

FIGURE 1

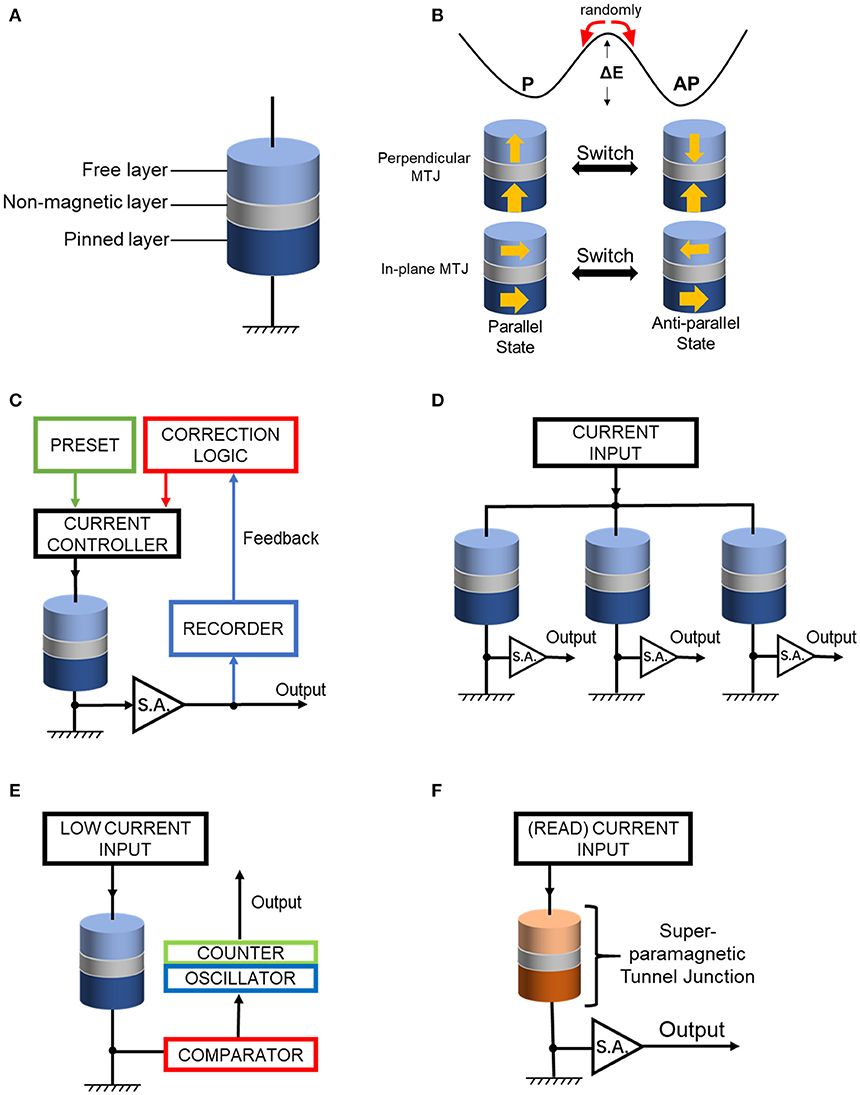
Figure 1. (A) The simplified version of the typical sandwich structure of MTJ. (B) The switching between a parallel state and anti-parallel state for in-plane and perpendicular MTJ. The arrows inside the MTJ indicate the magnetization direction of free and pinned FM layers. Schematic of the four main strategies for optimizing the randomness of spintronic TRNG. (C) Peripheral Current Correction Circuit. The perturb current is determined by correction logic based on previous output or preset. (D) Parallel designed MTJ cells. The overall deviation is leveraged by this structure. (E) Switching-time Dependent Stochasticity. The counter together with the oscillator records switching time as entropy instead of recording final states. (F) Adoption of Superparamagnetic tunnel junction. The switching happens spontaneously and the sensing amplifier gives output directly.

As illustrated in Figure 1B, once the MTJs are perturbed by appropriate approaches, they would resolve into AP or P states that can be read by sensing amplifiers (S.A.) as “0” or “1” correspondingly. As long as the probability to generate “0” or “1” is equal, the MTJ functions as a TRNG. Compared to the CMOS transistors, the dynamics of the MTJ switching process can happen within the time scale of around 10 ns [27] at an energy cost down to 80 to 200 fJ for spin torque driven mechanism [28, 29]. These fundamental advantages guarantee a high throughput capability and low energy consumption, which makes the spintronic devices a promising candidate for the next generation of high performance TRNGs.

This mini review introduces recent technology developments in spintronic TRNGs. In particular, it is focused on TRNGs that are built on the MTJs with P or AP states driven electrically by the current induced spin torques. The design concepts, testing methods, and performances of MTJ-based TRNGs (hereafter referred to as MTJ-TRNG for simplicity) are emphasized at the device and circuit levels. Section Different Designs of MTJ-TRNGs first briefly introduces the main obstacle to realize a random bit in the MTJ, followed by a detailed discussion of different proposed strategies in the literature. Based on the operation principles or hardware requirements, the strategies are divided into four main categories, which include: (i) the addition of peripheral current correction circuit, (ii) the adoption of parallel sensing MTJ arrays, (iii) the alternative method to harness switching-time stochasticity, and (iv) the replacement of superparamagnetic free layer in the MTJ structure. Consequently, Section III compares state-of-art performances for these strategies with regards to the key criteria including throughput, energy-efficiency, randomness, and circuit area size. Finally, the possible research trends and challenges are forecasted and discussed to stimulate more studies on spintronic TRNGs in the future.

Different Designs of MTJ-TRNGs

The general principle to create a random bit from an MTJ is to perturb it with an appropriate external stimulus to a metastable state at which the MTJ has an exactly equal tendency to settle into the P or AP state (Figure 1B). After the MTJ is stabilized in either one of the states, a randomly generated “0” or “1” is thus obtained. This process is as if throwing the so-called “spin dice” with two facets of “0” and “1.” In a practical STT driven MTJ device, one operation cycle to generate a random bit usually includes three main steps [30]: the reset step to initialize MTJ into either a stable AP or P state; followed by the perturb step to destabilize MTJ, and the final read step to wait and readout the final MTJ state. By repeating the cycle a few times in a single MTJ or operating multiple MTJs at the same time, a true random binary number with required bits can eventually be generated.

Although MTJs are fundamentally superior in terms of operation speed and energy consumption a major issue still exists in the perturb step, which brings the MTJ into a state with switching probability (P_sw) of exactly 50%. Any deviation of P_sw from the ideal value of 50% would lead to a compromise in the randomness of the TRNG. Hereafter, we use the word “bias” interchangeably with the deviation of P_sw from the ideal balanced value of 50% for simplicity. However, the switching of MTJ depends on many parameters, not only the material properties of MTJ itself, but also the environmental parameters, and thus it is not an easy task to perturb into the desired metastable state. For example, the switching probability of a nanopillar p-MTJ driven by thermally activated STT mechanism could be expressed as [31, 32]:

$\begin{array}{ll}{P}_{sw}=1-exp\left\{-\frac{t}{{\tau }_0}exp\left[-\Delta {\left(1-\frac{I}{I_{C0}}\right)}^2\right]\right\}& (1)\end{array}$

where I and t are the pulse current amplitude and pulse duration, respectively, τ₀ the attempt time, and I_C0 the critical switching current at 0 K. Δ is the thermal stability parameter that is further defined as E_b/k_BT, where E_b is the energy barrier between the P or AP states, k_B the Boltzmann constant, and T the absolute temperature. As can be seen, during the normal operation cycle, the input of I and t are actively controlled to achieve the state with P_sw = 50%. But the passive temperature drift of the working environment, and/or the common fluctuation of the current source, could cause an unwanted deviation of P_sw even for a single MTJ during multiple operation cycles. Different MTJs on the same wafer tend to exhibit slightly different material properties (e.g., E_b), which could lead to variation in the switching phase diagram, and cause troubles in the operation of multiple MTJs. Therefore, it is crucial to take proper actions to eliminate the deviation of P_sw from 50% so that the randomness of MTJ-TRNG can be ensured.

There are various proposals to tackle the difficult and stably extract bits with sufficient randomness. Depending on the methodology, they can be mainly categorized into four types. Intuitively, based on the importance of the input current, the peripheral current correction with preset configurations or external logic can be added to restrict the switching probability (Figure 1C). Alternatively, parallel arranged MTJ-TRNGs can be used to leverage the biases of different MTJs by reading several MTJs at the same time (Figure 1D). Other examples manage to find an entropy source from the switching-time characteristic of the MTJ under a low current that is several times smaller than the critical one, known as switching-time dependent MTJ-TRNGs (Figure 1E). Finally, the design of MTJ itself could be optimized to give random bits without an extra control unit, such as the incorporation of a superparamagnetic free layer (Figure 1F). These proposed MTJ-TRNGs are introduced in detail in the following section.

Peripheral Current Correction Circuit

In the seminal work by Fukushima et al. [31], a functional MTJ-TRNG device with eight p-MTJs was implemented. The schematic of one of such p-MTJ unit is illustrated in Figure 1C. The p-MTJ consists of a 2 nm FeB free layer, a 1 nm MgO non-magnetic layer, a CoPt/Ru/CoPt pinned layer, and the switching of the p-MTJs is driven by the current induced STT. As a result, the phase diagram of P_sw with respect to current and temperature is pre-calibrated from 4 × 10³ events so that any P_sw drift during normal operation can be compensated by presetting the amplitude of the input current (green frame in Figure 1C) through the current control unit (black frame in Figure 1C). Experimental evidence after generating 10⁹ bits shows that the numbers generated by different MTJs are independent without correlation, which ensures the randomness between output bits. But as mentioned above, the simple current correction circuit cannot eliminate all P_sw deviation sources, especially the disturbance caused by current source fluctuation. Indeed, it is found that the P_sw of two MTJs collected after the generation of 10⁹ bits exhibits an evident difference, and deviates from the ideal value of 50% by more than 10%. To perfect the quality of random bits, an additional exclusive OR operation (XOR) is applied on the two MTJs. The output P_sw was improved to 50.036% compared with 51.3% for one MTJ and 48.7% for the other. Nested XOR operation was later tested on these MTJs. XOR∧2 (two rounds of XOR operations) and XOR∧3 could further narrow the distribution of P_sw and improve the output distribution to close-binomial. The overall NIST pass rate after XOR∧3 operation climbs up to 99.7% for 188 tests. The throughput of this TRNG is estimated to be 0.6 Mb/s by generating one bit through the complete cycle with a XOR∧3 operation.

In the same year, 2014, another TRNG based on the STT mechanism was designed and simulated by Won Ho Choi et al. [33]. They proposed a feedback system that corrects the input current in real time, which consists of two 10-bit counters working as recorders (blue frame in Figure 1C). For every 1 Kbit generated from the MTJ, one counter counts the number of the generated “1”s and the other counter records the total number of bits. The count number from the former counter is multiplied by two and compared with the total bit number by a correction logic (red frame in Figure 1C). Depending on the result, the perturb current pulse width is adjusted through the current controller (black frame in Figure 1C) to optimize the randomness. Additionally, a conditional perturb scheme was proposed to improve the MTJ endurance, which replaces the conventional reset step with another reading step to checking the status of MTJ. Afterward, the control circuit decided whether to apply a positive or a negative perturb current. The improvement of MTJ endurance comes from the absence of a strong reset current. This TRNG device passed all NIST randomness tests after 65 Kbits of adjusting process, but no energy consumption and throughput capacity were mentioned.

Another digitally controlled probability tracking circuit design was simulated by Satoshi Oosawa et al. [34]. The correction logic works similarly to the tracking-feedback circuit in another example [33]. It records output random bits and adjusts the amplitude of current so that the output current limits the MTJ's switching probability between 48.625% and 51.375%. Compared with previous works, this probability-locked loop replaces all high-gain analog amplifiers in the circuit with digital components, which is more suitable for the integration in scaled CMOS process. Later in 2016, an array of MTJs with similar feedback circuits was simulated and passed 151 of 187 NIST tests [35].

Novel spintronic device technologies are also introduced into current correction TRNG designs. In the past decade, other than the STT driven p-MTJs as mentioned above, SOT is a more efficient mechanism to switch the state of p-MTJ at faster operation speed and lower power consumption [27]. As a result, SOT driven p-MTJs have also proved to be reliable random number sources as long as the input current can be properly controlled [36–38]. Different from the conventional STT one, the reset and perturb steps in SOT based MTJ-TRNG can be combined in a single step. Due to the additional symmetry requirements, the torque of SOT drives the free layer magnetization to in-plane orientation so that the input current always perturbs the MTJ into a metastable state regardless of its previous state.

It is worth pointing out that the SOT based MTJ-TRNG with p-MTJs can improve the pass rate of NIST to 95–100% and decrease the energy consumption down to 57.1 fJ/bit in simulation [37]. Similarly, in the unconventional orthogonal MTJs based TRNG, the current induced torque is also orthogonal to the free layer magnetization since the magnetizations of the free and pinned layer are built-in to be orthogonal during fabrication. Because of the short perturb time and resolve time for orthogonal MTJs, the throughput could hit as high as 208 Mb/s [39] under simulation by solving the Landau-Lifshitz-Gilbert equation, which describes magnetic dynamics. The adoption of these novel technologies opens a new avenue for the optimization of MTJ-TRNG performances.

Parallel Designed MTJ Cells

Aside from the strategy to stabilize P_sw with preset static parameters or external correction circuits, efforts have been made to find a design that can obtain high quality random numbers directly from the MTJ bit cells. One method abstracts the random numbers from different MTJs as independent Gaussian distributed random variables, it is natural to minimize the total deviation by a simple average operation [40]:

$\begin{array}{ll}\frac{{\sigma }_{x_1+\dots +x_N}}{N}=\frac{\sqrt{{\sigma }_1^2+\dots +{\sigma }_N^2}}{N}\left(=\frac{{\sigma }_N}{\sqrt{N}},if{x}_1=\dots =x_N\right)& (2)\end{array}$

where x_N is a random variable, N is the total number of variables, σ_x1+…+xN is the overall standard deviation and σ_N is the deviation of variable x_N. This equation indicates that N paralleled MTJs will have their overall probability deviation divided by $\sqrt{N}$.

Based on this approach, Qu et al. proposed a design with N paralleled MTJs, as shown in Figure 1D, which could in principle adjust the overall probability to close to 50% without any external correction circuits. These parallel MTJs are reset and then perturbed simultaneously, which is counted as two operations, and followed by N read operations after perturbance. Assuming that each of the operations (including reset, perturb, and read) takes only 5 ns, one operation cycle would thus take (N + 2) × 5 ns. With N = 16 MTJs, the throughput capacity reaches 177.8 Mb/s ($throughput=N\times \frac{1s}{(N+2)\times 5ns}$, N bits per cycle multiplied by total cycle number in 1 s). The simulation also shows that the average energy consumption is 0.64 pJ/bit. The passing rate of NIST is above 98.1% for all tests and will increase with more MTJs. More importantly, the area of core circuits is improved to 7.64 μm² as compared to hundreds or thousands of μm² in CMOS TRNG designs.

The same research group also simulated another design of multiple MTJs in 2018 with a focus to minimize the effect from global parameters rather than decreasing the overall P_sw bias [41]. Assuming that the switching probabilities of two identical MTJs are noted as x₁ and x₂, the probability that x₁ is smaller than x₂ always equals 50% since they are equally affected by external parameters. Based on this concept, this design places two identical MTJs in symmetric positions to leverage any possible disturbance caused by global parameters. The output bit is determined by the first switched MTJ after perturbance. In the ideal case, the switching of one of the two MTJs would cause a decrease of the overall current (a decrease by 33% if the resistance of MTJ in P state is half of that in AP state) in the circuit, which is sensed by a current detector (not shown in Figure 1). The writing process is interrupted immediately to ensure that only one of the MTJs switches and its state is output. To avoid malfunction situations where both or neither one flips, the perturb pulse width is moderated to 5 ns, which is a balance between bit-generating speed and switching effectiveness. Additionally, the switching properties of two MTJs cannot be identical in reality, and therefore it is necessary to apply a quality improvement circuit to minimize any inherent bias by the adoption of XOR gates. Under simulation, the pass rates of NIST tests are also no less than the critical line of 98% with a throughput of 66.7 Mbit/s and energy consumption of 0.81 pJ/bit. Compared to their previous work in the last paragraph, the area of the core circuit is further improved to 3.84 μm².

Switching-Time Dependent Stochasticity

The TRNGs discussed thus far in this review all use MTJ switching success rate as the entropy source. The physical nature of this method needs either peripheral circuits or a sophisticated anti-bias design, both of which are relatively expensive and complex to manufacture. Hence, Yang et al. proposed another TRNG design based on the fact that MTJ switching time itself can be a practical entropy source, and the proposal was verified with a commercial MRAM die [42].

The key experimental finding in their work is that when writing “1”s into MTJs with a low current, two or three times smaller than the nominal values, the switching time follows a skewed distribution (mean value of 28–56 ns). Such skewed distribution might be a result of both systematic delay mismatch and random jitter, which is similar to CMOS oscillation collapse time [43]. The stochasticity of the MTJ switching time allows it to record time itself as the random bit. To realize such a function, a ring oscillator (the blue frame in Figure 1E) together with an asynchronous counter (the green frame in Figure 1E) records the time circles that the MTJ writing process takes. A continuous comparator (red frame in Figure 1E) also works as a sensing amplifier to monitor the bit line and sends the stop signal to the counter once the MTJ flips to a P state. Consequently, the counter's least significant bits are used directly as random bits output. To avoid any false triggering, the comparator is activated slightly after the bit line sets up. To save energy, the random numbers are only harvested while writing “1”s after resetting all MTJs into AP state (“0”s). This design with an area of 180 μm² experimentally achieved the NIST pass rate above 98%. The maximum random number generation speed is 66 Mbps and the best energy efficiency is 18 pJ/bit (11 pJ/bit if neglecting the shared reference current used by comparator S.A.). Moreover, these performance indexes can be further improved by expanding the circuit and arranging more MTJs in parallel.

In 2019, Ben Perach proposed STT-ANGIE—an asynchronous MTJ based TRNG that can work in low frequency circuits [44], and tested it with simulation. The entropy of this TRNG also comes from switching time but random bits are still read from MTJs' final AP/P states. The perturbance is carried out by capacitors which give out charge to each MTJ asynchronously. Without strict current control, the final states of MTJs are different due to switching time variation, which can be used as a random bit. The generation speed of this type of TRNG with 8 MTJs could hit 99.7–127.8 Mb/s and the energy consumption is merely 6–7.7 pJ/bit. However, the area of the circuit is relatively large, being over 400 μm².

Superparamagnetic Tunnel Junction

As mentioned in Section Introduction, the MTJs with low thermal energy barriers between AP and P states inherently have stochasticity against thermal noise. Figure 1F shows the extreme case to replace the FM free layer in MTJ with a superparamagnetic layer, which is dubbed as the superparamagnetic tunnel junction (SP-MTJ). Consequently, thermal fluctuation at room temperature would be strong enough to switch the SP-MTJ repeatedly without invoking any external power source. In 2017, Vodenicarevic et al. experimentally tested SP-MTJs as a random number source, then demonstrated SP-MTJ based TRNG through circuit-level simulation. The energy consumption under simulation was decreased to 20 fJ/bit, and the core circuit was simplified to 2 μm² [45].

The fabrication of their SP-MTJ follows standard sputtering procedure [46] with common MTJ materials. The structure from top to bottom is Au(200)/Cr (5)/Ru (8)/Ta (7)/Free Layer(not specified)/MgO(1.075)/CoFeB (3)/Ru(0.85)/CoFe(2.5)/PtMn (15) (the number in the parenthesis indicates the thickness in nanometers). However, the lateral size of this type of MTJ should be carefully controlled (50 × 150 nm² elliptic pillar) to attain a superparamagnetic free layer with low thermal stability. In addition, to read the state without biasing its switching behavior, a negligibly small current is also needed to eliminate any current induced thermal fluctuation. The experimental test upon SP-MTJs over a 10-s period shows that the dwell times of both AP and P status follow a Poisson characteristic and the mean switching frequency is 1.66 kHz. Since the superparamagnetic switching happens spontaneously, a random number array could be generated by simply sampling the voltage outcome, with the maximum frequency of 100 kHz.

However, the P_sw deviation still exists due to the stray field induced by pinned layer. The free layer tends to stay longer in the P state than in the AP state, producing a mean state of 60.5% if AP is “0” and P is “1.” Again, XOR operation is introduced in the randomness optimization. The outcome random bits get exponentially closer to 50% after several rounds of XOR operations. Ultimately, with eight raw numbers and three rounds of XOR operations for one bit output, at a sampling rate under 5.9 kHz, the passing rate of NIST tests reaches 100%. This design also employs a special CMOS pre-charge sensing amplifier [47] to further eliminate any disturbance on MTJ switching performance. The whole circuit is simulated in CADENCE which shows that the reading current is relatively independent from the tunnel junctions, with an ultra-low reading energy consumption of approximately 2 fJ per bit. While using 8 bits to generate 1 bit through XOR operations, the average energy consumption is 20 fJ/bit. Unfortunately, the switching process is dominated by environment temperature, which limits the generating speed to merely several kHz. This design may only be suitable for slow missions such as neuro-inspired computing.

Comparison and Perspective

Up till now, four main types of strategies have been proposed to realize MTJ-TRNGs with sufficient randomness, fast speed, low energy, and compact area. As described in the last section, the TRNG performances in most of these spintronic devices are tested under simulation except [31, 42] where the circuit-board of the MRAM die was used for verification. Bearing this fact in mind, the comparison of the best performances of each strategy is summarized in Table 1. As listed in the table, all the strategies can achieve sufficient randomness in the sense that the pass rates for NIST tests are no <95%. Due to the existence of an upper monitor or external logic, the area of the peripheral current correction circuit is hard to be quantified; while other types of MTJ-TRNGs are significantly smaller than their CMOS counterparts. Even for the mediocre output speed of 66.6 Mb/s [34], it is still three times better than the CMOS-TRNG [11]. It is worth pointing out that the maximum throughput can be elevated to above 200 Mb/s when orthogonal MTJs are adopted. The TRNG with parallel-designed MTJ cells hits the second highest output speed, but it may pose fabrication difficulty in the requirement of identical MTJs. The TRNG based on SP-MTJ has the lowest throughput of 100 Kb/s, which is limited by the thermal agitation process. As for the energy consumption, the typical value is a few pJ per bit with STT driven MTJs, and it could be improved to fJ level with the assist of SOT technology. It should be noted that with superparamagnetic nature, SP-MTJ has a neglectable energy consumption of merely 2 fJ/bit in best cases. In general, there are always pros and cons accompanied with each strategy, and thus the adoption of a specific existing strategy would depend on the real application scenes of the TRNG.

TABLE 1

Table 1. A comparison of the best performances of the four main categories of MTJ-TRNGs described in Section Different Designs of MTJ-TRNGs.

From a fundamental point of view, further research on novel MTJ technologies are needed to optimize the performance of MTJ-TRNG devices. MTJs with shorter perturb and resolve times and smaller perturb current are always in demand, as they decrease energy consumption and increase throughput. Development of these requires efforts in terms of materials and the device, for example, it has been demonstrated that the antiferromagnetic material has a much faster spin dynamic than the FM one [48], which could boost the switching speed of the MTJ down to ps level once adopted as the free layer. The stochasticity of certain spin textures, such as domain walls [49, 50] or skyrmions [51, 52] could be utilized as another type of entropy source, which could potentially lead to a simpler circuit structure. A novel spin torque mechanism beyond STT or SOT [53, 54] could also be a direction to improve the performance of MTJs, as it has the switching energy of several fJ per bit, as mentioned above. In addition, more engineering works are required to verify and optimize the scalability and reliability of existing MTJ-TRNG designs at the circuit level. The ideal size of the core circuit for MTJ-TRNGs should be <10 μm² to achieve a significant advantage over CMOS TRNGs in scalability. In particular, since one of the TRNG applications is in data security, it is necessary to conduct a failure analysis on MTJ-TRNG considering the fact that spintronic devices are typically vulnerable to environmental magnetic fields. Possible attack methods against MTJ-TRNGs and the solutions to these limitations need to be carefully evaluated to eliminate the possibility of manipulating the behavior of the MTJ, but this issue is scarcely considered in existing works [44]. All this progress is needed for the commercialization of MTJ-TRNGs as the next generation of high performance TRNG with a simpler structure, compact area, higher throughput, and better energy-efficiency.

Author Contributions

YY and YT conceived the idea. XZ, KL, YD, AS, and ZZ contributed to the data collection and analyses. ZF, YT, and YY wrote the manuscript with input from all the authors. All authors contributed to the article and approved the submitted version.

Funding

ZF, AS, and YY are supported by the National Science Foundation of China Grants No. 62074099, Shanghai Pujiang Program No. 20PJ1411500, and ShanghaiTech University Startup Fund. KL acknowledges support by the Shanghai Sailing Program under grant No. 19YF1456300, and ZZ acknowledges the Shanghai Sailing Program No. 20YF1430400. YT and XZ are supported by the Zhejiang Qianjiang Program.

Conflict of Interest

YT and XZ are employed by Zhejiang Hikstor Technology Co., LTD.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Diffie W, Hellman M. New directions in cryptography. IEEE Trans Inform Theory. (1976) 22:644–54. doi: 10.1109/TIT.1976.1055638

CrossRef Full Text | Google Scholar

2. Maass W. Noise as a resource for computation and learning in networks of spiking neurons. Proc IEEE. (2014) 102:860–80. doi: 10.1109/JPROC.2014.2310593

CrossRef Full Text | Google Scholar

3. Habenschuss S, Puhr H, Maass W. Emergence of optimal decoding of population codes through STDP. Neural Comput. (2013) 25:1371–407. doi: 10.1162/NECO_a_00446

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Brederlow R, Prakash R, Paulus C, Thewes R. A low-power true random number generator using random telegraph noise of single oxide-traps. In: IEEE International Solid State Circuits Conference—Digest of Technical Papers. San Francisco, CA (2006). doi: 10.1109/ISSCC.2006.1696222

CrossRef Full Text | Google Scholar

5. Petrie CS, Connelly JA. A noise-based IC random number generator for applications in cryptography. IEEE Trans Circuits Syst I Fund Theory Applic. (2000) 47:615–21. doi: 10.1109/81.847868

CrossRef Full Text | Google Scholar

6. Kinniment DJ, Chester EG. Design of an on-chip random number generator using metastability. In: Proceedings of the 28th European Solid-State Circuits Conference. Florence (2002).

Google Scholar

7. Bucci M, Germani L, Luzzi R, Trifiletti A, Varanonuovo M. A high-speed oscillator-based truly random number source for cryptographic applications on a smart card IC. IEEE Trans. Comp. (2003) 52:403–9. doi: 10.1109/TC.2003.1190581

CrossRef Full Text | Google Scholar

8. Wold K, Tan CH. Analysis and enhancement of random number generator in fpga based on oscillator rings. In: International Conference on Reconfigurable Computing and FPGAs. Cancun (2008). doi: 10.1109/ReConFig.2008.17

CrossRef Full Text | Google Scholar

9. Liu N, Pinckney N, Hanson S, Sylvester D, Blaauw D. A true random number generator using time-dependent dielectric breakdown. In: Symposium on VLSI Circuits—Digest of Technical Papers (2011).

Google Scholar

10. Mathew SK, Srinivasan S, Anders MA, Kaul H, Hsu SK, Sheikh F, et al. 2.4 Gbps, 7 mW ALL-digital PVT-variation tolerant true random number generator for 45 nm CMOS high-performance microprocessors. IEEE J Solid-State Circuits. (2012) 47:2807–21. doi: 10.1109/JSSC.2012.2217631

CrossRef Full Text | Google Scholar

11. Yang K, Fick D, Henry MB, Lee Y, Blaauw D, Sylvester D. 16.3 A 23Mb/s 23pJ/b fully synthesized true-random-number generator in 28nm and 65nm CMOS. In: IEEE International Solid-State Circuits Conference Digest of Technical Papers (ISSCC). (2014). doi: 10.1109/ISSCC.2014.6757434

CrossRef Full Text | Google Scholar

12. Michal V. On the low-power design, stability improvement and frequency estimation of the CMOS ring oscillator. In: Proceedings of 22nd International Conference Radioelektronika. Brno (2012).

Google Scholar

13. Mathew SK, Johnston D, Satpathy S, Suresh V, Newman P, Anders MA, et al. μ RNG: A 300–950 mV, 323 Gbps/W All-Digital Full-Entropy True Random Number Generator in 14 nm FinFET CMOS. IEEE J Solid-State Circuits. (2016) 51:1695–704. doi: 10.1109/JSSC.2016.2558490

CrossRef Full Text | Google Scholar

14. Chatterjee D, Kottantharayil A. A CMOS compatible bulk finfet-based ultra low energy leaky integrate and fire neuron for spiking neural networks. IEEE Electron Device Lett. (2019) 40:1301–4. doi: 10.1109/LED.2019.2924259

CrossRef Full Text | Google Scholar

15. Tehrani S, Engel B, Slaughter JM, Chen E, DeHerrera M, Durlam M, et al. Recent developments in magnetic tunnel junction MRAM. IEEE Trans. Magn. (2000) 36:2752–7. doi: 10.1109/20.908581

CrossRef Full Text | Google Scholar

16. Engel BN, Akerman J, Butcher B, Dave RW, DeHerrera M, Durlam M, et al. A 4-Mb toggle MRAM based on a novel bit and switching method. IEEE Trans Magn. (2005) 41:132–6. doi: 10.1109/TMAG.2004.840847

CrossRef Full Text | Google Scholar

17. Kubota H, Fukushima A, Ootani Y, Yuasa S, Ando K, Maehara H, et al. Current induced magnetization switching in magnetic tunnel junction with MgO [001] tunnel barrier. In: IEEE International Magnetics Conference (INTERMAG). (2005). doi: 10.1109/INTMAG.2005.1463935

CrossRef Full Text | Google Scholar

18. Park J, Park C, Zhu J. Interfacial oxidation enhanced perpendicular magnetic anisotropy in low resistance magnetic tunnel junctions composed of co/pt multilayer electrodes. IEEE Trans. Magnet. (2008) 44:2577–80. doi: 10.1109/TMAG.2008.2003071

CrossRef Full Text | Google Scholar

19. Yoshikawa M, Kitagawa E, Nagase T, Daibou T, Nagamine M, Nishiyama K, et al. Tunnel magnetoresistance over 100% in MgO-based magnetic tunnel junction films with perpendicular magnetic L1₀-FePt electrodes. IEEE Trans. Magn. (2008) 44:2573–6. doi: 10.1109/TMAG.2008.2003059

CrossRef Full Text | Google Scholar

20. Hu G, Topuria T, Rice PM, Jordan-Sweet J, Worledge DC. Optimization of tunneling magnetoresistance in perpendicular magnetic tunnel junctions with co|pd reference layers. IEEE Magn Let. (2013) 4:3000104. doi: 10.1109/LMAG.2013.2270454

CrossRef Full Text | Google Scholar

21. Lee H, Sukegawa H, Liu J, Wen Z, Mitani S, Hono K. Tunnel magnetoresistance of ferromagnetic antiperovskite MnGaN/MgO/CoFeB perpendicular magnetic tunnel junctions. IEEE Trans. Magn. (2016) 52:1–4. doi: 10.1109/TMAG.2016.2519283

CrossRef Full Text | Google Scholar

22. Miron IM, Garello K, Gaudin G, Zermatten P-J, Costache MV, Auffret S, et al. Perpendicular switching of a single ferromagnetic layer induced by in-plane current injection. Nature. (2011) 476:189–93. doi: 10.1038/nature10309

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Cubukcu M, Boulle O, Drouard M, Garello K, Onur Avci C, Mihai Miron I, et al. Spin-orbit torque magnetization switching of a three-terminal perpendicular magnetic tunnel junction. Appl Phys Lett. (2014) 104:042406. doi: 10.1063/1.4863407

CrossRef Full Text | Google Scholar

24. Silva AV, Ferreira R, Paz E, Leitao DC, Devolder T, Cardoso S, et al. Thermal FMR spectral characterization of very low Ra in-plane MgO magnetic tunnel junctions. IEEE Trans Magn. (2017) 53:1–5. doi: 10.1109/TMAG.2017.2707798

CrossRef Full Text | Google Scholar

25. Suzuki KZ, Miura Y, Ranjbar R, Bainsla L, Ono A, Sasaki Y, et al. Perpendicular magnetic tunnel junctions with Mn-modified ultrathin MnGa layer. Appl Phys Lett. (2018) 112:062402. doi: 10.1063/1.5002616

CrossRef Full Text | Google Scholar

26. Kent AD, Özyilmaz B, del Barco E. Spin-transfer-induced precessional magnetization reversal. Appl Phys Lett. (2004) 84:3897–9. doi: 10.1063/1.1739271

CrossRef Full Text | Google Scholar

27. Wang Z, Zhao W, Deng E, Klein J-O, Chappert C. Perpendicular-anisotropy magnetic tunnel junction switched by spin-Hall-assisted spin-transfer torque. J Phys D Appl Phys. (2015) 48:065001. doi: 10.1088/0022-3727/48/6/065001

CrossRef Full Text | Google Scholar

28. Kang G, Jang Y, Park J. Charge-recycling based redundant write prevention technique for low power SOT-MRAM. In: IEEE International Symposium on Circuits and Systems (ISCAS). Florence (2018). doi: 10.1109/ISCAS.2018.8351277

CrossRef Full Text | Google Scholar

29. Wang Z, Zhang L, Wang M, Wang Z, Zhu D, Zhang Y, et al. High-density NAND-like spin transfer torque memory with spin orbit torque erase operation. IEEE Electron Dev Lett. (2018) 39:343–6. doi: 10.1109/LED.2018.2795039

CrossRef Full Text | Google Scholar

30. Yuasa S, Fukushima A, Yakushiji K, Nozaki T, Konoto M, Maehara H, et al. Future prospects of MRAM technologies. In: IEEE International Electron Devices Meeting. Washington, DC (2013). doi: 10.1109/IEDM.2013.6724549

CrossRef Full Text | Google Scholar

31. Fukushima A, Seki T, Yakushiji K, Kubota H, Imamura H, Yuasa S, et al. Spin dice: a scalable truly random number generator based on spintronics. Appl Phys Express. (2014) 7:083001. doi: 10.7567/APEX.7.083001

CrossRef Full Text | Google Scholar

32. Suzuki Y, Tulapurkar AA, Chappert C. CHAPTER 3—Spin-Injection Phenomena and Applications. Nanomagnetism and Spintronics. Amsterdam: Elsevier. (2009). p. 93–153. doi: 10.1016/B978-0-444-53114-8.00003-0

CrossRef Full Text | Google Scholar

33. Won Ho C, Yang L, Jongyeon K, Deshpande A, Gyuseong K, Jian-Ping W, et al. A Magnetic Tunnel Junction based True Random Number Generator with conditional perturb and real-time output probability tracking. In: IEEE International Electron Devices Meeting. (2014). doi: 10.1109/IEDM.2014.7047039

CrossRef Full Text | Google Scholar

34. Oosawa S, Konishi T, Onizawa N, Hanyu T. Design of an STT-MTJ based true random number generator using digitally controlled probability-locked loop. In: IEEE 13th International New Circuits and Systems Conference (NEWCAS). Grenoble (2015). doi: 10.1109/NEWCAS.2015.7182089

CrossRef Full Text | Google Scholar

35. Vatajelu EI, Natale GD, Prinetto P. STT-MTJ-based TRNG with on-the-fly temperature/current variation compensation. In: IEEE 22nd International Symposium on On-Line Testing and Robust System Design (IOLTS). (2016). doi: 10.1109/IOLTS.2016.7604694

CrossRef Full Text | Google Scholar

36. Liu Y, Wang Z, Li Z, Wang X, Zhao W. A spin orbit torque based true random number generator with real-time optimization. In: IEEE 18th International Conference on Nanotechnology (IEEE-NANO). Cork (2018). doi: 10.1109/NANO.2018.8626347

CrossRef Full Text | Google Scholar

37. Kim Y, Fong X, Roy K. Spin-orbit-torque-based spin-dice: a true random-number generator. IEEE Magn Lett. (2015) 6:1–4. doi: 10.1109/LMAG.2015.2496548

CrossRef Full Text | Google Scholar

38. Chen H, Zhang S, Xu N, Song M, Li X, Li R, et al. Binary and ternary true random number generators based on spin orbit torque. In: IEEE International Electron Devices Meeting (IEDM). San Francisco, CA (2018). doi: 10.1109/IEDM.2018.8614638

CrossRef Full Text | Google Scholar

39. Li X, Luo S, Qin H, Hong J, You L. Spin dice based on orthogonal spin-transfer devices with planar polarizer. IEEE Trans Magn. (2018) 54:1–4. doi: 10.1109/TMAG.2018.2832194

CrossRef Full Text | Google Scholar

40. Qu Y, Han J, Cockburn BF, Pedrycz W, Zhang Y, Zhao W. A true random number generator based on parallel STT-MTJs. In: Design, Automation & Test in Europe Conference & Exhibition (DATE). (2017). doi: 10.23919/DATE.2017.7927058

CrossRef Full Text | Google Scholar

41. Qu Y, Cockburn BF, Huang Z, Cai H, Zhang Y, Zhao W, et al. Variation-resilient true random number generators based on multiple STT-MTJs. IEEE Trans Nanotech. (2018) 17:1270–81. doi: 10.1109/TNANO.2018.2873970

CrossRef Full Text | Google Scholar

42. Yang K, Dong Q, Wang Z, Shih Y, Chih Y, Chang J, et al. A 28NM integrated true random number generator harvesting entropy from MRAM. In: IEEE Symposium on VLSI Circuits. (2018). doi: 10.1109/VLSIC.2018.8502431

CrossRef Full Text | Google Scholar

43. Yang K, Blaauw D, Sylvester D. An all-digital edge racing true random number generator robust against PVT variations. IEEE J Solid-State Circuits. (2016) 51:1022–31. doi: 10.1109/JSSC.2016.2519383

CrossRef Full Text | Google Scholar

44. Perach B, Kvatinsky S. STT-ANGIE: asynchronous true random number generator using STT-MTJ. In: Design, Automation & Test in Europe Conference & Exhibition (DATE). (2019). doi: 10.23919/DATE.2019.8715257

CrossRef Full Text | Google Scholar

45. Vodenicarevic D, Locatelli N, Mizrahi A, Friedman JS, Vincent AF, Romera M, et al. Low-energy truly random number generation with superparamagnetic tunnel junctions for unconventional computing. Phys Rev Appl. (2017) 8:054045. doi: 10.1103/PhysRevApplied.8.054045

CrossRef Full Text | Google Scholar

46. Jang Y, Nam C, Kim JY, Cho BK, Cho YJ, Kim TW. Magnetic field sensing scheme using CoFeBnetic fiel tunneling junction with superparamagnetic CoFeB layer. Appl Phys Lett. (2006) 89:163119. doi: 10.1063/1.2370876

CrossRef Full Text | Google Scholar

47. Zhao W, Chappert C, Javerliac V, Noziere J. High speed, high stability and low power sensing amplifier for MTJ/CMOS hybrid logic circuits. IEEE Trans Magn. (2009) 45:3784–7. doi: 10.1109/TMAG.2009.2024325

CrossRef Full Text | Google Scholar

48. Ghosh B, Dwivedi K. Micromagnetic analysis of Heusler alloy-based perpendicular double barrier synthetic antiferromagnetic free layer MTJs. J Theor Appl Phys. (2015) 9:207–12. doi: 10.1007/s40094-015-0181-9

CrossRef Full Text | Google Scholar

49. Kianirad H, Laurell F, Canalias C. Domain wall motion in stoichiometric LiTaO3 induced by low-energy electron beam. Appl Phys Lett. (2019) 115:052901. doi: 10.1063/1.5101039

CrossRef Full Text | Google Scholar

50. Li D, Cui B, Yun J, Chen M, Guo X, Wu K, et al. Current-induced domain wall motion and tilting in perpendicularly magnetized racetracks. Nanoscale Res Lett. (2018) 13:238. doi: 10.1186/s11671-018-2655-6

CrossRef Full Text | Google Scholar

51. Jiang W, Upadhyaya P, Zhang W, Yu G, Jungfleisch MB, Fradin FY, et al. Blowing magnetic skyrmion bubbles. Science. (2015) 349:283. doi: 10.1126/science.aaa1442

CrossRef Full Text | Google Scholar

52. Martinez JC, Jalil MBA. Current-induced motion in a skyrmion lattice. J Appl Phys. (2015) 117:17E509. doi: 10.1063/1.4916754

CrossRef Full Text | Google Scholar

53. Baek S-hC, Amin VP, Oh Y-W, Go G, Lee S-J, Lee G-H, et al. Spin currents and spin–orbit torques in ferromagnetic trilayers. Nat Mater. (2018) 17:509–13. doi: 10.1038/s41563-018-0041-5

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Davidson A, Amin VP, Aljuaid WS, Haney PM, Fan X. Perspectives of electrically generated spin currents in ferromagnetic materials. Phys Lett A. (2020) 384:126228. doi: 10.1016/j.physleta.2019.126228

CrossRef Full Text | Google Scholar