Monte-Carlo Simulations of Soft Matter Using SIMONA: A Review of Recent Applications

Molecular simulations such as Molecular Dynamics (MD) and Monte Carlo (MC) have gained increasing importance in the explanation of various physicochemical and biochemical phenomena in soft matter and help elucidate processes that often cannot be understood by experimental techniques alone. While there is a large number of computational studies and developments in MD, MC simulations are less widely used, but they offer a powerful alternative approach to explore the potential energy surface of complex systems in a way that is not feasible for atomistic MD, which still remains fundamentally constrained by the femtosecond timestep, limiting investigations of many essential processes. This paper provides a review of the current developments of a MC based code, SIMONA, which is an efficient and versatile tool to perform large-scale conformational sampling of different kinds of (macro)molecules. We provide an overview of the approach, and an application to soft-matter problems, such as protocols for protein and polymer folding, physical vapor deposition of functional organic molecules and complex oligomer modeling. SIMONA offers solutions to different levels of programming expertise (basic, expert and developer level) through the usage of a designed Graphical Interface pre-processor, a convenient coding environment using XML and the development of new algorithms using Python/C++. We believe that the development of versatile codes which can be used in different fields, along with related protocols and data analysis, paves the way for wider use of MC methods. SIMONA is available for download under http://int.kit.edu/nanosim/simona.

Introduction

Over the past decades, computer simulation methods have been extensively used to explore the potential energy surface (PES) in molecular systems in order to get valuable thermodynamic information. In the study of large atomistic systems, Molecular Dynamics (MD) and Monte Carlo (MC) simulations are the most popular and useful tools to contribute to the understanding of physico-chemical phenomena at the nanoscale level. The common ground of both methods is the use of specially parameterized potential functions, i.e., Force Fields (FF), that describe the system of interest and its behavior at finite conditions. Nevertheless, they use different approaches. MD trajectories are the result of solving the integration of Newton’s laws of motion obtaining several configurations or states of a molecule that depend on the previous state describing the atomic positions and velocities over the simulation time [1]. This approach is suitable to study dynamical processes, such as protein stabilization or binding of receptor-ligand complexes during a limited time scale. The challenge in simulating such processes is the trapping of conformations in local minimum of the PES and rare transitions between minima, leading to poor sampling of the wide conformational space of a molecular system. This can be overcome in MC simulations with Markov chains (MCMC), where the state/conformation of a molecule does not depend on the previous state, i.e., there is no memory, resulting in the sampling of different local minima potentially being faster than MD [2]. MD integration algorithms become unstable at large time steps. This limitation can be solved using MC simulations where applying the right “moves” can guide the system to different local minima. In MC simulations, novel conformations are created by applying moves affecting the whole structure (translations, rotations and dihedral rotations) to generate candidates that could be accepted/rejected according to energy acceptance criteria. The move-construction is a key feature affecting the efficiency of the MC approach. Single and local moves are not sufficient for complex systems where the acceptance rate commonly shows an exponential decrease for high energy intermediates and the efficiency of the method decreases due to the big number of steps required. These types of moves involve just one or a few degrees of freedom of the system whereas “collective” moves involve many more degrees of freedom from the entire configurational space. In systems where collective effects play a major role making “collective” moves is essential in finding moves which fulfill the acceptance criteria. Methods with a force-biased move construction, using an energy estimator to increase the MC simulation efficiency, are suitable to generate moves with many degrees of freedom. Examples are forced bias MC [3, 4] and AROMoCa (Acceptance Rate Optimized Monte-Carlo) approach [5], which is a generic MC protocol that has been proven to be effective compared with generic MC methods.

The conformations of a condensed-phase system can be significantly affected by the surrounding. To accurately predict the conformational space of a molecule in specific conditions, the implementation of solvation methods is necessary but challenging. For MD simulations, it is possible to simulate the solvent explicitly but for MC simulations, only a small part of the system is modulated in a single move. Explicit solvation in MC increases the number of degrees of freedom which, in many cases, makes efficient algorithms for multi-particle moves too expensive. Even though some strategies to add explicit solvation in MC simulation have been proposed in MC_PRO [6, 7], the solute conformations in MC simulations can be predicted faster using implicit solvation methods in order to achieve accurate convergence. The most widely used implicit solvent models that provide approximate descriptions of the effect of the solvent on the solute are Poisson-Boltzmann (PB), Generalized Born (GB) and Solvent-accessible Surface Area (SASA) models.

PB solvation method, which solves the PB equation numerically, describes the electrostatic interactions of charges in a dielectric continuum. The GB method uses a high dielectric continuum to represent the solvent and substrate as a spherical point of charge with a low dielectric cavity to obtain potential energy values [8]. While the PB method is an accurate model for calculating polar solvation energy, it is not widely used as the computational cost of solving the PB equation and its derivatives is very high [9]. Instead, GB-based calculations that were shown to have a reasonably accurate and cost-effective performance are more popular [10]. GB efficiency can also be improved using a faster method to calculate the Born radii for large scale biomacromolecules using octree integration and Barnes−Hut tree code scheme [11], as is discussed in the SIMONA Engine section.

Many other approaches exist for increasing the computational efficiency and for speeding up conformational sampling in atomistic MC simulations. Replica Exchange MC (REMC) or Hyper-parallel tempering MC has been used to study phase transition on Lennard-Jones fluids [12, 13]. The REMC method performs temperature jumps in several independent simulations copies generated with MC simulations, maintaining the equilibrium ensemble distribution of the temperatures in order to get a transition probability that allows the exchange between the ensembles of the simulations [14]. Another approach is Multiple Try MC, which is a variant of the classical Metropolis algorithm with the advantage that in each new step the selection of the new conformation is over several proposals improving the exploration over a large zone of the sample space [15, 16]. Also, some studies employed advanced protocols to simulate open systems such as simulation of surface adsorption. Grand Canonical Ensemble MC simulations are affected by the impediment regarding the insertion/deletion probability of molecules near the surface, especially at higher densities due to probable overlaps between the adsorbed molecules and the new molecule unit [17]. Methods such as Configurational Bias MC (CBMC) [18, 19] and Continuous Fractional Component MC (CFCMC) [20–22] method had been proposed for adsorption simulations. The CBMC method tries to insert the gas phase optimized molecules with a growth process that has the preference to a minimum energy configuration, meanwhile CFCMC insert molecules in a fractional way considering the absorbed molecules as in a framework, scaling the strength of the neighbor interactions to decide the insertion or deletion of molecule units. Torres-Knoop et al. [23] have compared both methods investigating the adsorption of alkanes in Fe₂(BDP), small rigid molecules on MgMOF-74 and xylenes in MTW-type zeolite showing that CFCMC is superior to CBMC in accuracy and efficiency. Furthermore, they proposed a hybrid method combining both methods achieving higher insertion acceptance ratios [23].

Several software packages have been developed to perform MC simulations for specific systems implementing different MC algorithms. Popular packages were created to perform de novo design on peptides and protein modeling, such as Rosetta with structural-based potential function [24] or MC_PRO (Monte Carlo for Proteins) that is part of BOSS (Biochemical and Organic Simulation System) able to use the OPLS-AA FF for the MC simulation of proteins [25]. In the same way, other programs have been developed for MC simulation of soft materials namely, RASPA MC package which is capable of performing simulations on the adsorption of organic molecules [26] and FEASST a Python module to perform Wang–Landau MC, transition-matrix MC and Metropolis MC simulations [27]. Grand Canonical MC (GCMC) has been implemented in LAMMPS, one of the most widely used and flexible open-source MD software packages. However, it does not incorporate enhanced sampling methods and its application is limited to specific problems such as hybrid Monte Carlo (HMC) simulations [28, 29]. Many packages are specifically oriented to a particular MC application and specific soft matter system (specifically designed MC FF is necessary) or are limited to users with advanced programming knowledge.

Here, we present a generic simulation package for stochastic simulations, SIMONA (Simulation Molecular and Nanoscale System) [30]. SIMONA code was designed to offer a versatile, efficient and adaptable tool to perform MC simulations in different molecular systems such as polymers, including bio-polymers (such as proteins or DNA), synthetic organic polymers, and also single molecules and their deposition on films. The paper is organized as follows: the first part of this paper explains the basis of the preprocessor steps, its adaptable engine and its performance. In the second part, we present representative applications of SIMONA in various fields (Figure 1) including 1) MC simulation of protein folding and sampling conformational ensembles using two different implicit solvation approaches providing thermodynamic averages and understanding on major kinetic processes, 2) MC simulations of reversible self-assembly of single-chain polymers inspired from protein folding, with designed donor-acceptor terminals providing a full thermodynamic characterization of their folding behavior, 3) a special supporting tool for polymer modeling, the Oligomer Encoder, which is able to create code-based polymer sequences from SMILES monomer codes for further SIMONA MC simulations, 4) deposition of molecules on a substrate or an empty simulation box using a sticking potential and investigating their interaction using electrostatic and Lennard-Jones grids, 5) the implementation of a layered implicit membrane model (SLIM) to study membrane proteins using MC simulations and application of SIMONA as a complement to bioinformatics programs to study the effect of mutations on protein stability. These applications show promising perspectives toward further code development and usage with SIMONA.

FIGURE 1

FIGURE 1. Possible applications of SIMONA described in this review.

SIMONA Engine

SIMONA can be used at different levels of programming expertise (basic, expert or developer). The basic user level allows users to perform generic MC simulations with molecules parametrized with previously implemented methods and force fields. The parameter files needed can be obtained from EPQR files that must include partial charges and van der Waals radii provided by the user and it will be converted in a SIMONA parameter file with extension SPF (Structure Parameter File). Coordinate inputs, such as PDB and mol2, are supported. SIMONA offers a graphical user interface (GUI) to guide the user in the configuration of the settings to perform the simulation (Figure 2). The package includes Python tools to prepare the input files required by the GUI and analyze the simulation output files. Additionally, SIMONA is adapted to use GROMACS input files to generate inputs for MC simulations.

FIGURE 2

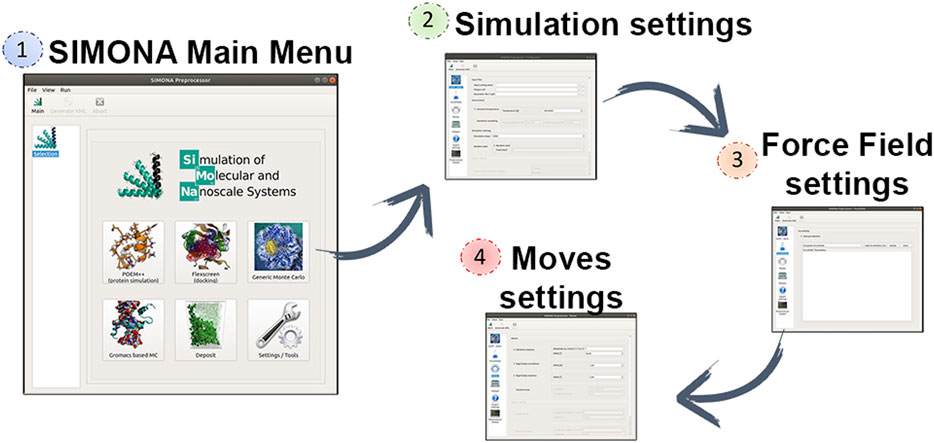
FIGURE 2. Captions of SIMONA pre-processor and required steps using the GUI to generate SIMONA input files.

The Generic Monte Carlo Simulation settings include the selection of moves, which can be translation and rotation moves. Rotational moves can be identified as “id moves” which denote the dihedral locations where the moves are going to be applied. Those ids are previously identified by SIMONA and specified in the SPF file. Part of the simulation settings must be provided by the user such as maximum angle distribution and temperature regime for constant temperature simulations or simulated annealing. The next step is the selection of the Force Field (FF) terms that will describe the interactions of the system and they will be used to calculate the conformational energies. FF energy contributions such as van der Waals (vdW), Coulomb or special physics-based FF are offered by SIMONA to perform simulations on proteins. Finally, the user must provide the simulation details, such as the number of the simulation steps and the frequency of data storage. Before performing the MC simulation, a global simulation input file is written in XML format, where all the information about the system is collected, it describes the system’s structural details, movements and the MC algorithm that is going to be applied.

At the expert level it is possible to directly manipulate XML files created by the preprocessor step. In Figure 3, the main parts of the XML code, corresponding to the Coordinates specification, the Structural moves definition, the FF terms and the Algorithm, are shown. The modular structure of the XML is organized to permit the creation of workflows, without modifying the C++ source code, to allow new features such as iterations, administration of subtasks and applying a conditional execution besides the standard protocols, such as nested MC or Simulated Annealing, which are included in the GUI. These special workflows can be achieved with logical statements on the Algorithm part with keywords, such as Repeatedmoved, TranformationSequence, SetDihedralRelativeRandom or Absolute, MetropolisAcceptanceCriterion and others.

FIGURE 3

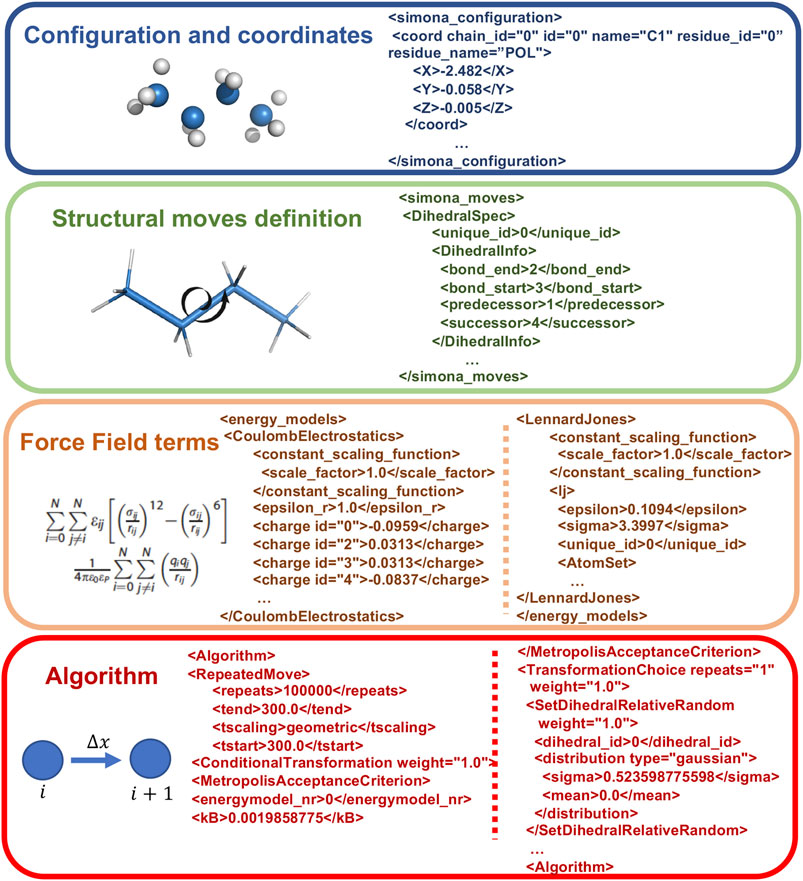
FIGURE 3. Example of Structure of XML SIMONA input file describing its main parts, such as the Configuration and coordinates, the Structural moves definition, FF terms to describe the system interactions and the Algorithm related to the moves generation.

Some molecular systems require a new force field implementation to evaluate special interactions, such as coordination bonds on metal-organic compounds or binding energies of molecules interacting with a specific surface. For this problem, the developer level in SIMONA offers a solution to generate new FF terms. The new FF contributions can be added, including new Python classes to call functions in the source code written in object-oriented C++ engine, including a Function Parser library that can convert text functions into C++ code from XML inputs. This procedure can be applied to subgroups of atoms or more complex general schemes for (3, 4, 5,...N)-body interactions.

Two methods for MC move generation are provided in SIMONA: the Generic Metropolis MC [31] and AROMoCa [5]. The total rates of states (Γ) moving from a point p–p′, Γ(p → p′) must be equal to the backwards rate Γ(p′ → p) to satisfy the detailed balance condition. The transition probability, W, can be expressed as a product of two parts π and ⍴ where π is the probability that a move is constructed and ⍴ is the probability that it is accepted.

$W= \pi \left(p\to p^{\prime }\right)\rho \left(p\to p^{\prime }\right)(1)$

If moves are drawn at random from a distribution of coordinates, orientations, spins etc. then an acceptable approximation is that π (p → p′) = π (p′ → p). Furthermore, the acceptance probability can be chosen via the widely used Metropolis acceptance criteria [32]:

$\rho \left(p\to p^{\prime }\right)=\{\begin{array}{cc}\exp \left(\frac{-\Delta E}{k_{b}T}\right),& \Delta E<0\\ 1,& \Delta E\ge 0\end{array}(2)$

Here, the construction of each move is inefficient compared with MD simulations because only one or a few degrees of freedom are changed at once whereas in MD simulations all degrees of freedom change simultaneously. Furthermore, in order to reach thermodynamically relevant configurations collective moves often need to be made. Such changes are often difficult to propose as a sequence of local moves and efforts to construct such moves in large systems may lead to low acceptance rates.

Another approach to satisfying detailed balance is by postulating that ρ (p → p′) = ρ (p′ → p) = 1 i.e., a near perfect move construction algorithm is needed where all moves constructed will be accepted. Advanced sampling schemes such as AROMoCa are able to increase the acceptance rates achieved by identifying regions of the phase space where the forces are high, and the system is out of equilibrium and preferentially move there instead of to states near equilibrium. An approach of this nature is viable for systems the potential energy can be easily approximated at each point. The major advantages of these accelerated schemes are much higher acceptance rates and faster exploration of the configurational space compared to the Metropolis MC methods.

In AROMoCa energy estimator for systems with classical interactions, the change of the energy between both states (ΔE) is approximated to the energy calculated with the Taylor expansion of the energy using the force (F) and the displacement (Δx). Since the evaluation of the forces and the probability of accepting a move are high, the move is evaluated by the energy acceptance criteria in order to accomplish the probability distribution during the MC sampling. Every MC step with AROMoCa is calculated in three main parts (Figure 4). First, for each degree of freedom the probability to perform a displacement between two maximum values (−Δx_max and Δx_max) is calculated to have a set of moves. Second, a move is picked up from the previous array that correspond to a new displacement (Δx_ij) that is a fraction of the maximum displacement used in the previous step. The selection is made from a uniform and random distribution equation to choose a random coefficient. Finally, the moves with large forces and probabilities are evaluated by the acceptance criteria [5] (further details are in Ref. [5]).

FIGURE 4

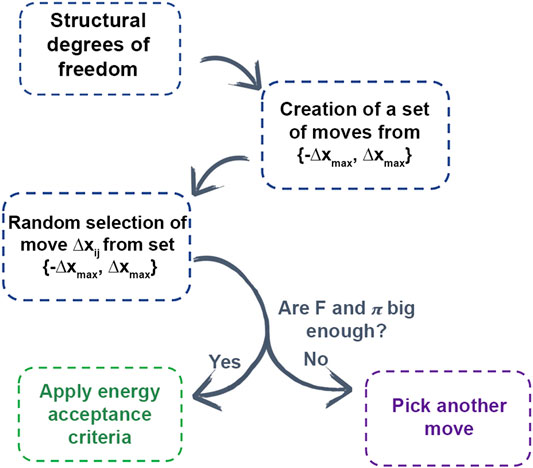
FIGURE 4. Scheme of AROMOCA moves generation. Degrees of freedom are used to generate moves to create a set of moves in a specific displacement. The moves are selected randomly from the set and if they obtain a high probability of acceptance and a high value of force, the energy acceptance criteria is applied.

To get an approximate potential of mean force from an effective solvation model, the calculation with implicit solvation models in SIMONA is currently separated into two components: polar and non-polar interactions. Non-polar contributions are the free energies in a SASA model, which can account for hydrophobic/hydrophilic effects. Their contribution is proportional to the surface area accessible to the solvent (solvent accessible surface area, SASA). The numerical evaluation of the accessible surface or volume of solute using MC, involves a substantial amount of integration points. POWERSASA is a C++ template library, available in the SIMONA framework, that employs exact analytical formulas to obtain the accessible surface and volume of molecules from the creation of iterative power diagrams of groups of atoms [33]. It was demonstrated that this approach is very stable and efficient (linear scaling), enabling simulations of large molecular systems.

Polar contributions to the free solvation energy are commonly calculated by the PB or GB method. As we mentioned before, GB-based methods are more popular in MC simulations because of their lower computational cost compared to PB-based methods. However, since GB calculation captures a considerable part of the computing effort in macromolecular simulations, development of efficient implementation for faster GB models is still required [34–37]. To increase the efficiency in the GB method, we have developed PowerBorn, implemented in C++, which presents a new method for Born radii calculation. It enhances the performance of GB solvation method in SIMONA simulations by creating an octree representation of the water region around the molecule (supported by POWERSASA) by means of subdividing the three-dimensional space and storing the data related to each subspace. Finally, the Barnes−Hut tree code scheme integration is performed walking through the octree. The accuracy of this method was tested in relation to PB method and a good agreement was observed for computed Born radii with major correlation coefficients of 0.9978 and root-mean-square error of ∼1% for polar solvation free energies [11].

In addition to the efficient MC simulation scheme, presented above, SIMONA is implemented for parallel computing architectures such as Open Multi-Processing (OpenMP). To illustrate SIMONA’s performance, a benchmark with different polymer chain lengths, i.e., 10-mer (280 atoms), 20-mer (344 atoms) and 30-mer (600 atoms) using OpenMP was performed (Figure 5). The simulation times reached no more than 1–2 min for 10⁹ steps using a supercomputer module AMD EPYC 7702 64-Core Processor, suitable for extremely cheap screening. The inverse relation of cores vs. CPU time in Figure 5 shows that for the different system sizes, the simulations get faster by increasing the number of cores, however, for smaller system sizes, simulation speed reaches a limit at 16 cores (Figure 5). The experience with the simulation performance can be additionally enhanced by including PLUMED libraries in calculation of properties such as distances, angles, conformation energies etc. necessary for further analysis [38, 39].

FIGURE 5

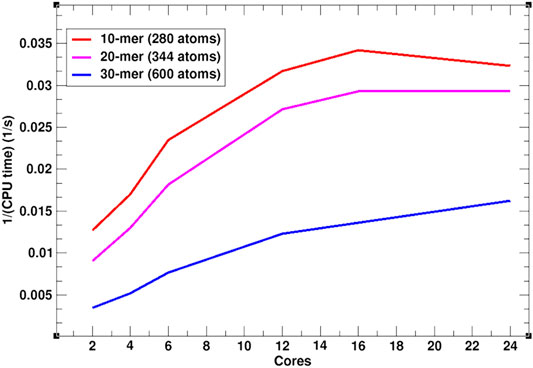
FIGURE 5. OpenMP SIMONA performance in 300 K constant temperature calculation of a polymer with 10, 20 and 30 monomers.

Biomolecular Simulations

Proteins are a very important group of biologically active macromolecules, whose specific function is steered by small conformational changes. The computational analysis of their structure-property relationships is still a widely investigated issue in modern science, therefore folding of proteins in different environmental conditions and efficient sampling of their conformational space are of extreme importance. Since a conformational change of a protein and many natural processes occur on timescale, ranging from microseconds to seconds, the use of MD simulations remains fundamentally constrained by the short individual timestep that arises from the discretization of the underlying equations of motion, which hovers in the femtosecond range for decades. The development of special-purpose computers, e.g., by DE Shaw Research, has resulted in a quantum-leap in performance and illustrated the potential of the method and high importance of MD simulations [40–43]. Unfortunately, special-purpose computers are not publicly accessible, therefore, there is an overwhelming majority of researchers who could not and who cannot perform competitive investigations.

Protein Folding

An MC-based simulation strategy, that can solve the underlying challenge to simulate large-scale biomolecular conformational change, is an alternative approach to understanding biomolecular structure and function. Here, a large set of points in the multidimensional space of the conformational degrees of freedom of a protein is generated with relatively low computational cost. This set contains folded and unfolded structures, as well as intermediates and transition states, representing the thermodynamic equilibrium ensembles that can be also extracted from long-time MD simulations. Thermodynamic averages in MC methods, that permit reconstruction of the large scale kinetics of proteins even on the basis of a thermodynamic simulation, are used to calculate barriers between distinct conformational ensembles sampled in MD [44]. Several MC simulation schemes for protein folding, that employ specifically designed force fields and algorithms, were reported. Among them are PROFASI [45], SMMP [46], Rosetta [24, 47, 48], CABS [49, 50], MMTSB [51]. Recently, we have illustrated a new efficient MC algorithm for modeling the large-scale conformational change of proteins using the standard all-atom force fields for proteins and efficient implementation of implicit solvent model in SIMONA [30, 52]. Two simulation protocols were used: 1) Amber99 force field Lennard-Jones and Coulomb terms and Amber99SB for dihedral potentials with generalized Born (GB) implicit solvent using PowerBorn [11] for Born radii computation and Stills GB formula with exponential factor of 4 [30]; 2) AMBER99SB*-ILDN force field with GBSA implicit solvent with Born radii computed with the PowerBorn [11] method and the SASA radii with the POWERSASA method [33, 52].

In both cases, the dielectric constant of the protein and water was taken to be e_p = 1 and e_w = 80, respectively, and the surface tension of the nonpolar solvation term was γ = 5.42 cal/mol·Å². MC calculations were performed with no long-range cutoffs or approximate methods in the evaluation of the force field or implicit solvent model. While the first strategy was applied for folding of 20-residue based Trp-cage protein (PDB code 1L2Y) and the native conformation was defined by a mean square deviation (RMSD) below 3 Å, it initiated our further developments of the MC algorithm in the second approach, where we have demonstrated successful usage of an accurate intramolecular force field (developed for all-atom MD simulations) and our efficient implicit solvent implementation for reversible folding also of 36-residue Villin headpiece (PDB code 1vii) and 35-residue WW-domain (PDB code 2f21) using MC [52].

To sample the conformational landscape of these proteins, we designed an individual MC step composed of either a combination of a randomly selected backbone and sidechain dihedral rotation or a concerted backbone move with equal probability. The angle change in the dihedral moves was drawn from a Gaussian distribution with a width of 18.3° for Villin Headpiece and 20° for Trp-cage and WW domain. In the case of a “concerted move”, a segment of four residues was modified, changing all dihedral angles under the constraint that the endpoints of the segment do not change. Rigid body rotations were applied by rotating the molecule around a random axis through its geometric center with a uniformly distributed rotation angle of up to 5°. The Metropolis acceptance criterion with Markov chain model was used to construct collective moves with the average acceptance probability of 0.6 (60%), preserving detailed balance. In such a way, the obtained effective time step of MC simulations was 260 fs/MC step, therefore, accelerated the sampling of the conformations by about two orders of magnitude over all-atom explicit-solvent MD simulations.

We have illustrated the efficiency of the MC protocol and its implementation in SIMONA in reversible folding of three proteins, where five to ten MC simulations, each comprising up to 200 million MC-steps at different simulation temperatures, were performed. Similarly to the longest, to our knowledge, MD simulations, multiple folding and unfolding events, starting from both native and unfolded structures, e.g., for the Villin headpiece (Figures 6A,C), were observed [40, 53–55]. Here, an all-atom/backbone RMSD of the refolded to the NMR native structure [56] reached 1.49 Å/0.76 Å, showing good quality of the sampled protein conformations. The complementary analysis was also monitoring the fraction of the native contacts, Q (Figure 6B), which is a widely used reaction coordinate of the folding process. The potential of mean force (PMF) projected on the fraction of Q-values was used to calculate the folding thermodynamic equilibrium and predict the folding temperature (Figure 6D), i.e., 354 K after temperature calibration of MC runs.

FIGURE 6

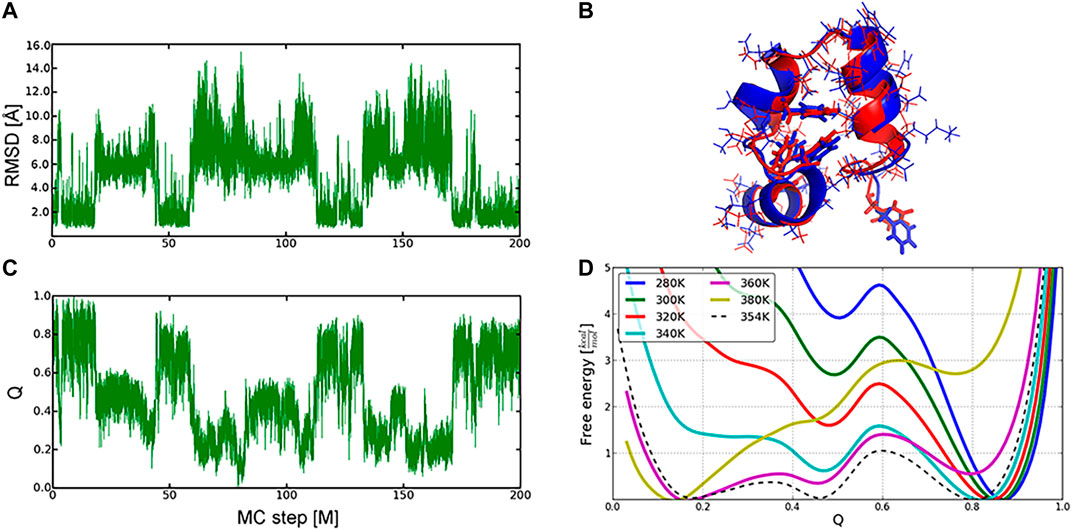
FIGURE 6. Sampling of the conformational landscape of the Villin headpiece protein (1VII): folding and unfolding events described by RMSD (A) and Q-values (B) changes in the MC run at 360 K (C) Overlay of the refolded (in red, Q −0.8) and the experimental (in blue) conformation of the protein (D), Free energy profiles as a function of Q‐values at different temperatures. Native, intermediate, and unfolded ensembles were found at Q∼0.8, 0.45, 0.2, respectively. Graphics reprinted from Heilmann et al. Sci. Rep. 10, 18211 (2020) [52] under Creative Commons Attribution 4.0 International License.

The obtained Cα-RMSD of the refolded Trp-cage protein using our MC in SIMONA was also of good accuracy, i.e., 0.86 Å (Figure 7) with the Q-values of the refolded structure of ∼0.73 (Figure 1 in Ref. 49 [52]). This value is slightly lower in comparison to what was observed in MD simulations with explicit water (Q around 0.9–1) [57]. Nevertheless, the absolute Q-value at the minimum depends on the definition of the protein native contacts taken from the NMR ensemble.

FIGURE 7

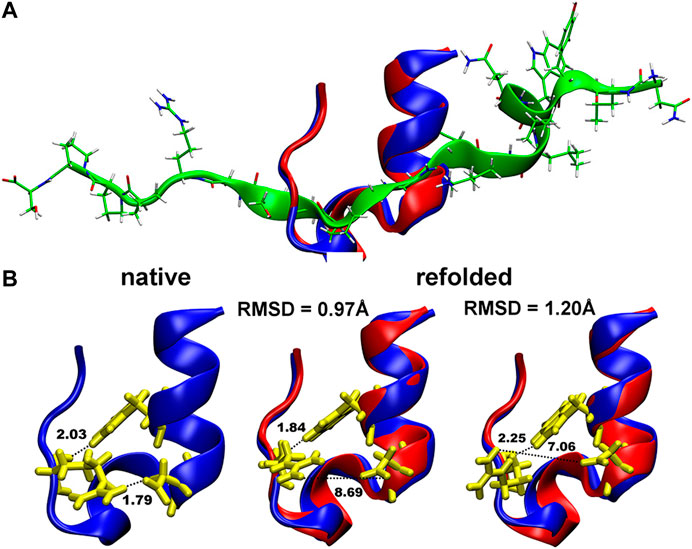
FIGURE 7. (A) Folding of the Trp-cage miniprotein (1L2Y) in MC simulations in SIMONA: Overlay of the native structure (in blue) and the refolded structure (in red) obtained inMCrun at 370 K starting from unfolded protein depicted in green (B), Structures of the native 1L2Y and refolded local minima with different RMSD and formed hydrogen bonds (described in the text). Graphics reprinted from Heilmann et al. Sci. Rep. 10, 18211 (2020) under Creative Commons Attribution 4.0 International License [52].

Even if the quality of the refolded structures is in good agreement with the experimental data, the estimated folding temperatures are overestimated, e.g., 370 K for Trp-cage, while in MD with explicit water and in experiment temperatures of 321–326 K [58, 59] and 315–317 K [60, 61], respectively, were reported. We assume the effect originates from the lack of the temperature dependence in the used GBSA implicit solvent model and the proper description of the solvent exposed hydrogen bonding [62]. It is known that folding and unfolding of Trp-cage is modulated by cooperative interactions between water and polar groups of the protein and by the H-bonded salt bridge between Asp-9 and Arg-16 (N–H⋯O bond of 1.79 Å in Figure 7B) exposed to the solvent. This bond is not properly reproduced in the refolded structures in MC shown in Figure 7B. At the same time, the second N–H⋯O hydrogen bond: between Trp-6 and Arg-16 (N–H⋯O bond of 2.03 Å in Figures 7B, is correctly reproduced, enabling refolding of the protein after unfolding (structure depicted in green in Figure 7A). Implementations of new implicit solvent models, e.g., with advanced fitting of the GB solvation energies and the relative solvation energies like in ff14SBonlysc + GB-Neck2, are necessary, and can be performed using SIMONA.

SIMONA was also used to investigate the all-atom level folding and unfolding kinetics of the Trp zipper one protein (PDB code 1LE0) [63], a small polypeptide that forms a β-hairpin at the room temperature [64]. Here, dynamical properties of protein conformational space were obtained using MC with a transition network algorithm that permitted calculation of the “absolute” conformational free energy and folding mechanism of Trp zipper 1, using protein force field PFF02 with implicit solvent [65]. This transition network consisted of the nodes that correspond to the discrete number of conformations sampled by the MC process. Protein dynamics was represented by a walker that moves across the network and “jumps” from one neighboring node to another with a certain probability. The probability was dependent on the transition rate between nodes connected by edges, characterized by the edge length, i.e., RMSD distance between the corresponding nodes. Using this approach, approximate estimations of the relative folding times for the whole ensemble of protein conformations were obtained, which is not possible in conventional MC simulations.

Membrane Peptides

We have also used SIMONA to investigate the function of membrane proteins in biological membranes [66] and the phenotypic effect of protein mutations [67]. Membrane proteins are part of the biological membranes and medically important proteins as they are targets for about half of all available drugs. The computational simulations of these molecules can be used as a supporting evidence for experimental findings, elucidating protein mechanisms, and validating protein crystal structures [68]. The transition time between the functional states of membrane proteins is generally much longer than what one can currently capture with the standard simulation methods [69]. To facilitate their simulation, approximate membrane models with coarse-graining or implicit membrane modeling have been proposed [70, 71]. In the most implicit continuum models, membranes are represented as heterogeneous dielectric environments, but their treatment within computationally efficient GB models is challenging. GB models are limited to two dielectric regions by construction, which are typically chosen as the solvent and the solute. Standard GB models cannot be embedded for a membrane region with different dielectric properties. Therefore, incorporating biological membranes in implicit solvent models is an important prerequisite for their simulations, which has been offered by SIMONA as SLIM (SIMONA layered implicit membrane) model [66].

The SLIM model has been tested in MC studies of three well-studied membrane proteins: Melittin from bee venom (PDB code: 2MLT), a single transmembrane domain of the M2 protein (PDB code: 1MP6), and the transmembrane domain of the Glycophorin A (PDB code:1AFO) [66]. For every system and parameter set, 20 independent SIMONA simulations were performed at 300 K with no force field cutoffs. Simulations were performed for 2 × 10⁴ MC steps including random rigid body rotations and translations, as well as all backbone and side chain dihedral rotations. Results showed that upon the use of the proper membrane model parameters, the SLIM model is able to reproduce known properties of these proteins, e.g., sampling of the protein conformations in the lipid environment. Simulation performance of SLIM-SIMONA model was compared with heterogeneous dielectric generalized Born (HDGB) model of Tanizaki and Feig [72], which is implemented in CHARMM (version 35b) [73]. It was shown that SIMONA simulation with SLIM achieves about 4.4 times more simulation steps without using any long-range interaction cutoffs.

SIMONA has also been used to predict the phenotypic effect of mutations on protein mutational landscapes, which quantifies how mutations affect the biological functionality of a protein. Figliuzzi et al. [67] developed and successfully tested a novel inference scheme for mutational landscapes based on the statistical analysis of large alignments of homologs of the protein of interest. They have used extensive all-atom SIMONA simulations along with bioinformatics programs to estimate TEM-1 (286 amino acids) protein stability changes, ΔΔG, induced by single point mutations. The complete PFF03v4-all parallel OpenMP force field was applied, which uses the AMBER99SB*-ILDN dihedral potential with an implicit solvent model. Locally stable configurations were explored by performing small structural relaxations from a reference structure, with the wild-type amino acid replaced by the mutant amino acid. The energy function was locally minimized and the resulting energy change ΔE = E_mut−E_wt was determined.

Polymer Folding

Reminiscent of protein folding, polymer chains can be folded to individual, single-chain polymer nanoparticles (SCNPs) by means of intrachain interacting groups. Synthesis of well-designed single chain polymers is one of the profound and constantly increasing interests in polymer chemistry [74]. Novel experimental techniques of controlling nanoscale architecture make it possible to synthesize polymeric single chain nanoparticles where single polymer folding is driven by a specially designed hydrogen donor–acceptor moieties [74–76]. In this regard, molecular simulation techniques can shorten the demanding experimental trial-and-error process by identifying “well-behaved” polymer architectures for single-chain polymer folding and establish design principles [74]. However, the individual macromolecular nature of the polymer molecules and the broad spectrum of time and length scales encountered in polymeric materials, make the efficient equilibration and sampling of their equilibrium properties tedious sometimes even impossible via nonstochastic approaches [77]. MC sampling techniques proved to be ideal for problems concerning structural equilibration or calculation of static properties of polymers [78, 79]. In this regard, various MC simulation techniques have been applied in polymer science to study the structure and elastic response of end-linked polymer networks [80], polymerization mechanism and chain relaxation of polymer brushes [81], phase behavior of copolymer blends [82], and the effect of chain branching on the topological properties of entangled polymer melt etc [83].

In this section, we focus only on the overview of MC simulations and advances to a specific problem related to the polymer science i.e., reversible self-assembly of single polymer chains. We have developed a MC simulation technique to study polymer systems functionalized by reactive sites [84] that bind/unbind forming reversible hydrogen bonds shown in Figure 8. Polystyrenes chains of lengths L = 10, 20, 30, 40 and 50 monomers with two hydrogen bonding recognition units based on six-point cyanuric acid(CA)–Hamilton wedge (HW) interaction (α,ω-donor–acceptor) were designed. For each chain length L, all-atom Metropolis Monte Carlo with 10⁹ steps at constant temperatures in the temperature range from 220 to 340 K were performed using SIMONA. To sample the conformations of the whole polymer, a molecular mechanics approach with General Amber force field (GAFF) parameters were applied with the partial charges computed according to the AM1-BCC method. The dielectric constant of the solvent was set to ε = 2.6 in all simulations in order to match the energy difference between the bound and unbound α and ω molecules with the QM calculations. To implicitly take into account the effect of van der Waals (vdW) interaction with a solvent, the vdW contribution in the force field was scaled by factor 0.1 based on the experimental data of the vdW dispersion forces between alkyl chains in different solvents.

FIGURE 8

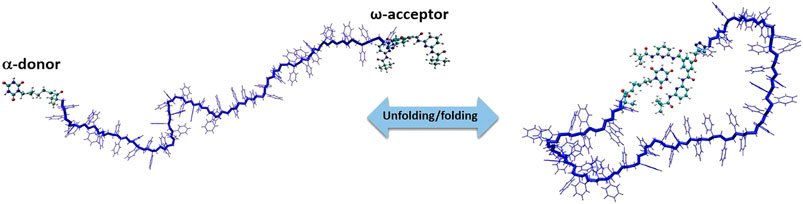
FIGURE 8. Model system of a polystyrene precision designed polymer with a,ω‐donor–acceptor for single chain self‐assembly.

Based on MC trajectories in a wide temperature range, hundreds of open and closed conformations were observed for each polymer chain, which is the result of reversible hydrogen bond formation between the designed binding sites. From a MC trajectory at a given temperature T, a probability density function p(E) as a function of the potential energy E (illustrated in Figure 9) was computed. It was used to deduce transition temperature (Tm), entropy and enthalpy difference between the closed and open states. Two measures were applied to describe the folded structure: 1) characterizing the shape of polymer chains in terms of anisotropy, asphericity and acylindricity and 2) calculating chain radius of gyration along the MC trajectory. Both disk-like and hairpin structures were observed for the long chain polymer L = 50. Furthermore, calculated radius of gyration for closed conformations showed that for shorter linker lengths (L = 10–20), polymers fold into a unique conformation with the root mean square deviation (RMSD) of the backbone atoms being smaller than 2.5 Å (see Figure 9C). For longer chain polymer (L = 50), no unique conformation was recognized (Figure 9D).

FIGURE 9

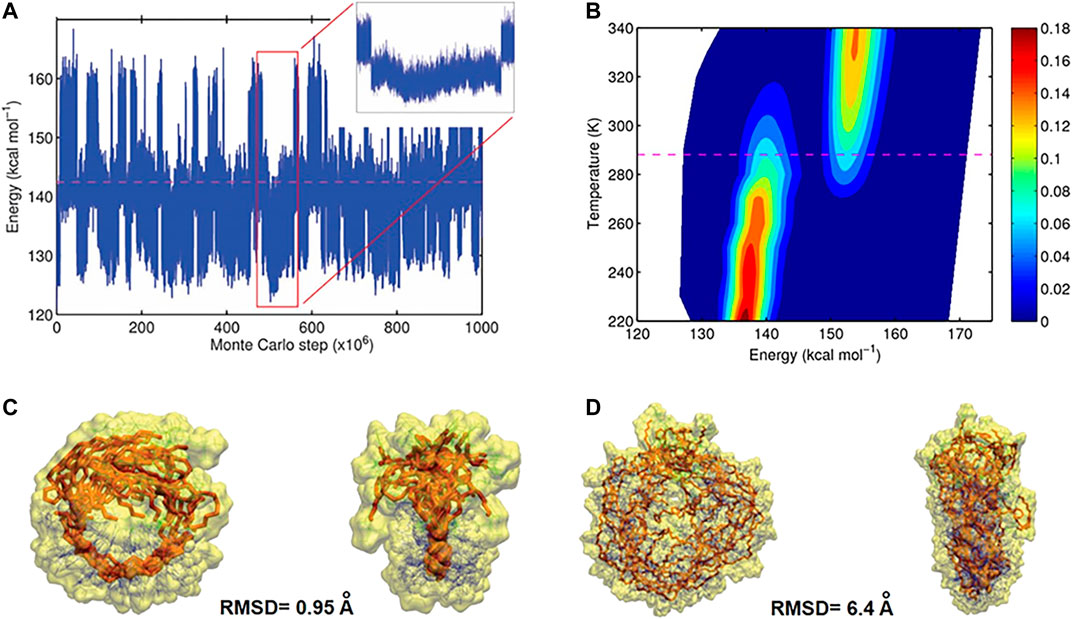
FIGURE 9. (A) Energy of the conformations for L 50 as function of the number of steps. Large values of the energy correspond to open, small values closed conformations (B), probability density profile computed from the trajectory (red regions are more occupied than blue regions), indicating two-state folding behavior. At the transition temperature (dashed line) the occupation of both states is equally probable (C), Front and side views of ten closed conformations obtained from uncorrelated closed intervals for polymers with L 10 (D) Front and side views of ten closed conformations obtained from uncorrelated closed intervals for polymers with L 50 (Reproduced by permission of The Royal Society of Chemistry).

Besides the chain length, the stereochemistry of the polymer chain also influences the folding behavior and thermodynamics. We applied the same MC technique to study the effect of tacticity of the polystyrenes chain of lengths L = 10, 12, 14, 16, 18, 20 and 30 monomers on their folding behavior [85]. Thermodynamic properties of reversible folding of atactic, syndiotactic and isotactic single polymer chains (see Figure 9A) were calculated using probability density histograms obtained from long MC trajectories containing hundreds of opening-closing transitions. We demonstrated that tacticity dependence of folding temperatures is especially pronounced for polymers of shorter chains (shorter than L = 20) compared to longer polymer chains (L = 30) (see Figure 10A). Reduced fluctuations of radius of gyration showed that for small linker lengths, polymers of diverse stereochemistry collapse into unique folded structures (see Figure 10C).

FIGURE 10

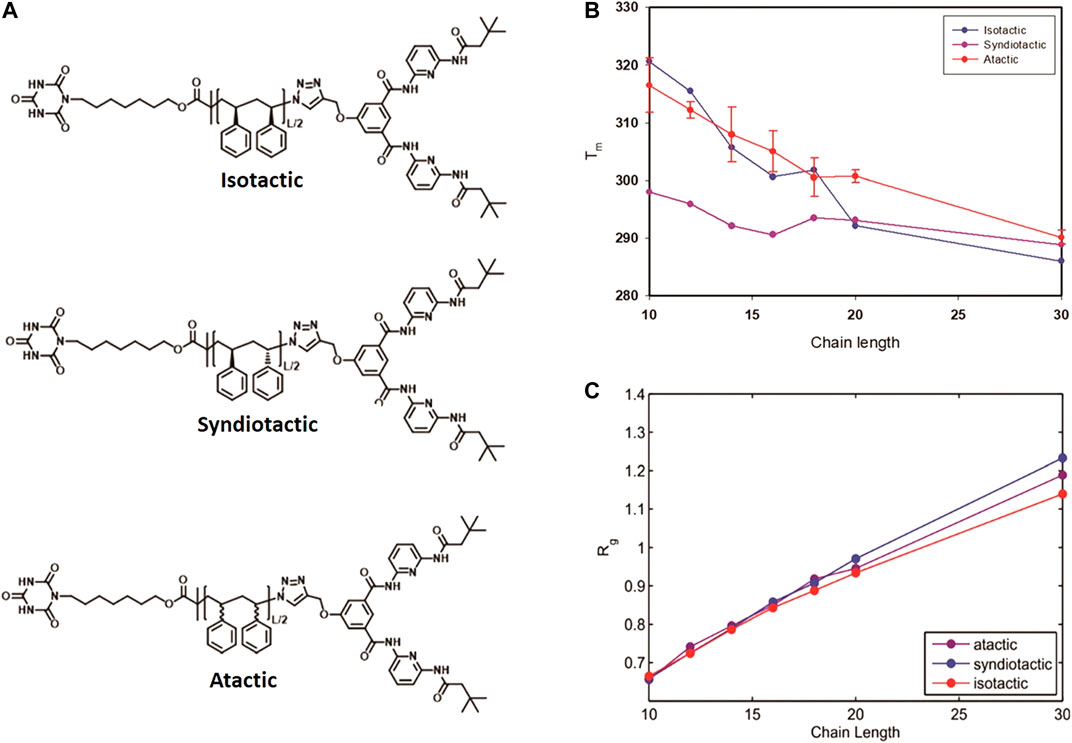
FIGURE 10. Molecular structure of Isotactic, Syndiotactic and atactic polymers (A), Folding temperature as a function of chain length for isotactic, syndiotactic and atactic polymers (B), Radius of gyration (Rg) as a function of chain length (C), for atactic, isotactic and syndiotactic polymers (Reproduced by permission of The Royal Society of Chemistry).

Oligomer Encoder

Natural storage information systems, such as DNA, are well-known as sequence-defined macromolecules where long chain sequences keep information encoded in building blocks called nucleobases. They are the foundation to create a new living entity, regulate processes and preserve the genetic information from one individual to another. Recently, there has been increasing interest in sequence-defined macromolecular synthesis for their potential application in the field of polymer chemistry in order to mimic enzyme activity or used as data storage systems [86]. This new area of research aims to obtain a high degree of synthesis control of non-natural macromolecules. They are considered as a new class of polymers combining the classic definition of a polymer (several repeating units) and characteristics such as monodispersity, chemical nature and conformational topology. A recent work by Wetzel et al. [87] revealed a synthesis strategy using the Passarini reaction to create sequence-controlled oligomers inspired in the genetic code and a protocol to decode their sequences using Mass Spectroscopy [87]. They defined a dual monomer scheme considering side chains and backbone modifications in order to create binary codes. Nevertheless, the synthesis of all possible code combinations is not feasible (nearly 10²² candidates) and the experimental challenge to determine their three-dimensional structures, by techniques such as NMR or Dynamic Light scattering, is limited to small sequences. As a complement to experiment, MC methods can provide insights regarding probable folded states, determining their potential applications as nanostructured materials for data storage.

As a special supporting feature to generate arbitrary synthetic oligomers for SIMONA simulations, we developed the Oligomer Encoder (OE). OE creates oligomer chains {X_i} (i = 1, … , N), where X_i monomer type is X_i = A_iB_i, while head and tails are Terminal 1 (T₁) and Terminal 2 (T₂), respectively. A_i and B_i are defined as side chains and backbone modifications, respectively, that are defined in a library (see Figure 11A). Here, we create oligomer structures and extract structural parameters of the respective monomer structures to reduce the computational cost. First, the oligomer structure is generated from the SMILES code database and then, monomer structures with head and tail terminal are generated and parameterized. Finally, information, such as coordinates, parameters and charges are extracted and transferred to the final model of a polymer/oligomer. The workflow of the OE program comprises three main steps. 1) Creation of Monomer structures and Optimization. The monomers required to build the sequences are created using the SMILES code [88] and optimized at DFT level using TURBOMOLE [89, 90]. 2) Oligomer chain ensemble. The optimized monomer structures are used to calculate charges using AM1-BCC method [91], provided for Ambertools [92], and parameters from the General Amber FF [93] are extracted with Acpype [94] to generate GROMACS input files. 3) SIMONA input file generation. At this step, GROMACS input files are used to generate the input files for the Monte Carlo simulation using the Python protocol provided by SIMONA [30]. This strategy allows OE to be a highly scalable molecule builder.

FIGURE 11

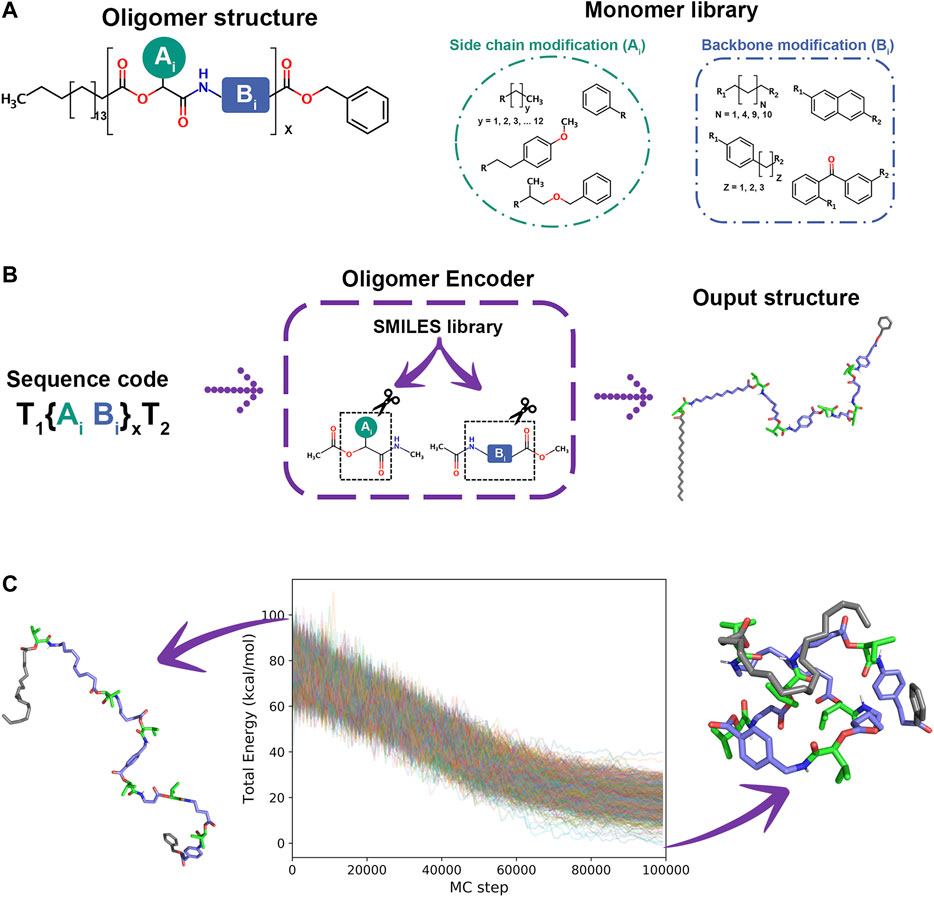
FIGURE 11. (A) Oligomer structure and monomer Library (B). OE workflow (C) Folded and unfolded structure of oligomer sequence and energy converged during 1000 MC annealing simulations from 900 to 100 K.

As an example, an hexamer oligomer inspired by the sequence B7 from Wetzel’s work [87] was created with OE. The sequence includes aliphatic and aromatic backbone modifications while all side chain modifications have isopropyl groups. The monomers were optimized using hybrid B3LYP functional [95, 96] with def2-SV(P) basis set functions [97]. A workflow simulation was performed generating 1000 different conformations from an annealing MC simulation heating the system from 300 to 900 K in 10⁶ steps and cooling from 900 to 100 K in 10⁶ steps, starting from different oligomer conformations. The energy convergence of MC simulations, presented in Figure 11C, shows attainment of the local minima. Even though MC simulations can explore the conformational space of every single sequence in a couple of minutes of simulation time, determining the most probable ensemble of unique folded structures is challenging. Currently, we are developing protocols to identify stable sequences in a minuscule fraction of the conformational space using design rules to identify the subspace of the library that is likely to fold. We are considering also the impact of organic solvent, hydrogen bonding between the backbone units, and specific interactions, like vdW or π-π, that stabilize specific sequences. We believe that this massively parallel iterative search is a promising tool to identify novel foldable structures that are not accessible with any other current technique.

Thin Films

The MC implementation in SIMONA can be used not only to obtain for obtaining the three-dimensional structure of single macromolecules, but also for generating nanoscale assemblies and films of smaller organic molecules. The latter, for example, lies in the basis for modern smartphone and TV displays technology, i.e., OLED (organic light-emitting diodes), where thin films are generated by physical vapor deposition (PVD) of organic molecules [98–102].

Due to the typically amorphous nature of the PVD generated films, their structure prediction, with the succeeding electronic property calculation, is the basis for all further microscopic simulations. To simulate the PVD thin film formation process, the SIMONA framework is used along with the Deposit protocol [103]. This protocol is split into three parts (see Figure 12): Parametrizer, Dihedral-Parametrizer and Deposit. The molecules are deposited either on a pre-existing substrate or into an empty simulation box with a sticky potential at the bottom. The total energy of a molecule is described by the intermolecular interactions consisting of an electrostatic part, E_ES, and a Lennard-Jones part, E_LJ, as well as the intramolecular interaction energy, E_DH, due to the dihedral rotations:

$E_{\text{total}}=E_{ES}+E_{LJ}+E_{DH}(3)$

To achieve a linear scaling behavior with system size, the molecules are kept fixed after deposition and the intermolecular interactions are computed by interpolating interactions with electrostatic and Lennard-Jones grids. The electrostatic grid represents the electrostatic potential created by charges of all previously deposited molecules in the simulation box. For the Lennard-Jones part, a separate grid for each element combination in the simulation is created. Therefore, each energy evaluation of the intermolecular part can be reduced to a lookup and a set of arithmetic operations, which do not scale with the total system size.

FIGURE 12

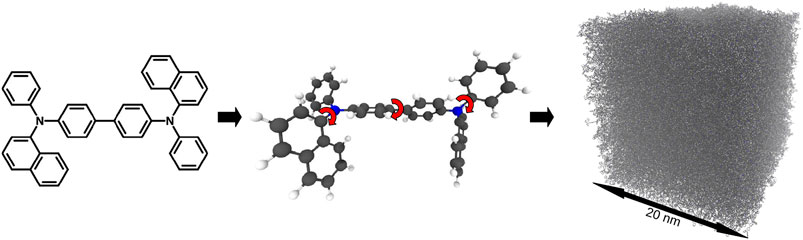
FIGURE 12. Thin film deposition simulation on the example of N,N′-Di(1-naphthyl)-N,N′-diphenyl-(1,1′-biphenyl)-4,4′-diamine (NPB): (i) Parametrizer: The molecular geometry gets optimized at the def2-TZVP/b3-lyp level with Turbomole. For the final geometry partial charges are calculated with an ESP fit. (ii) Dihedral- Parametrizer: The dihedral potential is scanned by turning the dihedral angles in 20° steps and performing DFT calculations at the def2-SVP/b3-lyp level. Additional internal charges and Lennard-Jones parameters are fitted to improve the dihedral forcefield. The final forcefield energy is tested against random configurations. (iii) Deposit: The molecule is deposited either onto a pre-existing substrate or into an empty box, where the first layers will stick to the bottom of the box via an externally applied force field.

In order to generate a molecule-specific potential, the intramolecular interactions are usually parametrized by turning each dihedral angle in 20° steps and relaxing all other dihedral angles. On each conformation, a single point DFT calculation is performed. After reaching a full rotation of an angle, a spline is fitted to the DFT energies. This method, though widely used, neglects correlations between different dihedral angles. However, it has been shown that such effects can be learned with a machine learning approach [104].

The deposition step is split into several simulated-annealing (SA) cycles, which run in parallel. In each cycle, the molecular position or conformation is changed, and the energy is re-evaluated. Each move is accepted on the basis of the Metropolis Monte-Carlo algorithm. The temperature of the simulation is adjusted from a high starting value, T_high, to a final temperature, T_low, during N steps via:

$T_n=T_{\text{high}}{\left(\frac{T_{\text{low}}}{T_{\text{high}}}\right)}^{\frac{n}{N}}(4)$

From the final positions of each SA-cycle, the deposited position is drawn with a Boltzmann probability. The described workflow was successfully applied for PVD of OLEDs and the structures generated by the DEPOSIT protocol have been used to calculate bulk mobility [105]. Due to its versatility and computational cost, it pathed the way for predicting and systematically improving new OLED materials [106].

Besides charge carrier mobility of thin OLED films and stacks, the outcoupling efficiency of dyes co-deposited in the film is another important property [107]. Since a dye molecule emits mostly perpendicular to the transition dipole moment (TDM) of the specific emission, the outcoupling efficiency is higher for TDMs oriented parallel to the surface of the OLED. This is usually quantified in an orientation parameter $\text{Θ}$, which equals to ∼0.33 for a completely isotropic orientation and to 0 for a perfect in-plane orientation:

$\Theta ={\langle \cos }^2{\alpha }_z\rangle (5)$

where α_z is the angle between the TDM and the axis perpendicular to the surface. To demonstrate the functionality of Deposit in reproducing experimentally observed orientation parameters, different iridium emitter complexes inside an 4,4′-bis(N-carbazolyl)-1,1′-biphenyl (CBP) host were calculated at 10 and 20% dye concentration. The obtained results are depicted in Figure 13. The simulation underestimates the orientation parameter, $\text{Θ}$, for all three emitters, which corresponds to a more anisotropic orientation of the emitter molecules. This may result from the neglection of the thermally activated collective moves of the surface molecules in the simulation protocol, which leads to a more isotropic distribution of orientations. The best calculation accuracy is observed for the Ir(bppo)_2(acac) film, compared to the other two emitters.

FIGURE 13

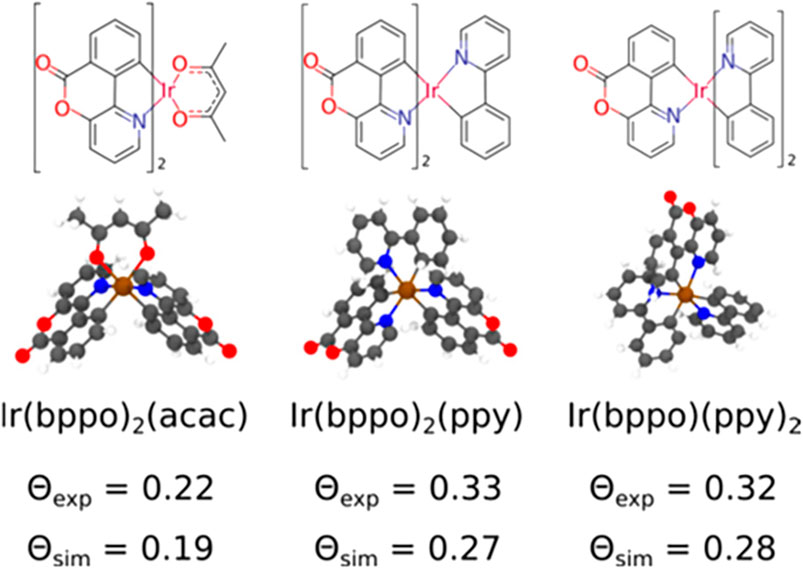
FIGURE 13. Molecular structure of the iridium-emitters: Ir(bppo)2(acac), Ir(bppo)2(ppy), and Ir(bppo) (ppy)2, and the experimental and simulated values of the orientation parameter ⊝, which characterizes the average orientation of the TDM with respect to the film normal, averaged in films with a 10 and 20% dye concentration. Here, bppo, acac, and ppy are benzopyranopyridinone, acetylacetonate, and 2-phenylpyridinate, respectively. Reprinted (adapted) with permission from Friederich et al. [101]. Copyright 2017 American Chemical Society.

Conclusion

With the help of ever-growing computational resources and algorithm design, MC simulation has contributed a lot to elucidate the underlying mechanisms involved on the microscopic scale and has been proved to be a powerful tool in complement to experiment. Here we have presented SIMONA, a MC multi-purpose package with high versatility, which is distributed free for academic users. It enables the user to select between different options, use GUI, create advanced workflows modifying the XML input files or implement new potential functions to describe special interactions in the C++ source code. Such features make SIMONA a high adaptable MC framework to study versatile phenomena in molecular systems including protein folding, sampling their conformational ensemble and studying the effect of mutation on protein stability, MC simulations of reversible self-assembly of polymers and deposition of molecules on a substrate allowing a deep and thorough understanding of some phenomena observed. New features such as the Oligomer Encoder for generating arbitrary synthetic oligomers, will be added to SIMONA which facilitates its application in polymer simulation. SIMONA is available for download under http://int.kit.edu/nanosim/simona.

Author Contributions

MP-A wrote the Introduction, SIMONA Engine and Oligomer Encoder sections. ES wrote the Polymer Folding and membrane peptide sections. MK wrote the Protein Folding section. CD wrote the Thin Films section. CP and MP-A made code implementation on Oligomer Encoder. ES and MK reviewed the manuscript. Supervision, review of the manuscript, project administration and funding acquisition were done by WW. All authors discussed the results and reviewed the final manuscript.

Funding

This research was funded by the Deutscher Akademischer Austauschdienst (DAAD) within the scholarship of MP-A (91683960), the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) within Collaborative Research Center (SFB) 1176 “Molecular Structuring of Soft Matter” (project Q3) and the priority program DiSPBiotech (SPP1934, project number WE1863/30–2). ES and WW acknowledge the financial support by Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – 2082/1–390761711 (Thrust A1), the Carl Zeiss Foundation through the "Carl-Zeiss-Focus@HEiKa", MK acknowledges funding by the Ministry of Science, Research and Art of Baden-Württemberg (Germany) under Brigitte-Schlieben-Lange-Programm. This work was performed on the supercomputer ForHLR II funded by the Ministry of Science, Research and the Arts Baden-Württemberg and by the Federal Ministry of Education and Research. We acknowledge support by the KIT-Publication Fund of the Karlsruhe Institute of Technology.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Hansmann UH, Okamoto Y. New Monte Carlo algorithms for protein folding. Curr Opin Struct Biol (1999) 9:177. doi:10.1016/S0959-440X(99)80025-6

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Dubbeldam D, Torres-Knoop A, Walton KS. On the inner workings of Monte Carlo codes. Mol Simulat (2013) 39:1253–92. doi:10.1080/08927022.2013.819102

CrossRef Full Text | Google Scholar

3. Mees MJ, Pourtois G, Neyts EC, Thijsse BJ, Stesmans A. Uniform-acceptance force-bias Monte Carlo method with time scale to study solid-state diffusion. Phys Rev B (2012) 85:134301. doi:10.1103/PhysRevB.85.134301

CrossRef Full Text | Google Scholar

4. Bal KM, Neyts EC. On the time scale associated with Monte Carlo simulations. J Chem Phys (2014) 141:204104. doi:10.1063/1.4902136

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Neumann T, Danilov D, Wenzel W. Multiparticle moves in acceptance rate optimized Monte Carlo. J Comput Chem (2015) 36:2236–45. doi:10.1002/jcc.24205

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Michel J, Tirado-Rives J, Jorgensen WL. Prediction of the water content in protein binding sites. J Phys Chem B (2009) 113:13337–46. doi:10.1021/jp9047456

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Michel J, Harker EA, Tirado-Rives J, Jorgensen WL, Schepartz A. In silico improvement of β3-peptide inhibitors of p53hDM2 and p53hDMX. J Am Chem Soc (2009) 131:6356–7. doi:10.1021/ja901478e

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Cramer CJ. Essentials of computational chemistry: theories and models. 2nd ed. Hoboken, NJ: Wiley (2004).

9. Still WC, Tempczyk A, Hawley RC, Hendrickson T. Semianalytical treatment of solvation for molecular mechanics and dynamics. J Am Chem Soc (1990) 112:6127–9. doi:10.1021/ja00172a038

CrossRef Full Text | Google Scholar

10. Zhang H, Yin C, Yan H, van der Spoel D. Evaluation of generalized Born models for large scale Affinity prediction of cyclodextrin host-guest complexes. J Chem Inf Model (2016) 56:2080–92. doi:10.1021/acs.jcim.6b00418

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Brieg M, Wenzel W. PowerBorn: a barnes-hut tree implementation for accurate and efficient Born radii computation. J Chem Theor Comput (2013) 9:1489–98. doi:10.1021/ct300870s

CrossRef Full Text | Google Scholar

12. Okabe T, Kawata M, Okamoto Y, Mikami M. Replica-exchange Monte Carlo method for the isobaric-isothermal ensemble. Chem Phys Lett (2001) 335:435–9. doi:10.1016/S0009-2614(01)00055-0

CrossRef Full Text | Google Scholar

13. Matsubara D, Okamoto Y. Analysis of liquids, gases, and supercritical fluids by a two-dimensional replica-exchange Monte Carlo method in temperature and chemical potential space. J Chem Phys (2020) 152:194108. doi:10.1063/5.0001874

CrossRef Full Text | Google Scholar

14. Yan Q, de Pablo JJ. Hyper-parallel tempering Monte Carlo: application to the Lennard-Jones fluid and the restricted primitive model. J Chem Phys (1999) 111:9509–16. doi:10.1063/1.480282

CrossRef Full Text | Google Scholar

15. Craiu RV, Lemieux C. Acceleration of the multiple-try metropolis algorithm using antithetic and stratified sampling. Stat Comput (2007) 17:109–20. doi:10.1007/s11222-006-9009-4

CrossRef Full Text | Google Scholar

16. Liu JS, Liang F, Wong WH. The multiple-try method and local optimization in metropolis sampling. J Am Stat Assoc (2000) 95:121–34. doi:10.1080/01621459.2000.10473908

CrossRef Full Text | Google Scholar

17. Frenkel D, Smit B. Understanding molecular simulation: from algorithms to applications. 2nd ed. San Diego, CA: Academic Press (2002).

18. Rosenbluth MN, Rosenbluth AW. Monte Carlo calculation of the average extension of molecular chains. J Chem Phys (1955) 23:356–9. doi:10.1063/1.1741967

CrossRef Full Text | Google Scholar

19. Siepmann JI, Frenkel D. Configurational bias Monte Carlo: a new sampling scheme for flexible chains. Mol Phys (1992) 75:59–70. doi:10.1080/00268979200100061

CrossRef Full Text | Google Scholar

20. Shi W, Maginn EJ. Continuous fractional component Monte Carlo: an adaptive biasing method for open system Atomistic simulations. J Chem Theor Comput (2007) 3:1451–63. doi:10.1021/ct7000039

CrossRef Full Text | Google Scholar

21. Shi W, Maginn EJ. Improvement in molecule exchange efficiency in Gibbs ensemble Monte Carlo: development and implementation of the continuous fractional component move. J Comput Chem (2008) 29:2520–30. doi:10.1002/jcc.20977

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Rosch TW, Maginn EJ. Reaction ensemble Monte Carlo simulation of complex molecular systems. J Chem Theor Comput (2011) 7:269–79. doi:10.1021/ct100615j

CrossRef Full Text | Google Scholar

23. Torres-Knoop A, Balaji SP, Vlugt TJ, Dubbeldam D. A comparison of advanced Monte Carlo methods for open systems: CFCMC vs CBMC. J Chem Theor Comput (2014) 10:942–52. doi:10.1021/ct4009766

CrossRef Full Text | Google Scholar

24. Rohl CA, Strauss CE, Misura KM, Baker D. Protein structure prediction using Rosetta. Meth Enzymol (2004) 383:66–93. doi:10.1016/S0076-6879(04)83004-0

CrossRef Full Text | Google Scholar

25. Jorgensen WL, Tirado-Rives J. Molecular modeling of organic and biomolecular systems using BOSS and MCPRO. J Comput Chem (2005) 26:1689–700. doi:10.1002/jcc.20297

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Dubbeldam D, Calero S, Ellis DE, Snurr RQ. RASPA: molecular simulation software for adsorption and diffusion in flexible nanoporous materials. Mol Simulat (2016) 42:81–101. doi:10.1080/08927022.2015.1010082

CrossRef Full Text | Google Scholar

27. Hatch HW, Mahynski NA, Shen VK. FEASST: free energy and advanced sampling simulation toolkit. J Res Natl Inst Stan (2018) 123:123004. doi:10.6028/jres.123.004

CrossRef Full Text | Google Scholar

28. Plimpton S. Fast parallel algorithms for short-range molecular dynamics. J Comput Phys (1995) 117:1–19. doi:10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

29. Guo J, Haji-Akbari A, Palmer JC. Hybrid Monte Carlo with LAMMPS. J Theor Comput Chem (2018) 17:1840002. doi:10.1142/S0219633618400023

CrossRef Full Text | Google Scholar

30. Strunk T, Wolf M, Brieg M, Klenin K, Biewer A, Tristram F, et al. SIMONA 1.0: an efficient and versatile framework for stochastic simulations of molecular and nanoscale systems. J Comput Chem (2012) 33:2602–13. doi:10.1002/jcc.23089

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Robert C, Casella G. Monte Carlo statistical methods. Berlin, Germany: Springer Science & Business Media (2013).

32. Metropolis N, Rosenbluth A, Rosenbluth M, Teller A, Teller E. Monte Carlo and molecular dynamics simulations in polymer science. J Chem Phys (1953) 21:6. doi:10.1063/1.1699114

CrossRef Full Text | Google Scholar

33. Klenin KV, Tristram F, Strunk T, Wenzel W. Derivatives of molecular surface area and volume: simple and exact analytical formulas. J Comput Chem (2011) 32:2647–53. doi:10.1002/jcc.21844

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Romanov AN, Jabin SN, Martynov YB, Sulimov AV, Grigoriev FV, Sulimov VB. Surface generalized Born method: a simple, fast, and precise implicit solvent model beyond the Coulomb approximation. J Phys Chem A (2004) 108:9323–7. doi:10.1021/jp046721s

CrossRef Full Text | Google Scholar

35. Feig M, Brooks CL. Recent advances in the development and application of implicit solvent models in biomolecule simulations. Curr Opin Struct Biol (2004) 14:217–24. doi:10.1016/j.sbi.2004.03.009

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Fan H, Mark AE, Zhu J, Honig B, Berne BJ. Comparative study of generalized Born models: protein dynamics. Proc Natl Acad Sci USA (2005) 102:6760–4. doi:10.1073/pnas.0408857102

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Mahmoud SSM, Esposito G, Serra G, Fogolari F. Generalized Born radii computation using linear models and neural networks. Bioinformatics (2020) 36:1757–64. doi:10.1093/bioinformatics/btz818

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Bonomi M, Branduardi D, Bussi G, Camilloni C, Provasi D, Raiteri P, et al. PLUMED: a portable plugin for free-energy calculations with molecular dynamics. Computer Phys Commun (2009) 180:1961–72. doi:10.1016/j.cpc.2009.05.011

CrossRef Full Text | Google Scholar

39. Tribello GA, Bonomi M, Branduardi D, Camilloni C, Bussi G. PLUMED 2: new feathers for an old bird. Computer Phys Commun (2014) 185:604–13. doi:10.1016/j.cpc.2013.09.018

CrossRef Full Text | Google Scholar

40. Shaw DE, Maragakis P, Lindorff-Larsen K, Piana S, Dror RO, Eastwood MP, et al. Atomic-level characterization of the structural dynamics of proteins. Science (2010) 330:341–6. doi:10.1126/science.1187409

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Lindorff-Larsen K, Maragakis P, Piana S, Eastwood MP, Dror RO, Shaw DE. Systematic validation of protein force fields against experimental data. PLoS ONE (2012) 7:e32131. doi:10.1371/journal.pone.0032131

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Dror RO, Mildorf TJ, Hilger D, Manglik A, Borhani DW, Arlow DH, et al. SIGNAL TRANSDUCTION. Structural basis for nucleotide exchange in heterotrimeric G proteins. Science (2015) 348:1361–5. doi:10.1126/science.aaa5264

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Robustelli P, Piana S, Shaw DE. Developing a molecular dynamics force field for both folded and disordered protein states. Proc Natl Acad Sci U S A (2018) 115:E4758–66. doi:10.1073/pnas.1800690115

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Liang F, Wong WH. Evolutionary Monte Carlo for protein folding simulations. J Chem Phys (2001) 115:3374–80. doi:10.1063/1.1387478

CrossRef Full Text | Google Scholar

45. Irbäck A, Mohanty S. PROFASI: a Monte Carlo simulation package for protein folding and aggregation. J Comput Chem (2006) 27:1548–55. doi:10.1002/jcc.20452

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Eisenmenger F, Hansmann UHE, Hayryan S, Hu C-K. [SMMP] A modern package for simulation of proteins. Computer Phys Commun (2001) 138:192–212. doi:10.1016/S0010-4655(01)00197-7

CrossRef Full Text | Google Scholar

47. Shimada J, Shakhnovich EI. The ensemble folding kinetics of protein G from an all-atom Monte Carlo simulation. Proc Natl Acad Sci USA (2002) 99:11175–80. doi:10.1073/pnas.162268099

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Cragnell C, Durand D, Cabane B, Skepö M. Coarse-grained modeling of the intrinsically disordered protein Histatin 5 in solution: Monte Carlo simulations in combination with SAXS. Proteins (2016) 84:777–91. doi:10.1002/prot.25025

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Kurcinski M, Kolinski A, Kmiecik S. Mechanism of folding and binding of an intrinsically disordered protein as revealed by ab initio simulations. J Chem Theor Comput (2014) 10:2224–31. doi:10.1021/ct500287c

CrossRef Full Text | Google Scholar

50. Pulawski W, Jamroz M, Kolinski M, Kolinski A, Kmiecik S. Coarse-Grained simulations of membrane insertion and folding of small helical proteins using the CABS model. J Chem Inf Model (2016) 56:2207–15. doi:10.1021/acs.jcim.6b00350

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Feig M, Karanicolas J, Brooks CL. MMTSB Tool Set: enhanced sampling and multiscale modeling methods for applications in structural biology. J Mol Graph Model (2004) 22:377–95. doi:10.1016/j.jmgm.2003.12.005

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Heilmann N, Wolf M, Kozlowska M, Sedghamiz E, Setzler J, Brieg M, et al. Sampling of the conformational landscape of small proteins with Monte Carlo methods. Sci Rep (2020) 10:18211. doi:10.1038/s41598-020-75239-7

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Lindorff-Larsen K, Piana S, Dror RO, Shaw DE. How fast-folding proteins fold. Science (2011) 334:517–20. doi:10.1126/science.1208351

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Wang E, Tao P, Wang J, Xioa Y. A novel folding pathway of the villin headpiece subdomain HP35. Phys Chem Chem Phys (2019) 21:8. doi:10.1039/C9CP01703H

CrossRef Full Text | Google Scholar

55. Kubelka J, Henry ER, Cellmer T, Hofrichter J, Eaton WA. Chemical, physical, and theoretical kinetics of an ultrafast folding protein. Proc Natl Acad Sci USA (2008) 105:18655–62. doi:10.1073/pnas.0808600105

PubMed Abstract | CrossRef Full Text | Google Scholar

56. McKnight CJ, Matsudaira PT, Kim PS. NMR structure of the 35-residue villin headpiece subdomain. Nat Struct Biol (1997) 4:180–4. doi:10.1038/nsb0397-180

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Best RB, Mittal J. Balance between alpha and beta structures in ab initio protein folding. J Phys Chem B (2010) 114:8790–8. doi:10.1021/jp102575b

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Paschek D, Day R, García AE. Influence of water-protein hydrogen bonding on the stability of Trp-cage miniprotein. A comparison between the TIP3P and TIP4P-Ew water models. Phys Chem Chem Phys (2011) 13:19840–7. doi:10.1039/C1CP22110H

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Day R, Paschek D, Garcia AE. Microsecond simulations of the folding/unfolding thermodynamics of the Trp-cage miniprotein. Proteins (2010) 78:1889–99. doi:10.1002/prot.22702

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Barua B, Lin JC, Williams VD, Kummler P, Neidigh JW, Andersen NH. The Trp-cage: optimizing the stability of a globular miniprotein. Protein Eng Des Sel (2008) 21:171–85. doi:10.1093/protein/gzm082

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Streicher WW, Makhatadze GI. Unfolding thermodynamics of Trp-cage, a 20 residue miniprotein, studied by differential scanning calorimetry and circular dichroism spectroscopy. Biochemistry (2007) 46:2876–80. doi:10.1021/bi602424x

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Anandakrishnan R, Izadi S, Onufriev AV. Why computed protein folding landscapes are sensitive to the water model. J Chem Theor Comput (2019) 15:625–36. doi:10.1021/acs.jctc.8b00485

CrossRef Full Text | Google Scholar

63. Klenin KV, Wenzel W. Transition network based on equilibrium sampling: a new method for extracting kinetic information from Monte Carlo simulations of protein folding. J Chem Phys (2011) 135:235105. doi:10.1063/1.3670106

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Cochran AG, Skelton NJ, Starovasnik MA. Tryptophan zippers: stable, monomeric beta-hairpins. Proc Nat Acad Sci USA (2002) 99:9081–6. doi:10.1073/pnas.091100898

CrossRef Full Text | Google Scholar

65. Klenin KV, Wenzel W. Calculation of the "absolute" free energy of a β-hairpin in an all-atom force field. J Chem Phys (2013) 139:054102. doi:10.1063/1.4817195

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Setzler J, Seith C, Brieg M, Wenzel W. Modeling membrane proteins with slim, a new implciit membrane model. Biophys J (2014) 106:89A. doi:10.1016/j.bpj.2013.11.562

CrossRef Full Text | Google Scholar

67. Figliuzzi M, Jacquier H, Schug A, Tenaillon O, Weigt M. Coevolutionary landscape inference and the context-dependence of mutations in beta-lactamase TEM-1. Mol Biol Evol (2016) 33:268–80. doi:10.1093/molbev/msv211

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Goossens K, De Winter H. Molecular dynamics simulations of membrane proteins: an overview. J Chem Inf Model (2018) 58:2193–202. doi:10.1021/acs.jcim.8b00639

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Mori T, Miyashita N, Im W, Feig M, Sugita Y. Molecular dynamics simulations of biological membranes and membrane proteins using enhanced conformational sampling algorithms. Biochim Biophys Acta (2016) 1858:1635–51. doi:10.1016/j.bbamem.2015.12.032

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Scott KA, Bond PJ, Ivetac A, Chetwynd AP, Khalid S, Sansom MS. Coarse-Grained MD simulations of membrane protein-bilayer self-assembly. Structure (2008) 16:621–30. doi:10.1016/j.str.2008.01.014

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Tanizaki S, Feig M. Molecular dynamics simulations of large integral membrane proteins with an implicit membrane model. J Phys Chem B (2006) 110:548–56. doi:10.1021/jp054694f

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Tanizaki S, Feig M. A generalized Born formalism for heterogeneous dielectric environments: application to the implicit modeling of biological membranes. J Chem Phys (2005) 122:124706. doi:10.1063/1.1865992

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Brooks BR, Brooks CL, Mackerell AD, Nilsson L, Petrella RJ, Roux B, Won Y, et al. CHARMM: the biomolecular simulation program. J Comput Chem (2009) 30:1545–614. doi:10.1002/jcc.21287

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Hanlon AM, Lyon CK, Berda EB. What is next in single-chain nanoparticles?. Macromolecules (2016) 49:2–14. doi:10.1021/acs.macromol.5b01456

CrossRef Full Text | Google Scholar

75. Frisch H, Kodura D, Bloesser FR, Michalek L, Barner-Kowollik C. Wavelength-selective folding of single polymer chains with different colors of visible light. Macromol Rapid Commun (2020) 41:e1900414. doi:10.1002/marc.20207000110.1002/marc.201900414

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Galant O, Donmez HB, Barner‐Kowollik C, Diesendruck CE. Flow photochemistry for single‐chain polymer nanoparticle synthesis. Angew Chem Int Ed (2020) 60:2042. doi:10.1002/anie.202010429

PubMed Abstract | CrossRef Full Text | Google Scholar

77. McLeish TCB. Tube theory of entangled polymer dynamics. Adv Phys (2002) 51:1379–527. doi:10.1080/00018730210153216

CrossRef Full Text | Google Scholar

78. Baschnagel J, Wittmer JP, Meyer H. Monte Carlo SImulation of polymers: coarse-grained models (2004) Available from: http://arxiv.org/abs/cond-mat/0407717 (Accessed November 10, 2020).

79. Meimaroglou D, Kiparissides C. Review of Monte Carlo methods for the prediction of distributed molecular and morphological polymer properties. Ind Eng Chem Res (2014) 53:8963–79. doi:10.1021/ie4033044

CrossRef Full Text | Google Scholar

80. Gilra N, Panagiotopoulos AZ, Cohen C. Monte Carlo simulations of polymer network deformation. Macromolecules (2001) 34:6090–6. doi:10.1021/ma0021895

CrossRef Full Text | Google Scholar

81. Polanowski P, Jeszka JK, Matyjaszewski K. Polymer brush relaxation during and after polymerization - Monte Carlo simulation study. Polymer (2019) 173:190–6. doi:10.1016/j.polymer.2019.04.023

CrossRef Full Text | Google Scholar

82. Jiang W, Shi T, Jiang S, An L, Yan D, Jiang B. Monte Carlo simulation of phase behavior of polymer blends with special interactions. Macromol Theory Simul (2001) 10:750–5. doi:10.1002/1521-3919(20011001)

CrossRef Full Text | Google Scholar

83. Jeong SH, Kim JM, Yoon J, Tzoumanekas C, Kröger M, Baig C. Influence of molecular architecture on the entanglement network: topological analysis of linear, long- and short-chain branched polyethylene melts via Monte Carlo simulations. Soft Matter (2016) 12:3770–86. doi:10.1039/C5SM03016A

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Danilov D, Barner-Kowollik C, Wenzel W. Modelling of reversible single chain polymer self-assembly: from the polymer towards the protein limit. Chem Commun (Camb) (2015) 51:6002–5. doi:10.1039/c4cc10243f

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Danilov D, Sedghamiz E, Fliegl H, Frisch H, Barner-Kowollik C, Wenzel W. Tacticity dependence of single chain polymer folding. Polym Chem (2020) 11:3439–45. doi:10.1039/d0py00133c

CrossRef Full Text | Google Scholar

86. Boukis AC, Meier MAR. Data storage in sequence-defined macromolecules via multicomponent reactions. Eur Polym J (2018) 104:32–8. doi:10.1016/j.eurpolymj.2018.04.038

CrossRef Full Text | Google Scholar

87. Wetzel KS, Frölich M, Solleder SC, Nickisch R, Treu P, Meier MAR. Dual sequence definition increases the data storage capacity of sequence-defined macromolecules. Commun Chem (2020) 3:63. doi:10.1038/s42004-020-0308-z

CrossRef Full Text | Google Scholar

88. Weininger D. SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules. J Chem Inf Model (1988) 28:31–6. doi:10.1021/ci00057a005

CrossRef Full Text | Google Scholar

89. Furche F, Ahlrichs R, Hättig C, Klopper W, Sierka M, Weigend F. Turbomole. Wires Comput Mol Sci (2014) 4:91–100. doi:10.1002/wcms.1162

CrossRef Full Text | Google Scholar

90. Balasubramani SG, Chen GP, Coriani S, Diedenhofen M, Frank MS, Franzke YJ, et al. TURBOMOLE: modular program suite for ab initio quantum-chemical and condensed-matter simulations. J Chem Phys (2020) 152:184107. doi:10.1063/5.0004635

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Jakalian A, Jack DB, Bayly CI. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and validation. J Comput Chem (2002) 23:1623–41. doi:10.1002/jcc.10128

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Duke R, Giese T, Gohlke H, Goetz A, Homeyer N, Izadi S, et al. AmberTools 16. San Fransisco, CA: University of California (2016).

93. Ozpinar GA, Peukert W, Clark T. An improved generalized AMBER force field (GAFF) for urea. J Mol Model (2010) 16:1427–40. doi:10.1007/s00894-010-0650-7

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Sousa da Silva AW, Vranken WF. ACPYPE - AnteChamber Python parser interfacE. BMC Res Notes (2012) 5:367. doi:10.1186/1756-0500-5-367

PubMed Abstract | CrossRef Full Text | Google Scholar

95. Becke AD. Density‐functional thermochemistry. III. The role of exact exchange. J Chem Phys (1993) 98:5648–52. doi:10.1063/1.464913

CrossRef Full Text | Google Scholar

96. Becke AD. A new mixing of Hartree-Fock and local density‐functional theories. J Chem Phys (1993) 98:1372–7. doi:10.1063/1.464304

CrossRef Full Text | Google Scholar

97. Zheng J, Xu X, Truhlar DG. Minimally augmented Karlsruhe basis sets. Theor Chem Acc (2011) 128:295–305. doi:10.1007/s00214-010-0846-z

CrossRef Full Text | Google Scholar

98. Van Slyke S, Pignata A, Freeman D, Redden N, Waters D, Kikuchi H, et al. 27.2: linear source deposition of organic layers for full-color OLED. SID Symp Dig (2002) 33:886. doi:10.1889/1.1830925

CrossRef Full Text | Google Scholar

99. Eritt M, May C, Leo K, Toerker M, Radehaus C. OLED manufacturing for large area lighting applications. Thin Solid Films (2010) 518:3042–5. doi:10.1016/j.tsf.2009.09.188

CrossRef Full Text | Google Scholar

100. Templier F. OLED microdisplays: technology and applications. Hoboken, NJ: Wiley Online Library (2014).

101. Gaspar DJ, Polikarpov E. OLED fundamentals: materials, devices, and processing of organic light-emitting diodes. Boca Raton, FL: CRC Press (2015).

102. Zhang L, Lloyd K, Fennimore A. Characterization of organic light emitting diodes (OLED) using depth-profiling XPS technique. J Electron Spectrosc Relat Phenomena (2019) 231:88–93. doi:10.1016/j.elspec.2018.02.004

CrossRef Full Text | Google Scholar

103. Neumann T, Danilov D, Lennartz C, Wenzel W. Modeling disordered morphologies in organic semiconductors. J Comput Chem (2013) 34:2716–25. doi:10.1002/jcc.23445

PubMed Abstract | CrossRef Full Text | Google Scholar

104. Friederich P, Konrad M, Strunk T, Wenzel W. Machine learning of correlated dihedral potentials for atomistic molecular force fields. Sci Rep (2018) 8:2559. doi:10.1038/s41598-018-21070-0

PubMed Abstract | CrossRef Full Text | Google Scholar

105. Friederich P, Symalla F, Meded V, Neumann T, Wenzel W. Ab initio treatment of disorder effects in amorphous organic materials: toward parameter free materials simulation. J Chem Theor Comput (2014) 10:3720–5. doi:10.1021/ct500418f

CrossRef Full Text | Google Scholar

106. Friederich P, Gómez V, Sprau C, Meded V, Strunk T, Jenne M, et al. Rational in silico design of an organic semiconductor with improved electron mobility. Adv Mater Weinheim (2017) 29:3505. doi:10.1002/adma.201703505

CrossRef Full Text | Google Scholar

107. Frischeisen J, Yokoyama D, Endo A, Adachi C, Brütting W. Increased light outcoupling efficiency in dye-doped small molecule organic light-emitting diodes with horizontally oriented emitters. Org Electronics (2011) 12:809–17. doi:10.1016/j.orgel.2011.02.005

CrossRef Full Text | Google Scholar