- Department of Physics, Naragh Branch, Islamic Azad University, Naragh, Iran
The photofission fragment mass yields of actinides are evaluated using a systematic statistical scission point model. In this model, all energies at the scission point are presented as a linear function of the mass numbers of fission fragments. The mass yields are calculated with a new approximated relative probability for each complementary fragment. The agreement with the experimental data is quite good, especially with a collective temperature Tcol of 2 MeV at intermediate excitation energy and Tcol = 1 MeV for spontaneous fission. This indicates that the collective temperature is greater than the value obtained by the initial excitation energy. The generalized superfluid model is applied for calculating the fragment temperature. The deformation parameters of fission fragments have been obtained by fitting the calculated results with the experimental values. This indicates that the deformation parameters decrease with increasing excitation energy. Also, these parameters decrease for fissioning systems with odd mass numbers.
1 Introduction
Since the fission discovery, the experimental and theoretical fission mass yields have been continuously developed. The most widely used theoretical model to study mass yields is the statistical model which was founded by Fong and Wilkins [1, 2]. This model has been developed in many branches, such as the Gaussian model [3, 4] and modified scission point models [6–13]. The time-dependent model has been significantly developed by Randrup [14–16] and others [17–22] to predict the shape of mass yields (symmetric or asymmetric modes). Because all of them have sophisticated computations, a systematic method is needed to evaluate the mass distribution of fission fragments in an easy way.
Although the statistical model can predict transitions between symmetric and asymmetric modes in the region of heavy actinides, the calculated results are inaccurate compared to the experimental data. This problem is found where the calculated results were smeared (refined) by the Gaussian model with the width 1.5 amu to obtain a smoother curve [8].
On the other hand, some researchers [6–9] added some terms to neutron kinetic energy or gamma endpoint energy, E (as the initial excitation energy), to obtain the excitation energy of the fissioning nucleus, E*, for example, Pasca [7, 9] added the Q-factor and the difference between the potential energy of the fissioning nucleus and the potential energy of one of the fragments at the scission point to the initial excitation energy to obtain excitation energy (i.e., E* = Q+E+Ucn−Ui). Some others [10, 11] took available energy as the difference between the potential energy of the fissioning system at the scission point and the energy of the excited compound nucleus, which is the sum of Q-factor and initial excitation energy (E* = Q+E). This addition of energies to the initial excitation energy is more pronounced in time-dependent models [14] when nuclear excitation energy measured relative to potential energy (E* = E-U). Also, fragment temperature, instead of collective temperature, has been used to calculate the mass yield of 238U in my previous work [13]. Also, collective temperature is usually calculated by the excitation energy of fissioning systems. Here, the role of collective temperature is examined by selecting two values (1 and 2 MeV) independently.
In the next section, a systematic method is presented to calculate mass yields for actinides; the fewer parameters and refinements are included in this framework. For this reason, all energies at the scission point are formulated as a function of the mass number of fission fragments. Then, all mass yields for photofission of actinides are calculated and compared with the experimental data (Section 3).
2 Theoretical Framework
The relative yield is usually calculated as the ratio between the probabilities of a given fragmentation and the sum of probabilities of all possible fragmentations as follows:
where
where
The total potential energies at the scission point are defined as follows:
The first term is the interaction energy between complementary fragments,
2.1 Interaction Energy
The nuclear proximity potential (
where the width (diffuseness) of the nuclear surface is b
In Eq. 4, γ is the surface tension coefficient of the nucleus and obtained from the Lysekil mass formula (Ref. 25) by
where
Coulomb energy is written as [4, 12] follows:
where
where θ is the angle made by the axis of symmetry with fission axis, βi is the quadrupole deformation parameter of fragments, and Y20 is the spherical harmonic functions.
2.2 Individual Energies
The individual energies include the macroscopic energy, shell correction energy, and pairing energy. The macroscopic energy is calculated in the framework of the FRLDM model from Ref. 26, and the spheroidally deformed is applied as [27].
where the quantity B1 is the relation generalized surface or nuclear energy in a model that accounts for the effect of infinite range of nuclear force. The quantity f is the proton form factor correction to Coulomb energy. Relative Coulomb energy B3 is used in the first approximate. All parameters are chosen from Ref. 26.
The pairing correction energy (Epair in MeV) is calculated by a simple relation as follows:
The shell correction energy is calculated according to Ref. 13. The systematic formalism of this method is used to calculate the shell correction energy of fragments. Also, the results of this method agree with the results of the Strutinsky model [28].
2.3 Temperature
The temperature-dependent relation for pairing energy is given by Ref. 29.
Temperature dependence of shell energy is applied as [29] follows:
where
Temperature (T) usually calculate with Fermi gas relation, but we used the generalized superfluid model as follows:
where E is the excitation energy and Econ is the condensation energy for the even–even nucleus. We have
where
where
3 Results and Discussion
Similar to Refs. 30 and 31, the atomic number of fission fragments are obtained with the unchanged charge density distribution as [32] follows:
where Zcn is the atomic number of compound nucleus, Acn is the mass number of compound nucleus, and ν is post-scission neutrons and is defined by Refs. 33 and 34.
Pasca [9] added the height of the fission barrier to the potential energy at the scission point to calculate the collective temperature. In this study, the height of the fission barrier is chosen as the excitation energy for spontaneous fission. Thus, for photofission, the height of the fission barrier is added to the initial excitation energy (the bremsstrahlung endpoint energy) (i.e., 6+E MeV for 238U). Thus, E* in Eqs 15, 16 is the height of the fission barrier of the target nucleus plus the initial excitation energies.
On the other hand, the collective temperature is not dependent on the excitation energy in this study such as Ref. 2. Therefore, here, the excitation energy only affects the total potential energy of the fissioning system. These calculations indicate that the excitation energy has little change in the values of fission fragment mass distributions. For example, by increasing the excitation energy by 20 MeV, the mass distribution changes by less than 1 percent. Therefore, this small effect indicates that the major effect of the excitation energy in mass yield values is due to the change in collective temperature. Of course, the excitation energies are divided between the fragments proportional to their masses.
Equation 2 is an exponential function that is strongly upward-sloping, and the collective temperature is usually taken to be constant in Refs. 2 and 7 (the change in collective temperature is discussed later). Therefore, the values of deformation parameters provide the minimal value of the total potential energy. On the other hand, the minimal values of the total potential energy of the fissioning system at the scission point correspond to the minimal values of the deformation parameters. Therefore, only the maximum values of deformation parameters could be considered in Eq. 2 as follows:
Here,
3.1 Investigation on Fission of 238U
The mass yield for spontaneous fission of 238U is presented in Figure 1. In the left side of Figure 1, the results of systematic calculation are presented for Tcoll = 1 MeV, and the results of systematic calculation are presented for Tcoll = 2 MeV in the right side of this figure. The deformation parameters have been changed to fit the calculated results and the experimental values, so when Tcoll = 1 MeV, we have
It can be seen that
also, for
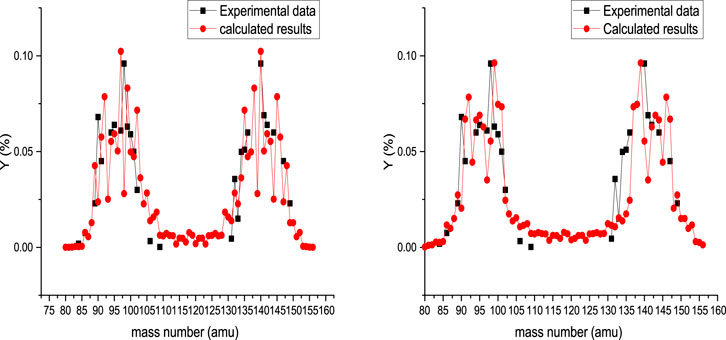
FIGURE 1. Calculated mass yield for spontaneous fission of 238U accompanied by experimental data [35]. In the left and right sides are presented the calculated results obtained for Tcoll = 1 MeV and Tcoll = 2 MeV, respectively.
Also, the obtained
The photofission mass yield of 238U is presented in Figure 2 at 8 MeV bremsstrahlung endpoint energy. In the left side of Figure 2, the results of systematic calculation are presented for Tcoll = 1 MeV, and the results of systematic calculation are presented for Tcoll = 2 MeV in the right side of this figure. The changing of deformation parameters are the same as the deformation parameters for spontaneous fission of 238U for Tcoll = 1 MeV. This shows that with increasing excitation energy up to 8 MeV, the behavior of photofission and spontaneous fission is the same. But for Tcoll = 2 MeV, the deformation parameters are obtained as
also, when
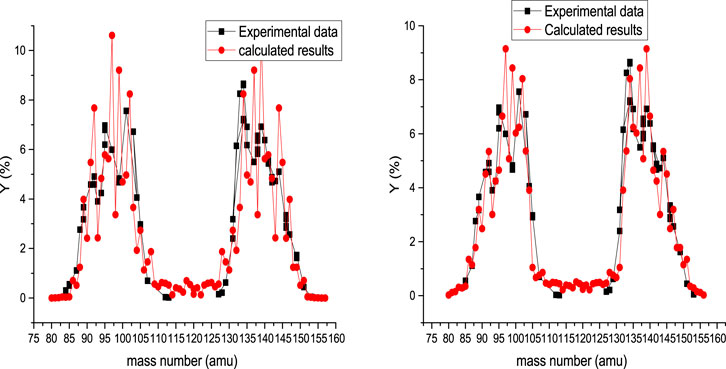
FIGURE 2. Calculated mass yield for photofission of 238U at 8 MeV bremsstrahlung endpoint energy, accompanied by experimental data [36]. In the left and right sides are presented the calculated results obtained for Tcoll = 1 MeV and Tcoll = 2 MeV, respectively.
In Figure 3, the photofission mass yield of 238U is presented at 67.8 MeV bremsstrahlung endpoint energy. In the left and right sides of this figure, the calculated results, along with the experimental data, are presented for Tcoll = 1 MeV and Tcoll = 2 MeV, respectively. When the deformation parameters are obtained by fitting the calculated results to the experimental values for Tcoll = 1 MeV, we have
Also, for
Also, for
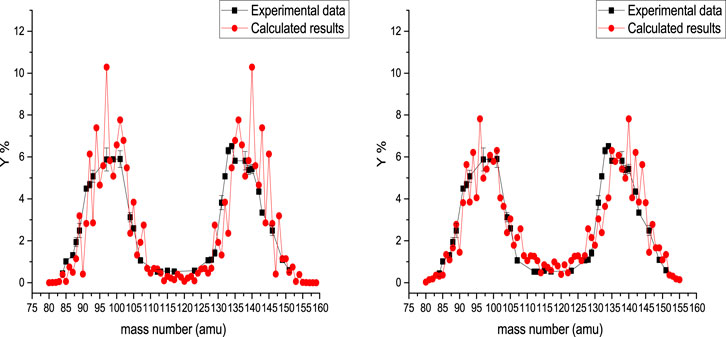
FIGURE 3. Calculated mass yield for photofission of 238U at 67.8 MeV bremsstrahlung endpoint energy, accompanied by experimental data [37]. In the left and right sides are presented the calculated results obtained for Tcoll = 1 MeV and Tcoll = 2 MeV, respectively.
As the excitation energy increases from 8 to 68 MeV,
But why does the fission fragment with the mass number AL = 102, corresponding to the heavy fission fragment
3.2 Investigation on the Plutonium Isotopes
The photofission mass yield of 240Pu is presented in Figure 4 at 10 MeV bremsstrahlung endpoint energy. In the left side of Figure 4, the results of systematic calculation are presented for Tcoll = 1 MeV, and the results of systematic calculation are presented for Tcoll = 2 MeV in the right side of this figure. The deformation parameters of fission fragments are obtained by fitting the calculated results with the experimental values for Tcoll = 1 MeV, so we have
Also, for
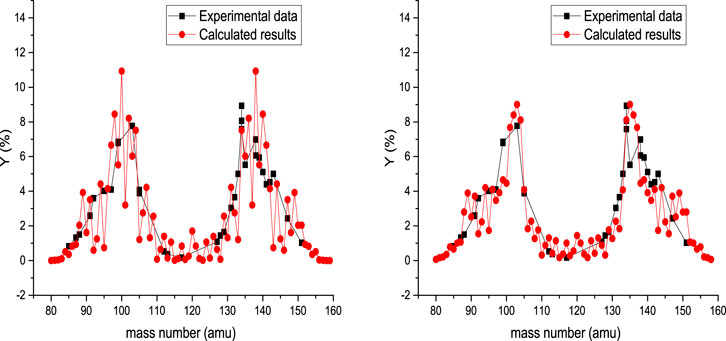
FIGURE 4. Calculated mass yield for photofission of 240Pu at 10 MeV bremsstrahlung endpoint energy, accompanied by experimental data [39]. In the left and right sides are presented the calculated results obtained for Tcoll = 1 MeV and Tcoll = 2 MeV, respectively.
For Tcoll = 2 MeV, the deformation parameters are obtained as
Also, for
The photofission mass yield of 239Pu is presented in Figure 5 at 28 MeV bremsstrahlung endpoint energy. In the left side of Figure 5, the results of systematic calculation are presented for Tcoll = 1 MeV, and the results of systematic calculation are presented for Tcoll = 2 MeV in the right side of this figure. The deformation parameters of fission fragments are obtained by fitting the calculated results with the experimental values for Tcoll = 1 MeV, so we have
Also, for
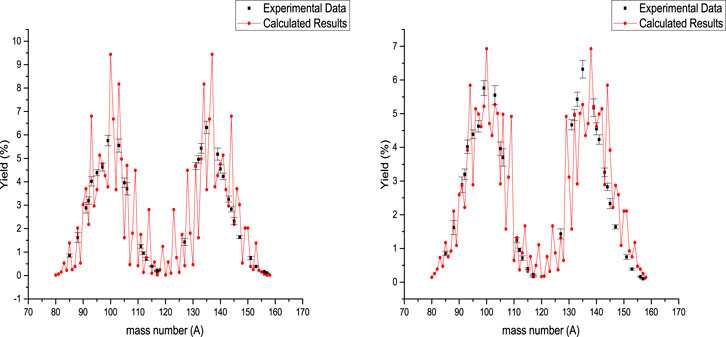
FIGURE 5. Calculated mass yield for photofission of 239Pu at 28 MeV bremsstrahlung endpoint energy, accompanied by experimental data [40]. In the left and right sides are presented the calculated results obtained for Tcoll = 1 MeV and Tcoll = 2 MeV, respectively.
For Tcoll = 2 MeV, the deformation parameters are obtained as
Also, for
Also, the
3.3 Investigation on Neptunium Isotopes
The photofission mass yield of 237Np is presented in Figure 6 at 28 MeV bremsstrahlung endpoint energy. In the left side of Figure 6, the results of systematic calculation are presented for Tcoll = 1 MeV, and the results of systematic calculation are presented for Tcoll = 2 MeV in the right side of this figure. The deformation parameters of fission fragments are obtained by fitting the calculated results with the experimental values for Tcoll = 1 MeV, so we have
It can be seen that
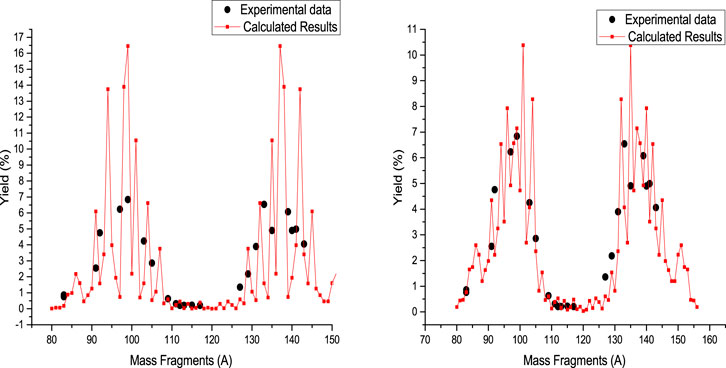
FIGURE 6. Calculated mass yield for photofission of 237Np at 25 MeV bremsstrahlung endpoint energy, accompanied by experimental data [41]. In the left and right sides are presented the calculated results obtained for Tcoll = 1 MeV and Tcoll = 2 MeV, respectively.
For Tcoll = 2 MeV, the deformation parameters are obtained as
and for
The photofission mass yield of 237Np is presented in Figure 7 at 9.5 MeV bremsstrahlung endpoint energy. In the left side of Figure 7, the results of systematic calculation are presented for Tcoll = 1 MeV, and the results of systematic calculation are presented for Tcoll = 2 MeV in the right side of this figure. The deformation parameters of fission fragments are obtained by fitting the calculated results with the experimental values for Tcoll = 1 MeV, so we have
Unlike plutonium fission,
The calculated results for the neptunium even–odd nucleus are in good agreement with the experimental values, and the deformation parameters have the least variations. Also, the deformation parameters reduce oscillations when Tcoll = 2 MeV. These conditions are true for all actinides, so it is best to use Tcoll = 2 MeV for intermediate energy of photofission.
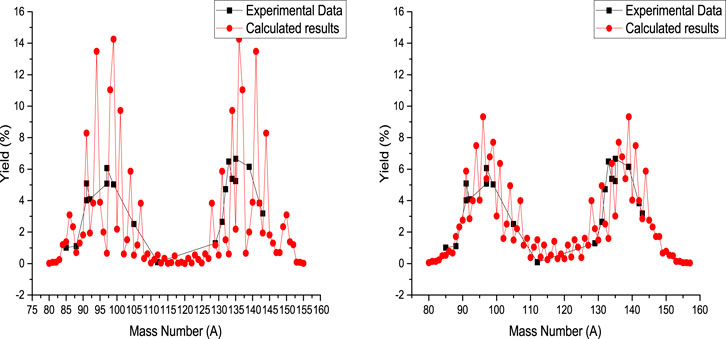
FIGURE 7. Calculated mass yield for photofission of 237Np at 9.5 MeV bremsstrahlung endpoint energy, accompanied by experimental data [43]. In the left and right sides are presented the calculated results obtained for Tcoll = 1 MeV and Tcoll = 2 MeV, respectively.
Therefore, by using the fragment temperature, instead of collective temperature in Eq. 2, the values of mass distribution are better obtained like in Ref. 13. Unlike the Gaussian models to calculate mass yields [5], where the excitation energy (bremsstrahlung endpoint energy) is used to evaluate mass distribution, in the statistical scission point model, the Q-factor energy and the height of the fission barrier are better added to the initial excitation energy.
Naik and Pomme [39, 44, 45] showed that the fission fragment mass yields around mass numbers 94–95, 99–100, and 104–105 are higher than other fission fragment mass yields for photofission of 238U and 240Pu in the low-energy region. Therefore, our calculated results confirm the changes in the mass yields of experimental data in some fragments. But these changes are seen for all nuclei studied in this systematic study.
4 Summary
The mass yield for spontaneous fission and photofission of actinides are calculated within a systematic scission point model. The calculated results are compared with the available experimental data. There is good agreement with the experimental data, especially for a collective temperature of 2 MeV.
For intermediate excitation energy, the calculated results with Tcoll = 2 MeV have better agreement with the experimental data, so it is better to add initial excitation energy (E) with the height of the fission barrier (and other energies such as Q-factor) to evaluate the mass yields. But for spontaneous fission, it is better not to change the excitation energy because the calculated results with Tcoll = 1 are in good agreement with the experimental data. Therefore, by using the fragment temperature, instead of collective temperature and adding other energies to initial excitation energy, the values of mass yield are closer to the experimental data.
In this study, the collective temperature is constant and also the change in mass distribution values was small with the change in excitation energy; therefore, the major effect of excitation energy (in other studies) is due to change in collective temperature.
The deformation parameters of fission fragments are presented by fitting the calculated results to the experimental data. There are close to the values in other studies obtained by the total kinetic energy and the integral form. The deformation values increase with increasing mass numbers of fission fragments (symmetric fragments) for all fissioning systems, which is due to the dominance of the asymmetric fission mode for photofission of actinides. On the other hand, the deformation parameter values decrease with increasing excitation energy. This increase in excitation energy also causes the deformation parameter changes to be irregular. Also, these parameters decrease for odd mass number fissioning systems. Also, the fissioning systems with odd neutron numbers have less deformation parameter values than the fissioning systems with even neutron numbers. The mass yield values for photofission of other actinides can be predicted by this method.
It is seen that the higher values in mass numbers of fission fragments around 104–105 and 99–100 in experimental data for photofission are related to the potential energy of the fissioning system at the scission point, and it can be seen for all photofission of nuclei actinide. But for some nuclei, these peaks are so small that they are not seen in the measurements.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Fong P. Statistical theory of nuclear fission: asymmetric fission. Phys. Rev (1956) 102:434. doi:10.1103/physrev.102.434
2. Wilkins BD, Steinberg EP, Chasman RR. Scission-point model of nuclear fission based on deformed-shell effects. Phys Rev C (1976) 14:1832. doi:10.1103/physrevc.14.1832
3. Brosa U, Grossmann S, Müller A. Nuclear scission. Phys Rep (1990) 197(4):167–262. doi:10.1016/0370-1573(90)90114-h
4. Denisov VY, Margitych TO, Sedykh IY. Mass yields and kinetic energy of fragments from fission of highly-excited nuclei with A ≲ 220. Nucl Phys (2017) 958:101–128. doi:10.1016/j.nuclphysa.2016.11.007
5. Mehdipour Kaldiani P. The perusal of photofission fragments mass yields for actinide isotopes by systematics neutron models. Phys Atom Nucl (2019) 82(5):450–461. doi:10.1134/s1063778819050089
6. Andreev AV, Adamian GG, Antonenko NV. Mass distributions for induced fission of different Hg isotopes. Phys Rev C (2012) 86:044315. doi:10.1103/physrevc.86.044315
7. Pasca H, Andreev AV, Adamian GG, Antonenko NV. Extraction of potential energy in charge asymmetry coordinate from experimental fission data. Eur Phys J A (2016) 52:369. doi:10.1140/epja/i2016-16369-5
8. Pasca H, Andreev AV, Adamian GG, Antonenko NV. Physical origin of the transition from symmetric to asymmetric fission fragment charge distribution. Acta Phys Pol Ser B (2017) 48(3):431. doi:10.5506/aphyspolb.48.431
9. Pasca H, Andreev AV, Adamian GG, Antonenko NV. Transitions between symmetric and asymmetric modes in the region of heavy actinides. Nucl Phys (2018) 969:226–236. doi:10.1016/j.nuclphysa.2017.10.001
10. Lemaître J-F, Dubray N, Hilaire S, Panebianco S, Sida J-L. SPY: a new scission point model based on microscopic ingredients to predict fission fragments properties. EPJ Web Conf (2013) 62:04002. doi:10.1051/epjconf/20136204002
11. Lemaître JF, Goriely S, Hilaire S, Sida J-L. Fully microscopic scission-point model to predict fission fragment observables. Phys Rev C (2019) 99:034612. doi:10.1103/physrevc.99.034612
12. Karthika C, Balasubramaniam M. Scission point model for the mass distribution of ternary fission. Eur Phys J A (2019) 55:59. doi:10.1140/epja/i2019-12729-y
13. Mehdipour Kaldiani P. Mass yield of spontaneous fission of 238 U within the systematic statistical scission-point model. Phys Scripta (2020) 95(7):075306. doi:10.1088/1402-4896/ab93a9
14. Randrup J, Möller P. Brownian shape motion on five-dimensional potential-energy surfaces: nuclear fission-fragment mass distributions. Phys Rev Lett (2011) 106:132503. doi:10.1103/physrevlett.106.132503
15. Randrup J, Möller P. Energy dependence of fission-fragment mass distributions from strongly damped shape evolution. Phys Rev Lett (2013) 88:064606. doi:10.1103/physrevc.88.064606
16. Möller P, Randrup J. Calculated fission-fragment yield systematics in the region 74 ≤ Z ≤94 and 90 ≤ N ≤ 150. Phys Rev C (2015) 91:044316. doi:10.1103/physrevc.91.044316
17. Nadtochy PN, Karpov AV, Vanin DV, Adeev GD. Mass-energy distribution of fragments from the fission of excited nuclei within three-dimensional Langevin dynamics. Phys Atom Nucl (2001) 64(5):861–869. doi:10.1134/1.1378876
18. Ivanyuk F, Chiba S, Aritomo Y. Scission-point configuration within the two-center shell model shape parameterization. Phys Rev C (2014) 90(5). doi:10.1103/physrevc.90.054607
19. Ivanyuk F, Kawano T, Chiba S, Paris MW, Talou P. The scission point configuration of fissioning nuclei. EPJ Web Conf (2016) 122:01002. doi:10.1051/epjconf/201612201002
20. Mirea M, Delion DS, Sandulescu A. Microscopic cold fission yields ofCf252. Phys Rev C (2010) 81:044317. doi:10.1103/physrevc.81.044317
21. Pomorski K, Nerlo-Pomorska B, Bartel J, Schmitt C. Fission fragment mass and total kinetic energy distributions of spontaneously fissioning plutonium isotopes. EPJ Web Conf (2018) 169:00016. doi:10.1051/epjconf/201816900016
22. Goutte H, Casoli P, Berger J-F. Mass and kinetic energy distributions of fission fragments using the time dependent generator coordinate method. Nucl Phys (2004) 734:217. doi:10.1016/j.nuclphysa.2004.01.038
23. Blocki J, Świątecki WJ. A generalization of the proximity force theorem. Ann Phys (1981) 132:53–65. doi:10.1016/0003-4916(81)90268-2
24. Blocki J, Randrup J, Swiatecki WJ, Tsang CF. Proximity forces. Anna Phys NY (1977) 105:427–462. doi:10.1016/0003-4916(77)90249-4
25. Bao X, Zhang H, Royer G, Li J. Spontaneous fission half-lives of heavy and superheavy nuclei within a generalized liquid drop model. Nucl Phys A (2013) 906:1–13. doi:10.1016/j.nuclphysa.2013.03.002
26. Moller P, Nix JR, Myers WD, Swiatecki WJ. Nuclear ground-state masses and deformations. At Data Nucl Data Tables (1995) 59:185–381. doi:10.1006/adnd.1995.1002
27. Duijvestijn MC, Koning AJ, Hambsch F-J. Mass distributions in nucleon-induced fission at intermediate energies. Phys Rev C (2001) 64:014607. doi:10.1103/physrevc.64.014607
28. Strutinsky VM. Shell effects in nuclear masses and deformation energies. Nucl Phys (1967) 95:420. doi:10.1016/0375-9474(67)90510-6
29. Ivanyuk FA, Ishizuka C, Usang MD, Chiba S. Temperature dependence of shell corrections. Phys Rev C (2018) 97:054331. doi:10.1103/physrevc.97.054331
30. Manailescu C, Tudora A, Hambsch F-J, Morariu C, Oberstedt S. Possible reference method of total excitation energy partition between complementary fission fragments. Nucl Phys (2011) 867(1):12–40. doi:10.1016/j.nuclphysa.2011.08.001
31. Morariu C, Tudora A, Hambsch F-J, Oberstedt S, Manailescu C. Modelling of the total excitation energy partition including fragment deformation and excitation energies at scission. J Phys G Nucl Part Phys (2012) 39:055103. doi:10.1088/0954-3899/39/5/055103
32. Sugarman N, Turkevich A. Radiochemical studies: the fission product In: CD Coryell, and N Sugarman, editors , Vol. 3. New York: McGraw-Hill (1951). p 1396.
33. Pahlavani MR, Mehdipour P. Product yields for the photofission of 232Th, 234,238U, 237Np, and 239,240,242Pu actinides at various incident photon energies. Nucl Sci Tech (2018) 29:146. doi:10.1007/s41365-018-0482-1
34. Umezawa H, Baba S, Baba H. Systematic behaviour of the most probable charge in the medium-energy fission. Nucl Phys (1971) 160:65. doi:10.1016/0375-9474(70)90174-0
35. Swindle DL, Wright RJ, Kuroda PK. Yields of ruthenium isotopes from the spontaneous fission of 238U. J Inorg Nucl Chem (1971) 33:876–879. doi:10.1016/0022-1902(71)80491-8
36. Naik H, Shivashankar BS, Raj Prakash HG, Raj D, Sanjeev G, Karunakara N, et al. Measurements of fission yield in 8 MeV bremsstrahlung induced fission of 232Th and 238U. J Radioanal Nucl Chem (2014) 299:127. doi:10.1007/s10967-013-2719-0
37. Belyshev SS, Ishkhanov BS, Kuznetsov AA, Stopani KA. Mass yield distributions and fission modes in photofission ofU238below 20 MeV. Phys Rev (2015) 91:034603. doi:10.1103/physrevc.91.034603
38. Mehdipour Kaldiani P. Kinetic energy distribution for photofission of light actinides. Phys Rev C (2020) 102:044612. doi:10.1103/physrevc.102.044612
39. Naik H, Nimje VT, Raj D, Suryanarayana SV, Goswami A, Singh S, et al. Mass distribution in the bremsstrahlung-induced fission of 232Th, 238U and 240Pu. Nucl Phys (2011) 853:1–25. doi:10.1016/j.nuclphysa.2011.01.009
40. Kondratko MY, Mosesov AV, Petrzhak KA. Yields of products of the photofission of239Pu. Sov Atom Energy (1981) 50:41–43. doi:10.1007/BF01141251
42. Zhao YL, Nishinaka I, Nagame Y, Tanikawa M, Tsukada K, Ichikawa S, et al. Symmetric and asymmetric scission properties: identical shape elongations of fissioning nuclei. Phys Rev Lett (1999) 82:3408–3411. doi:10.1103/physrevlett.82.3408
43. Parlag OO. EXFOR experimental nuclear reaction data base; targets: Np-237. In: International conference current problems in nuclear physics atomic energy, Kyiv (2006), p 369, Reactions: (g,f), quantity: FY.
44. Naik H, Carrel F, Kim GN, Laine F, Sari A, Normand S, et al. Mass yield distributions of fission products from photo-fission of 238U induced by 11.5–17.3 MeV bremsstrahlung. Eur Phys J A (2013) 49:94. doi:10.1140/epja/i2013-13094-7
Keywords: photofission, mass yields, statistical scission point model, fragment mass yields, deformation parameters
Citation: Kadiani PM (2021) Deformation Parameters and Collective Temperature Changes in Photofission Mass Yields of Actinides Within the Systematic Statistical Scission Point Model. Front. Phys. 9:629978. doi: 10.3389/fphy.2021.629978
Received: 19 November 2020; Accepted: 13 January 2021;
Published: 23 February 2021.
Edited by:
Giuseppe Mandaglio, University of Messina, ItalyReviewed by:
Giuseppe Verde, Universities and Research, ItalyGiorgio Giardina, University of Messina, Italy
Copyright © 2021 Kadiani. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: P. Mehdipour Kadiani, UGF5YW1tZWhkaXBvdXJAZ21haWwuY29t
 P. Mehdipour Kadiani
P. Mehdipour Kadiani