Laser-Induced Control of the Optical Response of Aluminum Phthalocyanine Chloride Complexes Dissolved in Ethanol

We show that absorption spectra of aluminum chloride phthalocyanine (AlClPc) in the liquid phase can be dynamically modified through the time-resolved interaction with a second laser pulse during a time window on the order of 100 fs. The observed effects can be explained by laser-induced coherent coupling dynamics between the ground state and a bath of excited states as reproduced by a few-level toy model. The presented results help to understand how intense laser fields interact with complex molecules in solution, but in their laser-controlled response still much alike isolated atoms in the gas phase. This understanding can, in the future, be used to modify and control the dynamics in complex systems.

1 Introduction

Coherent laser-control concepts are widely used to efficiently control matter [1–3]. In the gaseous phase the optical response of atomic and molecular targets can be controlled by XUV-NIR multi-pulse experiments which have been understood through laser-induced couplings between isolated electronic states [4–7], and also including vibrational couplings [8–12]. This approach also includes the possibility to selectively modify and control the dipole response with intense fields [13–15]. For more complex systems of molecules dissolved in the liquid phase, the intricacy of coherent light-matter interaction increases, where typically the coupling to a bath leads to rather rapid decoherence effects [16–20]. Nevertheless, coherent control concepts have been realized in these systems [21–23] and can also be understood through atom-like modeling [24, 25]. Based on existing dynamic coherent-control concepts which have been already established in the XUV-NIR spectral region on gas phase targets [14, 26, 27] it is the goal of this work to expand the dynamic control of absorption spectra to the liquid phase using time-resolved absorption spectroscopy in the visible (VIS) to near-infrared (NIR) regime.

The conceptual idea of measuring and controlling the optical dipole response of the system is presented in Figure 1. A weak excitation pulse induces a freely decaying dipole moment at time $t=0$, which itself interferes with the electric field of the excitation pulse. This interference leads to the characteristic (unperturbed) static absorption spectrum of the system that is imprinted on the excitation pulse spectrum. When a control pulse subsequently interacts (at time $t=\tau >0$) with the initially induced dipole moment it can be coherently modified, which is also known as perturbed free-induction decay [28–30]. This leads to characteristic spectral modifications of the absorption spectrum of the excitation pulse [5, 7, 14]. Hereby it should be noted that a grating-based spectrometer (not shown in Figure 1) intrinsically performs the Fourier transform and thus a time-integrated spectral measurement is carried out, which includes both the excitation pulse at $t=0$ and its (possibly perturbed; in the presence of the control pulse) dipole response for $t>0$. This concept thus invokes a time-domain picture of light-matter interaction where the absorption of light is understood in the impulsive limit of a time-domain (dipole) response function, the laser control of which is only possible while the system still reacts coherently upon the initial (excitation-induced) impulsive stimulus, which is here realized experimentally. The full real-time action of the control pulse on the system’s dynamics can in principle be retrieved from the measured absorption spectrum provided a sufficiently short excitation pulse is used [15].

FIGURE 1

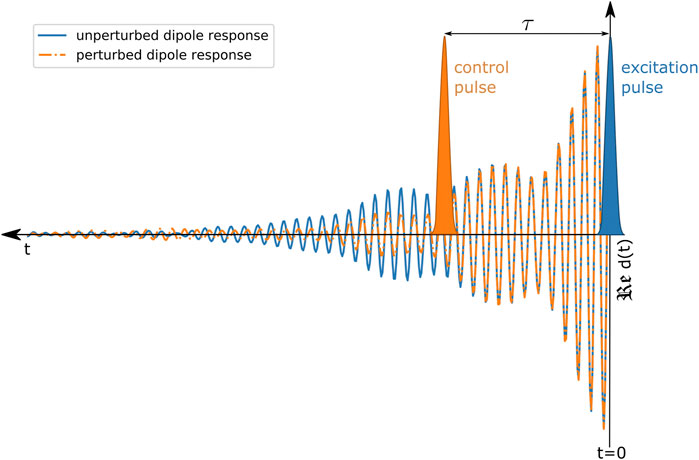
FIGURE 1. Schematic illustration of controlling the optical dipole response. The excitation pulse (depicted in blue) initiates the system’s dipole response $d\left(t\right)$ at time $t=0$ which thereafter evolves freely in time (blue solid curve) for $t>0$. At time $t=\tau$ a control pulse (depicted in orange) interacts with the dipole response, leading to a perturbed dipole response (orange dashed curve), which thereafter deviates from the unperturbed dipole response (evolving in absence of the control pulse) for $t>\tau$. See also Ref. [14] for further discussions of this concept.

With this understanding laser-induced coupling dynamics can be extracted across isolated atomic [6, 13, 31], molecular [9, 10] and also more complex resonances [25]. Here, we apply these laser-control concepts of absorption spectra and the dipole response to a larger system of an organo-metallic complex in the liquid phase to explore new possibilities to dynamically control the system’s absorption properties. Therefore we experimentally and computationally explore the impact of a laser field on a molecular coherence, which is encoded in the weak-field excitation-only absorption spectrum, by applying the concept of the induced dipole moment and its manipulation. We further confirm this approach by reproducing the measured coherent effects of the dynamically modified dipole response by using a numerical atom-like few-level toy model.

In this work our target of interest are aluminum phthalocyanine chloride (AlClPc) complexes dissolved in ethanol. Due to their outstanding electronic and optical properties phthalocyanines in general enjoy a variety of industrial and medical applications such as solar cells [32, 33] and photodynamic therapy (PDT) of tumors [34–36]. Phthalocyanines are thermally and chemically stable and can therefore sustain also slightly more intense electromagnetic radiation, which makes them adequate candidates for the interaction with intense laser fields in the liquid phase. Their absorption is mostly governed by a $\pi -{\pi }^{\ast }$ transition of the 18 delocalized π-electrons of the phthalocyanine ring resulting in two characteristic absorption bands, the Soret- (300–350 nm) and the Q-band (600–700 nm) [37]. The Q-band of AlClPc shows a substructure consisting of the strong Q3 and weak Q2 and Q1 bands which are maintained also in solution in ethanol [38].

2 Materials and Methods

To exert laser-induced control of the optical response of AlClPc in the liquid phase we use a transient-absorption measurement scheme “in reverse”: A weak (excitation) pulse to excite the system, and a second stronger pulse—referred to as control pulse—arriving later. Both pulses are in the visible spectral range.

The measurement concept is depicted in Figure 2. The preceding weak pulse induces in the sample a freely decaying dipole moment (blue) which can be understood as the coupling between the ground state GS and the excited states of the Q-band. The interference of the induced dipole response in time with the weak pulse itself—both are in a fixed phase relationship—leads to an (unperturbed) absorption spectrum which is dispersed by a grating and measured as a function of energy (see the corresponding blue spectrum). If the control pulse arrives in time before the coherent dipole response has decayed completely, it is able to disturb the system by modifying the dipole response, leading to changes in the measured weak-field absorption spectrum (depicted in red color).

FIGURE 2

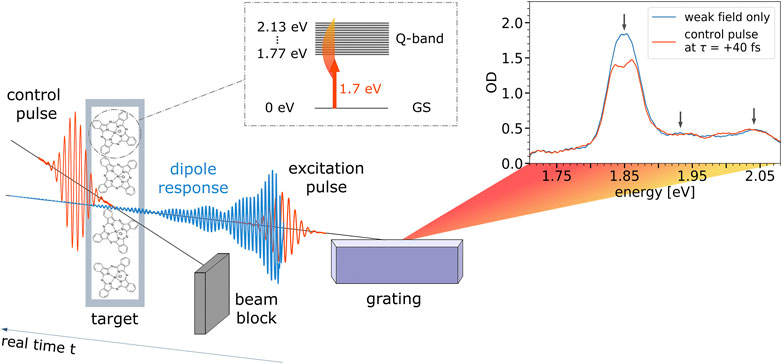
FIGURE 2. Measurement concept. Pulses propagate from left to right, so, if considered temporally, real time increases from right to left. Therefore, the depicted pulse arrangement shows a configuration for positive delay times, where the delayed control pulse modifies the excitation-pulse-induced dipole moment (depicted in blue). Exemplary absorption spectra are shown for the case of very late control delays in blue (effectively “weak field only”) where the control pulse does not change the dipole response anymore, as well as for the time delay τ = +40 fs, where the control pulse significantly perturbs the induced dipole moment. Black arrows denote the position of the Q3-, Q2-, and Q1-band. The inset shows an atom-like level scheme which is used for our toy model.

For the case of control-pulse first, that pulse does induce a dipole moment with which the later arriving weak pulse can interact. This effect is not seen in our measurements, since the control pulse (and therefore the co-propagating control-induced dipole moment) is spatially blocked after the sample. This is the reason why in our case we are only sensitive to the weak-field induced dipole moment. The difference in our experiment is thus rooted in the slightly non-collinear geometry where in the far field (after the sample) the pulses are detected spatially separate. Please note, due to the non-collinear geometry, measuring the excitation pulse together with its dipole response perturbed by the control pulse, any higher-order coherent effects induced by the control pulse itself, including stimulated emission induced by the control pulse [39], are not observed in the measurement direction of the excitation pulse.

To generate broadband ultrashort laser pulses in the visible spectral range we use a commercially available Ti:Sapphire multi-pass amplifier laser system (Femtolasers FEMTOPOWER^™ HE/HR CEP4) with a 3 kHz repetition rate, approximately 3 mJ pulse energy and a pulse duration of 20 fs full-width at half maximum (FWHM). After nonlinear propagation in a hollow-core fiber, a supercontinuum is generated which approximately covers the spectral range from 500 to 1000 nm. Subsequently the pulses are compressed with chirped mirrors. For this measurement we use chirped supercontinuum pulses of 32.7 ± 0.8 fs (FWHM), determined by fitting the instrumental response function on the lineout of the ground-state bleach of the Q3-band over the time delay, as can be seen in Figure 3. This helps to attenuate the peak intensities of the laser pulses to avoid permanent damage of the sample. As a fit function we used a convolution between a Gaussian, a Heaviside and an exponential function:

$f_{fit}\left(t\right)=\left(\left(\frac{A}{\sqrt{2\pi {\sigma }^2}}{e}^{-\frac{t^2}{2{\sigma }^2}}\right)\ast \left(\Theta (t)·\left(c+B\cdot e^{-\frac{t}{\tau }}\right)\right)\right)+b(1)$

with c and b being constants representing the depth and the total offset of the step, while A and B are constants for the amplitude of the instrumental response function (IRF) and the exponential decay, respectively, and σ denotes the width of the IRF and τ the exponential relaxation time. We apply this fit in the gray shaded pulse overlap area (Figure 3) near temporal overlap, i.e. before the onset of more complex molecular dynamics at later times.

FIGURE 3

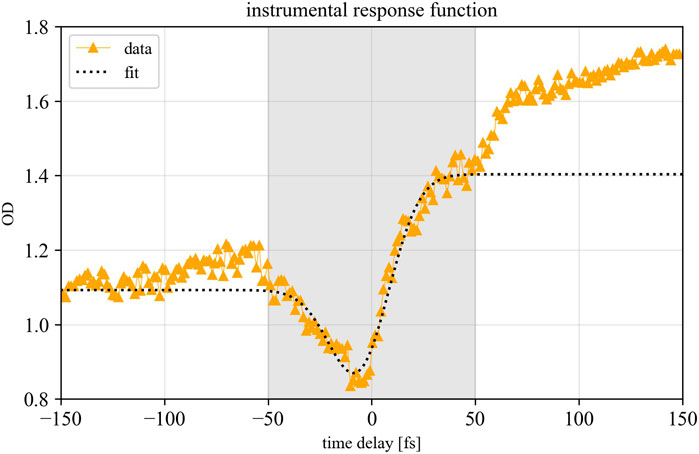
FIGURE 3. Fit of the instrumental response function on the mean lineout of the Q3-band as a function of the time delay. The fit function (1) was applied in the grey shaded pulse-overlap area.

The experimental response-control setup is depicted in detail in Figure 4. The collimated beam is divided into phase-synchronized excitation and control beams by a custom-built array of two iris apertures. The iris parameters are adjusted for the control beam to obtain a bigger focus diameter than the excitation beam. This ensures that the excitation-pulse-induced dipole response can be globally modified by the control beam, fully illuminating the excited sample volume. The preceding variable metallic neutral-density (ND) filters allow for an independent adjustment of the intensity of the beams. The time delay between both beams is introduced by a two-component mirror consisting of two mirrors separately mounted on piezo micrometer delay stages (PIHera Piezo Linearstage P-622.1CD, Physik Instrumente) which are hit by the laser beams under close-to normal angle of incidence, allowing to access time delays up to ±1.7 ps. Shortly after the focusing mirror (with a focal length of 50 cm), both beams pass a broadband beamsplitter (Layertech 110105) which reflects 80$\%$ and transmits 20$\%$ of the two beamlets. The transmitted part is used as a reference while the reflected part is guided into the sample where control and excitation beams spatially overlap with an intersection angle of 1.72 degree and a spot size of 150 μm FWHM diameter for the excitation beam and 400 μm for the control beam. In both pathways the control beam is blocked and only the excitation beam and its reference replica are refocussed using two additional focusing mirrors with a focal length of 50 cm each onto the slit of a Czerny-Turner-type spectrometer (Acton SpectraPro, Princeton Instruments). The excitation signal and reference beams are spectrally resolved with a resolution of 1.7 meV by a concave grating of 600 grooves/mm and detected with a spatial offset on the same CCD camera chip (CoolSnap K4, Teledyne Photometrics) as a function of the excitation-control time delay.

FIGURE 4

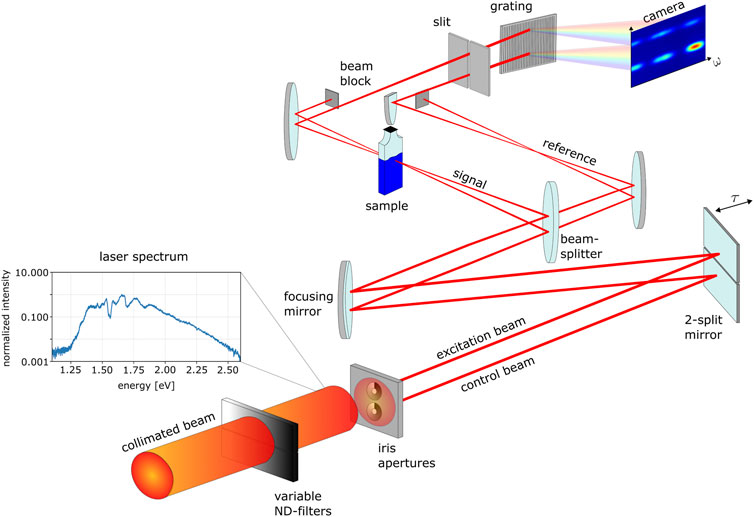
FIGURE 4. Experimental response-control setup. See text for details.—Note: The 2-split mirror, as well as the focusing mirror are experimentally hit under close-to-normal angle of incidence. Increased angles are depicted in the illustration for a better schematic overview of the experimental setup.

As a sample container, cyclic olefin copolymer cuvettes (SpecVette^™ manufactured by Aline Inc.) with 0.5 mm path length and 25 μl volume were used. The solution of AlClPc was prepared by dissolving 0.0042 g of AlClPc (purchased from Sigma Aldrich) in 0.01 ml of 99.9% ethanol (Uvasol^® by Sigma Aldrich) and was further diluted with distilled water with a ratio of 3:1 which results in a solution with a concentration of 55 nmol/ml.

3 Results

3.1 Experimental Results

For the measurements the excitation-beam average power was set to 0.28 mW and the control average power to 4.0 mW which correspond to on-target peak intensities of $3.2\cdot {10}^{10}$ and $1.7\cdot {10}^{11}$ W/cm² respectively. The transmitted signal and reference spectra were recorded for excitation-control time delays between −180 and +150 fs with a step size of 1.33 fs, where positive delays denote the excitation pulse preceding the control pulse. Laser-induced modifications of the excitation-pulse induced dipole response can therefore only take place for positive time delays $\left(\tau >0\right)$. With this in mind the optical density $\mathrm{OD}\left(\omega ,\tau \right)$ is calculated according to Beer-Lambert’s law:

$\mathrm{OD}\left(\omega ,\tau \right)=-{\log }_{10}\frac{I_{sig}\left(\omega ,\tau \right)}{c\left(\omega \right)\cdot I_{ref}\left(\omega ,\tau \right)}(2)$

with the signal and reference spectral intensity $I_{sig}$ and $I_{ref}$ depending on both time delay τ and frequency ω. The factor $c\left(\omega \right)$ is a calibration factor which corrects for the relative intensities between the signal and reference beams which are dependent on ω and mainly introduced by the beamsplitter. To determine $c\left(\omega \right)$ a measurement is conducted beforehand with an empty cyclic olefin copolymer cuvette in the focus. To additionally ensure that the solvent does not introduce effects which might be interpreted as a contribution from the coherent response of the AlClPc complexes, a time-delay scan in the neat solvent was conducted which showed no significant time-dependent spectro-temporal structures. After this step the actual measurement in the AlClPc complexes in ethanol are conducted with the same settings.

The static absorption of AlClPc’s Q-band is depicted in blue in Figure 2 and spans the spectral range between 1.80 and 2.08 eV. The highest contribution to the ground-state absorption is attributed to the Q3-band centered at 1.85 eV. The Q1-band is centered at 2.04 eV, while the Q2-band at 1.93 eV is only faintly visible. The measured time-delay-dependent absorption $OD\left(\omega ,\tau \right)$ can be seen in Figure 5. For a better visibility of the dynamic changes the relative optical density $\left[\text{ΔOD}\left(\omega ,\tau \right)\right]$ was calculated by subtracting the weak-field static absorption spectrum. The latter has been determined through the average of the optical density for control-pulse time delays between +150 and +140 fs, where the excitation-pulse induced absorption is no longer influenced as can be seen in Figure 5A. This can be rationalized since for late time delays the laser control of the dipole response is no longer possible. The most prominent feature which can be observed in Figure 5 is the decrease in absorption of the Q3-band for negative time delays. This effect can be explained by a ground-state bleach [40, 41]. In this case the control pulse itself, when arriving first, triggers a significant amount of population transfer into the excited states, which then leads to a lowered ground-state absorption of the excitation pulse as expected in conventional pump-probe transient absorption spectroscopy. For positive times (control pulse arrives later than the excitation pulse) a time-dependent modulation in the measured absorption spectrum between 1.85 and 2.10 eV is observed. For a better visibility the area of interest is marked in Figure 5B with a grey box. These slow modulations can be observed for positive time delays only and up to approximately +100 fs which implies that coherent modification of the excitation-pulse induced dipole response is still possible at these relatively long time scales even in the liquid phase. In addition a slight splitting of the Q3-band for positive time delays between 0 and +50 fs can be found.

FIGURE 5

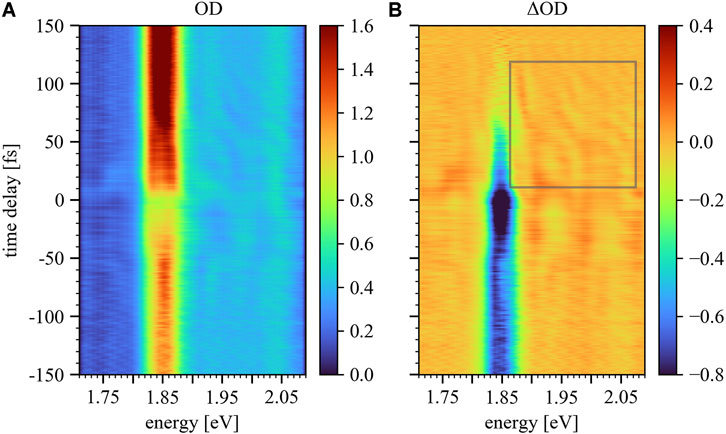
FIGURE 5. Time-delay trace $\mathrm{OD}\left(\omega ,\tau \right)$(A) and $\Delta \mathrm{OD}\left(\omega ,\tau \right)$(B) of AlClPc complexes dissolved in ethanol. The $\Delta$OD (B) underlines the control-induced changes of the excitation-pulse induced dipole response in AlClPc. Faint rapid fringes along the time-delay axis are due to residual stray light of the control beam which optically interferes with the excitation beam and occur symmetrically for both positive and negative times. At negative/positive times, the control pulse arrives before/after the excitation pulse, where the latter is centered at time $t=0$ and induces a coherent dipole response for times $t>0$. The grey box marks the area of interest where slow spectro-temporal modulations of the measured absorption are visible. The color bars represent the magnitude of OD.

To verify the origin of the observed effects a Fourier transform along the time-delay axis for positive and negative times of the $\Delta$OD trace is performed separately and depicted in Figure 6. In atoms, this procedure was used to reveal couplings of different energy levels by plotting the Fourier energy over absorption spectral energy [14, 26, 31]. In these two-dimensional Fourier energy vs. spectral energy representations, diagonals of slope ±1 that intersect the energy axis have been previously identified to indicate the modification of the coherent dipole response of that particular state for a variable time delay between excitation and control pulses [14]. Furthermore, enhancements in the Fourier amplitude along these diagonals are indicative of a coherent coupling between different states [31]. Such diagonals of slope ±1 can be observed in Figure 6A which arise at a spectral energy of approximately 1.84 eV and hence can be further associated to the Q3-band. Comparing the Fourier plots for positive and negative time delays, Figure 6A shows rich structure, while in Figure 6B only a globally enhanced signal around the Q3-band is visible.

FIGURE 6

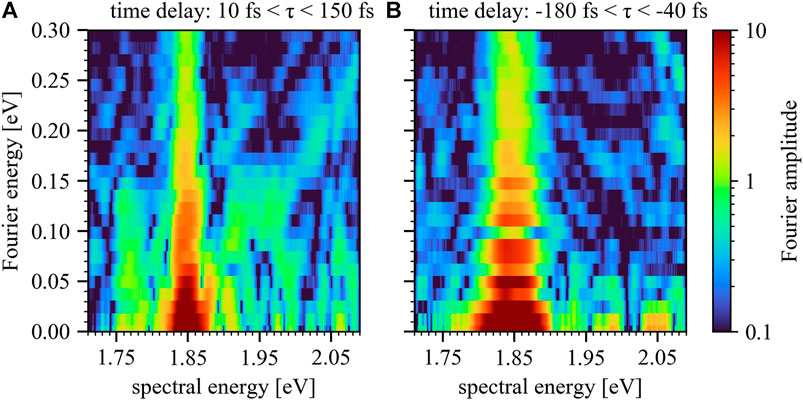
FIGURE 6. Fourier plot for positive (A) and negative (B) time delays of the $\Delta \mathrm{OD}\left(\omega ,\tau \right)$ depicted in Figure 5B. Diagonals of slope ±1 pointing at a spectral energy of approximately 1.84 eV can be observed in the Fourier plot only for positive time delays.

The significant qualitative difference between both Fourier plots confirms that the observed diagonal features are associated with laser-driven excited-state dipoles: for positive time delays the control field is able to modify the freely evolving dipole response of the excitation pulse. This qualitative difference between Figure 6A,B therefore strongly suggests that the previously introduced mechanism (Figure 1, 2) plays a significant role. Further confirmation of the underlying origin of the observed effects will be discussed in the following section by employing an atom-like multi-level model calculation.

3.2 Atom-Like Multi-Level Toy Model

We implement a numerical toy model through the propagation of the time-dependent Schrödinger equation in a multi-level system. Hereby we approximate the Q-bands through an ensemble of $N=300$ closely spaced states with respective energy widths of 2.2 meV each. We have ascertained that this choice of linewidth is sufficiently small to reproduce quantum interferences over the time-delay range of the measured data. In order to approximate the weak-field-only white-light absorption spectrum (depicted by the blue curve in the inset of Figure 2), the 300 states are brought to a mutual overlap and are equidistantly distributed over an energy range between 1.61 and 2.21 eV. Their respective real-valued transition dipole moments to the ground state are set such that the simulated white-light absorption spectrum agrees with the measurement, which is shown for comparison in Figure 7A. To solve the time-dependent Schrödinger equation

$i\frac{\partial }{\partial t}|\psi \left(t\right)\rangle =\mathrm{\mathscr{H}}|\psi \left(t\right)\rangle (3)$

with

$\mathrm{\mathscr{H}}={\mathrm{\mathscr{H}}}_0+{\mathrm{\mathscr{H}}}_{\mathrm{int}}(4)$

a split-step algorithm [42] has been used. Under the assumption that the Hamiltonian $\mathrm{\mathscr{H}}$ is constant during each time step, this routine solves the equations of motion iteratively for every time step by changing between the diagonalized Hilbert spaces of the unperturbed Hamiltonian ${\mathrm{\mathscr{H}}}_0$ and the interaction Hamiltonian ${\mathrm{\mathscr{H}}}_{\mathrm{int}}=\widehat{d}\cdot E\left(t\right)$ in the dipole approximation with the dipole operator $\widehat{d}$ and the time-dependent electric field $E\left(t\right)$. The wavefunction $|\psi \left(t\right)\rangle ={{\displaystyle \sum }}_i{c}_i\left(t\right)|{\Phi }_i\rangle$ can be represented as a sum of time-dependent state coefficients $c_i\left(t\right)$ and the spatial eigenstates of the system $|{\Phi }_i\rangle$. The dipole response $d\left(t\right)$ of the system can therefore be calculated by

$d\left(t\right)=\langle \psi \left(t\right)|\widehat{d}|\psi \left(t\right)\rangle ={\displaystyle \sum }_{m,n}{d}_{nm}{c}_n\left(t\right)c_m^{\ast }\left(t\right)+c.c.,(5)$

where $d_{nm}=\langle {\Phi }_m|\widehat{d}|{\Phi }_n\rangle$. The $d_{nm}$ are chosen with the aim to reproduce the measured (weak-field, excitation pulse only) absorption spectrum. Therefore the dipole matrix elements were set such that the thereby generated absorption spectrum closely matches the experimental data (Figure 7A). The final Hamiltonian matrix then reads

$\mathrm{\mathscr{H}}=\left[\begin{array}{ccccc}{\omega }_0& d_{\mathrm{1,0}}E\left(t\right)& d_{\mathrm{2,0}}E\left(t\right)& \dots & d_{\mathrm{300,0}}E\left(t\right)\\ d_{\mathrm{0,1}}E\left(t\right)& {\omega }_1& 0& \dots & 0\\ d_{\mathrm{0,2}}E\left(t\right)& 0& {\omega }_2& \dots & 0\\ ⋮& ⋮& ⋮& \ddots & 0\\ d_{\mathrm{0,300}}E\left(t\right)& 0& 0& 0& {\omega }_{300}\end{array}\right],(6)$

where $E\left(t\right)=E_{excitation}\left(t\right)+E_{control}\left(t-\tau \right)$ is the sum electric fields of both excitation and control pulses, and ${\omega }_i$ represent the complex eigenenergies of the states. The arrival time of the excitation pulse is kept constant at $t=0$ while the control pulse is temporally varied with the relative time delay τ. The pulses are implemented with a Gaussian envelope, an intensity FWHM of 3 fs and a central photon energy of 1.70 eV.

FIGURE 7

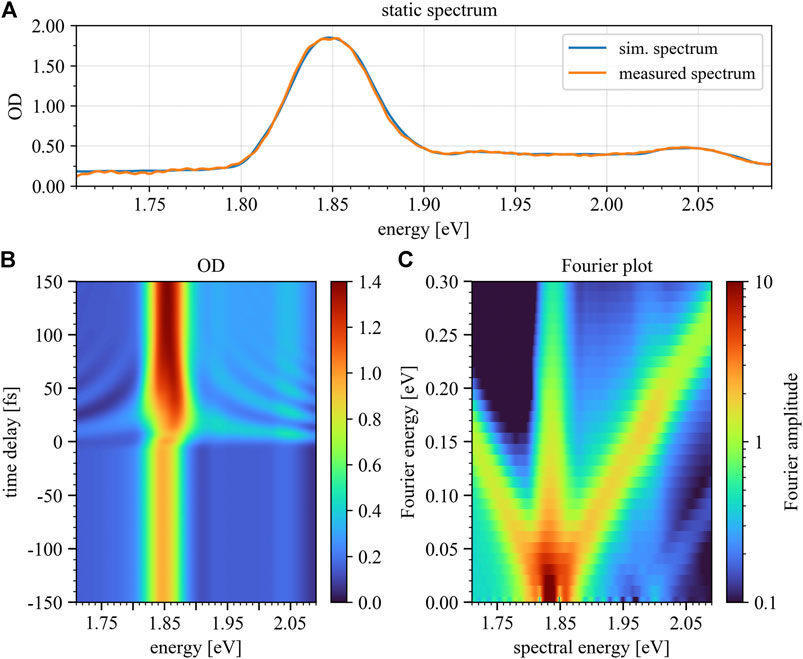
FIGURE 7. Simulated static absorption spectrum (A), time-delay trace (B) and Fourier plot (C) for positive time delays only. Panel 7B depicts the modeled optical density over a time-delay range of 300 fs, where the color bar marks the magnitude of OD. The Fourier plot (Panel 7C) reveals diagonals with slope ±1 in a similar fashion as seen in the experimental data. Negative time delays refer to control-pulse first, positive to excitation-pulse first.

The dipole spectrum $\tilde{d}\left(\omega \right)$ is obtained by Fourier-transforming the dipole response $d\left(t\right)$, and together with the spectral representation of the electric field $\widetilde{E_s}\left(\omega \right)$, the absorption cross section $\sigma \left(\omega \right)$ can be calculated according to

$\sigma \left(\omega \right)\propto \omega \cdot \mathrm{Im}\left[\frac{\tilde{d}\left(\omega \right)}{{\tilde{E}}_s\left(\omega \right)}\right],(7)$

which reflects the interference of the excitation-pulse induced dipole response with the excitation pulse itself, and their propagation through the medium according to Maxwell’s equations. The OD is in turn proportional to the absorption cross section via

$\mathrm{OD}\left(\omega \right)=-{\log }_{10}\left(\frac{I\left(\omega \right)}{I_0\left(\omega \right)}\right)=\frac{N_{a}l\sigma \left(\omega \right)}{\ln \left(10\right)},(8)$

where $N_a$ represents the number density of absorbers (i.e. AlClPc molecules) and l is the length of the absorption volume. A more detailed derivation of Eqs 7, 8 can be found [7].

To mimic the non-collinear experimental setup, an additional wave-front averaging { Refs. [43, 44]} is performed by calculating the absorption spectra with different carrier-envelope-phase (CEP) values for the control pulse, while keeping the CEP of the excitation pulse fixed, and subsequently taking the average of the resulting absorption spectra. Using this procedure the optical interference (heterodyne effect) between both optical pulses is suppressed in the toy model. Experimentally this optical interference is suppressed by the intersection angle of 1.72 degree which corresponds, together with the focal size of 150 μm, to a spread in delay of approximately seven full cycles of the wavelength. Finally, the simulated time-delay trace was convoluted with the instrumental response function, to account for the finite temporal and spectral resolution of the experiment. The resulting time-delay trace, as well as the corresponding Fourier plot (see discussion of Figure 5 above) are depicted in Figures 7B,C.

To show the impact of the control-pulse intensity on the manipulation of the excitation-pulse induced dipole response the numerical toy model was additionally conducted for two more intensities, half (Figure 8) and double (Figure 9) of the case shown in Figure 7. Hereby the results shown in Figure 7 reproduce the experimental results best.

FIGURE 8

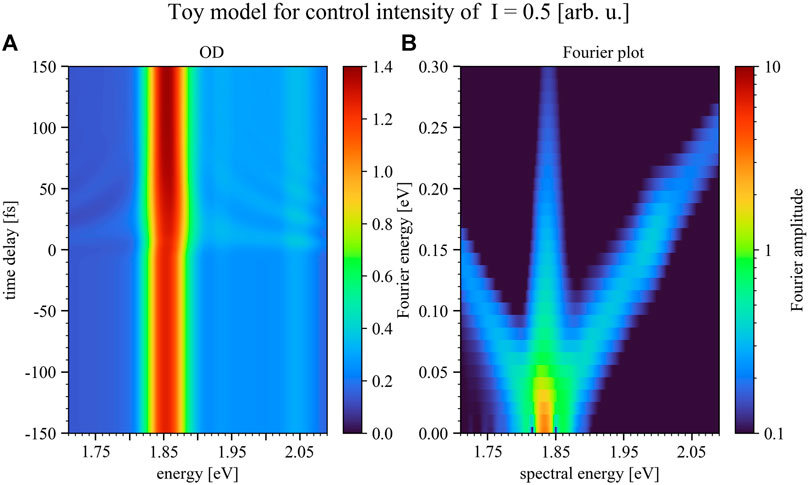
FIGURE 8. Simulated time delay trace (A) and Fourier plot (B) for positive time delays only, but for the case of half the control-pulse intensity compared to Figure 7. Panel 8A depicts the modeled optical density over a time-delay range of 300 fs, where the color bar marks the magnitude of the OD. The Fourier plot (Panel 8B) reveals less pronounced diagonals with slope ±1 compared to the experimental data. As can be seen by lowering the intensity of the control pulse the structures upon the absorption decrease. Negative time delays refer to control-pulse first, positive to excitation-pulse first.

FIGURE 9

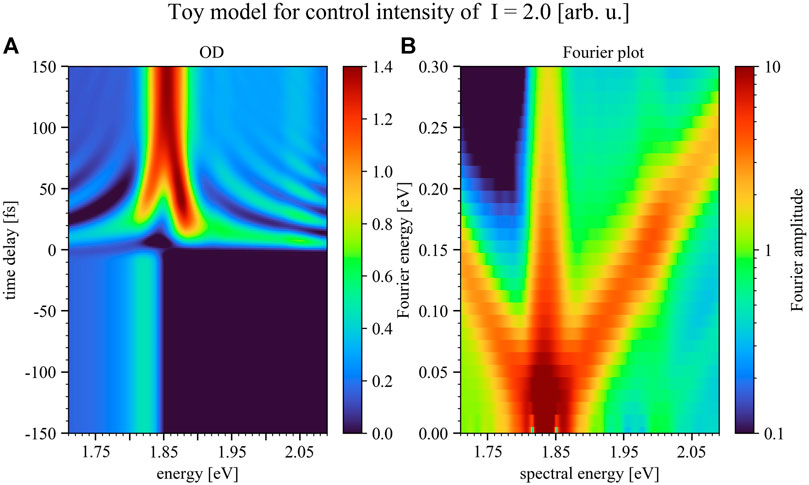
FIGURE 9. Simulated time delay trace (A) and Fourier plot (B) for positive time delays only, but for the case of double the control-pulse intensity of Figure 7. Panel 9A depicts the modeled optical density over a time-delay range of 300 fs, where the color bar marks the magnitude of the OD. The Fourier plot (Panel 9B) reveals diagonals with slope ±1 in a more pronounced fashion compared to the experimental data. The Rabi-/Autler-Townes splitting for small time delays near resonance can be observed to set in and grow with increasing control pulse intensity. Negative time delays refer to control-pulse first, positive to excitation-pulse first.

As can be seen in Figure 8 by lowering the intensity of the control pulse the structures upon the absorption decrease, while for increasing the control-pulse intensity one enters the strong-coupling limit. In this intensity region the control pulse is able to strongly modify the excitation-pulse induced dipole moment, leading to the splitting of the Q3-band which can already be seen in Figure 7B and increases toward higher control-pulse intensity (Figure 9). This band splitting is a Rabi-/Autler-Townes splitting involving light-induced level shifts of strongly coupled states, which can be observed to set in and grow with increasing control-pulse intensity.

In our toy model we only consider states up to a total excitation energy of 2.21 eV. Excitation of higher-lying states might also take place in our measurement but were neglected in the toy model due to lower relative population and thus have only a minor effect on the strong coupling of the lower-lying states. A prominent representative of such energetically higher-lying states is the Soret-band, which could imprint coupling signatures induced by the strong control pulse, which one could also try to identify by measuring its subsequently decay to the Q-band by fluorescence emission [40, 45]. Additional influence due to the coupling to higher excited states, like the Soret-band, may give rise to additional fine structures of the observed time-delay dependent interference.

4 Discussion

Comparing the measured time-delay-dependent absorbance (Figure 5A) with the simulated trace (Figure 7B), a good qualitative agreement can be observed for energies $>$1.80 eV. A discrepancy between the experimental and simulated data in the low-energy region is present since not all coupling channels are taken into account yet in the toy model to fully describe the experiment. Including more couplings currently lies outside the scope of this first study. Nevertheless the model reproduces the slight splitting of the Q3-band between 0 and 50 fs, the decrease in the overall absorption for negative time delays as well as the hyperbolic structures converging toward the Q3-band. Furthermore, also the Fourier energy plot in Figure 7C reveals diagonals of slope ±1 linked to the center of the Q3 band at spectral energy 1.84 eV, in qualitative agreement with the experiment. All these effects can thus be realized and understood with the described simplified atom-like multi-level toy model, with its level scheme depicted in Figure 2. The good structural agreement between experimental observation and the model results shows that the dynamical mechanism at work in this laser-driven AlClPc solution can be effectively approximated in the coupled system of ground and excited states.

To summarize, we have observed time-dependent coherent modifications of the ground-state absorption spectrum attributed to the Q-band of AlClPc complexes in the liquid phase. By comparing our measurements with an atom-like multi-level toy model, we were able to qualitatively reproduce and identify the spectro-temporal structures in the optical density as a laser-induced coupling between the ground state and a bath of excited states. Thus, by controlling the dipole response with a time-delayed laser pulse it is possible to understand the coherent ultrafast dynamics of complex systems in solution under the influence of intense light fields.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

CC and AP conducted the experiment and evaluated the experimental data together. CC wrote the paper manuscript, while AP conducted the numerical simulation using a part of the code provided from PB. CO and TP supervised the research project and gave input to the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Shapiro M, Brumer P. Coherent Control of Atomic, Molecular, and Electronic Processes. Adv At Mol Opt Phys (2000) 42:287–345. doi:10.1016/S1049-250X(08)60189-5

CrossRef Full Text | Google Scholar

2. Dantus M. Coherent Nonlinear Spectroscopy: From Femtosecond Dynamics to Control. Annu Rev Phys Chem (2001) 52:639–79. doi:10.1146/annurev.physchem.52.1.639

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Ohmori K. Wave-packet and Coherent Control Dynamics. Annu Rev Phys Chem (2009) 60:487–511. doi:10.1146/annurev.physchem.59.032607.093818

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Wang H, Chini M, Chen S, Zhang CH, He F, Cheng Y, et al. Attosecond Time-Resolved Autoionization of Argon. Phys Rev Lett (2010) 105:143002. doi:10.1103/PhysRevLett.105.143002

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Chen S, Bell MJ, Beck AR, Mashiko H, Wu M, Pfeiffer AN, et al. Light-induced States in Attosecond Transient Absorption Spectra of Laser-Dressed Helium. Phys Rev A (2012) 86:063408. doi:10.1103/PhysRevA.86.063408

CrossRef Full Text | Google Scholar

6. Kaldun A, Ott C, Blättermann A, Laux M, Meyer K, Ding T, et al. Extracting Phase and Amplitude Modifications of Laser-Coupled Fano Resonances. Phys Rev Lett (2014) 112:103001. doi:10.1103/PhysRevLett.112.103001

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Wu M, Chen S, Camp S, Schafer KJ, Gaarde MB. Theory of Strong-Field Attosecond Transient Absorption. J Phys B: At Mol Opt Phys (2016) 49:062003. doi:10.1088/0953-4075/49/6/062003

CrossRef Full Text | Google Scholar

8. Reduzzi M, Chu WC, Feng C, Dubrouil A, Hummert J, Calegari F, et al. Observation of Autoionization Dynamics and Sub-cycle Quantum Beating in Electronic Molecular Wave Packets. J Phys B: At Mol Opt Phys (2016) 49:065102. doi:10.1088/0953-4075/49/6/065102

CrossRef Full Text | Google Scholar

9. Warrick ER, Cao W, Neumark DM, Leone SR. Probing the Dynamics of Rydberg and Valence States of Molecular Nitrogen with Attosecond Transient Absorption Spectroscopy. J Phys Chem A (2016) 120:3165. doi:10.1021/acs.jpca.5b11570

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Cheng Y, Chini M, Wang X, González-Castrillo A, Palacios A, Argenti L, et al. Reconstruction of an Excited-State Molecular Wave Packet with Attosecond Transient Absorption Spectroscopy. Phys Rev A (2016) 94:23403. doi:10.1103/PhysRevA.94.023403

CrossRef Full Text | Google Scholar

11. Warrick ER, Fidler AP, Cao W, Bloch E, Neumark DM, Leone SR. Multiple Pulse Coherent Dynamics and Wave Packet Control of the Dark State by Attosecond Four-Wave Mixing. Faraday Discuss (2018) 212:157–74. doi:10.1039/C8FD00074C

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Drescher L, Reitsma G, Witting T, Patchkovskii S, Mikosch J, Vrakking MJJ. State-resolved Probing of Attosecond Timescale Molecular Dipoles. J Phys Chem Lett (2019) 10:265–9. doi:10.1021/acs.jpclett.8b02878

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Ott C, Kaldun A, Raith P, Meyer K, Laux M, Evers J, et al. Lorentz Meets Fano in Spectral Line Shapes: A Universal Phase and its Laser Control. Science (2013) 340:716–20. doi:10.1126/science.1234407

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Blättermann A, Ott C, Kaldun A, Ding T, Pfeifer T. Two-dimensional Spectral Interpretation of Time-dependent Absorption Near Laser-Coupled Resonances. J Phys B: At Mol Opt Phys (2014) 47:124008. doi:10.1088/0953-4075/47/12/124008

CrossRef Full Text | Google Scholar

15. Stooß V, Cavaletto S, Donsa S, Blättermann A, Birk P, Keitel C, et al. Real-Time Reconstruction of the Strong-Field-Driven Dipole Response. Phys Rev Lett (2018) 121:173005. doi:10.1103/PhysRevLett.121.173005

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Nuernberger P, Ruetzel S, Brixner T. Multidimensional Electronic Spectroscopy of Photochemical Reactions. Angew Chem Int Edition (2015) 54:11368–86. doi:10.1002/anie.201502974

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Nairat M, Webb M, Esch MP, Lozovoy VV, Levine BG, Dantus M. Time-resolved Signatures across the Intramolecular Response in Substituted Cyanine Dyes. Phys Chem Chem Phys (2017) 19:14085–95. doi:10.1039/C7CP00119C

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Kumpulainen T, Lang B, Rosspeintner A, Vauthey E. Ultrafast Elementary Photochemical Processes of Organic Molecules in Liquid Solution. Chem Rev (2017) 117:10826–939. doi:10.1021/acs.chemrev.6b00491

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Oliver TAA. Recent Advances in Multidimensional Ultrafast Spectroscopy. R Soc Open Sci (2018) 5:171425. doi:10.1098/rsos.171425

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Buckup T, Léonard J. Multidimensional Time-Resolved Spectroscopy. Switzerland: Springer (2018).

21. Brixner T, Damrauer NH, Niklaus P, Gerber G. Photoselective Adaptive Femtosecond Quantum Control in the Liquid Phase. Nature (2001) 414:57–60. doi:10.1038/35102037

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Pearson BJ, White JL, Weinacht TC, Bucksbaum PH. Coherent Control Using Adaptive Learning Algorithms. Phys Rev A (2001) 63:063412. doi:10.1103/PhysRevA.63.063412

CrossRef Full Text | Google Scholar

23. Herek JL, Wohlleben W, Cogdell RJ, Zeidler D, Motzkus M. Quantum Control of Energy Flow in Light Harvesting. Nature (2002) 417:533–5. doi:10.1038/417533a

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Schneider J, Wollenhaupt M, Winzenburg A, Bayer T, Köhler J, Faust R, et al. Efficient and Robust Strong-Field Control of Population Transfer in Sensitizer Dyes with Designed Femtosecond Laser Pulses. Phys Chem Chem Phys (2011) 13:8733–46. doi:10.1039/C0CP02723E

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Meyer K, Liu Z, Müller N, Mewes JM, Dreuw A, Buckup T, et al. Signatures and Control of Strong-Field Dynamics in a Complex System. Proc Natl Acad Sci (2015) 112:15613–8. doi:10.1073/pnas.1509201112

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Chini M, Wang X, Cheng Y, Wu Y, Zhao D, Telnov DA, et al. Sub-cycle Oscillations in Virtual States Brought to Light. Scientific Rep (2013) 3:1105.

CrossRef Full Text | Google Scholar

27. Ott C, Kaldun A, Argenti L, Raith P, Meyer K, Laux M, et al. Reconstruction and Control of a Time-dependent Two-Electron Wave Packet. Nature (2014) 516:374–8. doi:10.1038/nature14026

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Brito Cruz CH, Gordon JP, Becker PC, Fork RL, Shank CV. Dynamics of Spectral Hole Burning. IEEE J Quan Electron (1988) 24:261–9. doi:10.1109/3.122

CrossRef Full Text | Google Scholar

29. Sasaki F, Kobayashi S. Femtosecond Dynamics of Frenkel Excitons in Pseudoisocyanine J Aggregates. Jpn J Appl Phys (1995) 34:188. doi:10.7567/jjaps.34s1.188

CrossRef Full Text | Google Scholar

30. Bengtsson S, Larsen EW, Kroon D, Camp S, Miranda M, Arnold CL, et al. Space–time Control of Free Induction Decay in the Extreme Ultraviolet. Nat Photon (2017) 11:252–8. doi:10.1038/nphoton.2017.30

CrossRef Full Text | Google Scholar

31. Ding T, Ott C, Kaldun A, Blättermann A, Meyer K, Stooss V, et al. Time-resolved Four-Wave-Mixing Spectroscopy for Inner-Valence Transitions. Opt Lett (2016) 41:709–12. doi:10.1364/OL.41.000709

PubMed Abstract | CrossRef Full Text | Google Scholar

32. de la Torre G, Claessens CG, Torres T. Phthalocyanines: Old Dyes, New Materials. Putting Color in Nanotechnology. Chem Commun (2007) 2000–15. doi:10.1039/B614234F

CrossRef Full Text | Google Scholar

33. Walter MG, Rudine AB, Wamser CC. Porphyrins and Phthalocyanines in Solar Photovoltaic Cells. J Porphyrins Phthalocyanines (2010) 14:759–92. doi:10.1142/S1088424610002689

CrossRef Full Text | Google Scholar

34. Bonnett R. Photosensitizers of the Porphyrin and Phthalocyanine Series for Photodynamic Therapy. Chem Soc Rev (1995) 24:19–33. doi:10.1039/CS9952400019

CrossRef Full Text | Google Scholar

35. Py-Daniel KR, Namban JS, de Andrade LR, de Souza PEN, Paterno LG, Azevedo RB, et al. Highly Efficient Photodynamic Therapy Colloidal System Based on Chloroaluminum Phthalocyanine/pluronic Micelles. Eur J Pharm Biopharm (2016) 103:23–31. doi:10.1016/j.ejpb.2016.03.028

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Jayme CC, Calori IR, Tedesco AC. Spectroscopic Analysis of Aluminum Chloride Phthalocyanine in Binary Water/ethanol Systems for the Design of a New Drug Delivery System for Photodynamic Therapy Cancer Treatment. Spectrochimica Acta A: Mol Biomol Spectrosc (2016) 153:178–83. doi:10.1016/j.saa.2015.08.027

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Edwards L, Gouterman M. Porphyrins: XV. Vapor Absorption Spectra and Stability: Phthalocyanines. J Mol Spectrosc (1970) 33:292–310. doi:10.1016/0022-2852(70)90040-8

CrossRef Full Text | Google Scholar

38. Vilsinski B, Gerola A, Lemos É, Magalhães Barbosa P, Katieli C, Cesar G, et al. Spectroscopic Study of Aluminum Phthalocyanine Chloride (AlPcCl) in Homogeneous and Micro-heterogeneous Media Consisting of P-123 and F-127 Polymeric Micelles. Química Nova (2015) 38:631–9. doi:10.5935/0100-4042.20150056

CrossRef Full Text | Google Scholar

39. Konar A, Shah JD, Lozovoy VV, Dantus M. Optical Response of Fluorescent Molecules Studied by Synthetic Femtosecond Laser Pulses. J Phys Chem Lett (2012) 3:1329–35. doi:10.1021/jz300363t

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Gan Q, Li S, Morlet-Savary F, Wang S, Shen S, Xu H, et al. Photophysical Properties and Optical Limiting Property of a Soluble Chloroaluminum-Phthalocyanine. Opt Express (2005) 13:5424–33. doi:10.1364/OPEX.13.005424

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Melnikov MY. Aluminum Phthalocyanine on Silica Nanoparticles: Aggregation and Excited States. Macroheterocycles (2015) 8:279–83. doi:10.6060/mhc150459l

Google Scholar

42. Feit MD, Fleck JA. Solution of the Schrödinger Equation by a Spectral Method II: Vibrational Energy Levels of Triatomic Molecules. J Chem Phys (1983) 78:301–8. doi:10.1063/1.444501

CrossRef Full Text | Google Scholar

43. Liu Z, Cavaletto SM, Ott C, Meyer K, Mi Y, Harman Z, et al. Phase Reconstruction of Strong-Field Excited Systems by Transient-Absorption Spectroscopy. Phys Rev Lett (2015) 115:033003. doi:10.1103/PhysRevLett.115.033003

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Becquet V, Cavaletto SM. Transient-absorption Phases with Strong Probe and Pump Pulses. J Phys B: At Mol Opt Phys (2018) 51:035501. doi:10.1088/1361-6455/aa8e6a

CrossRef Full Text | Google Scholar

45. Chahraoui D, Valat P, Kossanyi J. Fluorescence of Phthalocyanines: Emission from an Upper Excited State. Res Chem Intermediates (1992) 17:219–32. doi:10.1163/156856792X00146

CrossRef Full Text | Google Scholar