Effects of the Background Turbulence on the Relaxation of Ion Temperature Anisotropy in Space Plasmas

Turbulence in space plasmas usually exhibits two regimes separated by a spectral break that divides the so called inertial and kinetic ranges. Large scale magnetic fluctuations are dominated by non-linear MHD wave-wave interactions following a −5/3 or −2 slope power-law spectrum. After the break, at scales in which kinetic effects take place, the magnetic spectrum follows a steeper power-law k^−α shape given by a spectral index α > 5/3. Despite its ubiquitousness, the possible effects of a turbulent background spectrum in the quasilinear relaxation of solar wind temperatures are usually not considered. In this work, a quasilinear kinetic theory is used to study the evolution of the proton temperatures in an initially turbulent collisionless plasma composed by cold electrons and bi-Maxwellian protons, in which electromagnetic waves propagate along a background magnetic field. Four wave spectrum shapes are compared with different levels of wave intensity. We show that a sufficient turbulent magnetic power can drive stable protons to transverse heating, resulting in an increase in the temperature anisotropy and the reduction of the parallel proton beta. Thus, stable proton velocity distribution can evolve in such a way as to develop kinetic instabilities. This may explain why the constituents of the solar wind can be observed far from thermodynamic equilibrium and near the instability thresholds.

1. Introduction

In many space environments the media is filled by a weakly collisional plasma. Although Coulomb collisions represent an efficient mechanism for relaxing plasma parcels toward a thermodynamic equilibrium state in which the particle Velocity Distribution Functions (VDFs) achieve a Maxwellian profile [1, 2], when collisions are scarce Coulomb scattering becomes ineffective in establishing equilibrium. Subsequently, kinetic collisionless processes may dominate the dynamics of the system and be responsible for many of the observed macroscopic and microscopic properties of the plasma. Under these conditions the plasma VDF usually develops non-Maxwellian characteristics that can provide the necessary free energy to excite micro-instabilities that subsequently can induce changes on the macroscopic properties of the plasma [3–7]. Among the fundamental problems of plasma physics belongs the understanding of the excitation and relaxation processes of these poorly collisional plasmas and the resultant state of nearly equipartition energy density between plasma particles and electromagnetic turbulence [8]. In particular, these processes play an important role in space plasma environments, such as the solar wind [9–12] and the Earth's magnetosphere [13–15], specially at kinetic scales [4, 16, 17].

It is well-known that in space plasmas, turbulence usually exhibits two distinct regimes separated by a spectral break dividing the fluctuations power spectrum. In the case of magnetic field fluctuations these two regimes are known as the inertial MHD range (at larger scales) and the kinetic range (at ionic and sub-ionic scales) [12, 18]. Large scale magnetic fluctuations are dominated by MHD non-linear wave-wave interactions following a −5/3 or −2 slope power-law spectrum [19]. After the break the spectrum follows a steeper power-law k^−α shape given by a spectral index α > 5/3, as it has been shown from observations [20], 2.5D simulations [21], and full 3D simulations [22]. The break is related with the scales in which kinetic effects, such as wave-particle interactions [23–25] take place, or ion-scale current sheets are disrupted due to the onset magnetic reconnection [26–30]. Depending on the local plasma conditions the break can coincide with the ion inertial length λ_i, or the ion gyroradius ${\rho }_i=\sqrt{\beta }{\lambda }_i$, where β is the plasma beta parameter, as observed in space plasmas [31, 32] and numerical simulations [33]. In particular, for small values of the proton plasma beta, the scale of the break seems to be related to λ_i; while for larger values of beta to ρ_i. Also, different plasma environments can exhibit different spectral indices. For example, considering Van Allen Probes observations, Gamayunov et al. [34] have found α ~ 2 in the inner magnetosphere, and Chaston et al. [35] and Moya et al. [16] observed α ~ 4 associated with Kinetic Alfvén Waves turbulent spectra measured during geomagnetic storms in the Ring Current region. Similarly, Alexandrova et al. [36] found α ~ 7/3 using Cluster data, and Goldstein et al. [37] observed α ~ 4.2 considering Wind observations in the case of the solar wind at 1 AU from the Sun. In addition, using data from the recent Parker Solar Probe mission, Franci et al. [38] have found α ~ 7/2 during the first perihelion of the spacecraft, at about 36 solar radii from the Sun. Further, all these results are consistent with kinetic scale simulations [22, 38, 39]. Besides the recent progress, how the turbulent energy is dissipated in all these almost collisionless plasma systems is still under debate and corresponds to one of the outstanding open questions in space plasma physics [20, 40].

In a magnetized plasma, such as the solar wind or the Earth's magnetosphere, one of the most typical deviations from the Maxwellian equilibrium is the bi-Maxwellian distribution, i.e., a composed Maxwellian VDF that exhibits different thermal spreads (different temperatures) in the directions along and perpendicular to the background magnetic field. These distributions are susceptible to temperature anisotropy driven micro-instabilities that can effectively reduce the anisotropy and relax the plasma toward more isotropic states. However, in the absence of enough collisions, these instabilities are usually not able to lead the system fully into thermodynamic equilibrium, and the plasma allows a certain level of anisotropy up to the so called kinetic instability thresholds [4, 41]. From the theoretical kinetic plasma physics point of view, on the basis of the linear and quasilinear theory approximations of the dynamics of the plasma, it is possible to predict the thresholds in the temperature anisotropy and plasma beta parameter space that separate the stable and unstable regimes, and how the plasma evolves toward such states. These models are useful to study the generation and first saturation of the electromagnetic energy at the expense of the free energy carried by the plasma. To do so, in general quasilinear calculations consider initial conditions with a small level of magnetic field energy that grows as the temperature anisotropy relaxes. A comprehensive review of linear and quasilinear analysis of these instabilities considering a bi-Maxwellian model can be found in Yoon [42] and references therein.

Since the first studies by Weibel [43] and Sagdeev and Shafranov [44], the research about temperature anisotropy driven modes and the stability of the plasma have been widely studied in the last decades, and represent an important topic for space plasmas physics [45–49]. Predictions based on a bi-Maxwellian description of the plasma are qualitatively in good agreement with observations of solar wind protons (see e.g., Hellinger and Trávníček [6], Bale et al. [11]) and electrons (see e.g., Hellinger et al. [50], Adrian et al. [51]). However, as mentioned, turbulence is ubiquitous in space environments and all these relaxation processes should occur in the presence of a background turbulent magnetic spectrum. To the best of our knowledge, only a few quasilinear studies, such as Moya et al. [49, 52] have considered a background spectrum but nonetheless a study focused on the possible effects of a magnetic field background spectrum is yet to be done. Here we perform such systematic study by computing the quasilinear relaxation of the ion-cyclotron temperature anisotropy instability, considering different choices of the initial level of the magnetic field fluctuations, and the shape of the spectrum. We analyze their effect on the relaxation of the instability and the time evolution of the macroscopic properties of the plasma that are involved.

Several studies of the solar wind electromagnetic turbulence near the spectral break as a function of wave number $\left|k\right|=\sqrt{k_{\perp }^2+k_{\parallel }^2}$, where k_⊥ and k_∥ are the wave vector components parallel and perpendicular to the magnetic field, respectively, have shown that the fluctuation spectrum is anisotropic and that the power spectrum sometimes is greater at quasi-perpendicular propagation k_⊥ ≫ k_∥ (see e.g., Dasso et al. [53], Horbury et al. [54]) than at quasi-parallel propagation k_⊥ ≪ k_∥. However, for small plasma beta (β < 1) as in this study, the compressibility of the magnetic fluctuations is small in the solar wind at 1 AU (see e.g., Bale et al. [11]), which is consistent with propagation of Alfvén ion-cyclotron waves. Therefore, as a first approximation we consider the fluctuations to be magnetically non-compressive and propagating strictly along the background magnetic field (k = k_∥), and also have and focused on small β values. In the next section we present the details of our quasilinear model, and then, in sections 3 and 4 we present and discuss all our numerical results. Finally, in the last section we summarize our findings and present the main conclusions of our work.

2. Quasilinear Temperature Evolution

We consider a magnetized plasma composed of bi-Maxwellian protons and cold electrons. The kinetic dispersion relation of left-handed circularly polarized waves, propagating along a background magnetic field ${\overrightarrow{B}}_0$ is given by [52, 55, 56].

$\begin{array}{ll}\frac{v_A^2{k}_{\parallel }^2}{{\Omega }_p^2}=A+(A{\xi }^{-}+\xi )Z({\xi }^{-})-\frac{{\omega }_k}{{\Omega }_p},& (1)\end{array}$

where ω_k = ω+iγ is the complex frequency that depends on the wavenumber k_∥; $v_A=B_0/\sqrt{4\pi n_p{m}_p}$ is the Alfvén speed, with n_p and m_p the density and mass of protons, respectively; Ω_p = eB₀/m_pc is the proton gyrofrequency with c the speed of light; A = T_⊥/T_∥ − 1 where T_⊥/T_∥ is the temperature anisotropy; T_⊥ and T_∥ are the proton temperatures perpendicular and parallel with respect to ${\overrightarrow{B}}_0$, respectively; ξ = ω_k/k_∥u_∥ and ${\xi }^{-}=({\omega }_k-{\Omega }_p)/k_{\parallel }{u}_{\parallel }$ are resonance factors [57]; $u_{\parallel }=\sqrt{2k_B{T}_{\parallel }/m_p}$ is the parallel proton thermal speed, and k_B the Boltzmann constant. Z(ξ) is the plasma dispersion function [58], which is calculated numerically with the Faddeeva function provided by scipy. We also define the parallel proton ${\beta }_{\parallel }=u_{\parallel }^2/v_A^2$. In Equation (1), we have assumed charge neutrality (i.e., zero net charge such that the electron density is n_e = n_p), and v_A/c ≪ 1. Numerical roots of Equation (1) are calculated through the Muller's method [59] using our own Python code. The dispersion relation Equation (1) supports an infinite number of solutions for ω_k for each value of k_∥, most of them being sound-like heavily damped modes with frequencies above and below the proton gyrofrequency [5, 60]. Here, we focus on the quasilinear evolution of the plasma due to Alfvén-Cyclotron Wave (ACW) instabilities (for more details about this instability in the context of space plasmas see e.g., Moya et al. [61], Jian et al. [62], Wicks et al. [63], Yoon [42], and references therein).

Figure 1A shows the real part of the ACW complex frequency for β_∥ = 0.1 and several values of the temperature anisotropy T_⊥/T_∥. Similarly, Figure 1B shows the effects of β_∥ on the ACW real frequency at a fixed anisotropy T_⊥/T_∥ = 3. In all cases with β_∥ < 0.1, the real part of the frequency seems to approach asymptotically to ω = Ω_p at large wavenumbers. This description is very similar to the solutions of the dispersion relation Equation (1) in the cold-plasma approximation [64, 65]. However, for T_⊥/T_∥ > 1 (Figure 1A) or β_∥ > 0.01 (Figure 1B), the frequency curve deviates from the cold-plasma approximation for wavelengths around the proton inertial length v_A/Ω_p.

FIGURE 1

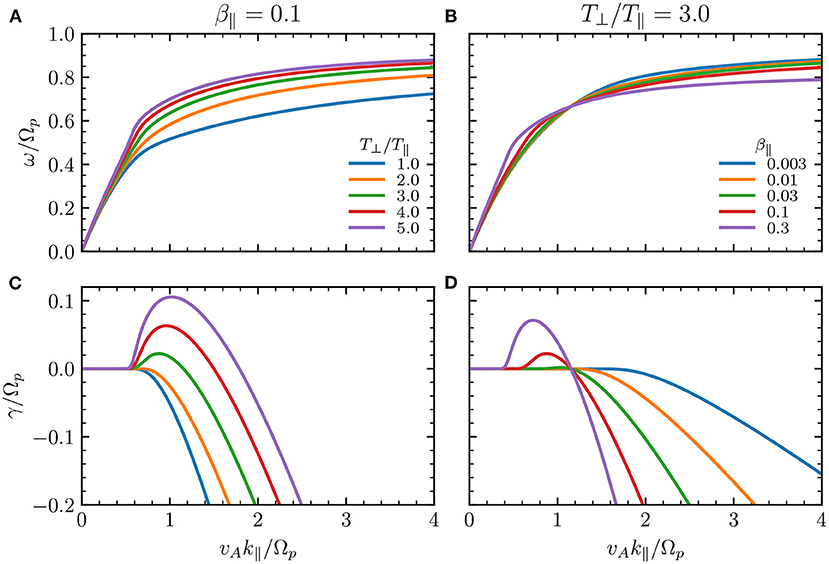
Figure 1. (A,B) Frequency and (C,D) growth/damping rate of Alfvén-cyclotron waves as a function of wavenumber, as calculated from the dispersion relation Equation (1). (A,C) β_∥ = 0.1 and different values of T_⊥/T_∥. (B,D) T_⊥/T_∥ = 3 and different values of β_∥. Plots for k_∥ < 0 can be obtained through the parity condition ${\omega }_{-k}=-{\omega }_k^{*}$.

Kinetic effects can damp ACWs of large wavenumbers even at low beta, and large temperature anisotropies can drive part of the wave spectrum unstable. Figures 1C,D show the imaginary part of the complex frequency for the same parameters as in Figures 1A,B, respectively. The wave is damped if its frequency satisfies Im(ω_k) = γ < 0, or it is unstable if γ > 0. Figure 1C shows that even a small value of β_∥ = 0.1 allows the growth of a kinetic instability when T_⊥/T_∥ ≳ 2 in a small range of wavenumbers 0.6 ≲ v_Ak_∥/Ω_p ≲ 2. The maximum value of γ increases, and its wavenumber also increases, as the anisotropy rises above T_⊥/T_∥ ≳ 2. On the other hand, for v_Ak_∥/Ω_p ≳ 2 and β_∥ = 0.1 the ACW is always damped, with damping rate γ decreasing almost linearly with k_∥. The wave is also marginally stable (γ ≈ 0) for long wavelengths compared with the ion inertial length (v_Ak_∥/Ω_p ≲ 0.5).

Notice in Figure 1D that the ACW is marginally stable (γ = 0) at a fixed wavenumber value v_Ak_∥/Ω_p ~ 1.15 and T_⊥/T_∥ = 3 independently of the value of β_∥. It can be shown from Equation (1) that this happens at ${(v_A{k}_{\parallel }/{\Omega }_p)}^2={(R-1)}^2/R$ [66]. Thus, for a lower value of the temperature anisotropy the waves are marginally stable at lower wavenumbers, as seen in Figure 1C, and the damping becomes stronger as the anisotropy approaches T_⊥/T_∥ = 1. Also, the instability decreases both with lower β_∥ and lower T_⊥/T_∥. It is important to mention that a semi-cold approximation of the plasma (ξ⁻ ≫ 1) fails to describe these properties, making it inappropriate for the quasilinear evolution of the plasma temperature.

The quasilinear moments approximation assumes that the macroscopic parameters of the plasma evolve adiabatically, thus ω_k = ω_k(t) solves the dispersion relation Equation (1) instantaneously at all times. The quasilinear evolution of the perpendicular and parallel thermal speeds are given by [52, 61]

$\begin{array}{l}\frac{\partial u_{\perp }^2}{\partial t}=-\text{Im}\frac{4}{L}\frac{e^2}{m_p^2}{\displaystyle {\int }_{-\infty }^{\infty }d}{k}_{\parallel }\frac{|B_k{|}^2}{c^2{k}_{\parallel }^2}[\frac{|B_k{|}^2}{c^2{k}_{\parallel }^2}(2i\gamma -{\Omega }_p)\\ \left(\frac{v_A^2{k}_{\parallel }^2}{{\Omega }_p^2}+\frac{{\omega }_k}{{\Omega }_p}\right)+{\omega }_k],& (2)\end{array}$

$\begin{array}{l}\frac{\partial u_{\parallel }^2}{\partial t}=\text{Im}\frac{8}{L}\frac{e^2}{m_p^2}{\displaystyle {\int }_{-\infty }^{\infty }d}{k}_{\parallel }\frac{|B_k{|}^2}{c^2{k}_{\parallel }^2}[\frac{|B_k{|}^2}{c^2{k}_{\parallel }^2}({\omega }_k-{\Omega }_p)\\ \left(\frac{v_A^2{k}_{\parallel }^2}{{\Omega }_p^2}+\frac{{\omega }_k}{{\Omega }_p}\right)+{\omega }_k].& (3)\end{array}$

where L is the characteristic length of the plasma, and $|B_k{|}^2$ is the spectral wave energy satisfying

$\begin{array}{ll}\frac{\partial |B_k{|}^2}{\partial t}=2\gamma (t)|B_k{|}^2,& (4)\end{array}$

such that Equations (1)–(4) form a closed system to address the quasilinear evolution of the ACW instability. The quasilinear approach summarized in Equations (1)–(4) is a widely used theoretical approach to study non-linear effects in the evolution of plasma waves as they interact with the media. Comparisons between quasilinear solutions and hybrid or particle-in-cell simulations [42, 67, 68] have shown that the approach is valid (theoretical and numerical results are in relatively good agreement) when the amplitude of the waves is finite but relatively small, especially for resonant instabilities (such as the ACW instability). Moreover, comparisons have also shown that the agreement between simulations and quasi-linear models is remarkable during the exponential growth of the instability (see e.g., Yoon [42]). Thus, for our calculations we have restricted the initial magnetic energy to $W_B(0)=\int d{k}_{\parallel }|B_k(0){|}^2/B_0^2\le 0.1$ (corresponding to B_k/B₀ ≲ 0.1 for a uniform spectrum), and have followed the quasilinear time evolution up to Ω_pt = 150 ensuring that the plasma reaches a stationary state.

In the next sections we explore the effects of the B_k spectrum on the relaxation of the proton anisotropy.

3. Numerical Results. The Effect of a Background Spectrum

In order to solve numerically the system of differential equations given by Equations (1)–(4) we use a fourth order Runge-Kutta method. In this section, for academic purposes, we consider three distinct shapes for the magnetic spectrum $|B_k{|}^2$ to illustrate the effects that different initial magnetic field background spectra can produce on the quasilinear evolution of the macroscopic parameters of the plasma. The three initial background spectra considered here are a uniform noise $|B_k(0){|}^2=A$, a Gaussian spectrum

$\begin{array}{ll}|B_k(0){|}^2=A{e}^{-{(v_A{k}_{\parallel }/{\Omega }_p)}^2},& (5)\end{array}$

and a Lorentzian spectrum

$\begin{array}{ll}|B_k(0){|}^2=\frac{A}{1+{(v_A{k}_{\parallel }/{\Omega }_p)}^{\alpha }},& (6)\end{array}$

where the normalization constant A is adjusted depending on the initial total magnetic energy W_B(0), with the integral calculated in the range $10^{-3}<v_A{k}_{\parallel }/{\Omega }_p<8$. The large-wavenumber tails v_Ak_∥/Ω_p > 8 of the spectrum shapes considered here do not contribute to the quasilinear plasma evolution. For these k_∥ values the waves are heavily damped as Figure 1 shows for β_∥ > 0.003. Thus, if energy is stored at those k_∥ values, they are quickly transferred to the particles until the wave energy is depleted. For greater values of k_∥, this process is faster. Therefore, most of the quasilinear evolution at late stages will be carried by energy transfer around v_Ak_∥/Ω_p = 1 where the wave is marginally stable and an instability is likely to appear.

Figure 2 shows the quasilinear time evolution of the temperature anisotropy, the perpendicular β_⊥ and parallel β_∥, and the total magnetic energy W_B. The initial conditions are chosen as T_⊥(0)/T_∥(0) = 1 and β_∥ = 0.1, parameters that are close to the most observed values in the solar wind at 1 AU in which quasi-parallel propagation seems to be dominant [11]. For every magnetic shape spectrum, we also compare the effects of different values of the initial level of magnetic fluctuations W_B(0) = 0.003 through 0.1. According to linear theory, the plasma is stable for the chosen initial parameters. In fact, for β_∥ = 0.1, an isotropic velocity distribution T_⊥/T_∥ = 1 has no free energy to excite an instability (see blue line in Figure 1C). Thus, we should expect that the temperatures will remain almost constant in time [60]. However, an striking feature for all the spectrum shapes, is that the anisotropy can grow in time if a sufficient level of magnetic energy is provided.

FIGURE 2

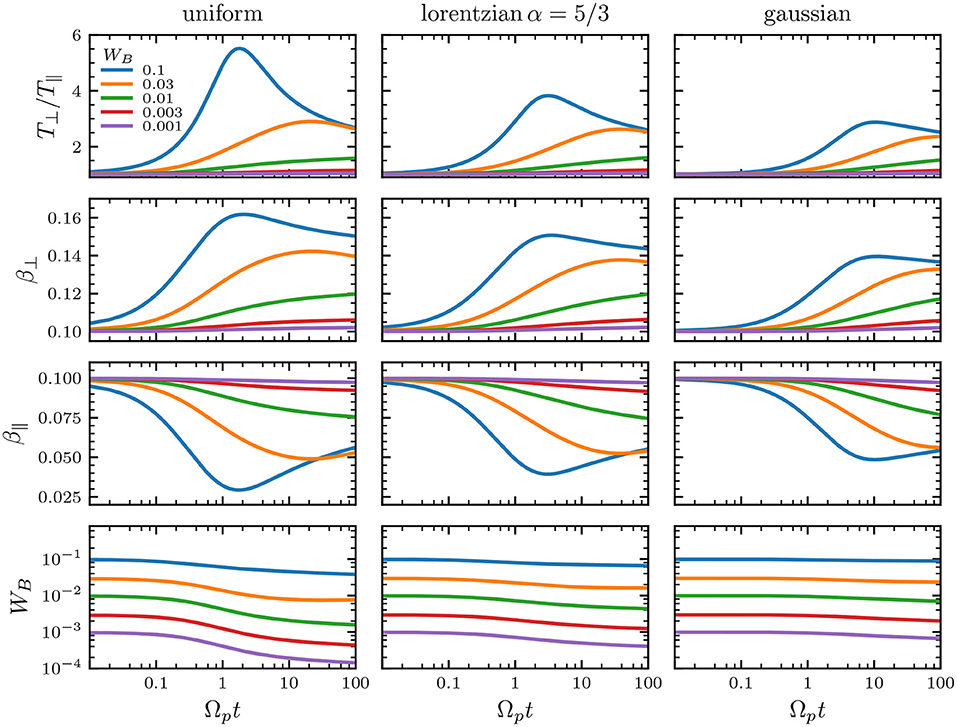
Figure 2. Quasilinear evolution of (upper row) the temperature anisotropy, (second row) perpendicular β_⊥, (third row) parallel β_∥, and (lower row) total magnetic energy. Initial conditions for all cases were chosen as β_∥(0) = 0.1, T_⊥(0)/T_∥(0) = 1, and different values of the initial magnetic energy: (blue) W_B(0) = 0.001, (orange) W_B(0) = 0.003, (green) W_B(0) = 0.01, (red) W_B(0) = 0.03, and (purple) W_B(0) = 0.1. Each column shows (left) a uniform, (middle) α = 5/3 Lorentzian, and (right) Gaussian initial background spectrum. Time and W_B axes are in logarithmic scale.

For an uniform spectrum of total level W_B(0) = 0.1 (blue lines in Figure 2), the anisotropy can grow up to high values T_⊥/T_∥ ≃ 5 in a small time frame. This results in a sharp increase in the perpendicular beta from β_⊥ = 0.1 to ≈ 0.16, and consistently a rapid fall in the parallel β_∥ = 0.1 toward ≈ 0.03. Afterwards, the anisotropy decreases while β_∥ rises, both steadily, toward a quasi-stationary state around T_⊥/T_∥ ≃ 3 and β_∥ ≈ 0.6. We note that this anisotropy growth is not as explosive for a Lorentzian (with α = 5/3, right column in Figure 2) and a Gaussian spectrum (middle column) compared to a uniform spectrum, although they all relax to a final state around the same temperature anisotropy. This shows that high levels of a power spectrum may play a role on the regulation of the temperature anisotropies observed in different plasma environments.

For a smaller value of W_B(0) = 0.03 (orange lines in Figure 2), the anisotropy also grows until it reaches a stationary state around T_⊥/T_∥ ≃ 3. However, this growth is monotonous and does not show a sharp increase nor a saturation in the early stages of the simulation, compared with W_B(0) = 0.1. Similarly, β_∥ decreases almost monotonically from 0.1 toward 0.05. For even smaller values of the magnetic field intensity, e.g., W_B(0) = 0.01, 0.003, 0.001 (green, red, and purple lines in Figure 2), the anisotropy growth is limited and a stationary stage is reached at lower values near T_⊥/T_∥ ≃ 1. As W_B(0) is lowered to noise levels $W_B(0)<10^{-5}$ (not shown), the anisotropy and other parameters remain almost constant, which is consistent with the fact that the plasma is in an equilibrium state for β_∥ = 0.1, T_⊥/T_∥ = 1, and low levels of the magnetic energy. In all cases, we observe that the total magnetic energy decreases monotonously, meaning that the quasilinear approximation is valid through every step of simulation runs.

In the earlier stages of the simulation runs, most of the energy transfer from the waves to the particles occurs at v_Ak_∥/Ω_p ≳ 2 since, according to the linear dispersion relation, the ACWs are heavily damped. This explains why a sufficient level of magnetic energy can heat the particles such that the anisotropy rises. Also, in this wavenumber range an initially uniform wave spectrum stores more energy compared to the Lorentzian one, meaning that the former can transfer more energy to particles compared to the latter in the same time lapse. A similar description holds as the Lorentzian is more energetic than the Gaussian in the v_Ak_∥/Ω_p ≳ 2 range, explaining why the anisotropy can reach higher values for the uniform spectrum compared to the Lorentzian and Gaussian cases. After the field energy is exhausted for long wavenumbers, the anisotropy saturates. If this occurs for anisotropy values in which a kinetic instability is excited, which should happen around v_Ak_∥/Ω_p = 1, then the energy transfer is reversed from the particles to the wave so that the anisotropy starts to decrease, and the wave energy around v_Ak_∥/Ω_p = 1 grows at an instantaneous growth-rate 2γ. However, as Figure 2 shows, this localized wave energy growth does not translate to total growth in W_B, probably because other parts of the spectrum are still transferring energy to the particles. If the saturated anisotropy is not enough to excite kinetic instabilities, or if the instability is weak, then energy transfer is a slow process and the plasma reaches a quasi-stationary state just after saturation, as shown in all cases with W_B ≤ 0.03 in Figure 2.

Figure 3 shows the time evolution of β_∥, T_⊥/T_∥, and W_B. A set of numerical simulations with evenly spaced (in log space) initial conditions were chosen in the range 0.003 ≤ β_∥ ≤ 0.3 and 1 ≤ T_⊥/T_∥ ≤ 5, marked with white circles, with an initial uniform magnetic wave spectrum of power W_B(0) = 0.01 for all cases. The colored lines represent the quasilinear path of the system in the diagram, and their colors represent the instantaneous magnetic energy W_B. The colored circles represent the final state of the system at Ω_pt = 150, long after the system has reached a stationary state, with color matching the instantaneous W_B.

FIGURE 3

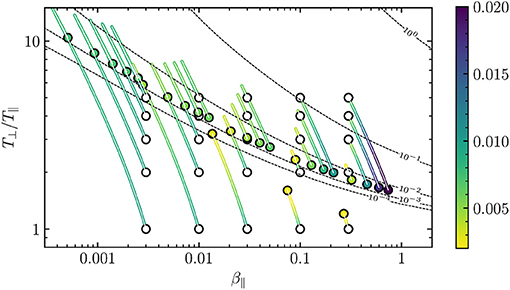
Figure 3. Quasilinear evolution of the proton β_∥ and anisotropy T_⊥/T_∥. Initial conditions (white circles) were chosen evenly spaced in the range 0.003 ≤ β_∥ ≤ 0.3 and 1 ≤ T_⊥/T_∥ ≤ 5, with a uniform magnetic wave spectrum of power W_B(0) = 0.01 for all cases. The colorbar represents the instantaneous value of W_B(t). Dashed lines are contours of the proton-cyclotron instability with maximum growth-rates $\gamma /{\Omega }_p=10^{-4}$ through 10⁰, as calculated from the dispersion relation Equation (1). Colorized circles correspond to the final (stationary) state of the plasma simulations.

A subset of these initial conditions can excite an instability as shown in Figures 1C,D. Thus, in Figure 3, contours of the maximum growth-rate γ_max/Ω_p are included as segmented lines. For numerical reasons, we will refer to the contour $\gamma /{\Omega }_p=10^{-4}$ as the instability threshold, and points below this line will be considered as stable according to the numerical solutions of the dispersion relation Equation (1). In general, the simulations with initial conditions below the instability threshold evolve so that the wave energy W_B decreases monotonously from W_B(0) = 0.01 to values between 0.002 < W_B(t_sat) < 0.01, which is consistent with results from Figure 2. On the other hand, for initially unstable conditions, the magnetic energy W_B rises up to values below 0.01 < W_B < 0.02.

In almost all simulated cases starting below the instability threshold, β_∥ drops rapidly while the temperature anisotropy increases to high values above the stability thresholds. Afterwards, the magnetic wave power is not enough to supply energy to protons, so that T_⊥/T_∥ slowly relaxes toward values where the maximum growth-rate of the ACW instability is of the order of γ/Ω_p ≃ 0.001. Of all the cases, however, there are three exceptions for T_⊥(0)/T_∥(0) = 1 and β_∥(0) = 0.03, 0.1, and 0.3, whose evolution reaches the final stationary state far below the instability threshold because the initial supplied energy W_B(0) = 0.1 is insufficient to push the system to higher anisotropies. This may explain why most of the observed plasma parameters in the solar wind are close to β_∥ = 1 and T_⊥/T_∥ = 1, since plasmas in this state are not heavily influenced by the background spectrum.

Notice that for simulations starting far below or far above the instability threshold, e.g., β_∥(0) = 0.003 and T_⊥/T_∥(0) = 1, or β_∥(0) = 0.3 and T_⊥/T_∥(0) = 5, the anisotropy can grow up to very high values above the instability thresholds. This effect is damped as the starting anisotropy is near the instability threshold. Thus, the effects of the starting anisotropy, which is a measure of the free energy available to excite an instability, can compete with the effects of the starting magnetic energy to regulate the anisotropy growth. Although not shown here, the quasilinear evolution in the cases of a Gaussian or Lorentzian power spectrum are similar. They all excite some level of proton perpendicular heating in the initial stage of the simulations, and then relax slowly toward a quasi-stationary state near the instability threshold, with properties similar to the ones shown in Figure 2.

In summary, we have illustrated how the initial shape magnetic field background spectrum can produce different results on the evolution of macroscopic parameters of the plasma. However, solar wind observations show that the plasma is mostly in a state below the instability thresholds, far from the isotropic state [6, 9], with a non-negligible level of magnetic fluctuations [11, 60], and that the magnetic field has a spectral break around the ion inertial length [31, 32]. The inertial range for transverse fluctuations propagating along the magnetic field v_Ak_∥/Ω_p < 1 typically shows a power-law spectrum $B_k^2\propto k_{\parallel }^{-2}$ [19]. For ion or sub-ions scales (in the kinetic range) the turbulent spectrum steepens to $k_{\parallel }^{-\alpha }$, with α ≥ 2.0, arguably due to the characteristics of the dispersion relation of Alfvén or other waves in that range [69–72]. Thus, the results presented here for three arbitrary spectral shapes may not remain the same when a solar wind-like spectrum is considered. This will be the focus of the next section.

4. Numerical Results. The Effect of a Turbulent Spectrum With a Spectral Break

Here we compute the quasilinear relaxation considering a quasi-parallel solar wind-like spectrum, including a spectral break at the ion inertial range scale, given by:

$\begin{array}{ll}|B_k(0){|}^2=\{\begin{array}{ll}A{k}_{\parallel }^{-2}\hfill & v_A{k}_{\parallel }/{\Omega }_p<1,\hfill \\ A{k}_{\parallel }^{-\alpha }\hfill & v_A{k}_{\parallel }/{\Omega }_p>1,\hfill \end{array}& (7)\end{array}$

where A is chosen depending on the initial total magnetic energy W_B(0), with the integral calculated in the range $10^{-3}<v_A\left|k_{\parallel }\right|/{\Omega }_p<8$. Notice that we are restricting to a reduced 1D background spectrum in k_∥. In this case, a $k_{\parallel }^{-2}$ reduced spectrum in the MHD range is the result of the integration in k_⊥ of a 2D spectrum of quasi-perpendicular fluctuations, whose corresponding reduced k_⊥ spectrum exhibit a −5/3 power law and a spectral anisotropy of $k_{\parallel }~k_{\perp }^{2/3}$. In general, the spectral slopes are determined by the conservation of total energy, i.e., that ∫dk_∥E(k_∥) = ∫dk_⊥E(k_⊥); and by the assumed spectral anisotropy, e.g., $k_{\parallel }~k_{\perp }^{d/3}$. So, if the reduced perpendicular 1D spectrum is $k_{\perp }^{-\mu }$, then the corresponding parallel reduced spectrum scales as $k_{\parallel }^{-\alpha }$ with α = [3(μ−1)+d]/d. The spectral anisotropy (represented by the parameter d) is still a matter of great debate. Typical values of such anisotropy are d = 1 [standard kinetic-Alfvén-wave (KAW) turbulence for which μ = 7/3, giving α = 5], d = 2 (intermittency corrected KAW turbulence [73], for which μ = 8/3, giving α = 7/2), or some reconnection-mediated scenario where d = 3 (i.e., k_∥ ~ k_⊥, to which α = μ). Sometimes it has been found α = μ = 3 in simulations [74].

Therefore, following the several observations mentioned here and in the Introduction section, we have considered four values of the spectral index, namely α = 2, 7/3, 7/2, and 5. Notice that the case with α = 2 corresponds to fluctuations without a break spectrum, which is unrealistic as a break is always observed around the ion characteristic scales and the spectrum is always steeper at smaller scales. Nevertheless we include such case for comparison purposes. Also notice that existing theories of plasma turbulence predict power laws in k_∥ with e.g., α = 2 in the MHD range (see e.g., Howes [75]), in consistency with solar wind observations [19], although this heavily relies on the assumed spectral anisotropy of the turbulent fluctuations, which is still a matter of great debate when it comes to the kinetic range. Moreover, regarding the validity of a purely parallel (instead of quasi-parallel) model, it is important to mention that, as shown by Gaelzer et al. [76] and Kim et al. [77], results considering quasi-parallel propagation may differ only by a multiplicative scaling factor with respect to the purely parallel propagation case considered in this work.

In what follows, the initial anisotropy and total magnetic energy are chosen as T_⊥(0)/T_∥(0) = 1 and W_B(0) = 0.1 for all simulation runs. For an initially low β_∥(0) = 0.001, Figure 4 (left column) shows that the proton distribution is cooled in the parallel direction with respect to the background magnetic field, as the parallel β_∥ decreases in time. Similarly, protons are heated in the transverse direction for all tested values of α. It is interesting to note that the magnetic energy decreases just 1% from the initial value, but causing a monotonous growth in the temperature anisotropy from T_⊥/T_∥ = 1 to ≃1.4 for α = 2. For larger values of α, this parallel cooling and transverse heating is less efficient. This can be explained as a steepened magnetic field spectrum for v_Ak_∥/Ω_p > 1 do not contain enough energy to be transferred to the particles compared to the α = 2 case.

FIGURE 4

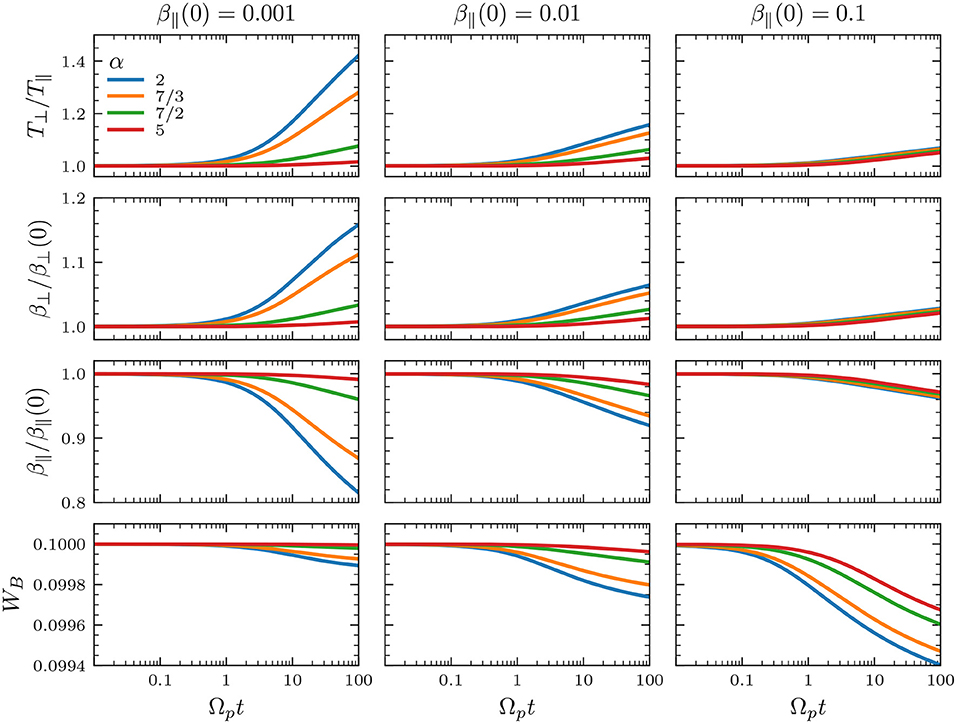
Figure 4. Quasilinear evolution of T_⊥/T_∥, β_⊥, β_∥, and total magnetic energy W_B for a solar-wind like spectrum Equation (7) with different values of 2 ≤ α ≤ 5. Initially, T_⊥/T_∥(0) = 1, W_B(0) = 0.1, and (left column) β_∥(0) = 0.001, (middle column) β_∥(0) = 0.01, and (right column) β_∥(0) = 0.1.

For β_∥(0) = 0.01 and 0.1, we see in Figure 4 that the parallel cooling and transverse heating still occurs. It is worth noticing that the magnetic energy actually decreases more, but the parallel cooling and transverse heating is less efficient than in cases with the same value of α and lower β_∥(0) = 0.001. Comparing with Figure 3, we see that all three cases β_∥ = 0.001, 0.01, and 0.1, with T_⊥/T_∥ = 1, correspond to linearly stable plasmas. However, β_∥ = 0.1 is closer to the instability thresholds, meaning that the quasilinear evolution will likely reach a stationary state with lower anisotropies near the stability margins. Also, in the cases we tested for high β_∥(0) ≥ 0.1, the temperature evolution seems to be independent of α. Moreover, as an initially anisotropic plasma can drive instabilities depending on the plasma beta, in order to compare with the initially isotropic case (always stable) shown in Figures 4, 5 shows results for the same set of parameters as in Figure 4, but for an initially anisotropic plasma with T_⊥/T_∥(0) = 3. The cases with β_∥(0) = 0.001 and 0.01 show similar qualitative characteristics for both Figures 4, 5. However, the case with β_∥(0) = 0.1 is initially unstable (see the green line in Figure 1C). This results in the reduction of the anisotropy and the increase in β_∥.

FIGURE 5

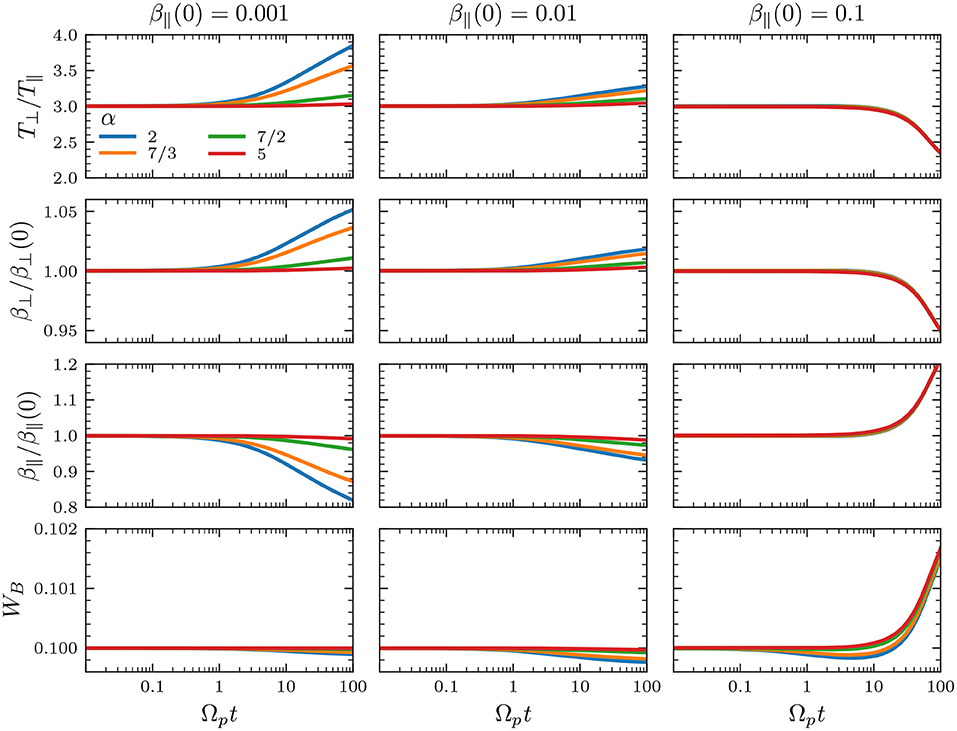
Figure 5. Same as in Figure 4 but for an initial anisotropy T_⊥/T_∥(0) = 3.

Finally, Figure 6 shows the spectral wave energy density at several intermediate time steps between Ω_pt = 0 and Ω_pt = 140, considering the initial conditions W_B(0) = 0.1, α = 7/2, T_⊥(0)/T_∥(0) = 1 (top), T_⊥(0)/T_∥(0) = 3 (bottom), and the same three values of β_∥(0) as in Figures 4, 5. For other values of α the description of these figures are almost identical. As time goes on, the wave spectrum is dampened for high values of k_∥ in all cases, which is consistent with results of Figure 1. For β_∥(0) = 0.001, the spectral break is unmodified at all times of the simulation run, but the spectrum steepens for v_Ak_∥/Ω_p > 2 for both T_⊥(0)/T_∥(0) = 1 and 3. For β_∥(0) = 0.01 and T_⊥(0)/T_∥(0) = 1 and 3, this happens at v_Ak_∥/Ω_p > 1.2 and the spectral break is still visible. For β_∥(0) = 0.1, the spectral break disappears and the wave spectrum becomes smooth around v_Ak_∥/Ω_p = 1. In all these cases, transference of energy from the wave to protons results in a monotonous drop in magnetic energy as discussed in Figures 4, 5.

FIGURE 6

Figure 6. Spectral wave energy $|B_k{|}^2$ as a function of the normalized wavenumber v_Ak_∥/Ω_p for several time steps. Initial conditions are W_B(0) = 0.1 for a solar wind-like spectrum with α = 7/2. (Top) T_⊥/T_∥(0) = 1 and (Bottom) T_⊥/T_∥(0) = 3. (Left) β_∥(0) = 0.001, (Middle) β_∥(0) = 0.01, and (Right) β_∥(0) = 0.1.

For β_∥(0) = 0.1 and T_⊥/T_∥(0) = 3, in the first stages of the simulation the electromagnetic wave loses energy at high values of v_Ak_∥/Ω_p > 1 as in the previous cases. However, since the wave is unstable in this case around 0.6 < v_Ak_∥/Ω_p ≲ 1.2 (see green line in Figure 1C), then the magnetic field amplitude starts to grow for those wavenumbers resulting in a bump in the spectral wave energy just below the spectral break. This results in the decrease of the temperature anisotropy and increment of β_∥, as shown in Figure 5, which is also consistent with the discussion of Figure 3. Comparing with Figure 1, this implies that the range of unstable wavenumbers shifts toward smaller values, which in turns means that the bump in the spectral wave energy also shifts to smaller values of k_∥. At the same time, previously unstable modes with higher v_Ak_∥/Ω_p > 1 become damped. Thus, the wave transfers energy to protons for values of v_Ak_∥/Ω_p > 1, resulting in a steep spectrum near the initial spectral break. At larger times and since the rate at which the wave damps is negligible compared to its growth, this results in a total growth of magnetic energy as shown in the lower right panel of Figure 5, which is consistent with the description of Figure 3 for initially unstable plasma states.

5. Discussion and Conclusions

Turbulence is ubiquitous in space environments and any relaxation process should occur in the presence of a background turbulent magnetic spectrum, e.g., relaxation to quasi-stationary states out of thermodynamic equilibrium, non-Maxwellian characteristics in poorly collisional plasmas, and temperature anisotropy regulation by micro-instabilities or other processes, among others. Here, we have focused on the possible effects of a magnetic field background spectrum on the quasilinear relaxation of the Alfvén ion-cyclotron temperature anisotropy instability. We have compared four different choices of the initial magnetic field spectrum shape $|B_k{|}^2$: (a) uniform noise, (b) Lorentzian, (c) Gaussian, and (d) the more realistic solar wind-like spectrum with a spectral break at v_Ak_∥/Ω_p = 1 and the kinetic ion or sub-ion range v_Ak_∥/Ω_p > 1 with a spectrum ∝k^−α with varying α ≥ 2.

Considering a plasma composed of bi-Maxwellian protons and cold electrons, with electromagnetic fluctuations propagating along a background magnetic field ${\overrightarrow{B}}_0$, it is shown that all the spectrum shapes considered here can heat protons preferentially in the direction perpendicular with respect to ${\overrightarrow{B}}_0$, provided the initial wave has enough energy power to be transferred to protons, even if the plasma is initially stable. Thus, isotropic protons can be heated toward high anisotropies T_⊥/T_∥ > 1. If T_⊥/T_∥ reaches high enough values, then an Alfvén-cyclotron instability is excited during the quasilinear evolution. Afterwards, the anisotropy production saturates and the plasma relaxes to a quasi-stationary state with a maximum instability growth-rate $\gamma /{\Omega }_p\approx 10^{-3}$. If the initial wave energy is insufficient then kinetic instabilities are not excited, although transverse heating may still occur.

It is noted that for simulations starting far below the instability threshold (defined here as the contour where ${\gamma }_{\mathrm{\text{max}}max}/{\Omega }_p=10^{-4}$ in the β_∥ and T_⊥/T_∥ parameter space), the anisotropy grows, and β_∥ and the wave energy are reduced, such that the final quasi-stationary state lies near the instability thresholds. This means that simulations of stable protons (T_⊥/T_∥ = 1) starting with low β_∥ < 0.01 experience stronger perpendicular heating compared to simulations starting with β_∥ > 0.01 for the same initial wave energy W_B. For higher values of β_∥ > 0.1, a wave energy W_B < 0.1 may not be sufficient to be transferred to protons, as it must compete with kinetic effects as measured by the beta parameter, thus the quasi-stationary state is reached for anisotropy values far below the instability thresholds although transverse heating can still be observed. On the other hand, simulations where the plasma is initially unstable (for anisotropies above the instability thresholds), the kinetic instability is dominant over the effects of energy transfer from the turbulent wave to protons. This results in an effective transverse cooling, i.e., reduction of the anisotropy and growth of β_∥. The wave energy also grows due to the presence of the instability. Nevertheless, and similarly to the previous description, the quasilinear evolution reaches a stationary state around the instability thresholds. Thus, there exists competition between the energy transfer from turbulent waves and the presence of kinetic instabilities, and they are effectively balanced near the instability thresholds.

Our numerical results show that the proton transverse heating by the waves is efficient depending on the energy stored in the tail of the magnetic spectrum (v_Ak_∥/Ω_p > 1 which lies in the kinetic range). This happens because the waves are heavily damped in the kinetic range according to the linear kinetic dispersion relation, and energy transfer from the waves to protons should occur first for those wavenumbers according to the quasilinear description. As anticipated from the previous results, in the case of a solar wind-like turbulent power-law spectra with a spectral break, the perpendicular heating is more effective for lower values of α as the tails of the spectrum can store more energy to be transferred to the particles. For values of β_∥(0) > 0.01, transverse preferential heating still occurs, however it seems to be independent of α, and it is less efficient than for lower values of β_∥(0) < 0.01. This means that for high values of β_∥, the shape of the wave spectrum is less relevant for perpendicular heating, and other kinetic effects become dominant. Finally, if the plasma is initially unstable, i.e., with large enough temperature anisotropy (e.g., T_⊥/T_∥ = 3 for β_∥ = 0.1), then the wave spectrum grows in time because it absorbs energy from the particles in a range of wavenumbers v_Ak_∥/Ω_p < 1. This produces a bump in the spectral wave energy just below the spectral break, the growth of the total magnetic energy, and the subsequent reduction of the proton temperature anisotropy toward the instability thresholds. It is worth mentioning that a bump has been sometimes observed in the magnetic field spectrum in correspondence of the ion characteristic scales near the Sun [78]. Thus, our results suggest that such characteristic may be related with resonant wave-particle interactions between unstable ion populations and turbulence near the spectral break.

The above being said, it is important to mention that turbulence in the solar wind correspond to an anisotropic cascade following critical balance with k_⊥ ≠ 0. However, as a first approximation here we have considered the fluctuations to follow the parallel propagating (k_⊥ = 0) Alfvén Ion-Cyclotron mode dispersion relation, since for small values of plasma beta, the compressibility of the fluctuations is small as pointed out by Bale et al. [11], which is consistent with Alfvén Ion-Cyclotron modes. Under this context we have considered that the plasma will only interact with transverse fluctuations with respect to the mean field, and therefore we have neglected the effect of other fluctuations with k_⊥ ≠ 0. We recognize, however, that this may be considered a crude approximation but at the same time we believe that our simplified approach provides valuable insights to the problem of the heating of the solar wind, that is generally observed in an anisotropic state. We expect to expand the scope of our approach and results with a subsequent study considering oblique propagating waves, hopefully corroborating or improving the results of our reduced model.

In summary, our results suggest a possible mechanism to explain why the solar wind plasma can be observed in a stationary state with T_⊥/T_∥ > 1 near the instability thresholds or far from thermodynamic equilibrium, as has been observed in the Earth's magnetosphere or the solar wind. A sufficient level of turbulent magnetic spectrum can drive an initially stable proton plasma toward higher values of the temperature anisotropy, i.e., far from thermodynamic equilibrium and preventing the plasma to remain in an isotropic state. However, measurements of solar wind protons at different space environments show that proton velocity distributions can also exhibit anisotropic states with T_⊥/T_∥ < 1 [11]. There are several possible explanations for this apparent discrepancy, as in this work we have not considered other effects that can effectively reduce the production of anisotropy, or compete with the Alfvén-cyclotron instability and the turbulent energy transfer, but are nonetheless worth of study. For example, radial expansion from the Sun [52, 79, 80], collisional effects [42], the role of compressive fluctuations [81], oblique propagation and the corresponding anisotropic turbulent cascade [19, 54, 75], oblique instabilities, such as the mirror or oblique firehose instabilities [48], other non-Maxwellian distributions, such as kappa distributions, the presence of heavy ions [56], or the kinetic effects of electrons. Also, the amplitude of magnetic fluctuations decays mostly with β_∥ [11, 60], imposing a severe restriction on the wave energy available for anisotropy production in space plasmas. However, steep spectra (larger α values) have been typically observed in association with small values of the plasma beta and large levels of turbulent fluctuations, both recently in near-Sun environment by Parker Solar Probe, and also previously in the near-Earth environment by WIND [82]. Moreover, Parker Solar Probe measurements have also shown an enhanced perpendicular proton heating possibly due to stochastic heating related to the strong turbulent fluctuations particularly in the fast solar wind (see e.g., Martinović et al. [83]) that could compete with all the mentioned mechanisms, including the heating mechanism suggested in this paper.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication. All authors contributed equally to this work.

Funding

This work was supported by ANID, Chile, through FONDECyT grants No. 11180947 (RN), and No. 1191351 (PM), and CONICyT-PAI grant No. 79170095 (RN).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Spitzer L. Physics of Fully Ionized Gases. New York, NY: John Wiley & Sons, Inc. (1962).

Google Scholar

2. Marsch E, Goldstein H. The effects of Coulomb collisions on solar wind ion velocity distributions. J Geophys Res. (1983) 88:9933–40. doi: 10.1029/JA088iA12p09933

CrossRef Full Text | Google Scholar

3. Marsch E, Mühlhäuser KH, Rosenbauer H, Schwenn R, Neubauer F. Solar wind helium ions: observations of the Helios solar probes between 0.3 and 1 AU. J Geophys Res. (1982) 87:35–51. doi: 10.1029/JA087iA01p00035

CrossRef Full Text | Google Scholar

4. Gary SP. Theory of Space Plasma Microinstabilities. Cambridge: Cambridge University Press (1993).

Google Scholar

5. Astudillo HF. High-order modes of left-handed electromagnetic waves in a solar-wind-like plasma. J Geophys Res. (1996) 101:24433. doi: 10.1029/96JA01586

CrossRef Full Text | Google Scholar

6. Hellinger P, Trávníček P. Parallel and oblique proton fire hose instabilities in the presence of alpha/proton drift: hybrid simulations. J Geophys Res. (2006) 111:A01107. doi: 10.1029/2005JA011318

CrossRef Full Text | Google Scholar

7. López RA, Lazar M, Shaaban SM, Poedts S, Moya PS. Alternative high-plasma beta regimes of electron heat-flux instabilities in the solar wind. Astrophys J Lett. (2020) 900:L25. doi: 10.3847/2041-8213/abaf56

CrossRef Full Text | Google Scholar

8. Klimontovich YL. Physics of collisionless plasma. Physics-Uspekhi. (1997) 40:21. doi: 10.1070/PU1997v040n01ABEH000200

CrossRef Full Text | Google Scholar

9. Kasper JC, Lazarus AJ, Gary SP. Wind/SWE observations of firehose constraint on solar wind proton temperature anisotropy. Geophys Res Lett. (2002) 29:20–1–20-4. doi: 10.1029/2002GL015128

CrossRef Full Text | Google Scholar

10. Marsch E. Kinetic physics of the solar corona and solar wind. Living Rev Solar Phys. (2006) 3:1. doi: 10.12942/lrsp-2006-1

CrossRef Full Text | Google Scholar

11. Bale SD, Kasper JC, Howes GG, Quataert E, Salem C, Sundkvist D. Magnetic fluctuation power near proton temperature anisotropy instability thresholds in the solar wind. Phys Rev Lett. (2009) 103:211101. doi: 10.1103/PhysRevLett.103.211101

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Bruno R, Carbone V. The solar wind as a turbulence laboratory. Living Rev Solar Phys. (2013) 10:2. doi: 10.12942/lrsp-2013-2

CrossRef Full Text | Google Scholar

13. Heinemann M. Role of collisionless heat flux in magnetospheric convection. J Geophys Res Space Phys. (1999) 104:28397–410. doi: 10.1029/1999JA900401

CrossRef Full Text | Google Scholar

14. Matsumoto Y, Hoshino M. Turbulent mixing and transport of collisionless plasmas across a stratified velocity shear layer. J Geophys Res Space Phys. (2006) 111:A05213. doi: 10.1029/2004JA010988

CrossRef Full Text | Google Scholar

15. Espinoza CM, Stepanova M, Moya PS, Antonova EE, Valdivia JA. Ion and electron κ distribution functions along the plasma sheet. Geophys Res Lett. (2018) 45:6362–70. doi: 10.1029/2018GL078631

CrossRef Full Text | Google Scholar

16. Moya PS, Pinto VA, Viñas AF, Sibeck DG, Kurth WS, Hospodarsky GB, et al. Weak kinetic Alfvén waves turbulence during the 14 November 2012 geomagnetic storm: Van Allen Probes observations. J Geophys Res Space Phys. (2015) 120:5504–23. doi: 10.1002/2014JA020281

CrossRef Full Text | Google Scholar

17. Narita Y, Roberts OW, Vörös Z, Hoshino M. Transport ratios of the kinetic Alfvén mode in space plasmas. Front Phys. (2020) 8:166. doi: 10.3389/fphy.2020.00166

CrossRef Full Text | Google Scholar

18. Sahraoui F, Goldstein ML, Belmont G, Canu P, Rezeau L. Three dimensional anisotropic $k$ spectra of turbulence at subproton scales in the solar wind. Phys Rev Lett. (2010) 105:131101. doi: 10.1103/PhysRevLett.105.131101

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Horbury TS, Forman M, Oughton S. Anisotropic scaling of magnetohydrodynamic turbulence. Phys Rev Lett. (2008) 101:175005. doi: 10.1103/PhysRevLett.101.175005

CrossRef Full Text | Google Scholar

20. Chen CHK. Recent progress in astrophysical plasma turbulence from solar wind observations. J Plasma Phys. (2016) 82:535820602. 535820602. doi: 10.1017/S0022377816001124

CrossRef Full Text | Google Scholar

21. González CA, Parashar TN, Gomez D, Matthaeus WH, Dmitruk P. Turbulent electromagnetic fields at sub-proton scales: two-fluid and full-kinetic plasma simulations. Phys Plasmas. (2019) 26:012306. doi: 10.1063/1.5054110

CrossRef Full Text | Google Scholar

22. Cerri SS, Grošelj D, Franci L. Kinetic plasma turbulence: recent insights and open questions from 3D3V simulations. Front Astron Space Sci. (2019) 6:64. doi: 10.3389/fspas.2019.00064

CrossRef Full Text | Google Scholar

23. Howes GG, Cowley SC, Dorland W, Hammett GW, Quataert E, Schekochihin AA. A model of turbulence in magnetized plasmas: implications for the dissipation range in the solar wind. J Geophys Res Space Phys. (2008) 113:A05103. doi: 10.1029/2007JA012665

CrossRef Full Text | Google Scholar

24. Maneva Y, Viñas AF, Moya PS, Wicks RT, Poedts S. Dissipation of parallel and oblique Alfvén-cyclotron waves-Implications for heating of alpha particles in the solar wind. Astrophys J. (2015) 814:33. doi: 10.1088/0004-637X/814/1/33

CrossRef Full Text | Google Scholar

25. Sulem PL, Passot T. Landau fluid closures with nonlinear large-scale finite Larmor radius corrections for collisionless plasmas. J Plasma Phys. (2015) 81:325810103. doi: 10.1017/S0022377814000671

CrossRef Full Text | Google Scholar

26. Cerri SS, Califano F. Reconnection and small-scale fields in 2D-3V hybrid-kinetic driven turbulence simulations. New J Phys. (2017) 19:025007. doi: 10.1088/1367-2630/aa5c4a

CrossRef Full Text | Google Scholar

27. Franci L, Cerri SS, Califano F, Landi S, Papini E, Verdini A, et al. Magnetic reconnection as a driver for a sub-ion-scale cascade in plasma turbulence. Astrophys J. (2017) 850:L16. doi: 10.3847/2041-8213/aa93fb

CrossRef Full Text | Google Scholar

28. Loureiro NF, Boldyrev S. Collisionless reconnection in magnetohydrodynamic and kinetic turbulence. Astrophys J. (2017) 850:182. doi: 10.3847/1538-4357/aa9754

CrossRef Full Text | Google Scholar

29. Mallet A, Schekochihin AA, Chandran BDG. Disruption of Alfvénic turbulence by magnetic reconnection in a collisionless plasma. J Plasma Phys. (2017) 83:905830609. doi: 10.1017/S0022377817000812

CrossRef Full Text | Google Scholar

30. Papini E, Franci L, Landi S, Verdini A, Matteini L, Hellinger P. Can hall magnetohydrodynamics explain plasma turbulence at sub-ion scales? Astrophys J. (2019) 870:52. doi: 10.3847/1538-4357/aaf003

CrossRef Full Text | Google Scholar

31. Chen CHK, Leung L, Boldyrev S, Maruca BA, Bale SD. Ion-scale spectral break of solar wind turbulence at high and low beta. Geophys Res Lett. (2014) 41:8081–8. doi: 10.1002/2014GL062009

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Wang X, Tu CY, He JS, Wang LH. Ion-scale spectral break in the normal plasma beta range in the solar wind turbulence. J Geophys Res Space Phys. (2018) 123:68–75. doi: 10.1002/2017JA024813

CrossRef Full Text | Google Scholar

33. Franci L, Landi S, Matteini L, Verdini A, Hellinger P. Plasma beta dependence of the ion-scale spectral break of solar wind turbulence: high-resolution 2D hybrid simulations. Astrophys J. (2016) 833:91. doi: 10.3847/1538-4357/833/1/91

CrossRef Full Text | Google Scholar

34. Gamayunov KV, Engebretson MJ, Zhang M, Rassoul HK. Source of seed fluctuations for electromagnetic ion cyclotron waves in Earth's magnetosphere. Adv Space Res. (2015) 55:2573–83. doi: 10.1016/j.asr.2015.02.024

CrossRef Full Text | Google Scholar

35. Chaston CC, Bonnell JW, Wygant JR, Mozer F, Bale SD, Kersten K, et al. Observations of kinetic scale field line resonances. Geophys Res Lett. (2014) 41:209–15. doi: 10.1002/2013GL058507

CrossRef Full Text | Google Scholar

36. Alexandrova O, Carbone V, Veltri P, Sorriso–Valvo L. Small–scale energy cascade of the solar wind turbulence. Astrophys J. (2008) 674:1153–7. doi: 10.1086/524056

CrossRef Full Text | Google Scholar

37. Goldstein ML, Wicks RT, Perri S, Sahraoui F. Kinetic scale turbulence and dissipation in the solar wind: key observational results and future outlook. Phil Trans R Soc A. (2015) 373:20140147. doi: 10.1098/rsta.2014.0147

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Franci L, Sarto DD, Papini E, Giroul A, Stawarz JE, Burgess D, et al. Evidence of a “current-mediated” turbulent regime in space and astrophysical plasmas. arXiv. (2020) 2010.05048. Available online at: https://arxiv.org/abs/2010.05048

Google Scholar

39. Franci L, Landi S, Matteini L, Verdini A, Hellinger P. High-resolution hybrid simulations of kinetic plasma turbulence at proton scales. Astrophys J. (2015) 812:21. doi: 10.1088/0004-637X/812/1/21

CrossRef Full Text | Google Scholar

40. Matthaeus WH, Yang Y, Wan M, Parashar TN, Bandyopadhyay R, Chasapis A, et al. Pathways to dissipation in weakly collisional plasmas. Astrophys J. (2020) 891:101. doi: 10.3847/1538-4357/ab6d6a

CrossRef Full Text | Google Scholar

41. Viñas AF, Moya PS, Navarro RE, Valdivia JA, Araneda JA, Muñoz V. Electromagnetic fluctuations of the whistler cyclotron and firehose instabilities in a Maxwellian and Tsallis-kappa-like plasma. J Geophys Res. (2015) 120, 3307–17. doi: 10.1002/2014JA020554

CrossRef Full Text | Google Scholar

42. Yoon PH. Kinetic instabilities in the solar wind driven by temperature anisotropies. Rev Mod Plasma Phys. (2017) 1:4. doi: 10.1007/s41614-017-0006-1

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Weibel ES. Spontaneously growing transverse waves in a plasma due to an anisotropic velocity distribution. Phys Rev Lett. (1959) 2:83–4. doi: 10.1103/PhysRevLett.2.83

CrossRef Full Text | Google Scholar

44. Sagdeev R, Shafranov V. On the instability of a plasma with an anisotropic distribution of velocities in a magnetic field. J Exptl Theoret Phys (USSR). (1960) 29:181.

Google Scholar

45. Kennel CF, Petschek HE. Limit on stably trapped particle fluxes. J Geophys Res. (1966) 71:1–28. doi: 10.1029/JZ071i001p00001

CrossRef Full Text | Google Scholar

46. Viñas AF, Goldstein ML, Acuña MH. Spectral analysis of magnetohydrodynamic fluctuations near interplanetary shocks. J Geophys Res. (1984) 89:3762–74. doi: 10.1029/JA089iA06p03762

CrossRef Full Text | Google Scholar

47. Brinca AL, Tsurutani BT. Unusual characteristics of electromagnetic waves exited by cometary newborn ions with large perpendicular energies. Astron Astrophys. (1987) 187:311–9. doi: 10.1007/978-3-642-82971-0_57

CrossRef Full Text | Google Scholar

48. Yoon PH. Quasilinear evolution of Alfvén-ion-cyclotron and mirror instabilities driven by ion temperature anisotropy. Phys Fluids B. (1992) 4:3627–37. doi: 10.1063/1.860371

CrossRef Full Text | Google Scholar

49. Moya PS, Navarro R, Viñas AF, Muñoz V, Valdivia JA. Weak turbulence cascading effects in the acceleration and heating of ions in the solar wind. Astrophys J. (2014) 781:76. doi: 10.1088/0004-637X/781/2/76

CrossRef Full Text | Google Scholar

50. Hellinger P, Trávníček PM, Decyk VK, Schriver D. Oblique electron fire hose instability: particle-in-cell simulations. J Geophys Res. (2014) 119:59–68. doi: 10.1002/2013JA019227

CrossRef Full Text | Google Scholar

51. Adrian ML, Viñas AF, Moya PS, Wendel DE. Solar wind magnetic fluctuations and electron non-thermal temperature anisotropy: survey of wind-SWE-VEIS observations. Astrophys J. (2016) 833:49. doi: 10.3847/1538-4357/833/1/49

CrossRef Full Text | Google Scholar

52. Moya PS, Viñas AF, Muñoz V, Valdivia JA. Computational and theoretical study of the wave-particle interaction of protons and waves. Ann Geophys. (2012) 30:1361–9. doi: 10.5194/angeo-30-1361-2012

CrossRef Full Text | Google Scholar

53. Dasso S, Milano LJ, Matthaeus WH, Smith CW. Anisotropy in fast and slow solar wind fluctuations. Astrophys J. (2005) 635:L181–4. doi: 10.1086/499559

CrossRef Full Text | Google Scholar

54. Horbury TS, Forman MA, Oughton S. Spacecraft observations of solar wind turbulence: an overview. Plasma Phys Controll Fusion. (2005) 47:B703–17. doi: 10.1088/0741-3335/47/12B/S52

CrossRef Full Text | Google Scholar

55. Gomberoff L, Muñoz V, Valdivia JA. Ion cyclotron instability triggered by drifting minor ion species: Cascade effect and exact results. Planet Space Sci. (2004) 52:679–84. doi: 10.1016/j.pss.2004.01.004

CrossRef Full Text | Google Scholar

56. Navarro RE, Muñoz V, Valdivia JA, Moya PS. Feasibility of ion-cyclotron resonant heating in the solar wind. Astrophys J. (2020) 898:L9. doi: 10.3847/2041-8213/aba0ae

CrossRef Full Text | Google Scholar

57. Gary SP, Tokar RL. The second-order theory of electromagnetic hot ion beam instabilities. J Geophys Res. (1985) 90:65–72. doi: 10.1029/JA090iA01p00065

CrossRef Full Text | Google Scholar

58. Fried BD, Conte SD. The Plasma Dispersion Function. San Diego, CA: Academic (1961).

Google Scholar

59. Muller DE. A method for solving algebraic equations using an automatic computer. Math Tables Other Aids Comput. (1956) 10:208–15. doi: 10.2307/2001916

CrossRef Full Text | Google Scholar

60. Navarro RE, Moya PS, Muñoz V, Araneda JA, Viñas AF, Valdivia JA. Solar wind thermally induced magnetic fluctuations. Phys Rev Lett. (2014) 112:1–5. doi: 10.1103/PhysRevLett.112.245001

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Moya PS, Muñoz V, Rogan J, Valdivia JA. Study of the cascading effect during the acceleration and heating of ions in the solar wind. J Atmos Solar Terres Phys. (2011) 73:1390–7. doi: 10.1016/j.jastp.2011.01.009

CrossRef Full Text | Google Scholar

62. Jian LK, Moya PS, Viñas AF, Stevens M. Electromagnetic cyclotron waves in the solar wind: wind observation and wave dispersion analysis. AIP Conf Proc (Weihai). (2016) 1720:040007. doi: 10.1063/1.4943818

CrossRef Full Text | Google Scholar

63. Wicks RT, Alexander RL, Stevens M, III LBW, Moya PS, Viñas A, et al. A proton-cyclotron wave storm generated by unstable proton distribution functions in the solar wind. Astrophys J. (2016) 819:6. doi: 10.3847/0004-637X/819/1/6

CrossRef Full Text | Google Scholar

64. Krall NA, Trivelpiece AW. Principle of Plasma Physics. San Francisco Press Inc. (1986).

Google Scholar

65. Stix TH. Waves in Plasmas. American Institute of Physics (1992). Available online at: http://books.google.com/books?id=OsOWJ8iHpmMC

Google Scholar

66. Yoon PH, Seough JJ, Kim KH, Lee DH. Empirical versus exact numerical quasilinear analysis of electromagnetic instabilities driven by temperature anisotropy. J Plasma Phys. (2012) 78:47–54. doi: 10.1017/S0022377811000407

CrossRef Full Text | Google Scholar

67. Seough J, Yoon PH, Hwang J. Quasilinear theory and particle-in-cell simulation of proton cyclotron instability. Phys Plasmas. (2014) 21:062118. doi: 10.1063/1.4885359

CrossRef Full Text | Google Scholar

68. Seough J, Yoon PH, Hwang J. Simulation and quasilinear theory of proton firehose instability. Phys Plasmas. (2015) 22:012303. doi: 10.1063/1.4905230

CrossRef Full Text | Google Scholar

69. Galtier S, Bhattacharjee A. Anisotropic weak whistler wave turbulence in electron magnetohydrodynamics. Phys Plasmas. (2003) 10:3065–76. doi: 10.1063/1.1618648

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Gary SP, Smith CW. Short-wavelength turbulence in the solar wind: linear theory of whistler and kinetic Alfvén fluctuations. J Geophys Res Space Phys. (2009) 114:A12105. doi: 10.1029/2009JA014525

CrossRef Full Text | Google Scholar

71. Schekochihin AA, Cowley SC, Dorland W, Hammett GW, Howes GG, Quataert E, et al. Astrophysical gyrokinetics: kinetic and fluid turbulent cascades in magnetized weakly collisional plasmas. Astrophys J Suppl Ser. (2009) 182:310–77. doi: 10.1088/0067-0049/182/1/310

CrossRef Full Text | Google Scholar

72. Boldyrev S, Horaites K, Xia Q, Perez JC. Toward a theory of astrophysical plasma turbulence at subproton scales. Astrophys J. (2013) 777:41. doi: 10.1088/0004-637X/777/1/41

CrossRef Full Text | Google Scholar

73. Boldyrev S, Perez JC. Spectrum of kinetic-Alfvén turbulence. Astrophys J. (2012) 758:L44. doi: 10.1088/2041-8205/758/2/L44

CrossRef Full Text | Google Scholar

74. Arzamasskiy L, Kunz MW, Chandran BDG, Quataert E. Hybrid-kinetic simulations of ion heating in Alfvénic turbulence. Astrophys J. (2019) 879:53. doi: 10.3847/1538-4357/ab20cc

CrossRef Full Text | Google Scholar

75. Howes GG. A dynamical model of plasma turbulence in the solar wind. Phil Trans R Soc A. (2015) 373:20140145. doi: 10.1098/rsta.2014.0145

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Gaelzer R, Yoon PH, Kim S, Ziebell LF. On the dimensionally correct kinetic theory of turbulence for parallel propagation. Phys Plasmas. (2015) 22:032310. doi: 10.1063/1.4916054

CrossRef Full Text | Google Scholar

77. Kim S, Yoon PH, Choe GS. Spontaneous emission of electromagnetic and electrostatic fluctuations in magnetized plasmas: quasi-parallel modes. Phys Plasmas. (2016) 23:022111. doi: 10.1063/1.4941707

CrossRef Full Text | Google Scholar

78. Bowen TA, Bale SD, Bonnell JW, Dudok de Wit T, Goetz K, Goodrich K, et al. A merged search-coil and fluxgate magnetometer data product for parker solar probe FIELDS. J Geophys Res Space Phys. (2020) 125:e2020JA027813. doi: 10.1029/2020JA027813

CrossRef Full Text | Google Scholar

79. Hellinger P, Matteini L, Landi S, Verdini A, Franci L, Trávnícek PM. Plasma turbulence and kinetic instabilities at ion scales in the expanding solar wind. Astrophys J. (2015) 811:L32. doi: 10.1088/2041-8205/811/2/L32

CrossRef Full Text | Google Scholar

80. Yoon PH, Sarfraz M. Interplay of electron and proton instabilities in expanding solar wind. Astrophys J. (2017) 835:246. doi: 10.3847/1538-4357/835/2/246

CrossRef Full Text | Google Scholar

81. Yan H, Lazarian A. Cosmic ray transport through gyroresonance instability in compressible turbulence. Astrophys J. (2011) 731:35. doi: 10.1088/0004-637X/731/1/35

CrossRef Full Text | Google Scholar

82. Bruno R, Trenchi L, Telloni D. Spectral slope variation at proton scales from fast to slow solar wind. Astrophys J. (2014) 793:L15. doi: 10.1088/2041-8205/793/1/L15

CrossRef Full Text | Google Scholar

83. Martinović MM, Klein KG, Kasper JC, Case AW, Korreck KE, Larson D, et al. The enhancement of proton stochastic heating in the near-sun solar wind. Astrophys J Suppl Ser. (2020) 246:30. doi: 10.3847/1538-4365/ab527f

CrossRef Full Text | Google Scholar