- National Centre for Physics, Islamabad, Pakistan
The formation of nonlinear ion-acoustic waves is studied in a degenerate magnetoplasma accounting for quantized and trapped electrons. Relying on the reductive perturbation technique, a three-dimensional Zakharov–Kuznetsov (ZK) equation is derived, admitting a solitary wave solution with modified amplitude and width parameters. The stability of the ZK equation is also discussed using the k-expansion method. Subsequently, numerical analyses are carried out for plasma parameters of a dense stellar system involving white dwarf stars. It has been observed that the quantized magnetic field parameter η and degeneracy of electrons (determined by small temperature values T) affect the amplitude and width of the electric potential. The critical point at which the nature of the solitary structure changes from compressive to rarefaction is evaluated. Importantly, the growth rate of the instability associated with a three-dimensional ZK equation depends on the plasma parameters, and higher values of η and T tend to stabilize the solitons in quantized degenerate plasmas. The results of the present study may hold significance to comprehend the properties of wave propagation and instability growth in stellar and laboratory dense plasmas.
1 Introduction
Quantum plasmas have been the focus of interest in the past few decades for many researchers owing to their significance in astrophysical environments [1–3], ultracold plasmas [4], intense laser plasma interaction experiments [5], microelectronic devices [6], and micro plasmas [7]. In particular, quantum mechanical effects can be taken into account in plasmas when the thermal de Broglie wavelength is larger or equal to the interparticle distance. The dispersive properties of the electrostatic and electromagnetic waves with quantum effects become modified. These waves are usually described by the quantum hydrodynamic (QHD) model (which is considered as an extension of classical fluid model) only valid in the long wavelength limit, kλFe ≪ 1, as well as by the quantum magnetohydrodynamic (QMHD) model involving the magnetic field and electron spin-1/2 effects apart from the fluid MHD equations in plasmas [8–14].
In degenerate plasmas, the strong external magnetic field affects the motion of electrons in two different ways. First, through the intrinsic spin of electrons that produces the Pauli paramagnetism. Second, through the quantization of orbital motion of electrons that could lead to Landau quantization/Landau diamagnetism [15]. The latter is a pure quantum phenomenon without any classical analogy, and charged particles propagating along the magnetic field lines are usually unaffected from the influence of magnetic field. However, the external magnetic field may enhance the total energy of the system in the form of quantized energy levels due to diamagnetism and alters thermodynamic properties in dense magnetoplasmas. In this context, the linear and nonlinear electrostatic waves with quantization effects have attracted lots of attention of the plasma community. Specifically, Tsintsadze [16] discussed the thermodynamic quantities in the presence of a magnetic field and showed the impact of quantized electrons on the dispersion of longitudinal waves, identifying its novel branches with quantum corrections.
The electron trapping is a nonlinear phenomenon which arises from the wave potential in which the electrons are confined to a certain region of phase space. The potential field essentially provides the potential energy to the electrons, which may be equivalent to or greater than the kinetic energy of electrons. When the net energy of electrons becomes negative or equal to zero, that is, ϵ ≤ 0, the free movement of the electrons is restrained within a certain region and the condition is then termed as adiabatic trapping. Moreover, the electrons can be treated as free particles, provided the net energy should be positive, that is, ϵ > 0. Hence, the electron trapping phenomenon may affect the nonlinear dynamics of the waves and its propagation characteristics in degenerate dense plasmas. Bernstein et al. [17] were the first who determined the nonlinear stationary electrostatic structures accounting for trapped particles in plasmas by utilizing a kinetic model. It was shown that adding a suitable amount of trapped particles in the potential energy trough leads to traveling wave solutions. Later, Gurevich [18] identified a collisionless electron trapping for a nonstationary electric field and a distribution function for captured electrons to examine a slowly varying field as well as for a rapidly varying field. In 1996, the phenomenon of adiabatic electron trapping was verified by laboratory experiments [19] and numerical works [20] at the microscopic level in plasmas. Recently, numerous efforts [21–24] have been made to investigate nonlinear structures with applications to space and laboratory plasmas by taking into account the trapping effects.
Furthermore, Shah et al. [25] examined the effects of trapping and quantized magnetic field on the profiles of large-amplitude ion-acoustic waves (IAWs) in degenerate plasmas. Using the framework of the Sagdeev potential, they obtained both compressive and rarefaction solitons for different conditions of temperature and magnetic field. They also confirmed these coherent structures in fully and partially degenerate plasmas to account for quantized magnetic field. Later on, the ion-acoustic shocks accounting for trapping and Landau quantization parameters were investigated [26] in quantum dense magnetoplasmas showing the impact of Landau quantization on the height of shock profiles.
In literature, different waves and instabilities have been studied for different plasma compositions and orientations. One of the fundamental plasma modes is the IAW. In recent studies, the propagation characteristics of IAWs have been investigated both in classical [27, 28] and quantum plasmas [29]. In particular, Mandi et al. [33] have considered the dynamics of IAWs in Thomas–Fermi plasmas comprising electrons, positrons, and positive ions and accounted for the source term effect. They examined the impact of the positron concentration, the speed of space debris, and the strength of the source term on the profiles of periodic, quasiperiodic, and chaotic motions of IAWs. Quite recently, the nonlinear features of IAWs have been identified in space plasmas to exhibit chaotic structures, which can be exploited to design efficient algorithms for image encryption [34]. For small (but finite) amplitude IAWs, a Zakharov-Kuznetsov (ZK) equation (35) was first derived in a classical plasma taking hot isothermal electrons and cold ions in a uniform magnetic field. The ZK equation governs two- or three-dimensional modulation of the KdV equation and can only be obtained in magnetized plasmas. Mamun [36] considered a three-component magnetized dusty plasma and studied the properties of nonlinear structures and analyzed instability of these waves by utilizing the small-k perturbation expansion method. It was found that the growth rate of the unstable wave structures varies with the external magnetic field and the direction of propagation. Infeld and Rowlands [37] discussed the stability of ZK solitons in transverse direction using the direct k-method. The multi-dimensional instability of IAWs was further investigated in a degenerate magnetoplasma for the basic instability criterion, exploring the effects of the external magnetic field on solitary structures [38]. Quite recently, the instability growth rate with different plasma parameters has been analyzed [39] in collisionless magnetized multi-ion plasmas with Landau quantization and polarization effects.
In this study, we investigate the small-amplitude properties of IAWs in a degenerate quantum plasma to account for trapped electrons and the quantized magnetic field. Using the reductive perturbation technique, we derive a ZK equation, which admits a solitary solution and stability analysis in the presence of trapped electrons. The critical point at which the compressive solitary structures changes to rarefactive solitons has also been determined.
The layout of the article is as follows: Section 2 presents a mathematical model containing the fluid equations of classical ions and degenerate-trapped electrons through the density distribution for a quantized dense magnetoplasma. Within the framework of the reductive perturbation technique, a ZK equation and its solution are obtained in Sections 3 and 4, respectively. Section 5 presents the stability analysis of the ZK equation, and Section 6 deals with the results and discussion to understand nonlinear characteristics of IAWs in the environment of white dwarf stars. A brief summary of the work is also given in Section 7.
2 Mathematical Model for Quantized Magnetoplasmas
To study the formation and propagation of small-amplitude IAWs with trapping effects, we consider a uniform collisionless quantized magnetoplasma, whose constituents are the degenerate-trapped electrons and non-degenerate cold dynamical positive ions. Since quantum effects may account for lighter species, that is, electrons, the ion species are treated as classical because of their larger mass compared to electronic mass. Such a plasma is also subjected to an external magnetic field B0, which is directed along the z-axis. At equilibrium, the plasma holds the charge–neutrality condition ni0 ≃ ne0 = n0, where ni0 (ne0) is the equilibrium ion (electron) number density. The dynamics of IAWs in a degenerate-quantized magnetoplasma is governed by the following normalized three-dimensional ion-continuity, ion-momentum, and Poisson equations, respectively, as
and
where
The electrons can be considered as degenerate, Landau quantized, and trapped. In this context, we need to express the number density of the quantized electrons [15] which are trapped in the electric potential of ions. The quantized energy of the electrons within the potential well in a nonrelativistic limit is given by the following:
where the potential and cyclotron energies are, respectively, denoted by −eϕ and ℏωce; pz is the z-component of the electron momentum and l = 0, 1, 2, ‥ are the quantized Landau levels with
The occupation number of degenerate electrons can be expressed as
where μ is the chemical potential, pFe is the Fermi momentum, and
In obtaining Eq. 6, we have used
3 Evaluation of the Zakharov-Kuznetsov Equation
To study the propagation of small but finite amplitude IAWs in a three-dimensional quantized degenerate plasma, we utilize the well-known reductive perturbation technique (RPT) [40] with following space-time stretching coordinates:
where λ shows the normalized phase speed of the IAWs and ϵ (0 < ϵ < 1) is the dimensionless smallness parameter measuring the amplitude of perturbations. For simplicity, we drop out the tilda notation (∼) from the variables in Eqs (1)–(3) and expand the dependent variables, such as ni, ϕ, vX, vY, and vZ in terms of ϵ, respectively, as
where vX, vY, and vZ are the scalar components of the ion fluid velocity vi. It is important to mention here that many authors [41–44] have previously studied the trapped electrons using the framework of RPT and derived the modified Korteweg–de Vries (mKdV), modified Kadomstev–Petviashvili (mKP), and modified Zakharov-Kuznetsov (mZK) equations, where quadratic nonlinearity changes to 3/2−order nonlinearity. However, the present model not only includes the trapping electrons but also magnetic field quantization. In this context, the small potential limit [i.e., ϕ ≪ 1] is utilized to expand the normalized electron density from Eq. 6, as
where the expansion coefficients are defined as
Since the number density expansion does not include the ϕ3/2-order term, so the resultant contribution to nonlinearity in the ZK equation is quadratic instead of fractional. Now employing the stretchings and expansions [i.e., Eqs. (7)–(9)] into the governing Eqs. (1)–(3) along with (6), we may obtain the set of equations by collecting the various orders of ϵ. The lowest order terms in ϵ (i.e., ϵ3/2-order) lead to the following:
These first order perturbed quantities give rise to the linear phase speed of IAWs, given as
Collecting the next order terms of ϵ (i.e., ϵ2-order), we get the following:
Also, collecting the ϵ5/2-order, we readily obtain equations containing the second order–perturbed quantities in the form of first order–perturbed variables, as
After some algebraic manipulations, the set of Eqs. (11)–(13) can be solved to obtain the ZK equation, as
where
are the nonlinearity and dispersion coefficients. Note that these coefficients are significantly modified in a partially degenerate plasma by the Landau quantization affect.
4 Solitary Solution of the Zakharov-Kuznetsov Equation
The nonlinear partial differential equations (nPDEs) play a significant role in describing the physical phenomena. To find the exact solutions of nPDEs, different useful methods have been proposed in the literature. In particular, for solving the ZK equation, we may transform different independent variables to a single moving frame (single variable) as given below:
where U0 is the soliton speed and the direction cosines are represented by lX, lY, and lZ, respectively, along the X-, Y-, and Z-axes, such that
The new coefficients are now defined as A0 = PlZ and
This is a localized stationary solitary wave solution describing the formation and propagation of a nonlinear structure in a quantized degenerate plasma. This solution can only be obtained when nonlinearity and dispersion are balanced out. The amplitude and width of the soliton are given, respectively, by the following:
It may be noted that the solution (19) has almost the similar analytical form as that of the well-known solution of the KdV equation. The only difference is the argument on the sech-squared function that has been complicated, corresponding to oblique propagation of soliton with respect to the magnetic field.
5 Stability Analysis of the Zakharov-Kuznetsov Equation
In a three-dimensional plasma, the solitary wave becomes unstable due to transverse perturbations. The stability of such solitary wave solution can be investigated by using variety of methods, including the linear variation-of-action method [45], the k-expansion method [46], and the direct stability analysis method [47, 48]. In this model, we carry out the stability analysis for the solitary waves in the presence of trapped electrons and Landau quantization by using the k-expansion method [37]. Thus, we first reduce the ZK equation (15) to its canonical form by making it identical to Equations (8), (6), and (1) of Ref. [37] and transform the normalized parameters, as
Then the ZK Equation 15 can be expressed as
where
with ∇2 = ∂2/∂ρ′2 + ∂2/∂χ′2, while ϕ0, L⊥ and τ0 are defined, respectively, as
The stationary solution of the canonical equation (23) is as follows:
To check the stability, we consider the following solution:
where λ is the instability growth rate when Re(λ) ≠ 0 and k is the expansion constant. Substituting the solution in Eq. 23 and linearizing the resulting equation we obtain the following:
We can expand g(ξ) and λ in terms of k, as
Using the k-expansions from Eq. 28 into Eq. 27, we obtain equations in terms of various k−orders. For the lowest order, we have the following:
Substituting f0 from Eq. 25 into Eq. 23 and differentiating give
By comparing the above two equations, the value of g0(ζ) is then obtained as
The bounded solution g1(ζ) is obtained from the next order, as g1(ζ) = −3λ1 (sec h2ζ − ζ sec h2ζ tanh ζ), and for the next order
For solving this equation, the kernal of the left hand side with f0 must be zero, that is,
which results into the following:
Solving these integrals, we get
The growth rate given by Eq. 28 can be written as
Here L∥ is arbitrary. The result (36) shows that the growth rate is dependent on the plasma parameters of the system under consideration through the dispersion coefficients Q and R. The k-expansion method can be further used to find the second and higher order growth rate instabilities.
6 Results and Discussion
For numerical evaluation, we need to identify quantum parameters and scales for a quantized nonrelativistic degenerate plasma, which is characterized by strong magnetic fields. We also focus on the region of application involving the compact stellar objects, such as white dwarf stars, neutron stars, and magnetars. These objects are highly dense, degenerate, and magnetized systems, where plasma number density is taken up to the order of 1032cm−3 for white dwarf stars and 1036cm−3 or even more for neutron stars [49, 50]. The typical values of densities and magnetic fields used in the present model are 1026cm−3–1032cm−3 and 109G − 1012G, respectively. The temperature of the system is typically found of the order of 106K, whereas electron Fermi (TFe) and ion Fermi (TFi) temperatures are estimated to be 0.904 × 107K and 4.92 × 103K, respectively, for densities ne0 ≃ ni0 = n0 ≡ 1026cm−3. Note that electrons behave as degenerate species under the condition TFe > T, while ions as classical non-degenerate species for TFi < T. One can also confirm that electrons remain in nonrelativistic regime as long as the Fermi energy
For the quantum fluid model, the electron Fermi length (λFe) should be greater than the interparticle distance (d), which can be approximated by the Wigner–Seitz radius, as
Figure 1A displays the variation of normalized electric potential perturbation ϕ1 [given by Eq. 19] by changing the quantization parameter η in a fully degenerate plasma (T = 0). The curves represent the small-amplitude ion-acoustic compressive solitons that are formed and affected by the parameters of dense white dwarf stars. It is found that as the parameter η increases, the amplitude and width of the electric potential also increase. The percentage increase of the maximum amplitude of soliton for the change of the values of η from 0.1 to 0.6 can thus be estimated from Figure 1A as
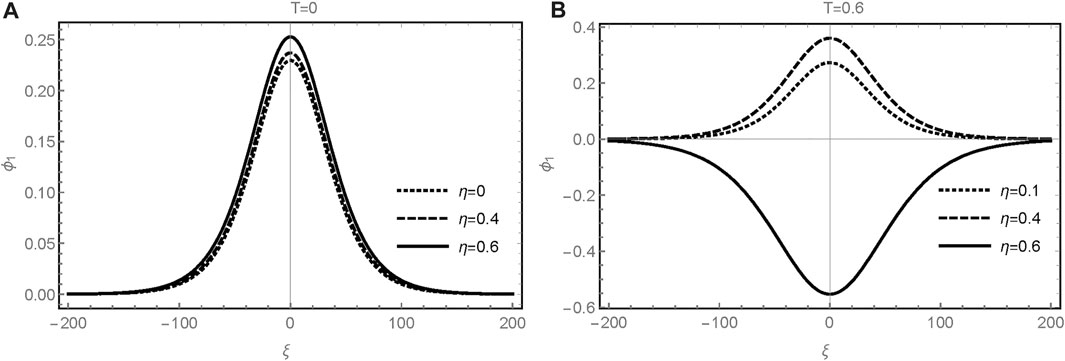
FIGURE 1. Electric potential ϕ1 (ξ, τ) of the ion-acoustic solitons is plotted across the quantized magnetic field parameter η for (A): completely degenerate plasma (T =0) and (B): partially degenerate plasma (T = 0.6). Here lZ = 0.8,
Figure 2A illustrates how the normalized electric potential perturbations ϕ1 (as function of spatial distance ξ) alter with variation of temperature when the quantizing magnetic field parameter is turned off (η = 0). Note that the amplitudes of the electric potential are significantly modified with increasing the temperature in a partially degenerate plasma. Thus, the percentage increase for the maxima of amplitude of solitary wave occurs when the temperature T changes from 0.1 to 0.6, which can be given as
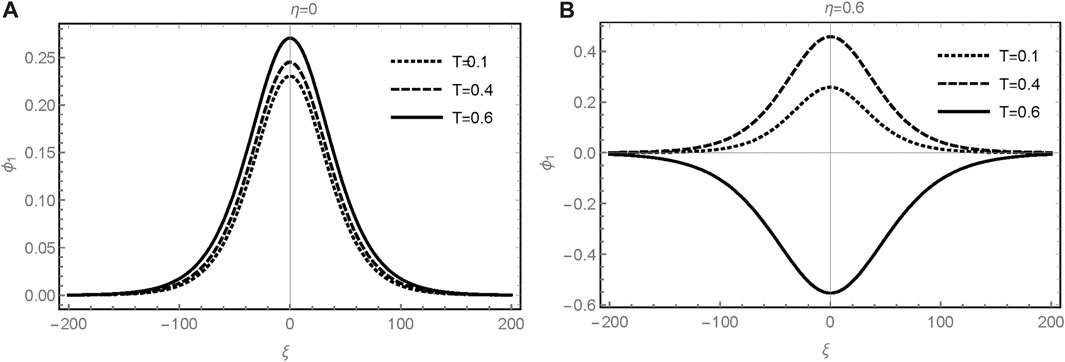
FIGURE 2. Electric potential ϕ1 (ξ, τ) of the ion-acoustic solitons is plotted across the temperature T in (A): absence of quantized magnetic field (η = 0) and (B): quantized magnetic field (η = 0.6). Here lZ = 0.8,
The nature of soliton strongly depends on the nonlinearity coefficient (P). If P = 0, then Eq. 16 reduces to
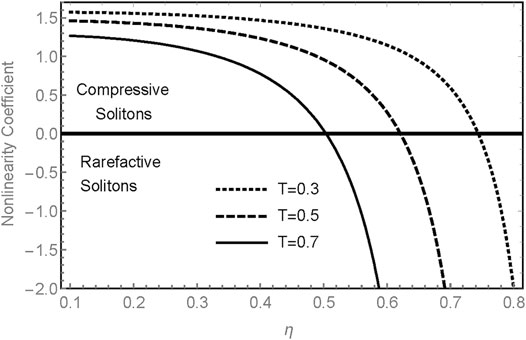
FIGURE 3. Nonlinearity coefficient P is plotted across the quantized magnetic field parameter η for different values of temperature T.
To investigate the stability of three-dimensional ion-acoustic soliton using Eq. 36, we show the growth rate numerically in Figure 4. It can be seen from Figure 4A that the growth rate instability not only reduces with increasing value of quantizing magnetic field but also decreases with increasing temperature effect. Figure 4B confirms that the variation of the parameter Ω causes a reduction in the magnitude of the growth rate. These figures determine that ZK solitons become more stable by increasing parameters such as η, T, and Ω.
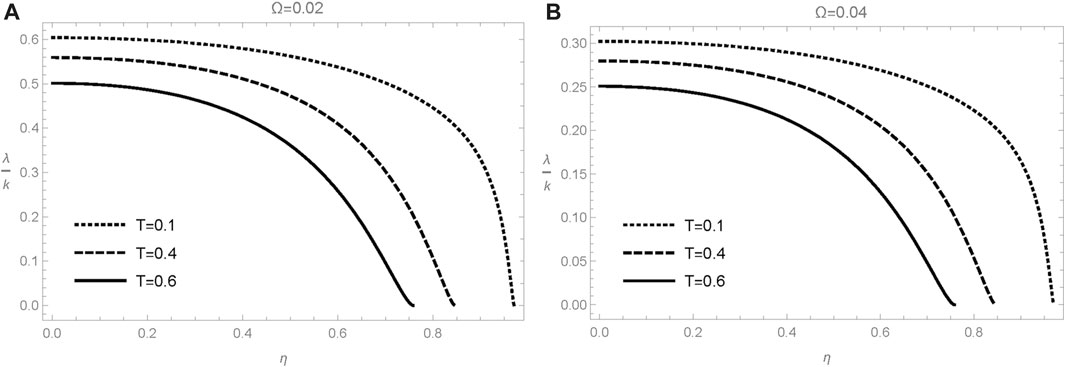
FIGURE 4. First order growth rate of the instability with arbitrary k (i.e., λ/k) is plotted across the quantized magnetic field parameter η for L∥ = 0.2.
7 Summary
We have investigated the propagation characteristics of the ion-acoustic solitary waves in a three-dimensional dense magnetoplasma consisting of cold non-degenerate ions and degenerate quantized trapped electrons. The ZK equation has been derived using the reductive perturbation technique, admitting solitary solution. The parametric analysis has been carried out using the plasma parameters involving the dense stellar system of white dwarf stars. It has been found that augmenting the temperature (which determines the degeneracy) and the quantized magnetic field parameter enhance the amplitudes of electric potential perturbations. Furthermore, the critical point at which the solitary structures change their nature has been determined and analyzed. The critical point arises from the complex nature of plasma and the interplay of degeneracy and quantized magnetic field. The stability analysis of the ZK equation in the presence of trapped quantized electrons has been carried out using the framework of the k-expansion method. The parametric investigations show that the growth rate of the instability varies with the quantizing parameter (η) and temperature (T) effects. Therefore, the higher values of η and T stabilize the ZK solitons in three-dimensional quantized dense plasmas. The present results may hold significance to comprehend the properties of wave propagation and instability growth in stellar and laboratory dense plasmas.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Jung Y-D. Quantum-mechanical Effects on Electron-Electron Scattering in Dense High-Temperature Plasmas. Phys Plasmas (2001) 8:3842–4. doi:10.1063/1.1386430
2. Hossen MA, Hossen MR, Mamun AA. Modified Ion-Acoustic Shock Waves and Double Layers in a Degenerate Electron-Positron-Ion Plasma in Presence of Heavy Negative Ions. Braz J Phys (2014) 44:703–10. doi:10.1007/s13538-014-0267-x
3. Atteya A, Behery EE, El-Taibany WF. Ion Acoustic Shock Waves in a Degenerate Relativistic Plasma with Nuclei of Heavy Elements. Eur Phys J Plus (2017) 132(1–8):109. doi:10.1140/epjp/i2017-11367-2
5. Marklund M, Shukla PK. Nonlinear Collective Effects in Photon-Photon and Photon-Plasma Interactions. Rev Mod Phys (2006) 78:591–640. doi:10.1103/RevModPhys.78.591
6. Becker K, Koutsospyros A, Yin S-M, Christodoulatos C, Abramzon N, Joaquin JC, et al. Environmental and Biological Applications of Microplasmas. Plasma Phys Control Fusion (2005) 47:B513–B523. doi:10.1088/0741-3335/47/12B/S37
8. Manfredi G. How to Model Quantum Plasmas. Fields Inst Commun (2005) 46:263–87. doi:10.1090/fic/046/10
9. Brodin G, Marklund M. Spin Magnetohydrodynamics. New J Phys (2007) 9:277. doi:10.1088/1367-2630/9/8/277
10. Masood W, Eliasson B, Shukla PK. Electromagnetic Wave Equations for Relativistically Degenerate Quantum Magnetoplasmas. Phys Rev E (2010) 81:066401. doi:10.1103/PHYSREVE.81.066401
11. Shukla PK, Eliasson B. Nonlinear Aspects of Quantum Plasma Physics. Phys Usp (2010) 53:51–76. doi:10.3367/UFNe.0180.201001b.0055
12. Bonitz M, Moldabekov ZA, Ramazanov TS. Quantum Hydrodynamics for plasmas-Quo Vadis? Phys Plasmas (2019) 26:090601. doi:10.1063/1.5097885
13. Sahu B, Sinha A, Roychoudhury R. Ion-acoustic Waves in Dense Magneto-Rotating Quantum Plasma. Phys Plasmas (2019) 26:072119. doi:10.1063/1.5082868
14. Haas F. Kinetic Theory Derivation of Exchange-Correlation in Quantum Plasma Hydrodynamics. Plasma Phys Control Fusion (2019) 61:044001. doi:10.1088/1361-6587/aaffe1
16. Tsintsadze LN, Eliasson B, Shukla PK. Quantization and Excitation of Longitudinal Electrostatic Waves in Magnetized Quantum Plasmas. AIP Conf Proc (2010) 1306:89–102. doi:10.1063/1.3533197
17. Bernstein IB, Greene JM, Kruskal MD. Exact Nonlinear Plasma Oscillations. Phys Rev (1957) 108:546–50. doi:10.1103/PhysRev.108.546
18. Gurevich AV. Distribution of Captured Particles in a Potential Well in the Absence of Collisions. Sov Phys JETP (1968) 26:575–80.
20. Erokhin NS, Zolnikova NN, Mikhailovskaya LA. Asymptotic Theory of the Nonlinear Interaction between a Whistler and Trapped Electrons in a Nonuniform Magnetic Field. Plasma Phys Rep (1996) 22:125–36. doi:10.1134/1.952264
21. Mushtaq A, Shah HA. Study of Non-maxwellian Trapped Electrons by Using Generalized (R,q) Distribution Function and Their Effects on the Dynamics of Ion Acoustic Solitary Wave. Phys Plasmas (2006) 13:012303. doi:10.1063/1.2154639
22. Shah HA, Qureshi MNS, Tsintsadze N. Effect of Trapping in Degenerate Quantum Plasmas. Phys Plasmas (2010) 17:032312. doi:10.1063/1.3368831
23. Aziz T, Masood W, Qureshi MNS, Shah HA, Yoon PH. Linear and Nonlinear Coupling of Electromagnetic and Electrostatic Fluctuations with One Dimensional Trapping of Electrons Using Product Bi (R,q) Distribution. Phys Plasmas (2016) 23:062307. doi:10.1063/1.4953428
24. Irfan M, Ali S, Mirza AM. Solitary Waves in a Degenerate Relativistic Plasma with Ionic Pressure Anisotropy and Electron Trapping Effects. Phys Plasmas (2017) 24:052108. doi:10.1063/1.4981932
25. Shah HA, Iqbal MJ, Tsintsadze N, Masood W, Qureshi MNS. Effect of Trapping in a Degenerate Plasma in the Presence of a Quantizing Magnetic Field. Phys Plasmas (2012) 19:092304. doi:10.1063/1.4752416
26. Hussain S, Ur-Rehman H, Mahmood S. The Effect of Magnetic Field Quantization on the Propagation of Shock Waves in Quantum Plasmas. Phys Plasmas (2019) 26:052105. doi:10.1063/1.5090181
27. Roy K, Misra AP, Chatterjee P. Ion-acoustic Shocks in Quantum Electron-Positron-Ion Plasmas. Phys Plasmas (2008) 15:032310. doi:10.1063/1.2896231
28. Tamang J, Saha A. Dynamical Properties of Nonlinear Ion-Acoustic Waves Based on the Nonlinear Schrödinger Equation in a Multi-Pair Nonextensive Plasma. Naturforsch (2020) 75(8):687–97. doi:10.1515/zna-2020-0018)
29. Haas F, Garcia LG, Goedert J, Manfredi G. Quantum Ion-Acoustic Waves. Phys Plasmas (2003) 10:3858–66. doi:10.1063/1.1609446
30. Ali S, Moslem WM, Shukla PK, Schlickeiser R. Linear and Nonlinear Ion-Acoustic Waves in an Unmagnetized Electron-Positron-Ion Quantum Plasma. Phys Plasmas (2007) 14:082307. doi:10.1063/1.2750649
33. Mandi L, Saha A, Chatterjee P. Dynamics of Ion-Acoustic Waves in Thomas-Fermi Plasmas with Source Term. Adv Space Res (2019) 64:427–35. doi:10.1016/j.asr.2019.04.028
34. Tamang J, Dieu Nkapkop JD, Ijaz MF, Prasad PK, Tsafack N, Saha A, et al. Dynamical Properties of Ion-Acoustic Waves in Space Plasma and its Application to Image Encryption. IEEE Access (2021) 9:18762–82. doi:10.1109/access.2021.3054250
36. Mamun AA. Instability of Obliquely Propagating Electrostatic Solitary Waves in a Magnetized Nonthermal Dusty Plasma. Phys Scr (1998) 58:505–9. doi:10.1088/0031-8949/58/5/014
37. Infeld E, Rowlands G. Nonlinear Waves, Solitons and Chaos. 2nd ed. Cambridge University Press (2000).
38. Haider MM, Mamun AA. Ion-acoustic Solitary Waves and Their Multi-Dimensional Instability in a Magnetized Degenerate Plasma. Phys Plasmas (2012) 19:102105. doi:10.1063/1.4757218
39. Zedan NA, Atteya A, El-Taibany WF, El-Labany SK. Stability of Ion-Acoustic Solitons in a Multi-Ion Degenerate Plasma with the Effects of Trapping and Polarization under the Influence of Quantizing Magnetic Field. Waves in Random and Complex Media (2020) 1–15. doi:10.1080/17455030.2020.1798560
40. Washimi H, Taniuti T. Propagation of Ion-Acoustic Solitary Waves of Small Amplitude. Phys Rev Lett (1966) 17:996–8. doi:10.1103/PhysRevLett.17.996
41. Alinejad H. Non-linear Localized Ion-Acoustic Waves in Electron-Positron-Ion Plasmas with Trapped and Non-thermal Electrons. Astrophys Space Sci (2010) 325:209–15. doi:10.1007/s10509-009-0177-5
42. Haider MM, Ferdous T, Duha SS. Instability Due to Trapped Electrons in Magnetized Multi-Ion Dusty Plasmas. J Theor Appl Phys (2015) 9:159–66. doi:10.1007/s40094-015-0174-8
43. Hafez MG, Roy NC, Talukder MR, Hossain Ali M. Effects of Trapped Electrons on the Oblique Propagation of Ion Acoustic Solitary Waves in Electron-Positron-Ion Plasmas. Phys Plasmas (2016) 23:082904. doi:10.1063/1.4961960
44. Masood W, Hamid N, Ilyas I, Siddiq M. Nonlinear Dissipative and Dispersive Electrostatic Structures in Unmagnetized Relativistic Electron-Ion Plasma with Warm Ions and Trapped Electrons. Phys Plasmas (2017) 24:062308. doi:10.1063/1.4985316
45. Bettinson DC, Rowlands G. Transverse Stability of Plane Solitons Using the Variational Method. J Plasma Phys (1998) 59:543–54. doi:10.1017/S0022377898006448
46. Allen MA, Rowlands G. Stability of Obliquely Propagating Plane Solitons of the Zakharov-Kuznetsov Equation. J Plasma Phys (1995) 53:63–73. doi:10.1017/S002237780001802X
47. Frycz P, Infeld E. Self-focusing of Nonlinear Ion-Acoustic Waves and Solitons in Magnetized Plasmas. Part 3. Arbitrary-Angle Perturbations, Period Doubling of Waves. J Plasma Phys (1989) 41:441–6. doi:10.1017/S0022377800013994
48. Das KP, Verheest F. Ion-acoustic Solitons in Magnetized Multi-Component Plasmas Including Negative Ions. J Plasma Phys (1989) 41:139–55. doi:10.1017/S0022377800013726
49. Padmanabhan T. Theoretical Astrophysics, Volume II: Stars and Stellar Systems. London: Cambridge University Press (2001).
Keywords: ion acoustic wave, instability analysis, Landau quantization, electron trapping, Degenerate plasma, white dwarfs
Citation: Jahangir R and Ali S (2021) Nonlinear Ion-Acoustic Waves in Degenerate Plasma with Landau Quantized Trapped Electrons. Front. Phys. 9:622820. doi: 10.3389/fphy.2021.622820
Received: 10 November 2020; Accepted: 26 July 2021;
Published: 13 September 2021.
Edited by:
Luca Sorriso-Valvo, Institute for Space Physics (Uppsala), SwedenReviewed by:
Prasanta Chatterjee, Visva-Bharati University, IndiaAta ur Rahman, Islamia College University, Pakistan
Copyright © 2021 Jahangir and Ali. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: R. Jahangir, cmFiaWFqQG5jcC5lZHUucGs=
 R. Jahangir
R. Jahangir S. Ali
S. Ali