
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Phys. , 27 September 2021
Sec. Statistical and Computational Physics
Volume 9 - 2021 | https://doi.org/10.3389/fphy.2021.599767
This article is part of the Research Topic Peregrine Soliton and Breathers in Wave Physics: Achievements and Perspectives View all 25 articles
This article discusses a limiting behavior of breather solutions of the focusing nonlinear Schrödinger equation. These breathers belong to the family of solitons on a non-vanishing and constant background, where the continuous-wave envelope serves as a pedestal. The rational Peregrine soliton acts as a limiting behavior of the other two breather solitons, i.e., the Kuznetsov-Ma breather and Akhmediev soliton. Albeit with a phase shift, the latter becomes a nonlinear extension of the homoclinic orbit waveform corresponding to an unstable mode in the modulational instability phenomenon. All breathers are prototypes for rogue waves in nonlinear and dispersive media. We present a rigorous proof using the ϵ-δ argument and show the corresponding visualization for this limiting behavior.
Although the study of wave phenomena traces its history back to the time of Pythagoras, research on nonlinear and rogue waves has attracted great scientific interest recently, both theoretically and experimentally. In particular, the focusing nonlinear Schrödinger (NLS) equation and its exact analytical solutions that belong to the family of soliton on constant background have been adopted as models and prototypes for rogue wave phenomena. The purpose of this article is to provide an overview of the relationship between these soliton solutions in this context. It also fills the gap in the details of limiting behavior. While the connection is well-known, the rigorous proof seems to be absent, and the visualizations found in the literature are incomplete. We will present this connection of the limiting behavior both analytically and visually. This introduction section covers a brief history of the NLS equation, exact solutions of the NLS equation, and a literature review on rogue waves.
The NLS equation is a nonlinear evolution equation that models slowly varying envelope dynamics of a weakly nonlinear quasi-monochromatic wave packet in dispersive media. The model has an infinite set of conservation laws and belongs to a completely integrable system of nonlinear partial differential equations. It has a wide range of applications in various physical settings, such as surface water waves, nonlinear optics, plasma physics, superconductivity, and Bose-Einstein condensates (BEC) [1–8].
Among early derivations of the NLS equation were found in nonlinear optics [9, 10], plasma physics [11–15], and hydrodynamics [16–18]. In BEC, the NLS equation with the non-zero potential term is known as the Gross-Pitaevskii equation [19, 20]. In superconductivity, the time-independent NLS equation resembles some similarities with a simplified
There are various techniques to derive analytical solutions of the NLS equation, among others, are the phase-amplitude algebraic ansatz [27–30], the Hirota method [31–34], nonlinear Fourier transform of inverse scattering transform (IST) [6, 35–40], symmetry reduction methods [41], variational formulation and displaced phase-amplitude equations [42–44]. Another derivation using IST with asymmetric boundary conditions is given in [45].
Throughout this article, we adopt the following
Usually, the variables x and t denote the space and time variables, respectively. The simplest-solution is called the “plane-wave” or “continuous-wave” solution:
We focus our discussion on the family of exact solutions with constant and non-vanishing background, also called “breather soliton solutions” [46]. There are three types of breather, and all of them are considered as weakly nonlinear prototypes for freak waves. Other solutions of the NLS equation include cnoidal wave envelopes that can be expressed in terms of the Jacobi elliptic functions and can be derived using the Hirota bilinear transformation, theta functions, or with some clever algebraic ansatz [30, 47].
In this subsection, the coverage follows the historical order of the time when the breathers were found. Furthermore, the term “breather” and “soliton” can be used interchangeably in this article, and they can also appear as a single term “breather soliton”. All of them refer to the same object, i.e., the exact analytical solutions of the NLS equation with a non-vanishing, constant pedestal, or background of continuous-wave solution.
The first found solution is called the “Kuznetsov-Ma breather”, where Kuznetsov derived it for the first time in the 1970s [48]. The original Russian version of his paper was published as a preprint in 1976 by the Institute of Automation and Electrometry of the Siberian Branch of the USSR (now Russian) Academy of Sciences in Novosibirsk. This preprint was then reproduced in English and appeared in the Proceedings of the 13th International Conference on Phenomena in ionized Gases and Plasma, held in East Berlin, German Democratic Republic, on 12–17 September 1977 [49].
Although some authors stated that Kawata and Inoue, as well as Ma, also derived this solution independently, understanding the history behind its development might change our perspective [50, 51]. Between 1976 and 1977, Evgenii A. Kuznetsov met Tutomu Kawata (also spelled Tsutomu, 川田 勉) many times because the latter was a postdoctoral researcher in the Landau Institute for Theoretical Physics in Chernogolovka, near Moscow, under the mentorship of Professor Vladimir E. Zakharov. Kuznetsov personally gave Kawata his preprint on the soliton solution of the NLS equation. Furthermore, although Yan-Chow Ma has never really met with Kuznetsov, Ma was surely aware of Kuznetsov’s paper. In his work [51], Ma has cited another Kuznetsov’s paper that was written together with Alexander V. Mikhailov on the stability of stationary waves using the Korteweg-de Vries (KdV) equation [49, 52].
Although the term “Kuznetsov-Ma soliton” has been introduced earlier [53], we will adopt and use the terminology “Kuznetsov-Ma breather” throughout this article. When the breather dynamics were observed experimentally for the first time in optical fibers by Kibler and collaborators, this term is getting popular since then [54]. We denote it as
where
A minor typographical error found in Kawata and Inoue’s paper [50] has been corrected by Gagnon [56]. Kawata and Inoue [50], as well as Ma [51], derived the Kuznetsov-Ma breather solution using the IST for finite boundary conditions at
Defining the amplitude amplification factor (AF) as the quotient of the maximum breather amplitude and the value of its background [43], we obtain that the amplitude amplification for the Kuznetsov-Ma breather is always larger than the factor of three, and it is explicitly given by
The function is bounded below and is increasing as the parameter μ also increases. The plot of this AF can be found in [43, 44], and different expressions of the AF for this breather also appear in [59–62].
The Kuznetsov-Ma breather finds applications as a rogue wave prototype in nonlinear optics [30, 54, 63] and deep-water gravity waves [38, 39, 61, 64]. A numerical comparison of the Kuznetsov-Ma breather indicated that a qualitative agreement was reached in the central part of the corresponding wave packet and on the real face of the modulation [59]. The stability analysis of the Kuznetsov-Ma breather using a perturbation theory based on the IST verified that although the soliton is rather robust with respect to dispersive perturbations, damping terms strongly influence its dynamics [65].
The dynamics of the Kuznetsov-Ma breather in a microfabricated optomechanical array showed an excellent agreement between theory and numerical calculations [66]. The spectral stability analysis of this breather has been considered using the Floquet theory [67]. The mechanism of the Kuznetsov-Ma breather has been discussed and two distinctive mechanisms are paramount: modulational instability and the interference effects between the continuous-wave background and bright soliton [68]. New scenarios of rogue wave formation for artificially prepared initial conditions using the Kuznetsov-Ma and superregular breathers in small localized condensate perturbations are demonstrated numerically by solving the Zakharov-Shabat eigenvalue problem [69].
A higher-order Kuznetsov-Ma breather can be derived using the Hirota method and utilized in studying soliton propagation with an influence of small plane-wave background [70, 71]; or using the bilinear method [72].
The second one is called the Akhmediev-Eleonskiĭ-Kulagin breather and was found in the 1980s [27–29]. In short, we simply call it the “Akhmediev soliton” and denote it as
Here, the parameter ν,
The amplitude amplification for the Akhmediev soliton is at most of the factor of three, and it is explicitly given by
This function is bounded above and below,
The Akhmediev soliton is rather well-known due to its characteristics being a nonlinear extension of linear modulational instability. This instability is also known as sideband (or Bespalov-Talanov) instability in nonlinear optics [82–84], or Benjamin-Feir instability in water waves [17, 85]. Some authors studied the modulational instability in plasma physics [11, 86–88] and in BEC [89–94]. Modulational instability is defined as the temporal growth of the continuous-wave NLS solution due to a small, side-band modulation, in a monochromatic wave train. A geometric condition for wave instability in deep water waves is given in [95] and for a historical review of modulational instability, see [96].
It has been shown numerically and experimentally that the modulated unstable wave trains grow to a maximum limit and then subside. In the spectral domain, the wave energy is transferred from the central frequency to its sidebands during the wave propagation for a certain period, and then it is recollected back to the primary frequency mode [97–101]. It turns out that the long-time evolution of these unstable wave trains leads to a sequence of modulation and demodulation cycles, known as the Fermi-Pasta-Ulam-Tsingou (FPUT) recurrence phenomenon [102, 103]. Although the FPUT recurrence using the NLS model has been observed experimentally in surface gravity waves in the late 1970s [98], it took more than 2 decades for the phenomenon to be successfully recovered in nonlinear optics [104].
Since the modulational instability extends nonlinearly to the Akhmediev soliton, it is no surprise that the former is considered as a possible mechanism for the generation of rogue waves while the latter acts as one prototype [105–107]. For wave trains with amplitude and phase modulation, there is a competition between the nonlinearity and dispersive factors. After the modulational instability occurs, the growth predicted by linear theory is exponential, and the nonlinear effect in the form of the Akhmediev soliton takes over before the wave trains return to the stage similar to the initial profiles with a phase-shift difference [64, 108]. On the other hand, Biondini and Fagerstrom argued that the major cause of modulational instability in the NLS equation is not the breather soliton solutions per se, but the existence of perturbations where discrete spectra are absence [109].
Experimental attempts on deterministic rogue wave generation using the Akhmediev solitons suggested that the symmetric structure is not preserved and the wave spectrum experiences frequency downshift even though wavefront dislocation and phase singularity are visible [43, 110–114]. A numerical calculation of rogue wave composition can be described in the form of the collision of Akhmediev breathers [115]. Another comparison of the Akhmediev breathers with the North Sea Draupner New Year and the Sea of Japan Yura wave signals also show some qualitative agreement [116]. The characteristics of the Akhmediev solitons have also been observed experimentally in nonlinear optics [117].
A theoretical, numerical, and experimental report of higher-order modulational instability indicates that a relatively low-frequency modulation on a plane-wave induces pulse splitting at different phases of evolution [118]. Second-order breathers composed of nonlinear combinations of the Kuznetsov-Ma breather and Akhmediev soliton reveal the dependence of the wave envelope on the degenerate eigenvalues and differential shifts [119]. Similar higher-order Akhmediev solitons visualized in [118, 119] have been featured earlier in [43, 120] and similar illustrations can also be found in [60, 121–127].
The third one is called the “Peregrine soliton”, also known as the “rational solution” [128]. This soliton is localized in both spatial and temporal variables
This solution is neither a traveling wave nor contains free parameters. Johnson called it a “rational-cum-oscillatory solution” [129]. Others referred to it as the “isolated Ma soliton” [130], an “explode-decay solitary wave” [131], the “rational growing-and-decaying mode” [71], the “algebraic breather” [132], or the “fundamental rogue wave solution” [124].
The amplitude amplification for the Peregrine soliton is exactly of factor three, and this can be obtained by taking the limit of the parameters toward zero in the previous two breathers:
Although the other two breather solitons are also proposed as rogue wave prototypes, some authors argued that the Peregrine soliton is the most likely freak wave event due to its appearance from nowhere and disappearance without a trace [79] as well as its closeness to all initial supercritical humps of small uniform envelope amplitude [133]. Some numerical and experimental studies may support this reasoning.
Henderson et al. studied numerically unsteady surface gravity wave modulations by comparing the fully nonlinear and NLS equations [130]. For steep-waves, their computations produced striking similarities with the Peregrine soliton. On the other hand, Voronovich et al. confirmed numerically that the bottom friction effect, even when it is small in comparison to the nonlinear term, could hamper the formation of a breather freak wave at the nonlinear stage of instability [134]. Investigations on linear stability demonstrated that the Peregrine soliton is unstable against all standard perturbations, where the analytical study is supported by numerical evidence [135–138].
An important breakthrough in the study of rogue waves is the observation of the Peregrine soliton in nonlinear media. In nonlinear optics, the existence of strongly localized temporal and spatial peaks on a non-vanishing background, which indicates near-ideal Peregrine soliton characteristics, was successfully implemented for the first time in optical fiber generating femtosecond pulses in 2010 [139]. Not long after that, the Peregrine soliton was also observed experimentally for the first time in a water wave tank [140]. A comparison between the predictions from the theoretical model and the measurement results exhibits an excellent qualitative agreement in terms of wave signal pattern, its amplification factor, and its symmetric structure. Another successful experimental observation of the Peregrine solitons is reported in ion-acoustic waves of a multicomponent plasma with negative ions when the density of negative ions is equal to the critical value [141].
A sequence of related experimental studies using the Peregrine soliton demonstrated reasonably good qualitative agreement with the theoretical prediction. Some discrepancies occur in the modulational gradients, spatiotemporal symmetries, and for larger steepness values [142], as well as the frequency downshift [143]. Interestingly, Chabchoub et al. shown further experimentally that the dynamics of the Peregrine soliton and its spectrum characteristics persist even in the presence of wind forcing with high velocity [144]. By selecting a target location and determining an initial steepness, an experiment using the Peregrine soliton of wave interaction with floating bodies during extreme ocean condition has also been successfully implemented [145].
The Peregrine soliton also finds applications in the evolution of the intrathermocline eddies, also known as the oceanic lenses [146]. It appeared as a special case of stationary limit in the solutions of the spinor BEC model [147], and it was observed experimentally emerging from the stochastic background in deep-water surface gravity waves [148].
Nonlinear spectral analysis using the finite gap theory showed that the spectral portraits of the Peregrine soliton represent a degenerate genus two of the NLS equation solution [149]. Higher-order Peregrine solitons in terms of quasi-rational functions are derived in [150]. Higher-order Peregrine solitons up to the fourth-order using a modified Darboux transformation has been presented with applications in rogue waves in the deep ocean and high-intensity rogue light wave pulses in optical fibers [151]. Super rogue waves modeled with higher-order Peregrine soliton with an amplitude amplification factor of five times the background value are observed experimentally in a water-wave tank [122].
There are various excellent reviews on rogue wave phenomena based on the NLS equation as a mathematical model and its corresponding breather solitons. Onorato et al. covered rogue waves in several physical contexts including surface gravity waves, photonic crystal fibers, laser fiber systems, and 2D spatiotemporal systems [60]. Dudley et al. reviewed breathers and rogue waves in optical fiber systems with an emphasis on the underlying physical processes that drive the appearance of extreme optical structures [125]. They reasoned that the mechanisms driving rogue wave behavior depend very much on the system. Residori et al. presented physical concepts and mathematical tools for rogue wave description [62]. They highlighted the most common features of the phenomenon include large deviations of wave amplitude from the Gaussian statistics and large-scale symmetry breaking. Chen et al. discussed rogue waves in scalar, vector, and multidimensional systems [152] while Malomed and Mihalache surveyed some theoretical and experimental studies on nonlinear waves in optical and matter-wave media [153].
Rogue waves come from and are closely related to modulational instability with resonance perturbation on continuous background [154]. A comparison of breather solutions of the NLS equation with emergent peaks in noise-seeded modulational instability indicated that the latter clustered closely around the analytical predictions [155]. “Superregular breathers” is the term coined indicating creation and annihilation dynamics of modulational instability, and the evidence of the broadest group of these superregular breathers in hydrodynamics and optics has been reported [156]. An interaction between breather and higher-order rogue waves in a nonlinear optical fiber is characterized by a trajectory of localized troughs and crests [157].
Breather soliton solutions find several applications, among others in beam-plasma interactions [158], in the transmission line analog of nonlinear left-handed metamaterials [159], in a nonlinear model describing an electron moving along the axis of deformable helical molecules [160], and in the mechanisms underlying the formation and real-time prediction of extreme events [161]. Additionally, optical rogue waves also successfully simulated in the presence of nonlinear self-image phenomenon in the near-field diffraction of plane waves from lightwave grating, known as the Talbot effect [162].
Since the definitions of “rogue waves” and “extreme events” are varied, a roadmap for unifying different perspectives could stimulate further discussion [163]. Theoretical, numerical, and experimental evidence of the dissipation effect on phase-shifted FPUT dynamics in a super wave tank, which is related to modulational instability, can be described by the breather solutions of the NLS equation [164]. Since the behavior of a large class of perturbations characterized by a continuous spectrum is described by the identical asymptotic state, it turns out that the asymptotic stage of modulational instability is universal [165]. Surprisingly, the long-time asymptotic behavior of modulationally unstable media is composed of an ensemble of classical soliton solutions of the NLS equation instead of the breather-type solutions [166].
General N-solitonic solutions of the NLS equation in the presence of a condensate derived using the dressing method describe the nonlinear stage of the modulational instability of the condensate [167]. Rogue waves on a periodic background in the form of cnoidal functions that exhibit modulational instability not only generalize the Peregrine’s soliton but also potentially stimulate further discussion [168]. Recently, both theoretical description and experimental observation of the nonlinear mutual interactions between a pair of copropagative breathers are presented and it is observed that the bound state of breathers exhibits a behavior similar to a molecule with quasiperiodic oscillatory dynamics [169].
The paper will be presented as follows. After this introduction, Section 2 discusses rigorous proof for the limiting behavior of the breather wave solutions using the ϵ-δ argument. The limiting behavior will continue in Section 3, where we cover it from the visual viewpoint. We present the corresponding contour plots for various values of parameters and the parameterization sketches of the non-rapid oscillating complex-valued breather amplitudes. Finally, Section 4 concludes our discussion and provide remarks for potential future research.
This section provides rigorous proof of the limiting behavior of breather wave solutions using the ϵ-δ argument. We have the following theorem:
Theorem 1. The Peregrine soliton is a limiting case for both the Kuznetsov-Ma breather and Akhmediev soliton:
We split the proof into four parts, and each limit consists of two parts corresponding to the real and imaginary parts of the solitons.
Proof. The following shows that the limit for the real parts of the Kuznetsov-Ma breather and Peregrine soliton is correct, i.e.,
For each
it then implies
It follows that
The following verifies that the limit for the imaginary parts of the Kuznetsov-Ma breather and Peregrine soliton is accurate, i.e.,
For each
It follows that
In what follows, we present the limit of the real part of the Akhmediev soliton as
For each
it then implies
We also have
it follows that
In what follows, we demonstrate that the limit of the imaginary part of the Akhmediev soliton becomes the imaginary part of the Peregrine soliton, i.e.,
For each
Since
We have completed the proof.
In the following section, we will visualize the limiting behavior of the breather solutions as they approach toward the Peregrine soliton.
In this section, we will visually confirm the limiting behavior of the Kuznetsov-Ma and Akhmediev breathers toward the Peregrine soliton as both parameter values approach zero. Subsection 3.1 presents the contour plots of the amplitude modulus, and Subsection 3.2 discusses the spatial and temporal parameterizations of the breathers. We select several parameter values in sketching the plots. Figure 1 displays the chosen parametric values for both breather solutions, where they can be visualized in the complex-plane for the parameter pair
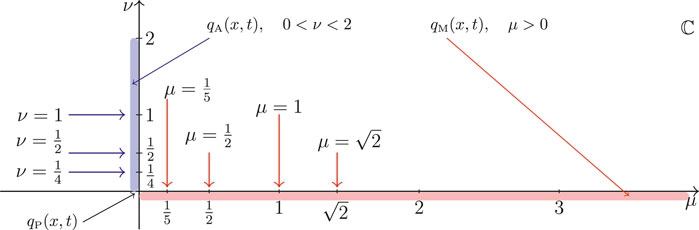
FIGURE 1. Selected parametric values ν and
In this subsection, we observe the contour plots of the amplitude modulus of the breather and how the changes in the parameter values affect the envelope’s period and wavelength. Similar contour plots have been presented in the context of electronegative plasmas with Maxwellian negative ions [170]. In particular, the contour plot of the Peregrine soliton is also displayed in [142].
Figures 2A-E display the contour plots of the Kuznetsov-Ma breather for several values of parameters μ:
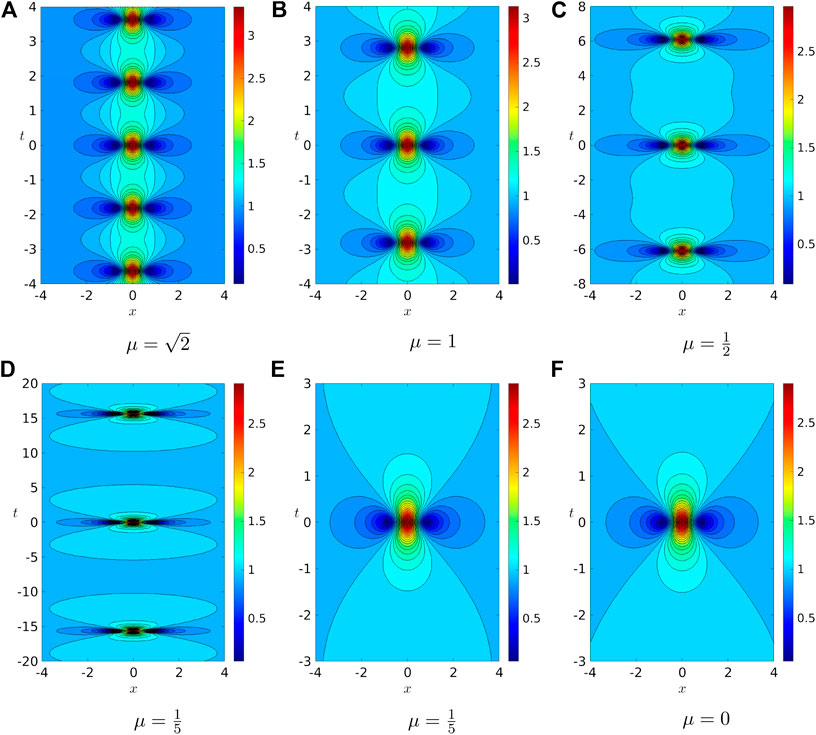
FIGURE 2. Contour plots for the moduli of the Kuznetsov-Ma breather for (A)
Let

TABLE 1. Exact values of the temporal envelope period
Figures 3A–C display the contour plot of the Akhmediev soliton for selected values of its parameters ν: 1,
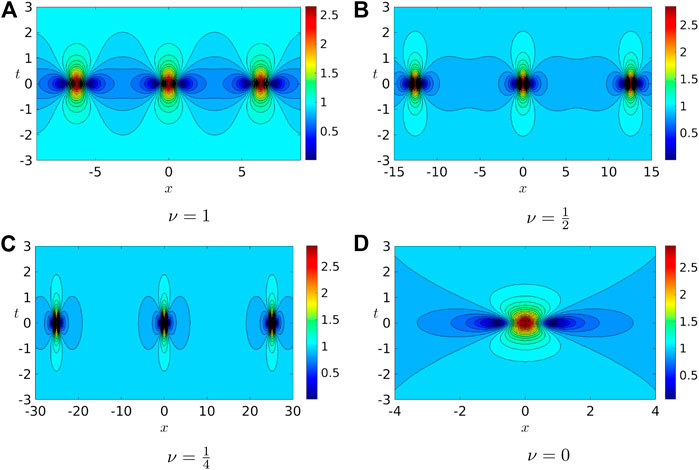
FIGURE 3. Contour plots for the moduli of the Akhmediev breather for (A)
Let

TABLE 2. Exact values of the spatial envelope wavelength
In this subsection, we write the breather solutions as
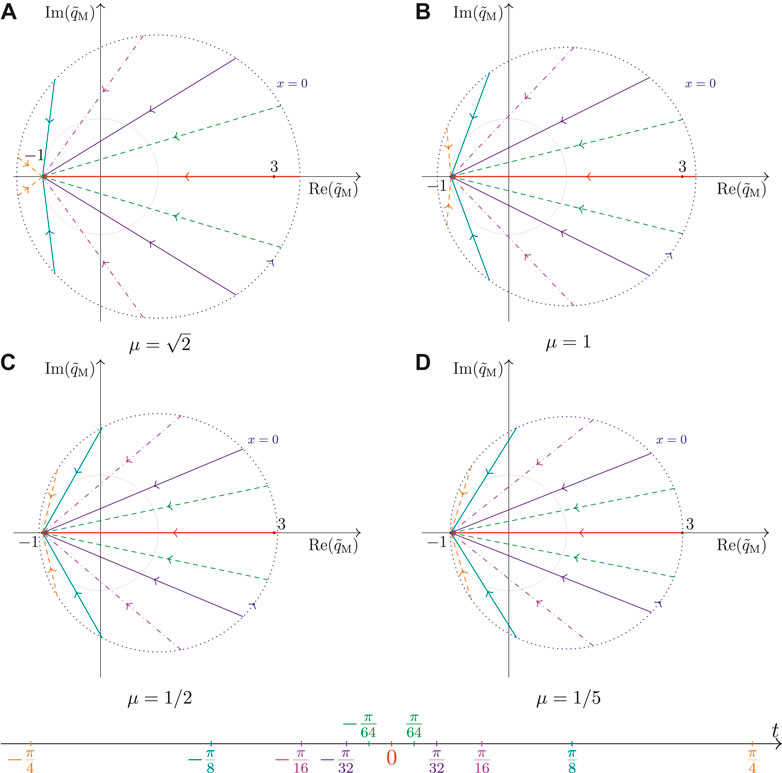
FIGURE 4. Parameterization of the non-rapid-oscillating complex-valued amplitude of the Kuznetsov-Ma breather
Figure 4 displays the parameterization of the non-rapid oscillating Kuznetsov-Ma breather
In particular, for
Additionally,
Figure 5 displays the sketch of the non-rapid-oscillating Kuznetsov-Ma breather
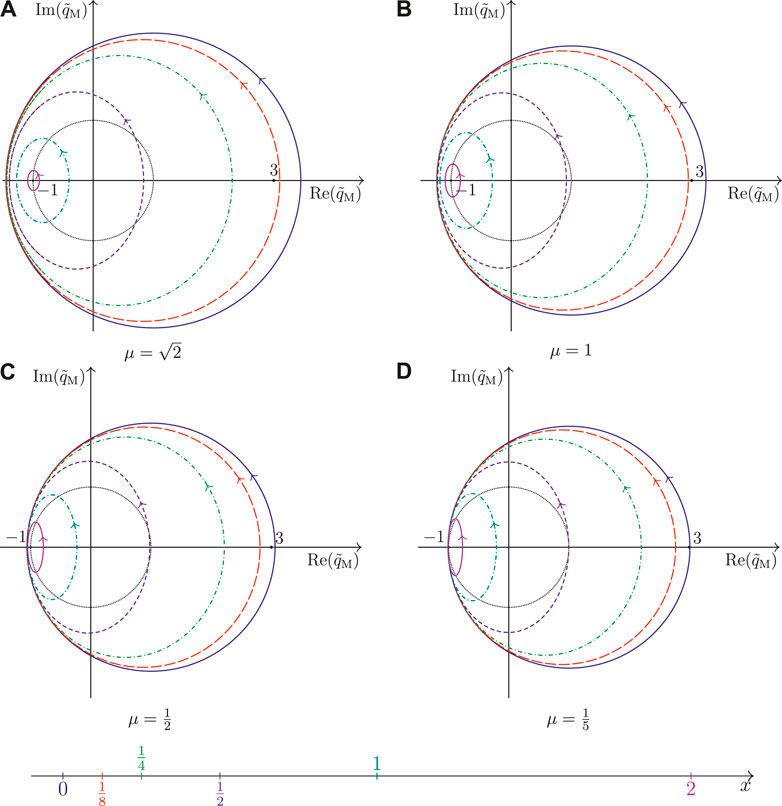
FIGURE 5. Parameterization of the non-rapid oscillating complex-valued amplitude of the Kuznetsov-Ma breather
The special case of a circle is obtained for
In Figure 4, the starting points of the trajectories for
Figure 6 displays the sketch in the complex-plane of the non-rapid-oscillating Akhmediev soliton
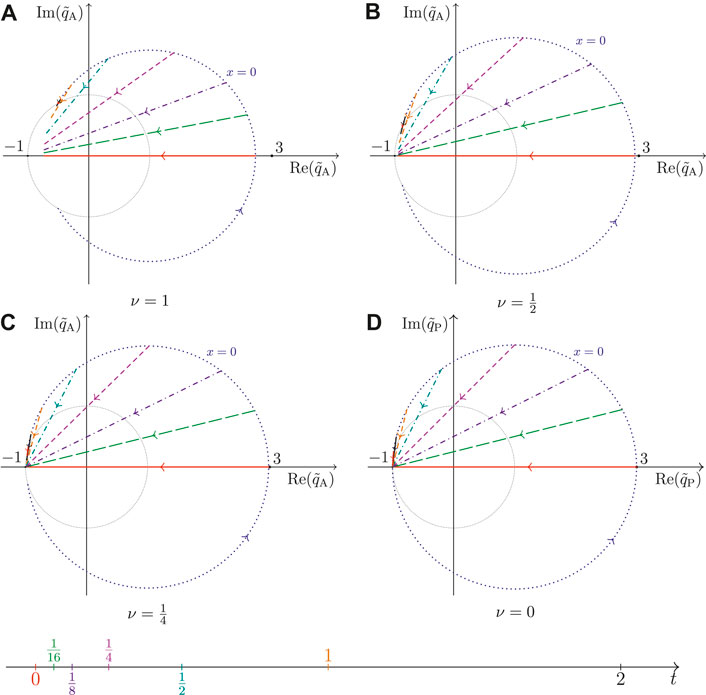
FIGURE 6. Parameterization of the non-rapid oscillating complex-valued amplitude
For each panel, we only sketch the trajectories for an interval of half the spatial envelope wavelength, i.e.,
In Figure 6, a prominent difference in the trajectories for different values of the parameter ν is its lengths. The length of the trajectories is increasing for decreasing values of ν. While the starting points for the Kuznetsov-Ma breathers are shrinking, for this family of Akhmediev solitons, they are expanding as
Figure 7 displays the sketch of the non-rapid-oscillating part of the Akhmediev soliton
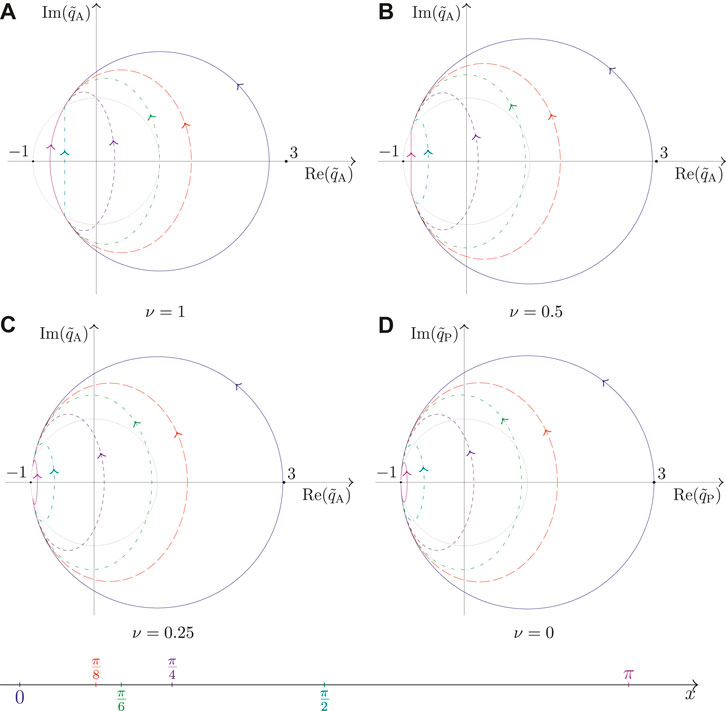
FIGURE 7. Parameterization of the non-rapid oscillating complex-valued amplitude
The circular sectors are attained for
For the Peregrine soliton, the trajectories of time parameterization in the complex-plane are either a circle (for
Nearly all trajectories in Figure 7 follow the right-hand side paths instead of the left-hand side. For decreasing values of ν, the trajectories are generally expanding in size, except for the curve at
Figure 8 should be viewed in connection to Figures 6D, 7D. It displays the plots of the real and imaginary parts of the non-rapid-oscillating complex-valued amplitude for the Peregrine soliton
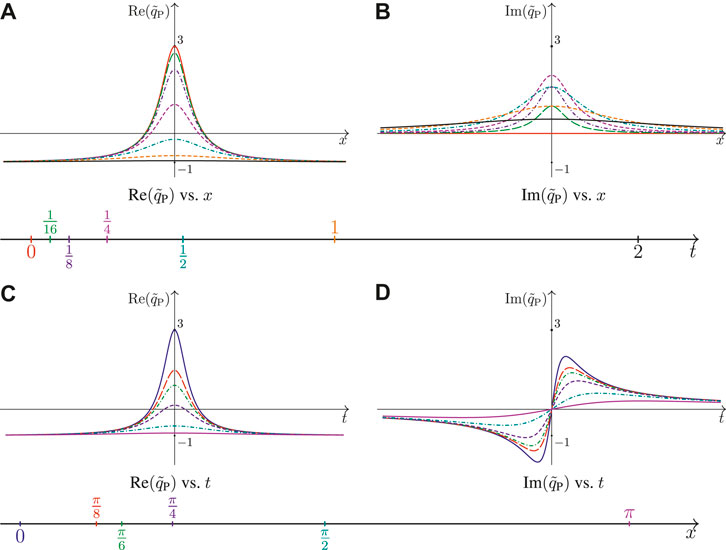
FIGURE 8. Plots of the real and imaginary parts of the non-rapid oscillating complex-valued amplitude for the Peregrine soliton with respect to the spatial and temporal variables, x (upper panels) and t (lower panels), respectively. For upper panels (A) and (B), various curves indicates different time:
We have considered the exact analytical breather solutions of the focusing NLS equation, where the wave envelopes at infinity have a nonzero but constant background. These solutions have been adopted as weakly nonlinear prototypes for freak waves in dispersive media due to their fine agreement with various experimental results. We have provided not only a brief historical review of the breathers but also covered some recent progress in the field of rogue wave modeling in the context of the NLS equation.
In particular, we have discussed the Peregrine soliton as a limiting case of the Kuznetsov-Ma breather and Akhmediev soliton. We have verified rigorously using the ε-δ argument that as each of the parameter values from these two breathers is approaching zero, they reduce to the Peregrine soliton. We have also presented this limiting behavior visually by depicting the contour plots of the breather amplitude modulus for selected parameter values. We displayed the parameterization plots of the non-rapid-oscillating complex-valued breather amplitudes both spatially and temporally.
The trajectories for the spatial parameterization in the complex-plane exhibit a set of straight lines for all the breathers. From
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
The author confirms being the sole contributor of this work and has approved it for publication.
The author would like to dedicate this article to his late father Zakaria Karjanto (Khouw Kim Soey, 許金瑞) who not only taught him the alphabet, numbers, and the calendar in his early childhood but also cultivated the value of hard work, diligence, discipline, perseverance, persistence, and grit. Karjanto Senior was born in Tasikmalaya, West Java, Japanese-occupied Dutch East Indies on 1 January 1944 (Saturday Pahing) and died in Bandung, West Java, Indonesia on 18 April 2021 (Sunday Wage).
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The author wishes to thank Bertrand Kibler, Amin Chabchoub, and Heremba Bailung for the invitation to contribute to the article collection “Peregrine Soliton and Breathers in Wave Physics: Achievements and Perspectives” and Marlena Radomska from the Production Team of Frontiers in Physics for her excellent and outstanding administrative assistance. The author also acknowledges E. (Brenny) van Groesen, Mark Ablowitz, Constance Schober, Frederic Dias, Roger Grimshaw, Panayotis Kevrekidis, Boris Malomed, Evgenii Kuznetsov, Nail Akhmediev, Alfred Osborne, Miguel Onorato, Gert Klopman, René Huijsmans, Andonowati, Stephan van Gils, Guido Schneider, Anthony Roberts, Shanti Toenger, Omar Kirikchi, Ardhasena Sopaheluwakan, Hadi Susanto, Alexander Iskandar, Agung Trisetyarso, Ade Irma Suriajaya, and Defrianto Pratama for fruitful discussion.
1. Osborne AR. Nonlinear Ocean Wave and the Inverse Scattering Transform. Cambridge, MA: Academic Press (2010).
2. Debnath L. Nonlinear Partial Differential Equations for Scientists and Engineers. Berlin, Germany: Springer Science + Business Media (2012).
4. Kivshar YS, Agrawal GP. Optical Solitons: From Fibers to Photonic Crystals. Cambridge, MA: Academic Press (2003).
5. Infeld E, Rowlands G. Nonlinear Waves, Solitons and Chaos. 2nd ed. Cambridge, United Kingdom: Cambridge University Press (2000).
7. Sulem C, Sulem PL. The Nonlinear Schrödinger Equation: Self-Focusing and Wave Collapse. Berlin, Germany: Springer-Verlag (1999).
8. Kevrekidis PG, Frantzeskakis DJ, Carretero-González R. Emergent Nonlinear Phenomena in Bose-Einstein Condensates: Theory and Experiment. Berlin, Germany: Springer Science + Business Media (2007).
9. Chiao RY, Garmire E, Townes CH. Self-trapping of Optical Beams. Phys Rev Lett (1964) 13:479–82. doi:10.1103/physrevlett.13.479
10. Kelley PL. Self-focusing of Optical Beams. Phys Rev Lett (1965) 15:1005–1008. doi:10.1103/physrevlett.15.1005
11. Taniuti T, Washimi H. Self-trapping and Instability of Hydromagnetic Waves along the Magnetic Field in a Cold Plasma. Phys Rev Lett (1968) 21:209–212. doi:10.1103/physrevlett.21.209
12. Karpman VI, Krushkal EM Modulated Waves in Nonlinear Dispersive Media. Soviet Phys JETP (1969) 28:277. doi:10.1007/3-540-46629-0_2
13. Taniuti T, Yajima N. Perturbation Method for a Nonlinear Wave Modulation. I. J Math Phys (1969) 10:1369–1372. doi:10.1063/1.1664975
14. Asano N, Taniuti T, Yajima N. Perturbation Method for a Nonlinear Wave Modulation. II. J Math Phys (1969) 10:2020–2024. doi:10.1063/1.1664797
15. Tappert FD, Varma CM. Asymptotic Theory of Self-Trapping of Heat Pulses in Solids. Phys Rev Lett (1970) 25:1108–1111. doi:10.1103/physrevlett.25.1108
16. Benney DJ, Newell AC The Propagation of Nonlinear Wave Envelopes. J Math Phys (1967) 46:133–139. doi:10.1002/sapm1967461133
17. Zakharov VE. Stability of Periodic Waves of Finite Amplitude on the Surface of a Deep Fluid. J Appl Mech Tech Phys (1968) 9:190–194. doi:10.1007/BF00913182
18. Hasimoto H, Ono H. Nonlinear Modulation of Gravity Waves. J Phys Soc Jpn (1972) 33:805–811. doi:10.1143/jpsj.33.805
19. Gross EP. Structure of a Quantized Vortex in Boson Systems. Il Nuovo Cimento (1955–1965) 20:454–477. doi:10.1007/BF02731494
21. Ginzburg VL, Landau LD. On the Theory of Superconductivity. On Superconductivity and Superfluidity. Berlin Heilderberg, Germany: Springer (2009). 113–137.
22. Malomed BA. Nonlinear Schrödinger Equation. In: A Scott, editor. Encyclopedia of Nonlinear Science. New York, NY: Routledge (2005). 639–643.
23. Ablowitz M, Prinari B. Nonlinear Schrodinger Systems: Continuous and Discrete. Scholarpedia (2008) 3:5561. doi:10.4249/scholarpedia.5561
24. Huang J. Nonlinear Schrödinger Equation. In: B Lembrikov, editor. Nonlinear Optics: Novel Results in Theory and Applications. London, UK and Rijeka, Croatia: IntechOpen (2018). 11–29.
25. Karjanto N. The Nonlinear Schrödinger Equation: A Mathematical Model with its Wide Range of Applications. In: V Simpao, and H Little, editors. Understanding the Schrödinger Equation: Some (Non)Linear Perspectives. Hauppauge, New York: Nova Science Publishers (2020). 135–179. Accessible online at arXiv, preprint arXiv:1912.10683.
26. Fibich G. The Nonlinear Schrödinger Equation: Singular Solutions and Optical Collapse. Cham, Switzerland: Springer (2015).
27. Akhmediev NN, Eleonskiĭ VM, Kulagin NE. Generation of Periodic Trains of Picosecond Pulses in an Optical Fiber: Exact Solutions. Soviet Phys JETP (1985) 62:894–899.
28. Akhmediev NN, Korneev VI. Modulation Instability and Periodic Solutions of the Nonlinear Schrödinger Equation. Theor Math Phys (1986) 69:1089–1093. doi:10.1007/bf01037866
29. Akhmediev NN, Eleonskii VM, Kulagin NE. Exact First-Order Solutions of the Nonlinear Schrödinger Equation. Theor Math Phys (1987) 72:809–818. doi:10.1007/bf01017105
30. Akhmediev NN, Ankiewicz A. Solitons: Nonlinear Pulses and Beams. London, United Kingdom: Chapman & Hall (1997).
31. Hirota R. A New Form of Backlund Transformations and its Relation to the Inverse Scattering Problem. Prog Theor Phys (1974) 52:1498–1512. doi:10.1143/ptp.52.1498
32. Hirota R. Direct Method of Finding Exact Solutions of Nonlinear Evolution Equations. In: Bäcklund Transformations, the Inverse Scattering Method, Solitons, and Their Applications. Lecture Notes in Mathematics, 515. Berlin, Germany: Springer (1976). 40–68. doi:10.1007/bfb0081162
33. Hirota R, Satsuma J. A Variety of Nonlinear Network Equations Generated from the Bäcklund Transformation for the Toda Lattice. Prog Theor Phys Suppl (1976) 59:64–100. doi:10.1143/ptps.59.64
34. Ablowitz MJ, Herbst BM. On Homoclinic Structure and Numerically Induced Chaos for the Nonlinear Schrödinger Equation. SIAM J Appl Math (1990) 50:339–351. doi:10.1137/0150021
35. Zakharov VE, Shabat AB. Exact Theory of Two-Dimensional Self-Focusing and One-Dimensional Self-Modulation of Waves in Nonlinear Media. Soviet Phys JETP (1972) 34:62.
36. Zakharov VE, Shabat AB. Interaction between Solitons in a Stable Medium. Soviet Phys JETP (1973) 37:823–828.
37. Ablowitz MJ, Segur H. Solitons and the Inverse Scattering Transform. Philadelphia, PA: SIAM (1981).
38. Osborne AR, Onorato M, Serio M. The Nonlinear Dynamics of Rogue Waves and Holes in Deep-Water Gravity Wave Trains. Phys Lett A (2000) 275:386–393. doi:10.1016/s0375-9601(00)00575-2
39. Osborne AR. The Random and Deterministic Dynamics of ‘Rogue Waves' in Unidirectional, Deep-Water Wave Trains. Mar Structures (2001) 14:275–293. doi:10.1016/s0951-8339(00)00064-2
40. Biondini G, Kovačič G. Inverse Scattering Transform for the Focusing Nonlinear Schrödinger Equation with Nonzero Boundary Conditions. J Math Phys (2014) 55:031506. doi:10.1063/1.4868483
41. Olver PJ. Applications of Lie Groups to Differential Equations. 2nd ed. Berlin, Germany: Springer Science + Business Media (1993).
42. van Groesen E, A ndonowati, Karjanto N. Displaced Phase-Amplitude Variables for Waves on Finite Background. Phys Lett A (2006) 354:312–319. doi:10.1016/j.physleta.2006.02.037
43. Karjanto N. Mathematical Aspects of Extreme Water Waves (Enschede and Zutphen, the Netherlands: The University of Twente and Wöhrmann Print Service). [PhD thesis] (2006). Accessible online at arXiv, preprint arXiv:2006.00766.
44. Karjanto N, van Groesen E. Derivation of the NLS Breather Solutions Using Displaced Phase-Amplitude Variables. In: S Wahyuni, IE Wijayanti, and D Rosadi, editors. Proceedings of SEAMS-GMU Conference 2007. Indonesia: Applied Mathematics (Department of Mathematics, Gadjah Mada University (2007). 357–368. Accessible online at arXiv, preprint arXiv:1110.4704.
45. Demontis F, Prinari B, Van Der Mee C, Vitale F. The Inverse Scattering Transform for the Focusing Nonlinear Schrödinger Equation with Asymmetric Boundary Conditions. J Math Phys (2014) 55:101505. doi:10.1063/1.4898768
46. Dysthe KB, Trulsen K. Note on Breather Type Solutions of the NLS as Models for Freak-Waves. Physica Scripta (1999) T82:48. doi:10.1238/physica.topical.082a00048
47. Chow KW. A Class of Exact, Periodic Solutions of Nonlinear Envelope Equations. J Math Phys (1995a) 36:4125–4137. doi:10.1063/1.530951
48. Kuznetsov EA. Solitons in a Parametrically Unstable Plasma. Akademiia Nauk SSSR Doklady (1977) 236:575–577. English translation: Soviet Physics Doklady22 (1977) 507–508.
50. Kawata T, Inoue H, Adachihara H, McLaughlin DW, Moloney JV, Newell AC. Solitary Waves as Fixed Points of Infinite‐dimensional Maps for an Optical Bistable Ring Cavity: Analysis. J Math Phys (1988) 29:63–85. doi:10.1063/1.528136
51. Ma Y-C. The Perturbed Plane-Wave Solutions of the Cubic Schrödinger Equation. Stud Appl Math (1979) 60:43–58. doi:10.1002/sapm197960143
52. Kuznetsov EA, Mikhailov AV. Stability of Stationary Waves in Nonlinear Weakly Dispersive Media. Zhurnal Eksperimentalnoi I Teoreticheskoi Fiziki 67 (1974). p. 1717–1727. English translation: Soviet Physics JETP40(2)1975855859.
53. Slunyaev A. Nonlinear Analysis and Simulations of Measured Freak Wave Time Series. Eur J Mech - B/Fluids (2006) 25:621–635. doi:10.1016/j.euromechflu.2006.03.005
54. Kibler B, Fatome J, Finot C, Millot G, Genty G, Wetzel B, et al. Observation of Kuznetsov-Ma Soliton Dynamics in Optical Fibre. Scientific Rep (2012) 2:463. doi:10.1038/srep00463
55. Grimshaw R, Pelinovsky D, Pelinovsky E, Talipova T. Wave Group Dynamics in Weakly Nonlinear Long-Wave Models. Physica D: Nonlinear Phenomena (2001) 159:35–57. doi:10.1016/s0167-2789(01)00333-5
56. Gagnon L. Solitons on a Continuous-Wave Background and Collision between Two Dark Pulses: Some Analytical Results. J Opt Soc Am B (1993) 10:469–74. doi:10.1364/josab.10.000469
57. Adachihara H, McLaughlin DW, Moloney JV, Newell AC. Solitary Waves as Fixed Points of Infinite‐dimensional Maps for an Optical Bistable Ring Cavity: Analysis. J Math Phys (1988) 29:63–85. doi:10.1063/1.528136
58. Mihalache D, Lederer F, Baboiu D-M. Two-parameter Family of Exact Solutions of the Nonlinear Schrödinger Equation Describing Optical-Soliton Propagation. Phys Rev A (1993) 47:3285–3290. doi:10.1103/physreva.47.3285
59. Clamond D, Francius M, Grue J, Kharif C. Long Time Interaction of Envelope Solitons and Freak Wave Formations. Eur J Mech - B/Fluids (2006) 25:536–553. doi:10.1016/j.euromechflu.2006.02.007
60. Onorato M, Residori S, Bortolozzo U, Montina A, Arecchi FT. Rogue Waves and Their Generating Mechanisms in Different Physical Contexts. Phys Rep (2013) 528:47–89. doi:10.1016/j.physrep.2013.03.001
61. Chabchoub A, Kibler B, Dudley JM, Akhmediev N. Hydrodynamics of Periodic Breathers. Phil Trans R Soc A (2014) 372:20140005. doi:10.1098/rsta.2014.0005
62. Residori S, Onorato M, Bortolozzo U, Arecchi FT. Rogue Waves: a Unique Approach to Multidisciplinary Physics. Contemp Phys (2017) 58:53–69. doi:10.1080/00107514.2016.1243351
63. Akhmediev NN, Wabnitz S. Phase Detecting of Solitons by Mixing with a Continuous-Wave Background in an Optical Fiber. J Opt Soc Am B (1992) 9:236–242. doi:10.1364/josab.9.000236
64. Kharif C, Pelinovsky E, Talipova T, Slunyaev A. Focusing of Nonlinear Wave Groups in Deep Water. JETP Lett (2001) 73:170–175. doi:10.1134/1.1368708
65. Garnier J, Kalimeris K. Inverse Scattering Perturbation Theory for the Nonlinear Schrödinger Equation with Non-vanishing Background. J Phys A: Math Theor (2011) 45:035202. doi:10.1088/1751-8113/45/3/035202
66. Xiong H, Gan J, Wu Y. Kuznetsov-Ma Soliton Dynamics Based on the Mechanical Effect of Light. Phys Rev Lett (2017) 119:153901. doi:10.1103/physrevlett.119.153901
67. Cuevas-Maraver J, Kevrekidis PG, Frantzeskakis DJ, Karachalios NI, Haragus M, James G. Floquet Analysis of Kuznetsov-Ma Breathers: A Path towards Spectral Stability of Rogue Waves. Phys Rev E (2017) 96:012202. doi:10.1103/physreve.96.012202
68. Zhao LC, Ling L, Yang ZY. Mechanism of Kuznetsov-Ma Breathers. Phys Rev E (2018) 97:022218. doi:10.1103/physreve.97.022218
69. Gelash A. Formation of Rogue Waves from a Locally Perturbed Condensate. Phys Rev E (2018) 97:022208. doi:10.1103/physreve.97.022208
70. Bélanger N, Bélanger P-A. Bright Solitons on a CW Background. Opt Commun (1996) 124:301–308. doi:10.1016/0030-4018(95)00659-1
71. Tajiri M, Watanabe Y. Breather Solutions to the Focusing Nonlinear Schrödinger Equation. Phys Rev E (1998) 57:3510–3519. doi:10.1103/physreve.57.3510
72. Chow KW. Solitary Waves on a Continuous Wave Background. J Phys Soc Jpn (1995) 64:1524–1528. doi:10.1143/jpsj.64.1524
73. Rajaraman R. Solitons and Instantons: An Introduction to Solitons and Instantons in Quantum Field Theory. Amsterdam, Netherlands: Elsevier/North Holland (1982).
74. Falkovich G, Kolokolov I, Lebedev V, Migdal A. Instantons and Intermittency. Phys Rev E (1996) 54:4896–907. doi:10.1103/physreve.54.4896
75. Turitsyn SK, Bale BG, Fedoruk MP. Dispersion-managed Solitons in Fibre Systems and Lasers. Phys Rep (2012) 521:135–203. doi:10.1016/j.physrep.2012.09.004
76. Calini A, Schober CM. Homoclinic Chaos Increases the Likelihood of Rogue Wave Formation. Phys Lett A (2002) 298:335–349. doi:10.1016/s0375-9601(02)00576-5
77. Onorato M, Osborne AR, Serio M, Damiani T. Occurrence of Freak Waves from Envelope Equations in Random Ocean Wave Simulations. In: Rogue Waves 2000. editors M Olagnon, and M Prevosto, (Brest, France: IFREMER, French Research Institute for Exploitation of the Sea). (2001). 11.
78. Karjanto N, van Groesen E, Peterson P. Investigation of the Maximum Amplitude Increase from the Benjamin-Feir Instability. J Indonesian Math Soc (2002) 8:39.
79. Akhmediev N, Ankiewicz A, Taki M. Waves that Appear from Nowhere and Disappear without a Trace. Phys Lett A (2009) 373:675–678. doi:10.1016/j.physleta.2008.12.036
80. Onorato M, Proment D, Toffoli A. Triggering Rogue Waves in Opposing Currents. Phys Rev Lett (2011) 107:184502. doi:10.1103/physrevlett.107.184502
81. Slunyaev AV, Shrira VI. On the Highest Non-breaking Wave in a Group: Fully Nonlinear Water Wave Breathers versus Weakly Nonlinear Theory. J Fluid Mech (2013) 735:203–248. doi:10.1017/jfm.2013.498
82. Bespalov VI, Talanov VI. Filamentary Structure of Light Beams in Nonlinear Liquids. Soviet Phys JETP Lett (1966) 3:307–312.
83. Ostrovskii L. Propagation of Wave Packets and Space-Time Self-Focusing in a Nonlinear Medium. Soviet Phys JETP (1967) 24:797–800.
84. Karpman VI. Self-modulation of Nonlinear Plane Waves in Dispersive Media. JETP Lett (1967) 6:277.
85. Benjamin TB, Feir JE. The Disintegration of Wave Trains on Deep Water Part 1. Theory. J Fluid Mech (1967) 27:417–30. doi:10.1017/s002211206700045x
86. Tam CKW. Amplitude Dispersion and Nonlinear Instability of Whistlers. Phys Fluids (1969) 12:1028–1035. doi:10.1063/1.2163663
87. Hasegawa A. Observation of Self-Trapping Instability of a Plasma Cyclotron Wave in a Computer Experiment. Phys Rev Lett (1970) 24:1165–1168. doi:10.1103/physrevlett.24.1165
88. Hasegawa A. Theory and Computer Experiment on Self-Trapping Instability of Plasma Cyclotron Waves. Phys Fluids (1972) 15:870–881. doi:10.1063/1.1693996
89. Robins NP, Zhang W, Ostrovskaya EA, Kivshar YS. Modulational Instability of Spinor Condensates. Phys Rev A (2001) 64:021601. doi:10.1103/physreva.64.021601
90. Konotop V, Salerno M. Modulational Instability in Bose-Einstein Condensates in Optical Lattices. Phys Rev A (2002) 65:021602. doi:10.1103/physreva.65.021602
91. Smerzi A, Trombettoni A, Kevrekidis P, Bishop A. Dynamical Superfluid-Insulator Transition in a Chain of Weakly Coupled Bose-Einstein Condensates. Phys Rev Lett (2002) 89:170402. doi:10.1103/physrevlett.89.170402
92. Baizakov BB, Konotop VV, Salerno M. Regular Spatial Structures in Arrays of Bose Einstein Condensates Induced by Modulational Instability. J Phys B: Mol Opt Phys (2002) 35:5105–5119. doi:10.1088/0953-4075/35/24/312
93. Salasnich L, Parola A, Reatto L Modulational Instability and Complex Dynamics of Confined Matter-Wave Solitons. Phys Rev Lett (2003) 91:080405. doi:10.1103/physrevlett.91.080405
94. Theocharis G, Rapti Z, Kevrekidis P, Frantzeskakis D, Konotop V. Modulational Instability of Gross-Pitaevskii-type Equations in 1 + 1 Dimensions. Phys Rev A (2003) 67:063610. doi:10.1103/physreva.67.063610
95. Lighthill MJ. Contributions to the Theory of Waves in Non-linear Dispersive Systems. IMA J Appl Math (1965) 1:269–306. doi:10.1093/imamat/1.3.269
96. Zakharov VE, Ostrovsky LA. Modulation Instability: The Beginning. Physica D: Nonlinear Phenomena (2009) 238:540–548. doi:10.1016/j.physd.2008.12.002
97. Yuen HC, Lake BM. Nonlinear Deep Water Waves: Theory and Experiment. Phys Fluids (1975) 18:956–960. doi:10.1063/1.861268
98. Lake BM, Yuen HC, Rungaldier H, Ferguson WE. Nonlinear Deep-Water Waves: Theory and Experiment. Part 2. Evolution of a Continuous Wave Train. J Fluid Mech (1977) 83:49–74. doi:10.1017/s0022112077001037
99. Yuen HC, Ferguson WE Relationship between Benjamin-Feir Instability and Recurrence in the Nonlinear Schrödinger Equation. Phys Fluids (1978a) 21:1275–1278. doi:10.1063/1.862394
100. Yuen HC, Ferguson WE Fermi-Pasta-Ulam Recurrence in the Two-Space Dimensional Nonlinear Schrödinger Equation. Phys Fluids (1978b) 21:2116–2118. doi:10.1063/1.862122
101. Yuen HC, Lake BM. Instabilities of Waves on Deep Water. Annu Rev Fluid Mech (1980) 12:303–334. doi:10.1146/annurev.fl.12.010180.001511
102. Fermi E, Pasta P, Ulam S, Tsingou M. Studies of the Nonlinear Problems. Technical Report No. LA-1940. New Mexico: Los Alamos Scientific Laboratory (1955). doi:10.2172/4376203
103. Janssen PAEM. Modulational Instability and the Fermi-Pasta-Ulam Recurrence. Phys Fluids (1981) 24:23–26. doi:10.1063/1.863242
104. Van Simaeys G, Emplit P, Haelterman M. Experimental Demonstration of the Fermi-Pasta-Ulam Recurrence in a Modulationally Unstable Optical Wave. Phys Rev Lett (2001) 87:033902. doi:10.1103/physrevlett.87.033902
105. Janssen PAEM. Nonlinear Four-Wave Interactions and Freak Waves. J Phys Oceanogr (2003) 33:863–884. doi:10.1175/1520-0485(2003)33863
106. Dysthe K, Krogstad HE, Müller P. Oceanic Rogue Waves. Annu Rev Fluid Mech (2008) 40:287–310. doi:10.1146/annurev.fluid.40.111406.102203
107. Kharif C, Pelinovsky E, Slunyaev A. Rogue Waves in the Ocean. Berlin, Germany: Springer Science + Business Media (2009).
108. Slunyaev A, Kharif C, Pelinovsky E, Talipova T. Nonlinear Wave Focusing on Water of Finite Depth. Physica D: Nonlinear Phenomena (2002) 173:77–96. doi:10.1016/s0167-2789(02)00662-0
109. Biondini G, Fagerstrom E. The Integrable Nature of Modulational Instability. SIAM J Appl Math (2015) 75:136–163. doi:10.1137/140965089
110. Huijsmans RH, Klopman G, Karjanto N, Andonowati. Experiments on Extreme Wave Generation Using the Soliton on Finite Background. in Rogue Waves 2004 (Brest, France: IFREMER, French Research Institute for Exploitation of the Sea) editors M. Olagnon, and M. Prevosto. (2005). 10. Accessible online at arXiv, preprint arXiv:1110.5119
111. van Groesen E, Andonowati , Karjanto N. Deterministic Aspects of Nonlinear Modulation Instability. in Rogue Waves 2004 (Brest, France: IFREMER, French Research Institute for Exploitation of the Sea) editors. M Olagnon, and M Prevosto. (2005). 12. Accessible online at arXiv, preprint arXiv:1110.5120
112. Andonowati, , Karjanto N, van Groesen E. Extreme Wave Phenomena in Down-Stream Running Modulated Waves. Appl Math Model (2007) 31:1425–1443. doi:10.1016/j.apm.2006.04.015
113. Karjanto N, van Groesen E. Qualitative Comparisons of Experimental Results on Deterministic Freak Wave Generation Based on Modulational Instability. J Hydro-environment Res (2010) 3:186–192. doi:10.1016/j.jher.2009.10.008
114. Karjanto N, van Groesen E. Note on Wavefront Dislocation in Surface Water Waves. Phys Lett A (2007b) 371:173–179. doi:10.1016/j.physleta.2007.06.064
115. Akhmediev N, Soto-Crespo JM, Ankiewicz A. Extreme Waves that Appear from Nowhere: on the Nature of Rogue Waves. Phys Lett A (2009) 373:2137–2145. doi:10.1016/j.physleta.2009.04.023
116. Chabchoub A, Vitanov N, Hoffmann N. Experimental Evidence for Breather Type Dynamics in Freak Waves. Proc Appl Math Mech (2010) 10:495–496. doi:10.1002/pamm.201010240
117. Dudley JM, Genty G, Dias F, Kibler B, Akhmediev N. Modulation Instability, Akhmediev Breathers and Continuous Wave Supercontinuum Generation. Opt Express (2009) 17:21497–21508. doi:10.1364/oe.17.021497
118. Erkintalo M, Hammani K, Kibler B, Finot C, Akhmediev N, Dudley JM, et al. Higher-order Modulation Instability in Nonlinear Fiber Optics. Phys Rev Lett (2011) 107:253901. doi:10.1103/physrevlett.107.253901
119. Kedziora DJ, Ankiewicz A, Akhmediev N. Second-order Nonlinear Schrödinger Equation Breather Solutions in the Degenerate and Rogue Wave Limits. Phys Rev E (2012) 85:066601. doi:10.1103/physreve.85.066601
120. Karjanto N, van Groesen E. Mathematical Physics Properties of Waves on Finite Background. In: SP Lang, and SH Bedore, editors. Handbook of Solitons: Research, Technology and Applications. Hauppauge, NY: Nova Science Publishers) (2009). 501–539.
121. Branger H, Chabchoub A, Hoffmann N, Kimmoun O, Kharif C, Akhmediev N. Evolution of a Peregrine Breather: Analytical and Experimental Studies. In: Presented in the 13th Hydrodynamics Days (Saint-Venant Hydrodynamic Laboratory, Île des Impressionnistes, Chatou, Seine River. France): Yvelines department, Île-de-France region (2012). 12. The typographical error contained in the English version of the title has been corrected in this reference.
122. Chabchoub A, Hoffmann N, Onorato M, Akhmediev N. Super Rogue Waves: Observation of a Higher-Order Breather in Water Waves. Phys Rev X (2012) 2:011015. doi:10.1103/physrevx.2.011015
123. Calini A, Schober CM. Observable and Reproducible Rogue Waves. J Opt (2013) 15:105201. doi:10.1088/2040-8978/15/10/105201
124. Ling L, Zhao LC. Simple Determinant Representation for Rogue Waves of the Nonlinear Schrödinger Equation. Phys Rev E (2013) 88:043201. doi:10.1103/physreve.88.043201
125. Dudley JM, Dias F, Erkintalo M, Genty G. Instabilities, Breathers and Rogue Waves in Optics. Nat Photon (2014) 8:755–764. doi:10.1038/nphoton.2014.220
126. Chabchoub A, Fink M. Time-reversal Generation of Rogue Waves. Phys Rev Lett (2014) 112:124101. doi:10.1103/physrevlett.112.124101
127. Bilman D, Miller PD. A Robust Inverse Scattering Transform for the Focusing Nonlinear Schrödinger Equation. Comm Pure Appl Math (2019) 72:1722–1805. doi:10.1002/cpa.21819
128. Peregrine DH. Water Waves, Nonlinear Schrödinger Equations and Their Solutions. J Aust Math Soc Ser B, Appl. Math (1983) 25:16–43. doi:10.1017/s0334270000003891
129. Johnson RS. A Modern Introduction to the Mathematical Theory of Water Waves. Cambridge, United Kingdom: Cambridge University Press (1997).
130. Henderson KL, Peregrine DH, Dold JW. Unsteady Water Wave Modulations: Fully Nonlinear Solutions and Comparison with the Nonlinear Schrödinger Equation. Wave Motion (1999) 29:341–361. doi:10.1016/s0165-2125(98)00045-6
131. Nakamura A, Hirota R A. New Example of Explode-Decay Solitary Waves in One-Dimension. J Phys Soc Jpn (1985) 54:491–499. doi:10.1143/jpsj.54.491
132. Yan Z. Nonautonomous “rogons” in the Inhomogeneous Nonlinear Schrödinger Equation with Variable Coefficients. Phys Lett A (2010) 374:672–679. doi:10.1016/j.physleta.2009.11.030
133. Shrira VI, Geogjaev VV. What Makes the Peregrine Soliton So Special as a Prototype of Freak Waves? J Eng Math (2010) 67:11–22. doi:10.1007/s10665-009-9347-2
134. Voronovich VV, Shrira VI, Thomas G. Can Bottom Friction Suppress “Freak Wave” Formation? J Fluid Mech (2008) 604:263–296. doi:10.1017/s0022112008001171
135. Klein C, Haragus M. Numerical Study of the Stability of the Peregrine Solution. Ann Math Sci Appl (2017) 2:217–239. doi:10.4310/amsa.2017.v2.n2.a1
136. Muñoz C Instability in Nonlinear Schrödinger Breathers. Proyecciones (2017) 36:653–683. doi:10.4067/s0716-09172017000400653
137. Calini A, Schober CM, Strawn M. Linear Instability of the Peregrine Breather: Numerical and Analytical Investigations. Appl Numer Math (2019) 141:36–43. doi:10.1016/j.apnum.2018.11.005
138. Klein C, Stoilov N. Numerical Study of the Transverse Stability of the Peregrine Solution. Stud Appl Math (2020) 145:36–51. doi:10.1111/sapm.12306
139. Kibler B, Fatome J, Finot C, Millot G, Dias F, Genty G, et al. The Peregrine Soliton in Nonlinear Fibre Optics. Nat Phys (2010) 6:790–795. doi:10.1038/nphys1740
140. Chabchoub A, Hoffmann NP, Akhmediev N. Rogue Wave Observation in a Water Wave Tank. Phys Rev Lett (2011) 106:204502. doi:10.1103/physrevlett.106.204502
141. Bailung H, Sharma SK, Nakamura Y. Observation of Peregrine Solitons in a Multicomponent Plasma with Negative Ions. Phys Rev Lett (2011) 107:255005. doi:10.1103/physrevlett.107.255005
142. Chabchoub A, Akhmediev N, Hoffmann N. Experimental Study of Spatiotemporally Localized Surface Gravity Water Waves. Phys Rev E (2012) 86:016311. doi:10.1103/physreve.86.016311
143. Shemer L, Alperovich L. Peregrine Breather Revisited. Phys Fluids (2013) 25:051701. doi:10.1063/1.4807055
144. Chabchoub A, Hoffmann N, Branger H, Kharif C, Akhmediev N. Experiments on Wind-Perturbed Rogue Wave Hydrodynamics Using the Peregrine Breather Model. Phys Fluids (2013) 25:101704. doi:10.1063/1.4824706
145. Onorato M, Proment D, Clauss G, Klein M. Rogue Waves: From Nonlinear Schrödinger Breather Solutions to Sea-Keeping Test. PLOS One (2013) 8:e54629. doi:10.1371/journal.pone.0054629
146. Yurova A. A Hidden Life of Peregrine's Soliton: Rouge Waves in the Oceanic Depths. Int J Geom Methods Mod Phys (2014) 11:1450057. doi:10.1142/s0219887814500571
147. Li S, Prinari B, Biondini G. Solitons and Rogue Waves in Spinor Bose-Einstein Condensates. Phys Rev E (2018) 97:022221. doi:10.1103/physreve.97.022221
148. Cazaubiel A, Michel G, Lepot S, Semin B, Aumaître S, Berhanu M, et al. Coexistence of Solitons and Extreme Events in Deep Water Surface Waves. Phys Rev Fluids (2018) 3:114802. doi:10.1103/physrevfluids.3.114802
149. Randoux S, Suret P, Chabchoub A, Kibler B, El G. Nonlinear Spectral Analysis of Peregrine Solitons Observed in Optics and in Hydrodynamic Experiments. Phys Rev E (2018) 98:022219. doi:10.1103/physreve.98.022219
150. Gaillard P. Multi-parametric Deformations of Peregrine Breathers Solutions to the NLS Equation. Adv Res (2015) 4:346–364. doi:10.9734/air/2015/16827
151. Akhmediev N, Ankiewicz A, Soto-Crespo JM. Rogue Waves and Rational Solutions of the Nonlinear Schrödinger Equation. Phys Rev E (2009c) 80:026601. doi:10.1103/physreve.80.026601
152. Chen S, Baronio F, Soto-Crespo JM, Grelu P, Mihalache D. Versatile Rogue Waves in Scalar, Vector, and Multidimensional Nonlinear Systems. J Phys A: Math Theor (2017) 50:463001. doi:10.1088/1751-8121/aa8f00
153. Malomed BA, Mihalache D. Nonlinear Waves in Optical and Matter-Wave Media: A Topical Survey of Recent Theoretical and Experimental Results. Rom J Phys (2019) 64:106.
154. Zhao L-C, Ling L. Quantitative Relations between Modulational Instability and Several Well-Known Nonlinear Excitations. J Opt Soc Am B (2016) 33:850–856. doi:10.1364/josab.33.000850
155. Toenger S, Godin T, Billet C, Dias F, Erkintalo M, Genty G, et al. Emergent Rogue Wave Structures and Statistics in Spontaneous Modulation Instability. Scientific Rep (2015) 5:10380. doi:10.1038/srep10380
156. Kibler B, Chabchoub A, Gelash A, Akhmediev N, Zakharov VE. Superregular Breathers in Optics and Hydrodynamics: Omnipresent Modulation Instability beyond Simple Periodicity. Phys Rev X (2015) 5:041026. doi:10.1103/physrevx.5.041026
157. Liu XS, Zhao LC, Duan L, Gao P, Yang ZY, Yang WL. Interaction between Breathers and Rogue Waves in a Nonlinear Optical Fiber. Chin Phys Lett (2018) 35:020501. doi:10.1088/0256-307x/35/2/020501
158. Veldes G, Borhanian J, McKerr M, Saxena V, Frantzeskakis D, Kourakis I. Electromagnetic Rogue Waves in Beam-Plasma Interactions. J Opt (2013) 15:064003. doi:10.1088/2040-8978/15/6/064003
159. Shen Y, Kevrekidis P, Veldes G, Frantzeskakis D, DiMarzio D, Lan X, et al. From Solitons to Rogue Waves in Nonlinear Left-Handed Metamaterials. Phys Rev E (2017) 95:032223. doi:10.1103/physreve.95.032223
160. Albares P, Díaz E, Cerveró JM, Domínguez-Adame F, Diez E, Estévez P. Solitons in a Nonlinear Model of Spin Transport in Helical Molecules. Phys Rev E (2018) 97:022210. doi:10.1103/physreve.97.022210
161. Farazmand M, Sapsis TP. Extreme Events: Mechanisms and Prediction. Appl Mech Rev (2019) 71. doi:10.1115/1.4042065
162. Zhang Y, Belić MR, Zheng H, Chen H, Li C, Song J, et al. Nonlinear Talbot Effect of Rogue Waves. Phys Rev E (2014) 89:032902. doi:10.1103/physreve.89.032902
163. Akhmediev N, Kibler B, Baronio F, Belić M, Zhong WP, Zhang Y, et al. Roadmap on Optical Rogue Waves and Extreme Events. J Opt (2016) 18:063001. doi:10.1088/2040-8978/18/6/063001
164. Kimmoun O, Hsu H, Branger H, Li M, Chen YY, Kharif C, et al. Modulation Instability and Phase-Shifted Fermi-Pasta-Ulam Recurrence. Scientific Rep (2016) 6:28516. doi:10.1038/srep28516
165. Biondini G, Mantzavinos D. Universal Nature of the Nonlinear Stage of Modulational Instability. Phys Rev Lett (2016) 116:043902. doi:10.1103/physrevlett.116.043902
166. Biondini G, Li S, Mantzavinos D Oscillation Structure of Localized Perturbations in Modulationally Unstable Media. Phys Rev E (2016) 94:060201. doi:10.1103/physreve.94.060201
167. Gelash AA, Zakharov VE. Superregular Solitonic Solutions: a Novel Scenario for the Nonlinear Stage of Modulation Instability. Nonlinearity (2014) 27:R1–38. doi:10.1088/0951-7715/27/4/r1
168. Chen J, Pelinovsky DE. Rogue Periodic Waves of the Focusing Nonlinear Schrödinger Equation. Proc R Soc A (2018) 474:20170814. doi:10.1098/rspa.2017.0814
169. Xu G, Gelash A, Chabchoub A, Zakharov V, Kibler B. Breather Wave Molecules. Phys Rev Lett (2019) 122:084101. doi:10.1103/physrevlett.122.084101
Keywords: nonlinear Schrödinger equation, Kuznetsov-Ma breather, Akhmediev soliton, Peregrine soliton, modulational instability, rogue waves, homoclinic orbit, limiting behavior
Citation: Karjanto N (2021) Peregrine Soliton as a Limiting Behavior of the Kuznetsov-Ma and Akhmediev Breathers. Front. Phys. 9:599767. doi: 10.3389/fphy.2021.599767
Received: 28 August 2020; Accepted: 18 January 2021;
Published: 27 September 2021.
Edited by:
Bertrand Kibler, UMR6303 Laboratoire Interdisciplinaire Carnot de Bourgogne (ICB), FranceReviewed by:
Gang Xu, The University of Auckland, New ZealandCopyright © 2021 Karjanto. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Natanael Karjanto, bmF0YW5hZWxAc2trdS5lZHU=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.