Generation of Hybrid Optical Trap Array by Holographic Optical Tweezers

Enabled by multiple optical traps, holographic optical tweezers can manipulate multiple particles in parallel flexibly. Spatial light modulators are widely used in holographic optical tweezers, in which Gaussian point (GP) trap arrays or special mode optical trap arrays including optical vortex (OV) arrays, perfect vortex (PV) arrays, and Airy beam arrays, etc., can be generated by addressing various phase holograms. However, the optical traps in these arrays are almost all of the same type. Here, we propose a new method for generating a hybrid optical trap array (HOTA), where optical traps such as GPs, OVs, PVs, and Airy beams in the focal plane are combined arbitrarily. Also, the axial position and peak intensity of each them can be adjusted independently. The energy efficiency of this method is theoretically studied, while different micro-manipulations on multiple particles have been realized with the support of HOTA experimentally. The proposed method expands holographic optical tweezers’ capabilities and provides a new possibility of multi-functional optical micro-manipulation.

Introduction

Since the pioneering works of Ashkin [1, 2], optical tweezers have become a non-invasive technology for manipulating micro/nano particles. They have been widely used in physics, biology, medicine, and other fields [3–10]. Spatial light modulators (SLMs) have promoted the development of optical tweezers into a universal micro-manipulation tool [11], called holographic optical tweezers [12, 13], which surpass the original configuration of using a single laser spot to trap particles. SLMs use computer-generated-holograms (CGHs) to flexibly shape the wavefront of the laser beam, generating Gaussian point (GP) trap arrays or arrays of special optical modes, such as optical vortex (OV), perfect vortex (PV), and Airy beam. These are essential for a range of applications, including beam shaping, multi-beam laser processing, and optical micro-manipulation [14–17].

Due to the excellent flexibility of holographic beam shaping, complexly optical patterns can be tailored in favor of specific applications, such as high-resolution optical imaging, optical lithography, metamaterial manufacturing, and optical trapping and manipulation [14–21]. In holographic optical tweezers, the most commonly used light field distribution is the optical trap array. GP trap arrays can be realized by the Gerchberg-Saxton (GS) algorithm, weighted Gerchberg-Saxton (GSW) algorithm, and other improved iterative Fourier transform methods [22, 23]. Some unique methods were used to generate multifocal arrays, such as using fractional Talbot effect [24], two-dimensional (2D) pure-phase modulation gratings [25], and multizone phase plates [26], etc. OV arrays containing multiple vortices have been extensively studied [27–29]. Harshith et al. [30] used a dielectric microlens-array (MLA) and a plano-convex lens to generate OV arrays. OV arrays were also produced by interference methods [31–33]. In addition, the arrangement of multiple OVs can be a rectilinear, a square array [34], or along an arbitrary curve [35]. PV arrays were generated by various approaches, including the use of two-dimensional continuous phase gratings [36], and curved fork gratings [37]. Deng et al. [38] reported a three-dimensional (3D) PV array with high quality and uniform intensity by a special designed hybrid phase plate. Multiple Airy beams can also form arrays [39]. Jin et al. [40] defined a square array composed of four Airy beams, and each Airy beam can carry a different vortex. Qian et al. [41] developed a circular array consisting of multiple Airy beams. Moreover, hybrid arrays composed of GPs and OVs were reported [42, 43]. PV arrays composed of different topological charges were also generated by unique methods such as multi-zone plates and holographic gratings [44, 45]. However, it seems that little work has been reported on hybrid arrays composed of arbitrary combination of GPs, OVs, PVs, and Airy beams.

In this paper, we propose using the phase-only liquid crystal SLM to generate a hybrid optical trap array (HOTA), in which arbitrary combinations of optical traps such as GPs, OVs, PVs, and Airy beams appear in the focal plane simultaneously. We propose a new method to calculate the required CGH in the objective lens's back focal plane. By using the improved GSW algorithm to iterate all the holograms corresponding to the targeted traps, a single hologram that can produce the desired HOTA is obtained. The experimental measurement results are almost consistent with the intensity distributions obtained by the theoretical simulation. We studied the improvement of energy efficiency with the number of iterations, the movement of the axial position of the optical trap, and the change of peak intensity. We experimentally prove that our method can be applied to holographic optical tweezers, and may significantly expand their manipulation capabilities and provide a new possibility of multi-functional optical micro-manipulation.

Methods

Principle of Generating HOTA

The technique of using a computer-generated-hologram (CGH) or computer-designed diffractive optical element (DOE) to modulate the wavefront of the incident light field and then generating the target light field through Fourier transform is called holographic beam shaping [42, 46]. The principle is shown in Figure 1. The phase-only liquid crystal SLM acts as a DOE and displays a hologram to modulate the incident light field. The SLM is located on the back focal plane (Hologram plane) of the Fourier lens with a focal length of f. A combination of different optical traps, such as GPs, OVs, PVs, and Airy beams, etc., is generated near the front focal plane (Fourier plane). The OV carrying the orbital angular momentum (OAM) has a hollow intensity distribution, and the radius of its bright ring depends on the topological charge l. In contrast, the ring radius of the PV is independent of the topological charge. For the convenience of description, we use OV_l and PV_l to denote the OV and PV with a topological charge of l, respectively. The Airy beam has the characteristic of freely accelerating along a curved trajectory. The holograms addressed on the SLM and corresponding intensity patterns on the Fourier plane of the GP, OV₊₁₅, PV_0, and Airy beam are shown in Figure 2.

FIGURE 1

FIGURE 1. Schematic diagram of holographic beam shaping.

FIGURE 2

FIGURE 2. Holograms and intensity patterns of the Gaussian point (GP), optical vortex (OV₊₁₅), perfect vortex (PV₀), and Airy beam.

Assume the incident optical field is a uniform plane wave with a unit amplitude of 1. After modulated by the SLM, the field’s complex amplitude at the jth pixel on the Hologram plane is $u_j=\exp \left(i{\varphi }_j\right)$, where ${\varphi }_j$ is the phase of the jth pixel. By the Fresnel diffraction theory, the complex amplitude v_m of the mth optical trap is the sum of the contribution from all pixels of the SLM [47, 48]:

$v_m=\frac{e^{i2\pi \left(2f+z_m\right)/\lambda }}{i}\frac{d^2}{\lambda f}{\displaystyle \sum }_{j=1}^N{e}^{i\left({\varphi }_j-{\Delta }_j^m-{\psi }_j^m\right)},(1)$

with

${\Delta }_j^m=\frac{\pi z_m}{\lambda f^2}\left(x_j^2+y_j^2\right)+\frac{2\pi }{\lambda f}\left(x_j{x}_m+y_j{y}_m\right).(2)$

Here, λ is the wavelength of the incident light, d is the size of a single pixel of SLM, and N is the total number of pixels; f represents the focal length of the Fourier lens, (x_j, y_j), are the coordinates of the jth pixel on the Hologram plane, and (x_m, y_m, z_m) are the coordinates of the mth optical trap. Since we deal with generic traps, not only point traps, an additional phase ${\psi }_j^m$ corresponding to the mth optical trap is added to the phase part in Eq. 1.

Algorithm for HOTA

Our primary objective is to seek the phase ${\varphi }_j$. Using the GSW algorithm [48], the phase ${\varphi }_j$ is found to be:

${\varphi }_j=arg\left[{\displaystyle \sum }_{m=1}^M{e}^{i{\Delta }_j^m}\frac{w_m{\alpha }_m{V}_m}{\left|V_m\right|}\right],(3)$

where

$V_m=\frac{1}{N}{\displaystyle \sum }_{j=1}^N{e}^{i\left({\varphi }_j-{\Delta }_j^m-{\psi }_j^m\right)}. (4)$

Here w_m is the weighting factor, and M is the total number of optical traps. Unlike the standard GSW, we have introduced a new parameter ${\alpha }_m$ in Eq. 3 to adjust the energy of the optical trap m.

The improved GSW algorithm, depicted in Figure 3, starts with the given ${\psi }_j^m$, ${\alpha }_m$ and K. ${\psi }_j^m$ is the phase of generating the target trap m, and the four phase patterns of ${\psi }_j^m$ are shown in the first column of Figure 2${\alpha }_m$ is a constant with respect to the optical trap m. K is the maximum number of iterations, which is generally set to 30 in our simulation. Before entering the iteration loop, w_m, ${\varphi }_j$, and V_m need to be initialized. The initial values of w_m and ${\varphi }_j$ are $w_m^{\left(0\right)}=1$ and ${\varphi }_j^{\left(0\right)}= 2\pi \cdot \text{rand}\left(\mathrm{0,1}\right)$, respectively. The ${\varphi }_j^{\left(0\right)}$ is an arbitrary guessed phase. The function of rand (0,1) means to generate a uniform random number between 0 and 1. The initial value of V_m is:

$V_m^{\left(0\right)}=\frac{1}{N}{\displaystyle \sum }_{j=1}^N{e}^{i\left({\varphi }_j^{\left(0\right)}-{\Delta }_j^m-{\psi }_j^m\right)}.(5)$

FIGURE 3

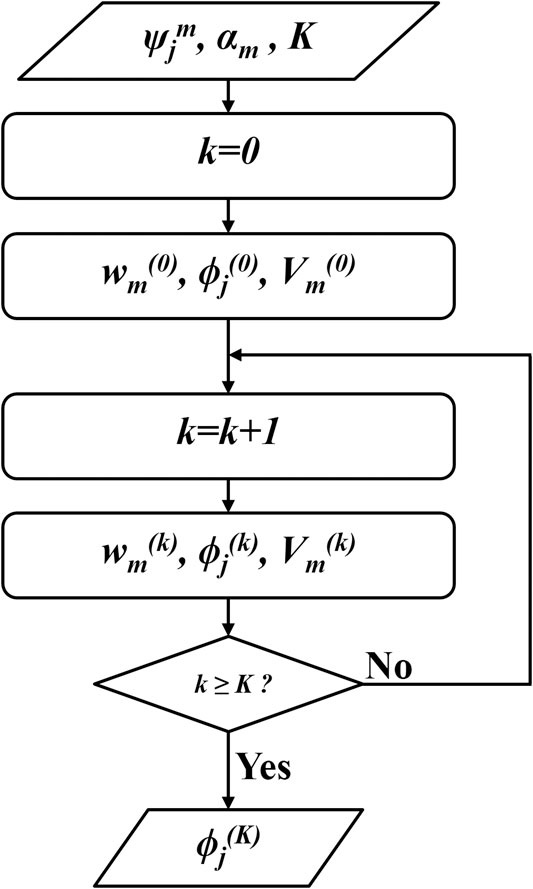
FIGURE 3. The flow chart of the improved GSW algorithm for HOTA. ${\varphi }_j$ is updated in each loop and reaches the estimated value ${\varphi }_j^{\left(k\right)}$ after K iterations, generating the required HOTA.

Then the program enters iterative loops. In the kth iteration, $w_m^{\left(k\right)}$, ${\varphi }_j^{\left(k\right)}$ and $V_m^{\left(k\right)}$ are

$w_m^{\left(k\right)}=\frac{\langle \left|V_m^{\left(k-1\right)}\right|/{{\alpha }_m\rangle }_{{ }_m}}{\left|V_m^{\left(k-1\right)}\right|/{\alpha }_m}{w}_m^{\left(k-1\right)},(6)$

${\varphi }_j^{\left(k\right)}=arg\left[{\displaystyle \sum }_{m=1}^M{e}^{i{\Delta }_j^m}\frac{w_m^{\left(k\right)}{\alpha }_m{V}_m^{\left(k-1\right)}}{\left|V_m^{\left(k-1\right)}\right|}\right],(7)$

$V_m^{\left(k\right)}=\frac{1}{N}{\displaystyle \sum }_{j=1}^N{e}^{i\left({\varphi }_j^{\left(k\right)}-{\Delta }_j^m-{\psi }_j^m\right)}, (8)$

where $<•{>}_m$ denotes the average value with respect to the index m. This completes one iteration. Subsequent iterations lead to continuous updates of ${\varphi }_j$. After K iterations, the loops end. When the program reaches this step, ${\varphi }_j^{\left(K\right)}$ is a relatively ideal estimation, which can produce the HOTA we need.

Experimental Setup

Figure 4 is an illustration of the holographic optical tweezers system used in our experiment. A linearly polarized laser beam (λ = 1064 nm) is expanded and collimated by a telescope composed of lenses L1 and L2. After passing through a half-wave plate (HWP) and a polarizing beam splitter (PBS), the input beam is polarized horizontally. The HWP adjusts the power of the laser. To miniaturize the experimental setup, a specially designed 96° prism is used to reflect the beam to the phase-only liquid crystal SLM (Pluto-HED6010-NIR-049-C, Holoeye Photonics AG Inc., Germany, 1,920 × 1,080 pixels, pixel pitch: 8.0 μm) while only the central area of 1,080 × 1,080 pixels (i.e., N = 1,080 × 1,080) is used. Lenses L3 and L4 form a 4f system, which relays the SLM plane to the back focal plane of the objective lens (Nikon Plan Apo IR, Japan, ×60, NA = 1.27, water immersion). The QWP is used to convert the linearly polarized beam into the circularly polarized one. After the objective lens focuses the beam, the required HOTA is observed in a region near the front focal plane. To map the intensity distribution of the generated field, a mirror M5, placed near the front focal plane, is employed to reflect the light to pass through in sequence objective lens, filter F and tube lens L5 and finally onto CMOS camera (Point Gray GS3-U3-41C6M-C, FLIR System Inc., United States, 2048 × 2,048 pixels, pixel pitch: 5.5 μm). When micro-manipulation experiments operate, the mirror M5 is replaced by a sample. The sample chamber consisting of double-sided tape, a cover-slip, and a slide, contains an aqueous solution of 2 μm in diameter polystyrene (PS) microspheres. Currently, there are already some softwares that can be used for optical trapping [49–51]. They can generate a variety of holograms and call the SLM to address holograms. In our experiment, we use MATLAB program to implement our proposed algorithm. After obtaining the hologram, the software provided by the SLM manufacturer is used to address the hologram. Simultaneously, the software also provides a method to correct the aberration, which is an essential factor that affects the quality of HOTA. The aberration of our system is mainly astigmatism caused by the uneven reflective surface of the SLM. In the commercial SLM software, we corrected that to improve the quality and manipulation performance of the HOTA by using the preset Zernike polynomials.

FIGURE 4

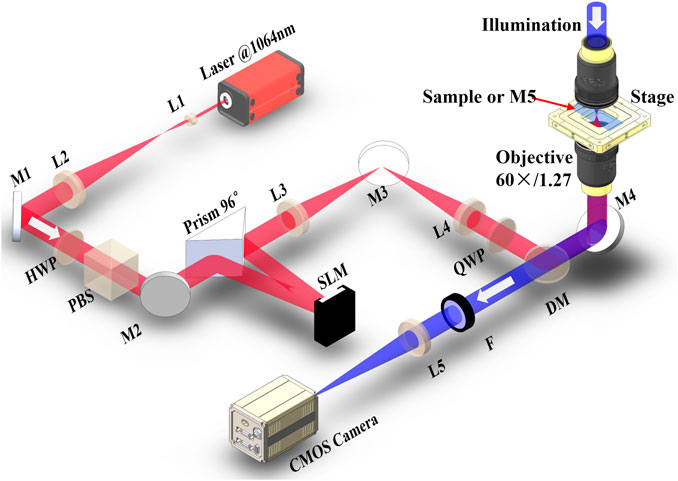
FIGURE 4. Schematic diagram of the holographic optical tweezers system used to generate HOTAs. L, lens; M, mirror; HWP, half-wave plate; PBS, polarizing beam splitter; QWP, quarter-wave plate; DM, dichroic mirror; F, filter; SLM, spatial light modular; CMOS, complementary metal oxide semiconductor.

Results and Discussion

Generation and Characterization of HOTA

We first generate an array composed of four types of optical traps: GPs, OVs, PVs, and Airy beams, as shown in Figure 5. Figure 5A shows ${\varphi }_j$ obtained after 30 iterations. In Figure 5B, columns 1 to 4 present four GPs, four OVs with a topological charge of l = +15, four PVs with a topological charge of l = 0, and four Airy beams, respectively. Figure 5C shows the xz-plane (y = 7.5 μm) intensity distribution of the field in Figure 5B. Figures 5D,E are the intensity distributions in the yz-plane, corresponding to x = −7.5 μm and x = 7.5 μm in Figure 5B, respectively. Although both OV₊₁₅ and PV₀ are of a ring shape in the xy-plane, they are quite different in the yz-plane. Due to the difficulty of detecting the intensity distribution in the axial plane, only the xy-plane intensity distribution is presented, as shown in Figure 5F, from which we see a good agreement between the experiment and the simulation results.

FIGURE 5

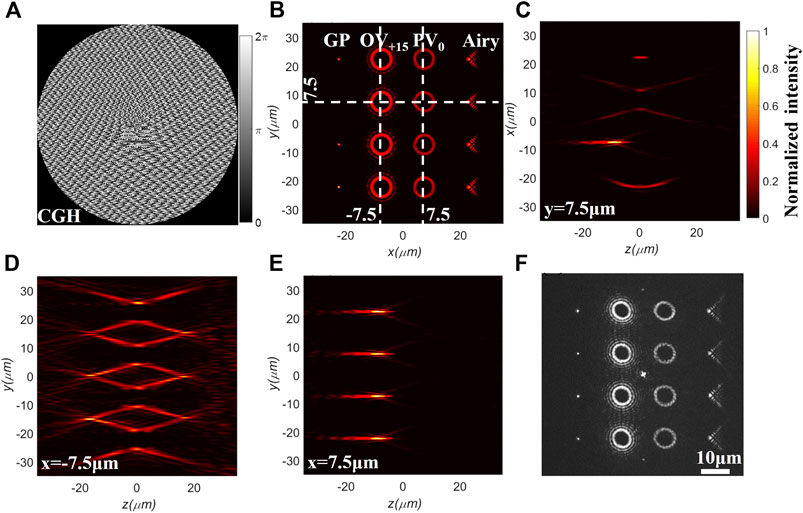
FIGURE 5. An array composed of four types of optical traps: GPs, OVs, PVs, and Airy beams. (A) Hologram addressed on SLM. (B) The intensity distribution of the xy-plane obtained by the simulation. (C) The intensity distribution of the xz-plane obtained by the simulation corresponding to the dashed line y = 7.5 μm in (B). (D,E) The intensity distributions in yz-plane obtained by simulation corresponding to the dashed line x = −7.5 μm and x = 7.5 μm in (B), respectively. (F) The intensity distribution of the xy-plane obtained from the experiment. The center highlight is the zero-order spot of SLM.

The Dependence of the Energy Efficiency on the Number of Iterations

We next investigate the energy efficiency of the proposed HOTA and define that as [48].

$e={\displaystyle \sum }_{m=1}^M{\left|V_m\right|}^2.(9)$

It measures the ratio of the energy diffracted to all M optical traps to the incident energy. Higher energy efficiency means more energy is used and less energy is diffracted into ghost traps. The traditional GSW algorithm can improve the energy efficiency of multiple optical traps through iterations. Here, the improved GSW also helps to increase the light energy utilization. Figure 6 shows that as the number of iterations increases, the light energy is gradually concentrated into the designed optical traps. The energy efficiency is gradually increased from ∼0.55 at the beginning of the iteration to ∼0.907 after 30 iterations. In this example, the average time for each iteration is ∼0.67 s on our computer (Intel Core i5 CPU 760@2.80GHz). After 16 iterations, energy efficiency no longer increases, indicating that the algorithm has converged.

FIGURE 6

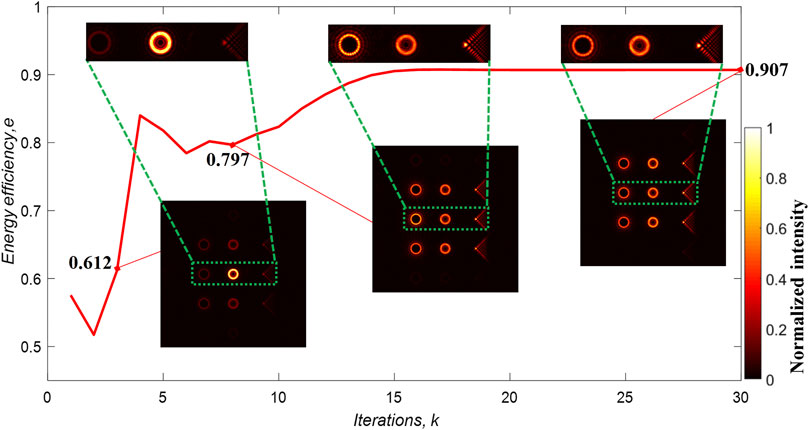
FIGURE 6. The behavior of energy efficiency is shown as a function of the number of iterations. After 3, 8, and 30 iterations, the energy efficiency becomes 0.612, 0.797, and 0.907, respectively. In the bottom insets, the first to third columns of each one are OVs with l = +15, PVs with l = +5, and Airy beams, respectively.

Individual Adjustment of the Axial Position

In Eq. 2, the coordinates of the optical trap m are x_m, y_m, and z_m, which can be changed to adjust three-dimensional (3D) positions of optical traps. x_m and y_m can adjust positions of optical traps in the xy-plane. They change the lateral distance between optical traps. In order to show that the proposed method can control the three-dimensional position of optical traps, we change z_m to adjust the axial position of optical traps. In Figure 7, the optical traps in the red, green and blue dashed areas are located at z = −15 μm, z = 0, and z = 15 μm, respectively. The simulation results demonstrate that different holograms can be used to make optical traps move along the optical axis. Combined with the movement in the lateral plane, the generated HOTA can realize the control of the 3D position.

FIGURE 7

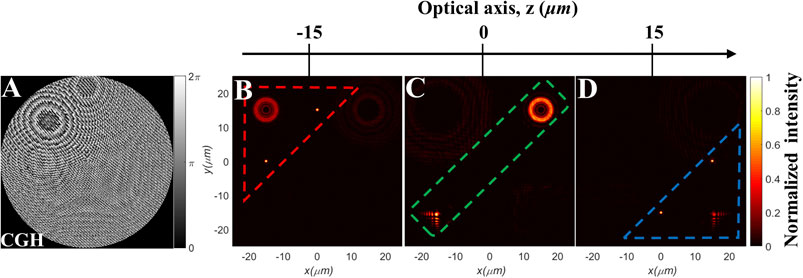
FIGURE 7. The generated hybrid optical traps at different axial positions. (A) Hologram. (B) A PV₊₅ and two GPs inside the red dashed line, located in the plane of z = −15 μm. (C) A PV_-5 and an Airy beam inside the green dashed line, located in the plane of z = 0. (D) An Airy beam and two GPs inside the blue dashed line, located in the plane of z = +15 μm.

Individual Adjustment of Peak Intensity

The ability to regulate the energy ratio between multiple optical traps allows researchers to customize force magnitude flexibly. Xu et al. [52] used a complementary random phase encoding technique to separately regulate each trap energy of multiple traps. However, all optical traps are Gaussian point traps, which are different from the HOTA we need as it contains various types of optical traps. If the GSW algorithm in [48] is used directly (that is, all types of beams are weighted equally), the energy allocated to GPs, OVs, PVs, and Airy beams will be equal. However, in the optical trapping and manipulation experiments, GPs and Airy traps demand much lower working energy than the OVs and PVs. Therefore, it is necessary to make the energy of different types of beams unequal. In order to achieve this goal, we introduce a new parameter ${\alpha }_m$ to the original GSW algorithm to adjust the energy ratio among the optical traps. The values of ${\alpha }_m$ are given based on empirical estimation: the energy obtained by an optical trap increases with increasing the value of the corresponding ${\alpha }_m$. In Figure 8, when we change the ratio among α₁, α₂, α₃, and α₄, the peak intensity of the corresponding optical trap changes. In Figure 8A, α₁, α₂, α₃, and α₄ are 2.6, 2.6, 1, and 1, respectively. We keep α₁ and α₃ unchanged and reduce α₂ to 1.3, and α₄ to 0.5. The corresponding peak intensities decrease, as shown in Figure 8B. By the comparison among Figure 8(A), (B), and (C), we can find that an optical trap with a larger α_m will have more energy. Therefore, if we change the relative value of the ${\alpha }_m$, we can indeed control the energy obtained by the optical trap m.

FIGURE 8

FIGURE 8. Adjusting the peak intensity of different optical traps. (A) The peak intensities of the four optical traps are approximately equal. α₁, α₂, α₃, and α₄ are 2.6, 2.6, 1, and 1, respectively. (B) Keep the peak intensities of optical traps 1 and 3, while the peak intensities of optical traps 2 and 4 are relatively weakened. α₁, α₂, α₃, and α₄ are 2.6, 1.3, 1, and 0.5, respectively. (C) Keep the peak intensities of optical traps 2 and 3, while the peak intensities of optical traps 1 and 4 are relatively weakened. α₁, α₂, α₃, and α₄ are 1.3, 2.6, 1, and 0.5, respectively.

Micro-Particles Trapping and Manipulation With HOTA

Figures 9B,C show the simulation and experimental results for a trap array: four vortices (OV₊₁₅, PV₊₁₀, OV₋₁₅, and PV₋₁₀) and four GPs. From Figures 9D–I, the difference between the direction of rotation among different vortices can be seen: OV₊₁₅ and PV₊₁₀ trap PS microspheres and rotate them counterclockwise, while OV₋₁₅ and PV₋₁₀ give rise to an opposite rotational sense. Each of the four GPs traps a PS microsphere, and the zero-order diffracted focal spot (center) also traps a PS microsphere. But each GP can also trap more than one PS microsphere (see the Supplementary Material Video S1). In Figures 9D–I, the optical trap in the upper left corner (OV₊₁₅) drives the PS microsphere to rotate counterclockwise, and it takes about 0.42 s to complete one full cycle. The optical trap in the lower right corner (PV₊₁₀) drives the PS microsphere to rotate counterclockwise and takes about 0.46 s per cycle. Our experimental results on trapping and manipulating micro-particles demonstrate that HOTA can provide multiple types of manipulation simultaneously.

FIGURE 9

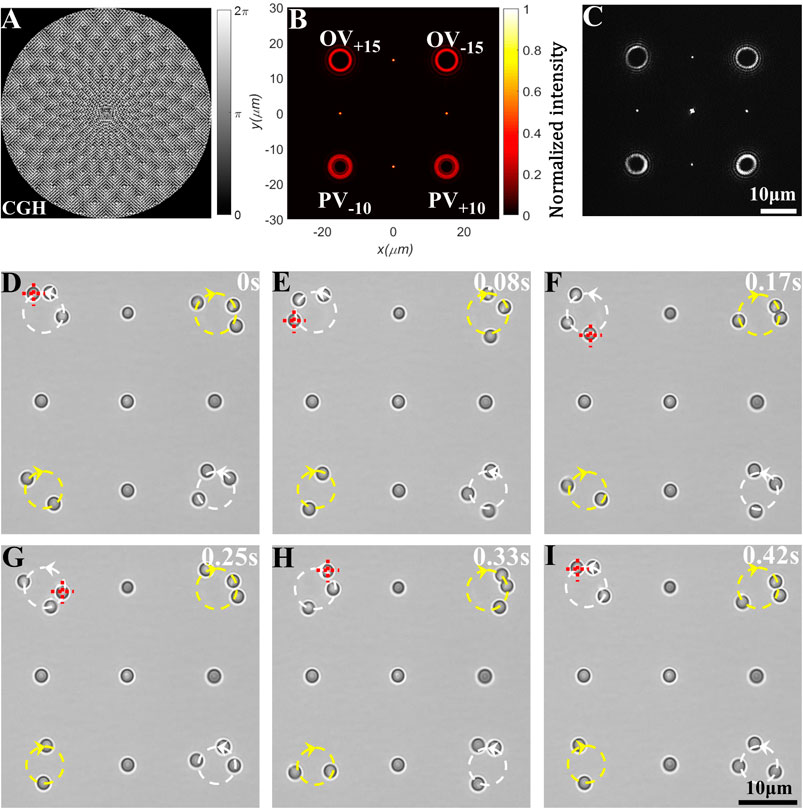
FIGURE 9. Various types of manipulation of PS microspheres with HOTA by holographic optical tweezers. (A) Hologram addressed on SLM. (B) The intensity pattern in the focal plane obtained by simulation, which is composed of OV_±15, PV_±10, and 4 GPs. (C) The intensity pattern in the focal plane measured experimentally. The bright spot in the center is the zero-order beam of the SLM. (D–I) Snapped video frames of manipulating PS microspheres at a sequential time point. At the optical trap of OV₊₁₅ in the upper left corner, the PS microspheres undergo a counterclockwise rotation of about 0.42 s per cycle.

Conclusion

We have proposed a method for generating a hybrid optical trap array. Addressing a hologram on the phase-only SLM can generate various types of optical traps near the focal plane of the objective lens. Our simulation results reveal that the energy efficiency can be improved by increasing the number of iterations and stabilized after a dozen iterations. The optical traps' axial positions can be independently controlled, and multiple optical traps are located on different planes. The peak intensity of the optical traps can be adjusted by the parameter ${\alpha }_m$. Experimental and simulation results of intensity distributions are in good agreement. Our method has two main differences compared with the previous method: one is that the energy ratio among different optical traps can be adjusted to meet the need for optical trapping and manipulation. The second is that it can generate hybrid optical trap arrays formed by arbitrary combinations of GPs, OVs, PVs, and Airy beams, etc. Furthermore, we demonstrate that the generated HOTA can trap and rotate 2 μm PS microspheres in expected manners. These experimental results strongly support the theoretical simulation and prove that the proposed method can simultaneously generate different types of optical traps, such as GPs, OVs, PVs, and Airy beams, etc., with good energy efficiency, adjustable axial positions, and controllable peak intensities of the optical traps. The proposed method has potential applications in the fields of beam shaping, optical trapping, and optical processing.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

XL conceived the idea. XL, YuZ, and YC constructed the experimental setup and experimented. YaZ, SY, ML, and RL contributed to discussing the results and the theoretical simulation. XL wrote and edited the manuscript. BY supervised the study. All the authors reviewed and revised the manuscript.

Funding

National Natural Science Foundation of China (NSFC) (11974417 and 11904395).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.591747/full#supplementary-material.

References

1. Ashkin A. Acceleration and trapping of particles by radiation pressure. Phys Rev Lett (1970) 24:156–9. doi:10.1103/physrevlett.24.156

CrossRef Full Text | Google Scholar

2. Ashkin A, Dziedzic JM, Bjorkholm JE, Chu S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt Lett (1986) 11:288–90. doi:10.1364/OL.11.000288

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Chu S. Nobel Lecture: the manipulation of neutral particles. Rev Mod Phys (1998) 70:685–706. doi:10.1103/REVMODPHYS.70.685

CrossRef Full Text | Google Scholar

4. Phillips WD. Nobel Lecture: laser cooling and trapping of neutral atoms. Rev Mod Phys (1998) 70:721–41. doi:10.1103/REVMODPHYS.70.721

CrossRef Full Text | Google Scholar

5. Diekmann R, Wolfson DL, Spahn C, Heilemann M, Schüttpelz M, Huser T. Nanoscopy of bacterial cells immobilized by holographic optical tweezers. Nat Commun (2016) 7:13711. doi:10.1038/NCOMMS13711

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Landenberger B, Höfemann H, Wadle S, Rohrbach A. Microfluidic sorting of arbitrary cells with dynamic optical tweezers. Lab Chip (2012) 12:3177–83. doi:10.1039/C2LC21099A

PubMed Abstract | CrossRef Full Text | Google Scholar

7. McAlinden N, Glass DG, Millington OR, Wright AJ. Accurate position tracking of optically trapped live cells. Biomed Opt Express (2014) 5:1026–37. doi:10.1364/BOE.5.001026

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Perkins T, Quake SR, Smith DE, Chu S. Relaxation of a single DNA molecule observed by optical microscopy. Science (1994) 264:822–6. doi:10.1126/SCIENCE.8171336

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Neuman KC, Nagy A. Single-molecule force spectroscopy: optical tweezers, magnetic tweezers and atomic force microscopy. Nat Methods (2008) 5:491–505. doi:10.1038/NMETH.1218

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Polimeno P, Magazzù A, Iatì MA, Patti F, Saija R, Boschi CDE, et al. Optical tweezers and their applications. J Quant Spectrosc Radiat Transfer (2018) 218:131–50. doi:10.1016/J.JQSRT.2018.07.013

CrossRef Full Text | Google Scholar

11. Forbes A, Dudley A, McLaren M. Creation and detection of optical modes with spatial light modulators. Adv Opt Photon (2016) 8:200–27. doi:10.1364/AOP.8.000200

CrossRef Full Text | Google Scholar

12. Grier DG. A revolution in optical manipulation. Nature (2003) 424:810–6. doi:10.1038/NATURE01935

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Dholakia K, MacDonald M, Spalding G. Optical tweezers: the next generation. Phys World (2002) 15:31–5. doi:10.1088/2058-7058/15/10/37

CrossRef Full Text | Google Scholar

14. Obata K, Koch J, Hinze U, Chichkov BN. Multi-focus two-photon polymerization technique based on individually controlled phase modulation. Opt Express (2010) 18:17193–200. doi:10.1364/OE.18.017193

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Gan Z, Cao Y, Evans RA, Gu M. Three-dimensional deep sub-diffraction optical beam lithography with 9 nm feature size. Nat Commun (2013) 4:2061. doi:10.1038/NCOMMS3061

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Paterson L, MacDonald MP, Arlt J, Sibbett W, Bryant PE, Dholakia K. Controlled rotation of optically trapped microscopic particles. Science (2001) 292:912–4. doi:10.1126/SCIENCE.1058591

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Woerdemann M, Alpmann C, Esseling M, Denz C. Advanced optical trapping by complex beam shaping. Laser Photon Rev (2013) 7:839–54. doi:10.1002/LPOR.201200058

CrossRef Full Text | Google Scholar

18. Shao Y, Qu J, Li H, Wang Y, Qi J, Xu G, et al. High-speed spectrally resolved multifocal multiphoton microscopy. Appl Phys B: Lasers Opt (2010) 99:633–7. doi:10.1007/S00340-010-4066-Y

CrossRef Full Text | Google Scholar

19. Arai Y, Yasuda R, Akashi K, Harada Y, Miyata H, Kinosita K, et al. Tying a molecular knot with optical tweezers. Nature (1999) 399:446–8. doi:10.1038/20894

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Jia B, Kang H, Li J, Gu M. Use of radially polarized beams in three-dimensional photonic crystal fabrication with the two-photon polymerization method. Opt Lett (2009) 34:1918–20. doi:10.1364/OL.34.001918

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Zhuang X. Molecular biology. Unraveling DNA condensation with optical tweezers. Science (2004) 305:188–90. doi:10.1126/SCIENCE.1100603

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Duadi H, Zalevsky Z. Optimized design for realizing a large and uniform 2-D spot array. J Opt Soc Am A Opt Image Sci Vis (2010) 27:2027–32. doi:10.1364/JOSAA.27.002027

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Kim D, Keesling A, Omran A, Levine H, Bernien H, Greiner M, et al. Large-scale uniform optical focus array generation with a phase spatial light modulator. Opt Lett (2019) 44:3178–81. doi:10.1364/OL.44.003178

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Zhu L, Yu J, Zhang D, Sun M, Chen J. Multifocal spot array generated by fractional Talbot effect phase-only modulation. Opt Express (2014) 22:9798–808. doi:10.1364/OE.22.009798

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Zhu L, Sun M, Zhu M, Chen J, Gao X, Ma W, et al. Three-dimensional shape-controllable focal spot array created by focusing vortex beams modulated by multi-value pure-phase grating. Opt Express (2014) 22:21354–67. doi:10.1364/OE.22.021354

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Mu T, Chen Z, Pacheco S, Wu R, Zhang C, Liang R. Generation of a controllable multifocal array from a modulated azimuthally polarized beam. Opt Lett (2016) 41:261–4. doi:10.1364/OL.41.000261

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Liu J, Min C, Lei T, Du L, Yuan Y, Wei S, et al. Generation and detection of broadband multi-channel orbital angular momentum by micrometer-scale meta-reflectarray. Opt Express (2016) 24:212–8. doi:10.1364/OE.24.000212

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Yu J, Zhou C, Jia W, Hu A, Cao W, Wu J, et al. Generation of dipole vortex array using spiral Dammann zone plates. Appl Opt (2012) 51:6799–804. doi:10.1364/AO.51.006799

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Lin YC, Lu TH, Huang KF, Chen YF. Generation of optical vortex array with transformation of standing-wave Laguerre-Gaussian mode. Opt Express (2011) 19:10293–303. doi:10.1364/OE.19.010293

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Harshith BS, Samanta GK. Controlled generation of array beams of higher order orbital angular momentum and study of their frequency-doubling characteristics. Sci Rep (2019) 9:10916. doi:10.1038/S41598-019-47403-1

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Vaity P, Aadhi A, Singh RP. Formation of optical vortices through superposition of two Gaussian beams. Appl Opt (2013) 52:6652–6. doi:10.1364/AO.52.006652

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Huang S, Miao Z, He C, Pang F, Li Y, Wang T. Composite vortex beams by coaxial superposition of Laguerre–Gaussian beams. Opt Lasers Eng (2016) 78:132–9. doi:10.1016/J.OPTLASENG.2015.10.008

CrossRef Full Text | Google Scholar

33. Vyas S, Senthilkumaran P. Interferometric optical vortex array generator. Appl Opt (2007) 46:2893–8. doi:10.1364/AO.46.002893

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Fu S, Wang T, Zhang Z, Zhai Y, Gao C. Selective acquisition of multiple states on hybrid poincare sphere. Appl Phys Lett (2017) 110:191102. doi:10.1063/1.4983284

CrossRef Full Text | Google Scholar

35. Li L, Chang C, Yuan X, Yuan C, Feng S, Nie S, et al. Generation of optical vortex array along arbitrary curvilinear arrangement. Opt Express (2018) 26:9798–812. doi:10.1364/OE.26.009798

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Yu J, Zhou C, Lu Y, Wu J, Zhu L, Jia W. Square lattices of quasi-perfect optical vortices generated by two-dimensional encoding continuous-phase gratings. Opt Lett (2015) 40:2513–6. doi:10.1364/OL.40.002513

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Karahroudi MK, Parmoon B, Qasemi M, Mobashery A, Saghafifar H. Generation of perfect optical vortices using a Bessel-Gaussian beam diffracted by curved fork grating. Appl Opt (2017) 56:5817–23. doi:10.1364/AO.56.005817

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Deng D, Li Y, Han Y, Su X, Ye J, Gao J, et al. Perfect vortex in three-dimensional multifocal array. Opt Express (2016) 24:28270–8. doi:10.1364/OE.24.028270

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Yu X, Li R, Yan S, Yao B, Gao P, Han G, et al. Experimental demonstration of 3D accelerating beam arrays. Appl Opt (2016) 55:3090–5. doi:10.1364/AO.55.003090

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Jin L, Li H, Zhao C, Gao W. Generation of airy vortex beam arrays using computer-generated holography. J Opt Soc Am A-Opt Image Sci Vis (2019) 36:1215–20. doi:10.1364/JOSAA.36.001215

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Qian Y, Shi Y, Jin W, Hu F, Ren Z. Annular arrayed-Airy beams carrying vortex arrays. Opt Express (2019) 27:18085–93. doi:10.1364/OE.27.018085

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Curtis JE, Koss BA, Grier DG. Dynamic holographic optical tweezers. Opt Commun (2002) 207:169–75. doi:10.1016/S0030-4018(02)01524-9

CrossRef Full Text | Google Scholar

43. Moreno I, Davis JA, Cottrell DM, Zhang N, Yuan XC. Encoding generalized phase functions on Dammann gratings. Opt Lett (2010) 35(10):1536–8. doi:10.1364/OL.35.001536

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Deng D, Li Y, Han Y, Ye J, Guo Z, Qu S. Multifocal array with controllable orbital angular momentum modes by tight focusing. Opt Commun (2017) 382:559–64. doi:10.1016/j.optcom.2016.08.049

CrossRef Full Text | Google Scholar

45. Fu S, Wang T, Gao C. Perfect optical vortex array with controllable diffraction order and topological charge: erratum. J Opt Soc Am A Opt Image Sci Vis (2016) 33:2076–1842. doi:10.1364/JOSAA.33.001836

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Liesener J, Reicherter M, Haist T, Tiziani HJ. Multi-functional optical tweezers using computer-generated holograms. Opt Commun (2000) 185:77–82. doi:10.1016/S0030-4018(00)00990-1

CrossRef Full Text | Google Scholar

47. Goodman JW. Introduction to fourier Optics. New York, NY: McGraw-Hill (1996).

48. Leonardo RD, Ianni F, Ruocco G. Computer generation of optimal holograms for optical trap arrays. Opt Express (2007) 15:1913–22. doi:10.1364/OE.15.001913

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Preece D, Bowman R, Gibson G, Padgett M. A comprehensive software suite for optical trapping and manipulation. Proc SPIE (2009) 7400. doi:10.1117/12.826924

CrossRef Full Text | Google Scholar

50. Lenton ICD, Stilgoe AB, Nieminen TA, Rubinsztein-Dunlop H. OTSLM toolbox for structured light methods. Comput Phys Commun (2020) 253:107199. doi:10.1016/J.CPC.2020.107199

CrossRef Full Text | Google Scholar

51. Sinclair G, Leach J, Jordan P, Gibson G, Yao E, Laczik Z, et al. Interactive application in holographic optical tweezers of a multi-plane Gerchberg-Saxton algorithm for three-dimensional light shaping. Opt Express (2004) 12(8):1665–70. doi:10.1364/OPEX.12.001665

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Xu T, Wu S, Jiang Z, Wu X, Zhang Q. Regulating trapping energy for multi-object manipulation by random phase encoding. Opt Lett (2020) 45:2002–5. doi:10.1364/OL.387223

PubMed Abstract | CrossRef Full Text | Google Scholar