The Effect of An Emergency Evacuation on the Spread of COVID19

In an emergency evacuation, people almost always come in close proximity as they quickly leave a built environment under a potential threat. With COVID19, this situation presents yet another challenge: that of getting unintentionally exposed to an infected individual. To assess the epidemiological consequences of an emergency evacuation, we expanded a popular pedestrian dynamic model to enable social distancing during a normal exit and analyze the effect of possible transmission through respiratory droplets and aerosol. Computer simulations point to a troubling outcome, whereby the benefits of a quick exit could be outweighed by the risk of infection.

Introduction

As schools and universities continue to evaluate various social distancing strategies to mitigate the spread of COVID19, a critical feature of human behavior is being overlooked—the response to a sudden alarm in a built environment that may trigger an emergency evacuation. The alarm may come from a fire in the building, the presence of an active shooter, or even a simple drill to prepare for true emergencies. Perhaps, in the current context, even someone blatantly unwilling to comply with social distancing regulations and use of masks could trigger an alarm. Whatever the source of the alarm is, during an evacuation, individuals will likely weigh the risks of being injured from the perceived threat heavily against the possibility of contracting an infection from a classmate or the instructor. Upon exiting however, people may wonder if they got too close to an infected person and if they breathed the same air for too long. These aspects represent an important discussion in relation to airborne transmission of COVID19 [1, 2].

The recommended separation distance of 2 m (six feet) is largely based on the transport of “respiratory droplets produced when an infected person coughs, sneezes, or talks.” [2]. These droplets can be propelled through air for up to 2 m and “land in the mouths or noses of people who are nearby or possibly be inhaled into the lungs.” [2]. More recently, results from fluid mechanics research have shown that aerosol could be the dominant driving mechanism for transmission between people in close proximity [3]. In comparison with respiratory droplets, aerosol includes much smaller particles that remain suspended in air for long periods of time to be inhaled by others. Irrespective of the driving mechanism, proximity to an infected individual is likely to increase the risk of infection, especially in the presence of screaming.

Risk of Infection From an Individual as a Function of Their Physical Proximity

Under the premise that the risk of an infection increases with the proximity to an infected individual, we could quantify the epidemiological consequences of an evacuation by tracking the separation distance within the crowd. We assume that the risk of infection decays exponentially with distance [3], and that this risk accumulates over time. More specifically, we measure the risk of exposure in a crowd of N people from an infected individual I as the instantaneous exposure integrated over time for the duration of the evacuation: $E=\underset{j\ne I}{\max }\underset{t}{{\displaystyle \int }}{e}^{-\tau d_{Ij}\left(t\right)}dt$, where $d_{Ij}\left(t\right)$ is the instantaneous distance between individual I and any other individual in the crowd (Figure 1A), and $\tau$ is the spatial decay rate of the transmission. The maximization ensures that we select the individual who receives the highest exposure within the crowd and quantifies the risk in terms of a worst-case scenario. The higher the value of E, the more likely the infected individual will create a new infection in the crowd. This definition is agnostic to the specific mechanism of transmission, be it respiratory droplets or aerosol, and allows for a direct comparison among feasible scenarios.

An estimate of the value of $\tau$ can be obtained through a linear regression of the plots in logarithmic scale presented in Figure 7 of Chen et al. [3]. These plots include exposure from both talking and coughing for droplets of size more than 100 µM (respiratory droplets) and short-range airborne (aerosol) as functions of distance. Hence, we obtain the following estimates: talking/respiratory droplets: $\tau =16.29 {\text{m}}^{-1}$; talking/aerosol: $\tau =9.46 {\text{m}}^{-1}$; coughing/respiratory droplets: $\tau =7.64 {\text{m}}^{-1}$; and coughing/aerosol: $\tau =5.29 {\text{m}}^{-1}$. As a reference for values of E that could lead to an infection, we can follow guidelines of the Centers for disease Control and Prevention (CDC)[4] that define a “close contact” as one that may trigger an infection by being within 2 m of an infected individual for more than 15 min. By considering the most extreme case of aerosol transmission during coughing, the value of E that corresponds to close contact is 2.29 × 10^–2 s. This value can be used as a simple threshold to assess a close contact in an evacuating crowd.

Simulating Emergency Evacuations and Normal Exit With Social Distancing

Emergency evacuations represent a dire situation where people exit a built environment as quickly as possible to escape the perceived danger. In an evacuation, the resulting crowd dynamics arise from a complex interplay between psychological, social, and physical factors. Individuals use social, cognitive, visual, and physical cues to stay with friends and family [5], look for the exit [6], and avoid collisions and injury [7]. Evacuation is therefore a cognitively demanding situation, which makes it inevitable for individuals to come close to each other—much less than the stipulated 2-m distance. Could this increase the risk of contracting COVID19?

Experiments on evacuation are impractical and potentially dangerous to conduct. A number of agent-based, mathematical models have been proposed over the years to predict human response and support hypothesis-driven experiments to clarify the mechanisms of the crowd dynamics. Among those, the social force model originally proposed by Helbing et al. [8] constitutes a viable compromise between model complexity and predictive power. The social force model is a physics-based model that captures interactions between finite-sized particles (agents) in the form of four kinds of forces: a social force that keeps agents apart; a goal force that makes them orient and move toward a goal location; a physical force in the event of friction and collision between agents; and a wall force, which is the same as the social force but captures interaction with walls and obstacles instead of other agents. Computer simulations can reproduce several real-world phenomena, including occurrences of bottlenecks near exits, injuries during an evacuation of a large crowd, and lane formation in corridors. The social force model has been validated in laboratory experiments [9], as well as real-world scenarios [7], thereby constituting a valid framework for exploring the potential epidemiological implications of an evacuation. By combining the classical evacuation model from Helbing et al. [8] with the proposed definition of risk of exposure, it is possible to provide a first assessment of the epidemiological consequences of an evacuation, compared to a normal exit where people can exercise social distancing.

The social force model [8] captures the motion of agent $i$ as the combination of three effects, a desire to move toward the exit goal, maintain separation from others, and maintain distance from walls. This is mathematically written as $m\ddot{{\mathit{x}}_i}={\mathit{f}}_g+{\displaystyle \sum }_j{\mathit{f}}_{ij}+{\displaystyle \sum }_W{\mathit{f}}_{iW}$, where m is the common mass of each agent (80 kg), x_i is the two-dimensional position vector of agent $i$, ${\mathit{f}}_g$ is the goal force, ${\mathit{f}}_{ij}$ includes the social force and the physical force between agents $i$ and $j$, and ${\mathit{f}}_{iW}$ is the wall interaction force for agent $i$ with respect to the wall W. The goal force is modeled as ${\mathit{f}}_g=\frac{v_0\mathit{e}-\mathit{v}}{\alpha }$, where $v_0$ is the desired speed that encapsulates the urgency with which the agent must leave the built environment, $\mathit{e}$ is the direction toward the exit, $\mathit{v}$ is the instantaneous velocity, and $\alpha =0.5 \text{s}$ is the relaxation time. The interaction force is ${\mathit{f}}_{ij}=\left\{A{e}^{\frac{(r_{ij}-d_{ij})}{B}}+kg(r_{ij}-d_{ij})\right\}{\mathit{n}}_{ij}+\kappa g\left(r_{ij}-d_{ij}\right)\text{Δ}{v}_{ji}{\mathit{t}}_{ij}$, where $r_{ij}$ is the sum of the radii of agents $i$ and $j$ (modeled as circles); $d_{ij}$ is the distance between agents $i$ and $j$ ; ${\mathit{n}}_{ij}$ identifies the direction from $j$ to $i$, and ${\mathit{t}}_{ij}$ denotes the direction that is perpendicular to ${\mathit{n}}_{ij}$; A and B are constants that determine the strength of social interaction, with higher values leading to larger distances between agents; and $k=1.2 \times {10}^5 {\text{kg s}}^{-2}$ and $\kappa =2.4 \times {10}^5 {\text{kg m}}^{-1}{\text{s}}^{-1}$ determine the strength of physical interaction and friction effects, with the function $g$ being equal to $r_{ij}-d_{ij}$ if $r_{ij}>d_{ij}$ and is zero otherwise. The wall interaction force ${\mathit{f}}_{iW}$ has the same form of the social interaction force, so that an agent stays away from the wall and experiences physical force when in contact.

To quantify and compare the risk associated with an emergency evacuation, we simulated two scenarios: evacuation and normal exit with social distancing. To simulate these two scenarios, we varied the interaction range (parameter B in the model), interaction repulsive force (parameter A in the model), and desired speed (parameter $v_o$ in the model) within the social force model (Figure 1). For a normal exit where people exercise social distancing (Figure 1B), we set a large interaction range and a strong interaction repulsive force, along with a low desired speed of 1 m/s. On the other hand, for an evacuation, we utilize a low interaction range and a weak repulsive force (Figure 1C), accompanied by a high desired speed of 5 m/s. The selection of these desired speeds reflect walking and running speeds during normal and emergency situations [8].

FIGURE 1

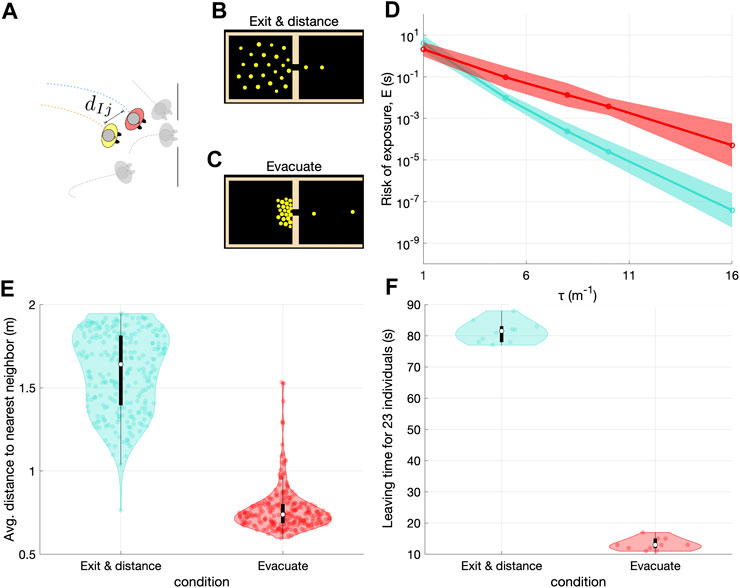
FIGURE 1. The epidemiological risks from coming close to an individual during an evacuation could outweigh the benefits of being able to quickly leave a room under a potential threat (A) The framework used here combines a pedestrian dynamic model and an exposure model to quantify the risk of exposure during an emergency evacuation (B) and (C), Snapshots from a simulation of the social force model [8] as 25 agents exit a 10 × 10 m room through a 1-m wide door while maintaining social distance or evacuate without maintaining social distance (D), Risk of exposure of an individual in the crowd as a function of the decay rate of the transmission; a low value of τ indicates high transmission at larger separation distances (red denotes evacuating, and turquoize identifies exiting and social distancing) (E), Average distance to the nearest neighbor during the two types of simulations performed (red denotes evacuation without distancing, and turquoize identifies exiting with distancing) (F), Leaving time for more than ninety percent of the crowd for the two scenarios.

Specifically, evacuation was simulated by setting $A=20 \text{kN}, B=0.08 \text{m}, v_0=5 {\text{m s}}^{-1}$, which were the default values proposed in Helbing et al. [8] to simulate an evacuation; the A and B parameter values for exit with social distancing were selected by simulating exit scenarios with a range of values $A\in \left\{\mathrm{20,40}, 60, \dots , 200\right\}\text{ kN}, B=\left\{0.08, 0.16, 0.24, \dots , 0.72\right\}\text{ m},$ for a normal walking speed of $v_0=1 {\text{m s}}^{-1}$ and calculating the average distance to the nearest neighbor for all agents in the room for the first 10 s; we found that the average distance to nearest neighbor increased steadily with A and B before it plateaued at approximately 1.7 m due to the wall and room size constraints. The dependence of average distance to the nearest neighbor on parameters A and B is highly nonlinear and multiple parameter choices could yield the same value. Specifically, we record an average distance of 1.7 m for $\mathit{A}\times \mathit{B}\approx 5\mathit{ }$ kNm as we vary A from 6 kN to 14 kN and B from 0.4 m to 0.72 m. We selected A = 10 kN, and $\mathit{B}=0.48$ m as the centroid of this region. In the event that experimental data is available, the parameters of the pedestrian dynamics model can be set by minimizing the difference between simulated and experimental trajectories [9], or between distribution of individual speeds [10]. All other parameter values were kept the same as set in the open source code provided as part of Helbing et al [8]. Simulations were performed using the C source code provided as Supplement to the paper by Helbing et al. [8].

To prevent goal and interaction forces from balancing out to an equilibrium for the exit with social distancing scenario, the goal force was multiplied by a factor $k_g$ that was a function of the distance to the exit $d_e$. This distance-dependent factor was set to an exponentially decaying value, namely, $k_g=1+C_1\text{exp}(-C_2{d}_e)$, with $C_1=100$, and $C_2=1 {\text{m}}^{-1}$ so that agents felt a stronger pull toward the exit as they got closer to it.

For each simulation, we randomly placed 25 agents (modeled as finite-sized circles) within a 10 × 10 m room with a single 1 m wide exit; this number of individuals is sufficiently low to allow for maintaining a separation distance of 2 m within the room. Randomness in the simulation was introduced through two means: first, ten simulations were performed in each scenario, where each simulation corresponded to a different initial condition and the distribution of agent size (circles with diameters ranging uniformly between 0.5 and 0.7 m), and, second, by selecting a different agent as the single infected agent within the crowd. This amounted to hundred different realizations of each scenario. The risk of exposure, E, was computed for each scenario for different values of $\tau$.

Figure 1D shows that the exposure for an agent within the evacuating crowd without social distancing is much larger than when the crowd leaves normally and maintains social distance, despite the evacuating crowd leaves the arena much sooner than a crowd that normally exits and maintains social distance (Figure 1F). Figure 1E confirms that the agents maintain larger distances as a result of the higher interaction range and repulsive force encoded into the model. Should the simulation be performed with a larger group of 100 agents within a room of $20\times 20$ m dimensions, the results would be statistically indistinguishable from those presented herein. This evidence suggests that our claims should be robust with respect to size of the room and the evacuating crowd.

Discussion

Our simulations show that despite the evacuating crowd taking only a sixth of the time to leave the room than when the crowd which is exiting normally, evacuation presents a far greater threat for possible transmission of COVID19 than a crowd that is exiting with social distancing. For example, in the case of aerosol transmission, evacuating in the presence of an infected individual who is coughing will yield a risk of exposure due to aerosol transmission of about 0.1 s (above the estimate of the threshold of close contact), while exit with social distancing will cause an average exposure ten time smaller (below the estimate of the threshold of close contact).

A vast community of researchers is focused on understanding how the flow of individuals during an emergency evacuation can be eased to avoid bottlenecks and high pressures that could lead to injuries and fatalities [11]. COVID19 presents yet another complication, where we must also weigh our compulsion to run away from a potential threat against the possible risks involved in being in proximity to an infected individual. Our results indicate that maintaining social distancing during an exit could increase the time required to leave the built environment by a factor of ten, which may be fatal in the case of a fire or a mass shooting. At the same time, evacuating without maintaining a social distance dramatically increases the risk of exposure, potentially leading to further infections. Face coverings can certainly help mitigate these risks, although more research is required to precisely evaluate the reduction in the decay rate associated with the proper use of masks, especially in the context of aerosol intake. Overall, this study points to a critical gap in the current guidelines for resuming in-presence learning, as well as opening up businesses during the coming fall.

Our analysis is not free of limitations, which should be investigated in further efforts, beyond the scope of this perspective. First of all, the pedestrian dynamics is described by one of the very first mathematical models in the field [8], which has seen several refinements throughout the last 20 years [12]. As such, one may attempt at more complex simulation of the evacuation process to capture perceptual and psychological factors that are missing in this model. Second, the simple evacuation scenario presented here is not able to fully capture the combination of exposure risks one may face when evacuating a building with multiple rooms, floors, stairways, and doorways. In such a complex scenario, it will also be important to trace the individuals who have experienced the strongest exposure; toward this aim it may be possible to borrow techniques from community detection in networks [13–15]. Third, the contact process examined herein does not account for individual orientation, which is likely to play an important role on droplet-based exposure, and, to a lesser extent, on airborne transmission [3]. This limitation for example could be overcome by following the approach proposed by Ronchi & Lovreglio [16] to combine risks of infections across a range of viable scenarios in a built environment. Overall, this study contributes to the general topic of safety-related issues during the current pandemic [17], by bringing forward preliminary evidence for the expected risks of infection during evacuations.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

SB was supported by the National Science Foundation, under grant # CMMI-2027988, and MP was supported by the National Science Foundation, under grant # CMMI-2027990.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Morawska L, Tang JW, Bahnfleth W, Bluyssen PM, Boerstra A, Buonanno G, et al. How can airborne transmission of COVID-19 indoors be minimised?. Environ Int (2020) 142:105832. doi:10.1016/j.envint.2020.105832

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Seibert T, Allen DB, Eickhoff JC, Carrel AL. How to protect yourself and others. Centers for Disease Control and prevention (CDC) (2020). https://www.cdc.gov/coronavirus/2019-ncov/prevent-getting-sick/prevention.html.

Google Scholar

3. Chen W, Zhang N, Wei J, Yen H-L, Li Y. Short-range airborne route dominates exposure of respiratory infection during close contact. Build Environ (2020) 176:106859. doi:10.1016/j.buildenv.2020.106859

CrossRef Full Text | Google Scholar

4. Seibert T, Allen DB, Eickhoff JC, Carrel AL. When to quarantine. Centers for Disease Control and prevention (CDC) (2020). https://www.cdc.gov/coronavirus/2019-ncov/if-you-are-sick/quarantine.html.

Google Scholar

5. Mawson AR. Mass panic and social attachment: the dynamics of human behavior. London: Routledge (2017).

CrossRef Full Text

6. Moussaïd M, Helbing D, Theraulaz G. How simple rules determine pedestrian behavior and crowd disasters. Proc Natl Acad Sci USA (2011) 108(17):6884–8. doi:10.1073/pnas.1016507108

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Helbing D, Buzna L, Johansson A, Werner T. Self-organized pedestrian crowd dynamics: experiments, simulations, and design solutions. Transport Sci (2005) 39(1):1–24. doi:10.1287/trsc.1040.0108

CrossRef Full Text | Google Scholar

8. Helbing D, Farkas I, Vicsek T. Simulating dynamical features of escape panic. Nature (2000) 407:487–90. doi:10.1038/35035023

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Moussaïd M, Helbing D, Garnier S, Johansson A, Combe M, Theraulaz G. Experimental study of the behavioural mechanisms underlying self-organization in human crowds. Proc Biol Sci (2009) 276(1668):2755–62. doi:10.1098/rspb.2009.0405

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Lee HRL, Bhatia A, Brynjarsdóttir J, Abaid N, Barbaro A, Butail S. Speed modulated social influence in evacuating pedestrian crowds. Collect Dyn (2020) 5:1–24. doi:10.17815/cd.2020.25

CrossRef Full Text | Google Scholar

11. Schadschneider A, Klingsch W, Klüpfel H, Kretz T, Rogsch C, Seyfried A. Evacuation dynamics: Empirical results, modeling and applications In: R Meyers, editor Encyclopedia of complexity and systems science. New York: Springer (2009) p 3142–3176.

Google Scholar

12. Martinez-Gil F, Lozano M, García-Fernández I, Fernández F. Modeling, evaluation, and scale on artificial pedestrians. ACM Comput Surv (2017) 50(5):1–35. doi:10.1145/3117808

CrossRef Full Text | Google Scholar

13. Li HJ, Wang L, Zhang Y, Perc M. Optimization of identifiability for efficient community detection. New J Phys (2020) 22(6):063035. doi:10.1088/1367-2630/ab8e5e

CrossRef Full Text | Google Scholar

14. Fortunato S, Hric D. Community detection in networks: a user guide. Phys Rep (2016) 659:1–44. doi:10.1016/j.physrep.2016.09.002

CrossRef Full Text | Google Scholar

15. Cazabet R, Boudebza S, Rossetti G. Evaluating community detection algorithms for progressively evolving graphs. arXiv:2007.08635 (2020).

Google Scholar

16. Ronchi E, Lovreglio R. EXPOSED: an occupant exposure model for confined spaces to retrofit crowd models during a pandemic. arXiv:2005.04007 (2020).

Google Scholar

17. Haghani M, Bliemer MC, Goerlandt F, Li J. The scientific literature on Coronaviruses, COVID-19 and its associated safety-related research dimensions: a scientometric analysis and scoping review. Saf Sci (2020) 129:104806. doi:10.1016/j.ssci.2020.104806

PubMed Abstract | CrossRef Full Text | Google Scholar