Turbulence Upstream and Downstream of Interplanetary Shocks

The paper reviews the interaction of collisionless interplanetary (IP) shocks with the turbulent solar wind. The coexistence of shocks and turbulence plays an important role in understanding the acceleration of particles via Fermi acceleration mechanisms, the geoeffectiveness of highly disturbed sheaths following IP shocks and, among others, the nature of the fluctuations themselves. Although our knowledge of physics of upstream and downstream shock regions has been greatly improved in recent years, many aspects of the IP-shock/turbulence interaction are still poorly known, for example, the nature of turbulence, its characteristics on spatial and temporal scales, how it decays, its relation to shock passage and others. We discuss properties of fluctuations ahead (upstream) and behind (downstream) of IP shock fronts with the focus on observations. Some of the key characteristics of the upstream/downstream transition are 1) enhancement of the power in the inertial range fluctuations of the velocity, magnetic field and density is roughly one order of magnitude, 2) downstream fluctuations are always more compressible than the upstream fluctuations, and 3) energy in the inertial range fluctuations is kept constant for a significant time after the passage of the shock. In this paper, we emphasize that–for one point measurements–the downstream region should be viewed as an evolutionary record of the IP shock propagation through the plasma. Simultaneous measurements of the recently launched spacecraft probing inner parts of the Solar System will hopefully shed light on some of these questions.

1 Introduction

The physical processes connected with the formation and propagation of MHD shocks, the role of these shocks in acceleration of particles and their coupling to the Earth’s magnetosphere has been studied for decades. Although many discoveries were made within these areas, the nature of upstream and downstream fluctuations in the framework of turbulence has been studied less intensively and basic questions have not been fully addressed yet. For example, what regime of turbulence, if any, would describe the observed level of upstream or downstream fluctuations, how intermittent are these fluctuations, etc. Considering that the energy of the downstream fluctuations can reach levels unmatched in a pristine solar wind, with a potential to couple with the Earth’s magnetic field, this phenomenon is worthy of further investigations.

Shocks and their drivers have been so far studied in frame of space weather because they are often associated with significant disturbances of the geomagnetic field–geomagnetic storms. Two major types of drivers of geomagnetic storms were identified: 1) interplanetary coronal mass ejections (ICMEs) that is preceded by a shock and sheaths and 2) corotating interaction regions (CIRs) where a fast stream from a coronal hole overtakes a leading slow stream [16, 17, 34, 111].

ICMEs are the solar wind counterparts of coronal mass ejections (CMEs) observed near the Sun and they play a role in the variation of the strength of the Interplanetary Magnetic Field (IMF) during the solar cycle [99]. They are of interest because, apart of the effects in the geomagnetic field (e.g., [38, 147]), they are responsible for energetic particle events through acceleration by shocks they drive (e.g., [23, 24]).

Magnetic clouds (MCs), a subset of ICMEs, are formed as twisted magnetic flux tubes that carry a large amount of magnetic helicity from the Sun to the interplanetary medium and they transport significant amount of magnetic flux, mass, and energy [22]. MCs are responsible for some major geomagnetic storms [16, 133] because they are often associated with shocks and large southward IMF [69].

The turbulent region bounded by the shock ramp on one side and the front surface of a particular ICME on the other side is called the ICME sheath. Magnetic field fluctuations in the sheaths can be transmitted from the upstream solar wind and/or generated within the sheath, due to physical processes at the shock and due to draping of the magnetic field around the driving ejecta (e.g., [47, 61, 121]). [122] have simulated and compared ICMEs and other heliophysical sheaths and have shown that the sheath of expanding ICMEs (the so-called the expansion sheath that forms around an object that expands but does not propagate relative to the solar wind) differs from the sheath formed by the propagation of steady-state ICMEs (the propagation sheath). Sheaths have been identified also as important drivers of geomagnetic storms (e.g., [38, 64, 128, 139, 147]). Southward excursions of the magnetic field due to fluctuating magnetic fields in the sheath can occasionally generate super-intense storms (e.g., [38, 147]), similarly as can southward fields in the ICME, especially if this is a magnetic cloud with a flux rope structure.

Geomagnetic storms associated with the other type of large-scale solar-wind structures, the quasi-steady CIRs (e.g., [8, 146]) are usually only weak to moderate in strength but they are more frequent than ICMEs, especially during solar minimum [57, 58]. If the relative speed gradients between interacting streams are sufficiently large, fast forward and reverse MHD shocks form and Alfvénic fluctuations in the rarefaction region at the CIR trailing edge may drive prolonged high-latitude activity [63].

In addition, the shock impact angle (i.e., the angle between the shock normal and the Sun–Earth line) affects the geomagnetic response. We note that CIRs are generally associated with larger impact angle, i.e., being more inclined than ICME-driven shocks [59, 67, 95].

The characteristics of fluctuations in the upstream/downstream plasma would be of value to understanding the geoeffectivness of the downstream fluctiations. For example, if one could predict the character of the downstream fluctuations, e.g., the IMF Bz component, from the upstream ones, then we can make a qualitative judgment about the influence of the incoming ICME on the space weather [47].

As discussed above, the connection between upstream and downstream interplanetary (IP) shock fluctuations and space weather effects is a subject of numerous review papers (e.g., [63, 64]). However, the nature of the IP shock induced changes of turbulence has been addressed by a few authors only. For this reason, the present paper concentrates on these fluctuations themselves with a focus on observable characteristics. First, we introduce collisionless shocks and discuss their main drivers within the heliosphere, ICMEs, and CIRs. Next, we focus on the nature of upstream fluctuations of quasi-parallel shocks and downstream fluctuations of both quasi-parallel and quasi-perpendicular shocks, addressing their turbulent nature and their spatial and temporal decay. Finally, we summarize the review and suggest directions for future investigations.

2 Collisionless Shocks

Collisionless shocks arise from the interaction of a large obstacle with a supersonic plasma flow, where “large” refers to a characteristic dimension of the obstacle being larger than characteristic ion kinetic scales and “supersonic” means that characteristic upstream wave speed ${\mathit{V}}_{\mathrm{w}}$, is smaller than the relative speed of the obstacle and the flow ${\mathit{V}}_{\mathrm{flow}}$, i.e., Mach number, $M\mathrm{=}{V}_{\mathrm{flow}}/V_{\mathrm{w}}\mathrm{>1}$. The wave speed refers to the group velocity of either the Alfvén, fast or slow magnetosonic wave modes. The flow is deflected around the obstacle and at some distance, a region where the flow is decelerated to the Mach number below unity is termed the shock front. The thickness of the shock front is of the order of characteristic kinetic scales [93], therefore it can be viewed as a discontinuity.

Unlike the hydrodynamic shocks, where we can create, control, and display the formation of a shock in a controlled set-up, the collisionless shocks are difficult to study in laboratory conditions (see references in [6]). The solar wind introduces a unique environment where we can investigate both macrostructure and microstructure of these shocks in details. In last decades, a great progress has been made in the understanding of shock formation, its characteristic scales, dissipation rate, an important role of the reflected paricles and wave-particle interactions and other topics (e.g., [6, 21, 43, 93, 114, 126, 129]).

A standard set of Rankine-Hugoniot (R-H) jump conditions that couple the parameters of upstream and downstream plasma of any MHD discontinuity can be derived from the macroscopic MHD equations (for a full set of the R-H equation see, e.g., [94]. We introduce the two most transparent conditions,

$\mathit{n}\cdot \left[N\mathit{V}\right]\mathrm{=0}(1)$

and

$\mathit{n}\times \left[\mathit{B}\right]\mathrm{=0,}(2)$

where $\mathit{n}$ is the shock normal unit vector, N is the plasma density, $\mathit{V}$ is the plasma speed and B is the magnetic field vector. Square brackets indicate that the quantities are conserved across the discontinuity. We focus on the solutions that exclude contact, tangential and rotational discontinuities, i.e., the solutions with the increase of the entropy, normal speed and plasma density across the boundary.

One of the most important shock characteristics is its criticality [81]. For a shock with Mach number above some critical value, $M\mathrm{>}{M}_{\mathrm{c}}$, the dissipation mechanism that supports the shock front (responsible for entropy production, heating and retardation of the flow) changes [6]. The reflection of some fraction of the incoming particles back upstream now serves as an additional dissipation mechanism.

The angle between the shock normal and upstream magnetic field, ${\mathit{\theta }}_{\mathrm{Bn}}$, plays an important role in the shock dynamics. An angle of ${\mathit{\theta }}_{\mathrm{Bn}}\mathrm{=4}{\mathrm{5}}^{\mathrm{o}}$ serves as a boundary between two types of shocks: the quasi-perpendicular, ${\mathit{\theta }}_{\mathrm{Bn}}\mathrm{>4}{\mathrm{5}}^{\mathrm{o}}$ and quasi-parallel, ${\mathit{\theta }}_{\mathrm{Bn}}\mathrm{<4}{\mathrm{5}}^{\mathrm{o}}$ shocks. For quasi-perpendicular supercritical shocks, the reflected particles cannot escape from the shock front into upstream and they perform one gyration orbit and return back to the shock. A collective effect of the reflected particles creates a so-called foot of the shock ramp (e.g., [71]). For quasi-parallel shocks, particles reflected from the shock escape along magnetic field lines, stream upstream and via multiple ion-beam instabilities they significantly affect the upstream (and thus downstream) plasma, therefore putting R-H relations into question. One point of view is that the whole region affected by the reflected particles is generally the shock transition itself, a highly structured region dominated by wave-particle interactions with continuously reforming shock ramp. On the other hand, there certainly should be a region upstream of the shock ramp that we could call “unaffected”, however, defining the boundary between the “unaffected” plasma and the shock transition is difficult. Indeed, observations show that the reflected particles can travel huge distances into upstream [10]. The waves excited by a plethora of wave-particle instabilities [42] would deplete the free energy residing in the non-Maxwellian Velocity Distribution Function (VDF) and interfere with the waves already present in the upstream plasma. The behavior of these new-born waves depends on the parameters of both waves and background plasma. For example, if the wave has a sufficient amplitude, a Parametric Instability Decay (PID) may play a major role in its evolution [25, 125].

In the solar wind, we encounter two types of shocks, fast and slow IP shocks; the former being more frequent than the later. The fast shock forms when the upstream speed of the plasma (relative to an obstacle) exceeds the fast magnetosonic speed within the upstream. On the other hand, the slow shock forms when the upstream speed exceeds the slow magnetosonic speed, while the plasma should not support the growth of fast waves. Thus, formation of a slow shock requires special solar wind conditions [95] and therefore, there are only sparse measurements and reports on them (e.g., [134, 136]) and we will not discuss them.

A shock that propagates away from the Sun is called forward shock while the shock propagating towards the Sun in the plasma frame is called reverse. Thus the jumps of plasma parameters in the spacecraft frame of reference differ for forward/reverse, fast/slow shocks. Figure 1 shows the qualitative changes of the density, pressure, magnetic field strength, and bulk solar wind speed across the shock in the s/c frame.

FIGURE 1

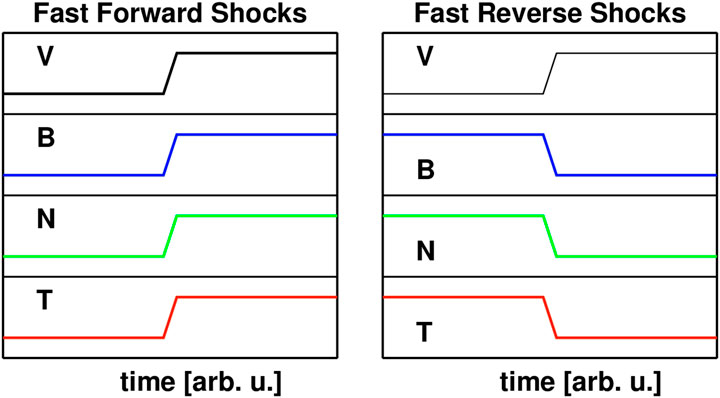
FIGURE 1. Profiles of the solar wind velocity, V, magnetic field magnitude, B, density, N, and temperature, T, across Fast Forward and Fast Reverse shocks.

These basic characteristics are crucial in understanding upstream (prior to or shock generated) and downstream fluctuations in the framework of turbulence. As an example, one would make a natural conclusion that the upstream medium of supercritical fast forward quasi-perpendicular IP shocks cannot be affected by the reflected particles that are confined to the shock foot. Locally, this should hold true, however, two factors distort this picture: 1) the level of upstream turbulent fluctuations, $\mathit{\delta }\mathit{B}/B_{\mathrm{0}}$ can reach a value of the order of 1 at scales that are relatively small ($\mathit{l}\approx \mathrm{0}\mathrm{.01}\mathrm{AU}$) compared to the whole region in which the shock expands into. These fluctuations change a shock geometry and one can find the reflected particles far upstream of shock that was at a given time and location characterized as quasi-perpendicular. These suprathermal particles then can excite waves that become a part of the prior upstream turbulence. The upstream medium can be thus affected by the microphysical processes within the shock ramp and can influence the level of turbulent fluctuations. On the other hand, the downstream medium should be influenced by the shock even more, e.g., the levels of downstream fluctuations can be order of magnitude higher than in upstream [14, 66, 80].

3 ICME VS CIR

Apart from bow shocks arising from the interactions of the solar wind with, the magnetospheres of planets and comets, two sources of collisionless shocks in the heliosphere are ICMEs and CIRs, as noted. Figure 2A shows schematically a formation of forward and reverse IP shocks associated with a CIR. The interaction region develops when the solar wind from a coronal hole interacts with preceding slower solar wind. The shocks bounding this region are predominantly formed at distances beyond the Earth’s orbit [112], however, already developed CIRs can also be found at $\mathrm{1}\mathrm{AU}$ [36, 67]. Due to the average IMF orientation and the overall CIR topology, both of which follow a Parker spiral [100, 102], shocks that arise from the interaction of slow and fast winds in the region of stream interface are mainly quasi-perpendicular fast shocks.

FIGURE 2

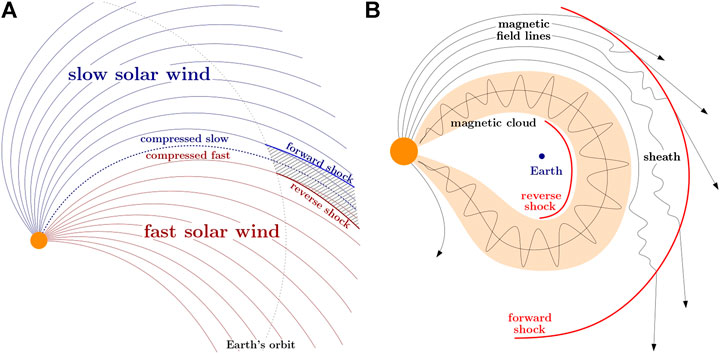
FIGURE 2. (A) Schematics of the Co-rotating Interaction Region (CIR) which leads to a formation of CIR bounded by forward and reverse shocks; (B) A fast forward shock formation in front of an ICME and a possible reverse shock at the trailing edge of the magnetic cloud.

Figure 2B presents a sketch of ICME with a leading fast forward magnetosonic shock, the sheath region, and the driver—a flux rope. Unlike the CIR shocks, the ICME-driven shock fronts form very close to the Sun and can be readily identified on coronographic images, e.g., of the SOHO mission [35, 96]. Again, taking into account the average direction of the Parker spiral, a parallel shock should be formed close to the Sun (e.g., [45]) and as the shock propagates further into the heliosphere, the normal of the shock front will be gradually more perpendicular to the IMF, thus eventually transforming into a quasi-perpendicular shock. This scenario can be applied for the CME head whereas shocks (if any) at the CME flanks can be quasi-perpendicular even near the Sun. However, a majority of observations come from $\sim \mathrm{1}\mathrm{AU}$ where the angle between the average magnetic field orientation and velocity is approx. $\mathrm{4}{\mathrm{5}}^{\mathrm{o}}$ that is also the transition from quasi-parallel to quasi perpendicular shock geometry but the IMF fluctuations can change the shock geometry significantly [132]. Moreover, if a pressure inside ICME is larger than that of the surrounding solar wind, the reverse shock can form at the trailing edge of such overexpanding ICME at larger distances from the Sun as Ulysses observations have shown [48].

It should be noted that the processes reported in upstream and downstream of the Earth’s bow shock have also been observed at ICMEs and/or CIRs (e.g., presence of ULF waves in the upstream of fast magnetosonic IP shocks [60]). However, the spatial extent of shocks connected with ICMEs and CIRs is orders of magnitude larger than that of the Earth’s bow shock, thus, new phenomena can emerge from the interaction of the pristine solar wind with these huge structures, such as accumulation of a plasma in front of a magnetic cloud that drives an ICME shock [63], the formation of Planar Magnetic Structures (PMSs) within ICME sheaths [91, 101] and many others.

One could expect that the changing of ${\mathit{\theta }}_{\mathrm{Bn}}$ of ICME shocks as they move away from the Sun will have consequences on the nature of downstream turbulence within the sheath region. At $\mathrm{1}\mathrm{AU}$, the leading part of the sheath can be characterized as a downstream region of the quasi-perpendicular shock, whereas the sheath region close to the driving CME was affected by shock passage much earlier when the shock was quasi-parallel (see chapter 5). These two regions could exhibit different characteristics because they were shocked at different times and the trailing region had more time for its evolution.

Considering both ICME and CIR related reverse shocks (see Figure 1) schematically depicted in Figures 2A,B, there are virtually no studies that address the changes of fluctuations from upstream to downstream medium. This is because they are much less frequent and much weaker than the fast shocks at $\mathrm{1}\mathrm{AU}$. Nonetheless, they may provide a new insight into the evolution of downstream fluctuations (see chapter 5.2) because spacecraft inherently detect first a plasma that was shocked closer to the Sun (thus it had more time for its evolution) and only later a plasma that is being shocked more recently. In the case of a forward shock, the situation is opposite. The difference between two scenarios is most clearly seen in the reference frame of an IP shock: for a forward shock, a spacecraft moves from upstream to downstream and for a reverse shock, from downstream to upstream. Therefore, a comparison of the evolution of the turbulent fluctuations along two paths through a shocked plasma would be interesting.

Finally, apart from the geoeffectievness of IP shock sheaths, it is of great importance to understand the nature and evolution of sheath fluctuations alone. What energy resides within these fluctuations? What compressibility they exhibit? These and many other questions arise.

We attempt to answer some of these questions in the following sections. The discussion above implies that sheaths of CIR driven shocks are much simple than those in front of CMEs for two reasons. First, CIR driven shocks are quasi-perpendicular on a global scale although we cannot rule out local deviations toward parallel geometry due to variations in the upstream region. Second, the CIR forward shocks propagate always into the slow solar wind whereas both slow and fast winds can be observed upstream the CME driven shocks. In order to cover the whole spectrum of possible scenarios, we discuss mainly CME driven shocks in the manuscript.

4 Solar Wind Turbulence

In this section, we briefly summarize the turbulent nature of the solar wind fluctuations. We note that this topic is still heavily debated and it is not yet fully understood. However, the main properties of the turbulent fluctuations have been established from decades of solar wind observations, i.e., the character of slow and fast solar wind plasma and magnetic field variations and their evolution with the heliocentric distance (e.g., [18]).

According to the present understanding, the solar wind fluctuations can be viewed as a system of nonlinearly interacting Alfvén-like wave packets traveling in opposite directions [56, 70]. The nonlinear interaction between counter streaming Alfvén waves of similar wavelengths is responsible for the generation of Alfvén waves with smaller wavelengths, i.e., the energy within the Alfvénic fluctuations is transferred to smaller scales and the fluctuations become gradually more anisotropic [120]. Furthermore, observations of [9, 39, 85] supported by theoretical works of [143, 144] suggest that solar wind fluctuations are dominated by quasi-2D turbulent fluctuations with a minority “slab” component, meaning that there are two populations of fluctuations, the first have their wave vectors parallel to the background magnetic field, ${\mathit{B}}_{\mathrm{0}}$, while the second have the wave vectors perpendicular to ${\mathit{B}}_{\mathrm{0}}$. The ratio of energies residing within the quasi-2D and slab fluctuations is roughly $\mathrm{4:1}$ (e.g., [9]. Figure 3 shows the composite power spectral density of magnetic field fluctuations measured by the Helios 2 and Wind spacecraft [18]. This triple power law is systematically observed in the solar wind and it is frequently interpreted as follows: 1) on large scales, where the power spectrum is a power law with the exponent $\mathrm{-1}$ [19], fluctuations are not yet turbulent and they become part of the turbulent cascade later on, 2) in the inertial range, the energy injected from large scales cascades into smaller scales, exhibiting a power law with the exponent ranging from −1.5 to −2 [28]. Finally, the cascaded energy reaches the characteristic ion scales below which a power spectrum steepens into the power law with even greater variability of the exponent from $\approx \mathrm{-2}$ to $\mathrm{-4}$ [74, 115]. It is believed that within this so-called kinetic/dissipation range, the cascaded energy is dissipated into random particle motion.

FIGURE 3

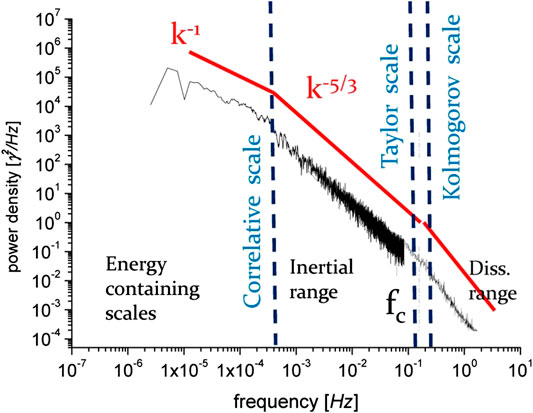
FIGURE 3. Power spectrum of magnetic field fluctuations at $\mathrm{1}\mathrm{AU}$. The figure is adapted from [18]; copyright by Springer Nature, licensed under CC BY 4.0.

Focusing on the large scale fluctuations in the solar wind, many authors investigated their characteristics to explain their origin. Their findings are consistent with the picture that the fluctuations within the so-called “1/f” range are not a simple mixture of non-interacting waves, but more likely these waves may undergo a nonlinear evolution, for example, parametric decay (e.g., [33, 83] and/or nonlinear cascade (e.g., [25, 131]). [84] found that the break between the injection and inertial ranges corresponds to condition $\mathit{\delta }\mathit{B}\mathrm{/}{\mathit{B}}_{\mathrm{0}}\sim \mathrm{1}$, implying that some process limits the compressibility of the fluctuations at largest scales. Recently, due to Parker Solar Probe (PSP) and Solar orbiter launches, much progress has already been made or is expected. [27] investigated the radial dependence of the power spectra of magnetic fluctuations with the heliocentric distance employing PSP measurements and noted consistency with aforementioned results. Furthermore, the evolution of fluctuations within $\mathrm{1}\mathrm{AU}$ in the framework of Nearly Incompressible (NI) turbulence transport equations [140] was studied by [2]. Using PSP measurements, they estimated the evolution of the kinetic energy, correlation length, density variance and temperature between $\sim \mathrm{35}{\mathit{R}}_{\mathrm{s}}$ and $\mathrm{130}{\mathit{R}}_{\mathrm{s}}$ and have found a good correspondence with the NI turbulent transport model that assumed an 80:20 ratio between quasi-2D and slab turbulent populations.

Within the inertial range, which is usually inferred from the estimated power spectrum of the magnetic field fluctuations, the energy flux through the scales $\varepsilon \left(l\right)$ is constant, i.e., the free energy that is cascading from the large scales with the rate ${\varepsilon }_{\mathrm{inj}}$ is equal to the dissipation rate ${\varepsilon }_{\mathrm{k}}$. The physical reason for the existence of the inertial range is that the energy supplied at the correlative scale (see Figure 3) cannot be effectively dissipated. It is transferred into smaller scales, eventually reaching the scales where, in the case of MHD turbulence, dissipative processes act and the cascaded energy is transformed into random particle motion. It follows that the nature of the inertial range cascade should not be sensitive to the dissipative processes, at least in the first approximation. The typical characteristic of the inertial range fluctuations is their anisotropy [52] in a multiple sense: (a) the power within the fluctuations perpendicular to the mean magnetic field is larger than the power within the parallel ones [8], (b) the fluctuations wave vectors are not populated isotropically within the inertial range [85] and (c) power spectrum of fluctuations exhibit different scaling $\mathit{P}\left(\mathit{k}\right)\propto {\mathit{k}}^{\mathrm{-}\mathit{\alpha }}$ for different sampling directions [51]. The scaling laws of power spectral densities of the physical fields (N, B, V, T) and the relevant anisotropies inferred from spacecraft observations (e.g., [13, 28, 115, 130]), or state-of-the-art computer simulations (see, [40]; and references therein) serve as key factors in understanding the dynamics of the inertial range. Specifically, they can answer the question which turbulent framework [98, 144, 149] is consistent with observations.

It is believed that the dissipative processes that are responsible for the heating of the solar wind act at the sub-ion range. Therefore, physics of this range has been studied observationally (e.g., [4, 30, 106, 109, 116]), theoretically [11, 53, 119] and by computer simulations [40, 49, 54]. Both observations and simulations show that the transition from inertial to dissipation range corresponds to the spatial scale of the proton thermal gyroradius ${\mathit{\rho }}_{\mathrm{gp}}$ or to the inertial length of the proton ${\mathit{\rho }}_{\mathrm{ip}}$ [31, 41]. The character of the fluctuations at the transition and below these characteristic ion scales is still an unresolved issue. A natural candidate for the plasma mode that the fluctuation may exhibit is the kinetic Alfvén wave (KAW) because it is a continuation of a shear Alfvén wave mode for highly perpendicular wave vectors, ${\mathit{k}}_{\perp }\gg k_{\parallel }$, for which a condition ${\mathit{k}}_{\mathrm{\perp }}{\mathit{\rho }}_{\mathrm{gp}}\mathrm{\gtrsim }1$ is satisfied. Since the KAW mode is low frequency [11] wave, i.e., $\mathit{\omega }\gg k_{\mathrm{\perp }}{\mathit{v}}_{\mathrm{th,i}}$, ${\mathit{v}}_{\mathrm{th,i}}$ being the ion thermal speed, it exhibits non-negligible density fluctuations around the scale of ${\mathit{\rho }}_{\mathrm{gp}}$, which are manifested as a plateau around the transition from inertial to dissipation range [26, 30, 115]. Recently, a number of authors [73, 106, 113, 137] shows that the character of fluctuations below the scale of the proton thermal gyroradius, i.e., $\mathit{k}{\mathit{\rho }}_{\mathrm{gp}}\mathrm{\gtrsim }1$, is consistent with KAW-like fluctuations and recently developed KAW turbulent phenomenology [11, 148]. However, the nature of the kinetic range is still heavily debated and alternative/complementary hypotheses are investigated [15].

Due to large spatial dimensions, the spectrum of fluctuations as depicted in Figure 3 can be significantly affected by the IP shocks. In principle, all three power-law segments can change their slope and amplitude or a power law may not even be formed and the power spectral density profile could be fitted by an exponential function [104].

5 IP Shocks and Turbulence

An excellent opportunity to illustrate the complexity of the interaction of turbulence and IP shocks and its dependence on surrounding environment is presented by an example of three consecutive IP shocks observed at $\mathrm{1}\mathrm{AU}$ on June 21 and 22, 2015 [46, 78]. We follow [78] and mark the IP shocks as shown in Figure 4: the first shock (S1) was detected at the Wind spacecraft at 16:05 UT on June 21, 2015, the second shock (S2) at 05:02 UT on June 22, 2015 and the third shock (S3) at 18:08 UT on June 22, 2015. Parameters of the shocks are listed in Table 1. One of the most important factors that distinguish these three shocks are the upstream conditions. Upstream of S1, the solar wind plasma has extremely high proton beta, ${\mathit{\beta }}_{\mathrm{p}}\approx \mathrm{30}$ and a very low level of magnetic field fluctuations. Upstream of S2 seems to be the driver of S1, i.e., the magnetic cloud. Finally, upstream of S3 looks like the sheath of S2.

FIGURE 4

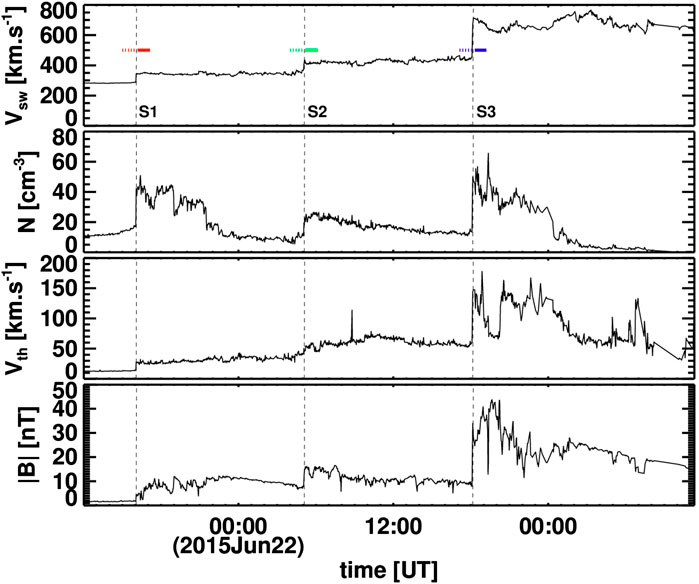
FIGURE 4. Bulk parameters of the solar wind during 2 days when Wind encountered three quasi-perpendicular fast forward IP shocks. From top to bottom: Profiles of the solar wind velocity, ${\mathit{V}}_{\mathrm{sw}}$, density, N, thermal speed, ${\mathit{V}}_{\mathrm{th}}$, and magnetic field magnitude, B. Dashed vertical lines show IP shock fronts. Colored horizontal lines mark the intervals for estimations of the power spectra of magnetic field fluctuations in Figure 5. Dashed/solid lines cover 1 h upstream/downstream of each shock (excluding 5 min adjacent to the shock front).

TABLE 1

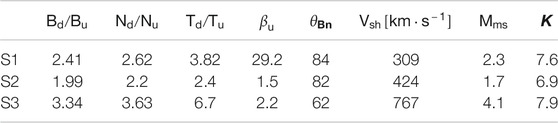
TABLE 1. Parameters of the shocks S1, S2, and S3 at $\mathrm{1}\mathrm{AU}$ as measured by Wind; parameters are taken from the database of http://ipshocks.fi. ${\mathit{B}}_{\mathrm{d}}/B_{\mathrm{u}}$, ${\mathit{N}}_{\mathrm{d}}/N_{\mathrm{u}}$, and $T_{\mathrm{d}}/T_{\mathrm{u}}$ are the ratios of downstream/upstream magnetic field magnitude, proton number density, and proton temperature, respectively. $V_{\mathrm{sh}}$ is the shock speed in the spacecraft frame of reference, $M_{\mathrm{ms}}$ is the fast magnetosonic Mach number and K is the time conversion constant estimated from the shock parameters by Eq. 4.

Figure 5 shows the power spectra of upstream and downstream fluctuations of the magnetic field components, the magnetic field strength and the magnetic field strength normalized by the average background magnetic field ${\mathit{B}}_{\mathrm{0}}$ for all three shocks at the time scale of 1 h. The intervals used for computations are shown by color bars in the top panel of Figure 4. Note that the difference in the fluctuation power between the downstream of S3 (solid blue) and upstream of S1 (dashed red) is roughly four orders of magnitude. Focusing on the changes of levels of fluctuations from upstream to downstream, one can see that S1 and S3 are similar, i.e., the enhancement in $\mathit{\delta }\mathit{B}$, $\mathit{\delta }\left|\mathit{B}\right|$, and $\mathit{\delta }\left|B\right|/B_0$ is roughly the same, while the enhancement of these quantities is much less for S2. Considering an overall level of fluctuations, downstream of S3 is unique because: 1) the IP shock propagates into already disturbed medium of the S2 sheath and 2) the compression ratio of this shock reaches the theoretical limit of 4 for adiabatic index $\mathit{\gamma }=5/3$ [6].

FIGURE 5

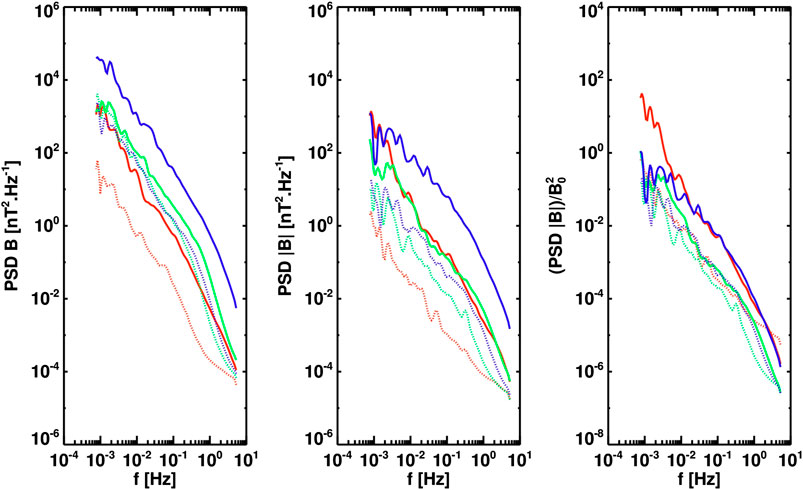
FIGURE 5. Left: Trace power spectral densities of magnetic field fluctuations for upstream (dashed) and downstream (solid) intervals of S1 (red), S2 (green), and S3 (blue); middle: power spectrum of magnetic field magnitude fluctuations, and right: the same power spectrum but normalized to the average $\mathrm{|}\mathit{B}\mathrm{|}$ in the particular interval.

5.1 Upstream Fluctuations

As it has been pointed out in Section 2, the upstream regions of supercritical IP shocks can be substantially disturbed by the microphysical processes that take place at the shock front. These processes influence both upstream and downstream regions. In this section, we discuss upstream fluctuations and how they are coupled with processes such as shock reformation.

Particles reflected from the quasi-parallel shock escape in the upstream region and move away from the shock along the magnetic field lines. These ions interact with the incoming solar wind through a number of wave generation mechanisms and plasma instabilities, which basically develop into an extended foreshock. The complex and highly coupled interaction between waves and particles in the foreshock, where waves are generated by energetic particles and, on the other hand, the energetic particles are scattered by these waves, also defines the energetic coupling between waves and particles. The coupling was described in a self-consistent model by [75, 76, 110]. The main approach of this model is a linear relationship between the energetic particle energy density and the wave energy density. The wave energy density is a partial energy density, calculated in the frequency range that is in resonant condition with the energetic particles. In other words, the energy density of the waves and fluctuations is determined by the energetic and/or accelerated particles. [89] analyzed two upstream ion events and found a good agreement between the measured and predicted wave energy density. In a statistical study by [127]; about 300 events were studied and they found a very good correlation value of 0.89 between the observed and predicted wave energy density. This study also demonstrates that the correlation does not depend on the velocity jump across the event. It has been shown by [62] that also in the case of interplanetary shocks, the predicted wave power (spectral) density agrees well with the observed wave intensity values. Lately, [68, 97] demonstrated that in the case when a strong Field Aligned Beam (FAB) is formed at the Earth’s bow shock, the waves generated by the beam can influence the wave field in the foreshock region resulting in a significantly higher wave intensity than usual.

In the context of upstream turbulence generated by the suprathermal particles, [7] reported that the upstream magnetic field spectra exhibit a power law scaling of $\mathrm{-3}/\mathrm{2}$. They argued that the estimated power spectra show the competition of wave growth [76] and turbulent wave diffusion of the Iroshnikov-Kraichnan weak turbulence theory. Their finding is consistent with the current models of imbalanced turbulence [77, 103, 107] that predict the spectral index of $\mathrm{-3}/\mathrm{2}$. In the upstream region, cross helicity ${\mathit{\sigma }}_{\mathrm{c}}$ may be significantly increased because the energetic ions amplify the anti-sunward propagating Alfvén waves. Moreover, [27, 28], have shown that the IMF in the solar wind exhibits −3/2 scaling for intervals with high cross helicity.

On the other hand, [92] have shown that in the Earth’s foreshock, power spectra in the wave number domain extracted from four-point Cluster measurements exhibit Kolmogorov scaling of $\mathrm{-5}/\mathrm{3}$, i.e., $\mathit{P}\left(\mathit{k}\right)\propto {\mathit{k}}^{\mathrm{-5/3}}$. They argued that the classical concept of an inertial range can be applicable, i.e., the first waves are excited at low wave numbers, and then they resonantly interact with other waves, creating daughter waves that interact again, etc.

A few studies reported observations of ULF waves (spacecraft frame frequencies $\mathrm{1}{\mathrm{0}}^{\mathrm{-2}}\mathrm{-1}{\mathrm{0}}^{\mathrm{-1}}\mathrm{Hz}$) upstream both quasi-parallel and quasi-perpendicular IP shocks. [10] reported that unlike the ULF waves in the Earth’s foreshock, where these waves can be highly compressive and may steepen into shocklets or Short Large Amplitude Magnetic Structures (SLAMS) (e.g., [135]), ULF waves upstream of IP shocks are only weakly compressional. The Alfvénic nature of ULF waves may be explained by a small average Mach number of the shocks they investigated. Since their dataset contained both CIR and ICME shocks, they estimated the extent of the foreshocks for both types. They found that quasi-parallel CIR shocks exhibit foreshocks with a small spatial extent $\mathrm{\Delta }\mathit{r}\approx \mathrm{0}\mathrm{.05}\mathrm{AU}$, while for ICME shocks $\mathrm{\Delta }\mathit{r}\approx \mathrm{0}\mathrm{.1}\mathrm{AU}$. They attributed this difference to the shock age; CIR shocks form at larger distances from the Sun (compared to ICME shocks), thus they have less time for acceleration of particles that are the ultimate source of the extended foreshock.

A simulation study of [72] focused on the Mach number dependence of upstream and downstream properties of quasi-parallel shocks. Other simulation studies (e.g., [20]; and references therein), have shown that the reformation of the shock front and its cyclic nature could play a pivotal role in understanding the downstream fluctuations. Due to the shock front reformation that is characteristic of high Mach number shocks, the upstream large amplitude fluctuations are directly convected into the downstream region. In other words, the energy of the reflected and accelerated particles is converted into the downstream wave energy. Even for low Mach number shocks, ULF waves impact the shock front, change the local ${\mathit{\theta }}_{\mathrm{Bn}}$ and lead to larger than expected amplification of the wave amplitude.

Focusing on quasi-perpendicular shocks, it is difficult to imagine how multiple crossings of the shock front (essential for particle acceleration) could be achieved because the reflected particles return to the shock in one gyroperiod. However, large amplitude turbulence that the particle would follow may enhance the cross-field diffusion [44]. [142] have shown that power-law spectra of energetic particles upstream of highly quasi-perpendicular IP shocks can be successfully explained in the framework of diffusive shock acceleration.

5.2 Downstream Fluctuations

A key relation that connects the time of observation of the downstream plasma in the spacecraft frame, ${\mathit{t}}_{\mathrm{sp}}$, with the age of this shocked plasma relative to the shock passage, ${\mathit{t}}_{\mathrm{sh}}$ was derived by [105] and it reads,

${\mathit{t}}_{\mathrm{sh}}\mathrm{=}{\mathit{t}}_{\mathrm{sp}}\mathit{K}\mathrm{,}(3)$

where $\mathit{K}$ is a time conversion constant that characterizes a particular shock and it is defined as

$\mathit{K}\mathrm{=}\frac{v_{\mathrm{sh}}}{v_{\mathrm{sh}}\mathrm{-}{\mathit{v}}_{\mathrm{d}}\cdot \mathit{n}}\mathrm{,}(4)$

$v_{\mathrm{sh}}$ is the shock speed, $v_{\mathrm{d}}$ is the downstream solar wind speed and $\mathit{n}$ is the shock normal. Calculation of $\mathit{K}$ for S1 yields $\mathit{K}\mathrm{=7}\mathrm{.6}$. This value is not universal, it changes with the shock and wind parameters. [105] reported an average value of $\mathit{K}\mathrm{=6}$ for a set of 174 IP shocks, while [14] proposed to use a value of $\mathit{K}\mathrm{=5}\mathrm{.5}$. A rough estimation of maximum $t_{\mathrm{sh}}$ for $\mathit{S}\mathrm{1}$ yields¹$t_{\mathrm{sh}}\mathrm{=5}\mathrm{.5}\mathrm{h}\cdot \mathrm{7}\mathrm{.6=42}\mathrm{h}$, that is shorter than the propagation time of the ICME from the solar surface up to L1, ${\mathit{t}}_{\mathrm{prop}}\mathrm{\approxeq }70\text{\hspace{0.17em}h}$ [46]. Consequently, the downstream region of the IP shock captures the evolution of the shocked plasma from a close proximity of the Sun to L1. It suggests that estimations of the power spectrum of the whole ICME sheath (e.g., S1 sheath in Figure 4) is problematic due to its inherent “non-stationarity” in the following sense: the leading edge of a sheath is a plasma that has been just shocked, while the trailing edge of the sheath is a plasma that has been shocked closer to the Sun, tens of hours ago. Thus, the determined energy levels of the power spectrum at largest scales seem to lack a proper physical meaning. This leads to the following question: what is the largest scale at which the spectrum can be estimated? Later on, we will introduce a phenomenological argument that addresses this question.

As already mentioned above, two aspects affect the character of sheath fluctuations, 1) the gradual change of the average magnetic field that should roughly follow the Parker spiral and 2) changes of the magnetic field direction due to its inherent fluctuations. The later effect was addressed by [14] who showed that it might enhance the levels of compressibility of downstream fluctuations.

The character of upstream and downstream fluctuations differs for the quasi-parallel and quasi-perpendicular geometry. Ignoring any complicating factors, the simple condition on conservation of the normal component (Eq. 2) leads to a conclusion that upstream and downstream magnetic field vectors are the same for ${\mathit{\theta }}_{\mathrm{Bn}}\mathrm{=}{\mathrm{0}}^{\mathrm{o}}$, implying that small deviations in the upstream magnetic field magnitude are not enhanced by the shock, whereas the perpendicular fluctuations can be. On the other hand, for ${\mathit{\theta }}_{\mathrm{Bn}}\mathrm{=9}{\mathrm{0}}^{\mathrm{o}}$, a shock can enhance both Alfvén-like (non-compressive) and compressive fluctuations. This leads to a conclusion that the relative change of the compressibility, ${\left(\mathit{\delta }{\mathit{B}}_{\parallel }/\mathit{\delta }{\mathit{B}}_{\perp }\right)}^2$ is different for these two shock geometries. A more realistic scenario of oblique shocks was treated by [88]. They analytically calculated the transmission coefficients of incident Alfvén wave striking the bow shock on the basis of hydromagnetic shocks. They deduced that an incident Alfvén wave excites two downstream Alfvén waves. This process was consistent with the findings of [79] who used two-dimensional hybrid simulation of the interaction of Alfvén waves with the quasi-perpendicular shock. Both studies report that the fluctuation level of downstream waves is roughly order of magnitude larger than the level of the upstream fluctuations. They found that a shape of the shock front is affected by upstream turbulence, e.g., it exhibits an irregular shape when the upstream is populated by a mix of Alfvén waves. This confirms the finding of [5]; who investigated the interaction of turbulence and IP shock by perturbation analysis of 2D inviscid Burgers’ equation. They found that a shape of the quasi-perpendicular shock front is significantly affected by upstream waves which results in complex downstream state and, moreover, they predict the variability of a compression ratio for different regions.

The interaction of turbulence and shocks was investigated both theoretically and observationally by [1, 145]. [1] compared solutions of equations for a turbulent transport with the observations of IP shocks by the Wind spacecraft. They derived four-coupled equations for a perpendicular shock and six-coupled equations for a parallel shock from the turbulent transport equations of [141]. In particular, they have found that the sum of kinetic and magnetic energies within turbulent fluctuations increases across the shock, while the normalized cross-helicity can either increase or decrease. Although the simplified equations are 1D, many important turbulent quantities like total turbulent energy, cross-helicity, residual energy can be reasonably estimated. They have found a good agreement between numerical solutions and observations of both upstream/downstream fluctuations.

However, the uncertainties in estimation of turbulent energies from observations are often huge because each upstream/downstream profile is significantly “noisy” and it may put the analysis of each particular IP shock into question. An approach that solves the problem of under-sampling of turbulent quantities can be based on a large statistical set of IP shocks (e.g., [14]).

[66] studied dynamic pressure and magnetic field fluctuations in the inertial range via a superposed analysis of sheaths driven by ICMEs. The authors estimated the power of the fluctuations in the range of periods $\mathrm{3-10}\min$. They observed a mismatch between the occurrence of the peaks in the ULF power of magnetic field fluctuations and the peaks in dynamic pressure ${\mathit{P}}_{\mathrm{dyn}}$ fluctuations. The ULF power was enhanced at the leading part of the sheath, while the ${\mathit{P}}_{\mathrm{dyn}}$ was enhanced at its trailing part. They attributed this mismatch to the effect of piling of the solar wind in front of ICME and geometric constraints of the magnetic field within the sheath. They also analyzed magnetic field ULF power for each ${\mathit{B}}_{\mathit{x}}$, ${\mathit{B}}_{\mathit{y}}$, and $B_z$ (GSM) component for the estimation of space weather effects. The ULF power for ${\mathit{B}}_{\mathit{z}}$ and ${\mathit{B}}_{\mathit{y}}$ showed enhancements at the sheath leading part, while the ULF power of the ${\mathit{B}}_{\mathit{x}}$ component did not. They focused the analysis mainly on a role of the ${\mathit{B}}_{\mathit{z}}$ component and divided 41 sheath regions into various subgroups (fast vs slow ICMEs, central vs intermediate encounters with ICMEs), and reported that the greatest difference of power profiles of ULF ${\mathit{B}}_{\mathit{z}}$ fluctuations is between fast and slow ICMEs. While there is a strong increase of the power towards the shock for fast ICMEs, slow ICMEs show a relatively flat profile through the whole sheath.

A different approach in analyzing ICME sheath fluctuations was used by [90]; they focused on carefully constructed averages of magnetic field anisotropy $\mathit{A}\mathrm{=}{\mathit{P}}_{\mathrm{\perp }}/\left(\mathrm{2}{\mathit{P}}_{\parallel }\right)$, compressibility $\mathit{C=}{\mathit{P}}_{\parallel }/\left({\mathit{P}}_{\parallel }\mathrm{+}{\mathit{P}}_{\mathrm{\perp }}\right)$, where ${\mathit{P}}_{\parallel }$ and ${\mathit{P}}_{\mathrm{\perp }}$ are the fluctuation powers parallel and perpendicular to a local magnetic field, and total fluctuation power P, in the solar wind, sheath and magnetic cloud. They discussed 42 events from the [82] list of well-defined and isolated magnetic cloud driven sheaths. The frequency range for the estimation of relevant quantities was set to $\mathrm{2}\cdot \mathrm{1}{\mathrm{0}}^{\mathrm{-3}}\mathrm{-5}\cdot \mathrm{1}{\mathrm{0}}^{\mathrm{-2}}\mathrm{Hz}$, i.e., similar as in [66]. The main results of their analysis is that the upstream solar wind and driving magnetic cloud have similar fluctuation powers (${\mathit{P}}_{\mathrm{sw}}\sim P_{\mathrm{mc}}\sim \mathrm{0}\mathrm{.9}\mathrm{n}{\mathrm{T}}^{\mathrm{2}}$), while the fluctuation power within the sheath is roughly order of magnitude larger (${\mathit{P}}_{\mathrm{sh}}\sim \mathrm{9}\mathrm{n}{\mathrm{T}}^{\mathrm{2}}$). Moreover, the power anisotropy in the sheaths (${\mathit{A}}_{\mathrm{sh}}\sim \mathrm{5}$) tends to be much lower than that in the solar wind (${\mathit{A}}_{\mathrm{sw}}\sim \mathrm{10}$) and in the magnetic cloud (${\mathit{A}}_{\mathrm{mc}}\sim \mathrm{36}$). The authors found a good correlation ($\mathit{Cor}\sim \mathrm{0}\mathrm{.54}$) between the power, ${\mathit{P}}_{\mathrm{sh}}$ and the speed of the magnetic cloud ${\mathit{v}}_{\mathrm{mc}}$, which can be expected because high-speed MCs drive stronger shocks [65] with a higher compression ratio that leads in average to the enhancement of the fluctuation power. A level of sheath fluctuations, ${\mathit{P}}_{\mathrm{sh}}$ correlates ($\mathit{Cor}\sim \mathrm{0}\mathrm{.42}$) with the level of upstream solar wind fluctuations, ${\mathit{P}}_{\mathrm{sw}}$, consistent with [14] who reported a similar correlation ($\mathit{Cor}\sim \mathrm{0}\mathrm{.48}$).

Perhaps the greatest limitation of the [90] study is the use of average values because the level of magnetic field fluctuations generally decreases with the distance from the shock [66, 105]. However, the authors show that significant correlations revealing true physical phenomena can be found even when one omits a time evolution within the sheaths. On the other hand, it would be important to estimate the above mentioned characteristics of fluctuations in different regions of ICME sheaths, and more generally, downstream of any IP shock.

Recently [65] addressed the evolution of magnetic field fluctuations starting from the upstream solar wind and in three separate sheath regions: near the shock, in middle of the sheath and close to the ejecta. Each studied interval have 1 h duration in the spacecraft frame of reference. Their study was based on analysis of three distinctly different IP shocks observed at L1 by the Wind spacecraft. They analyzed magnetic field fluctuation amplitudes, compressibility, spectral properties in inertial and kinetic ranges, and various intermittency measures. Their findings are consistent with the previous studies, e.g., the inertial range spectral indices are mostly steeper in the sheath region compared to the preceding solar wind, but not for the case where the IP shock propagates into a high speed solar wind [14]. However, no ultimate conclusion can be made because the value of the upstream spectral index is likely to be influenced by foreshock-related wave activity. They concluded that the sheath regions exhibit characteristics of turbulence in the slow solar wind (higher compressibility, $\mathit{\delta |B|}/\mathit{\delta }\mathit{B}\mathrm{\lesssim }0.2$) and suggested that sheath turbulence is not fully developed.

A number of studies focus on the nature of compressive fluctuations downstream of IP shocks or/and on the change of the compressibility from upstream to downstream. The basic analysis of three IP shocks in Section 5 suggests that the compressibility defined as $\mathit{\delta }{\mathit{B}}^{\mathit{2}}/{\mathit{B}}_{\mathit{0}}^{\mathit{2}}$ is higher in the downstream. Indeed [14] showed that both $\mathit{\delta }\mathit{N}/{\mathit{N}}_{\mathrm{0}}$ and $\mathit{\delta }\mathit{B}/{\mathit{B}}_{\mathrm{0}}$ increase across the shock by a factor of $\sim \mathrm{1}\mathrm{.5}$ and $\sim \mathrm{2}$, respectively. The author observed the increase for all four distinct types of solar wind plasma [138] the shock propagates through. They explained the increase in inhomogeneity (lumpiness) by invoking the spaghetti-like structure of the solar wind [12]. The main idea is that the change of average magnetic field vector between adjacent flux tubes causes the change of the shock ${\mathit{\theta }}_{\mathrm{Bn}}$ which drives the changes of the compression ratio of the shock. The increase of the lumpiness was also reported by [104]; who analyzed the changes of upstream/downstream power spectra of the ion flux (which served as a proxy for density fluctuations).

Important characteristics of turbulence are spectral slopes. Recently [14] comprehensively analyzed upstream/downstream trace-B and ${\mathit{V}}_{\mathrm{sw}}$ spectral indexes in the inertial range. He has shown that there is a little correlation between the corresponding upstream and downstream values ($\mathit{Cor}\mathrm{\lesssim 0}\mathrm{.20}$) for both B and ${\mathit{V}}_{\mathrm{sw}}$ while there is a small steepening of both spectral indices from upstream to downstream in average (see Figure 12 in [14]). Interestingly, when an IP shock propagates into a coronal-hole-origin plasma, virtually no steepening is observed (based on 15 shocks). Considering the Alfvén ratio ${\mathit{r}}_{\mathrm{A}}$ (ratio of the kinetic and magnetic energies of the fluctuations), IP shocks propagating through each type of solar wind exhibit a decrease of this ratio, with the greatest reduction occurring for shocks propagating through plasma of coronal hole origin.

Considering the evolution of the upstream and downstream spectral slopes of trace-B and ${\mathit{V}}_{\mathrm{sw}}$ with respect to the distance from the shock front [14] observed flatter spectra (spectral indices $\sim \mathrm{-1}\mathrm{.5}$) within 1 h adjacent to the shock front. A similar finding was reported by [55] who analyzed inertial and kinetic range magnetic field fluctuations in different regions of the terrestrial magnetosheath. They showed that closer to the bow shock, the inertial range power spectra of B exhibit ‘1/f’ scaling. The flattening reported by both studies is in a qualitative agreement, though the values of indices are substantially different. The difference may be elucidated by examining the spatial/time scales of the fluctuations in these two studies. The significant difference is between the measurements of Cluster [55] and Wind [14]; the Cluster is virtually standing still with respect to the IP shock front, while at Wind, the downstream fluctuations are sweeping past the spacecraft at the speed of the downstream solar wind velocity (with respect to shock front). The corresponding spacecraft time frame for a simulated Wind measurement of the magnetosheath region (e.g., at the nose) can be roughly estimated as ${\mathit{t}}_{\mathrm{sp}}^{\mathrm{W}}\mathrm{=}{\mathit{L}}_{\mathrm{magnetosheath}}/{\mathit{v}}_{\mathrm{sw}}$. For typical solar wind conditions, ${\mathit{t}}_{\mathrm{sp}}^{\mathrm{W}}$ is in the order of minutes. Therefore, the whole magnetosheath region would correspond to just a fraction of the immediate downstream region analyzed by [14] using Wind. Nonetheless, the qualitative similarity of the flattening probably indicates a common physical origin.

Finally, we note that the range of upstream spectral indices is roughly two times wider than the range of the downstream indices (see Figure 12 in [14]). A similar behavior was shown by [104] for the spectral index of the ion flux power spectra in the inertial range (Figure 6). We believe that this is not accidental, however, there is no explanation for such observation.

FIGURE 6

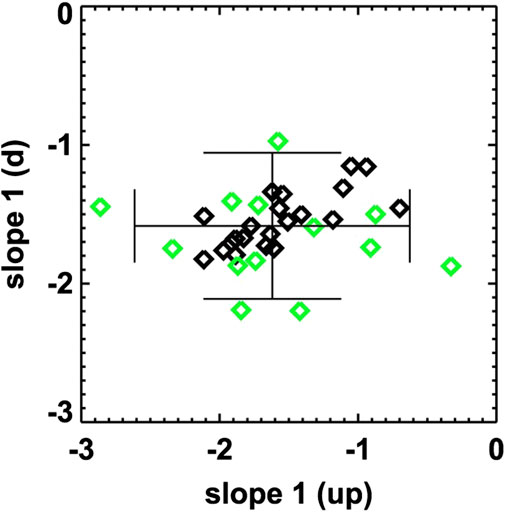
FIGURE 6. Upstream vs. downstream spectral indices of inertial range fluctuations of the ion flux for a set of 34 IP shocks of [104]. Color symbols show the reliability of estimated slopes (black denotes a more reliable estimation). The horizontal and vertical lines in the middle mark the average spectral index of slope1 in the downstream and upstream regions, respectively. The shorter horizontal and vertical lines denote 2 standard deviations from the averages of the downstream and upstream spectral indices, respectively. The plot shows that for more reliable estimated slopes, the upstream and downstream indices seem to be correlated. On the other hand, the whole set (34 cases) shows that the spread of the indices is roughly two times larger in the upstream than in the downstream region. Image adapted from [104] and reproduced by permission of the AAS.

5.2.1 Kinetic Range

The properties of kinetic range fluctuations, for example, which kinetic wave mode they resemble, what power-law scaling they obey, what levels of compressibility they have, etc., are not fully established yet, in particular because obtaining observations of these fluctuations upstream/downstream of IP shocks is challenging.

The number of studies that have analyzed the downstream IP shock kinetic range spectra is very limited but there are plenty of observations of kinetic turbulence in the terrestrial magnetosheath (e.g., [118]; and references therein). However, their relevance to the large scale sheaths of IP shocks is limited due to a small spatial extent of the magnetosheath. Immediately downstream the bow shock, the character of wave/turbulence should not be strongly affected by the presence of the magnetopause. However, deeper in the magnetosheath, magnetospheric processes like reconnection can influence the fluctuations and thus we will focus on the studies that investigated kinetic scale fluctuations closer to the bow shock.

[108] analyzed the 6 years of ion flux measurements of the Spektr-R spacecraft. In the magnetosheath, they found that the ion flux power spectra can be divided into three categories, a) two power laws separated by a break, b) two power laws with a bump around the break, and c) two power laws connected by a plateau (power law with spectral index −1). They reported that the bumpy spectra are more likely to occur close to the bow shock and they attributed this bump to kinetic instabilities such as mirror instability but they were not able to give a definitive answer due to the lack of magnetic field measurements. They observed a power law index of $\mathrm{-3}\mathrm{.2}$ in the vicinity of the bow shock, which is steeper than values reported in the solar wind [30, 115]. This finding is consistent with [104] who reported that ion flux spectrum is steeper within the downstream region of IP shocks.

[104] have shown that the scaling of fluctuations downstream of IP shocks of the ion flux in the kinetic range can be modeled as an exponentially truncated power law $\mathit{P}\left(\mathit{f}\right)\propto \mathit{a}\mathrm{\times }{\mathit{f}}^{\mathit{b}}\mathrm{\times }{\mathit{e}}^{\mathrm{-}\mathit{f}/{\mathit{f}}_{\mathrm{0}}}$ (Figure 7), which has not been reported in previous studies of kinetic-range spectra. A rule-of-thumb for these spectra in the solar wind is that they obey a power law with the scaling index that ranges from $\sim \mathrm{-2}$ to $\sim \mathrm{-4}$ [74, 115, 116]. An exponential power law may imply a fundamentally different physical mechanism that operates at sub-ion scales in the sheaths of IP shocks.

FIGURE 7

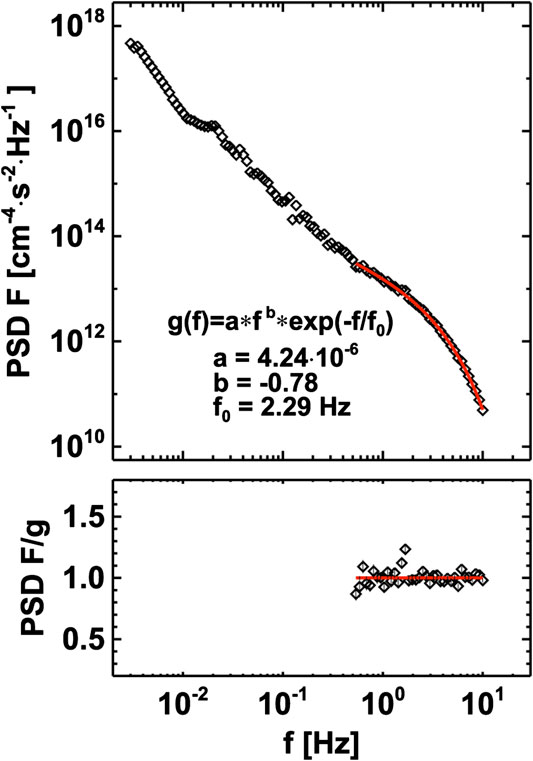
FIGURE 7. Upper plot: The power spectral density of the ion flux downstream of a particularly strong IP shock detected at Spektr-R on September 12, 2014. The red line shows the fit by an exponentially truncated power-law model function, $\mathit{g}\left(\mathit{f}\right)$. Lower plot: The ratio of the measured spectrum, $PSDF$, and the resulted fit, g. Image adapted from [104] and reproduced by permission of the AAS.

Employing fast MMS measurements [29] combined observations and theory to study plasma turbulence at kinetic scales in the Earth’s magnetosheath. They estimated the spectra of the magnetic field, density and electric field, and found that just below characteristic ion scales the spectra follow the predictions for the kinetic Alfvén turbulence. Namely, the dimensionless ratio of normalized density and magnetic field fluctuations $\mathit{\delta }{\mathit{n}}^{\mathrm{2}}/\mathit{\delta }{\mathit{b}}^{\mathrm{2}}$ [11, 30, 106] follows the kinetic Alfvén prediction over a wide range of sub-ion frequencies. Similarly [137] concluded that the sub-ion fluctuations are consistent with the two-fluid predictions of KAWs for various dimensionless ratios. [29] proposed a new mode of KAWs–inertial kinetic Alfvén wave–that arises when the plasma exhibits temperature anisotropy ${\mathit{T}}_{\mathrm{i}}\gg {\mathit{T}}_{\mathrm{e}}$ while ${\mathit{\beta }}_{\mathrm{i}}\sim \mathrm{1}$. In this regime, compressibility of fluctuations below the electron inertial length increases from the KAW-predicted value toward inertial KAW-predicted value of $\sim \mathrm{1}$ at electron gyroradius. This wave mode and its nonlinear dynamics could play an important role in the sheaths of IP shocks since the ions are often hotter than electrons there.

Although the solar wind is populated predominantly with Alfvénic and slow mode fluctuations [117], the mirror mode (MM) waves are frequently observed in shock sheaths. Due to the quasi-perpendicular shock compression, ions heat preferentially in the perpendicular direction which leads to an increase of temperature anisotropy and the instability threshold (${\mathit{\beta }}_{\mathrm{\perp }}/{\mathit{\beta }}_{\parallel }\mathrm{-}\mathit{1}\mathrm{-}\mathit{1}/{\mathit{\beta }}_{\mathrm{\perp }}\mathit{=0}$) can be easily reached. Several studies identified peak and dip like large amplitude fluctuations in the Earth magnetosheath (e.g. [123, 124]). [3] investigated MMs in sheaths of 91 ICME driven shocks and among other findings, they reported that 1) the key shock parameter that controls the occurrence of MMs is the Mach number (higher ${\mathit{M}}_{\mathrm{A}}$ means higher occurrence rate), 2) the amplitudes of MMs were largest near the shock and (3) MMs are predominantly dip like structures and occurred in the mirror stable plasma. They concluded that the source of free energy for MMs is the shock compression and that MMs found deeper in the sheath are remnants of MMs generated closer to the shock front.

Since the average duration of MMs (in the spacecraft frame) in the study of [3] is $\mathrm{\Delta }\mathit{T}\sim \mathrm{12}\mathrm{s}$, their large average amplitude is $\mathit{A}\sim \mathrm{3}\mathrm{.5}\mathrm{nT}$, a fact that MMs are compressive structures and their occurrence rate is higher for high Mach number IP shocks, these observations may provide a basis for an explanation of the exponential power spectra reported by [104]. However, a definitive answer could only be made by analyzing both the magnetic field vector and number density in IP shock sheaths with sufficient cadence. Then, the nature of fluctuations (KAWs, MMs, Alfvén Ion Cyclotron waves, Whistler mode waves) and their particular contribution to the overall shape of the power spectrum can be estimated.

5.2.2 Decay of Turbulent Fluctuations

[66] have shown that the power within ULF ${\mathit{B}}_{\mathit{z}}$ fluctuations decreases with a distance from the shock front. Generally, Figure 8 (adapted from [63]) shows a relatively flat (although spiky) profile of ULF $B_z$ power in a few hours downstream of the shock front and then decreases roughly from the middle of the sheath. This observation is qualitatively consistent with the findings of [105] who showed that the enhanced power of downstream fluctuations in the inertial range does not decrease immediately after the passage of an IP shock.

FIGURE 8

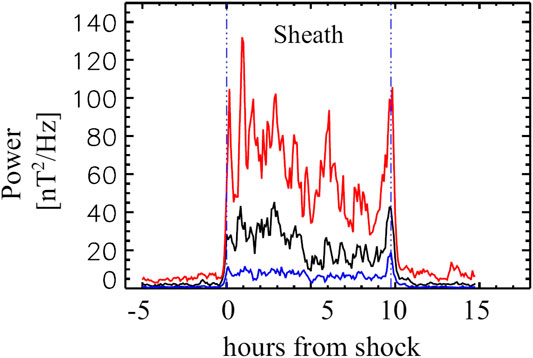
FIGURE 8. ULF power of ${\mathit{B}}_{\mathrm{z}}$ component of IMF in sheaths of ICMEs (superposed analysis of sheath profiles that have been re-scaled to 10 h). The black line in the middle shows the median while the red and blue lines denote the upper and lower quartiles, respectively. For details, see [66]. The figure is adapted from [63]; copyright by Springer Nature, licensed under CC BY 4.0.

[105] analyzed a set of 174 fast forward IP shocks with respect to the evolution of the kinetic and magnetic fluctuations in the downstream region. They estimated the kinetic and magnetic energies, ${\mathit{E}}_{\mathrm{k}}$ and $E_{\text{m}}$, in the fluctuations on the time scale of $30\text{\hspace{0.17em}min}$. A superposed analysis of energy profiles is depicted in Figure 9. The profile of each shock was normalized by its immediate downstream value ${\mathit{E}}_{\mathrm{0}}$. The main difference between their study and [66] is that the time is transformed into the natural units for turbulent energy decay, i.e., the eddy turnover time, ${\mathit{\tau }}_{\mathrm{nl}}$. The average energy profile for ${\mathit{E}}_{\mathrm{k}}$ and ${\mathit{E}}_{\mathrm{m}}$ is very similar and can be fitted by a phenomenological model function

$\mathit{E}\left({\mathit{t}}_{\mathrm{nl}}\right)\mathrm{=}{\left(\frac{{\mathit{t}}_{\mathrm{nl}}\mathrm{-}{\mathit{t}}_{\mathrm{0}}}{{\mathit{t}}_{\mathrm{d}}\mathrm{-}{\mathit{t}}_{\mathrm{0}}}\right)}^{\mathit{n}}(5)$

where ${\mathit{t}}_{\mathrm{0}}$ and $\mathit{n}$ are free parameters of the model, while ${\mathit{t}}_{\mathrm{d}}\mathrm{=10}$ is a constant determined from the profiles in Figure 9. This constant may be interpreted as an average time that turbulence needs to adjust itself after the amplification at the shock. The constant profile up to $\mathit{t}\mathrm{=}{\mathit{t}}_{\mathrm{d}}$ and a Kolmogorov like power-law in the inertial range suggest that turbulence is in a forced state. This forcing can have two origins (1) the kinetic processes in the shock front provide a free energy that can favor an inverse cascade of the fluctuation energy [105] and (2) the forcing from the large scales is constant. An important caveat for the constant $t_{\text{d}}=10$ is that the time scale of $\mathrm{30}\min$ for the estimation of the nonlinear time may not be the proper time scale. One should estimate ${\mathit{\tau }}_{\mathrm{nl}}$ on the spatial scale of the injection scale ${\mathit{\tau }}_{\mathrm{nl}}\left({\mathit{k}}_{\mathrm{inj}}\right)$ that is usually attributed to the low frequency break in the power spectrum of the magnetic field (see Figure 3). Invoking a standard formula for Kolmogorov turbulence, ${\mathit{\tau }}_{\mathrm{nl}}\mathrm{\sim }{\mathit{k}}^{\mathrm{-2/3}}\mathrm{\sim }{f}^{\mathrm{-2/3}}$ and assuming that the factor of ${\mathit{t}}_{\mathrm{d}}\mathrm{=10}$ comes from the underestimation of the true nonlinear time, one can estimate the spacecraft frame frequency corresponding to ${\mathit{\tau }}_{\mathrm{nl}}\left(f_{\mathrm{inj}}\right)$ using the ratio ${\mathit{\tau }}_{\mathrm{nl}}\left(f_{\mathrm{inj}}\right)/{\mathit{\tau }}_{\mathrm{nl}}\left(f_{\mathrm{30}}\right)\mathrm{=}{\left(f_{\mathrm{inj}}/f_{\mathrm{30}}\right)}^{\mathrm{-2/3}}\mathrm{=10}$, where $f_{30}$ is simply the spacecraft frame frequency that corresponds to the time scale of 30 min, which yields $f_{\mathrm{inj}}/f_{\mathrm{30}}\sim \mathrm{0}\mathrm{.03}$. This implies that the time scale in the spacecraft frame for the injection scale would correspond to roughly 15 h. That seems to be an overestimation of ${\mathit{f}}_{\mathit{i}\mathrm{n}\mathrm{j}}$, at least for the fast solar wind where this time scale is usually lower than 1 h. However, in the slow wind, it may reach such values [19]. In any case, the conclusions of [105] that the power-law decay in time does not start immediately after the IP shock front will not change.

FIGURE 9

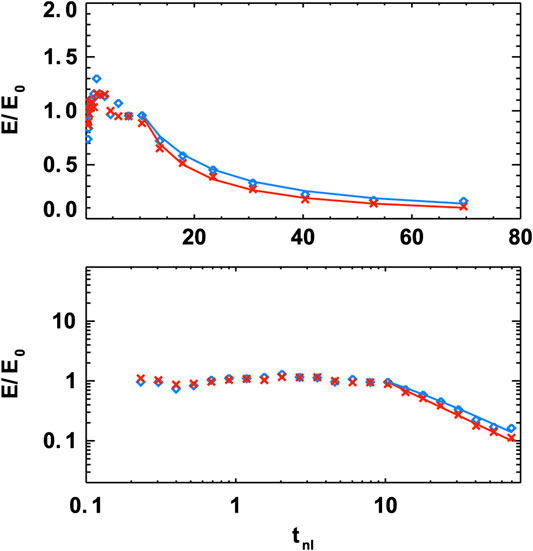
FIGURE 9. Average downstream evolution of the kinetic (red crosses) and magnetic (blue diamonds) energies for the set of 174 IP shocks analyzed by [105]. Upper/lower panel shows the evolution in a linear scale/log-log scale, respectively. ${\mathit{E}}_{\mathrm{0}}$ signifies that the profile of each shock was normalized by its immediate downstream value. Corresponding colored lines show the fit by a phenomenological power law function defined by Eq. 5. Image adapted from [105] and reproduced by permission of the AAS.

One could expect that the turbulent energy within the enhanced level of fluctuations downstream of the shock eventually cascades to smaller scales and dissipates into heat. Consequently, we should observe an increase of the temperature further in the downstream. The temperature profiles downstream of three shocks (see Figure 4) show a gradual rise of the temperature in time for S1 and S2. This rise could be caused by 1) the turbulent heating due to the enhancement of turbulent energy at the shock (left panel in Figure 5), 2) it could be just accidental or 3) caused by some another physical mechanism. A superposed analysis of 109 temperature profiles by [14] shows that there is no such an increase even 3 h after the passage of the IP shock (see Figure 6 in [14]). Our example of three consecutive shocks in Figure 4 shows that the downstream temperature profiles can be very different and thus the superposed profile can depend on the set of shocks used for analysis. In order, to check downstream temperature independently, Figure 10 shows the evolution of profiles of the proton temperature T, proton number density N, magnetic field strength B and specific entropy S, 5 h upstream and downstream from the shock passage for 174 IP shocks analyzed by [105]. The profiles are qualitatively similar to those reported by [14]; e.g., a slight increase of the temperature and density towards the shock front in upstream, roughly constant temperature and a slight decrease of the density in downstream. On the basis of the constant downstream temperature profile, [14] suggested that no new active turbulence is generated. However, two observational facts: i) an increased level of turbulent energy and ii) no temperature increase seems to be in contradiction and should be further addressed.

FIGURE 10

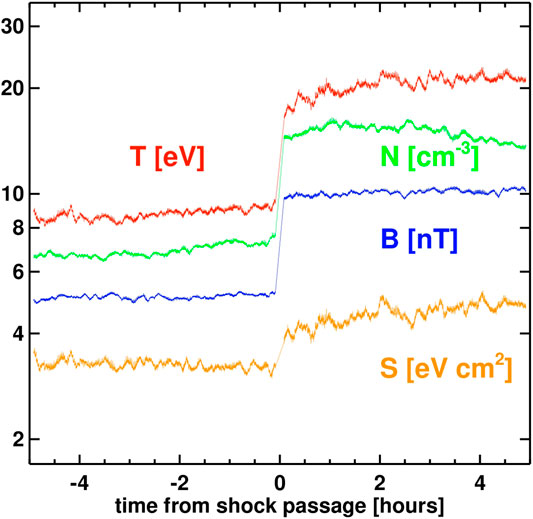
FIGURE 10. A superposed epoch analysis of 140 fast forward IP shocks analyzed in [105]. The plot shows average profiles of proton temperature (red), proton number density (green), magnetic field magnitude (blue) and specific entropy (orange) for 5 h of upstream/downstream plasma. Note that the statistical set is reduced from the original set of 174 IP shocks due to additional requirements on the temperature measurements.

An explanation for this discrepancy may be as it follows. A higher level of fluctuations implies a higher level of the turbulent cascade rate. However, this only means that the energy is dissipated with the higher rate while the temperature increase is proportional to the energy contained within the largest turbulent eddies. In the solar wind, this scale is of the order of $\mathrm{1}{\mathrm{0}}^{\mathrm{6}}\mathrm{km}$ [87], which translates into roughly $\mathrm{1}\mathrm{h}$ of data in the spacecraft frame. If one estimates the power spectrum of fluctuations during the first hour of downstream plasma, it may be unwise to infer the levels of turbulent energy contained within the largest scales from such a spectrum, because the interval is highly non-stationary. Generally, it is a mix that consists of just shocked plasma, on the one side, and the plasma evolved by $\mathrm{5-6}\mathrm{h}$ on the other side; it is due to the fact that the time at which the plasma was shocked ${\mathit{t}}_{\mathrm{sh}}$ is usually much longer than the downstream time of a particular plasma parcel observation $t_{\mathrm{sp}}$ (see chapter 5). A rule of thumb is, $t_{\mathrm{sh}}\mathrm{=5}\mathrm{.5}\cdot t_{\mathrm{sp}}$ [14, 105]. One may even ask a question, whether the energy in the injection scale can be estimated. Empirical finding that the temperature is not increasing with the distance from the shock [14] may suggest that there is no new turbulent energy added/enhanced on the largest scale that would eventually heat the plasma.

On the other hand, the constant temperature profile can be consistent with the solar wind turbulent heating. Under assumptions that 1) the heat needed for the non-adiabatic cooling of the solar wind is provided by the turbulent cascade and 2) the cooling rate does not depend on the temperature, the amount of the heat needed for the observed cooling rate $\mathit{T}\left(\mathit{r}\right)\hspace{0.17em}\propto \hspace{0.17em}{r}^{\mathrm{0}\mathrm{.8}}$ [37, 50] should increase with a temperature. The temperature increases across the shock by a factor of 4 (Figure 10) and thus the amount of heat that should be provided by the turbulent cascade to keep the same rate of non-adiabatic cooling should increase by a similar factor. It means that the average increase of the fluctuation power and average increase of temperature would be related. This suggestion is in line with observations shown in Figures 4, 5. The thermal velocity ${\mathit{V}}_{\mathrm{th}}$ increases by a factor of 2 across S1 but two orders of magnitude enhancement of PSD B is observed (Figure 5, red lines). This large enhancement of the fluctuation level leads to a gradual rise of the downstream temperature. On the other hand, similar enhancement of PSD B across S3 is not sufficient to support much larger rise of $V_{\mathrm{th}}$ and rather a decrease of $V_{\mathrm{th}}$ is observed through downstream. These speculations need an extended statistical study to be confirmed or rejected. In addition, two aspects that make the analysis even more difficult are: 1) the ratio of downstream/upstream temperatures $T_{\mathrm{d}}/T_{\mathrm{u}}$ can change with the heliocentric distance on the spatial scales of interest and 2) the relative temperature increase with respect to the adiabatic cooling may be too small to discern it in data on small spatial/temporal scales of few hours² (e.g., Figure 10).

5.3 Comment to the Ratio of Characteristic Time Scales

Further insight into the question of an amplification of turbulence due to shock passage may come from the understanding of how this enhancement develops. Generally, in order to increase the level of turbulent fluctuations, the simplest and straightforward way how to achieve this, is to increase it simultaneously for every wave vector. However, the IP shock is “increasing” the level of fluctuations by an opposite way. At each moment, only local magnetic field increases. Two extreme scenarios are: 1) when the characteristic time of evolution of Alfvénic fluctuations (characteristic eddy nonlinear time, ${\mathit{\tau }}_{\mathrm{nl}}$ or characteristic time of decay according to the WKB prediction) is much larger than the time it takes for the shock to travel across this fluctuation, then the enhancement can be viewed as sudden and simultaneous. However, when the opposite is true, i.e., 2) the fluctuations evolve much quicker than the characteristic time of IP shock passage, then the situation becomes more complex.

We can quantify the above considerations by defining a ratio $\mathit{R}$: the ratio of the characteristic time of a significant change of Alfvénic fluctuations, $t_{\mathrm{ch}}$, and the time for which an IP shock sweeps through fluctuations, ${\mathit{t}}_{\mathrm{sh}}$:

$\mathit{R}\mathrm{=}\frac{t_{\mathrm{ch}}}{t_{\mathrm{sh}}}(6)$

This ratio can be estimated in the upstream and downstream regions separately. We introduce a simple considerations for the both regions, thus illustrating the relevance of $\mathit{R}$.

In upstream, $R^{\mathrm{u}}$ may be estimated if we identify $t_{\mathrm{ch}}$ with the characteristic nonlinear time of turbulent fluctuations, ${\mathit{\tau }}_{\mathrm{nl}}^{\mathrm{u}}\mathrm{=}\mathrm{1}/\left(k{Z}^{\mathrm{u}}\right)$ [86], ${\left({\mathit{Z}}^{\mathrm{u}}\right)}^{\mathrm{2}}$ is the sum of kinetic and magnetic energies; and we express $t_{\mathrm{sh}}^{\mathrm{u}}\mathrm{=}\mathrm{1}/\left(k{v}_{\mathrm{A}}^{\mathrm{u}}{M}_{\mathrm{A}}\right)$, where $v_{\mathrm{A}}^{\mathrm{u}}$ is the upstream Alfvén speed and $M_{\mathrm{A}}$ is the Alfvén Mach number. Thus, $R^{\mathrm{u}}\mathrm{=}{v}_{\mathrm{A}}^{\mathrm{u}}{M}_{\mathrm{A}}/Z^{\mathrm{u}}$. For a sub-Alfvénic turbulence ($Z\mathrm{\sim }\mathit{\delta }{v}_{\mathrm{sw}}\mathrm{<}{v}_{\mathrm{A}}$), $R^{\mathrm{u}}\mathrm{\gtrsim }{M}_{\mathrm{A}}$ should then hold. We see that for large scales, $R^{\mathrm{u}}$ may serve as a proxy for $M_{\mathrm{A}}$. As anticipated, $R^{\mathrm{u}}$ should be larger than unity even for scales comparable to the coherence length.

In downstream, $R^{\mathrm{d}}$ may be evaluated in a similar manner, $t_{\mathrm{ch}}\mathrm{=}\mathrm{1}/\left(k{Z}^{\mathrm{d}}\right)$ and $t_{\mathrm{sh}}^{\mathrm{d}}\mathrm{=}\mathrm{1}/\left(k{v}_{\mathrm{sh}}^{\mathrm{d}}\right)$, where $v_{\mathrm{sh}}^{\mathrm{d}}$ is the downstream plasma speed in the shock frame. Hence, $R^{\mathrm{d}}\mathrm{=}{v}_{\mathrm{sh}}^{\mathrm{d}}/Z^{\mathrm{d}}$. We know that $v_{\mathrm{sh}}^{\mathrm{d}}\mathrm{<}{v}_{\mathrm{A}}^{\mathrm{d}}$, therefore $R^{\mathrm{d}}\mathrm{\lesssim }{v}_{\mathrm{A}}^{\mathrm{d}}/Z^{\mathrm{d}}$. Note, that $R^{\mathrm{d}}\sim \mathrm{1}$ signifies a change from sub-Alfvénic into super-Alfvénic turbulence [32]. In general, this condition seems hard to be ever satisfied in the solar wind, however, for shocks that propagate into coronal-hole-origin plasma, it may be possible due to the large levels of downstream fluctuations (see Figure 14 of [14]). We hypothesize that for some downstream IP shocks, the regime of super-Alfvénic turbulence may be relevant.

In the previous paragraphs, we derived the expressions for R in a convenient reference frame where the shock is stationary. Focusing on the downstream, we may roughly estimate this ratio from the spacecraft measurements as it follows: expression for $t_{\text{ch}}$ is the same as before, ${\mathit{\tau }}_{\mathrm{nl}}^{\mathrm{d}}\mathrm{=}\mathrm{1}/\left(k{Z}^{\mathrm{d}}\right)$ while $t_{\mathrm{sh}}^{\mathrm{d}}\mathrm{=}{t}_{\mathrm{sp}}\cdot K$ (Eq. 3), where $t_{\mathrm{sp}}\mathrm{=}\mathrm{1}/\left(k{v}_{\mathrm{sp}}^{\mathrm{d}}\right)$, $v_{\text{sp}}^{\text{d}}$ being the downstream solar wind speed in the spacecraft frame of reference. Then, $R^{\mathrm{d}}\mathrm{=}{v}_{\mathrm{sp}}^{\mathrm{d}}/\left(Z^{\mathrm{d}}K\right)$. Note that $R^{\mathrm{d}}\mathrm{=}{R}^{\mathrm{d}}\left(k\right)$ since $Z^{\mathrm{d}}\mathrm{=}{Z}^{\mathrm{d}}\left(k\right)$. Assuming Kolmogorov scaling in the inertial range, $Z\propto k^{\mathrm{-5}/\mathrm{6}}$, then $R^{\mathrm{d}}\propto k^{\mathrm{5/6}}$ and $R^{\text{d}}$ decreases for larger scales. If we directly evaluate $R^{\text{d}}$ for some average conditions at large scales, e.g., $K=5.5$, $v_{\mathrm{sp}}^{\mathrm{d}}\mathrm{=400}\mathrm{km}\cdot {\mathrm{s}}^{\mathrm{-1}}$, ${\left(Z^{\mathrm{d}}\right)}^{\mathrm{2}}\mathrm{=2000}\mathrm{k}{\mathrm{m}}^{\mathrm{2}}\cdot {\mathrm{s}}^{\mathrm{-2}}$, then $R^{\mathrm{d}}\mathrm{=1}\mathrm{.6}$. Whether the value of $R^{\mathrm{d}}$ corresponds to the injection scale or to the break between the inertial and injection ranges depends on specific values of $v_{\mathrm{sp}}^{\mathrm{d}}$, K and $Z^{\mathrm{d}}$.

Finally, the question whether the constant energy profile up to $t_{\mathrm{d}}$ and the constant temperature profile (Figure 10) are causally related, remains open. However, in the view of the new parameter R (Eq. 6), this issue should be investigated in the future studies. Analyses of the energy and temperature profiles with respect to the type of a plasma through which an IP shock propagates, as it was suggested by [14] can help in this respect.

6 Concluding Remarks

The interaction of interplanetary shocks and solar wind turbulence has been investigated for decades focusing mainly on the particle acceleration and geoeffectiveness of IP shocks and their sheaths. The nature of the fluctuations alone were addressed in more detail only recently.

The key aspects of this interaction have been discussed in this paper. Considering the changes from upstream to downstream of quasi-perpendicular IP shocks: 1) enhancement of the power in the inertial range fluctuations of the velocity, magnetic field and density is roughly one order of magnitude, 2) IP shock reduces the Alfvénicity of fluctuations, 3) the power in the inertial range fluctuations is kept constant for a significant time after the passage of the shock, 4) lumpiness of fluctuations is enhanced due to the changing ${\mathit{\theta }}_{\mathrm{Bn}}$ induced by the non-compressive fluctuations, 5) power spectra of inertial range fluctuations resemble those in the solar wind, though they are steeper on average.

A major point of this review is that the downstream region of an IP shock should be viewed as a history of the IP shock propagation through the plasma. This simple perspective then serves as a starting point for the interpretation of the observed phenomena, it constrains the potential questions and most importantly it opens new questions about the nature and evolution of the downstream turbulent fluctuations.

While our knowledge of the processes in upstream and downstream regions of IP shocks has greatly improved in recent years, there are still more questions than answers. Focusing on downstream quasi-perpendicular shocks, the major open problem is what state/regime of turbulence can be ascribed to these fluctuations? On one hand, the inertial range spectra closely resemble those of the turbulent solar wind, while these fluctuations do not evolve (decay) significantly within many hours after the shock passage. Closely connected with this issue is a questionable estimation of the scale of the break between the injection and inertial ranges and the energy that resides within the injection scales. Connected to the issue still is a role of the solar wind expansion: a simple fact that a time for the shock front to propagate through a structure with the spatial extent of correlative/integral scale may be smaller than the characteristic time of evolution of such a structure (WKB/turbulent decay/other). A ratio of these two time scales may prove to be a useful tool in future analysis of upstream/downstream IP shock turbulence.

Finally, understanding the evolution of the IP shock sheath’s fluctuations using single point measurements is difficult. Upcoming simultaneous measurements of Parker Solar Probe, Solar Orbiter and the spacecraft located at L1 will hopefully provide a unique opportunity to study the aforementioned evolution of the shock sheaths through the rising phase of the current solar cycle.

Data Availability Statement

All used data are from open-access sources via (http://cdaweb.gsfc.nasa.gov/cdaweb/), the Spektr-R data are available via http://aurora.troja.mff.cuni.cz/spektr-r/project/. Parameters of IP shocks can be accessed at http://ipshocks.fi.

Author Contributions

AP drafted the initial manuscript and performed the analysis of the data. JS and ZN significantly improved the manuscript and provided interpretation of the data. TD provided one figure and suggested improvements of the manuscript. AK worked on one section and on the finalization of the manuscript.

Funding

The work of the Czech authors was supported partly by the Czech Science Foundation under Contract 19-18993S and by the Grant Agency of the Charles University under the project number 264220.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors thank all spacecraft teams for the velocity and magnetic field data.

Footnotes

¹A rough estimation of the sheath crossing time ($t_{\mathrm{sp}}\mathrm{=5}\mathrm{.5}\mathrm{h}$) was inferred from the density and magnetic field profiles in Figure 4.

²For example, 3 h in the spacecraft frame translates into $\sim \mathrm{17}$ hours for the age of the shocked plasma (see Eq. 3). Assuming the solar wind speed of 500 km·s⁻¹, then the shock encountered the plasma at a distance of $\sim \mathrm{0}\mathrm{.8}\mathrm{AU}$. If the whole temperature increase from 0.8 to $\mathrm{1}\mathrm{AU}$ is due to the turbulent heating, we can estimate the relative temperature increase, $R_{\mathrm{t}}\mathrm{=}T\left(\mathrm{1}\mathrm{AU}\right)/T_{\mathrm{a}}\left(\mathrm{1}\mathrm{AU}\right)\sim \mathrm{1}\mathrm{.13}$, where $T_{\mathrm{a}}\left(\mathrm{1}\mathrm{AU}\right)$ is the prediction for the adiabatic temperature decrease.

References

1. Adhikari L, Zank GP, Hunana P, Hu Q. The Interaction of Turbulence with Parallel and Perpendicular Shocks: theory and Observations at 1 au. Astrophys J (2016) 833:218. doi:10.3847/1538-4357/833/2/218

CrossRef Full Text | Google Scholar

2. Adhikari L, Zank GP, Zhao LL, Kasper JC, Korreck KE, Stevens M, et al. Turbulence transport modeling and first orbit parker solar Probe (PSP) observations. Astrophys J Suppl Ser (2020) 246:38. doi:10.3847/1538-4365/ab5852

CrossRef Full Text | Google Scholar

3. Ala-Lahti MM, Kilpua EKJ, Dimmock AP, Osmane A, Pulkkinen T, Souček J. Statistical analysis of mirror mode waves in sheath regions driven by interplanetary coronal mass ejection. Ann Geophys (2018) 36:793–808. doi:10.5194/angeo-36-793-2018

CrossRef Full Text | Google Scholar

4. Alexandrova O, Lacombe C, Mangeney A, Grappin R, Maksimovic M. Solar wind turbulent spectrum at plasma kinetic scales. Astrophys J (2012) 760:121. doi:10.1088/0004-637X/760/2/121

CrossRef Full Text | Google Scholar

5. Ao X, Zank GP, Pogorelov NV, Shaikh D. Interaction of a thin shock with turbulence. I. Effect on shock structure: analytic model. Phys Fluids (2008) 20:127102. doi:10.1063/1.3041706

CrossRef Full Text | Google Scholar

6. Balogh A, Treumann RA. Physics of collisionless shocks. 1st ed. edn. New York: Springer-Verlag (2013).

7. Bamert K, Kallenbach R, le Roux JA, Hilchenbach M, Smith CW, Wurz P. Evidence for iroshnikov-kraichnan-type turbulence in the solar wind upstream of interplanetary traveling shocks. Astrophys J Lett (2008) 675:L45–8. doi:10.1086/529491

CrossRef Full Text | Google Scholar

8. Belcher JW, Davis L. Large-amplitude Alfvén waves in the interplanetary medium, 2. J Geophys Res (1971) 76:3534–63. doi:10.1029/JA076i016p03534

CrossRef Full Text | Google Scholar

9. Bieber JW, Wanner W, Matthaeus WH. Dominant two-dimensional solar wind turbulence with implications for cosmic ray transport. J Geophys Res (1996) 101:2511–22. doi:10.1029/95JA02588

CrossRef Full Text | Google Scholar

10. Blanco-Cano X, Kajdič P, Aguilar-Rodríguez E, Russell CT, Jian LK, Luhmann JG. Interplanetary shocks and foreshocks observed by STEREO during 2007-2010. J Geophys Res Space Phys (2016) 121:992–1008. doi:10.1002/2015JA021645

CrossRef Full Text | Google Scholar

11. Boldyrev S, Horaites K, Xia Q, Perez JC. Toward a theory of astrophysical plasma turbulence at subproton scales. Astrophys J (2013) 777:41. doi:10.1088/0004-637X/777/1/41

CrossRef Full Text | Google Scholar

12. Borovsky JE. Flux tube texture of the solar wind: strands of the magnetic carpet at 1 AU? J Geophys Res Space Phys (2008) 113:A08110. doi:10.1029/2007JA012684

CrossRef Full Text | Google Scholar

13. Borovsky JE. The velocity and magnetic field fluctuations of the solar wind at 1 AU: statistical analysis of Fourier spectra and correlations with plasma properties. J Geophys Res Space Phy (2012) 117:A05104. doi:10.1029/2011JA017499

CrossRef Full Text | Google Scholar

14. Borovsky JE. A statistical analysis of the fluctuations in the upstream and downstream plasmas of 109 strong-compression interplanetary shocks at 1 au. J Geophys Res Space Phys (2020) 125:e2019JA027518. doi:10.1029/2019JA027518

CrossRef Full Text | Google Scholar

15. Borovsky JE, Burkholder BL. On the fourier contribution of strong current sheets to the high-frequency magnetic power SpectralDensity of the solar wind. J Geophys Res Space Phys (2020) 125:e27307. doi:10.1029/2019JA027307

CrossRef Full Text | Google Scholar

16. Borovsky JE, Denton MH. Differences between CME-driven storms and CIR-driven storms. J Geophys Res Space Phys (2006) 111:A07S08. doi:10.1029/2005JA011447

CrossRef Full Text | Google Scholar

17. Borovsky JE, Denton MH. The differences between storms driven by helmet streamer CIRs and storms driven by pseudostreamer CIRs. J Geophys Res Space Phys (2013) 118:5506–21. doi:10.1002/jgra.50524

CrossRef Full Text | Google Scholar

18. Bruno R, Carbone V. The solar wind as a turbulence laboratory. Living Rev Solar Phys (2013) 10:2. doi:10.12942/lrsp-2013-2

CrossRef Full Text | Google Scholar

19. Bruno R, Carbone V, Vörös Z, D’Amicis R, Bavassano B, Cattaneo MB, et al. Coordinated study on solar wind turbulence during the venus-express, ACE and Ulysses alignment of august 2007. Earth Moon and Planets (2009) 104:101–4. doi:10.1007/s11038-008-9272-9

CrossRef Full Text | Google Scholar

20. Burgess D, Scholer M. Microphysics of quasi-parallel shocks in collisionless plasmas. Space Sci Rev (2013) 178:513–33. doi:10.1007/s11214-013-9969-6

CrossRef Full Text | Google Scholar

21. Burgess D, Scholer M. Microphysics of quasi-parallel shocks in collisionless plasmas. Boston, MA: Springer US (2014). p. 437–57.

22. Burlaga L, Sittler E, Mariani F, Schwenn R. Magnetic loop behind an interplanetary shock: voyager, Helios, and IMP 8 observations. J Geophys Res (1981) 86:6673–84. doi:10.1029/JA086iA08p06673

CrossRef Full Text | Google Scholar

23. Cane HV, Lario D. An introduction to CMEs and energetic particles. Space Sci Rev (2006) 123:45–56. doi:10.1007/s11214-006-9011-3

CrossRef Full Text | Google Scholar

24. Cane HV, Reames DV, von Rosenvinge TT. The role of interplanetary shocks in the longitude distribution of solar energetic particles. J Geophys Res (1988) 93:9555–67. doi:10.1029/JA093iA09p09555

CrossRef Full Text | Google Scholar

25. Chandran BDG. Parametric instability, inverse cascade and the 1/f range of solar-wind turbulence. J Plasma Phys (2018) 84:905840106. doi:10.1017/S0022377818000016

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Chandran BDG, Quataert E, Howes GG, Xia Q, Pongkitiwanichakul P. Constraining low-frequency alfvénic turbulence in the solar wind using density-fluctuation measurements. Astrophys J (2009) 707:1668–75. doi:10.1088/0004-637x/707/2/1668

CrossRef Full Text | Google Scholar

27. Chen CHK, Bale SD, Bonnell JW, Borovikov D, Bowen TA, Burgess D, et al. The evolution and role of solar wind turbulence in the inner heliosphere. Astrophys J Suppl Ser (2020) 246:53. doi:10.3847/1538-4365/ab60a3

CrossRef Full Text | Google Scholar

28. Chen CHK, Bale SD, Salem CS, Maruca BA. Residual energy spectrum of solar wind turbulence. Astrophys J (2013) 770:125. doi:10.1088/0004-637X/770/2/125

CrossRef Full Text | Google Scholar

29. Chen CHK, Boldyrev S. Nature of kinetic scale turbulence in the earth’s magnetosheath. Astrophys J (2017) 842:122. doi:10.3847/1538-4357/aa74e0

CrossRef Full Text | Google Scholar

30. Chen CHK, Boldyrev S, Xia Q, Perez JC. Nature of subproton scale turbulence in the solar wind. Phys Rev Lett (2013) 110:225002. doi:10.1103/PhysRevLett.110.225002

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Chen CHK, Leung L, Boldyrev S, Maruca BA, Bale SD. Ion-scale spectral break of solar wind turbulence at high and low beta. Geophys Res Lett (2014) 41:8081–8. doi:10.1002/2014GL062009

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Cho J, Lazarian A. Compressible magnetohydrodynamic turbulence: mode coupling, scaling relations, anisotropy, viscosity-damped regime and astrophysical implications. Monthly Notices R Astron Soc (2003) 345:325–39. doi:10.1046/j.1365-8711.2003.06941.x

CrossRef Full Text | Google Scholar

33. Del Zanna L. Parametric decay of oblique arc-polarized Alfvén waves. Geophys Res Lett (2001) 28:2585–8. doi:10.1029/2001GL012911

CrossRef Full Text | Google Scholar

34. Denton MH, Borovsky JE, Skoug RM, Thomsen MF, Lavraud B, Henderson MG, et al. Geomagnetic storms driven by ICME- and CIR-dominated solar wind. J Geophys Res Space Phys (2006) 111:A07S07. doi:10.1029/2005JA011436

CrossRef Full Text | Google Scholar

35. Domingo V, Fleck B, Poland AI. The SOHO mission: an overview. Solar Phys (1995) 162:1–37. doi:10.1007/BF00733425

CrossRef Full Text | Google Scholar

36. Ďurovcová T, Němeček Z, Šafránková J. Evolution of the α-proton differential motion across stream interaction regions. Astrophys J (2019a) 873:24. doi:10.3847/1538-4357/ab01c8

CrossRef Full Text | Google Scholar

37. Ďurovcová T, Šafránková J, Němeček Z. Evolution of relative drifts in the expanding solar wind: Helios observations. Solar Phys (2019b) 294:97. doi:10.1007/s11207-019-1490-y

CrossRef Full Text | Google Scholar

38. Echer E, Gonzalez WD, Tsurutani BT. Interplanetary conditions leading to superintense geomagnetic storms (Dst <= -250 nT) during solar cycle 23. Geophys Res Lett (2008) 35:L06S03. doi:10.1029/2007GL031755

CrossRef Full Text | Google Scholar

39. Forman MA, Wicks RT, Horbury TS. Detailed fit of “critical balance” theory to solar wind turbulence measurements. Astrophys J (2011) 733:76. doi:10.1088/0004-637X/733/2/76

CrossRef Full Text | Google Scholar

40. Franci L, Landi S, Matteini L, Verdini A, Hellinger P. High-resolution hybrid simulations of kinetic plasma turbulence at proton scales. Astrophys J (2015) 812:21. doi:10.1088/0004-637X/812/1/21

CrossRef Full Text | Google Scholar

41. Franci L, Landi S, Matteini L, Verdini A, Hellinger P. Plasma beta dependence of the ion-scale spectral break of solar wind turbulence: high-resolution 2D hybrid simulations. Astrophys J (2016) 833:91. doi:10.3847/1538-4357/833/1/91

CrossRef Full Text | Google Scholar

42. Gary SP. Theory of space plasma microinstabilities. CambridgeCambridge, UK: Cambridge University Press (1993).

CrossRef Full Text

43. Gedalin M. Ion reflection at the shock front revisited. J Geophys Res (1996) 101:4871–8. doi:10.1029/95JA03669

CrossRef Full Text | Google Scholar

44. Giacalone J, Jokipii JP. Injection and acceleration at non-parallel shocks. In: B Sripathi Acharya, S Gupta, P Jagadeesan, A Jain, S Karthikeyan, S Morriset al. editors. 29th International Cosmic Ray Conference (ICRC29); 2005 August 3-10; Pune, India. Mumbai: Tata Institute of Fundamental Research (2005). Vol 3:265

Google Scholar

45. Good SW, Ala-Lahti M, Palmerio E, Kilpua EKJ, Osmane A. Radial evolution of magnetic field fluctuations in an interplanetary coronal mass ejection sheath. Astrophys J (2020) 893:110. doi:10.3847/1538-4357/ab7fa2

CrossRef Full Text | Google Scholar

46. Gopalswamy N, Mäkelä P, Akiyama S, Yashiro S, Xie H, Thakur N. Sun-to-earth propagation of the 2015 June 21 coronal mass ejection revealed by optical, EUV, and radio observations. J Atmos Solar-Terrestrial Phys (2018) 179:225–38. doi:10.1016/j.jastp.2018.07.013

CrossRef Full Text | Google Scholar

47. Gosling JT, McComas DJ. Field line draping about fast coronal mass ejecta: a source of strong out-of-the-ecliptic interplanetary magnetic fields. Geophys Res Lett (1987) 14:355–8. doi:10.1029/GL014i004p00355

CrossRef Full Text | Google Scholar

48. Gosling JT, Riley P, McComas DJ, Pizzo VJ. Overexpanding coronal mass ejections at high heliographic latitudes: observations and simulations. J Geophys Res Space Phys (1998) 103:1941–54. doi:10.1029/97JA01304

CrossRef Full Text | Google Scholar

49. Grošelj D, Mallet A, Loureiro NF, Jenko F. Fully kinetic simulation of 3D kinetic alfvén turbulence. Phys Rev Lett (2018) 120:105101. doi:10.1103/PhysRevLett.120.105101

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Hellinger P, Matteini L, Štverák Š, Trávníček PM, Marsch E. Heating and cooling of protons in the fast solar wind between 0.3 and 1 AU: Helios revisited. J Geophys Res Space Phys (2011) 116:A09105. doi:10.1029/2011JA016674

CrossRef Full Text | Google Scholar

51. Horbury TS, Forman M, Oughton S. Anisotropic scaling of magnetohydrodynamic turbulence. Phys Rev Lett (2008) 101:175005. doi:10.1103/PhysRevLett.101.175005

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Horbury TS, Wicks RT, Chen CHK. Anisotropy in space plasma turbulence: solar wind observations. Space Sci Rev (2012) 172:325–42. doi:10.1007/s11214-011-9821-9

CrossRef Full Text | Google Scholar

53. Howes GG, Cowley SC, Dorland W, Hammett GW, Quataert E, Schekochihin AA. Astrophysical gyrokinetics: basic equations and linear theory. Astrophys J (2006) 651:590–614. doi:10.1086/506172

CrossRef Full Text | Google Scholar

54. Howes GG, Dorland W, Cowley SC, Hammett GW, Quataert E, Schekochihin AA, et al. Kinetic simulations of magnetized turbulence in astrophysical plasmas. Phys Rev Lett (2008) 100:065004. doi:10.1103/PhysRevLett.100.065004

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Huang SY, Hadid LZ, Sahraoui F, Yuan ZG, Deng XH. On the existence of the Kolmogorov inertial range in the terrestrial magnetosheath turbulence. Astrophys J Lett (2017) 836:L10. doi:10.3847/2041-8213/836/1/L10

CrossRef Full Text | Google Scholar

56. Iroshnikov PS. Turbulence of a conducting fluid in a strong magnetic field. Sov Astron (1963) 40:742.

Google Scholar

57. Jian LK, Russell CT, Luhmann JG. Comparing solar minimum 23/24 with historical solar wind records at 1 AU. Solar Phys (2011) 274:321–44. doi:10.1007/s11207-011-9737-2

CrossRef Full Text | Google Scholar

58. Jian LK, Russell CT, Luhmann JG, Galvin AB, Simunac KDC. Solar wind observations at STEREO: 2007 - 2011. In: GP Zank, J Borovsky, R Bruno, J Cirtain, S Cranmer, H Elliottet al. editors. 13th International Solar Wind Conference (Solar Wind); 2012 Jun 17–22; HI. Melville, NY: AIP Publishing LLC. Vol. 1539 (2013). p. 191–4.

Google Scholar

59. Jurac S, Kasper JC, Richardson JD, Lazarus AJ. Geomagnetic disturbances and their relationship to Interplanetary shock parameters. Geophys Res Lett (2002) 29:1463. doi:10.1029/2001GL014034

CrossRef Full Text | Google Scholar

60. Kajdič P, Blanco-Cano X, Aguilar-Rodriguez E, Russell CT, Jian LK, Luhmann JG. Waves upstream and downstream of interplanetary shocks driven by coronal mass ejections. J Geophys Res Space Phys (2012) 117. doi:10.1029/2011JA017381

CrossRef Full Text | Google Scholar

61. Kataoka R, Watari S, Shimada N, Shimazu H, Marubashi K. Downstream structures of interplanetary fast shocks associated with coronal mass ejections. Geophys Res Lett (2005) 32:L12103. doi:10.1029/2005GL022777

CrossRef Full Text | Google Scholar

62. Kennel CF, Coroniti FV, Scarf FL, Livesey WA, Russell CT, Smith EJ, et al. A test of Lee’s quasi-linear theory of ion acceleration by interplanetary traveling shocks. J Geophys Res (1986) 91:11917–28. doi:10.1029/JA091iA11p11917

CrossRef Full Text | Google Scholar

63. Kilpua E, Koskinen HEJ, Pulkkinen TI. Coronal mass ejections and their sheath regions in interplanetary space. Living Rev Solar Phys (2017a) 14:5. doi:10.1007/s41116-017-0009-6

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Kilpua EKJ, Balogh A, von Steiger R, Liu YD. Geoeffective properties of solar transients and stream interaction regions. Space Sci Rev (2017b) 212:1271–314. doi:10.1007/s11214-017-0411-3

CrossRef Full Text | Google Scholar

65. Kilpua EKJ, Fontaine D, Good SW, Ala-Lahti M, Osmane A, Palmerio E, et al. Magnetic field fluctuation properties of coronal mass ejection-driven sheath regions in the near-earth solar wind. Ann Geophys (2020) 38:999–1017. doi:10.5194/angeo-38-999-2020

CrossRef Full Text | Google Scholar

66. Kilpua EKJ, Hietala H, Koskinen HEJ, Fontaine D, Turc L. Magnetic field and dynamic pressure ulf fluctuations in coronal-mass-ejection-driven sheath regions. Ann Geophys (2013) 31:1559–67. doi:10.5194/angeo-31-1559-2013

CrossRef Full Text | Google Scholar

67. Kilpua EKJ, Lumme E, Andreeova K, Isavnin A, Koskinen HEJ. Properties and drivers of fast interplanetary shocks near the orbit of the earth (1995–2013). J Geophys Res Space Phys (2015) 120:4112–25. doi:10.1002/2015JA021138

CrossRef Full Text | Google Scholar

68. Kis A, Matsukiyo S, Otsuka F, Hada T, Lemperger I, Dandouras I, et al. Effect of upstream ULF waves on the energetic ion diffusion at the earth’s foreshock. II. Observations. Astrophys J (2018) 863:136. doi:10.3847/1538-4357/aad08c

CrossRef Full Text | Google Scholar

69. Klein LW, Burlaga LF. Interplanetary magnetic clouds at 1 AU. J Geophys Res (1982) 87:613–24. doi:10.1029/JA087iA02p00613

CrossRef Full Text | Google Scholar

70. Kraichnan RH. Inertial range spectrum of hydromagnetic turbulence. Phys Fluids (1965) 8:1385–7. doi:10.1063/1.1761412

CrossRef Full Text | Google Scholar

71. Krasnoselskikh V, Balikhin M, Walker SN, Schwartz S, Sundkvist D, Lobzin V, et al. The dynamic quasiperpendicular shock: cluster discoveries. Space Sci Rev (2013) 178:535–98. doi:10.1007/s11214-013-9972-y

CrossRef Full Text | Google Scholar

72. Krauss-Varban D, Omidi N. Structure of medium mach number quasi-parallel shocks: upstream and downstream waves. J Geophys Res (1991) 96:17715–31. doi:10.1029/91JA01545

CrossRef Full Text | Google Scholar

73. Lacombe C, Alexandrova O, Matteini L. Anisotropies of the magnetic field fluctuations at kinetic scales in the solar wind: cluster observations. Astrophysical J (2017) 848:45. doi:10.3847/1538-4357/aa8c06

CrossRef Full Text | Google Scholar

74. Leamon RJ, Smith CW, Ness NF, Matthaeus WH, Wong HK. Observational constraints on the dynamics of the interplanetary magnetic field dissipation range. J Geophys Res (1998) 103:4775. doi:10.1029/97JA03394

CrossRef Full Text | Google Scholar

75. Lee MA. Coupled hydromagnetic wave excitation and ion acceleration upstream of the earth’s bow shock. J Geophys Res (1982) 87:5063–80. doi:10.1029/JA087iA07p05063

CrossRef Full Text | Google Scholar

76. Lee MA. Coupled hydromagnetic wave excitation and ion acceleration at interplanetary traveling shocks. J Geophys Res (1983) 88:6109–20. doi:10.1029/JA088iA08p06109

CrossRef Full Text | Google Scholar

77. Lithwick Y, Goldreich P, Sridhar S. Imbalanced strong MHD turbulence. Astrophys J (2007) 655:269–74. doi:10.1086/509884

CrossRef Full Text | Google Scholar

78. Liu YD, Hu H, Wang R, Yang Z, Zhu B, Liu YA, et al. Plasma and magnetic field characteristics of solar coronal mass ejections in relation to geomagnetic storm intensity and variability. Astrophys J Lett (2015) 809:L34. doi:10.1088/2041-8205/809/2/L34

CrossRef Full Text | Google Scholar

79. Lu Q, Hu Q, Zank GP. The interaction of alfvén waves with perpendicular shocks. Astrophys J (2009) 706:687–92. doi:10.1088/0004-637X/706/1/687

CrossRef Full Text | Google Scholar

80. Luttrell AH, Richter AK. A study of MHD fluctuations upstream and downstream of quasi-parallel interplanetary shocks. J Geophys Res (1987) 92:2243–52. doi:10.1029/JA092iA03p02243

CrossRef Full Text | Google Scholar

81. Marshall W, Bullard EC. The structure of magneto-hydrodynamic shock waves. Proc R Soc Lond Ser A. Math Phys Sci (1955) 233:367–76. doi:10.1098/rspa.1955.0272

CrossRef Full Text | Google Scholar

82. Masías-Meza JJ, Dasso S, Démoulin P, Rodriguez L, Janvier M. Superposed epoch study of ICME sub-structures near Earth and their effects on Galactic cosmic rays. Astron Astrophys (2016) 592:A118. doi:10.1051/0004-6361/201628571

CrossRef Full Text | Google Scholar

83. Matteini L, Landi S, Del Zanna L, Velli M, Hellinger P. Parametric decay of linearly polarized shear Alfvén waves in oblique propagation: one and two-dimensional hybrid simulations. Geophys Res Lett (2010) 37:L20101. doi:10.1029/2010GL044806

CrossRef Full Text | Google Scholar

84. Matteini L, Stansby D, Horbury TS, Chen CHK. On the 1/f spectrum in the solar wind and its connection with magnetic compressibility. Astrophys J Lett (2018) 869:L32. doi:10.3847/2041-8213/aaf573

CrossRef Full Text | Google Scholar

85. Matthaeus WH, Goldstein ML, Roberts DA. Evidence for the presence of quasi-two-dimensional nearly incompressible fluctuations in the solar wind. J Geophys Res (1990) 95:20673–83. doi:10.1029/JA095iA12p20673

CrossRef Full Text | Google Scholar

86. Matthaeus WH, Oughton S, Osman KT, Servidio S, Wan M, Gary SP, et al. Nonlinear and linear timescales near kinetic scales in solar wind turbulence. Astrophys J (2014) 790:155. doi:10.1088/0004-637X/790/2/155

CrossRef Full Text | Google Scholar

87. Matthaeus WH, Smith CW, Oughton S. Dynamical age of solar wind turbulence in the outer heliosphere. J Geophys Res (1998) 103:6495–502. doi:10.1029/97JA03729

CrossRef Full Text | Google Scholar

88. McKenzie JF, Westphal KO. Transmission of Alfvén waves through the Earth’s bow shock. Planet Space Sci (1969) 17:1029–37. doi:10.1016/0032-0633(69)90107-X

CrossRef Full Text | Google Scholar

89. Möbius E, Scholer M, Sckopke N, Lühr H, Paschmann G, Hovestadt D. The distribution function of diffuse ions and the magnetic field power spectrum upstream of Earth’s bow shock. Geophys Res Lett (1987) 14:681–4. doi:10.1029/GL014i007p00681

CrossRef Full Text | Google Scholar

90. Moissard C, Fontaine D, Savoini P. A study of fluctuations in magnetic cloud-driven sheaths. J Geophys Res Space Phys (2019) 124:8208–26. doi:10.1029/2019JA026952

CrossRef Full Text | Google Scholar

91. Nakagawa T, Nishida A, Saito T. Planar magnetic structures in the solar wind. J Geophys Res Space Phys (1989) 94:11761–75. doi:10.1029/JA094iA09p11761

CrossRef Full Text | Google Scholar

92. Narita Y, Glassmeier KH, Treumann RA. Wave-number spectra and intermittency in the terrestrial foreshock region. Phys Rev Lett (2006) 97:191101. doi:10.1103/PhysRevLett.97.191101

PubMed Abstract | CrossRef Full Text | Google Scholar

93. Němeček Z, Š afránková J, Goncharov O, Přech L, Zastenker GN. Ion scales of quasi-perpendicular low-Mach-number interplanetary shocks. Geophys Res Lett (2013) 40:4133–7. doi:10.1002/grl.50814

CrossRef Full Text | Google Scholar

94. Oliveira D. Magnetohydrodynamic shocks in the interplanetary space: a theoretical review. Braz J Phys (2016) 47:81–95. doi:10.1007/s13538-016-0472-x

CrossRef Full Text | Google Scholar

95. Oliveira D, Samsonov A. Geoeffectiveness of interplanetary shocks controlled by impact angles: a review. Adv Space Res (2018) 61:1–44. doi:10.1016/j.asr.2017.10.006

CrossRef Full Text | Google Scholar

96. Ontiveros V, Vourlidas A. Quantitative measurements of coronal mass ejection-driven shocks from LASCO observations. Astrophys J (2009) 693:267–75. doi:10.1088/0004-637X/693/1/267

CrossRef Full Text | Google Scholar

97. Otsuka F, Matsukiyo S, Kis A, Nakanishi K, Hada T. Effect of upstream ULF waves on the energetic ion diffusion at the earth’s foreshock. I. Theory and simulation. Astrophysical J (2018) 853:117. doi:10.3847/1538-4357/aaa23f

CrossRef Full Text | Google Scholar

98. Oughton S, Matthaeus WH. Critical balance and the physics of magnetohydrodynamic turbulence. Astrophys J (2020) 897:37. doi:10.3847/1538-4357/ab8f2a

CrossRef Full Text | Google Scholar

99. Owens MJ, Crooker NU. Coronal mass ejections and magnetic flux buildup in the heliosphere. J Geophys Res (Space Physics) (2006) 111:A10104. doi:10.1029/2006JA011641

CrossRef Full Text | Google Scholar

100. Owens MJ, Forsyth RJ. The heliospheric magnetic field. Living Rev Solar Phys (2013) 10:5. doi:10.12942/lrsp-2013-5

CrossRef Full Text | Google Scholar

101. Palmerio E, Kilpua EKJ, Savani NP. Planar magnetic structures in coronal mass ejection-driven sheath regions. Ann Geophys (2016) 34:313–22. doi:10.5194/angeo-34-313-2016

CrossRef Full Text | Google Scholar

102. Parker EN. Dynamics of the interplanetary gas and magnetic fields. Astrophys J (1958) 128:664. doi:10.1086/146579

CrossRef Full Text | Google Scholar

103. Perez JC, Boldyrev S. Role of cross-helicity in magnetohydrodynamic turbulence. Phys Rev Lett (2009) 102:025003. doi:10.1103/PhysRevLett.102.025003

PubMed Abstract | CrossRef Full Text | Google Scholar

104. Pitňa A, Šafránková J, Němeček Z, Goncharov O, Němec F, Přech L, et al. Density fluctuations upstream and downstream of interplanetary shocks. Astrophys J (2016) 819:41. doi:10.3847/0004-637X/819/1/41

CrossRef Full Text | Google Scholar

105. Pitňa A, Šafránková J, Němeček Z, Franci L. Decay of solar wind turbulence behind interplanetary shocks. Astrophys J (2017) 844:51. doi:10.3847/1538-4357/aa7bef

CrossRef Full Text | Google Scholar

106. Pitňa A, Šafránková J, Němeček Z, Franci L, Pi G, Montagud Camps V. Characteristics of solar wind fluctuations at and below ion scales. Astrophys J (2019) 879:82. doi:10.3847/1538-4357/ab22b8

CrossRef Full Text | Google Scholar

107. Podesta JJ, Borovsky JE. Scale invariance of normalized cross-helicity throughout the inertial range of solar wind turbulence. Phys Plasmas (2010) 17:112905. doi:10.1063/1.3505092

CrossRef Full Text | Google Scholar

108. Rakhmanova LS, Riazantseva MO, Zastenker GN, Verigin MI. Effect of the magnetopause and bow shock on characteristics of plasma turbulence in the earth’s magnetosheath. Geomagnetism Aeronomy (2018) 58:718–27. doi:10.1134/S0016793218060129

CrossRef Full Text | Google Scholar

109. Riazantseva MO, Rakhmanova LS, Zastenker GN, Yermolaev YI, Lodkina IG, Chesalin LS. Small-scale plasma fluctuations in fast and slow solar wind streams. Cosmic Res (2020) 57:434–42. doi:10.1134/S0010952519060078

CrossRef Full Text | Google Scholar

110. Rice WKM, Zank GP, Li G. Particle acceleration and coronal mass ejection driven shocks: shocks of arbitrary strength. J Geophys Res Space Phys (2003) 108:1369. doi:10.1029/2002JA009756

CrossRef Full Text | Google Scholar

111. Richardson IG. Identification of interplanetary coronal mass ejections at Ulysses using multiple solar wind signatures. Solar Phys (2014) 289:3843–94. doi:10.1007/s11207-014-0540-8

CrossRef Full Text | Google Scholar

112. Richardson IG. Solar wind stream interaction regions throughout the heliosphere. Living Rev Solar Phys (2018) 15:1. doi:10.1007/s41116-017-0011-z

PubMed Abstract | CrossRef Full Text | Google Scholar

113. Roberts OW, Toledo-Redondo S, Perrone D, Zhao J, Narita Y, Gershman D, et al. Ion-scale kinetic alfvén turbulence: MMS measurements of the alfvén ratio in the magnetosheath. Geophys Res Lett (2018) 45:7974–84. doi:10.1029/2018GL078498

CrossRef Full Text | Google Scholar

114. Russell CT. Physics of collisionless shocks. Adv Space Res (1995) 15:403.

Google Scholar

115. Safránková J, Němeček Z, Němec F, Přech L, Pitňa A, Chen CHK, et al. Solar wind density spectra around the ion spectral break. Astrophys J (2015) 803:107. doi:10.1088/0004-637X/803/2/107

CrossRef Full Text | Google Scholar

116. Safránková J, Němeček Z, Němec F, Přech L, Chen CHK, Zastenker GN. Power spectral density of fluctuations of bulk and thermal speeds in the solar wind. Astrophysical J (2016) 825:121. doi:10.3847/0004-637X/825/2/121

CrossRef Full Text | Google Scholar

117. Safránková J, Němeček Z, Němec F, Verscharen D, Chen CHK, Ďurovcová T, et al. Scale-dependent polarization of solar wind velocity fluctuations at the inertial and kinetic scales. Astrophys J (2019) 870:40. doi:10.3847/1538-4357/aaf239

CrossRef Full Text | Google Scholar

118. Sahraoui F, Hadid L, Huang S. Magnetohydrodynamic and kinetic scale turbulence in the near-Earth space plasmas: a (short) biased review. Rev Mod Plasma Phys (2020) 4:4. doi:10.1007/s41614-020-0040-2

CrossRef Full Text | Google Scholar

119. Schekochihin AA, Cowley SC, Dorland W, Hammett GW, Howes GG, Quataert E, et al. Astrophysical gyrokinetics: kinetic and fluid turbulent cascades in magnetized weakly collisional plasmas. Astrophys J Suppl (2009) 182:310–77. doi:10.1088/0067-0049/182/1/310

CrossRef Full Text | Google Scholar

120. Shebalin JV, Matthaeus WH, Montgomery D. Anisotropy in MHD turbulence due to a mean magnetic field. J Plasma Phys (1983) 29:525–47. doi:10.1017/S0022377800000933

CrossRef Full Text | Google Scholar

121. Siscoe G, MacNeice PJ, Odstrcil D. East-west asymmetry in coronal mass ejection geoeffectiveness. Space Weather (2007) 5:S04002. doi:10.1029/2006SW000286

CrossRef Full Text | Google Scholar

122. Siscoe G, Odstrcil D. Ways in which ICME sheaths differ from magnetosheaths. J Geophys Res Space Phys (2008) 113:A00B07. doi:10.1029/2008JA013142

CrossRef Full Text | Google Scholar

123. Soucek J, Escoubet CP, Grison B. Magnetosheath plasma stability and ulf wave occurrence as a function of location in the magnetosheath and upstream bow shock parameters. J Geophys Res Space Phys (2015) 120:2838–50. doi:10.1002/2015JA021087

CrossRef Full Text | Google Scholar

124. Soucek J, Lucek E, Dandouras I. Properties of magnetosheath mirror modes observed by cluster and their response to changes in plasma parameters. J Geophys Res Space Phys (2008) 113. doi:10.1029/2007JA012649

CrossRef Full Text | Google Scholar

125. Spangler SR, Leckband JA, Cairns IH. Observations of the parametric decay instability of nonlinear magnetohydrodynamic waves. Phys Plasmas (1997) 4:846–55. doi:10.1063/1.872183

CrossRef Full Text | Google Scholar

126. Stone RG, Tsurutani BT. Collisionless shocks in the heliosphere. A tutorial review. Geophysical Monograph Series. Washington DC: American Geophysical Union (1985), 34. doi:10.1029/GM034

CrossRef Full Text

127. Trattner KJ, Mobius E, Scholer M, Klecker B, Hilchenbach M, Luehr H. Statistical analysis of diffuse ion events upstream of the Earth’s bow shock. J Geophys Res (1994) 99:13389–400. doi:10.1029/94JA00576

CrossRef Full Text | Google Scholar

128. Tsurutani BT, Gonzalez WD, Tang F, Akasofu SI, Smith EJ. Origin of interplanetary southward magnetic fields responsible for major magnetic storms near solar maximum (1978-1979). J Geophys Res (1988) 93:8519–31. doi:10.1029/JA093iA08p08519

CrossRef Full Text | Google Scholar

129. Tsurutani BT, Stone RG. Collisionless shocks in the heliosphere: reviews of current research. Geophysical Monograph Series. Washington, DC: American Geophysical Union (1985), 35.

130. Tu C-Y, Marsch E. MHD structures, waves and turbulence in the solar wind: observations and theories. Space Sci Rev (1995) 73:1–210. doi:10.1007/BF00748891

CrossRef Full Text | Google Scholar

131. Velli M, Grappin R, Mangeney A. Turbulent cascade of incompressible unidirectional alfvén waves in the interplanetary medium. Phys Rev Lett (1989) 63:1807–10. doi:10.1103/PhysRevLett.63.1807

PubMed Abstract | CrossRef Full Text | Google Scholar

132. Volkmer PM, Neubauer FM. Statistical properties of fast magnetoacoustic shock waves in the solar wind between 0.3 AU and 1 AU: Helios-1, 2 observations. Ann Geophys (1985) 3:1–12.

Google Scholar

133. Webb DF, Cliver EW, Crooker NU, Cry OCS, Thompson BJ. Relationship of halo coronal mass ejections, magnetic clouds, and magnetic storms. J Geophys Res (2000) 105:7491–508. doi:10.1029/1999JA000275

CrossRef Full Text | Google Scholar

134. Whang YC, Zhou J, Lepping RP, Ogilvie KW. Interplanetary slow shock observed from wind. Geophys Res Lett (1996) 23:1239–42. doi:10.1029/96GL01358

CrossRef Full Text | Google Scholar

135. Wilson LB, Koval A, Sibeck DG, Szabo A, Cattell CA, Kasper JC, et al. Shocklets, SLAMS, and field-aligned ion beams in the terrestrial foreshock. J Geophys Res Space Phys (2013) 118:957–66. doi:10.1029/2012JA018186

CrossRef Full Text | Google Scholar

136. Wu CC, Wu ST, Dryer M. Generation and evolution of interplanetary slow shocks. Ann Geophysicae (1996) 14:375–82. doi:10.1007/s00585-996-0375-1

CrossRef Full Text | Google Scholar

137. Wu H, Verscharen D, Wicks RT, Chen CHK, He J, Nicolaou G. The fluid-like and kinetic behavior of kinetic alfvén turbulence in space plasma. Astrophys J (2019) 870:106. doi:10.3847/1538-4357/aaef77

CrossRef Full Text | Google Scholar

138. Xu F, Borovsky JE. A new four-plasma categorization scheme for the solar wind. J Geophys Res Space Phys (2015) 120:70–100. doi:10.1002/2014JA020412

CrossRef Full Text | Google Scholar

139. Yermolaev YI, Lodkina IG, Nikolaeva NS, Yermolaev MY. Statistical study of interplanetary condition effect on geomagnetic storms. Cosmic Res (2010) 48:485–500. doi:10.1134/S0010952510060018

CrossRef Full Text | Google Scholar

140. Zank GP, Adhikari L, Hunana P, Shiota D, Bruno R, Telloni D. Theory and transport of nearly incompressible magnetohydrodynamic turbulence. Astrophys J (2017) 835:147. doi:10.3847/1538-4357/835/2/147

CrossRef Full Text | Google Scholar

141. Zank GP, Dosch A, Hunana P, Florinski V, Matthaeus WH, Webb GM. The transport of low-frequency turbulence in astrophysical flows. I. Governing equations. Astrophys J (2012) 745:35. doi:10.1088/0004-637X/745/1/35

CrossRef Full Text | Google Scholar

142. Zank GP, Li G, Florinski V, Hu Q, Lario D, Smith CW. Particle acceleration at perpendicular shock waves: model and observations. J Geophys Res Space Phys (2006) 111:A06108. doi:10.1029/2005JA011524

CrossRef Full Text | Google Scholar

143. Zank GP, Matthaeus WH. Nearly incompressible fluids. II: magnetohydrodynamics, turbulence, and waves. Phys Fluids A (1993) 5:257–73. doi:10.1063/1.858780

CrossRef Full Text | Google Scholar

144. Zank GP, Nakanotani M, Zhao LL, Adhikari L, Telloni D. Spectral anisotropy in 2D plus slab magnetohydrodynamic turbulence in the solar wind and upper corona. Astrophys J (2020) 900:115. doi:10.3847/1538-4357/abad30

CrossRef Full Text | Google Scholar

145. Zank GP, Zhou Y, Matthaeus WH, Rice WKM. The interaction of turbulence with shock waves: a basic model. Phys Fluids (2002) 14:3766–74. doi:10.1063/1.1507772

CrossRef Full Text | Google Scholar

146. Zhang J, Richardson IG, Webb DF. Interplanetary origin of multiple-dip geomagnetic storms. J Geophys Res Space Phys (2008) 113:A00A12. doi:10.1029/2008JA013228

CrossRef Full Text | Google Scholar

147. Zhang J, Richardson IG, Webb DF, Gopalswamy N, Huttunen E, Kasper JC, et al. Solar and interplanetary sources of major geomagnetic storms (Dst <= -100 nT) during 1996-2005. J Geophys Res Space Phys (2007) 112:A10102. doi:10.1029/2007JA012321

CrossRef Full Text | Google Scholar

148. Zhao JS, Voitenko Y, Yu MY, Lu JY, Wu DJ. Properties of short-wavelength oblique alfvén and slow waves. Astrophys J (2014) 793:107. doi:10.1088/0004-637X/793/2/107

CrossRef Full Text | Google Scholar

149. Zhou Y, Matthaeus WH, Dmitruk P. Colloquium: magnetohydrodynamic turbulence and time scales in astrophysical and space plasmas. Rev Mod Phys (2004) 76:1015–35. doi:10.1103/RevModPhys.76.1015

CrossRef Full Text | Google Scholar