Weighted Low-Rank Tensor Representation for Multi-View Subspace Clustering

Multi-view clustering has been deeply explored since the compatible and complementary information among views can be well captured. Recently, the low-rank tensor representation-based methods have effectively improved the clustering performance by exploring high-order correlations between multiple views. However, most of them often express the low-rank structure of the self-representative tensor by the sum of unfolded matrix nuclear norms, which may cause the loss of information in the tensor structure. In addition, the amount of effective information in all views is not consistent, and it is unreasonable to treat their contribution to clustering equally. To address the above issues, we propose a novel weighted low-rank tensor representation (WLRTR) method for multi-view subspace clustering, which encodes the low-rank structure of the representation tensor through Tucker decomposition and weights the core tensor to retain the main information of the views. Under the augmented Lagrangian method framework, an iterative algorithm is designed to solve the WLRTR method. Numerical studies on four real databases have proved that WLRTR is superior to eight state-of-the-art clustering methods.

Introduction

The advance of information technology has unleashed a multi-view feature deluge, which allows data to be described by multiple views. For example, an article can be expressed in multiple languages; an image can be characterized by colors, edges, and textures. Multi-view features not only contain compatible information, but also provide complementary information, which boost the performance of data analysis. Recently, [1] applied multi-view binary learning to obtain the supplementary information from multiple views. [2] proposed a kernelized multi-view subspace analysis method via self-weighted learning. Due to the lack of label, clustering using multiple views has become a popular research direction [3].

A large number of clustering methods have been developed in the past several decades. The most classic clustering method is the k-means method [4–6]. However, it cannot guarantee the accuracy of clustering since it is based on the distance of the original features and them are easily affected by outliers and noises. Many researchers have pointed out that the subspace clustering method can effectively overcome the above problem. As a promising technique, subspace clustering aims to find clusters within different subspaces by the assumption that each data point can be represented as a linear combination of the other samples [7]. The subspace clustering-basaed methods can be roughly divided into three types: matrix factorization methods [8–11], statistical methods [12] and spectral clustering methods [7,13,14]. The matrix factorization-based subspace clustering methods perform low-rank matrix factorization on the data matrix to achieve clustering, but they are only suitable for noise-free data matrices and thus loss of generalization. Although the statistical-based subspace clustering methods can clearly deal with the influence of outliers or noise, their clustering performance is also affected by the number of subspaces, which hinders their practical applications. At present, the spectral clustering-based subspace clustering methods are widely used because they can well deal with high-dimensional data with noise and outliers. Among them, two representative examples includes sparse subspace clustering (SSC) [13] and low-rank representation (LRR) [7] by obtaining a sparse or low-rank linear representation of datasets, respectively. When encountering multi-view features, SSC and LRR can not well discover the high correlation among them. To overcome this limitation, Xia et al. [15] applied LRR for multi-view clustering to learn a low-rank transition probability matrix as the input of the standard Markov chain clustering method. Taking the different types of noise in samples into account, Najafi et al. [16] combined the low-rank approximation with error learning to eliminate noise and outliers. The work in [17] used low-rank and sparse constraints for multi-view clustering simultaneously. One common limitation of them is that the above methods only capture the pairwise correlation between different views. Considering the possible high-order correlation of multiple views, Zhang et al. [3] proposed a low-rank tensor constraint-regularied multi-view subspace clustering method. The study in [18] was inspired by [3] to introduce Hyper-Laplacian constraint to preserve the geometric structure of the data. Compared with most matrix-based methods [15,17], the tensor-based multi-view clustering methods have achieved satisfactory results, which demonstrates that the high-order correlation of the data is indispensable. The above methods impose the low-rank constraint on the constructed self-representative tensor through the unfolding matrix nuclear norm. Unfortunately, this rank-sum tensor norm lacks a clear physical meaning for general tensor [19].

In this paper, we proposed the weighted low-rank tensor representation (WLRTR) method for multi-view subspace clustering. Similar to the above tensor-based methods [3,18], WLRTR still stacks the self-representation matrices of all views into a representation tensor, and then applies low-rank constraint on it to obtain the high-order correlation among multiple views. Different from them, we exploits the classic Tucker decomposition to encode the low-rank property, which decomposes the representation tensor into one core tensor and three factor matrices. Considering that the information contained in different views may be partially different, and the complementary information between views contributes differently to clustering, the proposed WLRTR treats the singular values differently to improve the capability. The main contributions of this paper are summarized as follows:

(1) We propose a weighted low-rank tensor representation (WLRTR) method for multi-view subspace clustering, in which all representation matrices are stored as a representation tensor with two spatial and one view modes.

(2) Tucker decomposition is used to calculate the core tensor for the representation tensor and the low-rank constraints are applied to capture high-order correlation among multiple views and remove redundant information. WLRTR assigns different weights on the singular values in the core tensor to differently treat singular values.

(3) Based on the augmented Lagrangian multiplier method, we design an iterative algorithm to solve the proposed WLRTR model, and conduct experiments on four challenging databases to verify the superiority of WLRTR method over eight state-of-the-art single-view and multi-view clustering methods.

The remainder of this paper is organized as follows. Section 2 summarizes the notations, basic definitions and related content of subspace clustering involved in this paper. In Section 3, we introduce the proposed WLRTR model, and design an iterative algorithm to solve it. Extensive experiments and model analysis are reported in Section 4. The conclusion of this paper is summarized in Section 5.

Related Works

In this section, we aim to introduce the notations, basic definitions through this paper and the framework of subspace clustering methods.

Notations

For a third-order tensor, we represent it using bold calligraphy letter (e.g., $\mathcal{X}$). The matrices and vectors are represented by upper case letters (e.g., X) and lower case letters (e.g., x), respectively. The elements of tensor and matrix are defined as ${\mathcal{X}}_{ijk}$ and $x_{ij}$, respectively. The $l_{\mathrm{2,1}}$ norm of matrix X is defined as ${\left|\left|X\right|\right|}_{\mathrm{2,1}}={\displaystyle \sum _i\sqrt{{\displaystyle \sum }_j|x_{ij}{|}^2}={\displaystyle \sum }_j{\left|\left|x_j\right|\right|}_2}$, where $x_j$ represents the j-th column vector of X. The Frobenius norm of X is defined as ${\left|\left|X\right|\right|}_F=\sqrt{{\displaystyle \sum _{ij}|x_{ij}{|}^2}}$. We denote the i-th horizontal, lateral and frontal slice by $\mathcal{X}\left(i,:,:\right)$, $\mathcal{X}\left(:,i,:\right)$, $\mathcal{X}\left(:,:,i\right)$. The Frobenius norm and ${\mathrm{ℒ}}_1$ norm of tensor are ${\left|\left|\mathcal{X}\right|\right|}_F=\sqrt{{\displaystyle \sum _{ijk}|{\mathcal{X}}_{ijk}{|}^2}}$ and ${\left|\left|\mathcal{X}\right|\right|}_1={\displaystyle \sum _{i,j,k}\left|{\mathcal{X}}_{ijk}\right|}$. For $3-mode$ tensor $\mathcal{X}\in {\mathrm{ℛ}}^{n_1\times n_2\times n_3}$, the Tucker decomposition of $\mathcal{X}$ is $\mathcal{X}=\mathcal{S}{\times }_1{U}_1{\times }_2{U}_2{\times }_3{U}_3$. $\mathcal{S}\in {\mathrm{ℛ}}^{n_1\times n_2\times n_3}$ is the core tensor and $U_i\in {\mathrm{ℛ}}^{n_i\times n_i} (i=\mathrm{1,2,3})$ is the orthogonal factor matrix. The Tucker decomposition will be exploited to depict the low-rank property of the representation tensor.

Subspace Clustering

Subspace clustering is an effective method for processing high-dimensional data clustering. It divides the original feature space into several subspaces and then imposes constraints on each subspace to construct the similarity matrix. Suppose $X=[x_1,x_2,\cdots ,x_n]\in {\mathrm{ℛ}}^{d\times n}$ is a feature matrix with n samples, and d represents the dimension of one sample. The subspace clustering model based on LRR is expressed as follows:

$\begin{array}{c}\underset{Z,E}{\text{min}}{\left|\left|Z\right|\right|}_{\text{*}}+\beta {\left|\left|E\right|\right|}_{\mathrm{2,1}}\\ s.t. X=XZ+E,\end{array}(1)$

where ${\left|\left|Z\right|\right|}_{\text{*}}$ denotes the nuclear norm (sum of all singular values of Z). This model has achieved the promising clustering effect, because the self-representation matrix Z represents the correlation between samples, which is convenient to obtain the final similarity matrix $C=\frac{\left|Z\right|+\left|Z^T\right|}{2}$. However, the above LRR method is only suitable for single-view clustering. For the dataset ${\left\{X^{\left(v\right)}\right\}}_{v=1}^V$ with V views, the effective single-view clustering method is usually extended to multi-view clustering:

$\begin{array}{l}\underset{Z,E^{\left(v\right)}}{\text{min}}{\left|\left|Z\right|\right|}_{\text{*}}+\beta {\displaystyle \sum _{v=1}^V{\left|\left|E^{\left(v\right)}\right|\right|}_{\mathrm{2,1}}}\hfill \\ s.t. X^{\left(v\right)}=X^{\left(v\right)}Z+E^{\left(v\right)},\left(v=\mathrm{1,2},\cdots ,V\right),\hfill \end{array}(2)$

The LRR-based multi-view method not only improves the accuracy of clustering, but also detects outliers from multiple angles [20]. However, with the increase of feature views, the above models will inevitably suffer from information loss when fusing high-dimensional data views. It is urgent to explore efficient clustering methods.

Weighted Low-Rank Tensor Representation Model

In this section, we first introduce an existing tensor-based multi-view clustering method, and then propose a novel weighted low-rank tensor representation (WLRTR) method. Finally, the WLRTR is solved by the augmented Lagrangian multiplier (ALM) method.

Model Formulation

In order to make full use of the compatible and complementary information among multiple views, Zhang et al. [3] used LRR to perform tensor-based multi-view clustering. The main process is to stack the self-representation matrix of each view as a frontal slice of the third-order representation tensor which is imposed low-rank constraint. The whole model is formulated as follows

$\begin{array}{l}\underset{\mathcal{Z},E}{\text{min}}{\left|\left|\mathcal{Z}\right|\right|}_{\text{*}}+\beta {\left|\left|E\right|\right|}_{\mathrm{2,1}}\hfill \\ s.t. X^{\left(v\right)}=X^{\left(v\right)}{Z}^{\left(v\right)}+E^{\left(v\right)},\left(v=\mathrm{1,2},\cdots ,V\right),\hfill \\ \mathcal{Z}=\text{Φ}\left(Z^{\left(1\right)},Z^{\left(2\right)},\cdots ,Z^{\left(V\right)}\right),E=\left[E^{\left(1\right)};E^{\left(2\right)};\cdots ;E^{\left(V\right)}\right],\hfill \end{array}(3)$

where the tensor nuclear norm is directly extended from the matrix nuclear norm: ${\left|\left|\mathcal{Z}\right|\right|}_{\text{*}}={\displaystyle \sum _{m=1}^3{\xi }_m\Vert Z_{\left(m\right)}}{\Vert }_{\ast }$, $Z_{\left(m\right)}$ is the unfolding matrix along the m-th mode, ${\xi }_m$ is a constant that satisfies ${\displaystyle \sum _{m=1}^3{\xi }_m=1,{\xi }_m>0}$. However, this rank-sum tensor norm lacks a clear physical meaning for general tensor [19]. In addition, the meaningful information contained in each view is not completely equal, so it is unreasonable to use the same weight to penalize the singular values of $Z_{\left(m\right)}$ in the tensor nuclear norm. In order to overcome these limitations, we propose a novel weighted low-rank tensor representation (WLRTR) method, which uses Tucker decomposition to simplify the calculation of the tensor nuclear norm and assigns different weights to the core tensor to take advantage of the main information in different views. The proposed WLRTR is formulated as:

$\begin{array}{l}\underset{\mathcal{Z},\mathcal{S},E,U_1,U_2,U_3}{\text{min}}{\left|\left|\mathcal{Z}-\mathcal{S}{\times }_1{U}_1{\times }_2{U}_2{\times }_3{U}_3\right|\right|}_F^2+\alpha {\left|\left|\omega \circ \mathcal{S}\right|\right|}_1+\beta {\left|\left|E\right|\right|}_{\mathrm{2,1}}\hfill \\ s.t. X^{\left(v\right)}=X^{\left(v\right)}{Z}^{\left(v\right)}+E^{\left(v\right)},\left(v=\mathrm{1,2},\cdots ,V\right),\hfill \\ \mathcal{Z}=\text{Φ}\left(Z^{\left(1\right)},Z^{\left(2\right)},\cdots ,Z^{\left(V\right)}\right),E=\left[E^{\left(1\right)};E^{\left(2\right)};\cdots ;E^{\left(V\right)}\right],\hfill \end{array}(4)$

where $\omega =c/\left|\sigma \left(\mathcal{Z}\right)\right|+\mathit{ϵ}$, c and ϵ are constants. α and β are two nonnegative parameters. The WLRTR model consists of three parts: the first term obtains the core tensor through Tucker decomposition; the second term weights the core tensor to preserve the main feature information, and uses the $l_1$ norm to encode the low-rank structure of the self-representing tensor; since the errors are specific with respect to samples, the third term uses the $l_{\mathrm{2,1}}$ norm to encourage columns sparse and eliminate noise and outliers.

Optimization of WLRTR

In this section, we aim to use the ALM to solve the proposed WLRTR model in Eq. 4. Since the variable $\mathcal{Z}$ is involved in the objective function and constraint conditions, it is difficult to directly solve the proposed WLRTR model. To solve this problem, we use the variable-splitting technique and introduce one auxiliary tensor variable $\mathcal{Y}$. Therefore, the Eq. 4 can be transformed into the following formulation:

$\begin{array}{l}\underset{\mathcal{Z},\mathcal{S},E,U_1,U_2,U_3}{\text{min}}{\left|\left|\mathcal{Z}-\mathcal{S}{\times }_1{U}_1{\times }_2{U}_2{\times }_3{U}_3\right|\right|}_F^2+\alpha {\left|\left|\omega \circ \mathcal{S}\right|\right|}_1+\beta {\left|\left|E\right|\right|}_{\mathrm{2,1}}\hfill \\ s.t. X^{\left(v\right)}=X^{\left(v\right)}{Y}^{\left(v\right)}+E^{\left(v\right)},\left(v=\mathrm{1,2},\cdots ,V\right),\hfill \\ \mathcal{Z}=\text{Φ}\left(Z^{\left(1\right)},Z^{\left(2\right)},\cdots ,Z^{\left(V\right)}\right),E=\left[E^{\left(1\right)};E^{\left(2\right)};\cdots ;E^{\left(V\right)}\right],\mathcal{Z}=\mathcal{Y}.\hfill \end{array}(5)$

Correspondingly, the augmented Lagrangian function of constrained model in Eq. 5 is obtained by

$\begin{array}{l}\mathrm{ℒ}\left(\mathcal{Z},\mathcal{Y},\mathcal{S},E;U_1,U_2,U_3,\text{Θ},\text{Π},\rho \right)={\left|\left|\mathcal{Z}-\mathcal{S}{\times }_1{U}_1{\times }_2{U}_2{\times }_3{U}_3\right|\right|}_F^2+\alpha {\left|\left|\omega \circ \mathcal{S}\right|\right|}_1+\hfill \\ \beta {\left|\left|E\right|\right|}_{\mathrm{2,1}}+\frac{\rho }{2}\left({\displaystyle \sum _{v=1}^V\Vert X^{\left(v\right)}-X^{\left(v\right)}{Y}^{\left(v\right)}-E^{\left(v\right)}+{\frac{{\text{Θ}}^{\left(v\right)}}{\rho }\Vert }_F^2}+{\left|\left|\mathcal{Z}-\mathcal{Y}+\frac{\text{Π}}{\rho }\right|\right|}_F^2\right),\hfill \end{array}(6)$

where $\text{Θ}$ and $\text{Π}$ are the Lagrange multipliers. $\rho >0$ is the penalty parameter. Then, each variable is updated iteratively by fixing the other variables. The detailed iteration procedure is shown as follows:

Update self-representation tensor$\mathcal{Z}$: When other variables are fixed, $\mathcal{Z}$ can be updated by

$\begin{array}{c}{\mathcal{Z}}^{\text{*}}=\text{arg}\underset{\mathcal{Z}}{\text{min}}{\left|\left|\mathcal{Z}-\mathcal{S}{\times }_1{U}_1{\times }_2{U}_2{\times }_3{U}_3\right|\right|}_F^2+\frac{\rho }{2}\left({\left|\left|\mathcal{Z}-\mathcal{Y}+\frac{\text{Π}}{\rho }\right|\right|}_F^2\right).\end{array}(7)$

By setting the derivative of Eq. 7 with respect to $\mathcal{Z}$ to zero, we have

$\begin{array}{c}{\mathcal{Z}}^{\text{*}}=\frac{2\mathcal{S}{\times }_1{\mathit{U}}_1{\times }_2{\mathit{U}}_2{\times }_3{\mathit{U}}_3+\rho \mathcal{Y}-\text{Π}}{2+\rho }.\end{array}(8)$

Update auxiliary variable$Y^{\left(v\right)}$: Update auxiliary variable $Y^{\left(v\right)}$ with fixed residual variables is equivalent to optimizing

$\begin{array}{c}{Y}^{\left(v\right)\text{*}}=\text{arg}\underset{Y^{\left(v\right)}}{\text{min}}\frac{\rho }{2}\left({\left|\left|X^{\left(v\right)}-X^{\left(v\right)}{Y}^{\left(v\right)}-E^{\left(v\right)}+\frac{{\text{Θ}}^v}{\rho }\right|\right|}_F^2+{\left|\left|{\mathit{Z}}^{\left(v\right)}-{\mathit{Y}}^{\left(v\right)}+\frac{{\text{Π}}^{\left(v\right)}}{\rho }\right|\right|}_F^2\right).\end{array}(9)$

The closed-form of $Y^{\left(v\right)\text{*}}$ can be calculated by setting the derivative of Eq. 9 to zero

$Y^{\left(v\right)\text{*}}={\left(\rho I+\rho X^{\left(v\right)T}{X}^{\left(v\right)}\right)}^{-1}\times \left(\rho X^{\left(v\right)T}{X}^{\left(v\right)}-\rho X^{\left(v\right)T}{E}^{\left(v\right)}+X^{\left(v\right)T}{\text{Θ}}^v+\rho Z^{\left(v\right)}+{\text{Π}}^{\left(v\right)}\right).(10)$

Update core tensor$\mathcal{S}$: By fixing other variables, the subproblem of updating $\mathcal{S}$ can be written as follows

$\begin{array}{cc}{\mathcal{S}}^{\text{∗}}=\text{arg}\underset{\mathcal{S}}{\text{min}}{\left|\left|\mathcal{Z}-\mathcal{S}{\times }_1{\mathit{U}}_1{\times }_2{U}_2{\times }_3{U}_3\right|\right|}_F^2+\alpha {\left|\left|\omega \circ \mathcal{S}\right|\right|}_1.& \end{array}(11)$

According to [21], the Eq.(11) can be rewritten as

${\mathcal{S}}^{\text{∗}}=\text{arg}\underset{\mathcal{S}}{\text{min}}{\left|\left|\mathcal{S}-\mathcal{O}\right|\right|}_F^2+\alpha {\left|\left|\omega \circ \mathcal{S}\right|\right|}_1,(12)$

where $O=\mathcal{Z}{\times }_1{U}_1^T{\times }_2{U}_2^T{\times }_3{U}_3^T$. The closed solution ${\mathcal{S}}^{\text{*}}$ is as follows

${\mathcal{S}}^{\text{*}}=sign\left(\mathcal{O}\right)\text{max}\left(\left|\mathcal{O}\right|-\omega \alpha /\mathrm{2,0}\right).(13)$

Update error matrixE: Similar to the subproblems $\mathcal{Z}$ ,$Y^{\left(v\right)}$ and $\mathcal{S}$, the subproblem E is expressed as:

$\begin{array}{c}{E}^{\text{*}}=\text{arg}\underset{E}{\text{min}}\beta {\left|\left|E\right|\right|}_{\mathrm{2,1}}+\frac{\rho }{2}\left({\displaystyle \sum _{v=1}^M{\left|\left|X^{\left(v\right)}-X^{\left(v\right)}{Y}^{\left(v\right)}-E^{\left(v\right)}+\frac{{\text{Θ}}^{\left(v\right)}}{\rho }\right|\right|}_F^2}\right)\\ =\text{arg}\underset{E}{\text{min}}\frac{\beta }{\rho }{\left|\left|E\right|\right|}_{\mathrm{2,1}}+\frac{1}{2}{\left|\left|E-F\right|\right|}_F^2,\end{array}(14)$

where F represents the matrix that vertically concatenates the matrix $X^{\left(v\right)}-X^{\left(v\right)}{Y}^{\left(v\right)}+\left(1/\rho \right){\text{Θ}}^v$ along the column. The j-th column of optimal solution $E^{\text{*}}$ can be obtained by

$E^{\text{*}}(:,j)=\{\begin{array}{l}\frac{\parallel F\left(:,j\right){\parallel }_2-\frac{\beta }{\rho }}{\parallel F\left(:,j\right){\parallel }_2}F\left(:,j\right),if \frac{\beta }{\rho }<\parallel F\left(:,j\right){\parallel }_2;\hfill \\ 0,otherwise.\hfill \end{array}(15)$

Update Lagrangian multipliers$\text{Θ},\text{Π}$ and penalty parameter ρ: The Lagrangian multipliers $\text{Θ},\text{Π}$ and the penalty parameter ρ can be updated by

$\begin{array}{l}{\text{Θ}}^{v^{\text{∗}}}={\text{Θ}}^v+\rho \left(X^{\left(v\right)}-X^{\left(v\right)}{Y}^{\left(v\right)}-E^{\left(v\right)}\right);\\ \text{Π}\text{∗}=\text{Π}+\rho \left(\mathcal{Z}-\mathcal{Y}\right);\\ \rho \text{∗}=\text{min}\left\{\lambda \ast \rho ,{\rho }_{max}\right\},\end{array}(16)$

where $\lambda >0$ is to facilitate the convergence speed [22]. In order to increase ρ, we set $\beta =1.5$. ${\rho }_{max}$ is the max value of the penalty parameter ρ. The WLRTR algorithm is summarized in Algorithm 1.

Algorithm 1: WLRTR for multi-view subspace clustering

Input: multi-view features $\left\{X^{\left(v\right)},v=\mathrm{1,2},\cdots ,V\right\}$ ; parameter α, λ, c;

Initialize:$\mathcal{Z}$, $\mathcal{S}$, E, ${\text{Θ}}_1$, ${\text{Π}}_1$ initialized to 0; ${\rho }_1={10}^{-3}$, $\beta =1.5$, $tol={10}^{-7}$, $t=1$;

1: while not converged do

2: Update ${\mathcal{Z}}_{t+1}$ according to Eq. 8;

3: Update $Y_{t+1}^{\left(v\right)}$ according to Eq. 10;

4: Update ${\mathcal{S}}_{t+1}$ according to Eq. 13;

5: Update $E_{t+1}$ according to Eq. 15;

6: Update ${\text{Θ}}_{t+1}^{\left(v\right)}$, ${\text{Π}}_{t+1}$, and ${\rho }_{t+1}$ according to Eqs. 16;

7: Check the convergence condition:

8: ${\left|\left|X^{\left(v\right)}-X^{\left(v\right)}{Y}^{\left(v\right)}-E^{\left(v\right)}\right|\right|}_{\infty }\le tol$, ${\left|\left|Y^{\left(v\right)}-Z^{\left(v\right)}\right|\right|}_{\infty }\le tol$;

9: end while

Output:${\mathcal{Z}}^{\text{*}}$ and ${\mathcal{Y}}^{\text{*}}$.

Experimental Results

In this section, we conduct experiments on four real databases and compare with eight state-of-the-art methods to verify the effectiveness of the proposed WLRTR. In addition, we reported a detailed analysis of the parameter selection and convergence performance of the proposed WLRTR method.

Experimental settings

(1) Datasets: We evaluate the performance of WLRTR on three categories of databases: news stories (BBC4view, BBCSport), face images (ORL), handwritten digits (UCI-3views). BBC4view contains 685 documents and BBCSport consists of 544 documents, which belong to 5 clusters. We use 4 and 2 features to construct multi-view data, respectively. ORL includes 400 face images with 40 clusters. We use 3 features for clustering on ORL database, i.e., $4096d$ (dimension, d) intensity, $3304d$ LBP, and $6750d$ Gabor. UCI-3views includes 2000 instance with 10 clusters. For UCI-3views database, we adopted the $240d$ Fourier coefficients, the $76d$ pixel averages and the $6d$ morphological features to construct 3 views. Some examples of ORL and UCI-3views are shown in Figure 1. Table 1 summarizes the statistic information of these four databases.

(2) Compared methods: We compared WLRTR with eight state-of-the-art methods, including three single-view clustering methods and five multi-view clustering methods. Single-view clustering methods: SSC [13], LRR [7] and LSR [23], which use nuclear norm, $l_1$ norm and least squares regression to learn a self-representing matrix, respectively. Multi-view clustering methods: RMSC [15]: RMSC utilized the low-rank and sparse matrix decomposition to learn the shared transition probability matrix; LT-MSC [3]: LT-MSC is the first tensor-based multi-view clustering by the tensor nuclear norm constraint to learn a representation tensor; MLAN [24]: MLAN performed clustering and local structure learning using adaptive neighbors simultaneously; GMC [25]: GMC is a graph-based multi-view clustering method; AWP [26]: AWP is a multi-view clustering via adaptively weighted procrustes. SMSC [27]: SMSC used non-negative embedding and spectral embedding for multi-view clustering.

(3) Evaluation metrics: We exploit six popular clustering metrics, including, accuracy (ACC), normalized mutual information (NMI), adjusted rank index (AR), F-score, Precision and Recall to comprehensively evaluate the clustering performance. The closer the values of all evaluation metrics are to 1, the better the clustering results are. We run 10 trials for each experiment and report its average performance.

FIGURE 1

FIGURE 1. Samples of (A) ORL and (B) UCI-3views databases.

TABLE 1

TABLE 1. Information of four real multi-view databases.

Experimental Results

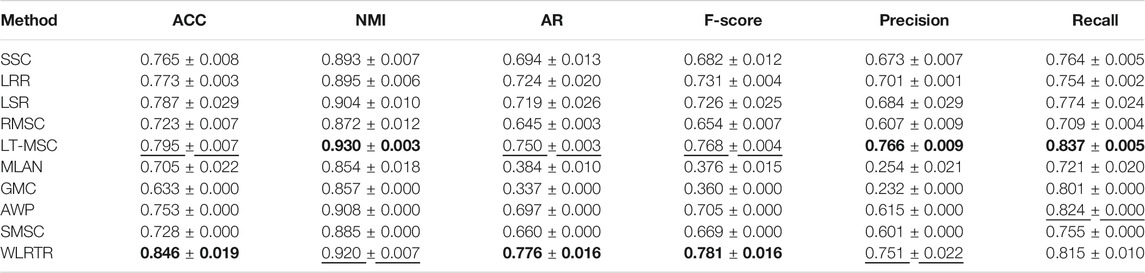
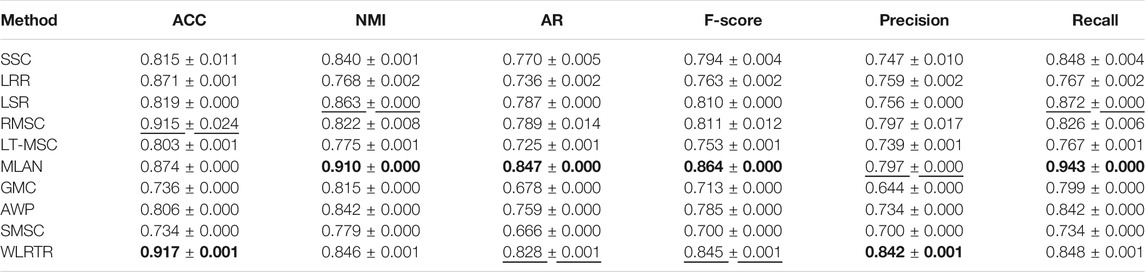
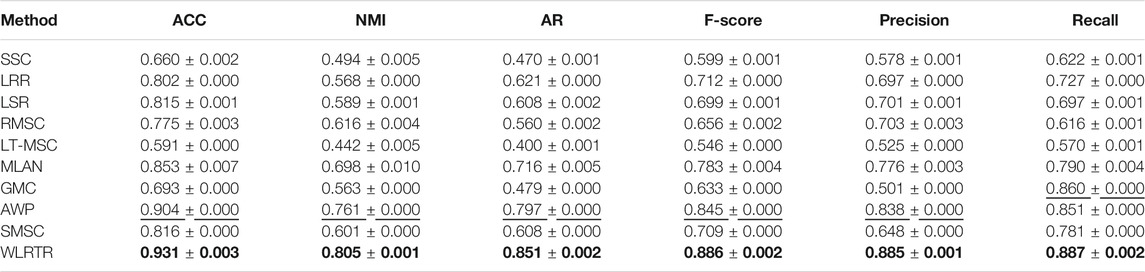
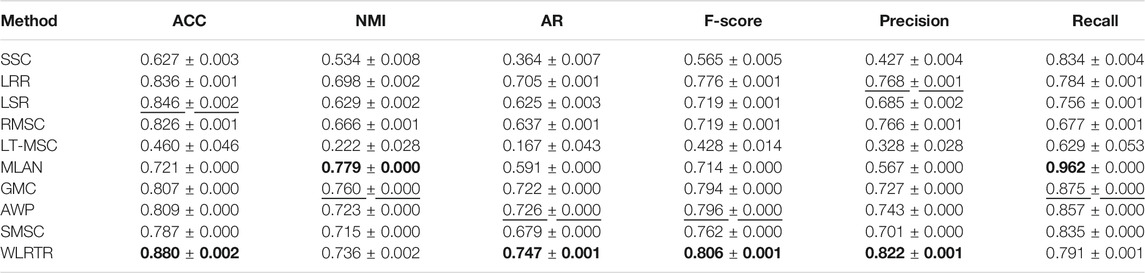
Tables 2–5 report the clustering performance of all comparison methods on the four databases. The best results are highlighted in bold and the second best results are underlined. From four tables, we can draw the following conclusions: Overall, the proposed WLRTR method has achieved better or comparable clustering results on all databases over all competing methods. Especially on the BBC4view database, WLRTR method outperforms all competing methods on six metrics. As for the ACC metric, the proposed WLRTR is higher than all methods on all datasets. In particular, WLRTR method shows better results than single-view clustering methods: SSC, LRR, LSR in most cases. This is because the multi-view clustering methods fully capture the complementary information among multiple views. The above conclusions have verified the effectiveness of the proposed WLRTR method.

TABLE 2

TABLE 2. Clustering results on ORL database.

TABLE 3

TABLE 3. Clustering results on UCI-3views database.

TABLE 4

TABLE 4. Clustering results on BBC4view database.

TABLE 5

TABLE 5. Clustering results on BBCSport database.

On the ORL database, the proposed WLRTR and LT-MSC methods have the best clustering effect among all the comparison methods. This shows that the tensor-based clustering methods can well explore the high-order correlation of multi-view features. Compared with LT-MSC method, WLRTR has improved ACC, AR and F-score metrics by $5.1$, $2.6$, and $1.3\text{\%}$, respectively. The main reason is that WLRTR takes the different contribution of each view to the construction of the affinity matrix into consideration, and assigns weights to it to retain important information. On the other hand, WLRTR uses Tucker decomposition technology to impose low-rank constraints on the core tensor instead of directly calculating the tensor nuclear norm based on the matrix.

On UCI-3views and BBCSport databases, although MLAN is better than WLRTR in some metrics, the clustering results of MLAN on different databases are unstable, and even lower than all single-view clustering methods on ORL database. In addition, we can find that the results of the recently proposed GMC method on the four databases cannot achieve satisfactory performance. The reason may be the graph-based clustering methods: MLAN and GMC usually use the original features to construct the affinity matrix, however, the original features usually are destroyed by noise and outliers.

Model Analysis

In this section, we conduct the parameter selection and convergence analysis of the proposed WLRTR method.

Parameter Selection

We perform experiments on ORL and BBCSport databases to investigate the influence of three parameters, i.e., α, β and c for the proposed WLRTR method, where parameters α and β are empirically selected from $\left[0.001,0.1\right]$ and c is selected from $\left[0.01,0.2\right]$. The influence of α and β on ACC is shown in the first column of Figure 2. After fixing c, we find that when α is set to a larger value, WLRTR can achieve the best result, which shows that noise has a greater impact on clustering. Similarly, we fix the parameters α and λ to analyze the influence of c on ACC. As shown in the second column of Figure 2, for the ORL database, when $c=0.2$, ACC reaches the maximum value. For the BBCSport database, the value of ACC has a peak at $c=0.04$, and when c becomes larger, the value of ACC decreases. The results show that c is very important for the weight distribution of the core tensor.

FIGURE 2

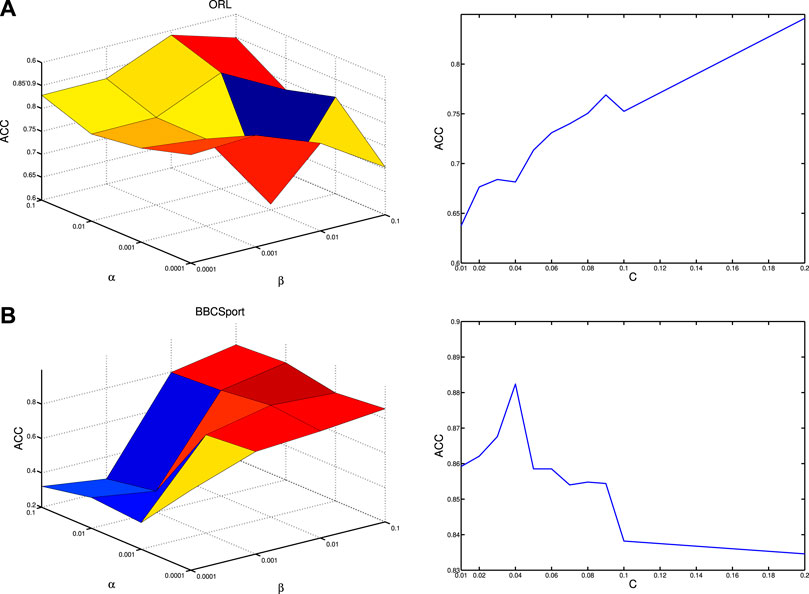
FIGURE 2. ACC versus different values of parameters α and β(left), and parameter c(right) on (A) ORL and (B) BBCSport.

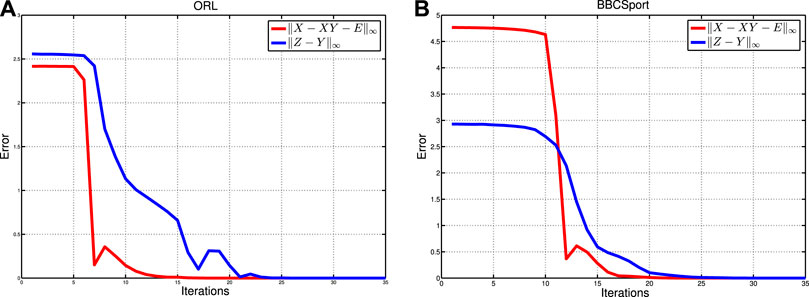
Numerical Convergence

This subsection investigates the numerical convergence of the proposed WLRTR method. Figure 3 shows the iterative error curves on the ORL and BBCSport databases. The iterative error is calculated by ${\left|\left|X^{\left(v\right)}-X^{\left(v\right)}{Y}^{\left(v\right)}-E^{\left(v\right)}\right|\right|}_{\infty }$ and ${\left|\left|Y^{\left(v\right)}-Z^{\left(v\right)}\right|\right|}_{\infty }$. One can be seen that the error curves gradually decrease with the increase of iterations and the error are close to 0 after 25 iterations. In addition, the error curves stabilized only after a few fluctuations. The above conclusions show that the proposed WLRTR method has strong numerical convergence and the similar conclusions can be obtained on the BBC4view and UCI-3views databases.

FIGURE 3

FIGURE 3. Errors versus iterations on (A) ORL and (B) BBCSport databases.

Conclusion and Future Work

In this paper, we developed a novel clustering method called weighted low-rank tensor representation (WLRTR) for multi-view subspace clustering. The main advantage of WLRTR is to encode the low-rank structure of the tensor through Tucker decomposition and $l_1$ norm, avoiding the error in calculating the tensor nuclear norm with the sum of nuclear norms of the unfolded matrices, and assigning different weights to the core tensor to exploit the main feature information of the views. In addition, the $l_{\mathrm{2,1}}$ norm is used to remove sample-specific noise and outliers. Extensive experimental results showed that the proposed WLRTR method has promising clustering performance. In future work, we will further explore the structural information representing tensors and use other tensor decomposition to improve the performance of multi-view clustering.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

SW conducted extensive experiments and wrote this paper. YC proposed the basic idea and revised this paper. FZ contributed to multi-view clustering experiments and funding support.

Funding

This work was supported by Natural Science Foundation of Zhejiang Province, China (Grant No. LY19A010025).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Jiang G, Wang H, Peng J, Chen D, Fu X (2019). Graph-based multi-view binary learning for image clustering. Available at: https://arxiv.org/abs/1912.05159

CrossRef Full Text | Google Scholar

2. Wang H, Wang Y, Zhang Z, Fu X, Li Z, Xu M, et al. Kernelized multiview subspace analysis by self-weighted learning. IEEE Trans Multimedia (2020) 32. doi:10.1109/TMM.2020.3032023

CrossRef Full Text | Google Scholar

3. Zhang C, Fu H, Liu S, Liu G, Cao X. Low-rank tensor constrained multiview subspace clustering. in: 2015 IEEE International Conference on Computer Vision (ICCV); Santiago, Chile; December 7–13, 2015 (IEEE), 1582–1590. (2015). doi:10.1109/ICCV.2015.185

CrossRef Full Text | Google Scholar

4. Bickel S, Scheffer T. Multi-view clustering. in: Fourth IEEE International Conference on Data Mining (ICDM'04); Brighton, UK; November 1–4, 2004 (IEEE), 19–26. (2004). doi:10.1109/ICDM.2004.10095

CrossRef Full Text | Google Scholar

5. Macqueen JB. Some methods for classification and analysis of multivariate observations. in: Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, (University of California Press), 281–297. (1967).

Google Scholar

6. Wu X, Kumar V, Quinlan JR, Ghosh J, Yang Q, Motoda H, et al. Top 10 algorithms in data mining. Know Inf Syst (2008) 14:1–37. doi:10.1007/s10115-007-0114-2

CrossRef Full Text | Google Scholar

7. Liu G, Lin Z, Yan S, Sun J, Yu Y, Ma Y. Robust recovery of subspace structures by low-rank representation. IEEE Trans Pattern Anal Mach Intell (2013) 35:171–184. doi:10.1109/TPAMI.2012.88

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Gao J, Han J, Liu J. Multi-view clustering via joint nonnegative matrix factorization. in: Proceedings of the 2013 SIAM International Conference on Data Mining; Austin, TX; May 2–4, 2013, 252–60. (2013). doi:10.1137/1.9781611972832.28

CrossRef Full Text | Google Scholar

9. Shao W, He L, Yu P. Multiple incomplete views clustering via weighted nonnegative matrix factorization with l2,1 regularization. Proc Joint Eur Conf Mach Learn Knowl Disc Data (2015) 9284:318–34. doi:10.1007/978-3-319-23528-8_20

CrossRef Full Text | Google Scholar

10. Zong L, Zhang X, Zhao L, Yu H, Zhao Q. Multi-view clustering via multi-manifold regularized non-negative matrix factorization. Neural Networks (2017) 88:74–89. doi:10.1016/j.neunet.2017.02.003

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Huang S, Kang Z, Xu Z. Auto-weighted multiview clustering via deep matrix decomposition. (2020) Pattern Recognit 97:107015. doi:10.1016/j.patcog.2019.107015

CrossRef Full Text | Google Scholar

12. Rao SR, Tron R, Vidal R., Ma Y. Motion segmentation via robust subspace separation in the presence of outlying, incomplete, or corrupted trajectories. in: 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, June 23–28, 2008, 1–8. (2008). doi:10.1109/CVPR.2008.4587437

CrossRef Full Text | Google Scholar

13. Elhamifar E, Vidal R. Sparse subspace clustering: Algorithm, theory, and applications. IEEE Trans Pattern Anal Mach Intell (2013) 35, 2765–2781. doi:10.1109/TPAMI.2013.57

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Chen Y, Xiao X, Zhou Y. Jointly learning kernel representation tensor and affinity matrix for multi-view clustering. IEEE Trans on Multimedia (2020) 22, 1985–1997. doi:10.1109/TMM.2019.2952984

CrossRef Full Text | Google Scholar

15. Xia R, Pan Y, Du L, Yin J. Robust multi-view spectral clustering via low-rank and sparse decomposition. Proc AAAI Conf Artif Intell (2014) 28, 2149–2155.

Google Scholar

16. Najafi M, He L, Yu PS. Error-robust multi-view clustering. Proc Int Conf on big data (2017) 736–745. doi:10.1109/BigData.2017.8257989

CrossRef Full Text | Google Scholar

17. Brbic M, Kopriva I. Multi-view low-rank sparse subspace clustering. Pattern Recognit (2018) 73, 247–258. doi:10.1016/j.patcog.2017.08.024

CrossRef Full Text | Google Scholar

18. Lu G, Yu Q, Wang Y, Tang G. Hyper-laplacian regularized multi-view subspace clustering with low-rank tensor constraint. Neural Networks (2020) 125:214–223. doi:10.1016/j.neunet.2020.02.014

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Xie Y, Tao D, Zhang W, Liu Y, Zhang L, Qu Y. On unifying multi-view self-representations for clustering by tensor multi-rank minimization. Int J Comput Vis (2018) 126:1157–1179. doi:10.1007/s11263-018-1086-2

CrossRef Full Text | Google Scholar

20. Li S, Shao M, Fu Y. Multi-view low-rank analysis with applications to outlier detection. ACM Trans Knowl Discov Data (2018) 12:1–22. doi:10.1145/3168363

CrossRef Full Text | Google Scholar

21. Chang Y, Yan L, Fang H, Zhong S, Zhang Z. Weighted low-rank tensor recovery for hyperspectral image restoration. Comput Vis Pattern Recognit (2017) 50:4558–4572. doi:10.1109/TCYB.2020.2983102

CrossRef Full Text | Google Scholar

22. Chen Y, Guo Y, Wang Y, Wang D, Peng C, He G. Denoising of hyperspectral images using nonconvex low rank matrix approximation. IEEE Transactions on Geoscience Remote Sensing (2017) 55:5366–5380. doi:10.1109/TGRS.2017.2706326

CrossRef Full Text | Google Scholar

23. Lu C-Y, Min H, Zhao Z-Q, Zhu L, Huang D-S, Yan S. Robust and efficient subspace segmentation via least squares regression. Proc Eur Conf Comput Vis (2012) 7578:347–360. doi:10.1007/978-3-642-33786-4_26

CrossRef Full Text | Google Scholar

24. Nie F, Cai G, Li J, Li X. Auto-weighted multi-view learning for image clustering and semi-supervised classification. IEEE Trans Image Process (2018a) 27:1501–1511. doi:10.1109/TIP.2017.2754939

CrossRef Full Text | Google Scholar

25. Wang H, Yang Y, Liu B. GMC: Graph-based multi-view clustering. IEEE Trans Knowl Data Eng (2019) 32:1116–1129. doi:10.1109/TKDE.2019.2903810

CrossRef Full Text | Google Scholar

26. Nie F, Tian L, Li X. Multiview clustering via adaptively weighted procrustes. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge, July 2018, 2022–2030. (2018b). doi:10.1145/3219819.3220049

CrossRef Full Text | Google Scholar

27. Hu Z, Nie F, Wang R, Li X. Multi-view spectral clustering via integrating nonnegative embedding and spectral embedding. Information Fusion 55:251–259. (2020). doi:10.1016/j.inffus.2019.09.005

CrossRef Full Text | Google Scholar