- 1Department of Mathematics, Faculty of Science, King Mongkut’s University of Technology Thonburi (KMUTT), Bangkok, Thailand
- 2Department of Mathematical Sciences, Bayero University, Kano, Nigeria
- 3KMUTT-Fixed Point Theory and Applications Research Group, Theoretical and Computational Science Center (TaCS), Science Laboratory Building, Faculty of Science, King Mongkut’s University of Technology Thonburi (KMUTT), Bangkok, Thailand
- 4Center of Excellence in Theoretical and Computational Science (TaCS-CoE), SCL 802 Fixed Point Laboratory, Science Laboratory Building, King Mongkut’s University of Technology Thonburi (KMUTT), Bangkok, Thailand
- 5Division of Science and Technology, Department of Mathematics, University of Education Lahore, Lahore, Pakistan
- 6Department of Mathematics, University of Lakki Marwat, Lakki Marwat, Pakistan
- 7Department of Medical Research, China Medical University Hospital, China Medical University, Taichung, Taiwan
- 8Department of Mathematics and Statistics, Hazara University Mansehra, Khyber Pakhtunkhwa, Pakistan
- 9Department of Mathematics and Statistics, University of Swat, Khyber Pakhtunkhwa, Pakistan
The analysis is carried out to analyze the flow through double stretchable rotating disks with the theory of radiative Cross nanofluid under the influence of variable thermal conductivity, the Hall current, Arrhenius activation energy, and binary chemical reactions. The Buongiorno nanofluid model is adopted for the governing equations of the problem which are transformed into ordinary differential equations through similarity transformations and then solved using the homotopy analysis method. The impact of dimensionless parameters on all profiles and physical quantities is presented and discussed. The radial velocity of the two disks increases with their corresponding ratio stretching rate parameter and decreases with the Hall parameter and the bioconvection Rayleigh number. The heat transfer at the lower disk enhances with the variable thermal conductivity parameter, while at the upper disk, opposite trend is observed. Mass transfer increases with the chemical reactions and temperature difference parameters at the lower disk and decreases with Arrhenius activation energy, whereas an opposite trend is observed at the upper disk. The local density number is enhanced for the larger values of Peclet and Lewis numbers. The comparison of the present work with the published literature authenticates the validation of the present work.
Introduction
Cross [1] carried out an innovative work on the Cross model in 1965. Cross fluid is a separate generalization of non-Newtonian fluid types, which has served as a model offering a wide range of shearing rates for the dilatant and pseudoplastic origin of the fluids. A variety of applications involves polymerization in the Cross-fluid model. Xie and Jin [2] reported a Cross rheological equation analysis for the surface free layer of non-Newtonian fluid. Manzur et al. [3] studied the Cross-fluid model with flow through the extended vertical sheet stretching layer by examining the mixed convection and radiative heat transfer. Abbas et al. [4] considered the Cross nanofluid flow subject to entropy generation mathematical modeling and analysis. Hayat et al. [5] performed a numeric simulation of MHD stagnation of Cross-fluid model flow and heat transfer in a stretched surface. Naz et al. [6] studied the Cross nanofluid dynamics with magnetohydrodynamics, entropy, and gyrotactic motile microbiological characteristics.
The thermal transformation process is characterized by the thermal conductivity of the basic fluid due to poor thermal conductivity of nonmetallic materials such as mud, oils, and glycol mixture in contrast to some metallic materials like copper, aluminum, iron, bronze, etc. The properties of low thermal-conducting nanoparticles, usually made up of oxides and metals, significantly increase the base fluid thermal conductivity. The conductivity and convection coefficients of metals and oxides increase the efficiency of heat transfer in nanofluids. Choi and Eastman [7] in 1995 first suggested the term “nanofluid” by using very small (1–100 nm) nanoparticles added to the base fluid. Boungiorno [8] suggested the slips mechanisms like inertia, dissipation, magnus, fluid drainage, gravity, Brownian diffusion, and thermophoresis effects in the dynamics of nanofluids. Kuznetsov and Nield [9] used the Buongiorno model to address the nanoparticles’ effects on natural convective boundary flow via a vertical plate. The main work focusing on normal cases using nanofluids for all purposes began in 1995 with Choi and Eastman on their study to assign the suspension of solid nanoparticles to the base fluid, where they found that the thermal conductivity of the water–
Bioconvective phenomena are common in suspension, usually due to the swimming of microorganisms that are marginally denser than water. If the upper surface of the suspension is too thick due to the accumulation of microorganisms, it becomes brittle and the microorganisms collapse to induce the bioconvection. The development of gyrotactic nanofluid microorganisms enables mass transfer, microscale mixing, primarily in microvolumes, and improves nanofluid stability. Li and Xu [22] studied the unsteady mixed bioconvection flow of a nanofluid between two contracting or expanding rotating disks. Qayyum et al. [23] examined the analysis of radiation in a suspension of nanoparticles and gyrotactic microorganism for rotating disk of variable thickness. Shehzad et al. [24] investigated the Maxwell nanofluid bioconvection on isolated rotating disks under the influence of the double-diffusive Cattaneo–Christov theory. Khan et al. [25] reported the study of entropy generation in bioconvection nanofluid flow between two stretchable rotating disks. More studies on bioconvection can be found in Refs. 26–30.
Scientists and engineers, particularly in the areas of oil, chemical and petroleum engineering, oil and water emulsion, cooling reactors, geothermal, mechanical chemistry, and material degradation, have been very interested in multi-specific applications such as energy activation and species response. Generally, the relation between chemical reactions and mass transfer is highly complex and can only be studied by producing and digesting reagent species at different fluid flow and mass transfer rates. Arrhenius [31] for the first time suggested the concept of activation energy. However, Bestman [32] recognized a principal model of a boundary layer of flow problem due to binary chemical reactions with Arrhenius activation energy. Shahzad et al. [33] investigated the transport of radiative heat transfer with entropy generation and activation energy in dissipative nanofluid flow. Dhlamini et al. [34] suggested the mixed convective nanofluid flow with convective boundary conditions under binary chemical reaction and Arrhenius activation energy. Azam et al. [35] investigated the Arrhenius activation energy effects on radiative Cross-nanofluid axisymmetric flow through covalent bonding development. More studies on Arrhenius activation energy and binary chemical reaction can be seen in Refs. 36–40.
The idea of flow into a rotating disk system is an important area for future industrial process optimization and development. Scientists all over the world have drawn attention to this idea with the applications in the fields of electrochemistry, energy engineering, aerodynamics, chemical engineering, food processing, and medical equipment. To the best of knowledge, Karman [41] initially investigated the flow of liquid through an infinite disk with the introduction of famous similarity transformations in his study. Hayat et al. [42] investigated the viscous dissipation in the second-grade fluid flow in rotating disk with the Joule heating. Yao and Lian [43] reported the flow due to rotation, in which they provided analytical and numerical solutions when the fluid is rigidly rotated. Hayat et al. [44] investigated the flow between two stretchable rotating disks with the Cattaneo–Christov heat flux model. More studies on a rotating disk system can be consulted in Refs. 45 and 46.
In the light of the abovementioned literature, no one has, to the best of our knowledge, studied the flow between two stretchable rotating disks under the radiative Cross-nanofluid theory in the following context. The objective, here is, to explore the flow of Cross nanofluid in the presence of variable thermal conductivity, the Hall effect, and Arrhenius activation energy effect. The Buongiorno nanofluid model is used to develop Brownian diffusion and thermophoresis effects in both the energy and concentration equations. The problem is solved through HAM [47, 48] presented by Liao in 1992. However, due to its rapid convergence, various researchers [49–74] used HAM and various potential techniques to solve their problems. The effects of the parameters on the profiles are explained through graphs and tables whose detail is given in the Discussion section.
Problem Formulation
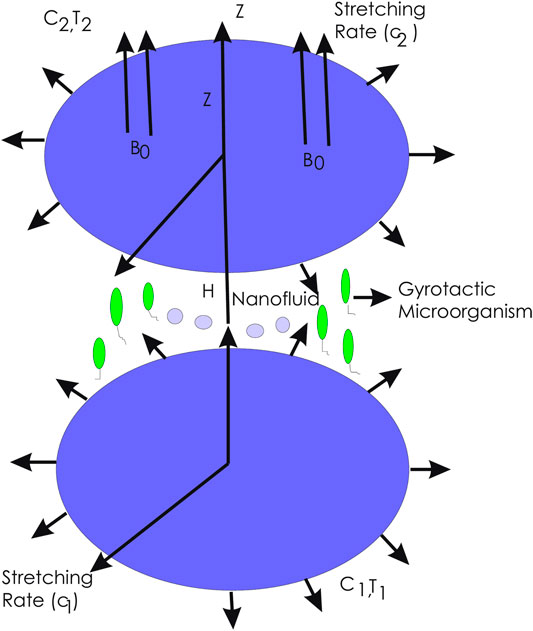
A three-dimensional, steady, axisymmetric motion of MHD flow of incompressible radiative Cross nanofluid through rotating double disks is considered. The lower disk is at the plane
The Hall current is influencing many fields such as medical sciences and engineering. Cosmological fluid dynamics, geophysics, and the Hall accelerator can be listed as various engineering applications of the Hall current. The Hall current is induced by the significantly strong magnetic field. Generalized form of Ohm’s law in the existence of the electric fields is given by
assuming that the thermoelectric pressure and ion slip conditions for weakly ionized gas are negligible. Hence, the equations reduced in the form as
where
The Cauchy stress tensor (Cross-viscosity model) is displayed as
where
where
by taking viscosity infinite shear rate to zero
Taking the assumption
The Cross-viscosity model shear rate in the existence of simulation is given as
where
Now the continuity, momentum, energy, concentration, and gyrotactic microorganism equations [1, 3, 5, 6, 34] are
where
The boundary conditions are
The following transformations are used
with boundary conditions
Physical Quantities
The physical quantities of interests are given below.
Skin Friction Coefficients
These are defined as
Therefore, the skin friction coefficients for the lower and upper disks are respectively, as
where
Nusselt Number
These are defined as
Sherwood Number
These are defined as
Local Density Motile Flux
These are defined as
Solution of the Problem by HAM
The current problem is solved with the HAM (homotopy analysis method) software in Mathematica 10 computer-based programing. HAM has been used to solve the problem because this method has the following good aspects.
Without discretization and linearization of the nonlinear differential equations, this technique is applicable to the system for the best answer.
This technique is also applicable to those systems which have small or large natural parameters.
This technique produces the convergent solution of the problem.
This method is free from a set of base functions and linear operators.
Taking the initial guesses and the linear operators as
which satisfy the following properties
where
The zeroth order form of the problems is given as
where
For
Obviously, when
The convergence of the series in Eqs 44–48 depends strongly upon
The result of the problems at order
where
By solving the
in which
Results and Discussion
Velocity Profile
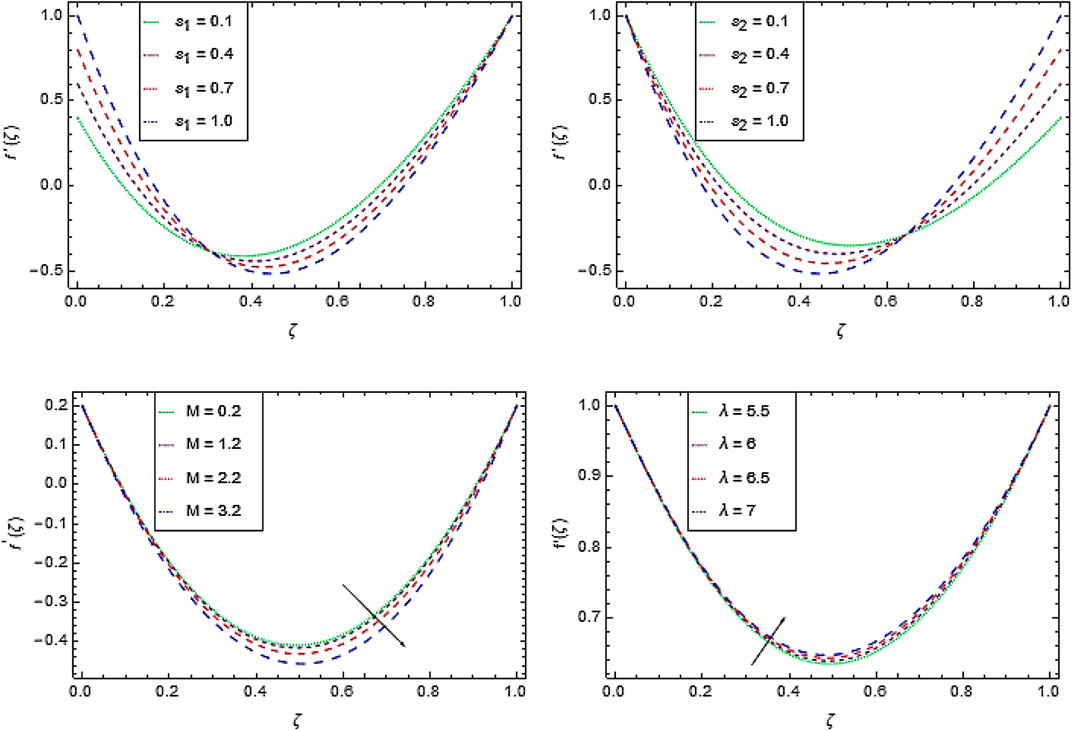
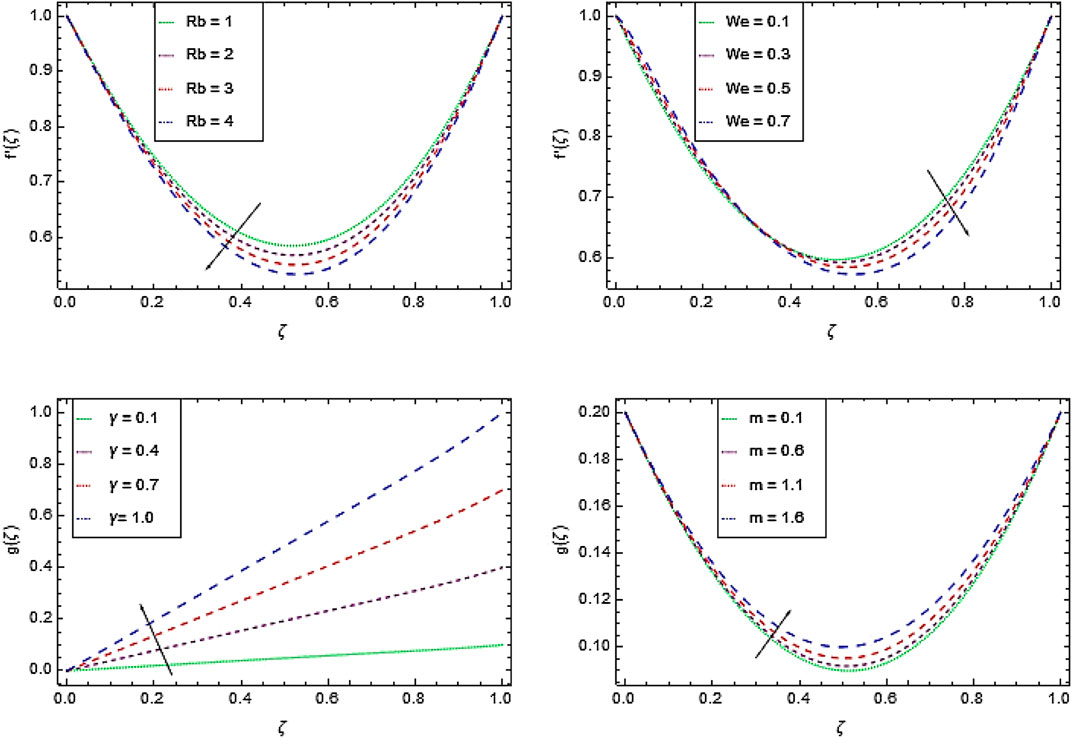
Figures 2A–D depict the effect of
Figure 3C discloses that the rotation paves a long way to enhance the velocity component
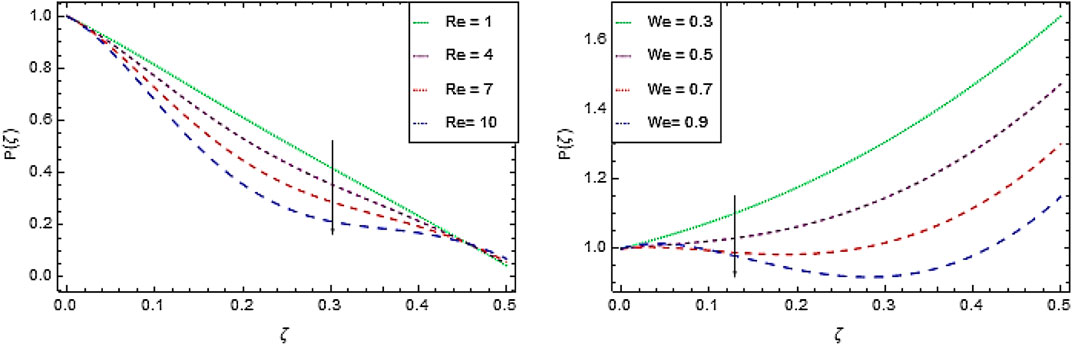
Pressure Profile
Figures 4A,B depicts the effect of Reynolds number
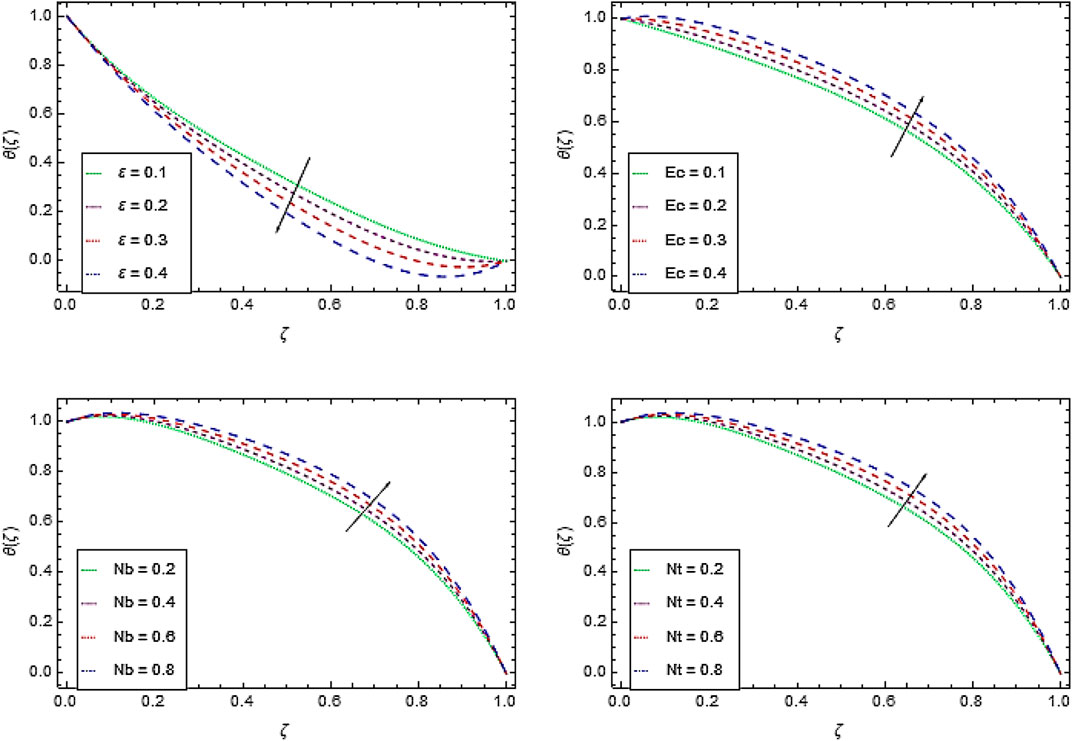
Temperature Profile
The temperature decreases by increasing the values of thermal conductivity parameter
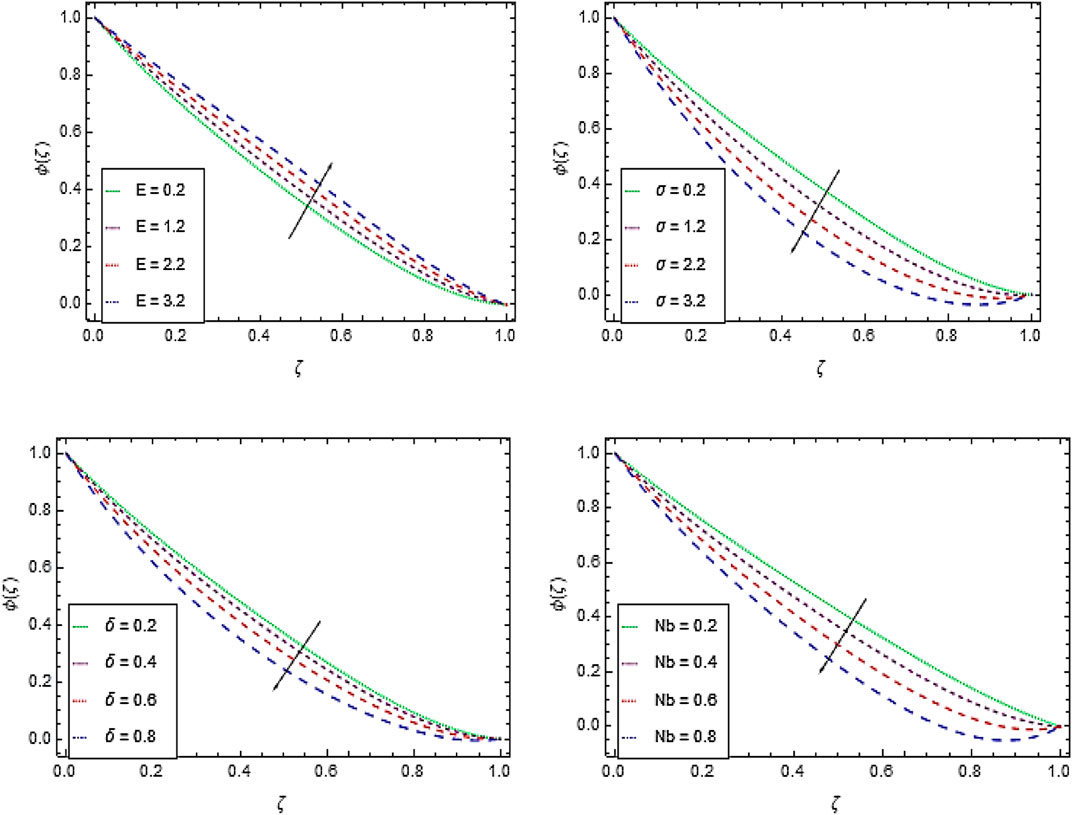
Nanoparticles Concentration Profile
The increase in Arrhenius activation energy
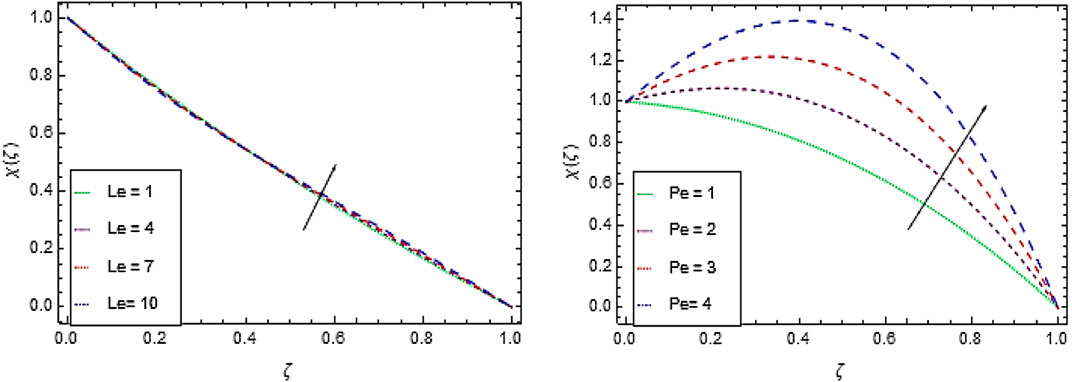
Gyrotactic Microorganism Concentration Profile
Heat treatment makes the system quite fragile and improves production of bioconvection. Figure 7A shows that the increment in the motile microorganism’s concentration
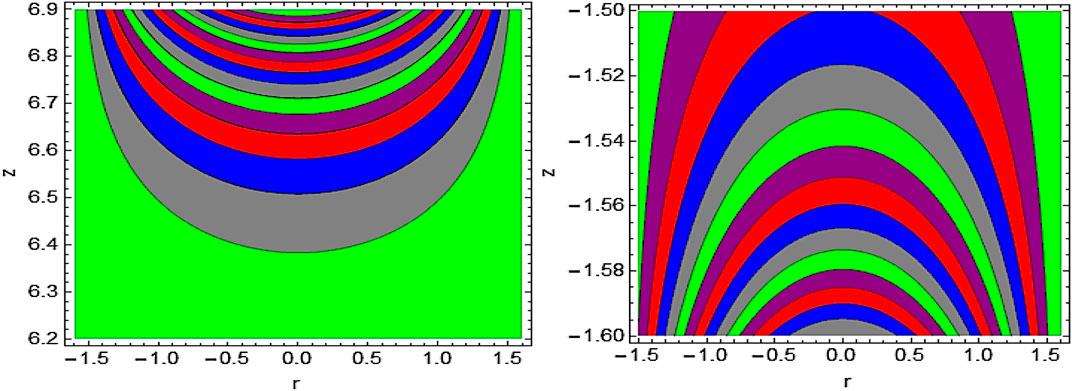
Streamlines
The trapping for different values of the Hall parameter
Validation of the Present Work and Physical Quantities
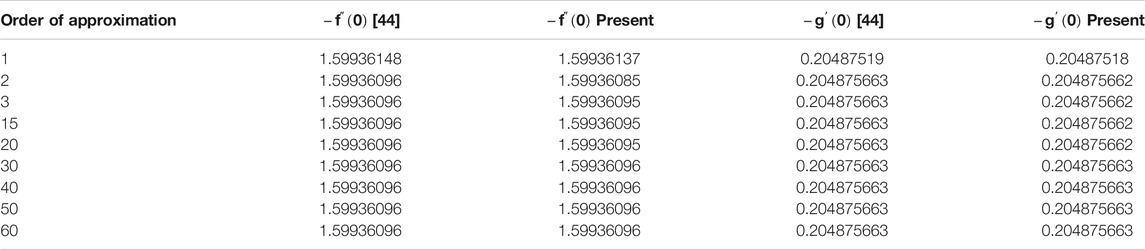
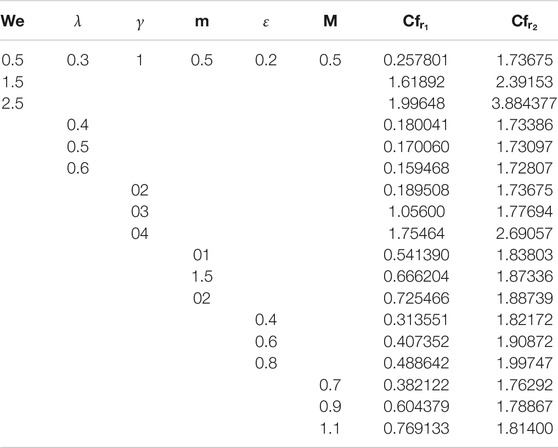
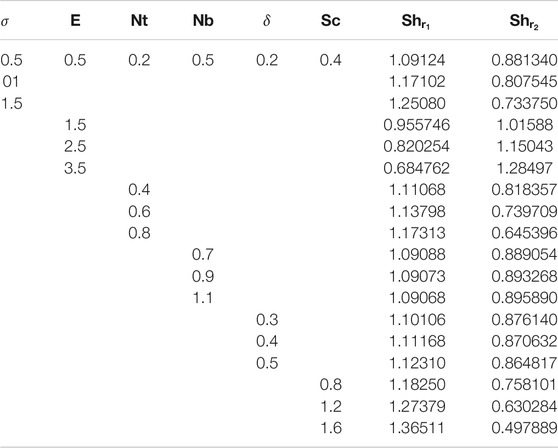
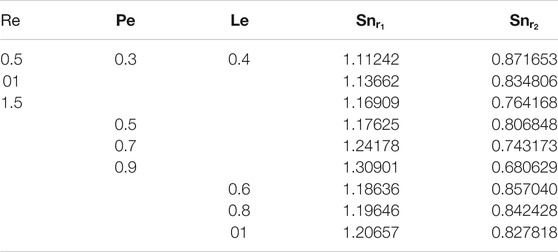
The comparison between the present work and the previous work is shown in Table 1. The results show that there is a close agreement of the present problem. The numerical values of the skin frictions on both the disks are displayed in Table 2. The lower disk skin friction is increased with
Conclusion
The current work has analyzed the influence of variable thermal conductivity, the Hall current, and activation energy on the flow of double stretchable rotating disks under the theory of radiative Cross nanofluid in the presence of a uniform magnetic field. The fluid functions have been analyzed using graphs and tables explaining the details of the findings in the Discussion section. In summary,
The Cross-nanofluid velocity decreases at the boundary layer with the magnetic field parameter
The azimuthal velocity
Pressure profile
The temperature of the Cross nanofluid enhances with increasing the
The nanofluid concentrations decreases with higher values of
Motile gyrotactic microorganism’s density increases through larger value of
The lower disk skin frictions is increased with
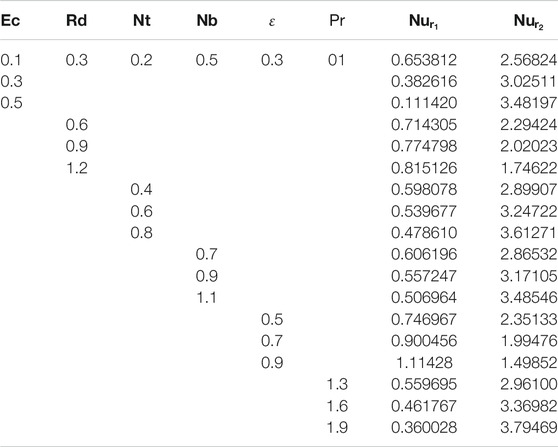
The rate of heat transport on the lower disk decreases with
The local density number is enhanced for the larger values of
There exists a nice agreement between the present and published work in Table 1.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding authors.
Author Contributions
NK, AU, UH, ZS, PK, WK, AK, SR, ZU completed the research work.
Funding
The research is funded by Petchra Pra Jom Klao Doctoral Scholarship for Ph.D. program of King Mongkut’s University of Technology Thonburi (KMUTT) (Grant No. 13/2562) and Theoretical and Computational Science (TaCS) Center. The authors appreciate the financial support allotted by King Mongkut’s University of Technology Thonburi through the “KMUTT 55th Anniversary Commemorative Fund.” The first author is supported by the Petchra Pra Jom Klao Doctoral Scholarship Academic for PhD studies at KMUTT. This research was accomplished with the help of the Theoretical and Computational Science (TaCS) Center, Faculty of Science, KMUTT.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest
Acknowledgments
The authors are obliged to the respectable editor and referees for their important and fruitful comments to enhance the quality of this article. The authors acknowledge the financial support provided by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT. Moreover, this research project is supported by Thailand Science Research and Innovation (TSRI) Basic Research Fund: Fiscal year 2021 under project number 64A306000005.
Glossary
References
1. Cross MM. Rheology of non-newtonian fluids: a new flow equation for pseudoplastic systems. J Colloid Sci (1965) 20:417–37. doi:10.1016/0095-8522(65)90022-x
2. Xie J, Jin Y-C. Parameter determination for the cross rheology equation and its application to modeling non-Newtonian flows using the WC-MPS method. Eng Appl Comput Fluid Mech (2016) 10:111–29. doi:10.1080/19942060.2015.1104267
3. Manzur M, Khan M, Rahman Mu. Mixed convection heat transfer to cross fluid with thermal radiation: effects of buoyancy assisting and opposing flows. Int J Mech Sci (2018) 138–139:515–23. doi:10.1016/j.ijmecsci.2018.02.010
4. Abbas SZ, Khan WA, Sun H, Ali M, Irfan M, Shahzed M, et al. Mathematical modeling and analysis of cross nanofluid flow subjected to entropy generation. Appl Nanosci (2020) 10:3149–60. doi:10.1007/s13204-019-01039-9
5. Hayat T, Khan MI, Tamoor M, Waqas M, Alsaedi A. Numerical simulation of heat transfer in MHD stagnation point flow of cross fluid model towards a stretched surface. Results Phy (2017) 7:1824–7. doi:10.1016/j.rinp.2017.05.022
6. Naz R, Noor M, Hayat T, Javed M, Alsaedi A. Dynamism of magnetohydrodynamic cross nanofluid with particulars of entropy generation and gyrotactic motile microorganisms. Int Commun Heat Mass Tran (2020) 110:104431. doi:10.1016/j.icheatmasstransfer.2019.104431
7. Choi SU, Eastman JA. Enhancing thermal conductivity of fluids with nanoparticles (1995). Report Nos. ANL/MSD/CP-84938; CONF-951135-29. Lemont, IL: Argonne National Lab.
8. Buongiorno J. Convective transport in nanofluids. J Heat Trans-T ASME (2006) 128:240–50. doi:10.1115/1.2150834
9. Kuznetsov AV, Nield DA. Natural convective boundary-layer flow of a nanofluid past a vertical plate. Int J Therm Sci (2010) 49(2):243–7. doi:10.1016/j.ijthermalsci.2009.07.015
10. Turkyilmazoglu M. Nanofluid flow and heat transfer due to a rotating disk. Comput Fluids (2014) 94:139–46. doi:10.1016/j.compfluid.2014.02.009
11. Ahmad L, Khan M, Khan WA. Numerical investigation of magneto-nanoparticles for unsteady 3D generalized Newtonian liquid flow. Eur Phys J Plus (2017) 132(9):373. doi:10.1140/epjp/i2017-11658-6
12. Hafeez A, Khan M, Ahmed A, Ahmed J. Rotational flow of Oldroyd-B nanofluid subject to Cattaneo-Christov double diffusion theory. Appl Math Mech (2020) 41:1083–94. doi:10.1007/s10483-020-2629-9
13. Khan M, Ahmad L, Gulzar MM. Unsteady Sisko magneto-nanofluid flow with heat absorption and temperature dependent thermal conductivity: a 3D numerical study. Results Phy (2018) 8:1092–103. doi:10.1016/j.rinp.2018.01.034
14. Ahmad L, Khan M. Numerical simulation for MHD flow of Sisko nanofluid over a moving curved surface: a revised model. Microsyst Technol (2019) 25(6):2411–28. doi:10.1007/s00542-018-4128-3
15. Khan M, Ahmed J, Sultana F, Sarfraz M. Non-axisymmetric Homann MHD stagnation point flow of Al2O3-Cu/water hybrid nanofluid with shape factor impact. Appl Math Mech (2020) 41:1125–38. doi:10.1007/s10483-020-2638-6
16. Khan M, Irfan M, Khan WA, Ahmad L. Modeling and simulation for 3D magneto eyring-powell nanomaterial subject to nonlinear thermal radiation and convective heating. Results Phy (2017) 7:1899–906. doi:10.1016/j.rinp.2017.06.002
17. Ahmed A, Khan M, Ahmed J. Thermal analysis in swirl motion of Maxwell nanofluid over a rotating circular cylinder. Appl Math Mech (2020) 41:1417–30. doi:10.1007/s10483-020-2643-7
18. Khan M, Ahmad L, Khan WA. Numerically framing the impact of radiation on magnetonanoparticles for 3D Sisko fluid flow. J Braz Soc Mech Sci Eng (2017) 39:4475–87. doi:10.1007/s40430-017-0842-5
19. Ahmed J, Khan M, Ahmad L. Radiative heat flux effect in flow of Maxwell nanofluid over a spiraling disk with chemically reaction. Phys Stat Mech Appl (2020) 551:123948. doi:10.1016/j.physa.2019.123948
20. Ahmed J, Shahzad A, Farooq A, Kamran M, Khan SUD, Khan SUD. Thermal analysis in swirling flow of titanium dioxide–aluminum oxide water hybrid nanofluid over a rotating cylinder. J Therm Anal Calorim (2020):1–11. doi:10.1007/s10973-020-10190-3
21. Ahmed J, Shahzad A, Farooq A, Kamran M, Khan SUD, Khan SUD. Radiative heat transfer in Homann stagnation-point flow of hybrid nanofluid. Appl Nanosci (2020) 10:1–10. doi:10.1007/s13204-020-01464-1
22. Li JJ, Xu H, Raees A, Zhao QK. Unsteady mixed bioconvection flow of a nanofluid between two contracting or expanding rotating discs. Z Naturforsch (2016) 71:261–72. doi:10.1515/zna-2015-0518
23. Qayyum S, Imtiaz M, Alsaedi A, Hayat T. Analysis of radiation in a suspension of nanoparticles and gyrotactic microorganism for rotating disk of variable thickness. Chin J Phys (2018) 56:2404–23. doi:10.1016/j.cjph.2018.06.020
24. Shehzad SA, Reddy MG, Rauf A, Abbas Z. Bioconvection of Maxwell nanofluid under the influence of double diffusive Cattaneo–Christov theories over isolated rotating disk. Phys Scr (2020) 95:045207. doi:10.1088/1402-4896/ab5ca7
25. Khan NS, Shah Q, Bhaumik A, Kumam P, Thounthong P, Amiri I. Entropy generation in bioconvection nanofluid flow between two stretchable rotating disks. Sci Rep (2020) 10:1–26. doi:10.1038/s41598-020-61172-2 |
26. Khan NS, Shah Q, Sohail A. Dynamics with Cattaneo–Christov heat and mass flux theory of bioconvection Oldroyd-B nanofluid. Adv Mech Eng (2020) 12. doi:10.1177/1687814020930464
27. Khan NS. Mixed convection in mhd second grade nanofluid flow through a porous medium containing nanoparticles and gyrotactic microorganisms with chemical reaction. Filomat (2019) 33:4627–53. doi:10.2298/fil1914627k
28. Zuhra S, Khan NS, Islam S. Magnetohydrodynamic second-grade nanofluid flow containing nanoparticles and gyrotactic microorganisms. Comput Appl Math (2018) 37:6332–58. doi:10.1007/s40314-018-0683-6
29. Zuhra S, Khan NS, Shah Z, Islam S, Bonyah E. Simulation of bioconvection in the suspension of second grade nanofluid containing nanoparticles and gyrotactic microorganisms. AIP Adv (2018) 8:105210. doi:10.1063/1.5054679
30. Palwasha Z, Islam S, Khan NS, Ayaz H. Non-Newtonian nanoliquids thin-film flow through a porous medium with magnetotactic microorganisms. Appl Nanosci (2018) 8:1523–44. doi:10.1007/s13204-018-0834-5
31. Arrhenius S. Über die dissociationswärme und den Einfluss der temperatur auf den dissociationsgrad der elektrolyte. Z Phys Chem (1889) 4:96–116. doi:10.1515/zpch-1889-0108
32. Bestman AR. Natural convection boundary layer with suction and mass transfer in a porous medium. Int J Energy Res (1990) 14:389–96. doi:10.1002/er.4440140403
33. Shahzad M, Sun H, Sultan F, Khan WA, Ali M, Irfan M. Transport of radiative heat transfer in dissipative cross nanofluid flow with entropy generation and activation energy. Phys Scr (2019) 94:115224. doi:10.1088/1402-4896/ab2caf
34. Dhlamini M, Kameswaran PK, Sibanda P, Motsa S, Mondal H. Activation energy and binary chemical reaction effects in mixed convective nanofluid flow with convective boundary conditions. J Comput Des Eng (2019) 6:149–58. doi:10.1016/j.jcde.2018.07.002
35. Azam M, Xu T, Shakoor A, Khan M. Effects of Arrhenius activation energy in development of covalent bonding in axisymmetric flow of radiative-cross nanofluid. Int Commun Heat Mass Tran (2020) 113:104547. doi:10.1016/j.icheatmasstransfer.2020.104547
36. Khan NS, Shah Z, Islam S, Khan I, Alkanhal T, Tlili I. Entropy generation in MHD mixed convection non-newtonian second-grade nanoliquid thin film flow through a porous medium with chemical reaction and stratification. Entropy (2019) 21:139. doi:10.3390/e21020139
37. Khan NS, Kumam P, Thounthong P. Second law analysis with effects of Arrhenius activation energy and binary chemical reaction on nanofluid flow. Sci Rep (2020) 10:1226–6. doi:10.1038/s41598-020-57802-4 |
38. Abdelmalek Z, Mahanthesh B, Md Basir MF, Imtiaz M, Mackolil J, Khan NS, et al. Mixed radiated magneto Casson fluid flow with Arrhenius activation energy and Newtonian heating effects: flow and sensitivity analysis. Alex Eng J (2020) 59:3991–4011. doi:10.1016/j.aej.2020.07.006
39. Khan NS, Zuhra S, Shah Q. Entropy generation in two phase model for simulating flow and heat transfer of carbon nanotubes between rotating stretchable disks with cubic autocatalysis chemical reaction. Appl Nanosci (2019) 9:1797–822. doi:10.1007/s13204-019-01017-1
40. Khan NS, Shah Z, Shutaywi M, Kumam P, Thounthong P. A comprehensive study to the assessment of Arrhenius activation energy and binary chemical reaction in swirling flow. Sci Rep (2020) 10:1–21. doi:10.1038/s41598-020-64712-y |
41. Kármán TV. Über laminare und turbulente Reibung. Z Angew Math Mech (1921) 1:233–52. doi:10.1002/zamm.19210010401
42. Hayat T, Khan MI, Alsaedi A, Khan MI. Joule heating and viscous dissipation in flow of nanomaterial by a rotating disk. Int Commun Heat Mass Tran (2017) 89:190–7. doi:10.1016/j.icheatmasstransfer.2017.10.017
43. Yao B, Lian L. A new analysis of the rotationally symmetric flow in the presence of an infinite rotating disk. Int J Mech Sci (2018) 136:106–11. doi:10.1016/j.ijmecsci.2017.12.023
44. Hayat T, Qayyum S, Imtiaz M, Alsaedi A. Flow between two stretchable rotating disks with Cattaneo-Christov heat flux model. Results Phys (2017) 7:126–33. doi:10.1016/j.rinp.2016.12.007
45. Khan M, Ahmed J, Ahmad L. Chemically reactive and radiative von Kármán swirling flow due to a rotating disk. Appl Math Mech (2018) 39:1295–310. doi:10.1007/s10483-018-2368-9
46. Hafeez A, Khan M, Ahmed J. Oldroyd-B fluid flow over a rotating disk subject to Soret–Dufour effects and thermophoresis particle deposition. Proc IME C J Mech Eng Sci (2020) 24. doi:10.1177/0954406220946075
47. Liao SJ. The proposed homotopy analysis technique for the solution of nonlinear problems. [PhD thesis]. Shanghai (China): Shanghai Jiao Tong University (1992).
48. Liao S-J. An explicit, totally analytic approximate solution for Blasius’ viscous flow problems. Int J Non Lin Mech (1999) 34:759–78. doi:10.1016/s0020-7462(98)00056-0
49. Shah Z, Gul T, Khan AM, Ali I, Islam S, Husain F. Effects of hall current on steady three-dimensional non-Newtonian nanofluid in a rotating frame with Brownian motion and thermophoresis effects. J Eng Technol (2017) 6:e296. doi:10.1115/1.2969753
50. Usman AH, Humphries UW, Kumam P, Shah Z, Thounthong P. Double diffusion non-isothermal thermo-convective flow of couple stress micropolar nanofluid flow in a Hall MHD generator system. IEEE Access (2020) 8:78821–35. doi:10.1109/access.2020.2986021
51. Khan NS, Shah Q, Sohail A, Kumam P, Thounthong P, Bhaumik A, et al. Lorentz forces effects on the interactions of nanoparticles in emerging mechanisms with innovative approach. Symmetry (2020) 12:1700. doi:10.3390/sym12101700
52. Shah Z, Islam S, Gul T, Bonyah E, Altaf Khan M. The electrical MHD and hall current impact on micropolar nanofluid flow between rotating parallel plates. Results Phys (2018) 9:1201–14. doi:10.1016/j.rinp.2018.01.064
53. Usman AH, Shah Z, Humphries UW, Kumam P, Thounthong P. Soret, Dufour, and activation energy effects on double diffusive convective couple stress micropolar nanofluid flow in a Hall MHD generator system. AIP Adv (2020) 10:075010. doi:10.1063/5.0014897
54. Zuhra S, Khan NS, Islam S, Nawaz R. Complexiton solutions for complex KdV equation by optimal homotopy asymptotic method. Filomat (2019) 33:6195–211. doi:10.2298/fil1919195z
55. Khan NS, Zuhra S, Shah Z, Bonyah E, Khan W, Islam S, et al. Hall current and thermophoresis effects on magnetohydrodynamic mixed convective heat and mass transfer thin film flow. J Phys Commun. (2019) 3:035009. doi:10.1088/2399-6528/aaf830
56. Khan NS, Kumam P, Thounthong P. Renewable energy technology for the sustainable development of thermal system with entropy measures. Int J Heat Mass Tran (2019) 145:118713. doi:10.1016/j.ijheatmasstransfer.2019.118713
57. Khan NS, Gul T, Islam S, Khan I, Alqahtani A, Alshomrani A. Magnetohydrodynamic nanoliquid thin film sprayed on a stretching cylinder with heat transfer. Appl Sci (2017) 7:271. doi:10.3390/app7030271
58. Khan NS. Bioconvection in second grade nanofluid flow containing nanoparticles and gyrotactic microorganisms. Braz J Phys (2018) 48:227–41. doi:10.1007/s13538-018-0567-7
59. Khan NS, Gul T, Islam S, Khan W. Thermophoresis and thermal radiation with heat and mass transfer in a magnetohydrodynamic thin film second-grade fluid of variable properties past a stretching sheet. Eur Phys J Plus (2017) 132:11. doi:10.1140/epjp/i2017-11277-3
60. Palwasha Z, Khan NS, Shah Z, Islam S, Bonyah E. Study of two-dimensional boundary layer thin film fluid flow with variable thermo-physical properties in three dimensions space. AIP Adv (2018) 8:105318. doi:10.1063/1.5053808
61. Khan NS, Gul T, Islam S, Khan A, Shah Z. Brownian motion and thermophoresis effects on MHD mixed convective thin film second-grade nanofluid flow with Hall effect and heat transfer past a stretching sheet. J Nanofluids (2017) 6:812–29. doi:10.1166/jon.2017.1383
62. Khan NS, Zuhra S, Shah Z, Bonyah E, Khan W, Islam S. Slip flow of Eyring-Powell nanoliquid film containing graphene nanoparticles. AIP Adv (2019) 8:115302. doi:10.1063/1.5055690
63. Khan NS, Gul T, Kumam P, Shah Z, Islam S, Khan W, et al. Influence of inclined magnetic field on Carreau nanoliquid thin film flow and heat transfer with graphene nanoparticles. Energies (2019) 12:1459. doi:10.3390/en12081459
64. Khan NS. Study of two dimensional boundary layer flow of a thin film second grade fluid with variable thermo-physical properties in three dimensions space. Filomat (2019) 33:5387–405. doi:10.2298/fil1916387k
65. Khan NS, Zuhra S. Boundary layer unsteady flow and heat transfer in a second-grade thin film nanoliquid embedded with graphene nanoparticles past a stretching sheet. Adv Mech Eng (2019) 11:1–11. doi:10.1177/1687814019884428
66. Khan NS, Gul T, Islam S, Khan W, Khan I, Ali L. Thin film flow of a second-grade fluid in a porous medium past a stretching sheet with heat transfer. Alex Eng J (2017) 57:1019–31.
67. Zuhra S, Khan NS, Alam A, Islam S, Khan A. Buoyancy effects on nanoliquids film flow through a porous medium with gyrotactic microorganisms and cubic autocatalysis chemical reaction. Adv Mech Eng (2020) 12:1–17. doi:10.1177/1687814019897510
68. Zuhra S, Khan NS, Khan MA, Islam S, Khan W, Bonyah E. Flow and heat transfer in water based liquid film fluids dispensed with graphene nanoparticles. Results Phys (2018) 8:1143–57. doi:10.1016/j.rinp.2018.01.032
69. Liaqat A, Asifa T, Ali R, Islam S, Gul T, Kumam P, et al. A new analytical approach for the research of thin-film flow of magneto hydrodynamic fluid in the presence of thermal conductivity and variable viscosityZAMM J Appl Math Mech (2020):1–13. doi:10.1002/zamm.201900292
70. Liaqat A, Khan NS, Ali R, Islam S, Kumam P, Thounthong P. Novel insights through the computational techniques in unsteady MHD second grade fluid dynamics with oscillatory boundary conditions. Heat Transf (2020) 1–23. doi:10.1002/htj.21989
71. Khan NS, Liaqat A, Ali R, Kumam P, Thounthong P. A novel algorithm for the computation of systems containing different types of integral and integro-differential equations. Heat Transf (2020) 1–14. doi:10.1002/htj.22018
72. Khan NS, Kumam P, Thounthong P. Computational approach to dynamic systems through similarity measure and homotopy analysis method for the renewable energy. Crystals (2020) 1–25. doi:10.3390/cryst10121086
73. Khan NS, Gul T, Khan MA, Bonyah E, Islam S. Mixed convection in gravity-driven thin film non-Newtonian nanofluids flow with gyrotactic microorganisms. Results Phys (2017) 7:4033–49. doi:10.1016/j.rinp.2017.10.017
Keywords: nanofluid, nanofluid (Buongiorno model), heat transfer, gyrotactic microorganism, rotating/stretching surface
Citation: Usman AH, Khan NS, Humphries UW, Shah Z, Kumam P, Khan W, Khan A, Rano SA and Ullah Z (2021) Development of Dynamic Model and Analytical Analysis for the Diffusion of Different Species in Non-Newtonian Nanofluid Swirling Flow. Front. Phys. 8:616790. doi: 10.3389/fphy.2020.616790
Received: 13 October 2020; Accepted: 23 December 2020;
Published: 22 February 2021.
Edited by:
Antonio F. Miguel, University of Evora, PortugalReviewed by:
Latif Ahmad, Shaheed Benazir Bhutto University, PakistanEda Aydin, Ontario Tech University, Canada
Jawad Ahmed, University of Engineering and Technology, Pakistan
Copyright © 2021 Usman, Khan, Humphries, Shah, Kumam, Khan, Khan, Rano and Ullah. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Usa Wannasingha Humphries, dXNhLndhbkBrbXV0dC5hYy50aA==; Noor Saeed Khan, bm9vcnNhZWVka2hhbmtoYXR0YWtAZ21haWwuY29t; Poom Kumam, cG9vbS5rdW1Aa211dHQuYWMudGg=
 Auwalu Hamisu Usman
Auwalu Hamisu Usman Noor Saeed Khan
Noor Saeed Khan Usa Wannasingha Humphries1*
Usa Wannasingha Humphries1*