Spreading Kinetics of Herschel-Bulkley Fluids Over Solid Substrates

The spreading kinetics of Herschel-Bulkley fluids on horizontal solid substrates were theoretically studied. The equations of film thickness were derived in both gravitational and capillary regimes. The dynamic contact angle for the capillary regime was also derived. Finally, a limiting result for the case of τ₀ = 0 was obtained, which was compared with the known solution for validation. The results show that the yield behavior of the fluids had a significant impact on the spreading kinetics in both cases. Only when stress was larger than the yield stress, would substantial flow occur. The spreading zone was divided into two parts by the yield surface: sheared zone and yield zone, which was completely different from common Newtonian fluids or power-law fluids. The thickness of the yield zone mainly depended on yield stress and pressure gradient along the z-direction. According to the final evolution, both the film thickness and dynamic contact angle were affected not only by the power-law index but also by the yield behavior.

Introduction

Many studies have addressed the spreading of Newtonian and power-law fluids over solid surfaces by experiments, simulations, and theories [1–7]. For Newtonian fluids, Tanner law is considered to be the classic theory [3]. For power-law fluids, Starov built a hydrodynamic model for the spreading of a complete wetting case [4]. Wang experimentally investigated both complete wetting and partial wetting cases of spreading, which agreed with the theory proposed by Starov [5-6]. Carré and Eustach proposed a simplified theoretical analysis and experimentally observed the drop shape [7].

Besides power-law fluids, Bingham and Herschel-Bulkley fluids also belong to the common non-Newtonian type, which present yielding behavior. For Bingham fluids, the spreading dynamics both in impact and spin-coating cases have been analyzed in detail. In the impact case, the results indicated that the film shape mainly depends on initial yield stress, power-law index, and the impact force [8–13]. In the spin-coating case, the analysis showed that film thickness is not homogeneous, the yield behavior, power-law index, and the centrifugal force are the key factors on spreading dynamics [14–17].

Because of the complex rheological model of Herschel-Bulkley fluids, a minority of theories of complete wetting have been proposed. In this paper, we will theoretically analyze the spreading of Heschel–Bulkley fluids in a complete wetting case based on some proper assumptions. We begins with the simple spreading schematic of Newtonian fluids and the Navier–Stokes equation. According to the analytical approach of the spreading of power-law fluids, the film thickness equations are derived in both gravitational and capillary regimes and the dynamic contact angle is also discussed.

Assumptions

To simplify the problem, the following assumptions are made [18, 19]. 1) The spreading process belongs to the complete wetting case. 2) The fluids are incompressible, which will ensure the Navier-Stokes equation is workable. 3) The gas viscosity is ignored. 4) The film is much thinner than the horizontal length, so the flow can be converted into 2D. 5) The Reynolds number is small enough to ignore inertial influence. And 6) complete wetting is applied here to ensure a small contact angle.

Theory

The Constitutive Model of Herschel-Bulkley Fluids

The constitutive model of Herschel-Bulkley fluids is similar to Bingham fluids or power-law fluids. The specific constitutive equation is given as follows:

$\{\begin{array}{l}\tau ={\tau }_0+k{\dot{\gamma }}^n,\left|\tau \right|>{\tau }_0\\ \dot{\gamma }=0,\left|\tau \right|\le {\tau }_0\end{array}(1)$

where τ is shear stress, k is viscosity coefficient,$\dot{\gamma }$is the shear rate, n is the power-law index, and τ₀ is the initial yield stress.

Thin Film Equation

The spreading schematic of the advancing system of Newtonian or power-law fluids is shown in Figure 1. The derivation of the Herschel-Bulkley case was also started in Figure 1. In Figure 1, u is the horizontal velocity of the fluid, which is affected by time t and position x, z. U is the framing moving velocity of the contact line, θ(U) is the dynamic contact angle, and h is the height of film thickness of any position x.

FIGURE 1

FIGURE 1. Spreading flow schematic figure of Newtonian fluids and power-law fluids.

With the proposed assumption (3), the pressure along the z-direction will meet the following equation.

$\frac{\partial p}{\partial z}=-\rho g(2)$

Applying the Young-Laplace equation to the free surface (z = h), there is

$p=p_G+\sigma \left(\frac{1}{R_1}+\frac{1}{R_2}\right)\approx p_G-\sigma \frac{{\partial }^{2}h}{\partial x^2}(3)$

where p_G represents the atmospheric pressure and σ is surface tension.

Integrating Eq. (2) with respect to the boundary condition listed in Eq. (3), the pressure can be further calculated as

$p=\rho g(h-z)+p_G-\sigma \frac{{\partial }^{2}h}{\partial x^2}(4)$

When z = 0, the stress on the horizontal substrate can be obtained from Eq. (4) as

${\tau }_s=p{|}_{z=0}=\rho gh+p_G-\sigma \frac{{\partial }^{2}h}{\partial x^2}(5)$

Consequently, when the initial yield stress τ₀ is larger than τ_s, substantial flow will not occur. Thus the approximate condition for substantial flow is

$\left|{\tau }_{\text{0}}\right|<\rho gh+p_G-\sigma \frac{{\partial }^{2}h}{\partial x^2}(6)$

Substantial flow will be discussed below. Owing to the initial yield stress, there must be a yield surface at z = h₀. Thus the spreading zone will be divided into two zones, the significant shear exists only below the yield surface. The shear rate is zero at or above the yield surface. The viewpoint is consistent with the spreading of Bingham fluids proposed by Liu [20]. Therefore, the actual flow schematic of the advancing systems of Herschel-Bulkley fluids is shown in Figure 2. The dashed line separates the zone into sheared and yield zones respectively. The schematic figure is completely different from the Newtonian or power-law case.

FIGURE 2

FIGURE 2. The actual spreading flow schematic figure of Herschel-Bulkley fluids.

For the Navier–Stokes equation, it can be written as

$\frac{\partial p}{\partial x}=\frac{\partial }{\partial z}\left(\mu \frac{\partial u}{\partial z}\right)(7)$

where p is the pressure and x is the distance of one point from the z-axis. According to Eq. (1), when the stress is larger than the yield initial stress, the viscosity can be expressed as

$\mu =\frac{{\tau }_0}{\left|\partial u/\partial z\right|}+k{\left|\frac{\partial u}{\partial z}\right|}^{n-1}(8)$

Substituting Eq. (8) into Eq. (7), there is

$\frac{\partial p}{\partial x}=\frac{\partial }{\partial z}\left[\left(\frac{{\tau }_0}{\left|\partial u/\partial z\right|}+k{\left|\frac{\partial u}{\partial z}\right|}^{n-1}\right)\frac{\partial u}{\partial z}\right](9)$

Based on the boundary condition of no shear at the yield surface (h(x) = h₀, ∂u/∂z = 0), integrating Eq. (9) with respect to z and the following equation can be acquired.

$\frac{\partial u}{\partial z}=sign\left(-\frac{\partial p}{\partial x}\right){\left[\left|-\frac{1}{k}\frac{\partial p}{\partial x}\right|\left(h_0-z\right)\right]}^{\frac{1}{n}}(10)$

With the boundary condition of no-slip at the solid surface (z = 0, u = 0), the expression of u can be obtained by integrating Eq. (10).

$u=\frac{n}{n+1}{\left(\frac{1}{k}\right)}^{\frac{1}{n}}sign\left(-\frac{\partial p}{\partial x}\right)\cdot {\left|-\frac{\partial p}{\partial x}\right|}^{\frac{1}{n}}\left[{h_0}^{\frac{n+1}{n}}-{\left(h_0-z\right)}^{\frac{n+1}{n}}\right](11)$

Equation (11) shows that the maximum velocity u_p occurs at the yield surface z = h₀ that can be obtained as

$u_p=\frac{n}{n+1}sign\left(\sigma \frac{{\partial }^{3}h}{\partial x^3}-\rho g\frac{\partial h}{\partial x}\right)\cdot {\left(\frac{1}{k}\right)}^{\frac{1}{n}}{\left(\sigma \frac{{\partial }^{3}h}{\partial x^3}-\rho g\frac{\partial h}{\partial x}\right)}^{\frac{1}{n}}{h_0}^{\frac{n+1}{n}}(12)$

When z > h₀, the velocity is still equal to the maximum velocity u_p. According to mass conservation, there is

$\frac{\partial h}{\partial t}+\frac{\partial q}{\partial x}=0(13)$

where q is the flow of fluids.

For Herschel-Bulkley fluids, q is made up of two parts as

$q={\displaystyle {\int }_0^{h_0}udz}+u_p(h-h_0)(14)$

The first term of the right side represents the shear zone below the yield surface and its detailed expression is

${\displaystyle {\int }_0^{h_0}udz}=\frac{n}{2n+1}\mathrm{sign}\left(\sigma \frac{{\partial }^{3}h}{\partial x^3}-\rho g\frac{\partial h}{\partial x}\right){\left(\frac{1}{k}\right)}^{\frac{1}{n}}{\left(\sigma \frac{{\partial }^{3}h}{\partial x^3}-\rho g\frac{\partial h}{\partial x}\right)}^{\frac{1}{n}}{h_0}^{\frac{2n+1}{n}}(15)$

Then the flow q will be acquired as follows:

$\begin{array}{l}q=\frac{n}{2n+1}\mathrm{sign}\left(\sigma \frac{{\partial }^{3}h}{\partial x^3}-\rho g\frac{\partial h}{\partial x}\right){\left(\frac{1}{k}\right)}^{\frac{1}{n}}{\left(\sigma \frac{{\partial }^{3}h}{\partial x^3}-\rho g\frac{\partial h}{\partial x}\right)}^{\frac{1}{n}}{h_0}^{\frac{2n+1}{n}}\\ +\frac{n}{n+1}\mathrm{sign}\left(\sigma \frac{{\partial }^{3}h}{\partial x^3}-\rho g\frac{\partial h}{\partial x}\right){\left(\frac{1}{k}\right)}^{\frac{1}{n}}{\left(\sigma \frac{{\partial }^{3}h}{\partial x^3}-\rho g\frac{\partial h}{\partial x}\right)}^{\frac{1}{n}}{h_0}^{\frac{n+1}{n}}\left(h-h_0\right)\end{array}(16)$

In Fig. 2, the velocity along the x-direction is parabolic, which can also be explained by Eqs. (11)–(12). When it refers to the velocity, the case here is similar to classical Poiseuille flow. Both of them are driven by the pressure gradient, and they have the same initial and boundary conditions, thus the relationship between h and h₀ can be obtained based on our previous work [21–22] as

$h_0=h-\frac{{\tau }_0}{\left|\partial p/\partial z\right|}=h-\frac{{\tau }_0}{\rho g}(17)$

Substituting Eq. (17) into Eq. (16), a new formula of flow q is generated as

$\begin{array}{l}q=\frac{n}{2n+1}\mathrm{sign}\left(\sigma \frac{{\partial }^{3}h}{\partial x^3}-\rho g\frac{\partial h}{\partial x}\right){\left(\frac{1}{k}\right)}^{\frac{1}{n}}{\left(\sigma \frac{{\partial }^{3}h}{\partial x^3}-\rho g\frac{\partial h}{\partial x}\right)}^{\frac{1}{n}}{h_0}^{\frac{2n+1}{n}}\\ +\frac{n}{n+1}\mathrm{sign}\left(\sigma \frac{{\partial }^{3}h}{\partial x^3}-\rho g\frac{\partial h}{\partial x}\right){\left(\frac{1}{k}\right)}^{\frac{1}{n}}{\left(\sigma \frac{{\partial }^{3}h}{\partial x^3}-\rho g\frac{\partial h}{\partial x}\right)}^{\frac{1}{n}}{h_0}^{\frac{n+1}{n}}\frac{{\tau }_0}{\rho g}\end{array}(18)$

Finally, substituting Eq. (18) into Eq. (13), the following equation is obtained as

$\begin{array}{l}\frac{\partial h}{\partial t}+\frac{n}{2n+1}\mathrm{sign}\left(\sigma \frac{{\partial }^{3}h}{\partial x^3}-\rho g\frac{\partial h}{\partial x}\right){\left(\frac{1}{k}\right)}^{\frac{1}{n}}\frac{\partial }{\partial x}\left[{\left|\sigma \frac{{\partial }^{3}h}{\partial x^3}-\rho g\frac{\partial h}{\partial x}\right|}^{\frac{1}{n}}{h_0}^{\frac{2n+1}{n}}\right]\\ +\frac{n}{n+1}\mathrm{sign}\left(\sigma \frac{{\partial }^{3}h}{\partial x^3}-\rho g\frac{\partial h}{\partial x}\right){\left(\frac{1}{k}\right)}^{\frac{1}{n}}\frac{\partial }{\partial x}\left[{\left|\sigma \frac{{\partial }^{3}h}{\partial x^3}-\rho g\frac{\partial h}{\partial x}\right|}^{\frac{1}{n}}{h_0}^{\frac{n+1}{n}}\frac{{\tau }_0}{\rho g}\right]=0\end{array}(19)$

According to Eq. (16), the pressure mainly depends on the gravity and capillary forces. In the following part, two limiting regimes will be considered further. One is only the gravitational regime taken into consideration by ignoring the capillary force, ρgR²>>σ. The other is only the capillary force regime considered, ignoring the gravity, σ>>ρgR².

Gravitational Spreading Regime

The capillary force is ignored here, so Eq. (19) can be simplified into the following equation.

$\frac{\partial h}{\partial t}+\mathrm{sign}\left(-\rho g\frac{\partial h}{\partial x}\right){\left(\frac{\rho g}{k}\right)}^{\frac{1}{n}}\frac{\partial }{\partial x}\left[{\left|-\frac{\partial h}{\partial x}\right|}^{\frac{1}{n}}{h_0}^{\frac{n+1}{n}}\left(\frac{n}{2n+1}{h}_0+\frac{n}{n+1}\frac{{\tau }_0}{\rho g}\right)\right]=0(20)$

When the contact line moves at velocity U, the above equation can be converted into the following form by introducing a new variable $\xi =x-Ut$.

$-U\frac{d{h}_0}{d\xi }+{\left(\frac{\rho g}{k}\right)}^{\frac{1}{n}}\frac{d}{d\xi }\left[{\left(\frac{d{h}_0}{d\xi }\right)}^{\frac{1}{n}}{h_0}^{\frac{n+1}{n}}\left(\frac{n}{2n+1}{h}_0+\frac{n}{n+1}\frac{{\tau }_0}{\rho g}\right)\right]=0(21)$

Integrating the above equation with respect to ξ, there is

$U^n={\left(\frac{n}{2n+1}\right)}^n\frac{\rho g}{k}\frac{d{h}_0}{d\xi }{h}_0{\left(h_0+\frac{2n+1}{n+1}\frac{{\tau }_0}{\rho g}\right)}^n(22)$

With the boundary condition: ξ = 0, h = 0, Eq. (22) can be solved as

$\frac{1}{n+2}\left[{\left(h+\frac{n}{n+1}\frac{{\tau }_0}{\rho g}\right)}^{n+2}-{\left(\frac{n}{n+1}\frac{{\tau }_0}{\rho g}\right)}^{n+2}\right]-\frac{2n+1}{{\left(n+1\right)}^2}\cdot \frac{{\tau }_0}{\rho g}\left[{\left(h+\frac{n}{n+1}\frac{{\tau }_0}{\rho g}\right)}^{n+1}-{\left(\frac{n}{n+1}\frac{{\tau }_0}{\rho g}\right)}^{n+1}\right]={\left(U\frac{2n+1}{n}\right)}^n\frac{k}{\rho g}\xi (23)$

Equation (23) addresses the fact that film thickness in capillary spreading is determined by initial yield stress τ₀ and power index n.

Capillary Spreading Regime

In the condition, the gravitational action is ignored, then Eq. (19) can be simplified as follows

$\frac{\partial h}{\partial t}+\mathrm{sign}\left(\sigma \frac{{\partial }^{3}h}{\partial x^3}\right){\left(\frac{1}{k}\right)}^{\frac{1}{n}}\frac{\partial }{\partial x}\left\{{\left(\sigma \frac{{\partial }^{3}h}{\partial x^3}\right)}^{\frac{1}{n}}{h_0}^{\frac{n+1}{n}}\left[\frac{n}{2n+1}{h}_0+\frac{n}{n+1}\frac{{\tau }_0}{\rho g}\right]\right\}=0(24)$

Introducing the above variable ξ and h₀ into Eq. (24),

$-U\frac{d{h}_0}{d\xi }+\mathrm{sign}\left(\sigma \frac{d^3{h}_0}{d{\xi }^3}\right){\left(\frac{1}{k}\right)}^{\frac{1}{n}}\frac{d}{d\xi }\left\{{\left(\sigma \frac{{\partial }^3{h}_0}{\partial {\xi }^3}\right)}^{\frac{1}{n}}{h_0}^{\frac{n+1}{n}}\left[\frac{n}{2n+1}{h}_0+\frac{n}{n+1}\frac{{\tau }_0}{\rho g}\right]\right\}=0(25)$

Integrating the above equation with respect to ξ,

$-U+\frac{n}{2n+1}{\left(\frac{1}{k}\right)}^{\frac{1}{n}}{\left(\sigma \frac{d^3{h}_0}{d{\xi }^3}\right)}^{\frac{1}{n}}{h_0}^{\frac{1}{n}}\left[h_0+\frac{2n+1}{n+1}\frac{{\tau }_0}{\rho g}\right]=0(26)$

Then it is supposed that $\frac{{\tau }_0}{\rho g}=\lambda h_0$, so Eq. (26) can be translated into

$U^n={\left[\frac{n}{2n+1}\cdot \frac{\left(2\lambda +1\right)n+\left(\lambda +1\right)}{n+1}\right]}^n\frac{\sigma }{k}\frac{d^3{h}_0}{d{\xi }^3}{h_0}^{n+1}(27)$

With the boundary condition: ξ = 0, h = 0, Eq. (27) can be solved as

${h_0}^{n+2}=\frac{k}{\sigma }{\left[U\frac{\left(2n+1\right)\left(n+1\right)}{n\left(n\left(2\lambda +1\right)+\left(\lambda +1\right)\right)}\right]}^n\left[\frac{{\left(n+2\right)}^3}{3\left(2n+1\right)\left|n-1\right|}\right]{\xi }^3\left(n\ne 1\right)(28)$

Further, the film thickness equation can be obtained by replacing h_0,

${\left(h-\frac{{\tau }_0}{\rho g}\right)}^{n+2}=\frac{k}{\sigma }{\left[U\frac{\left(2n+1\right)\left(n+1\right)}{n\left(n\left(2\lambda +1\right)+\left(\lambda +1\right)\right)}\right]}^n\left[\frac{{\left(n+2\right)}^3}{3\left(2n+1\right)\left|n-1\right|}\right]{\xi }^3\left(n\ne 1\right)(29)$

Based on Eq. (17), the variable λ can be calculated as

$\lambda =\frac{{\tau }_0/\rho g}{h-{\tau }_0/\rho g}(30)$

In this way, the equation of film thickness h can be obtained, which depends on the power index n and initial yield stress τ₀.

Dynamic Contact Angle

The inclination angle at x = ξ can be calculated by differentiating film thickness h as shown in Eq. (29) for the capillary spreading regime.

$\tan \theta =\frac{dh}{d\xi }=\frac{\frac{k}{\sigma }{U}^n\left[\frac{{\left(n+2\right)}^3}{\left(2n+1\right)\left|n-1\right|}\right]}{\left(h-{\tau }_0/\rho g\right){\left[\frac{n\left(n+1\right)h+n^2{\tau }_0/\rho g}{\left(2n+1\right)\left(n+1\right)}\right]}^{n-1}\left\{\left(n+2\right)\left[\frac{n\left(n+1\right)h+n^2{\tau }_0/\rho g}{\left(2n+1\right)\left(n+1\right)}\right]-\frac{n^2{\tau }_0/\rho g}{n+1}\right\}}{\xi }^2\left(n\ne 1\right)(31)$

In previous studies, many researchers found that the local microscopic contact angle can not be measured directly for boundary conditions. Thus dynamic contact angle θ is taken as the replacement, which is equal to the inclination angle at x = x_m. Furthermore, the dynamic contact angle can be obtained as

$\theta \approx \tan \theta =\frac{\frac{k}{\sigma }{U}^n\left[\frac{{\left(n+2\right)}^3}{\left(2n+1\right)\left|n-1\right|}\right]}{\left(h-{\tau }_0/\rho g\right){\left[\frac{n\left(n+1\right)h+n^2{\tau }_0/\rho g}{\left(2n+1\right)\left(n+1\right)}\right]}^{n-1}\left\{\left(n+2\right)\left[\frac{n\left(n+1\right)h+n^2{\tau }_0/\rho g}{\left(2n+1\right)\left(n+1\right)}\right]-\frac{n^2{\tau }_0/\rho g}{n+1}\right\}}{x_m}^2\left(n\ne 1\right)(32)$

To obtain Eq. (32), it is considered that when the angle θ is small enough, it is approximately equal to sin θ or tan θ.

Example

In a previous study [21, 22], the typical Herschel-Bulkley model was obtained as follows

$\{\begin{array}{l}\tau =3.899+1.103{\dot{\gamma }}^{0.633},{\tau }_0\ge 3.899\\ \dot{\gamma }=0,{\tau }_0<3.899\end{array}(33)$

The rheological figure is shown in Figure 3. The model was taken as an example to explain the spreading results.

FIGURE 3

FIGURE 3. The rheological model of Herschel-Bulkley fluids.

Figure 4 gives the film thickness in the gravitational regime. The area below the dashed line is the sheared zone. In Figure 5, the figure of the contact angle vs. the moving velocity at different film thicknesses is presented. It can be found that a thinner film will lead to a smaller contact angle.

FIGURE 4

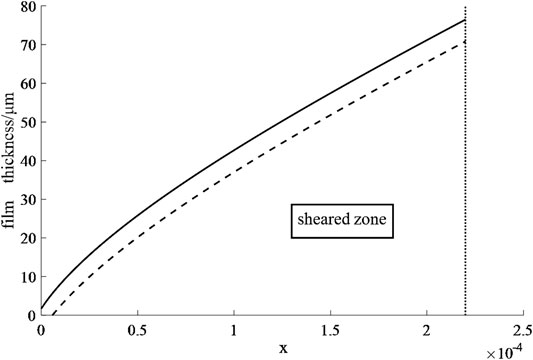
FIGURE 4. The figure of film thickness in gravitational regime (The detailed physical quantities are set as follows: ρ = 1950 kg/m³, n = 0.633, k = 1.103 Pa s^0.633, τ₀ = 3.899 Pa, g = 10 m/s². In Figure 4, U = 2*10⁻⁵ m/s, t = 0.3 s).

FIGURE 5

FIGURE 5. The contact angles at different film thicknesses.

Discussion and Conclusion

The spreading of Herschel-Bulkley fluids over solid substrates for a complete wetting case was theoretically studied here. The film thicknesses in both the gravitational and capillary regimes were derived and the dynamic contact angles were also explored. There was an obvious difference between other kinds of fluids (Newtonian fluids and power-law fluids). The flow was dramatically affected by the yield behavior of Herschel-Bulkley fluids. According to the analysis, only when the stress on the substrate was larger than the initial yield stress τ₀, would the flow be appreciable. Even if appreciable flow occurred, the spreading zone was also divided into two zones: one was the shear zone and the other was the yield zone. The dividing surface was named yield surface at z = h₀, which does not exist in common fluids such as Newtonian fluids or power-law fluids. In “Example” section, the detailed numerical examples are given to explain the results further.

It is noteworthy that when initial yield stress τ₀ = 0, the fluids become power-law fluids. The film thicknesses of the gravitational regime and the capillary regime will be obtained as follows

$h^{n+2}=\left(n+2\right)\frac{k}{\rho g}{\left(U\frac{2n+1}{n}\right)}^n\xi (34)$

$h^{n+2}=\frac{k}{\sigma }{\left[U\frac{2n+1}{n}\right]}^n\left[\frac{{\left(n+2\right)}^3}{3\left(2n+1\right)\left|n-1\right|}\right]{\xi }^3\left(n\ne 1\right)(35)$

Equations (34) and (35) represent the gravitational case and the capillary case, respectively. Also, the dynamic contact angle θ of the capillary regime will be

$\theta \approx \tan \theta =\frac{\frac{k}{\sigma }{U}^n\left[\frac{{\left(n+2\right)}^2}{{\left(2n+1\right)}^{1-2n}\left|n-1\right|}\right]}{\left(n+2\right)n^n{h}^{n+1}}{\xi }^2\left(n\ne 1\right)(36)$

Substituting Eq. (35) into Eq. (36), then the specific equation of the dynamic contact angle can be obtained as

${\theta }^{n+2}=\left(\frac{k}{\sigma }{U}^n\right)\left[\frac{3^{n+1}{\left(n+2\right)}^{1-n}}{{\left(2n+1\right)}^{1-n}\left|n-1\right|n^n}\right]{x_m}^{1-m}\left(n\ne 1\right)(37)$

It can be found that all of them are in agreement with the results obtained by Wang [5]. Another noticeable feature of the analysis is that some of the equations have a collective limitation $n\ne 1$, which means the theoretical results are not applicable for Bingham fluids, although the fluid corresponds to it when n = 1.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

JZ: idea, HG: method, JS: calculation, BL: calculation, JZ: calculation, WW: validation and writing.

Funding

This work was financially supported by the Young and Middle-Aged Scientific Research Backbone Training Project of Nantong Institute of Technology (Grant No. ZQNGG204), the Key University Science Research Project of Jiangsu Province (Grant No. 18KJA460006), the Priority Discipline Construction Program of Jiangsu Province (Grant No. 2016-9), the Top-Notch Academic Programs Project of Jiangsu Higher Education Institutions (Grant No. 2020-9), and the Key R&D plan of Jiangsu Province (Grant No. BE2018010-4).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.609926/full#supplementary-material.

Glossary

Nomenclature Symbols

g Gravitational acceleration
h The height of film thickness at position x
h₀ The film thickness of yield surface
k Viscosity coefficient
n The power-law index
p Pressure
p_G Atmospheric pressure
q Flow of fluids
t Time
u Velocity along the x-direction
u_p Maximum velocity of u
U Frame moving velocity
x/z Values at two directions in the Cartesian coordinate system
$\dot{\gamma }$ Shear rate
θ Dynamic contact angle
λ Variable
ξ Variable, ξ = x-Ut
ρ Density
σ Surface tension
τ Stress
τ₀ Initial yield stress
τ_s Stress on the substrate

References

1. Liang ZP, Wang XD, Lee DJ. Spreading dynamics of power-law fluid droplets. Phys-Condens Mat (2009) 21:3543–9. doi:10.1088/0953-8984/21/46/464117

CrossRef Full Text | Google Scholar

2. Neogi P, Ybarra RM. The absence of a rheological effect on the spreading of small drops. J Chem Phys (2001) 115:7811–3. doi:10.1063/1.1415455

CrossRef Full Text | Google Scholar

3. Tanner LH. The spreading of silicone oil drops on horizontal surfaces. J Phys D Appl Phys (1979) 12:1473. doi:10.1088/0022-3727/12/9/009

CrossRef Full Text | Google Scholar

4. Starov VM, Tyatyushkin AN, Velarde MG. Spreading of non-Newtonian liquids over solid substrates. J Colloid Interface Sci (2003) 257:284–90. doi:10.1016/s0021-9797(02)00034-6

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Zhdanov XD, Lee DJ, Peng XF. Spreading dynamics and dynamic contact angle of non-Newtonian fluids. Langmuir (2007) 23:8042–7. doi:10.1021/la0701125

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Lai XD, Zhang Y, Lee DJ. Spreading of completely wetting or partially wetting power-law fluid on solid surface. Langmuir (2007) 23:9258–62. doi:10.1021/la700232y

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Peng A, Eustache F. Spreading kinetics of shear-thinning fluids in wetting and dewetting modes. Langmuir (2000) 16:2936–41. doi:10.1021/la991021d

CrossRef Full Text | Google Scholar

8. German G, Bertola V. The spreading behaviour of capillary driven yield-stress drops. Colloid Surf Physicochem Eng Aspect (2010) 366:18–26. doi:10.1016/j.colsurfa.2010.05.019

CrossRef Full Text | Google Scholar

9. German G, Bertola V. Impact of shear-thinning and yield-stress drops on solid substrates. J Phys Condens Matter (2009) 21:375111. doi:10.1088/0953-8984/21/37/375111

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Nigen S. Experimental investigation of the impact of an (apparent) yield-stress material. Atomization Sprays (2005) 15:103–18. doi:10.1615/atomizspr.v15.i1.60

CrossRef Full Text | Google Scholar

11. Saïdi A, Martin C, Magnin A. Influence of yield stress on the fluid droplet impact control. J Non-Newtonian Fluid Mech (2010) 165:596–606. doi:10.1016/j.jnnfm.2010.02.020

CrossRef Full Text | Google Scholar

12. Luu L-H, Forterre Y. Drop impact of yield-stress fluids. J Fluid Mech (2009) 632:301–27. doi:10.1017/s0022112009007198

CrossRef Full Text | Google Scholar

13. Kim E, Baek J. Numerical study of the parameters governing the impact dynamics of yield-stress fluid droplets on a solid surface. J Non-Newtonian Fluid Mech (2012) 173–174:62–71. doi:10.1016/j.jnnfm.2012.02.005

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Burgess SL, Wilson SDR. Spin‐coating of a viscoplastic material. Phys Fluids (1996) 8(9):2291–7. doi:10.1063/1.869016

CrossRef Full Text | Google Scholar

15. Jenekhe SA, Schuldt SB. Flow and film thickness of Bingham plastic liquids on a rotating disk. Chem Eng Commun (1985) 33:135–47.

CrossRef Full Text | Google Scholar

16. Tabuteau H, Baudez JC, Chateau X. Flow of a yield stress fluid over a rotating surface. Rheol Acta (2007) 46:341–55. doi:10.1080/00986448508911165

CrossRef Full Text | Google Scholar

17. Tsamopoulos JA, Chen ME, Borkar AV. On the spin coating of viscoplastic fluids. Rheol Acta (1996) 35:597–615. doi:10.1007/bf00396510

CrossRef Full Text | Google Scholar

18. Fermigier M, Jenffer P. An experimental investigation of the dynamic contact angle in liquid–liquid systems. J Colloid Interface Sci (1991) 146:226–41. doi:10.1016/0021-9797(91)90020-9

CrossRef Full Text | Google Scholar

19. Chen J-D, Wada N. Edge profiles and dynamic contact angles of a spreading drop. J Colloid Interface Sci (1992) 148:207–22. doi:10.1016/0021-9797(92)90129-a

CrossRef Full Text | Google Scholar

20. Liu KF, Mei CC. Approximate equations for the slow spreading of a thin sheet of Bingham plastic fluid. Phys Fluids (1998) 2(1):30–6.

Google Scholar

21. Wu W, Huang X, Fang C. An improved MRT-LBM for Herschel-Bulkley fluids with high Reynolds number, Numer Heat Tr B-Fund (2017) 72(6):1–12. doi:10.1080/10407790.2017.1409521

CrossRef Full Text | Google Scholar

22. Wu W, Huang X, Li Y, Fangau C, Jiang X. A modified LBM for non-Newtonian effect of cement paste flow in 3D printing. Rpj (2019) 25(1):22–9. doi:10.1108/rpj-06-2017-0124

CrossRef Full Text | Google Scholar