Polarization Independent Achromatic Meta-Lens Designed for the Terahertz Domain

In recent years, metasurface-based focusing elements have gradually become an indispensable type of terahertz lenses. However, the meta-lens often suffers from chromatic aberration due to the intrinsic dispersion of each element, especially in the broadband application scenarios. In this paper, we design and demonstrate a silicon-based achromatic meta-lens working from 0.6 to 1.0 THz, which is polarization insensitive because of the adopted symmetrical structures. The simulated focal length and the full width at half maximum (FWHM) of the foci at different frequencies prove the achromatic behavior of our meta-lens compared with the chromatic counterpart. We also show that the focus shift incongruence of our design originates from the transmission amplitude distribution of the meta-lens. This article not only provides an achromatic planar lens working at terahertz domain but also reveals the importance of the amplitude distribution in the achromatic metasurface design.

1. Introduction

In recent years, the terahertz frequency domain has ushered in extensive and in-depth development. Various terahertz techniques and systems have been proposed for sensing, imaging, and communication scenarios, showing promising application prospects [1]. In almost all terahertz systems, the lens is an important component that can directly determine the performance of the system [2, 3]. Traditional terahertz lenses manipulate the output wavefront through phase accumulation along the propagation path via thickness variation, which is bound to a bulky size and curved shape, damaging the compactness of the lens. The metasurface, a 2D version metamaterial composed of an array of artificial subwavelength structures with the ability to engineer the phase, amplitude, and polarization features, has provided a new paradigm for the design of terahertz lenses. From the early metal gradient index terahertz lens to the all-dielectric meta-lens, which has attracted wide attention in recent years, metasurface-based focusing elements have gradually become an indispensable type of terahertz lenses. Compared with traditional terahertz lenses, terahertz meta-lenses composed of graphene [4, 5], silicon [6, 7], metals, etc. [8–14] can control the amplitude and/or phase distributions of the terahertz wavefront at quite a high freedom level to achieve novel focusing functions [15, 16]. Moreover, most meta-lenses have a planar shape and wavelength order thickness with potential outstanding integration capability.

However, compared with the silicon-based traditional terahertz lens, the meta-lens still faces the challenge of large chromatic aberration introduced by the mode dispersion of each meta-atom. For example, as the most mature terahertz technology, the time-domain spectroscopy uses a broadband terahertz pulse to analyze the spectrum of various materials, which has an natural demand for achromatic lenses. Recently in the visible domain, a huge line of meta-lens research has been dedicated to achieving the dispersion engineering. For instance, Khorasaninejad et al. [17] carried out a series of scientific researches on the achromatic meta-lens with a reflection mode. Chen et al. [18, 19] designed several achromatic meta-lenses with anisotropic nanostructures in the visible domain. Shrestha et al. [20] proposed an achromatic meta-lens working from 1,200 to 1,650 nm. Wang et al. [21, 22] demonstrated an achromatic meta-lens through integrated resonances for imaging. Despite those inspiring advances in the visible light domain, terahertz metasurfaces are critically different from visible light metasurfaces in terms of raw materials and structure design. Only sporadic study of achromatic meta-lenses has been conducted in the terahertz domain; Cheng et al. [23] proposed an achromatic lens based on silicon metasurface with a high aspect ratio. Though the achromatic behavior was demonstrated, the efficiency of their terahertz meta-lens is somehow limited, and the dispersion engineering capability is polarization sensitive due to the adopted geometrical phase modulation method.

In this paper, we propose and investigate a silicon based meta-lens with a focal length of 11 mm and a diameter of 6.4 mm. Etched silicon pillars with 190 µm height are adopted as the unit cells to accumulate the required transmissive phase distribution. By changing the cross section of the pillars, alteration of the linear dispersion slop of each unit cell is achieved, which satisfies the requirement of an achromatic lens. The numerical investigation shows that our meta-lens has an achromatic bandwidth ranging from 0.6 to 1.0 THz that is polarization insensitive due to the $C_4$ symmetry of the cross section geometry. The FWHMs of the foci at different frequencies are smaller than those of the chromatic counterpart. We also analyze the deviation between the simulated focal length and the designed value by the Rayleigh-Sommerfeld integration. This study has provided an effective method for solving the chromatic aberration problem in the terahertz lens design and paved the way for the research on terahertz achromatic devices that require dispersion engineering.

2. Design and Unit Cell Construction

The designed meta-lens is illustrated by Figure 1A. The desired phase distribution of a meta-lens working for a monochromatic wave can be expressed as

$\varphi \left(r,\omega \right)=\frac{-2\pi \omega }{c}\left(\sqrt{r^2+f^2}-\sqrt{r_0^2+f^2}\right)=\frac{-2\pi \omega }{c}L\left(r\right),(1)$

where ω is the wave frequency, c is the speed of light in vacuum, f is the focal length, and r and $r_0$ represent the positions of the unit cell and the reference cell on the meta-lens, respectively. $L\left(r\right)$ represents the required optical path difference to realize a focusing effect. However, for an achromatic meta-lens working in the frequency range $\left[{\omega }_1,{\omega }_2\right]$, $L\left(r\right)$ should also be equivalent at different frequencies because the focal point is fixed at different frequencies. [24]. With ${\omega }_1$ as the minimal frequency in the design process, the required phase distribution for an achromatic meta-lens is

$\varphi \left(r,\omega \right)=\varphi \left(r,{\omega }_1\right)+\text{Δ}\varphi =\frac{-2\pi {\omega }_1}{c}L\left(r\right)+\left[\frac{-2\pi }{c}L\left(r\right)\left(\omega -{\omega }_1\right)\right].(2)$

FIGURE 1

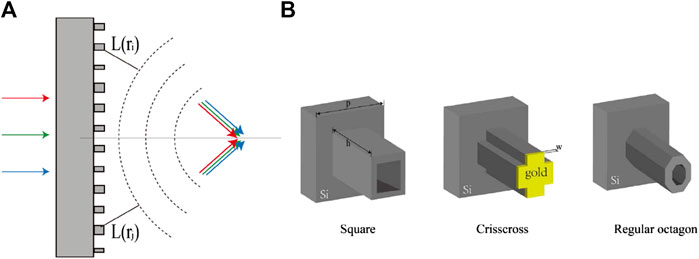
FIGURE 1. (A) The schematics of the achromatic meta-lens. The dashed lines represent the focusing wave front while the colored arrows represent the propagating directions of the terahertz waves at different frequencies. (B) The schematics of the adopted pillar structures with different cross section shapes; the height is 190 µm and the periodicity 130 µm. The yellow layer represents a gold layer of thickness 200 nm.

The unit cells for the achromatic meta-lens are thus expected to have a phase distribution $\varphi \left(r,{\omega }_1\right)$ similar to the chromatic lens designed for a monochromatic wave and a linear dispersed phase whose dispersion slope is determined by $L\left(r\right)$. To ensure the achromatic effect, the phase generated by the unit cells should be proportional to the frequency in the working frequency range.

The first step in the construction of the unit cells is to select the right raw material by using the commercial software CST Microwave Studio^TM and applying the periodic boundary condition with normal incidence wave. In the visible light domain, the substrate and the resonate cavity are often made of different materials in order to utilize the dispersion feature of the Mie scattering of a closed cavity. However, in the terahertz band, due to the ease of the fabrication and the consideration of absorption, dielectric metasurfaces prefer to etch structures directly onto the semi-insulating silicon substrates. As shown in Figure 2A, when both the substrate and the structure are made of silicon, a larger variation range of the phase and dispersion can be obtained by subwavelength pillar structure, compared to the fused silica structure with silicon substrate. Conversely, when the unit cell is made of a silicon pillar with fused silica substrate, its phase and dispersion have nearly the same ranges as the all silicon unit cells’, while the larger absorption and material dispersion of silica may cause problems in the design process.

FIGURE 2

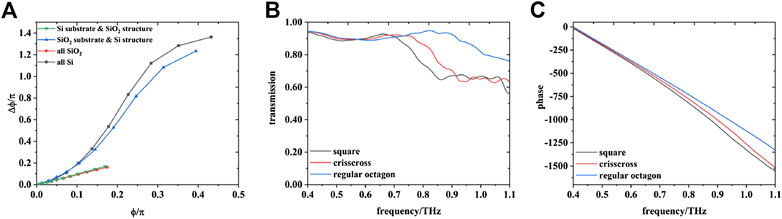
FIGURE 2. (A) The phase-dispersion comparison of unit cells composed of different raw materials. (B,C) The amplitude and phase of the unit cells’ transmission for different cross section shapes, respectively.

Considering the aspect ratio in the dry etching process, we set the height of the silicon pillars as 190 µm, and the fabrication accessibility of our selection is supported by our previous work [25]. The periodicity of the unit cell was set as 130 µm, and our meta-lens has 49 unit cells in total with a diameter of 6.4 mm. A focal length of 13.5 mm and the target frequency ranging from 0.6 to 1.0 THz were determined as well for the followed unit cell construction process. Inspired by the previous work of Shrestha et al [20], we appropriately changed the cross-section geometry of the silicon pillars while retaining the $C_4$ symmetry to hold the polarization-independent characteristics of the structures to engineer the phase and dispersion simultaneously. The specific cross section shapes are presented in Figure 1B, which are square ring, crisscross and hollow regular octagon, respectively. As depicted in Figures 2B,C, the three unit cells have different phases and amplitudes, while the phase has a quasi-linear dispersion and the transmission is relatively high in the target frequency range, indicating the silicon pillar structure proposed here has the capability to realize the desired phase range and liner dispersion. Besides, we found that adding a thin layer of pure gold on the dielectric silicon pillars could further endow the freedom level of the phase control. When the structure size was the same, the phase range of the metal-attached structure was significantly increased (Figure 3A). Hence we adopt this method in the construction of the reference unit cell. Next, by changing the cross section shape and scales in the simulation, we constructed a unit cell base and drew its phase-dispersion library in Figure 3B. We found that for all the investigated unit cells, the phase decreased linearly as the frequency increased from 0.6 to 1.0 THz, and the dispersion slope differs according to the specific cross section shape and geometric parameters. Finally, taking the lens edge as the reference position $r_0$ in the design, we calculated the phase distribution $\varphi \left(r,{\omega }_1\right)$ at ${\omega }_1=0.6THz$ and the dispersion slop $L\left(r\right)$ for each position r. Then, different shapes of unit cells whose phase and dispersion slop satisfy the required $\varphi \left(r,{\omega }_1\right)$ at ${\omega }_1=0.6THz$ as well as the dispersion slop $L\left(r\right)$ were chosen to form the metalens. The whole sketch of our metalens is depicted in Figure 4D. The adopted cross section shape and the geometric parameters are listed in Table 1. It can be seen in Figure 3C that the phase and dispersion of the selected unit cells fit the theoretical design quite well.

FIGURE 3

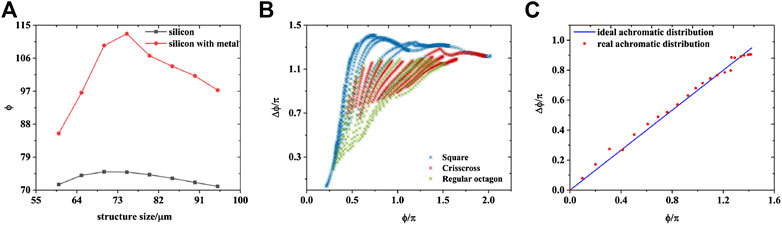
FIGURE 3. (A) The phase change ϕ of the structures as a function of size parameter a. The black line with squares and the red line with circles relate to the pure silicon structure and the corresponding meta-attached structure, respectively. (B) The phase-dispersion library of all the silicon pillars. Points in different colors in the figure represent different type of structures. (C) The phase-dispersion distributions of the achromatic meta-lens. The solid line is the ideal $\varphi -\text{Δ}\varphi$ distribution calculated by Eq. 2 while the red points are the $\varphi -\text{Δ}\varphi$ of the adopted unit cells in the constructed achromatic meta-lens.

FIGURE 4

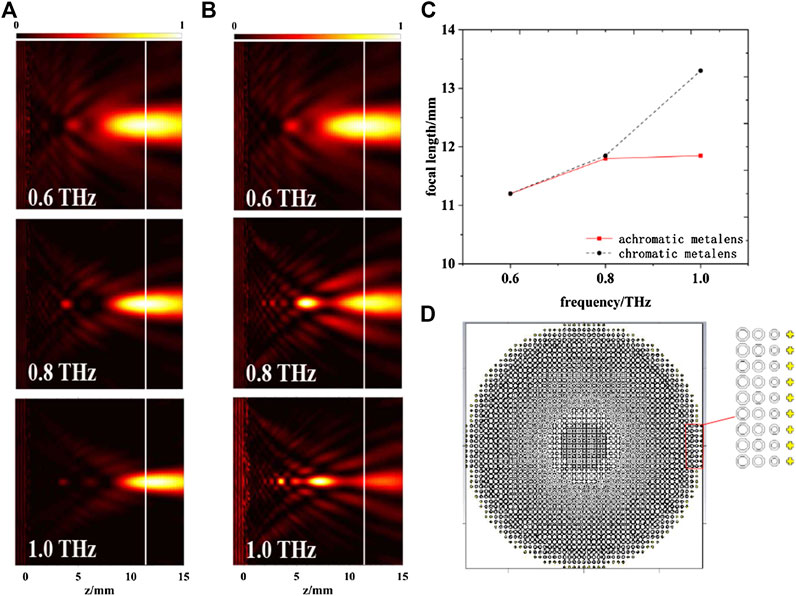
FIGURE 4. The simulated results of the focusing performance of the achromatic meta-lens and the chromatic counterpart. (A) The electric field intensity of the achromatic meta-lens in the $x=0$ plane for the normal incidence at 0.6, 0.8, and 1.0 THz, respectively. (B) The electric field intensity of the chromatic counterpart in the $x=0$ plane for the normal incidence at 0.6, 0.8, and 1.0 THz, respectively. (C) The evolution of the focal length as frequency changes. The red curve represents the focal length evolution of the achromatic meta-lens, and the black curve represents that of the counterpart. (D) The sketch of the achromatic meta-lens. The picture inset enlarges part of the structures used to form the metalens.

TABLE 1

TABLE 1. The parameters of the selected structures and the corresponding position on the meta-lens.

3. Numerical Demonstration and Analysis

The performance of our achromatic meta-lens was also evaluated using the CST Microwave Studio$\text{TM}$. A full meta-lens was constructed by the selected unit cells with the center of the meta-lens set at the origin of the simulation environment, the optical axis of which was set as the z-axis. With the open boundary conditions and a plane wave incidence with linear polarization, we obtained the electric field distributions of the achromatic focusing effects by setting three monitors at 0.6, 0.8, and 1.0 THz, respectively, and the $x=0$ cut of the distributions are shown in Figure 4. To inspect the achromatic feature of our meta-lens, a control meta-lens designed only for 0.6 THz and composed of pure crisscross pillars with other conditions remaining the same was investigated as well. It is quite clear that both the achromatic meta-lens and the control show focusing capabilities. By analyzing the maximal value of the electric field intensity, we verified that the foci of the achromatic meta-lens at 0.6, 0.8 and 1.0 THz lay at z = 11.20, 11.80 and 11.85 mm, respectively, which only has an maximal offset of 650 µm (Figure 4A). In contrast, the foci of the control meta-lens at the corresponding frequencies lay at z = 11.20, 11.80 and 13.30 mm, respectively, which has a much larger focal shifts of 2 mm as Figure 4B showed. Figure 4C depicts the evolution of the focal length as frequencies changes for the achromatic meta-lens and the control. The focal length of the achromatic meta-lens varies less than that of the control. We also found that the maximal electric field intensity point deviated 6 mm from the foci at 0.8 and 1.0 THz. Our achromatic meta-lens design is successful since it demonstrated a clearer focusing behavior and a more stable focal lengths over the whole interested frequency band than the control.

Figure 5A depicts the intensity distributions of our achromatic meta-lens at the focal planes ($z=11.2\text{mm}$) for the monitored frequencies, respectively. It can be seen that the focus spot shows a perfect circle shape and a typical Gaussian intensity distribution. Fringes around the spot are a common phenomenon in diffraction focusing devices caused by the limited unit cell periodicity. The horizontal cuts along the x-axis for the achromatic meta-lens and the control meta-lens are shown in Figures 5B,C. The FWHM of the achromatic meta-lens at 0.6, 0.8 and 1.0 THz are 1.628, 1.277, and 1.063 mm, respectively, yet the FWHM of the control at 0.6, 0.8, and 1.0 THz are 1.621, 1.382 and 1.892 mm, respectively. The evident reduction of the FWHM is a typical feature for achromatic lens, indicating a higher spatial resolution in broadband imaging or microscopy applications which is a well-known advantage of achromatic lens. The polarization dependence of the achromatic meta-lens was manifested by $y=0$ cut of the electric field intensities as shown in Figure 6 It is clear that the distributions of the electric field are almost the same, with only small variances compared with the electric field distribution shown in Figure 5, which confirms the $C_4$ symmetry of each unit cell.

FIGURE 5

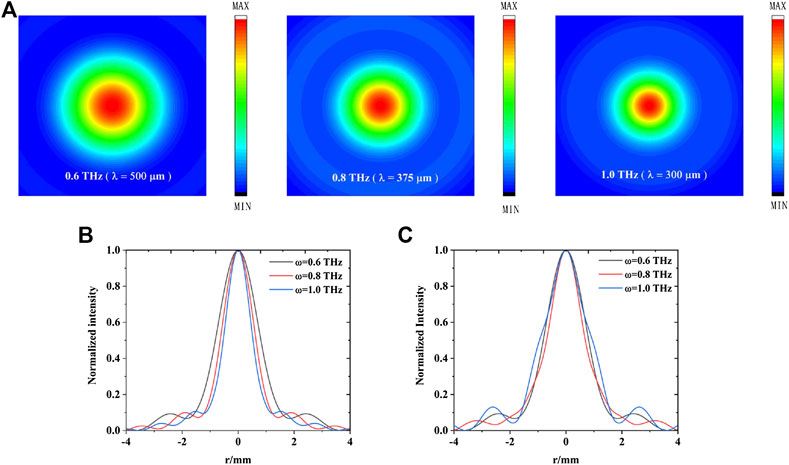
FIGURE 5. (A) The simulated focal spots of the achromatic meta-lens at 0.6, 0.8, and 1.0 THz of the achromatic meta-lens. (B) The horizontal cuts of the focal spots for achromatic meta-lens at 0.6 THz (black), 0.8 THz (red), and 1.0 THz (blue). (C) The horizontal cuts of the focal spots for the chromatic counterpart at 0.6 THz (black), 0.8 THz (red), and 1.0 THz (blue), respectively.

FIGURE 6

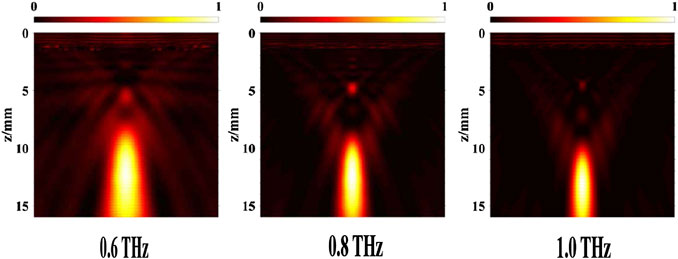
FIGURE 6. The simulated electric field intensity in the $y=0$ plane at 0.6, 0.8, and 1.0 THz, respectively.

4. Discussion

Although the simulation results have verified the feasibility of the designed achromatic meta-lens, the numerically obtained focal length is around 11.2 mm, which deviates 2.3 mm from the designed focal length of 13.5 mm. In addition, the focal lengths at 0.6 and 1.0 THz also differ by 650 µm. We believe this focal shift and the residual chromatic aberration are due to two reasons. The first one is the hexahedral mesh method in the simulation, which divides the space along Cartesian coordinates and will thus cause a calculation error because of the mismatch between the mesh grid and the tilted edge of the octagon pillars. The second reason is that focal shift is a prevalent phenomenon of the lens design [26], and we analyzed it from the perspective of the reversible light path. By assuming a point terahertz source located at $z=13.5\text{mm}$, it is easy to obtain the resulted amplitude and the phase distributions on the meta-lens. Though the phase distribution has been well satisfied in the whole interested bandwidth, the required amplitude variance, which equals $f/r$, was not considered in our numerical investigation. To investigate the influence of this amplitude distribution on the focal shift, we numerically testified an achromatic meta-lens with and without the amplitude distribution by the Rayleigh-Sommerfeld diffraction formula, respectively [27]. As shown in Figure 7, without the $f/r$ amplitude distribution, the calculated focal lengths of the achromatic meta-lens are in accordance with the simulated results, verifying our calculation program. While by adding the right $f/r$ amplitude distribution to the constructed achromatic meta-lens, the foci of this ‘ideal’ achromatic meta-lens at 0.6, 0.8, and 1.0 THz now all move to $z=13.5\text{mm}$, which is highly consistent with our design and shows even smaller chromatic features. This comparison inspires the researchers to pay more attention to the amplitude distribution in the design of achromatic meta-lenses, especially for meta-lenses with a large focal length.

FIGURE 7

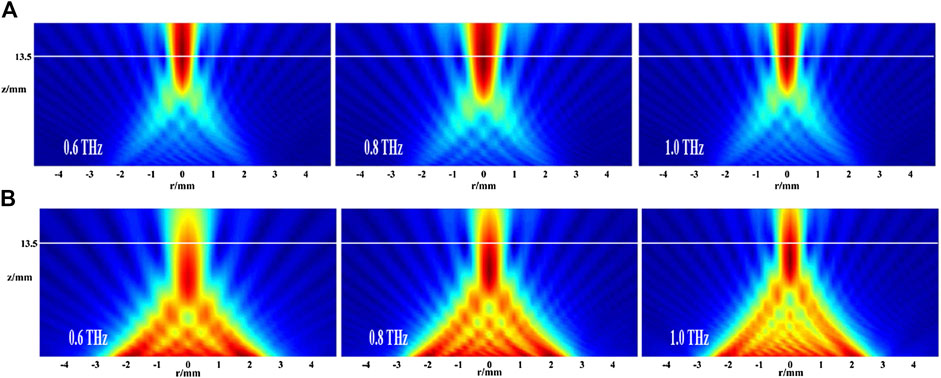
FIGURE 7. (A) The calculated ideal focusing performance of the achromatic meta-lens with the $f/r$ amplitude distribution at 0.6, 0.8, and 1.0 THz, respectively. The white lines mark the designed focal length of 13.5 mm. (B) The focusing performance of the achromatic meta-lens without $f/r$ amplitude distribution at 0.6, 0.8, and 1.0 THz, respectively.

5. Conclusion

In summary, we designed and numerically investigated an achromatic meta-lens composed of subwavelength silicon pillars working at terahertz frequencies. The achromatic behavior of the meta-lens was verified by the numerical simulation, which showed that its focal length changed by 650 µm when frequency ranged from 0.6 to 1.0 THz. The variation of the focal length is merely $5.80\text{\%}$. The FWHM of the achromatic meta-lens foci ranges from 1.063 to 1.628 mm, indicating a higher spatial resolution compared with that of the chromatic counterpart. The incongruence of the focal lengths with the design was well explained by adding the correct amplitude distribution in the Rayleigh-Sommerfeld diffraction calculation. The achromatic meta-lens proposed here not only provides an achromatic planar lens working at terahertz domain but also reveals the importance of the amplitude distribution in achromatic metasurface design.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

YG and JG discussed the design principle. YG and RJ completed the unit cell construction. YG performed the CST simulations, the matlab calculations, and the data analysis. YG wrote the paper, and JG modified the writing. All the authors commented on the paper.

Funding

National Natural Science Foundation of China (61307125, 61420106006, 61422509, 61575141, 61622505, 61975143); the US National Science Foundation (ECCS-1232081).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.606693/full#supplementary-material.

References

1. Zhang XC, Xu J. Introduction to THz wave photonics, Vol. 29. New York, NY: Springer (2010).

Google Scholar

2. Cooper KB, Dengler RJ, Llombart N, Thomas B, Chattopadhyay G, Siegel PH. Thz imaging radar for standoff personnel screening. IEEE Transactions on Terahertz Science and Technology (2011) 1:169–82. doi:10.1109/TTHZ.2011.2159556

CrossRef Full Text | Google Scholar

3. Trichopoulos GC, Mosbacker HL, Burdette D, Sertel K. A broadband focal plane array camera for real-time thz imaging applications. IEEE Trans Antenn Propag (2013) 61:1733–40. doi:10.1109/TAP.2013.2242829

CrossRef Full Text | Google Scholar

4. Liu W, Hu B, Huang Z, Guan H, Li H, Wang X, et al. Graphene-enabled electrically controlled terahertz meta-lens. Photon Res (2018) 6:703–8. doi:10.1364/PRJ.6.000703

CrossRef Full Text | Google Scholar

5. Huang Z, Hu B, Liu W, Liu J, Wang Y. Dynamical tuning of terahertz meta-lens assisted by graphene. JOSA B (2017) 34:1848–54. doi:10.1364/JOSAB.34.001848

CrossRef Full Text | Google Scholar

6. Yu Q, Gu J, Yang Q, Zhang Y, Li Y, Tian Z, et al. All-dielectric meta-lens designed for photoconductive terahertz antennas. IEEE Photonics J (2017) 9:1–9. doi:10.1109/JPHOT.2017.2721503

CrossRef Full Text | Google Scholar

7. Jia D, Tian Y, Ma W, Gong X, Yu J, Zhao G, et al. Transmissive terahertz metalens with full phase control based on a dielectric metasurface. Optic Lett (2017) 42:4494–7. doi:10.1364/OL.42.004494

CrossRef Full Text | Google Scholar

8. Yang Q, Gu J, Wang D, Zhang X, Tian Z, Ouyang C, et al. Efficient flat metasurface lens for terahertz imaging. Optic Express (2014) 22:25931–9. doi:10.1364/OE.22.025931

CrossRef Full Text | Google Scholar

9. Yang Q, Gu J, Xu Y, Zhang X, Li Y, Ouyang C, et al. Broadband and robust metalens with nonlinear phase profiles for efficient terahertz wave control. Advanced Optical Materials (2017) 5:1601084. doi:10.1002/adom.201601084

CrossRef Full Text | Google Scholar

10. Luo J, Yu H, Song M, Zhang Z. Highly efficient wavefront manipulation in terahertz based on plasmonic gradient metasurfaces. Optic Lett (2014) 39:2229–31. doi:10.1364/OL.39.002229

CrossRef Full Text | Google Scholar

11. Hu D, Moreno G, Wang X, He J, Chahadih A, Xie Z, et al. Dispersion characteristic of ultrathin terahertz planar lenses based on metasurface. Optic Commun (2014) 322:164–8. doi:10.1016/j.optcom.2014.02.017

CrossRef Full Text | Google Scholar

12. Hu D, Wang X, Feng S, Ye J, Sun W, Kan Q, et al. Ultrathin terahertz planar elements. Adv Opt Mater (2013) 1:186–91. doi:10.1002/adom.201200044

CrossRef Full Text | Google Scholar

13. Jiang XY, Ye JS, He JW, Wang XK, Hu D, Feng SF, et al. An ultrathin terahertz lens with axial long focal depth based on metasurfaces. Optic Express (2013) 21:30030–8. doi:10.1364/OE.21.030030

CrossRef Full Text | Google Scholar

14. Wang S, Wang X, Kan Q, Ye J, Feng S, Sun W, et al. Spin-selected focusing and imaging based on metasurface lens. Optic Express (2015) 23:26434–41. doi:10.1364/OE.23.026434

CrossRef Full Text | Google Scholar

15. Chang CC, Headland D, Abbott D, Withayachumnankul W, Chen HT. Demonstration of a highly efficient terahertz flat lens employing tri-layer metasurfaces. Opt Lett (2017) 42:1867–70. doi:10.1364/OL.42.001867

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Jiang X, Chen H, Li Z, Yuan H, Cao L, Luo Z, et al. All-dielectric metalens for terahertz wave imaging. Optic Express (2018) 26:14132–42. doi:10.1364/OE.26.014132

CrossRef Full Text | Google Scholar

17. Khorasaninejad M, Shi Z, Zhu AY, Chen WT, Sanjeev V, Zaidi A, et al. Achromatic metalens over 60 nm bandwidth in the visible and metalens with reverse chromatic dispersion. Nano Letters (2017) 17:1819–24. doi:10.1021/acs.nanolett.6b05137

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Chen WT, Zhu AY, Sanjeev V, Khorasaninejad M, Shi Z, Lee E, et al. A broadband achromatic metalens for focusing and imaging in the visible. Nat Nanotechnol (2018) 13:220–6. doi:10.1038/s41565-017-0034-6

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Chen WT, Zhu AY, Sisler J, Bharwani Z, Capasso F. A broadband achromatic polarization-insensitive metalens consisting of anisotropic nanostructures. Nat Commun (2019) 10:1–7. doi:10.1038/s41467-019-08305-y

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Shrestha S, Overvig AC, Lu M, Stein A, Yu N. Broadband achromatic dielectric metalenses. Light Sci Appl (2018) 7:1–11. doi:10.1038/s41377-018-0078-x

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Wang S, Wu PC, Su VC, Lai YC, Chu CH, Chen JW, et al. Broadband achromatic optical metasurface devices. Nat Commun (2017) 8:187. doi:10.1038/s41467-017-00166-7

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Wang S, Wu PC, Su VC, Lai YC, Chen MK, Kuo HY, et al. A broadband achromatic metalens in the visible. Nat Nanotechnol (2018) 13:227–32. doi:10.1038/s41565-017-0052-4

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Cheng Q, Ma M, Yu D, Shen Z, Xie J, Wang J, et al. Broadband achromatic metalens in terahertz regime. Sci Bull (2019) 64:1525–31. doi:10.1016/j.scib.2019.08.004

CrossRef Full Text | Google Scholar

24. Aieta F, Kats M, Genevet P, Capasso F. Applied optics. Multiwavelength achromatic metasurfaces by dispersive phase compensation. Science (2015) 347:1342–5. doi:10.1126/science.aaa2494

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Xu Y, Li Q, Zhang X, Wei M, Xu Q, Wang Q, et al. Spin-decoupled multifunctional metasurface for asymmetric polarization generation. ACS Photonics (2019) 6:2933–41. doi:10.1021/acsphotonics.9b01047

CrossRef Full Text | Google Scholar

26. Li Y, Wolf E. Focal shift in focused truncated Gaussian beams. Optic Commun (1982) 42:151–6. doi:10.1016/0030-4018(82)90128-6

CrossRef Full Text | Google Scholar

27. Lucke RL. Rayleigh–sommerfeld diffraction and Poisson’s spot. Eur J Phys (2006) 27:193–204. doi:10.1088/0143-0807/27/2/002

CrossRef Full Text | Google Scholar