Einstein, Planck and Vera Rubin: Relevant Encounters Between the Cosmological and the Quantum Worlds

In Cosmology and in Fundamental Physics there is a crucial question like: where the elusive substance that we call Dark Matter is hidden in the Universe and what is it made of? that, even after 40 years from the Vera Rubin seminal discovery [1] does not have a proper answer. Actually, the more we have investigated, the more this issue has become strongly entangled with aspects that go beyond the established Quantum Physics, the Standard Model of Elementary particles and the General Relativity and related to processes like the Inflation, the accelerated expansion of the Universe and High Energy Phenomena around compact objects. Even Quantum Gravity and very exotic Dark Matter particle candidates may play a role in framing the Dark Matter mystery that seems to be accomplice of new unknown Physics. Observations and experiments have clearly indicated that the above phenomenon cannot be considered as already theoretically framed, as hoped for decades. The Special Topic to which this review belongs wants to penetrate this newly realized mystery from different angles, including that of a contamination of different fields of Physics apparently unrelated. We show with the works of this ST that this contamination is able to guide us into the required new Physics. This review wants to provide a good number of these “paths or contamination” beyond/among the three worlds above; in most of the cases, the results presented here open a direct link with the multi-scale dark matter phenomenon, enlightening some of its important aspects. Also in the remaining cases, possible interesting contacts emerges. Finally, a very complete and accurate bibliography is provided to help the reader in navigating all these issues.

1 Introduction

The phenomenal roles in investigating the Universe and its content and governing rules, of these three great scientists is without discussion. However, despite that we have today a well organized system of laws of Nature and a formidable set of experimental and observational discoveries, the status of the Universe seems to require that researchers in Observational Cosmology, General Relativity and Quantum Physics concur together and join forces in building new effective paths of knowledge. In fact, it is well known that about 95% of the energy density of the Universe is of dubious invisible nature and cannot be framed within the “presently verified” physics. Moreover, a number of phenomena like e.g., “inflation”, “matter-antimatter asymmetry”, “cosmological and astrophysical quantum relativistic objects”, “ dark matter” just to name a few, are far from being understood and good ideas like “the Unification of Gravity with the other forces” and “the intrinsic Symmetry of the Universe” are also stalling.

In these circumstances, conceptually new directions of investigation have been proposed. The Universe is considered not only as the arena in which theories (e.g., on the Dark Matter) get falsified/verified, but, through the properties of its content, a strong motivator for creation of totally new ones. A contamination among Cosmology, Astrophysics, Relativity, Theoretical Physics, Physics of the Elementary particles theory is taking place in many recent investigations aimed at discovering new Physics. This is the leitmotiv of the Special Topic collection to which this work belongs; we want to contribute to it by providing a review of 17 examples of such new and in some case very different paths of contaminated knowledge.

This review confirms that just the complementary of physical, astrophysical and cosmological probes leads to a successful approach to the (always more required) New Physics and Cosmology. This is done by describing a substantial number of topics of the above kind. Of course this work is not fully complete in reporting such investigations, so as also in exhaustively discussing all the most pressing arguments of Cosmology and Fundamental Physics. About this, let us stress, however, that this review is conceived in relation to the collection of articles of the Special Issue for which it works as the Introductory Paper. In addition, in order to widen the scope of the present work, we indicate to the reader the following reviews on crucial issues of Cosmology and Fundamental Physics which are related to those accurately dealt in the present work: “Cosmology Intertwined: Perspectives for the Next Decade” [2, 3], “Lectures on Black Holes and linear waves” [4], “The distribution of dark matter in galaxies” [5], “Status of dark matter in the Universe” [6], “Testing dark energy models in the light of ${\sigma }_8$ tension” [7]. Finally, a large and accurate list of references will contribute to frame this review within the Cosmological and Fundamental Physics Literature.

2 Cosmography in General Relativity and in Extended Theories of Gravity

The standard cosmological model is also known as $\Lambda$CDM due to the dark components it takes on, i.e $\Lambda$ stands for the cosmological constant while CDM points to the Cold Dark Matter fluid. Such a model provides a successful description of the evolution and the structure of the Universe, requiring just six parameters, but leaves several questions open including the nature of the dark matter and the cosmological constant. Recently, with the improvement of the accuracy of the cosmological observations, tensions between different probes have emerged. Among the most debated at the moment, there is certainly the tension in the Hubble constant measurements, $H_0$ when it is derived at early Universe, $z=1100$, from the CMB measurements and when it is measured at low redshift by exploiting the SNIa distance indicator calibrated by Cepheids. Let us stress that, in the first case, the $H_0$ estimation strictly depends on the model used to describe the CMB data. In particular, the position of the main CMB peak reflects the size of the horizon at last scattering of the CMB photons and is determined almost entirely by the geometry of the Universe. The height of the peak is directly proportional to the fractional mass in baryons ${\Omega }_b$ and also varies according to the expansion rate of the Universe as specified by the Hubble constant $H_0$ [8]. In the latter case it is instead an accurate estimate of the magnitude μ of the SNIa distance indicator calibrated by Cepheids, which implies a series of accurate techniques which also consider the Cepheid period, metallicity and luminosity (see ref. 9 for details). The magnitude is then related to the luminosity distance, $D_L$, via $\mu =5\log D_L+25$, and it is possible to obtain the direct measurement (therefore independent of the model) of $H_0$ from the $D_L$ relationship, eg $D_L=\left(1+z\right)\frac{zc}{H_0}$, that is valid for low redshift.

The tension on H0 mentioned above is quantified in about $4.4\sigma$ between the Planck collaboration estimation [10] $H_0=\left(67.27\pm 0.60\right)$ km/s/Mpc and the SH0ES collaboration measurement [11]) $H_0=\left(74.03\pm 1.42\right)$ km/s/Mpc using the Hubble Space Telescope observations of 70 long-period Cepheids in the Large Magellanic Cloud.

Furthermore, the existence of other mutually discrepant probes with no common observational systematics reinforces the idea that the above tension is systematics-free and due to unknown properties of the actual cosmological scenario [12–14]. As an example, we can cite a joint data analysis of Baryon Acoustic Oscillation (BAO) from BOSS and eBOSS and Big Bang Nucleosyntesis (BBN) [15] that finds $H_0=\left(67.35\pm 0.97\right)$, while SPTpol [13] finds $H_0=\left(71.3\pm 2.1\right)$ km/s/M.

Moreover, standard distance ladder and time delay distances agree with the SH0ES estimate. Finally, the H0LiCOW [16] value $H_0=\left({73.3}_{-1.8}^{+1.7}\right)$ km/s/Mpc, based on strong gravitational lensing effects on quasars favor high values for the Hubble constant as the result of the Maser Cosmology Project [17]: $H_0=\left(73.9\pm 3.0\right)$ km/s/Mpc.

These tensions may indicate an inadequacy in the Standard Cosmological model in providing a correct description of the evolution of the Universe since the last scattering of the Cosmic Background Radiation till recent times.

Extensions of the standard model, i.e. including new physics in the $\Lambda$CDM theory to obtain changes in observational predictions, were explored to solve the $H_0$ tension. Among the proposals, we can mention the inclusion of extra relativistic species at recombination [18–22] and the dynamical interaction between dark matter and dark energy [23–25], as well as the investigation of the cosmological inflationary context [26]. Indeed, all these sectors can modify the value of the current expansion rate of the Universe. For example, in the case of further relativistic species at CMB epoch, it is worth mentioning that the standard cosmological model considers three families of neutrinos as relativistic species at decoupling epoch. Nevertheless, also extra contributions can be considered as, for example, non-standard particle physics like eV-scale sterile neutrinos, Goldstone Bosons, thermal axions and even relativistic dark matter, or also the stochastic background of primordial gravitational waves [27, 28]. These additional free-streaming relativistic particles are often called dark radiation [29]. Intuitively, increasing the number of species increases the contribution of these species in the calculation of background evolution, thus increasing the value of the expansion rate. Despite the efforts spent to cover the shortcomings of the standard model by including new factors, the current conclusion is that such tension cannot be dealt within reasonable physics beyond the standard cosmological model since any resolution of this disagreement produces even greater tensions with other parameters of the model such as ${\Omega }_m$ and ${\sigma }_8$ [30, 31, 32, 33, 160, 161].

The perspectives therefore open up, to explore drastically new theories, as the Extended Theories of Gravitation, or to discover the existence of subtle parameters’ degeneracies plaguing the standard model. Cosmographic studies can give important hints also about the existing cosmological tensions (as those on $H_0$ or ${\sigma }_8$) since they are able to fully describe the expansion of the Universe independently of any a-priori model, and therefore best highlight all the anomalies in the cosmological parameters that have not a priori a known theoretical explanation [34, 35].

The only assumptions cosmography relies on are the homogeneity and isotropy of the Universe. This model-independent technique permits the reconstruction of the dark energy dynamical evolution, with no need of assuming any particular cosmological model at late-time epochs [36, 37] (see Supplementary Appendix A19). Cosmography involves Taylor expansions of the observable quantities that get directly compared with data. The results of this procedure ensure the independence from a postulated equation of state for the Universe’s evolution and, thus, help us to break the above degeneracy. However, this approach is plagued [38] by the divergence of the Taylor polynomials at high redshifts that leads to non-accurate numerical results when data at $z>1$ are used. To alleviate this problem one can use other polynomial expansions like the rational Padé polynomials, which extend the convergence radius of the standard cosmographic series [39], or the Chebyshev polynomials which reduce the systematics on the fitting coefficients and remain stable at high-redshifts [40] (cf. Figure 1).

FIGURE 1

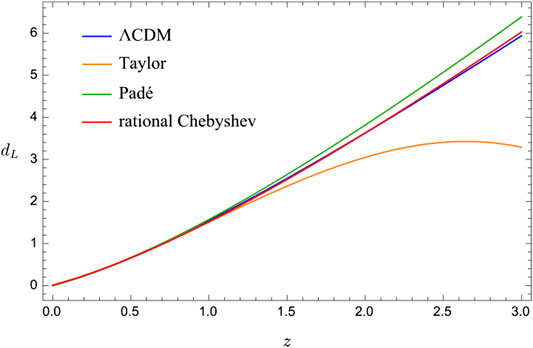
FIGURE 1. Dimensionless luminosity distance curves for the $\text{Λ}$CDM model, the Taylor expansion at fourth-order, the Padé(2,1) and Chebyshev(2,1) rational approximations.

At late times, assuming an arbitrary fiducial value for the current (dark + baryonic) matter density fraction, ${\Omega }_m$, the cosmography can be used to reconstruct the Hubble parameter in function of redshift using low redshift probes, as the Ia Supernovae. An extension of this strategy is to link together the parametric cosmographic behavior of the late Universe expansion with the small scale Universe, i.e. joining such a parametric late time evolution with a cosmological model as the $\text{Λ}$CDM (replacing the intake of dark energy with a cosmographic description of the current expansion of the Universe). In principle, one can obtain a snapshot of the Universe at any epoch. Following this strategy, it is possible to develop a $f\left(z\right)$CDM model, where z is the redshift and the function $f\left(z\right)$ is a suitable combination of polynomials which track the cosmic luminosity distance and replace the cosmological constant $\Lambda$ at any z. This allows one to avoid the assumption of a fiducial value for ${\Omega }_m$, since the latter can be constrained by early Universe data [41].

The background evolution reads as:

$E{\left(z\right)}^2={\left[\frac{H\left(z\right)}{H_0}\right]}^2={\Omega }_r{\left(1+z\right)}^4+{\Omega }_m{\left(1+z\right)}^3+{\Omega }_k{\left(1+z\right)}^2+{\Omega }_{f}f\left(z\right)(1)$

with ${\Omega }_k$ the spatial curvature density, ${\Omega }_r$ the radiation density and ${\Omega }_f$ the density that drives the current accelerated Universe expansion. In the Standard Model the last term reduces to ${\Omega }_{f}f\left(z\right)=\Lambda$. Clearly the class of cosmological models to test (or the given equations of state) can be reconstructed, in principle, starting from $f\left(z\right)$(for details see Section 3 of ref. 41. It is then possible to calculate the predictions of the various cosmological models and to compare them with the data by a Markov chain Monte Carlo process. This approach was applied to a second order Padé polynomials (see Figure 2) in order to analyze data at both small and large scales [41] i.e. by using recent $H\left(z\right)$ measurements from the 1,048 measurements, in the redshift range 0.01−2.3, of the Supernovae Pantheon sample [42], the galaxy clustering (DES sample) that combine galaxy clustering and weak gravitational lensing measurements, using 1,321 square degrees of imaging data [12] and the early Universe data i.e. the Cosmic Background Radiation anisotropies by Planck Collaboration and the Baryonic Acoustic Oscillation measurements [43–46].

FIGURE 2

FIGURE 2. $H\left(z\right)$ evolution expansion of $f\left(z\right)$CDM model, where $j_0=1.97$ and $s_0=l_0=0$ with different values of deceleration parameter: $q_0=-0.5$ (magenta curve), $q_0=-1$ (green curve), $q_0=-1.5$ (red curve). For comparison, the minimal $\text{Λ}$CDM model is also drawn (black solid line) and the Cosmic Clock data are reported (see ref. 41). Moreover, ${\text{Ω}}_m=0.3$, ${\text{Ω}}_{\text{Λ}}=1-{\text{Ω}}_m$, and $H_0=70$ Km/s/Mpc.

A dependence of the ${\Omega }_m$ value with the cosmographic parameters emerges in the analysis of ref. 41, indicating the importance of not fixing this parameter in cosmographic analyses. Furthermore, the authors show an improvement on the parameter constraint using the Cosmic Background Radiation temperature anisotropy power spectrum. Moreover, it has been found that the cosmographic series truncated at third order (i.e., one uses just two cosmographic parameters: the deceleration and the jerk), better describe the current observations with respect to the minimal $\Lambda$-CDM cosmological model, showing a better $\Delta {\chi }^2$ with respect to the minimal standard cosmological model (see ref. 41). This result acquires great significance when one recalls that General Relativity is a second order theory. Indeed, the evidence that the third order is required in cosmography to fully describe the data could be interpreted as that a higher order theory is needed to correctly describe the recent expansion of the Universe. In other words, $\Lambda$CDM may be a coarse-grained model that needs higher-order corrections in order to reproduce in a self-consistent way the existent phenomenology.

Furthermore, it is possible to go beyond General Relativity [47] and the related problems of the (homogeneous and isotropic) $\Lambda$CDM model that includes a cold dark matter (CDM) component and a no-evolving dark energy term with $w=-1$. This model provides the best fit to most of the available cosmological data [10] at present epoch but it is plagued with conceptual and theoretical shortcomings [48]. This state of art may indicate that General Relativity has to be, in some sense, “improved” at cosmological scales [35]. To this purpose one can look to the Extended Theories of Gravity representing a semi-classical approach, in which General Relativity is recovered in the weak energy limit [49]. Within this approach, beside the common metric formalism, one can also apply the Palatini formalism in which the field equations are obtained through the variation of the gravity action with respect to both metric and connection, treated as independent variables. This provides different field equations with respect to those of General Relativity when non-linear terms in the Ricci scalar R, or scalar fields non-minimally coupled to gravity are present [50]. One can adopt a priori the function of the Ricci scalar $f\left(R\right)$ but, in cosmographic context, it is possible to reconstruct the $f\left(R\right)$ function without assuming any specific functional form [51, 52]. The free parameters of the models are therefore obtained by observational data. The results indicate slight departures from the $\Lambda$CDM model, with a time-evolving dark energy term [40].

Therefore, better performing cosmographic series and more precise data at low redshift by future experiments [53–55], will help toward the final goal to reconstruct the actual cosmic history, to test the effectiveness of General Relativity at any redshift and to investigate the DM and DE mysteries. Indeed, cosmography allows us not only to avoid to choose a-priori a particular cosmological model, but also to reconstruct it by an inverse scattering procedure by which it is possible to obtain reliable equations of state.

From the current state of the art of this topic it can be concluded that the standard cosmological model shows significant gaps in describing low redshift data, and this is also confirmed using higher-redshift probes such as quasars, as shown in the following session.

3 Constraining Dark Energy Models at High Redshifts

Over the last decades, observations of high-redshift supernovae of type Ia revealed the current accelerated expansion of the Universe [56–59]. This result has been confirmed by temperature anisotropies of the cosmic microwave background radiation [60, 61], and by many different data. According to the most recent estimates, dark energy provides about 75% of matter-energy content in the Universe.

The nature of dark energy is unknown. Models of dark energy include, the standard one with the cosmological constant having a constant equation of state, w (in this case: $w=-1$), but also one or more of the following: 1) a potential energy of some scalar field [62–64], 2) effects due to a possible inhomogeneous distribution of matter or to errors in averaging procedures 3) the standard GR being substituted by extended theories of gravity where dark energy can be described in terms of scalar non minimally coupled scalar fields ([65, 66] and references therein). Moreover, these scalar fields might be not fundamental and consist of fermion condensates [67]. The effects of these condensates on the expansion of the Universe can be seen in ref. 68. There are also other possibilities for dark energy see refs. 69–72. Interacting dark matter/dark energy models have been recently introduced in different contexts [73–76]. In all these cases, in general, $w\ne -1$ and it is not constant with redshift.

Extracting the information on the effective equation of state $p_{\Lambda }=w{\rho }_{\Lambda }$ of dark energy from observational data is, therefore, at the same time a fundamental problem and a challenging task in Cosmology and Physics: new, independent measurements of the rate of expansion of the Universe, especially in different ranges of redshifts, can provide us with a non-trivial test of the standard cosmological model (see refs. 77 and 78).

Other cosmological probes of distances have entered the game. Ghirlanda et al. (2004), Fermiano et al. (2005) used long GRBs (gamma ray burst) to build up the Hubble diagram up to high redshifts ($z\simeq 9$) [79, 80]. GRBs are sudden bursts of hard X–ray/soft gamma–ray emissions, and can be as short as tens of millisecond and as long as several minutes. They are classified as long GRBs if the pulse lasts more than 2 s, and show a non-thermal spectrum that generally peaks at few hundreds keV. These objects release enormous amounts of energy (the isotropic equivalent radiated energy is of order of ${10}^{52}-{10}^{54}$ erg) and therefore are visible up to very high redshifts being so good candidates as cosmological probes. Their non-thermal spectra can be modeled with the Band function $N\left(E\right)$, a broken power law with the following parameters: the low–energy spectral index α, the high energy spectral index β and the roll–over energy $E_0$:

$N\left(E\right)=\{\begin{array}{cc}A{\left(\frac{E}{100keV}\right)}^{\alpha }\exp \left(\frac{-E}{E_0}\right),& \left(\alpha -\beta \right)\ge 0,\\ A{\left[\frac{\left(\alpha -\beta \right)E}{100keV}\right]}^{\alpha -\beta }\exp \left(\alpha -\beta \right){\left(\frac{E}{100keV}\right)}^{\beta },& \left(\alpha -\beta \right)E_0\le E,\end{array}(2)$

The spectra have a peak in correspondence of the photon energy $E_p=E_0\left(2+\alpha \right)$. For GRBs with measured spectrum and redshift it is possible to evaluate the intrinsic peak energy, $E_{p,i}=E_p\left(1+z\right)$ and the isotropic equivalent radiated energy

$E_{\mathrm{i}\mathrm{s}\mathrm{o}}=4\pi d_L\left(z,\theta \right){\left(1+z\right)}^{-1}{\displaystyle {\int }_{1/\left(1+z\right)}^{{10}^4/\left(1+z\right)}EN\left(E\right)dE}(3)$

It turns out that both $E_{\mathrm{p,i}}$ and $E_{\text{iso}}$ span orders of magnitude and their distributions can be approximated by Gaussians plus a tail at low values of energy. In 2002, for long GRBs the Amati relation was discovered: $E_{\text{p},\text{i}}$ was found strongly correlated with $E_{\text{iso}}$ [81]:

$\log \left[\frac{E_{\text{iso}}}{1\text{erg}}\right]=b+a\log \left[\frac{E_{\text{p},\text{i}}}{300\text{keV}}\right]$

This correlation can be properly calibrated and allows us to standardize the GRBs as a distance indicators in a way similar to that used for the Phillips relation concerning SNeIas ([82] and reference therein). Then, once the correlation between $E_{\text{p},\text{i}}$ and $E_{\text{iso}}$ is calibrated, it is possible to estimate the luminosity distance $d_L\left(z,\theta \right)$ by using Equation 3, and therefore to build up the Gamma Ray Burst Hubble diagram [83–87]. Furthermore, Eisenstein et al. (2005) introduced BAOs as standard rulers [88], Chavez (2016) used HII galaxies [89], and Negrete et al. (2017) used extreme quasars [90]. Recently Risaliti and Lusso [91, 92] found a physical relation between the ultraviolet (at $2500\AA$, $L_{UV}$) and the X-ray (at $2keV$, $L_X$) emissions in quasars. This correlation has an intrinsic dispersion between 0.35 and 0.4 dex. By eliminating quasars with host galaxy contamination, reddening, X-ray obscured objects and radio loudness [91] the dispersion decreases to 0.21–0.24 dex. This correlation provides a way to standardize quasars as distance indicators similar to SNeIa’s.

One investigates the dynamical evolution of dark energy by parametrizing the equation of state,

$w\left(z\right)=\frac{p\left(z\right)}{\rho \left(z\right)}$

assuming some analytical form of w as function of z [83]. Otherwise, we can follow a cosmographic approach relying upon quantities that are not model dependent. In refs. 91 and 92 a tension appears between the $\Lambda$CDM model and a Hubble diagram extended behind the supernovae of type Ia, built up by using a quasar sample with high-quality ultraviolet and X-ray flux measurements. This sample spans a huge range in red-shift, $0.04<z<5.1$. In ref. 93. By adding other 162 Gamma Ray Bursts data, with an even larger range in redshift: $0.03<z<9.3$, the existence of such tension has been reinforced (see Figure 3 in ref. 93). The fitting cosmographic models deviate from the standard $\Lambda$CDM model at $>4\sigma$ by using the high-redshift Hubble diagrams of SNe Ia, quasars and GRBs. Since the diagrams of quasars and GRBs are completely independent, the found tension with the standard model is unlikely to arise from unknown systematic effects and seems to imply new physics. Moreover, such tension is confirmed also in refs. 85 and 86 where the Gamma Ray Burst Hubble diagram was analyzed.

FIGURE 3

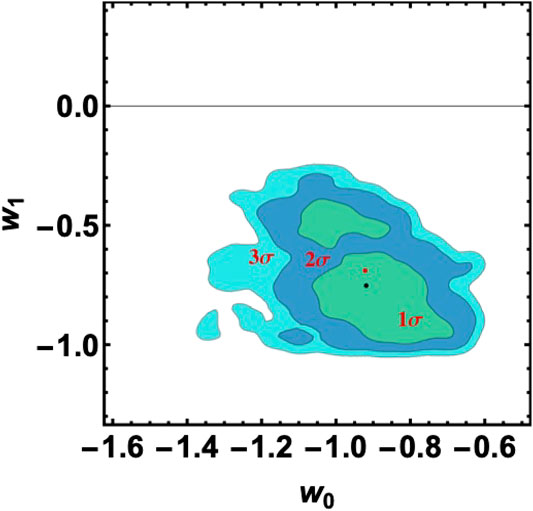
FIGURE 3. 2D confidence regions in the $w_0-w_1$ plane for the CPL model, obtained from our full data set. The red points correspond to the best fit value and the mean, respectively.

These results suggest investigating the $\Lambda$CDM tension by assuming several well known cosmological scenarios with different dark energy equation of state and comparing them by means of the Akaike Information Criterion [94]. These are:

1) a model with an evolving equation of state empirically parametrized, the CPL model [95, 96] see Equation 21 in Supplementary Appendix D.

2) a model where dark energy is due to a self-interacting scalar field, φ, which drives the acceleration. We consider the potential $V\left(\phi \right)\propto \exp \left\{-\sqrt{\frac{3}{2}}\phi \right\}$ [84, 87]. For this model exact solutions of the cosmological equations are known, and are shown in Supplementary Appendix C: it turns out that all basic cosmological functions surprisingly depend on a single parameter, ${\mathrm{\mathscr{H}}}_0$, which is the Hubble constant when we use the age of the Universe as a unit of time.

3) Early dark energy models, where a non-negligible fraction of dark energy exists at early stages of the Universe.

In these models the dark energy density parameter, ${\text{Ω}}_{DE}$, depends on the present matter fraction ${\Omega }_m$ dominated by the dark component, the early dark energy density parameter ${\Omega }_e$, and the present dark energy equation of state parameter $w_0$ [97]. The form of ${\text{Ω}}_{DE}$ and the Hubble function of these models are provided in Supplementary Appendix C by Equations 21, 43. The redshift investigation uses the Supernovae Cosmology Project Union 2.1 compilation, containing 580 SNIa, spanning the redshift range $0.015\le z\le 1.4$, a Gamma Ray Bursts (GRBs) Hubble diagram, consisting of 193 objects, a set of 28 independent measurements of the Hubble parameter, compiled in ref. 98, and several baryon acoustic oscillations (BAO) measurements compiled in ref. 99. The authors obtain the probability distributions of the cosmological parameters for each of the competing models. Their region of confidence is obtained by maximizing the appropriate likelihood functions by using the Monte Carlo Markov chains method.

In Table A1 of Supplementary Appendix A are shown the results of our analysis. In Figure 3 we plot the 2-dim confidence regions in the $w_0-w_1$ plane for the CPL model, obtained from the full data set. The $\Lambda$CDM model corresponds to the case $w_0=-1,w_1=0$, and is out at $>3\sigma$. It is worth noting that this result adds value to that obtained in Section 2 showing that third order cosmographic series describe the currently available cosmological observations better than the standard $\Lambda$CDM cosmological model. To bring out more clearly this result one plots, in Figure 4, the counterpart of the confidence regions in Figure 3 in terms of cosmographic parameters. We actually implemented a standard cosmographic series in the auxiliary variable $y=z/1+z$, which maps the z-range $\left[0,\infty \right]$ into the y-range $\left[\mathrm{0,1}\right]$. It turns out that the value $j_0=1.0$ is ruled out at 3 σ.

FIGURE 4

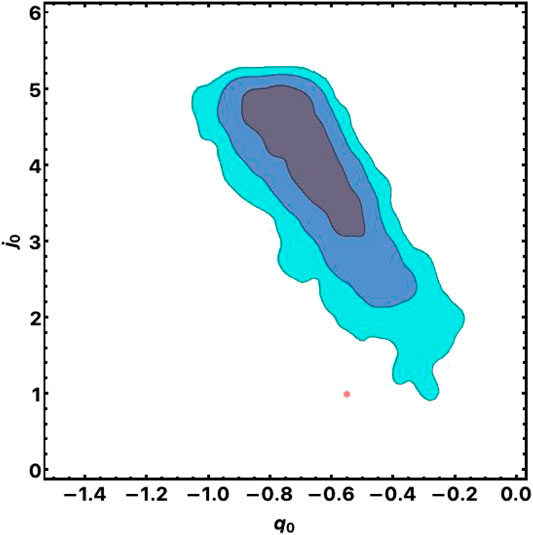
FIGURE 4. 2D confidence regions in the $q_0-j_0$ plane obtained from our full data set. For $\text{Λ}$ CDM we have: $j_0=1$, and $q_0=-1+\frac{3}{2}{\text{Ω}}_m$. The pink point corresponds to ${\text{Ω}}_m=0.3$.

We then apply to the above data the Bayesian Akaike criterion and found that among the three models the evolving dark energy, described by the exponential scalar field potential (EXP), is favored. Let us notice that such evolution of the Dark Energy reverberates also in the Dark Matter component, whose evolution of perturbations with redshift, will now differ from the $\Lambda$CDM case.

Future missions such as the THESEUS observatory for Gamma Ray bursts will substantially increase the number of Gamma Ray bursts in their Hubble diagram, therefore, providing us with the opportunity to confirm these results. Reliable high redshift cosmological probes alongside with the cosmography approach might indicate the actual dark energy model and the correct gravity theory.

4 The Scattering Angle of a Two-Body System

This research issue covers one of the most important topics in classical general relativity today. In fact, the last few years have witnessed the beginning of the era of gravitational-wave astronomy, with the detection of the first signals by the LIGO and Virgo interferometers (see e.g., the web sites https://www.ligo.caltech.edu/and http://www.virgo-gw.eu/). These detectors have the potential to accurately measure the two-body dynamics up to the region where the gravitational interaction is very strong, so that there is now a pressing need to go beyond the post-Newtonian approximation by combining results from different approaches. The Hamiltonian of a two-body system takes information (encoded in several building-block potentials) from any theoretical computation of gauge-invariant quantities. After having studied several orbital invariants like the redshift and the periastron advance, all recent literature is mainly focusing on the scattering angle in hyperbolic-like orbits. This is particularly promising in view of the bridge recently discovered between the classical scattering angle in post-Minkowskian context [100, 101] and the quantum scattering amplitudes for the same problem, computed by a completely different method of high-energy physics. The reached accuracy is now limited to the third post-Minkowskian order [102, 103] and to the local part of the associated Hamiltonian, but the aim is to go beyond this level, including gravitational self-force information and to study the effects related to the non-local (non-trivial) part of the Hamiltonian.

The topics included in this research involve, besides classical GR, also effective field theories and high-energy physics, with a direct superposition with other research interests. More in detail: in the gravitational interaction of a two-body system, i.e., the capture of one body by the other as well as the hyperbolic scattering, two different scenarios must be considered, in view of the detection of the associated gravitational wave signals. While several analytical and semi-analytical methods have been developed so far to study the first situation (“capture”), this is not the case for the second one (“scattering”). A renewed interest in the scattering problem has recently emerged with studies involving post-Newtonian (PN) and post-Minkowskian (PM) expansions of the scattering angle. The latter has been computed within the post-Newtonian theory at the fourth post-Newtonian level of accuracy in ref. 104, including both local and non-local (tail) contributions, whereas the general framework of the post-Minkowskian treatment of the scattering problem has been established in refs. 100and 101. The level-3 post-Minkowskian Hamiltonian, describing the conservative dynamics of a two-body system, has been obtained in refs. 102 and 103, where the two-loop scattering amplitude of the process and the associated scattering angle at third post-Minkowskian level were computed. This result in the high-energy limit can be properly compared with previous results [105]. In an effort to clarify this situation, ref. 106 suggested a novel approach, aiming at improving the current knowledge of the post-Newtonian Hamiltonian of a two-body system. This approach combines various different theoretical formalisms: post-Newtonian, post-Minkowskian, multipolar-post-Minkowskian, gravitational self-force, and effective-one-body [106] has given an independent check of the level-3 post-Minkowskian result, limited at the fifth post-Newtonian level of accuracy, in terms of the scattering angle ${\chi }_3$, i.e.,

$\begin{array}{c}{\chi }_3=-\frac{1}{3p_{\infty }^3}+\frac{4}{p_{\infty }}+\left(-8\nu +24\right)p_{\infty }+\left(-36\nu +\frac{64}{3}+8{\nu }^2\right)p_{\infty }^3\\ +\left(-\frac{91}{5}\nu +34{\nu }^2-8{\nu }^3\right)p_{\infty }^5+\left(\frac{69}{70}\nu +\frac{51}{5}{\nu }^2-32{\nu }^3+8{\nu }^4\right)p_{\infty }^7+o\left(p_{\infty }^7\right)\end{array}(4)$

where the label 3 refers to the third post-Minkowskian level, $\nu =m_1{m}_2/{\left(m_1+m_2\right)}^2$ denotes the symmetric mass ratio of the two bodies and the relation between the momentum at infinity and the (effective) energy of the process is given by $p_{\infty }\equiv \sqrt{{\widehat{\mathrm{ℰ}}}_{\text{eff}}^2-1}$. In the above expression, the last term proportional to $p_{\infty }^7$ is exactly the level-5 post-Newtonian contribution to ${\chi }_3$. In addition, Bini et al. have anticipated the level-5 post-Newtonian-accurate value for the level-4 post-Minkowskian scattering angle ${\chi }_4={\chi }_4^{\text{loc}}+{\chi }_4^{\text{nonloc}}$, with the local contribution ${\chi }_4^{\text{loc}}\left(p_{\infty }\right)$ given in Supplementary Appendix B20, Equation 20.

Finally, the analysis developed in ref. 106 has allowed to identify the local part of the level-5 post-Newtonian Hamiltonian modulo two unknown functions, $a_6^{{\nu }^2}$ and ${\overline{d}}_5^{{\nu }^2}$ that, however, are of the second order in the symmetric mass-ratio of the two bodies, see Supplementary Appendix B20.

Further studies and possible generalizations are currently being considered [107–111], including both the 6PN local and non-local contribution to the scattering angle.

We point out that measuring the scattering angle in a two-body system implies the determination of (gauge-invariant) information about the radiated gravitational wave energy along the full scattering process. Therefore, the analytical modeling for this quantity is important in the analysis of future detections of gravitational wave signals by gravitational wave interferometers. Noticeably, an accurate investigation of the merging of two BHs may yield to a precious test about them being the DM in galaxies.

5 Classical Physics In Curved Spacetime Backgrounds

1) Scalar wave equation and Ermakov-Pinney.

The field equations of classical field theory in curved spacetime, i.e., scalar wave equation, Maxwell equations and Einstein equations, are wave equations with variable coefficients, whose solution is known only in a few cases. Thus, a systematic technique for dealing with such hyperbolic equations may lead to a valuable physical insight.

In the work in ref. 112, the first part of the paper proves that a subset of the Ermakov-Pinney equations can be obtained by differentiation of a first-order non-linear differential equation. The second part of the paper proves that the equation for the amplitude function for the parametrix of the scalar wave equation can be obtained by differentiating covariantly a first-order non-linear equation. The construction of such a first-order non-linear equation relies upon a pair of auxiliary 1-forms $\left(\psi ,\rho \right)$. The 1-form ψ satisfies the vanishing divergence condition $\text{div}\left(\psi \right)=0$, whereas the 1-form ρ fulfills the non-linear equation

$\text{div}\left(\rho \right)+\langle \rho ,\rho \rangle =0$

The auxiliary 1-forms $\left(\psi ,\rho \right)$ are evaluated explicitly in Kasner spacetime. Therefore, amplitude and phase function in the parametrix are obtained. The novel method developed in this paper can be used in studying the electromagnetic field of binary systems in relativistic astrophysics.

The key property to be used is the fact that the technical difficulty of dealing with a coupled set of partial differential equations for the electromagnetic potential can be overcome by exploiting the Hertz potentials, that lead eventually to a linear wave equation for a complex scalar field [113]. The real and imaginary part of such a scalar field are then subject to a linear wave equation, and the original method relying upon two auxiliary 1-forms may come into play.

In ref. 114, the authors have solved the Ermakov-Pinney equation associated to the scalar wave equation in Schwarzschild, de Sitter and gravitational-wave spacetimes. For example, in the Schwarzschild case it is found that a positive coupling constant leads to spatially damped oscillations of the field (see Figure 5), whereas a negative or vanishing one is associated with a blow-up of the solutions.

FIGURE 5

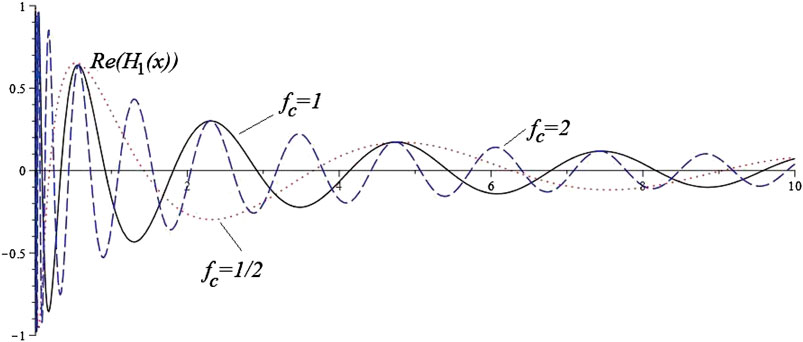
FIGURE 5. Amplitude function for a timelike current in Schwarzschild space-time. The real part of the Heun function $H_1\left(x\right)$ is plotted, which contributes to the amplitude for different values of the coupling constant $f_c=\frac{1}{2},\mathrm{1,2}$. All curves show a spatially damped oscillating behavior with a wavelength qualitatively proportional to the inverse of the coupling constant. The imaginary parts of the amplitude have a similar behavior.

In light of this, and bearing in mind the interest of studying in greater detail the quantization of fields, it seems more important to focus on the case of a positive coupling constant, a topic to be developed in future work. It would also be valuable to understand the relation (if it exists) with the asymptotic behavior of solutions of the scalar wave equation discovered by Schmidt and Stewart [115].

2) Trapped surfaces in general relativity.

After the proof by Christodoulou and Klainerman of the global non-linear stability of Minkowski spacetime [116], Christodoulou decided to apply his optical formalism in order to prove that, in the non-linear equation that describes the formation of trapped surfaces, some terms can be omitted while keeping under control the resulting error, that remains suitably small [117]. More recently, in order to deal with exact equations, without any approximation, in ref. 118 trapped surfaces have been studied instead from the point of view of local isometric embedding into three-dimensional Riemannian manifolds. When a two-surface is embedded into three-dimensional Euclidean space, the problem of finding all surfaces applicable upon it gives rise to a non-linear partial differential equation of the Monge-Ampère type, first discovered by Darboux [119], and later reformulated by Weingarten [120]. Even today, this problem remains very difficult, despite some remarkable results. In ref. 118, the authors have found an original way of generalizing the Darboux technique, which leads to a coupled set of six non-linear partial differential equations. For the 3-manifolds occurring in Friedmann-(Lemaitre)-Robertson-Walker cosmologies, they have shown that the local isometric embedding of trapped surfaces into such cosmologies can be proved by solving just one non-linear equation. Such an equation has been solved for the Friedmann models associated with positive, zero, negative curvature of the spatial sections, respectively. However, the task of solving such a non-linear equation in the most general case remains extremely difficult, and deserves a substantial effort, because there is a proliferation of terms in the non-linear equation, without any simplifying ansatz.

6 General Relativity as the Bridge Between Classical and Quantum Worlds

Motivated by recent efforts to apply the asymptotic symmetry group of asymptotically flat space-times to the investigation of black holes’ soft hair [121], in ref. 122 the authors remark that half of the Bondi-Metzner-Sachs (BMS) transformations are made of orientation-preserving homeomorphisms of the extended complex plane known as fractional linear (or Möbius) transformations. These can be of four kinds, i.e., they are parabolic, or hyperbolic, or elliptic, or loxodromic, depending on the number of fixed points and on the value of the trace of the associated $2\times 2$ matrix in the projective version of the $SL\left(2,\mathbf{C}\right)$ group. The resulting particular forms of $SL\left(2,\mathbf{C}\right)$ matrices affect also the other half of BMS transformations. They have been used in ref. 122 to propose four realizations of the asymptotic symmetry group that are called, again, parabolic, or hyperbolic, or elliptic, or loxodromic.

Moreover, it has been proved that a particular subset of hyperbolic and loxodromic transformations, i.e., those that have a trace that approaches $\infty$, correspond to the fulfillment of limit-point condition for singular Sturm-Liouville problems. Thus, a very deep link might exist between the language for describing asymptotically flat spacetimes and the world of complex analysis and self-adjoint problems in ordinary quantum mechanics. In other words, we are suggesting that General Relativity plays the role of gateway that establishes a correspondence between classical and quantum world. Such a viewpoint is of particular interest for the theoretical analysis of fundamental interactions.

So far, relativists have never considered the possibility of defining the concept of boundary in a measure-theoretic way. On the other hand, in a branch of mathematics known as geometric measure theory, the usefulness has been discovered long ago of yet another concept, i.e. the reduced boundary of a finite-perimeter set. In ref. 123 the authors have proposed therefore a definition of finite-perimeter sets and their reduced boundary in general relativity. Moreover, an integral formula of geometric measure theory has been evaluated explicitly in the relevant case of Euclidean Schwarzschild geometry, for the first time in the literature. This prepares the ground for a measure-theoretic approach to several concepts in gravitational physics, supplemented by geometric insight.

Interestingly, some observational tests of quantum gravity in the weak-gravity regime has become, in principle, conceivable by applying the effective-gravity picture of Donoghue [124]. In particular, within the framework of the Solar System, approximate realizations of the three-body problem occur when a comet approaches a planet; such a configuration was investigated by Tisserand [125] in Newtonian gravity. The exact relativistic treatment of the problem is not easy, but the work in ref. 126 develops an approximate computational scheme which evaluates for the first time the very tiny effective-gravity correction to the equation of the surface for all points of which it is equally legitimate to regard the heliocentric motion as being perturbed by the attraction of Jupiter, or the jovicentric motion as being perturbed by the gravitational attraction of the Sun. In the second part of ref. 126, comet trajectories for effective and Newtonian gravity are obtained and compared in detail. In the years to come, the relativistic analysis of cometary motions will require the inclusion of high orders of the post-Newtonian formalism, a task extremely difficult for three-body systems. This investigation will lead to a better understanding of the occurrence of chaotic behavior in general relativity.

Remarkably, such behavior is very distinct from the eventual effects, in the Solar System, of alternatives to the DM that, on the other hand, can affect the cometary motions at the level of the above high orders.

7 Quantum Field Theory in Curved Space-Time and Neutrino Physics

The search for a merging between General Relativity and Quantum Field Theory is the most demanding task of theoretical physics nowadays. Notwithstanding the zoo of models developed in recent years, the problem of finding a consistent theory of quantum gravity is still open, due to the lack of experimental guidance. Groping in the dark, significant progress is then expected to be achieved via indirect investigation. For instance, in ref. 127 it was argued that quantum gravity may involve foam models endowed with stochastic fluctuations of the space-time background. One of the most sensitive probes of these fluctuations could be neutrinos through decoherence effects on flavor oscillations. Similarly, in ref. 128 neutrinos were selected as best candidates to witness the gravity-induced entanglement between massive systems, being only affected by the weak and gravitational interactions.

On the other hand, in the cosmological framework it has been widely discussed [129–131] the active rôle played by primordial neutrinos in the formation of large-scale structures (LSS) of the Universe and, in particular, in giving a power at a large scale that otherwise could not be explained in the ordinary cold dark matter scenario at the critical density. Due to the considerable impact of neutrinos on the process of structure formation, observations of matter clustering in different epochs of the Universe have then contributed to build a solid bridge between cosmology and neutrino physics. This has also enabled us to put very competitive constraints on characteristic neutrino parameters, such as the neutrino mass sum ${\displaystyle \sum }_i{m}_{{\nu }_i}<0.72eV$ at 95% CL (through measurements of large scale polarization and CMB temperature anisotropies) or ${\displaystyle \sum }_i{m}_{{\nu }_i}<0.14eV$ at 95% CL (including measurements of Lyman-α forests), and the number of relativistic species at recombination $N_{eff}=3.03\pm 0.18$ at 68% CL (exploiting LSS and CMB data). More details can be found in ref. 132 and therein.

In light of the above discussion, it is believed that a deeper study of the fundamental nature of neutrinos could not only improve our knowledge of particle physics beyond the Standard Model, but also provide novel insights into a series of related problems, the most prominent ones being the development of a quantum theory of gravity and the understanding of the formation of the current Universe from small early density fluctuations.

Neutrinos are the most puzzling particles currently known. Although a series of findings have confirmed Pontecorvo’s idea of flavor mixing and oscillations, several questions remain unsolved. Among these, the problem of the very nature of asymptotic states—flavor or mass—is still a vibrant subject of analysis [133–135]. Recently, a challenging test bench has been provided in refs. 136 and 137 within the framework of the weak decay of uniformly accelerated protons (inverse β-decay). The idea that non-inertial protons are allowed to decay if exposed to sufficiently large accelerations traces back to ref. 138. In ref. 139 the inverse β-decay was exhibited as a theoretical proof of Unruh effect [140] for the consistency of QFT in curved space-time. However, in these works neutrinos were simplistically considered as massless. The first successful attempt to embed mixing was made in ref. 137, concluding that the use of the flavor basis is mandatory both to preserve the general covariance of QFT and to account for neutrino oscillations.

Starting from the outlined picture, let us review the rôle of the superposition of neutrino mass states in the inverse β-decay. By employing the S-matrix formalism, the scalar decay rate of accelerated protons is calculated in both the inertial and comoving frames in a two-flavour model (the three-flavour description including CP violation effects is contained in ref. 141). Perspectives and possible experimental implications are then discussed.

Laboratory frame. Concerning an inertial observer, the accelerating source supplies the proton with the missing energy to decay as $\left(i\right)p\to n+e^{+}+{\nu }_e$ (see the diagram (i) in Figure 6). If one assumes the acceleration to be much smaller than the masses of the $Z^0$ and $W^{\pm }$, the weak coupling can be described by a Fermi-like action $S_I$ with a classical (quantum) hadronic (lepton) current [137, 139]. Accordingly, the tree-level transition amplitude reads ${\mathcal{A}}^{\text{lab}}\equiv \langle n|\otimes \langle e^{+},{\nu }_e\left|S_I\right|0\rangle \otimes |p\rangle$. This leads to the following decay rate

${\text{Γ}}^{\left(\text{i}\right)}\equiv \frac{1}{T}{{\displaystyle \int }}^{\text{}}{d}^3{k}_{\nu }{d}^3{k}_e{\displaystyle \sum }_{{\sigma }_e,{\sigma }_{\nu }}|{\mathcal{A}}^{\text{lab}}{|}^2={\text{cos}}^4\theta {\text{Γ}}_1+{\text{sin}}^4\theta {\text{Γ}}_2+{\text{cos}}^2\theta {\text{sin}}^2\theta {\text{Γ}}_{12}(5)$

where the Pontecorvo state $|{\nu }_e\rangle =\cos \theta |{\nu }_1\rangle +\sin \theta |{\nu }_2\rangle$ has been used for the asymptotic neutrino, θ is the mixing angle and $|{\nu }_i\rangle$$\left(i=\mathrm{1,2}\right)$ denote the mass states (the expressions of ${\Gamma }_i$ and ${\Gamma }_{12}$ are given in ref. 137).

FIGURE 6

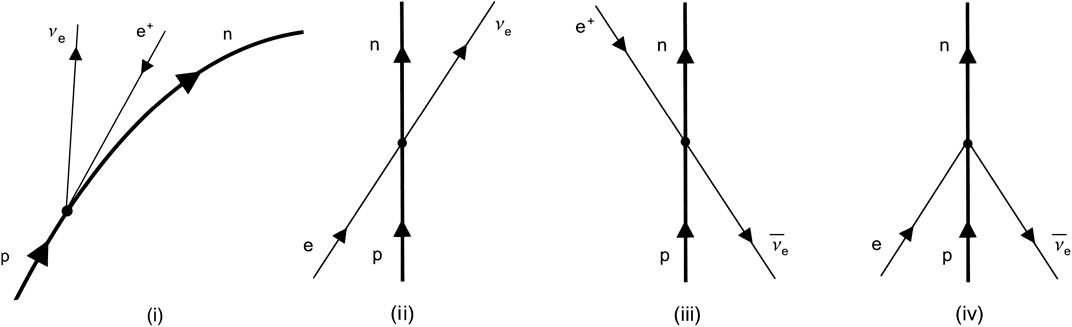
FIGURE 6. Proton decay in the laboratory (i) and comoving (ii, iii, iv) frames (time is on the vertical axis).

Remarkably, in ref. 142 it has been proved that the flavour-violating process $p\to n+e^{+}+{\nu }_{\mu }$ has a non-vanishing probability as well, due to the asymptotic occurrence of neutrino oscillations. Accounting for such a behavior further strengthens the use of flavor (rather than mass) states for neutrinos [142, 143].

Comoving frame. The question now arises as how to describe the above process for an observer comoving with the proton. Although one may envisage that the decay is kinematically forbidden in this frame, this is not the case, since the proton interacts with electrons and anti-neutrinos popping out from the thermal vacuum due to Unruh effect (see the last three diagrams in Figure 6). Details on the calculation of the decay rate are carried out in Supplementary Appendix E22, showing the result to be consistent with Equation 5. Therefore, unlike previous claims in literature [136], flavor mixing is perfectly consistent with the covariance of QFT, provided that asymptotic neutrinos are assumed to be flavor states.

The rôle of the non-thermality of Unruh spectrum for mixed fields [144–146] and the effects induced by gravity [49, 147–150] and acceleration [151–153] on the standard oscillation formula have still to be fully addressed. Worthy of attention are also the entanglement properties that emerge among neutrinos and other decay products in interaction processes. Beyond its inherent theoretical relevance, the tension between flavor and mass states may be of interest at the phenomenological level, as well. Recently, indeed, it has been shown that the predicted spectra of the neutrino capture on tritium and of the tritium β-decay are sensitive to whether neutrinos interact as massive or flavor eigenstates. Thus, it is expected that the output of experiments such as KATRIN [154] (that aims at measuring the mass of the electron antineutrino by investigating the spectrum of electrons emitted by the β-decay of tritium) or PTOLEMY [155, 156] (which is projected to reveal the Cosmic Neutrino Background via capture on tritium), may provide important pieces of information in the considered problem, deepening our understanding of neutrino physics. In addition, let us notice that neutrinos might add up to the total dark matter amount of the Universe. In this context, KATRIN and PTOLEMY setups could detect these particles in the keV mass range, that is the scale at which they should form the DM of the Universe. Potential connections between neutrinos (and, more general, particle) physics and dark matter are also under the active investigation of upcoming experiments such as AEDGE [157].

8 Dirac and Majorana Neutrinos

The fundamental nature of neutrinos has eluded physicists so far. Its determination is important due to the prominent role that neutrinos play in Cosmology. In particular, both the known active neutrinos and the hypothetical sterile neutrinos have been proposed as dark matter candidates, respectively as hot dark matter and warm dark matter [158]. The issue suffers from a substantial lack of experimental tests, the only attempts are based on the phenomenon of neutrinoless double beta decay [159]. While Dirac neutrinos have a distinct anti-particle (anti-neutrinos), Majorana neutrinos coincide with their own anti-particle.

The most promising way to reveal the possible Majorana nature of neutrinos is the experimental observation of the double beta decay without neutrinos [160] (see ref. 161–163 for alternative possibilities). The main difficulty in determining the Majorana character is that in theories with $V-A$ interactions, this is the case of the Standard Model, any observable difference between Dirac and Majorana neutrinos is suppressed by a factor ${\left(m_{\mu }/E\right)}^2$, being E the energy scale of the process [164]. However, an interesting possibility arises in the case in which neutrinos have new interactions beyond the SM [165]. In is worth of mentioning, for example, the proposal of ref. 166 in which the author considers the most general Lorentz-invariant form of neutrino-fermion interactions. This includes scalar, pseudo-scalar, vector, axial-vector and tensor couplings. In such a circumstance, it follows that in elastic neutrino-electron scattering, the ratio of forward to backward scattering cross sections $R_p$ could be used for distinguishing Dirac and Majorana neutrinos. More specifically, $R_p\le 2$ for Majorana neutrinos, and $R_p>4$ for Dirac neutrinos. Other alternative methods to determine the Majorana and Dirac nature stem from the differences that arise in presence of decoherence [167, 168] and in the propagation through a medium [169]. Let us recall the main distinctions between the two kinds of neutrinos. Let ν denote the neutrino field and let ${\nu }_{R,L}=\frac{1\pm {\gamma }_5}{2}\nu$ be its left–handed and right–handed components. The Dirac mass term in the neutrino Lagrangian has the form

$L_D=\frac{m_{LR}}{2}\left({\overline{\nu }}_L{\nu }_R+{\overline{\nu }}_R{\nu }_L\right)(6)$

with $\overline{\nu }={\nu }^{†}{\gamma }^0$. On the other hand the Majorana mass term has the structure

$L_{M,L}=\frac{m_{LL}}{2}\left[\overline{{\left({\nu }_L\right)}^c}{\nu }_L+{\overline{\nu }}_L{\left({\nu }_L\right)}^c\right](7)$

where the superscript c denotes the charge conjugated field. If right–handed neutrinos are allowed for, one has an analogous Majorana mass in terms of the right–handed components, namely

$L_{M,R}=\frac{m_{RR}}{2}\left[\overline{{\left({\nu }_R\right)}^c}{\nu }_R+{\overline{\nu }}_R{\left({\nu }_R\right)}^c\right](8)$

A heavy right–handed Majorana mass $m_{RR}$ might explain the smallness of the mass of the observed neutrinos via the see–saw mechanism (see ref. 170 for a review on several neutrino mass models). The different structure in terms of left–handed and right–handed components implies different transformation properties for the two kinds of neutrinos. Indeed, while the Dirac Lagrangian is invariant under global $U\left(1\right)$ transformations, the Majorana Lagrangian is not. As a consequence, Dirac neutrinos preserve the total lepton number, whereas Majorana neutrinos allow for lepton number violating processes. In addition, a different number of phases appears in the mixing matrix. For n flavors, there are $N_D=\left(n-1\right)\left(n-2\right)/2$ Dirac phases and $N_M=n\left(n-1\right)/2$ Majorana phases. This work is focused on 2-flavour mixing, which features a single Majorana phase ϕ. The Majorana mixing matrix admits various parametrizations

$U_1=\left(\begin{array}{cc}\cos \theta & \sin \theta e^{i\varphi }\\ -\sin \theta & \cos \theta e^{i\varphi }\end{array}\right) U_2=\left(\begin{array}{cc}\cos \theta & \sin \theta e^{-i\varphi }\\ -\sin \theta e^{i\varphi }& \cos \theta \end{array}\right)(9)$

which lead to the same oscillation formulae in absence of decoherence [171–173].

The Dirac mixing matrix is in any case obtained for $\varphi =0$. To study propagation with decoherence, it is necessary to model neutrinos as open quantum systems, described by means of density matrices $\rho \left(t\right)$. The time evolution of $\rho \left(t\right)$ is driven by a Lindblad-Kossakowski master equation [174, 175]: $\frac{\partial \rho \left(t\right)}{\partial t}=-\frac{i}{\hslash }[H_{eff},\rho \left(t\right)]+D\left[\rho \left(t\right)\right]$. The effect of decoherence is contained in the dissipator$D\left[\rho \left(t\right)\right]$, which for the case at hand is a $3\times 3$ matrix on the space of bounded operators $B\left(\mathrm{\mathscr{H}}\right)$ on the two-level Hilbert space $\mathrm{\mathscr{H}}$.

The elements of the dissipation matrix D are phenomenological parameters, to be extracted from the experimental setup. If D is diagonal, Dirac and Majorana neutrinos happen to obey the same oscillation formulae. For a non-diagonal dissipator, however, the two are distinct. One considers a dissipator with two off-diagonal components and plugs it in the master equation. Projecting on the $SU\left(2\right)$ basis, one obtains a linear system for the components ${\rho }_{\mu }\left(t\right)=\text{Tr}\left[\rho \left(t\right){\sigma }_{\mu }\right]$ which is easily solved. Then the transition probability from flavor σ to flavor ϱ can be computed as $P_{{\nu }_{\sigma }\to {\nu }_{\mathit{\varrho }}}\left(t\right)=\text{Tr}\left[{\rho }_{\mathit{\varrho }}\left(t\right){\rho }_{\sigma }\left(0\right)\right]$. Notice that, at this stage, the choice of a parametrization for the mixing matrix becomes relevant, as $U_1$ and $U_2$ produce different formulae. In particular, choosing $U_2$ results in probabilities that have an explicit dependence on the Majorana phase ϕ, which prompts an asymmetry between the particle and anti-particle transitions. One can introduce the $CP$-violating quantity ${\text{Δ}}_{CP}^{\sigma \to \mathit{\varrho }}\left(t\right)=P_{{\nu }_{\sigma }\to {\nu }_{\mathit{\varrho }}}\left(t\right)-P_{{\overline{\nu }}_{\sigma }\to {\overline{\nu }}_{\mathit{\varrho }}}\left(t\right)$ as a measure of the $CP$ asymmetry. For Majorana neutrinos, even the survival probability $P_{{\nu }_e\to {\nu }_e}\left(t\right)$ shows a $CP$ asymmetry. It should be remarked that this $CP$ violation, depending exclusively on the Majorana phase ϕ, is absent in the standard 3-flavour mixing of Dirac neutrinos, and is therefore distinct from the $CP$ violation arising from the Dirac phase ${\delta }_{CP}$. On the other hand, ${\Delta }_{CP}=0$ for any transition involving Dirac neutrinos. This can be generalized to three flavors in a straightforward way.

Another distinction between Dirac and Majorana neutrinos comes up from the analysis of geometric phases for neutrinos propagating in matter (see appendix). Using the Mukunda-Simon definition, one concludes that the geometric phase associated to a single flavor Equation 48 is not affected by the Dirac/Majorana distinction [169]. On the contrary, the phases associated with the mixing, Equations 49, 50 show an explicit dependence on the Majorana phase ϕ. As for decoherence, we find an asymmetry in the oscillations of Majorana neutrinos, which is absent in the Dirac case. The asymmetries in the transition probabilities and geometric phases are exemplified in Figure 7. In the upper panel we show the transition probability $P_{{\nu }_{\mu }\to {\nu }_{\tau }}\left(z\right)$ for Dirac and Majorana neutrinos when decoherence is taken into account, for a distance $z=300\text{km}$ as a function of energy. The dissipator parameters are chosen in correspondence with the bounds from long baseline experiments (see ref. 167 and the references therein). In the lower panel we plot the geometric phases associated to neutrino oscillations (see Supplementary Appendix F) as a function of energy.

FIGURE 7

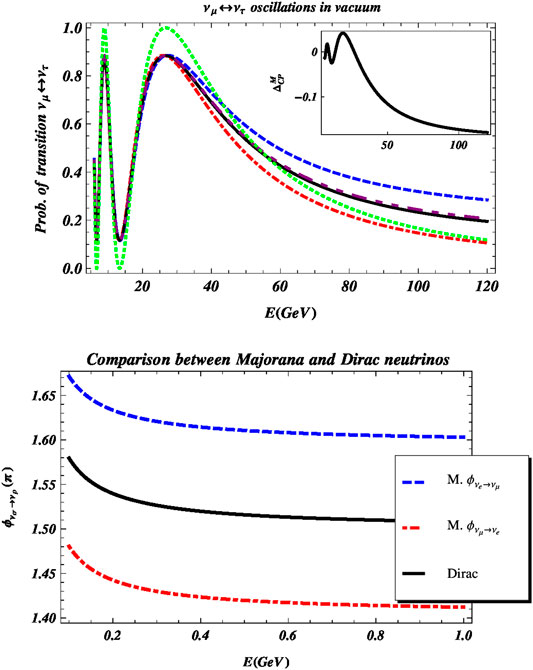
FIGURE 7. Upper panel: plot of the oscillation formula $P_{{\nu }_{\mu }\to {\nu }_{\tau }}$ for Majorana neutrinos and for Dirac neutrinos ($\varphi =0$, the black lines), as a function of the energy E. The experimental bounds from long baseline experiments on the decoherence parameters are used; Lower panel: plot of the geometric phases ${\text{Φ}}_{{\nu }_e\to {\nu }_{\mu }}^g$ (the blue dashed line) and ${\text{Φ}}_{{\nu }_{\mu }\to {\nu }_e}^g$ (the red dot–dashed line) for Majorana neutrinos as a function of the neutrino energy E, for a distance length $z=300km$. The geometric phase ${\text{Φ}}_{{\nu }_e\to {\nu }_{\mu }}^g={\text{Φ}}_{{\nu }_{\mu }\to {\nu }_e}^g$ for Dirac neutrinos is represented by the black solid line.

Future studies [176] shall be aimed at finding additional tools and phenomena that can highlight the fundamental nature of neutrinos. The determination of the latter is important to shed light on one of the most elusive particles in the Universe, which perhaps constitutes the strongest evidence for physics beyond the standard model of particles and may direct us toward the searched new “dark sector”.

9 Quantum Fields in Curved Space-Times

Several unresolved questions concerning the origin of our Universe, its very evolution and fate, are still waiting for quantum gravity - a theory allowing to manage and reconcile general relativity with quantum mechanics. In that respect, also the apparent presence in the Universe of “dark substances” such as Dark Energy and Dark Matter could play a crucial role. One of the difficulties of developing a quantum gravity theory is that quantum gravitational effects are expected near the Planck scale, around 10⁻³⁵ meters, so by far out of reach, given the present technology. On the other hand, the approach to quantum cosmology through a suitable quantum-mechanical translation of some known solutions in classical general relativity (and its possible extensions) could perhaps offer a back-door entry toward quantum gravity. Quantum effects involved in the early stages of a cosmological evolution may be of some relevance also at a low-energy microscopical level, influencing the microphysics in a classical background. In that respect, the study of the behavior of quantum fields in a curved space-time background represents an inescapable first step toward the quest for a comprehensive, self-consistent quantum theory of gravity [177]. In the semi-classical approach, the background - although allowed to evolve in time - is assumed not to be affected by the quantum field itself (i.e., back-reaction is not taken into account), the former being only sourced by some given classical distribution of mass-energy and completely described by the Einstein field equations. Nevertheless, even in such semi-classical scenario, several non-trivial manifestations of the background influence upon a quantum field appear, often related to the lack of a privileged reference frame in presence of a curved background. Hence, special attention has to be payed to the role of the physical observer's frame, in which the relevant measurements are performed.

Vacuum fluctuations are a distinctive feature pertaining to the quantum nature of a matter field. One of their most famous manifestations is the well-known Casimir effect [178–182]. Modification in the vacuum energy can be also induced by external fields, including gravity [183–186]. In such latter case, the space-time background and the quantum field confinement may conspire together, giving rise to several interesting effects [187, 188].

Looking at those effects, the Casimir energy has been extensively investigated, taking into account a small Casimir apparatus both in the weak and in the strong gravitational field limit. Analysis of a Casimir cavity at rest in a weak, static gravitational field has shown a small change in the value of the Casimir energy. Such a result has been first obtained by using a field mode decomposition technique [189]. Recently, the same result has been confirmed by means of a quite different approach based upon the Schwinger effective-action method [190]. Furthermore, a similar behavior has been obtained by considering a cavity in free fall into a black hole [191–193]. The Casimir effect has been investigated also in presence of (weak) gravitomagnetism. An interesting result is that - up to the lowest order of approximation - a gravitomagnetic field causes no distortion in the vacuum energy [194] (the extension to modified theories of gravity has been studied in refs. 195–refs. 197). However, a deeper and more exhaustive analysis in the field of a Kerr black hole, has revealed that the Casimir energy density is indeed sensitive to the Kerr gravitational dragging [198]. Actually, a small Casimir apparatus orbiting in the Kerr equatorial plane suffers a change in the Casimir energy density. Such a change vanishes in the case of a zero-angular-momentum-observer orbit, suggesting that modifications in the Casimir energy do appear when the azimuthal symmetry is broken by the equatorial circular motion of the cavity with respect to the local zero-angular-momentum-observer frame. A similar analysis has been carried on taking into account a Casimir apparatus orbiting an Ellis wormhole [199]. While obtaining basically the same results, e.g., a decrease in the absolute value of the vacuum energy density inside the cavity, the above work has shown that the Casimir energy is affected by the orbital motion of the cavity nearby the wormhole, also when other local classical measurements - performed by a co-moving observer–as the acceleration or the Fermi rotation coefficients - yield a vanishing result. In that respect, it is believed that the Casimir effect might represent an interesting quantum probe for testing the (non-inertial character of a given reference frame).

Concerning time-dependent backgrounds, particle creation out of quantum vacuum has been obtained by analyzing a “kicked” Casimir cavity [200] and, more recently, a Casimir cavity in free fall into a black hole [192, 193]. Such effect can be considered as a time-dependent tidal one, due to the non-uniformity of the gravitational field experienced by the quantum field confined to the cavity, as the black hole horizon is approached. In Figure 8 a schematic picture of a small Casimir cavity radially falling onto a Schwarzschild black hole is shown. The cavity is rigid, namely the plate separation L is constant with respect to a comoving observer.

FIGURE 8

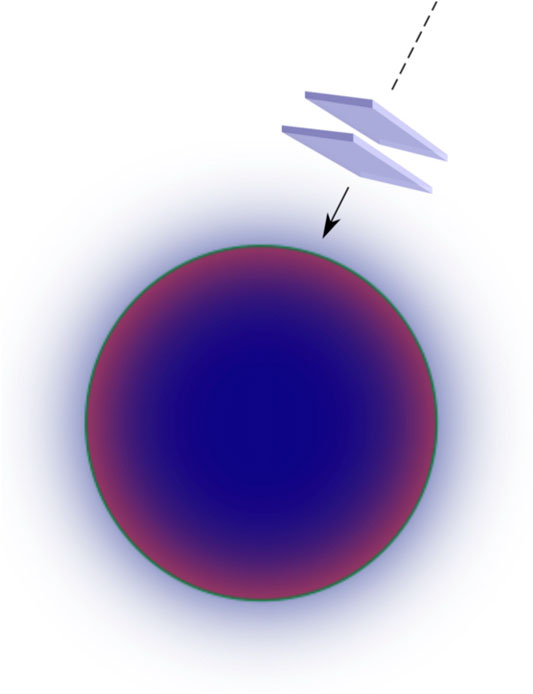
FIGURE 8. A Casimir cavity freely falling from infinity onto a Schwarzschild black hole. The cavity size is assumed to be small with respect to the Schwarzschild radius, ($L/r_g\ll 1$). The cavity is rigid, i.e., the plate separation L is constant according to a comoving observer.

Similar particle creation effects can be found when the confined quantum field experiences a time-dependent background describing a (weak) gravitational wave. In an early related study on a small three-dimensional cavity [201] hosting a scalar quantum field, the relevance of confinement from the point of view of a particle-creation effect has been highlighted. Last, within that framework the excitation of acoustic phonons out of the vacuum in a toy-model one-dimensional elastic medium has been considered, as a consequence of the interaction with a gravitational wave [191].

Future investigations will be devoted to a deeper understanding of the interplay between gravity and quantum fields both in the static and in the dynamical regime, the latter being typically related to particle creation. Moreover, mesoscopic quantum systems interacting with a gravitational wave [202] will be considered in detail. Quantum effects induced by gravitational waves at nanoscales might represent a new stimulating research arena, both from a theoretical and the experimental point of view.

Finally, quantum vacuum will be considered at cosmological level, being strongly related to the cosmological constant problem in non-trivial spacetime topologies as well as in models with compact extra dimensions. Let us stress that, along these lines, Gamma-Ray-Bursts [203]–will be investigated, as they could be deeply rooted in the intriguing interplay between GR and QFT and their capability to be indicators of the Universe expansion will be put in question.

10 Tomographic Description of Quantum and Classical States of the Universe

Modern cosmology was born after the formulation of general relativity by Albert Einstein. The evolution of the Universe is described by solutions of the Einstein equations. However, Hawking-Penrose theorems show that these solutions inescapably present singularities if the energy-momentum tensor has properties which are regular when ordinary matter and radiation are considered. The existence of these singularities, which appear to be a pathological aspect of the theory, can be interpreted as a signal that the theory is no longer reliable at particular conditions, for this reason many researchers postulated that general relativity, which is a classical theory, must be replaced by a quantum theory of gravitation. In particular, cosmology seems a topic that lends itself well to the study of the quantum properties of a gravitational system such as the Universe, which is homogeneous to a very high degree; it is therefore sufficient to study the problem of quantization in the minisuperspace, which is the space of all homogeneous three-metrics.

The study of the evolution of the Universe is the story of the evolution of the states of the Universe. The state of a particle in classical physics is described by its position and momentum in phase space. More generally, for a particle in a thermal bath, its state can be described by a probability function. For a constrained system where not all the dynamical variables are independent (for example the Friedmann equations show that expansion factor $a\left(t\right)$ and its time derivative $a\left(t\right)$ and are not independent), it is sufficient to use a smaller number of variables, and the states are confined in a subset of phase space. Given one state and the equation of motion, one can predict the evolution of the physical system.

On the other side, in quantum theory the state of a particle, or more generally a quantum system, is defined by a wave function (or functional in field theory). It can be used to evaluate the probability that a physical system is in a particular state and to obtain the probability amplitudes of its transition from a state to another. Alternatively to the wave function, other descriptions of the physical state have been introduced like the density matrix or the Wigner function. The last one describes the physical state in a phase space, even if, differently from the classical particle, it cannot be considered as a probability function since it can take negative values.

In general relativity the existence of singularities does not make it possible to predict the evolution of the Universe from an initial undetermined state. On the other side the quantum description of the initial states of the Universe needs to be extended to the final states crossed by the classical Universe. Unfortunately, there is no a simple way to perform this extension by using the kind of representations used so far. For this reason, we introduce a new description in terms of tomograms which are marginal probability functions, and as such they are positive-norm functions and are observables (see for example refs. 205 and 205) They describe equally well quantum and classical states. For this reason, tomograms are suitable for a good description of the quantum-to-classical transition of the Universe, and eventually can be defined phenomenologically by cosmological observations, leading to a reconstruction of the early Universe [206–212] with obvious relations with its dark components in matter and in energy.

For this purpose, recently a de Sitter Universe was considered and the wave functions, solutions of the cosmological quantum equation (the Wheeler-DeWitt equation) and were translated in the tomographic formalism [213, 214].

If we describe the de Sitter space-time with the closed metric

$d{s}^2=-\frac{N^2}{q}d{\tau }^2+\frac{q}{1-R^2}d{r}^2+q{r}^2\left(d{\theta }^2+{\sin }^2\theta d{\varphi }^2\right)(10)$

where $q=a^2$, N is the lapse function (related to the freedom of choice of the time variable). The classical distribution is represented by the delta function of the constraint equation

$f\left(q,p\right)=\delta \left(-4p^2+\lambda q-1\right)(11)$

where $p=-\dot{q}/4N$ is the conjugate momentum, and the corresponding classical tomogram is (see Figure 9)​

$\mathcal{W}\left(X,\mu ,\nu \right)={\displaystyle \int \delta \left(-4p^2+\lambda q-1\right)\delta \left(X-\mu q-\nu p\right)dqdp}=\frac{1}{2\left|\mu \right|}\frac{1}{\left|\sqrt{\frac{{\lambda }^2{\nu }^2}{16{\mu }^2}+\frac{\lambda X}{\mu }-1}\right|}(12)$

The tomogram corresponding to the Hartle-Hawking wave function is (see also Figure 10)

$\mathcal{W}\left(X,\mu ,\nu \right)=\frac{A^2}{\left|\mu \right|}|Ai\left[\frac{1}{{\left(2\hslash \lambda \right)}^{2/3}}\left(1-\frac{\lambda X}{\mu }-\frac{{\lambda }^2}{16}\frac{{\nu }^2}{{\mu }^2}\right)\right]{|}^2(13)$

where the constant $A=2^{5/6}\pi /{\hslash }^{1/6}{\lambda }^{2/3}$. These two tomograms can be compared. Then, first we see that the tomogram resulting from taking the limit for $\hslash \to 0$ or the limit for $\lambda \to 0$ is the same. This circumstance suggests that a decay of the cosmological constant from the Planck scale to its present value causes a transition from the quantum to the classical regime, as the quantum tomogram becomes

$\mathcal{W}\left(X,\mu ,\nu \right)\approx \frac{1}{2\left|\mu \right|}\frac{1}{|1-\frac{\lambda X}{\mu }-\frac{{\lambda }^2}{16}\frac{{\nu }^2}{{\mu }^2}{|}^{1/2}}|\cos \left(\frac{2}{3}{S}^{3/2}-\frac{\pi }{4}\right){|}^2(14)$

The Hartle-Hawking model does not converge to the classical tomogram and does not converge at all. But if nevertheless instead of taking $\lambda \to 0$, we take $\lambda \sim {10}^{-122}$ we have the possibility of examining a new “classical” model of Universe with peculiar features characterized by the presence of the cosine factor in Equation 14. Therefore, the Hartle-Hawking model is not ruled out, but its asymptotic expression is a possible “classical” description of the present Universe not derived from the classical equations. In other words quantum cosmology offers the possibility of formulating new classical models that are not necessarily derived from the classical general theory of relativity.

FIGURE 9

FIGURE 9. The tomogram of a classical de Sitter universe.

FIGURE 10

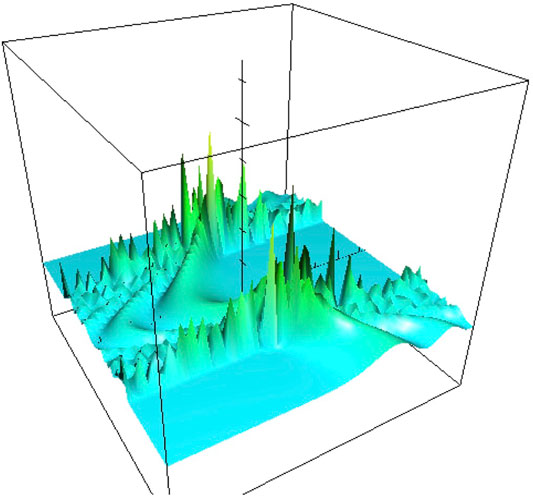
FIGURE 10. The tomogram of a quantum de Sitter universe according to the Hartle and Hawking initial conditions.

On the other side the tomogram

$\begin{array}{c}\mathcal{W}\left(X,\mu ,\nu \right)=\frac{A^2}{\left|\mu \right|}|\frac{1}{2}Ai\left[\frac{1}{{\left(2\hslash \lambda \right)}^{2/3}}\left(1-\frac{\lambda X}{\mu }-\frac{{\lambda }^2}{16}\frac{{\nu }^2}{{\mu }^2}\right)\right]\\ +iBi\left[\frac{1}{{\left(2\hslash \lambda \right)}^{2/3}}\left(1-\frac{\lambda X}{\mu }-\frac{{\lambda }^2}{16}\frac{{\nu }^2}{{\mu }^2}\right)\right]{|}^2\end{array}(15)$

which is the tomogram obtained from Vilenkin's initial conditions (see Figure 11) [215], in the limit ${\left(2\hslash \lambda \right)}^{2/3}\to 0$ converges asymptotically to

$\mathcal{W}\left(X,\mu ,\nu \right)\approx \frac{1}{2\left|\mu \right|}\frac{1}{|1-\frac{\lambda X}{\mu }-\frac{{\lambda }^2}{16}\frac{{\nu }^2}{{\mu }^2}{|}^{1/2}}(16)$

Remarkably, the quantum to classical transition found here can be extended to more general cosmological models involving either scalar fields or cosmological fluids [215]. Many of these models predict that a classical inflationary Universe emerges after the decay of the cosmological constant problem during the quantum epoch, and a further decay of the cosmological constant guarantees the exit from the inflationary epoch. A result of this analysis is that the so called “cosmological constant problem” can be addressed in quantum epoch rather than in the classical one.

FIGURE 11

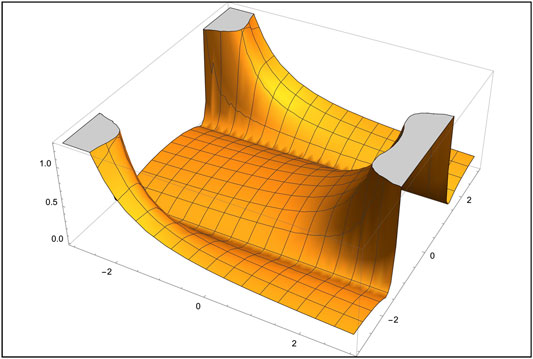
FIGURE 11. The tomogram of a quantum de Sitter universe according to Vilenkin’s “tunneling from nothing” initial conditions.

Last, tomograms are in principle observables. The form of the classical tomogram (11) suggests that the phenomenological tomogram of the Universe should be a function of the cosmographic parameters extending the analysis in Section 2 to the variables of the tomogram.

11 On the Origin of the Cosmological Constant: Planckian Fluctuations, Decoherence Scale

One of the biggest problems in modern physics and cosmology is the nature and origin of dark energy. There exist many attempts to explain the current acceleration phase of our Universe, by adopting ‘modified gravity theories’ or introducing ad hoc running (in time) scalar fields. In the standard cosmological model dark energy is interpreted as vacuum energy and it is simply depicted in terms of a cosmological constant $\Lambda$, both in time and space. The observed value for $\Lambda$ is very small and in complete disagreement with theoretical predictions (about 122 orders of magnitude smaller than the value predicted by Quantum Field Theory). Scarsely convincing explanations concerning the issues related to $\Lambda$ have been put forward (see for example refs. 216–220 and references therein). It is important to point out also that all the above bounces on the other great darkness of the Universe: the dark matter component, whose interaction with the dark energy is as important as presently unknown.

Remarkably, a completely new point of view, regarding the origin of $\text{Λ}$ has been recently put forward [221–223] The main idea relies on the nature of $\Lambda$ and its very small observed value and states that quantum fluctuations can explain the equation of state of the cosmological constant. In fact, a radiation field sufficiently close to the Planck scale can allow quantum fluctuations so strong to permit the transformation of this radiation field into one with the equation of state that $\Lambda$ shows. The effective value of the cosmological constant depends on the physical scale under consideration. Thus, in the new view, Planckian fluctuations average on bigger and bigger scales: the cosmological constant is watered down on scales bigger than the Planck one. The important concept of decoherence scale $L_D$ is also introduced: this is the scale determining the observed value of the cosmological constant and determines the crossover to classicality. The calculations concerning the formula of the observed cosmological constant $\overline{\Lambda }$ in terms of the decoherence scale $L_D$ are performed in the context of a semi-classical solution where the effective metric at the Planck scale is averaged. In formulas we have:

$\overline{\Lambda }=\frac{{\pi }^3}{90}\frac{L_P^2}{L_D^4}(17)$

where $L_P$ is the Planck length and the constant $\frac{{\pi }^3}{90}$ has been fixed in ref. 222 by analogy with Casimir effect. From a mathematical point of view the Buchert formalism in ref. 224, known since 2001 and used to model inhomogeneities in our Universe by means of a template homogeneous metric, is properly modified and applied at Planckian scales. Also this research field represents a novelty and, in absence of a sound quantum gravity proposal, provides a practical way to perform physically sound calculations.

A comparison with the Casimir effect is outlined in ref. 222. In this regard, it should be noticed that an expression for a quantum modification of the Misner-Sharp mass, introduced in ref. 225, can be written in the following way:

$E\left(L\right)=\frac{c^4}{2G}\frac{L^3}{L_A^2}+\xi \frac{c^4}{2G}\frac{L_P^2}{L}(18)$

In this context, as usual, the Casimir energy $E_C$ can be expressed as the difference between vacuum energy in presence of boundary conditions $E_B$ and the one of a space $E_0$ without boundary conditions:

$E_C=E_B-E_0(19)$

and as a result one obtains the expression

$E_C=E\left(L,\overline{\Lambda }\right)-E\left(L,\Lambda \right)=\frac{\xi c^4}{2G}\frac{L_P^2}{L}$

in perfect agreement with the Casimir energy $E_C$ obtained in the standard Casimir effect for a spherical conductor with $\xi ={\pi }^3/360$. This comparison allows to fix the decoherence scale $L_D$ to be of the order of about ${10}^{-2}$ millimeters. Note that this is the scale where thermodynamic fluctuations are expected to be of the same order of the quantum ones in the standard Casimir effect. Future studies must be focused in order to depict the decoherence scale in terms of Quantum Field Theory approach. By virtue of the well known lack of a well posed quantum gravity theory, we need an effective treatment of the Einstein’s equations at Planckian scales incorporating sound arguments of general relativity and quantum mechanics. The semi-classical models so obtained can guide us toward a complete and accepted quantum gravity theory. Moreover, extended theories of gravity naturally generalize the Misner-Sharp mass: it is thus intriguing to explore such modifications according to the Casimir effect for spherical configurations.

Finally, in the same line of research, in refs. 226 and 227 the logarithmic corrections to Black Hole entropy have been outlined in a very simple and physically sound way. A similar formula can be applied to the whole Universe represented by its apparent horizon, allowing the study of thermodynamics’ laws at a cosmological scales. Then, in refs. 228 and 229, a generalization of the well known Bekenstein-Hawking entropy formula at a cosmological level has been obtained: in an expanding Universe a further term arises depicting the degree of freedom due to the non-static nature of our Universe. Recently, in ref. 230 Saha showed that with this new proposal, according to recent astrophysical data, the phantom era is ruled out. This intriguing fact places in an even more important position the role of $\overline{\Lambda }$.

One can study a relation between the model above for the cosmological constant and the renormalization group (RG) approach. In particular, one chooses a suitable renormalization scale μ or a subtraction point, where the physics is calculated and fixed, as suggested by refs. 221–223 in a cosmological context. A physically sound well motivated expression for μ will represent the starting point to formulate a RG equation for the cosmological constant. In this regard, the main goal is to obtain a non-trivial (non-vanishing) infrared (IR) fixed point at $\mu ={\mu }_D$, thus identifying the fixed point ${\mu }_D$ with the decoherence scale $L_D$. This result will allow to firmly establish the decoherence scale $L_D$ as an invariant one where the value of the cosmological is fixed, thus representing the crossover to classicality.

The physical scales where quantum fluctuations act in a non-trivial way can be of interest, as an example, also in the fate of a collapsing star. In particular, are possible modifications of the Chandrasekhar-mass limit (i.e., the maximum mass of a stable white dwarf star) leading the formation of more massive stable stars without forming a black hole? For this purpose, it should be noticed that a possible presence of gravitational-echoes in the Ligo-Virgo detection [231] of post-merger signals of binary coalescent stars could model some deviations from General Relativity in the near-horizon structures or more generally for ultra-compact stars made of possible exotic matter, where quantum effects are expected to come into action. For example, gravitational-echoes are supposed to be generated by the collision of two black holes and may indicate possible new physics beyond General Relativity. Detections of gravitational-echoes will be the smoking gun of quantum effects in a very strong gravitational regime. Moreover, these objects may be part of the elusive Dark Matter component of the Universe.

12 Gravity Meets Quantum Mechanics: A Simple Quantum Low-Energy Gravity Model at Work

The idea that quantum mechanics (QM) should be characterized by a fundamental non-unitary time evolution of the state vector, where gravity plays a prominent role, has been put forward by a number of authors, on different grounds [232–234]. Thus two main questions arise, which require an answer: how to reconcile the basic processes of QM, i.e. the Schrödinger deterministic evolution and the non-unitary process associated with the act of measurement, and how to explain the transition to classicality.

These issues appear to be deeply connected with quantum gravity and, in particular, with the way in which gravitational fields are generated by quantum matter. It is still widely debated if gravity has to be quantized at all or it is intrinsically classic and should be properly treated. In the latter case a proposed route is the semi-classical gravity, based on the requirement that the energy-momentum tensor appearing in Einstein equations is taken as an expectation on the quantum state. This prescription, together with the Newtonian limit, leads to the Newton-Schrödinger equation [235]. While its solutions for a lump of matter show interesting properties, this equation cannot be a valid candidate to give self-gravity at low energies because the non-linearity allows for superluminal communications.

The effective low-energy model of Newtonian gravity introduced by S. De Fliippo twenty years ago, termed Non-unitary Newtonian Gravity (NNG) (see e.g., refs. 236–238, references therein), belongs to this line of research. It is obtained as the non-relativistic limit of a non-unitary version of higher derivative gravity, which is classically stable and allows in principle for regularization of gravitational collapse singularities [238], leading to results in agreement with Bekenstein-Hawking entropy [239, 240]. Among its appealing features, besides a non-Markov evolution, one finds that the ordinary Newton’s action-at-a-distance interaction is recovered at a macroscopic level. Furthermore it exhibits a mass threshold for dynamical self-localization, which amounts to ${10}^{11}$ proton masses for ordinary matter densities [236, 238, 241]. As a consequence, even for closed systems, macroscopic coherent superpositions of states evolve into ensembles of pure states thanks to the peculiar dynamics of NNG model. Thus, as a further bonus, density matrix emerges as the fundamental description of physical reality, characterized by a non-Markovian evolution even from a pure state.

Due to the above features the NNG model is among the best candidates to address the controversial and still unsolved issue of the quantum foundations of the Second Law of thermodynamics [242, 243]. Indeed, as elucidated in ref. 244, a microscopic derivation of the Second Law of thermodynamics for a closed system could be obtained only via a non-unitary quantum evolution and in correspondence of suitable initial conditions. This feature is also shared by the process of formation and evaporation of black holes [245]. In this respect a prominent, unifying role is played by the concept of von Neumann entropy as entanglement entropy with hidden degrees of freedom.

Preliminary steps in demonstrating the ability of NNG to give rise to a gravity-induced relaxation toward thermodynamic equilibrium even for a perfectly isolated system have been already performed in refs. 246 and 247. As a first case study, a system has been considered, built out of two particles trapped in a harmonic potential, interacting via delta-like and gravitational interaction [246]. By choosing an eigenstate of the physical Hamiltonian as initial condition, numerical simulations have been carried out in order to study the time evolution of von Neumann entropy. The picture is consistent with the interpretation of von Neumann entropy as an entanglement entropy with some hidden degrees of freedom, which is clearly reminiscent of well known black hole entropy calculations [248]. As a further result, entropy fluctuations have been found to take place, thanks to the non-unitary part of gravitational interactions, with the initial pure state evolving into a mixture.

These promising results have been confirmed by switching to a more involved system, i.e., a harmonic nanocrystal within a cubic geometry [247]. In this case a numerical simulation has been carried out as well, but the choice of initial conditions is much more involved. By following the procedure outlined in refs. 249 and 250, an initial pure state with mean energy E has been selected, built up uniformly at random as a superposition of a huge number of energy eigenstates within the energy interval $\Delta E$ around E. The von Neumann entropy as a function of time exhibits a sharp monotonic increase, followed by a stabilization at late times. These findings clearly show that a micro-canonical ensemble grew up within the initial energy levels, as a consequence of a non-unitary gravity-induced relaxation toward thermal equilibrium.

Now a further step has to be performed in order to confirm the above scenario, which implies the simulation of a real crystal. Of course, it is the fundamental non-unitarity of the NNG model which is responsible of a net entropy growth for the system as a whole. Thus a microscopic derivation of the Second Law of thermodynamics can be self-consistently carried out, which makes the NNG model the first low-energy gravity model leading in a natural way to the emergence of Thermodynamics even in a closed system [251].

A second topical issue, concerning causality violations in Newton-Schrödinger equation [235], has been fully addressed within the NNG model as well [252, 253]. Here the single particle Newton-Schrödinger equation has been obtained as the mean-field approximation of an equation of N identical copies of the particle, interacting each other via gravitational interaction, when N goes to infinity [254]. The starting point is a general N-copy model, which is a fully consistent quantum theory without causality violation problems thanks to the validity of the no-signaling condition [255, 256]. Furthermore, while superluminal communications are suppressed, new strange communications among Everett branches of the wave function [253] are shown to appear, in close agreement with previous findings by Polchinski [256]. Within NNG model the density matrix fully characterizes the state of a system. This may suggest to assume the Everett Many World Interpretation as the most natural conceptual framework of that theory. But, at odds with other non-linear approaches to quantum mechanics, here the possibility of constructing an Everett phone between different branches of the wave function appears to be strongly inhibited.

The implementation of an Everett phone deserves further investigations and is currently under study [257] together with the search for a general proof of the existence of gravity induced correlations between the different branches of the wave function within a path integral formulation of the NNG model a’ la Feynman-Vernon [258]. We strongly believe that this issue will help to clarify the role of gravity induced de-coherence in wave function collapse and stimulate to look for the answer to a further question: how to discriminate in principle this kind of fundamental de-coherence against the usual environmental de-coherence and, finally, how to experimentally detect such a difference. To consider astrophysical consequences of NNG model is premature but one can forecast non- GR violation of Newtonian law at interesting scales.

13 Physics Meets Cosmology: Turbulence In SPH Simulations of Galaxy Clusters

The author [259] presented results from a large set of N-body/SPH hydrodynamical cluster simulations aimed at studying the statistical properties of turbulence in the ICM (InterGalactic Cluster Medium). The cosmological model is a flat CDM model, with vacuum energy density ${\Omega }_{\Lambda }=0.7$, matter density parameter ${\Omega }_m=0.3$ and Hubble constant $h=0.7=H_0/\left(100\text{km}{\text{sec}}^{-1}{\text{Mpc}}^{-1}\right)$. ${\Omega }_b=0.019{\text{h}}^{-2}$ is the value of the baryonic density.

The numerical hydrodynamical scheme employs a SPH formulation in which gradient errors are strongly reduced by using an integral approach [260]. The ensemble of hydrodynamical cluster simulations has been constructed by performing a set of individual runs, with initial conditions for each cluster extracted from a cosmological N-body simulation with only dark matter. We consider both adiabatic and radiative simulations. For the cooling runs, the modeling of the gas incorporates radiative cooling, star formation and energy feedback from supernovae.

A gas particle is eligible to form a star particle if the gas flow is locally convergent and the gas density exceeds a given threshold. If these conditions are satisfied, star formation will occur with a characteristic dynamical time-scale. We refer to [261] for a detailed description of the recipes implemented.

We construct clusters subsamples according to the cluster dynamical status or gas physical modeling. We quantify the cluster dynamical state by using, as a morphological indicator, the power ratio method [259]. According to this method, the projected X-ray surface brightness ${\Sigma }_X\left(\overrightarrow{x}\right)$ is the source term of the pseudo potential $\Psi \left(\overrightarrow{x}\right)$ which satisfies the 2-D Poisson equation. A multipole expansion of the solution then gives the moments which are used to provide an unambiguous detection of asymmetric structures.

To analyze the turbulent velocity field of the simulated clusters we introduce a filtering procedure, aimed at decomposing the fluid velocity into a large-scale component and a small-scale part. We use an iterative multifilter approach, in which mean velocities are estimated locally using an adaptive filtering scheme [262]. We then extract from cluster subsamples small-scale turbulent velocities, obtained by applying to cluster velocities the multiscale filtering method. We also quantify the statistical properties of the small-scale turbulent velocity field by estimating the velocity power spectrum $E\left(k\right)$.

The main results of that work can be summarized as follows [259]. The velocity power spectra of non-radiative relaxed clusters are mostly solenoidal and exhibit a peak at wavenumbers set by the injection scales $\simeq R_{200}/10$. The radius $R_{\Delta }$ is defined such that

$M_{\Delta }=\left(4\pi /3\right)\Delta {\rho }_c{R}_{\Delta }^3(20)$

denotes the mass contained in a sphere of radius $R_{\Delta }$ with mean density $\Delta$ times the critical density ${\rho }_c$.

In the high wavenumber regime, the spectral behavior is steeper than in the Kolmogorov case. Radiative simulations are characterized by a shallower wavenumber dependency, which is due to the injection of turbulence at small scales. This in turn originates from the interaction of compact cool gas cores with the ICM. This small scale driving source acts in addition to the usual large scale injection mechanisms, thus showing that there are multiple injection scales which operate to generate turbulence in galaxy clusters. For cluster dynamically at equilibrium, the enstrophy profiles of cooling simulations show a power-law dependency over a large range of radii, and a very small turbulent-to-thermal energy ratio.

For an highly relaxed cluster we find in the core very low gas velocities, as seen by Hitomi. Similarly, the radial profile of the sloshing oscillation period is found in accord with Fornax observations. In particular, the associated Froude number $Fr$ satisfies $Fr\lesssim 0.1$ within $r/R_{200}\lesssim 0.1$. The number $Fr$ is introduced to assess the importance of buoyancy forces relative to stirring motions, so that very small values indicate that stratification is important.

Our findings suggest that in cluster cores ICM turbulence approaches a stratified anisotropic regime, with weak stirring motions dominated by gravity buoyancy forces and strongly suppressed along the radial direction. In accord with similar findings [263], we conclude that turbulent heating cannot be considered the main heating source in cluster cores and thus provide a viable solution to solve the so-called cooling flow problem. The center of relaxed clusters is often characterized by the presence of cool dense cores with cooling times much shorter than the age of the Universe. This implies radiative losses which will lead to an inward motion producing a ‘cooling flow’ [264] and large mass accretion rates. This is not observed, and some heating sources [265] must be operating in the cluster cores to regulate the cooling flows.

In a forthcoming work, we are planning to investigate the emergence of the cool-core/non-cool-core (CC/NCC) dichotomy in simulations of merging clusters. Specifically, we want to investigate the impact of radiative cooling on the survival of CC clusters in a merging environment.

14 A New Challenge for the $\Lambda$Cold Dark Matter Scenario: The Extremely Dense Environments Around Clusters of Galaxies

Galaxy clusters, the most massive gravitationally bound cosmic structures, are not isolated systems. Theoretical models within the framework of the $\Lambda$CDM cosmological model predict that they form in the highest-density regions of the underlying dark matter density field [266]. This is widely supported by cosmological numerical simulations that show a detailed picture of the so-called cosmic web, with massive galaxy clusters located in the highest-density nodes. The spatial correlation between the dark matter halos (hosting galaxy clusters) and the matter density field is described by the halo bias $b_h$ [267]:

$b_h=\frac{P_h\left(k\right)}{P_m\left(k\right)}(21)$

where $P_h$ and $P_m$ are the power spectrum of the dark matter halo distribution and the dark matter density field, respectively. Both quantities are direct function of the scale k. Hence, dark matter halos are not randomly distributed, but their clustering is enhanced relatively to the general mass distribution. Theoretical models also show that the matter density beyond the virial region is strongly correlated to the dark matter halo mass [267]. Recent observational works have confirmed this picture. In particular, refs. 268 and 269 have confirmed the predicted relation $b_h\left(M\right)$ between the halo bias and the mass M of the dark matter halo (the so-called 1-halo term). These works used the technique known as stacked weak gravitational lensing [270] (see also refs. 271 and 272). Weak gravitational lensing, i.e., the coherent and weak distortion of the image of background sources by means of a foreground gravitational field,is a fundamental tool to measure the mass distribution in cosmic structures. However, the typical small signal-to-noize due to the correlated matter distribution beyond the galaxy cluster virial radius is not large enough to allow the measurement of the halo bias in individual systems. This problem can be addressed by using stacked samples of galaxy clusters, where the signal-to-noize is enhanced by averaging the weak lensing signal over homogeneous samples, where clusters are grouped according to some observable quantity (such as, e.g., the optical richness). Therefore, stacked weak lensing provides an effective approach to test the statistical predictions of the theoretical formation scenarios, as the direct investigation of the correlated matter distribution around individual systems is hampered by the lack of deep and wide astronomical surveys around massive galaxy clusters.

However, the work in ref. 273 recently reported the first detection of an extremely dense environment around a massive galaxy cluster, PSZ2 G099.86 + 58.45, located at redshift $z=0.616$, from the PSZ2LenS [274] cluster sample. PSZ2LenS is a small but homogeneous and complete sample of 35 galaxy clusters, detected by the Planck mission in the sky regions observed by the CFHTLenS (Canada–France–Hawaii Telescope Lensing Survey) [275] and RCSLenS (Red Cluster Sequence Lensing Survey) [276]. Hence PSZ2LenS is an unbiased sub-sample of the Sunyaev-Zeldovich sources detected by Planck (PSZ2 catalog). PSZ2 G099.86 + 58.45 is a massive cluster (the cluster velocity dispersion is ${\sigma }_v=1040\pm 110\text{km}/\text{s}$) and the most distant system in the PSZ2LenS sample [273] performed the weak lensing analysis by using about $150\times {10}^3$ background galaxies, over a sky region about $2.5\times 2.5$ square degrees. Remarkably, PSZ2 G099.86 + 58.45 is unique in PSZ2LenS, as its large angular diameter distance ($D\simeq 0.98\text{Gpc}{\text{h}}^{-1}$) makes it possible to determine the weak lensing signal out to about 30 Mpc from the cluster center, well beyond the virial radius. The weak lensing analysis presented in ref. 273 reveals a galaxy cluster mass in broad agreement with previous measurements based on a dynamical study of the cluster's galaxies motions and on the X-ray temperature profile: $M_{200}=\left(8.2\pm 3.5\right)\times {10}^{14}{\text{M}}_{\odot }{\text{h}}^{-1}.$ However, beyond about 10 Mpc, the environment matter density largely exceeds the cosmological mean. Within the $\Lambda$CDM paradigm, the expected halo bias is $b_{h,\Lambda CDM}=11.1\pm 2.8$ [273]. We found a much larger signal from the second halo term: $b_h=72\pm 20,$ see Figure 12 for a comparison with the theoretical predictions from ref. 267. We note that the measured bias for the whole PSZ2LenS sample is well in agreement with the theoretical predictions, see Figure 12. The observational results obtained by ref. 273 present us with a new dilemma: is PSZ2 G099.86 + 58.45 a rare case, unexpectedly found in a small (yet complete) sample of galaxy clusters? Or, is this system the first example of a larger population of clusters whose existence requires a modification of the formation scenario within the $\Lambda CDM$ model? In the latter case, the immediate implication is that enhancing mechanisms around high-mass halos could be much more effective than previously thought.

FIGURE 12

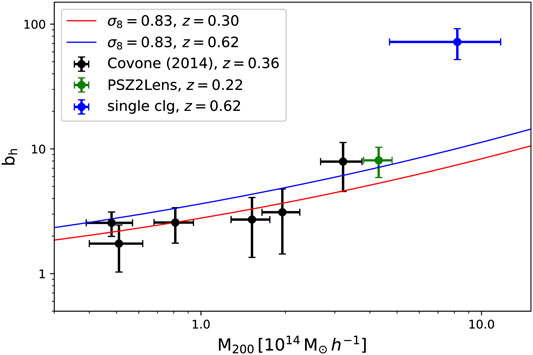
FIGURE 12. Comparison between the measured values of the halo bias and the theoretical predictions, as a function of the virial mass. Theoretical predictions are computed assuming a flat $\text{Λ}$CDM cosmological model with ${\sigma }_8=0.83$. Black points represent the measured values in the stacked sample from Covone et al. (2014) [269], at $z=0.36$. The blue point represents the single system at $z\simeq 0.62$.

In the next few years, the aim will be at determining the statistics of the halo bias values around single massive galaxy clusters, by completing a systematic study of the correlated matter distribution around a large sample of galaxy clusters, using recent and future data from wide surveys, such as KiDS and Euclid. KiDS (Kilo Degree Survey) is a public survey at the VLT Survey Telescope (Chile) which just completed the observations over about 1,500 deg₂ in the Southern hemisphere. Euclid, the forthcoming ESA space telescope, will survey about 15 thousand square degrees of the sky, detecting about ${10}^5$ galaxy clusters up to redshift z∼3. This wealth of data will allow both to trace the evolution of the correlated matter distribution and to robustly quantify the occurrence of rare systems such as PSZ2 G099.86 + 58.45. The statistics of these peculiar systems will tell us that our Cluster formation theory requires a critical revision.

15 Merging Rates of Compact Binaries in Galaxies and Stellar bhs

With the recent detections of gravitational waves (GWs) by the LIGO/Virgo collaborations, the era of multimessenger astronomy has begun. The future AdvLIGO/Virgo improved sensitivity configurations, together with the advent of the forthcoming detectors as Einstein Telescope (ET), will provide an enormous number of informations in many different fields: from astrophysics to cosmology and even to fundamental physics (e.g., refs. 277 and 278). In the last years the authors focused on forecasting the merging rates of compact binaries and the associated detection rates with different detectors as a function of redshift [279]. This issue depends on various astrophysical processes happening on different spatial and time scales: we must correctly model single stellar and binary evolution phenomena, GW physics and the environment in which binaries are formed; therefore also galaxy formation and evolution must be kept into account. In the approach of ref. 279 the authors have exploited the most recent observations of galaxies’ properties (i.e., their UV + far-IR/submillimeter/radio luminosity functions, their spectral energy distribution, the mass metallicity relationships) and combined them with stellar evolution simulations outcomes. This approach can remarkably provide joint probability distribution functions of the host galaxy properties (star formation rate, stellar mass, metallicity, etc.) and the properties of the GW signal.

In order to compute the merging rates as a functions of redshift we rely on three main ingredients: 1) a statistics of galaxies, coming from their UV and IR luminosity functions. 2) a model able to reproduce the observations of the chemical enrichment history of each individual galaxy, 3) the outcome of stellar and binary evolution simulations.

The first ingredient, given the relation between the luminosity and the star formation rate (SFR) [280], can be translated into a star formation rate function at different redshifts; it provides the number density of galaxies producing stars at different star formation rates ψ at various cosmic times/redshifts $t$: $\text{dN}/\text{d}\psi \text{dV}$ (see refs. 279 and 281). The second ingredient allows to associate a metallicity to galaxies with different properties (SFR, mass, age or morphological type). The metallicity (z) stellar winds, supernova kicks, direct collapse, common envelope effects all depend on it. Using a very simple model, in agreement with observational data, featuring a rapid linear increase of the metallicity with the galactic age up to a saturation value, the authors of ref. 279 are able to assign a probability distribution function of metallicities at given SFR: $dp/dZ\left(Z|\psi \right)$ (see refs. 282–refs. 287). Finally, the outcomes of stellar evolution simulations can provide three crucial factors: the number of merging binaries in an Hubble time per unit of star forming mass $\left[\text{dN}/{\text{dM}}_{\text{SFR}}\left(\text{Z}\right)\right]$, the chirp mass probability distribution $\left[\text{dp}/{\text{dM}}_{\text{chirp}}\left({\text{M}}_{\text{chirp}}|\text{Z}\right)\right]$ and a time delay distribution between the formation of the binary and the merging $\left[\text{dp}/{\text{dt}}_{\text{delay}}\left({\text{t}}_{\text{delay}}|\text{Z}\right)\right]$ (see e.g., 288–293).

The ingredients described above can be combined to compute the merging Koushiappasrates per bin of redshift and chirp mass as follows:

$\begin{array}{c}\frac{{\text{dN}\dot{}}_{\text{merging}}}{{\text{dzdM}}_{\text{chirp}}}\left(z,M_{\text{chirp}}\right)=\frac{\text{dV}}{\text{dz}\left(1+\text{z}\right)}{\displaystyle \int {\text{dt}}_{\text{delay}}}{\displaystyle \int \text{d}\psi \psi \frac{\text{dN}}{\text{d}\psi \text{dV}}\left(\psi ,{\text{z}}_{\text{t}-{\text{t}}_{\text{delay}}}\right)}\times \\ \times {\displaystyle \int \text{dZ}\frac{\text{dp}}{\text{dZ}}\left(\text{Z}|\psi \right)\frac{\text{dp}}{{\text{dt}}_{\text{delay}}}\left({\text{t}}_{\text{delay}}|\text{Z}\right)\frac{\text{dN}}{{\text{dM}}_{\text{SFR}}}\left(\text{Z}\right)\frac{\text{dp}}{{\text{dM}}_{\text{chirp}}}\left({\text{M}}_{\text{chirp}}|\text{Z}\right)}\end{array}(22)$

where $\text{dV}/\text{dz}$ is the differential comoving volume, dependent on the cosmological parameters, the $1/\left(1+z\right)$ factor keeps into account the cosmological time dilation and $z_{t-t_{\text{delay}}}$ is the redshift computed at the time of formation of the binary (i.e., the cosmic time at merging minus the delay time $t-t_{\text{delay}}$). This equation can be easily convolved with the sensitivity curve of a GW detector (e.g., AdvLIGO/Virgo or Einstein Telescope) to get the detected rate per redshift bin by that detector:

$\frac{{\text{dN}\dot{}}_{\text{detected}}}{\text{dz}}\left(z\right)={\displaystyle \int {\text{dM}}_{\text{chirp}}\frac{{\text{dN}\dot{}}_{\text{merging}}}{{\text{dzdM}}_{\text{chirp}}}\left(\text{z},{\text{M}}_{\text{chirp}}\right)}{\displaystyle {\int }_{{\rho }_{\text{th}}}^{\infty }\text{d}\rho \frac{\text{dp}}{\text{d}\rho }\left(\rho |\text{z},{\text{M}}_{\text{chirp}}\right)}(23)$

where ρ is the signal to noise ratio (SNR), ${\rho }_{\text{th}}$ is the SNR threshold of detectability and $\text{dp}/\text{d}\rho$ depends on the properties of the GW signal and on the characteristics of the detector. The result of Equation 23 is shown in Figure 13 for the ET detector.

FIGURE 13

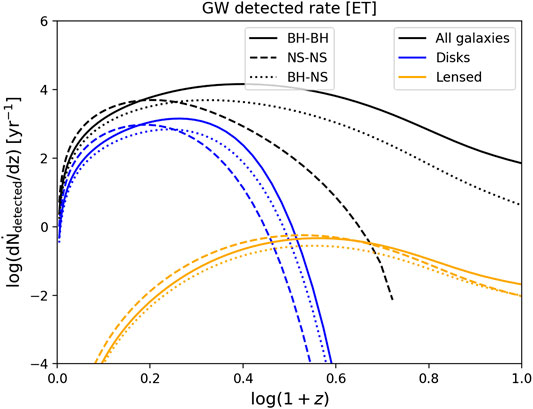
FIGURE 13. GW event rate per unit redshift expected for ET. Solid lines refer to BH-BH events, dashed lines to NS-NS events, and dotted lines to BH-NS events. Black lines refer to the total contribution from all galaxies, while blue lines represent only the contribution of disk galaxies at $z<2$. The orange lines refer to galaxy-scale gravitational lensing of GWs with magnification $\mu >10$.

The approach pursued in ref. 279 allows not only to compute the merging and detection rates, but also to relate the properties of the GW signal (chirp mass or SNR) to the properties of the host galaxy. First of all, since late type galaxies and early type galaxies show a completely different history of star formation and chemical enrichment, by using the approach of ref. 279, one can understand, depending on the characteristics of the signal, the galaxy type from which a GW event is likely to come. Moreover, one can take Equation 22 and not marginalizing over the star formation rate, obtain a joint probability distribution for the chirp mass and the SFR: $\text{dN}\dot{}/{\text{dzdM}}_{\text{chirp}}\text{d}\psi$. This quantity allows to relate a property directly measured from the GW signal, like the chirp mass, to a property of the host galaxy, i.e. the star formation rate, which can be converted into stellar mass or luminosity. This can result a powerful tool for cosmological investigation through GWs since alleviates the problem of the host galaxy association.

We can also perform tomographic cross correlations between galaxies and gravitational wave signals, as performed by the authors of ref. 294. The outcome of the cross correlations can give useful informations both on astrophysics and cosmology. Finally the approach described above can be also exploited to compute the number of lensed gravitational wave signals detected by different instruments. Lensed GWs, especially if they have an electromagnetic counterpart, can be a very strong tool to investigate both cosmology and the theory of gravity itself.

16 The Nature of Dark Matter

The existence of the “Dark Matter Phenomenon” is fully proven by the presence of a large number of (extremely strong) physical anomalies in the behavior of both the luminous matter and the radiation. These include, among others: the large-scale structures and the expansion rate of the Universe, the rotational speeds of galaxies (see Figure 14), the weak and strong gravitational lensing of background objects, the extraordinary cosmological object called the Bullet Cluster [295], the temperature radial distribution of the hot gas in galaxies and clusters of galaxies and the pattern of anisotropies in the cosmic microwave background (CMB) radiation as detected by Planck. Furthermore, the theory of Big Bang nucleosynthesis (BBN), by accurately predicting the cosmological abundance of the lightest chemical elements, indicates that most of the matter in the Universe, so as in every galaxy, cannot be made by baryons [296].

FIGURE 14

FIGURE 14. The observed Universal Rotation Curve (blue surface) of Spirals and its Luminous Matter component (red surface). $x\equiv R/R_D$, with $R_D$ the disk lenght-scale, $\tilde{V}$ is the double normalized URC: $\tilde{V}\equiv V\left(x,M_h\right)/V\left(3,M_h\right)$ with $M_h$ the galaxy halo virial mass and: $M_h={10}^{11+\mathrm{n}}{M}_{\odot }$. The discrepancy implies the presence of a dark massive component (see ref. 332).

Remarkably, the dark matter relates with the properties of the entire Universe supporting the case for which a modification of GR cannot explain, alone, all the above observational evidences.

An accurate discussion on various DM particle candidates can be found in (e.g., ref. 297), here we give a brief account of them. It is well known that, for this elusive massive component, there is a favored scenario: the $\Lambda$-cold dark matter ($\Lambda$CDM) one [298]; the dark particle is non-relativistic and can be described as a collisionless fluid; it interacts gravitationally with itself and with other massive particles and very weakly with the Standard Model (SM) particles [299, 300]. In detail, the Weakly Interacting Massive Particles (WIMPs) cross section with the SM ones is taken to be that of the Weak interactions: $\sigma \mathrm{\lesssim }{310}^{-26}{\text{cm}}^2$; particles in the (1–200) GeV mass range that interact via the electroweak force, with such self-annihilation cross section, imply a relic density of the same order of the observed matter density ${\rho }_c{\Omega }_m$. WIMPs are the relic particle from the early Universe, when all particles were in a state of thermal equilibrium. Being the temperatures of the Universe $T\gg m_{WIMP}$ the WIMP particles and their antiparticles were both created and annihilated into lighter Standard Model particles ($DMparticle+DMparticle\rightleftharpoons SMparticle+SMparticle$). As the Universe expanded and cooled down ($T\mathrm{\lesssim }{m}_{WIMP}$), the average thermal energy of the lighter particles decreased and eventually became too small to form a dark matter particle-antiparticle pair. The annihilation of the dark matter particle-antiparticle pairs did however continue and the number density of the DM particles started to decrease exponentially $\left[\propto exp\left(-m_{WIMP}/T\right)\right]$ so that the number density became so low that the DM particle-antiparticle interaction vanished. Since then, the number of dark matter particles has remained constant during the continued expansion of the Universe. Because of their large mass, WIMPs move non-relativistically since the Decoupling Time and are candidates of the CDM scenario. Noticeably, they clump together, from small structures to the largest ones according to the bottom-up scenario. They have a particular power spectrum of perturbations which guarantees unique initial conditions. It is relevant the fact that Supersymmetric extensions of the standard model of particle physics have new particles with the above properties including the “WIMP miracle”(e.g., refs. 298 and 301). Crucially, these particle, as any other which is collisionaless at galactic scale, lead to DM halos having an universal density profile that behaves as: ${\rho }_{DM}\propto r^{-1}$ in its innermost regions [302].

The Ultralight axion (ULA) with $m\sim {10}^{-22}eV$ is a scalar field [303, 304], that, at large scales mimics the behavior of a cold particle, while in (small) galaxies, where the inter-particle distance is much smaller than its de Broglie wave length, behaves in a collective way acquiring a Bose-Einstein condensates (BEC) equation of state that leads to cored dark halo density configurations, like those observed.

In self-interacting dark matter (SIDM) the DM particles do self-interact with a large scattering cross-section, but with a very small annihilation or dissipation. The relative cross-section is likely due to strong, short-range interactions, similar to neutron-neutron scattering at low-energies, or to weak interactions mediated by the exchange of light particles [305]. Then, the dark matter particles, inside the originally formed halo cusp, scatter elastically among themselves so that they are heated up and leave the region; this effect transforms the original cuspy density profile into a cored one. The SIDM collision rate is negligible during the early Universe epochs and during the period in which the cosmological structures form, so the relative cosmological scenario retains the large-scale successes of that of $\Lambda$CDM one, affecting the dark structures only at later times and at small scales. See refs. 306 and 307.

The sterile neutrino is a lepton particle beyond the SM of particle physics (e.g., refs. 308 and 309). Its existence is motivated also by arguments on the chirality of fermions and on the possibility to explain in a natural way the small active neutrino masses by means of the seesaw mechanism e.g., ref. 310. The mass of this particle when in the keV range (e.g., 311), being so a warm dark matter (WDM) particle. Created in the early Universe [312, 313] it decouples from the cosmological plasma when it is still mildly relativistic. WDM candidates may account for the various issues at small scales affecting the collisionless CDM scenario; in detail, the fermionic nature of this particle is be cosmologically crucial. In fact, for a ∼ keV mass the particle de-Broglie scale length is of the order ∼ tens kpc, i.e. the spirals's disks sizes; then,in the latter, a quantum pressure emerges balancing the gravitational force and shaping the inner DM density profile into a cored distribution [314].The different power spectrum of this particle might account for the observed lack of small mass halos in the local Universe with respect to the outcome of $\Lambda$ CDM N-Body simulations.

Recently, there appeared an unexpected new candidate for the Cold Dark Matter scenario that could raise an amazing connection between the DM in galaxies and the gravitational waves produced by the merging of stellar-mass black holes and detected by LIGO-Virgo experiments. The inferred masses of the merging Black Holes $\sim 50M_{\odot }$, infact, seems to be too high to be one of the dead ends of the evolution of the stars in galaxies, and these GW instead may signal the existence primordial black holes created in the very early Universe and working since then as collisionless Macroscopic particles The most interesting case is that in which they provide all the required galactic Dark Matter. Then, a reasonable number of detections of primordial black hole binaries could resolve the nature of this mysterious component [315]. Let us stress that these objects had continuous merging since recombination and this violent process could have generated a stochastic background of gravitational waves, likely detectable by LISA and PTA [316]. Of course, just substituting WIMPs with primordial BHs does not immediately relieve the severe tension with the observations at galactic scales that any cold particle has, independently of its mass.

The current status of the Universe features the crucial lack of any detection of Dark particles, expecially the WIMP ones, in a direct or indirect way or via super-collider experiment, allied with the lack of the distinctive central cusp in the DM halo density e.g., refs. 317 and 318 a set of observed scaling laws among the structure properties of the dark and the luminous matter components in galaxies that are too refined to arise from two of them that just share the same gravitational field (see ref. 5). This challenges the 30-year-old paradigm, that, resting on a priori knowledge of the DM nature, has led us to a quite small number of scenarios led by the collisionless Cold Dark Matter one. Motivated by such observational evidence, it is on the table the idea of resolving the dark matter mystery and its related not understood observations by following a new Paradigm: the nature of DM must be guessed/derived by deeply analyzing the properties of the dark and luminous mass distribution at any scales independently on whether the emerging scenario look to us “main stream” or “exotic”.

An application of this paradigm leads one to propose the existence of a direct interaction between Dark and Standard Model particles which has finely shaped the inner regions of galaxies [319]. Furthermore, other “exotic” DM candidates, including among many others eg the Mirror Dark Matter (e.g., ref. 320) and the Strongly Interacting Dark Matter (e.g., ref. 321), neutral dark atoms of composite dark matter [322] appear now reasonable and not anymore crushed by the existence of the WIMP particle a-priori nominated as the actual one.

17 Rotation Curves and Dark Matter in Galaxies at High Redshifts

17.1 Dark Halos and the RCs at High z

We can fairly understand the properties of Dark Matter (DM) in the local Universe (redshift $z\approx 0$) and, by means of the benefits of advancement in the instrumentation, we can now explore the DM properties at z∼1 to interpret the evolution of Dark and Luminous matter. The latter will certainly contribute to give us crucial information on the nature of DM. In detail, we have the KMOS-Redshift One Spectroscopic Survey (KROSS) data for investigating and understanding the Dark matter scenario at redshift one (z∼1) in rotation dominated galaxies (disk-type galaxies). KROSS is aimed to study the gas kinematics of redshift one Star-Forming galaxies (SFGs). Details of the observations can be found in first and foremost papers of KMOS (e.g., 323–325).

Ref. 326 investigated the samples in ref. 324 (hereafter H17) for the above explained purpose. The sample includes 409 objects with an integrated $H\alpha$ flux $F_{H\alpha }>1.5\times {10}^{-17}{\text{ergs}}^{-1}{\text{cm}}^{-2}$, i.e. with an acceptable Signal-to-noize (S/N) and an identified $H\alpha$ emission line. This sample has median redshift $z={0.85}_{-0.04}^{+0.13}$, $H\alpha$ luminosity $log\left(L_{H\alpha }\left[\text{erg}{\text{s}}^{-1}\right]\right)=41.47\pm 0.4$ and effective radii $log\left(R_e\left[kpc\right]\right)={0.45}_{0.33}^{+0.23}$ (see Table A1 of H17). Moreover, each galaxy is not an AGN and contains high quality $H\alpha$ spatially resolved data. Effective radii ($R_e$), position angles (PA), inclination angles (${\theta }_i$), absolute H-band magnitudes ($M_H$), $H\alpha$ Luminosities ($L_{H\alpha }$) and redshifts (z) and stellar masses ($M_{\ast }$) are also known.

They have modeled the kinematics of the samples under investigation with ${}^{3D}BAROLO$ code [327] that incorporates the instrumental and atmospheric effects (i.e. related to the point spread function (PSF) which determines the spatial resolution and the line spread function (LSF) which corresponds to spatial broadening, in combination these effects are known as beam-smearing.) This is done in a dynamical environment, differently from the 2D maps modeling which is strongly beam-smearing dominated in the inner region of galaxies. By using 3D-Barolo, it is possible to flawlessly compare the data and model in 3D observation space, thus correct for the beam-smearing and other effects dynamically [327, 328].

The modeling of 3D-Barolo requires three geometrical parameters, i.e., co-ordinate of galaxy center in the datacube ($x_0,y_0$), inclination angle (${\theta }_i$), position angle (PA) and three kinematic parameters, i.e., redshift (z), rotation velocity ($v_c$) and dispersion velocity from ionized gas (${\sigma }_{H\alpha }$). In their modeling, they precisely define the central co-ordinates of galaxy ($x_0,y_0$), ${\theta }_i$, z and keep the $v_c$, ${\sigma }_{H\alpha }$ and PA free to fit. This approach allows us to estimate the free parameters in annulii of increasing distance from the galaxy center without making any assumption on their evolution with radius, yielding a reliable approach on kinematic modeling of 3D datacube.

Figure 15: 1) $H\alpha$ image from chopped cube; 2) moment0 map; 2) moment1 map; 3) moment2 map; 4) Rotation Curve, black shade is data, red contour is the model and orange square is the best fit $v_{rot}$; 5) Dispersion curve, black shade is data, red contour is model and orange square is best fit, ${\sigma }_{H\alpha }$ of ionized gas.

FIGURE 15

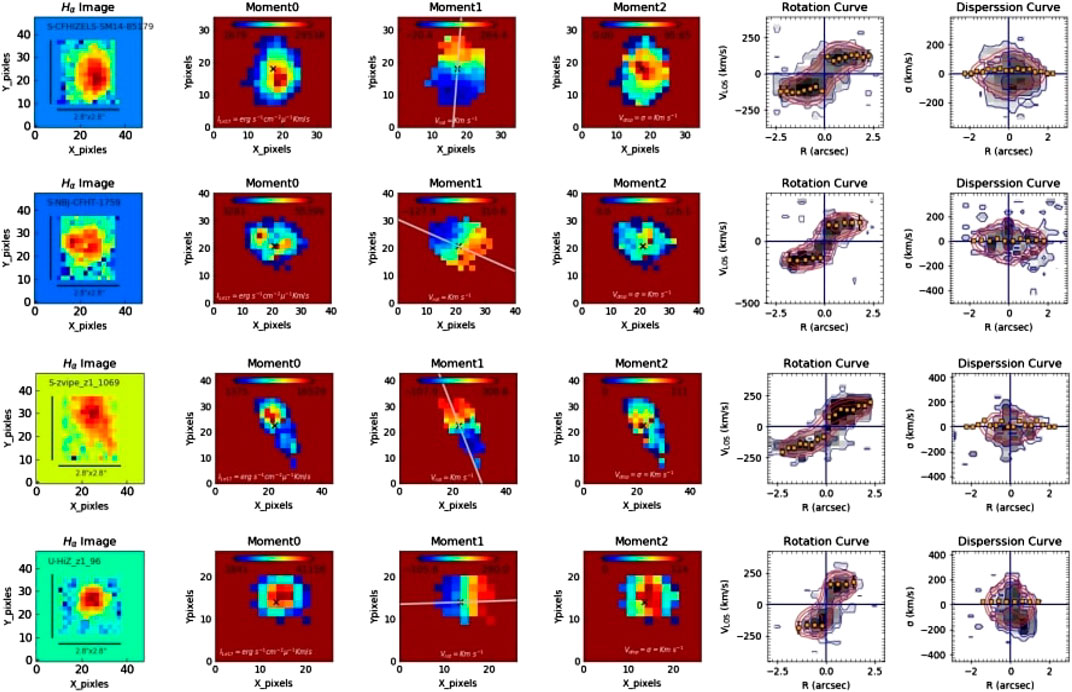
FIGURE 15. 1) $H\alpha$ image from chopped cube; 2) moment0 map; 2) moment1 map; 3) moment2 map; 4) Rotation Curve, black shade is data, red contour is the model and orange square is the best fit $v_{rot}$; 5) Dispersion curve, black shade is data, red contour is model and orange square is best fit, ${\sigma }_{H\alpha }$ of ionized gas.

They have obtained four co-added and binned RCs built out of from 201 individual RCs. Such a statistical approach has remarkable advantages: 1) it gives us a smooth distribution of RC without being affected by the random fluctuations that arise in each RC from bad data points, i.e., it virtually enhances the S/N in data; 2) it allows mass decomposition of galaxies of similar velocities but having different spatial sampling in the velocity field. This kind of approach in RC studies has been used for decades, pioneered by ref. 329 and later developed in several works [330–336]. In Figure 16 the results of co-added and binned RCs, in comparison with local RCs are shown. Within $2Kpc$, there is not data due to the low spatial and kinematical resolution, that affect also the first measure at $2kpc$. check this The RCs emerge surprisingly flattish from $R_{opt}=3.2R_D$ to 4 times $R_{opt}$, and the dark matter starts dominating within $R_{opt}$. The comparison with local RCs shows that in physical units (i.e. $V\left(R/kpc\right)/\left({\text{kms}}^{-1}\right)$ the z∼1 RCs are very similar to the local RCs, though only the mass modeling may clarify this.

FIGURE 16

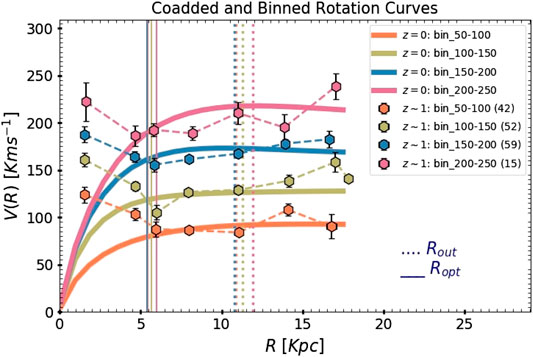
FIGURE 16. Comparison of $z\sim 1$ (hexagon connected dashed line curves) RCs and those of local spirals derived from the URC [330, 332] (solid line curves). Color code is given in the legend. Numbers in the bracket indicate the total number of RCs used in each bin. Dotted and solid vertical lines show $R_{out}$ and $R_{opt}$ for each RC (color coded as the velocity bins).

17.2 The Rotation Curves Profiles and the Nature of Dark Matter

The careful study of RCs both at low and high redshifts opens the way to pinpoint the nature of the dark particle and to follow the evolution of the DM halos during the galaxy formation era.

Among other recent works, by studying the RC of a sample of 30 dwarf irregular galaxies, it has been shown that these objects represent new targets for DM indirect searches in gamma rays: in fact, they are DM dominated object with astrophysical gamma-ray emission negligible with respect to the gamma-ray flux expected by DM annihilation events [337]. This claim have been already investigated not only at GeV energy scale, yet for heavy DM candidates at TeV energy scales, eg by the High Altitude Water Cherenkov (H.A.W.C) observatory [338]. Although multi-TeV DM candidates are not favored by benchmark models in particle physics - e.g., Super Symmetry, after decades of searching no experimental evidence of WIMP DM at GeV energy scale has been found at colliders so far. This fact has generated a crisis in physics and requires an epochal paradigm shift. In view of the new era of TeV observatories the study of particle physics nature of TeV DM candidate is a well-timed challenge and represents a new Frontier in physics.

There are few multi-TeV DM candidates available on a theoretical side. Among others, branons are WIMPs originated by a symmetry breaking mechanism in the extra-dimensional space-time. Thus, for the TeV energy scale new research windows will be opened by the current generation of cosmic-ray observatories (e.g., H.E.S.S. [339–341], IceCube [342]) and the next generation of experiments, e.g., Cherenkov Telescope Array (CTA) [343, 344] and the Square Kilometre Array (SKA) [345]. These experiments, beside the detection, will able to constraint the WIMPS mass to much higher value than the current one.

A careful analysis of high redshift RCs will be crucial for validating any new particle proposed to address the cusp-core issue emerging from all similar analysis of RCs of local galaxies.

One of these is fuzzy DM (FDM). FDM consists of ultra-light bosons that have mass in the range 10⁻²³–10⁻²⁰ eV, and arise from symmetry breaking due to the misalignment mechanism in the string theory landscape [303, 346]. Since the de Broglie wavelength of a FDM particle is a few kpc, the density fluctuations on a scale below the de Broglie wavelength are unstable and lead to the formation of a halo whose minimum mass is $\sim {10}^7{\text{M}}_{\odot }$ for a boson mass of ∼10⁻²² eV. Differently, density fluctuations on a scale above the de Broglie wavelength lead to a large scale structure of a DM halo indistinguishable from CDM [347]. As recently shown in numerical simulations, an imprint of FDM particles is the formation of a core of DM in the innermost part of each virialized halo that exhibits a flat density profiles [347]. In recent analyses of the kinematic of dwarf spheroidals, ultra-faint and ultra diffuse galaxies favor FDM with boson mass ∼10⁻²² eV over cuspy NFW profile [348–350]. Nevertheless, the debate on the fuzzy nature of DM is far to be closed. The existence of the core in each FDM halo enhances the circular velocity in the inner part of the rotation curve [351], questioning the model. Additionally, the boson mass constrained with the analysis of the Lyman-α forest data ($>7\times {10}^{-21}$ eV) [352] is almost two order of magnitudes larger than the one required to account for the kinematic of stars in dwarf galaxies (∼10⁻²² eV). Noticeably, for this particle, high redshift rotation curves will provide us with a decisive test, since in this scenario the DM halos are born with the central density core that we observe today, differently from other scenarios in which the DM cores develop with time from originally cuspy distributions [319]. At the same time, SKA and Pulsar Timing Array experiments may play an extremely important role providing us with the smoking gun for FDM by measuring the Compton and de-Broglie scale modulation of Pulsar Timing [353].

In general, it is very likely once we obtain ${\rho }_{DM}\left(r,z\right)$, where ρ is the DM density, r is the radial coordinate and z the redshift at which this quantity has been measured, we will be able to single out the DM particle.

18 Conclusion

The association of Einstein, Planck and Vera Rubin is made because these great scientists have at least two aspects in common. First, they, as seen together, represent the conjunction point of very different research lines of Physics. Always more people think that such point must be reached in order if we have to succeed in working out that New Physics which is required to frame a currently very large number of unexplained observations and experiment outcomes. The second is that they all provide examples of the time delay, often existing in Physics, between the formulation of a theory or the publication of an intriguing discovery and that of their general understanding and validation.

The idea of the great usefulness, for the growth of Physics and our understanding of the Universe, of a contamination between the fields of research of Astrophysics, Cosmology, GR and Elementary Particles is not a recent one but one has to date it 50 years back and recognize it as one of the extraordinary intuitions of Dennis Sciama [354]. Later on, other scientists have much contributed to it refs. 355–359.

Here, we have shown that this idea emerges naturally and roots many sub-fields of Astrophysic, Astroparticle and Cosmology. These include: the cosmological validation of the beyond GR scalar tensor theories, the (possibly not $\Lambda$CDM) cosmological model for the expansion of the Universe, tensions between different measurements of the same (cosmological model) parameters, the nature of dark matter, the evolution of galaxy halos and their stellar counterparts, the cosmological importance of the stellar BH in galaxies, the evolution of the dark matter perturbations at large scale, the properties of the biggest virialized objects of the Universe, the Fundamental Physics related to the scattering angle of two body systems and in curved space-time backgrounds, the bridge between classical and quantum world, the complex intrinsic neutrino nature and its cosmological importance, the tomographic description of the Universe, the origin of dark Energy, and the Holy Grail of the coupling between Gravity and Quantum Mechanics.

Let us stress that this list of fields of investigation covers only a part of all the active fields that also entangle the GR, the quantum world and the physics of the Universe and that can be successfully explored by means of the multi-lateral approach we have advocated. These are, therefore, subjects for the works of the present Special Topic. A short list of them includes: the baryogenesis, the inflation, the formation of primordial and Supermassive BH, the dark Ages of the Universe, the Astrophysical and cosmological impact of Gravitational Waves.

Finally, it could come as a surprise but, in the above discussion, an unknown entity, that we call dark matter, takes very often the center of the scene. In detail, a large number of issues related to this mystery emerge in many sub-fields of Cosmology, Physics and Elementary Particle Physics. However, one point must be stressed. The investigations of the past decades have not been able to tear the Maja veil off the Dark Matter Phenomenon. Our current knowledge presents mysterious evidences, lacks of congruence and shortcomings in both theoretical and experimental/observational sides. Theories like General Relativity and Standard Model of Elementary particles seem unable to account for the “darkness” of the Universe. As result the answers of our questions about dark Matter do not appear to be straightforward and shining but seem to follow the Nietzsche's directive: Beauty is False, Truth is Ugly. New, multi-lateral approaches to the mysteries of the Universe are likely to be the way to unveil the thick veil above.

Author Contributions

PS has conceived and coordinated this review. All authors have equally contributed in one of the sections.

Funding

The original research described in this work has been partially funded by INFN through the IS QGSKY.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationship that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.603190/full#supplementary-material.

References

1. Rubin VC, Ford WK, Thonnard N. “Rotational properties of 21 SC galaxies with a large range of luminosities and radii, from NGC 4605 (R=4kpc) to UGC 2885 (R=122kpc),”. Acta Pathol Jpn (1980) 238:471.

CrossRef Full Text | Google Scholar

2. Di Valentino E. Cosmology intertwined I: perspectives for the next decade. arXiv:2008.11283[astro-ph.CO].

Google Scholar

3. Di Valentino E. Cosmology intertwined II: the Hubble constant tension. arXiv:2008.11284[astro-ph.CO.

Google Scholar

4. Dafermos M, Rodnianski I. Lectures on black holes and linear waves. Clay Math Proc (2013) 17:97. arXiv:0811.0354 [gr-qc]

Google Scholar

5. Salucci P. The distribution of dark matter in galaxies. Astron Astro Phys Rev (2019) 27:2. doi:10.1086/115134

CrossRef Full Text | Google Scholar

6. Freese K. Status of dark matter in the universe. Int J Mod Phys (2017) 26:1730012. doi:10.1142/S0218271817300129

CrossRef Full Text | Google Scholar

7. Lambiase G, Mohanty S, Narang A, Parashari P. Testing dark energy models in the light of tension. Eur Phys J C (2019) 79:141. doi:10.1140/epjc/s10052-019-6634-6

CrossRef Full Text | Google Scholar

8. Hancock S, Rocha G. A first determination of the position of the ‘Doppler’ peak. arXiv:astro-ph/9612016.

Google Scholar

9. Riess AG. A 2.4 determination of the local value of the Hubble constant. Astrophys J (2016) 826(1):56. doi:10.3847/0004-637X/826/1/56

CrossRef Full Text | Google Scholar

10. Aghanim NPlanck collaboration. Planck 2018 results. VI. cosmological parameters. arXiv:1807.06209 astro-ph.CO].

Google Scholar

11. Riess AG, Casertano S, Yuan W, Macri LM, Scolnic D. Large magellanic Cloud Cepheid standards provide a 1% foundation for the determination of the Hubble constant and stronger evidence for physics beyond CDM. Astrophys J (2019) 876(1):85. doi:10.3847/1538-4357/ab1422

CrossRef Full Text | Google Scholar

12. Abbott TMCDES collaboration. Dark energy survey year 1 results: a precise H0 estimate from DES Y1, BAO, and D/H data. Mon Not Roy Astron Soc (2018) 480(3):3879. doi:10.1093/mnras/sty1939

Google Scholar

13. Henning JWSPT collaboration. Measurements of the temperature and E-mode polarization of the CMB from 500 square degrees of SPTpol data. Astrophys J (2018) 852(2):97. doi:10.3847/1538-4357/aa94

Google Scholar

14. Bonvin V. H0LiCOW–V.new cosmograil time delays of HE 0435-1223: to 3.8 percent precision from strong lensing in a flat CDM model. Mon Not Roy Astron Soc (2017) 465(4):4914.

CrossRef Full Text | Google Scholar

15. Alam SeBOSS Collaboration. The completed SDSS-IV extended baryon oscillation spectroscopic survey: cosmological implications from two decades of spectroscopic surveys at the apache point observatory. arXiv:2007.08991 [astro-ph.CO].

Google Scholar

16. Wong KC. H0LiCOW XIII A 2.4 measurement of $H_0$from lensed quasars: $5.3\sigma$tension between early and late-Universe probes. arXiv:1907.04869 [astro-ph.CO].

Google Scholar

17. Pesce DW. The megamaser cosmology project. XIII. combined Hubble constant constraints. Astrophys J Lett (2020) 891(1):L1. doi:10.3847/2041-8213/ab75f0

CrossRef Full Text | Google Scholar

18. Verde L, Feeney SM, Mortlock DJ, Peiris HV. Lack of cosmological evidence for dark radiation after planck. JCAP (2013) 1309:013. doi:10.1088/1475-7516/2013/09/013

CrossRef Full Text | Google Scholar

19. Trotta R, Hansen SH. Observing the helium abundance with CMB. Phys Rev D (2004) 69:023509. doi:10.1103/PhysRevD.69.023509

CrossRef Full Text | Google Scholar

20. Hou Z, Keisler R, Knox L, Millea M, Reichardt C. How massless neutrinos affect the cosmic microwave background damping tail. Phy Rev D (2013) 87:083008. doi:10.1103/physrevd.87.083008

CrossRef Full Text | Google Scholar

21. Graef LL, Benetti M, Alcaniz JS. Primordial gravitational waves and the H0-tension problem. Phys Rev D (2019) 99(4):043519. doi:10.1103/physrevd.99.043519

CrossRef Full Text | Google Scholar

22. Benetti M, Graef LL, Alcaniz JS. The H0 and σ8tensions and the scale invariant spectrum. J Cosmol Astropart Phys (2018) 1807:066. doi:10.1088/1475-7516/2018/07/066

CrossRef Full Text | Google Scholar

23. Di Valentino E, Melchiorri A, Mena O, Vagnozzi S. Interacting dark energy in the early2020s: a promising solution to the H0 and cosmic shear tensions. Phys Dark Univ (2020) 30:100666. doi:10.1016/j.dark.2020.100666

CrossRef Full Text | Google Scholar

24. Di Valentino E, Melchiorri A, Mena O, Vagnozzi S. Nonminimal dark sector physics and cosmological tensions. Phys Rev D (2020) 101(6):063502. doi:10.1103/physrevd.101.063502

CrossRef Full Text | Google Scholar

25. Benetti M, Miranda W, Borges HA, Pigozzo C, Carneiro S, Alcaniz JS, et al. Looking for interactions in the cosmological dark sector. arXiv:1908.07213 [astro-ph.CO].

Google Scholar

26. Benetti M, Graef L, Ramos RO. Observational constraints on warm inflation in loop quantum cosmology. J Cosmol Astropart (2019) 1910(10):066. doi:10.1088/1475-7516/2019/10/066

CrossRef Full Text | Google Scholar

27. Giovanni Cabass, Luca Pagano, Laura Salvati, Martina Gerbino, Elena Giusarma, Alessandro Melchiorri. Improved dark matter search results from PICO-2L Run 2. Phys. Rev. D (2016) 93:063508. doi:10.1103/PhysRevD.93,063508

Google Scholar

28. Meerburg PD, Hlozek R, Hadzhiyska B, Meyers J. Multi-wavelength constraints on the inflationary consistency relation. Phys Rev D (2015) 91(10):103505. doi:10.1103/PhysRevD.91.103505

CrossRef Full Text | Google Scholar

29. Tram T, Vallance R, Vennin V. The international school for advanced studies (SISSA), find out more. J Cosmol Astropart Phys (2017) 1701(1):046. doi:10.1088/1475-7516/2017/01/046

CrossRef Full Text | Google Scholar

30. Hill JC, McDonough E, Toomey MW, Alexander S. Early dark energy does not restore cosmological concordance. arXiv:2003.07355.

Google Scholar

31. Benevento G, Hu W, Raveri M. Can late dark energy transitions raise the hubble constant. arXiv(2002). p. 11707[astro-ph.CO].

Google Scholar

32. Knox L, Millea M. The hubble hunter’s guide. arXiv:1908.03663 [astro-ph.CO]

Google Scholar

33. Evslin J, Sen AA, Ruchika . Price of shifting the Hubble constant. Phys Rev D (2018) 97(10):103511. doi:10.1103/PhysRevD.97.103511

CrossRef Full Text | Google Scholar

34. Shafieloo A, Linder EV. Cosmographic degeneracy. Phys Rev D (2011) 84:063519. doi:10.1103/physrevd.84.063519

CrossRef Full Text | Google Scholar

35. Capozziello S, D’Agostino R, Luongo O. Extended gravity cosmography. Int J Mod Phys (2019) 28:1930016. doi:10.1142/s0218271819300167

CrossRef Full Text | Google Scholar

36. Visser M. Cosmography: cosmology without the einstein equations. Gen Relat Gravit (2005) 37:1541. doi:10.1007/s10714-005-0134-8

CrossRef Full Text | Google Scholar

37. Capozziello S, D’Agostino R, Luongo O. Cosmographic reconstruction to discriminate between modified gravity and dark energy. Acta Phys Polon Supp (2020) 13:271. doi:10.5506/aphyspolbsupp.13.271

CrossRef Full Text | Google Scholar

38. Dunsby PKS, Luongo O. On the theory and applications of modern cosmography. Int J Geomet Methods Mod Phys (2016) 13:1630002. doi:10.1142/s0219887816300026

CrossRef Full Text | Google Scholar

39. Gruber C, Luongo O, Aviles A, Bravetti A, Capozziello SO. Cosmographic analysis of the equation of state of the universe through padé approximations. Phys Rev D (2014) 89:103506. doi:10.1103/physrevd.89.103506

CrossRef Full Text | Google Scholar

40. Capozziello S, D’Agostino R, Luongo O. Cosmographic analysis with chebyshev polynomials. Mon Not Roy Astron Soc (2018) 476:3924. doi:10.1093/mnras/sty422

CrossRef Full Text | Google Scholar

41. Benetti M, Capozziello S. Connecting early and late epochs by f(z) CDM cosmography. J Cosmol Astropart Phys (2019) 1912:008. doi:10.1088/1475-7516/2019/12/008

CrossRef Full Text | Google Scholar

42. Scolnic DM. The complete light-curve sample of spectroscopically confirmed SNe Ia from pan-STARRS1 and cosmological constraints from the combined pantheon sample. Astrophys J (2018) 859(2):101. doi:10.3847/1538-4357/aab9bb

CrossRef Full Text | Google Scholar

43. Aghanim NPlanck Collaboration. Planck 2018 results. V. CMB power spectra and likelihoods. Astron Astrophys (2020) 641:A5. doi:10.1051/0004-6361/201936386

Google Scholar

44. Beutler F. The 6dF galaxy survey: baryon acoustic oscillations and the local hubble constant. Mon Not Roy Astron Soc (2011) 416:3017. doi:10.1111/j.1365-2966.2011.19250.x

CrossRef Full Text | Google Scholar

45. Ross AJ, Samushia L, Howlett C, Percival WJ, Burden A, Manera M, et al. The clustering of the SDSS DR7 main galaxy sample–I. A 4 per cent distance measure at $z=0.15$. Mon Not Roy Astron Soc (2015) 449(1):835. doi:10.1093/mnras/stv154

CrossRef Full Text | Google Scholar

46. Alam SBOSS Collaboration. The clustering of galaxies in the completed SDSS-III Baryon oscillation spectroscopic survey: cosmological analysis of the DR12 galaxy sample. Mon Not Roy Astron Soc (2017) 470(3):2617. doi:10.1093/mnras/stu2465

CrossRef Full Text | Google Scholar

47. Sahni V, Starobinsky A, Peebles PJE, Ratra B. The case for a positive cosmological lambda-term. Int J Mod Phys D (2000) 9:373. doi:10.1142/s0218271800000542

CrossRef Full Text | Google Scholar

48. Weinberg S. The cosmological constant problem. Rev Mod Phys (1989) 61:1.

CrossRef Full Text | Google Scholar

49. Capozziello S, De Laurentis M. Extended theories of gravity. arXiv:1108.6266.

Google Scholar

50. Borunda M, Janssen B, Bastero-Gil M. Palatini versus metric formulation in higher curvature gravity. J Cosmol Astropart Phys (2008) 0811. doi:10.1088/1475-7516/2008/11/008

CrossRef Full Text | Google Scholar

51. Capozziello S, D’Agostino R, Luongo O. Rational approximations of cosmography through Pad’e polynomials. J Cosmol Astropart Phys (2018) 1805:008. doi:10.1088/1475-7516/2018/05/008

CrossRef Full Text | Google Scholar

52. Capozziello S, D’Agostino R, Luongo O. Kinematic model-independent reconstruction of palatini cosmology. Gen Relat Gravit (2019) 51:2. doi:10.1007/s10714-018-2483-0

CrossRef Full Text | Google Scholar

53. Levi ME. The dark energy spectroscopic instrument (DESI). arXiv:1907.10688 [astro-ph.IM].

CrossRef Full Text | Google Scholar

54. Jha SW. Next generation LSST science. arXiv:1907.08945 [astro-ph.IM].

Google Scholar

55. Schlegel DJ. Astro2020 APC white paper: the MegaMapper: a $z>2$spectroscopic instrument for the study of inflation and dark energy. arXiv:1907.11171 [astro-ph.IM].

CrossRef Full Text | Google Scholar

56. Perlmutter S, Aldering G, Della Valle M, Deustua S, Ellis RS. Discovery of a supernova explosion at half the age of the universe. Nature (1998) 391:51–4. doi:10.1038/34124

CrossRef Full Text | Google Scholar

57. Perlmutter S, Aldering G, Goldhaber G, Knop RA, Nugent P. Measurements of $\text{Ω}$ and $\text{Λ}$ from 42 high-redshift supernovae. Astrophys J (1999) 517:565. doi:10.1086/307221/meta

CrossRef Full Text | Google Scholar

58. Riess AG, Filippenko AV, Challis P, Clocchiatti A, Diercks A. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron J (1998) 116:1009.

CrossRef Full Text | Google Scholar

59. Suzuki NThe supernova cosmology project. The Hubble space telescope cluster supernova survey. V. improving the dark-energy constraints above and building an early-type-hosted supernova sample. arXiv:1105.3470.

Google Scholar

60.Planck Collaboration. Planck 2015 results. XIII. cosmological parameters. Astron Astrophys (2016) 594:A13. doi:10.1063/1.4953315

CrossRef Full Text | Google Scholar

61. Ade PARPlanck Collaboration. Planck 2015 results. XIII. cosmological parameters. Astron Astrophys (2016) 594:A13. doi:10.1063/1.4953315

CrossRef Full Text | Google Scholar

62. Peebles PJE, Ratra B. Cosmology with a time-variable cosmological constant. Astrophys J (1988) 325:17.

CrossRef Full Text | Google Scholar

63. Ratra B, Peebles PJ. Cosmological consequences of a rolling homogeneous scalar field. Phys Rev D (1988) 37:3406.

CrossRef Full Text | Google Scholar

64. Copeland JE, Sami M, Tsujikawa S. Dynamics of dark energy. Int J Mod Phys (2006) 15:1753. doi:10.1142/S021827180600942X

CrossRef Full Text | Google Scholar

65. Clarkson C, Maartens R. Inhomogeneity and the foundations of concordance cosmology. Classical Quant Grav (2010) 27:124008. doi:10.1088/0264-9381/27/12/124008

CrossRef Full Text | Google Scholar

66. Boisseau B, Esposito-Farese G, Polarski D, Starobinsky AA, Reconstruction of a scalar-tensor theory of gravity in an accelerating universe. Phys Rev Lett (2000) 85:2236. doi:10.1103/PhysRevLett.85.2236

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Weinberg S. Implications of dynamical symmetry breaking. Phys Rev D (1976) 13:974.

CrossRef Full Text | Google Scholar

68. Carloni S, Cianci R, Feola P, Piedipalumbo E, Vignolo S. Non minimally coupled condensate cosmologies: matching observational data with phase space. J Cosmol Astrophys Particles (2019) 9:14. doi:10.1088/1475-7516/2019/09/014

CrossRef Full Text | Google Scholar

69. Piedipalumbo E, Scudellaro P, Esposito G, Rubano C. A matter-dominated cosmological model with variable G and and its confrontation with observational data. Gen Relat Gravit (2012) 44:2477. doi:10.1007/s10714-012-1409-5

CrossRef Full Text | Google Scholar

70. Demianski M, Piedipalumbo E. Observational tests of the Glavan, Prokopec and Starobinsky model of dark energy. Eur Phys J C (2019) 79:575. doi:10.1140/epjc/s10052-019-7045-4

CrossRef Full Text | Google Scholar

71. Piedipalumbo E, Della Moglie E, Cianci R. Updated f(T) gravity constraints from high-redshift cosmography. Int J Mod Phys (2014) 24:1550100. doi:10.1142/s021827181550100x

CrossRef Full Text | Google Scholar

72. Bahamonde S, Boehmer C, Christian G, Carloni S, Copeland EJ, Fang W, et al. Dynamical systems applied to cosmology: dark energy and modified gravity. Phys Rep (2018) 775:1–22. doi:10.1016/j.physrep.2018.09.001

CrossRef Full Text | Google Scholar

73. Piedipalumbo E, De Laurentis M, Capozziello S. Noether symmetries in interacting quintessence cosmology. Phys Dark Universe (2020) 27:100444. doi:10.1016/j.dark.2019.100444

CrossRef Full Text | Google Scholar

74. Amendola L. Coupled quintessence. Phys Rev D (2000) 62:043511. doi:10.1142/9789812772923_0007

CrossRef Full Text | Google Scholar

75. Bonometto SA, Mezzetti M, Mainini R. Strongly coupled dark energy with warm dark matter vs LCDM. J Cosmol Astropart Phys (2017) 10:11. doi:10.1088/1475-7516/2017/10/011

CrossRef Full Text | Google Scholar

76. Bonometto SA, Mainini R, Mezzetti M. Strongly coupled dark energy cosmologies yielding large-mass primordial black holes. Mon Not Roy Astron Soc (2019) 486:2321–35. doi:10.1093/mnras/stz846

CrossRef Full Text | Google Scholar

77. Riess AG, Rodney SA, Scolnic DM, Shafer DL, . Strolger L-G, Ferguson HC, et al. Type Ia supernova distances at redshift >1.5 from the Hubble space telescope multi-cycle treasury programs: the early expansion rate. Acta Pathol Jpn (2018) 853:126. doi:10.3847/1538-4357/aaa5a9

CrossRef Full Text | Google Scholar

78. Riess AG, Casertano S, Yuan W, Macri L, Bucciarelli B, Lattanzi MG, et al. Milky way cepheid standards for measuring cosmic distances and application to gaia DR2: implications for the Hubble constant. Acta Pathol Jpn (2018) 861:126. doi:10.3847/1538-4357/aac82e

CrossRef Full Text | Google Scholar

79. Ghirlanda G, Ghisellini G, Lazzati D, Firmani C. Gamma-ray bursts: new rulers to measure the universe. Acta Pathol Jpn (2004) 613:L13. doi:10.1086/424915

CrossRef Full Text | Google Scholar

80. Firmani C, Ghisellini G, Ghirlanda G, Avila-Reese V. A new method optimized to use gamma-ray bursts as cosmic rulers. MNRAS (2005) 360:L1–5. doi:10.1111/j.1745-3933.2005.00023.x

CrossRef Full Text | Google Scholar

81. Amati L, Frontera F, Tavani M, J in’t Zand JJ, Antonelli A, Costa E, et al. Intrinsic spectra and energetics of BeppoSAX gamma-ray bursts with known redshifts. Astron Astrophys (2002) 390:81. doi:10.1051/0004-6361:20020722

CrossRef Full Text | Google Scholar

82. Amati L, Guidorzi C, Frontera F, Della Valle M, Finelli F, Landi R, et al. Measuring the cosmological parameters with the–correlation of gamma-ray bursts. Marcel Grossmann Meet (2008) 391:577. doi:10.1142/9789814623995_0038

CrossRef Full Text | Google Scholar

83. Piedipalumbo E, Della Moglie E, De Laurentis M, Scudellaro P. High-redshift investigation on the dark energy equation of state. Mon Not Roy Astron Soc (2014) 441:3643. doi:10.1093/mnras/stu790

CrossRef Full Text | Google Scholar

84. Demianski M, Piedipalumbo E. Standardizing the gamma-ray bursts with the amati–relation: the updated Hubble diagram and implications for cosmography. Mon Not Roy Astron Soc 415:3580. doi:10.1111/j.1365-2966.2011.18975.x

CrossRef Full Text | Google Scholar

85. Demianski M, Piedipalumbo E, Sawant D, Amati L. Cosmology with gamma-ray bursts. I. The Hubble diagram through the calibrated–correlation. Astron Astrophys (2017) 598:A112. doi:10.1051/0004-6361/201628909

CrossRef Full Text | Google Scholar

86. Demianski M, Piedipalumbo E, Sawant D, Amati L. Cosmology with gamma-ray bursts. II. Cosmography challenges and cosmological scenarios for the accelerated universe. Astron Astrophys (2017) 598:A113. doi:10.1051/0004-6361/201628911

CrossRef Full Text | Google Scholar

87. Demianski M, Piedipalumbo E, Rubano C. The gamma-ray bursts Hubble diagram in quintessential cosmological models. Mon Not Roy Astron Soc (2011) 411:1213. doi:10.1111/j.1365-2966.2010.17751.x

CrossRef Full Text | Google Scholar

88. Eisenstein DJ, Zehavi I, Hogg DW, Scoccimarro R. Detection of the baryon acoustic peak in the large-scale correlation function of SDSS luminous red galaxies. Acta Pathol Jpn (2005) 633:560. doi:10.1086/466512

CrossRef Full Text | Google Scholar

89. Chávez R, Plionis M, Basilakos S, Terlevich R. Constraining the dark energy equation of state with H II galaxies. Mon Not R Astron Soc Lett (2016) 462:2431–39. doi:10.1093/mnras/stw1813

CrossRef Full Text | Google Scholar

90. Negrete CA, Dultzin D, Marziani P, Sulentic JW. Quasars as cosmological standard candles. Front Astron Space Sci (2017) 4:59. doi:10.3389/fspas.2017.00059

CrossRef Full Text | Google Scholar

91. Lusso E, Risaliti G. The tight relation between X-ray and ultraviolet luminosity of quasars. Astrophys J (2016) 819:154. doi:10.3847/0004-637x/819/2/154

CrossRef Full Text | Google Scholar

92. G RisalitiLusso EE. Cosmological constraints from the Hubble diagram of quasars at high redshifts. Nature Astron (2018) 3:272–277. doi:10.1038/s41550-018-0657-z

CrossRef Full Text | Google Scholar

93. Lusso E, Piedipalumbo E, Risaliti G, Paolillo M. Tension with the flat CDM model from a high-redshift Hubble diagram of supernovae, quasars, and gamma-ray bursts. Astron Astrophys (2019) 628:L4. doi:10.1051/0004-6361/201936223

CrossRef Full Text | Google Scholar

94. Akaike HH. A new look at the statistical model identification. IEEE Trans Automat Contr (1974) 19:716.

CrossRef Full Text | Google Scholar

95. Chevallier M, Polarski D. Accelerating universes with scaling dark matter. Int J Mod Phys (2001) 10:213–223. doi:10.1142/s0218271801000822

CrossRef Full Text | Google Scholar

96. Linder EV. Exploring the expansion history of the universe. Phys Rev Lett (2003) 90:091301. doi:10.1103/PhysRevLett.90.091301

PubMed Abstract | CrossRef Full Text | Google Scholar

97. Doran M, Robbers G. Early dark energy cosmologies. J Cosmol Astrophys Particles (2006) 06:026. doi:10.1088/1475-7516/2006/06/026

CrossRef Full Text | Google Scholar

98. Farooq O, Ratra B. Hubble parameter measurement constraints on the cosmological deceleration-acceleration transition redshift. Astrophys J (2013) 766:L7. doi:10.1088/2041-8205/766/1/l7

CrossRef Full Text | Google Scholar

99. Aubourg EBOSS Collaboration. Cosmological implications of baryon acoustic oscillation measurements. Phys Rev D (2015) 92:123516. doi:10.1103/PhysRevD.92.123516

Google Scholar

100. Damour T. Gravitational scattering, post-minkowskian approximation and effective one-body theory. Phys Rev D (2016) 94(10):104015. doi:10.1103/physrevd.94.104015

CrossRef Full Text | Google Scholar

101. Damour T. High-energy gravitational scattering and the general relativistic two-body problem. Phys Rev D (2018) 97(4):044038. doi:10.1103/physrevd.97.044038

CrossRef Full Text | Google Scholar

102. Bern Z, Cheung C, Roiban R, Shen CH. Scattering amplitudes and the conservative Hamiltonian for binary systems at third post-Minkowskian order. Phys Rev Lett (2019) 122(20):201603. doi:10.1103/PhysRevLett.122.201603

PubMed Abstract | CrossRef Full Text | Google Scholar

103. ZengSolon Z, Cheung C, Roiban R, Shen CH. Black hole binary dynamics from the double copy and effective theory. J High Energy Phys (2019) 10:206. doi:10.1007/jhep10(2019)206

CrossRef Full Text | Google Scholar

104. Bini D, Damour T. Gravitational scattering of two black holes at the fourth post-Newtonian approximation. Phys Rev D (2017) 96(6):064021. doi:10.1103/physrevd.96.064021

CrossRef Full Text | Google Scholar

105. Amati D, Ciafaloni M, Veneziano G. Higher order gravitational deflection and soft bremsstrahlung in planckian energy superstring collisions. Nucl Phys B (1990) 347:550.

CrossRef Full Text | Google Scholar

106. Bini D, Damour T, Geralico A. Novel approach to binary dynamics: application to the fifth post-newtonian level. Phys Rev Lett (2019) 123(23):231104. doi:10.1103/PhysRevLett.123.231104

PubMed Abstract | CrossRef Full Text | Google Scholar

107. Damour T. Classical and quantum scattering in post-Minkowskian gravity. Phys Rev D (2020) 102(2):024060. doi:10.1103/physrevd.102.024060

CrossRef Full Text | Google Scholar

108. Bini D, Damour T, Geralico A. Binary dynamics at the fifth and fifth-and-a-half post-newtonian orders. Phys Rev D (2020) 102(2):024061. doi:10.1103/physrevd.102.024062

CrossRef Full Text | Google Scholar

109. Kälin G, Porto RA. From boundary data to bound states. Part II. scattering angle to dynamical invariants (with twist). J High Energy Phys (2020) 2:120. doi:10.1007/jhep02(2020)120

CrossRef Full Text | Google Scholar

110. Kälin G, Porto RA. Post-Minkowskian effective field theory for conservative binary dynamics. arXiv:2006.01184 hep-th].

Google Scholar

111. Bern Z, Luna A, Roiban R, Shen CH, Zeng M. Spinning black hole binary dynamics, scattering amplitudes and effective field theory. arXiv:2005.03071 hep-th]].

Google Scholar

112. Esposito G, Minucci M. A new perspective on the Ermakov-Pinney and scalar wave equations. Lett High Energy Phys (2019) 3:5. doi:10.31526/lhep.3.2019.134

CrossRef Full Text | Google Scholar

113. Cohen JM, Kegeles LS. Electromagnetic fields in curved spaces: a constructive procedure. Phys Rev D (1974) 10:1070. doi:10.1103/physrevd.10.1070

CrossRef Full Text | Google Scholar

114. Bini D, Esposito G. New solutions of the Ermakov-Pinney equation in curved spacetime. Gen Relativ Gravit (2020) 52:60. doi:10.1007/s10714-020-02713-y

CrossRef Full Text | Google Scholar

115. Schmidt BG, Stewart JM. The scalar wave equation in a Schwarzschild spacetime. Proc Roy Soc Lond (1979) 367:503. doi:10.1016/j.physletb.2018.10.010

CrossRef Full Text | Google Scholar

116. Christodoulou D, Klainerman S. The global non-linear stability of the Minkowski space. Princeton, NJ: Princeton University Press (1993).

Google Scholar

117. Christodoulou D. the formation of black holes in general relativity: Berlin, Germany: European Mathematical Society (2009).

CrossRef Full Text | Google Scholar

118. Bini D., Esposito G. On the local isometric embedding of trapped surfaces into three-dimensional Riemannian manifolds. Class. Quantum Grav (2018) 35:195003. doi:10.1088/1361-6382/aadb39

CrossRef Full Text | Google Scholar

119. Darboux G. Leçons sur la Théorie Générale des Surfaces et les Applications Géometriques du Calcul Infinitesimal. III. Lignes Géodesiques et Courbure Géodesique. Parameters Différentiels. Déformation des Surfaces. Paris: Gauthier-Villars (1894).

Google Scholar

120. Weingarten J. Sur la déformation des surfaces. Acta Math (1896) 20:159.

Google Scholar

121. Hawking SW, Perry MJ, Strominger A. Soft hair on black holes. Phys Rev Lett (2016) 116:231301. doi:10.1103/PhysRevLett.116.231301

PubMed Abstract | CrossRef Full Text | Google Scholar

122. Esposito G., Alessio F. From parabolic to loxodromic BMS transformations. Gen Relativ Gravit (2018) 50:141. doi:10.1007/s10714-018-2465-2

CrossRef Full Text | Google Scholar

123. Battista E, Esposito G. What is a reduced boundary in general relativity? in progress (2020). Work in progress.

Google Scholar

124. Donoghue JF. Leading quantum correction to the Newtonian potential. Phys Rev Lett (1994) 72:2996. doi:10.1103/PhysRevLett.72.2996

PubMed Abstract | CrossRef Full Text | Google Scholar

125. Tisserand F. F. Traité de Mécanique Céleste. Paris: Gauthier-VillarsJacques Gabay (1889-1896), Vols. 1-4.

Google Scholar

126. Battista E, Esposito G, Tartaglia A. An effective-gravity perspective on the sun-jupiter-comet three-body system. Int J Geom Methods Mod Phys (2020) 17:2050168. doi:10.1142/s0219887820501686

CrossRef Full Text | Google Scholar

127. Mavromatos NE, Meregaglia A, Rubbia A, Sakharov A, Sarkar S. Quantum-gravity decoherence effects in neutrino oscillations: expected constraints from CNGS and J-PARC. Phys Rev D (2008) 77:053014. doi:10.1103/physrevd.77.053014

CrossRef Full Text | Google Scholar

128. Marletto C, Vedral V, Deutsch D. Quantum-gravity effects could in principle be witnessed in neutrino-like oscillations. New J Phys (2018) 20:083011. doi:10.1088/1367-2630/aad5d8

CrossRef Full Text | Google Scholar

129. Bond JR, Efstathiou G, Silk J. Massive neutrinos and the large scale structure of the universe. Phys Rev Lett (1980) 45:1980–4.

CrossRef Full Text | Google Scholar

130. Fukugita M, Liu GC, Sugiyama N. Limits on neutrino mass from cosmic structure formation. Phys Rev Lett (2000) 84:1082–5. doi:10.1103/PhysRevLett.84.1082

PubMed Abstract | CrossRef Full Text | Google Scholar

131. Blas D, Garny M, Konstandin T, Lesgourgues J. Structure formation with massive neutrinos: going beyond linear theory. J Cosmol Astrophys Phys (2014) 11:039. doi:10.1088/1475-7516/2014/11/039

CrossRef Full Text | Google Scholar

132. Lattanzi M., Gerbino M. Status of neutrino properties and future prospects–cosmological and astrophysical constraints. Front Physiol (2018) 5:70. doi:10.3389/fphy.2017.00070

CrossRef Full Text | Google Scholar

133. Blasone M, Vitiello G. Quantum field theory of fermion mixing. Ann Phys (1995) 244:283.

CrossRef Full Text | Google Scholar

134. Giunti C, Kim CW. Fundamentals of neutrino physics and astrophysics. Oxford, UK: Univ. Pr. (2007).

Google Scholar

135. Blasone M, Luciano GG, Petruzziello L, Smaldone L. Casimir effect for mixed fields. Phys Lett B (2018) 786:278. doi:10.1016/j.physletb.2018.10.004

CrossRef Full Text | Google Scholar

136. Ahluwalia DV, Labun L, Torrieri G. Neutrino mixing in accelerated proton decay. Eur Phys J A (2016) 52:189. doi:10.1103/physrevd.97.105008

CrossRef Full Text | Google Scholar

137. Blasone M, Lambiase G, Luciano GG, Petruzziello L. Role of neutrino mixing in accelerated proton decay. Phys Rev D (2018) 97:105008. doi:10.1103/physrevd.97.105008

CrossRef Full Text | Google Scholar

138. Ginzburg VL, Syrovatskii SI. Cosmic magnetobremsstrahlung (synchrotron radiation). Annu Rev Astron Astrophys (1965) 3:297.

CrossRef Full Text | Google Scholar

139. Matsas GEA, Vanzella DAT. Decay of protons and neutrons induced by acceleration. Phys Rev D (1999) 59:094004

CrossRef Full Text | Google Scholar

140. Unruh WG. Notes on black hole evaporation. Phys Rev D (1976) 14:870.

CrossRef Full Text | Google Scholar

141. Blasone M, Lambiase G, Luciano GG, Petruzziello L. On the β-decay of the accelerated proton and neutrino oscillations: a three-flavor description with CP violation. Eur Phys J C (2020) 80:130. doi:10.1140/epjc/s10052-020-7658-7

CrossRef Full Text | Google Scholar

142. Blasone M, Lambiase G, Luciano GG, Petruzziello L. Neutrino oscillations in Unruh radiation. Phys Lett B (2020) 800:135083. doi:10.1016/j.physletb.2019.135083

CrossRef Full Text | Google Scholar

143. Blasone M, Lambiase G, Luciano GG, Petruzziello L. Remarks on the unruh effect with mixed neutrinos. J Phys Conf Ser (2019) 1275:012063. doi:10.1088/1742-6596/1275/1/012063

CrossRef Full Text | Google Scholar

144. Blasone M, Lambiase G, Luciano GG. Nonthermal signature of the unruh effect in field mixing. Phys Rev D (2017) 96:025023. doi:10.1103/physrevd.96.025023

CrossRef Full Text | Google Scholar

145. Blasone M, Lambiase G, Luciano GG. Non-thermal unruh radiation for flavour neutrinos. J Phys Conf Ser (2018) 956:012021. doi:10.1088/1742-6596/956/1/012021

CrossRef Full Text | Google Scholar

146 Blasone M, Jizba P, Luciano GG. Unified formalism for thermal quantum field theories: a geometric viewpoint. Ann Phys (2018) 397:213. doi:10.1016/j.aop.2018.08.009

CrossRef Full Text | Google Scholar

147. Ahluwalia DV, Burgard C. Gravitationally induced quantum mechanical phases and neutrino oscillations in astrophysical environments. Gen Relat Gravit (1996) 28:1161.

CrossRef Full Text | Google Scholar

148. Cardall CY, Fuller GM. Neutrino oscillations in curved space-time: an heuristic treatment. Phys Rev D (1997) 55:7960–6.

CrossRef Full Text | Google Scholar

149. Blasone M, Lambiase G, Luciano GG, Petruzziello L, Smaldone L. Time-energy uncertainty relation for neutrino oscillations in curved spacetime. Classic Quant Grav (2020) 37:155004. doi:10.1088/1361-6382/ab995c

CrossRef Full Text | Google Scholar

150. Buoninfante L, Luciano GG, Petruzziello L, Smaldone L. Neutrino oscillations in extended theories of gravity. Phys Rev D (2020) 101:024016. doi:10.1103/physrevd.101.024016

CrossRef Full Text | Google Scholar

151. Capozziello S, Lambiase G. Inertial effects on neutrino oscillations. Eur Phys J C (2000) 12:343. doi:10.1007/s100529900212

CrossRef Full Text | Google Scholar

152. Dvornikov M. Neutrino interaction with background matter in a non-inertial frame. Mod Phys Lett A (2015) 30:1530017. doi:10.1142/s0217732315300177

CrossRef Full Text | Google Scholar

153. Blasone M, Lambiase G, Luciano GG, Petruzziello L. Neutrino oscillations in accelerated frames. Europhys Lett (2018) 124:51001. doi:10.1209/0295-5075/124/51001

CrossRef Full Text | Google Scholar

154. Aker MKATRIN. Improved upper limit on the neutrino mass from a direct kinematic method by KATRIN. Phys Rev Lett (2019) 123:221802. doi:10.1103/PhysRevLett.123.221802

PubMed Abstract | CrossRef Full Text | Google Scholar

155. Betts S. Development of a relic neutrino detection experiment at PTOLEMY: princeton tritium observatory for light, early-universe, massive-neutrino yield. arXiv:1307.4738 astro-ph.IM].

Google Scholar

156. Betti MGPTOLEMY. Neutrino physics with the PTOLEMY project: active neutrino properties and the light sterile case. J Cosmol Astrophys Phys (2019) 07:047. doi:10.1088/1475-7516/2019/07/047

CrossRef Full Text | Google Scholar

157. El-Neaj YA. AEDGE: atomic experiment for dark matter and gravity exploration in space. EPJ Quant Technol (2020) 7:6.

Google Scholar

158. Boyarsky A, Drewes M, Lasserre T, Mertens S, Ruchayskiy O. Sterile neutrino dark matter. Prog Part Nucl Phys (2019) 104:1–45. doi:10.1088/978-1-6817-4481-0

CrossRef Full Text | Google Scholar

159. Cardani L. Neutrinoless double beta decay overview. Sci Post Phys Proc (2019) 1:024. doi:10.21468/scipostphysproc.1.024

CrossRef Full Text | Google Scholar

160. Rodejohann W. Neutrino-less double beta decay and particle physics. Int J Mod Phys E (2011) 20:1833–930. doi:10.1142/s0218301311020186

CrossRef Full Text | Google Scholar

161. Menon A, Thalapillil AM. Interaction of Dirac and Majorana neutrinos with weak gravitational fields. Phys Rev D (2008) 78:113003. doi:10.1103/physrevd.78.113003

CrossRef Full Text | Google Scholar

162. Barranco J, Delepine D, Gonzalez-Macias V, Lujan-Peschard C, Napsuciale M. Scattering processes could distinguish Majorana from Dirac neutrinos. Phys Lett B (2014) 739:343–47. doi:10.1016/j.physletb.2014.11.008

CrossRef Full Text | Google Scholar

163. Rodejohann W, Xua XJ, Yaguna CE. Distinguishing between Dirac and Majorana neutrinos in the presence of general interactions: JHEP05 (2017). p. 024.

Google Scholar

164. Kayser B. Majorana neutrinos and their electromagnetic properties. Phys Rev. D (1982) 26:1662.

CrossRef Full Text | Google Scholar

165. Sobkow W, Blaut A. Probing neutrino nature at borexino detector with chromium neutrino source. Eur Phys J C (2016) 76:550. doi:10.1140/epjc/s10052-016-4406-0

CrossRef Full Text | Google Scholar

166. Rosen SP. Analog of the Michel parameter for neutrino-electron scattering: a test for Majorana neutrinos. Phys Rev Lett (1982) 48:842.

CrossRef Full Text | Google Scholar

167. Capolupo A, Giampaolo SM, Lambiase G. Decoherence in neutrino oscillations, neutrino nature and CPT violation. Phys Lett B (2019) 792:298.

CrossRef Full Text | Google Scholar

168. Buoninfante L, Capolupo A, Giampaolo SM, Lambiase G, Revealing neutrino nature and CPT violation with decoherence effects accepted for publication on EPJ C. arXiv:2001.07580 hep-ph] (2020).

Google Scholar

169. Capolupo A, Giampaolo SM, Hiesmayr BC, Vitiello G. Geometric phase of neutrinos: differences between Dirac and Majorana neutrinos. Phys Lett B (2018) 780:216. doi:10.1016/j.physletb.2018.03.016

CrossRef Full Text | Google Scholar

170. King SF. Neutrino mass models. Rep Prog Phys (2004) 67:107–57. doi:10.1063/1.2149691

CrossRef Full Text | Google Scholar

171. Giunti C. No effect of Majorana phases in neutrino oscillations. Phys Lett B (2010) 686:41–3. doi:10.1016/j.physletb.2010.02.020

CrossRef Full Text | Google Scholar

172. Capolupo A, Lambiase G, Quranta A. Neutrinos in curved spacetime: particle mixing and flavor oscillations. Phys Rev D (2020) 101:095022. doi:10.1103/physrevd.101.095022

CrossRef Full Text | Google Scholar

173. Capolupo A, Giampaolo SM, Quranta A. (2020). Neutrinos in a dense medium, CP and CPT violations: beyond the MSW effect. arXiv:2008.08119 hep-ph].

Google Scholar

174. Lindblad G. On the generators of quantum dynamical semigroups. Commun Math Phys (1976) 48(2):119–30.

CrossRef Full Text | Google Scholar

175. Gorini V, Kossakowski A, Sudarshan ECG. Completely positive dynamical semigroups of N-level systems. J Math Phys (1976) 17(5):821.

CrossRef Full Text | Google Scholar

176. Capolupo A, Giampaolo SM, Lambiase G, Quaranta A, Discerning the nature of neutrinos: decoherence and geometric phases. Universe (2020). 6 (11), 207. doi:10.3390/universe6110207

Google Scholar

177. Birrell ND, Davies PCV. Quantum fields in curved space. Cambridge: Cambridge University Press (1982).

Google Scholar

178. Casimir H. On the attraction between two perfectly conducting plates. Proc Koninklijke Nederl Akademie Wetenschappen (1948) 51:793.

Google Scholar

179. Lamoreaux SK. Demonstration of the Casimir force in the 0.6 to 6μm range. Phys Rev Lett (1997) 78:5.

CrossRef Full Text | Google Scholar

180. Bressi G, Carugno G, Onofrio R, Ruoso G. Measurement of the Casimir force between parallel metallic surfaces. Phys Rev Lett (2002) 88:041804. doi:10.1103/PhysRevLett.88.041804

PubMed Abstract | CrossRef Full Text | Google Scholar

181. Milton KA. The Casimir effect: physical manifestations of Zero-Point Energy. Singapore: World Scientific (2001).

CrossRef Full Text | Google Scholar

182. Bordag M, Klimchitskaya GL, Mohideen U, Mostepanenko VM. Advances in the Casimir effect. Oxford: Oxford Univ. Press (2009).

Google Scholar

183. Calloni E, Di Fiore L, Esposito G, Milano L, Rosa L. Vacuum fluctuation force on a rigid Casimir cavity in a gravitational field. Phys Lett (2002) 297:328. doi:10.1016/s0375-9601(02)00445-0

CrossRef Full Text | Google Scholar

184. Fulling SA, Milton KA, Parashar P, Romeo A, Shajesh KV, Wagner J, et al. How does Casimir energy fall?. Phys Rev D (2007) 76:025004. doi:10.1103/physrevd.76.025004

CrossRef Full Text | Google Scholar

185. Esposito G, Napolitano GM, Rosa L. Energy-momentum tensor of a Casimir apparatus in a weak gravitational field: scalar case. Phys Rev D (2008) 77:105011. doi:10.1103/physrevd.77.105011

CrossRef Full Text | Google Scholar

186. Nazari B. Casimir effect of two conducting parallel plates in a general weak gravitational field. Eur Phys J C (2015) 75:501. doi:10.1140/epjc/s10052-015-3732-y

CrossRef Full Text | Google Scholar

187. Calloni E, De Laurentis M, De Rosa R, Garufi F, Rosa L, Di Fiore L, et al. Towards weighing the condensation energy to ascertain the Archimedes force of vacuum. Phys Rev D (2014) 90:022002. doi:10.1103/physrevd.90.022002

CrossRef Full Text | Google Scholar

188. Avino S. Archimedes experiment: weighting the vacuum. Proc Sci (2018) 2018:20. doi:10.22323/1.325.0020

Google Scholar

189. Sorge F. Casimir effect in a weak gravitational field. Classical Quant Grav (2005) 22:5109. doi:10.1088/0264-9381/22/23/012

CrossRef Full Text | Google Scholar

190. Sorge F. Casimir effect in a weak gravitational field: Schwinger’s approach. Classical Quant Grav (2019) 36(23):235006. doi:10.1088/1361-6382/ab4def

CrossRef Full Text | Google Scholar

191. Sorge F. Gravitational waves and coherent phonon states in elastic media: 1D-analysis. J Phys Comm (2018) 2(12):125012. doi:10.1088/2399-6528/aaf33e

CrossRef Full Text | Google Scholar

192. Sorge F, Wilson JH. Casimir effect in free fall towards a Schwarzschild black hole. Phys Rev D (2019) 100(10):105007. doi:10.1103/physrevd.100.105007

CrossRef Full Text | Google Scholar

193. Wilson JH, Sorge F, Fulling SA. Tidal and non-equilibrium Casimir effect in free-fall. Phys Rev D (2020) 101(6):065007. doi:10.1103/physrevd.101.065007

CrossRef Full Text | Google Scholar

194. Sorge F. Casimir energy and gravitomagnetism. Class Quant Grav (2009) 26:235002. doi:10.1088/0264-9381/26/23/235002

CrossRef Full Text | Google Scholar

195. Lambiase G, Stabile A. Casimir effect in extended theories of gravity. Phys Rev D (2017) 95(8):084019. doi:10.1103/physrevd.95.084019

CrossRef Full Text | Google Scholar

196. Blasone M, Lambiase G, Petruzziello L, Stabile A. Casimir effect in post-Newtonian gravity with Lorentz-violation. Eur Phys J C (2018) 78(11):97611. doi:10.1140/epjc/s10052-018-6464-y

CrossRef Full Text | Google Scholar

197. Buoninfante L, Lambiase G, Petruzziello L, Stabile A. Casimir effect in quadratic theories of gravity. Eur Phys J C (2019) 79(1):41. doi:10.1140/epjc/s10052-019-6574-1

PubMed Abstract | CrossRef Full Text | Google Scholar

198. Sorge F. Cimir energy in Kerr space-time. Phys Rev D (2014) 90(8):084050. doi:10.1103/physrevd.90.084050

CrossRef Full Text | Google Scholar

199. Sorge F. Casimir effect around an Ellis wormhole. Int J Mod Phys (2020) 29(1):2050002. doi:10.1142/s0218271820500029

CrossRef Full Text | Google Scholar

200. Sorge F. Dynamical casimir effect in a kicked box. Int J Mod Phys A (2006) 21:6173. doi:10.1142/s0217751x0603429x

CrossRef Full Text | Google Scholar

201. Sorge F. Do gravitational waves create particles?. Classical Quant Grav (2000) 17:4655. doi:10.1088/0264-9381/17/22/306

CrossRef Full Text | Google Scholar

202. Sorge F. Quantum fluids, Josephson tunneling and gravitational waves. Classical Quant Grav (2010) 27:225001. doi:10.1088/0264-9381/27/22/225001

CrossRef Full Text | Google Scholar

203. Carlson CE, Swanson IJ. Casimir energy in astrophysics: gamma-ray bursts from QED vacuum transitions. Found Phys (2000) 30:775–83. doi:10.1023/A:1003741111963

Google Scholar

204. Man’ko VI. Conventional quantum mechanics without wave function and density matrix. AIP Conf Proc (1999) 464(1):191.

Google Scholar

205. Ibort A, Man’ko VI, Marmo G, Simoni A, Ventriglia F. An introduction to the tomographic picture of quantum mechanics. Phys Scripta (2009) 79:065013. doi:10.1088/0031-8949/79/06/065013

CrossRef Full Text | Google Scholar

206. Manko VI, Marmo G, Stornaiolo C. Radon transform of Wheeler-DeWitt equation and tomography of quantum states of the universe. Gen Relat Gravit (2005) 37:99–14. doi:10.1007/s10714-005-0005-3

CrossRef Full Text | Google Scholar

207. Man’ko VI, Marmo G, Stornaiolo C. Cosmological dynamics in tomographic probability representation. Gen Relat Gravit (2005) 37:2003. doi:10.1007/s10714-005-0161-5

CrossRef Full Text | Google Scholar

208. Man’ko VI, Marmo G, Stornaiolo C. Tomographic entropy and cosmology. Gen Relat Gravit (2008) 40:1449. doi:10.1007/s10714-007-0571-7

CrossRef Full Text | Google Scholar

209. Capozziello S, Man’ko VI, Marmo G, Stornaiolo C. Tomographic representation of minisuperspace quantum cosmology and noether symmetries. Gen Relat Gravit (2008) 40:2627. doi:10.1007/s10714-008-0643-3

CrossRef Full Text | Google Scholar

210. Capozziello S, Man’ko VI, Marmo G, Stornaiolo C. A tomographic description for classical and quantum cosmological perturbations. Phys Scripta (2009) 80:045901. doi:10.1088/0031-8949/80/04/045901

CrossRef Full Text | Google Scholar

211. Stornaiolo C. Tomographic represention of quantum and classical cosmology. Astrophys Space Sci Proc (2014) 38(3):211–19. doi:10.1007/978-3-319-02063-1_15

CrossRef Full Text | Google Scholar

212. Stornaiolo C. Tomographic cosmology. Phys Scripta (2015) 90(7):074032. doi:10.1088/0031-8949/90/7/074032

CrossRef Full Text | Google Scholar

213. Stornaiolo C. Tomographic analysis of the De Sitter model in quantum and classical cosmology. Int J Geom Meth Mod Phys (2018) 16(1):1950012. doi:10.1142/s0219887819500129

CrossRef Full Text | Google Scholar

214. Stornaiolo C. Tomographic analysis of quantum and classical de Sitter cosmological models. Int J Mod Phys D (2019) 28:2040009. doi:10.1142/s021827182040009x

CrossRef Full Text | Google Scholar

215. Stornaiolo C. Int J Geom Meth Mod Phys (2020) 17(11):2050167. doi:10.1142/S0219887820501674

CrossRef Full Text | Google Scholar

216. Buchdahl HA. Non-linear Emergent classical universes from initial quantum states in a tomographical description. Mont Not Roy Astr Soc (1970) 150:1.

CrossRef Full Text | Google Scholar

217. Colemann S. Why there is nothing rather than something: a theory of the cosmological constant. Nucl Phys B (1988) 310(3), 643.

CrossRef Full Text | Google Scholar

218. Peebles PJE, Ratra B. The cosmological constant and dark energy. Rev Mod Phys (2003) 75(2):559. doi:10.5772/51697

CrossRef Full Text | Google Scholar

219. Steinhardt PJ, Turok N. Why the cosmological constant is small and positive. Science (2006) 312:1180. doi:10.1126/science.1126231

PubMed Abstract | CrossRef Full Text | Google Scholar

220. Carlip S. Hiding the cosmological constant. Phys Rev Lett (2019) 123:131302. doi:10.1103/PhysRevLett.123.131302

PubMed Abstract | CrossRef Full Text | Google Scholar

221. Viaggiu S. On a physical description and origin of the cosmological constant Class. Quant Grav (2018) 35(21):215011. doi:10.1088/1361-6382/aae445

CrossRef Full Text | Google Scholar

222. Viaggiu S. The physical origin of the cosmological constant: continuum limit and the analogy with the casimir effect. Phys Scripta (2019) 94(12):125014. doi:10.1088/1402-4896/ab3d02

CrossRef Full Text | Google Scholar

223. Viaggiu S. The cosmological constant from Planckian fluctuations and the averaging procedure. Found Phys (2019) 49(1):1287. doi:10.1007/s10701-019-00308-5

CrossRef Full Text | Google Scholar

224. Buchert T. On average properties of inhomogeneous fluids in general relativity II: perfect fluid cosmologies. Gen Relat Gravit (2001) 33:1381. doi:10.1023/a:1012061725841

CrossRef Full Text | Google Scholar

225. Misner CW, Sharp CH. Relativistic equations for adiabatic, spherically symmetric gravitational collapse. Phys Rev B (1964) 136:571.

CrossRef Full Text | Google Scholar

226. Viaggiu S. Entropy, temperature and internal energy of trapped gravitons and corrections to the black hole entropy. Phys A (2017) 488:72–84. doi:10.1016/j.physa.2017.07.009

CrossRef Full Text | Google Scholar

227. Viaggiu S. Building a linear equation of state for trapped gravitons from finite size effects and the Schwarzschild black hole case. Int J Mod Phys (2018) 27:1850061. doi:10.1142/s021827181850061x

CrossRef Full Text | Google Scholar

228. Viaggiu S. Bekenstein-Hawking entropy in expanding universes from black hole theorems. Mod Phys Lett A (2014) 29:1450091. doi:10.1142/s0217732314500916

CrossRef Full Text | Google Scholar

229. Viaggiu S. First law of thermodynamics for dynamical apparent horizons and the entropy of Friedmann universes. Gen Relat Gravit (2015) 47:86. doi:10.1007/s10714-015-1928-y

CrossRef Full Text | Google Scholar

230. Saha S. Viaggiu entropy and the generalized second law in a flat FLRW Universe. Int J Mod Phys A (2019) 34(30):1950193. doi:10.1142/s0217751x19501938

CrossRef Full Text | Google Scholar

231. Abbot BP. Virgo, Ligo Scientific. Phys Rev Lett (2016) 116:241103. doi:10.1103/PhysRevLett.116.241103

PubMed Abstract | Google Scholar

232. Penrose R. On gravity’s role in quantum state reduction. Gen Relat Gravit (1996) 28:581.

CrossRef Full Text | Google Scholar

233. Diosi L. Models for universal reduction of macroscopic quantum fluctuations. Phys Rev A Gen Phys (1989) 40:1165.

PubMed Abstract | CrossRef Full Text | Google Scholar

234. Bassi A, Ghirardi GC. Dynamical reduction models. Phys Rep (2003) 379:257–426. doi:10.1016/s0370-1573(03)00103-0

CrossRef Full Text | Google Scholar

235. Bahrami M, Grobardt A, Donadi S, Bassi A. The Schrödinger–Newton equation and its foundations. New J Phys (2014) 16:115007. doi:10.1088/1367-2630/16/11/115007

CrossRef Full Text | Google Scholar

236. De Filippo S. Emergence of classicality in non relativistic quantum mechanics through gravitational self-interaction, arXiv:quant-ph/0104052.

Google Scholar

237. De Filippo S. Gravity-induced entropy in the quantum motion of a macroscopic body, arXiv:gr-qc/0105013.

Google Scholar

238. De Filippo S., Maimone F. Non-unitary higher derivative gravity classically equivalent to Einstein gravity and its Newtonian limit. Phys Rev D (2002) 66:044018. doi:10.1103/physrevd.66.044018

CrossRef Full Text | Google Scholar

239. Bekenstein JD. Black holes and entropy. Phys Rev D (1973) 7:2333.

CrossRef Full Text | Google Scholar

240. Hawking SW. Particle creation by black holes. Commun Math Phys (1975) 43:199.

CrossRef Full Text | Google Scholar

241. Maimone F, Scelza G, Naddeo A, Pelino V. Quantum superpositions of a mirror for experimental tests for nonunitary Newtonian gravity. Phys Rev A (2011) 83:062124. doi:10.1103/physreva.83.062124

CrossRef Full Text | Google Scholar

242. Landau L, Lifshitz M. Statistical physics. Oxford: Pergamon Press (1978).

Google Scholar

243. Zurek W, Paz J. Decoherence, chaos, and the second law. Phys Rev Lett (1994) 72:2508. doi:10.1103/PhysRevLett.72.2508

PubMed Abstract | CrossRef Full Text | Google Scholar

244. Wald RM. The thermodynamics of black holes. Living Rev Relat (2001) 4:6. doi:10.1007/978-94-017-2651-1_11

CrossRef Full Text | Google Scholar

245. Hawking SW. Breakdown of predictability in gravitational collapse. Phys Rev D (1976) 14:2460.

CrossRef Full Text | Google Scholar

246. Scelza G, Maimone F, Naddeo A. A two-particle simulation of nonunitary Newtonian gravity. J Phys Comm (2018) 2:015014. doi:10.1088/2399-6528/aaa374

CrossRef Full Text | Google Scholar

247. De Filippo S, Maimone F, Naddeo A, Scelza G. Microscopic foundation of the second law of thermodynamics within nonunitary Newtonian gravity. Int J Quant Inf (2019) 17:1941006. doi:10.1142/s0219749919410065

CrossRef Full Text | Google Scholar

248. Bombelli L, Koul RK, Lee J, Sorkin RD. Quantum source of entropy for black holes. Phys Rev D (1986) 34:373.

CrossRef Full Text | Google Scholar

249. Deutsch JM. Eigenstate thermalization hypothesis. Rep Prog Phys (2018) 81:082001. doi:10.1088/1361-6633/aac9f1

PubMed Abstract | CrossRef Full Text | Google Scholar

250. Rigol M, Dunjko V, Olshanii M. Thermalization and its mechanism for generic isolated quantum systems. Nature (2008) 452:854. doi:10.1038/nature06838

PubMed Abstract | CrossRef Full Text | Google Scholar

251. De Filippo S, Maimone F, Naddeo A, Scelza G, Quantum superpositions of a mirror for experimental tests for nonunitary Newtonian gravity. Phys Rev A (2011) 83:062124. doi:10.13140/2.1.1942.0164

CrossRef Full Text | Google Scholar

252. De Filippo S, Nonunitary Newtonian gravity makes semiclassical gravity viable for all practical purposes. arXiv:1807.10469.

CrossRef Full Text | Google Scholar

253. Maimone F, Scelza G, Naddeo A. A natural cure for causality violations in Newton-Schrödinger equation. Physica Scripta (2019) 94:075001. doi:10.1088/1402-4896/ab030d

CrossRef Full Text | Google Scholar

254. De Filippo S. The Schroedinger-Newton model as $N\to \infty$limit of a N color model. arXiv:gr-qc/0106057.

Google Scholar

255. Gisin N. Stochastic quantum dynamics and relativity. Helv Phys Acta (1989) 62:363.

Google Scholar

256. Polchinski J. Weinberg’s nonlinear quantum mechanics and the Einstein-Podolsky-Rosen paradox. Phys Rev Lett (1991) 66:397. doi:10.1103/PhysRevLett.66.397

PubMed Abstract | CrossRef Full Text | Google Scholar

257. De Filippo S, Maimone F, Naddeo A, Scelza G. Preparation.

Google Scholar

258. Feynman RP, Vernon FL. The theory of a general quantum system interacting with a linear dissipative system. Ann Phys (1963) 24:118. doi:10.3847/1538-4357/ab0964

CrossRef Full Text | Google Scholar

259. Valdarnini R. A multifiltering study of turbulence in a large sample of simulated galaxy clusters. Acta Pathol Jpn (2019) 874:42.

Google Scholar

260. Valdarnini R. Improved performances in subsonic flows of an SPH scheme with gradients estimated using an integral approach. Acta Pathol Jpn (2016) 831:103. doi:10.3847/0004-637X/831/1/103

Google Scholar

261. Valdarnini R. X-ray temperature spectroscopy of simulated cooling clusters. New Astron (2006) 12:71–93. doi:10.1016/j.newast.2006.06.005

CrossRef Full Text | Google Scholar

262. Vazza F, Roediger E, Brüggen M. Astron Astrophys (2012) 544:A103. doi:10.1051/0004-6361/201118688

Google Scholar

263. Mohapatra R, Sharma P. Turbulence in the ICM from mergers, cool-core sloshing, and jets: results from a new multi-scale filtering approach. Mon Not Roy Astron Soc (2019) 484:4881–896. doi:10.1093/mnras/stz328

CrossRef Full Text | Google Scholar

264. Fabian AC. Cooling flows in clusters of galaxies. Annu Rev Astron Astrophys (1994) 32:277–318.

CrossRef Full Text | Google Scholar

265. McNamara BR, Nulsen PEJ. Mechanical feedback from active galactic nuclei in galaxies, groups, and clusters. New J Phys (2012) 14:055023. doi:10.1088/1367-2630/14/5/055023

CrossRef Full Text | Google Scholar

266. Mo HJ, White SDM. An Analytic model for the spatial clustering of dark matter halos. Mon Not Roy Astron Soc (1996) 282:347.

CrossRef Full Text | Google Scholar

267. Tinker JL, Robertson BE, Kravtsov AV, Klypin A, Warren MS, Yepes G, et al. The large scale bias of dark matter halos: numerical calibration and model tests. Astrophys J (2010) 724:878. doi:10.1088/0004-637x/724/2/878

CrossRef Full Text | Google Scholar

268. Johnston DE[SDSS collaboration]. Cross-correlation weak lensing of SDSS galaxy clusters II: cluster density profiles and the mass–richness relation. arXiv:0709.1159 [astro-ph].

CrossRef Full Text | Google Scholar

269. Covone G, Sereno M, Kilbinger M, Cardone VF. Measurement of the halo bias from stacked shear profiles of galaxy clusters. Astrophys J (2014) 784:L25. doi:10.1088/2041-8205/784/2/l25

CrossRef Full Text | Google Scholar

270. Oguri M, Takada M. Combining cluster observables and stacked weak lensing to probe dark energy: self-calibration of systematic uncertainties. Phys Rev D (2011) 83:023008. doi:10.1103/physrevd.83.023008

CrossRef Full Text | Google Scholar

271. Campigotto MC, Diaferio A, Hernandez X, Fatibene L. Strong gravitational lensing in gravity. J Cosmol Astrophys Phys (2017) 06:057. doi:10.1088/1475-7516/2017/06/057

CrossRef Full Text | Google Scholar

272. Bozza V, Pietroni S, Melchiorre C. Caustics in gravitational lensing by mixed binary systems. Universe (2007) 6(8):106. doi:10.3390/universe6080106

CrossRef Full Text | Google Scholar

273. Sereno M. Gravitational lensing detection of an extremely dense environment around a galaxy cluster. Nat Astron (2018) 2(9):744. doi:10.1038/s41550-018-0508-y

CrossRef Full Text | Google Scholar

274. Sereno M, Covone G, Izzo L, Ettori S. PSZ2LenS. weak lensing analysis of the Planck clusters in the CFHTLenS and in the RCSLenS. Mon Not Roy Astron Soc (2017) 472(2):1946–971. doi:10.1093/mnras/stx2085

CrossRef Full Text | Google Scholar

275. Heymans C. CFHTLenS: the Canada-France-Hawaii telescope lensing survey. Mon Not Roy Astron Soc (2012) 427:146–66. doi:10.1111/j.1365-2966.2012.21952.x

CrossRef Full Text | Google Scholar

276. Hildebrandt H. RCSLenS: the red cluster sequence lensing survey. Mon Not Roy Astron Soc (2016) 463(1):635–54. doi:10.1093/mnras/stw2013

CrossRef Full Text | Google Scholar

277. Taylor SR. Cosmology using advanced gravitational-wave detectors alone. Phys Rev D (2012) 85, 023535. doi:10.1103/physrevd.85.023535

CrossRef Full Text | Google Scholar

278. Barack L. Black holes, gravitational waves and fundamental physics A Roadmap. Classical Quan Grav (2019) 36:14. doi:10.1088/1361-6382/ab0587

Google Scholar

279. Boco L. Merging rates of compact binaries in galaxies: perspectives for gravitational wave detections. Astrophys J (2019) 881:2. doi:10.3847/1538-4357/ab328e

CrossRef Full Text | Google Scholar

280. Kennicutt RC. Star formation in galaxies along the Hubble sequence. Ann Rev (1998) 36:189.

CrossRef Full Text | Google Scholar

281. Mancuso C. The quest for dusty star-foirming galaxies at high redshift. Astrophys J (2016) 823:2. doi:10.1016/j.physrep.2014.02.009

CrossRef Full Text | Google Scholar

282. Arrigoni M. Galactic chemical evolution in hierarchical formation models–I. early-type galaxies in the local universe. Mon Not Roy Astrono Soc (2010) 402:173–90. doi:10.1111/j.1365-2966.2009.15924.x

CrossRef Full Text | Google Scholar

283. Gallazzi A. Charting the evolution of the ages and metallicities of massive galaxies since. Astrophys J (2014) 788:72. doi:10.1088/0004-637x/788/1/72

CrossRef Full Text | Google Scholar

284. Andrews BH. The mass-metallicity relation with the direct method on stacked spectra of SDSS galaxies. Astrophys J (2013) 765:140. doi:10.1088/0004-637x/765/2/140

CrossRef Full Text | Google Scholar

285. Zahid HJ. The FMOS-COSMOS survey of star-forming galaxies at . II. the mass-metallicity relation and the dependence on star formation rate and dust extinction. Astrophys J (2014) 792:75. doi:10.1088/0004-637x/792/1/75

CrossRef Full Text | Google Scholar

286. Onodera M. ISM excitation and metallicity of star-forming galaxies at from near-IR spectroscopy. Astrophys J (2016) 822:42. doi:10.3847/0004-637x/822/1/42

CrossRef Full Text | Google Scholar

287. Pantoni L. New analytic solutions for galaxy evolution: gas, stars, metals, and dust in local ETGs and their high-z star-forming progenitors. Astrophys J (2019) 880:129. doi:10.3847/1538-4357/ab2adc

CrossRef Full Text | Google Scholar

288. Spera M, Mapelli M. Very massive stars, pair-instability supernovae and intermediate-mass black holes with the SEVN code. Mon Not Roy Astrono Soc (2017) 470, 4739–749. doi:10.1093/mnras/stx1576

CrossRef Full Text | Google Scholar

289. Dominik M. Double compact objects. I. The significance of the common envelope on merger rates. Astrophys J (2012) 759:52. doi:10.1088/0004-637x/759/1/52

CrossRef Full Text | Google Scholar

290. Belczynsky K. The first gravitational-wave source from the isolated evolution of two stars in the 40–100 solar mass range. Nature (2016) 534:512–15. doi:10.1038/nature18322

PubMed Abstract | CrossRef Full Text | Google Scholar

291. Dominik M. Double compact objects. III. gravitational-wave detection rates. Astrophys J (2015) 806:263. doi:10.1088/0004-637x/806/2/263

CrossRef Full Text | Google Scholar

292. de Mink SE, Belczynsky K. The progenitors of compact-object binaries: impact of metallicity, common envelope and natal kicks. Astrophys J (2015) 814:1. doi:10.1093/mnras/sty1999

Google Scholar

293. Chruslinska M. Double neutron stars: merger rates revisited. Mon Not Roy Astrono Soc (2018) 474:2937–58. doi:10.1093/mnras/stx2923

CrossRef Full Text | Google Scholar

294. Scelfo G. Galaxies-gravitational waves multimessenger cross-correlations: detectability and exploitation as an astrophysical probe. arXiv:2007.08534 [astro-ph.CO]].

Google Scholar

295. Clowe D, Gonzalez A, Markevitch M. Weak-lensing mass reconstruction of the interacting cluster 1E 0657-558: direct evidence for the existence of dark matter. Acta Pathol Jpn (2004) 604:596–603. doi:10.1086/381970

CrossRef Full Text | Google Scholar

296. Persic M, Salucci P. The baryon content of the universe. Mon Not Roy Astrono Soc (1992) 258:14.

CrossRef Full Text | Google Scholar

297. Bauer M, Plehn T. (2017). Yet another introduction to dark matter. ArXiv:1705.01987 hep-ph].

Google Scholar

298. Kolb EW, Turner MS. The early universe: Boston, MA: Addison-Wesley (1990).

Google Scholar

299. Jungman G, Kamionkowski M, Griest K. Supersymmetric dark matter. PhR (1996) 267:195.

CrossRef Full Text | Google Scholar

300. Bertone G. Particle dark matter: observations, models and searches: Cambridge, UK: Cambridge University Press (2010).

Google Scholar

301. Steigman G, Turner M. Cosmological constraints on the properties of weakly interacting massive particles. Nucl Phys B (1985) 253:375.

CrossRef Full Text | Google Scholar

302. Navarro JF, Frenk CS, White SDM A universal density profile from hierarchical clustering. Acta Pathol Jpn (1997) 490:493.

CrossRef Full Text | Google Scholar

303. Hu W, Barkana R, Gruzinov A. Fuzzy cold dark matter: the wave properties of ultralight particles. Phys Rev Lett (2000) 85:1158. doi:10.1103/PhysRevLett.85.1158

PubMed Abstract | CrossRef Full Text | Google Scholar

304. Hui L, Ostriker JP, Tremaine S, Witten E. Ultralight scalars as cosmological dark matter. Phys Rev (2017) 95:043541. doi:10.1103/physrevd.95.043541

CrossRef Full Text | Google Scholar

305. Spergel DN, Steinhardt PJ. Observational evidence for self-interacting cold dark matter. Phys Rev Lett (2000) 84:3760. doi:10.1103/PhysRevLett.84.3760

PubMed Abstract | CrossRef Full Text | Google Scholar

306. Zavala J, Vogelsberger M, Walker M. Constraining self-interacting dark matter with the milky way’s dwarf spheroidals. Mon Not Roy Astrono Soc (2013) 431:L20–24. doi:10.1093/mnrasl/sls053

CrossRef Full Text | Google Scholar

307. Kaplinghat M, Linden T, Yu H. Galactic center excess in γ rays from annihilation of self-interacting dark matter. Phys Rev Lett (2015) 114:211303. doi:10.1103/PhysRevLett.114.211303

PubMed Abstract | CrossRef Full Text | Google Scholar

308. Adhikari R, Agostini M, Ky N. A white paper on keV sterile neutrino dark matter. JCAP (2017) 01:025. doi:10.1088/1475-7516/2017/01/025

Google Scholar

309. Boyarsky A, Drewes M, Lasserre T. Sterile neutrino dark matter. Prog Part Nucl Phys (2019) 104:1. doi:10.1016/j.ppnp.2018.07.004

Google Scholar

310. Asaka T, Blanchet S, Shaposhnikov M. The ?MSM, dark matter and neutrino masses. Phys Lett B (2005) 631:151. doi:10.1016/j.physletb.2005.09.070

CrossRef Full Text | Google Scholar

311. Naumov DV. The sterile neutrino: a short introduction. EPJ Web Conf (2019) 207:04004. doi:10.1051/epjconf/201920704004

CrossRef Full Text | Google Scholar

312. Dodelson S, Widrow LM. Sterile neutrinos as dark matter. Phys Rev Lett (1994) 72:17. doi:10.1103/PhysRevLett.72.17

PubMed Abstract | CrossRef Full Text | Google Scholar

313. Kusenko A. Sterile neutrinos: the dark side of the light fermions. Phys Rep (2009) 481:1–28. doi:10.1016/j.physrep.2009.07.004

CrossRef Full Text | Google Scholar

314. Destri C, de Vega HJ, Sanchez NG. Warm dark matter primordial spectra and the onset of structure formation at redshift z. Phys Rev D (2013) 88:083512. doi:10.1103/physrevd.88.083512

CrossRef Full Text | Google Scholar

315. Green . Microlensing and dynamical constraints on primordial black hole dark matter with an extended mass function. PRD (2016) 94, 063530. doi:10.1103/PhysRevD.94.063530

CrossRef Full Text | Google Scholar

316. García-Bellido J. Massive primordial black holes as dark matter and their detection with gravitational waves. J Phys Conf Ser (2017) 840:012032. doi:10.1088/1742-6596/840/1/012032

CrossRef Full Text | Google Scholar

317.de Blok WJG. The core-cusp problem. Adv Astron (2010) 789293. doi:10.1155/2010/789293

Google Scholar

318. Gentile G, Burkert A, Salucci P. The cored distribution of dark matter in spiral galaxies. Mon Not Roy Astr Soc (2004) 351:903–22. doi:10.1111/j.1365-2966.2004.07836.x

CrossRef Full Text | Google Scholar

319. Salucci P, Turini N, di Paolo C. Paradigms and scenarios for the dark matter phenomenon. Universe (2020) 6:118. doi:10.3390/universe6080118

CrossRef Full Text | Google Scholar

320. Roux J, Cline JM. Constraining galactic structures of mirror dark matter. Phys Rev D (2020) 102f3518R. doi:10.1103/physrevd.102.063518

CrossRef Full Text | Google Scholar

321.Kamada. Strongly-interacting massive particle and dark photon in the era of the intensity Frontier. Phys Rev D (2020) 102:075001. doi:10.1103/physrevd.102.075001

CrossRef Full Text | Google Scholar

322. Khlopov , Yu M. Physics of dark matter in the light of dark atom. J Mod Phys Lett A (2011) 26:2823. doi:10.1142/S0217732311037194

CrossRef Full Text | Google Scholar

323. Stott JP. The KMOS redshift one spectroscopic survey (KROSS): dynamical properties, gas and dark matter fractions of typical z 1 star-forming galaxies. Mon Not Roy Astron Soc (2016) 457:1888–1904. doi:10.1093/mnras/stw129

CrossRef Full Text | Google Scholar

324. Harrison CHM. The KMOS redshift one spectroscopic survey (KROSS): rotational velocities and angular momentum of galaxies. Mon Not Roy Astron Soc (2017) 467:1965–83. doi:10.1093/mnras/stx217

CrossRef Full Text | Google Scholar

325. Tiley A. KROSS–sami: a direct IFS comparison of the Tully–Fisher relation across 8 Gyr since. Mon Not Roy Astron Soc (2019) 482:2166–88. doi:10.1093/mnras/sty2794

CrossRef Full Text | Google Scholar

326. Sharma G. Flat rotation curves of star-forming galaxies and evidence of disk-scale length evolution. arXiv:2005.00279.

Google Scholar

327. Di T, Di EM, Fraternali F. 3D barolo: a new 3D algorithm to derive rotation curves of galaxies. Mon Not Roy Astron Soc (2015) 451:3021–33. doi:10.1093/mnras/stv1213

CrossRef Full Text | Google Scholar

328. Di Teodoro EM, Fraternali F, Miller SH. Flat rotation curves and low velocity dispersions in KMOS star-forming galaxies at z 1. Astrophys J (2016) 594:77. doi:10.1051/0004-6361/201628315

CrossRef Full Text | Google Scholar

329. Persic M, Salucci P. The universal galaxy rotation curve. Astrophys J (1991) 368:60.

CrossRef Full Text | Google Scholar

330. Persic M, Salucci P, Stel F. The universal rotation curve of spiral galaxies—I. the dark matter connection. Mon Not Roy Astron Soc (1996) 281:27.

CrossRef Full Text | Google Scholar

331. Salucci P, Burkert A. Dark matter scaling relations. Astrophys J (2000) 537:9. doi:10.1086/312747

CrossRef Full Text | Google Scholar

332. Salucci P. The universal rotation curve of spiral galaxies–II. The dark matter distribution out to the virial radius. Mon Not Roy Astron Soc (2007) 378:41. doi:10.1111/j.1365-2966.2007.11696.x

CrossRef Full Text | Google Scholar

333. Catinella B, Giovanelli R, Haynes MP. Template rotation curves for disk galaxies. Astrophys J (2006) 640:751. doi:10.1086/500171

CrossRef Full Text | Google Scholar

334. Yegorova IA. Rotation curves of luminous spiral galaxies. Astronomische Nachrichten (2011) 332:846–53. doi:10.1002/asna.201111582

CrossRef Full Text | Google Scholar

335. Karukes EV, Salucci P. The universal rotation curve of dwarf disc galaxies. Mon Not Roy Astron Soc (2017) 465:4703–722. doi:10.1093/mnras/stw3055

CrossRef Full Text | Google Scholar

336. Lapi A, Salucci P, Danese L. Precision scaling relations for disk galaxies in the local universe. Astrophys J (2018) 859:2. doi:10.3847/1538-4357/aabf35

CrossRef Full Text | Google Scholar

337. Gammaldi V, Karukes E, Salucci P. Theoretical predictions for dark matter detection in dwarf irregular galaxies with gamma rays. Phys Rev D (2018) 98(8):083008. doi:10.1103/physrevd.98.083008

CrossRef Full Text | Google Scholar

338. Cadena SH. [HAWC], Constraints on cross-section and lifetime of dark matter with HAWC Observations of dwarf Irregular galaxies PoS. [arXiv:1908.08884 [astro-ph.HE]].

Google Scholar

339. Cembranos JAR, Gammaldi V, Maroto AL. Spectral study of the HESS J1745-290 Gamma-Ray Source as Dark Matter Signal. JCAP (2013) 4:051. doi:10.1088/1475-7516/2013/04/051

CrossRef Full Text | Google Scholar

340. Cembranos JAR, Gammaldi V, Maroto AL. Possible dark matter origin of the gamma ray emission from the galactic center observed by HESS. Phys Rev D (2012) 86:103506. doi:10.1103/physrevd.86.103506

CrossRef Full Text | Google Scholar

341. Gammaldi V. Analysis of the very inner milky way dark matter distribution and gamma-ray signals. Phys Rev D (2016) 94(12):121301. doi:10.1103/PhysRevD.94.121301

Google Scholar

342. Cembranos JAR, Gammaldi V, Maroto AL. Neutrino fluxes from dark matter in the HESS J1745-290 source at the galactic center. Phys Rev D (2014) 90(4):043004. doi:10.1103/physrevd.90.043004

CrossRef Full Text | Google Scholar

343. Aguirre-Santaella A. “Cherenkov Telescope Array sensitivity to branon dark matter models” JCAP (2020) 10:041.

CrossRef Full Text | Google Scholar

344. Acharyya A. The cherenkov telescope array consortium. [CTA], [arXiv:2007.16129 [astro-ph.HE]].

Google Scholar

345. Cembranos JAR. SKA-Phase 1 sensitivity to synchrotron radio emission from multi-TeV dark matter candidates. Phys Dark Univ (2020) 27:100448. doi:10.1016/j.dark.2019.100448

CrossRef Full Text | Google Scholar

346. Arvanitaki A, Dimopoulos S, Dubovsky S, Kaloper N, March-Russell J. String axiverse. Phys Rev D (2010) 81:123530. doi:10.1103/physrevd.81.123530

CrossRef Full Text | Google Scholar

347. Schive HY, Chiueh T, Broadhurst T. Cosmic structure as the quantum interference of a coherent dark wave. Nat Phys (2014) 10:496–9. doi:10.1038/nphys2996

CrossRef Full Text | Google Scholar

348. Chen SR, Schive HY, Chiueh T. Jeans analysis for dwarf spheroidal galaxies in wave dark matter. Mon Not Roy Astron Soc (2017) 468:1338–48. doi:10.1093/mnras/stx449

CrossRef Full Text | Google Scholar

349. Broadhurst T, de Martino I, Nhan Luu H, Smoot GF, Tye SHH. Ghostly galaxies as solitons of bose-einstein dark matter. Phys Rev D (2020) 101:083012. doi:10.1103/physrevd.101.083012

CrossRef Full Text | Google Scholar

350. Pozo A, Broadhurst T, de Martino I, Nhan Luu H, Smoot GF, Lim J, et al. Wave dark matter and ultra diffuse galaxies. arXiv:2003.0831 (2020).

Google Scholar

351. Bar N, Blum K, Eby J, Sato R. Ultralight dark matter in disk galaxies. Phys Rev D (2019) 99:103020. doi:10.1103/PhysRevD.99.103020

CrossRef Full Text | Google Scholar

352. Baur J, Palanque-Delabrouille N, Yleche C, Magneville C, Viel M. Lyman-alpha forests cool warm dark matter. J Cosmol Astropart Phys (2016) 2016:012. doi:10.1088/1475-7516/2016/08/012

CrossRef Full Text | Google Scholar

353. De Martino I, Broadhurst T, Tye SH, Chiueh T. Recognizing axionic dark matter by Compton and de Broglie scale modulation of pulsar timing. Phys Rev Lett (2017) 119:221103. doi:10.1103/PhysRevLett.119.221103

PubMed Abstract | CrossRef Full Text | Google Scholar

354. LazkozSchive DW. Modern cosmology. Cambridge: Cambridge University Press (1971).

Google Scholar

355. Sakharov AD. Cosmoparticle physics-a multidisciplinary science. Vestnik AN SSSR (1989) 4:39.

Google Scholar

356. Khlopov MY. Fundamental cross-disciplinary studies of microworld and universe. Vestnik Russ Acad Sci (2001) 71:1133.

Google Scholar

357. Khlopov MI. Cosmoparticle physics: Singapore World Scientific Singapore (1999).

Google Scholar

358. Khlopov MI. Fundamentals of cosmoparticle physics. UK: CISP-Springer Cambridge (2012).

Google Scholar

359. Peebles PJE. Cosmology’s century: an inside history of our modern understanding of the universe: Princeton, NJ: Princeton University Press (2020).

CrossRef Full Text | Google Scholar

360. Giacconi R. First results from the x-ray and optical survey of the chandra deep field south. Astrophys J (2001) 551:624. doi:10.1086/320222

CrossRef Full Text | Google Scholar

361. Lehmer BD. The extended chandra deep field-south survey: chandra point-source catalogs. Astrophys J (2005) 161:21. doi:10.1086/444590

CrossRef Full Text | Google Scholar

362 Scoville N. COSMOS: Hubble space telescope observations. Astrophys J (2007) 172:38. doi:10.1086/516580

Google Scholar

363. Lawrence A. The UKIRT infrared deep sky survey (UKIDSS). Mon Not Roy Astron Soc (2007) 379:1599. doi:10.1111/j.1365-2966.2007.12040.x

CrossRef Full Text | Google Scholar

364. Steidel C. A large structure of galaxies at redshift z 3 and its cosmological implications. Astrophys J (1998) 492:428.

CrossRef Full Text | Google Scholar

365. Davies RI. The software package for astronomical reductions with KMOS: SPARK. Astrophys J (2013) 558:56. doi:10.1051/0004-6361/201322282

CrossRef Full Text | Google Scholar