Creation of Silicon-Vacancy Color Centers in Diamond by Ion Implantation

Silicon-vacancy (SiV) centers in diamond are gaining an increased interest for application, such as in quantum technologies and sensing. Due to the strong luminescence concentrated in its sharp zero-phonon line at room temperature, SiV centers are being investigated as single-photon sources for quantum communication, and also as temperature probes for sensing. Here, we discussed strategies for the fabrication of SiV centers in diamond based on Si-ion implantation followed by thermal activation. SiV color centers in high-quality single crystals have the best optical properties, but polycrystalline micro and nanostructures are interesting for applications in nano-optics. Moreover, we discuss the photoluminescence properties of SiV centers in phosphorous-doped diamond, which are relevant for the creation of electroluminescent devices, and nanophotonics strategies to improve the emission characteristics of the SiV centers. Finally, the optical properties of such centers at room and high temperatures show the robustness of the center and give perspectives for temperature-sensing applications.

Introduction

Diamond offers plenty of attracting features for photonics applications: the large band-gap allows for a very large optical window and gives rise to the existence of hundreds of point defects presenting interesting optical and electrical characteristics [1, 2]. Its ¹²C lattice (especially if isotopically enriched [3]) offers a spin noise-free environment allowing for exceptionally long coherence times of spin states, and the high Debye-temperature of diamond maintains this feature at room temperature [4]. Recent success in n-type doping [5] (p-type doping has long been routinely performed) paves the way to electrically driven devices for light emission, taking advantage of the electrical properties of some of the point defects [6, 7].

The silicon-vacancy (SiV) complex is a point defect with D_3d symmetry, emerging from the splitting of a vacancy between two neighboring lattice sites with a silicon atom occupying the position in between. Both the neutral [8] (SiV⁰) and the negative [9] (SiV⁻) charge states are known to originate an optical transition with most of the intensity (70–90% at room temperature) concentrated in a zero-phonon line (ZPL) at 946 and 738 nm, respectively, with weak phononic sidebands. The linewidth of the ZPL is of the order of 1 nm at room temperature, with sub-nm peak dispersion, which is due to the inversion symmetry of the center, giving no static dipole moment for the environmental Stark effect. The SiV⁻, in the following SiV, if not otherwise stated, has the brightest, short-lived (≈1 ns) optical transition preserving the spin state, but the ground states are mixed by phonon interaction limiting the coherence time to a few tens of nanoseconds at room temperature [10]. On the other hand, the SiV⁰, whose electronic configuration is still poorly understood, exhibits ms-range coherence times [11], which makes it competitive with the best-known negatively charged nitrogen vacancy (NV⁻) center [12]. However, the ZPL of the NV⁻ contains only some percent of the overall luminosity. Therefore, the SiV, with its short excited-state lifetime and spectrally-narrow luminosity, is most promising for single-photon emission [9].

Silicon impurities, yet known in natural gems [13], are among the easier to incorporate in diamond during CVD growth, due to proximity of silicon-rich surfaces in contact with the plasma or impurities on the filament of hot-filament systems [9]. Si-ion implantation is a different fabrication strategy, having its own pros and drawbacks. The main advantage of implantation is undoubtfully the high precision attainable in the position of the implanted ions. Laterally, localization is limited either by the resolution of a focused micro-beam (down to hundreds of nm for high intensity beams and to a few tens of nm for low intensity ones), or by the diameter of a mechanical pinhole, mask, or any beam-shaping object, while the implantation depth depends on the ion energy, which also affects lateral and longitudinal straggling. The main drawback is the lattice damage determined by implantation, which is prominent in case of high fluences and which is the reason why thermal treatments are employed to favor Frenkel couples-recombination and to activate the implanted centers. Si ions generally occupy interstitial or substitutional positions in diamond lattice after implantation, so thermal diffusion of vacancies is necessary to favor formation of SiV color centers. Thermal annealing is not the only possible strategy for activation. Creation of NV color centers by native nitrogen has been obtained by local creation and mobilization of vacancies by means of focused pulsed laser irradiation [14], and the same concept could in principle be applied to other vacancy-related complexes.

In this work, we focus on Si-ion implantation and thermal annealing techniques in diamond (Implantation and Post Annealing), and on the optical behavior of implanted color centers in several types of substrates (Single-Crystal and Polycrystalline Samples) at room and high temperatures (Optical Properties at Room and High Temperatures). We discuss the optical properties of single centers (Optical Properties of Single Centers) and we briefly mention potential applications of SiV single centers in quantum information (Application in Quantum Information) and sensing (Application in Sensing).

Implantation and Post Annealing

Implantation Principles

If an ion is accelerated to energies up to some MeV, its energy loss in matter is mainly due to Coulomb interaction with charged particles. The energy loss of a charged ion of mass m_ion and energy E_ion during a close passage near an initially motionless charged particle with mass m_target is given with good approximation by $\Delta E=\frac{m_{\text{ion}}}{m_{\text{target}}}\frac{U_{\text{b}}^2}{E_{\text{ion}}}$, where U_b is the electrostatic potential energy of the couple ion-target at the minimum distance b (impact parameter). Thus, even if nuclei contribute to the deceleration of the ion, most of the energy loss is due to the lighter electrons. Since ΔE is generally much less than the ion energy, the deceleration of the ion in a material takes place quite smoothly and the path covered is approximately straight. Nevertheless, the stochastic nature of energy loss determines a straggling both in the range covered by a monochromatic beam and in the position projected on a plane orthogonal to beam direction (resp. called longitudinal and lateral straggling).

In ion implantation, we are interested in the distribution of the final positions of an implanted ion and possibly in the lattice damage produced by irradiation, usually expressed in term of the Frenkel couple's density induced by the dislocation of those nuclei kicked-off by incident ions. These are both studied by means of Monte Carlo simulations [15, 16], considering the characteristics of the ion (energy, charge, mass) and the target material (atom density and mass, atomic number, displacement energy of the nuclei). In these simulations the target material is usually assumed to be amorphous. If the ion travels through a high-symmetry direction of a crystalline material, channeling could occur [17], and the range of the ions is both longer (in average) and more dispersed than in the amorphous case. Channeling can be avoided either by inclining the sample with respect to the beam direction, in a way to avoid implantation through highly symmetric directions, or (for low-energy implantations) by depositing on the sample a thin amorphous metal layer, to make the ions enter the sample through casual directions.

In Figure 1, a plot of the position of the maximum of the depth distribution in diamond of Si-implanted ions as a function of the energy up to 20 MeV, along with the position of the 25th and the 75th percentile, is reported. In the inset of the same figure, the maximum number of vacancies per cm induced by a single ion is reported, to be multiplied by the ion fluence to obtain the maximum vacancy density (near end-of-range).

FIGURE 1

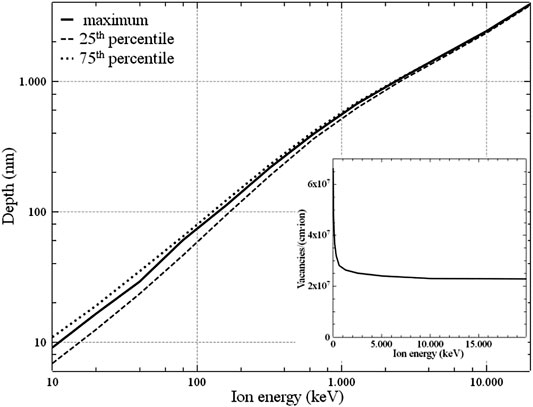
FIGURE 1. The depth of the maximum implanted ion density as a function of the energy, along with the depth of the 25th (lower dashed curve) and the 75th (upper dashed curve) percentile of the ion distribution. In the inset, the maximum number of vacancies per unit path-length produced by an ion, that is, the maximum vacancy density per unit fluence (in ions/cm²) as a function of the ion energy, near end-of-range.

Ion implantation is a routinely adopted strategy for semiconductor doping, in such a way that most of the accelerating machines installed worldwide have this specific purpose. The interest in quantum applications of the semiconductor industry has stimulated the development of deterministic strategies of ion implantation [18, 19], but these are limited in depth by the energies achievable by this kind of accelerator, generally up to a few tens of keV. In this work, we refer on the implantation activity performed at LABEC (Florence) with a 3 MV tandem accelerator, which was employed both in its optimal range of accelerating potentials (500–2,800 kV) and well below it, in a way to explore the minimum working conditions for the machine, which we successfully employed down to 50 kV of accelerating voltage. By selecting the appropriate state of charge emerging from the stripper, we have explored the entire range from 135 keV to about 14 MeV of implantation energies, thus obtaining single-photon sources in the entire range between some tens of nm and a few microns of depths. To the best of our knowledge, this is the first system devoted to ion implantation over such a large range of energies.

The Accelerating System and the DEFEL Line

Negative silicon ions are produced by a HVEE 860 cesium ion source (see Figure 2), accelerated by a ΔV_s = 35 kV static electric field and selected by a 90° deflecting magnet, which, with the help of an electrostatic focalizing system, introduces the beam in the HV 3MV Tandetron accelerator. Ions are first accelerated by the potential difference ΔV, then, in a section of the pipeline, where the stripper gas (Ar) pressure is maintained at the 10⁻⁶ mBar level, they lose the extra-electron along with one or more others, and finally (having inverted the original electric charge) they are further accelerated by the potential difference ΔV. The tandem concept, compared with conventional electrostatic accelerators, allows to keep both the source and the target at the ground potential, and permits to reach a generally higher energy, that is E = e[(N + 1)ΔV + ΔV_s], where N is the state of charge of the ion after the stripper. After acceleration, another analyzing magnet selects a definite state of charge and directs the beam to the selected beamline.

FIGURE 2

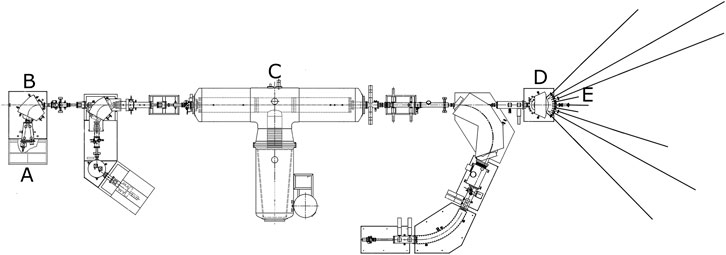
FIGURE 2. Sketch of the Tandetron system. (A) HVEE 860 cesium ion source; (B) 90° deflecting magnet; (C) 3MV Tandetron accelerator; (D) analyzing magnet; (E) DEFEL Line.

Comparison of the beam currents before acceleration and after the last analyzing magnet states that only about 10–20% of the injected Si ions are collected in the exit beamline. The others acquire a different state of charge or are lost due to scattering in the stripper. This brings the injected current from about 0.5–1 μA down to about 100 nA (scaled to the state of charge N = 1). Since we have also employed the machine for ΔV much lower than those for which it was designed (down to 50 kV vs. at least 500 kV) the beam current is further reduced by increased scattering in the stripper and by the out-of-design regime at which the switching magnet and the magnetic stirring and focalizing system in the final beamline operate. These are the factors, which determine a lower limit to the energies achievable with this system.

After the analyzing magnet, we use the electrostatic deflector (DEFEL) line at 15° from the accelerator axis, equipped with two orthogonally arranged parallel-plates electrostatic deflectors. The one closer to the exit slit is fed with +100 to –100 V square-wave pulses of potential difference, in a way to create a very short (a few ns) bunch passing through the exit slits. Before this deflector, an 800–0 V square wave pulse is applied to a pre-deflector, so that only the falling part of the deflector square wave pulse can send the beam to the exit slits (SL3 in Figure 3). This is important because the rising and the falling part of the deflector pulse do not have the same duration. The DEFEL system was designed to test particle detectors in the (Poisson statistic) 1 particle-per-bunch regime, but since we are interested in exploring the widest possible range of fluences, we have also employed the pre-deflector pulses (1–5 μs long) with grounded deflector, which, by selecting the pulse frequency (in the range from 1 to 100 Hz) allows to bring the particle flux from about 10¹² cm⁻²s⁻¹ to the range 10⁶–5 × 10⁸ cm⁻²s⁻¹, which is adequate to our purposes.

The DEFEL beam line is equipped with two magnetic quadrupoles (Q1–Q2 in Figure 3), which focalize the object formed by the entrance slits SL1 on the plane of the exit slits SL3, with a nearly unitary magnification factor. The divergence of the beam is also limited by the slits SL2 between SL1 and Q1-2, and its direction is controlled by two couples of stirring magnets (XY-ST1 and XY-ST2). In order to have a better definition of the implanted area, it is important to have the best possible beam collimation. Beam monitoring is performed, along the DEFEL line, by three stations QFC1-2-3 each carrying both an insertable Faraday cup (to measure the beam current) and a quartz plate whose luminescence, seen by an off-axis camera, allows to verify the shape of the beam. Three turbo-pumps assure a vacuum level of the order of 10⁻⁷ mbar, assuring negligibility of scattering and charge-exchange along the beam pipe.

FIGURE 3

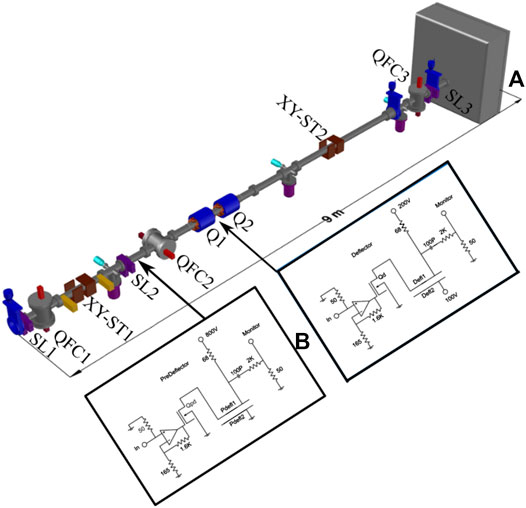
FIGURE 3. (A) Scheme of the DEFEL beamline: SL1-2-3, shaping slits; QFC1-2-3, beam monitor stations allowing insertion of a luminescent quartz plate or a Faraday cup along the beam path; XY-ST1-2, magnetic steerers. (B) Scheme of the electronics driving the electrostatic deflector (right) and pre-deflector (left). Figure reprinted from Ref. [20], Copyright (2018), with permission from Elsevier.

The unavoidable charge exchange with residual gases and with the slits edges before the deflecting plates are responsible for the formation of a weak neutral beam traveling through the beam pipe along with the ion beam. The former is not deflected by electric fields and determines a very weak, but constant, flux of neutral atoms on the target. To avoid undesired implantation, especially during deadtimes, a mechanical shutter has been inserted at the entrance of the implantation chamber.

The implantation chamber is a large vacuum chamber (0.5 m³), hosting two motorized x-y stages. The first, with a relatively low precision and reproducibility (20 μm) carrying a Faraday Cup and a p-i-n diode (Hamamatsu, S3590) for beam monitoring respectively during continuum and pulsed irradiation; the second is a Physik Instrumente PI Q-545.240 stage with nanometric resolution, carrying the sample. The beam, limited by the exit slits SL3, is shaped by a perforated quartz, whose luminescence is monitored off-axis by a second Aptina MT9v034 camera, employed to be sure that the beam hits the sample.

Implantation Procedure

Once having centered the beam (limited by the exit slits SL3 in a square region of width w) on the perforated quartz placed before the beam-shaping pinhole (see images A, B of Figure 4), we need to measure the ions flux ϕ, that is the number of ions impinging the unit surface in the unit time, in order to select pulse duration and frequency to perform the implantation at a desired fluence (in ion/cm²) in a reasonable time.

FIGURE 4

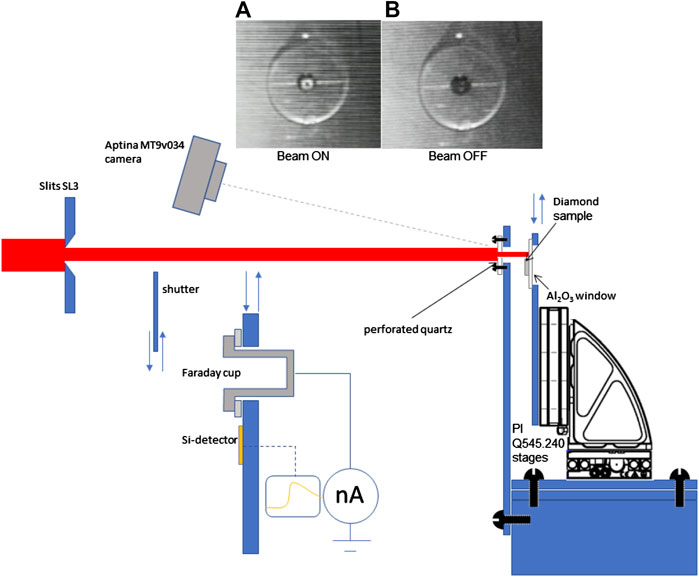
FIGURE 4. Schematic view of the implantation chamber setup. The function of the elements shown in the figures are described in the text (The Accelerating System and the DEFEL Line and Implantation Procedure). Images A and B show the luminescence produced by the beam (shaped by slits SL3) on the perforated quartz used to take aim at the sample placed behind it, (A) beam ON, (B) beam OFF.

In the ns-pulsed regime, obtained by activation of both deflector and pre-deflector plates, we find that, once verified that the luminosity of the quartz in the region limited by the slits is sensibly uniform, the number ΔN of ions impinging on the p-i-n diode is proportional to w², being ΔN = ϕΔt⋅w². Unfortunately, at this regime the pulse duration Δt is known only approximately (it is the time employed by the beam to pass through the slits during the deflector transition from +100 to −100 V of polarization), thus it is not possible to use the quantity ΔN/(Δt ⋅ w²) as a good estimation of ϕ. In the regime of μs (with only the pre-deflectors plates activated), the pulse duration is well known, because it is strictly imposed by the duration of the pre-deflector pulse, but the detector is not proportional for high ions number (moreover, it also accumulates high damage for long pulses). Consequently, the p-i-n diode was employed mainly to control the good functioning of the deflectors, while only the Faraday cup was extensively used for current measurements in continuous mode at all the energies.

To this aim, we insert the Faraday cup (see Figure 4) between the exit slits SL3 and the sample, and we measure the ion current as a function of the slit aperture w. We regularly find that, instead to measure a current depending on the flux ϕ as I = eNϕ⋅w², we also find a negative extra linear term: I = eNϕ⋅w² – a⋅w, in a way that, for small enough slit apertures, we measure a negative current. Since the particle flux in pulsed mode, as measured by the diode, is always proportional to w², the linear negative term was attributed to the interaction of the beam with the edges of the slits. Ions impinging on the slits edges causes the emission of secondary electrons not revealed by the diode, but partly collected by the Faraday cup, whose number is proportional to the perimeter of the area shaped by the slits themselves. The flux ϕ was then estimated by the quadratic term of the fit of the ion current as a function of w.

The nominal precision and reproducibility of the PI motorized stages is very good (about 1 nm) and allows precise placing of the sample behind the perforated quartz over a wide area (23 × 23 mm²). It relies on a combination of motorized stages (for long distances) and piezo-electric precision stages, controlled by optical interference devices. In the noisy environment of the accelerator laboratory, subject to slight, but sensitive vibrations by the vacuum pumps (especially scroll backing pumps), the stages must work during implantation to maintain a fixed position, so uncertainty in position is generally higher than the nominal one. We have mounted the stages on a massive aluminum holder separated by the body of the chamber by an anti-vibration layer, so that the dispersion in the position of the stage is kept well below 100 nm. This is the precision of the shape and dimension of the structures, which can be fabricated by implantation.

Post-Implantation Thermal Treatment

Ions are found, immediately after implantation, in interstitial or (less frequently) substitutional positions of a possibly highly damaged lattice. The formation of the SiV complex requires to increase the mobility of the defects, which is done by increasing the temperature. Long-range diffusion of impurities in diamond (excluding hydrogen) is negligible up to about 2000°C, even if the displacement of impurities in the vicinity of lattice defects seems to have a role in the formation of impurity complexes (see Ref. [21] and Single-Crystal and Polycrystalline Samples). Therefore, SiV formation relies on the thermal diffusion of native or radiation-induced vacancies. In CVD diamond the intrinsic vacancy density has values generally higher than those at thermal equilibrium [22], reaching the order of 10¹⁸ cm⁻³, which is the same density induced at end-of-range by the relatively high fluence of 3–5×10¹⁰ Si-ions/cm² at 0.1–1 MeV. This explains why interstitial-carbon diffusion, occurring above 400°C, contributes to the complete annealing of self-interstitials by recombination with vacancies, while residual vacancy diffusion, requiring temperatures above 600°C, leads to complete vacancy annealing only at temperatures of about 1,000°C. This is also the temperature necessary to the stable formation of the SiV complex, requiring first the occupation of a substitutional position of silicon (mainly by encounter of an interstitial silicon with a vacancy), then the recombination with a further vacancy, causing the positioning of the silicon atom between two lattice positions.

Diamond burns in oxygen-containing atmosphere above 500°C, and also 2 h at 1,400°C in a 10⁻⁷ mbar residual atmosphere, produce a nanometric graphitic layer [21]. Therefore, thermal annealing must be performed either in high-vacuum or in a reducing atmosphere, especially if very shallow implantations have been done. We performed thermal annealing of implanted diamond samples in an alumina cylindrical furnace of 5 cm diameter and 0.5 cm height (see Figure 5), electrically heated by two graphitic spirals above and below it. The sample itself is placed in a graphitic crucible inside the furnace, in order to avoid non-carbon contamination from surfaces during the heating. The furnace is placed in a cubic ultra-high vacuum chamber of about 3,000 cm³, and it is shielded by molybdenum sheets protecting the chamber walls from excessive heating. Ultra-high vacuum to the final level of about 3 × 10⁻⁷ mbar is obtained by a 200 m³/s turbo unit. The heating causes degassing of the furnace walls and components, which increases the residual pressure in the camera. To maintain the residual pressure at the level of 10⁻⁶ mbar, which is recommended, especially at temperatures above 500°C, slow temperature ramps are required. The usual annealing procedure adopted by us consists of a linear ramp of 2 h from room temperature to 1,150°C, followed by a constant temperature phase of 1 h, and then by the switch-off of the heaters. The temperature at this point falls below 700°C in a few minutes, while it takes several hours to go below 70°C.

FIGURE 5

FIGURE 5. (Top-left) the annealing cylindrical furnace (A) covered by one of the two spiral graphite heaters. A part of the molybdenum screen (B) is also visible. (C) The controlled-leakage valve for the insertion of a low-pressure inert gas. (Top-right) the vacuum chamber the oven is placed in. (Bottom-left) three diamond samples irradiated with silicon ions of 8 MeV energy at fluences of 6 × 10¹⁴, 3 × 10¹⁵ and 6 × 10¹⁵ cm⁻², not annealed. The loss of transparency can be evaluated by observing the pencil line below the samples. (Bottom-right) the same three samples after the annealing of the first and the third one, the second being left un-annealed for comparison. Figure reprinted from Ref. [20], Copyright (2018), with permission from Elsevier.

Single-Crystal and Polycrystalline Samples

Photoluminescence measurements have been performed on strongly implanted single-crystal and polycrystalline diamond at the level of ensemble, which clarified the nature of the processes occurring during annealing and the extent of the transformation of the silicon implanted ions in optically active SiV centers.

The comparison of the luminescent spectra of a strongly implanted sample before and after annealing shows features, which are similar to each other at a first sight (see Figure 6). The 738 nm strong peak after annealing is uniquely assignable to the ZPL of the SiV center, while before annealing the same implanted regions exhibit a weaker feature at 742 nm, along with a stronger background especially at higher wavelengths, which is reasonably assigned to the neutral vacancy-related GR1 defect.

FIGURE 6

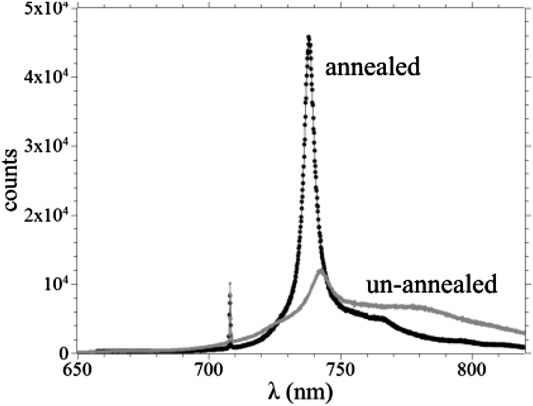
FIGURE 6. Spectra of a single-crystal diamond sample implanted at 3 × 10¹³ cm⁻² of Si-ion fluence, before and after 1 h annealing at 1,100°C. The luminescence has been excited by the 647 nm radiation of a Kr laser, the sharp peak at about 708 nm is the Raman line. The back-scattered radiation was analyzed by a 300 lines/mm monochromator equipped with a CCD cooled at 70 K. The system has an intrinsic resolution of 0.3 nm. Figure reprinted from Ref. [20], Copyright (2018), with permission from Elsevier.

The two kinds of defect show interaction in some cases [23], shifting the 738 nm luminescence toward higher wavelengths, but we can reasonably exclude the formation of SiV centers at low temperatures comparing the intensity maps of a sample irradiated at about 3 × 10¹³ cm⁻² fluence, at three different energies (see caption of Figure 7) passing through 0, 1 or 2 2.3 μm-thick aluminum shields. The strength of the 738-nm peak after annealing is the same everywhere the transmission efficiency is 100% (letting alone 15% fluctuations mainly due to the uncertainty in the fluence), but it is not the case with the 742-nm peak. In fact, its intensity is related to the penetration depth of the ions, that is, to the overall number of vacancies generated in diamond by the impinging ions during deceleration [see Figure 1]. The plain conclusion is that the 742 nm-peak is related to the amount of damage in diamond and not to the silicon impurity density, so the attribution to GR1 defects is confirmed.

FIGURE 7

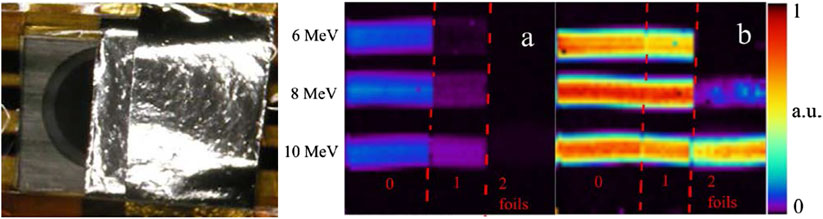
FIGURE 7. (Left) Single-crystal 5 × 5 mm² diamond sample, covered by 0, 1 or 2 foils of 2.3 μm-thick aluminum, and implanted along three 0.6 mm-wide parallel strips with 3 × 10¹³ Si-ions per cm², at the energies of 6, 8 and 10 MeV. The dark shadows on the sample are due to loss of transparency due to the damage, and are recovered after 1 h annealing at 1,100°C. (Right) Intensity map of the 742 nm-luminescence before annealing (A) and of the 738 nm SiV line after annealing (B). The color scale is arbitrary, but it is the same for the two samples, being the same the laser intensity and the integration time (1 s). Note that the transmission of the Si-ions through only 1 aluminum foil is 100% at all energies. Figures reprinted from Refs. [20,24], Copyright (2018), with permission from Elsevier

Moreover, comparison of pre- and post-annealing maps confirms the attribution of the SiV luminescence to the implanted Silicon, and not to a possible inclusion of Silicon atoms during diamond growth. In fact, if it was not so, the SiV signal would have been related not to the Si-ion fluence (as it is, as seen in Figure 7B), but to the number of vacancies, which were generated per unit surface (related to the GR1 luminescence shown in Figure 7A). In fact, if the activation of native, ubiquitous silicon by means of damage-related vacancy generation had a role in the SiV luminescence, the two intensity maps of Figures 7A,B would have been practically identical, within a proportionality factor. On the contrary, the SiV luminescence is nearly the same (within the uncertainty in the fluences) in all the 7 areas, where the implanted number of Si ions per unit area was the same, while the GR1 luminescence is related to the energy of the ions impinging the diamond surface. This is a strong evidence that the luminescence that we are observing comes from the implanted silicon, and not from the possible native one.

Even if the single centers are not distinguishable at a fluence of 10¹¹ cm⁻² or more, the grade of conversion of Si-implanted ions in SiV centers can be investigated by comparison of the overall SiV luminescence with the integrated Raman line peak. In fact, the Raman cross section for any given crystal orientation can be calculated (see Ref. [25] and Appendix of Ref. [24]) by the Raman polarizability tensors relative to the irreducible representations of the crystal point group, and for the (100) direction (the most common orientation of the growth surface), is $\frac{1}{4\pi }3.7\times {10}^{-29}{\text{cm}}^2$. Knowing the cross section and the excitation power, and given the geometrical size of the laser waist, one can calculate the number of backscattered Raman photons per unit solid angle, and if the Raman line is close enough to the SiV luminescence, the ratio between the two signals gives the number of photons per unit time dN_ph/dt from the SiV centers. At this point, from the quantum efficiency η (evaluated 30% for the SiV) and the lifetime τ of the excited level (measured 1.1 ns), the number of excited SiV centers N_SiV* is promptly $N_{SiV}^{\ast }=\frac{4\pi \tau }{\eta }\frac{d{N}_{ph}}{dt}$. Measuring the saturation power P_sat, the number of SiV centers in the beam waist is then $N_{SiV}=\frac{P + P_{sat}}{P}{N}_{SiV}^{\ast }$, and the SiV surface density is easily calculated and compared with the implantation fluence.

Inspection of Figure 7 (right) reveals that the activation yield is largely independent on the ion energy, at least in the MeV range. This was expected, because the vacancy density near end-of-range, the sole parameter reasonably related to the activation yield, is the same at constant fluence for a large energy range (see the inset of Figure 1). In order to investigate its dependence on the fluence, we have measured it for single-crystal and polycrystalline samples over a large range of fluences, and we found that the activation yield, which is evaluated as a few percent at the level of 10¹¹ cm⁻², decreases for increasing fluences, passing through 1% at the level of some 10¹² cm⁻², and reaching about 0.5%, when approaching 10¹⁴ cm⁻² (see Tables 1, 2).

TABLE 1

TABLE 1. Activation yield of the SiV center as a function of the implantation fluence for the single-crystal sample.

TABLE 2

TABLE 2. Activation yield of the SiV color center as a function of the implantation fluence for the polycrystalline sample.

These results are consistent with those reported in Ref. [26], obtained in the 1–100 keV regime in almost the same range of fluences, where the SiV surface density was measured by comparison of the overall luminescence from a unit area with the average obtained by single centers. There, Schröder, et al. also found only a weak dependence on energy and a general decrease of the yield at increasing fluences, from a few percent at 10¹² cm⁻² to less than 0.5% at 10¹⁴ cm⁻² [26]. At much lower fluences, suitable for the generation of single emitters (10⁸–10⁹ cm⁻², see Optical Properties of Single Centers) we measured, with the entirely different method of counting SiV centers, a value of the yield around 4%. A rationale for the decrement of the yield for increasing fluences could be the tendency of the vacancies to form complexes, when their density is high (at 10¹⁴ ions/cm² the density at end-of-range is as high as 2 × 10²¹ cm⁻³ for MeV ions), moreover, the un-combined Si centers are themselves bystanders, whose disturbance could compromise the emission of the SiV centers. Anyway, the substantial agreement between three entirely different methods of yield measurement (either comparison with the Raman line or with the single center intensity, or direct counting) testifies in favor of the reliability of this analysis.

In Table 2, the values reported for the polycrystals are taken in average. Close inspection of maps on the scale of the grain size reveals that the grain boundaries are preferential sites for the activation of the Si-ions. To this end, we distinguish between the Raman and the photoluminescence signals by placing different bandpass filters in front of two APDs. These generate two maps by confocal scanning of a polycrystalline sample (named here as poly sample) [20]²¹, as shown in Figures 8A,B. Filter 1 is centered at 720 nm with 10 nm bandwidth (corresponding to the diamond Raman peak at 718 nm, laser excitation at 656 nm) and Filter 2 is centered at 740 nm with 13 nm bandwidth (corresponding to the ZPL of the SiV center at 738 nm). The higher count rate is observed from the grain boundaries (GBs) due to the accumulation of activated SiV centers, whereas in the grain center (GC) the count rate is found to be less. Moreover, we performed a spectral analysis across the GBs and the GCs on the surface of the sample to identify the contributions of different spectral components to the overall emission. The spectral signal at each point along lines is analyzed at a 0.5 nm spectral resolution (150 L/mm grating, 357 nm bandpass). The intensity at Filters 1 and 2 is then reproduced by integrating the recorded signal over the wavelength range corresponding to the filters used in the mapping. Before performing this integration, the background is identified by introducing a baseline corresponding to the counts at the edges of Filter 2 spectral window. Finally, the distinction can be performed by integrating the background and the signal separately, where the contribution below the baseline corresponds to the background fluorescence, and above the baseline indicates the SiV luminescence. The same procedure is applied to Filter 1 to identify the Raman signal. However, only the background from Filter 2 is used as a reference. The result shown in Figure 8C reveals that the background around the ZPL emission of SiV centers, as well as the photoluminescence intensities from Filter 1 and Filter 2, increase along with the GB, while they drop as one moves to the GC (see black line in the Figures 8A,B).

FIGURE 8

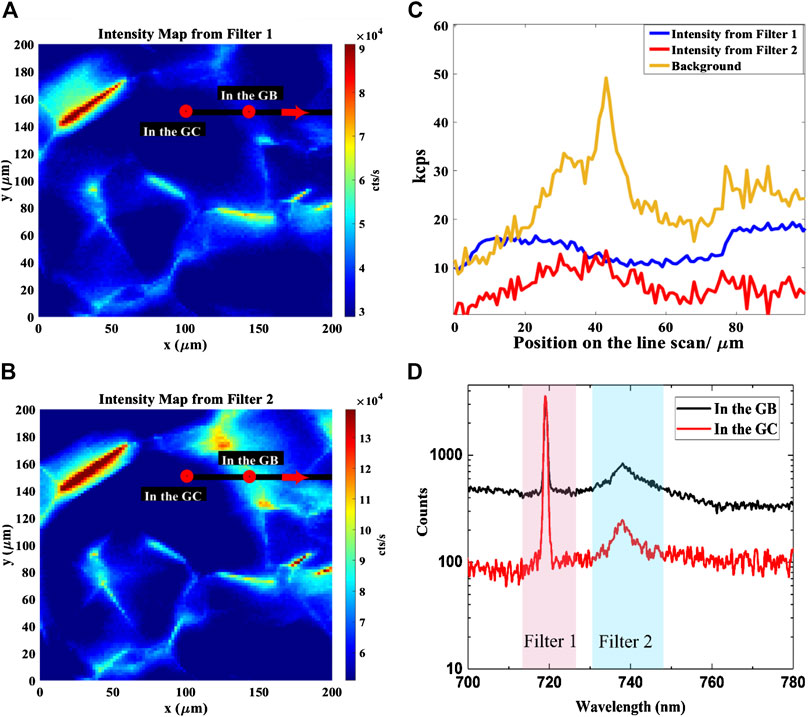
FIGURE 8. Optical properties of a polycrystalline sample. (A) Confocal map (1 µm step size) corresponding to the signal from Filter 1 (Raman signal). The dark regions correspond to the grain centers (In the GC) and the bright ones to the grain boundaries (In the GB). (B) Confocal map (1 µm step size) corresponding to the signal from Filter 2 (SiV photoluminescence signal). (C) Spectral acquisition with manual scanning (1 µm step size), performed along the black line indicated in Figures 8A,B, showing the background around the ZPL emission of SiV centers (yellow curve), the background-subtracted photoluminescence of SiV centers (red curve) and the background-subtracted Raman (blue curve). (D) Photoluminescence spectra in the GCs centers (red curve) and in the GBs (black curve) taken at the corresponding red points marked in Figures 8A,B. The bandpass filters for the Raman and SiV signals are represented as Filter 1 and Filter 2.

The photoluminescence spectra corresponding to the GC and the GB (the positions are marked as small red circles on the maps in Figures 8A,B) are shown in Figure 8D. It is confirmed that the signal-to-noise ratio is higher in the GCs compared along the GBs, since the photoluminescence background is higher in the GB due to poor crystal quality. Additionally, the intensity from Filter 1 is also varying from grain to grain, where the size of one grain is ranging from tens to hundreds of microns, as observed in Figure 8C. These interesting features that appeared on the photoluminescence spectra are mainly due to the random crystal orientations of the grains in polycrystalline diamond samples [24]. The close correlation between the higher photoluminescence intensity of the SiV signal (Filter 2) at the GB indicates that the concentration of activated SiV centers is relatively prominent [20].

Optical Properties at Room and High Temperatures

The variation of the optical properties of the SiV centers at different temperatures has both theoretical and practical implications. It enlightens the photophysics of the color centers, clarifying their level structure and transitions, it has important implications in temperature sensing, and it also has application in the band-gap engineering of electroluminescent single-photon devices [27–29]. Studies have been done on the temperature behavior of the SiV centers from cryogenic to room temperature [30, 31] and from room temperature to 860 K [32], and they showed consistent characteristics. Figure 9 reports the ensemble luminescence spectra of a densely implanted diamond sample at temperatures from 293 to 861 K, excited by the 647 nm, 36 mW radiation of a Kr ion laser. The sample was kept in vacuum during heating and observed through a quartz window by means of a long working-distance (2 cm) low-aperture (0.28 NA) objective. The intrinsic collection efficiency of such a system is no more than 0.3%, so the emitter density must be high to collect a measurable signal. In fact, the implantation fluence was 6 × 10¹⁴ cm⁻², and the effective number of emitters in the 2 μm-diameter spot was of the order of 10⁵, taking into account an activation yield of the order of 1% or less. Three main features are apparent: the peak wavelength increases at increasing temperatures as well as the dispersion of the distribution, while the integrated luminescence quenches at high temperatures. Moreover, the phononic sideband is indistinguishable above 500 K. Very importantly, the photostability of the centers at high temperatures is very good, since the luminescence does not show hysteresis for temperature cycles up to about 900 K. This was expected, since the sample was previously annealed at about 1400 K for 1 h so that all the lattice defects, intrinsic or radiation-induced, were annealed-out and the SiV center itself, once formed, is reputed highly stable. Figure 10 (left) shows the temperature dependence of the peak wavelength and the full width at half-maximum (FWHM) of the distribution.

FIGURE 9

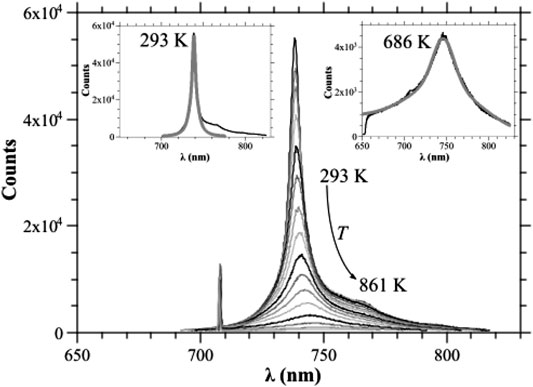
FIGURE 9. Luminescence spectra integrated for 4 s at increasing temperatures (the curves correspond to 293 K, 312 K, 321 K, 340 K, 356 K, 376 K, 399 K, 425 K, 454 K, 486 K, 524 K, 569 K, 623 K, 686 K, 762 K, 861 K with decreasing peak height), A linear background has been subtracted in order to take into account the thermal emission at high temperatures. Insets: fit of the ZPL at 293 and 686 K with a pseudo-Voigt distribution. The system is the same used for the measurements referred to in Figure 6. Figure reprinted from Ref. [32], Copyright (2015).

FIGURE 10

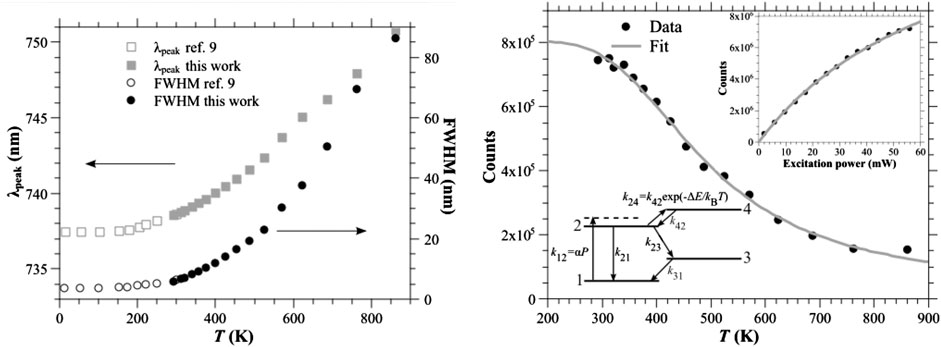
FIGURE 10. (Left) Dependence of the central wavelength of the luminescence peak λ_peak (squares, left vertical scale) and of the FWHM (circles, right vertical scale) on temperature. Filled (open) symbols refer to measurements performed in this work (in Ref. [31]). (Right) Dots: experimental dependence on temperature of the integrated luminescence of an ensemble of SiV centers. Line: fit of the experimental points by means of Eq. (1), with ΔE = 180 meV and Ap = 60. The inset in the upper-right part of Fig. 10 shows the experimental dependence of the observed luminescence on the excitation power at room temperature (dots) and the fit of the data by means of the expression I = I_s × P/(P_s + P), with P_s = 75 mW (curve). The bottom-left part shows the four-level scheme adopted to explain the photophysics of the SiV center at large temperatures. Figure reprinted from Ref. [32], Copyright (2015).

Apparently, the studies at low- and high-temperatures draw a coherent picture, the red shift, in particular, seems to be related to the shrinking of the diamond bandgap [33], which is likely to determine a change in the transition frequency of the deep levels.

The quenching of the luminescence, described in Figure 10 (right), tells us a different and more complicated story. The anticorrelation histograms obtained in g⁽²⁾ measurements performed on single SiV centers, exhibit generally an overshoot before settling on a constant value for large values of the delay time Δτ [34]. This is interpreted with the occurring of a non-radiative transition from the excited state to a third metastable state (“shelving state”, state 3 in the inset of Figure 10 (right)). If the system is initially in the ground state, the probability of occupation of the excited state (proportional to the emission probability) has a maximum after a definite time and then settles on an asymptotic value, when the meta-stable state occupation reaches its equilibrium value. On the other hand, the height of the overshoot tends to decrease for increasing excitation powers, and this is explained with the presence of a fourth state [“de-shelving state”, state 4 in the inset of Figure 10 (right)] radiatively bounded to the shelving state from which a non-radiative transition can occur with the excited state. Indeed, the inversion symmetry of a D_3d center provides two families of such opposed parity states with (dipole) radiative transitions only allowed between states with opposed parity. Assuming the de-shelving state is placed above the excited one at an energy difference ΔE of the same order (or lower than) K_BT, the thermal excitation from the excited level to the de-shelving state acts as an alternative channel to reach the shelving state, and this can effectively quench the luminescence of the center. In fact, one can prove that the depicted 4-levels scheme determines a dependence on temperature of the kind,

$I=\frac{I_0}{1+A\times \exp \left(-\frac{\Delta E}{K_{B}T}\right)}(1)$

which gives an excellent description of the integrated luminescence of the SiV centers between room temperature and 860 K (see Figure 10 (right)), with ΔE = 180 ± 10 meV and A = 60 ± 10. Indeed, Eq. (1) is a functional dependence emerging from a large class of different level schemes, but the large value of A imposes quite stringent bounds to the possibilities. For instance, a 3-levels scheme omitting level 3 and admitting a non-radiative transition from level 4 to 1, would give a value of A not exceeding 1, which is by far too small. On the contrary, the values of the transition rates obtained by the interpretation of the g⁽²⁾ measurements, which are wildly variable due to the uncontrolled boundary conditions of different nano-sized crystals, still gives a prevision for the value of A = 170 ± 75 [see supplementary material of Ref. (32)], which is at least of the correct order of magnitude.

Optical Properties of Single Centers

The versatility of the implantation technique permits the implantation of Si ions at low fluences 10⁸–10⁹ cm⁻² and different depth, ranging from a few tens of nm (100 keV ions, or 8–9 MeV ions moderated by two 2.3 μm-thick aluminum foils) to about 2 μm (10 MeV ions), for the production of single SiV color centers.

Figure 11A depicts the wide-field fluorescence image of SiV color centers implanted at a fluence of 10⁸ cm⁻² excited by 656 nm laser (PicoQuant, PDL 800-D, LDH-DC-660). Single SiV color centers are verified by measuring the intensity autocorrelation (second order correlation function, g⁽²⁾(τ)) using a Hanbury–Brown–Twiss interferometer. The spectra of single-emitters exhibit an intense and narrow ZPL-emission centred at 738 (±0.015) nm, with a linewidth of about 1.59 (±0.01) nm, as shown in Figure 11B. The small inhomogeneous broadening allows the possibility of finding color centers, whose difference in emission frequency lies within the ZPL transition, enabling quantum interference between single photons from separated sources [35, 36]. The strength of the ZPL is determined by the Debye–Waller factor (the ratio of the ZPL intensity to the overall emission band) and it amounts to be >0.94. This makes the color centers ideal for applications that require bright and narrowband emission. In addition, the SiV color centers show short excited-state lifetime of 1.03 (±0.06) ns. Figure 11C depicts the excited-state lifetime of single SiV color centers. The controlled shallow implantation of Si ions can allow coupling of SiV color centers with nanoresonators [37–39] to further increase the emission rate and make the emission of indistinguishable photons from different quantum emitters at room temperature possible.

FIGURE 11

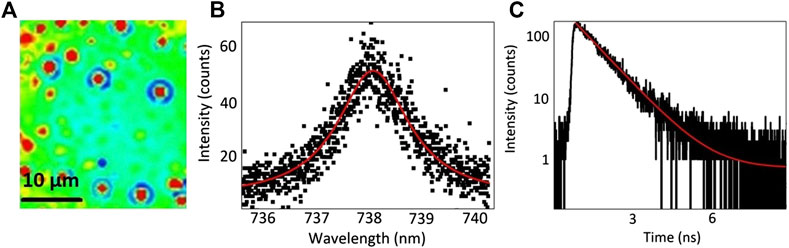
FIGURE 11. (A) Wide-field fluorescence image of single SiV centers in diamond implanted at 10⁸ cm⁻² fluence. (B) Emission spectrum of a SiV center. (C) Fluorescence lifetime measurement of a SiV center exhibiting an excited-state lifetime of ∼1 ns?

Some of the emitters show bunching behaviour, indicating the presence of two or more emitting centers below the spatial resolution of the optical system. This is attributed to the tendency of the activated centers to cluster. This is also manifested by the observation of higher count rates as compared to single color centers. The presence of defects (e.g., dislocations) around which the formation of a SiV center could be energetically favored could be an explanation. These points are currently under investigation. By counting the number of SiV color centers and determining the occurrence of clustering, the activation yield for the creation of SiV color centers amounts to 3.8 ± 0.8%. This value is not far from those reported by Schröder et al. [26] and it is consistent with that measured for the lowest implantation fluences in the single crystal with the method of the ratio between the SiV and the diamond Raman line intensity (see Table 1).

Unlike intrinsic diamond, the creation of single SiV color centers in doped diamond (p- or n-type diamond) is not straightforward. Single SiV color centers in doped diamond can facilitate the electronics integration of diamond-based quantum photonics devices, for instance SiV based single-photon sources operating upon electrical injection. The electrical excitation of the color centers is determined by electron- and hole-capture processes and this possibility has been recently demonstrated using p-i-n based diode structures, where the Si ions are implanted in the intrinsic layer [7, 29]. However, the creation of SiV color centers in p- or n-type diamond could avoid the need for complex semiconductor junctions. For example, SiV color centers in phosphorus-doped (P-doped) diamond would allow the implementation of a Schottky-diode. However, there are challenges to attain the conditions for single-photon emission in P-doped diamond. The crystal imperfections (structural distortion and degradation caused during the incorporation of phosphorus atoms during the growth process [40, 41]), phosphorus-based bound excitons [42] and phosphorus-related complex defects [43], photoluminescence related to phosphorus-nitrogen co-doping [44, 45] and ion-beam induced defects can compromise the signal-to-noise ratio required for single-photon emission. Particularly, nitrogen co-doping allows the formation of NV color centers as ion implantation creates vacancies and thermal annealing favours the formation of NV complexes in addition to the desired SiV color centers. Figure 12A shows the background related to the NV color centers (neutral and negatively charged states, NV⁰ and NV⁻, respectively), when the sample, Si-implanted single-crystal diamond grown by CVD with 4,300 ppm phosphorus concentration, is excited by the 532 nm laser (green curve). These features can be strongly suppressed by exciting the color centers at longer wavelengths (e.g., 656 and 690 nm, see red and black curves of Figure 12A, respectively), as NV complexes have less absorption. By reducing the nitrogen concentration in the technical gases during the growth of P-doped diamond, the luminescence background can be significantly suppressed even for high phosphorus doses (5,000 ppm) and the conditions for single-photon emission can be attained (below saturation) [46].

FIGURE 12

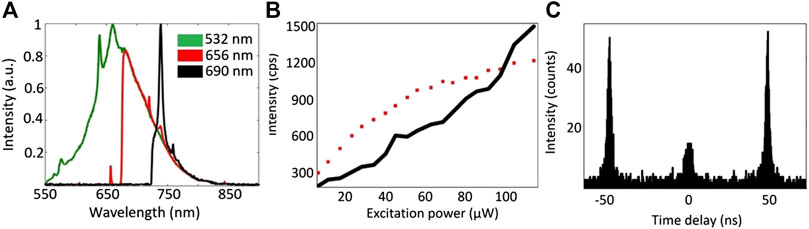
FIGURE 12. (A) Photoluminescence spectra of a Si-ion implanted and annealed P-doped diamond sample using 532 nm, 656 and 690 nm. The background due to NV color centers is reduced by choosing the 690 nm excitation wavelength, as NV complexes have less absorption in this spectral range. (B) Saturation (red curve) vs. background (black curve) as a function of excitation power. (C) Photon anti-bunching under pulsed excitation.

The intensity-dependent background (black curve in Figure 12B) of the sample prevents the observation of single-photon emission at high excitation power above saturation. The red curve in Figure 12B shows the count rate of the SiV color center as a function of the excitation power. The count rates are background corrected. The fluorescence count rate I of an emitter as a function of the excitation power P is described as I = I_∞/(1 + P_sat/P) + C_bgP, where P_sat is the excitation power at saturation and I_∞ is the maximum photon count rate. The background C_bgP is measured in the nearby region, where there is no SiV color center. This leads to a maximum photon count rate of I_∞ = 1.576 ± 0.035 × 10³ cps (at P_sat = 36 µW ± 3 µW). Taking into account light trapping in diamond due to total internal reflection and the overall detection efficiency of the setup, the count rate of a single SiV color center in P-doped diamond can reach about ∼4 × 10⁵ cps. This number is in the same order of magnitude as the count rate of SiV color centers in intrinsic bulk diamond [46]. The count rate of the color centers can be improved by selecting the emitters with the appropriate dipole moment orientation. Below saturation the single-photon emission of a SiV color center is verified by measuring the second order intensity autocorrelation function g²(τ) of the emitted photons in pulsed excitation (pulse width <90 ps, at the repetition rate of 20 MHz), as a function of the time delay τ. Figure 12C reveals the observation of a single-photon source in a P-doped diamond sample with g2(0) = 0.3. To the best of our knowledge, this is the first observation of single-photon emission from this kind of system.

Application in Quantum Information

The SiV center in diamond has attracted an ever-increasing interest as a single-photon emitter [34] and as a photon-spin interface [47] for quantum information. Experiments at cryogenic temperatures have indeed shown lifetime-limited linewidths and quantum interference between two SiV centers [35, 36] and spectroscopic investigations of its spin properties have identified a ground state with s = 1/2 [48]. Although the coherent properties of the spin states are relatively short, the high emission rate and the emission concentrated in the zero-photon line make them an interesting system for proof-of-principle studies and for certain applications. At room temperature, the situation is more problematic, because dephasing processes set in. Nonetheless, one could take advantage of nanophotonic structures to strongly enhance the radiative decay rate and thus make these emitters nearly lifetime limited at room temperature. Preliminary studies indicate that the ZPL transition of the SiV can be accelerated by orders of magnitude [39]. For example, Figure 13 shows how a SiV center inside a diamond membrane coupled to a plasmonic gold nanocone can be accelerated by more than four orders of magnitude, hence making the SiV ZPL transition in practice lifetime limited, with direct implications for solid-state quantum optics at room temperatures and for practical applications in quantum information science and technology.

FIGURE 13

FIGURE 13. (A) Emitter inside the dielectric membrane (diamond membrane) coupled to a gold nano-cone of 80-nm height and 80-nm base with gold coating thickness of 30 nm. The nano-cone-emitter distance P is 1 nm. The emitter is embedded at a depth Q of 2 nm in the diamond substrate (refractive index 2.4). (B) Corresponding total radiative decay rate normalized to the radiative decay rate (Purcell Factor) inside the diamond membrane and Antenna Efficiency as a function of the emission wavelength. Introducing a dielectric interface close to the emitter enhances the Purcell factor above four orders of magnitude.

Another important aspect for the application of color centers is the poor collection efficiency due to the large refractive index of diamond. Different strategies have been proposed to circumvent this challenge, such as solid-immersion lenses [49], photonic-crystal cavities [37] and plasmonic structures [50]. We have recently proposed a planar antenna structure based on thin metal films acting as director and reflector in a Yagi–Uda antenna configuration [51, 52]. We have shown strong directional emission from color centers in thin diamond membranes [53] and also theoretically shown that the antenna can be integrated into an optical fiber [54]. These studies could facilitate the use of quantum emitters and in particular of color centers for single-photon emission, since the antenna can be integrated into a cryostat and the emitted photons can be efficiently collected by an optical fiber.

Application in Sensing

Color centers in diamond are also becoming relevant for quantum sensing. Besides the nitrogen vacancy center, which has been widely investigated as a sensitive magnetometer [55], there is an emerging interest for their application as temperature sensors [56, 57]. In Optical Properties at Room and High Temperatures we have demonstrated the robustness of the SiV at high temperatures and the basic behavior of the photophysical properties as a function of temperature in a regime not previously explored. Our findings indicate that the SiV could be applied for temperature sensing applications where conventional sensors are less efficient or more complex. For instance, SiV could operate at high temperatures, be optically addressed and in principle could also provide temperatures maps with a very high resolution and fast temperature response.

To utilize the temperature dependence a calibration curve of the SiV-ZPL position was recorded (Figure 14B), by fitting a Lorentzian function to the SiV spectrum at the different temperatures (Figure 14A). From the slope of the calibration curve one can determine the sensitivity (response) of the ZPL position to a change in temperature. In the shown case the sensitivity was determined to be $\frac{\text{Δλ}}{\text{ΔT}}=(0.0137\pm 0.0004)\frac{\text{nm}}{°\text{C}}$, which is comparable with values found in literature [57]. After the calibration one can measure the temperature by determining the position of the ZPL. The precession of this measurement strongly depends on the resolution of the spectral measurements and therefore on the used equipment. The host of the SiV color center was here a bulk diamond. The usage of nano-diamonds enables the integration of the SiV color centers into different environments, such as organic systems or integrated circuits, where they can be used to probe the temperature at a microscopic level.

FIGURE 14

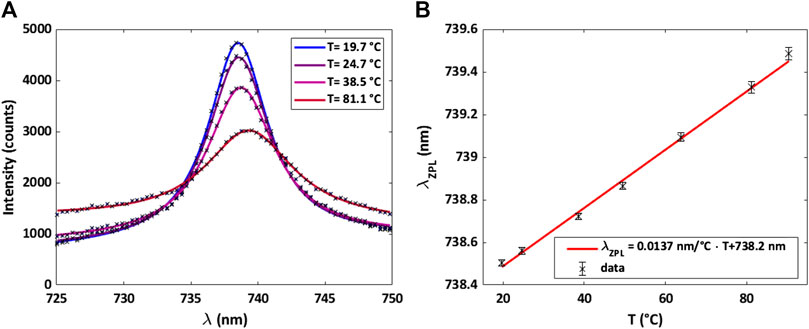
FIGURE 14. (A) SiV emission spectra at different temperatures. The markers show the measured data, while the solid lines show a Lorentzian-function fitted to the data. (B) Calibration curve for optical thermometry measurements by the SiV-ZPL position. The sensitivity of the peak to a change in temperature was determined by a linear regression to be Δλ/ΔT = (0.0137 ± 0.0004) nm/°C.

Conclusion and Outlook

We reviewed current efforts in the creation of SiV color centers in diamond by ion implantation and briefly mentioned their potential for quantum applications and sensing. First, we described the implantation and annealing procedures taking place at LABEC, which can be performed in a wide range of values for both ion fluence and implantation depth. Next, we discussed the optical properties of SiV centers in single crystal and polycrystalline samples. While single-crystal diamond offers a better host matrix for the SiV, the latter case can be interesting for certain applications, where it is difficult to process single crystals, such as ultrathin diamond membranes. The optical properties of the SiV investigated as a function of temperature indicated the robustness of the color center and the existence of a de-shelving state. Moreover, the variation of the SiV ZPL with temperature can find interesting applications, such as nanoscale thermometry, which is briefly discussed in terms of thermal sensitivity and calibration. The spectroscopic studies of single SiV centers in intrinsic and phosphorous-doped diamond lay the ground for the development of diamond-based single-photon sources at room temperature, also under electrical pumping. However, a substantial amount of basic research effort still needs to be done. In this regard, we discussed some strategies to improve the brightness of the SiV and also the modification of its photophysics by optical antennas in order to obtain transform-limited single-photons even at room temperatures. The SiV color center is thus an interesting platform for fundamental studies in quantum nano-optics and for the development of photonics-based quantum technologies for information processing and sensing.

Author Contributions

SL, SS, NG, MM, CC, and LG performed Si-ion implantation and annealing at LABEC. MM, CC, and LG are in charge of the accelerator and the beamline for ion implantation. SL, AF, HK, FS, LH, NS, PR performed optical experiments on SiV centers. MA supervised the projects. SL, AF, HK, FS, LG, MA analyzed the data and contributed to the manuscript.

Funding

The authors gratefully acknowledge financial support from the University of Siegen, the German Research Association (DFG) (INST 221/118-1 FUGG, 410405168). The authors also acknowledge INFN-CHNet, the network of laboratories of the INFN for cultural heritage, for support and precious contributions in terms of instrumentation and personnel.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors would like to thank C. Wild, E. Wörner, K. Haenen, S. Nicley, M. Becker, R. Rechenberg, K. de Hantsetters, C. Degen, S. Orlanducci for diamond sample supply, H. Galal, M. Santoro, F. Gorelli, F. Tantussi, F. De Angelis, F. Taccetti, G. Schulte and H. Schönherr for experimental support, C. Becher, D. Yu. Fedyanin and I. Khramtsov for helpful discussions. This work is based upon networking from the COST Action MP 1403 “Nanoscale Quantum Optics,” supported by COST (European Cooperation in Science and Technology).

References

1. Zaitsev AM. Optical properties of diamond [Internet]. Berlin, UK: Springer (2001) Available from: http://link.springer.com doi:10.1007/978-3-662-04548-0

CrossRef Full Text | Google Scholar

2. Sipahigil A, Lukin MD. “Quantum optics with diamond color centers coupled to nanophotonic devices”, in Current trends in atomic Physics [Internet]. Oxford, USA: Oxford University Press (2019) p. 1–28. Available from: https://oxford.universitypressscholarship.com/view/10.1093/oso/9780198837190.001.0001/oso-9780198837190-chapter-1.

Google Scholar

3. Itoh KM, Watanabe H. Isotope engineering of silicon and diamond for quantum computing and sensing applications. MRS Commun (2014) 4(4):143–57. doi:10.1557/mrc.2014.32

CrossRef Full Text | Google Scholar

4. Balasubramanian G, Neumann P, Twitchen D, Markham M, Kolesov R, Mizuochi N, et al. Ultralong spin coherence time in isotopically engineered diamond. Nat Mater (2009) 8(5):383–7. doi:10.1038/nmat2420

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Pinault-Thaury M-A, Temgoua S, Gillet R, Bensalah H, Stenger I, Jomard F, et al. Phosphorus-doped (113) CVD diamond: a breakthrough towards bipolar diamond devices. Appl Phys Lett (2019) 114(11):112106. doi:10.1063/1.5079924

CrossRef Full Text | Google Scholar

6. Mizuochi N, Makino T, Kato H, Takeuchi D, Ogura M, Okushi H, et al. Electrically driven single-photon source at room temperature in diamond. Nat Photon (2012) 6(5):299–303. doi:10.1038/nphoton.2012.75

CrossRef Full Text | Google Scholar

7. Tegetmeyer B, Schreyvogel C, Lang N, Müller-Sebert W, Brink D, Nebel CE. Electroluminescence from silicon vacancy centers in diamond p–i–n diodes. Diam Relat Mater (2016) 65:42–6. doi:10.1016/j.diamond.2016.01.022

CrossRef Full Text | Google Scholar

8. Green BL, Mottishaw S, Breeze BG, Edmonds AM, D'Haenens-Johansson UFS, Doherty MW, et al. Neutral silicon-vacancy center in diamond: spin polarization and lifetimes. Phys Rev Lett (2017) 119(9):096402. doi:10.1103/PhysRevLett.119.096402

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Neu E. Silicon vacancy color centers in chemical vapor deposition diamond : new insights into promising solid state single photon sources. [PhD Thesis], Germany: Universität des Saarlandes (2012).

Google Scholar

10. Rogers LJ, Jahnke KD, Metsch MH, Sipahigil A, Binder JM, Teraji T, et al. All-optical initialization, readout, and coherent preparation of single silicon-vacancy spins in diamond. Phys Rev Lett (2014) 113(26):263602. doi:10.1103/PhysRevLett.113.263602

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Rose BC, Huang D, Zhang ZH, Stevenson P, Tyryshkin AM, Sangtawesin S, et al. Observation of an environmentally insensitive solid-state spin defect in diamond. Science (2018) 361(6397):60–3. doi:10.1126/science.aao0290

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Oherty MW, Manson NB, Delaney P, Jelezko F, Wrachtrup J, Hollenberg LCL. The nitrogen-vacancy colour centre in diamond. Phys Rep (2013) 528(1):1–45. doi:10.1016/j.physrep.2013.02.001

CrossRef Full Text | Google Scholar

13. Breeding CM, Wang W. Occurrence of the Si–V defect center in natural colorless gem diamonds. Diam Relat Mater (2008) 17(7–10):1335–44. doi:10.1016/j.diamond.2008.01.075

CrossRef Full Text | Google Scholar

14. Chen Y-C, Griffiths B, Weng L, Nicley SS, Ishmael SN, Lekhai Y, et al. Laser writing of individual nitrogen-vacancy defects in diamond with near-unity yield. Optica (2019) 6(5):662. doi:10.1364/OPTICA.6.000662

CrossRef Full Text | Google Scholar

15. Ziegler JF, Biersack JP, Littmark U. The stopping and range of ions in solids. Oxford, UK: Pergamon (1985).(Stopping and ranges of ions in matter)

Google Scholar

16. Ziegler JF, Ziegler MD, Biersack JP. SRIM – the stopping and range of ions in matter (2010). Nucl Instrum Methods Phys Res Sect B Beam Interact Mater At (2010) 268(11–12):1818–23. doi:10.1016/j.nimb.2010.02.091

CrossRef Full Text | Google Scholar

17. Raatz N, Scheuner C, Pezzagna S, Meijer J. Investigation of ion channeling and scattering for single-ion implantation with high spatial resolution. Phys Status Solidi A (2019) 216(21):1970069. doi:10.1002/pssa.201970069

CrossRef Full Text | Google Scholar

18. Alves AD, Newnham J, van Donkelaar JA, Rubanov S, McCallum JC, Jamieson DN. Controlled deterministic implantation by nanostencil lithography at the limit of ion-aperture straggling. Nanotechnology (2013) 24(14):145304. doi:10.1088/0957-4484/24/14/145304

PubMed Abstract | CrossRef Full Text | Google Scholar

19. van Donkelaar J, Yang C, Alves AD, McCallum JC, Hougaard C, Johnson BC, et al. Single atom devices by ion implantation. J Phys Condens Matter (2015) 27(15):154204. doi:10.1088/0953-8984/27/15/154204

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Lagomarsino S, Sciortino S, Gelli N, Flatae AM, Gorelli F, Santoro M, et al. The center for production of single-photon emitters at the electrostatic-deflector line of the Tandem accelerator of LABEC. Nucl Instrum Methods Phys Res Sect B Beam Interact Mater At (2018) 422:31–40. doi:10.1016/j.nimb.2018.02.020

CrossRef Full Text | Google Scholar

21. Pezzagna S, Rogalla D, Wildanger D, Meijer J, Zaitsev A. Creation and nature of optical centres in diamond for single-photon emission—overview and critical remarks. New J Phys (2011) 13(3):035024. doi:10.1088/1367-2630/13/3/035024

CrossRef Full Text | Google Scholar

22.LS Pan, and DR Kania, editors. Diamond: electronic properties and applications [Internet]. Boston, MA: Springer US (1995) Available from: http://link.springer.com. doi:10.1007/978-1-4615-2257-7

CrossRef Full Text | Google Scholar

23. Tóth S, Himics L, Veres M, Balogh Z, Ralchenko VG, Koós M. Zero-phonon line characteristics of SiV center emission in microcrystalline diamond probed with intensive optical excitation. J Lumin (2015) 158:260–4. doi:10.1016/j.jlumin.2014.10.022

CrossRef Full Text | Google Scholar

24. Lagomarsino S, Flatae AM, Sciortino S, Gorelli F, Santoro M, Tantussi F, et al. Optical properties of silicon-vacancy color centers in diamond created by ion implantation and post-annealing. Diam Relat Mater (2018) 84:196–203. doi:10.1016/j.diamond.2018.03.010

CrossRef Full Text | Google Scholar

25. Loudon R. The Raman effect in crystals. Adv Phys (1964) 13(52):423–82. doi:10.1080/00018736400101051

CrossRef Full Text | Google Scholar

26. Schröder T, Trusheim ME, Walsh M, Li L, Zheng J, Schukraft M, et al. Scalable focused ion beam creation of nearly lifetime-limited single quantum emitters in diamond nanostructures. Nat Commun (2017) 8(May):15376–7. doi:10.1038/ncomms15376

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Khramtsov IA, Agio M, DYu F. Dynamics of single-photon emission from electrically pumped color centers. Phys Rev Appl (2017) 8(2):024031. doi:10.1103/PhysRevApplied.8.024031

CrossRef Full Text | Google Scholar

28. Fedyanin DY, Agio M. Ultrabright single-photon source on diamond with electrical pumping at room and high temperatures. New J Phys (2016) 18(7):073012. doi:10.1088/1367-2630/18/7/073012

CrossRef Full Text | Google Scholar

29. Berhane AM, Choi S, Kato H, Makino T, Mizuochi N, Yamasaki S, et al. Electrical excitation of silicon-vacancy centers in single crystal diamond. Appl Phys Lett (2015) 106:171102. doi:10.1063/1.4919388

CrossRef Full Text | Google Scholar

30. Feng T, Schwartz BD. Characteristics and origin of the 1.681 eV luminescence center in chemical‐vapor‐deposited diamond films. J Appl Phys (1993) 73(3):1415–25. doi:10.1063/1.353239

CrossRef Full Text | Google Scholar

31. Neu E, Hepp C, Hauschild M, Gsell S, Fischer M, Sternschulte H, et al. Low-temperature investigations of single silicon vacancy colour centres in diamond. New J Phys (2013) 15(4):043005. doi:10.1063/1.4807398

CrossRef Full Text | Google Scholar

32. Lagomarsino S, Gorelli F, Santoro M, Fabbri N, Hajeb A, Sciortino S, et al. Robust luminescence of the silicon-vacancy center in diamond at high temperatures. AIP Adv (2015) 5(12):127117. doi:10.1063/1.4938256

CrossRef Full Text | Google Scholar

33. Liu MS, Bursill LA, Prawer S, Beserman R. Temperature dependence of the first-order Raman phonon line of diamond. Phys Rev B (2000) 61(5):3391–5. doi:10.1103/PhysRevB.61.3391

CrossRef Full Text | Google Scholar

34. Neu E, Agio M, Becher C. Photophysics of single silicon vacancy centers in diamond: implications for single photon emission. Opt Express (2012) 20(18):19956–71. doi:10.1364/OE.20.019956

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Sipahigil A, Jahnke KD, Rogers LJ, Teraji T, Isoya J, Zibrov AS, et al. Indistinguishable photons from separated silicon-vacancy centers in diamond. Phys Rev Lett (2014) 113(11):113602–5. doi:10.1103/PhysRevLett.113.113602

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Rogers LJ, Jahnke KD, Teraji T, Marseglia L, Müller C, Naydenov B, et al. Multiple intrinsically identical single-photon emitters in the solid state. Nat Commun (2014) 5:4739–2. doi:10.1038/ncomms5739

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Riedrich-Möller J, Kipfstuhl L, Hepp C, Neu E, Pauly C, Mücklich F, et al. One- and two-dimensional photonic crystal microcavities in single crystal diamond. Nat Nanotechnol (2012) 7(1):69–74. doi:10.1038/nnano.2011.190

CrossRef Full Text | Google Scholar

38. Agio M. Optical antennas as nanoscale resonators. Nanoscale (2012) 4(3):692–706. doi:10.1039/c1nr11116g

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Kambalathmana H, Flatae AM, Lagomarsino S, Galal H, Tantussi F, Messina GC, et al. (2020) Exploring ultrafast single-photon emission of silicon-vacancy color centers in diamond nano-membranes coupled with gold nano-cones. In: M Agio, C Soci, and MT Sheldon, editors. Quantum nanophotonic materials, devices, and systems 2019. San Diego, United States: SPIE, 5. doi:10.1117/12.2528749

Google Scholar

40. Popovici G, Prelas MA. Prospective n-type impurities and methods of diamond doping. Diam Relat Mater (1995) 4(12):1305–10. doi:10.1016/0925-9635(95)00319-3

CrossRef Full Text | Google Scholar

41. Goss JP, Briddon PR, Jones R, Sque S. Donor and acceptor states in diamond. Diam Relat Mater (2004) 13(4–8):684–90. doi:10.1016/j.diamond.2003.08.028

CrossRef Full Text | Google Scholar

42. Barjon J. Luminescence spectroscopy of bound excitons in diamond. Phys Status Solidi A (2017) 214(11):1700402. doi:10.1002/pssa.201770169

CrossRef Full Text | Google Scholar

43. Jones R, Lowther JE, Goss J. Limitations to n-type doping in diamond: the phosphorus-vacancy complex. Appl Phys Lett (1996) 69(17):2489–91. doi:10.1063/1.117715

CrossRef Full Text | Google Scholar

44. Cao GZ, Driessen FAJM, Bauhuis GJ, Giling LJ, Alkemade PFA. Homoepitaxial diamond films codoped with phosphorus and nitrogen by chemical-vapor deposition. J Appl Phys (1995) 78(5):3125–31. doi:10.1063/1.359998

CrossRef Full Text | Google Scholar

45. te Nijenhuis J, Olsthoorn SM, van Enckevort WJP, Giling LJ. Red luminescence in phosphorous-doped chemically vapor deposited diamond. J Appl Phys (1997) 82(1):419–22. doi:10.1063/1.365831

CrossRef Full Text | Google Scholar

46. Flatae AM, Lagomarsino S, Sledz F, Soltani N, Nicley SS, Haenen K, et al. Silicon-vacancy color centers in phosphorus-doped diamond. Diam Relat Mater (2020) 105:107797. doi:10.1016/j.diamond.2020.107797

CrossRef Full Text | Google Scholar

47. Becker JN, Pingault B, Groß D, Gündoğan M, Kukharchyk N, Markham M, et al. All-optical control of the silicon-vacancy spin in diamond at millikelvin temperatures. Phys Rev Lett (2018) 120(5):053603. doi:10.1103/PhysRevLett.120.053603

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Hepp C, Müller T, Waselowski V, Becker JN, Pingault B, Sternschulte H, et al. Electronic structure of the silicon vacancy color center in diamond. Phys Rev Lett (2014) 112(3):036405. doi:10.1103/PhysRevLett.112.036405

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Jamali M, Gerhardt I, Rezai M, Frenner K, Fedder H, Wrachtrup J. Microscopic diamond solid-immersion-lenses fabricated around single defect centers by focused ion beam milling. Rev Sci Instrum (2014) 85(12):123703. doi:10.1063/1.4902818

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Dregely D, Lindfors K, Dorfmüller J, Hentschel M, Becker M, Wrachtrup J, et al. Plasmonic antennas, positioning, and coupling of individual quantum systems. Phys Stat Sol B (2012) 249(4):666–77. doi:10.1002/pssb.201100781

CrossRef Full Text | Google Scholar

51. Checcucci S, Lombardi P, Rizvi S, Sgrignuoli F, Gruhler N, Dieleman FB, et al. Beaming light from a quantum emitter with a planar optical antenna. Light Sci Appl (2017) 6(4):e16245. doi:10.1038/lsa.2016.245

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Galal H, Agio M. Highly efficient light extraction and directional emission from large refractive-index materials with a planar Yagi-Uda antenna. Opt Mater Express (2017) 7(5):1634. doi:10.1063/1.5096270

CrossRef Full Text | Google Scholar

53. Galal H, Flatae AM, Lagomarsino S, Schulte G, Wild C, Wörner E, et al. Highly efficient light extraction and directional emission from diamond color centers using planar Yagi-Uda antennas (2019) Available from: http://arxiv.org/abs/1905.03363.ArXiv190503363 Phys Physicsquant-Ph [Internet]

Google Scholar

54. Soltani N, Agio M. Planar antenna designs for efficient coupling between a single emitter and an optical fiber. Opt Express (2019) 27(21):30830. doi:10.1364/OE.27.030830

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Degen CL, Reinhard F, Cappellaro P. Quantum sensing. Rev Mod Phys (2017) 89(3):035002. doi:10.1103/RevModPhys.89.035002

CrossRef Full Text | Google Scholar

56. Kucsko G, Maurer PC, Yao NY, Kubo M, Noh HJ, Lo PK, et al. Nanometre-scale thermometry in a living cell. Nature (2013) 500(7460):54–8. doi:10.1038/nature12373

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Nguyen CT, Evans RE, Sipahigil A, Bhaskar MK, Sukachev DD, Agafonov VN, et al. All-optical nanoscale thermometry with silicon-vacancy centers in diamond. Appl Phys Lett (2018) 112(20):203102. doi:10.1063/1.5029904

CrossRef Full Text | Google Scholar