- 1Business School, Hohai University, Nanjing, China
- 2School of Mathematics and Information Sciences, Yantai University, Yantai, China
The resistance distance between any two vertices of a connected graph is defined as the net effective resistance between them in the electrical network constructed from the graph by replacing each edge with a unit resistor. In this article, using electric network approach and combinatorial approach, we derive exact expression for resistance distances between any two vertices of polyacene graphs.
1 Introduction
Let
Besides being an intrinsic graph metric and an important component of electrical circuit theory, resistance distance also turns out to have important applications in chemistry. For this reason, resistance distance has been widely studied in the mathematical, chemical, and physical literature. In the study of resistance distance, the main focus is placed on the problem of computation of resistance distance. This problem has been a classical problem in electrical network theory studied by numerous researchers for a long time. Besides, it is also relevant to a wide range of problems ranging from random walks, the theory of harmonic functions, to lattice Green’s functions. Consequently, this problem has attracted much attention, and many researchers have devoted themselves to it. Up to now, resistance distances have been computed for many interesting (classes of) graphs, with emphasis being placed on some highly concerned electrical networks and chemical interesting graphs. For example, resistance distances have been computed for Platonic solids [5], and for some fullerene graphs including buckminsterfullerene [6], circulant graphs [7], distance-regular graphs [8, 9], pseudo–distance-regular graphs [10], wheels and fans [11], Cayley graphs over finite abelian groups [12], complete graph minus N edges [13], resistor network embedded on a globe [14], Möbius ladder [15],
It is interesting to note that a good deal of attention has been paid on resistance distances in plane networks, such as Platonic solids, fullerene graphs, wheels, fans, ladder graphs, Apollonian network, Sierpinski Gasket Network,
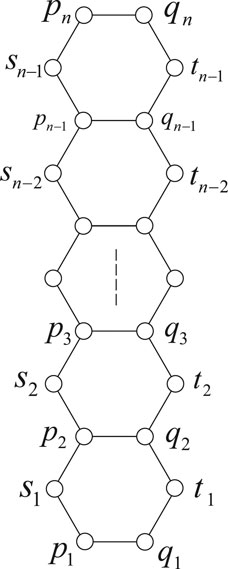
2 Resistance Distances in Linear Polyacene Graphs
Let
Before stating the main result, we introduce the elegant resistance distance local rules, which will be frequently used later. For any vertex
Lemma 2.1 [29]. Let
where
2) For any three different vertices
Now, we are ready for the main theorem. For simplicity, we let
Then, the main result is given in the following.
Theorem 2.2. The resistance distances between any two vertices in the linear polyacene graph
Proof. We divide the proof into two steps.
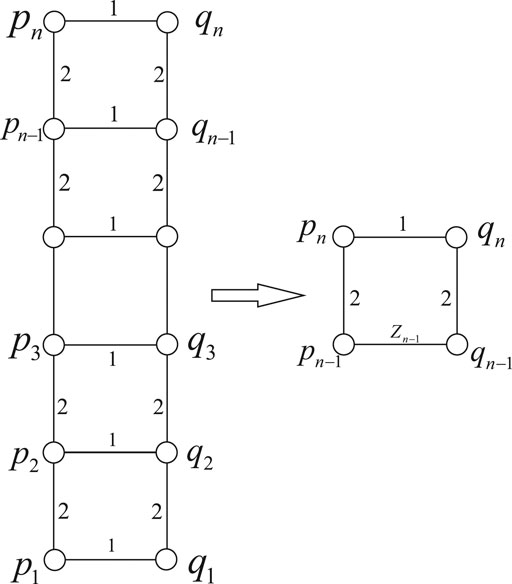
Step 1. Computation of resistance distances between any two vertices in
To compute resistance distances between vertices in
First, we compute resistance distances between the end vertices
with initial condition
Specially, we have
We proceed to use
On the other hand, by parallel and series connection rules, we have
with initial conditions
Set
Thus, we have
Since
This could also be rewritten as
Solving the recursion relation, we get
Now, by Eqs 2.14–2.16, together with the relation
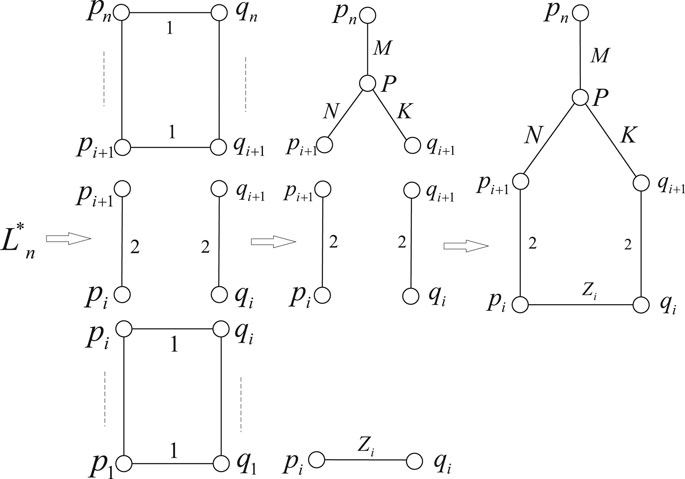
Next, we proceed to compute
Note that
Solving M, N, and K, we obtain
Then, applying parallel and series connection rules to the reduced circuit in Figure 3, we obtain
Substituting Eqs 2.8–2.20 into Eq. 2.21, we have
Finally, we compute
It follows that
On the other hand, by the series and parallel connection rules, we have
By Eqs. (2.8), Eqs 2.22–2.25, and doing some algebra using Mathematica [30], we obtain
It is easily verified that Eq. 2.27 is valid for
Step 2. Computation of resistance distances between
First, we compute
Multiplying Eq. 2.28 by 3 and then minus Eq. 2.29, we get
Then, substituting the value of
Substituting Eq. 2.31 into Eq. 2.30, we have
In the same way, we could obtain that
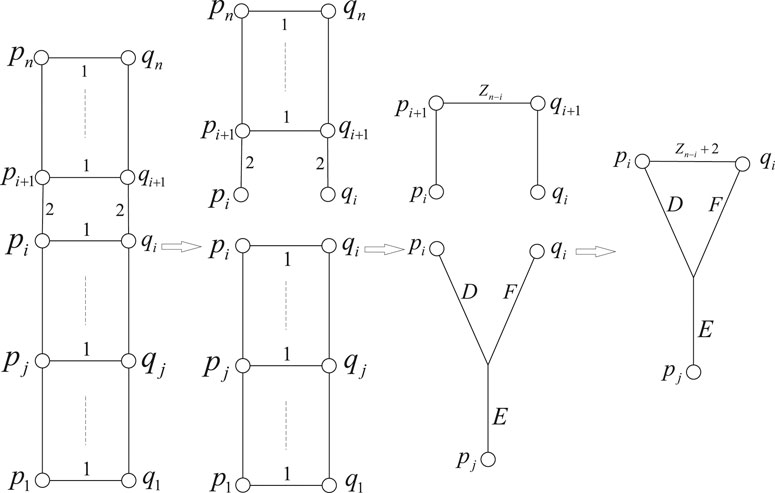
Second, we calculate the resistance distance between
By Eqs 2.32, 2.33, it follows that
For the sake of simplicity, we define
Then, Eq. 2.35 can be rewritten as
On the other hand, by Eq. 2.26, we have
Substituting Eqs. 2.37, 2.38 into Eq. 2.34, we draw the conclusion that
Third, we calculate the resistance distance between
By Eq. 2.37, we have
For simplicity, we define
On the other hand, by Eq. 2.27, we have
Substituting Eqs. 2.41–2.43 into Eq. 2.40, we get
Fourth, we calculate the resistance distance between
As
Fifth and finally, we calculate the resistance between
Note by the symmetry of
3 Conclusion
The computation of resistance distances is a classical problem in electrical circuit theory, which has attracted much attention. It is of special interest to investigate resistance distances in plane networks. Along this line, we have considered the linear polyacene network, with exact expression for resistance distances in this network being given. It is a primary attempt for the computation of resistance distances in plane hexagonal lattice. Resistance distances in more and more plane hexagonal lattices are greatly anticipated.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This research was funded by the National Natural Science Foundation of China through grant number 116711347, and project ZR2019YQ02 by Shandong Provincial Natural Science Foundation.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We would like to thank the anonymous reviewers for their useful comments.
References
3. Nash Williams JAC. Random walks and electric currents in networks. Proc. Cambridge Phil Soc (1959) 55:181–94. doi:10.1017/S0305004100033879
4. Doyle PG, Snell JL. Random walks and electric networks. Washington, DC: The Mathematical Association of America (1984) 118 p.
5. Lukovits I, Nikolić S, Trinajstić N. Resistance distance in regular graphs. Int J Quant Chem (1999) 71:217–25. doi:10.1002/(SICI)1097-461X(1999)71:3<217::AID-QUA1>3.0.CO;2-C
7. Zhang H, Yang Y. Resistance distance and Kirchhoff index in circulant graphs. Int J Quant Chem (2007) 107:330–9. doi:10.1002/qua.21068
8. Palacios JL. Closed-form formulas for Kirchhoff index. Int J Quant Chem (2001) 81:135–40. doi:10.1002/1097-461X(2001)81:2%3C135::AID-QUA4%3E3.0.CO;2-G
9. Jafarizadeh MA, Sufiani R, Jafarizadeh S. Recursive calculation of effective resistances in distance-regular networks based on Bose-Mesner algebra and Christoffel-Darboux identity. J Math Phys (2009) 50:023302. doi:10.1063/1.3077145
10. Jafarizadeh S, Sufiani R, Jafarizadeh MA. Evaluation of effective resistances in pseudo-distance-regular resistor networks. J Stat Phys (2010) 139:177–99. doi:10.1007/s10955-009-9909-8
11. Bapat RB, Gupta S. Resistance distance in wheels and fans. Indian J Pure Appl Math (2010) 41:1–13. doi:10.1007/s13226-010-0004-2
12. Gao X, Luo Y, Liu W. Resistance distances and the Kirchhoff index in Cayley graphs. Discrete Appl Math (2011) 159:2050–7. doi:10.1016/j.dam.2011.06.027
13. Chair N. Exact two-point resistance, and the simple random walk on the complete graph minus N edges. Ann Phys (2012) 327:3116–29. doi:10.1016/j.aop.2012.09.002
14. Tan Z, Essam JW, Wu FY. Two-point resistance of a resistor network embedded on a globe. Phys Rev E Stat Nonlinear Soft Matter Phys (2014) 90:012130. doi:10.1103/PhysRevE.90.012130
15. Chair N, Ali Dannoun EM. Two-point resistance of the Möbius ladder. Phys Scripta (2015) 90:035206. doi:10.1088/0031-8949/90/3/035206
16. Tan Z. Theory on resistance of m×n cobweb network and its application. Int J Circ Theor Appl (2015) 43:1687–702. doi:10.1002/cta.2035
17. Gervacio SV. Resistance distance in complete n-partite graphs. Discrete Appl Math (2016) 203:53–61. doi:10.1016/j.dam.2015.09.017
18. Tan Z. Two-point resistance of an m×n resistor network with an arbitrary boundary and its application in RLC network. Chin Phys B (2016) 25:050504. doi:10.1088/1674-1056/25/5/050504
19. Cinkir Z. Effective resistances and Kirchhoff index of a ladder graph. J Math Chem (2016) 54:955–66. doi:10.1007/s10910-016-0597-8
20. Tan Z, Asad JH, Owaidat MQ. Resistance formulae of a multipurpose 𝑛-step network and its application in LC network. Int J Circuit Theor Appl (2017) 45:1942–57. doi:10.1002/cta.2366
21. Vaskouski M, Zadorozhnyuk A. Resistance distances in Cayley graphs on symmetric groups. Discrete Appl Math (2017) 227:121–35. doi:10.1016/j.dam.2017.04.044
22. Shangguan Y, Chen H. Two-point resistances in an Apollonian network. Phys Rev E (2017) 96:062140. doi:10.1103/PhysRevE.96.062140
23. Jiang Z, Yan W. Some two-point resistances of the Sierpinski gasket network. J Stat Phys (2018) 172:824–32. doi:10.1007/s10955-018-2067-0
24. Owaidat MQ, Asad JH, Tan Z. Resistance computation of generalized decorated square and simple cubic network lattices. Results Phys (2019) 12:1621–7. doi:10.1016/j.rinp.2019.01.070
25. Shangguan Y, Chen H. Two-point resistances in a family of self-similar (x,y)-flower networks. Physica A (2019) 523:382–91. doi:10.1016/j.physa.2019.02.008
26. Ye L, Yan W. Resistance between two vertices of almost complete bipartite graphs. Discrete Appl Math (2019) 257:299–305. doi:10.1016/j.dam.2018.08.030
27. Barrett W, Evans EJ, Francis AE. Resistance distance in straight linear 2-trees. Discrete Appl Math (2019) 258:13–34. doi:10.1016/j.dam.2018.10.043
28. Jiang Z, Yan W. Resistances between two nodes of a path network. Appl Math Comput (2019) 361:42–6. doi:10.1016/j.amc.2019.05.006
29. Chen H, Zhang F. Resistance distance local rules. J Math Chem (2008) 44:405–17. doi:10.1007/s10910-007-9317-8
Keywords: hexagonal lattice, local rules, polyacene graph, resistance distance, circuit reduction
Citation: Wang D and Yang Y (2021) Resistance Distances in Linear Polyacene Graphs. Front. Phys. 8:600960. doi: 10.3389/fphy.2020.600960
Received: 31 August 2020; Accepted: 24 November 2020;
Published: 12 January 2021.
Edited by:
Andre P. Vieira, University of São Paulo, BrazilReviewed by:
Zhibin Du, South China Normal University, ChinaMohammad Reza Farahani, Iran University of Science and Technology, Iran
Copyright © 2021 Wang and Yang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yujun Yang, eWFuZ3lqQHlhaG9vLmNvbQ==
 Dayong Wang1
Dayong Wang1 Yujun Yang
Yujun Yang