The Suppression of Epidemic Spreading Through Minimum Dominating Set

COVID-19 has infected millions of people, with deaths in more than 200 countries. It is therefore essential to understand the dynamic characteristics of the outbreak and to design effective strategies to restrain the large-scale spread of the epidemic. In this paper, we present a novel framework to depress the epidemic spreading, by leveraging the decentralized dissemination of information. The framework is equivalent to finding a special minimum dominating set for a duplex network which is a general dominating set for one layer and a connected dominating set for another layer. Using the spin glass and message passing theory, we present a belief-propagation-guided decimation (BPD) algorithm to construct the special minimum dominating set. As a consequence, we could immediately recognize the epidemic as soon as it appeared, and rapidly immunize the whole network at minimum cost.

Introduction

In recent years, many different epidemic types have frequently erupted and spread worldwide, leading to not only great economic losses, but also widespread social disruption [7, 11, 14, 19]. The ongoing COVID-19 pandemic in particular has infected more than 10 million people causing deaths in more than 200 countries [5, 6, 10, 11, 24]. It is therefore essential to understand the dynamic characteristics of epidemic outbreaks and to design effective strategies to restrain the large-scale spread of the epidemic [4, 9, 13, 16–18].

The most traditional method of controlling an epidemic outbreak is network immunization, which cuts the path of the spread, by immunizing parts of the network nodes [2, 20, 23]. The common solution of network immunization uses the centrality index of the network, in which the nodes with large degree, k-shell, articulation points, betweenness, or spectral coefficients are selected as the immunized nodes. Recently, the control strategy of an epidemic, based on the competing spread on top of a duplex network, has attracted a lot of attention [1, 3, 15–17]. It is known that the information propagation in a virtual social network plays an important role in controlling epidemic spreading. A representative scenario is that the infectious diseases spread in a real physical contact network of individuals, will naturally lead to the propagation of crisis awareness information on virtual social networks. The individuals who obtained the awareness information will take measures to protect themselves, resulting in the suppression of the spread of the infectious disease. This is the framework of the competing spreading process of disease and awareness information on the duplex network coupled with the physical network and virtual network. Similarly, [21] introduced the competing spreading framework of the computer virus and patch, in which the patch dissemination restrains the virus propagation while they spread through different channels [21]. However, both of these competing spreading frameworks suffer the problem that it is surely improper to assume all network nodes have the ability to monitor their neighbors and recognize the epidemic and would like to distribute the awareness information or patch.

To compensate for the shortcomings of the competing spreading framework, Takaguchi et al. proposed a novel control method which takes advantage of both traditional network immunization and competing spreading [12]. They introduced the observer node into the networks, which could monitor the state of its neighbors and could therefore recognize the epidemic if its neighbors were infected. In addition, the observer node could send awareness information to its uninfected neighbors (i.e. immunize its uninfected neighbors) if it recognized the epidemic. However, such a method focusses on a single network which ignores the fact that physical monitoring and information propagation usually takes place in different channels. As an extension, [8] introduced an improved model of deploying an observer node on multiplex networks, consisting of an epidemic spreading layer and an information spreading layer. Though the observer node-based method could monitor all the network nodes and efficiently recognize the infection, it cannot immunize all the network nodes when infection spreading is confirmed.

In this sense, Zhao et al. introduced a strategy of controlling an epidemic through the minimum dominating set (MDS) of the multiplex network [22]. They proposed a framework coupled by a duplex network (one layer is the immunization distribution network, another is the epidemic spreading network layer) and a central node and let the nodes of the MDS of the duplex network be the observer nodes. When one neighbor is infected in the epidemic spreading network layer, the observer could immediately recognize the infection and send the information to the central node. The central node would then distribute the crisis information or patches to all the observers and the observers then spread them to their neighbors in the immunization distribution network. Under the definition of MDS of the multiplex network, such a method could recognize the infection immediately as it happened and could also immediately immunize all the network nodes using the smallest number of observer nodes.

However, Zhao’s method belongs to the centralization strategy. As an improvement, in this paper we propose an MDS-based decentralized strategy. We introduce a special MDS of the duplex network which is a general dominating set for one layer and a connected dominating set for another layer. Using the spin glass and message passing theory, we present a belief-propagation-guided decimation (BPD) algorithm to construct the special MDS. As a consequence, we could monitor all the network nodes and immediately recognize the infection, and rapidly immunize all the network nodes when infection spreading is confirmed, while the cost is minimized.

Deployment of Observer Node Based on Special MDS of Duplex Network

Different from the Zhao’s method, our method only contains one duplex network where one layer is the immunization distribution network (IL), and the other is the epidemic spreading network layer (EL). Here, we introduce a novel definition of special MDS of the duplex network (see Figure 1). It is a minimum node set which is a general dominating set for the EL and a connected dominating set for the IL; at the same time, the size of the node set is minimum.

FIGURE 1

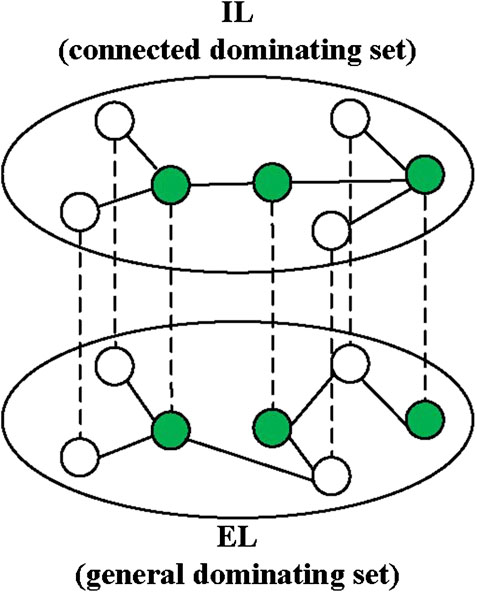
FIGURE 1. The set of green nodes is a special MDS of the duplex network. It is a general dominating set of the EL and a connected dominating set of the IL.

To control the epidemic spreading, we let the nodes of the special MDS of the duplex network be the observer nodes. The observer nodes could monitor its neighbors’ states in EL, thus could immediately recognize the infection after the neighbor was infected. In addition, the observer nodes could diffuse the information to its neighbors in IL after they recognized the infection or after receiving the information from its neighbors. Therefore, under the definition of the special MDS of the duplex network, the epidemic could be immediately recognized as soon as it appeared since all network nodes were monitored, and all network nodes could receive the related information due to the observer nodes being fully connected in IL.

Construction of Special MDS of Duplex Network

When considering the discussion in the above section, the problem of controlling epidemic spreading is converted to construct a special MDS of the duplex network. Obviously, the construction of the special MDS is NP-hard, and so we can only try to obtain a near optimal solution. Therefore, all the MDS discussed in the rest of the paper are actually a near-optimal special dominating set. In [22]; Zhao et al. proposed a framework of the construction method of the MDS of the multiplex network, but no detailed implementations are given. In this section, we first show the detailed procedure of the construction of general MDS of the duplex network, then a simple greedy strategy is given to construct the special MDS of the duplex network.

Construction of the General MDS of the Duplex Network

Let $G=\left(G^1,G^2\right)$ be a duplex network, where $G^i$ denotes the network layer i. In our framework, $G^1$ and $G^2$ represent the IL and EL, respectively. The two layers have the same set V of N nodes and a distinct set of edges. If D is a dominating set of G, it must be a dominating set of each network layer of G, which means every node in $V\backslash D$ must be connected to at least one node of D in every layer. The state of node $i\in D$ is called occupied, denoted by $c_i=1$. Otherwise $i\in V\backslash D$ is called empty but observed and denoted as $c_i=0$. For constructing the MDS of the duplex network, we introduce the following partition function

$Z={\displaystyle \sum }_{\underset{¯}{c}}{\displaystyle \prod }_{i\in V}\left\{e^{-x{c}_i}\left[1-\left(1-c_i\right){\displaystyle \prod }_{j\in {\text{Γ}}_i^1}\left(1-c_j\right)\right]\left[1-\left(1-c_i\right){\displaystyle \prod }_{j\in {\text{Γ}}_i^2}\left(1-c_j\right)\right]\right\}(1)$

where $\underset{¯}{c}=\left\{c_1,c_2,\dots ,c_N\right\}$ represents a configuration of node states, and ${\text{Γ}}_i^k$ denotes the set of neighbors of i in $G^k$. x is regarded as the positive re-weighting parameter. Obviously, in Eq. 1$\left[1-\left(1-c_i\right){\displaystyle \prod }_{j\in {\text{Γ}}_i^1}\left(1-c_j\right)\right]\left[1-\left(1-c_i\right){\displaystyle \prod }_{j\in {\text{Γ}}_i^2}\left(1-c_j\right)\right]=1$ implies i is occupied or observed in both layers; otherwise the term is equal to 0. Therefore, Z is only contributed by the configuration of the dominating set. In particular, only the MDS of the duplex network contributes to Z in the case of $x\to \infty$.

Solving Eq. 1 using the message passing theory, we have the expression of marginal probability $q_i^{c_i}$ of i being in state $c_i$ as follows

$q_i^{c_i}=\frac{Q_i^{c_i}}{{\displaystyle \sum _{c_i}{Q}_i^{c_i}}}(2)$

where

$Q_i^1=e^{-x}{\displaystyle \prod }_{j\in {\text{Γ}}_i^1\vee {\text{Γ}}_i^2}{\displaystyle \sum _{c_j}{q}_{j\to i}^{\left(c_j,1\right)}}(3)$

$Q_i^0={\displaystyle \prod }_{j\in {\text{Γ}}_i^1\mathrm{\vee }{\text{Γ}}_i^2}{\displaystyle \sum _{c_j}{q}_{j\to i}^{\left(c_j,0\right)}}-\left[{\displaystyle \prod }_{j\in {\text{Γ}}_i^1}{q}_{j\to i}^{\left(\mathrm{0,0}\right)}{\displaystyle \prod }_{\begin{array}{c}j\in {\text{Γ}}_i^2\\ j\notin {\text{Γ}}_i^1\end{array}}{\displaystyle \sum _{c_j}{q}_{j\to i}^{\left(c_j,0\right)}}+{\displaystyle \prod }_{j\in {\text{Γ}}_i^2}{q}_{j\to i}^{\left(\mathrm{0,0}\right)}{\displaystyle \prod }_{\begin{array}{c}j\in {\text{Γ}}_i^1\\ j\notin {\text{Γ}}_i^2\end{array}}{\displaystyle \sum _{c_j}{q}_{j\to i}^{\left(c_j,0\right)}}-{\displaystyle \prod }_{j\in {\text{Γ}}_i^1\mathrm{\vee }{\text{Γ}}_i^2}{q}_{j\to i}^{\left(\mathrm{0,0}\right)}\right].(4)$

${\text{Γ}}_i^1\mathrm{\vee }{\text{Γ}}_i^2$ represents the union of set ${\text{Γ}}_i^1$ and ${\text{Γ}}_i^2$, i.e. the set of all neighbors of nodes i in both layers. $q_{j\to i}^{\left(c_j,c_i\right)}$ denotes the joint probability of j being in state $c_j$ and i in $c_i$ under the assumption that node i is deleted from the network. $q_{j\to i}^{\left(c_j,c_i\right)}$ is given by

$q_{j\to i}^{\left\{c_j,c_i\right\}}=\frac{Q_{j\to i}^{\left\{c_j,c_i\right\}}}{{\displaystyle \sum _{c_j,c_i}{Q}_{j\to i}^{\left\{c_j,c_i\right\}}}}(5)$

where

$Q_{j\to i}^{\left\{\mathrm{1,0}\right\}}=e^{-x}{\displaystyle \prod }_{\begin{array}{c}k\in {\text{Γ}}_j^1\mathrm{\vee }{\text{Γ}}_j^2\\ k\ne i\end{array}}{\displaystyle \sum }_{c_k}{q}_{k\to j}^{\left(c_k,1\right)}(6)$

$Q_{j\to i}^{\left\{\mathrm{1,1}\right\}}=Q_{j\to i}^{\left\{\mathrm{1,0}\right\}}(7)$

$Q_{j\to i}^{\left\{\mathrm{0,1}\right\}}=\{\begin{array}{l}{\displaystyle \prod }_{\begin{array}{c}k\in {\text{Γ}}_j^1\vee {\text{Γ}}_j^2\\ k\ne i\end{array}}{\displaystyle \sum }_{c_k}{q}_{k\to j}^{\left(c_k,0\right)}-{\displaystyle \prod }_{\begin{array}{c}k\in {\text{Γ}}_j^2\\ k\ne i\end{array}}{q}_{k\to j}^{\left(\mathrm{0,0}\right)}{\displaystyle \prod }_{\begin{array}{c}k\in {\text{Γ}}_j^1\\ \begin{array}{l}k\notin {\text{Γ}}_j^2\\ k\ne i\end{array}\end{array}}{\displaystyle \sum }_{c_k}{q}_{k\to j}^{\left(c_k,0\right)},\text{if}j\in {\text{Γ}}_i^1,j\notin {\text{Γ}}_i^2\\ {\displaystyle \prod }_{\begin{array}{c}k\in {\text{Γ}}_j^1\vee {\text{Γ}}_j^2\\ k\ne i\end{array}}{\displaystyle \sum }_{c_k}{q}_{k\to j}^{\left(c_k,0\right)}-{\displaystyle \prod }_{\begin{array}{c}k\in {\text{Γ}}_j^1\\ k\ne i\end{array}}{q}_{k\to j}^{\left(\mathrm{0,0}\right)}{\displaystyle \prod }_{\begin{array}{c}k\in {\text{Γ}}_j^2\\ \begin{array}{l}k\notin {\text{Γ}}_j^2\\ k\ne i\end{array}\end{array}}{\displaystyle \sum }_{c_k}{q}_{k\to j}^{\left(c_k,0\right)},\text{if}j\notin {\text{Γ}}_i^1,j\in {\text{Γ}}_i^2\\ {\displaystyle \prod }_{\begin{array}{c}k\in {\text{Γ}}_j^1\mathrm{\vee }{\text{Γ}}_j^2\\ k\ne i\end{array}}{\displaystyle \sum }_{c_k}{q}_{k\to j}^{\left(c_k,0\right)},\text{if}j\in {\text{Γ}}_i^1\wedge {\text{Γ}}_i^2\end{array}(8)$

$Q_{j\to i}^{\left\{\mathrm{0,0}\right\}}={\displaystyle \prod }_{\begin{array}{c}k\in {\text{Γ}}_j^1\vee {\text{Γ}}_j^2\\ k\ne i\end{array}}{\displaystyle \sum }_{c_k}{q}_{k\to j}^{\left(c_k,0\right)}-\left[{\displaystyle \prod }_{\begin{array}{c}k\in {\text{Γ}}_j^1\\ k\ne i\end{array}}{q}_{k\to j}^{\left(\mathrm{0,0}\right)}{\displaystyle \prod }_{\begin{array}{c}k\in {\text{Γ}}_j^2\\ \begin{array}{l}k\notin {\text{Γ}}_j^1\\ k\ne i\end{array}\end{array}}{\displaystyle \sum }_{c_k}{q}_{k\to j}^{\left(c_k,0\right)}+{\displaystyle \prod }_{\begin{array}{c}k\in {\text{Γ}}_j^2\\ k\ne i\end{array}}{q}_{k\to j}^{\left(\mathrm{0,0}\right)}{\displaystyle \prod }_{\begin{array}{c}k\in {\text{Γ}}_j^1\\ \begin{array}{l}k\notin {\text{Γ}}_j^2\\ k\ne i\end{array}\end{array}}{\displaystyle \sum }_{c_k}{q}_{k\to j}^{\left(c_k,0\right)}-{\displaystyle \prod }_{\begin{array}{c}k\in {\text{Γ}}_j^1\mathrm{\vee }{\text{Γ}}_j^2\\ k\ne i\end{array}}{q}_{k\to j}^{\left(\mathrm{0,0}\right)}\right](9)$

Eq. 9 is called the belief propagation equation which has been widely used in different kinds of optimization problems.

Based on Eqs.1–9, we can use the classical Belief-Propagation-Guided Decimation Algorithm (BPD) to identify the MDS of a multiplex network. As discussed in [22]; we first simplify the calculation of $q_i^1$.

In case j has not been occupied but observed in at least one layer, the states of its neighbors in the corresponding layer could not be considered. Therefore, $Q_{j\to i}^{\left\{\mathrm{0,1}\right\}}$ and $Q_{j\to i}^{\left\{\mathrm{0,0}\right\}}$ can be further simplified as

$Q_{j\to i}^{\left\{\mathrm{0,1}\right\}}={\displaystyle \prod }_{\begin{array}{c}k\in {\text{Γ}}_j^1\mathrm{\vee }{\text{Γ}}_j^2\\ k\ne i\end{array}}{\displaystyle \sum }_{c_k}{q}_{k\to j}^{\left(c_k,0\right)}, \text{if}(j\in {\text{Γ}}_i^1,j\notin {\text{Γ}}_i^2,j\in O^2)\text{or}(j\in {\text{Γ}}_i^2,j\notin {\text{Γ}}_i^1,j\in O^1)(10)$

$Q_{j\to i}^{\left\{\mathrm{0,0}\right\}}=\{\begin{array}{l}{\displaystyle \prod }_{\begin{array}{c}k\in {\text{Γ}}_j^1\mathrm{\vee }{\text{Γ}}_j^2\\ k\ne i\end{array}}{\displaystyle \sum }_{c_k}{q}_{k\to j}^{\left(c_k,0\right)}-{\displaystyle \prod }_{\begin{array}{c}k\in {\text{Γ}}_j^1\\ k\ne i\end{array}}{q}_{k\to j}^{\left(\mathrm{0,0}\right)}{\displaystyle \prod }_{\begin{array}{c}k\in {\text{Γ}}_j^2\\ \begin{array}{c}k\notin {\text{Γ}}_j^1\\ k\ne i\end{array}\end{array}}{\displaystyle \sum }_{c_k}{q}_{k\to j}^{\left(c_k,0\right)},\text{if}j\notin O^1,j\in O^2\\ {\displaystyle \prod }_{\begin{array}{c}k\in {\text{Γ}}_j^1\mathrm{\vee }{\text{Γ}}_j^2\\ k\ne i\end{array}}{\displaystyle \sum }_{c_k}{q}_{k\to j}^{\left(c_k,0\right)}-{\displaystyle \prod }_{\begin{array}{c}k\in {\text{Γ}}_j^2\\ k\ne i\end{array}}{q}_{k\to j}^{\left(\mathrm{0,0}\right)}{\displaystyle \prod }_{\begin{array}{c}k\in {\text{Γ}}_j^1\\ \begin{array}{c}k\notin {\text{Γ}}_j^2\\ k\ne i\end{array}\end{array}}{\displaystyle \sum }_{c_k}{q}_{k\to j}^{\left(c_k,0\right)},\text{if}j\in O^1,j\notin O^2\\ {\displaystyle \prod }_{\begin{array}{c}k\in {\text{Γ}}_j^1\mathrm{\vee }{\text{Γ}}_j^2\\ k\ne i\end{array}}{\displaystyle \sum }_{c_k}{q}_{k\to j}^{\left(c_k,0\right)},\text{if}j\in O^1\wedge O^2\end{array}(11)$

where $O^k$ represents the set of nodes which have been observed in $G^k$, and $O^1\wedge O^2$ denotes the intersection of $O^1$ and $O^2$. In addition, $Q_i^0$ can also be simplified if i has been observed in at least one layer

$Q_i^0=\{\begin{array}{l}{\displaystyle \prod }_{j\in {\text{Γ}}_i^1\mathrm{\vee }{\text{Γ}}_i^2}{\displaystyle \sum }_{c_j}{q}_{j\to i}^{\left(c_j,0\right)}-{\displaystyle \prod }_{j\in {\text{Γ}}_i^1}{q}_{j\to i}^{\left(\mathrm{0,0}\right)}{\displaystyle \prod }_{\begin{array}{c}j\in {\text{Γ}}_i^2\\ j\notin {\text{Γ}}_i^1\end{array}}{\displaystyle \sum }_{c_j}{q}_{j\to i}^{\left(c_j,0\right)},\text{if}i\notin O^1,i\in O^2\\ {\displaystyle \prod }_{j\in {\text{Γ}}_i^1\mathrm{\vee }{\text{Γ}}_i^2}{\displaystyle \sum }_{c_j}{q}_{j\to i}^{\left(c_j,0\right)}-{\displaystyle \prod }_{j\in {\text{Γ}}_i^2}{q}_{j\to i}^{\left(\mathrm{0,0}\right)}{\displaystyle \prod }_{\begin{array}{c}j\in {\text{Γ}}_i^1\\ j\notin {\text{Γ}}_i^2\end{array}}{\displaystyle \sum }_{c_j}{q}_{j\to i}^{\left(c_j,0\right)},\text{if}i\in O^1,i\notin O^2\\ {\displaystyle \prod }_{j\in {\text{Γ}}_i^1\mathrm{\vee }{\text{Γ}}_i^2}{\displaystyle \sum }_{c_j}{q}_{j\to i}^{\left(c_j,0\right)},\text{if}i\in O^1\wedge O^2\end{array}(12)$

The procedure of BPD is now given by:

(1) The states of all nodes are initialized to be unoccupied and unobserved. The initial values of all joint probabilities $\left\{q_{j\to i}^{\left(c_j,c_i\right)}\right\}$ could set to be random numbers.

(2) Perform iterative calculations of the joint probabilities $\left\{q_{j\to i}^{\left(c_j,c_i\right)}\right\}$ based on Eq. 5 for $T_0$ rounds. Then calculate the occupation probability $\left\{q_i^1\right\}$ for all nodes using the obtained $\left\{q_{j\to i}^{\left(c_j,c_i\right)}\right\}$ according to Eq. 2.

(3) Select the first r unoccupied nodes with the highest occupation probabilities occupied. Then update the states of all remaining nodes.

(4) Remove the edges between the nodes that have been observed and remove all isolated observed nodes in every layer.

(5) If the remaining network still has unobserved nodes, calculate Eq. 5 for $T_1$ rounds and then calculate Eq. 2. Whether using Eq. 3 and Eq. 4 or Eq. 3 and Eq. 12 in Eq. 2, depends on whether i is unobserved or observed.

(6) Repeat operations (3)–(5) until all nodes are observed in all layers.

Greedy Construction of Special MDS of Duplex Network

In this section, we construct the special MDS of the duplex network based on the general MDS constructed via the BPD algorithm. We delete all of the nodes of layer IL which do not belong to the general MDS and denote the remaining network as IL’. If IL’ is not fully connected, it must have more than one cluster. We then remove nodes form $V/D$ into IL’ to reduce the number of clusters based on the following operations.

(1) If the insertion of one node into the IL’ can reduce the number of clusters, we select the node whose insertion can reduce the number of clusters to be inserted into the IL’ the most.

(2) If the insertion of one node into the IL’ cannot reduce the number of clusters, we select two linked nodes whose insertion can reduce the number of clusters to be inserted into the IL’ the most.

The operations are performed repeatedly until the IL’ is fully connected. In this way, a special MDS of the duplex network is constructed.

Result

In this section, we verify the effectiveness of our method by comparing it with the random algorithm and the simulated annealing algorithm.

The random algorithm is very simple. It randomly selects an unoccupied node and changes the node’s state to be occupied, until a special dominating set is constructed. The simulated annealing algorithm is widely used to solve many different kinds of optimization problems. To construct a special MDS of the duplex network, we define the following energy function

$E=u{\displaystyle \sum }_i{c}_i+v{\displaystyle \sum _i{f}_i}+w{\displaystyle \sum }_{\alpha }{\displaystyle \sum }_i\left(1-o_i^{\alpha }\right).(13)$

In the energy function, $f_i=1$ indicates that node i is occupied but has no occupied neighbor in layer IL, otherwise $f_i=0$. $o_i^{\alpha }=1$ indicates that node i is observed in layer α, that is it has at least one occupied neighbor in layer α, otherwise $o_i^{\alpha }=1$. In addition, u, v, and w are tunable parameters. At the beginning of the SA algorithm, we construct a special dominating set for the duplex network based on the random algorithm. Then we calculate the corresponding energy E based on Eq.13. At each time step of SA, we perform the following operations:

(1) Randomly select one node from the network. If the selected node is occupied, change its state to unoccupied. We then calculate the new energy $E^{new}$.

(2) Randomly select one node from the network. If the selected node is unoccupied, change its state to occupied. We then calculate the new energy $E^{new}$.

The operation is accepted with probability $e^{-\beta \left(E^{new}-E\right)}$, otherwise, the new occupation should be omitted. In this paper, we set $u=v=w=0.5$. β represents the inverse of the temperature. Its initial value is set to be 0.5 and then is increased by ${10}^{-6}$ at each time step. The SA algorithm terminates when β equals ${\beta }_{max}$. It should be noted that the SA algorithm could not ensure that the constructed dominating set is a special dominating set, therefore, a greedy process is still needed after the termination of the SA algorithm.

We performed experiments on four different kinds of duplex networks which are coupled by the SF network and ER random network. The results are given in Table 1. We can see that our method constructs the smallest special dominating set for any duplex network. Therefore, we could use the smallest observer nodes to control the epidemic spreading based on our deployment scheme.

TABLE 1

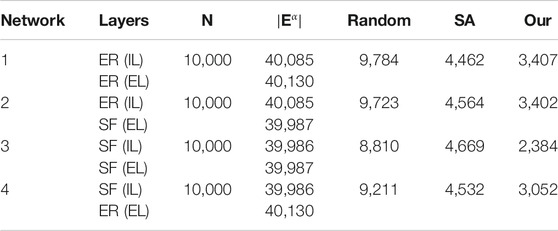
TABLE 1. The size of constructed dominating set of duplex network coupled by different network layers

Conclusion

In this paper, we designed a deployment scheme of observer nodes to control epidemic spreading based on the special MDS of the duplex network. Through the nodes of the special MDS of the duplex network, we could immediately recognize the epidemic as soon as it appeared and could immunize all network nodes—at the same time, the cost remains minimal. The deployment problem of the observer nodes is then converted to the construction problem of the special MDS of the duplex network. We used the BPD algorithm and a greedy algorithm to construct the special MDS of the duplex network. Our solution is verified to be very efficient on different kinds of duplex networks.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

LZ and DZ proposed the framework. JW, WZ, YZ, WW, and XX developed the mathematical theory. JW and WZ performed the experiment. All authors contributed to the article and approved the submitted version.

Funding

This work was supported in part by the National Natural Science Foundation of China (61702309), the Innovation and entrepreneurship training program of Civil Aviation University of China (201910059044), the National Key Research and Development Project (2018YFE0119700) and the Key Research and Development Project of Shandong Province (2019JZZY010132).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Gao B, Deng Z, Zhao D. (2016) Competing spreading processes and immunization in multiplex networks. Chaos, Solit Fractals 93, 175–181. doi:10.1016/j.chaos.2016.10.013

CrossRef Full Text | Google Scholar

2. Gao C, Liu J, Zhong N. (2010) Network immunization with distributed autonomy-oriented entities. IEEE Trans Parallel Distr Syst 22, 1222–1229. doi:10.1109/TPDS.2010.197

CrossRef Full Text | Google Scholar

3. Granell C, Gómez S, Arenas A. (2014) Competing spreading processes on multiplex networks: awareness and epidemics. Phys Rev E - Stat Nonlinear Soft Matter Phys 90, 012808. doi:10.1103/PhysRevE.90.012808

CrossRef Full Text | Google Scholar

4. Guo Z-G, Sun G-Q, Wang Z, Jin Z, Li L, Li C. (2020) Spatial dynamics of an epidemic model with nonlocal infection. Appl Math Comput 377, 125158. doi:10.1016/j.amc.2020.125158

CrossRef Full Text | Google Scholar

5. Kröger M, Schlickeiser R. (2020) Gaussian doubling times and reproduction factors of the covid-19 pandemic disease. Frontiers in Physics 8, 276. doi:10.3389/fphy.2020.00276

CrossRef Full Text | Google Scholar

6. Li H-J, Bu Z, Wang Z, Cao J. (2019a) Dynamical clustering in electronic commerce systems via optimization and leadership expansion. IEEE Transactions on Industrial Informatics 16, 5327–5334. doi:10.1109/TII.2019.2960835

CrossRef Full Text | Google Scholar

7. Li H-J, Wang L, Zhang Y, Perc M. (2020) Optimization of identifiability for efficient community detection. New J Phys 22, 063035. doi:10.1088/1367-2630/ab8e5e

CrossRef Full Text | Google Scholar

8. Li Z, Zhu P, Zhao D, Deng Z, Wang Z. (2019b) Suppression of epidemic spreading process on multiplex networks via active immunization. Chaos: An Interdisciplinary Journal of Nonlinear Science 29, 073111. doi:10.1063/1.5093047

CrossRef Full Text | Google Scholar

9. Liu C, Zhou N, Zhan X-X, Sun G-Q, Zhang Z-K. (2020) Markov-based solution for information diffusion on adaptive social networks. Appl Math Comput 380, 125286. doi:10.1016/j.amc.2020.125286

CrossRef Full Text | Google Scholar

10. Saberi M, Hamedmoghadam H, Madani K, Dolk HD, Morgan A, Morris JK, et al. (2020) Accounting for underreporting in mathematical modelling of transmission and control of covid-19 in Iran. Frontiers in Physics 8, 289. doi:10.3389/fphy.2020.00289

CrossRef Full Text | Google Scholar

11. Sun GQ, Wang SF, Li MT, Li L, Zhang J, Zhang W, et al. (2020) Transmission dynamics of covid-19 in wuhan, China: effects of lockdown and medical resources. Nonlinear Dyn 101, 1981–1993. doi:10.1007/s11071-020-05770-9

CrossRef Full Text | Google Scholar

12. Takaguchi T, Hasegawa T, Yoshida Y. (2014) Suppressing epidemics on networks by exploiting observer nodes. Phys Rev E - Stat Nonlinear Soft Matter Phys 90, 012807. doi:10.1103/PhysRevE.90.012807

CrossRef Full Text | Google Scholar

13. Wang X, Jia D, Gao S, Xia C, Li X, Wang Z. (2020a) Vaccination behavior by coupling the epidemic spreading with the human decision under the game theory. Appl Math Comput 380, 125232. doi:10.1016/j.amc.2020.125232

CrossRef Full Text | Google Scholar

14. Wang Z, Bauch CT, Bhattacharyya S, d’Onofrio A, Manfredi P, Perc M, et al. (2016) Statistical physics of vaccination. Phys Rep 664, 1–113. doi:10.1016/j.physrep.2016.10.006

CrossRef Full Text | Google Scholar

15. Wang Z, Guo Q, Sun S, Xia C. (2019) The impact of awareness diffusion on sir-like epidemics in multiplex networks. Appl Math Comput 349, 134–147. doi:1016/j.amc.2018.12.045

CrossRef Full Text | Google Scholar

16. Wang Z, Xia C, Chen Z, Chen G. (2020b) Epidemic propagation with positive and negative preventive information in multiplex networks. IEEE Transactions on Cybernetics. Available online at: https://ieeexplore.ieee.org/abstract/document/8957067.

CrossRef Full Text | Google Scholar

17. Xia C, Wang Z, Zheng C, Guo Q, Shi Y, Dehmer M, et al. (2019) A new coupled disease-awareness spreading model with mass media on multiplex networks. Inf Sci 471, 185–200. doi:10.1016/j.ins.2018.08.050

CrossRef Full Text | Google Scholar

18. Yin Q, Wang Z, Xia C, Dehmer M, Emmert-Streib F, Jin Z. (2020) A novel epidemic model considering demographics and intercity commuting on complex dynamical networks. Appl Math Comput 386, 125517. doi:10.1016/j.amc.2020.125517

CrossRef Full Text | Google Scholar

19. Zhao D, Li L, Peng H, Luo Q, Yang Y. (2014a) Multiple routes transmitted epidemics on multiplex networks. Phys Lett 378, 770–776. doi:10.1016/j.physleta.2014.01.014

CrossRef Full Text | Google Scholar

20. Zhao D, Wang L, Li S, Wang Z, Wang L, Gao B. (2014b) Immunization of epidemics in multiplex networks. PLoS One 9, e112018. doi:10.1371/journal.pone.0112018

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Zhao D, Wang L, Wang Z, Xiao G. (2018) Virus propagation and patch distribution in multiplex networks: modeling, analysis, and optimal allocation. IEEE Trans Inf Forensics Secur 14, 1755–1767. doi:10.1109/TIFS.2018.2885254

CrossRef Full Text | Google Scholar

22. Zhao D, Xiao G, Wang Z, Wang L, Xu L. (2020a) Minimum dominating set of multiplex networks: definition, application, and identification. IEEE Transactions on Systems, Man, and Cybernetics: Systems 99, 1–15. doi:10.1109/TSMC.2020.2987163

CrossRef Full Text | Google Scholar

23. Zhao D, Yang S, Han X, Zhang S, Wang Z. (2020b) Dismantling and vertex cover of network through message passing. IEEE Transactions on Circuits and Systems II: Express Briefs 99, 1–15. doi:10.1109/TCSII.2020.2973414

CrossRef Full Text | Google Scholar

24. Zhuang Z, Cao P, Zhao S, Lou Y, Wang W, Yang S, et al. (2020) Estimation of local novel coronavirus (covid-19) cases in wuhan, China from off-site reported cases and population flow data from different sources. Frontiers in Physics 8, 336. doi:10.3389/fphy.2020.00336

CrossRef Full Text | Google Scholar