
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys. , 25 September 2020
Sec. Computational Physics
Volume 8 - 2020 | https://doi.org/10.3389/fphy.2020.587419
This article is part of the Research Topic Computational Modeling of Spintronic Materials View all 18 articles
The promise of future spintronic devices with nanoscale dimension, high-density, and low-energy consumption motivates the search for van der Waals heterostructure that stabilize topologically protected whirling spin textures such as magnetic skyrmions and domain walls. To translate these compelling features into practical devices, a key challenge lies in achieving effective manipulation of the magnetic anisotropy energy and the Dzyaloshinskii-Moriya (DM) interaction, the two key parameters that determine skyrmions. Through the first-principles calculation, we demonstrate that the polarization-induced broken inversion symmetry in the two-dimensional Fe3GeTe2/In2Se3 multiferroic heterostructure does cause an interfacial DM interaction. The strong spin-orbit coupling triggers the magnetic anisotropy of the Fe3GeTe2/In2Se3 heterostructure. The magnetic anisotropy and the DM interaction in Fe3GeTe2 can be well-controlled by the ferroelectric polarization of In2Se3. This work paves the way toward the spintronic devices based on van der Waals heterostructures.
Two-dimensional (2D) van der Waals (vdW) materials have many novel properties compared to their three-dimensional (3D) counterparts, such as topology, spin frustration, and magnetic skyrmion [1]. The vdW bulks can be cleaved/exfoliated down to the monolayer limit with their structural integrities and chemical stabilities retained [2], which brings great convenience to the building of heterostructures (HSs). When cleaved, the specific surface area of the vdW material greatly increases, which is suitable to be tuned by many kinds of experimental stimuli. These advantages would provide completely new platforms with all magnetic atoms participating in the magnetoelectric coupling, and largely reshape the landscape of 2D vdW multiferroics [3, 4]. Inspired by the new physical picture of 2D materials, exploring the atom-thick vdW HS is the frontier of current spintronics research. The Dzyaloshinskii-Moriya (DM) interaction has recently received a lot of attention due to new findings on the magnetic skyrmions, spin waves, and chiral domain walls [5–8]. Magnetic skyrmion and domain wall are the smallest components that can be used in the next-generation magnetic race-track memories [9]. A critical constant of DM interaction is defined to evaluate the stability of the skyrmions [10], where J and K are the exchange coupling and magnetic anisotropy, respectively. The DM interaction and the magnetic anisotropy manipulated in 2D HS will greatly improve the practical applications of spintronic devices.
The coupling between ferroelectricity and ferromagnetism allows the control of spin via electric field or the control of charge via magnetic field, which leads to multifunctional performance of spintronic devices [11]. Thesore, the co-existence of these two ferroic orders in 2D materials is very attractive. The single-phase multiferroics are extremely rare because ferroelectricity arising from the off-center cations requires empty d-orbitals, while ferromagnetism usually results from partially occupied d-orbitals [12]. Scientists have built various heterostructures from the ferroelectric (FE) and ferromagnetic (FM) materials. Not only the coexistence of ferroelectricity and ferromagnetism, but also the magnetoelectric couplings were achieved in these HSs [1, 4, 12]. Since the first prediction of 2D FE hydroxyl-decorated graphene in 2013, more and more 2D FE materials have been discovered, e.g., SnSe, SnS, GeS, Bi2O2Se, and Bi2O2Te (in-plane FE) [13, 14], as well as MoS2, CuInP2S6, In2Se3, and MXenes (perpendicular FE) [13, 15]. The mechanisms involved in these in-plane and perpendicular polarizations are the polar functional groups, the hopping of halogen adatoms, or polar phonon modes [11]. In recent years, dozens of 2D ferromagnets have been found experimentally or predicted theoretically [14, 16]. The emerging of more novel 2D vdW ferroelectric materials and 2D vdW magnetic compounds indicates an enhanced probability to form multiferroic HSs.
The bulk Fe3GeTe2 (FGT) belongs to 2D vdW magnetic materials with a layered hexagonal lattice, where the weakly bonded Fe3Ge layers are sandwiched between two Te slabs. As a strongly correlated itinerant ferromagnet, FGT contains two inequivalent Fe coordinates: the Fe1 atoms form a hexagonal net, while the Fe2 atoms are bonded covalently with Ge. This compound has many excellent properties, for example: a mixed valence state (Fe2+)(Fe3+)2(Ge4−)(Te2−)2 [17], a [001] oriented easy axis [18], and a FM configuration down to the monolayer regime [19, 20]. In particular, FGT can be easily exfoliated along the [001] direction due to the weak vdW interaction [19]. Recently, Yi et al. [21] have demonstrated a new phase of FGT (namely a competing AFM configuration) and the FM slabs become AFM order below 152 K. Nevertheless, Tian et al. [22] reported that the AFM configuration originates from the movement of pinned magnetic domain walls. The above-mentioned arguments indicate that the fundamental properties of FGT are still under development. The experimentally confirmed 2D vdW ferromagnets are mainly focused on three materials: CrI3, Cr2Ge2Te6, and Fe3GeTe2 [23– 25]. Even though the Curie temperature (TC) of 230 K [17] is below (but not too far below) the room temperature, FGT show a much higher TC than the CrI3 (TC = 61 K) and Cr2Ge2Te6 (TC = 61 K) bulks [26, 27]. The combination of high TC and the above-mentioned properties makes FGT a promising candidate for exploring itinerant ferromagnetism in a truly 2D form.
Having the FM part at hand, we now investigate the FE part of our multiferroic HS. As an all-known fact, the perpendicular polarization is usually more important than the in-plane one because the perpendicular polarization can effectively penetrate the FM layers in a FE/FM HS, thus manipulating the magnetism of the FM slabs. The 2D vdW materials with perpendicular polarization are relatively rare, which is mainly due to the fact that incomplete screening of surface charges induced depolarization field opposes the spontaneous polarization of the vdW materials, thereby suppressing the ferroelectricity. Recently, In2Se3 has been widely used in spintronic devices for memory and logic applications. Ding et al. [28] have reported that α-In2Se3 is a room-temperature FE material (down to the stable single-layer regime) with intrinsic in-plane and controllable perpendicular polarizations, which may open avenues for developing new concepts of magnetoelectric devices.
Very recently, Huang et al. [29] have investigated the effect of asymmetric interfacial coupling on the FE stability of 2D Fe3GeTe2/In2Se3 HS through the first-principles calculation, but some important physical properties such as the MAE and DM interaction are not included in their work. Besides, a large hole doping induced magnetic anisotropy reduction is demonstrated in Fe3−xGeTe2 layered structure [30]. They also found the sharp decrease in magnetic anisotropy energy (MAE) caused by the change of electronic structure. Nevertheless, the reason for the change of electronic structure, hence the change of MAE is still unclear. Motivated by recent developments, we now study the DM interaction and magnetic anisotropy manipulated by a ferroelectric polarization in a truly 2D form. Control the magnetism of 2D materials, as well as modulate the magnetic order and electronic spin are of great importance in novel spintronic devices since they have smaller size and lower energy consumption compared with traditional electronic devices. We have first demonstrated the reversible control the DM interaction and MAE by the FE polarization in the Fe3GeTe2/In2Se3 HS, as well as its underlying mechanisms. A magnetoelectric coupling is expected in our FE/FM HSs, opening up the possibility to control the magnetic skyrmions by the FE-polarization.
The freestanding FGT monolayer is composed of two Fe1 layers, two Te layers and one mixed layer of Ge and Fe2 atoms, as shown in Figure 1A. The Fe atoms in the FGT monolayer can be divided into two inequivalent Fe1 and Fe2 atoms with the valence states of (Te2−)(Fe13+)/(Ge4−)(Fe22+)/(Te2−)(Fe13+) [31]. Excitingly, the exfoliation of mono-layer or few- layer Fe3GeTe2 has been experimentally achieved by Fei et al. [32] and Deng et al. [2]. Due to the relatively strong FE polarization, we choose In2Se3 as the substrate with its most stable structure [28] [see Figure 1B]. Figure 1C shows the coefficients of the DM interaction. Besides, the perpendicular FE polarization of the In2Se3 quintuple layers (QLs) can be easily reversed through several kinetic pathways given in Ding et al. [28]. In this work, four In2Se3 QLs are applied to form a substrate because the magnitude of the FE polarization reaches its maximum value at the thickness of 3 or 4 QLs [28]. Huang et al. [29] found that the energy difference between the up-polarization and down-polarization became a constant when the thickness of In2Se3 is more than 4 QLs. This result proven that our In2Se3 substrate is thick enough to get reliable results. The unit cell is chosen to be equal to that of ferromagnetic Fe3GeTe2 with the experimental lattice parameters a, b that also commensurate to the In2Se3 layers. In order to comprehensively describe the AFM configuration, we build a supercell with the x-y planes of FGT and In2Se3 changed from rhombus to rectangular, as shown in Figure 1D. Our HSs have idealized hard interfaces without any defects or adsorbates. More importantly, the calculation methods and detailed parameters are given in the Supplementary Information.
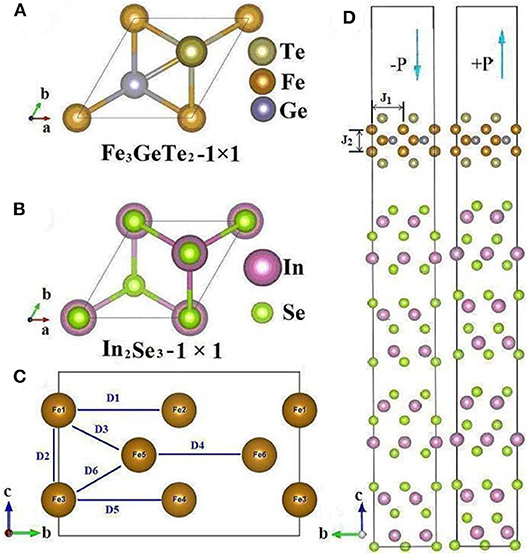
Figure 1. The crystal structures of the van der Waals Fe3GeTe2/In2Se3 HS. The top view of the bulk Fe3GeTe2 (A) and In2Se3 compounds (B); the side view of the coefficients of Dzyaloshinskii-Moriya (DM) interaction in the Fe3GeTe2 monolayer, only the Fe atoms are shown in the structure (C); and the side view of the Fe3GeTe2/In2Se3 HSs with the ferroelectric polarization directed downward (–P) and upward (+P) (D). These two HSs are built along the (001) direction within the in-plane supercells.
As it can be seen in Table 1, the lattice constants of the FGT monolayer agree well with the experimental data (a = 0.4050 nm, b = 0.7014 nm) [33]. Our calculated magnetic moments of the freestanding FGT monolayer are also in agreement with the experimental data (m1 = 2.18 μB, m2 = 1.54 μB) [34], which partially proved that our results are reliable. The lattice mismatch between FGT and In2Se3 is only 1.2% for both a and b axes, which indicates that these two materials can form heterostructures perfectly. It is worth noting that 2D FGT retains its FM configuration not only in the freestanding state, but also in the heterostructures. The orientation of the FE polarization has little effect on the magnetic moments and magnetic order of the FGT/In2Se3 HS.
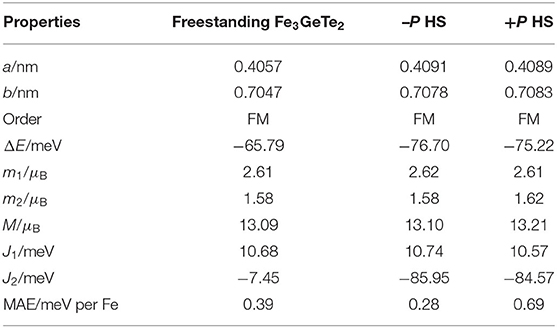
Table 1. The calculated lattice parameters a, b, the magnetic order, the energy difference between the FM order and the lowest-energy AFM order (ΔE = EFM−EAFM), the magnetic moments m1, m2 of the two inequivalent Fe atoms, the net magnetization M, the magnetic anisotropy energy (MAE) per Fe atom, the exchange parameters J1 and J2 of the freestanding Fe3GeTe2 monolayer and the FGT/In2Se3 HS.
Our calculated exchange parameters J1 and J2 are shown in Figure 1C, which are in general agreement with Deng's results (J1 =5.79 meV, J2 = −6.48 meV) [2]. Although the in-plane exchange interaction J1 is AFM, it is much weaker when compared to the FM interaction between the Fe1 and Fe2 atoms [2]. Hence the FM configuration can be retained in the freestanding FGT monolayer. When coupled with the In2Se3 substrate, J2 increases quickly. The sign of the exchange parameter for the FGT/In2Se3 HS, found positive for J1 and negative for J2, while J2 is predominantly stronger than J1. The parameter J2 is strong and negative so as to stabilize the FM order of the FGT/In2Se3 HS.
The MAE is calculated as the total energy difference between the HS with in-plane and perpendicular magnetization axes, which can be written as [35]
To obtain the MAE, we consider the SOC effect in our calculation. The calculated MAE is 0.39 meV per Fe atom, indicating strong easy axis anisotropy in the freestanding FGT monolayer. Our result is in good agreement with the data obtained by Zhuang et al. [19] (0.52 meV per Fe atom). The significant MAE exhibited by the freestanding FGT monolayer, which caused by strong SOC, suggests that the 2D FGT has potential for applications in magnetic data storage applications [19]. The FGT monolayer shows a perpendicular magnetic anisotropy in all cases involved, which agrees well with the experimental data of the bulk FGT [17]. The MAE of the HS is reduced by 28% and enhanced by 77% in the down-polarization and the up-polarization directions, respectively. Our calculated average orbital moment of Fe1 and Fe2 is ~0.08 μB, which is much smaller than that of an isolated Fe2+ ion (2 μB) according to Hund's rule. The relatively sizable value of 0.08 μB shows that orbital magnetic moment is not completely quenched and hence causing the strong SOC and a large MAE [19]. Therefore, we conclude that the strength of SOC is enhanced by the +P polarization, leading to the enhancement of MAE.
Figure 2 shows the spin-resolved total and partial DOS of the fully relaxed FGT monolayer, in which the Fermi level (EF) is set as zero. According to Figure 2A, we find that our system is metallic with several high peaks in the valence band (VB). The VB is mainly contributed by the non-localized Fe-3d, Ge-4p, and Te-5p states, while the Fe-3p, Ge-4s, and Te-5s states are small and negligible. The DOS just below the Fermi level is mainly contributed by the majority spin state of Te-4p, as well as the majority and minority states of Fe-3d. We observe the stronger Fe-Te hybridization and weaker Fe-Ge interaction mainly in the −4.5 — −2, eV and −5.5 — −4 eV region, respectively. According to the Stoner criterion [36], I·N(EF)>1 reflects the itinerant ferromagnetism of the material, where N(EF) is the spin-averaged DOS at the EF and I is the Stoner parameter [19]. From Figure 2B, our calculated value of I·N(EF) is 2.05, which reflects an itinerant ferromagnetic nature of the FGT monolayer. This is in agreement with the results given in Zhuang et al. [19]. Moreover, the ferromagnetic order of the freestanding FGT monolayer has also been confirmed in Table 1.
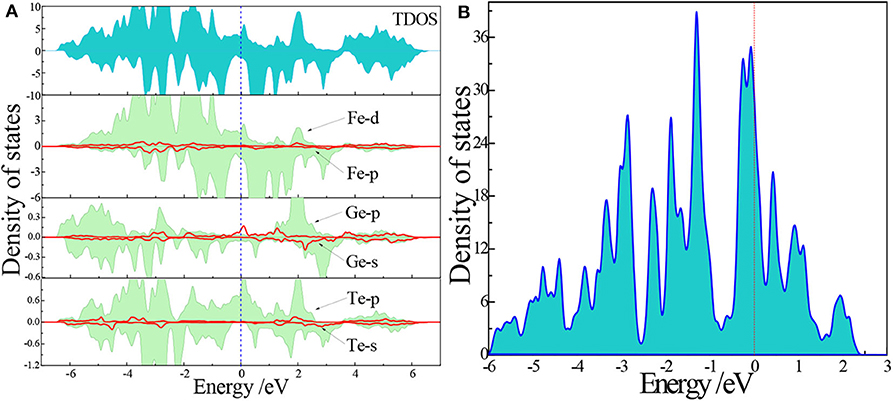
Figure 2. The spin-polarized total/partial DOS (A) and the spin-averaged total DOS (B) of the freestanding Fe3GeTe2 monolayer.
Figure 3 shows the total DOS (TDOS) and partial DOS (PDOS) of the Fe3GeTe2/In2Se3 HS for the –P case, which is useful in understanding the specific contributions of different atomic orbitals. We can see less TDOS near the EF in the freestanding FGT monolayer. When combined with the In2Se3 substrate, the TDOS near the EF increases dramatically, inducing a sizable DOS at the Fermi level. Namely, the metallicity is much better in the Fe3GeTe2/In2Se3 HSs than in the freestanding FGT monolayer. This novel feature is quite different from the case when the anisotropic SOC plays a decisive role in stabilizing the FM configuration in another famous 2D material CrI3 [37]. In the CrI3 monolayer, a spin gap at the center of the Brillouin zone can be found below the Curie temperature. The spin-up and spin-down DOSs are asymmetric, indicating significant spin polarization of our HS system. The spin polarizability can be defined as: SPF = [N(EF)α-N(EF)β]/[N(EF)α+ N(EF)β] × 100%, where N(EF)α and N(EF)β are the DOS at Fermi level for the spin-up and spin-down channels, respectively [38]. The SPF of the freestanding FGT monolayer, the –P HS, and the +P HS are 34.01, 35.57, and 29.69%, respectively. This indicates a much weaken quantum confinement effect in our HS system than in the strained FGT nanoribbons (SPF = 45–85.6%) shown in Han et al. [38].
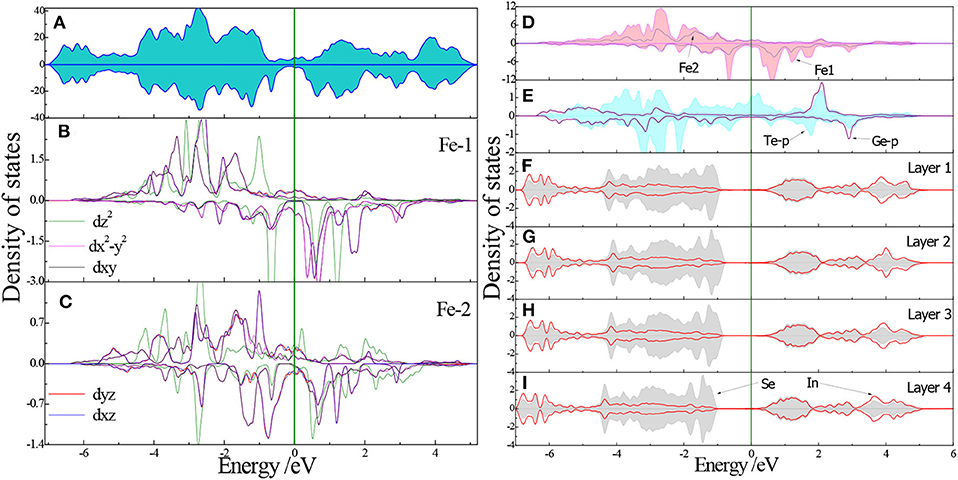
Figure 3. Total DOS of the Fe3GeTe2/In2Se3 HS for the –P case (A); the partial DOS of the five 3d orbitals for the four Fe1 (B); and two Fe2 atoms (C); the DOS of the inequivalent Fe1 and Fe2 atoms (D); the DOS of Te-5p and Ge-4p states (E); the layer-resolved DOS of the In2Se3 layers (F–I).
To further explore the difference between the two inequivalent Fe atoms, we show the PDOS of Fe1 and Fe2 in Figures 3B,C, respectively. Remarkably our HS system presents a metallic character, strictly confined in the FGT layer. The metallic FGT layer exhibits ferromagnetism, with a magnetic moment of 2.2 μB/Fe atom. Both the majority and minority spin states of the five split 3d orbitals are non-zero states near the EF. They mainly assemble between −4 to 1 eV, while the smaller spin-down states are around −3 to −0.5 eV, which produces large magnetic moments in Fe1 atoms. For the Fe2 atoms, there are more spin-down states between −3.5 to −0.5 eV than for Fe1 atoms, which compensate the difference between spin-up and spin-down states. This causes the Fe2 atoms to have lower magnetic moments than Fe1. In the VB region, the contribution of Fe atoms at the EF is mainly due to the Fe1 dxy, dyz, dxz, and orbitals as well as the Fe2 dxz, , and orbitals (dxy and dyz orbitals are almost degenerated). The rest of the orbitals are either too small or too far from the Fermi level. In the CB region, the Fe-3d PDOS is mainly contributed by the spin-down channels. The TDOS shown in Figures 3A, 4A and the PDOS shown in Figures 3B,C, 4B,C are quite similar, especially in the valence band region.
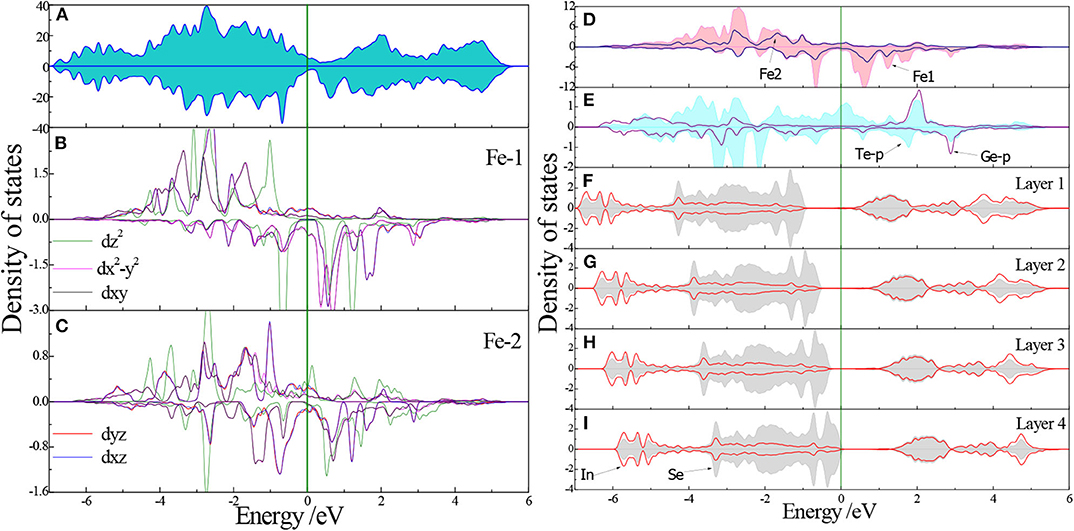
Figure 4. Total DOS of the Fe3GeTe2/In2Se3 HS for the +P case (A); the partial DOS of the five 3d orbitals for the four Fe1 (B); and two Fe2 atoms (C); the DOS of the inequivalent Fe1 and Fe2 atoms (D); the DOS of Te-5p and Ge-4p states (E); the layer-resolved DOS of the In2Se3 layers (F–I).
It is also shown in Figures 3D,E, 4D,E that the Fe and Te atoms contributing to the DOS near EF, but Fe1 does more than others [39]. Contrastingly, the Ge atoms, which can hardly be seen near the EF, play a less significant role in the FGT/In2Se3 HS. In Figures 3F–I, 4F–I, we can see that the upper VB is dominated by the states of selenium atoms and a slight contribution of indium atoms, while the lower VB and the CB are the results of strong hybridization of In and Se. The DOSs of the Layer 1 to Layer 4 are almost alike, but the –P DOS and +P DOS gradually move to the high energy and low energy regions, respectively. This is mainly due to the change of electric potential induced by polarization discontinuity. We found that all the insulating In2Se3 layers have little effects on the magnetic properties of our HSs. For the Fe1 and Fe2 atoms, we find essentially the same features with minor changes in the hybridization peaks when the FE-P reverses. The very similar DOS for both the ±P cases indicating the almost unchanged magnetic properties of the FGT/In2Se3 HSs. It is worthy of note that the DOS of FGT layer given by Huang et al. [29] is also metallic, and our DOS is in topological resemblance with the DOS shown in Huang et al. [29].
Figure 5 illustrates the charge density difference of the ferromagnetic Fe3GeTe2/In2Se3 HS for both the ±P cases. We only show the charge of the FGT/In2Se3 interface (not the whole HS) because the charge transfer mainly occurs near the interface. Here, the yellow (blue) region represents charge accumulation (depletion). For the –P case, there is obvious charge transfer between the Te-Se atoms than between the Te-Fe atoms. This reflects the importance of Te orbitals in bridging the exchange-coupling between the Fe atoms, which agrees well with the DOS result. For the +P case, the charge redistribution at the FGT/In2Se3 interface are less obvious. This is mainly due to the fact that the positive FE polarization leads to an increment of the distance between the FGT layer and the In2Se3 substrate, hence greatly reducing the interfacial charge transfer. Figure 5 reveals three features: (1) Fe1 and Fe2 atoms are non-equivalent; (2) when the FE-P reverses, the charge transfer of the Fe atoms is mainly along the z-axis, implying the importance of dz2 electrons that give rise to the inter- and intra-layer FM order; (3) The very little charge transfer of Fe leads to almost unchanged magnetic moments of the Fe1 and Fe2 atoms.
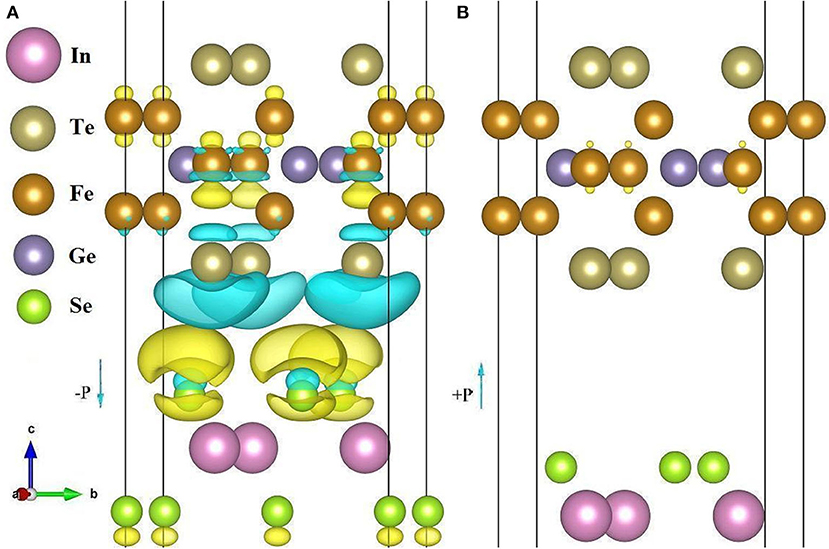
Figure 5. Charge density difference of the Fe3GeTe2/In2Se3 heterostructure for the –P (A) and +P cases (B). The isosurface value is set to be 0.00035 e/bohr3.
On the one hand, 2D vdW ferromagnetic materials with the FM orders are of great scientific interesting and technological importance for the next-generation storage devices. On the other hand, the DM interaction plays a key role in stabilizing the chiral domain walls and magnetic skyrmions in magnetic thin films with broken inversion symmetry. Therefore, it is important to control the DM interaction in 2D vdW materials with their FM orders unchanged. In order to obtain the coefficients of DM interaction, we have built a 2 × 2 × 1 supercell of our FGT/In2Se3 HS containing 24 Fe atoms. As shown in Figure 1C, the coefficients D (D1, D2, D3, D4, D5, and D6) can be obtained by mapping different spin configurations on the Hamiltonian H given in equation (1) [40]. For our rectangular HS along the z-axis, the Dx and Dy will cancel each other out due to the C3v symmetry of Fe atoms. Here only the Dz is calculated for simplicity. We first set all the spins along the z-axis, and then change the spins of two neighbors Fe positions 1 and 2 (S1 and S2) into four configurations: (i) S1 = (0, S, 0), S2 = (0, 0, S); (ii) S1 = (0, S, 0), S2 = (0, 0, –S); (iii) S1 = (0, –S, 0), S2 = (0, 0, S); (iv) S1 = (0, –S, 0), S2 = (0, 0, –S); where S represents the magnetic moment of Fe [41]. These energies of the four spin states are described as E1, E2, E3, and E4. Then, the coefficient D can be determined by D = (E1+E4-E2-E3)/(4S2) [41]. There are a large number of literatures calculate the coefficients of the DM interaction using VASP [42–44]. Although the coefficients are very small, these works confirm the accuracy of the VASP results. In this work, only the DM interactions between the nearest-neighboring Fe ions are considered.
To validate the plausible mechanism of ferroelectrically-driven DM interaction, we performed first-principles calculation on the FGT/In2Se3 HS (see Supplementary Information for details). The coefficients of the DM interaction D1-D6 for first-nearest neighbors are listed in Table 2, resulting in a magnitude D of −0.0224 (−0.0185) meV for the HS at the –P (+P) case, that is about two orders of magnitude smaller than the exchange parameter J1. When the FE polarization changes from +P to –P, the D2 and D3 change from positive to negative, and other coefficients D1, D4, D5, D6, and D [D=(D1+D4+D5)/3] vary −24, 102, −92, −65, and −58%, respectively. This indicates that the FE polarization effects on the in-plane D1, D6 and hence the average D is moderate. These DM interaction energies may be result of the broken inversion symmetry and the strong SOC effect [45, 46]. Our FGT/In2Se3 HS has the polarization-dependent DM interaction, which can be used in skyrmion-based racetrack memory. Although our results are small, there are many ways to enhance the DM interaction in experiments. For example, one way is enhancing the spin-orbit coupling [47], and doping of heavy atoms is another way [48]. Using criticality analysis, Tan et al. [20] have demonstrated that the coupling length between vdW layers in Fe3GeTe2 is estimated to be 5 layers. Wu et al. [45] have confirmed that the increasing of the thickness of FGT up to 4–60 layers will lead to greatly enhanced DM interaction. In short, we have demonstrated that the strong SOC in the In2Se3 layers does induce an interfacial DM interaction at the interface with FGT, and have achieved the robust manipulation of DM interaction in the Fe3GeTe2/In2Se3 heterostructure. Enhancing the DM interaction through the above-mentioned schemes can make our results more valuable in potential application of spintronics.
In this work, the vdW material In2Se3 with both in-plane and perpendicular spontaneous polarization and the vdW ferromagnetic compound Fe3GeTe2 are used to form a two-dimensional artificial 2D heterostructure. Through the first-principles calculation, we have demonstrated the magnetoelectric coupling in the two-dimensional Fe3GeTe2/In2Se3 system. This ferroelectric polarization of In2Se3 can manipulate the magnetic anisotropy and the DM interaction in Fe3GeTe2. When the FE polarization is switched from –P to +P, the DM interaction of the heterostructure varies moderately, which is affected by the strong spin-orbit coupling. Through the reorientation of the polarization, we also realized the robust control of DM interaction which originates from the broken inversion symmetry. The spin polarizations shown in the density of states reflect spin-polarized states in the FGT/In2Se3 system, which are important in spintronic devices. We hope that our results can promote the research on the spintronic devices with low power consumption, non-volatile, and high-speed.
All datasets generated for this study are included in the article/Supplementary Material.
JW and YW conceived the idea. DC, WS, and HL performed the calculations. DC and WS wrote the manuscript. All authors reviewed the manuscript.
This work was supported by the National Natural Science Foundation of China under research (Nos. 51571083 and 11674083), as well as the Key Scientific and Technological Projects in Henan Province (No. 162102210169) and the Key Projects of the Higher Education Institutions of Henan Province (No. 16A140033).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.587419/full#supplementary-material
1. Jiang Z, Wang P, Xing JP, Jiang X, Zhao JJ. Screening and design of novel 2D ferromagnetic materials with high Curie temperature above room temperature. ACS Appl Mater Interfaces. (2018) 10:39032–9. doi: 10.1021/acsami.8b14037
2. Deng Y, Yu Y, Song Y, Zhang J, Wang NZ, Sun Z, et al. Gate-tunable room-temperature ferromagnetism in two-dimensional Fe3GeTe2. Nature. (2018) 563:94–9. doi: 10.1038/s41586-018-0626-9
3. Sun W, Wang WX, Chen D, Cheng ZX, Jia TT, Wang YX. Giant magnetoelectric coupling and two-dimensional electron gas regulated by polarization in BiFeO3/LaFeO3 heterostructures. J Phys Chem C. (2019) 123:16393–9. doi: 10.1021/acs.jpcc.9b04499
4. Sun W, Wang WX, Chen D, Zhang GB, Cheng ZX, Wang YX. First-principles investigation on tunable electronic properties and magnetism by polarization in PbTiO3/BiFeO3 2D ferroelectric heterostructures. J Mater Chem C. (2019) 7:463–73. doi: 10.1039/C8TC04987D
5. Ding B, Li Z, Xu G, Li H, Hou Z, Liu E, et al. Observation of magnetic skyrmion bubbles in a van der Waals ferromagnet Fe3GeTe2. Nano Lett. (2020) 20:868–73. doi: 10.1021/acs.nanolett.9b03453
6. Di K, Zhang VL, Lim HS, Ng SC, Kuok MH, Qiu XP, et al. Asymmetric spin-wave dispersion due to dzyaloshinskii-moriya interaction in an ultrathin Pt/CoFeB film. Appl Phys Lett. (2015) 106:052403. doi: 10.1063/1.4907173
7. Fert A, Reyren N, Cros V. Magnetic skyrmions: advances in physics and potential applications. Nat Rev Mater. (2017) 2:17031. doi: 10.1038/natrevmats.2017.31
8. Dzyaloshinsky I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetis. J Phys Chem Solids. (1958) 4:241–55. doi: 10.1016/0022-3697(58)90076-3
9. Parkin S, Yang SH. Memory on the racetrack. Nat Nanotechnol. (2015) 10:195–8. doi: 10.1038/nnano.2015.41
10. Wang L, Feng Q, Kim Y, Kim R, Lee KH, Pollard SD, et al. Ferroelectrically tunable magnetic skyrmions in ultrathin oxide heterostructures. Nat Mater. (2018) 17:1087–94. doi: 10.1038/s41563-018-0204-4
11. Zhang J, Lin L, Zhang Y, Wu M, Yakobson BI, Dong S. Type-II multiferroic Hf2VC2F2 mxene monolayer wih high transiton temperature. J Am Chem Soc. (2018) 140:9768–73. doi: 10.1021/jacs.8b06475
12. Gong C, Kim EM, Wang Y, Lee G, Zhang X. Multiferroicity in atomic van der Waals heterostructures. Nat Commun. (2019) 10:2657. doi: 10.1038/s41467-019-10693-0
13. Wu MH, Jena P. The rise of two-dimensional van der Waals ferroelectrics. WIREs Comput Mol Sci. (2018) 8:e1365. doi: 10.1002/wcms.1365
14. Yin HB, Liu C, Zheng GP, Wang YX, Ren FZ. Ab initio simulation studies on the room-temperature ferroelectricity in two-dimensional β-phase GeS. Appl Phys Lett. (2019) 114:192903. doi: 10.1063/1.5097425
15. Liu FC, You L, Seyler KL, Li X, Yu P, Lin J, et al. Room-temperature ferroelectricity in CuInP2S6 ultrathin flakes. Nat Commun. (2016) 7:12357. doi: 10.1038/ncomms12357
16. Burch KS, Mandrus D, Park JG. Magnetism in two-dimensional van der Waals materials. Nature. (2018) 563:47–52. doi: 10.1038/s41586-018-0631-z
17. Deiseroth H, Aleksandrov K, Reiner C, Kienle L, Kremer RK. Fe3GeTe2 and Ni3GeTe2-two new layered transition-metal compounds: crystal structures, HRTEM investigations, and magnetic and electrical properties. Eur J Inorg Chem. (2006) 8:1561–7. doi: 10.1002/ejic.200501020
18. Johansen Ø, Risinggard V, Sudbø A, Linder J, Brataas A. Current control of magnetism in two-dimensional Fe3GeTe2. Phys Rev Lett. (2019) 122:217203. doi: 10.1103/PhysRevLett.122.217203
19. Zhuang HL, Kent PRC, Hennig RG. Strong anisotropy and magnetostriction in the two-dimensional stoner ferromagnet Fe3GeTe2. Phys Rev B. (2016) 93:134407. doi: 10.1103/PhysRevB.93.134407
20. Tan C, Lee J, Jung SG, Park T, Albarakati S, Partridge J, et al. Hard magnetic properties in nanoflake van der Waals Fe3GeTe2. Nat Commun. (2018) 9:1554. doi: 10.1038/s41467-018-04018-w
21. Yi J, Zhuang H, Zou Q, Wu Z, Cao G, Tang S, et al. Competing antiferromagnetism in a quasi-2D itinerant ferromagnet: Fe3GeTe2. 2D Mater. (2017) 4:011005. doi: 10.1088/2053-1583/4/1/011005
22. Tian CK, Wang C, Ji W, Wang JC, Xia TL, Wang L, et al. Domain wall pinning and hard magnetic phase in Co-doped bulk single crystalline Fe3GeTe2. Phys Rev B. (2019) 99:184428. doi: 10.1103/PhysRevB.99.184428
23. Albarakati S, Tan C, Chen ZJ, Partridge JG, Zheng G, Farrar L, et al. Antisymmetric magnetoresistance in van der Waals Fe3GeTe2/graphite/Fe3GeTe2 trilayer heterostructrues. Sci Adv. (2019) 5:eeaw0409. doi: 10.1126/sciadv.aaw0409
24. Song T, Cai X, Tu MWY, Zhang X, Huang B, Wilson NP, et al. Giant tunneling magnetoresistance in spin-filter van der Waals heterostructures. Science. (2018) 360:1214–8. doi: 10.1126/science.aar4851
25. Jiang S, Shan J, Mak KF. Electric-field switching of two-dimensional van der Waals magnets. Nat Mater. (2018) 17:406–10. doi: 10.1038/s41563-018-0040-6
26. McGuire MA, Dixit H, Cooper VR, Sales BC. Coupling of crystal structure and magnetism in the layered, ferromagnetic insulator CrI3. Chem Mater. (2015) 27:612–20. doi: 10.1021/cm504242t
27. Lohmann M, Su T, Niu B, Hou Y, Alghamdi M, Aldosary M, et al. Probing magnetism in insulating Cr2Ge2Te6 by induced anomalous Hall effect in Pt. Nano Lett. (2019) 19:2397–403. doi: 10.1021/acs.nanolett.8b05121
28. Ding W, Zhu J, Wang Z, Gao Y, Xiao D, Gu Y, et al. Prediction of intrinsic two-dimensional ferroelectrics in In2Se3 and other III2-VI3 van der Waals materials. Nat Commun. (2017) 8:14956. doi: 10.1038/ncomms14956
29. Huang XK, Li GN, Chen C, Nie X, Jiang XP, Liu JM. Interfacial coupling induced critical thickness for the ferroelectric bistability of two-dimensional ferromagnet/ferroelectric van der Waals heterostructure. Phys Rev B. (2019) 100:235445. doi: 10.1103/PhysRevB.100.235445
30. Park SY, Kim DS, Liu Y, Hwang J, Kim Y, Kim W, et al. Controlling the magnetic anisotropy of the van der Waals ferromagnet Fe3GeTe2 through hole doping. Nano Lett. (2020) 20:95–100. doi: 10.1021/acs.nanolett.9b03316
31. Zhao YH, Gu JX, Chen ZF. Oxygen evolution reaction on 2D ferromagnetic Fe3GeTe2: boosting the reactivity by the self-reduction of surface hydroxyl. Adv Funct Mater. (2019) 29:1904782. doi: 10.1002/adfm.201904782
32. Fei Z, Huang B, Malinowski P, Wang W, Song T, Sanchez J, et al. Two-dimensional itinerant ferromagnetism in atomically thin Fe3GeTe2. Nat Mater. (2018) 17:778–82. doi: 10.1038/s41563-018-0149-7
33. Kim D, Park S, Lee J, Yoon J, Joo S, Kim T, et al. Antiferromagnetic coupling of van der Waals ferromagnetic Fe3GeTe2. Nanotechnology. (2019) 30:245701. doi: 10.1088/1361-6528/ab0a37
34. May AF, Calder S, Cantoni C, Cao H, McGuire MA. Magnetic structure and phase stability of the van der Waals bonded ferromagnet Fe3−xGeTe2. Phys Rev B. (2016) 93:014411. doi: 10.1103/PhysRevB.93.014411
35. Lee M, Choi H, Chung YC. Ferroelectric control of magnetic anisotropy of FePt/BaTiO3 magnetoelectric heterojunction: a density functional theory study. J Appl Phys. (2013) 113:17C729. doi: 10.1063/1.4800499
36. Stoner EC. Collective electron ferromagnetism. Proc R Soc Lond A. (1938) 165:372–414. doi: 10.1098/rspa.1938.0066
37. Chen L, Chung JH, Chen T, Duan C, Schneidewind A, Radelytskyi I, et al. Magnetic anisotropy in ferromagnetic CrI3. Phys Rev B. (2020) 101:134418. doi: 10.1103/PhysRevB.101.134418
38. Han JN, Fan ZQ, Zhang ZH. Structure stability, magneto-electronic properties, and modulation effects of Fe3GeTe2 nanoribbons. Acta Phys Sin. (2019) 68:208502. doi: 10.7498/aps.68.20191103
39. Duan DD, Jin S, Liu N, Shen S, Lin Z, Li K, et al. Tuning magnetic properties in quasi-two-dimensional ferromagnetic Fe3−yGe1−xAsxTe2(0 ≤ x ≤ 0.85). Mater Res Express. (2017) 4:036103. doi: 10.1088/2053-1591/aa63b5
40. Cheng Y, Yu SS, Zhu ML, Hwang J, Yang FY. Evidence of the topological hall effect in Pt/antiferromagnetic insulator bilayers. Phys Rev Lett. (2019) 123:237206. doi: 10.1103/PhysRevLett.123.237206
41. Xiang HJ, Kan EJ, Wei SH, Whangbo MH, Gong XG. Predicting the spin-lattice order of frustrated systems from first principles. Phys Rev B. (2011) 84:224429. doi: 10.1103/PhysRevB.84.224429
42. Ma X, Yu G, Tang C, Li X, He H, Shi J, et al. Interfacial Dzyaloshinskii-Moriya interaction: effect of 5d band filling and correlation with spin mixing conductance. Phys Rev Lett. (2018) 120:157204. doi: 10.1103/PhysRevLett.120.157204
43. Luo HB, Zhang HB, Liu JP. Strong hopping induced dzyaloshinskii-moriya interaction and skyrmions in elemental cobalt. NPJ Comput Mater. (2019) 5:50. doi: 10.1038/s41524-019-0187-y
44. Beutier G, Collins SP, Dimitrova OV, Dmitrienko VE, Katsnelson MI, Kvashnin YO, et al. Band filling control of the dzyaloshinskii-moriya interaction in weakly ferromagnetic insulators. Phys Rev Lett. (2017) 119:167201. doi: 10.1103/PhysRevLett.119.167201
45. Wu Y, Zhang S, Yin G, Zhang J, Wang W, Zhu Y, et al. Néel-type skyrmion in WTe2/Fe3GeTe2 van der Waals heterostructure. Nat Commun. (2020) 11:3860. doi: 10.1038/s41467-020-17566-x
46. Yang H, Chen G, Cotta AAC, N'Diaye AT, Nikolaev SA, Soares EA, et al. Significant dzyaloshinskii-moriya interaction at graphene-ferromagnet interfaces due to the rashba effect. Nat Mater. (2018) 17:605–609. doi: 10.1038/s41563-018-0079-4
47. Moriya T. Anisotropic superexchange interaction and weak ferromagnetism. Phys Rev. (1960) 120:91–8. doi: 10.1103/PhysRev.120.91
Keywords: first-principles, multiferroic heterostructure, Dzyaloshinskii-Moriya interaction, magnetic anistropy, density of states
PACS: 63.20.dk, 74.78.Fk, 85.75.-d, 75.30.Gw
Citation: Chen D, Sun W, Li H, Wang J and Wang Y (2020) Tunable Magnetic Anisotropy and Dzyaloshinskii-Moriya Interaction in an Ultrathin van der Waals Fe3GeTe2/In2Se3 Heterostructure. Front. Phys. 8:587419. doi: 10.3389/fphy.2020.587419
Received: 01 August 2020; Accepted: 19 August 2020;
Published: 25 September 2020.
Edited by:
Xiaotian Wang, Southwest University, ChinaReviewed by:
Fang Hong, Institute of Physics Chinese Academy of Science, ChinaCopyright © 2020 Chen, Sun, Li, Wang and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jianli Wang, amlhbmxpQHVvdy5lZHUuYXU=; Yuanxu Wang, d2FuZ3l4QGhlbnUuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.