- 1International Space Science Institute (ISSI), Bern, Switzerland
- 2Geophysics, Department Geoscience and Environment, Munich University (LMU), Munich, Germany
- 3Space Research Institute (IWF), Austrian Academy of Sciences, Graz, Austria
It is proposed that reconnection would be a main mechanism governing the plasma processes on auroral time scales in the topside ionosphere/high-latitude magnetosphere transition. It occurs in the downward current region between two narrow parallel closely spaced though separated downward current sheets. The field-aligned currents are carried by upward cold upper-ionospheric electrons closing the upward current in an adjacent region. This local process does primarily not affect the ambient field but generates an anomalous diffusivity.
Introduction
In a recent paper [1] we suggested that strong-guide field reconnection may play a role in the generation of radiation in the topside auroral ionosphere by the electron cyclotron maser instability mechanism [2–4]. This idea was based on the assumption that at the boundary between the upward and downward current regions the magnetic fields of kinetic Alfvén waves might undergo reconnection, causing electron exhausts which are similar to electron holes while being of larger scale. Such a mechanism seems to be appropriate to explain intense emission in the auroral kilometric radiation band [5]. In a subsequent paper we explored a particular model of stronger amplification of the radiation if electron pairing would occur in the vicinity of the electron mirror points along the strong auroral magnetic field. This brings up the question whether, independent of the generation of radiation, reconnection might not be the dominant process of plasma dynamics in the topside auroral region.
The topside auroral region is characterized by a number of properties which at first glance do not seem in favor of reconnection. In order to have reconnection one needs contact between anti-parallel magnetic fields and plasma inflow perpendicular to the field, as is inherent to all the basic reconnection models (see Ref. 6, 7; for reviews separated by 40 years). The auroral region, at the contrary, hosts a very strong magnetic field which on the scales of aurora is parallel (except for some weak inclination and systematic geographic variation). It does not change sign across the auroral region on one hemisphere. Thus it seems highly improbable that such a field would undergo any reconnection and rearrange in some violent manner. Indeed, it does not. In order to rearrange it requires very strong external basically mechanical forces to twist or wrap it around. Such forces would be related to extremely strong currents which in the topside ionosphere-magnetosphere transition renders them completely improbable. They require conditions which are presumably realized in the lower solar atmosphere where the solar photospheric convection network rotates the frozen-in magnetic field at frequency of few minutes around causing the field to become highly warped into a spiral which stretches out into the corona and solar wind. The strong geomagnetic field in topside auroral region is in contrast fixed to the inert ionosphere and body of the earth. Deforming it substantially requires very strong outer forces which happens very rarely. It may, however, play a decisive role as catalyst of reconnection caused by other means.
The auroral region is comparably narrow in (geographic/geomagnetic) latitude while somewhat broader in its longitudinal extension. In each auroral event, it divides into two sections, one carrying downward fluxes of medium energy
There is no obvious local reason for field-aligned currents in the topside auroral ionosphere to be dispersed in the manner observed. Their most reasonable driving source is reconnection in the tail current sheet, however, which is well established. Upward currents/downward electrons originate from electron acceleration in the central tail plasma sheet. They flow down along the newly reconnected closed magnetic field into auroral latitudes causing the upward field aligned currents. Upward low energy electron fluxes belong to the downward closure currents and result from moderately accelerated ionospheric electrons present here in sufficiently large numbers. How this acceleration happens in detail remains unclear but can be taken as an observational fact. More than one up-down pair of currents indicates multiple tail reconnection. It seems that this is the only causally satisfactory picture. (Its gross geometry is depicted in Figure 1.)
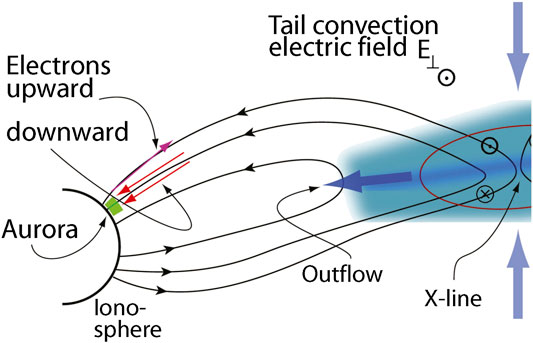
FIGURE 1. Schematic of connection between tail reconnection and auroral topside current system for one single tail X-point (after [32]). Downward and upward field-aligned electron fluxes are indicated in the topside ionosphere. They correspond to upward and downward field-aligned currents. Naturally, due to the geometry of the tailward source, the downward fluxes are distributed over a large spatial domain, while the returning upward fluxes occupy a narrow latitudinal interval only on the northern edge.
Some of the most violent auroral processes result from the dynamics of the downward/upward electron fluxes and the related upward/downward field-aligned currents. (A full sequence of Fast Auroral SnapshoT Explorer (FAST) observations when crossing a topside active auroral region during a substorm is given in Figure 2.) Of course, since reconnection in the tail is non-stationary, its longer temporal scale folds into the internal processes caused by the fluxes and currents. It modifies those while can be considered as waves flowing along the field with non-stationary currents coming in field-aligned electromagnetic wave pulses. These are assumed as belonging to one of the (kinetic) Alfvén modes. Thus, on the time-scale of the latter, auroral dynamics will be related to the electromagnetic stability of the field-aligned current pulses.
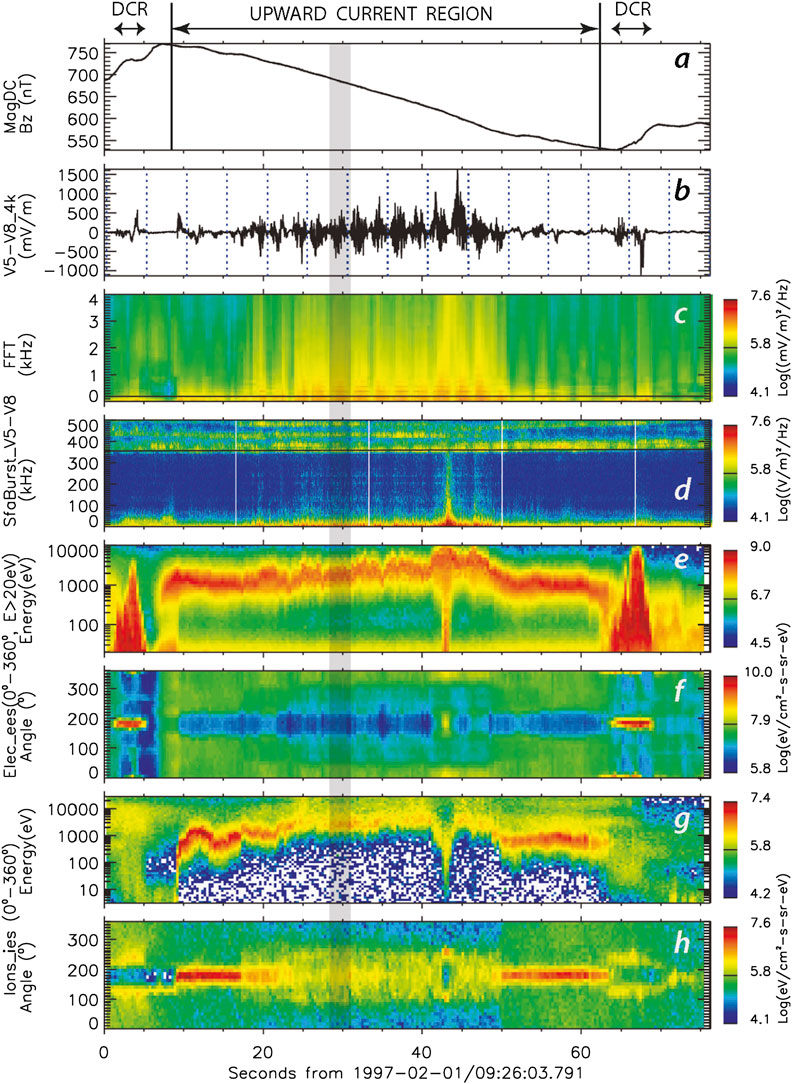
FIGURE 2. Full sequence of FAST measurements across dow-up-auroral current system on 02-01-1997 (after [16, 17]). (A) Magnetic field component
Field-Aligned Downward Current Sheets
The observations concerning auroral electron fluxes and the related currents are the following:
Upward Current Region Properties
Downward electrons/upward currents occupy an extended spatial interval of low density and barely structured fluxes. The variation of the perpendicular (to the main field) magnetic field is smooth; it changes about linearly from
Absence of an ionospheric electron background at (FAST) spacecraft altitude either suggests that the ionosphere does not reach up to those altitudes (
Upward Topside Electrons
Figure 3 shows simultaneous upward/downward FAST measurements of electron fluxes when crossing a very active substorm topside auroral ionosphere. The upward-electron downward-current region behaves differently. Its spatial extension is narrow. In view of the electron flux it consists of a large number of very closely spaced spikes. The flux in each spike (generally) maximizes at the lowest energies
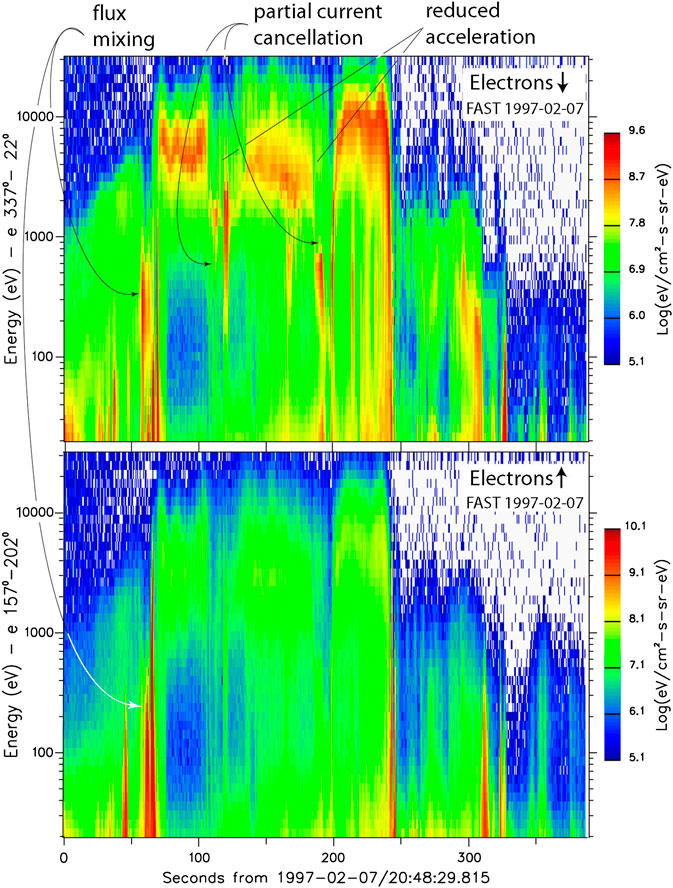
FIGURE 3. Sequence of downward (top) and upward (bottom) auroral electron fluxes observed by FAST on July 2, 1997 in the topside auroral region when crossing a substorm aurora (after [32]). The sequence distinguishes nicely between the intense downward electron fluxes at energies
The important observation is the high local structure of the downward currents, their obvious spatial closeness, and their differences in energies and flux level which is reflected in both the flux fluctuations across the narrow downward current region, and in the high spatial fluctuation of the main-field-perpendicular magnetic component
One might argue that the acceleration of electrons in the ionosphere below observation altitude is probably highly localized, depending on processes in the resistive ionospheric plasma. Therefore there would be no need for upward escaping electrons to merge laterally. This argument is invalid because they transport current. Lorentz attraction forces the currents to approach each other to form a broad unstructured downward current sheet. This is, however, inhibited by the strong main auroral geomagnetic field
Since anti-parallel currents reject each other the transition region between upward and downward currents is quiet. This is seen in panels (B–F) of Figure 2 and is in contrast to our previous investigation where we assumed that reconnection would happen there between parallel kinetic Alfvén waves. The Lorentz force between two equally strong sheet currents
where
which holds under very weak conditions in the topside auroral ionosphere. This implies that downward current sheets separated by say an electron inertial length
Kinetic (Shear) Alfvén Waves
In the complementary wave picture of field-aligned currents in the auroral region, the current is carried by (kinetic) Alfvén waves in the frequency range well below the local ion-cyclotron frequency. In addition, a large number of low-frequency electromagnetic waves are known to be present there [8]. We are in the downward current region with highly sheared upward particle flow along the magnetic field consisting of moderately fast electrons and much slower ions. Such flows are capable of generating Alfvén waves [11] on perpendicular scales of the ion inertial length
These Alfvén waves cannot be body waves like in the solar wind [12, 13] because they are strictly limited to the narrow field-aligned current sheets. Since they propagate in the strong auroral geomagnetic field, they are rather different from the usual kind of kinetic Alfvén waves which one refers to in solar wind turbulence [12], where the magnetic field ist very weak and the turbulence is dominated by the mechanics of the flow [14]. There the ion-temperature plays an important role imposing kinetic effects on the wave.
Under auroral conditions, in particular close to the ionosphere, the magnetic field is so strong that thermal ion effects on the wave are barely important. Their mass effect enters the Alfvén speed. Instead, however, under those conditions electron inertia on scales
where
The above dispersion relation, neglecting the ion contribution in the numerator, gives the well known relations for the parallel and perpendicular energy transport in the shear wave
Energy transport in the perpendicular direction is smaller than parallel by the ratio of wave numbers.
Repeating that we are in the downward current upward electron flux region causality requires that the upward electrons carry information from the ionosphere to the magnetosphere. Hence the kinetic Alfvén waves in this region also propagate upward being produced in the topside by the transverse shear on ion-inertial scales below
Reconnection Under Auroral Conditions
Assuming stationarity of the field aligned current
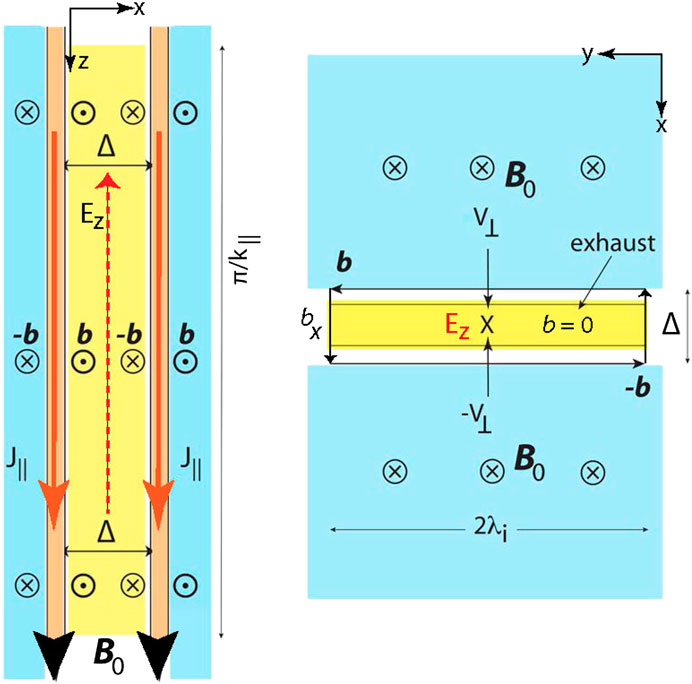
FIGURE 4. Schematic of the field configuration between two parallel field aligned flux tubes in the downward current region. Left: Geometry along the ambient field. Currents are in red. Included would be the (red dashed) fictitious return current which locally would correspond to the antiparallel wave magnetic fields
There are two essential differences between this type of reconnection and ordinary reconnection models. The first is that the ambient field serves as a strong guide field which, as noted, inhibits the adjacent field-aligned current to merge. The second is that initially the set-up lacks the presence of any central current sheet which in conventional models of reconnection is crucial and imposed from the beginning. In topside reconnection such a current flowing along the magnetic field inside the separation region would imply a return current which, however, is absent. Return currents flow through the bottomside ionosphere and close in the upward current region. Nevertheless formally a fictitious return current forms locally and temporarily in the center of the separator, which can be assumed as distributed over the separating region and belonging to the antiparallel fields
This current builds up dynamically and locally during the reconnection process itself when the two kinetic Alfvén waves slowly move perpendicular. This is a difficult dynamical problem in that reconnection will set on when the encountering magnetic fields exceed some threshold. Since electrons in this region are magnetized by the strong ambient field, they gyrate but do not take notice of the weak field b of the kinetic Alfvén waves which is transported across the separating region by the perpendicular phase and group speeds of the waves to get into contact and merge.
The reconnection process is thus solely between the two waves, primarily not affecting the ambient field and not based on any real central primary current sheet. Observations so far do not resolve the magnetic nor the particle effects of such fictitious return currents though some of the structure seen in the low energy electron fluxes in Figure 3 could be interpreted as such without proof. In fact, in order to avoid formation of the fictitious return current, which would imply that this current would be equally strong in the gap between the current sheets, reconnection is required over the full length of half a wavelength along z. Thus it necessarily generates elongated field-aligned vertical X-lines and electron exhausts in z.
First Step
All these effects are of vital interest. However, one particularly interesting question concerns the dissipation produced by this kind of reconnection. It is frequently argued that it leads to sliding of main-field field lines. In order to understand such a mechanism one needs to know the anomalous resistance caused by reconnection. In electrodynamic formulation, reconnection is conventionally dealing solely with the merging and energy transfer of fields. The microscopic mechanism of energy transfer is accounted for in the transport coefficients. Hence the appropriate way of inferring their value is referring to the electromagnetic energy exchange. This leads to the application of Poynting’s theorem
where the contribution of the electric field to the left-hand side is neglected as it is relativistically small, and
The above expression shows that reconnection in this case is a two-step process. In the first step the parallel field
Anomalous Collision Frequency
In this subsection we are not interested in this effect here as it is overwritten once reconnection really sets on but enters in the determination of the perpendicular inflow speed. It causes it to be different from tailward reconnection. Instead we proceed to an estimate of the anomalous collision frequency.
The parallel electric field
In order to get some information about the perpendicular velocity
This velocity apparently diverges for
The velocity
which, assuming a stationary state, enables us to estimate the anomalous resistivity of stationary reconnection (in the wave frame) where the inflow of magnetic energy attributed by the current, i.e., the field-aligned electron flux whose origin is found in reconnection in the magnetotail, is balanced by anomalous energy transfer to the plasma in the region separating the two current sheets. Putting the left-hand side to zero we thus find that in this kind of topside reconnection the anomalous resistivity is bound from above as
where
What concerns the spatial separation of the current sheets (see Figure 3), the best available observations (FAST) do not resolve any single sheets; it can however be assumed that their scales are the order of or below the ion-inertial length, such that
where we used that
Real reconnection will not occur between field-aligned current sheets of same strength. Thus the above resistivity respectively the collision frequency must be reduced by another factor proportional to the involved current and field fractions.
Second Step: Reconnection Electric Field
So far we just investigated the energy balance in order to obtain an anomalous collision frequency in this kind of reconnection. Reconnection however manifests itself in X points generating transverse magnetic fields and in addition electric fields. Since there is no primary return current flowing, it cannot be used as input into the two-dimensional reconnection equation for the vector potential
without prescribing the built-up of the central current profile
The important conclusion in the case of topside reconnection is rather different from usual reconnection. It tells that the exhaust is, over half the wavelength of the inertial Alfvén wave free of wave magnetic fields b, while being bounded by the reconnected wave fields
In case of the topside reconnection, a mesoscale first-order electric field
In order to circumvent the above named difficulty of calculating
and the right-hand side is the exchange of magnetic flux in the reconnection process within the typical time
Neglecting the small second term on the left then gives a simple order of magnitude estimate of the reconnection electric field
which could have been guessed from the beginning. This contains the reconnection time
The small additional term
Reconnection Time
In the above we have made use of the notion of reconnection time
With the above estimate of the anomalous resistivity in this kind of reconnection, we can proceed asking for the typical reconnection time scale. For this purpose we return to Poynting’s full theorem and take its variation with respect to the stationary state, indexing the latter with 0 while keeping the slow perpendicular velocity
This procedure, after some straightforward and simple algebra and rearranging, leads to the following expressions
and we obtain dimensionally for the typical time of reconnection
This seems a trivial result, but it tells that reconnection is a process which annihilates the excess magnetic field which is provided by the perpendicular inflow under the condition that we are close to a stationary state. This time can be compared with the times of energy flow in the shear Alfvén wave. Since clearly
a time the length of which depends essentially on the spacing of the current sheets. Since
for reconnection to occur in topside parallel field-aligned current sheets. This essentially is a condition on the spacing
Any current sheet separation is strictly limited. Since it must be larger than the upward electron gyro-radius we have
Conclusions
In the present letter we propose that reconnection might occur not only in given current sheets but also in the topside ionosphere-magnetosphere auroral transition region where the main magnetic field is very strong, almost vertical, and directly connects to the tail reconnection region. It serves as a guide for any particle flow exchange between the topside ionosphere and the tail plasma sheet, exchange between low frequency electromagnetic waves (in our case kinetic Alfvén waves) trapped in flux tubes and the accompanying field-aligned current sheets, and ultimately as an inhibitor for the field-aligned parallel current sheets to merge. This enables reconnection in the gap between the current sheets between the oppositely directed magnetic field of the sheets respectively the kinetic Alfvén wave magnetic fields.
Dealing with reconnection, one is not primarily interested in the change of magnetic topology but in energy transformation from magnetic into kinetic, diffusion of plasma and magnetic field across the reconnection region, generation of electric fields, and ultimately selective particle acceleration as these are the observed effects. The generality of reconnection is not the best argument. The decades old claim that reconnection converts magnetic energy into mechanical energy is no fundamental insight; in all processes involving reconnection, the main energy is stored in the basic mechanical motion and by no means in the magnetic field. This motion, convection in inhomogeneous media with boundaries, like the magnetotail or the magnetopause, or turbulence necessarily produces currents and transports magnetic fields to let them get into contact. The amount of energy released by reconnection is in all cases just the minor electromagnetic part, a fraction of the mechanical energy.
Topside reconnection is expected predominantly in the downward current region, which observationally seems to be highly structured, consisting of several adjacent parallel current sheets. Similar conditions may also occur in the upward current region though no such structuring is obvious from observations. If it exist, then the physics will be similar. We have shown that topside reconnection is possible, generates a elongated field-aligned regions (exhausts) where the fields of parallel current sheets merge, anomalous collisions are generated, energy is exchanged and dissipated, and most important a first order reconnection electric field
It is instructive to briefly inspect Figure 3. It shows the downward (upper panel) and upward (lower panel) electron fluxes. In addition to the temporally/spatially highly structured fluxes, still obeying the spatial differences between the downward and upward current regions imposed by the tail-source of the downward fluxes, resulting from variations in tail-reconnection, or several tail-reconnection sites, one occasionally observes the simultaneous presence of upward and downward fluxes in the downward current region. One particular case it at
Aside of acceleration, radiation generation may be taken as signature of topside reconnection. Radiation is preferably generated by the electron cyclotron maser mechanism. It requires low electron densities, strong magnetic fields, and a rather particular particle distribution with excess energy in its component perpendicular to the ambient magnetic field [2, 20]. Such a state in dilute plasmas lacks sufficiently many electrons for re-absorbing the spontaneously emitted radiation while the excited state causes inversion of the absorption coefficient. These conditions allow for the plasma to become an emitter [21–23, 33] by the electron cyclotron maser mechanism [4] based on a loss-cone distribution [24]. It requires weakly relativistic electrons (see Ref. 2, 3; for reviews) and a low density electron background embedded into a strong field. It nicely comes up for the weak auroral kilometric background radiation but fail explaining the intense narrow band observed and drifting emission seen in panel d of Figure 2.
To explain the latter, in earlier work we referred to electron hole formation [16, 17, 25]. Hole models favourably apply to electron depleted exhausts in topside reconnection where densities become low (see, e.g., Ref. 6 and the remaining trapped electron component maximizes at perpendicularly speeds having large anisotropy. Intense narrow band drifting emissions in the frequency range 300–600 kHz may be a signature of topside reconnection in the strong main auroral field. They were originally attributed to Debye scale electrostatic electron holes [26, 27] observed by Viking [28] and FAST [25, 29, 30] but are to small-scale for radiation sources. Topside reconnection exhausts instead have dimensions along the magnetic field of half a kinetic Alfvén length and transverse scales of few ion inertial lengths
Of course, details of this process should be developed both analytically as far as possible, and by numerical simulations. If confirmed, this mechanism would also map to any astrophysical moderately or strongly magnetized object with appropriate modification.
The present qualitative considerations which we spiced with a few simple estimates based on energy conservation arguments just propose that reconnection in the topside auroral ionosphere is a process which has so far been missed and probably is that mechanism which releases the largest amount of so-called magnetically stored energy available and from the smallest spatial regions. Reconnection in much weaker fields like in turbulence and broad current sheets will be substantially less efficient because of the weakness of the reconnecting magnetic fields. Nevertheless in very large extended systems with reconnection proceeding on the microscales [31] with the total number of reconnection regions very large, the emission measure is large as well, and radiation from reconnection may become a non-negligible signature even in weak fields. However, in very strong fields like those in magnetized planets and magnetized stars (predominantly neutron stars, white dwarfs but also including outer atmospheres of magnetized stars like the sun) reconnection following our argumentation may be more important than so far assumed.Very recently it has been observed [Brown, Z., Koskinen, T., Muller-Wodrag, I., West. R., Jouchoux, A., and Esposito, L. (2020). Nat. Astron. 4, 872-879. doi:10.1038/s41550-020-1060-0] that thermospheric temperatures at Saturn, as a paradigm of giant planets at large distance from the Sun, exceed those expected from solar radiation heating by several hundred degrees. The excess energy input is deposited in the planetary auroral region, a clear indication of auroral processes being responsible for the observed warming. This requires violent processes which presumably can hardly be provided by conventional wave heating. Reconnection in the topside auroral region may offer a promising solution for this conundrum.
Author's Note
Very recently it has been observed [Brown, Z., Koskinen, T., Muller-Wodrag, I., West. R., Jouchoux, A., and Esposito, L. (2020). Nat. Astron. 4, 872-879. doi:10.1038/s41550-020-1060-0] that thermospheric temperatures at Saturn, as a paradigm of giant planets at large distance from the Sun, exceed those expected from solar radiation heating by several hundred degrees. The excess energy input is deposited in the planetary auroral region, a clear indication of auroral processes being responsible for the observed warming. This requires violent processes which presumably can hardly be provided by conventional wave heating. Reconnection in the topside auroral region may offer a promising solution for this conundrum.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Author Contributions
Both authors contributed equally to this research and approved its publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was part of a brief Visiting Scientist Program at the International Space Science Institute Bern. RT acknowledges the interest of the ISSI directorate as well as the generous hospitality of the ISSI staff, in particular the assistance of the librarians Andrea Fischer and Irmela Schweitzer, and the Systems Administrator Saliba F. Saliba. We acknowledge discussions with R. Nakamura and Y. Narita. RT acknowledges the cooperation with R. Pottelette two decades ago on the data reduction and the radiation and electron hole problems.
References
1. Treumann RA, Baumjohann W. Electron cyclotron maser instability (ECMI) in strong magnetic guide field reconnection. Ann Geophys. (2017) 35:999–1013. doi:10.5194/angeo-35-999-2017
2. Melrose DB. Instabilities in space and laboratory plasmas. Cambridge, UK: Cambridge University Press (1989).
3. Treumann RA. The electron-cyclotron maser for astrophysical application. Astron Astrophys Rev. (2006) 13:229–315. doi:10.1007/s00159-006-0001-y
4. Wu CS, Lee LC. A theory of the terrestrial kilometric radiation. Acta Pathol Jpn. (1979) 230:621–6. doi:10.1086/157120
5. Gurnett DA. The Earth as a radio source: terrestrial kilometric radiation. J Geophys Res. (1974) 79:4227–38. doi:10.1029/ja079i028p04227
6. Treumann RA, Baumjohann W. Collisionless magnetic reconnection in space plasmas. Front Phys. (2013) 1:31. doi:10.3389/fphy.2013.00031
7. Vasyliunas VM. Theoretical models of magnetic field line merging. Rev Geophys. (1975) 13:303–36. doi:10.1029/rg013i001p00303
8. LaBelle J, Treumann RA. Auroral radio emissions, 1. Hisses, roars, and bursts. Space Sci Rev. (2002) 101:295–440. doi:10.1023/a:1020850022070
9. Paschmann G, Haaland S, Treumann RA, eds. Space sciences series of ISSI. In: Auroral plasma physics. Vol. 15. New York, NY: Springer-Verlag (2003).
10. Malara F, Veltri P, Carbone V. Magnetic neutral point stretching and coalescence in tearing‐generated magnetohydrodynamic structures. Phys Fluid Plasma Phys. (1991) 3:1801–3. doi:10.1063/1.859648
11. Hasegawa A, Uberoi C. The Alfvén wave. Oak Ridge, TN: U.S. Department of Energy, Technical Information Center 10. (1982).
12. Goldstein ML, Eastwood JP, Treumann RA, Lucek EA, Pickett J, Décréau P. The near-earth solar wind. Space Sci Rev. (2005) 118:7–39. doi:10.1007/1-4020-4582-4_2
13. Narita Y, Roberts OW, Vörös Z, Hoshino M. Transport ratios of the kinetic Alfvén mode in space plasmas. Front Phys. (2020) 8:00166. doi:10.3389/fphy.2020.00166
14. Maiorano T, Settino A, Malara F, Pezzi O, Pucci F, Valentini F. Kinetic Alfvén wave generation by velocity shear in collisionless plasmas. J Plasma Phys. (2020) 86:825860202, arXiv [physivs.plasm-ph] 2003.09394v1. doi:10.1017/s002237782000032x
15. Baumjohann W, Treumann RA. Basic space plasma physics. 2012 revised edition. London, UK: Imperial College Press (1996).
16. Treumann RA, Baumjohann W, Pottelette R. Electron-cyclotron maser radiation from electron holes: upward current region, Ann Geophys. (2011b) 29:1885–904. doi:10.5194/angeo-29-1885-2011
17. Treumann RA, Baumjohann W, Pottelette R. Electron-cyclotron maser radiation from electron holes: downward current region. Ann Geophys. (2012) 30:119–30. doi:10.5194/angeo-30-119-2012
18. Lysak RL, Lotko W. On the kinetic dispersion relation for shear Alfvén waves. J Geophys Res. (1996) 101:5085–94. doi:10.1029/95ja03712
19. Schindler K. A theory of the substorm mechanism. J Geophys Res. (1974) 79(19):2803–10. doi:10.1029/ja079i019p02803
20. Sprangle P, Drobot AT. The linear and self-consistent nonlinear theory of the electron cyclotron maser instability. IEEE Trans. Microwave Theory Techn. (1977) 25:528–44. doi:10.1109/tmtt.1977.1129151
21. Gaponov AV. Interaction between electron fluxes and electromagnetic waves in waveguides. Izvestiya Vyzsh. Uchebn. Zaved. Radiofizika. (1959) 2:450–6.
22. Schneider J. Stimulated emission of radiation by relativistic electrons in a magnetic field. Phys Rev Lett. (1959) 2:504–5. doi:10.1103/physrevlett.2.504
23. Twiss R. Radiation transfer and the possibility of negative absorption in radio astronomy. Aust J Phys. (1958) 11:564–79. doi:10.1071/ph580564
24. Louarn P, Le Quéau D. Generation of the auroral kilometric radiation in plasma cavities-I. Experimental study. Planet Space Sci. (1996) 44:199–210. doi:10.1016/0032-0633(95)00121-2
25. Pottelette R, Treumann RA. Electron holes in the auroral upward current region. Geophys Res Lett. (2005) 32:L12104. doi:10.1029/2005gl022547
26. Ergun RE, Carlson CW, McFadden JP, Mozer FS, Delory GT, Peria W, et al. FAST satellite observations of large-amplitude solitary structures. Geophys Res Lett. (1998b) 25:2041–4. doi:10.1029/98gl00636
27. Pottelette R, Ergun RE, Treumann RA, Berthomier M, Carlson CW, McFadden JP, et al. Modulated electron-acoustic waves in auroral density cavities: FAST observations. Geophys Res Lett. (1999) 26:2629–32. doi:10.1029/1999gl900462
28. de Feraudy H, Pedersen BM, Bahnsen A, Jespersen M. Viking observations of auroral kilometric radiation from the plasmasphere to night auroral oval source regions. Geophys Res Lett. (1987) 14:511–4. doi:10.1029/gl014i005p00511
29. Carlson CW, Pfaff RF, Watzin JG. The fast auroral snapshoT (FAST) mission. Geophys Res Lett. (1998) 25:2013–6. doi:10.1029/98gl01592
30. Ergun RE, Carlson CW, McFadden JP, Mozer FS, Muschietti L, Roth I, et al. Debye-scale plasma structures associated with magnetic-field-aligned electric fields, Phys Rev Lett. (1998a) 81:826–9. doi:10.1103/physrevlett.81.826
31. Treumann RA, Baumjohann W. Spontaneous magnetic reconnection. Collisionless reconnection and its potential astrophysical relevance. Astron AstroPhys Rev. (2015) 23:1–91. doi:10.1007/s00159-015-0087-1
32. Treumann RA, Nakamura R, Baumjohann W. Downward auroral currents from reconnection Hall-region. Ann Geophys. (2011a) 29:679–85. doi:10.5194/angeo-29-679-2011.
Keywords: reconnection, strong guide fields, downward current region, auroral processes, acceleration, radiation
Citation: Treumann RA and Baumjohann W (2020) Topside Reconnection. Front. Phys. 8:586082. doi: 10.3389/fphy.2020.586082
Received: 22 July 2020; Accepted: 17 September 2020;
Published: 06 October 2020.
Edited by:
Chi Wang, National Space Science Center (CAS), ChinaReviewed by:
Zhonghua Yao, Chinese Academy of Sciences (CAS), ChinaFrancesco Malara, University of Calabria, Italy
Copyright © 2020 Treumann and Baumjohann. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: W. Baumjohann, V29sZmdhbmcuQmF1bWpvaGFubkBvZWF3LmFjLmF0
 R. A. Treumann
R. A. Treumann W. Baumjohann
W. Baumjohann