- 1Laboratório de Física Estatística e Biologia Computacional, Faculdade de Filosofia, Ciências e Letras de Ribeirão Preto, Departmento de Física, Universidade de São Paulo, Ribeirão Preto, Brazil
- 2Departamento de Física, Universidade Federal de Pernambuco, Recife, Brazil
The critical brain hypothesis states that there are information processing advantages for neuronal networks working close to the critical region of a phase transition. If this is true, we must ask how the networks achieve and maintain this critical state. Here, we review several proposed biological mechanisms that turn the critical region into an attractor of a dynamics in network parameters like synapses, neuronal gains, and firing thresholds. Since neuronal networks (biological and models) are not conservative but dissipative, we expect not exact criticality but self-organized quasicriticality, where the system hovers around the critical point.
1 Introduction
Thirty-three years after the initial formulation of the self-organized criticality (SOC) concept [1] (and 37 years after the self-organizing extremal invasion percolation model [2]), one of the most active areas that employ these ideas is theoretical neuroscience. However, neuronal networks, similar to earthquakes and forest fires, are nonconservative systems, in contrast to canonical SOC systems like sandpile models [3, 4]. To model such systems, one uses nonconservative networks of elements represented by cellular automata, discrete time maps, or differential equations. Such models have distinct features from conservative systems. A large fraction of them, in particular neuronal networks, have been described as displaying self-organized quasi-criticality (SOqC) [5–7] or weak criticality [8, 9], which is the subject of this review.
The first person that made an analogy between brain activity and a critical branching process probably was Alan Turing, in his memorable paper Computing machinery and intelligence [10]. Decades later, the idea that SOC models could be important to describe the activity of neuronal networks was in the air as early as 1995 [11–16], eight years before the fundamental 2003 experimental article of Beggs and Plenz [17] reporting neuronal avalanches. This occurred because several authors, working with models for earthquakes and pulse-coupled threshold elements, noticed the formal analogy between such systems and networks of integrate-and-fire neurons. Critical learning was also conjectured by Chialvo and Bak [18–20]. However, in the absence of experimental support, these works, although prescient, were basically theoretical conjectures. A historical question would be to determine in what extent this early literature motivated Beggs and Plenz to perform their experiments.
Since 2003, however, the study of criticality in neuronal networks developed itself as a research paradigm, with a large literature, diverse experimental approaches, and several problems addressed theoretically and computationally (some reviews include Refs. [7, 21–27]). One of the main results is that information processing seems to be optimized at a second-order absorbing phase transition [28–42]. This transition occurs between no activity (the absorbing phase) and nonzero steady-state activity (the active phase). Such transition is familiar from the SOC literature and pertains to the directed percolation (DP) or the conservative-DP (C-DP or Manna) universality classes [7, 42–45].
An important question is how neuronal networks self-organize toward the critical region. The question arises because, like earthquake and forest-fire models, neuronal networks are not conservative systems, which means that in principle they cannot be exactly critical [5, 6, 45, 46]. In these networks, we can vary control parameters like the strength of synapses and obtain subcritical, critical, and supercritical behavior. The critical point is therefore achieved only by fine-tuning.
Over time, several authors proposed different biological mechanisms that could eliminate the fine-tuning and make the critical region a self-organized attractor. The obtained criticality is not perfect, but it is sufficient to account for the experimental data. Also, the mechanisms (mainly based on dynamic synapses but also on dynamic neuronal gains and adaptive firing thresholds) are biologically plausible and should be viewed as a research topic per se.
The literature about these homeostatic mechanisms is vast, and we do not intend to present an exhaustive review. However, we discuss here some prototypical mechanisms and try to connect them to self-organized quasicriticality (SOqC), a concept developed to account for nonconservative systems that hover around but do not exactly sit on the critical point [5–7].
For a better comparison between the models, we will not rely on the original notation of the reviewed articles, but will try to use a universal notation instead. For example, the synaptic strength between a presynaptic neuron j and a postsynaptic neuron i will be always denoted by
Last, before we begin, a few words about the fine-tuning problem. Even perfect SOC systems are in a sense fine-tuned: they must be conservative and require infinite separation of time scales with driving rate
To Tune or Not to Tune
In this article, we have shown how systems self-organize into a critical state through [homeostasis]. Thus, we became relieved from the task of fine-tuning the control parameter W, but instead, we acquire a new task: that of estimating the appropriate values for parameters
The issue of tuning or not tuning depends mainly on what we understand by control parameter. (…) a control parameter can be thought of a knob or dial that when turned the system exhibits some quantifiable change. We say that the system self-organizes if nobody turns that knob but the system itself. In order to achieve this, the elements comprising the system require a feedback mechanism to be able to change their inner dynamics in response to their surroundings. (…) The latter does not require an external entity to turn the dial for the system to exhibit critical dynamics. However, its internal dynamics are configured in a particular way in order to allow feedback mechanisms at the level of individual elements.
Did we fine-tune their configuration? Yes. Otherwise, we would have not achieved what was desired, as nothing comes out of nothing. Did we change control parameter from W to
2 Plastic Synapses
Consider an absorbing-state second-order phase transition where the activity is
for
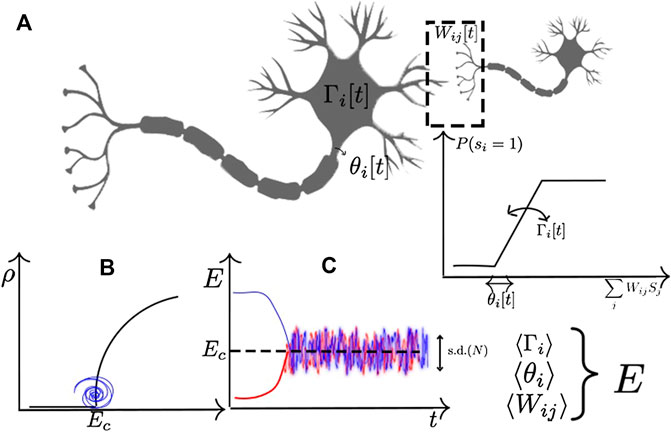
FIGURE 1. Example of homeostatic mechanisms in a stochastic neuron with firing probability
The basic idea underlying most of the proposed mechanism for homeostatic self-organization is to define a slow dynamics in the individual links
2.1 Short-Term Synaptic Plasticity
Markram and Tsodyks [49, 50] proposed a short-term synaptic model that inspired several authors in the area of self-organization to criticality. The Markram–Tsodyks (MT) dynamics is
where
In an influential article, Levina, Herrmann, and Geisel (LHG) [51] proposed to use depressing–recovering synapses. In their model, we have leaky integrate-and-fire (LIF) neurons in a complete-graph topology. As a self-organizing mechanism, they used a simplified version of the MT dynamics with constant u, that is, only Eq. 2. They studied the system varying A and found that although we need some tuning in the hyperparameter A, any initial distribution of synapses
Bonachela et al. [6] studied in depth the LHG model and found that, like forest-fire models, it is an instance of SOqC. The system presents the characteristic hovering around the critical point in the form of stochastic sawtooth oscillations in the
Note that the LHG dynamics can be written in terms of the synaptic efficacy
Brochini et al. [55] studied a complete graph of stochastic discrete time LIFs [56, 57] and proposed a discrete time LHG dynamics:
where the firing index
The discrete time LHG dynamics was also studied for cellular automata neurons in random networks with an average of K neighbors connected by probabilistic synapses
with an upper limit
It has been found that such depressing synapses induce correlations inside the synaptic matrix, affecting the global branching ratio
After examining this diverse literature, it seems that any homeostatic dynamics of the form
can self-organize the networks, where R and D are the recovery and depressing processes, for example:
In particular, the simplest mechanism would be
a usual dynamics in SOC models [5, 7]. This means that the full LHG dynamics, and also the full MT dynamics, is a sufficient but not a necessary condition for SOqC.
The average
where
Here, for biological plausibility, it is better to assume a large but finite recovery time, say
We observe that the original LHG model [6, 51] had
As early as 1998, Kinouchi [62] proposed the synaptic dynamics:
with small but finite τ and u. The difference here from the former mechanisms is that, like in Eq. 10, depression is not proportional to
Hsu and Beggs [63] studied a model for the activity
where
where
Hsu and Beggs found that for
where now
In another article, Hsu et al. [64] extended the model to include distance-dependent connectivity and Hebbian learning [64]. Changing the homeostasis equations to our standard notation, we have
where
Shew et al. [65] studied experimentally the visual cortex of the turtle and proposed a (complete graph) self-organizing model for the input synapses
where, like in Eq. 13,
Hernandez-Urbina and Herrmann [47] studied a discrete time IF model where they define a local measure called node success:
where A is the adjacency matrix of the network, with
The authors then define the node success–driven plasticity (NSDP):
where
They analyzed the relation among the avalanche critical exponents, the largest eigenvalue
Levina et al. [66] proposed a model in a complete graph in which the branching ratio σ is estimated as the local branching
2.2 Meta-Plasticity
Peng and Beggs [67] studied a square lattice (
where Θ is the Heaviside function. The self-organization is made by a LHG dynamics plus a meta-plasticity term:
where
2.3 Hebbian Synapses
Ever since Donald Hebb’s proposal that neurons that fire together wire together [68–70], several attempts have been made to implement this idea in models of self-organization. However, a pure Hebbian mechanism can lead to diverging synapses, so that some kind of normalization or decay needs also be included in Hebbian plasticity.
In 2006, de Arcangelis, Perrone-Capano, and Herrmann introduced a neuronal network with Hebbian synaptic dynamics [71] that we call the APH model. There are several small variations in the models proposed by de Arcangelis et al., but perhaps the simplest one [72] is given by the following neuronal dynamics on a square lattice of
where
where
Çiftçi [81] studied a neuronal SIRs model on the C. elegans neuronal network topology. The spontaneous activation rate (the drive) is
Ciftçi found robust self-organization to quasicriticality. The author notes, however, that S is nonlocal information.
Uhlig et al. [82] considered the effect of LHG synapses in the presence of an associative Hebb synaptic matrix. They found that, although the two processes are not irreconcilable, the critical state has detrimental effects to the attractor recovery. They interpret this as a suggestion that the standard paradigm of memories as fixed point attractors should be replaced by more general approaches like transient dynamics [83].
2.4 Spike Time–Dependent Plasticity
Rubinov et al. [84] studied a hierarchical modular network of LIF neurons with STDP plasticity. The synapses are modeled by double exponentials:
where
where
Del Papa et al. [85] explored the interaction between criticality and learning in the context of self-organized recurrent networks (SORN). The ratio between inhibitory to excitatory neurons is
where
where
Levina et al. [86] studied the combined effect of LHG synapses, homeostatic branching parameter
They found that there is cooperativity of these mechanisms in extending the robustness of the critical state to variations on the hyperparameter A (see Eq. 2).
Stepp et al. [87] examined a LIF neuronal network which has both Markram–Tsodyks dynamics and spiking time–dependent plasticity STDP (both excitatory and inhibitory). They found that, although MT dynamics produces some self-organization, the STDP mechanism increases the robustness of the network criticality.
Delattre et al. [88] included in the STDP synaptic change
where resource availability
Here,
2.5 Homeostatic Neurite Growth
Kossio et al. [89] studied IF neurons randomly distributed in a plane, with neurites distributed within circles of radii
where
Tetzlaff et al. [90] studied experimentally neuronal avalanches during the maturation of cell cultures, finding that criticality is achieved in a third stage of the dendrites/axons growth process. They modeled the system using neurons with membrane potential
where
Finally, the effective connection is defined as
where
3 Dynamic Neuronal Gains
For all-to-all topologies as used in Refs. 6, 51, 53, 55, the number of synapses is
The stochastic neuron has a probabilistic firing function, say, a linear saturating function or a rational function:
where
Now, let us assume that each neuron i has its neuronal gain
Costa et al. [91] and Kinouchi et al. [58] studied the stability of the fixed points of mechanisms given by Eqs 55 and 56 and concluded that the fixed point solution
Zierenberg et al. [92] considered a cellular automaton neuronal model with binary states
where
Indeed, for a cellular automata model similar to [60, 61], a probabilistic synapse with neuronal gains could be written as
where
4 Adaptive Firing Thresholds
Girardi-Schappo et al. [93] examined a network with
They noticed, however, that for these stochastic LIF systems, the critical point requires also a zero field
Notice the plus signal in the last term, since if the postsynaptic neuron fires (
As already seen, Del Pappa et al. [85] considered a similar threshold dynamics, Eq. 41. Bienenstock and Lehmann [95] also studied, at the mean field level, the joint evolution of firing thresholds and dynamic synapses (see Section 6.3).
5 Topological Self-Organization
Consider a cellular automata model [29, 32, 60, 61] in a network with average degree K and average probabilistic synaptic weights
In another sense, we call a network topology critical if there is a barely infinite percolating cluster, which for a random network occurs for
So, we can have a critical network with a
We present here a more advanced version of the BR model [97]. It follows the idea of deleting synapses from correlated neurons and increasing synapses of uncorrelated neurons. The correlation over time T is calculated as
where the stochastic neurons evolve as
The self-organization procedure is as follows:
Choose at random a pair
Calculate the correlation
Define a threshold α. If
Then, continue updating the network state
Interesting analytic results for this class of topological models were obtained by Droste et al. [105]. The self-organized connectivity is about
Zeng et al. [107] combined the rewiring rules of the BR model with the neuronal dynamics of the APH model. They obtained an interesting result: the final topology is a small-world network with a large number of neighbors, say
6 Self-Organization to Other Phase Transitions
6.1 First-Order Transition
Mejias et al. [108] studied a neuronal population model with firing rate
where
where
Millman et al. [109] obtained similar results at a first-order phase transition, but now in a random network of LIF neurons with average of K neighbors and chemical synapses. The synapses follow the LHG mechanism:
where
Di Santo et al. [110, 111] and Buendía et al. [7, 46] studied the self-organization toward a first-order phase transition (called self-organized bistability or SOB). The simplest self-organizing dynamics was used in a two-dimensional model:
where
Relaxing the conditions of infinite separation of time scales and bulk conservation, the authors studied the model with an LHG dynamics [7, 46, 111]:
where W is the synaptic weight and I a small input. They found that this is the equivalent SOqC version for first-order phase transitions, obtaining hysteretic up–down activity, which has been called self-organized collective oscillations (SOCOs) [7, 46, 111]. They also observed bistability phenomena.
Cowan et al. [112] also found hysteresis cycles due to bistability in an IF model from the combination of an excitatory feedback loop with anti-Hebbian synapses in its input pathway. This leads to avalanches both in the upstate and in the downstate, each one with power-law statistics (size exponents close to
6.2 Hopf Bifurcation
Absorbing-active phase transitions are associated to transcritical bifurcations in the low-dimensional mean-field description of the order parameter. Other bifurcations (say, between fixed points and periodic orbits) can also appear in the low-dimensional reduction of systems exhibiting other phase transitions, such as between steady states and collective oscillations. They are critical in the sense that they present phenomena like critical slowing down (power-law relaxation to the stationary state) and critical exponents. Some authors explored the homeostatic self-organization toward such bifurcation lines.
In what can be considered a precursor in this field, Bienenstock and Lehmann [95] proposed to apply a Hebbian-like dynamics at the level of rate dynamics to the Wilson–Cowan equations, having shown that the model self-organizes near a Hopf bifurcation to/from oscillatory dynamics.
The model has excitatory and inhibitory stochastic neurons. The neuronal equations are
where, as before, the binary variable
where
The authors proposed a covariance-based regulation for the synapses
where
The authors show that there are Hopf and saddle-node lines in this system and that the regulated system self-organizes at the crossing of these lines. So, the system is very close to the oscillatory bifurcation, showing great sensibility to external inputs.
As commented, this article is a pioneer in the sense of searching for homeostatic self-organization at a phase transition in a neuronal network in 1998, well before the work of Beggs and Plenz [17]. However, we must recognize some deficiencies that later models tried to avoid. First, all the synapses and thresholds have the same value, instead of an individual dynamics for each one, as we saw in the preceding sections. Most importantly, the network activities
Magnasco et al. [113] examined a very stylized model of neural activity with time-dependent anti-Hebbian synapses:
where
6.3 Edge of Synchronization
Khoshkhou and Montakhab [114] studied a random network with
The parameters
where
The inhibitory synapses are fixed, but the excitatory ones evolve with a STDP dynamics. If the firing difference is
This system presents a transition from out-of-phase to synchronized spiking. The authors show that a STDP dynamics self-organizes in a robust way the system to the border of this transition, where critical features like avalanches (coexisting with oscillations) appear.
7 Concluding Remarks
In this review, we described several examples of self-organization mechanisms that drive neuronal networks to the border of a phase transition (mostly a second-order absorbing phase transition, but also to first-order, synchronization, Hopf, and order-chaos transitions). Surprisingly, for all cases, it is possible to detect neuronal avalanches with mean-field exponents similar to those obtained in the experiments of Beggs and Plenz [17].
By using a standardized notation, we recognized several common features between the proposed homeostatic mechanisms. Most of them are variants of the fundamental drive-dissipation dynamics of SOC and SOqC and can be grouped into a few classes.
Following Hernandez-Urbina and Herrmann [47], we stress that the coarse tuning on hyperparameters of homeostatic SOqC is not equivalent to the fine-tuning of the original control parameter. This homeostasis is a bona-fide self-organization, in the same sense that the regulation of body temperature is self-organized (although presumably there are hyperparameters in that regulation). The advantage of these explicit homeostatic mechanisms is that they are biologically inspired and could be studied in future experiments to determine which are more relevant to cortical activity.
Due to nonconservative dynamics and the lack of an infinite separation of time scales, all these mechanisms lead to SOqC [5–7], not SOC. In particular, conservative sandpile models should not be used to model neuronal avalanches because neurons are not conservative. The presence of SOqC is revealed by stochastic sawtooth oscillations in the former control parameter, leading to large excursions in the supercritical and subcritical phases. However, hovering around the critical point seems to be sufficient to account for the current experimental data. Also, perhaps the omnipresent stochastic oscillations could be detected experimentally (some authors conjecture that they are the basis for brain rhythms [91]).
One suggestion for further research is to eliminate nonlocal variables in the homeostatic mechanisms. Another is to study how the branching ratio σ, or better, the synaptic matrix largest eigenvalue
Author Contributions
OK and MC contributed to conception and design of the study; RP organized the database of revised articles and made Figure 1; OK and MC wrote the manuscript. All authors contributed to manuscript revision, and read and approved the submitted version.
Funding
This article was produced as part of the activities of FAPESP Research, Innovation, and Dissemination Center for Neuromathematics (Grant No. 2013/07699-0, São Paulo Research Foundation). We acknowledge the financial support from CNPq (Grant Nos. 425329/2018-6, 301744/2018-1 and 2018/20277-0), FACEPE (Grant No. APQ-0642-1.05/18), and Center for Natural and Artificial Information Processing Systems (CNAIPS)-USP. Support from CAPES (Grant Nos. 88882.378804/2019-01 and 88882.347522/2010-01) and FAPESP (Grant Nos. 2018/20277-0 and 2019/12746-3) is also gratefully acknowledged.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors thank Miguel Muñoz for discussions and advice.
References
1. Bak P, Tang C, Wiesenfeld K. Self-organized criticality: an explanation of the 1/fnoise. Phys Rev Lett (1987). 59:381. doi:10.1103/physrevlett.59.381
2. Wilkinson D, Willemsen JF. Invasion percolation: a new form of percolation theory. J Phys A Math Gen (1983). 16:3365. doi:10.1088/0305-4470/16/14/028
3. Jensen HJ. Self-organized criticality: emergent complex behavior in physical and biological systems. Vol. 10. Cambridge: Cambridge University Press (1998).
4. Pruessner G. Self-organised criticality: theory, models and characterization. Cambridge: Cambridge University Press (2012).
5. Bonachela JA, Muñoz MA. Self-organization without conservation: true or just apparent scale-invariance? J Stat Mech (2009) 2009:P09009. doi:10.1088/1742-5468/2009/09/P09009
6. Bonachela JA, De Franciscis S, Torres JJ, Muñoz MA. Self-organization without conservation: are neuronal avalanches generically critical? J Stat Mech 2010 (2010). P02015. doi:10.1088/1742-5468/2010/02/P02015
7. Buendía V, di Santo S, Bonachela JA, Muñoz MA. Feedback mechanisms for self-organization to the edge of a phase transition. Front Phys 8 (2020). 333. doi:10.3389/fphy.2020.00333
8. Palmieri L, Jensen HJ. The emergence of weak criticality in soc systems. Epl 123 (2018). 20002. doi:10.1209/0295-5075/123/20002
9. Palmieri L, Jensen HJ. The forest fire model: the subtleties of criticality and scale invariance. Front Phys 8 (2020). 257. doi:10.3389/fphy.2020.00257
10. Turing AM. I.-computing machinery and intelligence. Mind LIX (1950). 433. doi:10.1093/mind/lix.236.433
11. Usher M, Stemmler M, Olami Z. Dynamic pattern formation leads to1fnoise in neural populations. Phys Rev Lett (1995). 74:326. doi:10.1103/PhysRevLett.74.326
12. Corral Á, Pérez CJ, Díaz-Guilera A, Arenas A. Synchronization in a lattice model of pulse-coupled oscillators. Phys Rev Lett (1995). 75:3697. doi:10.1103/PhysRevLett.75.3697
13. Bottani S. Pulse-coupled relaxation oscillators: from biological synchronization to self-organized criticality. Phys Rev Lett (1995). 74:4189. doi:10.1103/PhysRevLett.74.4189
14. Chen D-M, Wu S, Guo A, Yang ZR. Self-organized criticality in a cellular automaton model of pulse-coupled integrate-and-fire neurons. J Phys Math GenJ Phys A Math Gen (1995). 28:5177. doi:10.1088/0305-4470/28/18/009
15. Herz AVM, Hopfield JJ. Earthquake cycles and neural reverberations: collective oscillations in systems with pulse-coupled threshold elements. Phys Rev Lett (1995). 75:1222. doi:10.1103/PhysRevLett.75.1222
16. Middleton , Tang C. Self-organized criticality in nonconserved systems. Phys Rev Lett 74 (1995). 742. doi:10.1103/PhysRevLett.74.742
17. Beggs JM, Plenz D. Neuronal avalanches in neocortical circuits. J Neurosci 23 (2003). 11167–77. doi:10.1523/JNEUROSCI.23-35-11167.2003
18. Stassinopoulos D, Bak P. Democratic reinforcement: a principle for brain function. Phys Rev E (1995). 51:5033. doi:10.1103/physreve.51.5033
19. Chialvo DR, Bak P. Learning from mistakes. Neuroscience (1999). 90:1137–48. doi:10.1016/S0306-4522(98)00472-2
20. Bak P, Chialvo DR. Adaptive learning by extremal dynamics and negative feedback. Phys Rev E (2001). 63:031912. doi:10.1103/PhysRevE.63.031912
22. Hesse J, Gross T. Self-organized criticality as a fundamental property of neural systems. Front Syst Neurosci (2014). 8:166. doi:10.3389/fnsys.2014.00166
23.D Plenz, and E Niebur, editors. Criticality in neural systems. Hoboken: John Wiley & Sons (2014).
24. Cocchi L, Gollo LL, Zalesky A, Breakspear M. Criticality in the brain: a synthesis of neurobiology, models and cognition. Prog Neurobiol Prog Neurobiol (2017). 158:132–52. doi:10.1016/j.pneurobio.2017.07.002
25. Muñoz MA. Colloquium: criticality and dynamical scaling in living systems. Rev Mod Phys (2018). 90:031001. doi:10.1103/RevModPhys.90.031001
26. Wilting J, Priesemann V. 25 years of criticality in neuroscience—established results, open controversies, novel concepts. Curr Opin Neurobiol (2019). 58:105–11. doi:10.1016/j.conb.2019.08.002
27. Zeraati R, Priesemann V, Levina A. Self-organization toward criticality by synaptic plasticity. arXiv (2020) 2010.07888.
28. Haldeman C, Beggs JM. Critical branching captures activity in living neural networks and maximizes the number of metastable states. Phys Rev Lett (2005). 94:058101. doi:10.1103/PhysRevLett.94.058101
29. Kinouchi O, Copelli M. Optimal dynamical range of excitable networks at criticality. Nat Phys (2006). 2:348–351. doi:10.1038/nphys289
30. Copelli M, Campos PRA. Excitable scale free networks. Eur Phys J B (2007). 56:273–78. doi:10.1140/epjb/e2007-00114-7
31. Wu A-C, Xu X-J, Wang Y-H. Excitable Greenberg-Hastings cellular automaton model on scale-free networks. Phys Rev E (2007). 75:032901. doi:10.1103/PhysRevE.75.032901
32. Assis VRV, Copelli M. Dynamic range of hypercubic stochastic excitable media. Phys Rev E (2008). 77:011923. doi:10.1103/PhysRevE.77.011923
33. Beggs JM. The criticality hypothesis: how local cortical networks might optimize information processing. Phil Trans R Soc A 366 (2008). 29–343. doi:10.1098/rsta.2007.2092
34. Ribeiro TL, Copelli M. Deterministic excitable media under Poisson drive: Power law responses, spiral waves, and dynamic range. Phys Rev E (2008). 77:051911. doi:10.1103/PhysRevE.77.051911
35. Shew WL, Yang H, Petermann T, Roy R, Plenz D. Neuronal avalanches imply maximum dynamic range in cortical networks at criticality. J Neurosci (2009). 29:15595–600. doi:10.1523/JNEUROSCI.3864-09.2009
36. Larremore DB, Shew WL, Restrepo JG. Predicting criticality and dynamic range in complex networks: effects of topology. Phys Rev Lett (2018). 106:058101. doi:10.1103/PhysRevLett.106.058101
37. Shew WL, Yang H, Yu S, Roy R, Plenz D. Information capacity and transmission are maximized in balanced cortical networks with neuronal avalanches. J Neurosci (2011). 31:55–63. doi:10.1523/JNEUROSCI.4637-10.2011
38. Shew WL, Plenz D. The functional benefits of criticality in the cortex. Neuroscientist (2013). 19:88–100. doi:10.1177/1073858412445487
39. Mosqueiro TS, Maia LP. Optimal channel efficiency in a sensory network. Phys Rev E (2013). 88:012712. doi:10.1103/PhysRevE.88.012712
40. Wang C-Y, Wu ZX, Chen MZQ. Approximate-master-equation approach for the Kinouchi-Copelli neural model on networks. Phys Rev E (2017). 95:012310. doi:10.1103/PhysRevE.95.012310
41. Zierenberg J, Wilting J, Priesemann V, Levina A. Tailored ensembles of neural networks optimize sensitivity to stimulus statistics. Phys Rev Res (2020). 2:013115. doi:10.1103/physrevresearch.2.013115
42. Galera EF, Kinouchi O. Physics of psychophysics: two coupled square lattices of spiking neurons have huge dynamic range at criticality. arXiv (2020). 11254.
43. Dickman R., Vespignani A, Zapperi S. Self-organized criticality as an absorbing-state phase transition. Phys Rev E (1998). 57:5095. doi:10.1103/PhysRevE.57.5095
44. Muñoz MA, Dickman R, Vespignani A, Zapperi S. Avalanche and spreading exponents in systems with absorbing states. Phys Rev E (1999). 59:6175. doi:10.1103/PhysRevE.59.6175
45. Dickman R, Muñoz MA, Vespignani A, Zapperi S. Paths to self-organized criticality. Braz J Phys (2000). 30:27–41. doi:10.1590/S0103-97332000000100004
46. Buendía V., di Santo S., Villegas P., Burioni R, Muñoz MA. Self-organized bistability and its possible relevance for brain dynamics. Phys Rev Res (2020). 2:013318. doi:10.1103/PhysRevResearch.2.013318
47. Hernandez-Urbina V, Herrmann JM. Self-organized criticality via retro-synaptic signals. Front Phys (2017). 4:54. doi:10.3389/fphy.2016.00054
48. Lübeck S. Universal scaling behavior of non-equilibrium phase transitions. Int J Mod Phys B (2004). 18:3977–4118. doi:10.1142/s0217979204027748
49. Markram H, Tsodyks M. Redistribution of synaptic efficacy between neocortical pyramidal neurons. Nature (1996). 382:807–10. doi:10.1038/382807a0
50. Tsodyks M, Pawelzik K, Markram H. Neural networks with dynamic synapses. Neural Comput (1998). 10:821–35. doi:10.1162/089976698300017502
51. Levina A., Herrmann K, Geisel T. Dynamical synapses causing self-organized criticality in neural networks. Nat Phys (2007a). 3:857–860. doi:10.1038/nphys758
52. Levina A, Herrmann M. Dynamical synapses give rise to a power-law distribution of neuronal avalanches. Adv Neural Inf Process Syst (2006). 771–8.
53. Levina A., Herrmann M, Geisel T. Phase transitions towards criticality in a neural system with adaptive interactions. Phys Rev Lett(2009). 102:118110. doi:10.1103/PhysRevLett.102.118110
54. Wang SJ, Zhou C. Hierarchical modular structure enhances the robustness of self-organized criticality in neural networks. New J Phys (2012). 14:023005. doi:10.1088/1367-2630/14/2/023005
55. Brochini L, de Andrade Costa A, Abadi M, Roque AC, Stolfi J, Kinouchi O. Phase transitions and self-organized criticality in networks of stochastic spiking neurons. Sci Rep (2016). 6:35831. doi:10.1038/srep35831
56. Gerstner W, van Hemmen JL. Associative memory in a network of 'spiking' neurons. Netw Comput Neural SystNetw Comput Neural Syst (1992). 3:139–64. doi:10.1088/0954-898X_3_2_004
57. Galves A, Löcherbach E. Infinite systems of interacting chains with memory of variable length-A stochastic model for biological neural nets. J Stat Phys (2013). 151:896–921. doi:10.1007/s10955-013-0733-9
58. Kinouchi O, Brochini L, Costa AA, Campos JGF, Copelli M. Stochastic oscillations and dragon king avalanches in self-organized quasi-critical systems. Sci Rep (2019). 9:1–12. doi:10.1038/s41598-019-40473-1
59. Grassberger P, Kantz H. On a forest fire model with supposed self-organized criticality. J Stat Phys (1991). 63:685–700. doi:10.1007/BF01029205
60. Costa AdA, Copelli M, Kinouchi O. Can dynamical synapses produce true self-organized criticality? J Stat Mech (2015). 2015:P06004. doi:10.1088/1742-5468/2015/06/P06004
61. Campos JGF, Costa AdA, Copelli M, Kinouchi O. Correlations induced by depressing synapses in critically self-organized networks with quenched dynamics. Phys Rev E (2017). 95:042303. doi:10.1103/PhysRevE.95.042303
62. Kinouchi O. Self-organized (quasi-)criticality: the extremal Feder and Feder model. arXiv (1998). 9802311.
63. Hsu D, Beggs JM. Neuronal avalanches and criticality: a dynamical model for homeostasis. Neurocomputing 69 (2006). 1134–36. doi:10.1016/j.neucom.2005.12.060
64. Hsu D, Tang A, Hsu M, Beggs JM. Simple spontaneously active Hebbian learning model: homeostasis of activity and connectivity, and consequences for learning and epileptogenesis. Phys Rev E 76 (2007). 041909. doi:10.1103/PhysRevE.76.041909
65. Shew WL, Clawson WP, Pobst J, Karimipanah Y, Wright NC, Wessel R. Adaptation to sensory input tunes visual cortex to criticality. Nature Phys 11 (2015). 659–663. doi:10.1038/nphys3370
66. Levina A., Ernst U, Michael Herrmann JM. Criticality of avalanche dynamics in adaptive recurrent networks. Neurocomputing 70 (2007b). 1877–1881. doi:10.1016/j.neucom.2006.10.056
67. Peng J, Beggs JM. Attaining and maintaining criticality in a neuronal network model. Physica A Stat Mech Appl (2013). 392:1611–20. doi:10.1016/j.physa.2012.11.013
68. Hebb DO. The organization of behavior: a neuropsychological theory. Hoboken: J. Wiley; Chapman & Hall (1949).
69. Turrigiano GG, Nelson SB. Hebb and homeostasis in neuronal plasticity. Curr Opin Neurobiol (2000). 10:358–64. doi:10.1016/S0959-4388(00)00091-X
70. Kuriscak E, Marsalek P, Stroffek J, Toth PG. Biological context of Hebb learning in artificial neural networks, a review. Neurocomputing (2015). 152:27–35. doi:10.1016/j.neucom.2014.11.022
71. de Arcangelis L, Perrone-Capano C, Herrmann HJ. Self-organized criticality model for brain plasticity. Phys Rev Lett (2006). 96:028107. doi:10.1103/PhysRevLett.96.028107
72. Lombardi F, Herrmann HJ, de Arcangelis L. Balance of excitation and inhibition determines 1/f power spectrum in neuronal networks. Chaos (2017). 27:047402. doi:10.1063/1.4979043
73. Pellegrini G. L., de Arcangelis L., Herrmann HJ, Perrone-Capano C. Activity-dependent neural network model on scale-free networks. Phys Rev E (2007). 76:016107. doi:10.1103/PhysRevE.76.016107
74. de Arcangelis L. Are dragon-king neuronal avalanches dungeons for self-organized brain activity? Eur Phys J Spec Top (2012). 205:243–57. doi:10.1140/epjst/e2012-01574-6
75. de Arcangelis L, Herrmann HJ. Activity-dependent neuronal model on complex networks. Front Physiol (2012). 3:62. doi:10.3389/fphys.2012.00062
76. Lombardi F, Herrmann HJ, Perrone-Capano C, Plenz D, De Arcangelis L. Balance between excitation and inhibition controls the temporal organization of neuronal avalanches. Phys Rev Lett (2012). 108:228703. doi:10.1103/PhysRevLett.108.228703
77. de Arcangelis L, Lombardi F, Herrmann HJ. Criticality in the brain. J Stat Mech (2014). 2014:P03026. doi:10.1088/1742-5468/2014/03/P03026
78. Lombardi F, Herrmann HJ, Plenz D, De Arcangelis L. On the temporal organization of neuronal avalanches. Front Syst Neurosci (2014). 8:204. doi:10.3389/fnsys.2014.00204
79. Lombardi F, de Arcangelis L. Temporal organization of ongoing brain activity. Eur Phys J Spec Top (2014). 223:2119–2130. doi:10.1140/epjst/e2014-02253-4
80. Van Kessenich LM, De Arcangelis L, Herrmann HJ. Synaptic plasticity and neuronal refractory time cause scaling behaviour of neuronal avalanches. Sci Rep (2016). 6:32071. doi:10.1038/srep32071
81. Çiftçi K. Synaptic noise facilitates the emergence of self-organized criticality in the caenorhabditis elegans neuronal network. Netw Comput Neural Syst (2018). 29:1–19. doi:10.1080/0954898X.2018.1535721
82. Uhlig M, Levina A, Geisel T, Herrmann JM. Critical dynamics in associative memory networks. Front Comput Neurosci (2013). 7:87. doi:10.3389/fncom.2013.00087
83. Rabinovich M, Huerta R, Laurent G. Neuroscience: transient dynamics for neural processing. Science (2008). 321:48–50. doi:10.1126/science.1155564
84. Rubinov M., Sporns O., Thivierge JP, Breakspear M. Neurobiologically realistic determinants of self-organized criticality in networks of spiking neurons. PLoS Comput Biol (2011). 7:e1002038. doi:10.1371/journal.pcbi.1002038
85. Del Papa B., Priesemann V, Triesch J. Criticality meets learning: criticality signatures in a self-organizing recurrent neural network. PLoS One (2017). 12:e0178683. doi:10.1371/journal.pone.0178683
86. Levina A, Herrmann JM, Geisel T. Theoretical neuroscience of self-organized criticality: from formal approaches to realistic models. In D Plenz, and E Niebur, editors. Criticality in neural systems. Hoboken: Wiley Online Library (2014). 417–36. doi:10.1002/9783527651009.ch20
87. Stepp N, Plenz D, Srinivasa N. Synaptic plasticity enables adaptive self-tuning critical networks. PLoS Comput Biol (2015). 11:e1004043. doi:10.1371/journal.pcbi.1004043
88. Delattre V, Keller D, Perich M, Markram H, Muller EB. Network-timing-dependent plasticity. Front Cell Neurosci (2015). 9:220. doi:10.3389/fncel.2015.00220
89. Kossio FYK, Goedeke S, van den Akker B, Ibarz B, Memmesheimer RM. Growing critical: self-organized criticality in a developing neural system. Phys Rev Lett (2018). 121:058301. doi:10.1103/PhysRevLett.121.058301
90. Tetzlaff C, Okujeni S, Egert U, Wörgötter F, Butz M. Self-organized criticality in developing neuronal networks. PLoS Comput Biol (2010). 6, e1001013. doi:10.1371/journal.pcbi.1001013
91. Costa A., Brochini L, Kinouchi O. Self-organized supercriticality and oscillations in networks of stochastic spiking neurons. Entropy (2017). 19:399. doi:10.3390/e19080399
92. Zierenberg J., Wilting J, Priesemann V. Homeostatic plasticity and external input shape neural network dynamics. Phys Rev X (2018). 8:031018. doi:10.1103/PhysRevX.8.031018
93. Girardi-Schappo M., Brochini L., Costa AA, Carvalho TT, Kinouchi O. Synaptic balance due to homeostatically self-organized quasicritical dynamics. Phys Rev Res (2020). 2:012042. doi:10.1103/PhysRevResearch.2.012042
94. Brunel N Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J Comput Neurosci (2000). 8:183–208. doi:10.1023/A:1008925309027
95. Bienenstock E, Lehmann D. Regulated criticality in the brain? Advs Complex Syst (1998). 01:361–84. doi:10.1142/S0219525998000223
96. Bornholdt S, Rohlf T. Topological evolution of dynamical networks: global criticality from local dynamics. Phys Rev Lett (2000). 84:6114. doi:10.1103/PhysRevLett.84.6114
97. Bornholdt S, Röhl T. Self-organized critical neural networks. Phys Rev E (2003). 67:066118. doi:10.1103/PhysRevE.67.066118
98. Rohlf T. Self-organization of heterogeneous topology and symmetry breaking in networks with adaptive thresholds and rewiring. Europhys Lett (2008). 84:10004. doi:10.1209/0295-5075/84/10004
99. Gross T, Sayama H. Adaptive networks. Berlin: Springer (2009). 1–8. doi:10.1007/978-3-642-01284-6_1
100. Rohlf T, Bornholdt S. Self-organized criticality and adaptation in discrete dynamical networks. Adaptive Networks. Berlin: Springer (2009). 73–106.
101. Meisel C, Gross T. Adaptive self-organization in a realistic neural network model. Phys Rev E 80 (2009). 061917. doi:10.1103/PhysRevE.80.061917
102. Min L, Gang Z, Tian-Lun C. Influence of selective edge removal and refractory period in a self-organized critical neuron model. Commun Theor Phys 52 (2009). 351. doi:10.1088/0253-6102/52/2/31
103. Rybarsch M, Bornholdt S. Avalanches in self-organized critical neural networks: a minimal model for the neural soc universality class. PLoS One (2014). 9:e93090. doi:10.1371/journal.pone.0093090
104. Cramer B, Stöckel D, Kreft M, Wibral M, Schemmel J, Meier K, et al. Control of criticality and computation in spiking neuromorphic networks with plasticity. Nat Commun (2020). 11:1–11. doi:10.1038/s41467-020-16548-3
105. Droste F., Do AL, Gross T. Analytical investigation of self-organized criticality in neural networks. J R Soc Interface (2013). 10:20120558. doi:10.1098/rsif.2012.0558
106. Kuehn C. Time-scale and noise optimality in self-organized critical adaptive networks. Phys Rev E (2012). 85:026103. doi:10.1103/PhysRevE.85.026103
107. Zeng H-L, Zhu C-P, Guo Y-D, Teng A, Jia J, Kong H, et al. Power-law spectrum and small-world structure emerge from coupled evolution of neuronal activity and synaptic dynamics. J Phys: Conf Ser (2015). 604:012023. doi:10.1088/1742-6596/604/1/012023
108. Mejias JF, Kappen HJ, Torres JJ. Irregular dynamics in up and down cortical states. PLoS One (2010). 5:e13651. doi:10.1371/journal.pone.0013651
109. Millman D, Mihalas S, Kirkwood A, Niebur E. Self-organized criticality occurs in non-conservative neuronal networks during ‘up’ states. Nat Phys (2010). 6:801–05. doi:10.1038/nphys1757
110. di Santo S, Burioni R, Vezzani A, Muñoz MA. Self-organized bistability associated with first-order phase transitions. Phys Rev Lett (2016). 116:240601. doi:10.1103/PhysRevLett.116.240601
111. Di Santo S, Villegas P, Burioni R, Muñoz MA. Landau–Ginzburg theory of cortex dynamics: scale-free avalanches emerge at the edge of synchronization. Proc Natl Acad Sci USA (2018). 115:E1356–65. doi:10.1073/pnas.1712989115
112. Cowan JD, Neuman J, Kiewiet B, Van Drongelen W. Self-organized criticality in a network of interacting neurons. J Stat Mech(2013). 2013:P04030. doi:10.1088/1742-5468/2013/04/p04030
113. Magnasco MO, Piro O, Cecchi GA. Self-tuned critical anti-Hebbian networks. Phys Rev Lett (2009). 102:258102. doi:10.1103/PhysRevLett.102.258102
Keywords: self-organized criticality, neuronal avalanches, self-organization, neuronal networks, adaptive networks, homeostasis, synaptic depression, learning
Citation: Kinouchi O, Pazzini R and Copelli M (2020) Mechanisms of Self-Organized Quasicriticality in Neuronal Network Models. Front. Phys. 8:583213. doi: 10.3389/fphy.2020.583213
Received: 14 July 2020; Accepted: 19 October 2020;
Published: 23 December 2020.
Edited by:
Attilio L. Stella, University of Padua, ItalyReviewed by:
Srutarshi Pradhan, Norwegian University of Science and Technology, NorwayIgnazio Licata, Institute for Scientific Methodology (ISEM), Italy
Copyright © 2020 Kinouchi, Pazzini and Copelli. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Osame Kinouchi, b3NhbWVAZmZjbHJwLnVzcC5icg==
 Osame Kinouchi
Osame Kinouchi Renata Pazzini
Renata Pazzini Mauro Copelli
Mauro Copelli