Simultaneous Random Number Generation and Optical Tweezers Calibration Employing a Learning Algorithm Based on the Brownian Dynamics of a Trapped Colloidal Particle

True random number generators are in high demand for secure cryptographic algorithms. Unlike algorithmically generated pseudo-random numbers they are unclonable and non-deterministic. A particle following Brownian dynamics as a result of the stochastic Ornstein-Uhlenbeck process is a source of true randomness because the collisions with the ambient molecules are probabilistic in nature. In this paper, we trap colloidal particles in water using optical tweezers and record its confined Brownian motion in real-time. Using a segment of the initial incoming data we train our learning algorithm to measure the values of the trap stiffness and diffusion coefficient and later use those parameters to extract the “white” noise term in the Langevin equation. The random noise is temporally delta correlated, with a flat spectrum. We use these properties in an inverse problem of trap-calibration to extract trap stiffnesses, compare it with standard equipartition of energy technique, and show it to scale linearly with the power of the trapping laser. Interestingly, we get the best random number sequence for the best calibration. We test the random number sequence, which we have obtained, using standard tests of randomness and observe the randomness to improve with increasing sampling frequencies. This method can be extended to the trap-calibration for colloidal particles confined in complex fluids, or active particles in simple or complex environments so as to provide a new and accurate analytical methodology for studying Brownian motion dynamics using the newly-emerged but robust machine learning platform.

1 Introduction

Stochastic processes are excellent manifestations of statistical randomness and can be used for pedagogical study of probabilistic models [1, 2]. Such processes are widely used to expound phenomena like the Brownian motion of microscopic particles, radioactive decay, Johnson Noise in a resistor; they are even applied to financial markets [3] and population dynamics [4] where fluctuations play a central role. The most widely employed stochastic process is the Ornstein-Uhlenbeck process, which can model the trajectory of an inertia-less Brownian particle. As is well known, Brownian particles exhibit random motion due to collisions with the surrounding molecules that are in constant thermal motion in atomic timescales. However, Brownian motion - being one of the simplest stochastic processes - can be studied in an confined environment in conjunction with optical traps. Thus, optical traps may be employed to exert calibrated forces in order to induce deterministic perturbations on the particles, so that the interplay between random and deterministic forces may then be studied [5]. The motion of an optically trapped Brownian particle is determined by parameters such as temperature, viscosity of the fluid and trapping power—thus it embodies the perfect model to test parameter extraction in linear systems [6, 7]. These extracted parameters are also used to spatially calibrate the trap, i.e., find out the trapping potential, which is a cardinal prerequisite for position detection and force measurement experiments. Indeed, for the last few decades, optical tweezers are being widely used as tools to study forces in cellular adhesion [8], DNA nanopores [9], or Van der Waals interaction [10] only to name a few.

In recent works, machine learning (ML) has been applied to problems of parameter estimations in stochastic time series. Bayesian Networks [11–13] are in high demand to analyze such processes due to their speed and reliability. Neural networks [14] are also coming up to analyze complicated problems including data analysis in Optical Tweezers. We take a step in the same direction to learn the parameters of our system from the measured time series of the stochastic Brownian motion of a trapped particle, as well as employ the time series to generate strings of completely random numbers. Generation of secure random numbers underpins many aspects of internet and financial security protocols. True random numbers, unlike algorithmically generated pseudo-randoms, are non-cloneable and in high demand for cryptographic purposes. Many physical systems have been demonstrated to generate random bits, including photonic crystals, chaotic laser fluctuations, amplified spontaneous emission (ASE) [15], DRAM PUF circuits [16], and even self-assembled carbon nanotubes [17]. However, the stochasticity in the Ornstein-Uhlenbeck process—of which the Brownian motion of an optically trapped particle is a robust example—has not yet been considered to generate statistically random variables. Indeed, the string of random numbers obtained by this route is a by-product of a completely natural phenomenon, and thus superior to algorithmically generated random strings. It is important to remember that stochasticity is a statistical phenomenon that emerges due to the loss of classical variables in its description, and so—though it is has a pure classical description—it also has a ingrained probabilistic nature.

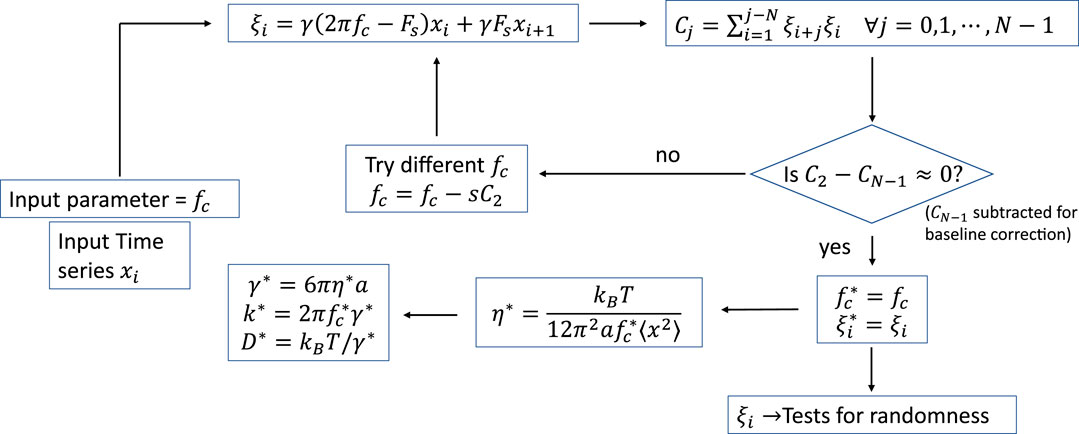
In this paper, we present a modus operandi for estimation of the parameters associated with the stochastic process which governs the Brownian motion of a microscopic particle confined in an optical trap from the partially observed samples [18] of the position (observable) using the simple properties of an autoregressive theory. Since such phenomena have components of both stochastic and deterministic processes, we can separate the fluctuations and study their aleatory traits. Note that the stiffness of the harmonic potential k, the drag-coefficient of the particle γ in the viscous fluid and the temperature $k_{B}T$ are the three parameters of the trapped Brownian dynamics. The Stoke's law $\gamma =6\pi \eta a$ relates the viscosity of the simple fluid η and the radius of the spherical particles a to the drag coefficient γ. The Einstein relation $D=\frac{k_{B}T}{\gamma }$ introduces the diffusion parameter in our equation which we choose to represent in terms of two independent variables k and γ. We commence our treatment by discretizing the trajectory of the particle into finite samples taken at equal intervals of time. Using a finite difference method we recast the Langevin equation describing the motion of the optically trapped Brownian particle into an iterative equation. Since we can measure the time series for the displacement (x), the knowledge of this parameter will enable us to solve for the stochastic part of the Langevin equation. We construct an inverse problem of parameter extraction, for which we use the temporal delta correlation and flattened nature of the spectral density of the white noise to estimate the parameters k and γ in the Langevin equation. For a particle of known size, estimation of γ by this method also allows us to find out the coefficient of viscosity if the position detection system is pre-calibrated. Thus it becomes a viable paradigm for performing viscometry even when the sample volumes are in nanoliter range. Additionally any change in the estimated parameters in our model will help to descry any heterogeneity present in the sample and eliminate unwanted systematic fluctuations. On the other hand, we can also use a fluid of known viscosity to find the position sensitivity of our detectors. It is important to note that existing methods of calibration such as the Power Spectrum analysis [19] or equipartition of energy per degree of freedom [20] are efficacious only in cases where there is no drift or electronic noise present in the system, and the presence of systematic or non-systematic variations meddle with the analyses which are typically done on the entire dataset. Now, the Ornstein-Uhlenbeck process is Gauss-Markov in nature [21] and harbors no memory earlier than the last step which makes it profoundly useful in dealing with small fluctuations concentrated locally in the dataset. In our treatment, we demonstrate the entropy of randomness to increase with increasing sampling rates asymptotically. We perform tests for randomness using the celebrated NIST test suite [22], and our extracted time-series pass all relevant tests at 99% confidence level. We plan to further extrapolate this procedure, using higher order parameter estimation, to subsume non-Markovian chains in our protocol that will describe fluctuations in viscoelastic fluids.

In a nutshell, the time-series data of the probe's displacement is used to construct an inverse problem of parameter estimation. The auto-correlation properties of the extracted noise term obtained from the initial section of the data are used to learn the parameters for trap-calibration (that closely concur with the values extracted through conventional techniques). Then these parameters are used to extract arrays of random numbers from the stochastic time-series, which efficiently pass statistical tests for randomness.

2 Theory of the Ornstein-Uhlenbeck Process and Algorithm

The dynamics of a Brownian particle in a simple fluid with a drag coefficient γ confined in a potential U is given by the Langevin equation.

$m\ddot{x}+\gamma \stackrel{\cdot }{x}+\text{Δ}U=\xi (1)$

where ξ is the zero-mean Gaussian stochastic white noise term noise term. As required by the fluctuation dissipation theorem the variance of ξ follows, $\langle \xi \left(t\right)\xi \left(t^{\prime }\right)\rangle =2k_{B}T\gamma \delta \left(t-t^{\prime }\right)$. Such a noise term is “white” in nature which means that it has a flat spectrum. In an overdamped system with vanishing inertial effects and a harmonic potential, $U=\frac{1}{2}k{x}^2$ we can reduce Eq. 1 to

$-x\left(t\right)-\frac{\gamma }{k}\dot{x}\left(t\right)+\sqrt{\frac{2k_{B}T}{\gamma }}\zeta \left(t\right)=0(2)$

where $\zeta \left(t\right)$ is zero mean, unit variance, Gaussian white noise. This is the form of Ornstein-Uhlenbeck process that gives rise to stochastic trajectories in $x\left(t\right)$. Fourier transform of Eq. 2 gives the power spectral density of the probe's displacement which is a Lorentzian function in angular frequency ω,

$C\left(\omega \right)=\langle {\left|x\left(\omega \right)\right|}^2\rangle =\frac{1}{{\omega }^2{\gamma }^2+k^2}(3)$

The correlation of the Brownian trajectories can be computed exactly for arbitrary values of $|t-t^{\prime }|$ from the power spectrum of the probe's displacement using the Weiner-Khinchin theorem [23] as:

$C\left(t-t^{\prime }\right)=\langle x\left(t\right)x\left(t^{\prime }\right)\rangle =\frac{k_{B}k}{T}{e}^{-\frac{k}{\gamma }|t-t^{\prime }|}(4)$

This exponential decay holds true for all Gauss-Markov processes. The Ornstein-Unhenbeck process is basically the continuous time analogue of an AR (1) process, and for experimental purposes we can discretise our time series into steps of $\text{Δ}t$ using the Euler method to write an iterative equation of ${\xi }_n$ as

${\xi }_n=k{x}_n+\gamma \frac{x_{n+1}-x_n}{\text{Δ}t}(5)$

The time series $x\equiv \left(x_1,x_2,\cdots ,x_N\right)$ now consists of observations from the trajectory at discrete times $t=n\text{Δ}t$ with $n=1,\cdots ,N$; the vector ξ is constructed from x using 0 padding or telomere deletion to make them of equal lengths. This simple manipulation allows us to restore the AR (0) variable ξ from the trajectory, if the parameter of the process is known. Thus it provides a principled solution to this inverse problem of parameter estimation where for the correct estimated parameters, $k^{\text{*}}$ and ${\gamma }^{\text{*}}$, we shall get back the expected autocorrelation properties of $\xi \left(t\right)$. We do that by finding out the corner frequency $f_c$ of the trap and viscosity η of the given fluid of which k and γ are direct functions givens as

$k=2\pi f_c\gamma (6)$

$\gamma =6\pi \eta a(7)$

Samples drawn from $\xi \left(t\right)$ are independent of each other—the delta correlation and flat spectrum renders it perfect for generation of random bits at a rate only limited by our temporal resolution.

3 Learning Algorithm

Such parameter extraction problems in linear systems can be easily solved using regression analysis and gradient descent on the linear equation ${\xi }_j={\theta }_1{x}_j+{\theta }_{2}B{x}_j$, where B is a positive bit-shift operator, defined as $B_{i,j}={\delta }_{i+1,j}$. But due to the prior knowledge of the form of the parameters pertaining to our Langevin equation, we can define ${\theta }_1=\gamma \left(2\pi f_c-\frac{1}{\text{Δ}t}\right)$ and ${\theta }_2=\frac{\gamma }{\text{Δ}t}$. Recasting the parameter in such a form allows effective minimization of the cost function without invoking parameter re-scaling algorithms. We achieve this in two main ways, by looking at the delta correlation of the extracted noise, and, by looking at the flatness of its power spectrum. We define the autocorrelation vector (‘autocorr’) as

$C_j={\displaystyle \sum }_{i=1}^{j-N}{\xi }_{i+j}{\xi }_i\forall j=\mathrm{0,1},\cdots ,N-1(8)$

We first inject test values of $f_c$ in our iterative equation which should change the width of the symmetric 2-sided auto-correlation function while the drag coefficient γ should change the height. In theory, for correct estimate $f_c^{\text{*}}$, we expect to get $C_0=1$ and to $C_{N-1}=0$ (In further discussion we shall call these as the center and off-centre values, respectively.) Keeping that in mind we normalize the autocorr vector, putting its maximum to 1. In practice, the entire off-centre values will never go to 0 (which is also true for algorithmically generated random numbers). We have observed different test values of $f_c$ changes the standard deviation (stdev) of the off-centre values considerably; but the stdev is least in the case of $f_c=0$ and vice versa. So this is not a good way to characterize the noise floor.

A good way to do it is to ask the question: At which value of $f_c$, does $C_2$ go to 0? Clearly, at $f_c=0$ the off-centre values do not reach 0. To create a robust framework, we define a parameter called “Autocorrelation parameter” as $C_2-C_{N-1}$, which goes to 0 for the best estimate of $f_c$. It is necessary to subtract the small amplitude in the tail of the autocorrelation vector $\left(C_{N-1}\right)$ since it has some very small positive value in the real scenario and can compromise the accuracy. We call this “Baseline subtraction”. Similarly, we can show that the flatness property of the PSD of ξ holds for the estimated parameter $f_c$. We use this property to generate ${\xi }_n$ by simply fitting the double-log binned power spectrum with a straight line. We expect that for the correct injected parameter $f_c$, we would retrieve an expected 0 slope of the linear fit. We shall call the slope of this fitted line as “PSD parameter” in further discussions. We observe a slight systematic shift of the PSD parameter for all the experimental data sets and modify our baseline accordingly. This allows us to unequivocally estimate $f_c$ from both the properties of ξ, namely the temporal delta correlation and flatness of spectral density.

To find out the corner frequency, it is not necessary to spatially calibrate the trap; the trap stiffness can also be found out just by using Eq. 6 by performing the experiment in water which has known viscosity. But to do viscometric measurement - as a bonus - within the same framework, we use the equipartition of energy formulation and write

${\eta }^{\text{*}}=\frac{k_{B}T}{12{\pi }^{2}a{f}_c^{\text{*}}\langle x^2\rangle },(9)$

and this enables us to obtain γ using Eq. 7 to complete the parameter estimation process.

Once our program learns the parameters from the incoming pool of data, it uses the iterative equation Eq. 5 to spill out the normally distributed random numbers with a white spectrum. This is different from the Brownian noise signature which is generally associated with such an Ornstein-Uhlenbeck process. To find $f_c$ we start with a guess value and then modify $f_c$ in step sizes of s simply using $f_c=f_c-s{C}_2$. We stop when $C_2\approx 0$ either using a threshold or a maximum iteration limit. We present a short summary of the algorithm in Figure 1.

FIGURE 1

FIGURE 1. Schematic of our algorithm for trap parameter extraction and random number generation.

3.1 Scope and Applicability

Our use of the learning algorithm falls in line with the basic philosophy of ML–that is to automate the process and leave less requirement for human intervention. This algorithm can be implemented easily to perform calibration of the optical tweezers in real time [24, 25] which is often necessary in the case of non-equilibrium systems [26, 27]. The main goal is to generate the random numbers; the “training” set is used to optimize the parameters, and then generate the random numbers from the “test” set–which improves upon feeding in more training examples. Additionally, our algorithm can be generalized to a wide range of scenarios, for example calibrating arbitrary potentials, other than the most common harmonic potential studied in this paper. Only the force term in the Langevin Equation will change on generalization, and one has to minimize the deviation of the autocorrelation of the extracted noise from the Dirac delta behavior for all the parameters individually. In addition, this algorithm can be extended to include stochastic motion in viscoelastic fluids, with multiple parameters. Clearly the conventional methods (which are mainly designed for the Markov time-series in harmonic potentials–which is actually a very special case) will be inadequate in these contexts.

4 Experimental Setup and Data Acquisition

We collect position fluctuation data of an optically trapped Brownian particle using a standard optical tweezers setup that is described in detail in Ref. [28]. Here we provide a brief overview for the sake of completeness. Our optical tweezers are built around an inverted microscope (Olympus IX71) with an oil immersion objective lens (Olympus 100 x, 1.3 numerical aperture) and a semiconductor laser (Lasever, 1W max power) of wavelength 1,064 nm which is tightly focused on the sample. We modulate the beam by using the first order diffracted beam off an acousto-optic modulator (AOM, Brimrose) placed at a plane conjugate to the focal plane of the objective lens. The modulation amplitude is small enough such that the power in the first order diffracted beam is modified very minimally (around 1%) as the beam is scanned. We employ a second stationary and co-propagating laser beam of wavelength 780 nm and very low power ($<5\text{\%}$ of the trapping laser power, such that the detection laser does not influence the motion of trapped particle in any way) to track the probe particle's position (we call this “detection laser”), which we determine from the back-scattered light that is incident on a balanced detection system. The balanced-detection-system together with a data acquisition card record the probe displacement data into a computer. We prepare a sample chamber of dimension around $20\text{mm}\times 10\text{mm}\times 0.2\text{mm}$ by attaching a cover slip to a glass slide by a double-sided tape which contains our sample. The samples are prepared by mixing mono-dispersed spherical polystyrene probe particles of radii $1.5\mu m$ in very low volume fraction $\left(\approx 0.1\text{\%}\right)$ into 10% NaCl-water solution. For each dataset of varying power, first, we trap a single probe particle around $30\mu m$ away from the nearest wall to get rid of any surface effects and record its Brownian motion with sampling frequency from 2–5 kHz over any desired timescale. We use the initial part of the incoming dataset to calibrate our trap. Once the trap is calibrated we re-sample our data into small batches of 5,000 data points, and make an estimate of the aforesaid parameters. Once these parameter values are learnt, subsequently we use them to isolate the stochastic term and scale it appropriately to generate the desired random variable. We note that the measured data is a result of a transformation by the detection apparatus of the physical sample paths. But we posit it to be true for all practical purposes and any deviation from theoretical behavior is therefore attributed to this limitation. To perform the experiment at different trap stiffnesses, we maximized the laser power to reduce the pointing fluctuations in the laser beam and maintained power at $\pm 0.1$ mW of the values in Table 1 for all cases. To vary the power at the objective lens we have used a combination of half-waveplate and polarizing beam cube, and the powers noted are the powers measured before filling the high numerical aperture lens. For the viscometry experiment, we mixed glycerol and water at four different concentrations. The voltage-distance sensitivity measurement was performed each time the sample was removed and reinstalled.

TABLE 1

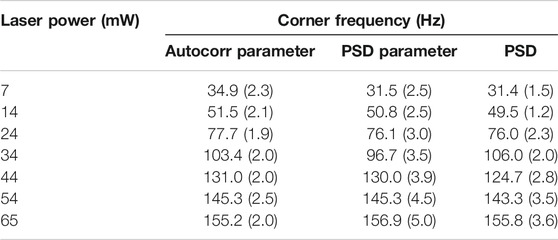
TABLE 1. Variation of corner frequency and related trap stiffness with varying laser power for experiments performed at 5 kHz. The standard deviation for each case is represented in parentheses.

5 Results and Discussions

5.1 Relation Between the Algorithms

The autocorrelation parameter estimation is directly linked theoretically to the Mean Squared Displacement (MSD) of the data, a measure often exploited to estimate the trap-stiffness. In addition, the Power Spectral Density (PSD) is related to the time-series using a Fourier Transform; further, autocorrelation at short time scales of measurement is related to the PSD by the Weiner-Khinchin theorem as shown in Eq. 4. It can be also related to the Mean Squared displacement (MSD) using time-averaged notation as $\langle \text{Δ}x{\left(\tau \right)}^2\rangle =\langle x^2\rangle -\langle x\left(\tau \right)x\left(0\right)\rangle$, where $\langle \text{Δ}x{\left(\tau \right)}^2\rangle$ is the Mean Squared Displacement, $\langle x^2\rangle$ is the variance and $\langle x\left(\tau \right)x\left(0\right)\rangle$ is the autocorrelation function of stochastic time-series. The variance is a good measure to calibrate optical traps by equating the translational kinetic energy per degree of freedom to $\frac{1}{2}{k}_{B}T$. In theory, all these methods–which analyze the probe's displacements—should give equivalent results. However, in practice, the issues with each method need to be addressed.

5.2 Equipartition of Energy

Figure 2A shows a typical time series obtained by discrete observations from the position fluctuations of the Brownian particle of diameter $3\mu m$. The data shown in this case is taken at 5 kHz sampling rate. The histogram of the data is plotted and it is well approximated by a bell curve in Figure 2B. The variance $\langle x^2\rangle$ is used in the conventional Equipartition method to estimate the spring constant k, where $\frac{1}{2}k\langle x^2\rangle =\frac{1}{2}{k}_{B}T$. However, if random fluctuations are prominent in some sections of the time-series, they can overestimate the variance, and thereby interfere with the parameter estimation procedure. These fluctuations may arise due to changes in laser power, which will ultimately cause small changes in the trap-stiffness. Also, local changes in the viscosity surrounding the probe and small random drifts can affect any parameter estimation process. For example, in Figure 2A, a section of the data is shown to have a greater fluctuation characterized by a greater variance from the mean than other sections of the dataset. To picture this effect clearly, we filter out the high-frequency components of the time-series by integrating over the short-timescales, thus revealing the low-frequency oscillation in the data. Thus, such unwanted perturbations can creep into the time-series, which is a clear deviation from the assumed Langevin dynamics of the Brownian probe.

FIGURE 2

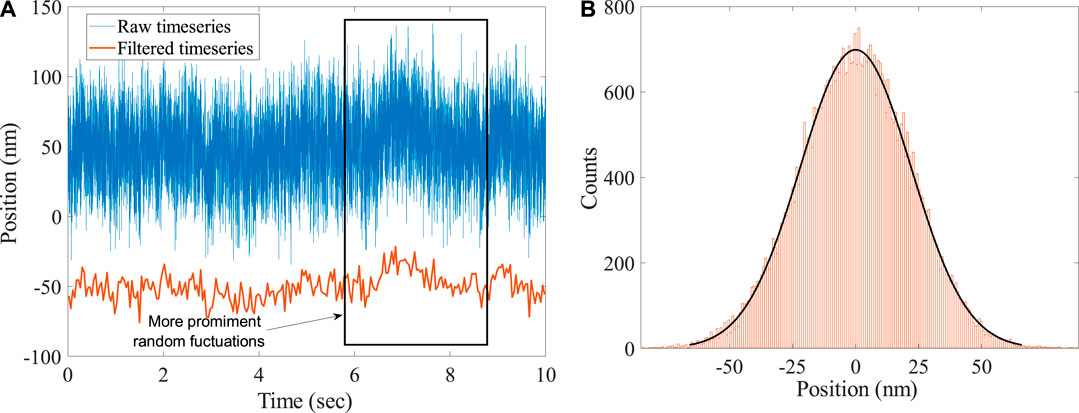
FIGURE 2. (A) Typical time series data of the position fluctuation of an optically trapped Brownian polystyrene bead of radius $a=1.5\text{μm}$. Discrete samples are taken from its trajectory along one coordinate at 5 kHz in this case. The box in the left shows the data where there is minimum fluctuation and the box on the right delineates a part of the time series where there is a minor fluctuation. (B) The histogram of the position fluctuation.

5.3 Addressing Random Fluctuations

This AR (1) variable of probe-displacement is a stationary variable—evident from the measure of the AR coefficient ${\psi }_1=\left(1-\frac{2\pi f_c}{F_s}\right)\ll 1$ (see pg-88, 90 of Ref. [29]), and the bell shape of the histogram. Fortunately, being a fast Markovian algorithm, which only depends on the difference in the consecutive points in the entire series, we can calculate the corner frequency for a particular region subject to systematic deviation from the linear behavior. This makes our method more immune to these local fluctuations interlaced in the time-series. In presence of any additional drift in the equation the drag term get modified to $\left(\gamma +\alpha \right)\dot{x}\left(t\right)$. This additional drift in the data just becomes a multiplicative factor on the overall noise term given by $\xi \left(t\right)=2\pi f_c\left(\gamma +\alpha \right)x\left(t\right)+\left(\gamma +\alpha \right)\dot{x}\left(t\right)$. We eventually normalize the multiplicative factor $\gamma +\alpha$ before using our parameter extraction algorithm to estimate $f_c^{\text{*}}$. To demonstrate this, we intentionally used our algorithm to compute the corner frequency of this selected region at 44 mW laser power, which turned out to be $132.1\pm 1.6$ Hz, well within the standard error of measurement. This provides a way to circumvent the reliability problem that many conventional measurement processes fail to address.

5.4 Conventional PSD Method

The squared modulus power of the Fourier Transformed time series follows a Lorentzian function given by Eq. 3. The parameters of this Lorentzian function gives us the required corner frequency. But often, fitting the data becomes a challenge because the fitted parameter values can be sensitive to the region of the fit. So, by following the procedures portrayed in Ref. [19], we bin every 25 points of the Fourier Transformed data. We leave behind the less reliable tail-ends at both high and low frequencies, which are prone to systematic errors. The estimates of the corner frequency using this conventional Power Spectral Density (PSD) are shown in Figures 3A,B for two different laser powers. We made sure that there is no unwanted leakage of the 50 Hz line or its harmonics in the power spectrum, the presence of which can alter the fitted parameters.

FIGURE 3

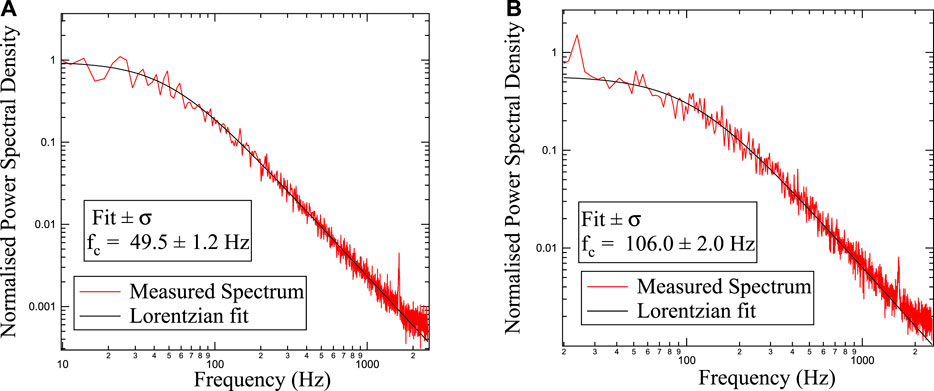
FIGURE 3. Calibration of the trap by fitting a Lorentzian to the power spectral data which has been binned over 25 points. The corner frequencies have been obtained for two different powers, 14 and 34 mW, shown respectively in (A) and (B).

5.5 Autocorrelation Parameter Estimation

The results obtained in the autocorrelation parameters inference is summarized in Table 1. In Figures 4A,B, the autocorr parameter obtained from the time series after normalization is plotted for two different laser powers. We observe that if the injected $f_c$ value is 0, then the two-sided autocorrelation plot will have a smooth off-centre distribution. But the entire off-centre region in the plot will be elevated from the 0 base-level which is not a desirable feature. Physically having a parameter value of $f_c$ close to 0 represents only the $\dot{x}$ part of the equation. It is no surprise that the velocity-autocorrelation function (VACF) will yield a near-monotonic function [30, 31]. We follow the iterative equation and generate the test values of $f_c$ to demonstrate how the autocorrelation parameter changes. Since $f_c^{\text{*}}$ is found out by looking at the particular test value where the autocorrelation parameter becomes zero, it can be considered an analogue to cost functions in many ML protocols. The negative parameter value results from the fact that we have performed baseline subtraction–subtracted the tail ends of the autocorrelation vectors from the original vector to scale it to 0, which is the expected case. It is reassuring to note that all pseudo-randoms time series also exhibit this small non zero correlation value at non-zero time-lags [32, 33]. In Figure 5A, we demonstrated how the correlation looks for the perfectly extracted random noise. Compared to it, the experimentally obtained Brownian temporal correlation is jittery at long time scales, as shown in Figure 5B, although it has exponential decay at the short time scales.

FIGURE 4

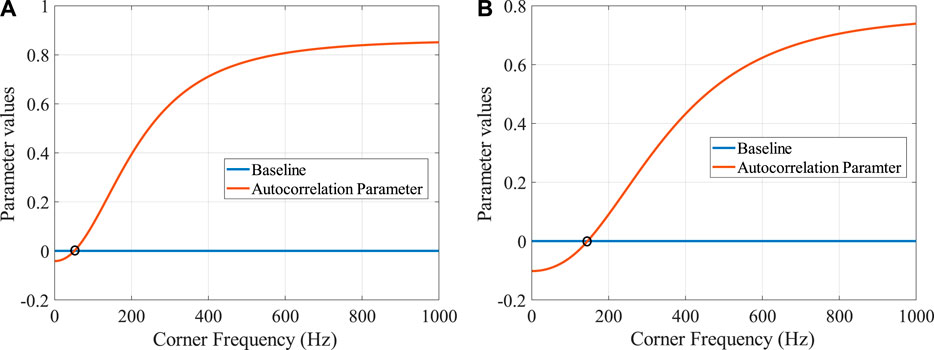
FIGURE 4. Autocorrelation Parameter values plotted for various corner frequencies used as a trail. As stated in the text, we look at the second point from the peak in the Autocorrelation curve. The corner frequency at which this parameter matches the zero baseline can be considered as the correct corner frequency for our system. Figures (A) and (B) are for two different laser powers, 14 and 54 mW, that is two different trap stiffnesses.

FIGURE 5

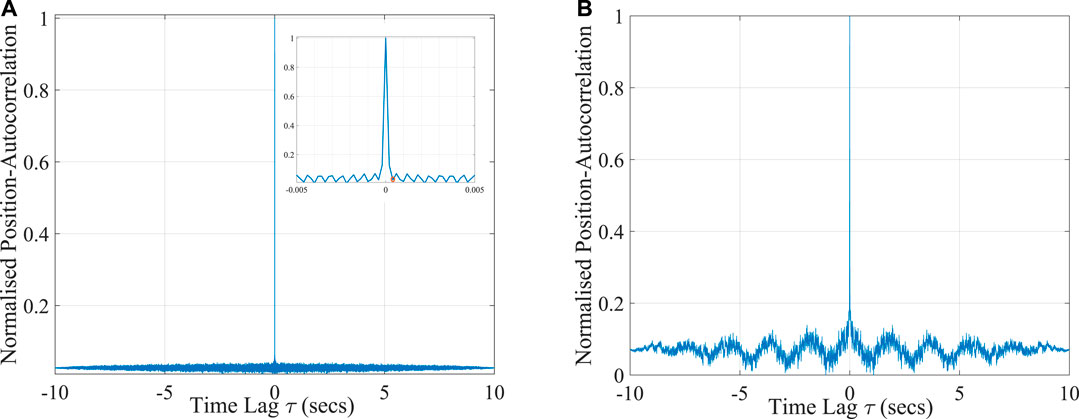
FIGURE 5. Normalized position autocorrelations for various time lags for (A) the extracted random noise, and (B) the Brownian time series. The former shows near perfect temporal delta correlation, the later exhibits exponential decay for small time lags, followed by jittery non-monotonicity.

5.6 Optimization Process

Every Learning algorithm is based on parameter optimization on a cost function defined by the algorithm. The algorithm minimizes this cost using training examples by optimizing the parameters, which often involves a gradient descent step. Mirroring on the same notion, we define a cost function that essentially is the deviation of the autocorrelation of the extracted noise from the Dirac delta behavior (or the deviation from the flat power spectrum for the noise term). There is no “label” associated with it–indeed, the cost function is calculated from the properties of the input data itself, so it can be classified under an “unsupervized” learning process. We initialize a guess value of the parameter $\left(f_c\right)$. Our goal is to reach at that value of the parameter where the deviation is zero. So we descend/ascend on this cost landscape until we reach sufficiently close to zero, or out-shoot a maximum number of iterations (we used this as a stopping point). But we do not use the gradient but the cost function itself, as for our case we intend to reach its zero, not its minimum. Depending on the calculated parameter values, we get in each step, $f_c\leftarrow f_c-s{C}_2$, for step size s, until our procedure converges. The convergence of this method depends on this step size (commonly referred to as learning rate in ML literature).

In Figure 6 we demonstrate a particular scenario for the case where the laser power is 54 mW. Depending on the learning rate, the convergence toward the solution can fast or slow. In Figure 6A two cases are shown where the parameter is initialized at 620 and 30 Hz respectively. The algorithm takes small steps in the direction of the solution until it converges. In Figure 6B$f_c$ is initialized at 200 Hz. The initial value is close to the expected value and the chosen learning rate is large, so it initially over-shoots the solution. In spite of that, in the next steps, the algorithm approaches the zero of the error function after oscillating on its sides. Since in each step the value of $s{C}_2$ decreases, the effective step size toward the solution decreases as we approach the solution, which guarantees convergence. Interestingly, when we started with a guess value within 500 Hz of the actual $f_c$ our algorithm always converged in $\sim 30$ iterations, for $s\sim 100$. We also follow the same procedure with the PSD parameter (described in the next subsection). Now, since the parameter value is 0 for the frequency $f_c^{\text{*}}$, which is the focal point of interest, any calibration of time series is redundant for this particular case. Depending on the datasets, there can be a small “bias” term associated. To take that into account, we perform a baseline-correction—where we subtract the tail end $C_{N-1}$ while computing the error function.

FIGURE 6

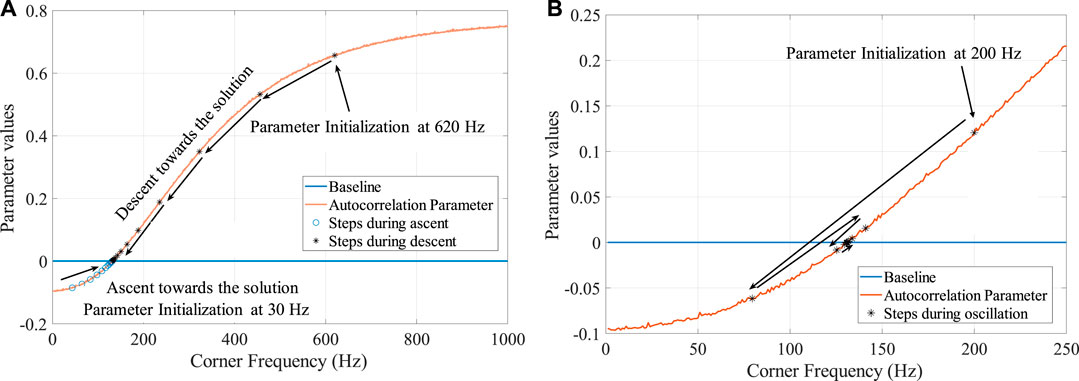
FIGURE 6. The convergence of the parameter value, corner frequency, is shown for two different learning rates, for the case where laser power is 54 mW. After initialization at the trail value the parameter steps toward the zero of the parameter value in small steps. Figure (A) shows the case where learning rate is small, and Figure (B) shows where for a larger learning rate the solution oscillates and moves toward the zero.

5.7 Parameter Extraction Through Flatness of Power Spectrum

We also fit the PSD of each parametrized time series by a straight line in a log scale and note its slope, which we had earlier defined as PSD parameter. The spectrum of a Brownian particle falls as $\frac{1}{f^2}$, while a white noise has $\frac{1}{f^0}$ signature or a constant spectral variation with frequency. To make the fitting more reliable, we do not bin the data into isolated blocks in this case but only fit till the one to two orders of the expected corner frequency (Upto 5 kHz in our case). Naturally, systematic errors creep into the analysis as a consequence of low-frequency noise coupling. Nonetheless, we see these two estimates are in close agreement (less than 5% deviation in all cases.) We compare these two protocols of stiffness estimation to the conventional method of trap calibration of fitting a binned PSD data by a Lorentzian function as mentioned earlier and also plotted for two different laser powers in Figure 7. These methods all render values of the corner frequency within 5% of each other, which corroborates the parameter estimation technique for trap calibration. In Figure 8, we show that the corner frequency scales linearly with the power of the trapping laser used in each case.

FIGURE 7

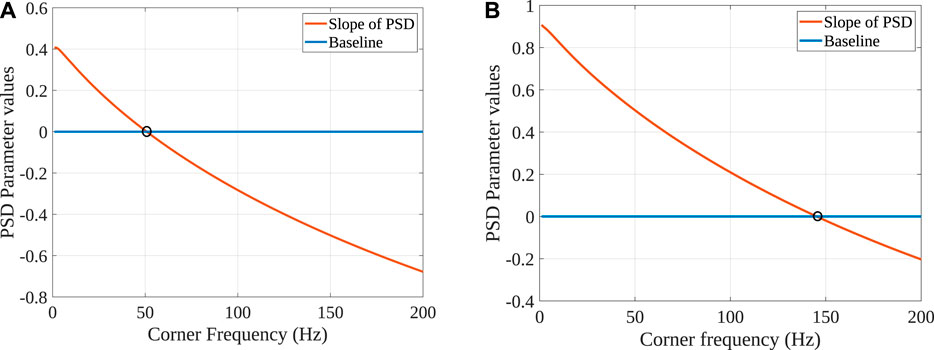
FIGURE 7. Slope of the power spectrum for time series $\xi \left(t\right)$ for various trial corner frequencies. The parameter at which after baseline correction the PSD parameter matches the zero baseline gives the corner frequency in our system. Again, Figures (A) and (B) are for two different laser powers, 14 and 54 mW, that is two different trap stiffnesses.

FIGURE 8

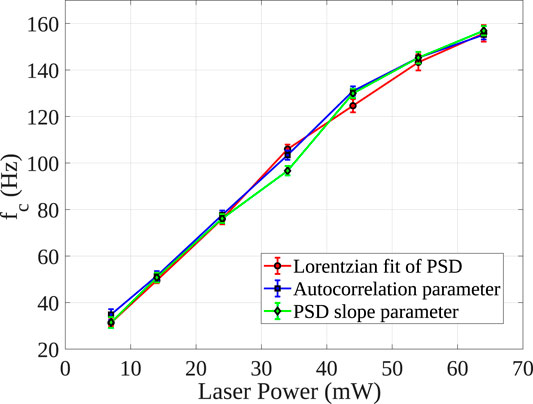
FIGURE 8. Linear variation of corner frequency with laser power, also at lower trapping potentials. The points are plotted with 1σ error bar. Note that the measurements from our method agree very well with that obtained by power spectrum analysis.

5.8 Error Analysis

In all the columns of Table 1, the figures in parentheses represent the $1\sigma$ standard deviations of the mean values of measured corner frequencies. For the autocorr parameter, it is interesting to note that the error in the correlation can be written as $\mathit{ϵ}\left(\tau \right)=\delta \left(\tau \right)-C\left(x;f_c\right)$, and C (the autocorr parameter) is also a function of τ (the time lag). The variance in the ϵ term (only at the non-zero τ) can be written as $Var\left(\mathit{ϵ}\right)=Var\left(\delta \right)+Var\left(C\right)-Cov\left(\delta ,C\right)$, where the first and third term will be zero, as all the values of δ at non-zero τ is zero. We calculate the associated variance in the autocorrelation parameter values from the variance of the error term. Then, from the graph (as seen in Figure 4), we calculate the particular value of standard deviation in the corner frequency $\left(f_c^{\text{*}}\right)$ (along the horizontal axis) which gives us the associated standard deviation in the autocorr parameter values (along the vertical axis). Thus from the difference between the theoretical delta function at the best estimate $f_c^{\text{*}}$ and the obtained position autocorrelation (for example, Figure 5A), we obtain the standard error in the estimate of the corner frequency.

For the second method (PSD parameter estimation), the errors are again computed from the standard errors associated with fitting the double logarithmic power spectrum vs. frequency curve with a straight line. The errors in fitting are directly related to the error in the estimate of corner frequency. Similarly, the standard error in fitting the binned PSD vs. frequency with the Lorentzian function returns the error in the estimated parameter. Generally, due to the ambient noise sources–systematic errors such as beam pointing fluctuations, laser drifts coupled to our signal are prominent in lower frequencies. So the standard error in the corner frequency measurement is rather large at low corner frequencies.

5.9 Viscometry

Viscosity measurement requires spatial calibration of the trap, which we do using “equipartition of energy”. Once the sensitivity measurement is performed, it is easy to estimate η using Eq. 9. Glycerol and water mixed at various concentrations create solutions at different viscosity. Finding η from it requires the variance of the actual time series (which we obtain by fitting the gaussian distribution) and $f_c$. The rest of the parameters, such as the probe size and the ambient temperature, are already known. So the standard error in η is computed from the standard error in fitting and standard error in parameter estimation discussed earlier. Note that we have used a temperature of 300 K, which is the same as the lab environment temperature. This assumption is based on studies in literature where the effects of laser heating in water have shown to be well below 1 K at the power levels we employ in the trap [34]. We calculate the diffusion coefficient for our probe size, $3\mu m$ using Stokes-Einstein's relation. We also perform a consistency-check measurement of viscosity for water and match all measured values of viscosity (water and glycerol-water mixtures) with the values measured using a conventional rheometer. All the measurements are tabulated in Table 2. This remarkable consistency in the successful estimation of both the parameters ($f_c$ and η or, k and γ) in a stochastic process—in our case the Ornstein-Uhlenbeck process—provides a fresh perspective to look at the calibration problem.

TABLE 2

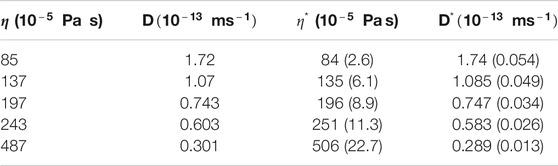
TABLE 2. The first column is the viscosity of the glycerol-water solution (first row only water) as measured in a classical rheometer, while the second column is the diffusion coefficient. The third column provides the viscosity values as obtained in our experiment using Eq. 9, while the fourth column again shows the diffusion coefficient for our case. The standard errors are noted in parentheses.

6 Generation of Unclonable Random Numbers: Measure of Randomness

6.1 Origin of Stochasticity

We now move on to the other aspect of our work: generating unclonable random numbers from the Brownian fluctuations of the optically trapped probe. As stated earlier, the Brownian motion of the particles in water follows Markov dynamics. The motion of the bead in water at any instant is only dependant on the previous instant. In other words, the system stores no memory in the process. The motion of the colloidal particle is a combined manifestation of millions of collisions it has with the ambient water molecules. The Brownian force due to all these collisions is summed up as $\xi \left(t\right)$. Being classical in nature, determinism is ingrained in theory. But from our vantage point, we omit most of the classical variables and describe the collisions by a statistical approximation that forms the radix to every stochastic process. Thus the random numbers obtained from the Ornstein-Uhlenbeck process are statistically random, not true random (true random numbers can only be generated from a quantum phenomenon). But these randoms are not algorithmically generated as is the case with pseudo-randoms; hence they are unclonable. This noise term being delta correlated in time and having a flat power spectrum forms the foundation for the generation of random bits. Non-overlapping sections of random numbers always have zero correlation between them. Moreover, the absence of any significant repetitive patterns also results in its equal power over all frequencies.

6.2 Sampling Rate

The standard deviation of the off-centre values (the autocorrelation values at non-zero time lag) is a good measure of stochasticity. For the best extracted random numbers, we expect to get the least standard deviation. In theory, the deviation should be 0 for perfectly delta correlated numbers, as discussed before. We have sampled our observable at different intervals and compared the standard deviation of the off-centre values. In Figure 9, we observe that with increasing sampling rates, this standard deviation decreases (as expected) until it saturates asymptotically around 2.5 kHz. When the data is sampled over shorter time intervals, fewer effective impacts with the surrounding molecules are averaged; naturally, the stochasticity improves.

FIGURE 9

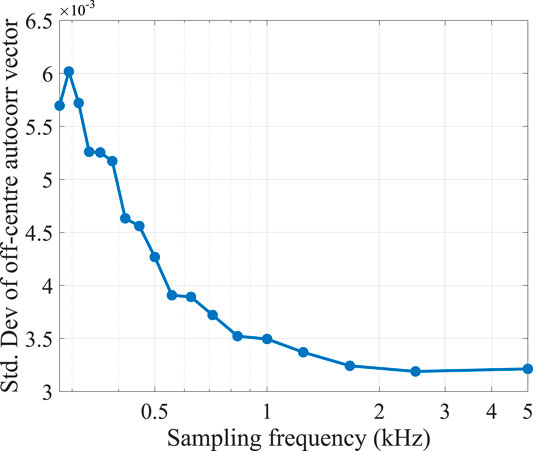
FIGURE 9. The standard deviation of the off-centre values are shown as an inverse measure of randomness; the randomness asymptotically improves with increasing sampling rates.

6.3 Tests for Randomness

We proceed to follow the relevant tests of randomness following the NIST-test for randomness suite [22]. We performed all our analyses using $\sim 50000$ data points. To test any physical random number generators, discretization and conversion into binary strings are often involved. In the binary conversion step, the values above and below the median of the time-series are marked as 1 and 0 respectively.

Our null-hypothesis states that the numbers in the time-series are randomly distributed. The alternative hypothesis against this is the opposite, viz. there exists a correlation between successive numbers (and numbers separated by finite a time interval). To test our null hypothesis against the alternative hypothesis, we employ various known statistical methods. Then, we test them against mainly standard-normal, half-normal and chi-squared distributions $\left({\chi }^2\right)$, depending on the type of NIST test we have employed (see Ref. [22]). We choose the critical value, $p_{\alpha }=0.01$, which defines the significance level of the hypothesis-testing (the maximum permissible limit of Type-I error). This critical p-value of 0.01 or the (99% confidence interval) is a ubiquitous choice in statistical inference theory. For each of the NIST-tests performed, we obtain a p-value of the test statistic. The region where $p>p_{\alpha }$ is where the null hypothesis cannot be rejected at $p_{\alpha }$ significance level and vice-versa.

In all the NIST sub-tests performed, we have obtained p-values greater than 0.01 which are tabulated in Table 3. This means that the test statistic falls outside the critical region, within the 99% confidence interval of the tests - which implies that we have failed to reject the null hypothesis at a 1% level of significance. Thus, we are more than 99% confident that the array of numbers which we obtain after solving the inverse problem of parameter estimation, is distributed randomly. Additionally, recovering this white-noize term ${\xi }_n$, helps us understand that our experimental Brownian probe correctly follows the stochastic model of Langevin dynamics.

TABLE 3

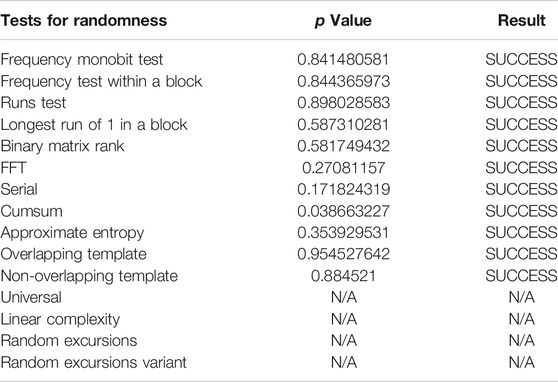
TABLE 3. Results and p values are shown for various tests of randomness provided in the NIST suite. In all the cases, the p-values are greater than 0.01 and result in successful randomness distributions at 99% confidence level. The statistical tests are performed with 40,000 bit long random numbers, N/A corresponds to those tests rendered non applicable due to the requirement of extremely long bit string length $>{10}^6$ as mentioned in Ref. [17].

7 Conclusion

The work we report here serves two primary goals. First and foremost, we describe a new approach to calculate the parameters associated with a confined Brownian motion in a fluid, exploiting the autocorrelation physics of the white noise. A crucial advantage of this method is that it can be implemented “online”, which implies that the parameter can be extracted while recording the data. Any significant fluctuation in the parameter values can be treated as a signature of non-linearity in the system, which precludes the need for further analysis and saves time. Thus, we initially discretize the trajectory of an optically trapped particle into equal-time finite samples, solve the Langevin equation by a finite-difference method, and then construct an inverse problem of parameter extraction by exploiting the temporal delta correlation and flattened nature of the spectral density of the white noise. Thus, we are able to estimate the parameters k (stiffness of the optical trap) and γ (friction constant of the fluid where the particle is immersed) - and use the latter to find out the coefficient of viscosity assuming that the position detection system is pre-calibrated. Our method of parameter estimation is thus virtually immune to electronic noise which is not the case for the other predominantly used methods of calibration such as the Power Spectrum analysis [19] or Equipartition theorem. We observe that the accuracy of the process depends on the number of data points employed, and the entropy of randomness increases with increasing sampling rates. We perform tests for randomness on the extracted time series using the celebrated NIST test suite [22], and observe that our extracted time-series pass all relevant tests at 99% confidence level. Also, since the analysis is solely based on time domain, it has a time complexity of $\sim O\left(N\right)$ for finding out the autocorr vector - and is thus faster than conventional PSD analysis. Most importantly, we demonstrate a new way to extract normally distributed unclonable random variable, which is invaluable to cryptography and financial security.

In summary, our learning algorithm uses “training” a set of incoming data to estimate the trap parameters. These parameters are used in the “test” set to obtain random strings. In future work, we plan to use a similar approach to calibrate the independent parameters of a higher-order AR process, namely Brownian motion in a viscoelastic fluid, which will have non-Markovian features.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

RD designed the protocol and performed the analysis. SG and AK carried out the experiments. RD and AB both wrote the manuscript as well as planned the project. AB supervised the project.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

RD would like to thank SERB, Dept of Science and Technology, Govt. of India, for scholarship support under the INSPIRE scheme. SG and AK would like to thank SERB, Dept of Science and Technology, Govt. of India, for fellowship support under the INSPIRE scheme. The authors acknowledge IISER Kolkata, an autonomous teaching and research institution under the Ministry of Human Resource and Development, Govt. of India. RD and AB thank R. K. Nayak and S. Banerjee of the Department of Physical Sciences at IISER-Kolkata for providing valuable insight during several deep discussions.

Abbreviations

PSD, power spectral density; Autocorr, autocorrelation; ML, machine learning; MSD, mean squared displacement.

References

1. Ross SM, Kelly JJ, Sullivan RJ, Perry WJ, Mercer D, Davis RM, et al. Stochastic processes. Vol. 2. New York: Wiley (1996).

Google Scholar

2. Cinlar E. Introduction to stochastic processes. Courier Corporation (2013).

Google Scholar

3. Steele JM. Stochastic calculus and financial applications. Vol. 45. Springer Science & Business Media (2012).

Google Scholar

4. Bressloff PC. Stochastic processes in cell biology. Vol. 41. Springer (2014).

Google Scholar

5. Volpe G, Volpe G. Simulation of a brownian particle in an optical trap. Am J Phys (2013) 81:224–30. doi:10.1119/1.4772632

CrossRef Full Text | Google Scholar

6. Hu Y, Nualart D. Parameter estimation for fractional ornstein–uhlenbeck processes. Stat Probab Lett (2010) 80:1030–8. doi:10.1016/j.spl.2010.02.018

CrossRef Full Text | Google Scholar

7. Lewis R, Reinsel GC. Prediction of multivariate time series by autoregressive model fitting. J Multivariate Anal (1985) 16:393–411. doi:10.1111/j.1467-9892.1988.tb00452.x

CrossRef Full Text | Google Scholar

8. Fällman E, Schedin S, Jass J, Andersson M, Uhlin BE, Axner O. Optical tweezers based force measurement system for quantitating binding interactions: system design and application for the study of bacterial adhesion. Biosens Bioelectron (2004) 19:1429–37. doi:10.1016/j.bios.2003.12.029

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Keyser U, Van der Does J, Dekker C, Dekker N. Optical tweezers for force measurements on dna in nanopores. Rev Sci Instrum (2006) 77:105105. doi:10.1063/1.2358705

CrossRef Full Text | Google Scholar

10. Kundu A, Paul S, Banerjee S, Banerjee A. Measurement of van der waals force using oscillating optical tweezers. Appl Phys Lett (2019) 115:123701. doi:10.1063/1.5110581

CrossRef Full Text | Google Scholar

11. Bera S, Paul S, Singh R, Ghosh D, Kundu A, Banerjee A, et al. Fast bayesian inference of optical trap stiffness and particle diffusion Sci Rep. (2017) 7:1–10. doi:10.1038/srep41638

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Singh R, Ghosh D, Adhikari R. Fast bayesian inference of the multivariate ornstein-uhlenbeck process. Phys Rev (2018) 98:012136. doi:10.1103/PhysRevE.98.012136

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Theodoridis S. Probability and stochastic processes. In Machine learning: a bayesian and optimization perspective (2015). 9–51.

CrossRef Full Text | Google Scholar

14. Aggarwal T, Salapaka M. Real-time nonlinear correction of back-focal-plane detection in optical tweezers. Rev Sci Instrum (2010) 81:123105. doi:10.1063/1.3520463

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Hart JD, Terashima Y, Uchida A, Baumgartner GB, Murphy TE, Roy R. Recommendations and illustrations for the evaluation of photonic random number generators. APL Photonics (2017) 2:090901. doi:10.1063/1.5000056

CrossRef Full Text | Google Scholar

16. Keller C, Gürkaynak F, Kaeslin H, Felber N. Dynamic memory-based physically unclonable function for the generation of unique identifiers and true random numbers. In: 2014 IEEE international symposium on circuits and systems (ISCAS); 2014 June 1–5; Melbourne, Australia. IEEE (2014). p. 2740–3.

Google Scholar

17. Hu Z, Comeras JM, Park H, Tang J, Afzali A, Tulevski GS, et al. Physically unclonable cryptographic primitives using self-assembled carbon nanotubes Nat Nanotechnol (2016) 11:559. doi:10.1038/nnano.2016.1

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Jeffreys H. The theory of probability. OUP Oxford (1998).

Google Scholar

19. Berg-Sørensen K, Flyvbjerg H. Power spectrum analysis for optical tweezers. Rev Sci Instrum (2004) 75:594–612. doi:10.1063/1.1645654

CrossRef Full Text | Google Scholar

20. Neuman KC, Block SM. Optical trapping. Rev Sci Instrum (2004) 75:2787–809. doi:10.1063/1.1785844

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Doob JL. The brownian movement and stochastic equations. Ann Math (1942) 351–69. doi:10.2307/1968873

CrossRef Full Text | Google Scholar

22. Rukhin A, Soto J, Nechvatal J, Smid M, Barker E, Leigh S. A statistical test suite for random and pseudorandom number generators for cryptographic applications va Tech. rep. Booz-allen and hamilton inc mclean (2001).

Google Scholar

23. Wiener N. Extrapolation, interpolation, and smoothing of stationary time series. The MIT press (1964).

Google Scholar

24. Gavrilov M, Jun Y, Bechhoefer J. Real-time calibration of a feedback trap. Rev Sci Instrum (2014) 85:095102. doi:10.1063/1.4894383

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Jun Y, Gavrilov M, Bechhoefer J. High-precision test of Landauer's principle in a feedback trap. Phys Rev Lett (2014) 113:190601. doi:10.1103/PhysRevLett.113.190601

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Martínez IA, Roldán É, Dinis L, Petrov D, Parrondo JMR, Rica RA. Brownian carnot engine. Nat Phys (2016) 12:67–70. doi:10.1038/NPHYS3518

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Blickle V, Bechinger C. Realization of a micrometre-sized stochastic heat engine. Nat Phys (2012) 8:143–6. doi:10.1038/nphys2163

CrossRef Full Text | Google Scholar

28. Pal SB, Haldar A, Roy B, Banerjee A. Measurement of probe displacement to the thermal resolution limit in photonic force microscopy using a miniature quadrant photodetector. Rev Sci Instrum (2012) 83:023108. doi:10.1063/1.3685616

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Shumway RH, Stoffer DS. Time series analysis and its applications: with R examples. Springer (2017).

CrossRef Full Text | Google Scholar

30. Li T, Raizen MG. Brownian motion at short time scales. Ann Phys (2013) 525:281–95. doi:10.1002/andp.201200232

CrossRef Full Text | Google Scholar

31. Grimm M, Franosch T, Jeney S. High-resolution detection of brownian motion for quantitative optical tweezers experiments. Phys Rev E Stat Nonlinear Soft Matter Phys (2012) 86:021912. doi:10.1103/PhysRevE.86.021912

CrossRef Full Text | Google Scholar

32. Stasev YV, Kuznetsov A, Nosik A. Formation of pseudorandom sequences with improved autocorrelation properties. Cybern Syst Anal (2007) 43:1–11. doi:10.1007/s10559-007-0021-2

CrossRef Full Text | Google Scholar

33. Simpson H. Statistical properties of a class of pseudorandom sequences. Proc Inst Electr Eng (1966) 113:2075–80. doi:10.1049/piee.1966.0361

CrossRef Full Text | Google Scholar

34. Peterman EJ, Gittes F, Schmidt CF. Laser-induced heating in optical traps. Biophys J (2003) 84:1308–16. doi:10.1016/S0006-3495(03)74946-7

PubMed Abstract | CrossRef Full Text | Google Scholar