Diverse Properties of Carbon-Substituted Silicenes

The theoretical framework, which is built from the first-principles results, is successfully developed for investigating emergent two-dimensional materials, as it is clearly illustrated by carbon substitution in silicene. By the delicate VASP calculations and analyses, the multi-orbital hybridizations are thoroughly identified from the optimal honeycomb lattices, the atom-dominated energy spectra, the spatial charge density distributions, and the atom and orbital-decomposed van Hove singularities, being very sensitive to the concentration and arrangements of guest atoms. All the binary two-dimensional silicon-carbon compounds belong to the finite- or zero-gap semiconductors, corresponding to the thoroughly/strongly/slightly modified Dirac-cone structures near the Fermi level. Additionally, there are frequent π and σ band crossings, but less anti-crossing behaviors. Apparently, our results indicate the well-defined π and σ bondings.

1. Introduction

Chemical substitutions on layered materials are capable of band structure tailoring which could lead to significant modifications of the properties of pristine lattices through very strong host-guest multi-orbital hybridizations. With the use of modern experimental growth techniques, ternary and binary compounds, which are characterized by B_xC_yN_z, have been successfully synthesized for three-dimensional (3D) bulk systems [12], two-dimensional (2D) layers [3], one-dimensional (1D) cylindrical nanotubes [4], 1D nanoribbons [5], and zero-dimensional (0D) quantum dots [6]. Their geometric structures vary from three to zero dimensions, as observed in carbon-related systems [78]. This clearly indicates that each atom possesses at least three half-filled orbitals. Similar syntheses have been performed for the high-potential C-Si compounds [9]. In general, it would be routine to produce the above-mentioned compounds, whereas the opposite might be true for specific components. For example, using high-performance experimental techniques, it may be difficult to manipulate the ratio between the C/Si atoms. Such non-monoelement condensed-matter systems have been predicted or found to exhibit the observable energy gaps or belong to specific semiconductors. The main reason lies in the distinct ionization energies of their components, being consistent with the tight-binding model for non-vanishing diagonal Hamiltonian matrix elements (the sublattice-dependent site energies). Gap engineering could be achieved by transforming the strengthful relations in the π, σ, and sp³ bondings the [p_z-, (s, p_x, p_y)-, and (s, p_x, p_y, p_z)-orbital hybridizations].

Chemisorption and substitution of carbon atoms on silicene are two very interesting procedures, since first-principles predictions are available for understanding the important differences between these two types of chemical modification [1011], and providing additional information regarding another approach for the formation of silicon-carbide compounds [12] or induce magnetism based on transition-metals are embedded in silicene [13]. Based on the viewpoint of a silicon-created honeycomb lattice, carbon atoms are regarded as adatoms and guest ones, respectively. Both silicon and carbon atoms have rather active dangling bonds, leadings to significant multi-orbital hybridizations in Si-C [Si-Si and C-C] bonds. Most importantly, the planar bondings between Si and C atoms are expected to be stronger and complicated, compared with the perpendicular configuration. That is to say, the π and σ bondings of silicene will be significantly modified by C-substitutions. This is directly reflected in the diversified properties, the spatial charge distributions, atom-dominated energy bands, and atom-as well as orbital-projected density-of-states.

The present work is focused on the diverse geometric, and electronic properties of C-substituted silicene. A theoretical framework, which is based on multi-orbital hybridizations, is further developed to clearly analyze the concentration- and configuration-dependent phenomena. For example, the zero- and finite-gap behaviors, the main features of π and σ bands could be understood from the specific relations among the hybridized π, σ, and sp³ chemical bondings. On the experimental side, a controllable synthesis way, using MTMS/hexane as precursors, is proposed to generate the large-area graphene-based Si-C binary 2D compounds [14]. Furthermore, the silicon-carbide nanosheets are successfully synthesized by a catalyst-free carbothermal method and post-sonication process [15], in which the AFM measurements show the average thickness of ∼2–3 nm and size of ∼2 μm.

2. Computational Details

Our investigation of the diverse properties of carbon-substituted silicene is based on density functional theory using VASP codes [16, 17]. The exchange and correlation energies due to many-particle Coulomb interactions were calculated with the use of the Perdew-Burke-Ernzerhof (PBE) functional under the generalized gradient approximation [18], whereas the electron-ion interactions can be characterized by the projector augmented wave (PAW) pseudopotentials [19]. A plane-wave basis set with a maximum kinetic energy cutoff of 500 eV was chosen to expand the wave function. In a direction perpendicular to the silicene plane, a vacuum layer with a thickness of 15 Å was added to avoid interactions between adjacent unit cells. The k-point mesh was set as 9 × 9 × 1 in geometry optimization, 100 × 100 × 1 for further calculations on electronic properties via the Monkhorst-Pack scheme. During the ionic relaxations, the maximum Hellmann-Feynman force acting on each atom is less than 0.01 eV/whereas the convergent energy scale was chosen as 10⁻⁵ eV between two consecutive steps.

3. Results and Discussions

3.1. Geometric Structures

Carbon-substituted silicon systems are capable of possessing unusual geometries, as it is clearly indicated in Table 1 and Figures 1A–L. Four types of typical C-substitution configurations, which cover meta, ortho, para, and single cases, are chosen for a model investigation. In general, the third and fourth types, respectively, possess the lowest and highest ground state energies, i.e., the para-configuration is the most stable among them, or it is expected to be relatively easily synthesized in experimental growths. Moreover, the percentage is considered as a measure of the concentration of the ratio between the guest and host atoms are determined by the following formula: n_C/(n_tot − n_C), where n_C, n_Si, and n_tot = n_C + n_Si are the numbers of carbon, silicon, and total atom, respectively, in the unit cell.

TABLE I

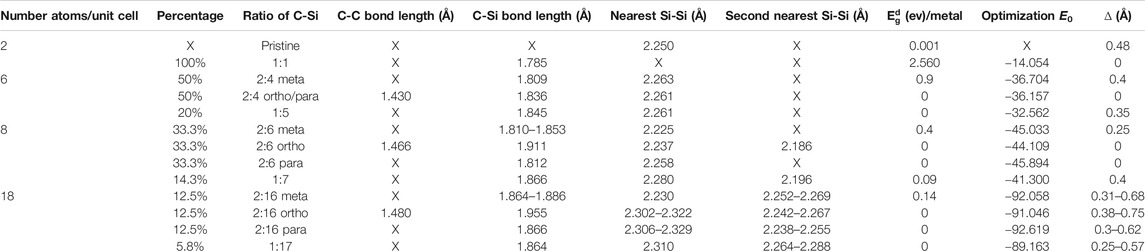
TABLE I. The optimal geometric structures of carbon-substituted silicene systems under various concentrations and configurations with the C-C, C-Si and Si-Si bond lengths, the band gaps, ground state energies per unit cell, together with the height differences between A and B sublattices.

FIGURE 1

FIGURE 1. The top and side views optimal geometric structures for C-substituted silicene systems; the (A) pristine, (B) full-, (C) 50%-meta-, (D) 50%-ortho-/para-, (E) 33.3%-meta, (F) 33%-ortho, (G) 3.3%-para-, (H) 12.5%-meta-, (I) 12.5%-ortho-, (J) 12.5%-para-, (K) 14.3%-single-, and (L) 5.8%-single-substitution cases. Also the red parallelogram/rhombus represent the unit cell.

Carbon and silicon atoms, respectively, possess four outer orbitals of [2p_x, 2p_y, 2p_z, 2s] and [3p_x, 3p_y, 3p_z, 3s]. Besides the pristine ones, the substitutions of carbon on silicene, as clearly illustrated in Figures 3A–L, will create the hybridized π and σ bondings [2p_z-3p_z and (2s, 2p_x, 2p_y)-(3s, 3p_x, 3p_y)] in silicene honeycomb lattice (the standard orbital hybridizations in Figures 2A). This seems to be responsible for the extremely non-uniform chemical/physical environments in an enlarged unit cell. Consequently, the Si-Si/Si-C bond lengths and the height difference between A and B sublattices might lie in specific ranges (Table 1). Specifically, the full C-substitution case, with the only uniform environment, is clearly different from the pristine one, since they, respectively, have the planar and buckled honeycomb lattices [Figures 1A,B; ∆ = 0∼0.48°Å]. When the C-concentration is sufficiently low, the buckled structures will recover, such as the C:Si ratio lower than 15%. For the other conditions, the existence of buckling strongly depends on the concentration and configuration of the substitution.

FIGURE 2

FIGURE 2. Brillouin zone folding for silicene systems.

In addition, the spin-dependent interactions are included in the numerical evaluations to see whether the magnetic configurations play an important role in the essential properties. However, the C- and Si-dependent spin configurations/interactions are fully suppressed by the very strong and complicated chemical bondings. That is to say, the spin-induced magnetic configuration is absent in any C-substituted silicene.

3.2. Band Structure Tailoring of Carbon-Substituted Silicene Systems

Apparently, the concentrations and configurations of carbon guest atoms play a crucial role in the diverse electronic properties. Figure 2 shows the Brillouin zone scheme for many unit cells in which all the electronic states are plotted along Γ-K-M-Γ paths. In pristine monolayer silicene, the specific relations among the π, σ, and sp³ bondings account for the main features of the band structure. The electron-hole symmetry around the Fermi level is only weakly modified at low energy, as illustrated in Figure 3A. The first pair of valence and conduction bands. being nearest to E_F = 0, are initiated from the stable K/K′ valley. A very narrow band gap of E_F ∼ 0.01 meV comes to exist between slightly separated Dirac cones, mainly due to the weak spin-orbital coupling (a single-particle interaction). This result is consistent with that obtained using the tight-binding model [20]. Additionally, they show the valence/conduction saddle M-point structure at −1.02/0.59 eV. Finally, the π band is ended at the stable Γ valley, in which the π-band energy width for valence states, the energy spacing between the initial K point and the final Γ point is about 3.2 eV. Apparently, such an electronic spectrum originates from the π bonding of pure 3p_z-3p_z orbital hybridizations in the buckled honeycomb lattice. On the other hand, the four-fold degenerate σ bands, which arise mainly from [3p_x, 3p_y]-orbital bondings, obey parabolic energy dispersion relations from the stable Γ valley at E^v ∼ −1.04 eV. The σ and π valence bands have the obvious or observable mixing behavior along the ΓK and ΓM directions since there exists a weak, but significant sp³ bonding. Additionally, the bandwidth of the first σ-electronic states along ΓMK is about 3.45 eV. Generally, all π- and σ-bands (three-band) widths could be well defined for monolayer silicene. In addition, all k-states in the energy bands are doubly degenerate in terms of the spin degree of freedom, since the spin-up- and spin-down-dominated states have identical energy spectra.

FIGURE 3

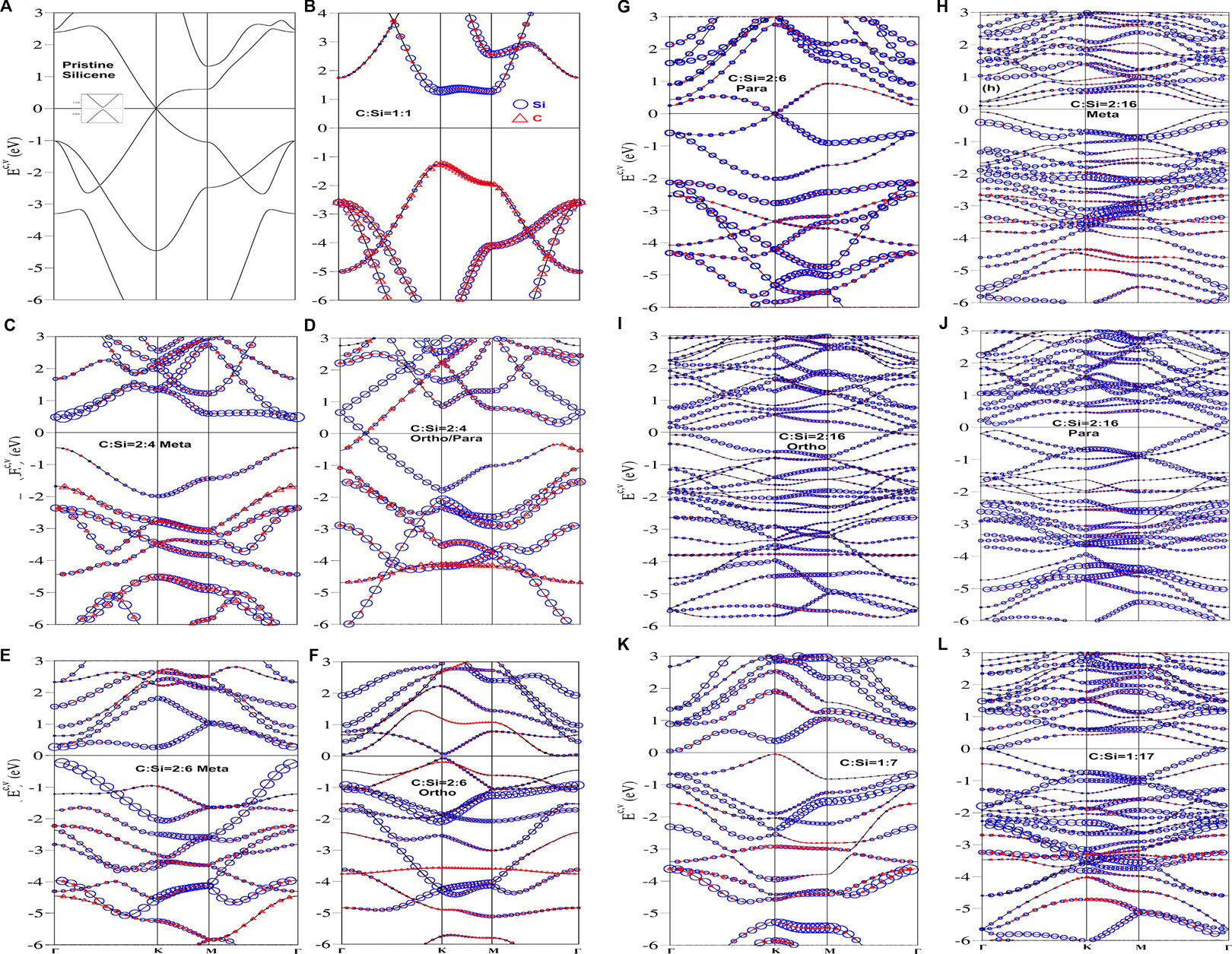
FIGURE 3. Electronic structures, with the dominance of silicon and carbon atoms (the blue circles and red triangle ones), for the C-substituted silicene systems; the (A) pristine, (B) [1:1]-, (C) [2:4]-meta-, (D) [2:4]-ortho-/para-, (E) [2:6]-meta-, (F) [2; 6]-ortho-, (G) [2:6]-para-, (H) [2:16]-meta-, (I) [2:16]-ortho-, (J) [2:16]-para-, (K) [1:7]-single-, (L) [1:17]-single substitution configurations.

The full carbon-substitution silicene system, i.e., the silicon-carbon binary compound [21], exhibits an unusual electronic energy spectrum as shown in Figure 3B, is totally different from the pristine case (Figure 3A). The occupied valence bands are highly asymmetric to the unoccupied conduction bands near E_F = 0. Such material is classified as a direct-gap insulator with a band gap larger than 2.56 eV at the K/K′ point, as observed in a wide-gap monolayer boron-nitride system [22]. This is closely related to the strongly modified Dirac-cone structure across the Fermi level with highly anisotropic energy dispersions (e.g., the partially flat conduction band along KM). Both valence and conduction bands nearest to E_F are, respectively, π and π^* bands due to the 2p_z-3p_z impure orbital hybridizations in Si-C bonds. The higher/lower ionization energy of 2p_z/3p_z orbitals further leads to the creation of a band gap for the honeycomb lattice, and the C-/Si-dominance of the π/π^* bands (the red and blue circles). The first pair of energy bands are highly anisotropic. For example, the valence/conduction π/π^* states, which are initiated from the K valley, show different group velocities along the KM and KΓ directions, especially for the saddle point/the partially flat dispersion related to the M point. Furthermore, the π-band energy width is (E_w = 3.71 eV) according to the difference between the K- and Γ-point energies (−1.50 and −5.20 eV). Compared with a pristine 3p_z-3p_z case (E_w ∼ 3.20 eV in Figure 3A), the larger bandwidth might indicate the stronger 2p_z-3p_z bonding. The two σ bands, which arise from [3p_x, 3p_y]-[2p_x, 2p_y] hybridizations, appear at E_v ∼ −2.60 eV initiated from the Γ point, but remain fourfold degenerate electronic states there. Furthermore, the contributions from the different orbitals are comparable in the [C,Si]-co-dominated energy bands. The concave-downward parabolic valley near the Γ point is dramatically transformed into concave-upward ones/the saddle-point forms along the ΓK/ΓM direction. Consequently, the first σ-bandwidth is approximately 4.30 eV. There exist direct crossings of the π and σ valence bands along any direction, e.g., MΓ and KΓ. This result clearly reveals no evidence of sp³ bonding [25]. As a result, the fundamental properties of the [1:1] Si-C compound are dominated by the well-behaved π and σ bondings in the absence of sp³ ones.

Electronic energy spectra are greatly enriched through the modulations of concentration and distribution configuration. The [2:4]-meta and [2:4]-ortho/para cases, as clearly displayed in Figures 3C,D, present finite- and zero-gap behaviors, respectively, corresponding to the highest occupied state and lowest one at the Γ point (E_g ∼ 0.90 eV) and the gapless Dirac-cone structure along the ΓK or ΓM direction. That the low-lying valence and conduction bands are initiated from the stable K and Γ valleys are associated with the zone-folding effect. According to the pristine and full-substitution configurations (Figures 3A,B), the valence and conduction bands in the energy range of |E^c,v < 1.30| eV, including the first pair, mainly arise from the [2p_z, 3p_z]-orbital hybridizations. Such bondings are responsible for the low-energy physical properties. This result is also confirmed by the orbital-projected density-of-states (discussed later in Figure 5B). It should be noted that the latter (Figure 5D) belongs to a zero-gap semiconductor because of the vanishing density of states at the Fermi level. The low-lying energy bands are dominated by the 3p_z orbitals of silicon-host atoms because of the higher weight. More energy subbands come to exist under the enlarged unit cells. Therefore, the band crossings and anti-crossings would happen frequently. In addition, it might be able to define the π-band energy widths through the ΓK → KM → MΓ direction (examinations from the 3p_z-projected density-of-states in Figures 5C,D), respectively, corresponding to 4.01 and 4.70 eV for the meta- and ortho-configurations. It would be very difficult or even meaningless, in characterizing bandwidths with a further decrease of guest-atom concentration, as a result of more complicated valence subbands. Concerning the first σ valence bands, they are roughly identified from the initial Γ-states at E^v ∼ −1.80 eV for the meta-case (Figure 3C), while the very strong zone-folding effects forbid their characterizations under the ortho-condition (Figure 3D).

Very interestingly, two kinds of band properties are also revealed in the [2:6] cases, as clearly indicated in Figures 3E–G. The meta-, ortho- and para-configurations, respectively, exhibit the small-, narrow- and zero-gap behaviors (the finite- and zero-gap semiconductors) according to the first pair of energy bands nearest to the Fermi level. The first case has an indirect band gap of E_g ∼ 0.31 eV, which is determined by the specific energy spacing between the highest occupied state at the K point and the lowest unoccupied state at the Γ point (Figure 3E). Furthermore, the first valence band has an oscillatory energy dispersion. As a result, two stable valleys dominate low-energy physical phenomena simultaneously. The significant overlaps of valence and conduction bands, which come to exist along any wave vector direction, appear under the second configuration in Figure 3F. There are five/three energy subbands, with weak oscillatory dispersion relations near the Γ point/the K and M points. They are responsible for the formation of partially flat bands and thus the high density-of-states near the Fermi level (discussed later in Figure 5F). The third case in 2:6 configurations (Figure 3G) shows a gapless Dirac cone structure at the K/K′ valley only with a single Fermi momentum state (a zero density-of-states at E_F in Figure 5G). There are more finite energy spacings between valence and conduction subbands at the Γ valley. For any guest-atom configurations, most electronic energy spectra are dominated by the silicon atoms, while the opposite is true for the carbon atoms.

Clearly, there appear more complex electronic energy spectra when the guest-atom concentrations are decreased (under the reduced/enhanced number of Si-C and C-C/Si-Si bonds). Typically, three sorts of distribution configurations are revealed under the specific [2:16] condition, the meta-, ortho-, and para-ones in Figures 3H–J. Their low-lying band structures exhibit strongly modified Dirac cones, respectively, with a direct gap of E_g ∼ 0.14 eV due to parabolic valence and conduction dispersion relations near the Γ valley, the gapless and crossing structure (the finite energy spacing) along the ΓM direction (the ΓK direction), and similar zero-gap behavior. Additionally, the single [1:7] substitution in Figure 3I creates an E_g ∼ 0.09 eV indirect band gap associated with the valence K state and conduction Γ state. It should be emphasized that the second and third electronic structures only belong to zero-gap semiconductors (the vanishing density-of-states at E_F in Figures 5I,J). The Moiré superlattices have created a substantial number of energy subbands within a smaller first Brillouin zone, leading to frequent band crossings and anti-crossings. As a consequence, it is very difficult to characterize the π-bandwidth (similarly for the σ bandwidths). However, the orbital-projected density ofstates might be useful in examining the relationship among the π, σ, and sp³ bondings. Interestingly, C-substituted silicene will gradually recover to the pristine case (Figure 3A) at very low guest-atom concentrations, e.g., the appearance of an almost gapless Dirac cone under the [1:17] case in Figure 3I. In summary, the energy subbands, with |E^c,v < 1.5| eV, are dominated by the [2p_z, 3p_z] orbital hybridization, and the other deeper-/higher-energy electronic states might be closely related to the [2p_x, 2p_y, 2s, 3p_x, 3p_y 3s] or eight orbitals in Si and C atoms. The carbon substitutions in silicene can only induce the modified Dirac cone structures, but not free carriers (the n- or p-type dopings).

3.3. Spatial Charge Density Distributions

The spatial charge density distributions are able to provide certain observable evidences regarding the existence of the impure/pure π and σ chemical bondings as well as their non-orthogonalities or orthogonalities. Pristine 2D silicene, as clearly displayed in Figure 4A with the [x,z]- and [x,y]-plane projections, shows the well-defined 3p_z-3p_z and [3s, 3p_x, 3p_y]-[3s, 3p_x, 3p_y] orbital hybridizations, especially for the latter. In our notation, ρ is a symmetric distribution around the Si-Si bond center. Most of the charge density is accumulated between two silicon atoms (the red region), corresponding to the very strong σ bonding of three orbitals. The neighboring Si-atoms are also attracted together through the parallel 3p_z orbitals perpendicular to the [x,y] plane, in which the π bonding appears in the outer region shown by the light green/blue color.

FIGURE 4

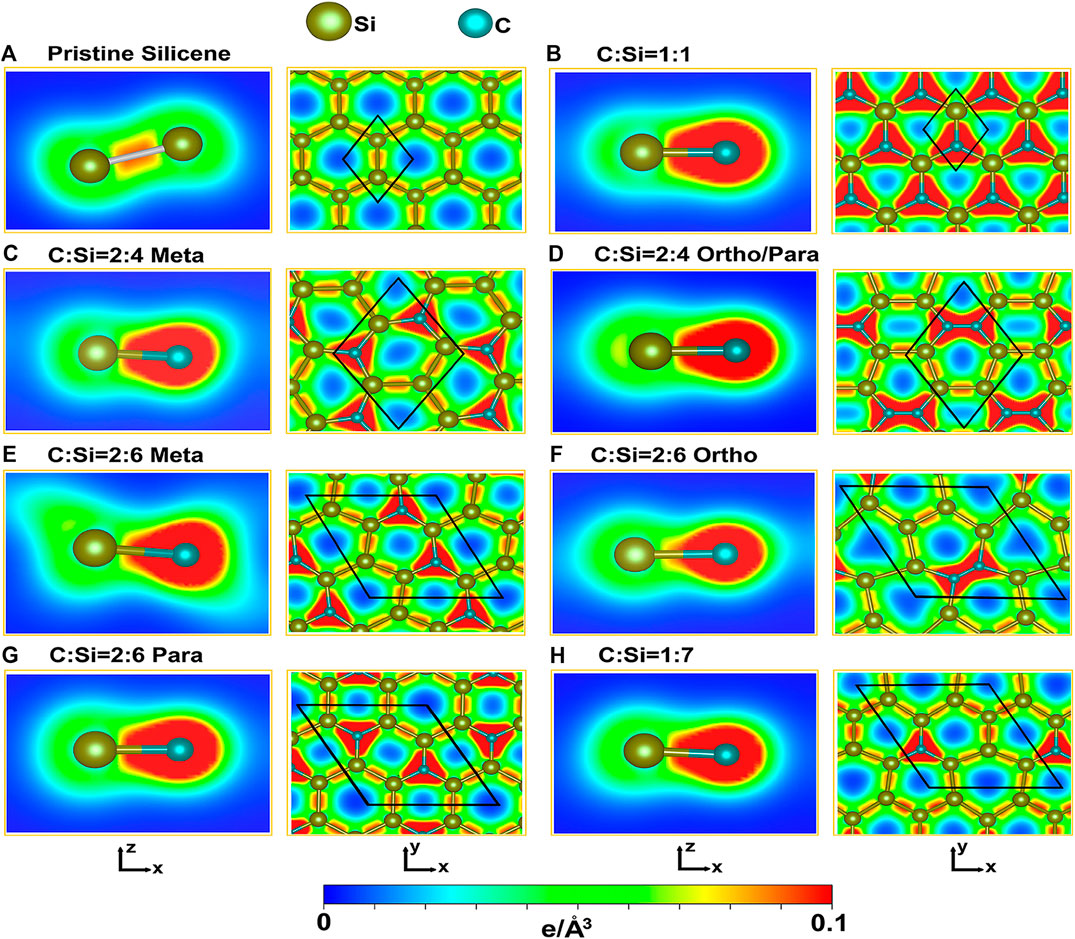
FIGURE 4. The spatial charge densities of the carbon-substituted silicene materials for the various concentrations and configurations: (A) the absence of guest atoms, (B) [1:1], (C) [2:4]-meta, (D) [2:4]-ortho-/para, (E) [2:6]-meta, (F) [2; 6]-ortho, (G) [2:6]-para, and (H) [1:7] conditions. They are shown on the [x,z] and [x,y] planes, clearly illustrating the π and σ chemical bondings and their orthogonality/non-orthogonality. The unit cells are represented by the black parallelogram/rhombus.

As a result of buckling, they have the weak, but significant sp³ hybridizations under the non-orthogonality of π and σ chemical bondings. When the Si-Si bonds become Si-C ones under full substitution, ρ presents a dramatic transformation, is clearly illustrated in Figure 4B. The charge density is highly asymmetric with respect to the C-Si bond center, mainly owing to the different electron affinities of the guest and host atoms. There exist more carriers around the guest C-atoms (the red region); that is, electrons are transferred from silicon to carbon atoms. The whole C-Si bonds consist of a planar honeycomb lattice with a stronger σ bonding, compared with those of a pristine one (Figure 4A). The σ and π bondings could be roughly defined under the impure 2p_z-3p_z and [2s, 2p_x, 2p_y]-[3s, 3p_x, 3p_y] orbital hybridizations, respectively. They are directly reflected in the π- and σ-electronic valence subbands, with direct crossings (Figure 3B). Most importantly, two kinds of chemical bondings are orthogonal to each other. Therefore, the sp³ orbital hybridizations are negligible in the [1:1] case. Each Si-C bond has an identical chemical environment, i. e., only one chemical bond in a unit cell. This clearly illustrates that it is relatively easy to simulate the first-principles band structure using the tight-binding model [24].

When the carbon concentrations are decreased (Figures 4C–H), the existence of π and σ chemical bondings is relatively easily examined from the spatial charge densities. There exist C-Si, Si-Si, and even C-C bonds, for which the last ones are stable under the specific ortho cases (Table 1). The almost symmetric carrier distributions are clearly revealed between two silicon atoms for any concentration and configuration, in which they possess the lowest charge density among three kinds of chemical bonds. Similar phenomena appear for C-C bonds with the highest carrier densities, e.g., ρ values in Figures 4D,F at [2:4] and [2:6] ortho conditions, respectively. Roughly speaking, the spatial charge densities in different chemical bonds are not sensitive to changes in various carbon substitutions. These further illustrates that the σ and π chemical bondings might be well separated from each other. Therefore, they could be roughly defined in the carbon-substituted silicene systems. As a result, the fundamental low-energy properties are expected to be dominated by the π-electronic states due to the modified Dirac cone structures. On the other hand, the different chemical bonds lead to complex orbital hybridizations and thus contribute to the difficulties in obtaining suitable phenomenological models. When the first principles electronic energy spectra along the high-symmetry paths are successfully simulated by the tight-binding model with the non-uniform and multi-/single-orbital hopping integrals [25], the diversified essential properties could be fully explored in the near future, e.g., the rich and unique magnetic quantization phenomena [23], as predicted/observed in layered graphene systems [26].

3.4. Density of States

There are four/five categories of van Hove singularities in carbon-substituted silicene systems or pristine one, as clearly illustrated in Figures 5A–F. The orbital- and atom-decomposed density-of-states are very useful in fully understanding the bonding-induced special structures. The critical points, i.e., the band-edge states, in the energy-wave vector space include the linear Dirac cone structure, local minima or maxima of parabolic energy dispersion, saddle points, constant energy loops, which are closely related to band anticrossings, and partially flat bands (Figures 3A–L). Their densities-of-states generate the V-shape form, discontinuous shoulders, logarithmic divergent peaks, asymmetric peaks in the square root divergence, and delta-function-like peaks, respectively. A pure monolayer silicene in Figure 5A displays an almost linear E-dependence across the Fermi energy with a vanishing density-of-states (a quasi-V shape in the range −0.5 eV ≤ E ≤ 0.5 eV; the purple curve of 3p_z orbitals), a logarithmic symmetric π-peak/π*-peak at −1.02/0.59 eV, the [π, σ]-mixing created square root asymmetric peaks at (−2.20, −2.65, −3.15 eV). The red, green and blue curves of (3p_x, 3p_x, 3p_y) orbitals, the Γ-valley π shoulder at −3.20 eV, the initial σ-[3p_x, 3p_y] shoulder at −1.03 eV at the Γ point, their M saddle point symmetric peak at −2.47 eV and the K valley shoulder at −4.40 eV. Consequently, the π and σ bandwidths are −3.15 and 3.36 eV, respectively. It should be noted that the 3s orbitals (the red curve) are frequently accompanied by [3p_x, 3p_y] ones, but their contributions become significant at the deeper/higher energies, e.g., density-of-states within E < −3.0 eV. The above mentioned features of van Hove singularities further illustrate the well behaved π and σ chemical bondings and their weak, but important hybridization.

FIGURE 5

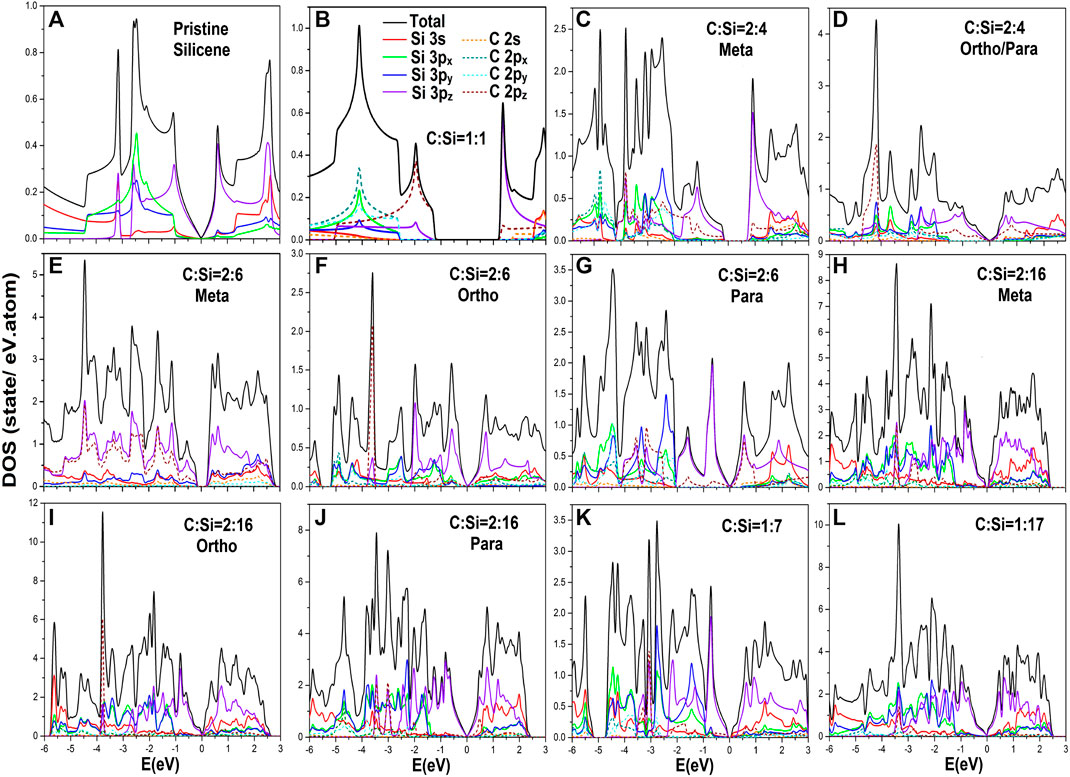
FIGURE 5. The various van Hove singularities in atom- and orbital-decomposed density-of-states for carbon-substituted silicene systems under the various cases: (A) pristine, (B) [1:1]-, (C) [2:4]-meta-, (D) [2:4]-ortho-/para-, (E) [2:6]-meta-, (F) [2:6]-ortho-, (G) [2:6]-para-, (H) [2:16]-meta-, (I) [2:16]-ortho-, (J) [2:16]-para-, (K) [1:7]-single-, and (L) [1:17]-single-configurations.

The structural features, energy and number of van Hove singularities exhibit a dramatic transformation under full carbon substitution, as indicated in Figure 5B. The special structures cover vanishing density-of-states within a band gap of E_g ∼ 2.56 eV at the K/K′ valley, the initial π shoulder/delta function-like π peak at −1.26/1.26 eV (also shows the low-lying π and π* bands in Figure 3B), the −1.95 eV symmetric π peak in the logarithmic divergence, the final π shoulder at −5.00 eV, the first σ shoulder at −2.75 eV, the −4.10 eV logarithmic peak, and the second discontinuous structure at −7.01 eV. We also, observe that the first valence/conduction structure is dominated by the C-2p_z orbitals/Si-3p_z ones due to an obvious difference of ionization energy. The widths of the π and first σ bands are −3.74 and 4.26 eV, respectively. Additionally, there is no evidence of π-σ band mixing. This is mainly due to the absence of the simultaneous four-orbital structures. The fact that the sp³ bonding is absent agrees with the direct π-σ subband crossings (Figure 3B).

Within the whole energy range, the van Hove singularities become more complex during the decrease of guest-C-atom concentration, as a result of zone-folding effects as well as the significant [3s, 3p_x, 3p_y, 3p_z]-[2s, 2p_x, 2p_y, 2p_z] multi-orbital hybridizations. For example, the [2:4]-meta and [2:4]-ortho configurations, as clearly illustrated in Figures 5C,D, exhibit diverse low-energy van Hove singularities arising from the dominant 3p_z-2p_z chemical bonding. The former has a π-electronic zero density-of-states in the 0.90 eV-gap region (the Γ valley in Figure 3C), a threshold valence shoulder at −0.45 eV (the first composite conduction state structure due to the discontinuous shoulder and delta function-like peak at 0.45 eV)–, a strong logarithmic peak at −1.41 eV, as well as the second and third step structures at −1.69 and −2.71 eV, respectively. Regarding the latter, the 3p_z-2p_z-diversified van Hove singularities show a gapless V-shape (a Dirac cone energy spectrum in Figure 3D), the first valence shoulder at −0.5 eV (the initial conduction shoulder at 0.30 eV), the logarithm-step composite structure at −1.01 eV, the symmetric peak arising from two opposite shoulders at −1.32 eV, a similar one at −2.10 eV, and the −2.65 eV asymmetric peak in the square root form. The widths of the π-band in the former and latter cases are estimated to be −4.05 and 4.70 eV, respectively. Furthermore, the first σ-bands are wider than 4.5 eV. Obviously, the low-energy physical phenomena are dominated by the 3p_z orbitals of Si-host atoms.

As the guest-atom concentration is declined, there appear additional van Hove singularities. Overall, in this way, one is able to characterize the width of the π-band from the effective distributions of the [3p_z, 2p_z] orbitals for any concentration and configuration (Figures 5A–L). However, the opposite is true for the first σ-band width except for full substitution and the pristine cases (Figures 5A,B). Certain van Hove singularities, close to the Fermi level, are very useful to comprehend the band-edge states in the first pair of the valence and conduction bands. The main features cover the vanishing density-of-states at/across the Fermi level (Figures 5C through E)/(Figures 5D through G), the electron-hole asymmetry near the first pair of clearly identifiable shoulders, the prominent π peak in logarithmic form, the second and third shoulders and so on. Finally, the dip structure at E_F, with a very small gap comparable to the broadening factor, will come to exist for a sufficiently low concentration, e.g., the almost gapless behavior in the [1:17] case (Figure 5L). We also noticed that the single-particle interactions of spin-orbital couplings cannot create any significant effects on the electronic properties and thus the other essential properties.

4. Concluding Remarks

The geometric and electronic properties of carbon-substituted silicene are investigated using DFT calculations. The systems present unusual geometric properties, which are directly reflected in the spatial charge distributions. At high carbon-concentrations, the planar structure clearly indicates a very small variation in the sigma bonding of C-[2s, 2p_x, 2p_y] orbitals. Therefore, they hardly take part in Si-C bonds and lead the C-C bond lengths in substitution cases to remain almost unchanged. The above mentioned important results directly reveal critical mechanisms, i.e., the multi-orbital hybridizations of sp³-p in Si-C bonds, sp³-sp³ in Si-Si bonds, and sp²-sp²/π in C-C bonds.

All substitution results in semiconducting behavior with a finite or zero band gap in which the Dirac cone structure presents a deviation from the Γ point, a strong distortion, or even destruction. The number of valence and conduction energy subbands remains the same after chemical substitutions. Furthermore, they are co-dominated by the C-guest and Si-host atoms. High-resolution ARPES measurements are very useful in verifying the low-lying valence bands near/crossing the Fermi level along ΓK and ΓM path and the rigid sigma bands initiated from the Γ valley.

Several unusual van Hove singularities in the atom and orbital decomposed density-of-states are created under the C-guest-atom chemical substitution. The strong bonding evidence is totally destroyed by substitutions except for the very diluted Si-adatoms. They are replaced by a finite density of states at E_F = 0, many shoulders, and peak structures. Furthermore, they are co-dominated by the four Si-[3s, 3p_x, 3p_y, 3p_z] orbitals and the single C-2p_z orbital, since their contributions are merged together. The above-mentioned significant features further support and illustrate the sp³-sp³ and sp²-sp² multi-orbital hybridizations in Si-C bonds and C-C bonds, respectively. The predicted van Hove singularities could be verified by the high-resolution STS experiments [27].

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

HP: collected the data, performed the analysis, wrote the paper. SL: contributed data or analysis tools. GG: performed the analysis, wrote the paper (checking English grammar). NK: contributed data or analysis tools. ML: methodology, checked and evaluated results, wrote the paper.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Funding

This work was financially supported by the Hierarchical Green-Energy Materials (Hi-GEM) Research Center, from The Featured Areas Research Center Program within the framework of the Higher Education Sprout Project by the Ministry of Education (MOE) and the Ministry of Science and Technology (MOST 108-3017-F-006 -003) in Taiwan.

Acknowledgments

This first version manuscript has been released as a pre-print at (http://export.arxiv.org/pdf/1912.00334) (Hai Duong Pham et al.).

References

1. Terrones M, Grobert N, Terrones H. Synthetic routes to nanoscale BxCyNz architectures. Carbon (2002). 40(10):1665–84. doi:10.1016/s0008-6223(02)00008-8

CrossRef Full Text | Google Scholar

2. Deng X, Kousaka H, Tokoroyama T, Umehara N. Deposition and tribological behaviors of ternary BCN coatings at elevated temperatures. Surf Coat Technol (2014). 259:2–6. doi:10.1016/j.surfcoat.2014.08.087

CrossRef Full Text | Google Scholar

3. Prakash A, Sundaram KB, Campiglia AD. Photoluminescence studies on BCN thin films synthesized by RF magnetron sputtering. Mater Lett (2016). 183:355–8. doi:10.1016/j.matlet.2016.07.140

CrossRef Full Text | Google Scholar

4. Terrones M, Benito AM, Manteca-Diego C, Hsu WK, Osman OI, Hare JP, et al. Pyrolytically grown BxCyNz nanomaterials: nanofibres and nanotubes. Chem Phys Lett (1996). 257:576–82. doi:10.1016/0009-2614(96)00594-5

Google Scholar

5. Erickson KJ, Sinitskii A, Alexander M, Rousseas N, Tour JM, Zettl AK, et al. Longitudinal splitting of boron nitride nanotubes for the facile synthesis of high quality boron nitride nanoribbons. Nano Lett (2011). 11(8):3221–6. doi:10.1021/nl2014857

CrossRef Full Text | Google Scholar

6. Zhang K, Zhang Z-Y, Liang R-P, Qiu J-D. Boron-doped graphene quantum dots for selective glucose sensing based on the "abnormal" aggregation-induced photoluminescence enhancement. Anal Chem (2014). 86(9):4423–30. doi:10.1021/ac500289c

CrossRef Full Text | Google Scholar

7. Zhu M, Diao G. Review on the progress in synthesis and application of magnetic carbon nanocomposites. Nanoscale (2011). 3:2748. doi:10.1039/c1nr10165j

CrossRef Full Text | Google Scholar

8. Chen L-F, Zhang X-D, Liang H-D, Kong M, Guan Q-F, Chen P, et al. Synthesis of nitrogen-doped porous carbon nanofibers as an efficient electrode material for supercapacitors. ACS Nano (2012). 6(8):7092–102. doi:10.1021/nn302147s

CrossRef Full Text | Google Scholar

9. Chabi S, Chang H, Xia Y, Zhu Y. From graphene to silicon carbide: ultrathin silicon carbide flakes. Nanotechnology (2016). 27(7):075602. doi:10.1088/0957-4484/27/7/075602

CrossRef Full Text | Google Scholar

10. Zheng H, Walter D. First-principles study of edge chemical modifications in graphene nanodots. Phys Rev B (2008). 78:045421. doi:10.1103/physrevb.78.045421

CrossRef Full Text | Google Scholar

11. Song Y-L, Zhang J-M, Lu D-B, Xu K-W. Structural and electronic properties of a single C chain doped zigzag silicene nanoribbon. Phys E Low-Dimens Syst Nanostruct (2013). 53:173–7. doi:10.1016/j.physe.2013.05.002

CrossRef Full Text | Google Scholar

12. Bekaroglu E, Topsakal M, Cahangirov S, Ciraci S. First-principles study of defects and adatoms in silicon carbide honeycomb structures. Phys Rev B (2010). 81:075433. doi:10.1103/physrevb.81.075433

CrossRef Full Text | Google Scholar

13. Sun X, Wang L, Lin H, Hou T, Li Y. Induce magnetism into silicene by embedding transition-metal atoms. Appl Phys Lett (2015). 106:222401. doi:10.1063/1.4921699

CrossRef Full Text | Google Scholar

14. Lv R, dos Santos MC, Antonelli C, Feng S, Fujisawa K, Berkdemir A, et al. Large-area Si-doped graphene: controllable synthesis and enhanced molecular sensing. Adv Mater (2014). 26(45):7593–9. doi:10.1002/adma.201403537

CrossRef Full Text | Google Scholar

15. Sun L, Han C, Wu N, Wang B, Wang Y. High temperature gas sensing performances of silicon carbide nanosheets with an n-p conductivity transition. RSC Adv (2018). 8:13697–707. doi:10.1039/c8ra02164c

CrossRef Full Text | Google Scholar

16. Kresse G, Furthmüller J. Efficient iterative schemes forab initiototal-energy calculations using a plane-wave basis set. Phys Rev B (1996). 54:11169. doi:10.1103/physrevb.54.11169

CrossRef Full Text | Google Scholar

17. Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys Rev B (1999). 59:1758. doi:10.1103/physrevb.59.1758

CrossRef Full Text | Google Scholar

18. Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett (1996). 77:3865. doi:10.1103/physrevlett.77.3865

CrossRef Full Text | Google Scholar

19. Blöchl PE. Projector augmented-wave method Phys Rev B (1994). 50:17953. doi:10.1103/physrevb.50.17953

CrossRef Full Text | Google Scholar

20. Liu C-C, Jiang H, Yao Y. Low-energy effective Hamiltonian involving spin-orbit coupling in silicene and two-dimensional germanium and tin. Phys Rev B (2011). 84:195430. doi:10.1103/physrevb.84.195430

CrossRef Full Text | Google Scholar

21. Badzian A. Stability of silicon carbonitride phases. J Am Ceram Soc (2002). 85(1):16–20. doi:10.1111/j.1151-2916.2002.tb00031.x

Google Scholar

22. Elias C, Valvin P, Pelini T, Summerfield A, Mellor CJ, Cheng TS, et al. Direct band-gap crossover in epitaxial monolayer boron nitride. Nat Commun (2019). 10:2639. doi:10.1038/s41467-019-10610-5

CrossRef Full Text | Google Scholar

23. Shih P-H, Do T-N, Godfrey G, Huang D, Pham H-D, Lin M-F. Rich magnetic quantization phenomena in AA bilayer silicene. Sci Rep (2019). 9:14799.

Google Scholar

24. Slater JC, Koster GF. Simplified LCAO method for the periodic potential problem. Phys Rev (1954). 94:1498. doi:10.1103/physrev.94.1498

CrossRef Full Text | Google Scholar

25. Chiu Y-H, Ho J-H, Ho Y-H, Chuu D-S, Lin M-F. Effects of a modulated electric field on the optical absorption spectra in a single-layer graphene. J Nanosci Nanotechnol (2009). 9(11):6579–86. doi:10.1166/jnn.2009.1340

CrossRef Full Text | Google Scholar

26. Do T-N, Lin C-Y, Lin Y-P, Shih P-H, Lin M-F. Configuration-enriched magneto-electronic spectra of AAB-stacked trilayer graphene. Carbon (2015). 94:619–32. doi:10.1016/j.carbon.2015.07.027

CrossRef Full Text | Google Scholar

27. Li G, Luican A, Lopes dos Santos JMB, Castro Neto AH, Reina A, Kong J, et al. Observation of Van Hove singularities in twisted graphene layers. Nat Phys (2010). 6:109–13. doi:10.1038/nphys1463

CrossRef Full Text | Google Scholar