Wide-Angle Circular Polarization Converter Based on a Metasurface of Z-Shaped Unit Cells

Since it is designable, metasurface was widely used in various fields, especially the design of polarization converters. However, most of the polarization converters currently designed can only work under normal incidence or small angle incidence, which hugely limits the application of the device. In this paper, a chiral metasurface based on the z-shaped unit cell, which can manipulate circular polarization wave, is proposed. The simulation result shows that this converter can maintain the polarization state of circular polarization after reflection from 8.18 to 13.988 GHz with a polarization conversion ratio of more than 90%. Moreover, the structure is insensitive to the incidence angle, which can keep a stable performance both for left-handed circularly polarized wave and right-handed circularly polarized waves as the incident angle increase to 75°. The proposed metasurface with simple structure and angular stability can be used in communication and polarization manipulating devices.

Introduction

Polarization, as one of the basic characteristics of electromagnetic (EM) waves, can be divided into three types: linear polarization, circular polarization, and elliptical polarization. Due to the features of circular polarization [1], circularly polarized (CP) antennas play an important role in communication systems such as satellites and rockets. With the diversification of application scenarios, it is necessary to manipulate the polarization state flexibly. Traditional polarization regulators are implemented using birefringent crystals, but such devices usually have a large volume, which greatly limits their application range. Therefore, people have always been working to find polarization converters with better performance and more relaxed application conditions.

Metasurfaces, artificially constructed two-dimensional materials, are periodically arranged by micro-units, showing unique EM properties that have not been found in nature [2]. Different unit structures, materials, and arrangements can achieve different functions, so metasurfaces have strong designability and functional customization. This new material that can design EM properties provides new ideas for the design of polarization regulators.

In recent years, various types of polarization converters based on metasurfaces have been successively proposed, including linear polarization (LP) to LP (that is 90° polarization rotator) [3–6], LP to circular polarization (CP) [7–9], CP to CP (that is circular polarization rotation direction regulator) [10], and multiple conversion modes [11, 12]. Great progress has been made in frequency band [13–15], bandwidth [16–18], volume [2], robustness [19, 20], etc. However, most of the attention was focused on the LP converter, and the research on CP regulators is relatively few. Recently, Akram et al. [18] proposed an ultra-wideband metasurface working at both transmission and reflection modes; however, they do not pay attention to oblique incidence. Huang [10] proposed one in 2017, which has a simple structure and can regulate the rotation direction of circularly polarized waves in the range of 8.16–15.32 GHz. However, the polarization converter is extremely sensitive to the angle. When the incident angle is >30°, the working bandwidth becomes obviously narrow and the polarization conversion ratio decreases rapidly. The existing polarization converters currently all have such a common defect that they can only work under small-angle incidence, which puts restrictions on the application of the device.

In this paper, we carried out works to overcome the shortcomings of the strong angle sensitivity of existing polarization converters and proposed a reflective CP regulator using a chiral metasurface based on the unit cell having a z-shaped structure. The polarization converter can maintain the polarization state of circular polarization after reflection from 8.18 to 13.988 GHz, basically covering the X-band that is 8–12 GHz. Compared with published designs, the proposed CP regulator has a simple geometry but a superior angular tolerance and hence can be used in many applications.

Model and Design

Our designed metasurface is composed of 20 × 20 unit cells as shown in Figure 1A. Every unit cell has three layers: the metal ground, the middle dielectric substrate, and the surface metal figure. The copper ground can prevent the transmission of the EM, reducing energy loss. The metal pattern on the surface is a copper material with a conductivity of 5.8 × 10⁷S/, and the intermediate dielectric layer is an FR-4 material with ε_r = 4.4, μ_r = 1, and tanδ = 0.025, which is rotated 45° with respect to the Y-axis. The thickness of the underlying layer is 0.3 mm, and the surface Z-shaped pattern with the thickness of 0.035 mm is placed along the diagonal position of the substrate material. Figure 1B shows the specific parameters of the structure, where p = 10.5mm, l = 6mm, w = 1.6mm.

FIGURE 1

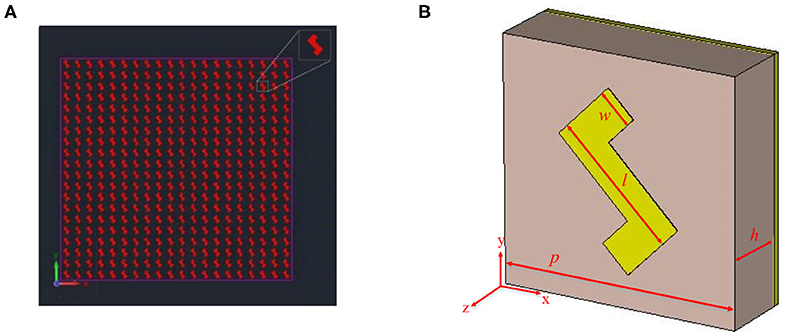
Figure 1. (A) Perspective view of designed metasurface. (B) Schematic picture of the unit cell structure.

The numerical simulation is carried out via the CST software, which utilizes a finite integration method and the Floquet mode to analyze the frequency response of the periodical structure. We set the unit cell conditions in the x and y directions, and the open and add space conditions in the z-direction. Incident left-handed circularly polarized (LCP) wave and right-handed circularly polarized (RCP) waves propagate along the opposite of the z-direction.

Simulation and Performance Analysis

When the circular waves were normally incident on the metasurface, the reflection wave can be expressed as [10]

$\begin{array}{l}\left(\begin{array}{c}{\text{E}}_{\text{+}}^r\\ {\text{E}}_{-}^r\end{array}\right)=\left(\begin{array}{cc}{\text{r}}_{++}& {\text{r}}_{+-}\\ {\text{r}}_{-+}& {\text{r}}_{--}\end{array}\right)\left(\begin{array}{c}{\text{E}}_{\text{+}}^i\\ {\text{E}}_{-}^r\end{array}\right)\end{array}$

where the superscripts i and r represent the incident and reflected waves, respectively, and the subscripts + and − denote the RCP and LCP, respectively. The first subscript indicates the polarization of the reflected wave, and the second subscript indicates the polarization of the incident wave. Thus, ${\text{E}}_{+}^i$,${\text{E}}_{-}^i$ represent the electric fields of incident RCP and LCP, respectively. Similarly, ${\text{E}}_{+}^r$ and ${\text{E}}_{-}^r$ represent the reflected ones. Elements in the matrix are all reflection coefficients; identical subscripts indicate co-polarized reflection coefficients, while different subscripts indicate cross-polarized reflected coefficients. The above reflection coefficients r_mn(m, n = +, − and m ≠ n) are the complex reflection coefficients, containing both amplitude r_mn = |r_mn| and phase information. We know that when EM waves are normally incident on the metasurface, the handedness of the reflected CP wave will be changed. We regulate the rotation direction of the reflected wave, that is, to maintain the handedness of the circularly polarized wave. Therefore, it is possible to define the polarization conversion rate (PCR) of two different modes of circularly polarized waves.

$\begin{array}{l}PC{R}_m=|r_{mm}{|}^2/\left({\left|r_{mm}\right|}^2+{\left|r_{\text{n}m}\right|}^2\right)\end{array}$

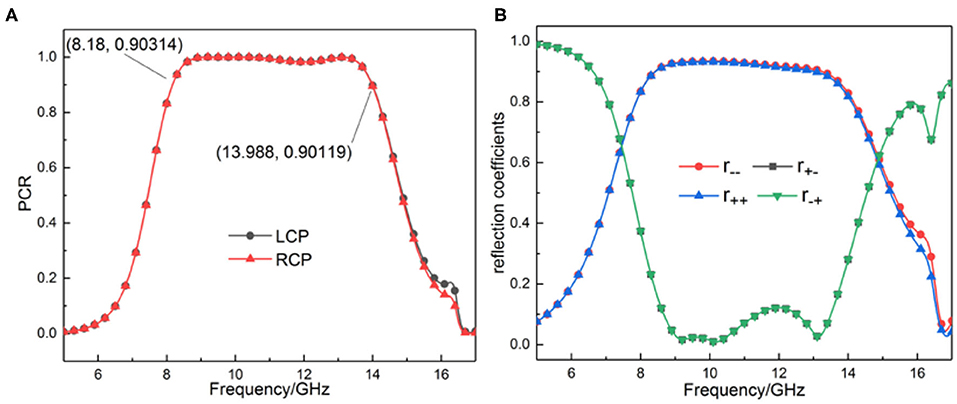
To show the performance of this device, we simulated the reflection coefficient and PCR of LCP and RCP at normal incidence, as shown in Figure 2. The results show that the reflection coefficients curves of the two cases almost wholly coincide; the PCR also satisfies this rule. For the reflection coefficient, the co-polarized reflection coefficient is > 0.9 in the range of 8.432–13.036 GHz, and the cross-polarized reflection coefficient is <0.2 in the range of 8.672–13.508 GHz, which indicates that the reflected CP does achieve a polarization regulation in this band. For the polarization conversion ratio, PCR is > 0.9 in the range of 8.18–13.988 GHz, covering all the X-band, which proves the high efficiency of the regulator. Besides, we can observe that there are three resonant frequencies (at 9.22, 10.17, and 13.12 GHz) in this range.

FIGURE 2

Figure 2. (A) PCR and (B) reflection coefficient under the normal incident CP waves.

In practical applications, we need to consider the situation of oblique incidence. So we calculate the bandwidth to discuss the oblique incidence performance. The schematic diagram of the incident angle is shown in Figure 3B. Figure 3A shows the relation between the bandwidth when the PCR is higher than 0.9 (the bandwidth in the paper all refers to the continuous bandwidth with a PCR > 0.9) and the incident angle. Obviously, for the two incident modes of LCP and RCP, the angle has different effects on the performance of the polarization converter, and the influence of the angle on the bandwidth is not monotonous. For the RCP waves, when the angle of incidence is <75°, the bandwidth decreases monotonically with an increasing angle, reaching a minimum value of 3.756 GHz at 75°. When the incident angle continually increases, the bandwidth expands rapidly. For the LCP waves, the bandwidth reaches a maximum of 5.988 GHz when the angle of incidence is around 30°; when the angle enlarges again, the bandwidth shows a downward trend, but the decline rate is slower, reaching a minimum value of 5.172 GHz when the incident angle reaches 70°. The bandwidth also increases when the incident angle increases again.

FIGURE 3

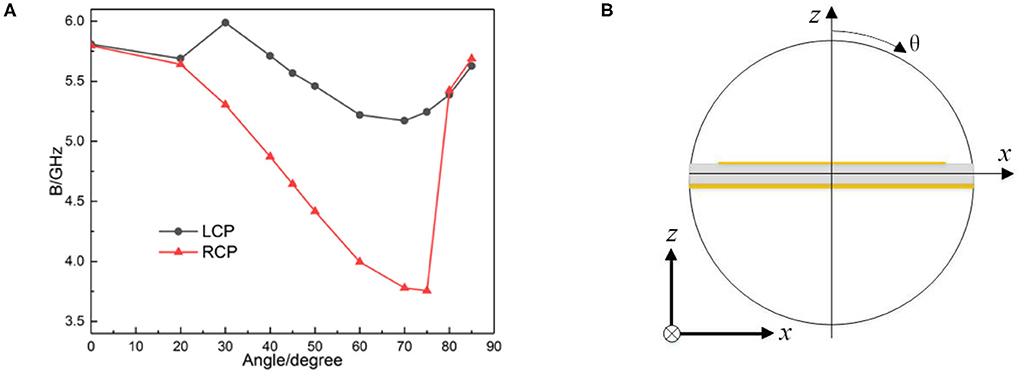
Figure 3. (A) Relation between the bandwidth and the angle. (B) Schematic diagram of the incident angle.

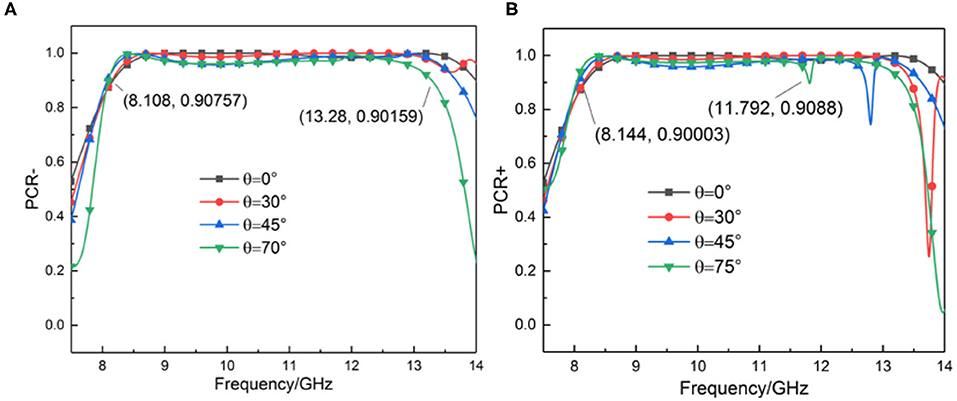
To show the influence of the angle on the performance of the converter in more detail, we simulated the PCR of the two types of CP waves at different incident angles, respectively. For LCP waves, the incidence angles are 0°, 30°, 45°, and 70°, respectively, as shown in Figure 4A. For RCP waves, the incidence angles are 0°, 30°, 45°, and 75°, respectively, as shown in Figure 4B. The result shows that the device still works well for both LCP and RCP in the X-band, though under a super large incident angle. For LCP waves, the incidence angle has little effect on the PCR and the bandwidth. According to Figure 3, under the LCP incoming wave, the bandwidth reaches the minimum when the incident angle is equal to 70°. In combination with Figure 4A, in the same angle, the PCR is > 0.9 in the range from 8.108 to 13.28 GHz, covering the 97.3% X-band. At other angles, the bandwidth coverage is broader, and the performance is better. For RCP waves, although the continuous bandwidth is narrow, the PCR is kept high, and the performance in the X-band is still great. With the analysis of Figure 3, the bandwidth reaches a minimum when the angle of incidence is 75°. According to Figure 4B, when the angle of incidence is 75°, the frequency band with a PCR > 0.9 is 8.144–11.792 GHz, which can still regulate the handedness of the CP waves in the X-band 91.2% frequency band. Besides, due to the drooping frequency point in the high-frequency band, the continuous bandwidth becomes smaller, and the working field changes from a single wideband to a dual band; in other words, the regulation performance outside the X-band is also excellent.

FIGURE 4

Figure 4. Simulation result of PCR under a different angle for (A) LCP and (B) RCP incident waves.

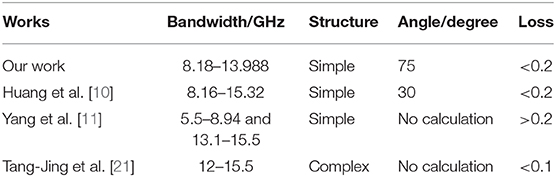
To show the advantages of the device more clearly, we provide a parameter comparison with a previous circular polarization regulator as shown in Table 1. It shows that our design has the advantages of simple structure, small loss, and strong angular tolerance.

TABLE 1

Table 1. Comparison with other published circular polarization regulator.

Mechanism Discussion

In the following, we explain the mechanism of the excellent performance of the device through formula derivation and simulation results. When the incident CP wave is decomposed into LP waves ${\text{E}}_x^i$ and ${\text{E}}_y^i$, the reflected wave can also be expressed as and ${\text{E}}_x^r$, and ${\text{E}}_y^r$ the relationship between the incident field and the reflected field can be expressed as [10]

$\begin{array}{l}\left(\begin{array}{c}{\text{E}}_x^r\\ {\text{E}}_y^r\end{array}\right)=\left(\begin{array}{cc}{\text{r}}_{xx}& {\text{r}}_{xy}\\ {\text{r}}_{yx}& {\text{r}}_{yy}\end{array}\right)\left(\begin{array}{c}{\text{E}}_x^i\\ {\text{E}}_y^i\end{array}\right)=R\left(\begin{array}{c}{\text{E}}_x^i\\ {\text{E}}_y^i\end{array}\right)\end{array}$

that is, ${\text{E}}_x^r={\text{r}}_{xx}{\text{E}}_x^i+{\text{r}}_{yx}{\text{E}}_y^i$, ${\text{E}}_y^r={\text{r}}_{yy}{\text{E}}_y^i+r_{xy}{\text{E}}_x^i$, where r_xx and r_yx represent the co-polarized and cross-polarized reflection coefficients under the x-polarized wave incidence; others are similar. Then, the reflected wave can be described as

$\begin{array}{l}{\text{E}}^r=\left({\text{r}}_{xx}{\text{E}}_x^i\text{+}{\text{r}}_{xy}{\text{E}}_y^i\right)\widehat{x}+\left({\text{r}}_{yy}{\text{E}}_y^i+{\text{r}}_{yx}{\text{E}}_x^i\right)ŷ\end{array}$

There are four cases in this expression: ${\text{r}}_{xx}{\text{E}}_x^i\widehat{x}+{\text{r}}_{yy}{\text{E}}_y^iŷ$, ${\text{r}}_{xy}{\text{E}}_y^i\widehat{x}+{\text{r}}_{yx}{\text{E}}_x^iŷ$, ${\text{r}}_{xx}{\text{E}}_x^i\widehat{x}+{\text{r}}_{xy}{\text{E}}_y^i\widehat{x}$, ${\text{r}}_{yy}{\text{E}}_y^iŷ+{\text{r}}_{yx}{\text{E}}_x^iŷ$. For convenience, they are expressed as f_xx + f_yy, f_xy + f_yx, f_xx + f_xy, and f_yy + f_yx, where f_xx + f_yy and f_xy + f_yx express the reflected co-polarization terms under the CP incoming wave; the other two items express the reflected LP wave under the same incident situation. Based on the above definition, to maintain the handedness of reflected waves, the structure must meet the conditions that r_yx = r_xy, ϕ_yx = ϕ_xy, r_xx = r_yy, |ϕ_yy − ϕ_xx| = π. Figure 5 shows the reflection coefficient and phase under the LP incoming wave. We can see that ϕ_xy and ϕ_yx are entirely coincident; the difference of ϕ_yy and ϕ_xx is close to 180°; r_yx and r_xy are completely coincident; the difference of r_xx and r_yy is > 0.13. In addition, at the three resonant frequencies (f= 9.22, 10.17, 13.12 GHz), |ϕ_yy − ϕ_xx| = π. We can see that the results satisfied all the amplitude and phase conditions mentioned above. Therefore, we confirmed that the circular polarization-keeping reflection is realized.

FIGURE 5

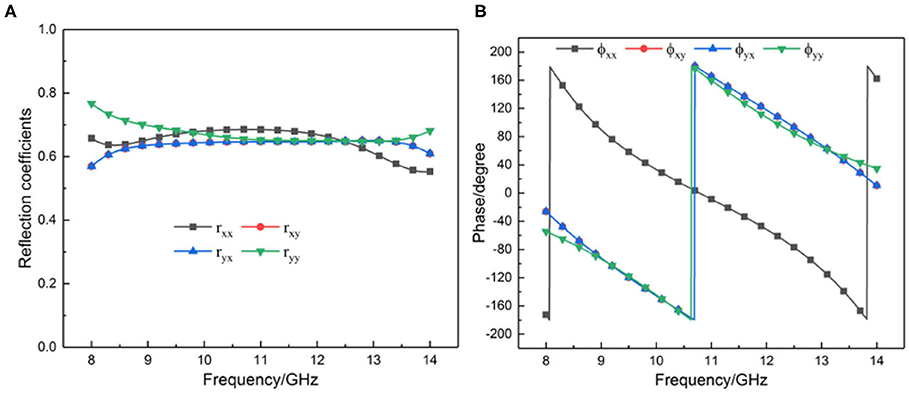
Figure 5. Simulation result of linearly polarized incoming wave under normal incidence. (A) Reflection coefficient. (B) Phase.

For the case of oblique incidence, we calculated the mean values of r_xx/r_yy, r_xy/r_yx, |ϕ_xx − ϕ_yy|, and |ϕ_xy − ϕ_yx| within the bandwidth with different incident angles, as shown in Figure 6. The result indicates that $\frac{{\mathrm{\text{r}}}_{xy}}{{\mathrm{\text{r}}}_{yx}}=1$ and the values of r_xx/r_yy are all larger than 0.96, which are close to 1, at any angle of incidence. In Figure 6B, ϕ_xy and ϕ_yx are wholly coincident, and the difference of ϕ_yy and ϕ_xx is close to 180°, meeting the regulation conditions. Therefore, the device has a robust angular-tolerance performance.

FIGURE 6

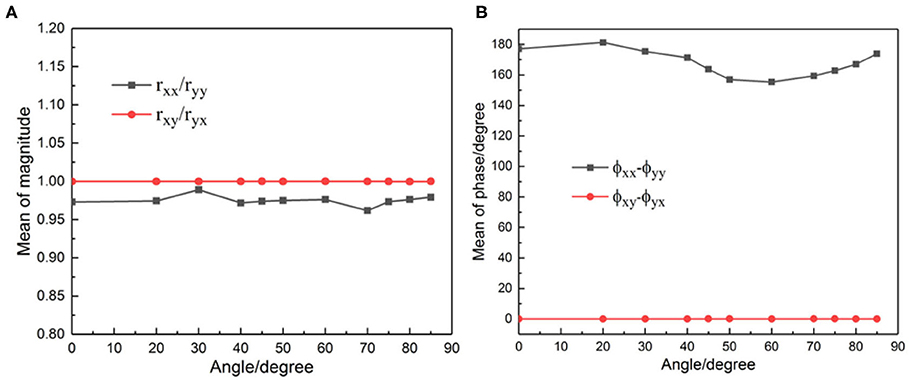
Figure 6. Simulation result of linearly polarized incoming wave under oblique incidence. (A) Mean of amplitude ratio. (B) Mean of phase difference.

Circular dichroism also can be used to explain the physical mechanism of the device. Our design is a reflective chiral device with circular dichroism, that is, it has different absorptivity for LCP waves and RCP waves. The selective absorption of waves by the device will reduce the component of co-polarized reflected waves, resulting in a drop in the PCR. The absorption spectra of different incident waves are shown in Figure 7.

FIGURE 7

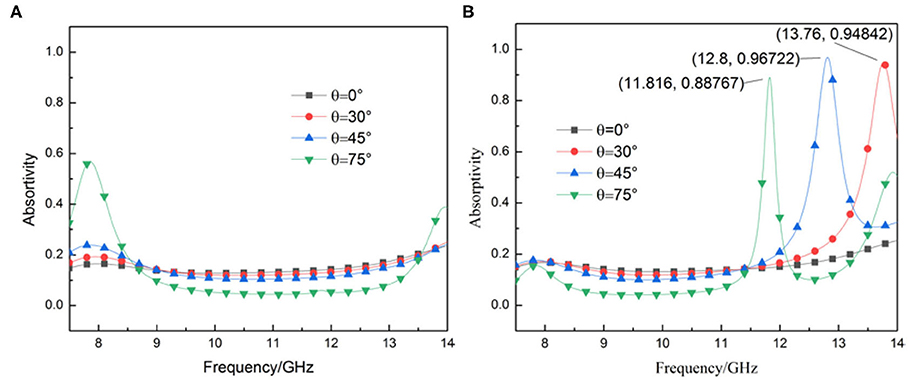
Figure 7. Absorption spectra for different incoming wave. (A) LCP incoming waves. (B) RCP incoming waves.

Comparing Figure 7A with Figure 7B, it can be found that the absorption rate of the LCP incident wave is kept at a low level in the working frequency band, basically below 0.2, with the increase in the incident angle. When the incident angle reaches 75°, absorption peaks appear at low frequency and high frequency, which leads to a slight narrowing of the bandwidth of the polarization converter, which is consistent with the results in Figure 4A. For the case of the RCP incident wave, with the increase in the incident angle, the absorption peak of the device for the RCP wave gradually shifts to the left, corresponding to the tips of the polarization conversion rate in Figure 4B.

Conclusion

We proposed a reflective circular polarization handedness regulator based on metasurface, which contains 20 × 20 resonant units. The structure is simple and easy to fabricate. Simulations and mechanisms have proven that our devices exhibit excellent performance in the X-band. Compared with previous papers, our design not only can achieve high-efficiency broadband polarization conversion performance under the normal incidence but also has robust angular tolerance. At large incident angles, they can also effectively keep circular polarization handedness. Indeed, the device also has disadvantages. Our work still does not address the problem of different responses to RCP and LCP waves, which should be considered in the application. Anyway, this metasurface has great significance for the application due to the good regulation function and robust angular tolerance.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

MW tutored and revised the paper. ZZ conducts deductive calculations, plots, and thesis writing. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (Grants No. 61771385), Science and Technology on Solid-State Laser Laboratory (Grants No. 6142404180301), and Science and Technology research plan of Xi'an city (Grant No. GXYD14.26).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Luo Q, Zhu F, Gao S. Circularly Polarized Antennas. West Sussex: John Wiley & Sons, Ltd (2013).

Google Scholar

2. Gao X, Han X, Cao WP, Li HO, Ma HF, Cui TJ. Ultrawideband and high-efficiency linear polarization converter based on double V-shaped metasurface. IEEE T Antenn Propag. (2015) 63:3522–30. doi: 10.1109/TAP.2015.2434392

CrossRef Full Text | Google Scholar

3. Xu Y, Shi Q, Zhu Z, Shi J. Mutual conversion and asymmetric transmission of linearly polarized light in bilayered chiral metamaterial. Opt Express. (2014) 22:411–4. doi: 10.1364/OE.22.025679

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Huang X, Yang D, Yang H. Multiple-band reflective polarization converter using U-shaped metamaterial. J Appl Phys. (2014) 115:13–9. doi: 10.1063/1.4868076

CrossRef Full Text | Google Scholar

5. Huang X, Xiao B, Yang D, Yang H. Ultra-broadband 90° polarization rotator based on bi-anisotropic metamaterial. Opt Commun. (2015) 338:416–21. doi: 10.1016/j.optcom.2014.11.010

CrossRef Full Text | Google Scholar

6. Zhang L, Zhou P, Lu H, Zhang L, Xie J, Deng L. Realization of broadband reflective polarization converter using asymmetric cross-shaped resonator. Opt Mater Express. (2016) 6:1393–404. doi: 10.1364/OME.6.001393

CrossRef Full Text | Google Scholar

7. Li Y, Zhang J, Qu S, Wang J, Zheng L, Pang Y, et al. Achieving wide-band linear-to-circular polarization conversion using ultra-thin bi-layered metasurfaces. J Appl Phys. (2015) 117:7. doi: 10.1063/1.4906220

CrossRef Full Text | Google Scholar

8. Zhuang YQ, Wang GM, Zhang XK, Zhang CX, Cai T, Li HP. Design of reflective linear-circular polarization converter based on phase gradient metasurface. Acta Phys Sin-Ch Ed. (2016) 65:154102. doi: 10.7498/aps.65.154102

CrossRef Full Text | Google Scholar

9. Jia Y, Liu Y, Zhang W, Wang J, Wang Y, Gong S, et al. Ultra-wideband metasurface with linear-to-circular polarization conversion of an electromagnetic wave. Opt Mater Express. (2018) 8:597. doi: 10.1364/OME.8.000597

CrossRef Full Text | Google Scholar

10. Huang X, Chen J, Yang H. High-efficiency wideband reflection polarization conversion metasurface for circularly polarized waves. J Appl Phys. (2017) 122:43102. doi: 10.1063/1.4996643

CrossRef Full Text | Google Scholar

11. Yang D, Lin H, Huang X. Dual broadband metamaterial polarization converter in microwave regime. Progress in electromagnetics research. Letters. (2016) 61:71–6. doi: 10.2528/PIERL16033004

CrossRef Full Text | Google Scholar

12. Lin B, Guo J, Chu P, Huo W, Xing Z, Huang B, et al. Multiple-band linear-polarization conversion and circular polarization in reflection mode using a symmetric anisotropic metasurface. Phys Rev Appl. (2018) 9:024038. doi: 10.1103/PhysRevApplied.9.024038

CrossRef Full Text | Google Scholar

13. Fu YN, Zhang XQ, Zhao GZ, Li YH, Yu JY. A broadband polarization converter based on resonant ring in terahertz region. Acta Phys Sin-Ch Ed. (2017) 66:180701. doi: 10.7498/aps.66.180701

CrossRef Full Text | Google Scholar

14. Grady NK, Heyes JE, Chowdhury DR, Zeng Y, Reiten MT, Azad AK, et al. Terahertz metamaterials for linear polarization conversion and anomalous refraction. Science. (2013) 340:1304–7. doi: 10.1126/science.1235399

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Mun SE, Kim SJ, Hong J, Lee B. Polarization conversion in toroidal metamaterial in optical spectral range. In: 2018 Conference on Lasers and Electro-Optics Pacific Rim, CLEO-PR. Hong Kong (2018). doi: 10.1364/CLEOPR.2018.W3A.146

CrossRef Full Text | Google Scholar

16. Yu JB, Ma H, Wang JF, Feng MD, Li YF, Qu SB. High-efficiency ultra-wideband polarization conversion metasurfaces based on split elliptical ring resonators. Acta Phys Sin-Ch Ed. (2015) 64:178101. doi: 10.7498/aps.64.178101

CrossRef Full Text | Google Scholar

17. Khan MI, Fraz Q, Tahir FA. Ultra-wideband cross polarization conversion metasurface insensitive to incidence angle. J Appl Phys. (2017) 121:45103. doi: 10.1063/1.4974849

CrossRef Full Text | Google Scholar

18. Akram MR, Ding G, Chen K, Feng Y, Zhu W. Ultrathin single layer metasurfaces with ultra-wideband operation for both transmission and reflection. Adv Mater. (2020) 32:1907308. doi: 10.1002/adma.201907308

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Xie Y, Yang C, Wang Y, Shen Y, Deng X, Zhou B, et al. Anomalous refraction and reflection characteristics of bend V-shaped antenna metasurfaces. Sci Rep. (2019) 9:6700. doi: 10.1038/s41598-019-43138-1

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Huan X, Yang H, Yu S, Hui W. Dual-functional metamaterial for reflection and transmission polarization conversion. Singapore: IEEE. (2017) 1–2. doi: 10.1109/CLEOPR.2017.8118652

CrossRef Full Text | Google Scholar

21. Tang-Jing L, Jian-Gang L, Hai-Peng L. Broadband circularly polarized high-gain antenna design based on single-layer reflecting metasurface. Acta Phys Sin-Ch Ed. (2016) 66:064102. doi: 10.7498/aps.65.104101

CrossRef Full Text | Google Scholar