Anomalous Diffusion in Systems with Concentration-Dependent Diffusivity: Exact Solutions and Particle Simulations

We explore the anomalous diffusion that may arise as a result of a concentration dependent diffusivity. The diffusivity is taken to be a power law in the concentration, and from exact analytical solutions we show that the diffusion may be anomalous, or not, depending on the nature of the initial condition. The diffusion exponent has the value of normal diffusion when the initial condition is a step profile, but takes on anomalous values when the initial condition is a spike. Depending on the sign of the exponent in the diffusivity the diffusive behavior will then be either sub-diffusive or super-diffusive. We introduce a particle model that behaves according to the non-linear diffusion equation in the macroscopic limit. This correspondence is demonstrated via kinetic theory, i.e. by means of Chapman-Kolmogorov equation, as well as by direct simulations.

1 Introduction

A wide range of interesting physical systems are described by a diffusion equation where the diffusivity depends on the concentration of the diffusing quantity. That is, we have a concentration $C\left(x,t\right)$ where x is the distance from some surface and t is the time. The concentration $C=C\left(x,t\right)$ is governed both by the diffusion equation and a necessary initial condition

$\frac{\partial }{\partial t}C\left(x,t\right)=\frac{\partial }{\partial x}\left(D\left[C\left(x,t\right)\right]\frac{\partial }{\partial x}C\left(x,t\right)\right)(1)$

$C\left(x,0\right)=C_{in}\left(x\right),(2)$

where $C_{in}\left(x\right)$ is the initial concentration profile and $D=D\left[C\right]$ is the concentration-dependent diffusivity. The typical and interesting case is when the diffusivity obeys the power law

$D=D_0{\left(\frac{C\left(x,t\right)}{C_0}\right)}^{-\gamma }.(3)$

Here $C_0$ is a constant reference concentration and $D_0$ is the diffusivity at that reference value.

We e.g., find such behavior when compressible gases flow through porous media [1, 2] or in filtration processes [3]. Another example is heat diffusion at high temperature [4, 5]. Population dynamics gives rise to this kind of behavior [6–8], as does water ingress in zeolites as studied by Azevedo et al. [9, 10] and Fischer et al. [11]. The diffusion of grains in granular media considered by Christov and Stone [12] is yet another example. Pritchard et al. [13] studied gravity-driven fluid flow in layered porous media finding that the fluid motion could be described by a concentration-dependent diffusivity as did Hansen et al. [14] for the spreading of wetting films in wedges.

Common to all of these examples is that γ is negative, ranging from $\gamma =-5$ [4] to $\gamma =-1/2$ [14]. That is, in all these examples the diffusivity increases with increasing concentration. But, what about the opposite case? This is where the diffusivity decreases with the concentration. Intuitively, this makes sense as anybody trying to move in a dense crowd as compared to in an open crowd will testify. Küntz and Lavallée consider high-concentration aqueous CuSO₄ diffusion in deionized water, and in this case, they find that the diffusivity decreases with increasing concentration [15]. Gosh et al. [16] also report decreasing diffusivity with increasing concentration in protein diffusion in crowded lipid bilayer membranes. Another system where such behavior would be seen may be outlined as follows: Imagine a tube filled with beads with diameter d slightly less than the tube. When the beads are all touching, there will be a relative fraction (porosity) ${\varphi }_0$ of the volume of the tube which is not occupied by the beads. If they do not touch each other, the porosity is increased to $\varphi ={\varphi }_0+\delta \varphi$ where $\delta \varphi$ is the excess porosity. Suppose now that there is a typical distance λ between each pair of beads not in contact. The excess porosity is then proportional to $\delta \varphi \propto v/\left(d^2\lambda \right)$, where v is the excess volume at a pair of beads not touching, i.e., were there is a hole. This hole moves a distance λ when all the touching beads move in the direction of the hole. If this motion is random, we will be dealing with diffusive behavior. The diffusivity is then proportional to ${\lambda }^2/t_{\lambda }$, where $t_{\lambda }$ is the time it takes to move the $\lambda /d$ beads. Assuming that this time is proportional to λ, the diffisivity is then proportional to λ which in turn is proporional to $1/\delta \varphi$. This leads to a diffusion equation

$\frac{\partial }{\partial t}\delta \varphi =\frac{\partial }{\partial x}\frac{\delta {\varphi }_0}{\delta \varphi }\frac{\partial }{\partial x}\delta \varphi ,(4)$

where $\delta {\varphi }_0$ is a reference excess porosity level. Comparing with Eqs 1 and 3, we see that $\gamma =1$ here.

There are two classes of examples in the list above: systems where there is a physical quantity that is diffusing due to random motion, and systems that are only described by the diffusion equation. The diffusion of excess porosity in the packing of beads is an example of the first class. On the other hand, the motion of a fluid-fluid interface under gravity in a porous layer [13] is an example of a system where there is no random diffusion.

In either case, there being physical diffusion or the system may be mapped onto equations having the form of a diffusion equation, we may consider an equivalent system consisting of diffusing particles. The concentration-dependent diffusivity may then be interpreted as mean-field type interaction between the particles, where the behavior of each particle is determined by the number of neighbors it has.

A key quantity to characterize diffusive behavior is the root mean square (rms) displacement traveled by the particles — i.e., random walkers — as a function of time. If a random walker in one dimension starts at position $x=0$ when time $t=0$, then the subsequent rms displacement is Refs. 17, 18

$\sqrt{\langle x^2\left(t\right)\rangle }\propto t^{\tau }.(5)$

When the diffusion exponent $0<\tau <1/2$, we are dealing with sub-diffusion and when $1/2<\tau \le 1$, we are dealing with super-diffusion. When $\tau =1$, the diffusion is ballistic. When $\tau >1$, the term hyper-ballistic is used [19, 20]. These are all examples of anomalous diffusion. Normal diffusion occurs when $\tau =1/2$.

There are several possible ways the behavior of the diffusivity in the diffusion equation may lead to anomalous diffusion. It may do so by having a position dependent diffusivity, see e.g., Refs. 21–24. The diffusivity we are considering in this work also depends on the position, but only through the concentration as in Eq. 3.

There is a relation between the exponent γ defined in Eq. 3 and the random walk exponent τ in Eq. 5,

$\tau =\frac{1}{2-\gamma }.(6)$

This equation was first worked out by Pattle [25] for negative γ indicating sub diffusion. We will in this paper extend this equation to positive γ, using the self-similarity approach [26–28]. We find that Eq. 6 is valid for the range $\gamma <2/3$, and that indeed there is super-diffusion for positive γ. This result comes from a closed form analytic solution that exists for the full range $\gamma <1$. In the $2/3<\gamma <1$ range the integral defining the second moment $\langle x^2\rangle$ diverges. We furthermore note that hyper-diffusion cannot occur in one dimension if the concentration-dependent diffusivity Eq. 3 is at play.

In spite of the relation Eq. 6 between γ and the exponent that defines anomalous diffusion, τ, it is sometimes believed that the Boltzmann transformation [29] demonstrates that there is no anomalous diffusion, even when the diffusivity depends on the concentration. This is, e.g., demonstrated in the famous textbook by Crank [30]. However, the random walk exponent τ, depends on the initial condition Eq. 2.

We support our analytical work by numerical simulations through the introduction of a particle model where random walkers move in discrete steps that depend on the local concentration. We show that the average description of this model, that is given by the Chapman-Kolmogorov equation, reduces to Eq. 7. Hence, we are able to reproduce the analytical results by particle simulations. These particle simulations are easily generalized to higher dimensions and different kinds of non-linearities in the diffusion equation that describes them.

2 Analytic Solutions

The analytic results are most conveniently obtained by rewriting Eq. 1 in the form [31]

$\frac{1-\gamma }{D_0{C}_0^{\gamma }}\frac{\partial }{\partial t}C\left(x,t\right)=\frac{{\partial }^2}{\partial x^2}C{\left(x,t\right)}^{1-\gamma }.(7)$

Hence, we see that we need $\gamma <1$ for the equation to be defined when $C\left(x,t\right)=0$.

2.1 Boltzmann Transformation and the Step

In order for the Boltzmann transformation to be applicable we take the initial conditions to be $C\left(x,0\right)=C_0\text{Θ}\left(-x\right)$, where $\text{Θ}\left(x\right)$ is the Lorentz-Heaviside function. The Boltzmann transformation consists in introducing the variable

$y=\frac{x}{\sqrt{t}}.(8)$

When the t and x derivatives are transformed to y-derivatives the diffusion Eq. 7 becomes the ordinary differential equation,

$\frac{1-\gamma }{2D_0{C}_0^{\gamma }}y\frac{dC}{dy}+\frac{d^2{C}^{1-\gamma }}{d{y}^2}=0(9)$

with the x and t dependence through y only. Now, the initial condition too may be written in terms of y alone: For $t>0$: $C\left(y\right)=C_0\text{Θ}\left(-y\right)$. For this reason the solution of the diffusion Eq. 7 takes the form

$C\left(x,t\right)=q\left(\frac{x}{t^{1/2}}\right)(10)$

for some function q that satisfies Eq. 9. This immediately leads to the conclusion

$\langle x^2\left(t\right)\rangle =\frac{{{\displaystyle \int }}^{\text{}}dx{x}^{2}C\left(x,t\right)}{{{\displaystyle \int }}^{\text{}}dxC\left(x,t\right)}\sim t,(11)$

i.e., that the diffusion is normal with $\tau =1/2$ in Eq. 6. In other words, the step function initial condition cannot lead to the anomalous diffusion behavior defined by Eq. 6 and Pattle’s solution. In the following we shall se that this conclusion is qualitatively changed by the introduction of a localized, and thus normalizable, δ-function inital condition.

2.2 Exact Solutions From Delta-Function Initial Condition

Solving Eq. 7 with a point source initial condition turns out to change the diffusion exponent τ. Hence, we start with

$C\left(x,0\right)=N_p\delta \left(x\right),(12)$

where $N_p$ is the particle number, and $\delta \left(x\right)$ is the Dirac δ-function, which obviously, yields the normalization

${{{\displaystyle \int }}^{\text{}}}_{-\infty }^{+\infty }dxC\left(x,t\right)=N_p.(13)$

There is no intrinsic length or time-scale in Eq. 7 since the diffusivity depends on C through the power law of Eq. 3. This means that as long as boundary- or initial conditions do not introduce such scales either, the solutions $C\left(x,t\right)$ must be scale-free too. More precisely, if $x\to \lambda x$, then there must be some rescaling of time $t\to t/f^{-1}\left(1/\lambda \right)$ so that the probability of finding the particle remains unchanged, that is,

$dxC\left(x,t\right)=\lambda dxC\left(\lambda x,\frac{t}{f^{-1}\left(1/\lambda \right)}\right).(14)$

This ensures that the normalization of Eq. 13 remains constant with time. We now choose λ so that $t/f^{-1}\left(1/\lambda \right)=1$. That is, we set

$\lambda =\frac{1}{f\left(t\right)}.(15)$

Combined with Eq. 14, this gives

$C\left(x,t\right)=\frac{1}{f\left(t\right)}C\left(\frac{x}{f\left(t\right)},1\right)=\frac{1}{f\left(t\right)}p\left(\frac{x}{f\left(t\right)}\right),(16)$

where we have set $p\left(y\right)\equiv C\left(y,1\right)$. Since $C\left(x,t\right)$ has dimension 1/length, we will take $p\left(y\right)$ to be dimensionless and $f\left(t\right)$ to have dimension of length.

We introduce the reduced variable

$y=\frac{x}{f\left(t\right)},(17)$

and so get

$\frac{\partial y}{\partial x}=\frac{1}{f\left(t\right)},(18)$

and

$\frac{\partial y}{\partial t}=-y\frac{\dot{f}\left(t\right)}{f\left(t\right)}.(19)$

Equation 7 may then be transformed into

$\frac{1}{D_0{C}_0^{\gamma }}\frac{1-\gamma }{2-\gamma }\frac{df{\left(t\right)}^{2-\gamma }}{dt}\frac{d}{dy}yp\left(y\right)+\frac{d^2}{d{y}^2}p{\left(y\right)}^{1-\gamma }=0.(20)$

This means that for some dimensionless separation constant c

$\frac{\frac{d^2}{d{y}^2}p{\left(y\right)}^{1-\gamma }}{\frac{d}{dy}yp\left(y\right)}=-c,(21)$

and

$\frac{1}{D_0{C}_0^{\gamma }}\frac{1-\gamma }{2-\gamma }\frac{df{\left(t\right)}^{2-\gamma }}{dt}=c.(22)$

The property expressed by Eq. 14 is that the right‐hand side is independent of λ. For this reason replacing $f\to c^{1/\left(2-\gamma \right)}f$ will leave the right‐hand side of Eq. 16 invariant. So, the c factor will cancel out in the final expression for $C\left(x,t\right)$, and we might as well set $c=1$. Then Eq. 22 for $f\left(t\right)$ is easily integrated assuming $f\left(0\right)=0$ since we are assuming Eq. 12, i.e., point-like initial conditions. This yields

$f\left(t\right)={\left(\frac{2-\gamma }{1-\gamma }{D}_0{C}_0^{\gamma }t\right)}^{\frac{1}{2-\gamma }}.(23)$

Our solution thus has the scaling form

$C\left(x,t\right)\sim \frac{g\left(x/t^{\tau }\right)}{t^{\tau }}(24)$

for some function g and with τ given by Eq. 6. Note that this form immediately gives

$\langle x^2\left(t\right)\rangle =\frac{{{\displaystyle \int }}^{\text{}}dx{x}^{2}C\left(x,t\right)}{{{\displaystyle \int }}^{\text{}}dxC\left(x,t\right)}\sim t^{2\tau }.(25)$

This is in contrast to the Boltzmann transformation, which assumes step-like initial conditions, thus leading to $\langle x^2\left(t\right)\rangle \propto t$.

We now turn to finding an expression for the probability density $p\left(y\right)$. Equation 21 yields

$\frac{d}{dy}yp\left(y\right)+\frac{d^2}{d{y}^2}p{\left(y\right)}^{1-\gamma }=0.(26)$

which may be integrated to

$yp\left(y\right)+\frac{d}{dy}p{\left(y\right)}^{1-\gamma }=K,(27)$

where K is an integration constant.

On physical grounds we require that Fick’s law be valid throughout the domain, and so C must be continuously differentiable. By symmetry it must also be symmetric around $x=0$ and so $p^{\prime }\left(0\right)=0$ and $p\left(0\right)$ finite. This implies that the integration constant $K=0$ so that we get the equation

$yp\left(y\right)+\frac{d}{dy}p{\left(y\right)}^{1-\gamma }=0.(28)$

which is integrable. Rewriting it as

$dp{\left(y\right)}^{-\gamma }=\frac{\gamma }{1-\gamma }d\left(\frac{y^2}{2}\right),(29)$

it may be integrated to yield

$p\left(y\right)={\left[\frac{\gamma }{2\left(1-\gamma \right)}{y}^2+k\right]}^{-\frac{1}{\gamma }},(30)$

where k is yet an integration constant. For $\gamma <0$, the factor multiplying $y^2$ is negative, $\gamma /2\left(1-\gamma \right)<0$, so that the solution is restricted to $\left|\gamma \right|<\sqrt{2k\left(\gamma -1\right)/\gamma }$, while for $0<\gamma <1$, the solution is valid for all y values.

The constant k is determined by the normalization condition

${{{\displaystyle \int }}^{\text{}}}_{-\infty }^{\infty }dyp\left(y\right)=N_p(31)$

which follows from Eq. 13. Since the two cases of positive and negative γ-values give either finite or infinite support for p , they give rise to different functions $k\left(\gamma \right)$ which we shall denote $k_{\pm }$ for $\gamma >0$ (+) and $\gamma <0$ ($-$). They are

$k_{\pm }={\left[\right|\frac{\gamma }{2\left(1-\gamma \right)}{|}^{1/2}\frac{N_P}{I_{\pm }}]}^{\frac{2\gamma }{\gamma -2}}(32)$

where the integrals

$I_{\pm }=\{\begin{array}{l}{{{\displaystyle \int }}^{\text{}}}_{-\infty }^{\infty }du{\left(1+u^2\right)}^{-1/\gamma }\text{for }+\\ {{{\displaystyle \int }}^{\text{}}}_{-1}^{1}du{\left(1-u^2\right)}^{-1/\gamma }\text{for }-\end{array}.(33)$

These integrals may be calculated numerically, or evaluated through the analytic expressions

$k_{-}={\left[\frac{N_p}{\sqrt{\pi }}{\left|\frac{\gamma }{2\left(\gamma -1\right)}\right|}^{\frac{1}{2}}\frac{\text{Γ}\left(\frac{3}{2}-\frac{1}{\gamma }\right)}{\text{Γ}\left(1-\frac{1}{\gamma }\right)}\right]}^{\frac{2\gamma }{\gamma -2}},(34)$

and

$k_{+}={\left[\frac{N_p}{\sqrt{\pi }}{\left|\frac{\gamma }{2\left(1-\gamma \right)}\right|}^{\frac{1}{2}}\frac{\text{Γ}\left(\frac{1}{\gamma }\right)}{\text{Γ}\left(\frac{1}{\gamma }-\frac{1}{2}\right)}\right]}^{\frac{2\gamma }{\gamma -2}},(35)$

where $\text{Γ}\left(z\right)$ is the Euler gamma function.

We may now reconstruct the normalized concentration field $C\left(x,t\right)$ using eq. 16. For $\gamma <0$ we get

$\begin{array}{l}C\left(x,t\right)=\text{Θ}\left(x_c-\left|x\right|\right){\left(\frac{2-\gamma }{1-\gamma }{D}_0{C}_0^{\gamma }t\right)}^{\frac{-1}{2-\gamma }}\\ {\left[\frac{\gamma }{2\left(1-\gamma \right)}{\left(\frac{2-\gamma }{1-\gamma }{D}_0{C}_0^{\gamma }t\right)}^{\frac{-2}{2-\gamma }}{x}^2+k_{-}\right]}^{-\frac{1}{\gamma }},\end{array}(36)$

where

$x_c={\left(\frac{2k_{-}\left(\gamma -1\right)}{\gamma }\right)}^{\frac{1}{2}}{\left(\frac{2-\gamma }{1-\gamma }{D}_0{C}_0^{\gamma }t\right)}^{\frac{1}{2-\gamma }},(37)$

and for $\gamma >0$

$\begin{array}{l}C\left(x,t\right)={\left(\frac{2-\gamma }{1-\gamma }{D}_0{C}_0^{\gamma }t\right)}^{\frac{-1}{2-\gamma }}\\ {\left[\frac{\gamma }{2\left(1-\gamma \right)}{\left(\frac{2-\gamma }{1-\gamma }{D}_0{C}_0^{\gamma }t\right)}^{\frac{-2}{2-\gamma }}{x}^2+k_{+}\right]}^{-\frac{1}{\gamma }}.\end{array}(38)$

We now calculate $x_{RMS}$ as,

$x_{RMS}^2=\frac{1}{N_p}{{{\displaystyle \int }}^{\text{}}}_{-\infty }^{\infty }dx{x}^{2}C\left(x,t\right)=A_{\pm }{t}^{\frac{2}{2-\gamma }},(39)$

where for $\gamma <0$,

$\begin{array}{l}{A}_{-}=\frac{1}{N_p}{k}_{-}^{\frac{3}{2}-\frac{1}{\gamma }}\frac{\sqrt{\pi }}{2}\frac{\text{Γ}\left(1-\frac{1}{\gamma }\right)}{\text{Γ}\left(\frac{5}{2}-\frac{1}{\gamma }\right)}\\ {\left(\frac{2\left(\gamma -1\right)}{\gamma }\right)}^{\frac{3}{2}}{\left(\frac{2-\gamma }{1-\gamma }{D}_0{C}_0^{\gamma }\right)}^{\frac{2}{2-\gamma }}.\end{array}(40)$

For $0<\gamma <\frac{2}{3}$,

$\begin{array}{l}{A}_{+}=\frac{1}{N_p}{k}_{+}^{\frac{3}{2}-\frac{1}{\gamma }}\frac{\sqrt{\pi }}{2}\frac{\text{Γ}\left(\frac{1}{\gamma }-\frac{3}{2}\right)}{\text{Γ}\left(\frac{1}{\gamma }\right)}\\ {\left(\frac{2\left(1-\gamma \right)}{\gamma }\right)}^{\frac{3}{2}}{\left(\frac{2-\gamma }{1-\gamma }{D}_0{C}_0^{\gamma }\right)}^{\frac{2}{2-\gamma }}.\end{array}(41)$

For $\gamma >2/3$, the integral in Eq. 25 does not converge. This means that as γ approaches 1 there is no continous transition to the ballistic regime as may be indicated by the $\tau =1$ value at $\gamma =1$. For $\gamma <2/3$ the diffusion exponent is given by Eq. 6 which is the result found by Pattle for $\gamma <0$. The fact that there is a gap of γ-values where the integral for $\langle x^2\left(t\right)\rangle$ is undefined does not mean that the solution of Eq. 30 is invalid; it only means that the $C\left(x,t\right)$ distribution becomes too broad. In fact, the one-sided $\langle x\left(t\right)\rangle$ for $x>0$ remains well-defined with $\langle x\left(t\right)\rangle \sim t^{\tau }$.

3 Derivation of the Diffusion Equation From Particle Dynamics

We now turn to stochastic modeling of the process we so far have described using the non-linear diffusion Eq. 7. Following the discussion in the van Kampen book Stochastic Processes in Physics and Chemistry [32], we derive the non-linear diffusion equation, which is an example of a Fokker-Planck equation.

3.1 Particle Model and the Fokker-Planck Equation

A population of $N_p$ particles are propagated by a sequence of random steps of zero mean using a concentration dependent step length. For every time the particle positions, which take on continuous values, are updated, the concentration field $C\left(x,t\right)$ is updated onto a discrete one-dimensional lattice of unit lattice constant. The value of $C\left(x,t\right)$ is simply set to the number of particles between $x_{int}-1/2$ and $x_{int}+1/2$ where $x_{int}$ is the closest integer to x. The particle positions $x_i$ are updated according to the following algorithm

$x_i\to x_i+\text{Δ}{x}_i,(42)$

where

$\text{Δ}{x}_i=\eta g\left(C\left(x_i\right)\right)\sqrt{\text{Δ}t}(43)$

is a Wiener process and η is a random variable with $\langle \eta \rangle =0$ and $\langle {\eta }^2\rangle =1$, where $g\left(C\right)$ may be the normalized concentration. Now, following the discussion in the van Kampen book, Chapter VIII.2 we derive the corresponding Fokker-Planck equation as follows. The Chapman-Kolmogorov or master equation describing the above stochastic process is

$\frac{\partial C\left(x,t\right)}{\partial t}={\displaystyle {\int }_{-\infty }^{\infty }dr}C\left(x-r,t\right)W\left(x-r,r\right)-C\left(x,t\right)W\left(x,-r\right),(44)$

where $W\left(x,r\right)$ is the number of particles per time and length that jump a distance r starting from x. We note that the formalism remains valid also when $W\left(x,t\right)$ depends on x via $C\left(x,t\right)$ itself. Using the standard assumption that $W\left(x,r\right)$ varies slowly with x, but rapidly with r, we may Taylor expand around x. This yields the Fokker-Planck equation

$\frac{\partial C\left(x,t\right)}{\partial t}=\frac{1}{2}\frac{{\partial }^2}{\partial x^2}\left(a_2\left(x\right)C\left(x,t\right)\right),(45)$

where $a_2\left(x\right)$ is the mean squared jump length per time,

$a_2\left(x\right)={\displaystyle \int dr}{r}^{2}W\left(x,r\right)=\frac{\langle \Delta x^2\rangle }{\Delta t}=g{\left(C\right)}^2,(46)$

according to Eq. 43. Setting $g\left(C\right)=b{C}^{-\gamma /2}$ gives

$\frac{\partial C}{\partial t}=\frac{b^2}{2}\frac{{\partial }^2}{\partial x^2}{C}^{1-\gamma },(47)$

and requiring equivalence with Eq. 7 thus implies that $b^2=2/\left(1-\gamma \right)$.

3.2 Itô-Stratonovitch Dilemma

However, the presence of a C-dependence in the diffusivity D introduces an ambiguity in the implementation of Eq. 42, since now $\text{Δ}x$ also depends on C, which in turn depends on all the Δx’s. So, the question is whether one should use $C\left(x\right)$ or $C\left(x+\text{Δ}x\right)$ or perhaps something in between? Since $\text{Δ}x\sim \sqrt{\text{Δ}t}$ these choices are not equivalent.

Stratonovitch read Eq. 42 as [32]

$x\to x+g\left(\frac{C\left(x+\text{Δ}x\right)+C\left(x\right)}{2}\right)\eta \sqrt{\text{Δ}t},(48)$

while Itô read it as

$x\to x+g\left(C\left(x\right)\right)\eta \sqrt{\text{Δ}t}.(49)$

It turns out that it is the choice opted for by Itô that gives Eq. 45, while the Stratonovitch choice gives

$\frac{\partial C}{\partial t}=\frac{1}{2}\frac{\partial }{\partial x}\left(g\frac{\partial }{\partial x}\left(gC\right)\right),(50)$

see the van Kampen book [32], Chapter VI.4 for a derivation of this result. By setting $g\left(C\right)=b{C}^{-\gamma /2}$ again we can write the above equation as

$\frac{\partial C}{\partial t}=\frac{b^2}{2}\frac{1-\gamma /2}{1-\gamma }\frac{{\partial }^2}{\partial x^2}{C}^{1-\gamma },(51)$

and equivalence with Eq. 7 now implies that $b^2=2/\left(1-\gamma /2\right)$.

It is also possible to read read Eq. 42 as

$x\to x+g\left(C\left(x+\text{Δ}x\right)\right)\eta \sqrt{\text{Δ}t},(52)$

This is known as the Hänggi-Klimontovich interpretation [22–24, 33, 34] Setting $g\left(C\right)=b{C}^{-\gamma /2}$ again leads to the equation

$\frac{\partial C}{\partial t}=\frac{b^2}{2\left(1-\gamma \right)}\frac{{\partial }^2}{\partial x^2}{C}^{1-\gamma },(53)$

and equivalence with Eq. 7 now implies that $b^2=2$.

This means that the only difference between the different implementations of Eq. 42 is the magnitude of the random step. In the Itô case the step length has to be a bit smaller than in the Stratonovitch case, which in turn is smaller than in the Hänggi-Klimontovich case, in order to correspond to the same macroscopic descriptions for $\gamma \ne 0$. When $\gamma =0$ the C-dependence of D goes away, and the three interpretations give the same b, as one would expect. In the simulations it is convenient to use the Itô implementation and thus

$\text{Δ}x=\eta \sqrt{\frac{2\text{Δ}t}{\left(1-\gamma \right)}}{C}^{-\gamma /2}.(54)$

The other implementations are complicated by the fact that the step length of the particles depends on the local concentration after the steps are taken. Numerically, this problem is similar to that of implicit solvers for partial differential equations.

4 Simulations

The numerical simulations are carried out using a population of $N_p$ random walkers that take on continous x-values but are sampled to yield a concentration profile $C\left(x,t\right)$ on a discrete set of x-values, as discussed above. First, the particles are initialized on the negative x-axis to produce a step profile, then they are initialized at the same location, so that the initial concentration is a δ-function. The time step is $dt=5{10}^{-5}$, unless otherwise stated, and $N_p=2000$ particles are used.

4.1 The Boltzmann Case

We start by considering the step initial conditions in the simulations by setting $C\left(x,0\right)=\text{Θ}\left(-x\right)$. In the simulations, which must be carried out over a finite domain, we truncate the initial condtion at some $x_{min}<0$. This value, which introduces a second step in $C\left(x,0\right)$, is chosen to be sufficiently large, so as to keep it from affecting the behavior for positive x. In all the simulations $D_0=1$, $C_0=1$.

Figure 1A shows the concentration profile $C\left(x,t\right)$ for different times plotted against the reduced variable $y=x/\sqrt{t}$ using $\gamma =\pm 0.5$. There is data collapse in accordance with Eq. 10, allthough, interestingly, the master curves do in fact depend on γ.

FIGURE 1

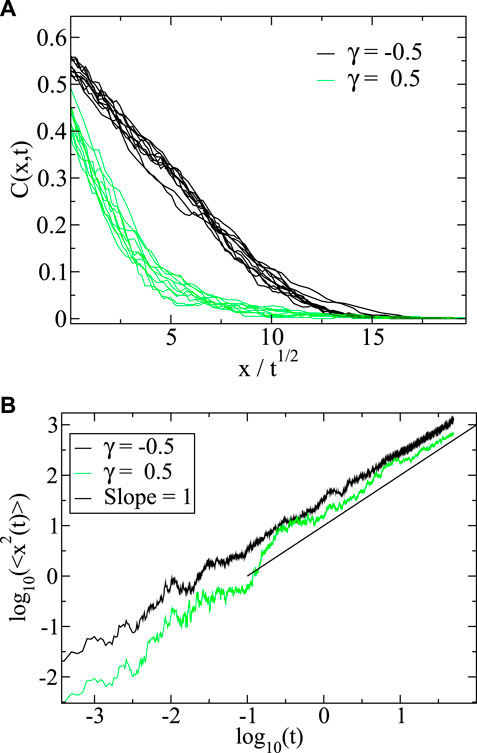
FIGURE 1. (A) Evolution of the step profile when $\gamma =\pm 1/2$ as a function of $x/\sqrt{t}$ at different times. (B) The corresponding right‐handed $\langle x^2\left(t\right)\rangle$, which is evaluated for $x>0$ only. In these simulations $N_p=10000$.

In Figure 1B we show the mean square displacement ${\displaystyle {\sum }_{i=1}^{N_p}{x}_i^2/N_p}$ where the sum runs over all particles with positions $x_i>0$. This quantity is easily calculated as the motion of each particle is traced. The black line shows a slope of 1, thus showing that the step profile leads to normal diffusion.

4.2 The Initial Delta-Function

In this case all the particles start at the origin for $t=0$, thus fulfilling the initial condition of Eq. 12. Figure 2 shows simulations of the concentration and how it evolves after a given time for different γ-values. It is seen that the positive γ-values yield a smaller diffusive spread but with more pronounced tails at larger x. The main effect is that the negative γ-values yield higher diffusivity in the high C regions, while the the positive γ-values suppress the spreading from these regions while enhancing the spread at small C-values.

FIGURE 2

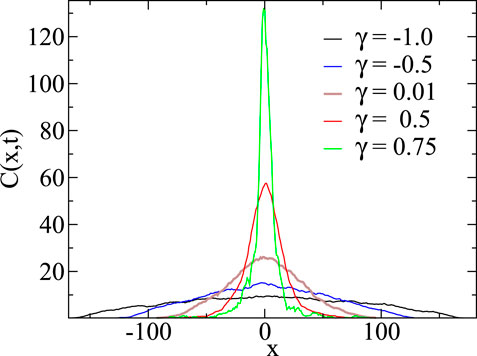
FIGURE 2. Concentration resulting from an initial δ-profile as a function of position for negative and positive γ-values after a time t = 50. For $\gamma \le 0.5$ and a running average over a window of 20 data points was applied, for $\gamma =0.75$ the running average was over 5 data points. In all cases $D_0=1$ (in units of the lattice constant²/timestep) , N_p = 2,000 and $dt={10}^{-4}$.

Figure 3 show simulations compared to the analytic prediction of Eq. 30. We plot $p\left(y\right)=C\left(x,t\right)/f\left(t\right)$ against $y=x/f\left(t\right)$. The figures show a good agreement with theory as well as the expected data collapse between curves sampled at different times. Figure 4A, which shows $\langle x^2\left(t\right)\rangle$, show that, unlike the Boltzmann case, the slopes are different for different γ values. Using a range of γ-values Figure 4B compares the measured values of τ to the prediction in Eq. 6 over the range of γ-values $\left[-1,2/3\right]$. Good agreement between simulations and theory is observed.

FIGURE 3

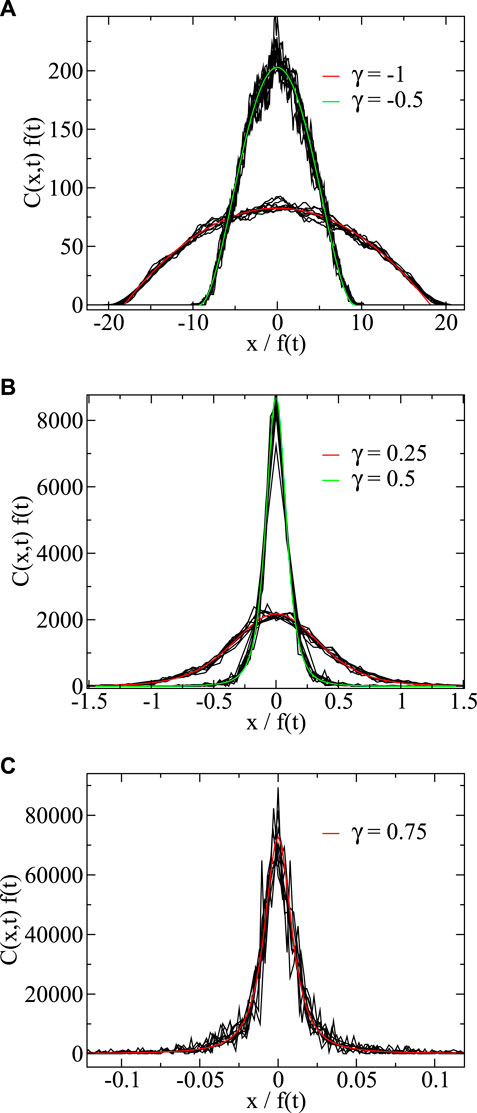
FIGURE 3. Scaled concentration as a function of scaled position for negative (A) and positive (B,C) γ-values. For the negative γ-values $dt={10}^{-5}$, and a running average over a window of 10 data points was applied. For the positive γ-values $dt={10}^{-4}$, no running average was applied. In all cases $D_0=1$ (in units of the lattice constant²/timestep) and N_p = 2,000. The red and green curves show the analytic solutions given in Eq. 30 and Eq. 32.

FIGURE 4

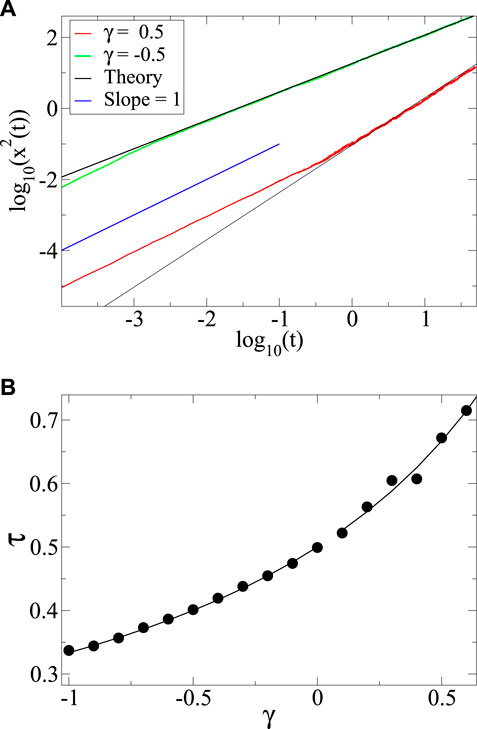
FIGURE 4. (A) Mean square displacement $\langle x^2\left(t\right)\rangle$ for $\gamma =\pm 1/2$. (B) The corresponding diffusion exponent ($•$) compared to the prediction of Eq. 6 (full line) for the range of γ-values where the integral of Eq. 39 converges.

5 Summary and Conclusion

With a power law diffusivity and a delta-function initial condition, there is no intrinsic length scale in the problem. In this case normalizability leads to the scaling form of Eq. 24 leading to the exponent relation Eq. 6 which is the defining characteristic of anomalous diffusion. With a step function initial condition however, as first studied by Boltzmann [26] the solution extends to $x=-\infty$ and cannot be normalized. Hence, in this case, Eq. 24 is replaced by Eq. 10 which gives normal $\tau =1/2$ diffusion. If the step function were modified to a normalizable profile, it would necessarily imply the introduction of a length scale, the width of the profile. In this case one would expect a late-time crossover to the anomalous diffusion of the δ-profile.

We have reviewed the Boltzmann result and demonstrated, as did Pattle 60 years ago [25], that when $D\left(C\right)\sim C^{-\gamma }$ where $\gamma <0$, the non-linear diffusion equation is analytically solvable and leads to anomalous diffusion. We have proceeded, however, to consider the case when $0<\gamma <1$ which is indeed analytically solvable and yields super-diffusion.

We have also constructed a stochastic particle dynamics that satisfies the non-linear diffusion equation at hand, and implemented it computationally. Using this approach, we were able to verify the central results that we were derived analytically, and shown agreement between simulations and theory. In future applications, the particle model may also serve as a stepping stone for generalizations of our present model, that are not analytically tractable.

Both Küntz and Lavallée [15] and Gosh et al. [16] report sub-diffusion when the diffusivity decreases with increasing concentration. Figure 2, where we show the concentration profile $C\left(x,t\right)$ at a given time for different γ seems consistent with this: the smaller (i.e., less positive) the value of γ, the broader the concentration profile. However, Eq. 6, which is verified numerically in Figure 4, concludes the opposite: For positive γ, the exponent $\tau >1/2$, indicating super-diffusion. The value of τ controls the shape of the concentration profile, not how fast it spreads. There is thus a lack of consistency between the results presented here and those of refs. [15] and [16]. A possible explanation is that the more general approach of Refs. [21–24] employing a position-dependent diffusivity that does not depend on the position through the concentration.

As mentioned in the introduction, anomalous diffusion originating from a concentration dependent diffusivity may have been seen in diffusion in granular media [11, 12]. These observations are based on rotating a bi-disperse composition of smaller and large glass beads in a horizontal cylindrical mixer. The mixer is filled with the larger beads except for a small disk of smaller beads. As the cylinder turns, the smaller beads diffuse into the larger beads and the concentration of smaller beads as a function of time and position along the cylinder is recorded. This setup mimics closely the initial conditions that we have studied here, except for Section 2.1, where we assumed a step initially. The connection with the present work is the proposal that the diffusivity of the smaller beads is larger when they are surrounded by other smaller beads than when they are surrounded by the larger beads; the higher the concentration of smaller beads, the larger their diffusivity is. We propose here to prepare the packing in a different way initially. Fill (say) the left half of the cylinder with the smaller beads and the right half with the larger beads. The system is therefore initiated with a step function in the concentration. One would then expect normal diffusion where the front evolves as $x^2\sim t$, i.e., the parabolic law as predicted by Boltzmann.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

AH derived the solution to the diffusion equation and EF designed the numerical simulations and derived the macroscopic description via a Fokker-Planck equation. BB expanded the analytic solution to the positive gamma case.

Funding

This work was partly supported by the Research Council of Norway through its Centers of Excellence funding scheme, project number 262644.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be constructed as a potential conflict of interest.

Acknowledgments

We thank M. R. Geiker, P. McDonald, and members of the ERICA network for interesting discussions. AH thanks Hai-Qing Lin and the CSRC for friendly hospitality.

References

1. Muskat M. The flow of fluids through porous media. J Appl Phys (1937) 8:274–82. doi:10.1063/1.1710292

CrossRef Full Text | Google Scholar

2. Barenblatt GI, Entov VM, Ryzhik VM. Theory of fluid flows through natural rocks. Dordrecht, Netherlands: Kluwer (1990).

CrossRef Full Text | Google Scholar

3. Kamenomostskaya SK. Similar solutions and the asymptotics of filtration equations. Arch Rational Mech Anal (1976) 60:171–83. doi:10.1007/BF00250678

CrossRef Full Text | Google Scholar

4. Zeldovich IB, Kompaneez AS. On the theory of heat propagation with heat conduction depending on temperature. Lectures dedicated on the 70th Anniversary of A. F. Joffe. Moscow, Russia: Akad Nauk SSSR (1950).

Google Scholar

5. Zeldovich Y, Raizer YP. Physics of shock waves and high-temperature hydrodynamic phenomena, Vol. 2. New York, NY: Academic Press (1968).

Google Scholar

6. Gurtin ME, MacCamy RC. On the diffusion of biological populations. Math Biosci (1977) 33:35–49. doi:10.1016/0025-5564(77)90062-1

CrossRef Full Text | Google Scholar

7. Newman WI. Some exact solutions to a non-linear diffusion problem in population genetics and combustion. J Theor Biol (1980) 85:325–34. doi:10.1016/0022-5193(80)90024-7

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Murray JD. Mathematical Biology. Biomathematics. Vol. 19. Berlin, Germany: Springer (1989).

Google Scholar

9. de Azevedo EN, de Sousa PL, de Souza RE, Engelsberg M, Miranda MdeN, Silva MA. Concentration-dependent diffusivity and anomalous diffusion: a magnetic resonance imaging study of water ingress in porous zeolite. Phys Rev E (2006) 73:011204. doi:10.1103/PhysRevE.73.011204

CrossRef Full Text | Google Scholar

10. de Azevedo EN, da Silva DV, de Souza RE, Engelsberg M. Water ingress in Y-type zeolite: anomalous moisture-dependent transport diffusivity. Phys Rev E (2006) 74:041108. doi:10.1103/PhysRevE.74.041108

CrossRef Full Text | Google Scholar

11. Fischer D, Finger T, Angenstein F, Stannarius R. Diffusive and subdiffusive axial transport of granular material in rotating mixers. Phys Rev E (2009) 80:061302. doi:10.1103/PhysRevE.80.061302

CrossRef Full Text | Google Scholar

12. Christov IC, Stone HA. Resolving a paradox of anomalous scalings in the diffusion of granular materials. Proc Natl Acad Sci USA (2012) 109:16012–7. doi:10.1073/pnas.1211110109

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Pritchard D, Woods AW, Hogg AJ. On the slow draining of a gravity current moving through a layered permeable medium. J Fluid Mech (2001) 444:23–47. doi:10.1017/S002211200100516X

CrossRef Full Text | Google Scholar

14. Hansen A, Skagerstam B-S, Tørå G. Anomalous scaling and solitary waves in systems with nonlinear diffusion. Phys Rev E (2011) 83:056314. doi:10.1103/PhysRevE.83.056314

CrossRef Full Text | Google Scholar

15. Küntz M, Lavallée P. Anomalous diffusion is the rule in concentration-dependent diffusion processes. J Phys D Appl Phys (2004) 37:L5. doi:10.1088/0022-3727/37/1/L02

CrossRef Full Text | Google Scholar

16. Gosh SK, Cherstvy AG, Grebenkov DS, Metzler R. Anomalous non-Gaussian tracer diffusion in crowded two-dimensional environments. New J Phys (2016) 18:013027. doi:10.1088/1367-2630/18/1/013027

CrossRef Full Text | Google Scholar

17. Bouchaud J-P, Georges A. Anomalous diffusion in disordered media: statistical mechanisms, models and physical applications. Phys Rep (1990) 195:127–293. doi:10.1016/0370-1573(90)90099-N

CrossRef Full Text | Google Scholar

18. Metzler R, Klafter J. The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Phys Rep (2000) 339:1–77. doi:10.1016/S0370-1573(00)00070-3

CrossRef Full Text | Google Scholar

19. Levi L, Krivolapov Y, Fishman S, Segev M. Hyper-transport of light and stochastic acceleration by evolving disorder. Nature Phys (2012) 8:912–7. doi:10.1038/nphys2463

CrossRef Full Text | Google Scholar

20. Peccianti M, Morandotti R. Beyond ballistic. Nat Phys (2012) 8:858–9. doi:10.1038/nphys2486

CrossRef Full Text | Google Scholar

21. Cherstvy AG, Chechkin AV, Metzler R. Anomalous diffusion and ergodicity breaking in heterogeneous diffusion processes. New J Phys (2013) 15:083039. doi:10.1088/1367-2630/15/8/083039

CrossRef Full Text | Google Scholar

22. Cherstvy AG, Chechkin AV, Metzler R. Particle invasion, survival, and non-ergodicity in 2D diffusion processes with space-dependent diffusivity. Soft Matter (2014) 10:1591–601. doi:10.1039/C3SM52846D

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Regev S, Grønbech-Jensen N, Farago O. Isothermal Langevin dynamics in systems with power-law spatially dependent friction. Phys Rev E (2016) 94:012116. doi:10.1103/PhysRevE.94.012116

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Leibovich N, Barkai E. Infinite ergodic theory for heterogeneous diffusion processes. Phys Rev E (2019) 99:042138. doi:10.1103/PhysRevE.99.042138

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Pattle RE. Diffusion from an instantaneous point source with a concentration-dependent coefficient. Q J Mechanics Appl Math (1959) 12:407–9. doi:10.1093/qjmam/12.4.407

CrossRef Full Text | Google Scholar

26. Barenblatt GI. Scaling, self-similarity, and intermediate asymptotics. Cambridge, UK: Cambridge University Press (1996). doi:10.1017/CBO9781107050242

CrossRef Full Text | Google Scholar

27. Witelski TP, Bernoff AJ. Self-similar asymptotics for linear and nonlinear diffusion equations. Stud Appl Math (1998) 100:153–93. doi:10.1111/1467-9590.00074

CrossRef Full Text | Google Scholar

28. Nabokov R. An inverse problem for the porous medium equation: identification of the permeability. In: J Gottlieb, and P DuChateau, editors Parameter identification and Inverse problems in hydrology, geology and ecology, water science and technology library. Vol. 23. Dordrecht, Netherlands: Springer (1996). doi:10.1007/978-94-009-1704-0_9

CrossRef Full Text | Google Scholar

29. Boltzmann L. Zur Integration der Diffusionsgleichung bei variabeln Diffusionscoefficienten. Ann Phys (1894) 289:959–64. doi:10.1002/andp.18942891315

CrossRef Full Text | Google Scholar

30. Crank J. The mathematics of diffusion. Oxford, UK: Oxford University Press (1975).

Google Scholar

31. Hristov J. Integral solutions to transient nonlinear heat (mass) diffusion with a power-law diffusivity: a semi-infinite medium with fixed boundary conditions. Heat Mass Tran (2016) 52:635–55. doi:10.1007/s00231-015-1579-2

CrossRef Full Text | Google Scholar

32. van Kampen NG. Stochastic processes in physics and chemistry. 3rd ed. Amsterdam, Netherlands: North-Holland (2007).

Google Scholar

33. Volpe G, Wehr J. Effective drifts in dynamical systems with multiplicative noise: a review of recent progress. Rep Prog Phys (2016) 79:053901. doi:10.1088/0034-4885/79/5/053901

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Li Y, Mei R, Xu Y, Kurths J, Duan J, Metzler R. Particle dynamics and transport enhancement in a confined channel with position-dependent diffusivity. New J Phys (2020) 22:053016. doi:10.1088/1367-2630/ab81b9

CrossRef Full Text | Google Scholar