
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Phys. , 07 October 2020
Sec. Nuclear Physics
Volume 8 - 2020 | https://doi.org/10.3389/fphy.2020.00379
This article is part of the Research Topic The Future of Nuclear Structure: Challenges and Opportunities in the Microscopic Description of Nuclei View all 11 articles
Over the last decade, new developments in Similarity Renormalization Group techniques and nuclear many-body methods have dramatically increased the capabilities of ab initio nuclear structure and reaction theory. Ground and excited-state properties can be computed up to the tin region, and from the proton to the presumptive neutron drip lines, providing unprecedented opportunities to confront two- plus three-nucleon interactions from chiral Effective Field Theory with experimental data. In this contribution, I will give a broad survey of the current status of nuclear many-body approaches, and I will use selected results to discuss both achievements and open issues that need to be addressed in the coming decade.
Over the past decade, the reach and capabilities of ab initio nuclear many-body theory have grown exponentially. The widespread adoption of Renormalization Group (RG) techniques, in particular the Similarity Renormalization Group (SRG) [1], and Effective Field Theory (EFT) [2–4] in the 2000s laid the foundation for these developments. Consistent two-nucleon (NN) and three-nucleon (3N) interactions from chiral EFT were quickly established as a new “standard” inputs for a variety of approaches, which made true multi-method benchmarks possible. The SRG equipped us with the ability to dial the resolution scale of nuclear interactions, accelerating model-space and many-body convergence alike. Suddenly, even (high-order) Many-Body Perturbation Theory (MBPT) became a viable tool for rapid benchmarking [5, 6], and exact diagonalization approaches were able to extend their reach into the lower sd-shell [7–9]. A variety of computationally efficient techniques with controlled truncations were readied, like the Self-Consistent Green's Function method (SCGF) [10], the In-Medium SRG (IMSRG) [11] and Coupled Cluster (CC) [12], the prodigal son [13, 14] who returned home after finding success in foreign lands, i.e., quantum chemistry and solid state physics.
At the start of the last decade the race was on, and Figure 1 documents the progress that ensued. Calculations started at closed-shell nuclei [15–19] and their vicinity before extending to semi-magic isotopic chains with the development of the Multi-Reference IMSRG [20, 21] and Gor'kov SCGF [22, 23] techniques, and just a couple of years later, the use of CC [24, 25] and IMSRG [26, 27] techniques to construct valence-space interactions opened all nuclei that were amenable to Shell Model calculations for exploration. Owing to very recent developments that extend these combined approaches to multi-shell valence spaces, the open region between the nickel and tin isotopic chain is poised to be filled in rapidly [28]. Development of the no-core versions of these methods has continued as well, and made direct calculations for intrinsically deformed nuclei possible [29].
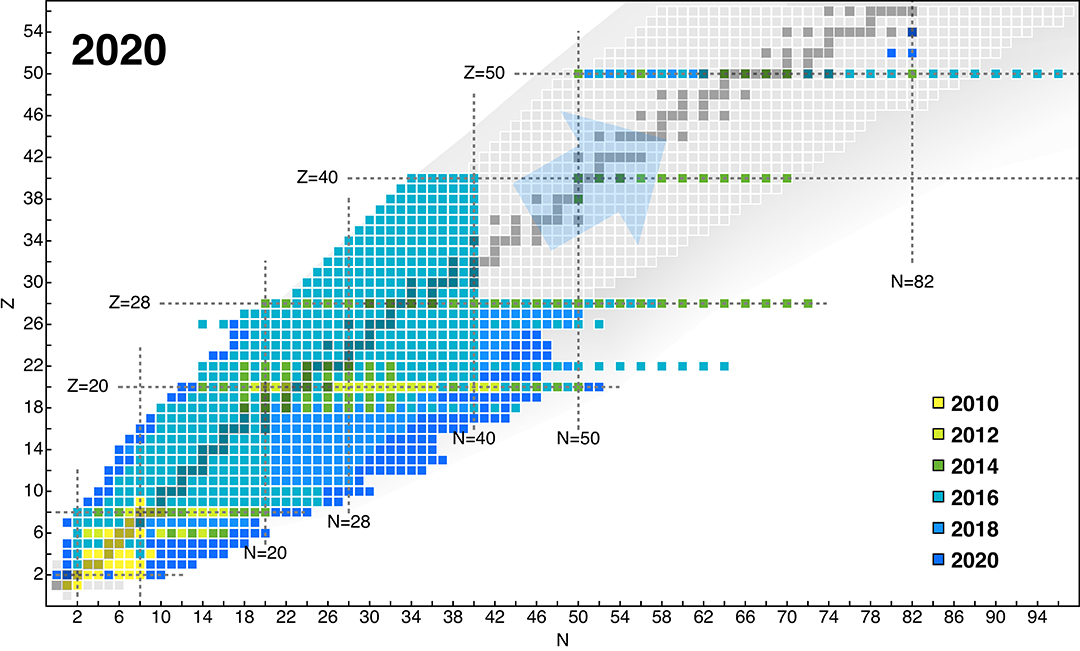
Figure 1. Progress in ab initio nuclear structure calculations over the past decade. The blue arrow indicates nuclei that will become accessible with new advances for open-shell nuclei in the very near term (see section 2.3).
The growing reach of ab initio many-body methods made it possible to confront chiral NN+3N forces with a wealth of experimental data, revealing shortcomings of those interactions and sparking new efforts toward their improvement. There were other surprises along the way, some good, some bad. Due to the benchmarking capabilities and further developments in many-body theory, we are now often able to understand the reasons for the failure of certain calculations (see, e.g., reference [27])—hindsight is 2020, as they say1.
The present collection of Frontiers in Physics contributions provides us with a timely and welcome opportunity to attempt a look back at some of the impressive results from the past decade and the developments that brought us here, as well as a look ahead at the challenges to come as we enter a new decade.
Let us conclude this section with a brief outline of the main body of this work. In section 2, I will discuss the main ingredients of modern nuclear many-body calculations: The input interactions from chiral EFT, the application of the SRG to process Hamiltonians and operators, and eventually a variety of many-body methods that are used to solve the Schrödinger equation. I will review key ideas but keep technical details to a minimum, touching only upon aspects that will become relevant again later on. Section 3 presents selected applications from the past decade, and discusses both the advances they represent as well as open issues. This will provide a starting point for section 4, which presents ideas for addressing the aforementioned issues and highlights important directions for the next decade.
Naturally, the discussion in sections 3 and 4 is highly subjective. While this work grew from a more restricted scope into a rambling, albeit not random, walk through the landscape of modern nuclear many-body theory, it still cannot encompass the field in its entirety. The upside is that this reflects the breadth of ideas that are being pursued by the ab initio nuclear theory community, including those with cross-disciplinary impact, as well as our community's ability to attract junior researchers. The downside is that the present work can only scratch the tip of the iceberg of impressive results from the past decade. I hope that the readers will use it as a jumping-off point for delving into the cited literature, including the contributions to this volume.
Quantum Chromodynamics (QCD) is the fundamental theory of the strong interaction between quarks and gluons. One of its characteristic features is that the strong coupling, which governs the strength of interaction processes, is sufficiently small to allow perturbative expansions at high energies, but large in the low-energy domain relevant for nuclear structure and dynamics [30, 31]. This makes the description of all but the lightest nuclei at the QCD level inefficient at best, and impossible at worst. However, strongly interacting matter undergoes a phase transition that leads to the confinement of quarks in composite hadronic particles, like nucleons and pions. These particles can be used as the degrees of freedom for a hierarchy of EFTs that describe the strong interaction across multiple scales.
Following Weinberg [32, 33], one can construct effective Lagrangians that consist of interactions that are consistent with the symmetries of QCD and organized by an expansion in (Q/Λ). Here, Q is a typical momentum of the interacting system, and Λ is the breakdown scale of the theory, which is associated with physics that is not explicitly resolved. In chiral EFT with explicit nucleons and pions, Λ = Λχ is traditionally considered to be in the range 700 − 1000 MeV, although newer analyses of observable truncation errors using Bayesian methods favor slightly lower values [34–36]. From a chiral EFT Lagrangian, one can then construct a systematic low-momentum expansion of nuclear interactions, as shown in Figure 2 (see references [2, 3, 32, 37, 39]). These interactions consist of (multi-)pion exchanges between nucleons, indicated by dashed lines, as well as nucleon contact interactions. The different types of vertices are proportional to the low-energy constants (LECs) of chiral EFT, which encode physics that is not explicitly resolved because it involves either a high momentum scale or excluded degrees of freedom. Eventually, one hopes to calculate these LECs directly from the underlying QCD either through matching or renormalization group evolution of the couplings (see section 2.2), but at present, the LECs are fit to experimental data [3, 4, 39–41].
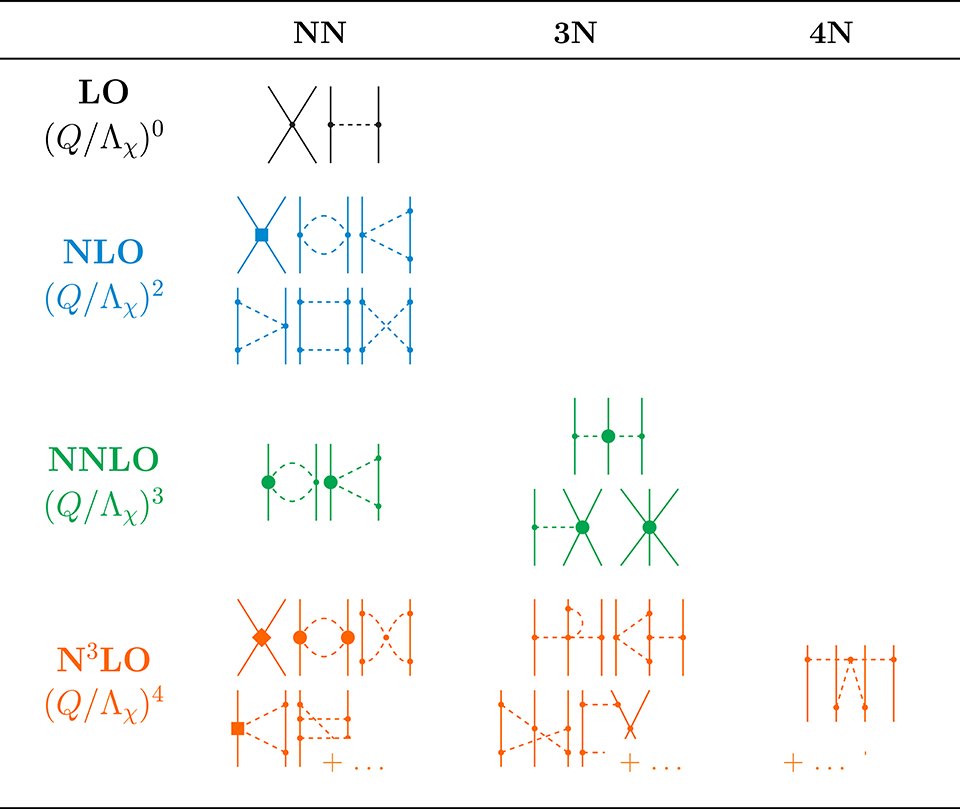
Figure 2. Chiral two-, three-, and four nucleon forces through next-to-next-to-next-to-leading order (N3LO) (see, e.g., [2, 37, 38]). Dashed lines represent pion exchanges between nucleons. The large solid circles, boxes and diamonds represent vertices that are proportional to low-energy constants (LECs) of the theory (see text).
The power counting scheme shown in Figure 2 yields consistent two-, three- and higher many-nucleon interactions, and explains their empirical hierarchy, i.e., VNN > V3N > V4N > …. Moreover, one can readily extend the chiral Lagrangian with couplings to the electroweak sector by gauging the derivatives. In this way, nuclear interactions and electroweak currents depend on the same LECs, and one can use electroweak observables to constrain their values [42–45]. Last but not least, the existence of a power counting scheme offers inherent diagnostics for assessing the theoretical uncertainties that result from working at a given chiral order [34–36]. This is especially useful since issues relating to the regularization and renormalization of these interactions remain (see, e.g., references [2, 46–51] and section 4.4).
Renormalization group methods are a natural companion to the hierarchy of EFTs for the strong interaction. They provide the means to systematically dial the resolution scales and cutoffs of these theories, and this makes it possible, at least in principle, to connect the different levels in our hierarchy of EFTs. The RGs also expand the diagnostic toolkit for assessing the inherent consistency of EFT power counting schemes, e.g., by tracing the enhancement or suppression of specific operators, or by identifying important missing operators.
In nuclear many-body theory, the SRG has become the method of choice. In contrast to Wilsonian RG [52], which is based on decimation, i.e., integrating out high-momentum degrees of freedom, SRGs decouple low- and high-momentum physics using continuous unitary transformations. Note that this concept is not limited to RG applications: we can construct transformations that adapt a many-body Hamiltonian or other observables of interest to our needs, e.g., to extract eigenvalues [11, 53], or impose specific structures on the operator [1, 26, 27, 54, 55].
We define the flowing Hamiltonian
where H(s = 0) is the starting Hamiltonian, and the flow parameter s parameterizes the unitary transformation. Instead of making an ansatz for U(s), we take the derivative of Equation (1) and obtain the operator flow equation
where the anti-Hermitian generator η(s) is related to U(s) by
We can choose η(s) to achieve the desired transformation of the Hamiltonian as we integrate the flow Equation (2) for s → ∞. Wegner [56] originally proposed a class of generators of the form
that is widely used in applications, although it gives rise to stiff flow equations, and more efficient alternatives exist for specific applications [1, 11, 53]. Wegner generators are constructed by splitting the Hamiltonian into suitably chosen diagonal (Hd(s)) and off-diagonal (Hod(s)) parts. These labels are a legacy of applying this generator to drive finite-dimensional matrices toward diagonality. For our purposes, they reflect the desired structure of the operator in the limit s → ∞: We want to keep the diagonal part and drive Hod(s) to zero by evolving it via Equation (2) (see references [1, 11, 53, 56, 57]).
To implement the operator flow equation (23), we need to express η(s) and H(s) in a basis of suitable operators {Oi}i∈ℕ,
where ηi(s) and Hi(s) are the running couplings of the operators. If the algebra of the operators Oi is closed naturally or with some truncation, we have
and Equation (2) becomes a system of flow equations for the coupling coefficients:
where the bold quantities collect the algebra's structure constants and the running couplings, respectively. From this discussion, it is clear that the choice of the Oi can have a significant effect on the size of the system of flow equations, as well as the quality of any introduced truncations.
An important application of the SRG in nuclear many-body theory is the dialing of the operators' resolution scales. This is achieved by using the Wegner-type generator
to band-diagonalize the Hamiltonian in momentum space, and thereby decouple low- and high-momentum physics in the operators and eigenstates. As indicated in Equation (9) the flow is typically re-parameterized by λ = s−1/4, which characterizes the width of the band in momentum space and controls the magnitude of the momentum transferred in an interaction process. For example, |ki − kf| ≲ λ in a two-nucleon system [1, 58].
Nowadays, the momentum space evolution is regularly performed for two- and three-nucleon forces [1, 59–62]. In light of the previous discussion, it can be understood as choosing the operator basis
with creation and annihilation operators referring to (discretized) single-particle momentum modes, and truncating four- and higher-body terms that appear when the commutators of the basis operators are evaluated. Since the commutator of an M-body and an N-body operator in the basis (10) acts at least on K = max(M, N) particles, the SRG evolution is exact for A ≤ 3 systems under this truncation [59, 61]. It is implemented by working with the matrix representations of H(s) in two- and three-nucleon systems, whose entries correspond to the coupling constants in our chosen operator basis (cf. Equation 6). For efficiency, an additional basis change is made to center-of-mass and relative coordinates.
In principle, the strategy for evolving nuclear interactions toward some form of “diagonality” could be used to determine eigenvalues of many-body Hamiltonians, but the computational cost for dealing either with exponentially growing matrix representations or induced terms of high particle rank is prohibitive. This motivates the implementation of the flow equation with a different choice of basis operators in the In-Medium SRG (see section 2.3.3).
Let us now discuss commonly used many-body methods for solving the nuclear Schrödinger equation. Roughly speaking, they fall into two categories: configuration space methods that expand the nuclear eigenstates on a basis of known many-body states, or coordinate-space methods that work directly with the wave function and optimize them in some fashion. Our goal is to use approaches that systematically converge to an exact result, e.g., by adding more and more particle-hole excitations of a selected reference state to the many-body basis of a configuration space, or by exhausting the distribution of meaningful wave function parameters.
The discussion in the following sections will be light on mathematical details, which can be found in more specialized articles and reviews, including other contributions to the present volume. The goal is to review only certain ideas that will become relevant later on.
Let us briefly discuss the general setup of the configuration-space approaches. We choose a single-particle basis, e.g., the eigenstates of a harmonic oscillator, and use it to construct a basis of Slater determinants for the many-body Hilbert space. Usually, the many-body basis is organized by selecting a reference state |Φ〉 and constructing its particle-hole excitations in order to account for the natural energy scales of the system under consideration. For further use, we define
where particle (a, b, …) and hole (i, j, …) indices run over unoccupied and occupied single-particle states, respectively2. The parentheses indicate that the strings of creation and annihilation operators are normal ordered with respect to the reference state. They are related to the original operators by
where the indices p, q, … run over all single-particle states, and the contractions are defined as
(see, e.g., references [11, 53] for more details).
Let us now consider a Hamiltonian containing up to two-body interactions, for simplicity. In normal-ordered form, it is given by
where E is the energy expectation value of the reference state, while f and Γ are the mean-field Hamiltonian and residual two-body interaction, respectively [11, 53]. Our task is to solve the many-body Schrödinger equation for this Hamiltonian to determine its eigenvalues and eigenstates, either in an approximate fashion or by exactly diagonalizing its matrix representation, which is shown in Figure 3A.
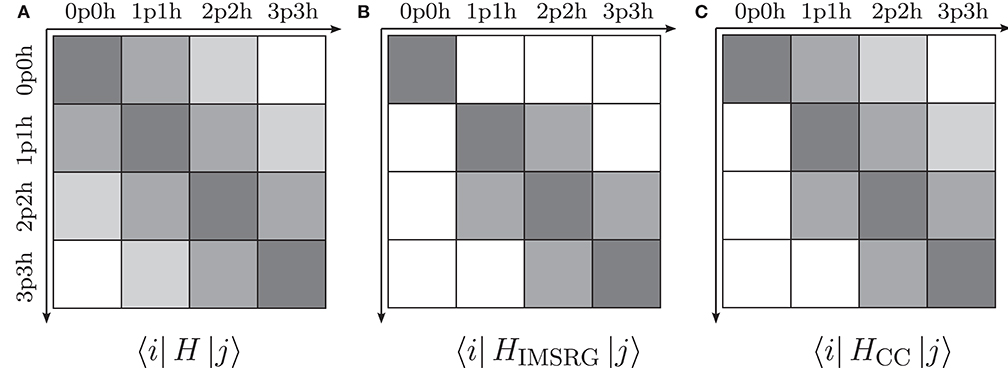
Figure 3. Decoupling of particle-hole excitations from a 0p0h reference state: the schematic matrix representation of the initial Hamiltonian H0 (A) and the transformed Hamiltonians obtained from IMSRG (B) and CC (C), respectively (see text for details).
Many-Body Perturbation Theory (MBPT) is the simplest configuration-space approach for capturing correlations in interacting quantum many-body systems. It has enjoyed widespread popularity in treatments of the many-electron system since the early days of quantum mechanics, and it comes in a myriad of flavors (see, e.g., reference [64] and references therein). A major factor in its success is that the Coulomb interaction is sufficiently weak to make perturbative treatments feasible. Applications in nuclear physics had long been hindered by the strong short-range repulsion and tensor interactions in realistic nuclear forces, despite the introduction of techniques like Brueckner's G matrix formalism that were meant to resum the strong correlations from these contributions [65–68]. These issues were overcome with the introduction of the SRG evolution to low resolution scales, which makes nuclear interactions genuinely perturbative, albeit at the cost of inducing three-and higher many-body interactions [1]. As a consequence, MBPT has undergone a renaissance in nuclear physics in the past decade [69], leading to efficient applications for the computation of ground-state properties [5, 6, 70] and the construction of effective Shell Model interactions and operators (see, e.g., references [71–74], or the reviews [75, 76], and references therein). These successes have also motivated the development of novel types of MBPTs [69, 77, 78].
In a nutshell, MBPT assumes that the Hamiltonian can be partitioned into a solvable part H0 and a perturbation HI,
which then allows an order-by-order expansion of its eigenvalues and eigenstates in powers of HI, usually starting from a mean-field solution. In the Rayleigh-Schrödinger formulation of MBPT, which is widely used for its convenience,
where E(0) is the unperturbed energy. If we assume that the reference Slater determinant |Φ〉 has been variationally optimized by solving the Hartree-Fock equations, E0 in Equation (15) is the Hartree-Fock energy and f is diagonal. Then we can introduce the so-called Møller-Plesset partitioning,
and note that the Slater determinants of the basis introduced in section 2.3.1 are eigenstates of H0:
The eigenvalues of H0 then become the unperturbed energies appearing in Equations (17), (18), and the energy including a finite number of correction terms can be evaluated straightforwardly. For example, the ground-state energy through second order is given by
For a more detailed discussion, we refer to reference [69] and references therein.
The expression (21) can serve to illustrate both advantages and drawbacks of an MBPT treatment of nuclei. We see that the second-order energy can be evaluated very efficiently, since it requires a non-iterative calculation whose computational effort scales polynomially in the single-particle basis size N, namely as . The reason is that the construction of the Hamiltonian matrix (Figure 3A) can be avoided. In fact, the computational scaling is even more favorable, because we can distinguish particle and hole states and achieve , and we typically have Nh ~ A ≪ Np. Although there is a proliferation of terms with increasing order [63, 69, 79], MBPT is still fundamentally polynomial and therefore more efficient than an exact diagonalization, whose cost scales exponentially with N. It is also clear from Equation (21) that the expansion of the exact eigenvalue will break down if one (or more) of the energy denominators become small due to (near-)degeneracies of the unperturbed energies. Thus, MBPT works best for ground states in systems with a strong energy gap, i.e., closed-shell nuclei, although extensions for more complex scenarios exist (see references [63, 68, 69] and references therein). A noteworthy new development is Bogoliubov MBPT, in which particle number symmetry is broken and eventually restored [77, 80, 81].
As mentioned at the beginning of this section, MBPT can be used to derive effective interactions and operators. The primary tool for such efforts is the -box or folded-diagram resummation of the perturbative series (see references [75, 76, 82] and references therein).
As already mentioned in our discussion of the SRG in section 2.2, we could envision applying SRG techniques not only to preprocess the nuclear interactions, but also to compute eigenvalues and eigenstates. For all but the lightest nuclei, applying the SRG to the Hamiltonian matrix is hopeless, so we work with the operators instead.
Let us again consider the matrix representation shown in Figure 3A. We want to design a transformation that will decouple the one-dimensional 0p0h block in the Hamiltonian matrix, spanned by a reference state Slater determinant |Φ〉, from all excitations as the flow equation (2) is integrated. The matrix element in this block will then be driven toward an eigenvalue (up to truncation errors), and the unitary transformation becomes a mapping between the reference Slater determinant and the exact eigenstate (see below). In principle, we could use a suitably chosen reference to target different eigenstates, e.g., by taking references which are expected to have a large overlap with the target state (see section 10.3 in reference [58]). In practice, we usually target the ground state by using a Hartree-Fock Slater determinant as our reference.
To implement the operator flow, we need to choose an operator basis to express H(s) and the generator η(s). Instead of using the basis (10), we switch to operators that are normal ordered with respect to the reference state |Φ〉:
Commutators of these operators can feed into terms of lower particle rank: For instance, a commutator of M-body and N−body operators generates |M − N|-body through (M + N − 1)-body operators, while the lower bound for the basis (10) is max(M, N) (cf. section 2.2). As a result, the complexity of the flow equations for the operators' coupling coefficients increases due to the appearance of additional terms that depend on the contractions introduced in Equations (12) and (13). These contractions translate into density matrices (or occupation numbers)—hence the name In-Medium SRG. At the same time, we achieve a reduction of the truncation error because only the residual, contraction-independent parts of the operators (12) and (13) are omitted. In the majority of applications to date, we truncate all operators and their commutators at the two-body level, defining the IMSRG(2) truncation scheme. More details can be found in references [11, 53, 58, 76].
In the chosen basis we now identify the parts of the Hamiltonian that are responsible for coupling the reference state to 1p1h and 2p2h excitations, and define the off-diagonal Hamiltonian (cf. 2.2) as
We use this Hod to construct a generator, either using Wegner's ansatz (4) or an alternative choice [11, 53]. Plugging the generator into the operator flow equation (2), we obtain a system of flow equations for the energy E(s) and the coefficients fpq(s), Γpqrs(s), … (cf. Equation 8 and references [11, 53, 76]). By integrating these flow equations, we evolve the Hamiltonian operator so that its matrix representation assumes the shape shown in Figure 3B. We note that the suppression of Hod not only leads to the desired ground-state decoupling, but also eliminates the outermost band in the Hamiltonian matrix. This simplification makes the evolved Hamiltonian an attractive input for other approaches, e.g., configuration interaction (CI) or equation-of-motion methods (see references [27, 29, 76, 83–86] and discussion below).
Valence-space IMSRG. Soon after introducing the IMSRG in nuclear physics [87], Tsukiyama, Bogner, and Schwenk proposed the use of the IMSRG flow to derive Hamiltonians (and other effective operators) for use in nuclear Shell Model calculations [88]. This is achieved by partitioning the single-particle basis into core, valence, and beyond-valence states, normal ordering all operators with respect to a Slater determinant describing the closed-shell core, and extending the definition of the off-diagonal Hamiltonian (23) to include all terms that couple valence and non-valence states. The eigenvalue problem for the evolved Hamiltonian can then be solved in the valence space with widely available Shell model codes [89–93]. After a study of the oxygen isotopic chain revealed an increasing overbinding away from the chosen core [26], we adopted a normal-ordering scheme that uses an ensemble of Slater determinants to account for partially filled shells in open-shell nuclei [27, 54]. This improved operator basis, along with the valence decoupling procedure and subsequent Shell Model diagonalization defines what is nowadays called the valence-space IMSRG (VS-IMSRG)—see reference [76] for a recent review.
Correlated reference states and multi-reference IMSRG. Another important development was the extension of the IMSRG formalism to correlated reference states, in the so-called Multi-Reference IMSRG (MR-IMSRG) [20, 53, 58]. The unitarity of the IMSRG transformation allows us to control to what extent correlations are described by either the Hamiltonian or the reference state. We can see this by considering the stationary Schrödinger equation and applying U(s):
The transformation shifts correlations from the wave function into the evolved, RG-improved Hamiltonian H(s) = U(s)HU†(s), and any many-body method that uses this Hamiltonian as input now needs to describe U(s)|Ψk〉, which should be less correlated than the exact eigenstate |Ψk〉. In the extreme cases, U(s) = 1 and the wave function carries all correlations, or U(s) has shifted all correlations into the Hamiltonian and |Φ〉 = U(s)|Ψ〉 is a simple Slater determinant.
Correlated reference states can be particularly useful for the description of systems with strong static or collective correlations, like open-shell nuclei with strong intrinsic deformation or shape coexistence. Reference states that describe these types of correlations efficiently, e.g., through symmetry breaking and restoration (also see section 2.3.4), are an ideal complement to the IMSRG transformation, which excels at capturing dynamic correlations, involving the excitation of a few particles up to high energies. This complementarity is schematically illustrated in Figure 4: Collective correlations that would require as much as an IMSRG(A) calculation in the conventional approach are built into the reference state, and an MR-IMSRG(2) calculation is sufficient to treat the bulk of the dynamical correlations in the system.
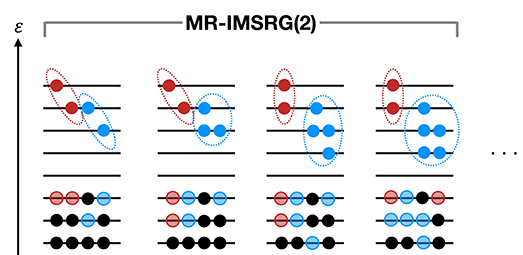
Figure 4. Schematic view of correlations in nuclei. Solid circles indicate nucleons, transparent circles hole states, and dashed ellipses indicate correlations between nucleons. Certain 2p2h, 3p3h and higher correlations (indicated in blue) are built into a correlated wave function that then serves as the reference state for an MR-IMSRG(2) calculation (capturing correlations indicated in red), while up to an IMSRG(A) calculation would be needed for an equivalent description in the conventional framework.
Reference state correlations are built into the MR-IMSRG framework by using a generalized normal ordering [53, 94, 95] that is extended with contractions of higher rank, namely the irreducible k-body density matrices λ(k):
etc. The irreducible densities matrices encode the correlation content of an arbitrary reference state |Φ〉, hence they vanish for Slater determinants. While the basis of normal-ordered operators superficially is the same as in the conventional IMSRG, shown in Equation (22), the inclusion of the irreducible densities (cf. Equations 12 and 13) equips the basis with the capability to describe the correlations that are present in the reference state, which in turn should help to reduce MR-IMSRG truncation errors. To understand this, let us assume that we know the ground state of our system, and we normal order the Hamiltonian with respect to this correlated state. Then the zero-body part of the normal ordered Hamiltonian already is the exact ground-state energy, and the normal-ordered one-, two-, and higher-body parts do not matter at all for our result, and neither does their evolution under an exact or truncated MR-IMSRG flow. Thus, the better the reference state matches the ground state, the less work the MR-IMSRG evolution and any subsequent many-body method have to do to obtain the correct ground-state energy.
Computational scaling and Magnus expansion. The computational scaling of all three IMSRG flavors discussed here—traditional, VS-IMSRG, and MR-IMSRG—is governed by the truncation scheme. If we truncate operators and commutators at the two-body level, as briefly mentioned above, the number of flow equations scales as with the single-particle basis size N, and the computational effort for evaluating the right-hand sides as . This holds despite the greater complexity of the MR-IMSRG flow equations, which contain terms containing irreducible two- and higher-body density matrices.
Any observables of interest must, in principle, be evolved alongside the Hamiltonian for consistency, which would create a significant overhead. In practice, we can address this issue by using the so-called Magnus formulation of the IMSRG [58, 76, 83, 96]: Assuming that the IMSRG transformation can be written as an explicit exponential, U(s) = expΩ(s), we can solve a single set of flow equations for the anti-Hermitian operator Ω(s) instead of evolving observables separately. All operators of interest can then be computed by applying the Baker-Campbell-Hausdorff expansion to O(s) = exp[Ω(s)]O exp[−Ω(s)].
IMSRG hybrid methods. As noted earlier in this section, the conventional IMSRG evolution makes the matrix representation of the Hamiltonian more diagonal by suppressing couplings between the npnh excitations of the reference state. This implies a decoupling of energy scales of the many-body system, analogous to the decoupling of momentum scales by the free-space SRG, although there are differences in detail that are associated with the operator bases in which the flow is expressed (cf. Equations 10 and 22).
From this realization, it is not a big step to consider using the IMSRG to construct RG-improved Hamiltonians for applications in other methods, defining novel hybrid approaches. In fact, even the original IMSRG formulation can be understood from this perspective: The evolution generates a Hamiltonian that yields the exact ground-state energy (up to truncations) in a Hartree-Fock calculation, except the HF equations are automatically satisfied for the evolved H, and we can read off the ground-state energy directly. The same Hamiltonian can then be used as input for EOM methods to compute excitation spectra [83]. Likewise, the VS-IMSRG produces an RG-improved Hamiltonian that serves as input for a Shell Model diagonalization.
Applying the same logic as in the VS-IMSRG case, the IMSRG has been merged with the No-Core Shell Model (NCSM, see section 2.3.6) into the In-Medium NCSM [84, 97]. In this approach, the IMSRG improves the Hamiltonian with dynamical correlations from high-energy few-nucleon excitations that would require enormously large model spaces in the conventional NCSM, and the exact diagonalization in a small model space describes the dynamics of many-nucleon excitations. The NCSM as the “host” method is rooted in the same particle-hole expansion picture as the IMSRG itself, but this is not a requirement. Another new hybrid method is the In-Medium Generator Coordinate Method (IM-GCM), which relies on the GCM as a host method to capture collective correlations [29, 85, 86]. In this approach, a many-body basis is generated by restoring the symmetries of mean field solutions with various types of shape and gauge configuration constraints, which is very different from the particle-hole excitation basis discussed so far.
The Coupled Cluster (CC) method [12, 63] is an older cousin of the IMSRG approach. It can also be understood as a decoupling transformation of the Hamiltonian, but in contrast to the IMSRG, it relies on a non-unitary similarity transformation (see Figure 3). Traditionally, CC is motivated by an exponential ansatz for the exact wave function of a system,
where |Φ〉 is a reference Slater determinant, and T is the so-called cluster operator. This operator is expanded on particle-hole excitations,
with the cluster amplitudes tai, tabij, …. In practical applications, the T is truncated to include up to 2p2h (CC with Singles and Doubles, or CCSD) or 3p3h terms (CCSDT, including Triples). Various schemes exist for iteratively or non-iteratively including subsets of Triples [12, 63, 98–100]. When it acts on the reference state |Φ〉, eT admixes arbitrary powers of few-particle, few-hole excitations. Note, however, that the cluster operator T is not anti-Hermitian because it lacks de-excitation operators, and therefore eT is not unitary.
The cluster amplitudes are determined by demanding that the transformed Hamiltonian,
does not couple the reference to 1p1h and 2p2h states (see Figure 3). Using notation introduced in section 2.3.1, the decoupling conditions lead to the following system of non-linear equations:
Here, ECC is the CC ground-state energy, which corresponds to the one-dimensional block in the upper left of Figure 3C and is analogous to the zero-body part of the IMSRG-evolved Hamiltonian, as discussed in the previous section. The other blocks in the first column of the matrix vanish because of the CC Equations (30)–(32).
Since the CC transformation is non-unitary, one needs to be careful when one evaluates observables using the CC wave function, or uses HCC as input for equation-of-motion calculations or other applications [12, 63]. For instance, the non-Hermiticity of HCC forces us to consider left and right eigenstates separately. This is a drawback compared to unitary transformation methods like the IMSRG. Coupled Cluster also has advantages, though: For instance, the Baker-Campbell-Hausdorff expansion appearing in Equations (30)–(32) automatically terminates at finite order because the cluster operator only contains excitation operators. For the same reason, Equation (31) will automatically solve the Hartree-Fock equations, so any Slater determinant is equally well-suited as a reference state, while MBPT, IMSRG, and even exact diagonalization approaches exhibit (some) reference-state dependence.
Symmetry breaking and collective correlations. While most applications of CC theory in nuclear physics have enforced and exploited spherical symmetry, the capabilities for performing M-scheme calculations that allow nuclei to develop intrinsic deformation have existed for more than a decade. This is a more natural approach for capturing collective correlations than the construction of Triples, Quadruples (4p4h), and ever higher particle-hole excitations of a spherical reference (cf. section 2.3.3). Converging such calculations is challenging because the single-particle basis typically grows by an order of magnitude or more, and the broken symmetries must eventually be restored. The formalism for symmetry restoration in CC has been developed in references [101–104]. In fact, the work of Duguet et al. forms the basis of recent works on symmetry breaking and restoration in MBPT [77, 80, 81]. Applications are currently underway.
Shell-model CC. Like the IMSRG, the CC framework can be used to construct effective interactions and operators for Shell model calculations. Initial work in that direction applied Hilbert space projection techniques (cf. section 2.3.6) to construct a so-called CC effective interaction (CCEI) [24, 105], but the construction of the model spaces via Equation-of-Motion CC methods proved to be computationally expensive. The CCEI approach is now superseded by the Shell Model CC method [25], which applies a second similarity transformation to HCC in Fock space, similar to VS-IMSRG decoupling (cf. section 2.3.3).
Unitary CC. While almost all applications of CC in nuclear physics use the traditional ansatz (27), unitary CC (UCC) approaches that parameterize the wave function as have been used in numerous studies in quantum chemistry (see, e.g., [106, 107]). Unitary CC wave functions have also become a popular ansatz for the Variational Quantum Eigensolver (VQE) algorithm on current and near-term quantum devices [108, 109]. It is also worth noting that the recently revived Unitary Model Operator Approach (UMOA) is closely related to UCC [110, 111].
Self-Consistent Green's Function (SCGF) theory is another prominent approach for solving the nuclear many-body problem with systematic approximations [112–115]. The Green's Functions in question are correlation functions of the form
which describe the propagation of nucleons in the exact ground state of the system. Using Wick's theorem, the exact A-body propagator (33) can be factorized into products of irreducible one-, two-, etc. propagators, similar to the decomposition of density matrices briefly touched upon in section 2.3.3. One can then formulate coupled equations of motion for propagators, and introduce truncations to obtain polynomially scaling methods, again somewhat analogous to IMSRG and CC. We must remain aware that the propagators of SCGF, the induced operators of IMSRG, and the CC amplitudes are all different objects, and while their definitions may make the seem complementary to each other, there are subtle distinctions. One of these is that the g(k) are formally defined with respect to the exact wave function, while IMSRG and CC use definitions with respect to a reference state.
Practical implementations of the SCGF technique usually work with the Fourier transforms of the propagators to the energy domain. One needs to solve integral equations of motion of the form
where g0 is the propagator of the non-interacting system and Σ a kernel that encodes the particles' interactions, which is constructed using diagrammatic techniques. For example, the one-body propagator is obtained by solving
the so-called Dyson equation. From this propagator, one can compute the one-body density matrix
where C+ indicates an integration contour in the complex upper half plane. Higher-body density matrices are connected to the corresponding higher-body propagators in analogous fashion. Using the density matrices, one can then evaluate any operator expectation values of interest. For more details, we refer to the contributions [10, 115] to the present volume, and the works cited therein.
Current applications of SCGF techniques in nuclear physics make use of the so-called Algebraic Diagrammatic Construction (ADC) scheme, with increasing orders, denoted by ADC(n), converging to an exact solution. For closed-shell nuclei, calculations up to ADC(3) are be performed regularly, which contain correlations that are roughly comparable to IMSRG(2) with a perturbative 3p3h correction (see section 2.3.3 and references [83, 86, 116]) and CCSD(T) (cf. section 2.3.4). Somà and collaborators have extended the ADC scheme to open-shell nuclei by using Gor'kov Green's Functions with explicitly broken particle number symmetry [117, 118]. Applications of this framework have used a self-consistent second-order scheme, denoted Gor'kov-ADC(2), and the extension to Gor'kov-ADC(3) as well the integration of particle-number projection to restore the broken number symmetry are in progress [80, 114].
While the computation of the Green's Functions tends to be a more involved task than solving the IMSRG flow equations or CC amplitude equations, the propagator contains more information from a single computation than these other methods. For instance, one can immediately extract spectral information about the neighboring nuclei and the response of the system [119, 120], which requires the application of additional techniques in the IMSRG [83] and CC approaches [12, 121, 122], or, indeed, the computation of the Green's Function using similarity-transformed operators. Furthermore, the kernels of the equations of motion (34) are energy-dependent effective interactions that govern the dynamics of (few-)nucleon-nucleus interactions. For example, the one-nucleon self-energy in Equation (35) is an ab initio version of an optical potential, as used in reaction theory [123–125]. We will return to this discussion in section 4.5.
No-core configuration interaction methods. The most straightforward but also most computationally expensive approach to solving the many-body Schrödinger equation is to exactly diagonalize the Hamiltonian in a basis of many-body states. In general, we refer to such approaches as No-Core Configuration Interaction (NCCI). “No core” makes it explicitly clear that all nucleons are treated as active degrees of freedom, in contrast to the nuclear Shell model discussed below.
In light nuclei, the exact diagonalization can be directly formulated in Jacobi coordinates, using translationally invariant harmonic oscillator [126] or hyperspherical harmonic wave functions [127, 128]. Since the construction of the basis states themselves and the matrix representation of the Hamiltonian becomes increasingly complicated and computationally expensive as the particle number grows, one eventually has to switch to Slater determinants in the laboratory system, using a construction along the lines discussed in section 2.3.1.
A common choice for the single-particle basis in the laboratory system are spherical harmonic oscillator (SHO) states, because they allow an exact separation of center-of-mass and intrinsic degrees of freedom provided one uses an energy-based truncation for the model space [129, 130]. These choices define what we specifically call the No-Core Shell Model (NCSM). A disadvantage of using SHO orbitals is that they are not optimized to the energy scales of specific nuclei, and they are poorly suited for describing physical features like extended exponential wave function tails. Other popular choices are Hartree-Fock single-particle states, and perturbatively [131] or non-perturbatively enhanced natural orbitals [132–134]. Model spaces built on these bases no longer guarantee the separation of center-of-mass and intrinsic coordinates, but fortunately, center-of-mass contaminations either remain small automatically [135], or they can be suppressed using techniques like the Lawson method [136].
Importance truncation and symmetry adaptation. As indicated above, the main issue with exact diagonalization approaches is the exponential (or greater) growth of the Hilbert space dimension, which is proportional to with single particle basis size N and particle number A. A variety of strategies can be used to address this often-quoted “explosion” of the basis size. One direction is to avoid the construction of the full model space basis by applying importance-based truncation or sampling methods, leading to the Importance-Truncated NCSM [9] or Monte-Carlo (No-Core) CI approaches [137, 138].
Another important research program is the exploration of many-body states that are constructed from the irreducible representations (irreps) of the symplectic group Sp(3,ℝ), which describes an approximate emergent symmetry of finite nuclei [139, 140]. An exact diagonalization in such a symmetry-adapted basis will offer a much more efficient description of nuclear states with intrinsic deformation than the conventional NCSM, which would need to use massive model spaces with many-particle-many-hole excitations. This reduction of the model space dimensions also allows such symmetry-adapted NCSM [139, 140] and NCCI approaches [141] to reach heavier nuclei than the conventional versions.
Interacting nuclear shell model with a core (valence CI). Instead of treating all of the nucleons as active, one can also factorize the nuclear wave function by introducing an inert core and only treat the interactions of a smaller number of valence nucleons via appropriately transformed interactions:
This, of course, is the traditional nuclear Shell model approach. Even with the substantial reduction of the single-particle basis to a relatively small number of valence orbitals, the numerical cost for an exact diagonalization quickly becomes unfeasible for many medium-mass and heavy nuclei, especially if one needs multi-shell valence-spaces to capture complex nuclear structure features like coexisting intrinsic shapes.
In previous sections, we have discussed how a variety of many-body methods can be used to derive valence-space interactions, hence it is not a surprise that this is possible in NCCI approaches as well. One strategy is to project solutions of no-core calculations for the core and its neighboring nuclei onto a valence-configuration space to extract the effective Hamiltonian. The viability of this approach has been demonstrated in several publications [142–145], although there are ambiguities in the extraction of the valence-space Hamiltonian, and the initial NCCI calculations that serve as input for the projection rapidly become expensive.
Description of continuum effects and nuclear dynamics. An important breakthrough in ab initio calculations for light nuclei has been the merging of the NCSM with resonating group method (RGM) techniques [130, 146]. This makes it possible to describe clustered states as well as reactions between light projectile(s) and targets. In the original NCSM/RGM approach, compact clusters of nucleons are described by NCSM states, which are then used to construct a basis of configurations |χi〉 that place such clusters at different relative distances. In this basis, one can then solve the generalized eigenvalue problem, known as the Griffin-Hill-Wheeler equation [147] in the RGM context:
where and are the so-called Hamiltonian and norm kernels. The latter appears because the chosen basis configurations are not orthogonal in general. The dimension of Equation (38) is typically small, certainly compared to the NCSM model space, but the computation of the kernels is computationally expensive since it relies on the construction of up to three-body transition density matrices. In recent years, the NCSM/RGM has been extended to the NCSM with Continuum (NCSMC), which accounts for the coupling between the NCSM and RGM sectors of the many-body basis [130]. It requires solving the generalized eigenvalue problem
where h and 𝟙 are the Hamiltonian and norm kernel in the NCSM sector (the latter being diagonal), and the corresponding kernels in the RGM sector (cf. Equation 38), and and encode the coupling between the sectors of the basis.
Alternative approaches to the description of continuum effects in the NCSM are the Single-State HORSE (Harmonic Oscillator Representation of Scattering Equations) method [148–150], for which the nomen is omen, as well as the No-Core Gamow Shell Model (GSM), a no-core CI approach that constructs Slater determinants from a single-particle Berggren basis [151] consisting of bound, resonant and scattering states [152–155].
The most commonly used Quantum Monte Carlo (QMC) techniques in nuclear physics make use of many-body wave functions in coordinate space representation [156–159]. As such, they are well-suited for the description of nuclear states with complex intrinsic structures, and they can readily use interactions with a high momentum cutoff, as opposed to the configuration space methods which would exhibit poor convergence in such cases. This allows QMC calculations to explore physics across the interfaces of the hierarchy of EFTs for the strong interaction (cf. sections 2.1 and 4.4), e.g., for processes that explore energies approaching the breakdown scale of chiral EFT [160–163].
A typical ansatz for a QMC trial state is
where is an operator that explicitly imprints correlations on the mean-field like state |Φ(b)〉, and a, b are vectors of tunable parameters. The first step of most QMC calculations is a variational minimization of the energy in the trial state,
followed by an imaginary-time evolution to project out the true ground state in a quasi-exact fashion:
This projection can be implemented using Monte Carlo techniques in a variety of ways, which gives rise to different approaches like Green's Function Monte Carlo (GFMC) or Auxiliary-Field Diffusion Monte Carlo (AFDMC) [156, 158].
A major challenge in QMC calculations is that most commonly used algorithms suffer from some form of sign problem [156, 158]. Many quantities of interest like the wave functions or local operator expectation values in these wave functions are not positive definite across their entire domain, which means that they cannot be immediately interpreted as probability distributions that the algorithms sample. This is one of the main reasons why QMC methods can only be used with Hamiltonians that are either completely local, or have a non-locality that is at most quadratic in the momenta, e.g., p2 or l2.
While QMC applications in ab initio nuclear structure have been focused on coordinate space, there are a wide variety of approaches that merge QMC techniques with the configuration space approaches discussed in previous sections. Examples include sampling the intermediate-state summations in MBPT [164], diagrammatic expansions [165–167], or the coefficients of correlated CC [168] or (No-Core) CI wave functions [137, 138, 169–171].
Lattice methods are nowadays widely used to simulate the dynamics of non-perturbative field theories on finite space-time lattices. The most prominent example is Lattice QCD, but implementations of various Effective Field Theories on the Lattice have been developed and applied with impressive outcomes in the past two decades—see, for example, references [172–175] and references therein, which also provide pedagogical introductions to Lattice EFT for nuclear systems.
Lattice EFT simulations are built around the partition function, which is defined for a pure state |Ψ〉 as
Here, H is an EFT Hamiltonian, typically truncated at a given order of the EFT's power counting scheme. In practice, the partition function is evaluated as a path integral in which field configurations are sampled using Monte Carlo techniques. At large τ, one can extract information about the ground state and low-lying excited states of the system directly from (cf. section 2.3.7), and general expectation values can be evaluated using
The use of discretized spatial lattices makes Lattice EFT particularly suited for the description of nuclear states with complex geometries like cluster structures [176–178]. Depending on the size of the lattices, it will also typically require less computational effort than the imaginary-time evolution of states that are formulated in continuum coordinates, as in AFDMC or GFMC (see section 2.3.7). Moreover, the development of the so-called adiabatic projection method (APM) [179, 180] in recent years has made it possible to compute scattering cross sections for reactions of (light) clusters on the lattice. Conceptually, the APM is reminiscent of the resonating-group method used to describe reactions in the NCSMC framework discussed in section 2.3.6.
Of course, Lattice EFT is not free of disadvantages, which are usually caused by the discretization of space(time). The finite size and lattice spacing are related to infrared (long-range, low-momentum) and ultraviolet (short-range, high-momentum) cutoffs of a calculation, which need to be carefully considered. Since the recognition of cutoff scales is an inherent aspect of EFTs, one can systematically correct for these effects [181, 182]. The discrete lattice also breaks continuous spatial symmetries that may need to be restored approximately or exactly before comparisons with experimental data are made [172, 182].
In this section, I will discuss selected achievements of the ab initio nuclear many-body community in the past decade, and the issues that were encountered in the process. As stated in the introduction, this selection is subjective, and giving full justice to the breadth of research accomplishments is beyond the scope of this work. I hope that the present discussion will serve as an invitation for further exploration, for which the cited literature may serve as a useful starting point.
One of the biggest issues in nuclear theory was the lack of comparability between different approaches for describing the structure of medium-mass or heavy nuclei. These nuclei were well in reach of the Shell Model and nuclear Density Functional Theory (DFT), but whenever issues emerged, it was unclear whether they resulted from approximations in the many-body method, or deficiencies in the effective interactions, i.e., the valence-space Hamiltonians or energy density functionals (EDF). Moreover, one cannot simply perform a valence CI calculation with an EDF, or a DFT calculation with a Shell Model interaction, because the interactions are tailored to their specific many-body method.
The development of the RG/EFT and many-body methods discussed in section 2 has opened up a new era for benchmarking the same nuclear interactions across multiple approaches, and on top of that, these methods provide a systematic framework for analyzing, and eventually quantifying, the reasons for differences between the obtained results.
One of the earliest testing grounds for ab initio calculations of medium-mass nuclei was the oxygen isotopic chain, which was accessible to all of the approaches that emerged at the beginning of the past decade. Figure 5 shows the ground-state energies of even oxygen isotopes for the same chiral NN+3N interaction, obtained with several of the configuration space approaches introduced in section 2.3. In addition, results for applying various types of MBPT to the same interaction and nuclei are presented in reference [69]—I only refrained from including them here to avoid overloading the figure. As we can see, the ground-state energies obtained from the different approaches are in good agreement with each other and with experiment. Since our results include quasi-exact IT-NCSM values, the deviation of the other methods' energies from these values provide us with an estimate of the theoretical uncertainties due to any employed truncations, which is on the order of 1–2%. As we can see from Figure 5, essentially all of the used many-body methods place the drip line in the oxygen isotopic chain at 24O, although the signal is exaggerated. Continuum effects that have been omitted in these calculations would lower the energy of the 26O resonance, which is experimentally constrained to be a mere 18(7) keV above the two-neutron threshold [185], and produce a very flat trend in the energies toward 28O. Similar features were found in calculations for other isotopic chains and other chiral interactions [21, 114, 118, 186]. The 16O ground state energies obtained for the employed chiral NN+3N Hamiltonian are also compatible with a Lattice EFT result that was obtained at a similar resolution scale [177].
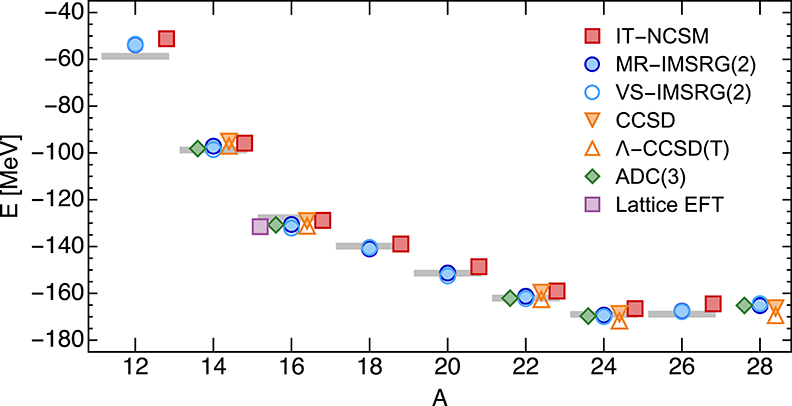
Figure 5. Ground-state energies of the oxygen isotopes for various many-body approaches, using the chiral NN+3N(400) interaction at λ = 1.88 fm−1 [183]. Details on the Lattice EFT calculation can be found in reference [177]. Gray bars indicate experimental data [184].
This last comparison shows that some obstacles to the ideal cross-validation scenario still remain. Since coordinate-space approaches like Lattice EFT or QMC are truly complementary to configuration-space methods, it would be highly desirable to test the same chiral NN+3N Hamiltonians in both types of calculations. However, the Hamiltonians used in configuration space are typically given in terms of harmonic oscillator matrix elements (especially if SRG evolved) instead of the coordinate-space operators required by Lattice EFT or QMC calculations. Furthermore, Lattice EFT and QMC cannot handle all possible types of non-locality in the Hamiltonian (cf. section 2.3.7), including the forms generated by the non-local regulators that are favored for configuration-space Hamiltonians. Conversely, local chiral interactions that have been constructed explicitly for QMC applications [4, 158, 187–190] exhibit slow model-space convergence in configuration-space calculations because they still tend to require a significant repulsive core at short distance to describe nucleon-nucleon scattering data, albeit a far weaker one than interactions like Argonne V18 [191].
The reach of ab initio many-body theory has increased dramatically over the past decade. Figure 1 illustrates this growing coverage of the nuclear chart, but it tells only part of the story. The expansion has happened in many “dimensions” besides the mass number A, namely by pushing toward exotic nuclei via improved treatments of the continuum degrees of freedom, filling in gaps in the coverage that are occupied by doubly open-shell nuclei with strong intrinsic deformation, and expanding the types of observables that can be computed from first principles. Recalling section 3.1, the ongoing push against the limitations of our many-body approaches will continue to grow the opportunities for benchmarking current- and next-generation chiral Hamiltonians.
First calculations for selected nuclei and semi-magic isotopic chains up to tin were already published in the first half of the last decade [19, 21, 23]. For the most part, they were using a family of chiral NN+3N interactions that gave a good description of the oxygen ground-state energies (cf. Figure 5) as well as the spectroscopy of the lower sd-shell region [24, 26]. However, the same interactions underpredict nuclear charge radii [192], and start to overbind as we approached the calcium chain (cf. Figure 7), eventually leading to an overbinding of 1 MeV per nucleon in tin. While model-space convergence in CC, IMSRG and SCGF calculations suggested that calculations for heavier nuclei would have been technically possible, it made little sense to pursue them.
The growing number of results for medium-mass nuclei and the problems they revealed motivated a new wave of efforts to refine chiral interactions. One direction of research aimed to achieve a simultaneous description of nuclear energies and radii up to 48Ca by including selected many-body data in the optimization protocol of the chiral LECs. This work resulted in the so-called NNLOsat interaction [194]. While NNLOsat definitely improved radii [195], its model-space convergence was found to become problematically slow already in lower pf-shell nuclei [114, 196, 197].
Simultaneously with the efforts to develop new interactions, attention also turned toward an older, less consistently constructed family of chiral NN+3N interactions that exhibited reasonable saturation properties in nuclear matter calculations [198, 199]. These forces are referred to as EMλ/Λ, where λ indicates the resolution scale of the NN interaction, the SRG-evolved N3LO potential of Entem and Machleidt [200], and Λ is the cutoff of an NNLO three-nucleon interaction whose low-energy constants have been adjusted to fit the triton binding energy and 4He charge radius [198, 199]. In CC calculations for the nickel isotopes, Hagen et al. demonstrated that the EM1.8/2.0 interaction, in particular, allowed a good description of the energies of nuclei in the vicinity of 78Ni [196]. As shown in Figure 6, these findings have been reinforced by subsequent VS-IMSRG calculations, as well as the experimental observation of the first excited 2+ state in this nucleus [201].
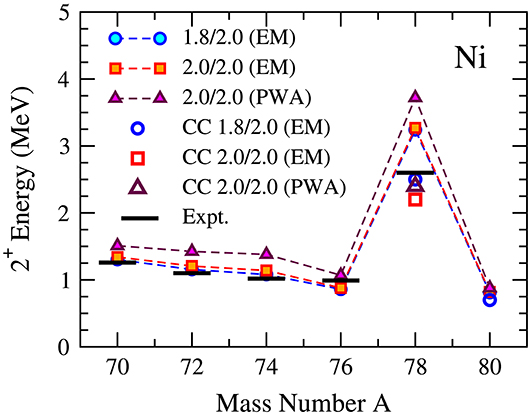
Figure 6. Energies of the first excited 2+ states from VS-IMSRG [201] and Equation-of-Motion CC [196] calculations for several chiral two- plus three-nucleon interactions. Experimental values [201, 202] are indicated as black bars. Data courtesy of J. D. Holt, J. Menéndez, and G. Hagen.
Since this initial application in medium-mass nuclei, the EMλ/Λ family has seen widespread use in ab initio calculations due to its empirical quality, although the Hamiltonian's theoretical uncertainties are less well-defined than for interactions that obey the chiral power counting more rigorously. Indeed the EM1.8/2.0 interaction was used in VS-IMSRG calculations to produce what is to my knowledge the first attempt at producing an ab initio mass table for nuclei up to the iron isotopes [186]. For selected nuclei up to the tin region, it also yields converged energies for ground and low-lying states that are in good agreement with experimental data [203, 204]. It also yields slightly larger radii than previous interactions, although the underprediction is not eliminated entirely (see references [195, 203] and section 3.2.3).
Multiple applications of the EMλ/Λ Hamiltonians in support of spectroscopy experiments have been published in recent years (see, e.g., [197, 205–208]), and additional studies are underway, including an effort to better understand what makes the EM1.8/2.0 Hamiltonian so successful. Furthermore, a new generation of chiral NN+3N interactions is now available for applications in medium-mass and heavy nuclei [46, 114, 209–211].
Neutron-rich nuclei are excellent laboratories for disentangling the interplay of nuclear interactions, many-body correlations and the continuum. Thus, data from the experimental push toward the drip line can offer important constraints for the refinement of chiral interactions if the many-body truncations and continuum effects are under control.
In practice, ab initio results for observables like the absolute energies of states still exhibit significant scale and scheme dependence due to truncations that are made in the EFT, the potential implementation of SRG evolutions, and the many-body methods. Since such variations tend to be systematic within families of interactions (and sometimes even across multiple families), differential quantities like separation and excitation energies or transition matrix elements often exhibit a weaker scale and scheme dependence—note, for example, the small systematic variation of the first excited 2+ states of the neutron-rich nickel isotopes for EMλ/Λ interactions. This makes energy differences an ideal observable for confronting ab initio results with experimental data.
Let us consider two-neutron separation energies as a concrete example. Sudden drops in these observables are a signal of (sub)shell closures (albeit not universally [195]) and in the neutron-rich domain, they are important indicators for the proximity of the drip line. Figure 7 shows MR-IMSRG ground-state and two-neutron separation energies of the calcium isotopes, obtained with the NN+3N(400) interaction used in Figure 5, as well as the NNLOsat and EM1.8/2.0 interactions briefly discussed in the previous section. We note the overbinding produced by NN+3N(400) and the baffling accuracy of the EM1.8/2.0 results, given the approximations that went into the construction of this force, as well as the MR-IMSRG truncation. Common to all three interactions is the emergence of a very flat trend in the ground-state and separation energies in neutron-rich calcium isotopes, which will likely be further enhanced by the inclusion of continuum effects, and extended beyond the shown mass range. Similar flat trends emerge in many isotopic chains, as shown both in ab initio surveys based on chiral interactions [10, 114, 186] as well as a sophisticated Bayesian analysis of empirical EDF models [212]. Naturally, this will make the precise determination of the neutron drip line in the medium-mass region a challenging task, but also suggests that interesting features like alternating patterns of unbound odd nuclei and weakly-bound even nuclei with multi-neutron halos could emerge. This is an exciting prospect for the experimental programs at rare-isotope facilities.
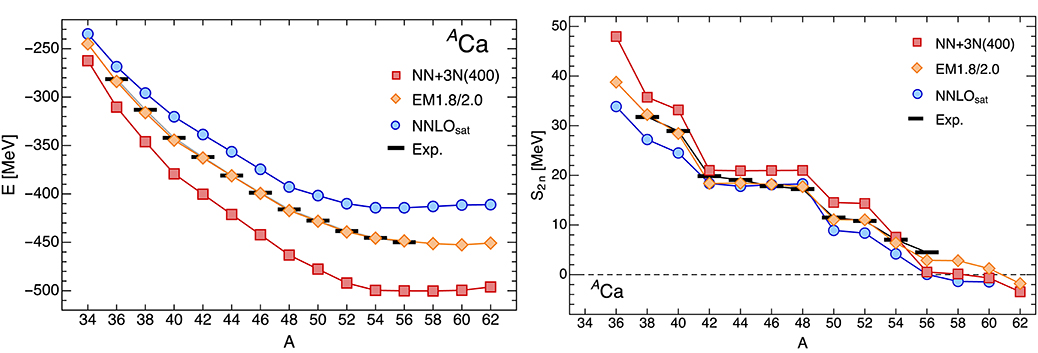
Figure 7. Ground-state and two-neutron separation energies for several chiral NN+3N interactions from MR-IMSRG(2) calculations. Experimental data are indicated by black bars [184, 193].
With the exception of the NCSMC and HORSE methods discussed in section 2.3.6, the inclusion of continuum degrees in configuration-space techniques has been focused on the use of the Berggren basis [151]. While such calculations are challenging due to the significantly increased single-particle basis size and the difficulties of handling the resulting complex symmetric Hamiltonians, applications in CC (see references [12, 213] and references therein), both valence and No-Core Gamow Shell Model [153–155, 214, 215] and IMSRG [216] calculations have been published. Common to all these approaches is that a configuration space interaction that is given in terms of SHO matrix elements is expanded on a basis containing SHO and Berggren states, hence it is still an open question how a direct implementation of the interactions in a basis with continuum degrees of freedom might modify existing results. It is worth noting that such a construction has been achieved for phenomenological GSM interactions that have been tuned for light nuclei [217–222].
In light nuclei, the NCSMC has been applied with impressive success to describe a variety of exotic nuclei with up to three-cluster structures. For example, Calci et al. [223] carried out NCSMC calculations for 11Be with several chiral NN+3N interactions to investigate the parity inversion of the ground and first-excited states in this nucleus from first principles. The authors found that the coupling between the NCSM and RGM sectors of the generalized eigenvalue has strong effects, but that among the tested interactions, only NNLOsat can produce the experimentally observed ordering of the states (see Figure 8). However, it still underpredicts the splitting of these levels and as a result, overestimates the cross section for the photodisintegration 11Be(γ, n)10Be. Additional applications of the NCSMC for exotic nuclei can be found in the review [130] and references therein, as well as the more recent works [224–226].

Figure 8. NCSMC spectrum of 11Be with respect to the n +10 Be threshold. Dashed black lines indicate the energies of the 10Be states. Light boxes indicate resonance widths. See reference [223] for details. Figure reprinted with permission from the American Physical Society.
The capabilities of ab initio approaches have also significantly expanded when it comes to the evaluation of observables other than the energies.
Nuclear radii. Figure 9 shows MR-IMSRG results for the charge radii of calcium isotopes. The left panel illustrates the reasonable reproduction of the 40Ca and 48Ca charge radii that can be obtained for NNLOsat. The MR-IMSRG(2) results are slightly smaller than the experimental data due to differences in the truncations from the CCSD charge radius calculations that were used in the NNLOsat optimization protocol [194]. Note the steep increase in the experimental charge radii beyond 48Ca: At the time of the measurement, NNLOsat was the only chiral NN+3N interaction exhibiting this feature, although other more recent interactions can replicate this trend as well [10, 114]. Also note that none of the calculations are able to reproduce the inverted arc of the charge radii between 40Ca and 48Ca. In a CI picture, it is caused by strong mixing with 4p4h excitations into the pf-shell [229]. Since the MR-IMSRG(2) calculations shown here included only up to (generalized) 2p2h excitations and used particle-number projected Hartree-Fock Bogoliubov vacua as reference states that do not contain collective correlations (cf. section 2.3.3), it is not surprising that the inverted arc cannot be reproduced. We will return to this issue of missing collectivity later.
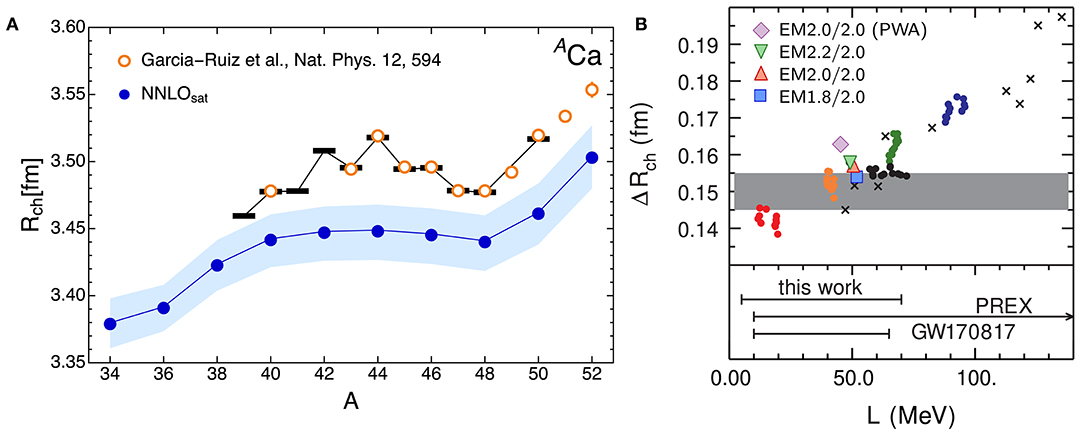
Figure 9. (A) Calcium charge radii from MR-IMSRG(2) calculations with NNLOsat The shaded area indicates uncertainties from basis convergence. Black bars and orange circles indicate experimental data [195, 227]. (B) Mirror charge radius difference of 36Ca and 36S vs. the slope of the symmetry energy, L, at nuclear saturation, for the EMλ/Λ interactions (symbols as indicated in the legend), compared to Skyrme functionals (solid circles) and Relativistic Mean Field models (crosses). The band indicates the experimental result from the BECOLA facility at NSCL. See reference [228] for details.
While the EMλ/Λ interactions underpredict the absolute charge radii, they fare quite well in the description of radius differences, as suggested in the previous section. Figure 9B is adapted from a recent study that suggests a correlation between the charge radius difference of mirror nuclei, ΔRch, and the slope of the symmetry energy in the nuclear matter equation of state [228]. We see that the MR-IMSRG results for ΔRch are actually compatible with results from a multitude of Skyrme EDFs, and the value for the magic EM1.8/2.0 interaction falls into the uncertainty band of the experimental result.
Electromagnetic transitions. Since the second half of the past decade, ab initio calculations for transitions in medium-mass nuclei have become more frequent, owing to the appropriate extensions of the IMSRG, CC and SCGF methods [205, 230, 231]. While results for transitions that are dominated by a few nucleons, e.g., M1 transitions [230] or β decays (see reference [232] and the discussion below) can be quite good, the description of collective transitions is hampered by inherent truncations of these many-body methods, which are better suited for dynamical, few-particle correlations (see sections 2.3.3 and 2.3.4). Results from the SA-NCSM [139, 140] and the IM-GCM discussed in section 2.3.3 show that the modern chiral interactions themselves adequately support the emergence of nuclear collectivity.
Consider for example Figure 10, which shows VS-IMSRG(2) results for the quadrupole transition from the first excited 2+ state to the ground state in 14C, 22O and 32S [230]. The picture is fairly consistent for all four chiral NN+3N interactions that were used in the study: The 2+ energies are described quite well, but energies are not very sensitive to the details of the nuclear wave functions. In 14C, the E2 transition is weakly collective, so the E2 matrix element is reasonably reproduced, while the matrix element for the collective transition in 32S is underpredicted by 25–50%. The NN+3N(400) interaction gives a particularly poor result, but this is also related to the significant underestimation of the point-proton radius we obtain for this Hamiltonian, as discussed earlier.
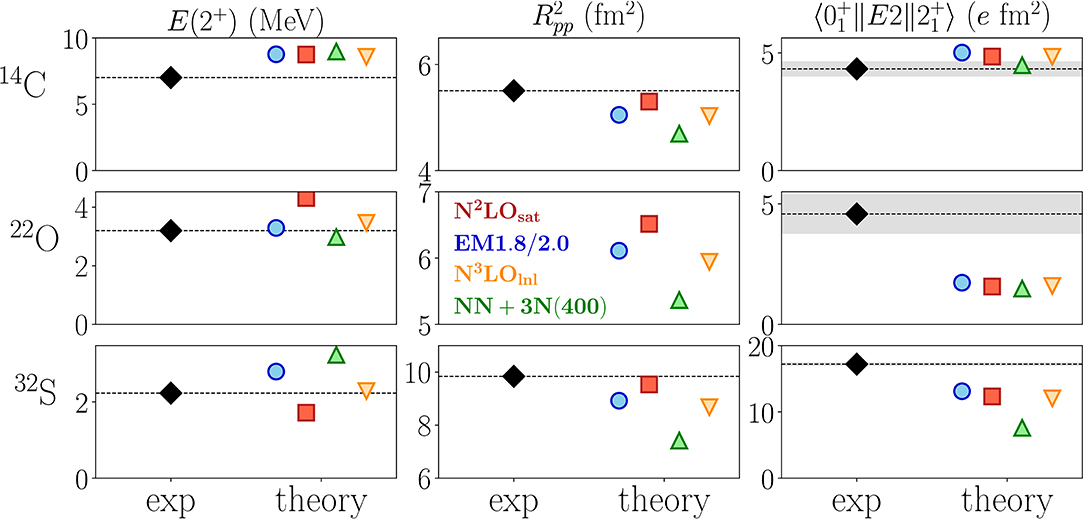
Figure 10. Energies of the first excited 2+ state, proton mean square radius and quadrupole transition matrix elements for selected nuclei, based on VS-IMSRG(2) calculations with multiple chiral NN+3N interactions. See references [76] and [230] for more details. Experimental values (with uncertainties indicated by bands) are taken from [227, 233]. Figure courtesy of R. Stroberg.
The result for 22O deserves special attention. The E2 transition matrix element is only a third of the experimental value, although the transition is only weakly collective. However, 22O only has neutrons in an sd valence space, so the E2 matrix element would vanish in a conventional Shell Model calculation unless the neutrons have an effective charge. Such effective charges must be introduced by hand and fit to data in phenomenological Shell Model calculations. Here, we see that the VS-IMSRG decoupling naturally induces a non-vanishing quadrupole moment through an effective neutron charge in the one-body transition operator as well as an induced two-body contribution (see reference [230], and reference [231] for an analogous effort in SCGF theory). It is likely that the E2 strength could be improved by performing the VS-IMSRG calculation in a psd valence space, so that the proton dynamics is treated explicitly instead of implicitly by valence-space decoupling. Until recently, we were unable to perform such a multi-shell decoupling because of the IMSRG version of the intruder-state problem, but a promising workaround was introduced in reference [28].
Gamow-Teller transitions. In recent years, there have been concerted efforts to understand the mechanisms behind the empirically observed quenching of Gamow-Teller (GT) transitions in medium-mass nuclei, in part due to its relevance to neutrinoless double-beta decay searches (see below). In reference [232], the authors show that this issue is largely resolved by properly accounting for the scale and scheme dependence of configuration-space calculations. By dialing the resolution scale to typical values favored by approaches like NCSM, CC, and VS-IMSRG, correlations are shifted from the wave functions into induced two- and higher-body contributions to the renormalized transition operator, just as in the quadrupole case discussed above.
The transition operator, including two-body currents, is consistently evolved to lower resolution scale alongside the nuclear interactions, keeping the induced contributions. The transition matrix elements of the evolved operator are then computed with the NCSM in light nuclei, and VS-IMSRG in sd- and pf-shell nuclei, leading to agreement with experimental GT strengths within a few %. In contrast, the bare GT operator must be quenched by 20–25% via the introduction of an effective axial coupling, , to yield agreement with experimental beta decay rates.
The GT transitions in light nuclei have also been evaluated in the GFMC, most recently with consistently constructed local chiral interactions and currents [234, 235]. Interestingly, the inclusion of two-body currents seems to consistently enhance the GT matrix elements, while it tends to quench the matrix element in NCSM calculations. Since this is almost certainly related to the differences in the resolution scale and calculation scheme, the disentanglement of these observables might yield further insights into the interplay of wave function correlations and the renormalization of the transition operators.
Neutrinoless double beta decay. Due to the high impact the observation of neutrinoless double beta decay (or lack thereof) would have on particle physics and cosmology, the computation of nuclear matrix elements (NMEs) for neutrinoless double beta decay is a high priority for nuclear structure theory. Precise knowledge of the NMEs for various candidate nuclei is required to extract key observables like the absolute neutrino mass scale from the measured lifetimes (or at least, any new bounds that would be provided by experiment). Most calculations of the NME to date were subject to the lack of comparability between phenomenological nuclear structure results that was discussed in section 3.1, hence a new generation of ab initio calculations with quantified uncertainties is required.
A major step in that direction was the first calculation of the NME for the decay 48Ca → 48Ti based on chiral interactions [29]. The IM-GCM approach discussed in section 2.3.3 was used to describe the structure of the intrinsically deformed daughter nucleus 48Ti, achieving a satisfactory reproduction of the low-lying states and their quadrupole transitions (see Figure 11). Since the initial publication (blue spectra in Figure 11A), the description of the excited states has been improved further through the admixing of cranked configurations (red spectra), without affecting the NME (Figure 11B). Work on quantifying the uncertainties due to the many-body method, the Hamiltonian, and the transition operator is underway, in preparation for the computation of the NMEs of more realistic candidate nuclei like 76Ge and 136Xe.
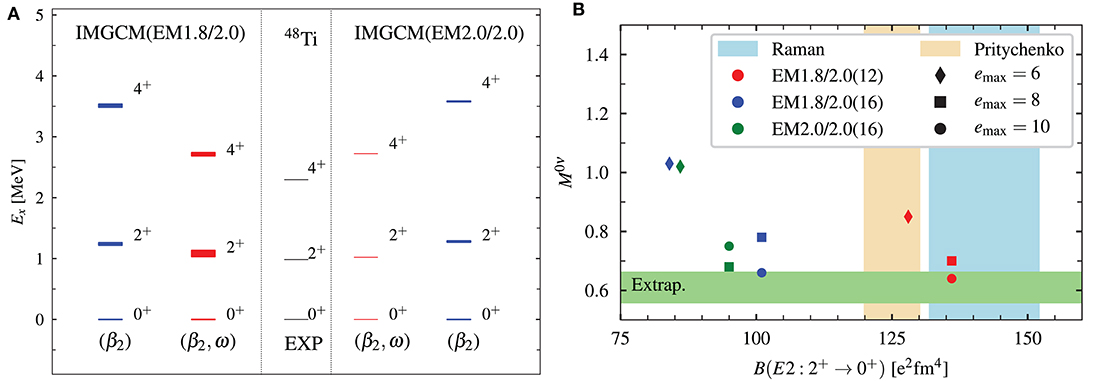
Figure 11. IM-GCM description of the neutrinoless double beta decay 48Ca →48 Ti, using EMλ/Λ interactions: Low-lying spectrum of 48Ti and its compression through the admixing of cranked configurations (A) and the nuclear matrix element vs. B(E2) transition probability (B). See text and reference [29] for details. (A) courtesy of J. M. Yao, (B) reprinted with permission from the American Physical Society.
From the computation of transitions between low-lying levels, it is only a small step to the computation of nuclear response functions and cross sections, although the implementation can be challenging and the applications are often computationally expensive.
Nuclear response functions. In light nuclei, GFMC is a powerful yet numerically heavy tool for computing exact nuclear response functions (see, e.g., references [236, 237]). In medium-mass nuclei, applications of SCGF and CC techniques to the computation of the nuclear response have been published in recent years. As mentioned in section 2.3.5, the Green's functions computed in the standard or Gor'kov ADC Green's function schemes inherently contain information about the nuclear response that has been used to study both electromagnetic and weak processes of medium-mass nuclei [119, 120, 238–240].
In the Coupled Cluster framework, response functions have been computed by merging CC with up to Triples excitations with the Lorentz Integral Transformation (LIT) technique [241–245]. Immediately after its inception, this approach was used to for the first ab initio calculations of dipole response and the related photodisassociation cross section of medium-mass closed-shell nuclei [241, 242]. More recently, it was used to compute the electric dipole polarizability αD of nuclei like 48Ca [243, 244, 246] and 68Ni [247]. Together with measurements of the charge radius, this quantity can be used to constrain ab initio calculations that will in turn allow the theoretical extraction of the neutron point radius as well as the thickness of the neutron skin.
An important application for nuclear response calculations is to map out the neutrino response of 40Ar, the primary target material in detectors for the short-baseline [248] and long-baseline neutrino experiments, like the Deep Underground Neutrino Experiment (DUNE) Far Detector [249, 250]. At low energies, the cross section for coherent neutrino elastic scattering is essentially determined by the weak form factor of 40Ar, which has recently been computed using CC techniques [251]. This work is complementary to SCGF calculations of the neutrino response in the region of the quasi-elastic peak by Barbieri et al. [238].
Nuclear reactions. As discussed in section 2.3, there has been enormous progress in the development of unified treatments of ab initio nuclear structure and reactions. Here, I want to highlight two among a bevy of impressive results. Figure 12A shows S− and D−wave phase shifts for α − α scattering, computed order by order in Lattice EFT [179, 180]. These calculations are made possible by the lattice's capability to describe clustered states (also see references [176–178]), as well the development of the APM and associated algorithms. The results for the phase shifts show the desired order-by-order improvement, and the inclusion of higher-order terms of the chiral expansion is expected to improve agreement with experimental data. The near identical NLO and NNLO phase shifts in the S−wave appear to be the result of an accidental cancellation that is not occurring in the D−wave phase shifts.
Figure 12. Ab initio calculations of nuclear reactions. (A) S (δ0) and D-wave phase shifts (δ2) for α-α scattering at various orders in Lattice EFT. For details, see references [179, 180]. Figure courtesy of S. Elhatisari. (B) NCSMC results for the deuterium-tritium (D–T) fusion cross section (top) and reaction rate (bottom). The figure compares the rates for unpolarized and polarized fuel, as well as rates obtained from widely adopted parametrization of the fusion cross section (see reference [252] for details). The arrows are included to the guide the reader's eye (see text). Figure reprinted from Hupin et al. [252] under a CC BY 4.0 license.
In reference [252], the authors studied deuterium-tritium (D-T) fusion using the NCSMC. One of the main results of this work is shown in Figure 12B, which compares the NCSMC D–T reaction rates for polarized and unpolarized fuels to each other, as well as rates obtained with several widely used parameterizations of the D–T fusion cross section. The NCSMC calculations indicate that for an experimentally realizable polarized fuel with aligned spins, a reaction rate of the same magnitude as for unpolarized fuel can be achieved at about half the temperature. Naturally, this suggests that polarized D-T fuels will allow a more efficient power generation in thermonuclear reactors.
The progress in ab initio calculations over the past decade has not only led to impressive results for nuclear observables, but also revealed the long-surmised underpinnings of empirical models of nuclear structure. In many cases, the ideas that led to the formulation of such models were shown to be correct, but they could not be verified at the time because RG and EFT techniques or sufficient computing power for a more thorough exploration were not available.
The Nuclear Shell Model. The first prominent example I want to discuss is the nuclear Shell Model and some of the “folklore” surrounding it. We can immediately make the observation that the Shell model picture is inherently a low-momentum description of nuclear structure. It is based on the assumption that nucleons are able to move (almost) independently in a mean field potential, and that nuclear spectra can be explained by the mixing of a few valence configurations above an inert core via the residual interaction. As we know now, the existence of a bound mean-field solution and a weak, possibly perturbative residual interaction relies on the decoupling of low and high momenta in the nuclear Hamiltonian [1, 6, 253], e.g., by an SRG transformation. Historical approaches to exploit this connection to construct the Shell model from realistic nuclear forces [254–256] failed in part because the decoupling of the momentum scales via Brueckner's G−matrix formalism [65–67] was not as good as believed [1].
In addition to the momentum-space decoupling, one must also decouple the valence space configurations from the excluded space. This can be achieved using a variety of techniques (cf. sections 2.3.3–2.3.6), and either by performing transformations in sequence, or designing a single procedure that achieves both types of decoupling simultaneously. In practice, the former strategy tends to be more efficient and less prone to truncation errors—an example is the VS-IMSRG decoupling of Hamiltonians that have been evolved to a low resolution scale by means of a prior SRG evolution (see sections 2.2 and 2.3.3, as well as reference [76]). An added benefit of using low-momentum interactions is that the Shell Model wave functions will qualitatively resemble those obtained by a no-core method using the same Hamiltonian without valence decoupling. This facilitates qualitative comparisons and allow us to apply the same intuitive picture. For quantitative comparisons, the effects of all unitary transformations must be carefully taken into account [257].
Figure 13 illustrates the effect of the discussed transformations via the deviations between the computed and experimental energies of close to 400 levels in the sd-shell. Since the EM1.8/2.0 interaction used in these calculations has a low resolution scale, simply using the valence-space matrix elements of the input Hamiltonian without any further valence-space decoupling yields a root-mean-square (rms) deviation of “only” about 1.7 MeV, which is not outright disastrous. When we apply the VS-IMRSG to decouple the valence space, the newly evolved interaction yields a much improved rms deviation of ~ 650 keV, which is better than for some of the older sd-shell interactions, albeit not as good as the USDB Hamiltonian, which is shown for comparison [258, 259]. This is not really surprising: USDB essentially represents the best possible fit to experimental data under the model assumptions, i.e., the choice of a pure sd-shell valence space, the restriction to a two-body Hamiltonian, the omission of isospin-breaking effects from the Coulomb interaction and the nuclear interactions, and the empirical A-dependence multiplying the two-body matrix elements (TBMEs). The accuracy of the VS-IMSRG results, on the other hand, is affected by possible deficiencies in the input Hamiltonian and the use of the VS-IMSRG(2) truncation. Naturally, both of these aspects will be improved systematically in future calculations.
Figure 13. Deviations between theoretical and experimental excitation energies of 391 sd-shell states, for (A) the EM1.8/2.0 interaction without valence decoupling, (B) the same interaction transformed with VS-IMSRG, and (C) the USDB interaction [258]. The points correspond to the respective root-mean-square deviations for each interaction. Figure courtesy of R. Stroberg.
Phenomenological adjustments of effective Shell Model interactions like the A-dependent scaling factors in the USD Hamiltonians or Zuker's monopole shift [260] are typically attributed to the changes in the nuclear mean field away from the core, as well as missing three-body interactions. In reference [76], the VS-IMSRG is used to demonstrate that this is indeed the case. As described in section 2.3.3, upon normal ordering, the three-body force gives contributions to operators of equal and lower particle rank, which in the Shell Model case amounts to the core energy, single-particle energy, and two-body matrix elements. All of these contributions become A-dependent in the VS-IMSRG, but one can shift the A-dependent parts completely into the TBMEs, like in phenomenological interactions, without changing the Hamiltonian matrix in the many-body Hilbert space or its eigenvalues.
Procedures like the VS-IMSRG decoupling also let us track in detail how operators besides the nuclear interactions evolve when they are subject to the valence-decoupling transformation. Recall from the discussion in section 3.2.3 that this can even quantitatively explain the quenching of the Gamow-Teller strength in phenomenological Shell Model calculations, provided two-body current contributions to the initial transition operator are taken into account as well. For electromagnetic transitions, the renormalization of the one-body transition operator and the appearance of induced terms generate at least some part of the usual phenomenological effective charges, but a more complete treatment of nuclear collectivity (cf. section 2.3.3) as well the inclusion of current contributions to these operators are developments that need to be undertaken in the coming years.
Emergence of collectivity. Both NCCI and VS-IMSRG calculations with chiral NN+3N interactions have demonstrated that these interactions do indeed produce the telltale features of collective behavior in nuclear spectra [26, 141, 213, 261, 262]. Upon a bit of reflection, it is not surprising that reasonable results on rotational bands, for instance, should be found in these approaches: While they rely on particle-hole type expansions, the exact diagonalization is done in a complete model space of up to AvhAvp excitations, where Av is the number of valence nucleons. In contrast, equation-of-motion methods that typically employ 1p1h or 2p2h truncations struggle with the description of collectivity in low-lying states [83, 122, 204], but they do work reasonably well for giant resonances [241, 242].
As argued in sections 2.3.3 and 2.3.6, bases built on particle-hole type expansions are not ideally suited to the description of collective correlations. The SA-NCSM [139] instead uses irreducible representations of SU(3) or Sp(3,ℝ), the dynamical symmetry groups of collective models [263], to achieve a much more efficient description of collective behavior in nuclei. This is illustrated for the case of 20Ne in Figure 14. The SA-NCSM calculations [140] based on the two-nucleon NNLOopt potential [264] describe the ground-state rotational band extremely well, all the way to the J = 8+ state. It is dominated by a single SU(3) irrep, associated with the axially elongated shape of the computed intrinsic density profile that is also shown in the figure.
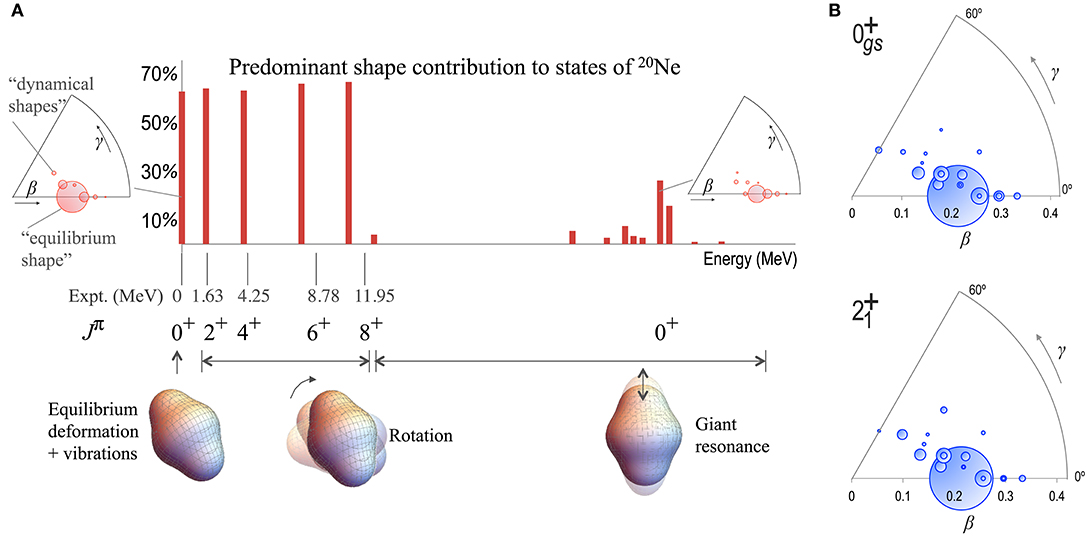
Figure 14. SA-NCSM results for 20Ne in an SU(3)-adapted basis, using the two-nucleon interaction [264]. (A) Excitation energies (horizontal axis) of the ground-state rotational band (Jπ = 0+ through 8+) and 0+ states, and the dominant shape in each state (vertical axis), indicated using the ab initio one-body density profiles in the intrinsic (body-fixed) frame. (B) Distribution of the equilibrium shapes that contribute to the ground state and first excited 2+ state, indicated by the average deformation parameters (β, γ). See reference [140] for additional details. Figure reprinted with permission from the American Physical Society.
A substantial part of the appeal of methods like CC, IMSRG and SCGF is their polynomial scaling. For the purposes of uncertainty quantification (UQ), we need to be able to evaluate at least two consecutive truncation levels to assess the convergence of the many-body expansion in nuclei for which exact calculations are not feasible. Efforts in that direction have been in progress for some time, and while some methods are at a more advanced stage than others, the improved truncations should be available for regular use within the next couple of years [10, 12, 86, 100, 116, 244, 265]. In part, this is owing to the development of computer tools that automate tasks like diagrammatic evaluation or angular momentum coupling [266, 267]. The computational scaling of these approaches will be of order or , which makes applications a task for leadership-class computing resources for the foreseeable future. It is clear that it will not be feasible to just push the calculations further, since we would then face a (naive) scaling.
Applications where we would expect to need high-order truncations involve nuclear states with strong collective correlations, provided we work from a spherical reference state. As explained in section 2.3, this issue can likely be addressed either by using mean-field reference states with spontaneously broken symmetries (cf. section 2.3.4) or using correlated reference states in the first place (cf. section 2.3.3), and the first applications of the IM-GCM give credence to that idea. Moreover, there is first evidence that the CC and IMSRG truncations converge much more rapidly for observables that are sensitive to collectivity [268], i.e., the current state-of-the-art truncations may be sufficiently precise.
The IMSRG framework also offers perspectives for the construction of further IMSRG hybrid methods (cf. section 2.3.3). Based on the successes of both the IM-NCSM and IM-GCM it would be worthwhile to use IMSRG-evolved Hamiltonians in the SA-NCSM or techniques like the Density Matrix Renormalization Group, which is also capable of efficiently describing strong collective correlations under certain conditions [269, 270].
The progress in ab initio many-body calculations is not simply due to the availability of increasingly powerful computational resources, but also due to dedicated collaborations with computer scientists to ensure that the available high-performance computers are used efficiently. Such collaborations will only grow more important as hardware architectures change rapidly and a growing demand for computing time requires users to demonstrate sufficient efficiency to be granted access to supercomputers.
Measures to boost the numerical efficiency can also be taken at the many-body theory level. Efficient calculations rely on finding optimal representations of the relevant physical information that is encoded in the Hamiltonian. Algorithmic gains are possible whenever there is a mismatch, either because we made convenient choices, e.g., by expanding many-body states in terms of simple Slater determinants, or because we were not able to recognize simplifications beforehand, e.g., due to hidden or dynamical symmetries.
The SRG has played a key role in addressing the first points at the level of the nuclear interaction over the past two decades, and SRG and IMSRG can be applied in novel ways to explore dynamical symmetries [55]. In the construction of a configuration space, the selection of the single-particle basis leaves room for optimization. Indeed, the natural orbitals introduced in reference [131] lead to faster model-space convergence in NCSM and CC calculations, implying a more compact Hamiltonian matrix in natural orbital representation. The efficiency of this representation can be leveraged further by making robust importance truncations based on analytical measures, e.g., in MBPT, CC, or IT-NCSM [9, 271].
The aforementioned steps make use of prior theoretical knowledge, e.g., to identify desired decoupling patterns in interactions, or define analytical measures for the importance of basis states. If such knowledge is not available, or we want to avoid bias, we can leverage a myriad of Principal Component Analysis (PCA) methods to factorize interactions or intermediate quantities in many-body calculations [271, 272]. This can potentially even give us control over the computational scaling of nuclear many-body methods (see, e.g., [273–277]).
A very noteworthy development with origins in nuclear physics is Eigenvector Continuation (EVC) [278, 279], a method for learning manifolds of eigenvector trajectories of parameter-dependent Hamiltonians. The method has been employed in several contexts, e.g., to stabilize high-order MBPT expansions [81] and to construct emulators for nuclear few- and many-body calculations [280, 281]. As an example, Figure 15 shows a global sensitivity analysis of CC results for 16O under variations of the chiral LECs [281]. Eigenvector continuation was used to learn representations of the CCSD Hamiltonian and charge radius operators in a 64-dimensional subspace of the space of CCSD ground-state wave functions for interactions with 16 varying LECs. The subspace-projected Hamiltonian was then sampled more than a million times on laptop, while full CCSD calculations of the same ensemble would be completely unfeasible. The successful applications of EVC suggest that the method should be further explored as a tool for improvement, emulation and UQ in other many-body methods in the (near) future.
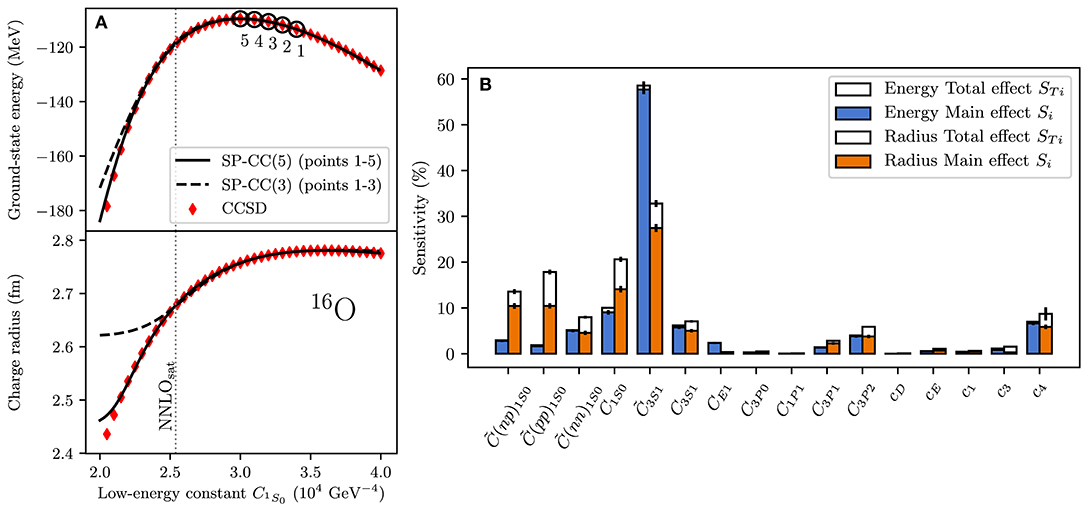
Figure 15. Sensitivity analysis using subspace-projected CC (SPCC) method [281]. (A) illustrates the capability of the SPCC Hamiltonian constructed from 3 to 5 sample points to predict full CCSD ground-state energies and charge radii for 16O over a wide range of values of the chiral LEC . (B) Shows the global sensitivity of the 16O ground-state energy and charge radius to chiral LECs, determined by evaluating over 1,000,000 quasi-MC samples from a 64-dimensional SPCC Hamiltonian. Vertical bars indicate 95% confidence intervals. For details, see reference [281]. Figure reprinted with permission from the American Physical Society.
In typical nuclear many-body calculations as discussed in sections 2 and 3 the main sources of theoretical uncertainties are the EFT truncation of the observables and the many-body wave function, either due to many-body expansion and/or model space truncations in configuration space approaches, lattice discretization effects in Lattice EFT, or the specific form of the wave function ansatz in QMC. If an SRG evolution is applied, there is an additional uncertainty associated with the truncation of induced operators (see section 2.2).
The application of Bayesian methods has led to enormous progress in the quantification of the EFT uncertainties [34–36, 282–285], and it would be highly desirable to apply the same approach to the many-body uncertainties as well. The most challenging amongst these are the truncation of the many-body expansion in methods like CC, IMSRG or SCGF, and the truncation of the free-space SRG flow of observables. In contrast, the infrared effects of finite-basis size truncations in HO bases—or general orbitals that are at some point expanded in an HO basis—are well-understood for the energy and other observables, and they can be systematically corrected for [286–290]. The situation is less clear for ultraviolet basis-size errors [291], but this error can be suppressed by working at appropriate values of the HO frequency.
An ideal uncertainty analysis would combine the exploration of EFT and many-body uncertainties for nuclear observables of interest, using EC or Machine Learning (ML) to construct emulators that allow an efficient sampling of the parameter space. In such an effort, the generation of sufficient training data poses a significant challenge, because it would require calculations at several truncation levels (see section 4.1). A possible strategy for mitigating this issue is to combine non-perturbative methods with cheaper high-order MBPT in Bayesian mixed models (see references [212, 292, 293] for applications in nuclear physics). The successful application of factorization methods to the nuclear many-body problem could likely resolve the issue once and for all by reducing the computational scaling of high-order truncations, at the cost of introducing an additional uncertainty from the factorization procedure.
On the road toward the destination represented by such a “complete” UQ framework, the intermediate milestones will already provide valuable insights into open issues in the EFTs of the strong interactions, and enable the design of better protocols for constraining and refining EFT-based interactions and operators (see, e.g., references [294, 295] and references therein).
Strong interaction physics is a multi-scale problem, and there are good reasons for making better use of the hierarchy of Effective (Field) Theories at our disposal. At the top level, we have QCD, followed by EFTs involving hyperons that can be eliminated progressively until we arrive at the “traditional” pionful and pionless chiral EFTs (see references [296, 297] and references therein). At even lower scales, one can formulate an EFT for nuclear halos (or clusters) [297] and make the connection to nuclear DFT and collective models, which can be understood as EFTs as well [298–305].
At least in principle, the different levels of this hierarchy can be connected either by computing observables with different theories and matching the LECs, or using RG flows to track in detail how the theories evolve from one into another. While matching procedures have been applied successfully to modern EFts in nuclear physics [306–311] as well as efforts to match more traditional models of nuclear structure to ab initio calculations [312–314], making the connection through RG methods is a more daunting task. While I must admit to bias in this regard, I still consider this an effort worth undertaking. The success of SRG techniques in nuclear physics demonstrate how these methods reveal the most effective degrees of freedom even in situations were the separation of scales is not perfectly clear. Moreover, RGs would also reveal unexpected features of the power counting schemes, like the enhancement or inadvertent omission of certain operators (see reference [51] and references therein).
Tackling power counting issues. Throughout this work, I have alluded to shortcomings and issues of the current generation of chiral interactions, like the struggle to achieve a good simultaneous description of nuclear binding energies and radii (see section 3.1). Recent efforts to construct new, accurate chiral interactions have revealed that this issue is connected to the use of local or non-local regulators, with the latter being favored for better descriptions [114, 209]. In another exploration of non-locally regularized chiral forces [210, 211], a tension between the simultaneous description of nuclear matter and finite was observed in the attempts to fit the chiral LECs. In QMC calculations, it was demonstrated that the use of local regulators breaks the equivalence of parameterizations of the interaction that are connected by Fierz identities, in certain cases with disastrous consequences [188]. Meanwhile, Epelbaum et al. have proposed the use of a more nuanced semilocal regularization scheme that applies local regulators to the long-range pion exchange and non-local regulators to the short-range contact terms [3, 46]. While physical arguments can be made in favor of different regularization schemes, perhaps especially the semilocal one, the significant scheme dependence is at odds with the principles of EFT, which would predict regulator artifacts to be pushed beyond the order at which one currently works.
It has also been suggested that the scales of the chiral EFT interaction and the inherent scales of the many-body configuration space (e.g., IR and UV cutoffs inherited from a HO basis, see section 4.3) or coordinate space wave functions should not be treated independently, and that by doing so, current many-body approaches might at least contribute to power counting issues. There have been a few efforts to explore this problem, but more work is clearly required [315–320].
Application needs. Aside from the formal need to make progress on the power counting issue, there are also concrete application needs that call for a tighter coupling between QCD and the nuclear EFTs. For example, the chiral EFT transition operator for neutrinoless double-beta decay (see section 3.2.3) contains counter terms whose LECs can only be determined from Lattice QCD [321–324].
The dawning of a new age in our understanding of neutron stars, heralded by the detection of gravitational waves from the neutron-star merger GW170817, has taken the demand for accurate neutron and nuclear matter equations of state to a new level (see, e.g., reference [159] and references therein). While ab initio calculations of infinite matter up to the saturation region based on chiral interactions are reasonably well-controlled [159, 190, 285, 325], the supranuclear densities probed in merger events are beyond the range of validity of regular pionful chiral EFT. To increase its validity, hyperons must be taken into account as dynamical degrees of freedom (see [296] and references therein), and the entire set of nuclear and hyperon LECs must be readjusted at the increased breakdown scale. For the NN sector, this is unproblematic due to the plethora of available scattering data. Since no direct experiments on three-neutron or three-proton systems are feasible, the only available experimental constraints come from finite nuclei, which implies that the corresponding channels of the 3N interaction are only constrained at sub-saturation densities. The world database of hyperon-nucleon scattering data is also quite limited. Thus, a high-precision interaction for describing the equation of state at high density can only be constructed with the help of Lattice QCD constraints on the 3N and hypernucleon LECs.
The final important research direction for the coming decade I want to discuss here are efforts to interface the advanced ab initio nuclear structure methods at our disposal with reaction theory [326].
As discussed in sections 2.3.6 and 3.2.4, the NCSMC has been applied with great success to the reactions of light nuclei at low energies, but its computational complexity makes this approach unfeasible for nuclei beyond A ≈ 10 − 20. Work has begun on a similar approach that combines SA-NCSM with the RGM, leveraging the efficiency of the symmetry-adapted basis to reach medium-mass nuclei [327] (cf. sections 2.3.6 and 3.3). Since the RGM is just a special case of a Generator Coordinate Method, the IM-GCM discussed in sections 2.3.3 and 3.2.3 is a promising candidate for extending this type of reaction calculations to even heavier nuclei.
Methods that are similar in spirit to these combinations of structure approaches with the RGM are the APM, which can provide an interface between structure and scattering in Lattice EFT (cf. sections 2.3.8 and 3.2.4), as well as the GSM Coupled Channel (GSM-CC) approach, which was developed to describe reactions between light projectiles and targets that are treated in the GSM with a core [221, 328, 329]. Thus far, applications of the GSM-CC have been based on phenomenological valence-space interactions, but new efforts are underway to directly construct suitable Hamiltonians based on EFT principles [220, 330], or derive the effective interactions from chiral forces with the techniques discussed in section 2.3 (see [214, 215]). Of course, the GSM-CC ideas could also be applied to the No-Core GSM [153, 155, 218], although the computational complexity would limit such an approach to light nuclei.
A complementary strategy for bridging nuclear structure and reactions for medium-mass nuclei is the construction of optical potentials for use in traditional reaction calculations. In SCGF theory, the optical potential for elastic nucleon-nucleus scattering is given by the one-body self energy, which is obtained as a byproduct of a nuclear structure calculation, and can be used with little effort in reaction codes [125]. Similarly, Rotureau et al. constructed optical potentials by extracting the self-energy from the Coupled Cluster Green's Function [123, 124, 331]. One can roughly view this procedure as performing a GF calculation with the similarity-transformed CC Hamiltonian, which does not require self-consistent iterations because of the CC decoupling (cf. section 2.3.4). Optical potentials can also be constructed by folding scattering T-matrices with ab initio density matrices. This technique was applied for NCSM density matrices by two collaborations in references [332, 333] and [334, 335], respectively, and more applications are underway.
While the published results from the optical-potential based approaches are promising, an important aspect of these calculations must be checked carefully in the near term: The optical potential depends on the resolution scale of the used chiral interactions, and the calculation scheme, which encompasses the truncations in the operators and many-body method, as well as the choice of regulator in the interaction [257, 336]. To produce scale- and scheme-independent observables, these choices must be matched by the reaction theory. Matching the resolution scales is probably the easier of the two checks, but it will require the analysis of free-space SRG transformations on the reaction theory side. Once structure and theory are defined at a matching resolution scale, any residual scheme dependence of the observables will give rise to the remaining theoretical uncertainty of the combined calculation.
Thus concludes our little excursion through the landscape of state-of-the-art ab initio nuclear many-body theory, but of course, the road goes ever on. I hope that this guided tour has contributed to your appreciation of the immense progress the community has made in the last 10 years, as well as the challenges that we are facing on the next stage of the road. None of the obstacles in our path are unsurmountable, and while we chip away at them, results from ab initio calculations can make meaningful contributions to the analysis and planning of nuclear physics and fundamental symmetry experiments. With new facilities launching in the next couple of years, the fun will begin in earnest, so here's looking forward to the next decade!
The author confirms being the sole contributor of this work and has approved it for publication.
The preparation of this work has been supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics under Awards No. DE-SC0017887, DE-SC0018083 (NUCLEI2 SciDAC-4 Collaboration), and DE-SC0015376 (DBD Topical Theory Collaboration).
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
This work has been shaped by an enormous amount of discussions over the past decade, and naming all discussion partners would likely require multiple pages—it is safe to say that if your work is cited here, we have likely talked in person at some point. I am deeply grateful for these conversations, and the spirit of the ab initio nuclear structure and reactions community that fosters such exchanges.
I would like to thank the current (and former) members of my research group as well as colleagues at NSCL/FRIB, who had the most immediate impact on this work by virtue of being a short walk away. Particular thanks go out to S. Bogner, K. Fossez, M. Hjorth-Jensen, R. Wirth, and J. M. Yao. Special thanks are owed to R. Stroberg and S. Elhatisari, who helped out with sudden requests for figures.
I am also grateful to the Institute of Nuclear Theory for its hospitality, which was the venue for many of the aforementioned discussions, most recently during the program INT-19-2a, Nuclear Structure at the Crossroads.
1. ^This exhausts my contractually allowed contingent of 2020 vision puns, I swear.
2. ^This labeling scheme is commonly used in chemistry [63], and it is used with increasing frequency in nuclear physics as well.
1. Bogner SK, Furnstahl RJ, Schwenk A. From low-momentum interactions to nuclear structure. Prog Part Nucl Phys. (2010) 65:94–147. doi: 10.1016/j.ppnp.2010.03.001
2. Machleidt R, Sammarruca F. Chiral EFT based nuclear forces: achievements and challenges. Phys Scripta. (2016) 91:083007. doi: 10.1088/0031-8949/91/8/083007
3. Epelbaum E, Krebs H, Reinert P. High-precision nuclear forces from chiral EFT: state-of-the-art, challenges, and outlook. Front Phys. (2020) 8:98. doi: 10.3389/fphy.2020.00098
4. Piarulli M, Tews I. Local nucleon-nucleon and three-nucleon interactions within chiral effective field theory. Front Phys. (2020) 7:245. doi: 10.3389/fphy.2019.00245
5. Roth R, Langhammer J. Padé-resummed high-order perturbation theory for nuclear structure calculations. Phys Lett B. (2010) 683:272–7. doi: 10.1016/j.physletb.2009.12.046
6. Tichai A, Langhammer J, Binder S, Roth R. Hartree-Fock many-body perturbation theory for nuclear ground-states. Phys Lett B. (2016) 756:283–8. doi: 10.1016/j.physletb.2016.03.029
7. Navrátil P, Gueorguiev VG, Vary JP, Ormand WE, Nogga A. Structure of A = 10˘13 nuclei with two- plus three-nucleon interactions from chiral effective field theory. Phys Rev Lett. (2007) 99:042501. doi: 10.1103/PhysRevLett.99.042501
8. Roth R, Navrátil P. Ab initio study of 40Ca with an importance-truncated No-core shell model. Phys Rev Lett. (2007) 99:092501. doi: 10.1103/PhysRevLett.99.092501
9. Roth R. Importance truncation for large-scale configuration interaction approaches. Phys Rev C. (2009) 79:064324. doi: 10.1103/PhysRevC.79.064324
10. Somà V. Self-consistent Green's function theory for atomic nuclei. arXiv. (2020) arxiv [Preprint] arXiv:2003.11321.
11. Hergert H, Bogner SK, Morris TD, Schwenk A, Tsukiyama K. The in-medium similarity renormalization group: a novel ab initio method for nuclei. Phys Rep. (2016) 621:165–222. doi: 10.1016/j.physrep.2015.12.007
12. Hagen G, Papenbrock T, Hjorth-Jensen M, Dean DJ. Coupled-cluster computations of atomic nuclei. Rept Prog Phys. (2014) 77:096302. doi: 10.1088/0034-4885/77/9/096302
13. Coester F. Bound states of a many-particle system. Nucl Phys. (1958) 7:421–4. doi: 10.1016/0029-5582(58)90280-3
14. Coester F, Kümmel H. Short-range correlations in nuclear wave functions. Nucl Phys. (1960) 17:477–85. doi: 10.1016/0029-5582(60)90140-1
15. Hagen G, Hjorth-Jensen M, Jansen GR, Machleidt R, Papenbrock T. Continuum effects and three-nucleon forces in neutron-rich oxygen isotopes. Phys Rev Lett. (2012) 108:242501. doi: 10.1103/PhysRevLett.108.242501
16. Hagen G, Hjorth-Jensen M, Jansen GR, Machleidt R, Papenbrock T. Evolution of shell structure in neutron-rich calcium isotopes. Phys Rev Lett. (2012) 109:032502. doi: 10.1103/PhysRevLett.109.032502
17. Hergert H, Bogner SK, Binder S, Calci A, Langhammer J, Roth R, et al. In-medium similarity renormalization group with chiral two- plus three-nucleon interactions. Phys Rev C. (2013) 87:034307. doi: 10.1103/PhysRevC.87.034307
18. Cipollone A, Barbieri C, Navrátil P. Isotopic chains around oxygen from evolved chiral two- and three-nucleon interactions. Phys Rev Lett. (2013) 111:062501. doi: 10.1103/PhysRevLett.111.062501
19. Binder S, Langhammer J, Calci A, Roth R. Ab initio path to heavy nuclei. Phys Lett B. (2014) 736:119–23. doi: 10.1016/j.physletb.2014.07.010
20. Hergert H, Binder S, Calci A, Langhammer J, Roth R. Ab initio calculations of even oxygen isotopes with chiral two-plus-three-nucleon interactions. Phys Rev Lett. (2013) 110:242501. doi: 10.1103/PhysRevLett.110.242501
21. Hergert H, Bogner SK, Morris TD, Binder S, Calci A, Langhammer J, et al. Ab initio multi-reference in-medium similarity renormalization group calculations of even calcium and nickel isotopes. Phys Rev C. (2014) 90:041302. doi: 10.1103/PhysRevC.90.041302
22. Somà V, Barbieri C, Duguet T. Ab initio Gorkov-Green's function calculations of open-shell nuclei. Phys Rev C. (2013) 87:011303. doi: 10.1103/PhysRevC.87.011303
23. Somà V, Cipollone A, Barbieri C, Navrátil P, Duguet T. Chiral two- and three-nucleon forces along medium-mass isotope chains. Phys Rev C. (2014) 89:061301. doi: 10.1103/PhysRevC.89.061301
24. Jansen GR, Engel J, Hagen G, Navratil P, Signoracci A. Ab-initio coupled-cluster effective interactions for the shell model: application to neutron-rich oxygen and carbon isotopes. Phys Rev Lett. (2014) 113:142502. doi: 10.1103/PhysRevLett.113.142502
25. Sun ZH, Morris TD, Hagen G, Jansen GR, Papenbrock T. Shell-model coupled-cluster method for open-shell nuclei. Phys Rev C. (2018) 98:054320. doi: 10.1103/PhysRevC.98.054320
26. Bogner SK, Hergert H, Holt JD, Schwenk A, Binder S, Calci A, et al. Nonperturbative shell-model interactions from the in-medium similarity renormalization group. Phys Rev Lett. (2014) 113:142501. doi: 10.1103/PhysRevLett.113.142501
27. Stroberg SR, Calci A, Hergert H, Holt JD, Bogner SK, Roth R, et al. Nucleus-dependent valence-space approach to nuclear structure. Phys Rev Lett. (2017) 118:032502. doi: 10.1103/PhysRevLett.118.032502
28. Miyagi T, Stroberg SR, Holt JD, Shimizu N. Ab initio multi-shell valence-space Hamiltonians and the island of inversion. arXiv. (2020) arxiv [Preprint] arXiv:2004.12969.
29. Yao JM, Bally B, Engel J, Wirth R, Rodríguez TR, Hergert H. Ab initio treatment of collective correlations and the neutrinoless double beta decay of 48Ca. Phys Rev Lett. (2020) 124:232501. doi: 10.1103/PhysRevLett.124.232501
30. Gross DJ, Wilczek F. Ultraviolet behavior of non-Abelian gauge theories. Phys Rev Lett. (1973) 30:1343–6. doi: 10.1103/PhysRevLett.30.1343
31. Politzer HD. Reliable perturbative results for strong interactions? Phys Rev Lett. (1973) 30:1346–9. doi: 10.1103/PhysRevLett.30.1346
32. Weinberg S. Effective chiral lagrangians for nucleon-pion interactions and nuclear forces. Nucl Phys B. (1991) 363:3–18. doi: 10.1016/0550-3213(91)90231-L
33. Weinberg S. The Quantum Theory of Fields, Vol. II. Modern Applications. 2nd ed. Cambridge: Cambridge University Press (1996).
34. Melendez JA, Wesolowski S, Furnstahl RJ. Bayesian truncation errors in chiral effective field theory: nucleon-nucleon observables. Phys Rev C. (2017) 96:024003. doi: 10.1103/PhysRevC.96.024003
35. Melendez JA, Furnstahl RJ, Phillips DR, Pratola MT, Wesolowski S. Quantifying correlated truncation errors in effective field theory. Phys Rev C. (2019) 100:044001. doi: 10.1103/PhysRevC.100.044001
36. Wesolowski S, Furnstahl RJ, Melendez JA, Phillips DR. Exploring Bayesian parameter estimation for chiral effective field theory using nucleon-nucleon phase shifts. J Phys G Nucl Part Phys. (2019) 46:045102. doi: 10.1088/1361-6471/aaf5fc
37. Epelbaum E, Hammer HW, Meißner UG. Modern theory of nuclear forces. Rev Mod Phys. (2009) 81:1773–825. doi: 10.1103/RevModPhys.81.1773
38. Machleidt R, Entem DR. Chiral effective field theory and nuclear forces. Phys Rept. (2011) 503:1–75. doi: 10.1016/j.physrep.2011.02.001
39. Rodriguez Entem D, Machleidt R, Nosyk Y. Nucleon-nucleon scattering up to N5LO in chiral effective field theory. Front Phys. (2020) 8:57. doi: 10.3389/fphy.2020.00057
40. Ekström A. Analyzing the nuclear interaction: challenges and new ideas. Front Phys. (2020) 8:29. doi: 10.3389/fphy.2020.00029
41. Ruiz Arriola E, Amaro JE, Navarro Pérez R. NN scattering and nuclear uncertainties. Front Phys. (2020) 8:1. doi: 10.3389/fphy.2020.00001
42. Gazit D, Quaglioni S, Navrátil P. Three-nucleon low-energy constants from the consistency of interactions and currents in chiral effective field theory. Phys Rev Lett. (2009) 103:102502. doi: 10.1103/PhysRevLett.103.102502
43. Pastore S, Girlanda L, Schiavilla R, Viviani M. Two-nucleon electromagnetic charge operator in chiral effective field theory (χEFT) up to one loop. Phys Rev C. (2011) 84:024001. doi: 10.1103/PhysRevC.84.024001
44. Kölling S, Epelbaum E, Krebs H, Meißner UG. Two-nucleon electromagnetic current in chiral effective field theory: one-pion exchange and short-range contributions. Phys Rev C. (2011) 84:054008. doi: 10.1103/PhysRevC.84.054008
45. Piarulli M, Girlanda L, Marcucci LE, Pastore S, Schiavilla R, Viviani M. Electromagnetic structure of A=2 and 3 nuclei in chiral effective field theory. Phys Rev C. (2013) 87:014006. doi: 10.1103/PhysRevC.87.014006
46. Reinert P, Krebs H, Epelbaum E. Semilocal momentum-space regularized chiral two-nucleon potentials up to fifth order. Eur Phys J A. (2018) 54:86. doi: 10.1140/epja/i2018-12516-4
47. Lynn JE, Tews I, Carlson J, Gandolfi S, Gezerlis A, Schmidt KE, et al. Chiral three-nucleon interactions in light nuclei, neutron-α scattering, and neutron matter. Phys Rev Lett. (2016) 116:062501. doi: 10.1103/PhysRevLett.116.062501
48. Lynn JE, Tews I, Carlson J, Gandolfi S, Gezerlis A, Schmidt KE, et al. Quantum Monte Carlo calculations of light nuclei with local chiral two- and three-nucleon interactions. Phys Rev C. (2017) 96:054007. doi: 10.1103/PhysRevC.96.054007
49. Valderrama MP, Sánchez MS, Yang CJ, Long B, Carbonell J, van Kolck U. Power counting in peripheral partial waves: the singlet channels. Phys Rev C. (2017) 95:054001. doi: 10.1103/PhysRevC.95.054001
50. Sánchez MS, Yang CJ, Long B, van Kolck U. Two-nucleon amplitude zero in chiral effective field theory. Phys Rev C. (2018) 97:024001. doi: 10.1103/PhysRevC.97.024001
51. van Kolck U. The problem of renormalization of chiral nuclear forces. Front Phys. (2020) 8:79. doi: 10.3389/fphy.2020.00079
52. Wilson KG. The renormalization group: critical phenomena and the Kondo problem. Rev Mod Phys. (1975) 47:773–840. doi: 10.1103/RevModPhys.47.773
53. Hergert H. In-medium similarity renormalization group for closed and open-shell nuclei. Phys Scripta. (2017) 92:023002. doi: 10.1088/1402-4896/92/2/023002
54. Stroberg SR, Hergert H, Holt JD, Bogner SK, Schwenk A. Ground and excited states of doubly open-shell nuclei from ab initio valence-space Hamiltonians. Phys Rev C. (2016) 93:051301. doi: 10.1103/PhysRevC.93.051301
55. Johnson CW. Unmixing symmetries. Phys Rev Lett. (2020) 124:172502. doi: 10.1103/PhysRevLett.124.172502
56. Wegner F. Flow equations for Hamiltonians. Ann Phys (Leipzig). (1994) 3:77. doi: 10.1002/andp.19945060203
57. Kehrein S. The Flow Equation Approach to Many-Particle Systems. Vol. 237 of Springer Tracts in Modern Physics. Berlin; Heidelberg: Springer Berlin Heidelberg (2006).
58. Hergert H, Bogner SK, Lietz JG, Morris TD, Novario SJ, Parzuchowski NM, et al. In-medium similarity renormalization group approach to the nuclear many-body problem. In: Hjorth-Jensen M, Lombardo MP, van Kolck U, editors. An Advanced Course in Computational Nuclear Physics: Bridging the Scales from Quarks to Neutron Stars. Cham: Springer International Publishing (2017). p. 477–570. doi: 10.1007/978-3-319-53336-0_10
59. Jurgenson ED, Navrátil P, Furnstahl RJ. Evolution of nuclear many-body forces with the similarity renormalization group. Phys Rev Lett. (2009) 103:082501. doi: 10.1103/PhysRevLett.103.082501
60. Hebeler K. Momentum-space evolution of chiral three-nucleon forces. Phys Rev C. (2012) 85:021002. doi: 10.1103/PhysRevC.85.021002
61. Wendt KA. Similarity renormalization group evolution of three-nucleon forces in a hyperspherical momentum representation. Phys Rev C. (2013) 87:061001. doi: 10.1103/PhysRevC.87.061001
62. Calci A. Evolved Chiral Hamiltonians at the Three-Body Level and Beyond. Darmstadt: TU Darmstadt (2014).
63. Shavitt I, Bartlett RJ. Many-Body Methods in Chemistry and Physics: MBPT and Coupled-Cluster Theory. Cambridge: Cambridge University Press (2009).
64. Kutzelnigg W. How many-body perturbation theory (MBPT) has changed quantum chemistry. Int J Quantum Chem. (2009) 109:3858–84. doi: 10.1002/qua.22384
65. Brueckner KA, Levinson CA, Mahmoud HM. Two-body forces and nuclear saturation. I. Central forces. Phys Rev. (1954) 95:217–28. doi: 10.1103/PhysRev.95.217
66. Brueckner KA, Levinson CA. Approximate reduction of the many-body problem for strongly interacting particles to a problem of self-consistent fields. Phys Rev. (1955) 97:1344–52. doi: 10.1103/PhysRev.97.1344
67. Day BD. Elements of the Brueckner-Goldstone theory of nuclear matter. Rev Mod Phys. (1967) 39:719–44. doi: 10.1103/RevModPhys.39.719
68. Brandow BH. Linked-cluster expansions for the nuclear many-body problem. Rev Mod Phys. (1967) 39:771–828. doi: 10.1103/RevModPhys.39.771
69. Tichai A, Roth R, Duguet T. Many-body perturbation theories for finite nuclei. Front Phys. (2020) 8:164. doi: 10.3389/fphy.2020.00164
70. Langhammer J, Roth R, Stumpf C. Spectra of open-shell nuclei with Padé-resummed degenerate perturbation theory. Phys Rev C. (2012) 86:054315. doi: 10.1103/PhysRevC.86.054315
71. Otsuka T, Suzuki T, Holt JD, Schwenk A, Akaishi Y. Three-body forces and the limit of oxygen isotopes. Phys Rev Lett. (2010) 105:032501. doi: 10.1103/PhysRevLett.105.032501
72. Holt JD, Engel J. Effective double-β-decay operator for 76Ge and 82Se. Phys Rev C. (2013) 87:064315. doi: 10.1103/PhysRevC.87.064315
73. Tsunoda N, Takayanagi K, Hjorth-Jensen M, Otsuka T. Multi-shell effective interactions. Phys Rev C. (2014) 89:024313. doi: 10.1103/PhysRevC.89.024313
74. Holt JD, Menéndez J, Simonis J, Schwenk A. Three-nucleon forces and spectroscopy of neutron-rich calcium isotopes. Phys Rev C. (2014) 90:024312. doi: 10.1103/PhysRevC.90.024312
75. Coraggio L, Covello A, Gargano A, Itaco N, Kuo TTS. Shell-model calculations and realistic effective interactions. Prog Part Nucl Phys. (2009) 62:135–82. doi: 10.1016/j.ppnp.2008.06.001
76. Stroberg SR, Hergert H, Bogner SK, Holt JD. Nonempirical interactions for the nuclear shell model: an update. Annu Rev Nucl Part Sci. (2019) 69:307–62. doi: 10.1146/annurev-nucl-101917-021120
77. Tichai A, Arthuis P, Duguet T, Hergert H, Somà V, Roth R. Bogoliubov many-body perturbation theory for open-shell nuclei. Phys Lett B. (2018) 786:195–200. doi: 10.1016/j.physletb.2018.09.044
78. Tichai A, Gebrerufael E, Vobig K, Roth R. Open-shell nuclei from No-core shell model with perturbative improvement. Phys Lett B. (2018) 786:448–52. doi: 10.1016/j.physletb.2018.10.029
79. Kucharski SA, Bartlett RJ. Fifth-order many-body perturbation theory and its relationship to various coupled-cluster approaches. Adv Quantum Chem. (1986) 18, 281–344. doi: 10.1016/S0065-3276(08)60051-9
80. Ripoche J, Tichai A, Duguet T. Normal-ordered k-body approximation in particle-number-breaking theories. Eur Phys J A. (2020) 56:40. doi: 10.1140/epja/s10050-020-00045-8
81. Demol P, Duguet T, Ekström A, Frosini M, Hebeler K, König S, et al. Improved many-body expansions from eigenvector continuation. Phys Rev C. (2020) 101:041302. doi: 10.1103/PhysRevC.101.041302
82. Hjorth-Jensen M, Kuo TTS, Osnes E. Realistic effective interactions for nuclear systems. Phys Rept. (1995) 261:125–270. doi: 10.1016/0370-1573(95)00012-6
83. Parzuchowski NM, Morris TD, Bogner SK. Ab initio excited states from the in-medium similarity renormalization group. Phys Rev C. (2017) 95:044304. doi: 10.1103/PhysRevC.95.044304
84. Gebrerufael E, Vobig K, Hergert H, Roth R. Ab initio description of open-shell nuclei: merging No-core shell model and in-medium similarity renormalization group. Phys Rev Lett. (2017) 118:152503. doi: 10.1103/PhysRevLett.118.152503
85. Yao JM, Engel J, Wang LJ, Jiao CF, Hergert H. Generator-coordinate reference states for spectra and 0νββ decay in the in-medium similarity renormalization group. Phys Rev C. (2018) 98:054311. doi: 10.1103/PhysRevC.98.054311
86. Hergert H, Yao JM, Morris TD, Parzuchowski NM, Bogner SK, Engel J. Nuclear structure from the in-medium similarity renormalization group. J Phys Conf Series. (2018) 1041:012007. doi: 10.1088/1742-6596/1041/1/012007
87. Tsukiyama K, Bogner SK, Schwenk A. In-medium similarity renormalization group for nuclei. Phys Rev Lett. (2011) 106:222502. doi: 10.1103/PhysRevLett.106.222502
88. Tsukiyama K, Bogner SK, Schwenk A. In-medium similarity renormalization group for open-shell nuclei. Phys Rev C. (2012) 85:061304. doi: 10.1103/PhysRevC.85.061304
89. Caurier E, Martínez-Pinedo G, Nowacki F, Poves A, Zuker AP. The shell model as a unified view of nuclear structure. Rev Mod Phys. (2005) 77:427–88. doi: 10.1103/RevModPhys.77.427
90. Brown BA, Rae WDM. The shell-model code NuShellX@MSU. Nucl Data Sheets. (2014) 120:115–8. doi: 10.1016/j.nds.2014.07.022
91. Engeland T, Hjorth-Jensen M. The Oslo FCI Code. (2017). Available online at: https://github.com/ManyBodyPhysics/ManybodyCodes
92. Johnson CW, Ormand WE, McElvain KS, Shan H. BIGSTICK: a flexible configuration-interaction shell-model code. arXiv. (2018) arxiv [Preprint] arXiv:180108432.
93. Shimizu N, Mizusaki T, Utsuno Y, Tsunoda Y. Thick-restart block Lanczos method for large-scale shell-model calculations. Comput Phys Commun. (2019) 244:372–84. doi: 10.1016/j.cpc.2019.06.011
94. Kutzelnigg W, Mukherjee D. Normal order and extended Wick theorem for a multiconfiguration reference wave function. J Chem Phys. (1997) 107:432–49. doi: 10.1063/1.474405
95. Kong L, Nooijen M, Mukherjee D. An algebraic proof of generalized Wick theorem. J Chem Phys. (2010) 132:234107. doi: 10.1063/1.3439395
96. Morris TD, Parzuchowski NM, Bogner SK. Magnus expansion and in-medium similarity renormalization group. Phys Rev C. (2015) 92:034331. doi: 10.1103/PhysRevC.92.034331
97. D'Alessio A, et al. Precision measurement of the E2 transition strength to the state of 12C. arXiv. (2020) arxiv [Preprint] arXiv:2005.04072.
98. Taube AG, Bartlett RJ. Improving upon CCSD(T): Lambda CCSD(T). I. Potential energy surfaces. J Chem Phys. (2008) 128:044110. doi: 10.1063/1.2830236
99. Taube AG, Bartlett RJ. Improving upon CCSD(T): Lambda CCSD(T). II. Stationary formulation and derivatives. J Chem Phys. (2008) 128:044111. doi: 10.1063/1.2830237
100. Binder S, Piecuch P, Calci A, Langhammer J, Navrátil P, Roth R. Extension of coupled-cluster theory with a noniterative treatment of connected triply excited clusters to three-body Hamiltonians. Phys Rev C. (2013) 88:054319. doi: 10.1103/PhysRevC.88.054319
101. Duguet T. Symmetry broken and restored coupled-cluster theory: I. Rotational symmetry and angular momentum. J Phys G. (2015) 42:025107. doi: 10.1088/0954-3899/42/2/025107
102. Signoracci A, Duguet T, Hagen G, Jansen GR. Ab initio Bogoliubov coupled cluster theory for open-shell nuclei. Phys Rev C. (2015) 91:064320. doi: 10.1103/PhysRevC.91.064320
103. Duguet T, Signoracci A. Symmetry broken and restored coupled-cluster theory: II. Global gauge symmetry and particle number. J Phys G Nucl Part Phys. (2017) 44:015103. doi: 10.1088/0954-3899/44/1/015103
104. Qiu Y, Henderson TM, Duguet T, Scuseria GE. Particle-number projected Bogoliubov-coupled-cluster theory: application to the pairing Hamiltonian. Phys Rev C. (2019) 99:044301. doi: 10.1103/PhysRevC.99.044301
105. Jansen GR, Schuster MD, Signoracci A, Hagen G, Navrátil P. Open sd-shell nuclei from first principles. Phys Rev C. (2016) 94:011301. doi: 10.1103/PhysRevC.94.011301
106. Taube AG, Bartlett RJ. New perspectives on unitary coupled-cluster theory. Int J Quantum Chem. (2006) 106:3393–401. doi: 10.1002/qua.21198
107. Bartlett RJ, Musiał M. Coupled-cluster theory in quantum chemistry. Rev Mod Phys. (2007) 79:291–352. doi: 10.1103/RevModPhys.79.291
108. Dumitrescu EF, McCaskey AJ, Hagen G, Jansen GR, Morris TD, Papenbrock T, et al. Cloud quantum computing of an atomic nucleus. Phys Rev Lett. (2018) 120:210501. doi: 10.1103/PhysRevLett.120.210501
109. Lu HH, Klco N, Lukens JM, Morris TD, Bansal A, Ekström A, et al. Simulations of subatomic many-body physics on a quantum frequency processor. Phys Rev A. (2019) 100:012320. doi: 10.1103/PhysRevA.100.012320
110. Miyagi T, Abe T, Okamoto R, Otsuka T. Introduction of the one-body correlation operator in the unitary-model-operator approach. Phys Rev C. (2017) 96:054312. doi: 10.1103/PhysRevC.96.054312
111. Miyagi T, Abe T, Kohno M, Navrátil P, Okamoto R, Otsuka T, et al. Ground-state properties of doubly magic nuclei from the unitary-model-operator approach with chiral two- and three-nucleon forces. Phys Rev C. (2019) 100:034310. doi: 10.1103/PhysRevC.100.034310
112. Dickhoff WH, Barbieri C. Self-consistent Green's function method for nuclei and nuclear matter. Prog Part Nucl Phys. (2004) 52:377–496. doi: 10.1016/j.ppnp.2004.02.038
113. Barbieri C, Carbone A. Self-consistent Green's function approaches. In: Hjorth-Jensen M, Lombardo M, van Kolck U, editors. An Advanced Course in Computational Nuclear Physics. No. 936 in Lecture Notes in Physics. Springer. (2017).
114. Somà V, Navrátil P, Raimondi F, Barbieri C, Duguet T. Novel chiral Hamiltonian and observables in light and medium-mass nuclei. Phys Rev C. (2020) 101:014318. doi: 10.1103/PhysRevC.101.014318
115. Rios A. Green's functions techniques for extended nuclear systems. arXiv. (2020) arxiv [Preprint] arXiv:2006.10610.
116. Morris TD. Systematic Improvements of Ab Initio In-Medium Similarity Renormalization Group Calculations. East Lansing, MI: Michigan State University (2016).
117. Somà V, Duguet T, Barbieri C. Ab initio self-consistent Gorkov-Green's function calculations of semimagic nuclei: Formalism at second order with a two-nucleon interaction. Phys Rev C. (2011) 84:064317. doi: 10.1103/PhysRevC.84.064317
118. Somà V, Barbieri C, Duguet T. Ab initio self-consistent Gorkov-Green's function calculations of semi-magic nuclei: numerical implementation at second order with a two-nucleon interaction. Phys Rev C. (2014) 89:024323. doi: 10.1103/PhysRevC.89.024323
119. Raimondi F, Barbieri C. Nuclear electromagnetic dipole response with the self-consistent Green's function formalism. Phys Rev C. (2019) 99:054327. doi: 10.1103/PhysRevC.99.054327
120. Rocco N, Barbieri C. Inclusive electron-nucleus cross section within the self-consistent Green's function approach. Phys Rev C. (2018) 98:025501. doi: 10.1103/PhysRevC.98.025501
121. Jansen GR, Hjorth-Jensen M, Hagen G, Papenbrock T. Toward open-shell nuclei with coupled-cluster theory. Phys Rev C. (2011) 83:054306. doi: 10.1103/PhysRevC.83.054306
122. Jansen GR. Spherical coupled-cluster theory for open-shell nuclei. Phys Rev C. (2013) 88:024305. doi: 10.1103/PhysRevC.88.024305
123. Rotureau J, Danielewicz P, Hagen G, Nunes FM, Papenbrock T. Optical potential from first principles. Phys Rev C. (2017) 95:024315. doi: 10.1103/PhysRevC.95.024315
124. Rotureau J, Danielewicz P, Hagen G, Jansen GR, Nunes FM. Microscopic optical potentials for calcium isotopes. Phys Rev C. (2018) 98:044625. doi: 10.1103/PhysRevC.98.044625
125. Idini A, Barbieri C, Navrátil P. Ab initio optical potentials and nucleon scattering on medium mass nuclei. Phys Rev Lett. (2019) 123:092501. doi: 10.1103/PhysRevLett.123.092501
126. Navrátil P, Kamuntavicius GP, Barrett BR. Few-nucleon systems in translationally invariant harmonic oscillator basis. Phys Rev C. (2000) 61:044001. doi: 10.1103/PhysRevC.61.044001
127. Barnea N, Leidemann W, Orlandini G. State-dependent effective interaction for the hyperspherical formalism with noncentral forces. Nucl Phys A. (2001) 693:565–78. doi: 10.1016/S0375-9474(01)00794-1
128. Barnea N, Efros VD, Leidemann W, Orlandini G. Incorporation of three-nucleon force in the effective-interaction hyperspherical-harmonic approach. Few Body Syst. (2004) 35:155–67. doi: 10.1007/s00601-004-0066-y
129. Barrett BR, Navrátil P, Vary JP. Ab initio no core shell model. Prog Part Nucl Phys. (2013) 69:131–81. doi: 10.1016/j.ppnp.2012.10.003
130. Navrátil P, Quaglioni S, Hupin G, Romero-Redondo C, Calci A. Unified ab initio approaches to nuclear structure and reactions. Phys Scripta. (2016) 91:053002. doi: 10.1088/0031-8949/91/5/053002
131. Tichai A, Müller J, Vobig K, Roth R. Natural orbitals for ab initio no-core shell model calculations. Phys Rev C. (2019) 99:034321. doi: 10.1103/PhysRevC.99.034321
132. Robin C, Pillet N, Peña Arteaga D, Berger JF. Description of nuclear systems with a self-consistent configuration-mixing approach: theory, algorithm, and application to the 12C test nucleus. Phys Rev C. (2016) 93:024302. doi: 10.1103/PhysRevC.93.024302
133. Robin C, Pillet N, Dupuis M, Le Bloas J, Peña Arteaga D, Berger JF. Description of nuclear systems with a self-consistent configuration-mixing approach. II. Application to structure and reactions in even-even sd-shell nuclei. Phys Rev C. (2017) 95:044315. doi: 10.1103/PhysRevC.95.044315
134. Pillet N, Robin C, Dupuis M, Hupin G, Berger JF. The self-consistent multiparticle-multihole configuration mixing. Eur Phys J A. (2017) 53:49. doi: 10.1140/epja/i2017-12232-7
135. Roth R, Gour JR, Piecuch P. Center-of-mass problem in truncated configuration interaction and coupled-cluster calculations. Phys Lett B. (2009) 679:334–9. doi: 10.1016/j.physletb.2009.07.071
136. Gloeckner DH, Lawson RD. Spurious center-of-mass motion. Phys Lett B. (1974) 53:313–8. doi: 10.1016/0370-2693(74)90390-6
137. Otsuka T, Honma M, Mizusaki T, Shimizu N, Utsuno Y. Monte Carlo shell model for atomic nuclei. Prog Part Nucl Phys. (2001) 47:319–400. doi: 10.1016/S0146-6410(01)00157-0
138. Shimizu N, Abe T, Honma M, Otsuka T, Togashi T, Tsunoda Y, et al. Monte Carlo shell model studies with massively parallel supercomputers. Phys Scripta. (2017) 92:063001. doi: 10.1088/1402-4896/aa65e4
139. Launey KD, Dytrych T, Draayer JP. Symmetry-guided large-scale shell-model theory. Prog Part Nucl Phys. (2016) 89:101–36. doi: 10.1016/j.ppnp.2016.02.001
140. Dytrych T, Launey KD, Draayer JP, Rowe DJ, Wood JL, Rosensteel G, et al. Physics of nuclei: key role of an emergent symmetry. Phys Rev Lett. (2020) 124:042501. doi: 10.1103/PhysRevLett.124.042501
141. Caprio MA, Fasano PJ, Maris P, McCoy AE, Vary JP. Probing ab initio emergence of nuclear rotation. Eur Phys J A. (2020) 56:120. doi: 10.1140/epja/s10050-020-00112-0
142. Lisetskiy AF, Barrett BR, Kruse MKG, Navrátil P, Stetcu I, Vary JP. Ab-initio shell model with a core. Phys Rev C. (2008) 78:044302. doi: 10.1103/PhysRevC.78.044302
143. Lisetskiy AF, Kruse MKG, Barrett BR, Navrátil P, Stetcu I, Vary JP. Effective operators from exact many-body renormalization. Phys Rev C. (2009) 80:024315. doi: 10.1103/PhysRevC.80.024315
144. Dikmen E, Lisetskiy AF, Barrett BR, Maris P, Shirokov AM, Vary JP. Ab initio effective interactions for sd-shell valence nucleons. Phys Rev C. (2015) 91:064301. doi: 10.1103/PhysRevC.91.064301
145. Smirnova NA, Barrett BR, Kim Y, Shin IJ, Shirokov AM, Dikmen E, et al. Effective interactions in the sd shell. Phys Rev C. (2019) 100:054329. doi: 10.1103/PhysRevC.100.054329
146. Kravvaris K, Volya A. Study of nuclear clustering from an ab initio perspective. Phys Rev Lett. (2017) 119:062501. doi: 10.1103/PhysRevLett.119.062501
148. Shirokov AM, Mazur AI, Mazur IA, Vary JP. Shell model states in the continuum. Phys Rev C. (2016) 94:064320. doi: 10.1103/PhysRevC.94.064320
149. Shirokov AM, Mazur AI, Mazur IA, Mazur EA, Shin IJ, Kim Y, et al. Nucleon-α scattering and resonances in 5He and 5Li with JISP16 and Daejeon16 NN interactions. Phys Rev C. (2018) 98:044624. doi: 10.1103/PhysRevC.98.044624
150. Bang JM, Mazur AI, Shirokov AM, Smirnov YF, Zaytsev SA. P-matrix and J-matrix approaches: coulomb asymptotics in the harmonic oscillator representation of scattering theory. Ann Phys. (2000) 280:299–335. doi: 10.1006/aphy.1999.5992
151. Berggren T. On the use of resonant states in eigenfunction expansions of scattering and reaction amplitudes. Nucl Phys A. (1968) 109:265–87. doi: 10.1016/0375-9474(68)90593-9
152. Michel N, Nazarewicz W, Płoszajczak M, Vertse T. Shell model in the complex energy plane. J Phys G. (2009) 36:013101. doi: 10.1088/0954-3899/36/1/013101
153. Papadimitriou G, Rotureau J, Michel N, Płoszajczak M, Barrett BR. Ab initio no-core Gamow shell model calculations with realistic interactions. Phys Rev C. (2013) 88:044318. doi: 10.1103/PhysRevC.88.044318
154. Rotureau J, van Kolck U. Effective field theory and the Gamow shell model. Few Body Syst. (2013) 54:725–35. doi: 10.1007/s00601-012-0455-6
155. Shin IJ, Kim Y, Maris P, Vary JP, Forssén C, Rotureau J, et al. Ab initio no-core solutions for 6Li. J Phys G Nucl Part Phys. (2017) 44:075103. doi: 10.1088/1361-6471/aa6cb7
156. Carlson J, Gandolfi S, Pederiva F, Pieper SC, Schiavilla R, Schmidt KE, et al. Quantum Monte Carlo methods for nuclear physics. Rev Mod Phys. (2015) 87:1067–18. doi: 10.1103/RevModPhys.87.1067
157. Lynn JE, Tews I, Gandolfi S, Lovato A. Quantum Monte Carlo methods in nuclear physics: recent advances. Annu Rev Nucl Part Sci. (2019) 69:279–305. doi: 10.1146/annurev-nucl-101918-023600
158. Gandolfi S, Lonardoni D, Lovato A, Piarulli M. Atomic nuclei from quantum Monte Carlo calculations with chiral EFT interactions. Front Phys. (2020) 8:117. doi: 10.3389/fphy.2020.00117
159. Tews I. Quantum Monte Carlo methods for astrophysical applications. Front Phys. (2020) 8:153. doi: 10.3389/fphy.2020.00153
160. Lonardoni D, Lovato A, Gandolfi S, Pederiva F. Hyperon puzzle: hints from quantum Monte Carlo calculations. Phys Rev Lett. (2015) 114:092301. doi: 10.1103/PhysRevLett.114.092301
161. Madeira L, Lovato A, Pederiva F, Schmidt KE. Quantum Monte Carlo formalism for dynamical pions and nucleons. Phys Rev C. (2018) 98:034005. doi: 10.1103/PhysRevC.98.034005
162. Cruz-Torres R, Lonardoni D, Weiss R, Barnea N, Higinbotham DW, Piasetzky E, et al. Scale and scheme independence and position-momentum equivalence of nuclear short-range correlations. arXiv. (2019) arxiv [Preprint] arXiv:1907.03658.
163. Lynn JE, Lonardoni D, Carlson J, Chen JW, Detmold W, Gandolfi S, et al. Ab initio short-range-correlation scaling factors from light to medium-mass nuclei. J Phys G Nucl Part Phys. (2020) 47:045109. doi: 10.1088/1361-6471/ab6af7
164. Hirata S, He X, Hermes MR, Willow SY. Second-order many-body perturbation theory: an eternal frontier. J Phys Chem A. (2014) 118:655–72. doi: 10.1021/jp410587b
165. Prokof'ev N, Svistunov B. Bold diagrammatic Monte Carlo technique: when the sign problem is welcome. Phys Rev Lett. (2007) 99:250201. doi: 10.1103/PhysRevLett.99.250201
166. Van Houcke K, Werner F, Kozik E, Prokof'ev N, Svistunov B, Ku MJH, et al. Feynman diagrams versus Fermi-gas Feynman emulator. Nat Phys. (2012) 8:366–70. doi: 10.1038/nphys2273
167. Scott CJC, Di Remigio R, Crawford TD, Thom AJW. Diagrammatic coupled cluster Monte Carlo. J Phys Chem Lett. (2019) 10:925–35. doi: 10.1021/acs.jpclett.9b00067
168. Roggero A, Mukherjee A, Pederiva F. Quantum Monte Carlo calculations of neutron matter with nonlocal chiral interactions. Phys Rev Lett. (2014) 112:221103. doi: 10.1103/PhysRevLett.112.221103
169. Booth GH, Thom AJW, Alavi A. Fermion Monte Carlo without fixed nodes: a game of life, death, and annihilation in Slater determinant space. J Chem Phys. (2009) 131:054106. doi: 10.1063/1.3193710
170. Blunt NS, Thom AJW, Scott CJC. Preconditioning and perturbative estimators in full configuration interaction quantum Monte Carlo. J Chem Theory Comput. (2019) 15:3537–51. doi: 10.1021/acs.jctc.9b00049
171. Ten-no S. Stochastic determination of effective Hamiltonian for the full configuration interaction solution of quasi-degenerate electronic states. J Chem Phys. (2013) 138:164126. doi: 10.1063/1.4802766
172. Nicholson AN. Lattice methods and effective field theory. In: Hjorth-Jensen M, Lombardo M, van Kolck U, editors. An Advanced Course in Computational Nuclear Physics. No. 936 in Lecture Notes in Physics. Springer. (2017). p. 155–236. doi: 10.1007/978-3-319-53336-0_5
173. Lee D. Recent progress in nuclear lattice simulations. Front Phys. (2020) 8:174. doi: 10.3389/fphy.2020.00174
174. Lähde TA, Meißner UG. Nuclear Lattice Effective Field Theory. No. 957 in Lecture Notes in Physics. Cham: Springer (2019).
175. Lee D. Lattice methods and the nuclear few- and many-body problem. In: Hjorth-Jensen M, Lombardo M, van Kolck U, editors. An Advanced Course in Computational Nuclear Physics. No. 936 in Lecture Notes in Physics. Springer (2017).
176. Epelbaum E, Krebs H, Lähde TA, Lee D, Meißner UG. Structure and rotations of the Hoyle State. Phys Rev Lett. (2012) 109:252501. doi: 10.1103/PhysRevLett.109.252501
177. Epelbaum E, Krebs H, Lähde TA, Lee D, Meißner UG, Rupak G. Ab initio calculation of the spectrum and structure of O16. Phys Rev Lett. (2014) 112:102501. doi: 10.1103/PhysRevLett.112.102501
178. Elhatisari S, Epelbaum E, Krebs H, Lähde TA, Lee D, Li N, et al. Ab initio calculations of the isotopic dependence of nuclear clustering. Phys Rev Lett. (2017) 119:222505. doi: 10.1103/PhysRevLett.119.222505
179. Elhatisari S, Lee D, Rupak G, Epelbaum E, Krebs H, Lähde TA, et al. Ab initio alpha-alpha scattering. Nature. (2015) 528:111–4. doi: 10.1038/nature16067
180. Elhatisari S. Adiabatic projection method with Euclidean time subspace projection. Eur Phys J A. (2019) 55:144. doi: 10.1140/epja/i2019-12844-9
181. Klein N, Lee D, Meißner UG. Lattice improvement in lattice effective field theory. Eur Phys J A. (2018) 54:233. doi: 10.1140/epja/i2018-12676-1
182. Klein N, Elhatisari S, Lähde TA, Lee D, Meißner UG. The Tjon band in nuclear lattice effective field theory. Eur Phys J A. (2018) 54:121. doi: 10.1140/epja/i2018-12553-y
183. Roth R, Langhammer J, Calci A, Binder S, Navrátil P. Similarity-transformed chiral NN+3N interactions for the ab initio description of 12C and 16O. Phys Rev Lett. (2011) 107:072501. doi: 10.1103/PhysRevLett.107.072501
184. Huang WJ, Audi G, Wang M, Kondev FG, Naimi S, Xu X. The AME2016 atomic mass evaluation (I). Evaluation of input data; and adjustment procedures. Chin Phys C. (2017) 41:030002. doi: 10.1088/1674-1137/41/3/030002
185. Kondo Y, Nakamura T, Tanaka R, Minakata R, Ogoshi S, Orr NA, et al. Nucleus 26O: a barely unbound system beyond the drip line. Phys Rev Lett. (2016) 116:102503. doi: 10.1103/PhysRevLett.116.102503
186. Holt JD, Stroberg SR, Schwenk A, Simonis J. Ab initio limits of atomic nuclei. arXiv. (2019) arxiv [Preprint] arXiv:1905.10475.
187. Gezerlis A, Tews I, Epelbaum E, Freunek M, Gandolfi S, Hebeler K, et al. Local chiral effective field theory interactions and quantum Monte Carlo applications. Phys Rev C. (2014) 90:054323. doi: 10.1103/PhysRevC.90.054323
188. Lonardoni D, Gandolfi S, Lynn JE, Petrie C, Carlson J, Schmidt KE, et al. Auxiliary field diffusion Monte Carlo calculations of light and medium-mass nuclei with local chiral interactions. Phys Rev C. (2018) 97:044318. doi: 10.1103/PhysRevC.97.044318
189. Piarulli M, Baroni A, Girlanda L, Kievsky A, Lovato A, Lusk E, et al. Light-nuclei spectra from chiral dynamics. Phys Rev Lett. (2018) 120:052503. doi: 10.1103/PhysRevLett.120.052503
190. Lonardoni D, Tews I, Gandolfi S, Carlson J. Nuclear and neutron-star matter from local chiral interactions. Phys Rev Res. (2020) 2:022033. doi: 10.1103/PhysRevResearch.2.022033
191. Wiringa RB, Stoks VGJ, Schiavilla R. Accurate nucleon-nucleon potential with charge-independence breaking. Phys Rev C. (1995) 51:38–51. doi: 10.1103/PhysRevC.51.38
192. Lapoux V, Somà V, Barbieri C, Hergert H, Holt JD, Stroberg SR. Radii and binding energies in oxygen isotopes: a challenge for nuclear forces. Phys Rev Lett. (2016) 117:052501. doi: 10.1103/PhysRevLett.117.052501
193. Michimasa S, Kobayashi M, Kiyokawa Y, Ota S, Ahn DS, Baba H, et al. Magic nature of neutrons in 54Ca: first mass measurements of 55−57Ca. Phys Rev Lett. (2018) 121:022506. doi: 10.1103/PhysRevLett.121.022506
194. Ekström A, Jansen GR, Wendt KA, Hagen G, Papenbrock T, Carlsson BD, et al. Accurate nuclear radii and binding energies from a chiral interaction. Phys Rev C. (2015) 91:051301. doi: 10.1103/PhysRevC.91.051301
195. Garcia Ruiz RF, Bissell ML, Blaum K, Ekstrom A, Frommgen N, Hagen G, et al. Unexpectedly large charge radii of neutron-rich calcium isotopes. Nat Phys. (2016) 12:594–8. doi: 10.1038/nphys3645
196. Hagen G, Jansen GR, Papenbrock T. Structure of 78Ni from first-principles computations. Phys Rev Lett. (2016) 117:172501. doi: 10.1103/PhysRevLett.117.172501
197. Leistenschneider E, Reiter MP, Ayet San Andrés S, Kootte B, Holt JD, Navrátil P, et al. Dawning of the N = 32 shell closure seen through precision mass measurements of neutron-rich titanium isotopes. Phys Rev Lett. (2018) 120:062503. doi: 10.1103/PhysRevLett.120.062503
198. Nogga A, Bogner SK, Schwenk A. Low-momentum interaction in few-nucleon systems. Phys Rev C. (2004) 70:061002. doi: 10.1103/PhysRevC.70.061002
199. Hebeler K, Bogner SK, Furnstahl RJ, Nogga A, Schwenk A. Improved nuclear matter calculations from chiral low-momentum interactions. Phys Rev C. (2011) 83:031301. doi: 10.1103/PhysRevC.83.031301
200. Entem DR, Machleidt R. Accurate charge-dependent nucleon-nucleon potential at fourth order of chiral perturbation theory. Phys Rev C. (2003) 68:041001. doi: 10.1103/PhysRevC.68.041001
201. Taniuchi R, Santamaria C, Doornenbal P, Obertelli A, Yoneda K, Authelet G, et al. 78Ni revealed as a doubly magic stronghold against nuclear deformation. Nature. (2019) 569:53–8. doi: 10.1038/s41586-019-1155-x
202. National Nuclear Data Center. NuDat 2 Database. Available online at: https://www.nndc.bnl.gov/nudat2
203. Simonis J, Stroberg SR, Hebeler K, Holt JD, Schwenk A. Saturation with chiral interactions and consequences for finite nuclei. Phys Rev C. (2017) 96:014303. doi: 10.1103/PhysRevC.96.014303
204. Morris TD, Simonis J, Stroberg SR, Stumpf C, Hagen G, Holt JD, et al. Structure of the lightest tin isotopes. Phys Rev Lett. (2018) 120:152503. doi: 10.1103/PhysRevLett.120.152503
205. Henderson J, Hackman G, Ruotsalainen P, Stroberg SR, Launey KD, Holt JD, et al. Testing microscopically derived descriptions of nuclear collectivity: Coulomb excitation of 22Mg. Phys Lett B. (2018) 782:468–73. doi: 10.1016/j.physletb.2018.05.064
206. Evitts LJ, Garnsworthy AB, Kibédi T, Smallcombe J, Reed MW, Stuchbery AE, et al. E0 transition strength in stable Ni isotopes. Phys Rev C. (2019) 99:024306. doi: 10.1103/PhysRevC.99.024306
207. Liu HN, Obertelli A, Doornenbal P, Bertulani CA, Hagen G, Holt JD, et al. How robust is the N = 34 subshell closure? First Spectroscopy of 52Ar. Phys Rev Lett. (2019) 122:072502. doi: 10.1103/PhysRevLett.122.072502
208. Xu X, Wang M, Blaum K, Holt JD, Litvinov YA, Schwenk A, et al. Masses of neutron-rich 52−54Sc and 54,56Ti nuclides: The N = 32 subshell closure in scandium. Phys Rev C. (2019) 99:064303. doi: 10.1103/PhysRevC.99.064303
209. Hüther T, Vobig K, Hebeler K, Machleidt R, Roth R. Family of chiral two- plus three-nucleon interactions for accurate nuclear structure studies. arXiv. (2019) arXiv:1911.04955. doi: 10.1016/j.physletb.2020.135651
210. Drischler C, Hebeler K, Schwenk A. Chiral interactions up to next-to-next-to-next-to-leading order and nuclear saturation. Phys Rev Lett. (2019) 122:042501. doi: 10.1103/PhysRevLett.122.042501
211. Hoppe J, Drischler C, Hebeler K, Schwenk A, Simonis J. Probing chiral interactions up to next-to-next-to-next-to-leading order in medium-mass nuclei. Phys Rev C. (2019) 100:024318. doi: 10.1103/PhysRevC.100.024318
212. Neufcourt L, Cao Y, Nazarewicz W, Olsen E, Viens F. Neutron drip line in the Ca region from Bayesian model averaging. Phys Rev Lett. (2019) 122:062502. doi: 10.1103/PhysRevLett.122.062502
213. Hagen G, Hjorth-Jensen M, Jansen GR, Papenbrock T. Emergent properties of nuclei from ab initio coupled-cluster calculations. Phys Scripta. (2016) 91:063006. doi: 10.1088/0031-8949/91/6/063006
214. Sun ZH, Wu Q, Zhao ZH, Hu BS, Dai SJ, Xu FR. Resonance and continuum Gamow shell model with realistic nuclear forces. Phys Lett B. (2017) 769:227–32. doi: 10.1016/j.physletb.2017.03.054
215. Hu BS, Wu Q, Li JG, Ma YZ, Sun ZH, Michel N, et al. An ab-initio Gamow shell model approach with a core. Phys Lett B. (2020) 802:135206. doi: 10.1016/j.physletb.2020.135206
216. Hu BS, Wu Q, Sun ZH, Xu FR. Ab initio Gamow in-medium similarity renormalization group with resonance and continuum. Phys Rev C. (2019) 99:061302. doi: 10.1103/PhysRevC.99.061302
217. Jaganathen Y, Betan RMI, Michel N, Nazarewicz W, Płoszajczak M. Quantified Gamow shell model interaction for psd-shell nuclei. Phys Rev C. (2017) 96:054316. doi: 10.1103/PhysRevC.96.054316
218. Fossez K, Rotureau J, Michel N, Płoszajczak M. Can tetraneutron be a narrow resonance? Phys Rev Lett. (2017) 119:032501. doi: 10.1103/PhysRevLett.119.032501
219. Fossez K, Rotureau J, Michel N, Nazarewicz W. Continuum effects in neutron-drip-line oxygen isotopes. Phys Rev C. (2017) 96:024308. doi: 10.1103/PhysRevC.96.024308
220. Fossez K, Rotureau J, Nazarewicz W. Energy spectrum of neutron-rich helium isotopes: complex made simple. Phys Rev C. (2018) 98:061302. doi: 10.1103/PhysRevC.98.061302
221. Wang SM, Nazarewicz W, Charity RJ, Sobotka LG. Structure and decay of the extremely proton-rich nuclei 11,12O. Phys Rev C. (2019) 99:054302. doi: 10.1103/PhysRevC.99.054302
222. Mao X, Rotureau J, Nazarewicz W, Michel N, Betan RMI, Jaganathen Y. Gamow shell model description of Li isotopes and their mirror partners. arXiv. (2020) arXiv:2004.02981. doi: 10.1103/PhysRevC.102.024309
223. Calci A, Navrátil P, Roth R, Dohet-Eraly J, Quaglioni S, Hupin G. Can Ab Initio theory explain the phenomenon of parity inversion in 11Be? Phys Rev Lett. (2016) 117:242501. doi: 10.1103/PhysRevLett.117.242501
224. Kumar A, Kanungo R, Calci A, Navrátil P, Sanetullaev A, Alcorta M, et al. Nuclear force imprints revealed on the elastic scattering of protons with 10C. Phys Rev Lett. (2017) 118:262502. doi: 10.1103/PhysRevLett.118.262502
225. Vorabbi M, Calci A, Navrátil P, Kruse MKG, Quaglioni S, Hupin G. Structure of the exotic 9He nucleus from the no-core shell model with continuum. Phys Rev C. (2018) 97:034314. doi: 10.1103/PhysRevC.97.034314
226. Vorabbi M, Navrátil P, Quaglioni S, Hupin G. 7Be and 7Li nuclei within the no-core shell model with continuum. Phys Rev C. (2019) 100:024304. doi: 10.1103/PhysRevC.100.024304
227. Angeli I, Marinova KP. Table of experimental nuclear ground state charge radii: an update. Atomic Data Nucl Data Tables. (2013) 99:69–95. doi: 10.1016/j.adt.2011.12.006
228. Brown BA, Minamisono K, Piekarewicz J, Hergert H, Garand D, Klose A, et al. Implications of the 36Ca−36S and 38Ca−38Ar difference in mirror charge radii on the neutron matter equation of state. Phys Rev Res. (2020) 2:022035. doi: 10.1103/PhysRevResearch.2.022035
229. Caurier E, Langanke K, Martínez-Pinedo G, Nowacki F, Vogel P. Shell model description of isotope shifts in calcium. Phys Lett B. (2001) 522:240–4. doi: 10.1016/S0370-2693(01)01246-1
230. Parzuchowski NM, Stroberg SR, Navrátil P, Hergert H, Bogner SK. Ab initio electromagnetic observables with the in-medium similarity renormalization group. Phys Rev C. (2017) 96:034324. doi: 10.1103/PhysRevC.96.034324
231. Raimondi F, Barbieri C. Core-polarization effects and effective charges in O and Ni isotopes from chiral interactions. Phys Rev C. (2019) 100:024317. doi: 10.1103/PhysRevC.100.024317
232. Gysbers P, Hagen G, Holt JD, Jansen GR, Morris TD, Navrátil P, et al. Discrepancy between experimental and theoretical Îs-decay rates resolved from first principles. Nat Phys. (2019) 15:428. doi: 10.1038/s41567-019-0450-7
233. Pritychenko B, Birch M, Singh B, Horoi M. Tables of E2 transition probabilities from the first 2+ states in even-even nuclei. Atomic Data Nucl Data Tables. (2016) 107:1–139. doi: 10.1016/j.adt.2015.10.001
234. Pastore S, Baroni A, Carlson J, Gandolfi S, Pieper SC, Schiavilla R, et al. Quantum Monte Carlo calculations of weak transitions in A = 6−−10 nuclei. Phys Rev C. (2018) 97:022501. doi: 10.1103/PhysRevC.97.022501
235. King GB, Andreoli L, Pastore S, Piarulli M, Schiavilla R, Wiringa RB, et al. Chiral effective field theory calculations of weak transitions in light nuclei. arXiv. (2020) arXiv:2004.05263. doi: 10.1103/PhysRevC.102.025501
236. Lovato A, Gandolfi S, Carlson J, Pieper SC, Schiavilla R. Neutral weak current two-body contributions in inclusive scattering from 12C. Phys Rev Lett. (2014) 112:182502. doi: 10.1103/PhysRevLett.112.182502
237. Lovato A, Gandolfi S, Carlson J, Lusk E, Pieper SC, Schiavilla R. Quantum Monte Carlo calculation of neutral-current ν−12C inclusive quasielastic scattering. Phys Rev C. (2018) 97:022502. doi: 10.1103/PhysRevC.97.022502
238. Barbieri C, Rocco N, Somà V. Lepton scattering from 40Ar and 48Ti in the quasielastic peak region. Phys Rev C. (2019) 100:062501. doi: 10.1103/PhysRevC.100.062501
239. Rocco N, Barbieri C, Benhar O, De Pace A, Lovato A. Neutrino-nucleus cross section within the extended factorization scheme. Phys Rev C. (2019) 99:025502. doi: 10.1103/PhysRevC.99.025502
240. Rocco N. Ab initio calculations of lepton-nucleus scattering. Front Phys. (2020) 8:116. doi: 10.3389/fphy.2020.00116
241. Bacca S, Barnea N, Hagen G, Orlandini G, Papenbrock T. First principles description of the giant dipole resonance in 16O. Phys Rev Lett. (2013) 111:122502. doi: 10.1103/PhysRevLett.111.122502
242. Bacca S, Barnea N, Hagen G, Miorelli M, Orlandini G, Papenbrock T. Giant and pigmy dipole resonances in 4He, 16,22O, and 40Ca from chiral nucleon-nucleon interactions. Phys Rev C. (2014) 90:064619. doi: 10.1103/PhysRevC.90.064619
243. Miorelli M, Bacca S, Barnea N, Hagen G, Jansen GR, Orlandini G, et al. Electric dipole polarizability from first principles calculations. Phys Rev C. (2016) 94:034317. doi: 10.1103/PhysRevC.94.034317
244. Miorelli M, Bacca S, Hagen G, Papenbrock T. Computing the dipole polarizability of 48Ca with increased precision. Phys Rev C. (2018) 98:014324. doi: 10.1103/PhysRevC.98.014324
245. Simonis J, Bacca S, Hagen G. First principles electromagnetic responses in medium-mass nuclei. Eur Phys J A. (2019) 55:241. doi: 10.1140/epja/i2019-12825-0
246. Birkhan J, Miorelli M, Bacca S, Bassauer S, Bertulani CA, Hagen G, et al. Electric dipole polarizability of 48Ca and implications for the neutron skin. Phys Rev Lett. (2017) 118:252501. doi: 10.1103/PhysRevLett.118.252501
247. Kaufmann S, Simonis J, Bacca S, Billowes J, Bissell ML, Blaum K, et al. Charge radius of the short-lived 68Ni and correlation with the dipole polarizability. Phys Rev Lett. (2020) 124:132502. doi: 10.1103/PhysRevLett.124.132502
248. Antonello M, et al. A proposal for a three detector short-baseline neutrino oscillation program in the fermilab booster neutrino beam. arXiv. (2015) arxiv [Preprint] arXiv:1503.01520.
249. Abi B, Acciarri R, Acero M, Adamov G, Adams D, Adinolfi M, et al. Deep underground neutrino experiment (DUNE), far detector technical design report, volume I: introduction to DUNE. arXiv. (2020) arxiv [Preprint] arXiv:2002.02967.
250. Abi B, Acciarri R, Acero M, Adamov G, Adams D, Adinolfi M, et al. Deep underground neutrino experiment (DUNE), far detector technical design report, volume II: DUNE physics. arXiv. (2020) arxiv [Preprint] arXiv:2002.03005.
251. Payne CG, Bacca S, Hagen G, Jiang WG, Papenbrock T. Coherent elastic neutrino-nucleus scattering on 40Ar from first principles. Phys Rev C. (2019) 100:061304. doi: 10.1103/PhysRevC.100.061304
252. Hupin G, Quaglioni S, Navrátil P. Ab initio predictions for polarized deuterium-tritium thermonuclear fusion. Nat Commun. (2019) 10:351. doi: 10.1038/s41467-018-08052-6
253. Hoppe J, Drischler C, Furnstahl RJ, Hebeler K, Schwenk A. Weinberg eigenvalues for chiral nucleon-nucleon interactions. Phys Rev C. (2017) 96:054002. doi: 10.1103/PhysRevC.96.054002
254. Bertsch GF. Role of core polarization in two-body interaction. Nucl Phys. (1965) 74:234–40. doi: 10.1016/0029-5582(65)90262-2
255. Kuo TTS, Brown GE. Structure of finite nuclei and the free nucleon-nucleon interaction: an application to 18O and 18F. Nucl Phys. (1966) 85:40–86. doi: 10.1016/0029-5582(66)90131-3
256. Kuo TTS. Structure of finite nuclei and the free nucleon-nucleon interactions. Nucl Phys A. (1967) 90:199–208. doi: 10.1016/0375-9474(67)90749-X
257. Duguet T, Hergert H, Holt JD, Somà V. Nonobservable nature of the nuclear shell structure: meaning, illustrations, and consequences. Phys Rev C. (2015) 92:034313. doi: 10.1103/PhysRevC.92.034313
258. Brown BA, Richter WA. New “USD” Hamiltonians for the sd-shell. Phys Rev C. (2006) 74:034315. doi: 10.1103/PhysRevC.74.034315
259. Magilligan A, Brown BA. New isospin-breaking “USD” Hamiltonians for the sd shell. Phys Rev C. (2020) 101:064312. doi: 10.1103/PhysRevC.101.064312
260. Zuker A. Three-body monopole corrections to realistic interactions. Phys Rev Lett. (2003) 90:042502. doi: 10.1103/PhysRevLett.90.042502
261. Caprio MA, Maris P, Vary JP. Emergence of rotational bands in ab initio no-core configuration interaction calculations of light nuclei. Phys Lett B. (2013) 719:179–84. doi: 10.1016/j.physletb.2012.12.064
262. Caprio MA, Maris P, Vary JP, Smith R. Collective rotation from ab initio theory. Int J Mod Phys E. (2015) 24:1541002. doi: 10.1142/S0218301315410025
263. Rowe DJ, McCoy AE, Caprio MA. The many-nucleon theory of nuclear collective structure and its macroscopic limits: an algebraic perspective. Phys Scripta. (2016) 91:033003. doi: 10.1088/0031-8949/91/3/033003
264. Ekström A, Baardsen G, Forssén C, Hagen G, Hjorth-Jensen M, Jansen GR, et al. Optimized chiral nucleon-nucleon interaction at next-to-next-to-leading order. Phys Rev Lett. (2013) 110:192502. doi: 10.1103/PhysRevLett.110.192502
265. Raimondi F, Barbieri C. Algebraic diagrammatic construction formalism with three-body interactions. Phys Rev C. (2018) 97:054308. doi: 10.1103/PhysRevC.97.054308
266. Arthuis P, Duguet T, Tichai A, Lasseri RD, Ebran JP. ADG: automated generation and evaluation of many-body diagrams I. Bogoliubov many-body perturbation theory. Comput Phys Commun. (2019) 240:202–27. doi: 10.1016/j.cpc.2018.11.023
267. Tichai A, Wirth R, Ripoche J, Duguet T. Symmetry reduction of tensor networks in many-body theory I. Automated symbolic evaluation of SU(2) algebra. arXiv. (2020) arxiv [Preprint] arXiv:2002.05011.
268. Novario SJ. Private Communication. arXiv [Preprint] (2020). Available online at: https://arxiv.org/abs/2008.09696
269. Rotureau J, Michel N, Nazarewicz W, Płoszajczak M, Dukelsky J. Density matrix renormalization group approach to two-fluid open many-fermion systems. Phys Rev C. (2009) 79:014304. doi: 10.1103/PhysRevC.79.014304
270. Legeza O, Veis L, Poves A, Dukelsky J. Advanced density matrix renormalization group method for nuclear structure calculations. Phys Rev C. (2015) 92:051303. doi: 10.1103/PhysRevC.92.051303
271. Tichai A, Ripoche J, Duguet T. Pre-processing the nuclear many-body problem. Eur Phys J A. (2019) 55:90. doi: 10.1140/epja/i2019-12758-6
272. Tichai A, Schutski R, Scuseria GE, Duguet T. Tensor-decomposition techniques for ab initio nuclear structure calculations: From chiral nuclear potentials to ground-state energies. Phys Rev C. (2019) 99:034320. doi: 10.1103/PhysRevC.99.034320
273. Hohenstein EG, Parrish RM, Martínez TJ. Tensor hypercontraction density fitting. I. Quartic scaling second- and third-order Møller-Plesset perturbation theory. J Chem Phys. (2012) 137:044103. doi: 10.1063/1.4732310
274. Parrish RM, Hohenstein EG, Martínez TJ, Sherrill CD. Tensor hypercontraction. II. Least-squares renormalization. J Chem Phys. (2012) 137:224106. doi: 10.1063/1.4768233
275. Hohenstein EG, Parrish RM, Sherrill CD, Martínez TJ. Communication: Tensor hypercontraction. III. Least-squares tensor hypercontraction for the determination of correlated wavefunctions. J Chem Phys. (2012) 137:221101. doi: 10.1063/1.4768241
276. Parrish RM, Sherrill CD, Hohenstein EG, Kokkila SIL, Martínez TJ. Communication: acceleration of coupled cluster singles and doubles via orbital-weighted least-squares tensor hypercontraction. J Chem Phys. (2014) 140:181102. doi: 10.1063/1.4876016
277. Parrish RM, Hohenstein EG, Schunck NF, Sherrill CD, Martínez TJ. Exact tensor hypercontraction: a universal technique for the resolution of matrix elements of local finite-range N-body potentials in many-body quantum problems. Phys Rev Lett. (2013) 111:132505. doi: 10.1103/PhysRevLett.111.132505
278. Frame D, He R, Ipsen I, Lee D, Lee D, Rrapaj E. Eigenvector continuation with subspace learning. Phys Rev Lett. (2018) 121:032501. doi: 10.1103/PhysRevLett.121.032501
279. Sarkar A, Lee D. Convergence of eigenvector continuation. arXiv. (2020) arxiv [Preprint] arXiv:2004.07651.
280. König S, Ekström A, Hebeler K, Lee D, Schwenk A. Eigenvector continuation as an efficient and accurate emulator for uncertainty quantification. arXiv. (2019) arxiv [Preprint] arXiv:1909.08446.
281. Ekström A, Hagen G. Global sensitivity analysis of bulk properties of an atomic nucleus. Phys Rev Lett. (2019) 123:252501. doi: 10.1103/PhysRevLett.123.252501
282. Furnstahl RJ, Phillips DR, Wesolowski S. A recipe for EFT uncertainty quantification in nuclear physics. arXiv. (2014) arxiv [Preprint] arXiv:1407.0657. doi: 10.1088/0954-3899/42/3/034028
283. Furnstahl RJ, Klco N, Phillips DR, Wesolowski S. Quantifying truncation errors in effective field theory. Phys Rev C. (2015) 92:024005. doi: 10.1103/PhysRevC.92.024005
284. Wesolowski S, Klco N, Furnstahl RJ, Phillips DR, Thapaliya A. Bayesian parameter estimation for effective field theories. J Phys G Nucl Part Phys. (2016) 43:074001. doi: 10.1088/0954-3899/43/7/074001
285. Drischler C, Melendez JA, Furnstahl RJ, Phillips DR. Quantifying uncertainties and correlations in the nuclear-matter equation of state. arXiv. (2020) arxiv [Preprint] arXiv:2004.07805.
286. More SN, Ekström A, Furnstahl RJ, Hagen G, Papenbrock T. Universal properties of infrared oscillator basis extrapolations. Phys Rev C. (2013) 87:044326. doi: 10.1103/PhysRevC.87.044326
287. Furnstahl RJ, More SN, Papenbrock T. Systematic expansion for infrared oscillator basis extrapolations. Phys Rev C. (2014) 89:044301. doi: 10.1103/PhysRevC.89.044301
288. Wendt KA, Forssén C, Papenbrock T, Sääf D. Infrared length scale and extrapolations for the no-core shell model. Phys Rev C. (2015) 91:061301. doi: 10.1103/PhysRevC.91.061301
289. Odell D, Papenbrock T, Platter L. Infrared extrapolations of quadrupole moments and transitions. Phys Rev C. (2016) 93:044331. doi: 10.1103/PhysRevC.93.044331
290. Forssén C, Carlsson BD, Johansson HT, Sääf D, Bansal A, Hagen G, et al. Large-scale exact diagonalizations reveal low-momentum scales of nuclei. Phys Rev C. (2018) 97:034328. doi: 10.1103/PhysRevC.97.034328
291. König S, Bogner SK, Furnstahl RJ, More SN, Papenbrock T. Ultraviolet extrapolations in finite oscillator bases. Phys Rev C. (2014) 90:064007. doi: 10.1103/PhysRevC.90.064007
292. Kejzlar V, Neufcourt L, Maiti T, Viens F. Bayesian averaging of computer models with domain discrepancies: a nuclear physics perspective. arXiv. (2019) arxiv [Preprint] arXiv:1904.04793.
293. Neufcourt L, Cao Y, Giuliani SA, Nazarewicz W, Olsen E, Tarasov OB. Quantified limits of the nuclear landscape. Phys Rev C. (2020) 101:044307. doi: 10.1103/PhysRevC.101.044307
294. Ekström A, Forssén C, Dimitrakakis C, Dubhashi D, Johansson HT, Muhammad AS, et al. Bayesian optimization in ab initio nuclear physics. J Phys G Nucl Part Phys. (2019) 46:095101. doi: 10.1088/1361-6471/ab2b14
295. Melendez JA, Furnstahl RJ, Grießhammer HW, McGovern JA, Phillips DR, Pratola MT. Designing optimal experiments: an application to proton compton scattering. arXiv. (2020) arxiv [Preprint] arXiv:2004.11307.
296. Haidenbauer J, Meißner UG, Nogga A. Hyperon-nucleon interaction within chiral effective field theory revisited. Eur Phys J A. (2020) 56:91. doi: 10.1140/epja/s10050-020-00100-4
297. Hammer HW, König S, van Kolck U. Nuclear effective field theory: status and perspectives. Rev Mod Phys. (2020) 92:025004. doi: 10.1103/RevModPhys.92.025004
298. Furnstahl RJ. EFT for DFT. In: Schwenk A, Polonyi J, editors. Renormalization Group and Effective Field Theory Approaches to Many-Body Systems. Lecture Notes in Physics, Vol. 852. Berlin; Heidelberg: Springer (2012). doi: 10.1007/978-3-642-27320-9_3
299. Furnstahl RJ. Turning the nuclear energy density functional method into a proper effective field theory: reflections. Eur Phys J A. (2020) 56:85. doi: 10.1140/epja/s10050-020-00095-y
300. Papenbrock T, Weidenmüller HA. Effective field theory for finite systems with spontaneously broken symmetry. Phys Rev C. (2014) 89:014334. doi: 10.1103/PhysRevC.89.014334
301. Papenbrock T, Weidenmüller HA. Effective field theory of emergent symmetry breaking in deformed atomic nuclei. J Phys G Nucl Part Phys. (2015) 42:105103. doi: 10.1088/0954-3899/42/10/105103
302. Coello Pérez EA, Papenbrock T. Effective field theory for nuclear vibrations with quantified uncertainties. Phys Rev C. (2015) 92:064309. doi: 10.1103/PhysRevC.92.064309
303. Coello Pérez EA, Papenbrock T. Effective theory for the nonrigid rotor in an electromagnetic field: toward accurate and precise calculations of E2 transitions in deformed nuclei. Phys Rev C. (2015) 92:014323. doi: 10.1103/PhysRevC.92.014323
304. Coello Pérez EA, Papenbrock T. Effective field theory for vibrations in odd-mass nuclei. Phys Rev C. (2016) 94:054316. doi: 10.1103/PhysRevC.94.054316
305. Papenbrock T, Weidenmüller HA. Effective field theory for deformed odd-mass nuclei. arXiv. (2020) arxiv [Preprint] arXiv:2005.11865.
306. Contessi L, Lovato A, Pederiva F, Roggero A, Kirscher J, van Kolck U. Ground-state properties of 4He and 16O extrapolated from lattice QCD with pionless EFT. Phys Lett B. (2017) 772:839–48. doi: 10.1016/j.physletb.2017.07.048
307. Hagen G, Hagen P, Hammer HW, Platter L. Efimov physics around the neutron-rich Ca60 isotope. Phys Rev Lett. (2013) 111:132501. doi: 10.1103/PhysRevLett.111.132501
308. Bogner SK, Furnstahl RJ, Hergert H, Kortelainen M, Maris P, Stoitsov M, et al. Testing the density matrix expansion against ab initio calculations of trapped neutron drops. Phys Rev C. (2011) 84:044306. doi: 10.1103/PhysRevC.84.044306
309. Dyhdalo A, Bogner SK, Furnstahl RJ. Applying the density matrix expansion with coordinate-space chiral interactions. Phys Rev C. (2017) 95:054314. doi: 10.1103/PhysRevC.95.054314
310. Navarro Pérez R, Schunck N, Dyhdalo A, Furnstahl RJ, Bogner SK. Microscopically based energy density functionals for nuclei using the density matrix expansion. II. Full optimization and validation. Phys Rev C. (2018) 97:054304. doi: 10.1103/PhysRevC.97.054304
311. Zhang YN, Bogner SK, Furnstahl RJ. Incorporating Brueckner-Hartree-Fock correlations in energy density functionals. Phys Rev C. (2018) 98:064306. doi: 10.1103/PhysRevC.98.064306
312. Pudliner BS, Smerzi A, Carlson J, Pandharipande VR, Pieper SC, Ravenhall DG. Neutron drops and Skyrme energy-density functionals. Phys Rev Lett. (1996) 76:2416–9. doi: 10.1103/PhysRevLett.76.2416
313. Duguet T, Lesinski T. Non-empirical pairing functional. Eur Phys J. (2008) 156:207–15. doi: 10.1140/epjst/e2008-00618-x
314. Shen S, Colò G, Roca-Maza X. Skyrme functional with tensor terms from ab initio calculations of neutron-proton drops. Phys Rev C. (2019) 99:034322. doi: 10.1103/PhysRevC.99.034322
315. Yang CJ. Chiral potential renormalized in harmonic-oscillator space. Phys Rev C. (2016) 94:064004. doi: 10.1103/PhysRevC.94.064004
316. Yang CJ. Do we know how to count powers in pionless and pionful effective field theory? Eur Phys J A. (2020) 56:96. doi: 10.1140/epja/s10050-020-00104-0
317. Binder S, Ekström A, Hagen G, Papenbrock T, Wendt KA. Effective field theory in the harmonic oscillator basis. Phys Rev C. (2016) 93:044332. doi: 10.1103/PhysRevC.93.044332
318. Bansal A, Binder S, Ekström A, Hagen G, Jansen GR, Papenbrock T. Pion-less effective field theory for atomic nuclei and lattice nuclei. Phys Rev C. (2018) 98:054301. doi: 10.1103/PhysRevC.98.054301
319. McElvain KS, Haxton WC. Nuclear physics without high-momentum potentials: constructing the nuclear effective interaction directly from scattering observables. Phys Lett B. (2019) 797:134880. doi: 10.1016/j.physletb.2019.134880
320. Drissi M, Duguet T, Somà V. Renormalization of pionless effective field theory in the A-body sector. Eur Phys J A. (2020) 56:119. doi: 10.1140/epja/s10050-020-00097-w
321. Cirigliano V, Dekens W, de Vries J, Graesser ML, Mereghetti E. A neutrinoless double beta decay master formula from effective field theory. J High Energy Phys. (2018) 2018:97. doi: 10.1007/JHEP12(2018)097
322. Cirigliano V, Dekens W, de Vries J, Graesser ML, Mereghetti E, Pastore S, et al. New leading contribution to neutrinoless double-β decay. Phys Rev Lett. (2018) 120:202001. doi: 10.1103/PhysRevLett.120.202001
323. Cirigliano V, Dekens W, Mereghetti E, Walker-Loud A. Neutrinoless double-β decay in effective field theory: the light-Majorana neutrino-exchange mechanism. Phys Rev C. (2018) 97:065501. doi: 10.1103/PhysRevC.97.065501
324. Cirigliano V, Dekens W, de Vries J, Graesser ML, Mereghetti E, Pastore S, et al. Renormalized approach to neutrinoless double-β decay. Phys Rev C. (2019) 100:055504. doi: 10.1103/PhysRevC.100.055504
325. Drischler C, Furnstahl RJ, Melendez JA, Phillips DR. How well do we know the neutron-matter equation of state at the densities inside neutron stars? A Bayesian approach with correlated uncertainties. arXiv. (2020) arxiv [Preprint] arXiv:2004.07232.
326. Johnson CW, et al. From bound states to the continuum. arXiv. (2019) arxiv [Preprint] arXiv:1912.00451.
327. Mercenne A, Launey KD, Escher JE, Dytrych T, Draayer JP. New symmetry-adapted ab initio approach to nuclear reactions for intermediate-mass nuclei. arXiv. (2019) arxiv [Preprint] arXiv:1910.00638.
328. Jaganathen Y, Michel N, Płoszajczak M. Gamow shell model description of proton scattering on 18Ne. Phys Rev C. (2014) 89:034624. doi: 10.1103/PhysRevC.89.034624
329. Mercenne A, Michel N, Płoszajczak M. Gamow shell model description of 4He(d, d) elastic scattering reactions. Phys Rev C. (2019) 99:044606. doi: 10.1103/PhysRevC.99.044606
330. Huth L, Durant V, Simonis J, Schwenk A. Shell-model interactions from chiral effective field theory. Phys Rev C. (2018) 98:044301. doi: 10.1103/PhysRevC.98.044301
331. Rotureau J, Potel G, Li W, Nunes FM. Merging ab initio theory and few-body approach for (d, p) reactions. J Phys G. (2020) 47:065103. doi: 10.1088/1361-6471/ab8530
332. Burrows M, Elster C, Popa G, Launey KD, Nogga A, Maris P. Ab initio translationally invariant nonlocal one-body densities from no-core shell-model theory. Phys Rev C. (2018) 97:024325. doi: 10.1103/PhysRevC.97.024325
333. Burrows M, Elster C, Weppner SP, Launey KD, Maris P, Nogga A, et al. Ab initio folding potentials for nucleon-nucleus scattering based on no-core shell-model one-body densities. Phys Rev C. (2019) 99:044603. doi: 10.1103/PhysRevC.99.044603
334. Gennari M, Vorabbi M, Calci A, Navrátil P. Microscopic optical potentials derived from ab initio translationally invariant nonlocal one-body densities. Phys Rev C. (2018) 97:034619. doi: 10.1103/PhysRevC.97.034619
335. Gennari M, Navrátil P. Nuclear kinetic density from ab initio theory. Phys Rev C. (2019) 99:024305. doi: 10.1103/PhysRevC.99.024305
336. Furnstahl RJ, Hebeler K. New applications of renormalization group methods in nuclear physics. Rept Prog Phys. (2013) 76:126301. doi: 10.1088/0034-4885/76/12/126301
Keywords: similarity renormalization group, nuclear theory, many-body theory, ab initio nuclear structure, ab initio nuclear reactions
Citation: Hergert H (2020) A Guided Tour of ab initio Nuclear Many-Body Theory. Front. Phys. 8:379. doi: 10.3389/fphy.2020.00379
Received: 01 July 2020; Accepted: 05 August 2020;
Published: 07 October 2020.
Edited by:
Luigi Coraggio, National Institute of Nuclear Physics of Naples, ItalyReviewed by:
Furong Xu, Peking University, ChinaCopyright © 2020 Hergert. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Heiko Hergert, aGVyZ2VydEBmcmliLm1zdS5lZHU=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.