Unorthodox Dimensional Interpolations for He, Li, Be Atoms and Hydrogen Molecule

We present a simple interpolation formula using dimensional limits D = 1 and D = ∞ to obtain the D = 3 ground-state energies of atoms and molecules. For atoms, these limits are linked by first-order perturbation terms of electron-electron interactions. This unorthodox approach is illustrated by ground-states for two, three, and four electron atoms, with modest effort to obtain fairly accurate results. Also, we treat the ground-state of H₂ over a wide range of the internuclear distance R, and compares well with the standard exact results from the Full Configuration Interaction method. Similar dimensional interpolations may be useful for complex many-body systems.

1. Introduction

Dimensional scaling, as applied to chemical physics, offers promising computational strategies and heuristic perspectives to study electronic structures and obtain energies of atoms, molecules, and extended systems [1–4]. Taking a spatial dimension other than D = 3 can make a problem much simpler and then use perturbation theory or other techniques to obtain an approximate result for D = 3. Years ago, a D-scaling technique used with quantum chromodynamics [5] was prompted for helium [2–4]. The approach began with the D → ∞ limit and added terms in powers of δ = 1/D. It was arduous and asymptotic but by summation techniques attained very high accuracy for D = 3 [6]. Other dimensional scaling approaches were extended to N-electron atoms [7], renormalization with 1/Z expansions [8], random walks [9], interpolation of hard sphere virial coefficients [10], resonance states [11], and dynamics of many-body systems in external fields [12, 13].

Recently, a simple analytical interpolation formula emerged using both the D = 1 and D → ∞ limits for helium [14]. It makes use of only the dimensional dependence of a hydrogen atom, together with the exactly known first-order perturbation terms with λ = 1/Z for the dimensional limits of the electron-electron 〈1/r₁₂〉 interaction. In the D = 1 limit, the Coulombic potentials are replaced by delta functions in appropriately scaled coordinates [15]. In the D → ∞ limit, the electrons assume positions fixed relative to another and to the nucleus, with wave functions replaced by delta functions [16]. Then at D = 3, the ground state energy of helium ϵ₃ can be obtained by linking ϵ₁ and ϵ_∞ together with the first-order perturbation coefficients ${ϵ}_1^{(1)}$ and ${ϵ}_{\infty }^{(1)}$ of the 1/Z expansion. The first-order terms actually provide much of the dimension dependence. This article exhibits the applicability of an unorthodox formula, a blend of dimensions with first-order perturbations, to more complex many-body systems.

We outline the following sections: in section 2 the interpolation formula; in section 3 treat helium; in section 4 lithium; in section 5 beryllium; in section 6 hydrogen molecule. Each atom section 3–5 has four subsections: A for D = 1; B for D → ∞; C for ${ϵ}_D^{(1)}$, the first-order perturbation terms; D for ϵ₃, the ground-state energy at D = 3 is obtained from the interpolation formula. For the hydrogen molecule section 6, the subsections deal how the internuclear distance R varies in the D = 1 and D → ∞ dimensions and mesh into D = 3. Finally, in section 7 we comment on prospects for blending dimensional limits to serve other many-body problems.

2. Dimensional Interpolation

For dimensional scaling of atoms and molecules the energy erupts to infinity as D → 1 and vanishes as D → ∞. Hence, we adopt scaled units (with hartree atomic units) whereby $E_D={(Z/\beta )}^2{ϵ}_D$ and $\beta =\frac{1}{2}(D-1)$, so the reduced energy ϵ_D remains finite in both limits. When expressed in a 1/Z perturbation expansion, the reduced energy is given by

$\begin{array}{ll}{ϵ}_D=-1+{ϵ}_D^{(1)}\lambda +{ϵ}_D^{(2)}{\lambda }^2+...& (1)\end{array}$

with λ = 1/Z, where Z is the total nuclear charge of the corresponding atom. The first-order perturbation coefficient is (1, 6):

$\begin{array}{ll}{ϵ}_D^{(1)}=f(D)=\frac{\Gamma (\frac{D}{2}+\frac{1}{2})\Gamma (D+\frac{1}{2})}{\Gamma (\frac{D}{2})\Gamma (D+1)}.& (2)\end{array}$

It represents the expectation value, $\langle \frac{1}{r_{12}}\rangle$, of the electron-electron repulsion evaluated with the zeroth-order hydrogenic wave function, exp(−r₁ − r₂). Accordingly, ${ϵ}_D^{(1)}$ is universal. For D = 1, 3, ∞ the corresponding term ${ϵ}_D^{(1)}=1/2,5/8,2^{-1/2}$, respectively.

Our interpolation for atoms, developed in [14], weights the dimensional limits by δ = 1/D, providing δϵ₁ and (1 − δ)ϵ_∞ in a simple analytic formula

$\begin{array}{ll}{ϵ}_D=\delta {ϵ}_1+(1-\delta ){ϵ}_{\infty }+[{ϵ}_D^{(1)}-\delta {ϵ}_1^{(1)}-(1-\delta ){ϵ}_{\infty }^{(1)}]\lambda ,& (3)\end{array}$

We aim to illustrate the interpolation formula more fully, presenting results with modest calculations having respectable accuracy for two, three, and four electrons.

For the hydrogen molecule, a different scaling scheme will be used and illustrated. The rescaling of the internuclear distance R→R′ is given by:

$\begin{array}{ll}R\to \delta R^{\prime }\text{ for }D\to 1;R\to (1-\delta )R^{\prime }\text{ for }D\to \infty .& (4)\end{array}$

An approximation for D = 3 (where R = R′) emerges:

$\begin{array}{ll}{ϵ}_3(R^{\prime })=\frac{1}{3}{ϵ}_1(\frac{1}{3}{R}^{\prime })+\frac{2}{3}{ϵ}_{\infty }(\frac{2}{3}{R}^{\prime }),& (5)\end{array}$

on interpolating linearly between the dimensional limits, developed by Loeser in [17–19]; especially see the paragraphs around Equations (23) and (24) of [17] for more details.

3. Two-Electrons: Helium

The formula worked very well for D = 3, helium with λ = 1/2:

$\begin{array}{ll}{ϵ}_3=\frac{1}{3}{ϵ}_1+\frac{2}{3}{ϵ}_{\infty }+\left[{ϵ}_3^{(1)}-\frac{1}{3}{ϵ}_1^{(1)}-\frac{2}{3}{ϵ}_{\infty }^{(1)}\right]\lambda & (6)\end{array}$

The input ingredients are exact limit energies: ϵ₁ = −0.788843 from Ref. [15]; ϵ_∞ = −0.684442 from [4]; and the three first-order perturbation terms ${ϵ}_D^{(1)}$ displayed in Equation (2). The interpolation delivered ϵ₃ = −0.725780, a result very close to the exact ground-state energy −0.725931 [4]. The interpolation accuracy of 2 millihartrees is better than current density functional theory.

3.1. One-Dimension: D = 1

We will calculate the ground-state energy of the Hamiltonian operator using the variational principle. It is less accurate than [15], but much easier to deal with two and more electrons [20]. The Hamiltonian with electrons in delta functions is:

$\begin{array}{ll}{H}=-\frac{1}{2}\frac{{\partial }^2}{\partial r_1^2}-\frac{1}{2}\frac{{\partial }^2}{\partial r_2^2}-\delta (r_1)-\delta (r_2)+\lambda \delta (r_1-r_2),& (7)\end{array}$

with λ = 1/Z. The electronic wave function is as follows:

$\begin{array}{ll}\varphi (r_1,r_2)={\chi }_1(r_1){\chi }_2(r_2),& (8)\end{array}$

where the normalized wave functions χ₁ and χ₂ are defined as:

$\begin{array}{ll}{\chi }_1(r_1)={(\xi )}^{1/2}{e}^{-\xi |r_1|}& (9)\end{array}$

and

$\begin{array}{ll}{\chi }_2(r_2)={(\xi )}^{1/2}{e}^{-\xi |r_2|}.& (10)\end{array}$

We optimize the parameter ξ, defined in (9, 10), and calculate the minimum value of the operator E_ϕ(ξ) defined as:

$\begin{array}{l}{E}_{\varphi }(\xi )=\langle \varphi |{H}|\varphi \rangle =\langle \varphi |-\frac{1}{2}\frac{{\partial }^2}{\partial r_1^2}-\frac{1}{2}\frac{{\partial }^2}{\partial r_2^2}\hfill \\ \hfill -\delta (r_1)-\delta (r_2)+\lambda \delta (r_1-r_2)|\varphi \rangle .& (11)\end{array}$

We divide the above Hamiltonian into three parts, where

$\begin{array}{ll}\langle \varphi |{{H}}_{KE}|\varphi \rangle =\langle \varphi |-\frac{1}{2}\frac{{\partial }^2}{\partial r_1^2}-\frac{1}{2}\frac{{\partial }^2}{\partial r_2^2}|\varphi \rangle ={\xi }^2& (12)\end{array}$

is the kinetic energy of the two electrons,

$\begin{array}{ll}\langle \varphi |{{H}}_{PE}|\varphi \rangle =\langle \varphi |-\delta (r_1)-\delta (r_2)|\varphi \rangle =-2\xi & (13)\end{array}$

is the potential energy of the two electrons due to nuclear attraction, and

$\begin{array}{ll}\langle \varphi |{{H}}_{ee}|\varphi \rangle =\lambda \langle \varphi |\delta (r_1-r_2)|\varphi \rangle =\lambda \frac{\xi }{2}& (14)\end{array}$

is the interaction energy for electron-electron repulsion in the system.

We minimize the Hamiltonian operator E_ϕ(ξ) with respect to ξ, with

$\begin{array}{ll}{E}_{\varphi }(\xi )={\xi }^2-2\xi +\lambda \frac{\xi }{2},& (15)\end{array}$

such that

$\begin{array}{ll}\frac{d{E}_{\varphi }}{d\xi }=2\xi -2+\frac{\lambda }{2}=0,& (16)\end{array}$

and obtain ξ₀ = 0.875, which put into Equation (15) gives the ground-state energy, ϵ₁ = −0.765625. This result is found in [20–22], but it is approximated by 2.9% since noted the exact value is ϵ₁ = −0.788843.

3.2. Infinite-Dimension: D → ∞

At large-D limit, the effective ground state Hamiltonian for a two electron atom, with inter-electronic correlation can be written as:

$\begin{array}{ll}{H}=\frac{1}{2{\text{ sin}}^2\theta }\left(\frac{1}{r_1^2}+\frac{1}{r_2^2}\right)-\frac{Z}{r_1}-\frac{Z}{r_2}+J(r_1,r_2,\theta ),& (17)\end{array}$

with

$\begin{array}{ll}J(r_1,r_2,\theta )=\frac{1}{\sqrt{r_1^2+r_2^2-2r_1{r}_2\text{ cos }\theta }},& (18)\end{array}$

where θ is the angle between r₁ and r₂; see [7] for more details.

We minimize the above effective-Hamiltonian with respect to the parameters r₁, r₂, and θ respectively, and obtain the corresponding ground state energy to be: ϵ_∞ = −0.684442 (see Table 1 in [14], and [22]).

3.3. First-Order Perturbations: ${ϵ}_D^{(1)}$

In a two-electron atom, with nuclear charge Z, the exact Hamiltonian in D-dimension using atomic units can be written as:

$\begin{array}{ll}{H}=-\frac{1}{2}{\nabla }_1^2-\frac{1}{2}{\nabla }_2^2-\frac{1}{r_1}-\frac{1}{r_2}+\lambda \frac{1}{r_{12}},& (19)\end{array}$

where the Laplacian operator ${\nabla }_r^2$ in D-dimension is defined as:

$\begin{array}{ll}{\nabla }_r^2=\frac{{\partial }^2}{\partial r^2}+\left(\frac{D-1}{r}\right)\frac{\partial }{\partial r}+\left(\text{angular part involving}{\partial }_{\theta },{\partial }_{\varphi }\text{etc}\right).& (20)\end{array}$

For helium-like atoms we consider the two electrons are in a 1s-like state with spatial part being symmetric (both electrons are in the same state) and the spin part in the antisymmetric spin singlet. The spatial part of the electronic wave function can be written as:

$\begin{array}{ll}\varphi (r_1,r_2)={\chi }_1(r_1){\chi }_2(r_2),& (21)\end{array}$

where the normalized wave functions χ₁(r₁) and χ₂(r₂) are defined as:

$\begin{array}{ll}{\chi }_1(r_1)={N}{e}^{-r_1}& (22)\end{array}$

and

$\begin{array}{ll}{\chi }_2(r_2)={N}{e}^{-r_2}.& (23)\end{array}$

The normalization constant ${N}$ is calculated as:

$\begin{array}{ll}{N}=\frac{2^{D/2}}{\sqrt{(D-1)!\Omega (D)}},& (24)\end{array}$

with

$\begin{array}{ll}\Omega (D)=\frac{2{\pi }^{D/2}}{\Gamma (D/2)}& (25)\end{array}$

is the surface area of an unit sphere in D-dimension.

In D-dimension, with the above wave functions, we obtain the following first-order coefficient [14]:

$\begin{array}{ll}{ϵ}_D^{(1)}=f(D)=\langle \varphi |\frac{1}{r_{12}}|\varphi \rangle =\frac{\Gamma (\frac{D}{2}+\frac{1}{2})\Gamma (D+\frac{1}{2})}{\Gamma (\frac{D}{2})\Gamma (D+1)}.& (26)\end{array}$

As shown in Equation (2) and for D = 1, 3, ∞, respectively ${ϵ}_D^{(1)}=\frac{1}{2},\frac{5}{8},\frac{1}{\sqrt{2}}$.

3.4. Interpolation for D = 3

We use the formula shown in Equation (6), already noting that the exact limit energies and first-order perturbation terms, gave ϵ₃ = −0.725780; accurate to 0.02%. If we replace the variational result ϵ₁ = −0.765625 (from section 3.1), the formula would give ϵ₃ = −0.71839, accurate to 2.9%. However, if we evaluate ϵ₁ by using Equation (3), a subformula is

$\begin{array}{ll}{ϵ}_D={ϵ}_{\infty }+\left[{ϵ}_D^{(1)}-{ϵ}_{\infty }^{(1)}\right]\lambda ,& (27)\end{array}$

with D = 1. This yielded a good approximation of 0.11% for ϵ₁ = −0.787996, near the exact ϵ₁ = −0.788843. With this better ϵ₁ we obtain ϵ₃ = −0.725496, with accuracy of 0.06%.

In conventional quantum chemistry textbooks treating D = 3 helium, the electron-electron interaction, 〈1/r₁₂〉, is evaluated by first-order perturbation theory. The result is ϵ₃ = −0.687529 with accuracy of 5.29%.

4. Three-Electrons: Lithium

The ground-state of the lithium atom had been calculated a long ago by using the variational method with complicated wave functions [23–25]. Here we present the interpolation formula, using the D = 1 and D = ∞ limits and the first-order perturbation terms. For the ground-state of the lithium atom our formula gave ϵ₃ = −0.839648, with approximation 1.04% compared the exact result ϵ₃ = −0.830896 [26].

4.1. One-Dimension: D=1

In a three-electron atom, with nuclear charge Z, the exact Hamiltonian in one-dimension using atomic units can be written as:

$\begin{array}{ll}{H}={\displaystyle \sum _{i=1}^3}\left(-\frac{1}{2}\frac{{\partial }^2}{\partial r_i^2}-\delta (r_i)\right)+\lambda {\displaystyle \sum _{i,j=1}^3}\delta (r_i-r_j),& (28)\end{array}$

with λ = 1/Z.

In the lithium atom we consider that two electrons are in the 1s state and the third electron is in a 2s state, with the spatial part being symmetric (both electrons are in the same state) and the spin part in the antisymmetric state. We write spatial part of the electronic wave function as:

$\begin{array}{ll}\varphi (r_1,r_2,r_3)={\chi }_1(r_1){\chi }_2(r_2){\chi }_3(r_3).& (29)\end{array}$

The two normalized wave functions χ₁(r₁), χ₂(r₂) are described in Equations (9) and (10). We assume that the 1s wave functions are orthogonal to the 2s wave function:

$\begin{array}{ll}{\chi }_3(r_3)={\left(\frac{9\xi }{20}\right)}^{1/2}\left(\frac{2}{3}-\xi |r_3|\right)e^{-\xi |r_3|/2}.& (30)\end{array}$

We calculate the ground state energy of a three-electron atom using variational principle. We optimize the parameter ξ, defined in the wave functions χ₁(r₁), χ₂(r₂), χ₃(r₃), and obtain the minimum value of the Hamiltonian operator E_ϕ(ξ), which is defined as

$\begin{array}{l}{E}_{\varphi }(\xi )=\langle \varphi |{H}|\varphi \rangle =\langle \varphi |{\displaystyle \sum _{i=1}^3\left(-\frac{1}{2}\frac{{\partial }^2}{\partial r_i^2}-\delta (r_i)\right)}\\ +\lambda {\displaystyle \sum _{i,j=1}^3\delta }(r_i-r_j)|\varphi \rangle .& (31)\end{array}$

We divide the above Hamiltonian (31) into five parts, where

$\begin{array}{ll}\langle \varphi |{{H}}_{KE}|\varphi \rangle =\langle \varphi |{\displaystyle \sum _{i=1}^3}-\frac{1}{2}\frac{{\partial }^2}{\partial r_i^2}|\varphi \rangle =\frac{1}{2}\left(2{\xi }^2+\frac{17}{20}{\xi }^2\right)& (32)\end{array}$

is the kinetic energy of the three electrons,

$\begin{array}{ll}\langle \varphi |{{H}}_{PE}|\varphi \rangle =\langle \varphi |-{\displaystyle \sum _{i=1}^3}\delta (r_i)|\varphi \rangle =-\left(2\xi +\frac{\xi }{5}\right)& (33)\end{array}$

is the potential energy of the three electrons due to nuclear attraction, and

$\begin{array}{ll}\langle \varphi |{{H}}_{12}|\varphi \rangle =\langle \varphi |\lambda \delta (r_1-r_2)|\varphi \rangle =\lambda \frac{\xi }{2},& (34)\end{array}$

$\begin{array}{ll}\langle \varphi |{{H}}_{13}|\varphi \rangle =\lambda \langle \varphi |\delta (r_1-r_3)|\varphi \rangle =\lambda \frac{\xi }{15},& (35)\end{array}$

$\begin{array}{ll}\langle \varphi |{{H}}_{23}|\varphi \rangle =\lambda \langle \varphi |\delta (r_2-r_3)|\varphi \rangle =\lambda \frac{\xi }{15},& (36)\end{array}$

are the interaction energies for inter-electronic repulsions in the system.

We minimize the Hamiltonian operator E_ϕ(ξ) with respect to ξ, with

$\begin{array}{ll}{E}_{\varphi }(\xi )=\frac{1}{2}\left(2{\xi }^2+\frac{17}{20}{\xi }^2\right)-\left(2\xi +\frac{\xi }{5}\right)+\lambda \frac{2\xi }{15}+\lambda \frac{\xi }{2},& (37)\end{array}$

such that

$\begin{array}{ll}\frac{d{E}_{\varphi }}{d\xi }=\frac{57}{20}\xi -\frac{11}{5}+\frac{19}{30}\lambda =0,& (38)\end{array}$

and obtain ξ₀ = 0.697856, which put into Equation (37) gives the ground-state energy, ϵ₁ = −0.693979.

4.2. Infinite-Dimension: D → ∞

At large-D-limit the effective ground state Hamiltonian for three-electron atoms, with correlation can be written as:

$\begin{array}{l}{H}=\frac{1}{2}\left(\frac{1}{r_1^2}\frac{{\Gamma }^{(1)}}{\Gamma }+\frac{1}{r_2^2}\frac{{\Gamma }^{(2)}}{\Gamma }+\frac{4}{r_3^2}\frac{{\Gamma }^{(3)}}{\Gamma }\right)-\frac{1}{r_1}-\frac{1}{r_2}-\frac{1}{r_3}\\ +\lambda J(r_1,r_2,r_3),& (39)\end{array}$

where

$\begin{array}{l}J(r_1,r_2,r_3)=\frac{1}{\sqrt{r_1^2+r_2^2-2r_1{r}_2{\gamma }_{12}}}\\ +\frac{1}{\sqrt{r_1^2+r_3^2-2r_1{r}_3{\gamma }_{13}}}+\frac{1}{\sqrt{r_2^2+r_3^2-2r_2{r}_3{\gamma }_{23}}},& (40)\end{array}$

with γ_ij = γ_ij = cos θ_ij, and θ_ij is the angle between r_i and r_j. The quantities Γ⁽ⁱ⁾ and Γ are called the Gramian determinants. In Equation (39) the quantity $\frac{{\Gamma }^{(i)}}{\Gamma }$ is effectively defined as:

$\begin{array}{ll}\frac{{\Gamma }^{(i)}}{\Gamma }=1+{\displaystyle \sum _{\begin{array}{c}i,j\\ (j\ne i)\end{array}}}{\gamma }_{ij}^2-{\displaystyle \sum _{\begin{array}{c}i,j,k\\ (j\ne i\ne k)\end{array}}}2{\gamma }_{ij}{\gamma }_{jk}{\gamma }_{ki}\text{ for }i,j,k=1,2,3.& (41)\end{array}$

See page 111, Equation (35) in [7] for more details.

We minimize the above effective-Hamiltonian with respect to the parameters r₁, r₂, r₃, and θ₁₂, θ₁₃, θ₂₃, respectively and obtain the corresponding ground state energy ϵ_∞ = −0.795453.

4.3. First-Order Perturbations: ${ϵ}_D^{(1)}$

As the electrons reside in two orbits, 1s²2s, there are three electron-electron pairs: one $\langle \frac{1}{r_{12}}\rangle$ from 1s², the two others $\langle \frac{1}{r_{13}}\rangle$ and $\langle \frac{1}{r_{23}}\rangle$ from 1s2s. Thus, each ${ϵ}_D^{(1)}$ coefficient is comprised from the three electron pairs:

$\begin{array}{ll}{ϵ}_1^{(1)}=1/2+2(1/15)=0.633333& (42)\end{array}$

$\begin{array}{ll}{ϵ}_{\infty }^{(1)}=2^{-1/2}+2(0.447212)=1.601531& (43)\end{array}$

$\begin{array}{ll}{ϵ}_3^{(1)}=5/8+2(17/81)=1.044753.& (44)\end{array}$

The D = 1 item is obtained via section 4.1. The D = 3 item is attained from [27]. Here we will develop both D = 3 and D → ∞ bringing the third electron akin with the two-electron treatment in section 3.3. As the Hamiltonian is evident in Equations (19) and (20), we start with the electronic wave function:

$\begin{array}{ll}\varphi (r_1,r_2,r_3)={\chi }_1(r_1){\chi }_2(r_2){\chi }_3(r_3).& (45)\end{array}$

The two normalized functions χ₁(r₁), χ₂(r₂) are taken care of in Equations (22), (23), (24), and (25). We assume that the 1s wave functions are orthogonal to the 2s wave function:

$\begin{array}{ll}{\chi }_3(r_3)={{N}}_1(1-\alpha r_3)e^{-r_3/2}.& (46)\end{array}$

The normalization is:

$\begin{array}{ll}{{N}}_1=\frac{1}{\sqrt{(1+{\alpha }^{2}D(D+1)-2\alpha D)(D-1)!\Omega (D)}},& (47)\end{array}$

with $\alpha =\frac{3}{2D}$.

To obtain the first-order terms for D = 3 and D → ∞ we need to assemble some integrals associated with the key f (D) function shown in Equations (2) and (26). The output is:

$\begin{array}{ll}\langle \frac{1}{r_{13}}\rangle =\langle \frac{1}{r_{23}}\rangle =f(D)F\left(\frac{1}{2},\frac{3-D}{2};\frac{D}{2};y\right)\left(\frac{ab}{a+b}\right),& (48)\end{array}$

with

$\begin{array}{ll}y={\left(\frac{a-b}{a+b}\right)}^2,& (49)\end{array}$

and the hypergeometric function $F\left(\frac{1}{2},\frac{3-D}{2};\frac{D}{2};y\right)$ enters in (26).

The parent integral is,

$\begin{array}{l}{G}_D(a,b)={\displaystyle \int d^D}{r}_1{\displaystyle \int d^D}{r}_2\frac{e^{-a{r}_1}}{r_1}\frac{e^{-b{r}_2}}{r_2}\frac{1}{r_{12}}\\ =N_{D}F\left(\frac{1}{2},\frac{3-D}{2};\frac{D}{2};y\right)\frac{1}{{(ab)}^{D-2}(a+b)},& (50)\end{array}$

and

$\begin{array}{ll}{N}_D=\frac{{(4\pi )}^{D-1}\Gamma (D-1)\Gamma (D-\frac{3}{2})\Gamma {(\frac{D-1}{2})}^3}{\Gamma {(D-1)}^2\Gamma (D/2)}.& (51)\end{array}$

From G_D(a, b) we compute the following integral:

$\begin{array}{l}{K}_D(i,j)={\displaystyle \int d^D}{r}_1{\displaystyle \int d^D}{r}_2{e}^{-a{r}_1}{e}^{-b{r}_2}{r}_1^{i-1}{r}_2^{j-1}\frac{1}{r_{12}}\\ ={\left(-\frac{\partial }{\partial a}\right)}^i{\left(-\frac{\partial }{\partial b}\right)}^j{G}_D(a,b).& (52)\end{array}$

In the integrals, we used the normalized wave functions χ₁(r₁), χ₂(r₂), and χ₃(r₃) already specified, such a typical term:

$\begin{array}{l}\langle \frac{1}{r_{13}}\rangle ~{\displaystyle \int }{d}^D{r}_1{\displaystyle \int }{d}^D{r}_3{\chi }_1^{\ast }{(r_1)}^{\ast }{\chi }_3^{\ast }(r_3)\frac{1}{r_{13}}{\chi }_1(r_1){\chi }_3(r_3)\hfill \\ ~{\displaystyle \int }{d}^D{r}_1{\displaystyle \int }{d}^D{r}_3{(1-\alpha r_3)}^2{e}^{-2r_1}{e}^{-r_3}\frac{1}{r_{13}}.\hfill & (53)\end{array}$

From Equation (53), we see that we have to put a = 2 and b = 1, so y = 1/9. In Equations (48) and (55) the hypergeometric function is available in tabulations [28]. We computed up to D = 10⁶ to see that the function converges to

$\begin{array}{ll}F\left(\frac{1}{2},-\frac{D}{2};\frac{D}{2};\frac{1}{9}\right)\to 0.948683\text{for }D\to \infty .& (54)\end{array}$

At the D → ∞ limit

$\begin{array}{ll}\langle \frac{1}{r_{13}}\rangle =\langle \frac{1}{r_{23}}\rangle =(2/3)2^{-1/2}(0.948683)=0.447212.& (55)\end{array}$

For D = 3, the function gives

$\begin{array}{ll}F\left(\frac{1}{2},0;\frac{3}{2};\frac{1}{9}\right)=0.503703& (56)\end{array}$

and,

$\begin{array}{ll}\langle \frac{1}{r_{13}}\rangle =\langle \frac{1}{r_{23}}\rangle =(2/3)(5/8)(0.503703)=17/81.& (57)\end{array}$

4.4. Interpolation for D = 3

Again we use the interpolation formula shown in Equation (6),

$\begin{array}{ll}{ϵ}_3=\frac{1}{3}{ϵ}_1+\frac{2}{3}{ϵ}_{\infty }+\left[{ϵ}_3^{(1)}-\frac{1}{3}{ϵ}_1^{(1)}-\frac{2}{3}{ϵ}_{\infty }^{(1)}\right]\lambda ,& (58)\end{array}$

now with λ = 1/Z = 1/3. The input from our A, B, C subsections was:

${ϵ}_1=-0.693979,{ϵ}_{\infty }=-0.795453,$

and

${ϵ}_3^{(1)}=1.044753,{ϵ}_1^{(1)}=0.633333,{ϵ}_{\infty }^{(1)}=1.601531.$

Our interpolation gave the Li atom ground-state energy with error 1%: ϵ₃ = −0.839648, compared with the exact result ϵ₃ = −0.830896 [26].

5. Four-Electron: Beryllium

The electronic structure of the beryllium atom is highly interesting because it's implication in different areas of modern science, for e.g. stellar astrophysics and plasmas, high-temperature physics, etc. The ground-state energy for the Be-atom has been calculated by applying various methods for e.g., the Configuration Interaction (CI) method with Slater-type orbitals (STOs) [29], the Hylleraas method (Hy) [30], the Hylleraas-Configuration Interaction method (Hy-CI) [31], and the Exponential Correlated Gaussian (ECG) method [32, 33]. In this section, we present the dimensional interpolation formula, by using the results from D = 1 and D = ∞ limit, to obtain the ground state energy of the four-electron atoms. With dimensional interpolation we obtain the ground state energy of beryllium atom to be ϵ₃ = −0.910325, compared to the exact energy ϵ₃ = −0.916709, with a percentage error of 0.6%.

5.1. One-Dimension: D=1

In Four-electron atoms, with nuclear charge Z = 1/λ, the exact Hamiltonian in one-dimension using atomic units can be written as:

$\begin{array}{ll}{H}={\displaystyle \sum _{i=1}^4}\left(-\frac{1}{2}\frac{{\partial }^2}{\partial r_i^2}-\delta (r_i)\right)+\lambda {\displaystyle \sum _{i,j=1}^4}\delta (r_i-r_j).& (59)\end{array}$

In beryllium atom we consider that two electrons are in the 1s state, and the other two electrons are in the 2s state with the spatial part being symmetric (both electrons are in the same state) and the spin part in the antisymmetric state. We write spatial part of the electronic wave function as follows:

$\begin{array}{ll}\varphi (r_1,r_2,r_3,r_4)={\chi }_1(r_1){\chi }_2(r_2){\chi }_3(r_3){\chi }_4(r_4),& (60)\end{array}$

The three normalized wave functions χ₁(r₁), χ₂(r₂), χ₃(r₃) are described in Equations (9), (10), and (30). We assume that the 1s wave functions are orthogonal to the two 2s wave functions χ₃(r₃) and

$\begin{array}{ll}{\chi }_4(r_4)={\left(\frac{9\xi }{20}\right)}^{1/2}\left(\frac{2}{3}-\xi |r_4|\right)e^{-\xi |r_4|/2}.& (61)\end{array}$

We calculate the ground state energy of a four-electron atom with variational principle. We optimize the parameter ξ, defined in the wave functions χ₁(r₁), χ₂(r₂), χ₃(r₃), χ₄(r₄), and obtain the minimum value of the Hamiltonian operator E_ϕ(ξ), which is defined as:

$\begin{array}{l}{E}_{\varphi }(\xi )=\langle \varphi |{H}|\varphi \rangle =\langle \varphi |{\displaystyle \sum _{i=1}^4\left(-\frac{1}{2}\frac{{\partial }^2}{\partial r_i^2}-\delta (r_i)\right)}\\ +\lambda {\displaystyle \sum _{i,j=1}^4\delta }(r_i-r_j)|\varphi \rangle .& (62)\end{array}$

We divide the above Hamiltonian into five parts, where

$\begin{array}{ll}\langle \varphi |{{H}}_{KE}|\varphi \rangle =\langle \varphi |{\displaystyle \sum _{i=1}^4}-\frac{1}{2}\frac{{\partial }^2}{\partial r_i^2}|\varphi \rangle =\left({\xi }^2+\frac{17}{20}{\xi }^2\right)& (63)\end{array}$

is the kinetic energy of the four electrons,

$\begin{array}{ll}\langle \varphi |{{H}}_{PE}|\varphi \rangle =\langle \varphi |-{\displaystyle \sum _{i=1}^4}\delta (r_i)|\varphi \rangle =-2\left(\xi +\frac{1}{5}\xi \right)& (64)\end{array}$

is the potential energy of the four electrons due to nuclear attraction, and

$\begin{array}{ll}\langle \varphi |{{H}}_{12}|\varphi \rangle =\langle \varphi |\lambda \delta (r_1-r_2)|\varphi \rangle =\lambda \frac{\xi }{2},& (65)\end{array}$

$\begin{array}{l}\langle \varphi |{{H}}_{i3}|\varphi \rangle =\langle \varphi |\lambda \delta (r_i-r_3)|\varphi \rangle =\lambda \frac{\xi }{15}\\ \begin{array}{l}=\langle \varphi |{{H}}_{i4}|\varphi \rangle ,\text{ for i}=1,2,\end{array}& (66)\end{array}$

$\begin{array}{ll}\langle \varphi |{{H}}_{34}|\varphi \rangle =\langle \varphi |\lambda \delta (r_3-r_4)|\varphi \rangle =\lambda \frac{71}{800}\xi & (67)\end{array}$

are the interaction energies for inter-electronic repulsions in the system.

We minimize the Hamiltonian operator E_ϕ(ξ) with respect to ξ, with

$\begin{array}{ll}{E}_{\varphi }(\xi )=\left({\xi }^2+\frac{17}{20}{\xi }^2\right)-2\left(\xi +\frac{\xi }{5}\right)+\lambda \frac{4\xi }{15}+\lambda \frac{\xi }{2}+\lambda \frac{71}{800}\xi ,& (68)\end{array}$

such that

$\begin{array}{ll}\frac{d{E}_{\varphi }}{d\xi }=\frac{37}{10}\xi -\frac{12}{5}+\frac{2053}{2400}\lambda =0,& (69)\end{array}$

and obtain ξ₀ = 0.590850, which put into Equation (68) gives the ground-state energy, ϵ₁ = −0.645842.

5.2. Infinite-Dimension: D → ∞

In large-D-limit the effective ground state Hamiltonian for four-electron atoms, with inter-electronic correlation can be written as:

$\begin{array}{l}{H}=\frac{1}{2}\left(\frac{1}{r_1^2}\frac{{\Gamma }^{(1)}}{\Gamma }+\frac{1}{r_2^2}\frac{{\Gamma }^{(2)}}{\Gamma }+\frac{4}{r_3^2}\frac{{\Gamma }^{(3)}}{\Gamma }+\frac{4}{r_4^2}\frac{{\Gamma }^{(4)}}{\Gamma }\right)\\ -\frac{1}{r_1}-\frac{1}{r_2}-\frac{1}{r_3}-\frac{1}{r_4}+\lambda J(r_1,r_2,r_3,r_4),& (70)\end{array}$

where

$\begin{array}{ll}J(r_1,r_2,r_3,r_4)={\displaystyle \sum _{i,j=1}^4}\frac{1}{\sqrt{r_i^2+r_j^2-2r_i{r}_j{\gamma }_{ij}}},& (71)\end{array}$

with γ_ij = γ_ij = cos θ_ij, and θ_ij are the angle between r_i and r_j. The quantities Γ⁽ⁱ⁾ and Γ are the Gramian determinants. In Equation (70) the quantity $\frac{{\Gamma }^{(i)}}{\Gamma }$ is effectively defined as follows:

$\begin{array}{l}\frac{{\Gamma }^{(i)}}{\Gamma }=1+{\displaystyle \sum _{\begin{array}{c}i,j\\ (j\ne i)\end{array}}}{\gamma }_{ij}^2-{\displaystyle \sum _{\begin{array}{c}i,j,k\\ (j\ne i\ne k)\end{array}}}2{\gamma }_{ij}{\gamma }_{jk}{\gamma }_{ki}\\ +{\displaystyle \sum _{\begin{array}{c}i,j,k,l\\ (j\ne i\ne k\ne l)\end{array}}}\left(2{\gamma }_{ij}{\gamma }_{jk}{\gamma }_{kl}{\gamma }_{li}-{\gamma }_{ij}^2{\gamma }_{kl}^2\right)\text{ for }i,j,k,l=1,2,3,4.& (72)\end{array}$

See page 111, Equation (35) in [7] for more details.

We minimize the above effective-Hamiltonian with respect to the parameters r₁, r₂, r₃, r₄, and θ₁₂, θ₁₃, θ₁₄, θ₂₃, θ₂₄, θ₃₄ respectively and obtain the corresponding ground state energy ϵ_∞ = −0.875837.

5.3. First-Order Perturbations: ${ϵ}_D^{(1)}$

As the electrons reside in two orbits, 1s²2s², there are six electron-electron pairs: one $\langle \frac{1}{r_{12}}\rangle$ from 1s², four others $\langle \frac{1}{r_{13}}\rangle$, $\langle \frac{1}{r_{14}}\rangle$, $\langle \frac{1}{r_{23}}\rangle$, $\langle \frac{1}{r_{24}}\rangle$ from 1s2s; and another lonely $\langle \frac{1}{r_{34}}\rangle$ from 2s². Each ${ϵ}_D^{(1)}$ coefficient is comprised from the six electron pairs:

$\begin{array}{ll}{ϵ}_1^{(1)}=1/2+4(1/15)+(71/800)=0.855417,& (73)\end{array}$

$\begin{array}{ll}{ϵ}_{\infty }^{(1)}=2^{-1/2}+4(0.447212)+0.353553=2.849508,& (74)\end{array}$

$\begin{array}{ll}{ϵ}_3^{(1)}=5/8+4(17/81)+0.275696=1.740202,& (75)\end{array}$

The D = 1 item is obtained via section 5.1. Here we will develop both D = 3 and D → ∞ bringing the fourth electron akin with the three-electron treatment in section 4.3. As the Hamiltonian is evident in Equations (19) and (20), we start with the electronic wave function:

$\begin{array}{ll}\varphi (r_1,r_2,r_3,r_4)={\chi }_1(r_1){\chi }_2(r_2){\chi }_3(r_3){\chi }_4(r_4),& (76)\end{array}$

The two normalized 1s wave functions χ₁(r₁), χ₂(r₂) are taken care of in Equations (22), (23), (24), and (25). We assume that the 1s wave functions are orthogonal to the 2s wave functions χ₂(r₂), defined in (46), and:

$\begin{array}{ll}{\chi }_4(r_4)={{N}}_1(1-\alpha r_4)e^{-r_4/2},& (77)\end{array}$

with normalization constant ${{N}}_1$ defined in (47).

We take the same approach as section 4.3 to calculate the first-order term (the 2s² electron-electron repulsion term) at D → ∞ limit with the help of Equations (50, 52):

$\begin{array}{ll}\langle \frac{1}{r_{34}}\rangle =f(D)F\left(\frac{1}{2},\frac{3-D}{2};\frac{D}{2};y\right)\left(\frac{ab}{a+b}\right)& (78)\end{array}$

with $y={\left(\frac{a-b}{a+b}\right)}^2$ and f (D) function shown in Equations (2) and (26). This is the same functional expression as in lithium atom (53), but the arguments are different.

To calculate the first-order perturbation coefficient $\langle \frac{1}{r_{34}}\rangle$ for beryllium we use the normalized wave functions χ₁(r₁), χ₂(r₂), χ₃(r₃), and χ₄(r₄) already specified, which gives rise to a typical term like

$\begin{array}{l}\langle \frac{1}{r_{34}}\rangle ~{\displaystyle \int }{d}^D{r}_3{\displaystyle \int }{d}^D{r}_4{\chi }_3^{*}(r_3){\chi }_4^{*}(r_4)\frac{1}{r_{34}}{\chi }_3(r_3)\chi (r_4)\\ ~{\displaystyle \int }{d}^D{r}_3{\displaystyle \int }{d}^D{r}_4{(1-\alpha r_3)}^2{(1-\alpha r_4)}^2{e}^{-r_3}{e}^{-r_4}\frac{1}{r_{34}}.& (79)\end{array}$

From the above Equation (79), we see that we have to put a = 1 and b = 1, so y = 0. In Equation (78) the hypergeometric function

$\begin{array}{ll}{\displaystyle \underset{D\to \infty }{\text{lim}}}F\left(\frac{1}{2},\frac{3-D}{2};\frac{D}{2};y\right)={\displaystyle \underset{D\to \infty }{\text{lim}}}F\left(\frac{1}{2},-\frac{D}{2};\frac{D}{2};0\right)=1,& (80)\end{array}$

and f (D) → 2^−1/2 at D → ∞ limit.

At D → ∞ limit (78) gives

$\begin{array}{ll}\langle \frac{1}{r_{34}}\rangle =0.353553.& (81)\end{array}$

For D = 3 we use the following formula from [1] and [28]:

$\begin{array}{l}{G}_3^k(a,b)={\displaystyle \int }{d}^3{r}_1{\displaystyle \int }{d}^3{r}_2\frac{e^{-a{r}_1}}{r_1}\frac{e^{-b{r}_2}}{r_2}{r}_{12}^{k-1}\\ ={(4\pi )}^2\Gamma (k+1){(a^2-b^2)}^{-1}\left(b^{-k-1}-a^{-k-1}\right),& (82)\end{array}$

From the above relation (82) we can compute the following integral:

$\begin{array}{l}{K}_3(i,j,k)={\displaystyle \int d^3}{r}_1{\displaystyle \int d^3}{r}_2{e}^{-a{r}_1}{e}^{-b{r}_2}{r}_1^{i-1}{r}_2^{j-1}{r}_{12}^{k-1}\\ ={\left(-\frac{\partial }{\partial a}\right)}^i{\left(-\frac{\partial }{\partial b}\right)}^j{G}_3^k(a,b).& (83)\end{array}$

At D = 3 the 2s wave function

$\begin{array}{ll}{\psi }_{2s}(r)=\sqrt{\frac{{\alpha }^3}{32\pi }}(2-\alpha r)e^{-\alpha r/2},& (84)\end{array}$

with α = 1 such that

$\begin{array}{ll}\langle \frac{1}{r_{34}}\rangle ={\displaystyle \int d^3{r}_3\int }{d}^3{r}_4|{\psi }_{2s}(r_3){|}^2\left(\frac{1}{r_{34}}\right)|{\psi }_{2s}(r_4){|}^2.& (85)\end{array}$

To calculate the inter-electronic repulsion energy $\langle \frac{1}{r_{34}}\rangle$ from (85) we use the above type of integrals $G_3^k(a,b)$ in Equation (82) and K₃(i, j, k) in Equation (83), with a = 1, b = 1, and k = 0.

With the help of (82, 83) we calculate the first-order coefficient (2s-2s part) for the beryllium atom in three dimension:

$\begin{array}{ll}\langle \frac{1}{r_{34}}\rangle =0.275696.& (86)\end{array}$

5.4. Interpolation for D=3

We again use the interpolation formula shown in Equation (6),

$\begin{array}{ll}{ϵ}_3=\frac{1}{3}{ϵ}_1+\frac{2}{3}{ϵ}_{\infty }+\left[{ϵ}_3^{(1)}-\frac{1}{3}{ϵ}_1^{(1)}-\frac{2}{3}{ϵ}_{\infty }^{(1)}\right]\lambda ,& (87)\end{array}$

now with λ = 1/Z = 1/4. The input from our A, B, C subsections was:

${ϵ}_1=-0.645842,{ϵ}_{\infty }=0.875837,$

and

${ϵ}_3^{(1)}=1.740202,{ϵ}_1^{(1)}=0.855417,{ϵ}_{\infty }^{(1)}=2.849508.$

Our interpolation gives the Be atom ground-state energy with error 0.6%: ϵ₃ = −0.910325, compared with the exact result ϵ₃ = −0.916709.

6. Hydrogen Molecule

The ground state potential energy function, V(R), of the hydrogen molecule has been calculated by many methods [34–37]. Recently, Olivares-Pilón and Turbiner [38] presented a general theory for obtaining the V(R) function for diatomic molecules. They dealt with the Born-Oppenheimer approximation, based on matching R in short and long distances via a two-point Padé approximation. Here, we present a simpler approach obtaining V(R) for H₂ at D = 3 by using interpolation between D = 1 and D → ∞ dimensional limits. Key aspects of dimensional scaling had been developed years ago by Tan and Loeser [18], Lòpez-Cabrera et al. [19] and Frantz and Herschbach [17]. They did an excellent treatment on ${\text{H}}_2^{+}$ and partial on H₂. Now we will complete V(R) for H₂ by interpolation.

6.1. One-Dimension: D=1

In H₂, with nuclear charge of each atom Z, the electronic part of the Hamiltonian in one-dimension using atomic units can be written as [20, 39]:

$\begin{array}{l}{H}=-\frac{1}{2}\frac{{\partial }^2}{\partial r_1^2}-\frac{1}{2}\frac{{\partial }^2}{\partial r_2^2}-\delta (r_1-a)\\ \begin{array}{l}-\delta (r_1+a)-\delta (r_2-a)-\delta (r_2+a)+\lambda \delta (r_1-r_2),\end{array}& (88)\end{array}$

with a = R/2, where R is the distance between the two nuclei located at r = ±a; also λ = 1/Z = 1. The Hamiltonian energy eigenvalues provide symmetric and antisymmetric states under exchange of the electrons. The symmetric state pertains to the ground-state potential energy [20]:

$\begin{array}{ll}{ϵ}_1(R)=-\frac{1+\left(4+2R+R^2\right)e^{-2R}}{1+{\left(1+R\right)}^2{e}^{-2R}},& (89)\end{array}$

The total binding energy is obtained by adding the nucleus-nucleus-interaction term (1/R) with the electronic energy.

6.2. Infinite-Dimension: D → ∞

Many important features of the H₂ molecule are calculated in cylindrical coordinates because this problem has a natural cylindrical symmetry about the z-axis. The D-dimensional space in cylindrical coordinates is described by a linear coordinate z and a (D − 1)-dimensional subspace specified by spherical coordinates, which are orthogonal to each other. The coordinate ρ is the radius of a (D − 1)-dimensional sphere; see section 2 of [17] for more details.

For H₂, convention locates the two nuclei A and B on the z-axis at −R/2 and R/2, respectively, with equal charges Z_A = Z_B = Z. The electrons are located at (ρ₁, z₁) and (ρ₂, z₂), with a dihedral angle ϕ specifying their relative azimuthal orientation about the molecular axis. The effective Hamiltonian for large-D limit in cylindrical coordinates is [17, 40]:

$\begin{array}{l}{H}=\frac{1}{2}\left(\frac{1}{{\rho }_1^2}+\frac{1}{{\rho }_2^2}\right)\frac{1}{{\text{sin}}^2\varphi }\\ \begin{array}{l}-{\displaystyle \sum _{i=1}^2}\left[\frac{Z}{\sqrt{{\rho }_i^2+{(z_i+a)}^2}}+\frac{Z}{\sqrt{{\rho }_i^2+{(z_i-a)}^2}}\right]\\ \begin{array}{l}+J({\rho }_1,{\rho }_2,z_1,z_2,\varphi ),\end{array}\end{array}& (90)\end{array}$

with a = R/2 and

$J({\rho }_1,{\rho }_2,z_1,z_2,\varphi )=\frac{1}{\sqrt{{(z_1-z_2)}^2+{\rho }_1^2+{\rho }_2^2-2{\rho }_1{\rho }_2\text{cos}\varphi }}.$

In the D → ∞ limit, the Hamiltonian has two locations for electrons, namely: symmetric, with ρ₁ = ρ₂ and z₁ = z₂, and antisymmetric, with ρ₁ = ρ₂ and z₁ = −z₂. When R has the nuclei well apart, in the symmetric case, both electrons cluster near one of the nuclei $({\text{H}}_2\to {\text{H}}^{-}+{\mathrm{\text{H}}}^{+})$; in the antisymmetric case, each electron resides near just one of the nuclei (H₂ → H + H). Thus, the antisymmetric case is much more favorable for the ground-state energy.

We minimize the Hamiltonian (90) with respect to ρ's and z's to obtain the ground state energy, ϵ_∞(R); we numerically evaluate the corresponding optimized parameters ${\rho }_1^{*},{\rho }_2^{*},z_1^{*},z_2^{*}$, and ϕ^* for different values of R.

The total binding energy is obtained by adding to ϵ_∞(R) the internuclear-interaction term (1/R).

6.3. Interpolation for D=3

Unlike the atoms, our interpolation will be different for a molecule. An atom has only one nucleus, with the electrons orbiting about the positive charge; our interpolation with the first-order perturbation works well for atoms but not for a molecule. For a diatomic molecule, V(R) is fundamental, with the internuclear distance R. As mentioned in Equations (4) and (5), our interpolation for H₂ uses a modified rescaling scheme developed by [17–19] with the D = 1 and D → ∞ dimensional limits:

$\begin{array}{ll}{ϵ}_3(R)=\frac{1}{3}{ϵ}_1(R)+\frac{2}{3}{ϵ}_{\infty }(R),& (91)\end{array}$

The rescaled distances are:

$\begin{array}{ll}\text{In }D=1:r_i\to r_i^{\prime }/3\text{ and }R\to R^{\prime }/3,\text{ for }i=1,2;& (\mathrm{92a})\end{array}$

$\begin{array}{l}\text{In }D\to \infty :{\rho }_i\to 2{\rho }_i^{\prime }/3,z_i\to 2z_i^{\prime }/3,\text{ and }R\to 2R^{\prime }/3,\\ \begin{array}{l}\text{ for }i=1,2.\end{array}& (\mathrm{92b})\end{array}$

The rescaled Hamiltonians have distinct factors in the kinetic and potential energy parts: In D = 1: Hamiltonian (88) becomes:

$\begin{array}{l}{{H}}_{D=1}=-\frac{9}{2}\frac{{\partial }^2}{\partial r_1^2}-\frac{9}{2}\frac{{\partial }^2}{\partial r_2^2}-3\delta (r_1-a)-3\delta (r_1+a)\\ -3\delta (r_2-a)-3\delta (r_2+a)+3\lambda \delta (r_1-r_2).& (\mathrm{93a})\end{array}$

In D → ∞: Hamiltonian (90) becomes:

$\begin{array}{l}{{H}}_{D=\infty }=\frac{9}{4}\left(\frac{1}{{\rho }^2{\text{sin}}^2\varphi }\right)\\ \begin{array}{l}-3\left[\frac{Z}{\sqrt{{\rho }^2+{(z+a)}^2}}+\frac{Z}{\sqrt{{\rho }^2+{(z-a)}^2}}\right]\\ \begin{array}{l}+\frac{3}{2}J(\rho ,z,\varphi ),\end{array}\end{array}& (\mathrm{93b})\end{array}$

with a = R/2 and

$J(\rho ,z,\varphi )=\frac{1}{\sqrt{{(2z)}^2+2{\rho }^2-2{\rho }^2\text{cos}\varphi }}.$

We minimized these rescaled Hamiltonians (93) with respect to the rescaled distances (92).

In Figure 1, we have plotted the binding energies of H₂ as functions of R, in the three dimensions (91), adding the nuclear repulsion term, 1/R. The curves are colored: red for D = 1, green for D → ∞, and blue for D = 3, the interpolation. It compares fairly well with the nominally exact V(R) curve, colored orange, for H₂ obtained from the full configuration interaction (FCI) method [41, 42]. We have obtained the FCI by using the OpenFermion quantum computational chemistry software [43].

FIGURE 1

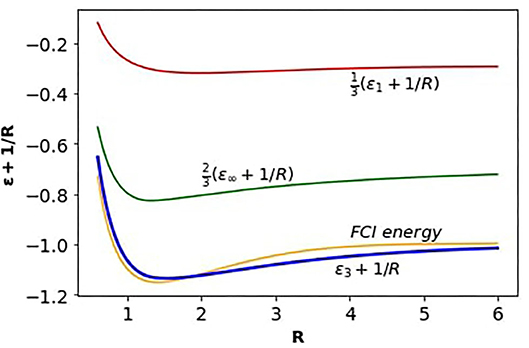
Figure 1. The binding V(R) curves for H₂, shown from different dimensions. The red and green curves pertain to D = 1 and D → ∞, respectively, parts from Equations (92) and (93) of the interpolaiton. The blue curve, ϵ₃(R) + 1/R, represents D = 3, the interpolation result at Equation (91). The orange curve is a highly accurate result obtained from computation [43].

7. Conclusion and Prospects

The formula used for atoms we consider unorthodox, as it recently emerged [14] whereas other D-interpolations are elderly [44, 45]. The fresh aspect links the energies ϵ₁ and ϵ_∞ together with the first-order perturbation coefficients ${ϵ}_1^{(1)}$ and ${ϵ}_{\infty }^{(1)}$ plus ${ϵ}_3^{(1)}$ from their 1/Z expansions. Those perturbations arise from of electron-electron pair interactions, 〈1/r_ij〉; they actually provide much of the dimension dependence. For H₂ we used a different scaling than with the atoms, since H₂ links the distance R between the two nuclei. Then the rescaling is: R → 1/3R′ for D → 1; R → 2/3R′ for D → ∞. Interpolating between the dimensional limits gave a fair approximation of the binding energy for D = 3, when compared with the full configuration interaction (FCI).

In tally, our sections 3, 4, and 5 treat He, Li, Be; in section 6 dealt with H₂. In subsections we describe the D = 1 limit, the D = ∞ limit, the first-order perturbations, and the interpolation output.

The ingredients of the interpolation are well suited for computing. In our calculation we treat the electrons exclusively in s states with spherical or, in the molecular case, cylindrical symmetry. However, we expect the possibility to extend our method to encompass atoms with electrons of finite angular momentum, although this could be more challenging. We also expect the method to hold true for larger atomic, molecular and extended systems. More than ground-state energies are accessible. However, there are prospects for combining dimensional limits to serve other many-body problems. One is examining dimensional dependence of quantum entanglement [46, 47]. Another is the isomorphism between the Ising model [48] and two-level quantum mechanics [49]. Long ago the Ising model was solved in one, two and infinite dimensions [50–52], as well much activity near four dimensions [53]. The unknown solution at D = 3 remains a challenge even by quantum computing [54, 55]. More light on the solution might come by blending of dimensions akin to our unorthodox interpolated formula.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors (SK and KG) acknowledge the partial financial support by the U.S. Department of Energy (Office of Basic Energy Sciences) under Award No. DE-SC0019215 and the Integrated Data Science Initiative Grant (IDSI F.90000303), Purdue University. This manuscript has been released as a pre-print at arXiv:2004.11489 [quant-ph] [56].

References

1. Herrick DR, Stillinger FH. Variable dimensionality in atoms and its effect on the ground state of the helium isoelectronic sequence. Phys Rev A. (1975) 11:42–53. doi: 10.1103/PhysRevA.11.42

CrossRef Full Text | Google Scholar

2. Mlodinow LD, Papanicolaou N. SO(2,1) algebra and the large N expansion in quantum mechanics. Ann Phys. (1980) 128:314–334.

Google Scholar

3. Yaffe LG. Large N limits as classical mechanics. Rev Mod Phys. (1982) 54:407.

Google Scholar

4. Herschbach DR. Dimensional interpolation for two-electron atoms. J Chem Phys. (1986) 84:838–51. doi: 10.1063/1.450584

CrossRef Full Text | Google Scholar

5. Witten E. Quarks, atoms, and the 1/N expansion. Phys Today. (1980) 33:38–43.

Google Scholar

6. Goodson DZ, López-Cabrera M, Herschbach DR, Morgan III JD. Large-order dimensional perturbation theory for two-electron atoms. J Chem Phys. (1992) 97:8481–96.

Google Scholar

7. Zhen Z, Loeser J. In: Herschbach DR, Avery J, Goscinski O. (eds.). Large-D Limit for N-Electron Atoms. Dordrecht: Springer Netherlands (1993). p. 83–114.

Google Scholar

8. Kais S, Herschbach DR. The 1/Z expansion and renormalization of the large-dimension limit for many-electron atoms. J Chem Phys. (1994) 100:4367–76.

Google Scholar

9. Rudnick J, Gaspari G. The shapes of random walks. Science. (1987) 237:384–9.

PubMed Abstract | Google Scholar

10. Loeser JG, Zhen Z, Kais S, Herschbach DR. Dimensional interpolation of hard sphere virial coefficients. J Chem Phys. (1991) 95:4525–44.

Google Scholar

11. Kais S, Herschbach DR. Dimensional scaling for quasistationary states. J Chem Phys. (1993) 98:3990–8.

Google Scholar

12. Wei Q, Kais S, Herschbach DR. Dimensional scaling treatment of stability of simple diatomic molecules induced by superintense, high-frequency laser fields. J Chem Phys. (2008) 129:214110. doi: 10.1063/1.3027451

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Wei Q, Kais S, Herschbach DR. Dimensional scaling treatment of stability of atomic anions induced by superintense, high-frequency laser fields. J Chem Phys. (2007) 127:094301. doi: 10.1063/1.2768037

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Herschbach DR, Loeser JG, Virgo WL. Exploring unorthodox dimensions for two-electron atoms. J Phys Chem A. (2017) 121:6336–40. doi: 10.1021/acs.jpca.7b06148

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Rosenthal CM. Solution of the delta function model for heliumlike ions. J Chem Phys. (1971) 55:2474–83. doi: 10.1063/1.1676436

CrossRef Full Text | Google Scholar

16. Loeser JG, Herschbach DR. Dimension dependence of correlation energies in two-electron atoms. J Chem Phys. (1987) 86:3512–21. doi: 10.1063/1.451954

CrossRef Full Text | Google Scholar

17. Frantz DD, Herschbach DR. Lewis electronic structures as the large-dimension limit for $H_2^{+}$ and H₂ molecules. Chem Phys. (1988) 126:59–71.

Google Scholar

18. Tan AL, Loeser JG. In: Herschbach DR, Avery J, Goscinski O, editors. Simple molecules and variant scalings. Dimensional Scaling in Chemical Physics. Dordrecht: Springer Netherlands (1993). p. 230–55. doi: 10.1007/978-94-011-1836-1_3

CrossRef Full Text

19. López-Cabrera M, Tan AL, Loeser JG. Scaling and interpolation for dimensionally generalized electronic structure. J Phys Chem. (1993) 97:2467–78.

Google Scholar

20. Lapidus IR. One-dimensional models for two-electron systems. Am J Phys. (1975) 43:790–2. doi: 10.1119/1.9708

CrossRef Full Text | Google Scholar

21. White RJ, Stillinger FH. Analytic approach to electron correlation in atoms. J Chem Phys. (1970) 52:5800–14. doi: 10.1063/1.1672862

CrossRef Full Text | Google Scholar

22. Loeser JG, Herschbach DR. Hylleraas-Pekeris treatment of D-dimensional two-electron atoms. J Chem Phys. (1986) 84:3882–92. doi: 10.1063/1.450099

CrossRef Full Text | Google Scholar

23. James HM, Coolidge AS. On the ground state of Lithium. Phys Rev. (1936) 49:688.

Google Scholar

24. Weiss AW. Configuration interaction in simple atomic systems. Phys Rev. (1961) 122:1826.

Google Scholar

25. Larsson S, Burke EA. Variational calculation of the ground state of the lithium atom. Phys Rev. (1969) 184:248.

Google Scholar

26. Scherr CW, Silverman JN, Matsen FA. Perturbation energy coefficients and ionization potentials of the ground state of three-to ten-electron isoelectronic atomic series. Phys Rev. (1962) 127:830.

Google Scholar

27. Wilson Jr EB. Wave functions for the ground state of lithium and three-electron ions. J Chem Phys. (1933) 1:210–8.

Google Scholar

28. Abramowitz M, Stegun IA. Handbook of Mathematical Functions With Formulas, Graphs, and Mathematical Tables, Vol. 55. US Government Printing Office (1948).

Google Scholar

29. Bunge CF. Configuration interaction benchmark for Be ground state. Theor Chem Acc. (2010) 126:139–50. doi: 10.1007/s00214-009-0601-5

CrossRef Full Text | Google Scholar

30. Büsse G, Kleindienst H, Lüchow A. Nonrelativistic energies for the Be atom: double-linked Hylleraas-CI calculation. Int J Quantum Chem. (1998) 66:241–7.

Google Scholar

31. Sims JS, Hagstrom SA. Hylleraas-configuration-interaction study of the 1s ground state of neutral beryllium. Phys Rev A. (2011) 83:032518. doi: 10.1103/PHYSREVA.83.032518

CrossRef Full Text | Google Scholar

32. Puchalski M, Komasa J, Pachucki K. Testing quantum electrodynamics in the lowest singlet states of the beryllium atom. Phys Rev A. (2013) 87:030502. doi: 10.1103/PhysRevA.87.030502

CrossRef Full Text | Google Scholar

33. Stanke M, Komasa J, Bubin S, Adamowicz L. Five lowest S 1 states of the Be atom calculated with a finite-nuclear-mass approach and with relativistic and QED corrections. Phys Rev A. (2009) 80:022514. doi: 10.1103/PhysRevA.80.022514

PubMed Abstract | CrossRef Full Text | Google Scholar

34. James HM, Coolidge AS. The ground state of the hydrogen molecule. J Chem Phys. (1933) 1:825–35. doi: 10.1063/1.1749252

CrossRef Full Text | Google Scholar

35. Kolos W, Roothaan CCJ. Accurate electronic wave functions for the H₂ molecule. Rev Mod Phys. (1960) 32:219. doi: 10.1103/RevModPhys.32.219

CrossRef Full Text | Google Scholar

36. Svidzinsky AA, Scully MO, Herschbach DR. Simple and surprisingly accurate approach to the chemical bond obtained from dimensional scaling. Phys Rev Lett. (2005) 95:080401. doi: 10.1103/PhysRevLett.95.080401

PubMed Abstract

37. Chen G, Chin SA, Dou Y, Kapale KT, Kim M, Svidzinsky AA, et al. The two electron molecular bond revisited: from Bohr orbits to two-center orbitals. Adv At Mol Opt Phys. (2005) 51:93–238. doi: 10.1016/S1049-250X(05)51015-2

CrossRef Full Text | Google Scholar

38. Olivares-Pilón H, Turbiner AV. Towards the theory of Potential Energy Curves for diatomic molecular ions: $H{e}_2^{+}$ case. arXiv [preprint]. arXiv:1904.06614. (2019). Available online at: https://arxiv.org/abs/1904.06614

Google Scholar

39. Lapidus IR. One-dimensional hydrogen molecule revisited. Am J Phys. (1982) 50:453–6. doi: 10.1119/1.12833

CrossRef Full Text | Google Scholar

40. Herrick DR. Degeneracies in energy levels of quantum systems of variable dimensionality. J Math Phys. (1975) 16:281–3. doi: 10.1063/1.522538

CrossRef Full Text | Google Scholar

41. Bauschlicher CW, Langhoff SR, Taylor PR. Accurate quantum chemical calculations. Adv Chem Phys. (1990) 77:103–61.

Google Scholar

42. Sherrill CD, Schaefer HF III. The configuration interaction method: advances in highly correlated approaches. In: Löwdin P-O, Sabin JR, Zerner MC, Brändas E, editors. Advances in Quantum Chemistry. Vol. 34. San Diego, CA: Elsevier (1999). p. 143–269.

Google Scholar

43. McClean JR, Rubin NC, Sung KJ, Kivlichan ID, Monroig XB, Cao Y, et al. OpenFermion: the electronic structure package for quantum computers. Quant Sci Technol. (2020) 5:034014. doi: 10.1088/2058-9565/ab8ebc

CrossRef Full Text | Google Scholar

44. Kais S, Sung SM, Herschbach DR. Large-Z and-N dependence of atomic energies from renormalization of the large-dimension limit. Int J Quantum Chem. (1994) 49:657–74. doi: 10.1002/qua.560490511

CrossRef Full Text | Google Scholar

45. Cardy J. Scaling and Renormalization in Statistical Physics. Vol. 5. Cambridge, UK: Cambridge University Press (1996).

Google Scholar

46. Kais S. Entanglement, electron correlation, and density matrices. Adv Chem Phys. (2007) 134:493. doi: 10.1002/9780470106600.ch18

CrossRef Full Text | Google Scholar

47. Huang Z, Wang H, Kais S. Entanglement and electron correlation in quantum chemistry calculations. J Mod Opt. (2006) 53:2543–58. doi: 10.1080/09500340600955674

CrossRef Full Text | Google Scholar

48. Chandler D. Introduction to Modern Statistical Mechanics. Oxford: Oxford University Press (1987).

Google Scholar

49. Loeser JG, Herschbach DR. In: Tsipis CA, Popov VS, Herschbach DR, Avery JS, editors. Dimensional Scaling. New Methods in Quantum Theory. 1st Edn. Dordrecht: Kluwer Academic Pub (1996) 1–32.

Google Scholar

50. Ising E. Beitrag zur theorie des ferromagnetismus. Z Phys. (1925) 31:253–8. doi: 10.1007/BF02980577

CrossRef Full Text | Google Scholar

51. Stanley HE. Spherical model as the limit of infinite spin dimensionality. Phys Rev. (1968) 176:718–22. doi: 10.1103/PhysRev.176.718

CrossRef Full Text | Google Scholar

52. Berlin TH, Kac M. The spherical model of a ferromagnet. Phys Rev. (1952) 86:821–35. doi: 10.1103/PhysRev.86.821

CrossRef Full Text | Google Scholar

53. Herschbach DR. Dimensional scaling and renormalization. Int J Quantum Chem. (1996) 57:295–308. doi: 10.1002/(SICI)1097-461X(1996)57:3<295::AID-QUA3>3.0.CO;2-T

CrossRef Full Text | Google Scholar

54. Xia R, Bian T, Kais S. Electronic structure calculations and the Ising Hamiltonian. J Phys Chem B. (2017) 122:3384–95. doi: 10.1021/acs.jpcb.7b10371

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Nielsen MA, Chuang IL. Quantum Computation and Quantum Information: 10th Anniversary Edition. Cambridge, UK: Cambridge University Press (2010).

PubMed Abstract | Google Scholar

56. Ghosh KJB, Kais S, Herschbach DR. Unorthodox dimensional interpolations for He, Li, Be atoms and hydrogen molecule. arXiv [preprint]. arXiv:2004.11489. (2020). Available online at: https://arxiv.org/abs/2004.11489

Google Scholar