
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys. , 11 September 2020
Sec. Interdisciplinary Physics
Volume 8 - 2020 | https://doi.org/10.3389/fphy.2020.00321
This article is part of the Research Topic Non-Local Thermodynamic Equilibrium (NLTE) Hydrogen-Boron Fusion View all 6 articles
Increasing absorption up to more than 90% with increasing intensity was observed in boron and gold laser plasmas heated by KrF laser pulses of high, but still non-relativistic, intensity. The pulses of 700 fs duration had a temporal contrast of 12 orders of magnitude; thus, the laser pulse of more than 1018 Wcm−2 intensity hit the steep surface of the boron and gold targets. Blue shift of the reflected radiation refers to extreme high acceleration resulting in velocities above 5 × 105 ms−1. Brunel absorption and ponderomotive effects are shown to play an important role in the observed phenomena.
Investigation of the light reflected from plasmas generated on solid surfaces is not only the most straightforward diagnostic of laser-plasma interactions, but also the so-called plasma mirrors [1] are frequently used for improving the temporal contrast of intense subpicosecond laser pulses. As a diagnostic tool its quantity measures the absorption in the plasma, whereas the spectral properties give information on the motion of the plasma and the non-linear interactions in it. The outward and inward motion of the plasma as derived from the reflectivity measurements resulted in the so-called block ignition idea which might become a way toward non-thermal ignition of ICF (inertial confinement fusion), reducing the requirements even for DT fusion or which might allow even the high temperature needed for p-B fusion [2, 3]. As based on earlier experiments [4, 5], the possible use of KrF lasers was also emphasized [6]. For this reason we aimed to get more insight into KrF laser-plasma interactions under “clean” conditions where the temporal background before the main pulse does not modify the interactions. As an appropriate light source, the recently upgraded KrF laser system incorporating the newly installed Fourier-filtering technique [7] could be used, offering a short laser pulse with 1012 temporal contrast.
Herewith we summarize some results on bulk plasma motion in laser-plasma interactions with ultrashort laser pulses. Spectral blue shift of the reflected radiation attributed to plasma expansion was studied by Milchberg and Freeman [8]. Later, with the increase of the available laser intensities, a red shift referring to inward motion was also observed when the oscillation velocity of the electrons in the laser field became relativistic [9]. Even the early works [10] gave explanation to the observations in the non-relativistic case, but the possible absorption and acceleration mechanisms are summarized in detail in the theoretical work of Wilks and Kruer [11] considering collisional, resonance-, and Brunel-absorption as well as the relativistic j × B heating. Recently experimental and theoretical studies were carried out in the relativistic regime [12, 13], but also the dependence of these processes on the contrast of the laser pulse generated renewed interest [14].
As a consequence of the short wavelength of the KrF laser, the interactions are non-relativistic up to several times 1018 Wcm−2. Due to the relative narrow bandwidth of KrF systems the reflectivity can be studied directly from the reflection of the main pulse, not requiring an auxiliary laser source or the use of the second harmonic of the laser pulse. The early investigations [4] gave detailed analysis of the processes, considering even the chirp of the laser pulse having a contrast of more than 8 orders of magnitude. A surprising statement of that paper was that in some—even non-relativistic—cases (the intensity was <3 × 1017 Wcm−2), a red shift was reported as a probable consequence of the inward acceleration of the plasma. However later it was shown [5] that a UV prepulse of low (i.e., ~107 Wcm−2) intensity may result in photoablation and photoionization, thus preformed plasma in the interaction range. New developments of pulse cleaning based on the Fourier-filtering technique [7] and its integration into our laser system [15] allowed us to achieve 1012 temporal contrast against the ASE prepulse of the KrF system. Detailed studies of the reflectivity and investigations of the spectral shape are then carried out on high-Z (Au) and low-Z (B) targets with the KrF laser system offering 700 fs on-target pulse duration and 1.15 × 1018 Wcm−2 intensity. With these experiments the interactions could be studied in well-defined conditions up to a high-intensity range which is still non-relativistic due to the short wavelength of radiation.
The laser system is based on a hybrid dye-excimer system [16]. The 500 fs long and 497 nm central wavelength output of a XeCl pumped distributed feedback dye laser is frequency doubled and amplified in a three tube, 6 pass KrF amplifier chain [15]. The pulse is sent through a so-called pre-imaging system which after the first pass consists of a two lens telescope and a conventional spatial filter. After the second pass of the first amplifier, the beam is sent through the recently introduced non-linear Fourier-filter which provided—after focusing—our high temporal contrast (~1012) of the laser intensity [7, 17]. Depending on the use of the Fourier-filter, the energy contrast ranged from 1:80 to 1:8 (when pulse cleaning was omitted). It is to be noted that without the Fourier-filter the temporal contrast of the laser intensity dropped drastically to ~5.5 × 105. A modification of the arrangement of the present work as compared with Gilicze et al. [15] is that the interferometric multiplexing was removed from the final amplifier in order to keep the polarization vertical or horizontal, which was selected in front of the amplifiers by a half-wave-plate. This, however, reduced the output energy to ~80 mJ.
The final energy on the target was 55 mJ, and after 4 m in sealed propagation the measured pulse duration was 700 fs at the position of the target. The 4 cm × 4 cm p-polarized beam had a positive chirp of 3.5 (±0.5) × 10−5 fs−2. The beam was focused by a 30° F/3 off-axis parabolic mirror (SORL). Focal spot and intensity contrast measurements were carried out using an f = 3 mm, three lens configuration UV microscope objective. The 40x magnified image on the CCD of a Hamamatsu T7040 UV sensitive camera revealed an elliptical focal spot size of 1.85 μm (± 0.1 μm) for the vertical axis and 1.95 μm (± 0.1 μm) for the horizontal axis (corresponding to a ~2x diffraction limit). At the same time the ASE spot size was 1.56 mm when using Fourier filtering, as shown in Figure 1.

Figure 1. ASE signal (A) and main pulse spot size (B) with 40x magnification. The main pulse spot in (B) is with the same magnification as the ASE on the left hand side, and then further magnified to make the full pattern visible.
The experimental arrangement is illustrated in Figure 2. The intensity was attenuated by a variable diaphragm, and for each aperture size, the focal spot size was measured, too. This enabled experimental studies for 3 orders of magnitude of intensity range, from 1015 Wcm−2 up to 1.15·1018 Wcm−2 on the target (taking into account the 45° angle of incidence). Experiments were carried out either with p- or with s-polarized radiation. In both cases the polarization contrast was only 7:1 due to the large number of the applied optical components. The targets were glass plates coated by 500 nm boron (B) or gold (Au) layers. Turbomolecular pumping resulted in <10−5 mbar oil-free vacuum in a chamber of 80 cm diameter. In order to avoid damage on the focusing optics from the debris of the irradiated targets, a 1 mm thick suprasil quartz plate was placed between the parabolic mirror and the target. This did not introduce new spectral components into the laser spectrum. The incident laser spectra were monitored using fractional reflection from a thin quartz plate by a spectrometer (Spectrometer 1) with a resolution of 0.027 nm. Target positioning was carried out by an xyz translation stage (STANDA 133373), with a step size of 1.25 μm. Target stability was also tested and found to deviate <3 μm over the 4 cm sample size along the Z-axis. This is well within the 6 μm Rayleigh-range of the F/3 focusing.
The focal plane was determined using the X-ray signal generated in the laser-plasma. For this, an IRD AXUV-100 silicon diode covered by a 2 μm thick Al foil was used and the output was recorded by an oscilloscope. The specularly reflected radiation from the 45° tilted targets was collimated and passed through the quartz window of the vacuum chambers (<10−5 mbar). The energy of the reflected radiation was measured by a calibrated energy meter with simultaneous monitoring of the incoming pulse. The boundary of the reflected radiation was sharp, therefore only the specular reflection was measured, and the diffuse reflection could be neglected. In order to measure the spectral change, the slightly divergent beam was sent to a second spectrometer (Spectrometer 2) having the same (0.027 nm) spectral resolution. This twin spectrometer configuration allowed avoiding errors due to the shot-to-shot deviation of the laser's central wavelength, which could be as high as 0.3 nm.
Detailed study of the reflectivity for high and low contrast pulses for p-polarized radiation has been discussed in detail elsewhere, together with the observed increasing x-ray conversion efficiency with increasing intensity [18]. Herewith Figure 3 shows the measured specular reflectivity from boron and gold targets both for p- and s-polarized 248 nm KrF laser pulses of 700 fs duration. The intensity of the prepulse was <107 Wcm−2 in the whole range, thus the main pulse hits an initially steep profile of the solid [5]. Figure 3 shows decreasing reflectivity with increasing intensity. Thus, the absorption reaches more than 90% for 1018 Wcm−2 p-polarized radiation, but it is nearly 85% for s-polarized pulses as well. The shot-to-shot scattering of the data was, however, high. Whereas, in the case of Au targets the reflectivity is significantly higher for s-polarized radiation for the lower intensity range, no significant difference in reflectivity was found between p- and s-polarized beam for B targets. It must be again emphasized that the polarization contrast was only 7:1, as the large number of optical elements prevented us to obtain a more precise experiment on polarization dependence.
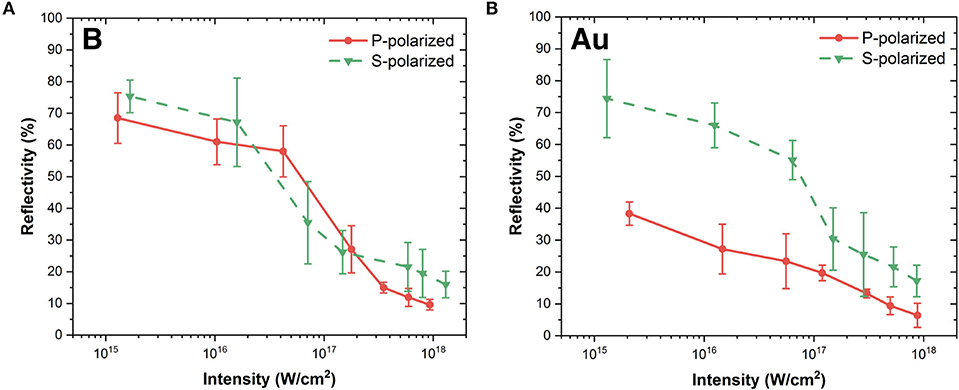
Figure 3. Intensity dependence of reflectivity from B (A) and Au (B) targets for p-polarized (red circles, solid line) and s-polarized radiation (green three angles, dotted line). The contrast is 1012.
The main purpose of the present paper is the detailed study of the spectrum of the reflected radiation. Figure 4 illustrates typical reflected spectra from boron targets for high contrast laser pulses, whereas Figure 5 shows similar data in the case when the prepulse intensity reached 5.5 × 105 of the main pulse. The choice of boron was due to its lower Z, for which theoretical considerations are easier. It is salient for Figure 4 that in case of high-contrast 248 nm pulse the reflected radiation has significant broadening. Whereas, the incident high intensity pulse has a 0.4 ± 0.2 nm bandwidth, that of the reflected one reaches 0.7 nm. Additionally, the spectral shift is increasing with increasing intensity, too. It can be noted that according to Figure 4 broadening shoulders are also appearing at the blue part of the scattered radiation, which may be attributed to the time-dependent reflection of the positively chirped laser pulse.
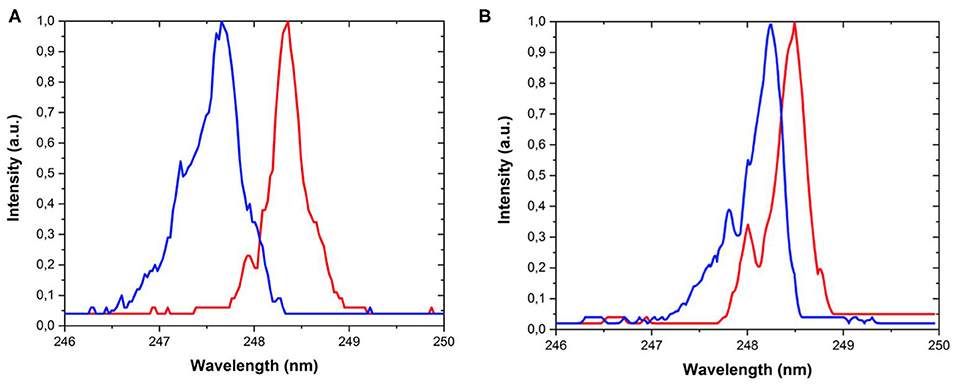
Figure 4. Incident (red) and reflected (blue) laser spectra from boron targets in the case of 1012 contrast for 1018 Wcm−2 (A), and 1016 Wcm−2 (B). The laser beam was p-polarized.
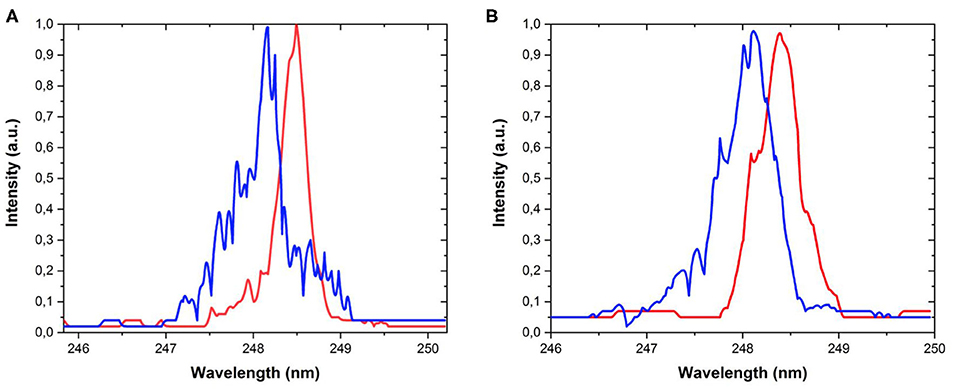
Figure 5. Incident (red) and reflected (blue) laser spectra from boron targets in the case of 5 × 105 contrast for 1018 Wcm−2 (A), and 1016 Wcm−2 (B). The laser beam was p-polarized.
As illustrated in Figure 4, spectral modulations are marginal in the case of high contrast. On the other hand, Figure 5 reveals strong modulation of the reflected radiation, similarly to the early investigations of Kalashnikov et al. [9]. This modulation can be attributed to the propagation in the preformed plasma which can be more pronounced in the case of a nanosecond ASE prepulse of 1012 Wcm−2 intensity. The new spectral components are introduced by the increasing weight of the non-linear processes, resulting—roughly speaking—in increasing higher order susceptibilities. The observed modulation is getting stronger for higher intensities, and at the same time the spectral shift seems to be less than for high contrast. These observations are similar to that observed in the case of Au targets for which the modulations are even stronger probably due to the lower ionization threshold of the material. Figure 6 illustrates quantitatively the measured spectral shift for both types of targets as a function of intensity from 1015 Wcm−2 up to 1.15 × 1018 Wcm−2 intensity. Each experimental point corresponds to an average of 4–8 shots. This shows a gradual increase of the Doppler-shift with intensity, a saturation above 1017 Wcm−2 and a maximum about 0.6 nm for both materials for the maximum intensity. The spectral shift is higher for pulses with higher contrast, showing an early saturation and even decrease in the case of the presence of preplasmas. Saturating behavior can also be observed at the highest intensity values even for the high contrast case. We emphasize here that the observed spectral shift is approximately 3–4 times as high as was observed earlier [4] when the laser contrast was only 8–10 orders of magnitude, and the intensity is lower. Additionally it must be mentioned that even the maximum intensity is non-relativistic for the 248 nm wavelength; therefore, no red shift can be observed because the light pressure is low (as we shall see below) and the relativistic j × B force is negligible as well.
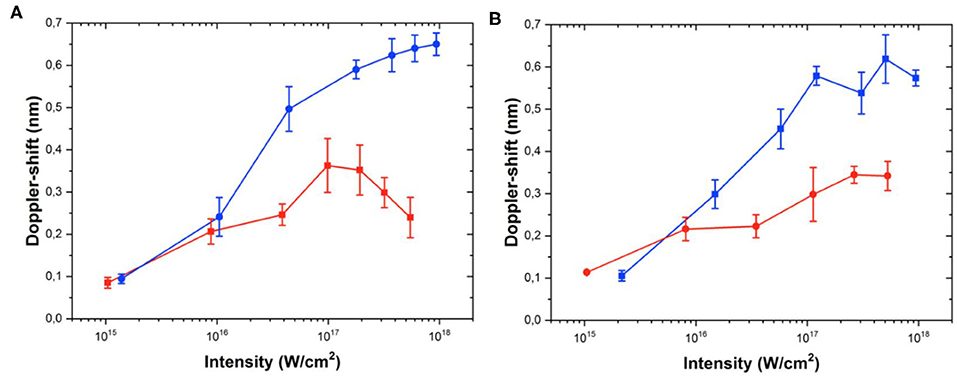
Figure 6. Intensity dependence of spectral blue shift for boron (A) and for gold (B) targets. The red circles are obtained with 5 × 105, the blue squares with 1012 temporal contrast laser pulses. The laser beam was p-polarized.
First of all we can easily explain the absence of the red shift of the spectrum. This is similar to most of the earlier observations but it contradicts with the results of Sauerbrey [4] who claimed the appearance of red shift for a laser pulse which had a similar chirp to ours. Looking at the spectrum in Figure 2 in the cited paper of Sauerbrey [4] we can see that it is practically a broadening in the pulse, comparable to the complicated reflected spectrum in the case of a low temporal contrast. In a similar manner we think that his observation was not a real spectral shift but a modulation and non-linear scattering in the preformed plasma. This is supported by the lower contrast applied therein. Even recently Singh et al. [14] showed the importance of the contrast not only for the relativistic case but in their intensity-dependent experiments in the non-relativistic case as well.
The maximum velocity can be estimated from the spectral shift with the non-relativistic Doppler formula applied to an expanding reflecting mirror:
Here c is the velocity of light, θ is the angle incidence, λ is the laser wavelength, and Δλ the wavelength shift. This yields about 5–6 × 105 ms−1 or a corresponding 1.7 × 1018 ms−2 acceleration for high contrast irradiation of both materials (assuming that the values correspond to the maximum of the laser pulse, i.e., half of the total FWHM of the laser pulse, 350 fs was taken into account).
The 6 × 105 ms−1 maximum velocity is ~50% higher than that of earlier observations.
An alternative method is to derive the acceleration and the velocity from the change of the spectral width [4]. A constant acceleration of the plasma mirror was assumed and the measured chirp of the incident laser pulse was taken into account. In case of a positive chirp the b acceleration of the plasma can be derived from the algebraic equation
Here the chirp of the laser pulse is a = 3.1 × 10−5fs−2, c is the velocity of light, ω is the laser radiation frequency. Similarly to the considerations for the Doppler shift here we assumed that τL is the half of the FWHM of the laser pulse duration, i.e., τL = 350 fs. We took the high intensity case for boron targets as shown in Figure 6A, where the incident pulse had a linewidth of ΔλL = 0.35 nm while the reflected pulse broadens to about Δλr = 0.7 nm. For the maximum intensity the acceleration b = 3.1 × 1018 ms−2 is obtained which is significantly higher than the result obtained from the simpler Doppler formula. It must be added that the result is very sensitive to the measurement of the spectral widths, the chirp, and the actual pulse duration which could cause a significant shot-to-shot variations in the derived acceleration, thus we think the approximations of Equation (1) is more appropriate. The derived maximum acceleration is the highest one observed up to now with KrF lasers. We can mention that according to the relativistic oscillating mirror model in the case of high harmonic generation the critical surface may obtain a significantly higher velocity during oscillation, e.g., using a ~2cycle laser pulse acceleration up to 7 × 1021 ms−2 was derived as based on spectral interferometry [19]. However in the present case we can speak about directional acceleration of a macroscopic material quantity [3, 4].
A possible way to give an interpretation of the observed high velocity is to assume that our high contrast 700 fs pulse hits a steep density profile, which can be really approximated by a step-function. Therefore, for our 1018 Wcm−2 intensity Brunel absorption (also called vacuum heating) may be present. Then resonance absorption steps in and in later stage of the 700 fs pulse duration—when the scale length of the plasma will be larger than λ/10—even collisional absorption may play a role. Resonance absorption occurs in general for lower intensity than vacuum heating. It might play a role in the absorption in Au targets, where the difference between p- and s-polarized pulses was found to be significant for low intensities in Figure 3. Herewith we consider Brunel absorption and a counteracting effect, the light pressure which acts against the plasma expansion [20]. According to Wilks and Kruer [11] the Brunel-absorption depends only on the oscillation velocity of electrons in the laser field which drags them out and in to the solid. The maximum oscillation velocity can be derived from the ponderomotive force equation as
where e and m denote the electron charge and mass, respectively, and I is the incident intensity. This velocity corresponds to 11.5 keV hot electron temperature. We can now assume that the plasma will expand outside of the solid with a sound velocity determined by the hot electron temperature. On the other hand the light pressure pushes it back toward the solid surface, and therefore the expansion velocity is
Here Z is the charge state, Te is the hot electron temperature, M the atomic mass, p the light pressure, ρ the density, and δ is the assumed scale length. Clearly the first term will dominate with a contribution of ~7 × 105 ms−1 whereas the second term is about 105 ms−1 depending on the parameters therein (e.g., boron, p ≈ 330 Mb, τ = 0.5τL and a scale length of 0.2λ). Thus, the final result is in close agreement with the observed velocity, and Brunel absorption may be an important mechanism of absorption. We must keep in mind that after the initial steplike profile the plasma will expand, and therefore the role of Brunel absorption may decrease, and the above mentioned resonance- and collisional absorption may play a more important role. On the other hand, as was observed earlier [21] the pressure term in Equation (4) will contain temporally increasing contribution from ponderomotive pressure, which will not be sufficient to stop the outward propagation for these intensities. On the other hand this may contribute to the profile steepening, keeping the plasma gradient steep around the critical density. Similarly to Teubner et al. [22] we cannot explain the observed high absorption for the s-polarized radiation. A possibility might be the earlier observed surface rippling [20] which might mix the polarizations on the target. In order to get more insight, 2D simulations will be needed.
Laser plasma experiments were carried out with 700 fs KrF laser pulses up to >1018 Wcm−2 intensities using the high contrast (1012) laser pulses for which the Fourier filtering technique was applied. The intensity of the ASE prepulse of nanosecond duration was well below 107 Wcm−2, consequently the main pulse could hit a steep initial density profile. Strong and increasing absorption was observed with increasing intensity both for the high-Z Au and for the low-Z B targets, which was found to be only slightly higher for p-polarized radiation. Doppler blue-shift and broadening of the initially chirped laser pulse refers to a plasma propagation moving away from the surface. Whereas, the Doppler shift was 0.6 nm as compared with the previous results of not higher than 0.2 nm, the derived velocity with our longer pulse duration was more than 5 × 105 ms−1, which is higher than observed previously, corresponding to a maximum acceleration of ~2 × 1018 ms−2.
Simple model estimations show that Brunel absorption may be one of the dominant accelerating mechanisms, but resonance absorption and inverse Bremsstrahlung must be also taken into account for understanding the high absorption and the strong acceleration when ponderomotive and light pressure effects are also taken into account. For a better understanding our observations 2D PIC simulations will be needed.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
ZK carried out the interaction experiments. BG and SS provided and controlled the high contrast KrF laser pulses. IF conceived the experiments and interpreted the experimental data with ZK. All authors contributed to the article and approved the submitted version.
This work has been carried out within the framework of the EUROfusion Consortium and has received funding from the Euratom research and training programme 2014–2018 and 2019–2020 under grant agreement 633053. The views and opinions expressed herein do not necessarily reflect those of the European Commission. The support of the Hungarian Scientific Research Fund—OTKA113222 and the European Social Fund EFOP-3.6.2-16-2017-00005—Ultrafast physical processes in atoms, molecules, nanostructures, and biological systems as well as the support Hungary grant TUDFO/47138-1/2019-ITM FIKP of Ministry of Innovation and Technology was also acknowledged.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The authors are indebted to Prof. Heinrich Hora who gave a strong motivation to carry out the experiments. The technical assistance of Krisztián Bali was acknowledged this way.
1. Ziener CH, Foster PS, Divall E, Hooker C, Hutchinson MHR, Langley AJ, et al. Specular reflectivity of plasma mirrors as a function of intensity, pulse duration, and angle of incidence. J Appl Phys. (2003) 93:768–70. doi: 10.1063/1.1525062
2. Hora H, Lalousis P, Moustaizis S. Fiber ICAN laser with exawatt-picosecond pulses for fusion without nuclear radiation problems. Laser Part Beams. (2014) 32:63–8. doi: 10.1017/S0263034613000876
3. Hora H, Eliezer S, Nissim N, Lalousis P. Non-thermal laser driven plasma-blocks for proton-boron avalanche fusion as direct drive option. Matter Radiat Extremes. (2017) 2:177–89. doi: 10.1016/j.mre.2017.05.001
4. Sauerbrey R. Acceleration in femtosecond laser-produced plasmas. Phys Plasmas. (1996) 3:4712–6. doi: 10.1063/1.872038
5. Földes IB, Bakos JS, Gál K, Juhász Z, Kedves MÁ, Kocsis G, et al. Properties of high harmonics generated by ultrashort UV laser pulses on solid surfaces. Laser Phys. (2000) 10:264–9.
6. Lalousis P, Földes IB, Hora H. Ultrahigh acceleration of plasma by picosecond terawatt laser pulses for fast ignition of fusion. Laser Part Beams. (2012) 30:233–42. doi: 10.1017/S0263034611000875
7. Szatmári S, Dajka R, Barna A, Gilicze B, Földes IB. Improvement of the temporal and spatial contrast of high-brightness laser beams. Laser Phys Lett. (2016) 13:075301. doi: 10.1088/1612-2011/13/7/075301
8. Milchberg HM, Freeman RR. Expansion-induced Doppler shifts from ultrashort-pulse laser-produced plasmas. Phys Rev A. (1990) 41:2211–4. doi: 10.1103/PhysRevA.41.2211
9. Kalashnikov MP, Nickles PV, Schlegel TH, Schnuerer M, Billhardt F, Will I, Sandner W, et al. Dynamics of laser-plasma interaction at 1018 W/cm2. Phys Rev Lett. (1994) 73:260–3. doi: 10.1103/PhysRevLett.73.260
10. Liu X, Umstadter D. Competition between ponderomotive and thermal forces in short-scale-length laser plasmas. Phys Rev Lett. (1992) 69:1935–8. doi: 10.1103/PhysRevLett.69.1935
11. Wilks SC, Kruer WL. Absorption of ultrashort, ultra-intense laser light by solids and overdense plasmas. IEEE J. Quant Electron. (1997) 33:1954–68. doi: 10.1109/3.641310
12. Ping Y, Shepherd R, Lasinski BF, Tabak M, Chen H, Chung HK, et al. Absorption of short laser pulses on solid targets in the ultrarelativistic regime. Phys Rev Lett. (2008) 100:085004. doi: 10.1103/PhysRevLett.100.085004
13. Ping Y, Kemp AJ, Divol L, Key MH, Patel PK, Akli KU, et al. Dynamics of relativistic laser-plasma interaction on solid targets. Phys Rev Lett. (2012) 109:145006. doi: 10.1103/PhysRevLett.109.145006
14. Singh PS, Cui YQ, Adak A, Lad AD, Chatterjee G, Brijesh P, et al. Contrasting levels of absorption at intense femtosecond laser pulses by solids. Sci Rep. (2015) 5:17870. doi: 10.1038/srep17870
15. Gilicze B, Homik Z, Szatmári S. High-contrast, high-brightness ultraviolet laser system. Opt Express. (2019) 27:17377–86. doi: 10.1364/OE.27.017377
16. Szatmári S, Schäfer FP. Simplified laser system for the generation of 60 fs pulses at 248 nm. Opt Commun. (1988) 68:196–202. doi: 10.1016/0030-4018(88)90184-8
17. Gilicze B, Dajka R, Földes IB, Szatmári S. Improvement of the temporal and spatial contrast of the nonlinear Fourier-filter. Opt Express. (2017) 25:20791–7. doi: 10.1364/OE.25.020791
18. Kovács Z, Bali K, Gilicze B, Szatmári S, Földes IB. Reflectivity and spectral shift from laser plasmas generated by high-contrast, high-intensity KrF laser pulses. Phil Trans Roy Soc. (2020) A378:2020043. doi: 10.1098/rsta.2020.0043
19. Kormin D, Borot A, Ma G, Dallari W, Bergues B, Aladi M, et al. Spectral interferometry with waveform-dependent relativistic high-order harmonics from plasma surfaces. Nat Commun. (2018) 9:4992. doi: 10.1038/s41467-018-07421-5
20. Rácz E, Földes IB, Kocsis G, Veres G, Eidmann K, Szatmári S. On the effect of surface rippling on the generation of harmonics in laser plasmas. Appl Phys B. (2006) 82:13–8. doi: 10.1007/s00340-005-2039-3
21. Teubner U, Uschmann I, Gibbon P, Altenbernd D, Förster E, Feurer T, et al. Absorption and hot electron production by high intensity femtosecond uv-laser pulses in solid targets. Phys Rev E. (1996) 54:4167–77. doi: 10.1103/PhysRevE.54.4167
Keywords: laser plasma, subpicosecond, reflectivity, ponderomotive force, vacuum heating
Citation: Kovács Z, Gilicze B, Szatmári S and Földes IB (2020) Large Spectral Shift of Reflected Radiation From Laser Plasmas Generated by High Contrast KrF Laser Pulses. Front. Phys. 8:321. doi: 10.3389/fphy.2020.00321
Received: 06 April 2020; Accepted: 13 July 2020;
Published: 11 September 2020.
Edited by:
Noaz Nissim, Soreq Nuclear Research Center, IsraelReviewed by:
Vladimir D. Zvorykin, The Lebedev Physical Institute (RAS), RussiaCopyright © 2020 Kovács, Gilicze, Szatmári and Földes. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: István B. Földes, Zm9sZGVzLmlzdHZhbkB3aWduZXIuaHU=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.