High-Energy Charged Particles for Spatially Fractionated Radiation Therapy

Spatially fractionated radiotherapy (SFRT) offers a gain in normal tissue sparing with respect to standard seamless irradiations. The benefits of SFRT may be further enhanced by replacing the commonly used photon beams by charged particles. Along this line, proton SFRT has already shown a significant widening of the therapeutic window for radioresistant tumors in preclinical studies. The goal of this work was to investigate whether the use of superior energies as compared to the clinical ones, as well as heavy ions could lead to a further improvement of SFRT. New facilities such as FAIR, RAON, or some others associated with the International Biophysics collaboration will be able to provide very intense high-energy ion beams, enabling the experimental evaluation of the Monte Carlo simulations reported in this work. Our results indicate that proton SFRT could benefit from the use of higher beam energies ($\tilde{1}$ GeV). Concerning heavy ions, such as carbon or neon, the main advantage would be the possible theragnostic use. Biological experiments are needed to validate these results, and they will be the subject of future experimental proposals at those new facilities.

1. Introduction

Spatial fractionation of the dose, such as in minibeam radiation therapy (MBRT), has already proven its capacity to spare normal tissues [1–4]. Spatially fractionated radiotherapy (SFRT) has been mainly explored using photons, such as in LINAC-based Grid therapy [2] or synchrotron micro and minibeam radiation therapies [1, 3–6].

However, SFRT may be further improved by partnering its benefits with the advantages of charged particles for therapy [7, 8]. Recently, proton minibeam radiation therapy (clinical beams) has demonstrated a net gain in normal tissue sparing [9–12]. An equivalent or superior tumor control than with standard seamless irradiations was observed after pMBRT [12, 13]. This holds even in cases where highly heterogeneous dose distributions were delivered.

In contrast to the flat dose profiles in conventional radiotherapy, the profiles in SFRT follow a pattern of areas of high dose (peaks) followed by areas of low dose (valley). The ratio between peak and valley doses, the so-called peak-to-valley-dose ratio (PVDR), is considered to be an important dosimetric parameter in SFRT, as it plays an important role in the biological response. Different studies suggest that high PVDR with low valleys favor tissue sparing, while low PVDR with high valleys increase tumor control [14].

Dosimetry evaluations in heavy ions MBRT have shown favorable dose distributions for normal tissue sparing [8, 15]. Indeed very high peak-to-valley dose ratios and minimal contribution of high linear energy transfer (LET) nuclear fragments to the valley regions, which are believed to be responsible for normal tissue sparing [14], were obtained. Additionally, the possible gain in normal tissue sparing of MBRT might allow a renewed use of very heavy ions (Ne, Ar, and Si) for the treatment of hypoxic tumors [15], which remains one of the main challenges in radiation therapy. Heavy ions, such as Neon, were used in the past, demonstrating a high capacity for hypoxic cell tumor killing [16, 17]. However, their use was discontinued due to important side effects [17]. The first biological experiments performed using Ne MBRT at HIMAC (NIRS-QST) seem to validate our hypothesis, namely, a gain in normal tissue sparing thanks to the combination of Ne ions with MBRT [18].

The advent of new accelerators, able to provide very intense high energy (up to 10 GeV/A) ions beams, opens up for new possibilities for the exploration of charged particles MBRT. This is the case of facilities such as FAIR (Facility for Antiproton and Ion Research, www.gsi.de), Rare Isotope Science Project (RAON, https://www.ibs.re.kr), or some others associated with the recently created International Biophysics collaboration (IBC). In particular, the use of high-energy beams (around 1 GeV/A) would reduce multiple coulomb scattering (MCS), which could lead to higher PVDR in normal tissues than with clinical-relevant energies. The resulting narrow penumbras could make the beams to act as “remote scalpels” for radiosurgery applications [7, 19]. This could find important applications in the treatment of non-cancer diseases, such as arteriovenous malformations or some types of epilepsy [20]. In addition, the reduction of MSC would allow the use of narrower beams, while keeping a good ratio between dose deposited in the trajectory of the primary beam and scattered dose. Moreover, high-energy beams may enable a theragnostics use, as the exiting beam could be employed for imaging purposes. The high beam intensity of those new facilities might allow to combine SFRT and FLASH therapy [21]. Very high dose rates will also open new possibilities in SFRT: moving targets (such as lung) could safely start to be considered without the risk of jeopardizing the spatial fractionation of the widows.

Indeed, the use of relativistic protons was already proposed for plateau (non-Bragg peak) stereotactic radiosurgery in the late 70s [22]. More than a thousand of patients have been treated at PNPI synchrocyclotron with 1GeV for image-guided stereotactic radiosurgery (IGSpRS) [23].

The aim of this dosimetry study was to assess whether the combination of high energy charged particles beams and MBRT could offer an advantage in SFRT. A very first evaluation of the use of high energy (1 GeV) protons for SFRT was reported by Prezado et al. [7]. This new investigation aims at completing that first study and extend it toward heavy ions, with the goal of evaluating the interest of this new approach.

2. Materials and Methods

Monte Carlo simulations were performed to evaluate the dose distributions of high energy protons, ¹²C and ²⁰Ne minibeam radiation therapy.

2.1. Monte Carlo Simulations

The GEANT4 (GEANT4.10.3)-based GATE (release 8.0) toolkit was employed. One of the recommended physics list for hadrontherapy by the GATE collaboration was employed [24]. The so-called QGSP₋BIC₋HP builder and standard option 3 were used to describe the hadronic and electromagnetic interactions, respectively. A range cut of 20 μm was considered for protons, electrons, positrons, and gammas. Values of 75 and 85.7 eV were used for the ionization potentials in water and air, respectively [24, 25].

The beams impinged into either (i) a cubic-shaped water phantom (20 x 20 x 500 cm) or (ii) computed tomography (CT) DICOM images of anonymized human patients, both embedded in air. The method described in [26] was followed to convert Hounsfield Units (HU), i.e., voxel values, into materials, for dose calculations.

Particle sources were modeled by means of General Particle Source (GPS), which considers a Gaussian shape for the energy spectrum. Three irradiation configurations were created: broad beam, single minibeam, and minibeam arrays. Different beam energies of 400, 700, and 1,000 MeV/u were used (maximum range of 3.25 m water equivalent for the highest proton energy). Energy spreads of 0.1% MeV of total energy were simulated in all cases. A realistic beam divergence of 3 mrad was assumed.

The dimensions of the beam source were 2 x 2 cm in the case of broad beam irradiations and 50 μm, 600 μm, and 1 mm x 2 cm in the case of MBRT. The narrowest beam width is the one used in Microbeam Radiation Therapy [1]. Beam widths of 600 μm are the most commonly used in MBRT studies. We decided to evaluate thicker beams as well, those around 1 mm, as they still provide a significant normal tissue sparing [12]. The sources were placed at 7 cm far away from the phantom. The minibeam arrays consisted of five minibeams with a center-to-center distances (ctc) of 1,200 μm (commonly used in MBRT) and 3,500 μm, which has been shown to minimize the contribution of heavy nuclear fragments to the valleys [8].

Doses were recorded by using the GATE dose-actor. They were tallied in bins of one tenth of the minibeam widths in each case, 2 mm, and 1 mm in the lateral, vertical, and beam directions, respectively. Depth dose profiles (PDD) and peak-to-valley dose ratios (PVDR) were assessed over the tally bin size along the beam transversal axis by taking the doses in the central peak and its adjacent valley. The statistical uncertainty in dose in each voxel was calculated as reported in [27].

The total number of primary particles simulated was 10⁸, leading to a global uncertainty of less than 1%.

3. Results

This section reports on the calculated dose distributions of both broad beam and MBRT irradiation with high energy proton, carbon, and neon beams. Dose are recorded along the tallies of the central axis.

3.1. Broad-Beam Dose Distributions

Figure 1 upper-left shows the depth dose curves in water for 2 x 2 cm large proton beams with energies going from 400 MeV to 1 GeV. In contrast to the dose deposition in depth with clinically relevant energies, there is a continuous decrease in the dose deposited in depth up to the Bragg peak [28]. The ratio between the dose deposited at the entrance and at the Bragg Peaks increases with the beam energy. Figure 1 upper-right to lower-right depicts the proportion of secondary particles as a function of depth for the three energies (400, 700, and 1,000 MeV) considered. The trend is the same for all the three energies: secondary nuclear products and electrons amount for roughly 10% of the total dose, being higher the contribution of the first ones. Gamma rays contribution is several orders of magnitude lower than other ones.

FIGURE 1

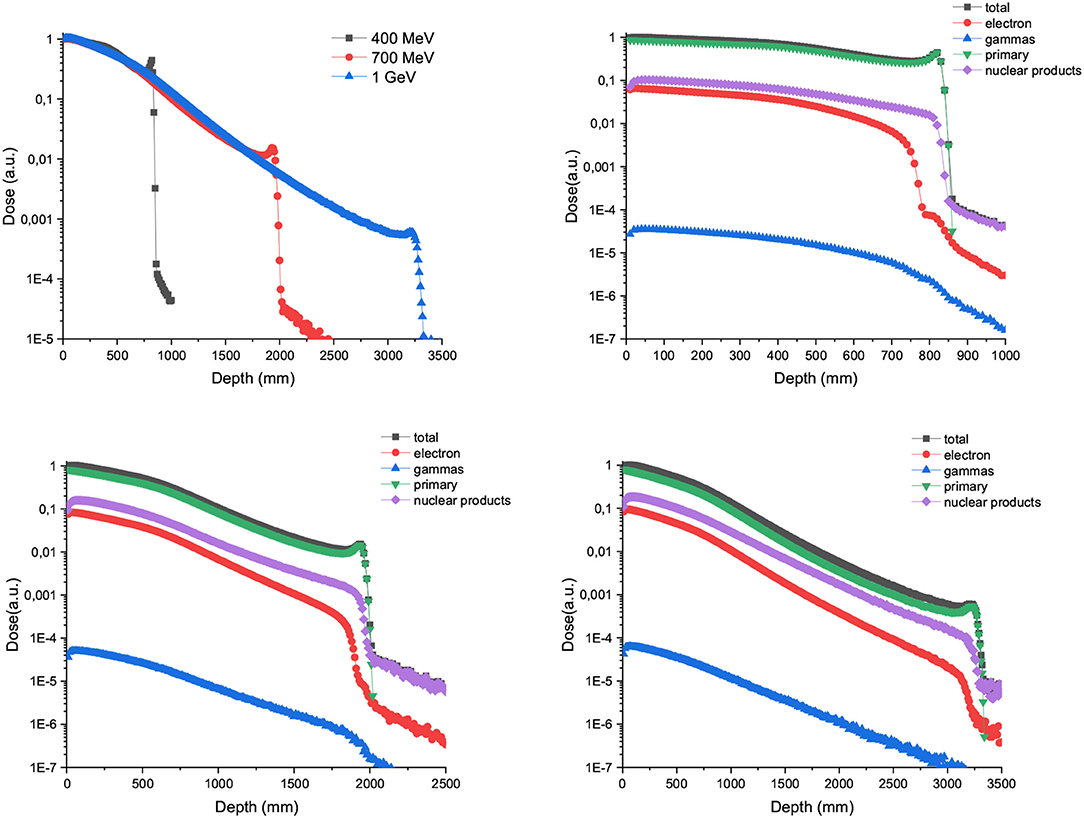
Figure 1. Left panel in the upper row: Depth dose curves resulting from broad-beam irradiations with 400, 700, and 1,000 MeV proton beams. The plots in the upper row right column and the lower row show the contribution of the secondary particles to the total dose for the three energies evaluated.

Figure 2 shows the contribution of both primary and secondary particles to the total dose in the case of 700 and 1,000 MeV/u of Carbon and Neons beams. The dose deposited by the secondary nuclear products increases with the atomic number of the ion at shallow depths and can overpass the dose contribution of the primary ions for the higher energies (1,000 MeV/u).

FIGURE 2

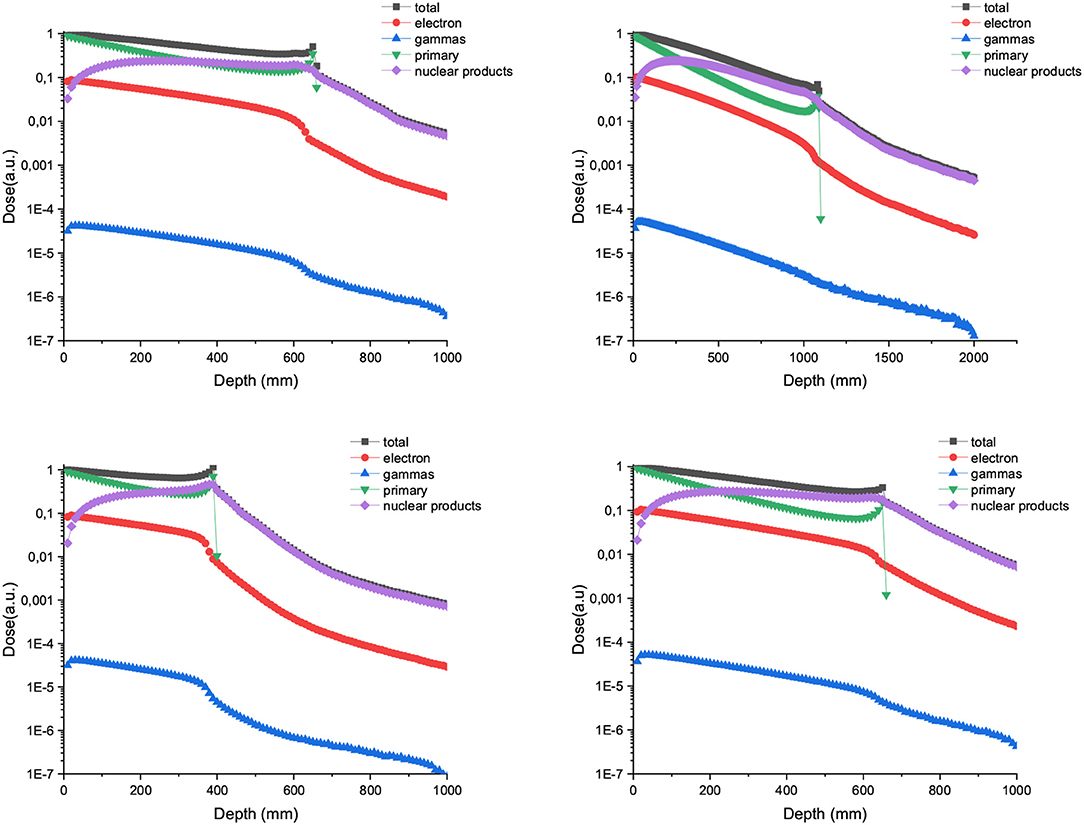
Figure 2. Relative dose deposition of primary and secondary particles to the total dose as a function of depth when a water tank is irradiated with 700 (left) and 1,000 MeV/u (right) carbon (up) and neon ions (bottom) broad beams.

3.2. Minibeam Radiation Therapy

Figure 3 upper-row shows the depth dose curves of one single 1,000 MeV proton minibeam (50 μm, 600 μm, and 1mm-wide beam). On the right side, the depth dose curves zoomed in the range from 0 to 160 mm (approximative lateral length of a human head [29]) are depicted. In the case of 50 μm-wide beams, the important lateral scattering results in a rapid fall off of the deposited dose after a few centimeters. Consequently, those narrow beams were deemed not to be suitable for charged particle SFRT. The curves are almost flat for the thicker beam widths evaluated (600 μm and 1 mm) up to 7 cm in depth. From that depth on, the depth dose curve decreases rapidly in the case of 600 μm-wide beam, helping to reduce the dose deposited upstream. This could be an interesting feature for the treatment of brain tumors. Central and lowest rows depict the depth dose curves for 700 and 1,000 MeV/u C and Ne ions, respectively. No important difference was observed for any of the configurations in the first 16 cm depth. In contrast, a more rapid fall off in the dose as a function of depth is observed for C and Ne in comparison with protons. This is a result of a more important attenuation in depth due to a higher rate of nuclear fragmentation [30].

FIGURE 3

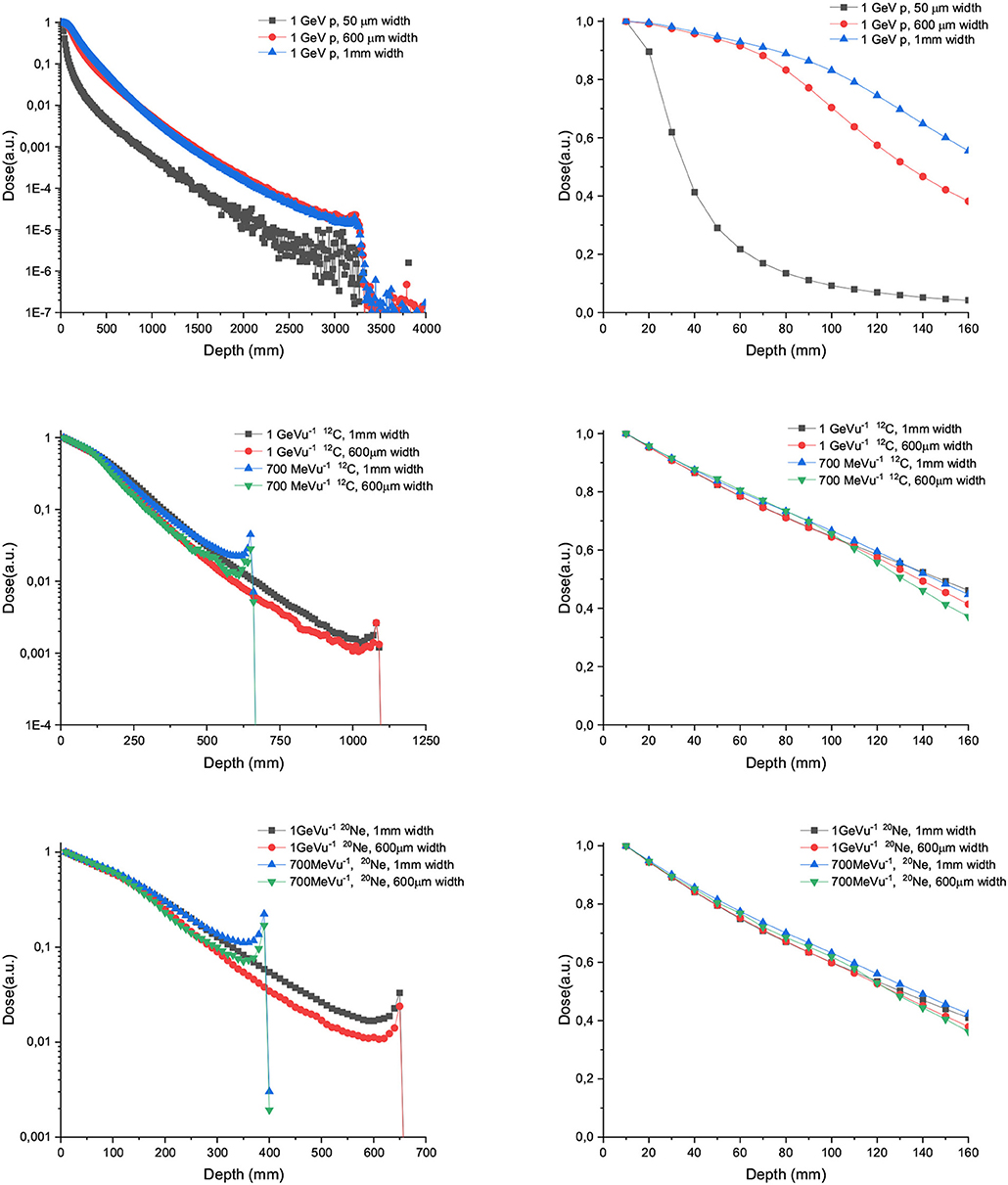
Figure 3. Depth dose curves for 50 μm, 600 μm, and 1 mm-wide 1,000/u GeV protons (upper row), carbon (central row), and Neon (lower row) beams in water tank. The left column shows the full range, while the right one depicts only the first 16 cm.

Figure 4 shows the depth dose curves for the central beam of arrays of proton minibeams of different energies, widths and ctc. The three rows corresponds to the three energies evaluated: 400 MeV (uppermost row), 700 MeV (central row), and 1,000 MeV (lowest row). The dose deposition along the total beam range and the first 16 cm depth are shown in the left and right columns, respectively. The curves are flatter with respect to the case of one unique minibeam. The larger the width and ctc of the array, the deeper the distance before the dose deposition starts decreasing rapidly. Figure 5 shows the contribution of the secondary products to the valley doses. The main contribution in the first 20 cm are nuclear products, particularly the secondary protons for all the beam energies evaluated.

FIGURE 4

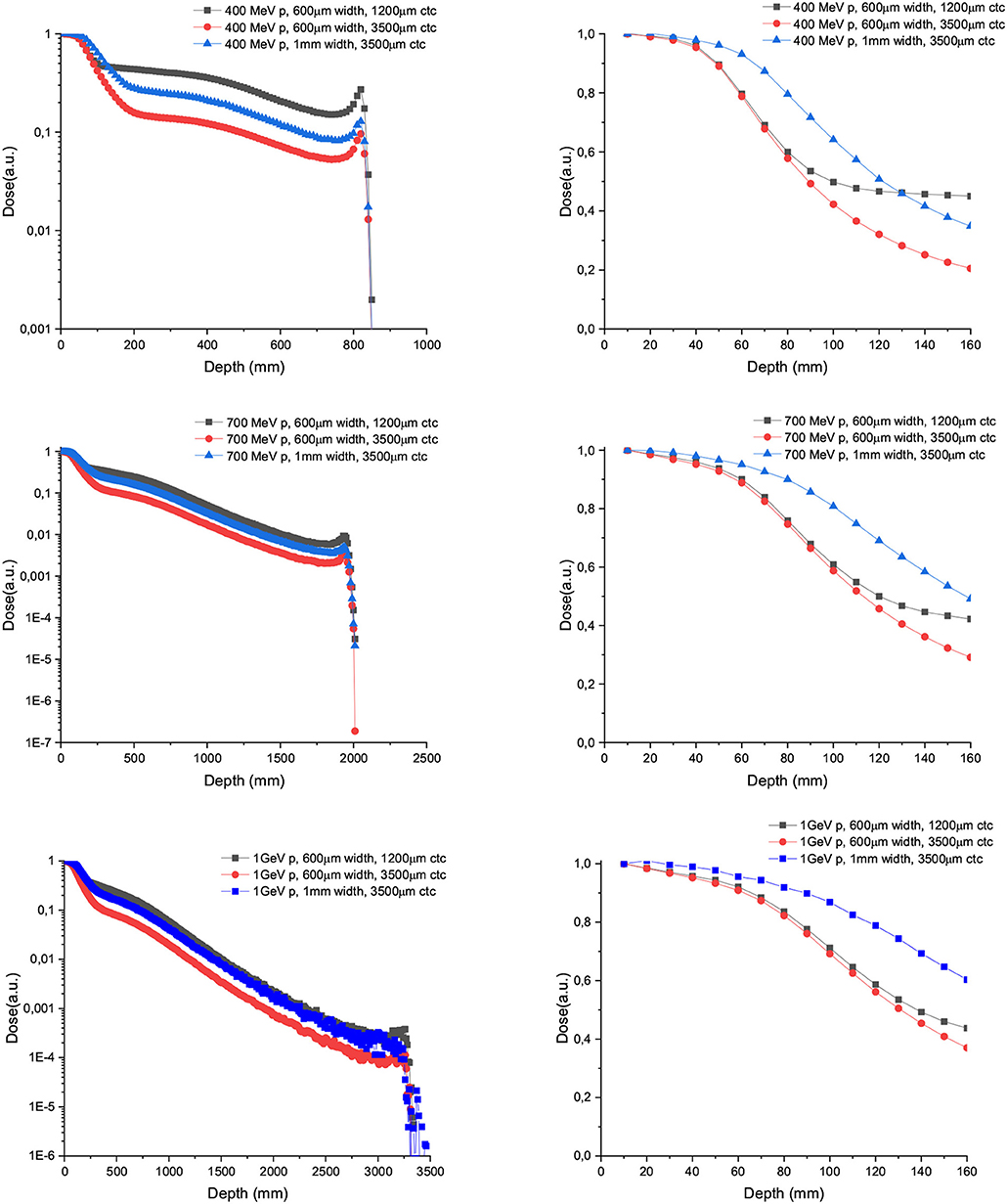
Figure 4. Depth dose curves for the central minibeam of arrays of 600 μm and 1 mm-wide protons of 400 (upper row), 700 (central row), and 1,000 MeV (lower row) minibeams in water tank. Two ctcs are compared. The left column shows the full range, while the right one depicts only the first 16 cm.

FIGURE 5

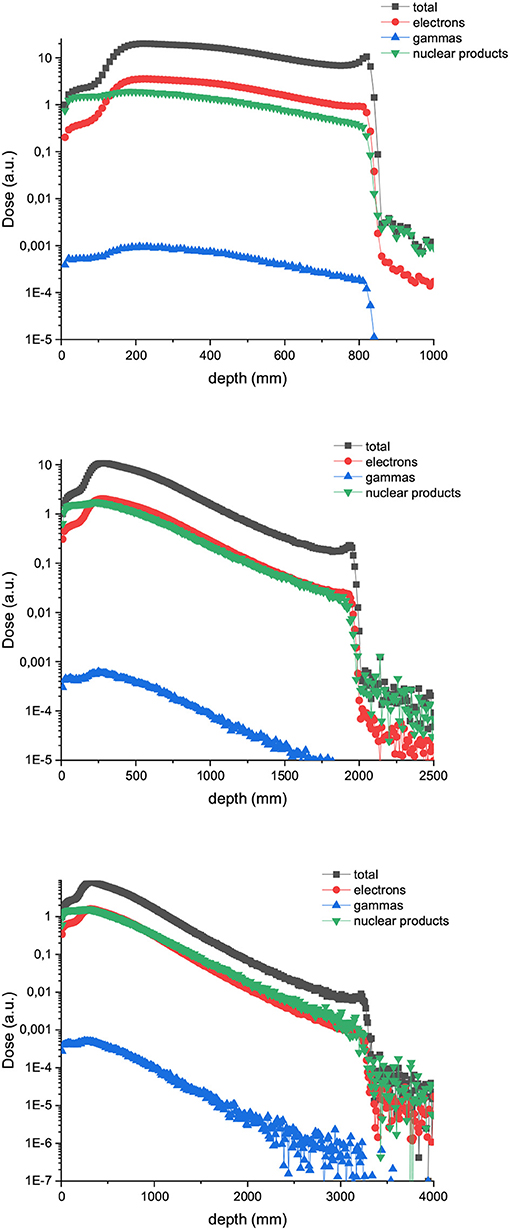
Figure 5. Composition of the valley doses in the case of 400 (up), 700 (middle), and 1,000 MeV (down) proton minibeams.

Figure 6 shows the PVDR values for the proton minibeams for the same aforementioned configurations. The highest PVDR are achieved with 600 μm-wide beams and ctc of 3,500 μm (middle), being around five times higher than the PVDR for a ctc of 1,200 μm (down). For this later case, a homogenization is reached at around 10 cm depth. Intermediate values are obtained in the case of one array of beams 1 mm wide. PVDR values are higher than the ones used previously in preclinical studies [11–13], and which had shown a net gain in normal tissue tolerances. Therefore, an even higher sparing of normal tissue might be expected. The PVDR values are similar or even lower than the values that could be obtained with magnetically focused 100 MeV proton beams [31]. The lower the beam energy is, the higher the PVDR in the first centimeters. The reason is that at these high beam energies, the stopping power follows an inverse relation with the beam energy (www.nist.gov). Consequently, the dose deposition by the primary beam follows an inverse relationship with the beam energy. In addition, the secondary products are more forward directed depositing their energy at deeper depths. This results in smaller peak doses at shallower depths for the highest energies. Since the valley doses are very small, the PVDR is dominated by the peaks at this range of beam energies.

FIGURE 6

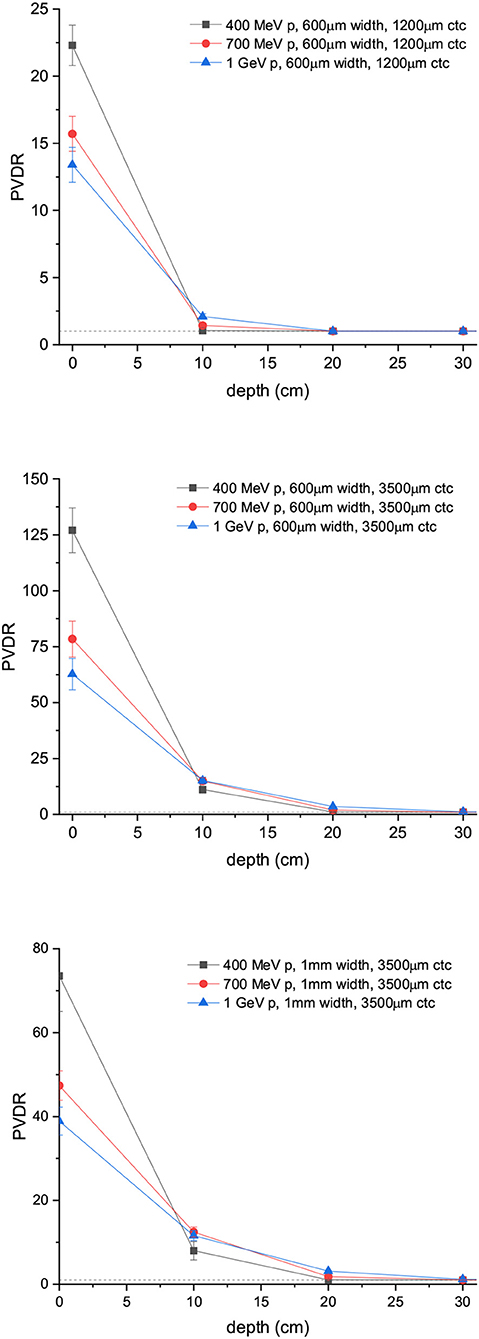
Figure 6. PVDR values for arrays of protons minibeams are shown: 600 μm-wide beams and 1,200 μm ctc (up); 600 μm-wide beams and 3,500 μm ctc (middle); 1 mm-wide beams and 3,500 μm ctc (down).

Figure 7 depicts the depth dose curves for the central minibeam in the case of C and Ne ions of 700 and 1,000 MeV/u. The beam width and ctc considered were 600 and 3,500 μm. Figure 8 shows the contribution of nuclear products, electrons and gammas to the valley doses for 700 MeV carbon and neon 600 μm-wide beams. Nuclear products are the dominant ones at almost all depths, which is in contrast to trends observed at lower beam energies [15].

FIGURE 7

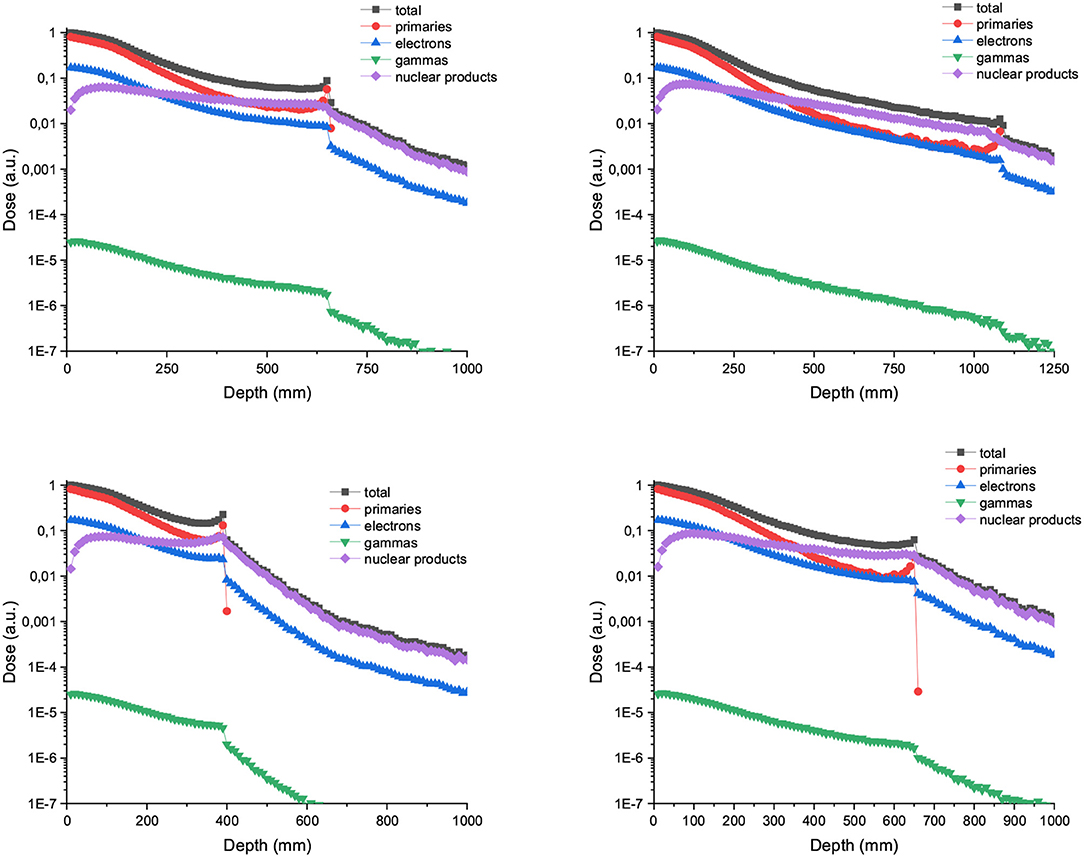
Figure 7. (Up) PDD curve for 700 (left) and 1,000 MeV/u (right) Carbon minibeams of 600 μm witdth and 3,500 μm ctc. (Bottom) PDD curve for 700 (left) and 1,000 MeV/u (right) Neon minibeams of 600 μm witdth and 3,500 μm ctc.

FIGURE 8

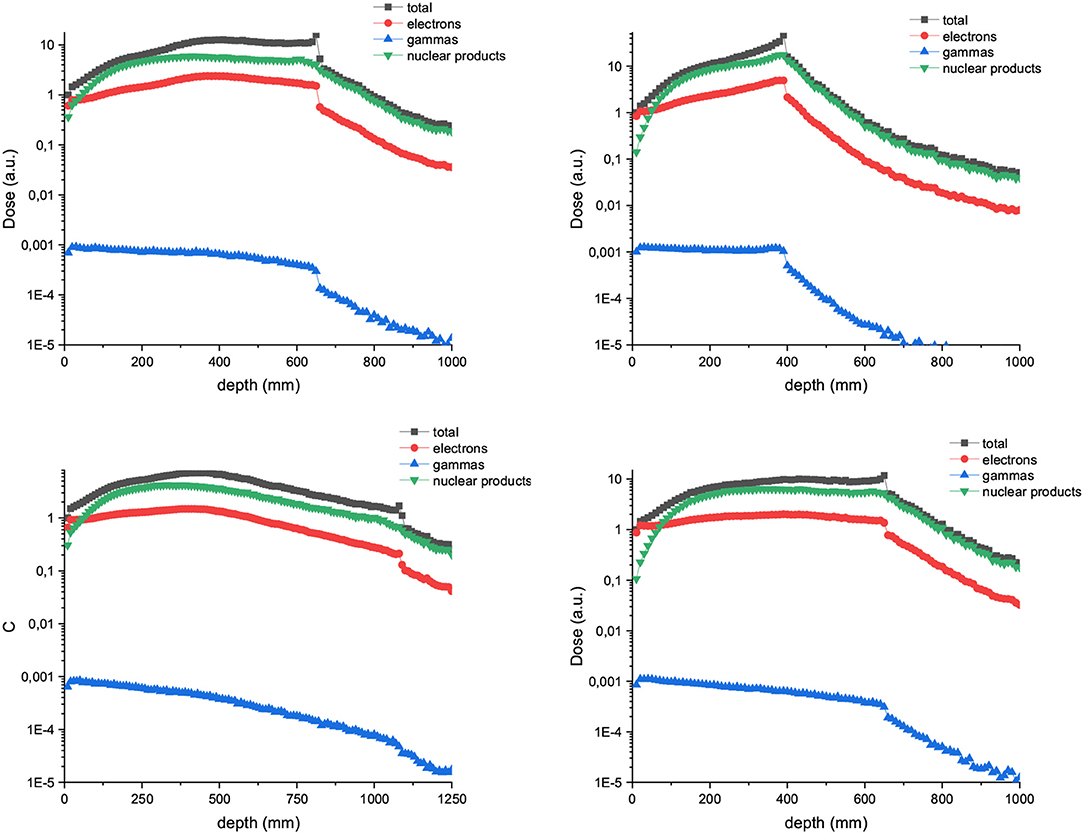
Figure 8. Composition of the valley doses in the case of arrays of 600 μm witdth and 3,500 μm ctc carbon (left) and neon (right). The beam energy is 700 MeV/u in the upper row and 1,000 MeV/u in the lower row.

PVDR values for Carbon and Ne MBRT are a factor 2 or higher than in the case of protons, with Ne ions offering the highest PVDR at the entrance (See Figure 9). Figure 10 showing how the peak and valley doses vary as a function of the ion and beam energy (same number of primary particle simulates) illustrates why the PVDR decreases with beam energy in the first centimeters.

FIGURE 9

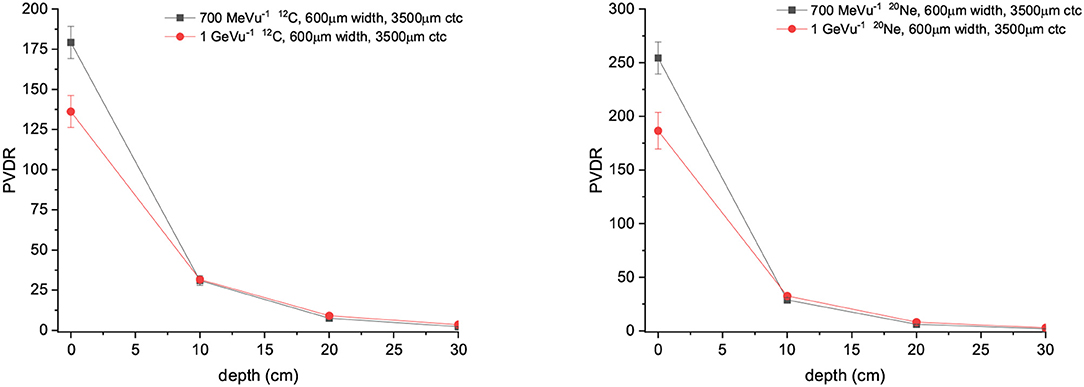
Figure 9. (Left) PVDR values for Carbons minibeams of 600 μm witdth and 3,500 μm ctc. (Right) PVDR for Neons minibeams of 600 μm witdth and 3,500 μm ctc.

FIGURE 10

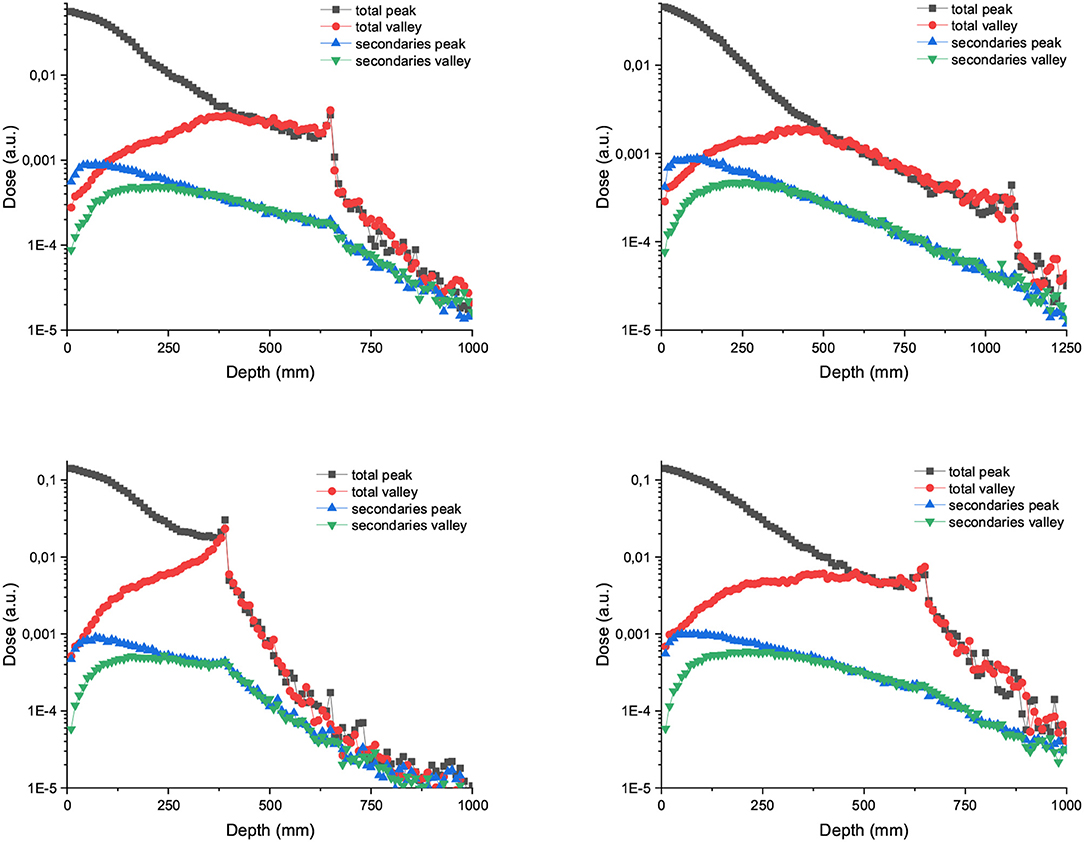
Figure 10. Left: Peak and valley doses in depth and distribution of secondaries for arrays of 600 μm width and 3,500 μm carbon (up) and neon (down) minibeams. The beam energies are 700 MeV/u in the left column and 1,000 MeV/u in the right column.

Finally, to illustrate a possible patient's scenario, we have evaluated the dose distribution in an anonymized human head anatomy. We have simulated an irradiation with 1,000 MeV/u proton MBRT. The beam width and ctc were 600 and 3,500 μm, respectively (See Figure 11). The depth dose curve shows that the dose deposition in the peak regions is almost constant in depth. The spatial fractionation can be maintained at all depths.

FIGURE 11

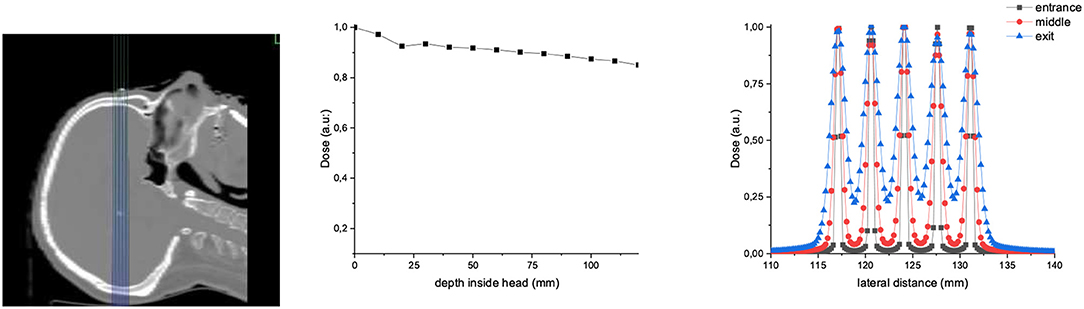
Figure 11. Dose distributions in an anonymized human patient irradiated with 1,000 MeV/u proton MBRT (600 μm width and 3,500 μm ctc). Two-dimensional dose distributions, PDD, and lateral dose profiles at different depths are shown on the left, middle, and right, respectively.

4. Discussion

Radiotherapy, despite being in the forefront of cancer treatments, continues to be limited by the tolerances of normal tissues. Different strategies based on distinct dose delivery methods, such as SFRT or FLASH therapy [32], offer promise to overcome that limitation. This would allow widening the therapeutic window for radioresistant tumors or pediatric cancers.

SFRT has been mainly explored with photons, both with medical LINACs [2] and at large synchrotrons [3]. The implementation at LINACs with MV photons suffers from important lateral scattering resulting in high valley doses, and a low flux, which results in the need of using large (around 1 cm²) beam sizes. On the other hand the beamtime at large synchrotrons is limited, and the penetration depth of the low-energy synchrotron x-rays provided is short. Charged particle SFRT has been proposed as a promising alternative [7] to fully profit from the advantages of the spatial fractionation of the dose. Among the main advantages, one can cite the possibility of achieving a homogenous dose coverage of the target with one unique array or the fact of having a negligible (or inexistent) dose deposition after the Bragg Peak. Biological experiments with clinically relevant energies have already shown the gain in normal tissue sparing provided by charged particles SFRT [10, 11, 18].

New accelerators, such as FAIR or Raon, will offer intense and high-energy beams (up to 10 Gev/u). The aim of this work was to investigate whether a further improvement in SFRT can be obtained by using those new beams. The rational was the possible benefit of the reduction of MSC for high energies. In addition, the use of higher beam energies (around 1 GeV/u) might enable theragnostic applications as the same beam can be used for treatment and online imaging. The ultrahigh dose rates that will be available would allow partnering FLASH and charged particle SFRT. This might allow using MBRT for moving targets like lung, today restricted due to possible blurring of the minibeam patterns due to respiratory motion.

Concerning protons, our study shows that energies slightly higher than the ones used in clinical practice (400 MeV) for protons offer very interesting features: an almost flat peak dose deposition in depth in the first centimeters and a rapid falloff after 7 cm depth for beams 1 mm wide (Figure 4). This could be of interest for a theragnostic treatment of brain tumors. Indeed a higher tumor-to-entrance ratio than with clinical energies could be obtained. Thanks to the rapid falloff after the first centimeters, the dose deposited in the contralateral hemisphere will be relatively low, and the existing beam could be used for image guidance. It should also be highlighted that energies up to 400 MeV could already be produced in some ion beam therapy centers. This energy leads to the highest PVDR values at shallow depths out of the three energies evaluated. Beam widths of 600μm combined with 700 or 1,000 MeV follow the same pattern just described. In all cases, an homogenization can be obtained at around 10 cm of depth with a ctc of 1,200 μm. For larger ctc distances, crossfiring, or interlacing several arrays could be used as a strategy to increase the valley dose in the tumor. One of the advantages of increasing the energy in proton minibeams is that the depth dose curve of each minibeam is flat in the first centimeters in comparison with that obtained with 100–200 MeV protons minibeams. This would result in a more favorable tumor to entrance dose ratio.

Higher PVDR are obtained with Carbon and Neon than with protons at all depths. The higher capacity of those ions to activate the immune system might compensate for those larger PVDR in the tumor with respect to protons. The PVDR are not significantly higher than the ones obtained in previous works with clinical relevant energies [15]. The secondary nuclear products represent a larger contribution to the valley doses than at currently clinically relevant energies [15].

Consequently, to increase the beam energy in proton SFRT seems to provide some advantages from dosimetric point of view, while in the case of heavier ions, such as carbon, no clear advantage could be extracted from this dosimetry evaluation other than a theragnostic use.

Indeed, 600 μm proton minibeams of 400 MeV lead to similar PVDR than C ions of 1 GeV/u in the phantom entrance (127 vs. 136 respectively), while a more homogeneous dose distribution could be obtained in the target. The valley doses will be less impacted by high-LET nuclear fragments contributions. Therefore, a further optimization in SFRT could be achieved by using high energy submillimetric proton beams. Biological experiments are needed to validate these results and they will be the subject of future experimental proposals at those new facilities.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

CG performed the Monte Carlo simulations and data analysis. YP conceived the project. CG and YP wrote the manuscript. All authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Calculation time was granted at MareNostrum Barcelona Supercomputing Center from the Partnership for Advanced Computing in Europe [PRACE Project Access Call 19th (proposal number 2019204903)] and the Centre de Calcul de lIN2P3 (CCIN2P3).

References

1. Slatkin DN, Spanne P, Dilmanian FA, Gebbers JO, Laissue JA. Subacute neuropathological effects of microplanar beams of x-rays from a synchrotron wiggler. Proc Natl Acad Sci USA. (1995) 92:8783–7. doi: 10.1073/pnas.92.19.8783

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Mohiuddin M, Fujita M, Regine WF, Megooni AS, Ibbott GS, Ahmed MM. High-dose spatially-fractionated radiation (GRID): a new paradigm in the management of advanced cancers. Int J Radiat Oncol Biol Phys. (1999) 45:721–7. doi: 10.1016/S0360-3016(99)00170-4

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Dilmanian FA, Zhong Z, Bacarian T, Benveniste H, Romanelli P, Wang R, et al. Interlaced x-ray microplanar beams: a radiosurgery approach with clinical potential. Proc Natl Acad Sci USA. (2006) 103:9709–14. doi: 10.1073/pnas.0603567103

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Prezado Y, Deman P, Varlet P, Jouvion G, Gil S, Le Clec'H C, et al. Tolerance to dose escalation in minibeam radiation therapy applied to normal rat brain: long-term clinical, radiological and histopathological analysis. Radiat Res. (2015) 184:314–21. doi: 10.1667/RR14018.1

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Bouchet A, Serduc R, Laissue JA, Djonov V. Effects of microbeam radiation therapy on normal and tumoral blood vessels. Phys Med. (2015) 31:634–41. doi: 10.1016/j.ejmp.2015.04.014

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Deman P, Vautrin M, Edouard M, Stupar V, Bobyk L, Farion R, et al. Monochromatic minibeams radiotherapy: from healthy tissue-sparing effect studies toward first experimental glioma bearing rats therapy. Int J Radiat Oncol Biol Phys. (2012) 82:693–700. doi: 10.1016/j.ijrobp.2011.09.013

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Prezado Y, Fois GR. Proton-minibeam radiation therapy: a proof of concept. Med Phys. (2013) 40:031712. doi: 10.1118/1.4791648

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Gonzalez W, Prezado Y. Spatial fractionation of the dose in heavy ions therapy: an optimization study. Med Phys. (2018) 45:2620–7. doi: 10.1002/mp.12902

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Zlobinskaya O, Girst S, Greubel C, Hable V, Siebenwirth C, Walsh DW, et al. Reduced side effects by proton microchannel radiotherapy: study in a human skin model. Radiat Environ Biophys. (2013) 52:123–33. doi: 10.1007/s00411-012-0450-9

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Girst S, Greubel C, Reindl J, Siebenwirth C, Zlobinskaya O, Walsh DWM, et al. Proton minibeam radiation therapy reduces side effects in an in vivo mouse ear model. Int J Radiat Oncol Biol Phys. (2016) 95:234–41. doi: 10.1016/j.ijrobp.2015.10.020

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Prezado Y, Jouvion G, Hardy D, Patriarca A, Nauraye C, Bergs J, et al. Proton minibeam radiation therapy spares normal rat brain: long-term clinical, radiological and histopathological analysis. Sci Rep. (2017) 7:14403. doi: 10.1038/s41598-017-14786-y

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Prezado Y, Jouvion G, Patriarca A, Nauraye C, Guardiola C, Juchaux M, et al. Proton minibeam radiation therapy widens the therapeutic index for high-grade gliomas. Sci Rep. (2018) 8:16479. doi: 10.1038/s41598-018-34796-8

PubMed Abstract | CrossRef Full Text

13. Prezado Y, Jouvion G, Guardiola C, Gonzalez W, Juchaux M, Bergs J, et al. Tumor control in RG2 glioma-bearing rats: a comparison between proton minibeam therapy and standard proton therapy. Int J Radiat Oncol Biol Phys. (2019) 104:266–71. doi: 10.1016/j.ijrobp.2019.01.080

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Dilmanian FA, Button TM, Le Duc G. Response of rat intracranial 9L gliosarcoma to microbeam radiation therapy. Neuro Oncol. (2002) 4:26–38. doi: 10.1215/15228517-4-1-26

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Peucelle C, Mart?nez-Rovira I, Prezado Y. Spatial fractionation of the dose using neon and heavier ions: a Monte Carlo study. Med Phys. (2015) 42:5928–36. doi: 10.1118/1.4930960

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Linstadt DE, Castro JR, Phillips TL. Neon ion radiotherapy: results of the phase I/II clinical trial. Int J Radiat Oncol Biol Phys. (1991) 20:761–9. doi: 10.1016/0360-3016(91)90020-5

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Castro JR, Linstadt DE, Bahary JP, Petti PL, Daftari I, Collier JM, et al. Experience in charged particle irradiation of tumors of the skull base: 1977-1992. Int J Radiat Oncol Biol Phys. (1994) 29:647–55. doi: 10.1016/0360-3016(94)90550-9

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Prezado Y, Bergs J. Ne-MBRT - a worldwide first implementation of spatial fractionation for very heavy ions. In: PTCOG58. (2019).

19. Bert C, Engenhart-Cabillic R, Durante M. Particle therapy for noncancer diseases. Med Phys. (2012) 39:1716–27. doi: 10.1118/1.3691903

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Larsson B, Leksell L, Rexed B, Sourander P, Mair W, Andersson B. The high-energy proton beam as a neurosurgical tool. Nature. (1958) 182:1222–3. doi: 10.1038/1821222a0

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Favaudon V, Caplier L, Monceau V, Pouzoulet F, Sayarath M, Fouillade C, et al. Ultrahigh dose-rate FLASH irradiation increases the differential response between normal and tumor tissue in mice. Sci Transl Med. (2014) 6:245ra93. doi: 10.1126/scitranslmed.3008973

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Tobias CA. Pretherapeutic investigations with accelerated heavy ions. Radiology. (1973) 108:145–58.

PubMed Abstract | Google Scholar

23. Abrosimov NK, Gavrikov YA, Ivanov ea E M. 1000 MeV proton therapy facility at Petersburg Nuclear Physics Institute Synchrocyclotron. J Phys. (2006) 41:424–32. doi: 10.1088/1742-6596/41/1/047

CrossRef Full Text | Google Scholar

24. Grevillot L, Frisson T, Zahra N, Bertrand D, Stichelbaut F, Freud N, et al. Optimization of GEANT4 settings for proton pencil beam scanning simulations using GATE. NIM B. (2010) 268:3295–305. doi: 10.1016/j.nimb.2010.07.011

CrossRef Full Text | Google Scholar

25. Seravalli E, Robert C, Bauer J, Stichelbaut F, Kurz C, Smeets J, et al. Monte Carlo calculations of positron emitter yields in proton radiotherapy. Phys Med Biol. (2012) 57:1659–73. doi: 10.1088/0031-9155/57/6/1659

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Schneider U, Pedroni E, Lomax A. The calibration of CT Hounsfield units for radiotherapy treatment planning. Phys Biol Med. (1996) 41:111–24. doi: 10.1088/0031-9155/41/1/009

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Chetty IJ, Rosu M, Kessler ML, Fraass BA, Ten Haken RK, Kong FM, et al. Reporting and analyzing statistical uncertainties in Monte Carlo-based treatment planning. Int J Radiat Oncol Biol Phys. (2006) 65:1249–59. doi: 10.1016/j.ijrobp.2006.03.039

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Yu Q. Energy deposition calculated by PHITS code in Pb spallation target. NIM B. (2016) 367:8–13. doi: 10.1016/j.nimb.2015.11.014

CrossRef Full Text | Google Scholar

29. Harling OK, Roberts KA, Moulin DJ, Rogus DR. Head phantoms for neutron boron capture therapy. Med Phys. (1995) 22:579–83. doi: 10.1118/1.597545

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Rovituso M, La Tessa C. Nuclear interactions of new ions in cancer therapy: impact on dosimetry. Transl Cancer Res. (2017) 6:S914–33. doi: 10.21037/tcr.2017.06.46

CrossRef Full Text

31. Schneider T, De Marzi L, Patriarca A, Prezado Y. Advancing proton minibeam radiation therapy: magnetically focussed proton minibeams at a clinical centre. Sci Rep. (2020) 10:1384. doi: 10.1038/s41598-020-58052-0

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Mazal A, Prezado Y, Ares C, de Marzi L, Patriarca A, Miralbell R, et al. FLASH and minibeams in radiation therapy: the effect of microstructures on time and space and their potential application to protontherapy. Br J Radiol. (2020) 93:20190807. doi: 10.1259/bjr.20190807

PubMed Abstract | CrossRef Full Text | Google Scholar