- 1Department of Mathematics, National College of Business Administration & Economics, Lahore, Pakistan
- 2Department of Mathematics, University of Sargodha, Sargodha, Pakistan
- 3Informetrics Research Group, Ton Duc Thang University, Ho Chi Minh City, Vietnam
- 4Faculty of Mathematics and Statistics, Ton Duc Thang University, Ho Chi Minh City, Vietnam
- 5Department of Mathematics, Government College University, Faisalabad, Pakistan
- 6Department of Mathematics, Faculty of Arts and Sciences, Cankaya University, Ankara, Turkey
- 7Department of Medical Research, China Medical University, Taichung, Taiwan
- 8Institute of Space Sciences, Bucharest, Romania
In this article we develop a numerical algorithm based on redefined extended cubic B-spline functions to explore the approximate solution of the time-fractional Klein–Gordon equation. The proposed technique employs the finite difference formulation to discretize the Caputo fractional time derivative of order α ∈ (1, 2] and uses redefined extended cubic B-spline functions to interpolate the solution curve over a spatial grid. A stability analysis of the scheme is conducted, which confirms that the errors do not amplify during execution of the numerical procedure. The derivation of a uniform convergence result reveals that the scheme is O(h2 + Δt2−α) accurate. Some computational experiments are carried out to verify the theoretical results. Numerical simulations comparing the proposed method with existing techniques demonstrate that our scheme yields superior outcomes.
1. Introduction
The subject of fractional-order differential equations has attracted considerable interest due to its applications in a wide range of fields, such as traffic flow, earthquakes and other physical phenomena, signal processing, finance, control theory, fractional dynamics, and mathematical modeling [1–10]. In recent years, the analytical and numerical study of fractional-order differential equations has become a dynamic area of research. Several numerical and analytical techniques have been developed to handle these types of equations [11–22]. There are a number of different definitions of fractional-order derivatives, with different applications. An excellent overview can be found in the works [23–31]. This article is concerned with the following time-fractional non-linear Klein–Gordon equation (KGE):
where ∂α∂tα represents the Caputo fractional time derivative, v = v(x, t) denotes the displacement of the wave at (x, t), α ∈ (1, 2] is the fractional order of the time derivative, f(x, t) is the source term, ρ, ρ1 and ρ2 are real numbers, and σ = 2 or 3.
The fractional KGE plays a significant role in quantum mechanics, the study of solitons, and condensed matter physics. Many approaches have been adopted to solve equations of Klein/sine–Gordon type efficiently, including the Adomian decomposition method, the variational iteration method [32–34], and the homotopy analysis method [35]; see also the references cited in these works. Jafari et al. proposed using fractional B-splines for approximate solution of fractional differential equations [36]. In Vong and Wang [37, 38] space compact difference schemes were applied to one- and two-dimensional time-fractional Klein–Gordon-type equations, and stability and convergence of the proposed numerical approaches were established with the aid of an energy method. In Dehghan et al. [39] the authors used a meshless method based on radial basis functions to develop an unconditionally stable numerical scheme for fractional Klein/sine–Gordon equations. The Adomian decomposition method and an iterative method were applied in Jafari [40] to solve Klein–Gordon-type equations involving fractional time derivatives. A fully spectral approach was employed in Chen et al. [41] that uses finite differences for time discretization and Legendre spectral approximation in the spatial direction to construct numerical solutions of non-linear partial differential equations involving fractional derivatives. A sinc–Chebyshev collocation method (SCCM) was developed in Nagy [42] for numerical treatment of the time-fractional non-linear KGE. Recently, in Kanwal et al. [43], Genocchi polynomials were employed together with the Ritz–Galerkin scheme to solve fractional KGEs and diffusion wave equations. A linearized second-order scheme was introduced in Lyu and Vong [44] to solve non-linear time-fractional Klein–Gordon-type equations. Later on, in Doha et al. [45], a space–time spectral approximation was proposed for solving non-linear variable-order fractional Klein/sine–Gordon differential equations.
In this article we propose using redefined extended cubic B-spline (RECBS) functions for numerical solution of the time-fractional KGE. RECBS functions are basically a generalization of typical cubic B-spline functions that involve a free parameter which provides the flexibility to fine-tune the solution curve. We employ the usual finite central difference approach to discretize the Caputo fractional time derivative and use RECBS functions for spatial integration.
This article is organized as follows. The Caputo definition of fractional time derivative and the finite difference formulation for temporal discretization are reviewed in section 2; this section also includes a brief introduction to extended cubic B-spline and RECBS functions and their applications to space discretization. The stability analysis of the proposed algorithm is presented in section 3, and the description of theoretical convergence is given in section 4. The approximate results are reported and discussed in section 5. Finally, concluding remarks are given in section 6.
2. Description of Numerical Technique
2.1. Time Discretization
Let the time domain [0, T] be divided into R subintervals of equal length Δ with endpoints 0 = t0 < t1 < ⋯ < tR = T, where tr = rΔt and r = 0:1:R. We first discretize the Caputo fractional derivative at t = tr+1 as [46]
where , ϵ = (tr+1 − w), and is the truncation error. The truncation error is bounded, i.e.,
where ψ is a constant. The coefficients pk in (4) possess the following attributes:
• the pk's are non-negative for k = 0, 1, 2, …, r;
• 1 = p0 > p1 > p2 > p3 > ⋯ > pn, and pn → 0 as n → ∞;
• .
Substituting Equation (4) into Equation (1), we get
Suppose and . Applying a θ-weighted scheme, Equation (6) takes the form
For θ = 1, we obtain the following semi-discretized numerical scheme:
2.2. Extended Cubic B-Spline Functions
Let the spatial domain [a, b] be partitioned into M parts of equal length with boundary points a = x0 < x1 < ⋯ < xM = b, where xm = x0 + mh for m = 0:1:M. For a sufficiently continuous function v(x, t), there always exists a unique extended cubic B-spline (ECBS) approximation V*(x, t):
where the ξm(t) are to be calculated and the fourth-degree ECBS blending functions Sm(x, λ) are defined as [47]
Here λ, with −n(n − 2) ≤ λ ≤ 1, is a real number responsible for fine-tuning the curve, and n gives the degree of the ECBS used to generate different forms of ECBS functions. The approximate solution and its first two derivatives with respect to the spatial variable x at the rth time step can be expressed in terms of ξm as [48]
where , , , , and .
2.3. Redefined Extended Cubic B-Spline Functions
In the typical ECBS collocation method, the basis functions S−1, S0, …, SM+1 do not vanish at the boundaries of the spatial domain when Dirichlet-type end conditions are imposed. Therefore, we need to redefine them so that the resulting set of basis functions will vanish at the boundaries. For this, a weight function Φ(x, t) is introduced to eliminate ξ−1 and ξM+1 from Equation (9) in the following manner [49]:
where the weight function Φ(x, t) and the redefined ECBS (RECBS) functions are given by
and.
2.4. Space Discretization
Using Equation (12) in Equation (8) at t = tr+1, we obtain
Discretizing at x = xj, we get
Using (12), the last expression takes the form
Consequently, we get the following system of M + 1 equations in M + 1 unknowns:
where
To start the numerical procedure, we use the given initial conditions to obtain the set of equations
The matrix representation of (19) is
where and . We solve (20) to obtain . The ξj values are then substituted into (12) to get V0. Now we can use (18) for r = 0, 1, 2, …, R − 1. However, for r = 0 the term involving V−1 appears in Equation (18). This issue is resolved by using the following substitution derived from the velocity condition given in (2):
3. Stability Analysis
We use the Fourier method to study the stability of the proposed numerical method. Let and denote, respectively, the exact and approximate growth factors of the Fourier modes. The error, , is given by
where .
For the sake of simplicity, we shall investigate the stability of the proposed scheme with f = 0. The equation for the round-off error is derived from Equations (8) and (21) as
The error equation satisfies the end conditions
and
We define the grid function as
Now, ϱr(x) can be written in the form of a Fourier series as follows:
where
Taking the ‖·‖2 norm, we get
From Parseval's equality we have , so the above expression can be written as
Next, we consider the solution in terms of Fourier series,
where and . Using Equation (29) in Equation (22) and then dividing by eiνkh gives
We know that eiνh + e−iνh = 2 cos(νh), so after collecting like terms, the following useful relation is obtained:
where . Now it is obvious that η ≥ 1 for ν > −2.
Lemma 3.1. Let εr be the solution of Equation (31). Then |εr| ≤ |ε0| for r = 0:1:R.
Proof: For r = 0 in (31), we have
Suppose that the result is true for r = 1:1:R. Then, from Equation (31) we get
Theorem 1. The implic it collocation technique presented in Equation (13) is unconditionally stable.
Proof: Using Lemma (3.1) and Equation (28), we obtain
4. Convergence of the Scheme
To investigate the convergence of the proposed scheme, we follow the approach in Khalid et al. [50]. Before proceeding, we state the following useful theorems [51, 52].
Theorem 2. Let Π = {a = x0, x1, …, xM = b} be a partition of [a, b] with xm = mh for m = 0, …, M, and let v ∈ C4[a, b] and f ∈ C2[a, b]. Suppose (x, t) is the spline that interpolates the solution curve of this problem at the knots xm ∈ Π. Then there exist constants Ϝm, not depending on h, such that
Lemma 4.1. The extended B-splines in (10) satisfy the inequality
Proof: By the triangle inequality we have
For any knot xm, we have
From (11) we obtain
Then, for x ∈ [xm−1, xm], Sm(x, λ) and Sm−1(x, λ) are bounded above by .
Similarly, Sm+1(x, λ) and Sm−2(x, λ) are bounded above by
For any point xm−1 ≤ x ≤ xm, we obtain
Since λ ∈ [−8, 1], we have . Hence,
Theorem 3. The extended cubic B-spline approximation V(x, t) for the analytical exact solution v(x, t) of problem (1)–(3) exists, and if f ∈ C2[0, 1] then
where h is reasonably small and is a constant not depending on h.
Proof: Let be the calculated spline for the approximate solution V(x, t) and the exact solution v(x, t).
Let Lv(xm, t) = LV(xm, t) = (xm, t), with m = 0:1:M, be the collocation conditions. Then
Now, at any time step, the problem can be expressed in the form of a difference equation L((xm, t) − V(xm, t)) as
The boundary conditions can be rewritten as
where
and
From (32) we have
We define , and .
For r = 0, Equation (35) transforms into the following relation:
Using the initial condition e0 = 0, we obtain
Taking absolute values of and and with adequately small h, we have
using the boundary conditions, from which we conclude that
where Ϝ1 is independent of the spatial grid spacing.
Using the induction technique, we assume that is true for k = 1:1:r.
Let Ϝ = max{Ϝk:0 ≤ k ≤ r}; then Equation (35) becomes
Again, taking absolute values of and , we have
Using the boundary conditions, we have
Hence, for all values of n,
Now,
Taking the infinity norm and applying Lemma (3.1), we obtain
Making use of the triangle inequality, we get
Using the inequalities (32) and (38) in (39), we obtain
where .
Using the above theorem with expression (5), it is easy to conclude that the numerical approach converges unconditionally. Therefore,
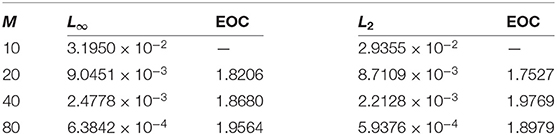
where is a constant and α ∈ (1, 2]. Hence, theoretically, the proposed scheme is O(h2 + Δt2−α) accurate.
5. Numerical Results and Discussion
To examine the accuracy of the proposed method, we conduct a numerical study of some test problems. The L∞ and L2 error norms are calculated as [53]
Also, the experimental order of convergence (EOC) is computed by the following important formula [54]:
All numerical computations were performed using Mathematica 9.0.
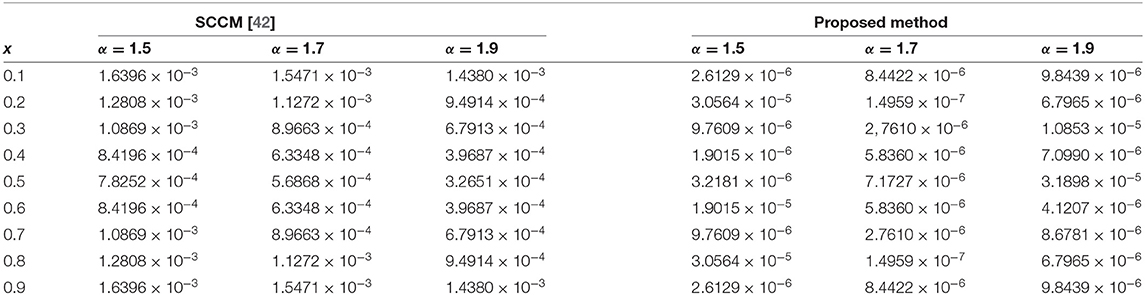
Example 5.1. Consider the non-linear time-fractional KGE [42]
where . The initial/end conditions can be extracted from the analytical exact solution .
For Example 5.1, the piecewise-defined approximate solution obtained using the proposed method with α = 1.25, 0 ≤ x ≤ 1, n = 100, and Δt = 0.01 is given by
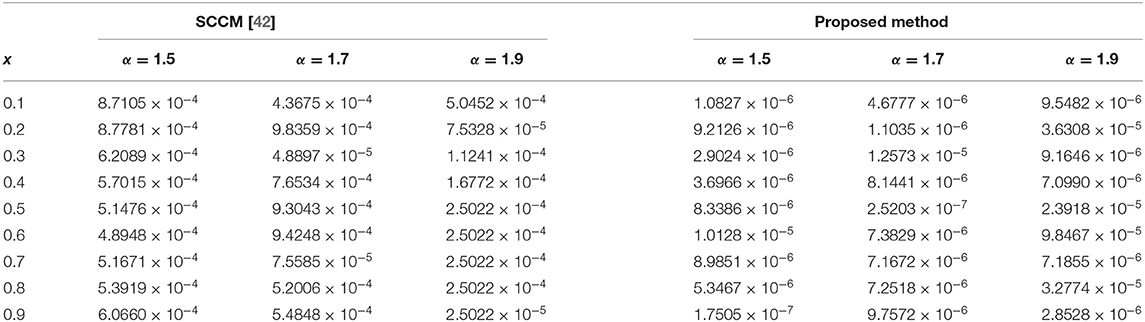
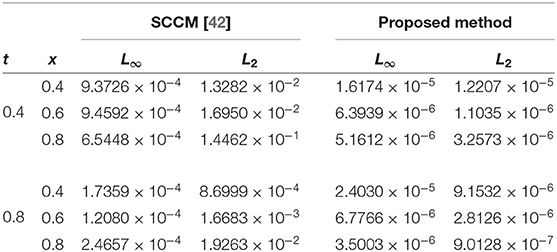
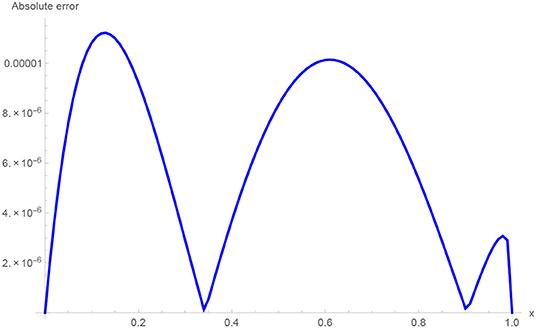
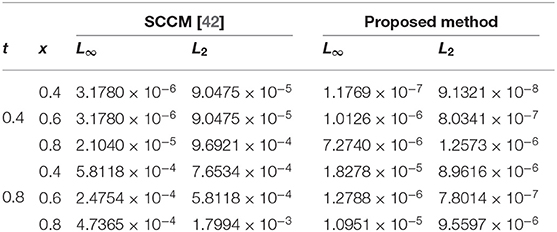
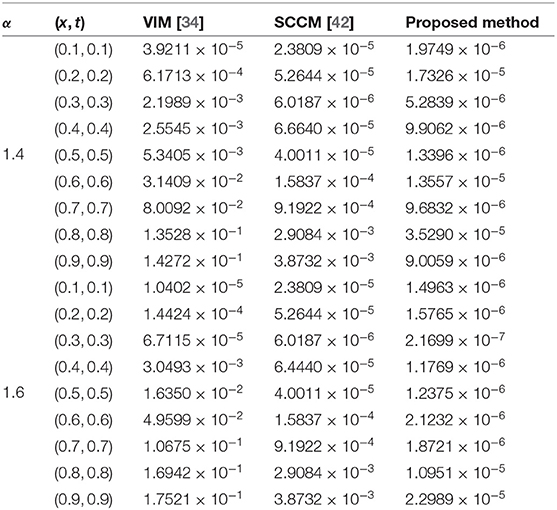
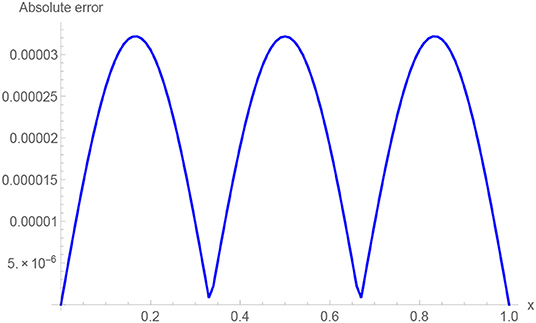
The absolute numerical errors at different grid points of the RECBS solution for Example 5.1 using Δt = 0.001 and M = 100 are reported in Table 1. It can easily be seen that our scheme is more accurate than the SCCM [42]. In Table 2 the absolute and relative numerical errors are listed for our method with M = 100, Δt = 0.001, and α = 1.6 at x = 0.4, 0.6, 0.8 when t = 0.4, 0.8. We can see that the computational results are superior to those obtained from the SCCM [42]. Table 3 compares the absolute errors of the proposed method, the variational iteration method (VIM) [34], and the SCCM [42] under different values of α. Figure 1 shows the behavior at different time stages of numerical solutions obtained using α = 1.5, M = 100, and Δt = 0.001. The 3D visuals of exact and numerical solutions with α = 1.5 and M = 100 are shown in Figure 2. The comparison between the exact and approximate solutions using M = 100 is plotted in Figure 3. Figure 4 depicts the absolute error between the exact and numerical solutions when α = 1.3, M = 100, and Δt = 0.001. The values of the EOC along the spatial grid, using Δt = 0.001 and α = 1.5, are given in Table 4. The experimental rate of convergence of the proposed method is found to be in line with the theoretical results.
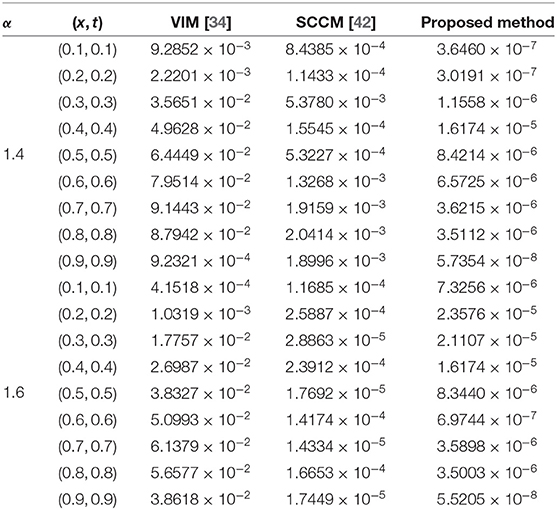
Table 3. Comparison of absolute errors for Example 5.1 using three different methods with M = 100, Δt = 0.001, and α = 1.4 or 1.6.
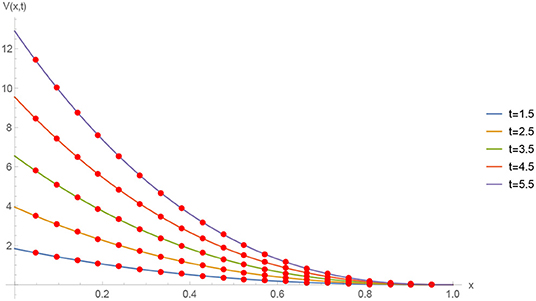
Figure 1. Numerical solution of Example 5.1 with Δt = 0.001, M = 100, and α = 1.5 at different time stages.
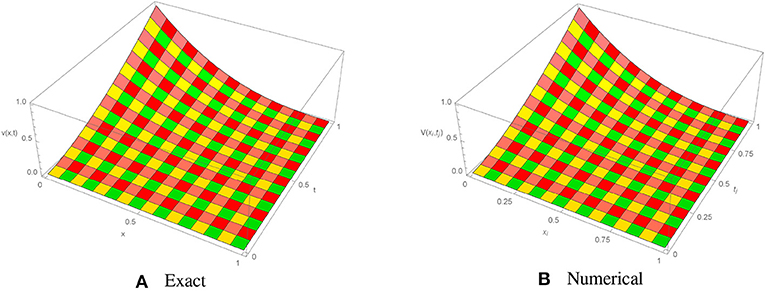
Figure 2. Exact and approximate solutions of Example 5.1 with M = 100, Δt = 0.001, and α = 1.50. (A) Exact. (B) Numerical.
Example 5.2. Consider the fractional KGE [34, 42]
where the forcing term f(x, t) on right-hand side is given by
For Example 5.2, the piecewise-defined numerical solution obtained using the proposed method with α = 1.5, 0 ≤ x ≤ 1, n = 100, and Δt = 0.01 is given by
The initial/boundary conditions can be extracted from the analytical exact solution v(x, t) = sin(πx)t2+α. The absolute numerical errors at different grid points of the RECBS solution for Example 5.2 using Δt = 0.001 and M = 100 are listed in Table 5. Again it can be observed that our scheme is more accurate than the SCCM [42]. Table 6 reports the absolute and relative errors in our numerical computation with M = 100, Δt = 0.001, and α = 1.6 at x = 0.4, 0.6, 0.8 when t = 0.4, 0.8. It is clear that the results are better than those obtained by the SCCM [42]. Table 7 compares the absolute errors of the proposed method, VIM [34], and SCCM [42] under different values of α. The EOC in the spatial direction, using Δt = 0.001 and α = 1.50, is tabulated in Table 8. The experimental rate of convergence of the proposed scheme is found to be in line with the theoretical prediction. Figure 5 shows the behavior at different time stages of numerical solutions obtained using α = 1.5, M = 100, and Δt = 0.001. The 3D plots of exact and numerical solutions with α = 1.5 and M = 100 are displayed in Figure 6. The absolute error between the exact and approximate solutions using α = 1.3, M = 100, and Δt = 0.001 is plotted in Figure 7.
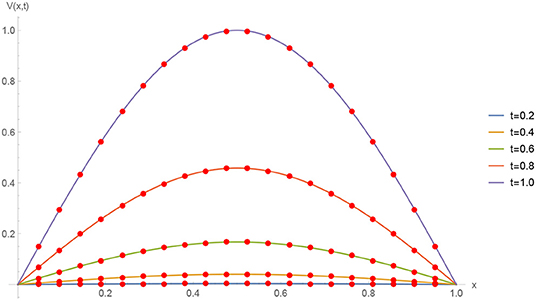
Figure 5. Numerical solution for Example 5.2 with Δt = 0.001, M = 100, and α = 1.5 at different time stages.
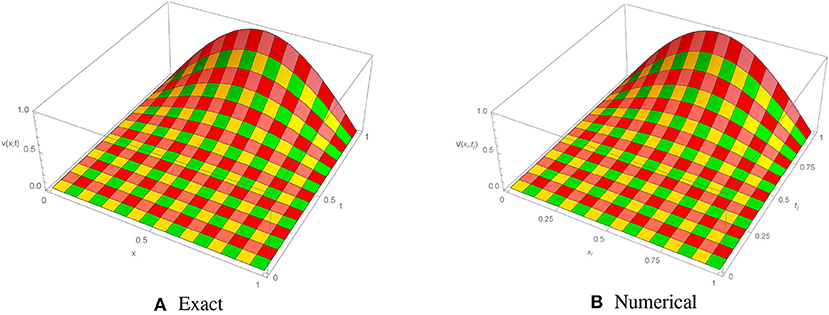
Figure 6. Exact and numerical solutions of Example 5.2 with M = 100, Δt = 0.001, and α = 1.5. (A) Exact. (B) Numerical.
6. Conclusion
In this work we have conducted a numerical investigation of the time-fractional Klein–Gordon equation by applying the redefined extended cubic B-spline collocation method. A finite central difference formulation is employed for temporal discretization, while a set of redefined extended cubic B-spline functions is used to interpolate the solution curve in the spatial direction. The unconditional stability of the proposed scheme is established, and the orders of convergence along the space and time grids are shown to be O(h2) and O(Δt)2−α, respectively. The computational outcomes of the proposed algorithm show that the order of convergence agrees with the theoretical results. The numerical scheme has been tested on different problems, and comparison of the results reveals our method's advantage over VIM [34] and SCCM [42].
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Rossikhin YA, Shitikova M. Application of fractional derivatives to the analysis of damped vibrations of viscoelastic single mass systems. Acta Mech. (1997) 120:109–25. doi: 10.1007/BF01174319
2. Rudolf H. Applications of FractionalCalculus in Physics. Singapore; River Edge, NJ: World Scientific (2000).
3. Metzler R, Klafter J. The restaurant at the end of the random walk: recent developments in the description of anomalous transport by fractional dynamics. J Phys A Math Gen. (2004) 37:R161. doi: 10.1088/0305-4470/37/31/R01
4. Luo MJ, Milovanovic GV, Agarwal P. Some results on the extended beta and extended hypergeometric functions. Appl Math Comput. (2014) 248:631–51. doi: 10.1016/j.amc.2014.09.110
5. Zhang Y. Time-fractional Klein-Gordon equation: formulation and solution using variational methods. WSEAS Trans Math. (2016) 15:206–14.
6. Ruzhansky M, Cho YJ, Agarwal P, Area I. Advances in Real and Complex Analysis With Applications. Singapore: Springer (2017).
7. Owolabi KM, Hammouch Z. Mathematical modeling and analysis of two-variable system with noninteger-order derivative. Chaos. (2019) 29:013145. doi: 10.1063/1.5086909
8. Agarwal P, Baleanu D, Chen Y, Momani S, Machado JAT. Fractional calculus. In: ICFDA: International Workshop on Advanced Theory and Applications of Fractional Calculus. Amman (2019). doi: 10.1007/978-981-15-0430-3
9. Babaei A, Jafari H, Ahmadi M. A fractional order HIV/AIDS model based on the effect of screening of unaware infectives. Math Methods Appl Sci. (2019) 42:2334–43. doi: 10.1002/mma.5511
10. Babaei A, Jafari H, Liya A. Mathematical models of HIV/AIDS and drug addiction in prisons. Eur Phys J Plus. (2020) 135:395. doi: 10.1140/epjp/s13360-020-00400-0
11. Yuste SB, Acedo L. An explicit finite difference method and a new von Neumann-type stability analysis for fractional diffusion equations. SIAM J Numer Anal. (2005) 42:1862–74. doi: 10.1137/030602666
12. Sweilam N, Nagy A. Numerical solution of fractional wave equation using Crank-Nicholson method. World Appl Sci J. (2011) 13:71–5.
13. Ur-Rehman M, Khan RA. The Legendre wavelet method for solving fractional differential equations. Commun Nonlin Sci Numer Simul. (2011) 16:4163–73. doi: 10.1016/j.cnsns.2011.01.014
14. Bhrawy A, Tharwat M, Yildirim A. A new formula for fractional integrals of Chebyshev polynomials: application for solving multi-term fractional differential equations. Appl Math Modell. (2013) 37:4245–52. doi: 10.1016/j.apm.2012.08.022
15. Rad J, Kazem S, Shaban M, Parand K, Yildirim A. Numerical solution of fractional differential equations with a Tau method based on Legendre and Bernstein polynomials. Math Methods Appl Sci. (2014) 37:329–42. doi: 10.1002/mma.2794
16. Mohebbi A, Abbaszadeh M, Dehghan M. High-order difference scheme for the solution of linear time fractional Klein-Gordon equations. Numer Methods Partial Differ Equat. (2014) 30:1234–53. doi: 10.1002/num.21867
17. Heydari M, Hooshmandasl M, Mohammadi F, Cattani C. Wavelets method for solving systems of nonlinear singular fractional Volterra integro-differential equations. Commun Nonlin Sci Numer Simul. (2014) 19:37–48. doi: 10.1016/j.cnsns.2013.04.026
18. Salahshour S, Ahmadian A, Senu N, Baleanu D, Agarwal P. On analytical solutions of the fractional differential equation with uncertainty: application to the basset problem. Entropy. (2015) 17:885–902. doi: 10.3390/e17020885
19. Sweilam N, Nagy A, El-Sayed AA. Second kind shifted Chebyshev polynomials for solving space fractional order diffusion equation. Chaos Solit Fract. (2015) 73:141–7. doi: 10.1016/j.chaos.2015.01.010
20. Ramezani M, Jafari H, Johnston SJ, Baleanu D. Complex b-spline collocation method for solving weakly singular Volterra integral equations of the second kind. Miskolc Math Notes. (2015) 16:1091–103. doi: 10.18514/MMN.2015.1469
21. Badr M, Yazdani A, Jafari H. Stability of a finite volume element method for the time-fractional advection-diffusion equation. Numer Methods Partial Differ Equat. Wiley online Library. (2018) 34:1459–71. doi: 10.1002/num.22243
22. Agarwal P, Agarwal RP, Ruzhansky M. Special Functions and Analysis of Differential Equations. (2020).
23. Atangana A, Secer A. A note on fractional order derivatives and table of fractional derivatives of some special functions. Abstr Appl Anal. (2013) 2013:279681. doi: 10.1155/2013/279681
24. Srivastava H, Agarwal P. Certain fractional integral operators and the generalized incomplete hypergeometric functions. Appl Appl Math. (2013) 8:333–45.
25. Goufo EFD. Solvability of chaotic fractional systems with 3D four-scroll attractors. Chaos Solit Fract. (2017) 104:443–51. doi: 10.1016/j.chaos.2017.08.038
26. Asif N, Hammouch Z, Riaz M, Bulut H. Analytical solution of a Maxwell fluid with slip effects in view of the Caputo-Fabrizio derivative. Eur Phys J Plus. (2018) 133:272. doi: 10.1140/epjp/i2018-12098-6
27. Singh J, Kumar D, Hammouch Z, Atangana A. A fractional epidemiological model for computer viruses pertaining to a new fractional derivative. Appl Math Comput. (2018) 316:504–15. doi: 10.1016/j.amc.2017.08.048
28. Atangana A, Goufo EFD. Conservatory of Kaup-Kupershmidt equation to the concept of fractional derivative with and without singular kernel. Acta Math Appl Sin. (2018) 34:351–61. doi: 10.1007/s10255-018-0757-7
29. Owolabi KM, Atangana A. Computational study of multi-species fractional reaction-diffusion system with ABC operator. Chaos Solit Fract. (2019) 128:280–9. doi: 10.1016/j.chaos.2019.07.050
30. Uçar S, Uçar E, Özdemir N, Hammouch Z. Mathematical analysis and numerical simulation for a smoking model with Atangana-Baleanu derivative. Chaos Solit Fract. (2019) 118:300–6. doi: 10.1016/j.chaos.2018.12.003
31. Goufo EFD, Toudjeu IT. Analysis of recent fractional evolution equations and applications. Chaos Solit Fract. (2019) 126:337–50. doi: 10.1016/j.chaos.2019.07.016
32. Batiha B, Noorani MSM, Hashim I. Numerical solution of sine-Gordon equation by variational iteration method. Phys Lett A. (2007) 370:437–40. doi: 10.1016/j.physleta.2007.05.087
33. Yusufoğlu E. The variational iteration method for studying the Klein-Gordon equation. Appl Math Lett. (2008) 21:669–74. doi: 10.1016/j.aml.2007.07.023
34. Odibat Z, Momani S. The variational iteration method: an efficient scheme for handling fractional partial differential equations in fluid mechanics. Comput Math Appl. (2009) 58:2199–208. doi: 10.1016/j.camwa.2009.03.009
35. Jafari H, Saeidy M, Arab Firoozjaee M. Solving nonlinear Klein-Gordon equation with a quadratic nonlinear term using homotopy analysis method. Iran J Optimiz. (2010) 2:130–38.
36. Jafari H, Khalique CM, Ramezani M, Tajadodi H. Numerical solution of fractional differential equations by using fractional B-spline. Central Eur J Phys. (2013) 11:1372–6. doi: 10.2478/s11534-013-0222-4
37. Vong S, Wang Z. A compact difference scheme for a two dimensional fractional Klein-Gordon equation with Neumann boundary conditions. J Comput Phys. (2014) 274:268–82. doi: 10.1016/j.jcp.2014.06.022
38. Vong S, Wang Z. A high-order compact scheme for the nonlinear fractional Klein-Gordon equation. Numer Methods Partial Differ Equat. (2015) 31:706–22. doi: 10.1002/num.21912
39. Dehghan M, Abbaszadeh M, Mohebbi A. An implicit RBF meshless approach for solving the time fractional nonlinear sine-Gordon and Klein-Gordon equations. Eng Anal Bound Elements. (2015) 50:412–34. doi: 10.1016/j.enganabound.2014.09.008
40. Jafari H. Numerical solution of time-fractional Klein-Gordon equation by using the decomposition methods. J Comput Nonlin Dyn. (2016) 11:041015. doi: 10.1115/1.4032767
41. Chen H, Lü S, Chen W, et al. A fully discrete spectral method for the nonlinear time fractional Klein-Gordon equation. Taiwan J Math. (2017) 21:231–51. doi: 10.11650/tjm.21.2017.7357
42. Nagy A. Numerical solution of time fractional nonlinear Klein-Gordon equation using Sinc-Chebyshev collocation method. Appl Math Comput. (2017) 310:139–48. doi: 10.1016/j.amc.2017.04.021
43. Kanwal A, Phang C, Iqbal U. Numerical solution of fractional diffusion wave equation and fractional Klein-Gordon equation via two-dimensional Genocchi polynomials with a Ritz-Galerkin method. Computation. (2018) 6:40. doi: 10.3390/computation6030040
44. Lyu P, Vong S. A linearized second-order scheme for nonlinear time fractional Klein-Gordon type equations. Numer Algorithms. (2018) 78:485–511. doi: 10.1007/s11075-017-0385-y
45. Doha E, Abdelkawy M, Amin A, Lopes AM. A space-time spectral approximation for solving nonlinear variable-order fractional sine and Klein-Gordon differential equations. Comput Appl Math. (2018) 37:6212–29. doi: 10.1007/s40314-018-0695-2
46. Amin M, Abbas M, Iqbal MK, Ismail AIM, Baleanu D. A fourth order non-polynomial quintic spline collocation technique for solving time fractional superdiffusion equations. Adv Differ Equat. (2019) 2019:1–21. doi: 10.1186/s13662-019-2442-4
47. Khalid N, Abbas M, Iqbal MK, Baleanu D. A numerical algorithm based on modified extended B-spline functions for solving time-fractional diffusion wave equation involving reaction and damping terms. Adv Differ Equat. (2019) 2019:378. doi: 10.1186/s13662-019-2318-7
48. Wasim I, Abbas M, Iqbal M. A new extended B-spline approximation technique for second order singular boundary value problems arising in physiology. J Math Comput Sci. (2019) 19:258–67. doi: 10.22436/jmcs.019.04.06
49. Sharifi S, Rashidinia J. Numerical solution of hyperbolic telegraph equation by cubic B-spline collocation method. Appl Math Comput. (2016) 281:28–38. doi: 10.1016/j.amc.2016.01.049
50. Khalid N, Abbas M, Iqbal MK, Baleanu D. A numerical investigation of Caputo time fractional Allen-Cahn equation using redefined cubic B-spline functions. Adv Differ Equat. (2020) 2020:1–22. doi: 10.1186/s13662-020-02616-x
51. De Boor C. On the convergence of odd-degree spline interpolation. J Approx Theory. (1968) 1:452–63. doi: 10.1016/0021-9045(68)90033-6
52. Hall CA. On error bounds for spline interpolation. J Approx Theory. (1968) 1:209–18. doi: 10.1016/0021-9045(68)90025-7
53. Iqbal MK, Abbas M, Zafar B. New quartic B-spline approximations for numerical solution of fourth order singular boundary value problems. Punjab Univ J Math. (2020) 52:47–63.
Keywords: redefined extended cubic B-spline, time fractional Klein-Gorden equation, Caputo fractional derivative, finite difference method, convergence analysis
Citation: Amin M, Abbas M, Iqbal MK and Baleanu D (2020) Numerical Treatment of Time-Fractional Klein–Gordon Equation Using Redefined Extended Cubic B-Spline Functions. Front. Phys. 8:288. doi: 10.3389/fphy.2020.00288
Received: 02 March 2020; Accepted: 25 August 2020;
Published: 23 September 2020.
Edited by:
Jordan Yankov Hristov, University of Chemical Technology and Metallurgy, BulgariaReviewed by:
Praveen Agarwal, Anand International College of Engineering, IndiaHossein Jaferi, University of South Africa, South Africa
Copyright © 2020 Amin, Abbas, Iqbal and Baleanu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Muhammad Abbas, bXVoYW1tYWRhYmJhc0B0ZHR1LmVkdS52bg==
 Muhammad Amin1,2
Muhammad Amin1,2