- 1Department of Mathematics, Erode Arts & Science College, Erode, India
- 2Department of Mathematics, University of Tabuk, Tabuk, Saudi Arabia
- 3Department of Mathematics and Statistics, Imam Mohammad Ibn Saud Islamic University, Riyadh, Saudi Arabia
- 4Department of Mathematics, Faculty of Arts and Science in Almandaq, Albaha University, Albaha, Saudi Arabia
The prime objective of this article is to explore the entropy analysis of third-order nanofluid fluid slip flow caused by a stretchable sheet implanted in a porous plate along with thermal radiation, convective surface boundary, non-Fourier heat flux applications, and nanoparticle concentration on zero mass flux conditions. The governing physical systems are modified into non-linear ordinary systems with the aid of similarity variables, and the outcomes are solved by a homotopy analysis scheme. The impression of certain governing flow parameters on the nanoparticle concentration, temperature, and velocity is illustrated through graphs, while the alteration of many valuable engineering parameters viz. the Nusselt number and Sherwood number are depicted in graphs. Entropy generation with various parameters is obtained and discussed in detail. The estimation of entropy generation using the Bejan number find robust application in power engineering and aeronautical propulsion to forecast the smartness of entire system.
Introduction
Nanoliquids are the type of liquids that have small volumetric quantities of nanoscale (10−9 − 10−7m) metallic (Cu, Ti, Hg, Fe, Ag, Au, etc.) or non-metallic particles (TiO2, SiO2, CuO, Al2O3, etc) taken as nano particles. Usually nanoliquids have a colloidal suspension of nanoparticles inside a base liquid for example water, oil, ethylene glycol, etc. Initially, Choi [1] proposed the “nanofluid” term. In general, the effective heat transfer enhancement has the reason of nanoliquids generally restrict up to volume fraction of nanoparticles. Therefore, in the latest technologies and engineering areas, nanoliquids receiving a phenomenal impact. Mushtaq et al. [2] attempted the numerical study of the nanoliquids induced by an exponentially stretchable sheet with rotating flow model. MHD nanoliquid flow toward a porous plate with internal heat generation effects was presented by Reddy and Chamka [3]. Shit et al. [4] studied the convective flow of hydromagnetic nanoliquid with entropy generation mechanism. Recently, Gireesha et al. [5] explained a Hall current effects of two-phase transient nanoliquid flow induced by a stretchable sheet. Reddy et al. [6] performed the combined convection flow of nanoliquid toward a semi-infinite vertical flat sheet with convectively heated boundary and Soret effect. Few more significant studies in this research area are seen in ref's [7–13].
Due to various applications in different technical and industrial areas, the fluid flow problems toward a stretching surface have developed. It finds application in rubber and plastic sheets production, melt-spinning, production of glass-fiber, and metallic plate cooling systems. Sakiadis [14] studied the uniform velocity of a magnetohydrodynamic flow past a solid medium. Magyari et al. [15] examined the first order chemical reaction and heat generation combination on micropolar fluid flow induced by a permeable stretching surface. Gupta [16] analyzed the heat and mass transfer effects of a boundary layer flow induced by a stretchy sheet with suction or blowing impact. Magyari and Keller [17] exposed the fluid flow over exponentially extending sheet with heat and mass transfer impacts. Significances of thermal boundary layer flow for a linearly stretchy sheet with viscous dissipation were examined by Cortell [18]. The cutting-edge research reports on stretching sheet flow are highlighted in these works of literature [19–24].
Fluid flow saturated in the porous surface have numerous applications in various fields like geothermal energy, fuel cell technologies, material processing, etc. Chamkha et al. [25] described the free convective flow past an inclined plate fitted in a porous medium of variable porosity with solar radiation. Khan and Aziz [26] studied the natural convective flow with double diffusion caused by a vertical porous sheet. Oyelakin et al. [27] analyzed the slip flow of unsteady radiative Casson nanofluid toward a stretchy surface. Gorla and Chamkha [28] studied the nanofluid flow toward a non-isothermal vertical plat entrenched in a porous sheet. The same research group extended their work for different models for various applications [29–32].
Heat transport problems in the flow of liquids have been examined by several researchers for the last decade. In 1822, Fourier [33] constructed the heat conduction law. This states that “the heat transfer in a medium with inertial rate.” A parabolic-type equation was used to state the heat conduction equation. The problem rising at this time is that there exists no such object or material that satisfies Fourier's law, as argued by Cattaneo [34] when using thermal relaxation time to customize Fourier's law. Later, Christov [35] developed and joined the upper convected Maxwell fluid. This developed model is called a Christov-Cattaneo heat flux model. Loganathan et al. [36] studied the thermal relaxation time effects on Oldroyd-B liquid with second-order slip and cross-diffusion impacts. The Christov-Cattaneo heat flux model for a third-grade liquid with chemical reaction effects was examined by Imtiaz et al. [37].
In the last decade, several scientists have researched entropy generation in the flow of fluids and heat transfer over a stretching surface. In various engineering and industrial divisions, the performance of heating and cooling are of massive importance in different electronic and energy issues. Aiboud and Saouli [38] examined the MHD viscoelastic fluid flow with the application of entropy analysis using Kummer's function. Makinde [39] presented the thermal radiation and Newtonian heating impacts of variable viscosity fluid caused by a semi-infinite plate using shooting quadrature and obtained the entropy generation number. Loganathan et al. [40, 41] verified the entropy analysis for the third grade and Williamson nanoliquid flow caused by a stretchable sheet with various effects. They employed HAM to solve the non-linear governing systems.
Based on our research in previously published works, entropy generation of third-grade nanofluid flow caused by a stretching sheet with a modified Fourier law has not been discussed with a high standard of scientific attention. As far as we noticed in literature, the studies taken for entropy generation are limited with some parameters viz the Brinkmann number, Reynolds number, Temperature difference parameter, and Hartmann number. We have extended our investigations to include thermal relaxation time, the Biot number, thermal radiation, slip parameter, porous parameter, etc. The effective collection and analysis of these results will open new gateways for diverse engineering application in various streams.
Problem Development
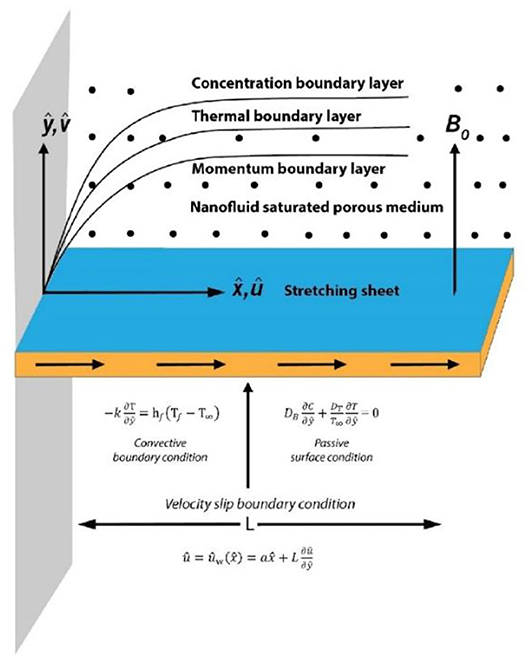
We were interested in analyzing the entropy and Bejan number of third-grade nanofluid saturated in a porous medium with Christov-Cattaneo heat flux. In Figure 1, the stretching parameter is taken along x direction where TW and CW are represented the wall temperature and concentration, respectively. T∞ and C∞ are used to index the ambient temperature and concentration, respectively. A convective heating temperature Tf is stimulated at the bottom of the sheet surface. The Buongiorno nanofluid [42] is used for the present case. Based on his consideration, the slip mechanisms, namely, the Brownian diffusion, inertia, Magnus effect, diffusiophoresis, thermophoresis, gravity, and fluid drainage, were analyzed. He recommended that the thermophoresis and Brownian diffusion are essential slip mechanism in low dimensional materials.
The following is an incompressible fluid model containing body forces with the equation of continuity and motion:
Here, ρ is the fluid density, which is taken as a constant, v is the velocity field, b indicates the body forces, J denotes the electric current, and T states the third-grade incompressible fluids Cauchy stress tensor [43]
where μ, (E1, E2, E3) and indicate the viscosity coefficient, kinematics tensors, and material modulis as in
is expressed as the material time derivative
The relationship between Clausius-Duhem inequality and thermodynamically compatible fluid is stated by Fosdick and Rajagopal [44]:
Boussinesq and normal boundary layer approximations were considered by Pakdemirli [45]. We made the following assumptions:
1. The nanoparticles are small and of equal size to the pores.
2. The zero-mass flux of the nanoparticles is included.
3. Christov-Cattaneo heat flux is considering instead of normal heat flux.
4. The magnetic field in the fluid flow is ignored due to a lower magnetic Reynolds number.
The energy equation with a Cattaneo-Christov heat flux model is stated as
Consider the transformation given below:
The non-linear governing equations are:
with the end points
The non-dimensional variables are
The application of physical entitles is such that
The local mass transfer rate becomes identically zero due to the zero mass flux state [46]
Entropy Optimization
The entropy minimization optimization for fluid friction, heat, and the irreversibility of mass transfer are given below:
Using Equation (25) modified with the help of Equation (17),
Dimensionless system of entropy generation is defined as:
The Bejan number states
Homotopy Solutions
There are several techniques available to solve non-linear problems. The homotopy analysis method (HAM) is initially constructed by Liao [47]. Moreover, he altered a non-zero auxiliary parameter [48]. This parameter shows the way to calculate the convergence rate. It also offers great independence with which to make the initial guesses of the solutions.
The initial guesses for satisfying the boundary conditions
Lf, Lθ, and Lϕ are the linear operators
while obeying the resulting properties
The zeroth order deformation is
where p ϵ [0, 1]
hf, hθ, and hϕ are the non-zero auxiliary constants, and , , and are the non-linear operators given by
The mth order deformation equations are
where
with boundary conditions
The appropriate solutions are
Convergence Analysis
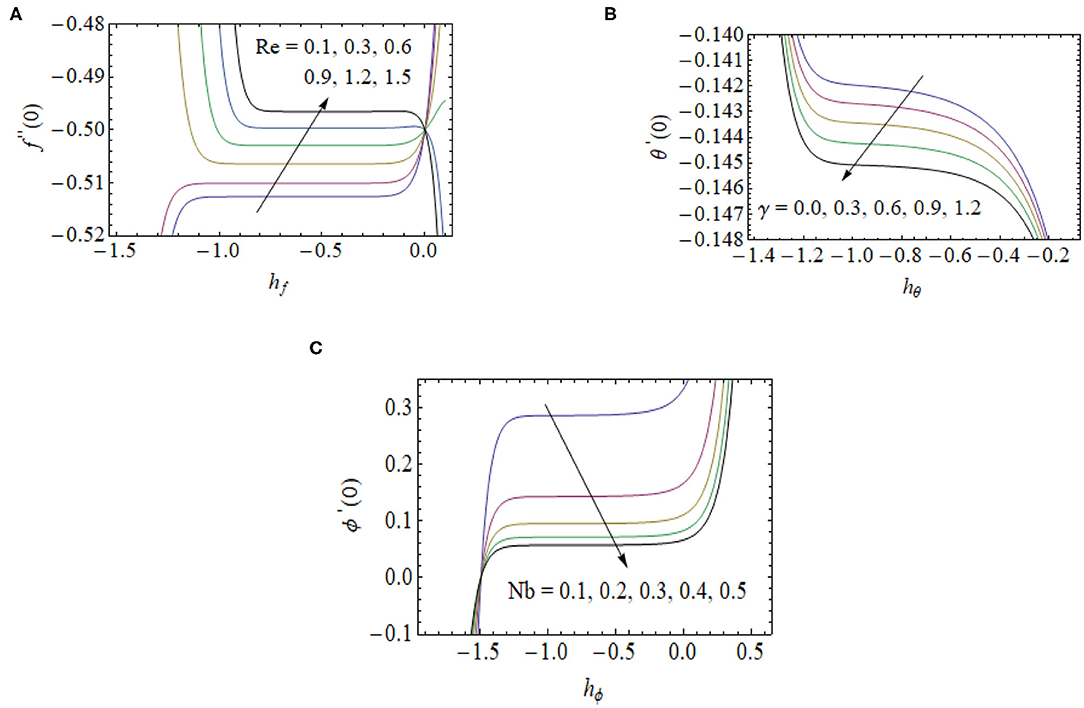
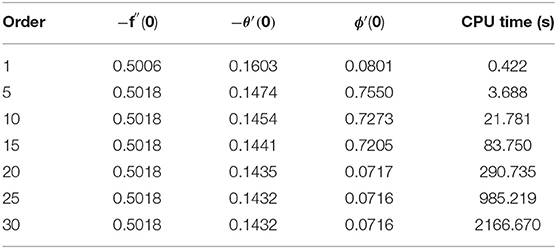
The auxiliary parameters hf, hθ, and hϕ act as a vital part of convergence series solutions. The h-charts of f″(0), θ′(0), and ϕ′(0) for Re, γ , and Nb are shown in Figure 2. From these curves, the straight line is referred as the h-curve. The convergent approximation is selected from this straight line of the curves. We note that h-curve of f″(0), θ′(0), and ϕ′(0) shrinks as we enhance the range of Re, γ , and Nb, which shows the larger order approximation will be needed if the larger value of Re, γ , and Nb is employed. Approximations values of HAM with CPU time is denoted in Table 1.
Computational Results and Discussion
The numerical calculations of velocity, concentration, temperature, entropy generation, and the Bejan number are discussed in this section. The homotopy technique is used for solving the non-linear governing Equations (18)–(20) with boundary conditions (21). The graphical results of entropy, Bejan number, temperature, Nusselt number, nanoparticle concentration, Sherwood number, and velocity profiles are computed via different flow parameters included in this study with the fixed values of α1 = α2 = β = Bi = fw = Nt = 0.2,Re = Pr = Le = Γ = 1.0, M = γ = 0.5, Rd = 0.3, Hg = −0.1, Nb = 0.4, Br = 5.0, and λ = Ω = ζ = 1.0.
Impact on Velocity
It is observed from Figure 3A that the velocity is reduced to increase the values of the velocity slip parameter due to the ratio of stretching velocity and the viscosity of the fluid. The effect of the slip parameter in velocity has had more impact in the absence of a porous medium. Figure 3B indicates that the velocity diminishes when the magnetic field (M) raises. Improved Lorentz force is observed because of the increasing the values of M that opposes the fluid motion. Thus, we conclude that the velocity profile diminishes.
Impact on Temperature
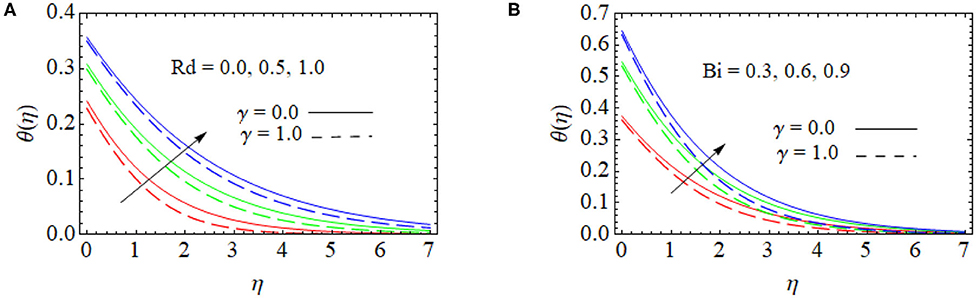
The impact of the radiation parameter Rd on the temperature profile is examined in Figure 4A. The temperature in the radiation parameter is high. Comparing the radiation effects with Christov-Cattaneo and normal heat flux, we observed that the radiation effect is quite low for Christov-Cattaneo heat flux. Figure 4B displays the influence of the Biot number on the temperature profile. From this figure, we observed that temperature is a rising function of Bi close to the sheet. Since Bi affects more temperature near the surface. Heat transfer resistance is higher within the body compared to the surface of the sheet for rising values Bi.
Impact on Nanoparticle Volume Concentration
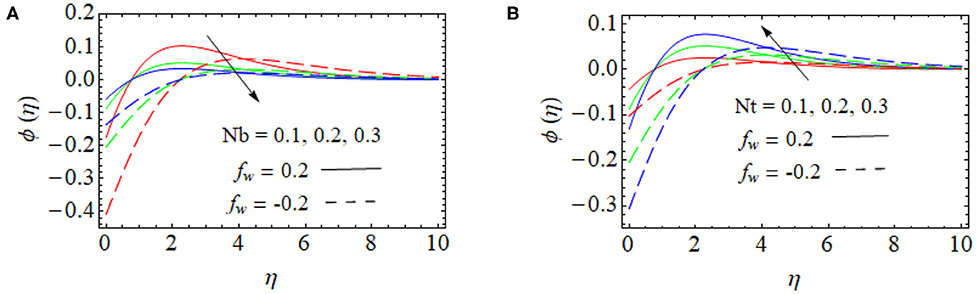
In Figure 5A, the effect of concentration profile with growing values of the Brownian motion parameter Nb is depicted. In suction cases, higher values of Nb increase the concentration profile close to that of the surface of the sheet, and, suddenly, the concentration begins to fall, stabilizing far away from the surface of the sheet. This is due to the appearance of passive surface conditions for the concentration profile. Moreover, the injection at the sheet shows the concentration is rising near the sheet, and it diminishes far away from the surface of the sheet. The influence of the thermophoresis parameter Nt in the concentration profile ϕ(η). is highlighted in Figure 5B. When there is suction in the sheet, with a rise in Nt, the concentration of the liquid decreases near to thsheet at certain stage starts to fall and stabilize away from the endpoints of the surface of the sheet. When there is an injection at the sheet, higher values of Nt decreases the concentration profile near the sheet, and it increases far away from the surface of the sheet.
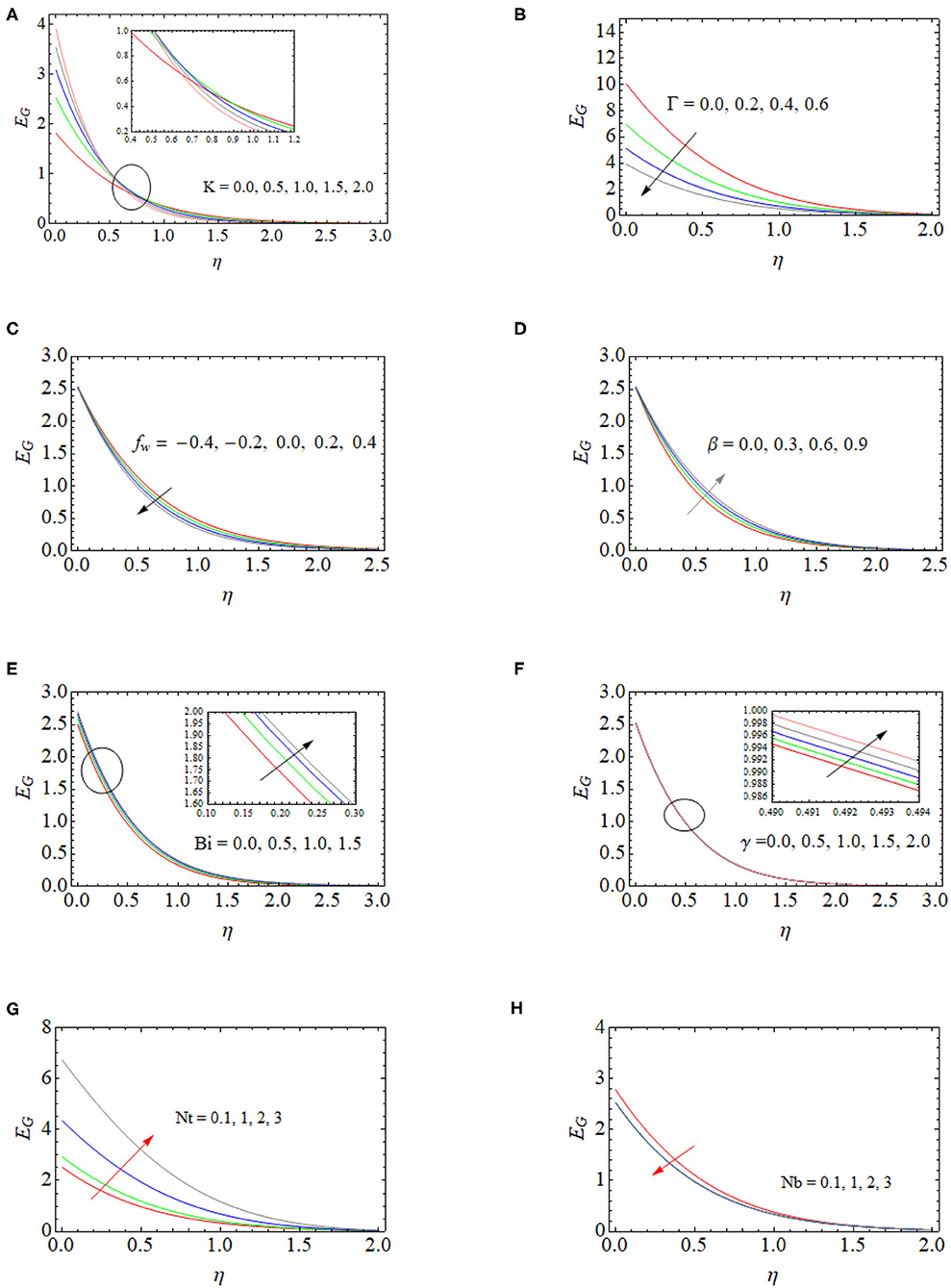
Impact on Entropy Generation
The Effects of distinct fluid parameters on the entropy generation profile are highlighted in Figures 6A–G. Figure 6A depicts the influence of porous parameter in entropy profile. Initially, the entropy rate increases for the porous parameter at a certain stage (η = 0.6) before it becomes to fall. The responses of the slip parameter on entropy generation were succinctly depicted in Figure 6B. From this figure, it was obviously noted that entropy generation was inversely proportional to slip parameter. This causes a decrease in large values of slip parameter and temperature gradients in the boundary layer when retaining the fluid friction as we proceed. This occurrence induces a suppression in entropy generation since heat transfer was committed. Figures 6C–E displayed the impact of the suction\ injection parameter (fw.), material parameter (β) and Biot number (Bi) on the entropy profile (EG). Our examination obtained that higher range of fw, reduces the entropy generation profile, and the entropy generation rate is enhanced for higher β and Bi.
The effect of thermal relaxation time (γ) on the entropy genation profile is sketched in Figure 6F. It is obvious that thermal relaxation time is small for temperature and heat transfer rates. In addition, domination of the irreversibility in heat transfer affected the heat flux. Thus, we have seen a small increase in the entropy of the system. Performance of Nt and Nb on entropy generation profile (EG) is shown in Figures 6G,H, which shows that entropy is increased with an increase of Nt, whereas EG is inversely proportional to Nb. The Brownian motion induces the nanoparticles temperature, but it reduces the temperature gradient on wall. As a result, entropy generation parameter reduces where Nt is directly proportional to temperature gradient and creates ambient atmosphere for higher values of EG.
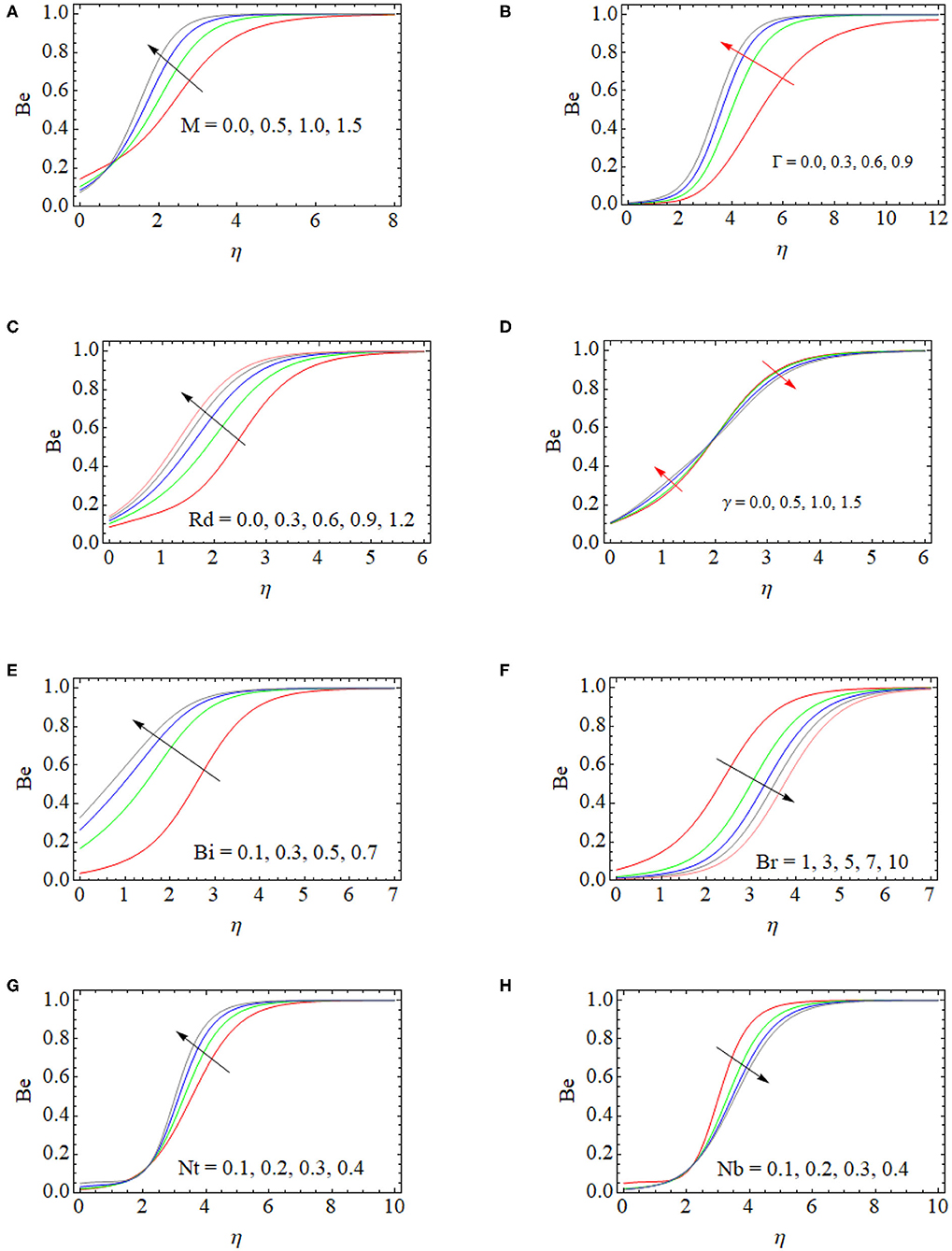
Impact on the Bejan Number
The Bejan number (Be) is a dimensionless quantity that specifies the ratio of entropy generation between heat transfer and the total entropy generation where Bejan numbers take values from 0 to 1. If Be is nearly equal to 1, the entropy generation will become more due to heat transfer. It is clear from Figure 7A that, with an escalation in the applied magnetic field, there is an augmentation in the Bejan number. The consequence of heat transfer entropy develops as we move up from the surface. The entropy effect has full domination because of the heat transfer while it is also outlying from the region. This is the reason behind how the augmenting value of M brings a stronger frictional effect, which leads to an increase in the liquid temperature. There is also a consequent development in the Be, as shown in Figure 7A. From Figure 7B, it is observed that the Be is increased for the increase in the slip parameter (Γ). Physically, larger values of (Γ) enhance the temperature gradient inside the regime, which induces the Bejan number and irreversibility of heat transfer.
Figure 7C states that, with the rise of the radiation constant Rd, the Bejan number is boosted. This is due to the total entropy generation dominated by thermal irreversibility. Figure 7D shows the effect of the thermal relaxation time (γ) on the Be. At first, the Be is augmented for higher values of γ at a sudden point (η = 2.2). Consequently, the Bejan number profile reduces for the values of γ. Figure 7E shows that the Bi displays a trend of raising the Be. The demonstration of such an increasing trend of the Bejan number explains how the entropy production near the surface is large due to the liquid friction—at least relative to that of the heat transfer irreversibility. The variation of the Brinkmann number Br is sketched in Figure 7F. This figure shows that the Bejan number is reduced, as we have to enhance the Br. Figures 7G,H shows the influence of thermophoresis (Nt) and Brownian motion (Nb) parameters on the Bejan number. From these plots, we note that Nt and Nb have inverse effects on the Bejan number profile.
Impact on Physical Entities
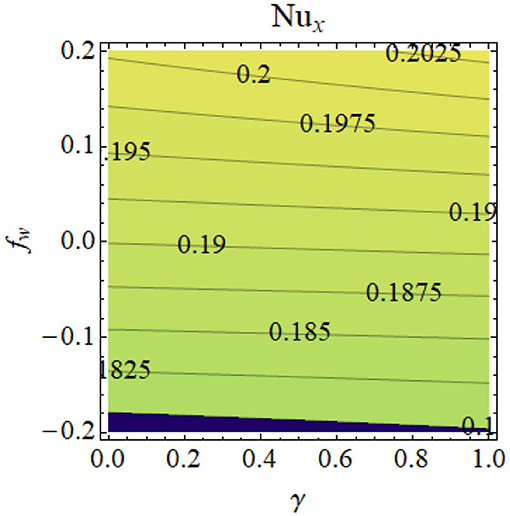
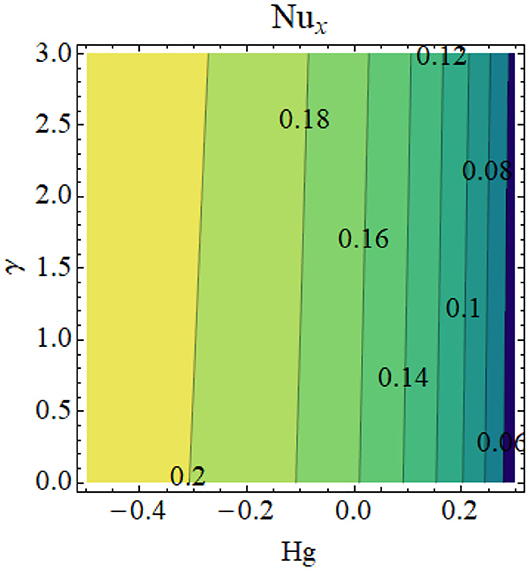
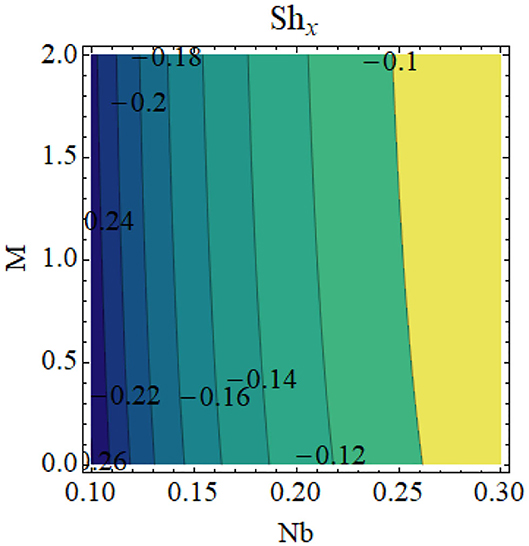
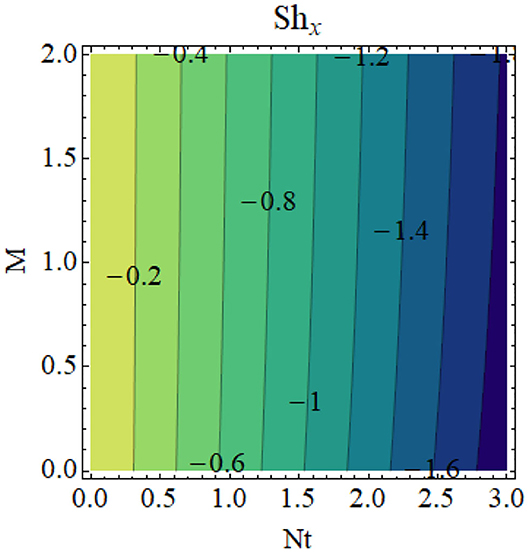
Figures 8–11 illustrate the effects of different physical parameters on the local Nusselt number and local Sherwood number. The influence of fw andγ on Nux is shown in Figure 8: heat transfer decays for higher values of fw and γ. The same phenomena can be observed for larger values Hg and γ on the Nusselt number profile, as presented in Figure 9. The combined effects of Nb and M as well as Nt and M are shown in Figures 10, 11, respectively. From these figures, we conclude that thermophoresis (Nt) and Brownian motion (Nb) parameters have produce the converse trend in the mass transfer rate.
Numerical Code Validation
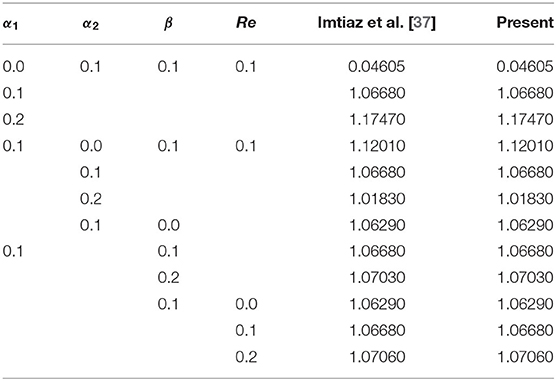
In this segment, we examine the code validation of early published works of literature. Table 2 validates the results of −f″(0) and −θ′(0) for the limiting case M = 0, K = 0, Nb = 0, Nt = 0, Rd = 0, S = 0, and Bi → ∞ with Imtiaz et al. [37]. Moreover, the skin friction rate is also validated by the same literature [37] when M = K = 0 (see Table 3). Table 4 exhibits the matching results of reduced Nusselt number with the references [20, 49–51]. From the above validation, results show that the current simulation is considered an efficient one.
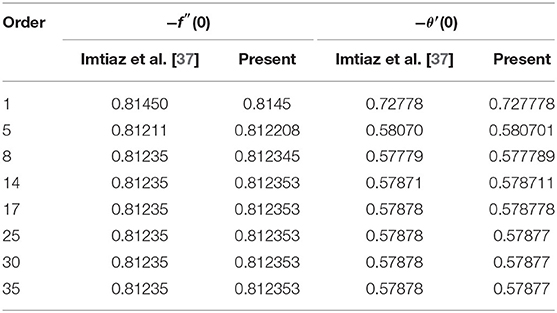
Table 2. Validation of −f″(0) and −θ′(0) for the limiting case M = 0, K = 0, Nb = 0, Nt = 0, Rd = 0, S = 0, and Bi → ∞.
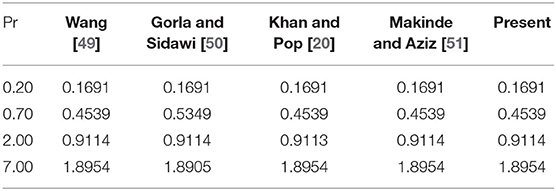
Table 4. Matching results of reduced Nusselt number with the restricting case Rd = Ec = M = Nt = Nb = γ = S = K = Γ = fw = 0, and Bi → ∞.
Key Results
The present research work examines the entropy generation influence on third-grade nanoliquid flow caused by a stretching sheet in the appearance of Magnetic field, radiation, and convective heating effects. Christov-Cattaneo heat flux replaces ordinary heat flux. HAM is employed to validate the non-linear governing equations. Results of velocity, temperature, nanoparticle volume concentration, the system of entropy, the Bejan number, mass, and heat transfer rates are presented graphically. We obtained the following main upshots:
1. A falling tendency of the velocity profile is detectable while we keep increasing the values of the velocity slip and magnetic field parameter.
2. An augmentation in the range of radiation parameter and Biot number causes an increasing trend.
3. The concentration of the nanoparticle volume fraction is found to be a diminishing function of the thermophoretic parameter. On the other hand, a contrary impact is identified for the Brownian motion parameter.
4. The irreversibility of the system rises as we keep enhancing the values of the Biot number, thermal relaxation time, material parameter, and the Brinkmann number, but an inverse occurrence takes place as we increase the slip parameter and suction/injection parameter.
5. The Bejan number increases with greater values of the slip parameter, Biot number, thermophoresis parameter, magnetic parameter, and radiation parameter, whereas it reduces for larger values of the Brinkmann number and Brownian motion parameter.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Funding
This research was supported by the Research Group Project (RGP), University of Tabuk, Tabuk 71491, Saudi Arabia, under Grant No. RGP-0207-14440.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Choi SUS, Eastman JA. Enhancing Thermal Conductivity of Fluids With Nanoparticles, Report No. ANL/MSD/CP 84938, Argonne National Laboratory, Lemont, IL, United States (1995). Available online at: https://ecotert.com/pdf/196525_From_unt-edu.pdf
2. Mushtaq A, Mustafa M, Hayat T, Alsaedi A. Numerical study for rotating flow of nanofluids caused by an exponentially stretching sheet. Adv Powder Technol. (2016) 27:2223–31. doi: 10.1016/j.apt.2016.08.007
3. Reddy PS, Chamkha AJ. Soret and dufour effects on MHD convective flow of Al2O3-water and TiO2-water nanofluids past a stretching sheet in porous media with heat generation/absorption. Adv Powder Technol. (2016) 27:1207–18. doi: 10.1016/j.apt.2016.04.005
4. Shit GC, Haldar R, Mandal S. Entropy generation on MHD flow and convective heat transfer in a porous medium of exponentially stretching surface saturated by nanofluids. Adv Powder Technol. (2017) 28:1519–30. doi: 10.1016/j.apt.2017.03.023
5. Gireesha BJ, Mahanthesh B, Thammanna GT, Sampathkumar P. Hall effects on dusty nanofluid two-phase transient flow past a stretching sheet using KVL model. J Mol Liq. (2018) 256:139–47. doi: 10.1016/j.molliq.2018.01.186
6. RamReddy Ch, Murthy PVSN, Chamkha AJ, Rashad AM. Soret effect on mixed convection flow in a nanofluid under convective boundary condition. Int J Heat Mass Transfer. (2013) 64:384–92. doi: 10.1016/j.ijheatmasstransfer.2013.04.032
7. Ghalambaz M, Behseresht A, Behseresht J, Chamkha AJ. Effects of nanoparticles diameter and concentration on natural convection of the Al2O3-water nanofluids considering variable thermal conductivity around a vertical cone in porous media. Adv Powder Technol. (2015) 26:224–35. doi: 10.1016/j.apt.2014.10.001
8. Joshi PS, Mahapatra PS, Pattamatta A. Effect of particle shape and slip mechanism on buoyancy induced convective heat transport with nanofluids. Phys Fluids. (2017) 29:122001. doi: 10.1063/1.4996824
9. Chamkha AJ, Abbasbandy S, Rashad AM, Vajravelu K. Radiation effects on mixed convection about a cone embedded in a porous medium filled with a nanofluid. Meccanica. (2013) 48:275–85. doi: 10.1007/s11012-012-9599-1
10. Reddy PS, Sreedevi P, Chamkha AJ. MHD boundary layer flow, heat and mass transfer analysis over a rotating disk through porous medium saturated by Cu-water and Ag-water nanofluid with chemical reaction. Powder Technol. (2017) 307:46–55. doi: 10.1016/j.powtec.2016.11.017
11. Anitha S, Loganathan K, Pichumani M. Approaches for modelling of industrial energy systems: correlation of heat transfer characteristics between magnetohydrodynamics hybrid nanofluids and performance analysis of industrial length-scale heat exchanger. J Therm Anal Calorim. doi: 10.1007/s10973-020-10072-8
12. Liu Z, Li D, Song Y, Pan X, Li D, Xuan X. Surface-conduction enhanced dielectrophoretic-like particle migration in electric-field driven fluid flow through a straight rectangular microchannel. Phys Fluids. (2017) 29:102001. doi: 10.1063/1.4996191
13. Zargartalebi H, Ghalambaz M, Noghrehabadi A, Chamkha AJ. Natural convection of a nanofluid in an enclosure with an inclined local thermal non-equilibrium porous fin considering buongiorno's model. Numer Heat Transf A. (2016) 70:432–45. doi: 10.1080/10407782.2016.1173483
14. Sakiadis BC. Boundary-layer behavior on continuous solid surfaces: I. Boundary layer equations for two-dimensional and axisymmetric flow. AIChE J. (1961) 7:26–28. doi: 10.1002/aic.690070108
15. Magyari E, ChamkhaA J. Combined effect of heat generation or absorption and first-order chemical reaction on micropolar fluid flows over a uniformly stretched permeable surface: the full analytical solution. Int J Therm Sci. (2010) 49:1821–8. doi: 10.1016/j.ijthermalsci.2010.04.007
16. Gupta PS, Gupta AS. Heat and mass transfer on a stretching sheet with suction or blowing. Can J Chem Eng. (1977) 55:744–46. doi: 10.1002/cjce.5450550619
17. Magyari E, Keller B. Heat mass transfer in the boundary layers on an exponentially stretching continuous surface. J Phys D Appl Phys B. (1999) 32:577. doi: 10.1088/0022-3727/32/5/012
18. Cortell R. Viscous flow and heat transfer over a nonlinearly stretching sheet. Appl Math Comput. (2007) 184:864–73. doi: 10.1016/j.amc.2006.06.077
19. Vajravelu K. Viscous flow over a nonlinearly stretching sheet. Appl Math Comput. (2001) 124:281–88. doi: 10.1016/S0096-3003(00)00062-X
20. Khan WA, Pop I. Boundary-layer flow of a nanofluid past a stretching sheet. Int J Heat Mass Transfer. (2010) 53:2477–83. doi: 10.1016/j.ijheatmasstransfer.2010.01.032
21. Rana P, Bhargava R. Flow and heat transfer of a nanofluid over a nonlinearly stretching sheet: a numerical study. Commun Nonlinear Sci Numer Simul. (2012) 17:212–26. doi: 10.1016/j.cnsns.2011.05.009
22. Khedr MEM, Chamkha AJ, Bayomi M. MHD flow of a micropolar fluid past a stretched permeable surface with heat generation or absorption. Nonlinear Anal Model. (2009) 14:27–40. doi: 10.15388/NA.2009.14.1.14528
23. Ghalambaz M, Izadpanahi E, Noghrehabadi A, Chamkha AJ. Study of the boundary layer heat transfer of nanofluids over a stretching sheet: passive control of nanoparticles at the surface. Can J Phys. (2014) 93:725–33. doi: 10.1139/cjp-2014-0370
24. Al-Mudhaf A, Chamkha AJ. Similarity solutions for MHD thermosolutal marangoni convection over a flat surface in the presence of heat generation or absorption effects. Heat Mass Transfer. (2005) 42:112–21. doi: 10.1007/s00231-004-0611-8
25. Chamkha AJ, Issa C, Khanafer K. Natural convection from an inclined plate embedded in a variable porosity porous medium due to solar radiation. Int J Therm Sci. (2002) 41:73–81. doi: 10.1016/S1290-0729(01)01305-9
26. Khan WA, Aziz A. Double-diffusive natural convective boundary layer flow in a porous medium saturated with a nanofluid over a vertical plate: prescribed surface heat, solute and nanoparticle fluxes. Int J Therm Sci. (2011) 50:2154–60. doi: 10.1016/j.ijthermalsci.2011.05.022
27. Oyelakin IS, Mondal S, Sibanda P. Unsteady Casson nanofluid flow over a stretching sheet with thermal radiation, convective and slip boundary conditions. Alexandria Eng J. (2016) 55:1025–35. doi: 10.1016/j.aej.2016.03.003
28. Gorla RSR, Chamkha AJ. Natural convective boundary layer flow over a nonisothermal vertical plat embedded in a porous medium saturated with a nanofluid. Nanosc Microsc Therm. (2011) 15:81–94. doi: 10.1080/15567265.2010.549931
29. Chamkha AJ, Mohamed RA, Ahmed SE. Unsteady MHD natural convection from a heated vertical porous plate in a micropolar fluid with joule heating, chemical reaction and radiation effects. Meccanica. (2011) 46:399–411. doi: 10.1007/s11012-010-9321-0
30. Chamkha AJ. Hydromagnetic natural convection from an isothermal inclined surface adjacent to a thermally stratified porous medium. Int J Eng Sci. (1997) 35:975–86. doi: 10.1016/S0020-7225(96)00122-X
31. Chamkha AJ. Solar radiation assisted natural convection in uniform porous medium supported by a vertical flat plate. ASME J Heat Transfer. (1997) 119:35–43. doi: 10.1115/1.2824104
32. Chamkha AJ, Al-Mudhaf AF, Pop I. Effect of heat generation or absorption on thermophoretic free convection boundary layer from a vertical flat plate embedded in a porous medium. Int Commun Heat Mass. (2006) 33:1096–102. doi: 10.1016/j.icheatmasstransfer.2006.04.009
33. Fourier J. Theorie analytique de la chaleur, par M. Fourier. Paris: Chez Firmin Didot, père et fils (1822).
34. Cattaneo C. Sulla conduzione del calore. In: Pignedoli A, editor. Some Aspects of Diffusion Theory. Berlin; Heidelberg: Springer (2011). doi: 10.1007/978-3-642-11051-1_5
35. Christov CI. On frame indifferent formulation of the Maxwell-Cattaneo model of finite-speed heat conduction. Mech Res Commun. (2009) 36:481–86. doi: 10.1016/j.mechrescom.2008.11.003
36. Loganathan K, Sivasankaran S, Bhuvaneshwari M, Rajan S. Second-order slip, cross-diffusion and chemical reaction effects on magneto-convection of oldroyd-B liquid using Cattaneo–Christov heat flux with convective heating. J Therm Anal Calorim. (2019) 136:401–9. doi: 10.1007/s10973-018-7912-5
37. Imtiaz M, Alsaedi A, Shaq A, Hayat T. Impact of chemical reaction on third grade fluid flow with Cattaneo–Christov heat flux. J Mol Liq. (2017) 229:501–7. doi: 10.1016/j.molliq.2016.12.103
38. Aiboud S, Saouli S. Entropy analysis for viscoelastic magnetohydrodynamic flow over a stretching surface. Int J Nonlinear Mech. (2010) 45:482–89. doi: 10.1016/j.ijnonlinmec.2010.01.007
39. Makinde OD. Second law analysis for variable viscosity hydromagnetic boundary layer flow with thermal radiation and Newtonian heating. Entropy. (2011) 13:1446–64. doi: 10.3390/e13081446
40. Loganathan K, Mohana K, Mohanraj M, Sakthivel P, Rajan S. Impact of third-grade nanofluid flow across a convective surface in the presence of inclined Lorentz force: an approach to entropy optimization. J Therm Anal Calorim. (2020). doi: 10.1007/s10973-020-09751-3
41. Loganathan K, Rajan S. An entropy approach of Williamson nanofluid flow with Joule heating and zero nanoparticle mass flux. J Therm Anal Calorim. (2020) 141:2599–612. doi: 10.1007/s10973-020-09414-3
42. Buongiorno J. Convective transport in nanofluids. J Heat Transfer. (2005) 128:240–50. doi: 10.1115/1.2150834
43. Rivlin RS, Thomas AG. Large elastic deformations of isotropic materials. In: Barenblatt GI, Joseph DD, editors. Collected Papers of RS Rivlin. New York, NY: Springer (1997). doi: 10.1007/978-1-4612-2416-7_13
44. Fosdick R, Rajagopal K. Thermodynamics and stability of fluids of third grade. In: Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. London: The Royal Society (1980).
45. Pakdemirli M. The boundary layer equations of third-grade fluids. Int J Nonlinear Mech. (1992) 27:785–93. doi: 10.1016/0020-7462(92)90034-5
46. Halim NA, Rizwan Ul Haq, Noor NFM. Active and passive controls of nanoparticles in Maxwell stagnation point flow over a slipped stretched surface. Meccanica. (2017) 52:1527–39. doi: 10.1007/s11012-016-0517-9
47. Liao SJ. The proposed homotopy analysis technique for the solution of nonlinear problems (Ph.D. thesis), Shanghai Jiao Tong University, Shanghai, China (1992).
48. Liao SJ. An explicit, totally analytic approximation of Blasius viscous flow problems. Int J Nonlinear Mech. (1999) 34:759–78. doi: 10.1016/S0020-7462(98)00056-0
49. Wang CY. Free convection on a vertical stretching surface. ZAMM Z Angew Math Mech. (1989) 69:418–20. doi: 10.1002/zamm.19890691115
50. Gorla RR, Sidawi I. Free convection on a vertical stretching surface with suction and blowing. Appl Sci Res. (1994) 52:247–57. doi: 10.1007/BF00853952
51. Makinde OD, Aziz A. Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Int J Therm Sci. (2011) 50:1326–32. doi: 10.1016/j.ijthermalsci.2011.02.019
LIST OF SYMBOLS
Keywords: entropy generation, Christov-Cattaneo heat flux, third-grade nanofluid, porous medium, homotopy analytic technique
Citation: Loganathan K, Muhiuddin G, Alanazi AM, Alshammari FS, Alqurashi BM and Rajan S (2020) Entropy Optimization of Third-Grade Nanofluid Slip Flow Embedded in a Porous Sheet With Zero Mass Flux and a Non-Fourier Heat Flux Model. Front. Phys. 8:250. doi: 10.3389/fphy.2020.00250
Received: 21 April 2020; Accepted: 08 June 2020;
Published: 24 November 2020.
Edited by:
Ahmed Zeeshan, International Islamic University, Islamabad, PakistanReviewed by:
Ali Chamkha, Prince Mohammad bin Fahd University, Saudi ArabiaPrecious Sibanda, University of KwaZulu-Natal, South Africa
Copyright © 2020 Loganathan, Muhiuddin, Alanazi, Alshammari, Alqurashi and Rajan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: G. Muhiuddin, Y2hpc2h0eWdtQGdtYWlsLmNvbQ==; K. Loganathan, bG9nYW5hdGhhbmthcnVwcHVzYW15MzA0QGdtYWlsLmNvbQ==
 K. Loganathan
K. Loganathan G. Muhiuddin
G. Muhiuddin A. M. Alanazi2
A. M. Alanazi2