Triple Diffusive Unsteady Flow of Eyring–Powell Nanofluid Over a Periodically Accelerated Surface With Variable Thermal Features

This research communicates the triple diffusion perspective of Eyring–Powell nano-materials configured by a periodically moving configuration. The thermal consequences of variable natures are utilized as a novelty. Combined magnetic and porous medium effects are also involved, which result in a magneto-porosity parameter. The thermophoretic and Brownian motion aspects are reported by using Buongiorno's nanofluid theory. The formulated flow equations in non-dimensional forms are tackled with the implementation of a homotopy analysis algorithm. A detailed physical investigation against derived parameters is presented graphically. Due to periodically accelerated surface, the oscillations in velocity and wall shear stress have been examined.

Introduction

Recent advances in nanotechnology have discovered an advanced source of energy based on utilization nanoparticles. Nanofluids have been interacted for the impressive thermal properties that turn into enhancement of energy transportation. The enhancement of thermo-physical features of conventional base liquids with the addition of micro-sized metallic particles is a relatively new and interesting development in nanotechnology. Nanoparticles attain microscopic size, having a range between 1 and 100 nm. Recently, the investigations on nano-materials become a new class of intense engineering research due to inherent significances in biomedical, chemical, and mechanical industries, electronic field, nuclear reactors, power plants, cooling systems, diagnoses, diseases, etc. The primary investigation on this topic was reported by Choi [1], which was further worked out by several scientists, especially in the current century. The convective features for nano-materials based on thermophoresis and Brownian movement phenomenon were notified by Buongiorno [2]. This investigation revealed that the role of thermophoresis and Brownian motion factors was quite essential for convective slip mechanism. Khan and Pop [3] discussed the feature of nanofluid immersed in base material confined by moving configuration. Sheikholeslami et al. [4] reported the features of thermal radiation in magneto-nanoparticle flow between circular cylinders. The slip flow in nano-material due to porous surface has been reported by Shahzadi et al. [5]. Khan et al. [6] directed their investigation regarding stability prospective of nanoliquids in a curved geometry and successfully estimated a dual solution for the formulated problem. Turkyilmazoglu [7] imposed zero mass flux constraints regarding asymmetric channels filled by nanoparticles. Vaidya et al. [8] enrolled the fundamental thermal characteristics in the three-dimensional (3D) flow of Maxwell nanofluid where analytical expressions were developed by using optimal homotopic procedure. Hayat et al. [9] focused on the thermal properties and developed the 3D flow of Oldroyd-B fluid featuring mixed convection effects. Some valuable closed-form expressions for a nanofluid flow problem in porous space have been computed by Turkyilmazoglu [10]. Krishna and Chamkha [11] investigated the ion and hall slip effects in the rotating flow of nanofluid configured by a vertical porous plate. The enhancement of heat transfer by using hybrid nanofluids having variable thermal viscosity was reported by Manjunatha et al. [12]. Sardar et al. [13] used non-Fourier's expressions for Carreau nanofluid and suggested some useful multiple numerical solutions successfully. Alwatban et al. [14] performed a numerical analysis to examine the rheological consequences in Eyring–Powell fluid subjected to the second-order slip along with activation energy. The stability analysis for bioconvection flow of nanofluid was reported by Zhao et al. [15]. Alkanhal et al. [16] involved thermal radiation and external heat source for nanofluid enclosed by a wavy shaped cavity. Kumar et al. [17] discussed the thermo-physical properties of hybrid ferrofluid in thin-film flow impacted by uniform magnetic field. Bhattacharyya et al. [18] evaluated the characteristics of different carbon nanotubes for coaxial movement of disks. Mekheimer and Ramdan [19] investigated the flow of Prandtl nanofluid in the presence of gyrotactic microorganisms over a stretching/shrinking surface.

Recently, researchers specified their attention toward the complex and interesting properties of non-Newtonian meterials due to their miscellaneous application in many industries and technologies. The non-Newtonian materials due to convoluted features attracted special attention especially in the current century. The novel physical importance of such non-Newtonian liquids in various engineering and physical processes, biological sciences, physiology, and manufacturing industries is associated due to complex rheological features. Some useful applications associated with the non-Newtonian fluids include polymer solutions, certain oil, petroleum industries, blood, honey, lubricants, and many more. It is commonly observed that distinctive features of such non-Newtonian fluid cannot be pointed out via single relation. Therefore, different non-Newtonian fluid models are suggested by investigators according to their rheology. Among these, Eyring–Powell fluid is inferred from kinetic laws of gases instead of any empirical formulas. This model reduces the viscous fluid at both low and high shear rates (see Powell and Eyring [19]). Gholinia et al. [20] carried out the homogenous and heterogeneous impact in flow of Powell–Eyring liquid due to rotating. Khan et al. [21] focused on viscosity-dependent mixed convection flow of Eyring–Powell nanofluid encountered by inclined surface. Salawu and Ogunseye [22] reported the entropy generation prospective in Eyring–Powell nanofluid featuring variable thermal consequences and electric field. Another useful continuation performed by Abegunrin et al. [23] examined the change in the boundary layer for the flow of Eyring–Powell fluid subjected by the catalytic surface reaction. Rahimi et al. [24] adopted a numerical technique to compute the numerical solution of a boundary value problem modeled due to the flow of Eyring–Powell fluid. Reddy et al. [25] involved some interesting thermal features, like activation energy, chemical reaction, and non-linear thermal radiation in the 3D flow of Eyring–Powell nanofluid induced via slandering surface. Hayat and Nadeem [26] examined the flow of Eyring–Powell fluid and suggested modification in energy and concentration expressions by using generalized Fourier's law. Ghadikolaei et al. [27] reported the Joule heating and thermal radiation features inflow of Eyring–Powell non-Newtonian fluid in a stretching walls channel.

The double diffusion convection is a natural phenomenon that encountered multiple novel applications in area soil sciences, groundwater, oceanography, petroleum engineering, food processing, etc. The double-diffusive convection refers to the intermixing of components of two fluid having different diffuse rates. However, the situation becomes quite interesting when double-diffusive convection depends upon more than two components of fluids. Examples of such multiple diffusive phenomenons include seawater, molten alloy solidification, and geothermally heated lakes. The triple diffusion flow appears in diverse engineering and scientific fields like geology, astrophysics, disposals of nuclear waste, deoxyribonucleic acid (DNA), chemical engineering, etc. [28–30].

After careful observation of the previously cited work, it is claimed that no efforts have been made to report the triple diffusion flow of Eyring–Powell nanofluid induced by an oscillatory stretching surface with variable thermal features. Although some investigations on flow that is due to periodical acceleration have been available in the literature, thermodiffusion features for Eyring–Powell nanofluid are not studied yet. Therefore, our prime objective of this contribution is to report the triple diffusion aspects of Eyring–Powell nanofluid flow by using variable thermal properties. The most interesting convergent technique homotopy analysis procedure is followed to simulate the solution [31–35]. The graphs are prepared to see the impact of different flow parameters with relevant physical consequence.

Flow Problem

To develop governing equations for unsteady flow of Eyring–Powell nanofluid, we have considered a periodically stretching surface where x-axis is assumed along with the stretched configuration, whereas y-axis is taken normally. The source of induced flow is based on the periodically moving surface where amplitude of oscillations are assumed to be small. Let velocity of the moving surface as u = u_ω = bx sin ωt, b as stretching rate, ω being angular frequency, whereas t represent time. The uniform features of the magnetic field are reported by implementing it vertically. Let T represent the temperature, C solutal concentration, whereas Φ report the nanoparticle volume fraction. Furthermore, T_∞, C_∞, and Φ_∞ denote free stream nanoparticle temperature, free stream solutal concentration, and volume fraction of nanofluid, respectively. After using such assumptions, the flow problem is modeled through the following equations [22, 33]:

$\begin{array}{ll}\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,& (1)\end{array}$

$\begin{array}{l}u\left(\frac{\partial u}{\partial x}\right)+v\left(\frac{\partial u}{\partial y}\right)+\frac{\partial u}{\partial t}=\left(\nu +\frac{1}{{\rho }_f{\beta }^{*}C}\right)\left(\frac{{\partial }^{2}u}{\partial y^2}\right)\\ -\frac{1}{2\rho {\beta }^{*}{C}^3}\left[{\left(\frac{\partial u}{\partial y}\right)}^2\frac{{\partial }^{2}u}{\partial y^2}\right]-\left(\frac{\sigma B_0^2}{{\rho }_f}+\frac{\nu \vartheta }{k^{\prime }}\right)u,& (2)\end{array}$

$\begin{array}{l}u\left(\frac{\partial T}{\partial x}\right)+\left(\frac{\partial T}{\partial y}\right)+\frac{\partial T}{\partial t}=\frac{1}{{\left(\rho c\right)}_p}\frac{\partial }{\partial y}\left(K\left(T\right)\frac{\partial T}{\partial y}\right)\\ +{\tau }_T\left[D_T\frac{\partial \varphi }{\partial y}\frac{\partial T}{\partial y}+\frac{D_T}{T_{\infty }}{\left(\frac{\partial T}{\partial y}\right)}^2\right]+D{K}_{TC}\left(\frac{{\partial }^{2}C}{\partial y^2}\right),& (3)\end{array}$

$\begin{array}{ll}u\left(\frac{\partial C}{\partial x}\right)+v\left(\frac{\partial C}{\partial y}\right)+\frac{\partial C}{\partial t}=D_s\left(\frac{{\partial }^{2}C}{\partial y^2}\right)+D{K}_{CT}\left(\frac{{\partial }^{2}T}{\partial y^2}\right),& (4)\end{array}$

$\begin{array}{ll}u\left(\frac{\partial \Phi }{\partial x}\right)+v\left(\frac{\partial \Phi }{\partial y}\right)+\frac{\partial \Phi }{\partial t}=D_B\left(\frac{{\partial }^2\Phi }{\partial y^2}\right)+\frac{D_T}{T_{\infty }}\left(\frac{{\partial }^{2}T}{\partial y^2}\right),& (5)\end{array}$

where ν is viscosity, ρ_f fluid density, (β^*, C) fluid parameters, ϑ permeability of porous medium, σ_e electrical conductivity, α₁ thermal diffusivity, DK_TC Dufour diffusivity, τ_T = (ρc)_p/(ρc)_f ratio of heat capacity of nanoparticles to heat capacity of fluid, D_B Brownian diffusion coefficients, D_s solutal diffusivity, D_T thermophoretic diffusion coefficient, whereas DK_CT Soret diffusivity.

Following boundary assumptions are articulated for current flow problem

$\begin{array}{l}u=u\left(x,t\right)=u_{w}sin\omega t=bxsin\omega t,v=0,\\ T=T_w,C=C_w,\Phi ={\Phi }_w\text{at }y=0,& (6)\end{array}$

$\begin{array}{ll}u\to 0,v\to 0,T\to T_{\infty },C\to C_{\infty },\Phi \to {\Phi }_{\infty }\text{at }y\to \infty .& (7)\end{array}$

In order to suggest modification in energy equation (3), we used the following relations for variable thermal conductivity [33, 34]

$\begin{array}{ll}K\left(T\right)=K_{\infty }\left[1+\epsilon \frac{\left(T-T_{\infty }\right)}{\Delta T}\right],& (8)\end{array}$

where K_∞ ambient fluid conductivity and ε thermal dependence conductivity constant. Now, before perfume analytical simulations, first, we reduce the number of independent variables in the governing equations by using the following variables:

$\begin{array}{l}\xi ={\left(\frac{b}{\nu }\right)}^{1/2}y,\tau =t\omega ,u=u_w{f}_y\left(\xi ,\tau \right),\\ v=-\sqrt{\nu b}f\left(\xi ,\tau \right),& (9)\end{array}$

$\begin{array}{l}\theta \left(\xi ,\tau \right)=\frac{\left(T-T_{\infty }\right)}{\left(T_w-T_{\infty }\right)},\phi \left(\xi ,\tau \right)=\left(\frac{\left(C-C_{\infty }\right)}{C_w-C_{\infty }}\right),\varphi \left(\xi ,\tau \right)\\ =\frac{\left(\Phi -{\Phi }_{\infty }\right)}{\left({\Phi }_w-{\Phi }_{\infty }\right)},& (10)\end{array}$

The dimensionless set of equations in view of the previously mentioned transformations is

$\begin{array}{ll}\left(1+K\right)f_{\xi \xi \xi }-S{f}_{\xi \tau }-f_{\xi }^2+f{f}_{\xi \xi }-\Omega f_{\xi }-\Gamma K{f}_{\xi \xi }^2{f}_{\xi \xi \xi }=0,& (11)\end{array}$

$\begin{array}{l}\left(1+\delta \theta \right){\theta }_{\xi \xi }+\delta {\left({\theta }_{\xi }\right)}^2+Pr[f{\varphi }_{\xi }-S{\varphi }_{\tau }+Nb{\theta }_{\xi }{\varphi }_{\xi }+Nt{\left({\theta }_{\xi }\right)}^2\\ +\left(Nd\right){\phi }_{\xi \xi }]=0,& (12)\end{array}$

$\begin{array}{ll}{\phi }_{\xi \xi }-S{\phi }_{\tau }+Le\left(f{\phi }_{\xi }\right)+Ld{\theta }_{\xi \xi }=0,& (13)\end{array}$

$\begin{array}{ll}{\varphi }_{\xi \xi }-S{\varphi }_{\tau }+Ln\left(f{\varphi }_{\xi }\right)+\frac{Nt}{Nb}{\theta }_{\xi \xi }=0,& (14)\end{array}$

The boundary constraints in the non-dimensional form are

$\begin{array}{l}{f}_{\xi }\left(0,\tau \right)=sin\tau ,f\left(0,\tau \right)=0,\\ \theta \left(0,\tau \right)=1,\phi \left(0,\tau \right)=1,\varphi \left(0,\tau \right)=1,& (15)\end{array}$

$\begin{array}{ll}{f}_y\left(\infty ,\tau \right)\to 0,\theta \left(\infty ,\tau \right)\to 0,\phi \left(\infty ,\tau \right)\to 0,\varphi \left(\infty ,\tau \right)\to 0,& (16)\end{array}$

where K = 1/μβ^*C and $\Gamma ={u_w}^{2}b/2\nu C^2$ denote the material parameters, $\Omega =\sigma B_0^2/{\rho }_{f}b+\nu \vartheta /k^{\prime }b$ is magneto-porosity constant, S = ω/b oscillating frequency-to-stretching rate ratio, N_t = (ρc)_pD_T (T_w − T_∞)/(ρc)_fT_∞ν thermophoresis parameter, Pr = ν/α_m is Prandtl number, N_b = (ρc)_pD_B (C_w − C_∞)/(ρc)_fν Brownian motion constant, Nd = D_TC (C_w − C_∞)/α_m (T_w − T_∞) modified Dufour number, Ld = D_CT (T_w − T_∞)/α_m (C_w − C_∞) Dufour Lewis number, Le = ν/D_s regular Lewis number, whereas Ln = ν/D_B nano-Lewis number.

We define the following relations associated with the definitions of wall shear stress, local Nusselt number, Sherwood number, and nano-Sherwood number:

$\begin{array}{l}{C}_f=\frac{{\tau }_w}{\rho u_w^2},N{u}_x=\frac{x{q}_s}{k\left(T_w-T_{\infty }\right)},S{h}_x=\frac{x{j}_s}{D_B\left(C_w-C_{\infty }\right)},\\ S{h}_{xn}=\frac{x{q}_m}{D_s\left({\phi }_w-{\phi }_{\infty }\right)},& (17)\end{array}$

where q_s, j_s, and g_s stand for surface heat flux, surface mass flux, and motile microorganisms flux, respectively. The dimensionless forms of the previously mentioned physical quantities are

$\begin{array}{ll}\begin{array}{l}{Re}_x^{1/2}{C}_f=\left(1+K\right)f_{\xi \xi }-\frac{K}{3}\beta {\left(f_{\xi \xi }\right)}_{\xi =0},\\ N{u}_x{Re}_x^{-1/2}=-{\theta }_{\xi }\left(0,\tau \right),\\ S{h}_x{Re}_x^{-1/2}=-{\phi }_{\xi }\left(0,\tau \right),\\ S{h}_n{Re}_x^{-1/2}=-{\varphi }_{\xi }\left(0,\tau \right).\end{array}\}& (18)\end{array}$

where ${Re}_x=u_w\bar{x}/\nu$ is mentioned for local Reynolds number.

Solution Methodology

The structured set of non-linear partial differential equations (12–16) with boundary conditions (17–18) are simulated analytically via homotopy analysis technique. Due to efficient and convincing accuracy, various physical problems in recent years have been solved by following this procedure. The initial guesses for the present flow problem are

$\begin{array}{l}{f}_0\left(\xi ,\tau \right)=sin\tau \left(1-e^{-\xi }\right),{\theta }_0\left(\xi \right)=e^{-\xi },{\phi }_0\left(\xi \right)=e^{-\xi },\\ {\varphi }_0\left(\xi \right)=e^{-\xi },& (19)\end{array}$

Following auxiliary linear operators that are followed to precede the solution

$\begin{array}{l}{\text{£}}_f=\frac{{\partial }^3}{\partial {\xi }^3}-\frac{\partial }{\partial \xi },{\text{£}}_{\theta }=\frac{{\partial }^2}{\partial {\xi }^2}-1,{\text{£}}_{\phi }=\frac{{\partial }^2}{\partial {\xi }^2}-1,\\ {\text{£}}_{\varphi }=\frac{{\partial }^2}{\partial {\xi }^2}-1,& (20)\end{array}$

satisfying

$\begin{array}{ll}{\text{£}}_f\left[a_1+a_2{e}^{\xi }+a_3{e}^{-\xi }\right]=0,& (21)\end{array}$

$\begin{array}{ll}{\text{£}}_{\theta }\left[a_4{e}^{\xi }+a_5{e}^{-\xi }\right]=0,& (22)\end{array}$

$\begin{array}{ll}{\text{£}}_{\phi }\left[a_6{e}^{\xi }+a_7{e}^{-\xi }\right]=0,& (23)\end{array}$

$\begin{array}{ll}{\text{£}}_{\varphi }\left[a_8{e}^{\xi }+a_9{e}^{-\xi }\right]=0,& (24)\end{array}$

where a₁, … a₉ are arbitrary constants.

Convergent Region

The convergence procedure in homotopic solution is regulated with auxiliary parameters h_f, h_θ, h_φ, and h_ϕ. On this end, we prepare h−curves to report the convincible range of such parameters. It is obvious from Figure 1 that the preferable range of these such parameters can be utilized from −2 ≤ h_f ≤ 0, −1.2 ≤ h_θ ≤ −0.2, −1.4 ≤ h_φ ≤ 0 and −1.2 ≤ h_ϕ ≤ −0.2.

FIGURE 1

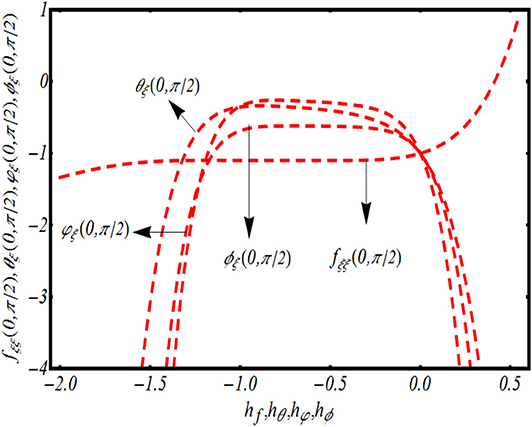
Figure 1. h− curves for f_ξξ (0, π/2), θ_ξ (0, π/2), φ_ξ (0, π/2), and ϕ_ξ (0, π/2) temperature, solutal concentration, and nanoparticle concentration.

Validation of Results

Table 1 shows the comparison of present results with Abbas et al. [35] as a limiting case. An excellent accuracy of results is noted with these reported investigations.

TABLE 1

Table 1. Comparison of f_ξξ (0, τ) for τ with Abbas et al. [35] when S = 1, Ω = 12, Γ = 0, and K = 0.

Discussion

This section aims to manifest the features of some interesting flow parameters that appeared in the dimensionless equations, where material parameter K, magneto-porosity constant Ω, oscillating frequency-to-rate of stretching ratio S, Brownian motion Nb, thermophoresis constant Nt, variable thermal conductivity δ, Prandtl number Pr, Dufour Lewis number Ld, modified Dufour constant Nd, regular Lewis number Le, and nano-Lewis number Ln. During variation of each flow parameter, we fixed some numerical values to remaining parameters, like K=0.2, Ω = 0.4, S = 0.2, Nt = 0.3, Pr = 0.7, Nb = 0.4, Nd,= 0.5, Ld = 0.3, Le = 0.2, and Ln = 0.3.

Skin Friction Coefficient

The impact of the skin friction coefficient against time τ for diverse variation of K and S is evaluated in Figures 2A,B. An interesting periodic oscillation in the wall shear stress is evaluated by both figures. Furthermore, the growing values of both parameters increase the amplitude of oscillation sufficiently. Due to no-slip conditions at the surface, the fluid particles accelerated together with surface in same amplitude and phase. However, the occurrence of a phase shift in both curves is almost negligible.

FIGURE 2

Figure 2. Impact of (A) K (B) S on skin friction coefficient.

Velocity Profile

The results reported in Figures 3A,B show the change in velocity f_ξ, verse time τ and leading values of material constant K, and magneto-porosity parameter Ω. Figure 3A characterized the influence of K on f_ξ, which shows that an increment in K leads to higher velocity amplitude. The physical justification of such enhancing velocity distribution is attributed to the lower viscosity of fluid associated with the higher values of K. However, reverse observations are predicated for Ω. In fact, magneto-porosity constant is the combination of magnetic field and porous space. The existence of a magnetic force encountered the effects of Lorentz force, in which a declining oscillation behavior is noticed. Similarly, the permeability of a porous medium also retards the velocity amplitude due to the loss of fluid. Moreover, the utilization of magnetic force enhances the apparent viscosity of fluid up to a certain point of becoming an elastic solid, and subsequently, the fluid stress can be managed upon changing the magnetic force. These interesting observations can be used in various processes, like magnetohydrodynamic drive ion propulsion, magnetohydrodynamic drive power generators, electromagnetic material casting, etc.

FIGURE 3

Figure 3. Impact of (A) K (B) Ω on velocity.

Temperature Distribution

To visualize the alter profile of nanoparticle temperature θ due to δ, K, and Nd, Figures 4A–C are prepared. Figure 4A reveals that temperature distribution θ increases with variable thermal conductivity constant δ. Figure 4B is constituted to observe the change in θ due to material parameter K. A fall in θ is associated with leading variation of K. An increment in viscosity would yield for arising values of K that increases the fluid velocity but a decline in the temperature of fluid. The change in θ with effect of modified Dufour number Nd has been reported in Figure 4C. A slightly dominant variation in θ is seen with larger values of Nd.

FIGURE 4

Figure 4. Impact of (A) δ, (B) K, (C) Nd.

Solutal Concentration Profile

Now, we observe the variation in solutal concentration profile φ by varying regular Lewis number (Le), Dufour Lewis constant (Ld), and material constant (K). Figure 5A is designed to observe the impact of Le on φ. A decreasing solutal concentration profile φ is notified due to Le. Physical explanation of such decling variation of φ can be justified on the fact that Le captures reverse relation with species diffusion, which means that when Le is maximum, species diffusion is lower, which leads to the decrement of the resulting solutal concentration. From Figure 5B, φ increases with the growth of Ld. Physically, Ld depends upon the Lewis number due to lower mass diffusivity. Figure 5C presents change in φ due to material constant K. Again, an enhanced distribution of solutal concentration profile φ has resulted for maximum values of K.

FIGURE 5

Figure 5. Impact of (A) Le, (B) Ld, and (C) K on solutal concentration.

Nanoparticle Concentration

The physical consequences of Ln, Nt, and Nb on concentration distribution ϕ are deliberated in Figures 6A–C. Figure 6A specified the input of Ln on ϕ. A declining concentration distribution ϕ is examined in the peak values of Ln. This decreasing behavior of ϕ is attributed to the fact that Ln is associated with the Brownian diffusion coefficient because Ln expresses the thermal diffusivity-to-mass diffusivity ratio. This parameter that is referred to the fluid flow in a phenomenon of heat and mass transfer occurs due to convection. The consequences for another important parameter, namely thermophoresis constant Nt, are analyzed in Figure 6B. As expected, a larger concentration distribution ϕ is reported due to involvement of Nt. The larger variation of Nt helps to improve the thermal conductivity of fluid. Physically, the thermophoretic process is based on collective migrated heat particles in the region of low temperature and plays a momentous role in many physical phenomenons. The curve of ϕ attained maximum level due to Nt. However, a reduced concentration distribution ϕ is associated with Nb, as shown in Figure 6C. The Brownian movement is based on random pattern moving fluid particles in flow surface. It is further justified from Equation (16), which clearly shows that reverse relation is developed between Nb and ϕ. In fact, the specified numerical values of Nb are associated to the more prominent nanoparticle moments that are being pushed back from accelerated plate to quiescent, which resulted in a retarded concentration distribution.

FIGURE 6

Figure 6. Impact of (A) Ln, (B) Nt, and (C) Nb.

Physical Quantities

To perform the numerical simulations for local Nusselt number −θ_ξ (0, τ), local Sherwood Number −φ_ξ (0, τ) and nanofluid Sherwood number −ϕ_ξ (0, τ), Table 2 is designed. It is observed that when Ω, ε, and K assigned larger numerical values, a decreasing trend in −θ_ξ (0, τ), −φ_ξ (0, τ), and −ϕ_ξ (0, τ) is reported. However, these physical quantities increase with the variation of Pr.

TABLE 2

Table 2. Numerical values of −θ_ξ (0, τ), −φ_ξ (0, τ), and −ϕ_ξ (0, τ), when τ = π/2.

Conclusions

We have focused on periodically accelerated unsteady flow of Eyring–Powell nanofluid with utilization of thermal diffusive features. The variable impact of thermal conductivity, porous medium, and magnetic field consequences are also utilized. The important observations from current flow problem are summarized as:

➢ The magneto-porosity parameter declined the periodic oscillation in the velocity, and subsequently, the magnitude of velocity declined.

➢ The wall shear stress oscillates periodically with time that increases by varying material parameter.

➢ The thermal conductivity with the variable nature is more effective in enhancing the nanoparticle temperature.

➢ The modified Dufour number increases the temperature distribution.

➢ It is noted that solutal concentration increases subject to Dufour Lewis number and material constant.

➢ An increasing change in nanoparticle concentration determined with nano-Lewis number and a material parameter.

The observation based on the reported results can be used to improve thermal extrusion processes, heat exchangers, solar technology, energy production, cooling processes, etc.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary materials, further inquiries can be directed to the corresponding author/s.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at Majmaah University for funding this work under project number: RGP-2019-1.

References

1. Choi S. Enhancing thermal conductivity of fluids with nanoparticles, development and applications of non-newtonian flow ASME. MD. (1995) 66:99–105.

Google Scholar

2. Buongiorno J. Convective transport in nanofluids. J Heat Transfer. (2010) 128:240–50. doi: 10.1115/1.2150834

CrossRef Full Text | Google Scholar

3. Khan WA, Pop I. Boundary layer flow of a nanofluid past a stretching sheet. Int J Heat Mass Transfer. (2010) 53:2477–83. doi: 10.1016/j.ijheatmasstransfer.2010.01.032

CrossRef Full Text | Google Scholar

4. Sheikholeslami M, Nimafar M, Ganji DD. Nanofluid heat transfer between two pipes considering brownian motion using AGM. Alexandria Eng J. (2017) 56:277–83. doi: 10.1016/j.aej.2017.01.032

CrossRef Full Text | Google Scholar

5. Shahzadi I, Nadeem S. Impinging of metallic nanoparticles along with the slip effects through a porous medium with MHD. J Braz Soc Mech Sci Eng. (2017) 39:2535. doi: 10.1007/s40430-017-0727-7

CrossRef Full Text | Google Scholar

6. Khan AU, Hussain ST, Nadeem S. Existence and stability of heat and fluid flow in the presence of nanoparticles along a curved surface by mean of dual nature solution. Appl Math Comput. (2019) 353:66–81. doi: 10.1016/j.amc.2019.01.044

CrossRef Full Text | Google Scholar

7. Turkyilmazoglu M. Buongiorno model in a nanofluid filled asymmetric channel fulfilling zero net particle flux at the walls. Int J Heat Mass Transfer. (2018) 126:974–9. doi: 10.1016/j.ijheatmasstransfer.2018.05.093

CrossRef Full Text | Google Scholar

8. Vaidya H, Prasad KV, Vajravelu K, Shehzad SA, Basha H. Role of variable liquid properties in 3d flow of maxwell nanofluid over convectively heated surface: optimal solutions. J Nanofluids. (2019) 8:1133–46. doi: 10.1166/jon.2019.1658

CrossRef Full Text | Google Scholar

9. Hayat T, Ullah I, Muhammad T, Alsaedi A. Thermal and solutal stratification in mixed convection three- dimensional flow of an oldroyd-B nanofluid. Result Phys. (2017) 7:3797–805. doi: 10.1016/j.rinp.2017.09.051

CrossRef Full Text | Google Scholar

10. Turkyilmazoglu M. MHD natural convection in saturated porous media with heat generation/absorption and thermal radiation: closed-form solutions. Arch Mech. (2019) 71:49–64. doi: 10.24423/aom.3049

CrossRef Full Text | Google Scholar

11. Krishna MV, Chamkha AJ. Hall and ion slip effects on MHD rotating boundary layer flow of nanofluid past an infinite vertical plate embedded in a porous medium. Results Phys. (2019) 15:102652. doi: 10.1016/j.rinp.2019.102652

CrossRef Full Text | Google Scholar

12. Manjunatha S, Kuttan A, Jayanthi S, Chamkha A, Gireesha BJ. Heat transfer enhancement in the boundary layer flow of hybrid nanofluids due to variable viscosity and natural convection. Heliyon. (2019) 5:e01469. doi: 10.1016/j.heliyon.2019.e01469

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Sardar H, Khan M, Alghamdi M. Multiple solutions for the modified Fourier and Fick's theories for Carreau nanofluid. Ind J Phys. (2019) doi: 10.1007/s12648-019-01628-y

CrossRef Full Text | Google Scholar

14. Alwatban AM, Khan SU, Waqas H, Tlili I. Interaction of Wu's slip features in bioconvection of Eyring Powell nanoparticles with activation energy. Processes. (2019) 7:859. doi: 10.3390/pr7110859

CrossRef Full Text | Google Scholar

15. Zhao M, Xiao Y, Wang S. Linear stability of thermal-bioconvection in a suspension of gyrotactic micro-organisms. Int J Heat Mass Transfer. (2018) 126:95–102. doi: 10.1016/j.ijheatmasstransfer.2018.05.030

CrossRef Full Text | Google Scholar

16. Alkanhal TA, Sheikholeslami M, Usman M, Haq R-U, Shafee A, SaadAl-Ahmadi A, et al. Thermal management of MHD nanofluid within the porous medium enclosed in a wavy shaped cavity with square obstacle in the presence of radiation heat source, Int J Heat Mass Transfer. (2019) 139:87–94. doi: 10.1016/j.ijheatmasstransfer.2019.05.006

CrossRef Full Text | Google Scholar

17. Anantha Kumar K, Sandeep N, Sugunamma V, Animasaun IL. Effect of irregular heat source/sink on the radiative thin film flow of MHD hybrid ferrofluid. J Therm Anal Calorim. (2020) 139:2145. doi: 10.1007/s10973-019-08628-4

CrossRef Full Text

18. Bhattacharyya A, Seth GS, Kumar R, Chamkha AJ. Simulation of cattaneo-christov heat flux on the flow of single and multi-walled carbon nanotubes between two stretchable coaxial rotating disks. J Therm Anal Calorim. (2020) 139:1655. doi: 10.1007/s10973-019-08644-4

CrossRef Full Text | Google Scholar

19. Mekheimer SKH, Shaimaa Ramadan F. New Insight into gyrotactic microorganisms for Bio-thermal convection of Prandtl nanofluid past a stretching/shrinking permeable sheet. SN Appl Sci. (2020) 2:450. doi: 10.1007/s42452-020-2105-9

CrossRef Full Text | Google Scholar

20. Powell RE, Eyring H. Mechanisms for the relaxation theory of viscosity. Nature. (1944) 154:427–28. doi: 10.1038/154427a0

CrossRef Full Text | Google Scholar

21. Gholinia M, Hosseinzadeh Kh, Mehrzadi H, Ganji DD, Ranjbar AA. Investigation of MHD eyring-Powell fluid flow over a rotating disk under effect of homogeneous-heterogeneous reactions. Case Stud Thermal Eng. (2019) 13:100356. doi: 10.1016/j.csite.2018.11.007

CrossRef Full Text | Google Scholar

22. Sami UK, Nasir A, Zaheer A. Soret and dufour effects on hydromagnetic flow of eyring powell fluid over an oscillatory stretching surface with heat generation/absorption and chemical reaction. Thermal Sci. (2018) 22:533–43. doi: 10.2298/TSCI150831018U

CrossRef Full Text | Google Scholar

23. Salawu SO, Ogunseye HA. Entropy generation of a radiative hydromagnetic powell-eyring chemical reaction nanofluid with variable conductivity and electric field loading. Res Eng. (2020) 5:100072. doi: 10.1016/j.rineng.2019.100072

CrossRef Full Text | Google Scholar

24. Abegunrin OA, Animasaun IL, Sandeep N. Insight into the boundary layer flow of non-newtonian eyring-powell fluid due to catalytic surface reaction on an upper horizontal surface of a paraboloid of revolution. Alexandria Eng J. (2018) 57:2051–60. doi: 10.1016/j.aej.2017.05.018

CrossRef Full Text | Google Scholar

25. Rahimi J, Ganji DD, Khaki M, Hosseinzadeh Kh. Solution of the boundary layer flow of an eyring-powell non-newtonian fluid over a linear stretching sheet by collocation method. Alexandria Eng J. (2017) 56:621–7. doi: 10.1016/j.aej.2016.11.006

CrossRef Full Text | Google Scholar

26. Reddy SRR, Bala Anki Reddy P, Bhattacharyya K. Effect of nonlinear thermal radiation on 3D magneto slip flow of eyring-powell nanofluid flow over a slendering sheet with binary chemical reaction and arrhenius activation energy. Adv Powder Technol. (2019) 30:3203–13. doi: 10.1016/j.apt.2019.09.029

CrossRef Full Text | Google Scholar

27. Hayat T, Nadeem S. Flow of 3D eyring-powell fluid by utilizing cattaneo-christov heat flux model and chemical processes over an exponentially stretching surface. Res. Phys. (2018) 8:397–403. doi: 10.1016/j.rinp.2017.12.038

CrossRef Full Text | Google Scholar

28. Ghadikolaei SS, Hosseinzadeh Kh, Ganji DD. Analysis of unsteady MHD Eyring-Powell squeezing flow in stretching channel with considering thermal radiation and Joule heating effect using AGM. Case Stud Thermal Eng. (2017) 10:579–94. doi: 10.1016/j.csite.2017.11.004

CrossRef Full Text | Google Scholar

29. Raghunatha KR, Shivakumara IS. Stability of triple diffusive convection in a viscoelastic fluid-saturated porous layer. Appl Math Mech Engl Ed. (2018) 39:1385–410. doi: 10.1007/s10483-018-2376-8

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Daba M, Devaraj P. Unsteady double diffusive mixed convection flow over a vertically stretching sheet in the presence of suction/injection. J Appl Mech Tech Phys. (2017) 58:232–43. doi: 10.1134/S0021894417020067

CrossRef Full Text | Google Scholar

31. Khan ZH, Culham JR, Khan WA, Pop I. Triple convective-diffusion boundary layer along a vertical flat plate in a porous medium saturated by a water-based nanofluid. Int J Thermal Sci. (2015) 90:53e61. doi: 10.1016/j.ijthermalsci.2014.12.002

CrossRef Full Text | Google Scholar

32. Liao SJ. Advances in the Homotopy Analysis Method. Singapore: World Scientific Publishing. (2014) doi: 10.1142/8939

CrossRef Full Text | Google Scholar

33. Khan SU, Shehzad SA, Abbasi FM, Arshad SH. Thermo diffusion aspects in Jeffrey nanofluid over periodically moving surface with time dependent thermal conductivity. Thermal Sci. (2019). doi: 10.2298/TSCI190428312U

CrossRef Full Text | Google Scholar

34. Mekheimer SKh, Abd elmaboud Y. Simultaneous effects of variable viscosity and thermal conductivity on peristaltic flow in a vertical asymmetric channel. Can J Phys. (2014) 92:1541–55. doi: 10.1139/cjp-2013-0465

CrossRef Full Text | Google Scholar

35. Abbas Z, Wang Y, Hayat T, Oberlack M. Hydromagnetic flow ina viscoelastic fluid due to the oscillatory stretching surface. Int J Non-Linear Mech. (2008) 43:783–97. doi: 10.1016/j.ijnonlinmec.2008.04.009

PubMed Abstract | CrossRef Full Text | Google Scholar