- 1Dipartimento di Matematica e Fisica, “Ennio de Giorgi”, Università del Salento, Lecce, Italy
- 2Dipartimento di Ingegneria dell' Innovazione, Università del Salento, Lecce, Italy
The quantum formula of the fluctuation dissipation theorem (FDT) was given by Callen and Welton in 1951 [1] for the case of conductors, and then expanded by Kubo in 1966 [2, 3]. The drawback of these quantum relations concerns with the appearance of a zero-point contribution, hω/2 with h the reduced Planck constant and ω the angular frequency of the considered photon, which implies a divergence of the fluctuation spectrum at increasing frequencies. This divergence is responsible for a vacuum-catastrophe, to keep the analogy with the well-known ultraviolet catastrophe of the classical black-body radiation spectrum. As a consequence, the quantum formulation of the FDT as given by Callen-Welton and Kubo introduces a Field Grand Challenge associated with the existence or less of a vacuum-fluctuations catastrophe for the energy-density spectrum. Here we propose a solution to this challenge by taking into account of the Casimir energy that, in turns, is found to be responsible for a quantum correction of the Stefan-Boltzmann law.
1. Introduction
The quantum form of the fluctuation dissipation theorem (FDT) was given by Callen and Welton in 1951 [1] for the case of conductors, and then expanded by Kubo in 1957–1966 [2, 3]. The drawback of these quantum relations concerns with the appearance of a zero-point contribution, ℏω/2 with ℏ the reduced Planck constant and ω = 2πf the angular frequency of the considered photon, which implies a divergence of the energy-spectrum radiated by a physical system at a given temperature at increasing frequencies. This divergence is responsible for a vacuum-catastrophe, to keep the analogy with the well-known ultraviolet catastrophe of the classical black-body radiation spectrum. As a consequence, the quantum form of the FDT as formulated by Callen-Welton and Kubo (CWK) introduces a Field Grand Challenge associated with the existence or less of a vacuum-fluctuations catastrophe for the energy spectrum. Here we propose a solution to this challenge by taking into account of the Casimir force [4].
In the next section we reformulate the FDT by accounting for the presence of the Casimir energy and the associated Casimir force, a genuine quantum phenomena neglected by CWK. Major conclusions are then drawn in the final section.
2. Formulation of the Fluctuation Dissipation Theorem
The essence of the problem addressed here is to consider u(f, T), i.e., “the energy-spectrum radiated into a single mode of the electromagnetic field by our physical system (i.e., a black-body) coupled to a reservoir at temperature T [5].” Accordingly, following Planck 1912 [6], Callen-Welton 1951 [1], and Kubo 1957–1966 [2, 3], the quantum formulation that includes zero-point contribution is found to be a universal function given by:
where KB is the Boltzmann constant and x = ℏω/(KBT).
The quantity uP(f, T) refers to Planck 1901 [7] quantum formulation. Figure 1 reports the different shapes of u(f, T)/u(0, T) as function of hf/(KBT) according to different models proposed in the literature [8–10]. The total energy, U, associated with the spectral density is defined as:
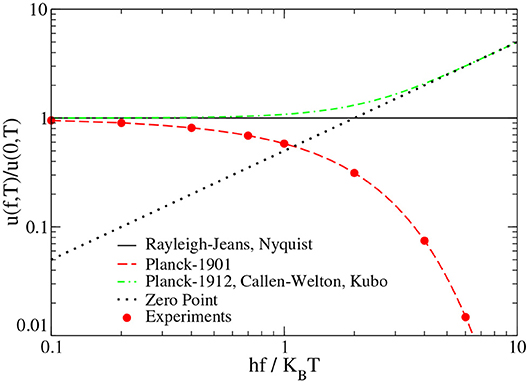
Figure 1. Different shapes of u(f, T)/u(0, T) as function of hf/(KBT) according to different models: continuous curve refers to Rayleigh-Jeans 1900 and Nyquist 1928, dashed curve refers to Planck 1901 black-body without zero-point contribution, dot-dashed curve refers to Planck 1912, Callen and Welton 1951, Kubo 1966 with zero-point contribution included, dotted curve refers to zero-point only, full circles report available experimental results.
where the sum is extended over all the photon modes, and V is the volume of the physical system. The sum can be carried out in the frequency or in the wavevector space according to convenience.
By inserting uP(f, T) it is obtained [5]
where is the mean number of photons inside the volume V of the physical system at the given temperature. We notice that, by analogy with the case of a classical gas, Equation (3) expresses the Stefan-Boltzmann law in terms of the mean number of photon times the average photon-energy. We notice that, the Stefan-Boltzmann law is here associated with the T3 increase of the average photon-number with temperature, a quantum effect associated with the Boson nature of photon statistics and implicitly accounted for by Boltzmann who set to zero the value of the chemical potential in his derivation of the law without any justification [11].
By adding the zero-point contribution, the quantum formulation including zero-point contribution leads to
the so called vacuum catastrophe, determined by the intuitive expectation that, using Callen-Welton words [1]: …the ℏω/2 term gives the familiar infinite zero-point contribution… Therefore, only the Planck-1901 form, uP(f, T), leads to a finite value of U(T), in agreement with experiments and Stefan-Boltzmann law, as reported in Figure 1. In particular, the separation into two contributions of u(f, T), as given by the last expression in the r.h.s. of Equation (1), is of most physical importance.
Indeed, the first term is the original Planck-contribution that represents a property of the coupling between the thermal reservoir and the physical system. As such, it is a universal function of the temperature and the volume of the system, which takes a finite value at any frequency and is independent of the external shape of the physical system. Furthermore, its spectrum can be directly measured by standard experimental techniques in a wide range of frequencies, typically from far infrared up to ultraviolet frequencies where excellent agreement between theory and experiments is a standard achievement, as reported in Figure 1. This contribution involves the photons inside the volume of the physical system and is the responsible of the thermal agitation at an atomic level of the electrical charge in conductors.
By contrast, the second term, ℏω/2, represents a quantum property of the vacuum and, by definition, it involves all the photons outside and inside the physical system. Furthermore, being independent of temperature it does not vanish at T = 0. However, as considered by Casimir in 1948 [4], by accounting for the boundary conditions of the physical system its expectation value gives a finite value, UC, that implies an attractive or a repulsive force, FC, acting between opposite surfaces of the physical system. Calculations of UC are not easy to be performed [12–15], and here we report the results obtained by Casimir [4] for the simple case when opposite surfaces consist of two thin parallel conducting plates in vacuum. The final result gives for the Casimir energy a finite and negative value as
with A the area of each metallic plate, c is the light speed in vacuum, and L the distance between the plates.
The negative value of the Casimir energy, UC, implies an attractive force (the Casimir force) between opposite conducting plates given by
To date, these Casimir forces are thought to pertain to a more general family of so called fluctuation-induced forces that are ubiquitous in nature covering many topics from biophysics to cosmology [16–20]. As a consequence of this force, the physical system becomes mechanically unstable and the opposite conducting plates forming the terminals of the physical system would tend to implode [21, 22] when left free to move. By following standard mechanical arguments, to keep the stability a reaction vincular force FRV = −FC, mostly attributed to the rigidity of the physical system (i.e., the black-body box) associated with its elastic properties [23, 24], should be introduced [25]. We remark, that for macroscopic physical systems of centimeter length scale both forces take negligible values (of the order of 10−23 N) and the corresponding Casimir energy is of about 14 orders of magnitude less than the Planck energy at room temperature [25]. By accounting for the Casimir force and the associated vincular reaction, at thermodynamic equilibrium the resultant of both forces is null, thus supporting the conjecture that once mechanical stability is established zero-point energy cannot be extracted, but its macroscopic effects are simply stored in the rigidity (implied by the mechanical stability) of the physical system [25]. Indeed, the omission of the whole zero-point energy in considering black-body radiation spectrum is often encouraged (without justification) for all practical calculations [26, 27]. This omission is here justified by the fact that “quantum agitation of vacuum does not interfere with carrier thermal-agitation in a medium, rather it can be exactly compensated by forcing the stability of the physical system” [5]. As a consequence, we are justified to drop the zero-point contribution in the expression (1) for the energy spectrum and recover the celebrated Planck distribution-law [7]. We conclude [5], that the original Planck 1901 [7] expression for the black-body radiation emission as well as the Nyquist relation for the electrical noise in dissipative conductors which replaces KBT by the Planck distribution (as originally suggested by Nyquist himself [28]) are physically justified for macroscopic physical systems, in full agreement with experimental evidence.
3. Conclusions
In this paper we reconsider the fluctuation dissipation theorem (FDT) in its quantum form as given in the seminal papers by Callen-Welton [1] and Kubo [2, 3] (CWK). We assert that the zero-point energy, that is present in the quantum formulation of CWK, does not contribute to the macroscopic electrical fluctuations but is responsible of the Casimir force [4], a genuine quantum-relativistic effect, that by implying a mechanical instability of the physical system under test should be exactly balanced by a reaction force in order to recover stability-conditions of the physical system. In most cases (e.g., macroscopic systems), the reaction force is negligible and can be absorbed by the elastic properties of the environment in which the physical system is embedded. As a consequence, the claim that CWK generalize Nyquist relation including quantum effects should more properly refer to the equation where zero-point contribution is neglected, as intuitively proposed by Nyquist himself in the very final paragraph of his 1928 paper [28]. Indeed, in the pioneer paper of Callen and Welton the sentence concerning the infinite zero-point contribution should be more properly changed in …gives the Casimir energy that, when correctly evaluated: (i) its value is finite and depends on the geometry and the material of the physical system under test and, (ii) is responsible of an attractive or repulsive force between opposite plates of the physical system that can be independently detected. By contrast, Kubo [2, 3] never discussed the problem of the infinite zero-point contribution, and in his work of 1957 simply remarked …The situation is more complicated for the antisymmetric part of the static conductivity. If one wish to use the correlation function instead of the response function, one has to be careful about a quantum effect which appears as (a quantum time scale) Γ(t) = 2/(πℏ) logcoth[πKBT|t|/(2ℏ)] in Equation (7.15) and which replaces the classical value limh → 0Γ(t) = δ(t)/(KBT), which is naturally to be expected.
We stress that the total energy associated with the radiation by the black-body should be written as the sum of two contributions:
Where UP can be referred to the original Stefan-Boltzmann law and UC to the quantum-relativistic Casimir contribution. In this we differ from CWK who did not evaluate the finite value of UC in the spirit of the Casimir effect. As a consequence, UC can be considered as a quantum correction to the Stefan-Boltzmann law that was originally obtained by using classical thermodynamics and classical electromagnetism only, thus without invoking explicitly any quantum arguments. The fact that for macroscopic systems UC takes negligible values is a reason why till now its contribution was not explicitly detected from fluctuations spectra. However, for microscopic systems (i.e., in the case of atomic scale lengths) and sufficiently low temperatures, its effect should become relevant, as evidenced by experiments on the Casimir effects [12–15]. An experimental analysis of the cross-over from the Planck to the Casimir energy remains a mandatory issue to be investigated.
We finally remark that a set of further relevant properties concerning the FDT appeared in the literature after the CWK seminal papers. To this purpose the interested reader is sent to a recent review by the same Authors [5] that provides a historical revisitation of the FDT since the middle of the nineteenth century. Also, it is worth mentioning the importance of the formulation presented here for a current cosmological problem, such as the horizon of black holes [29].
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
LR analyzed the history of the topics. EA detailed the calculations. All authors contributed to the article and approved the submitted version.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Dr. T. Kuhn from Münster University, Germany, is warmly thanked for valuable discussions on the subject.
References
1. Callen H, Welton T. Irreversibility and generalized noise. Phys Rev. (1951) 83:34–40. doi: 10.1103/PhysRev.83.34
2. Kubo R. Statistical-mechanical theory of irreversible processes I. Phys Soc Jpn. (1957) 12:570–86. doi: 10.1143/JPSJ.12.570
3. Kubo R. The fluctuation-dissipation theorem. Rep Prog Phys. (1966) 29:255–84. doi: 10.1088/0034-4885/29/1/306
4. Casimir H. On the attraction between two perfectly conducting plates. Proc Knowl Ned Akad Wet. (1948) 51:793–95.
5. Reggiani L, Alfinito E. Fluctuation dissipation theorem and electrical noise revisited. Fluct Noise Lett. (2018) 18:1930001. doi: 10.1142/S0219477519300015
6. Planck M. Uber die begrundung des gesetzes der schwarzen strahlung (on the grounds of the law of black body radiation). Ann Phys. (1912) 6:642–59. doi: 10.1002/andp.19123420403
7. Planck M. Ueber das gesetz der energieverteilung im normalspectrum (on the law of distribution of energy in the normal spectrum). Ann Phys. (1901) 4:553–63.
11. Montambauux G. Generalized Stefan-Boltzmann law. Found Phys. (2018) 48:395. doi: 10.1007/s10701-018-0153-4
12. Milton K. The Casimir Effect: Physical Manifestations of Zero-Point Energy. Singapore: World Scientific Publishing (2001).
13. Edery A. Casimir forces in Bose-Einstein condensate: finite size effects in three dimensional rectangular cavities. J Stat Mech. (2006) 06:P06007. doi: 10.1088/1742-5468/2006/06/P06007
14. Schmidt F, Diehl H. Crossover from attractive to repulsive casimir force and vice versa. Phys Rev Lett. (2008) 101:10601–4. doi: 10.1103/PhysRevLett.101.100601
16. Buenzli PR. Fluctuation-induced self-force and violation of action-reaction in a nonequilibrium steady state fluid. J Phys Conf Ser. (2009) 161:012036. doi: 10.1088/1742-6596/161/1/012036
17. Kardar M, Golestanian R. The “Friction” of vacuum, and other fluctuation–induced forces. Rev Mod Phys. (1999) 71:1233–47. doi: 10.1103/RevModPhys.71.1233
18. Mishonov T, Dimitrova I, Varonov A. Callen–Welton fluctuation dissipation theorem and nyquist theorem as a consequence of detailed balance principle applied to an oscillator. Phys A. (2019) 530:121577. doi: 10.1016/j.physa.2019.121577
19. Sciama D. The physical significance of the vacuum state of a quantum field. In: Saunders S, Brown HR, Editors. The Philosophy of Vacuum. Oxford: Oxford University Press (1991). p. 137–58.
20. Rugh S, Zinkernagel H. The quantum vacuum and the cosmological constant problem. Stud Hist Philos Modern Phys. (2002) 33:663–705. doi: 10.1016/S1355-2198(02)00033-3
22. Lebowitz J, Lieb E. Existence of thermodynamics for real matter with coulomb forces. Phys Rev Lett. (1969) 13:631–4. doi: 10.1103/PhysRevLett.22.631
24. Qu J, Benz S, Rogalla H, Tew W, White D, Zhou K. Johnson noise thermometry. Measure Sci Technol. (2019) 30:112001. doi: 10.1088/1361-6501/ab3526
25. Reggiani L, Alfinito E. The puzzling of zero-point energy contribution to black-body radiation spectrum: the role of casimir force, fluct. Noise Lett. (2017) 16:1771002. doi: 10.1142/S021947751771002X
26. Kogan S. Electronic Noise and Fluctuations in Solids. Cmbridge: Cambridge University Press (1996).
27. Prigogine I, Kondepudi D. Modern Thermodynamics: From Heat Engines to Dissipative Structures. Hoboken, NJ: Wiley (2014).
28. Nyquist H. Thermal agitation of electric charge in conductors. Phys Rev. (1928) 32:110–3. doi: 10.1103/PhysRev.32.110
Keywords: fluctuation dissipation theorem, Casimir effect, noise, vacuum fluctuations, zero-point energy, Stefan-Boltzmann law
Citation: Reggiani L and Alfinito E (2020) Beyond the Formulations of the Fluctuation Dissipation Theorem Given by Callen and Welton (1951) and Expanded by Kubo (1966). Front. Phys. 8:238. doi: 10.3389/fphy.2020.00238
Received: 27 April 2020; Accepted: 02 June 2020;
Published: 10 July 2020.
Edited by:
Fernando A. Oliveira, University of Brasilia, BrazilReviewed by:
Muktish Acharyya, Presidency University, IndiaIgnazio Licata, Institute for Scientific Methodology (ISEM), Italy
Copyright © 2020 Reggiani and Alfinito. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lino Reggiani, bGluby5yZWdnaWFuaUB1bmlzYWxlbnRvLml0
 Lino Reggiani
Lino Reggiani Eleonora Alfinito
Eleonora Alfinito