Different Types of Progressive Wave Solutions via the 2D-Chiral Nonlinear Schrödinger Equation

A versatile integration tool, namely the protracted (or extended) Fan sub-equation (PFS-E) technique, is devoted to retrieving a variety of solutions for different models in many fields of the sciences. This essay presents the dynamics of progressive wave solutions via the 2D-chiral nonlinear Schrödinger (2D-CNLS) equation. The solutions acquired comprise dark optical solitons, periodic solitons, singular dark (bright) solitons, and singular periodic solutions. By comparing the results gained in this work with other literature, it can be noticed that the PFS-E method is an useful technique for finding solutions to other similar problems. Furthermore, some new types of solutions are revealed that will help us better understand the dynamic behaviors of the 2D-CNLS model.

1. Introduction

The attainment of analytical solutions for different models described by NLPDEs plays a major role in applied mathematics, fluid mechanics, fluid dynamics, plasma and solid-state physics, nonlinear optics, and chemistry. Among these solutions, the optical solitons, which have significant applications in modern communication systems, and have attracted particular attention from physicists as well as mathematicians [1–5]. Optical solitons can propagate over extremely large distances without shape change when a balance between the linear dispersion and nonlinear effects is achieved. There are many types of solitons, including bright, dark, anti-dark, and singular solitons, amongst many others. Bright solitons exist on a zero-intensity background, while dark solitons arise as an intensity dip in an infinitely extended constant background. Moreover, dark solitons are less influenced by the perturbations, which means that dark solitons could be more preferable than bright ones in optical communication systems. The anti-dark solitons have profiles similar to those of the bright ones but exist on a nonzero background like the dark ones [6, 7]. Many effective methods have been presented to solve these equations [8–26].

The PFS-E method [27, 28] is a direct and concise method to solve nonlinear evolution equations. It is employed to find and study the wave solutions of the 2D-CNLS equation. The predominating equation is described by [29–32]:

$\begin{array}{l}i{\Phi }_t+{\mu }_1({\Phi }_{xx}+{\Phi }_{yy})\\ +i({\mu }_2(\Phi {\Phi }_x^{*}+{\Phi }^{*}{\Phi }_x)+{\mu }_3(\Phi {\Phi }_y^{*}+{\Phi }^{*}{\Phi }_y))\Phi =0,& (1)\end{array}$

where Φ = Φ(x, y, t) refers to the complex-valued function, μ₁ is the second-order dispersion coefficient, and μ₂, μ₃ are the self-steepening coefficients. The 2D-CNLS equation has been established by a one-dimensional reduction of the structure that defines the fractional quantum Hall effect (it is a quantum-mechanical version of the Hall effect existing in 2D electron systems related to strong magnetic fields and low temperatures). An extraordinary characteristic of Equation (1) is the nonlinearity of the current density, which informs the new execution for the SPM and self-focusing through the current [29–32]. This equation cannot pass the Painlevè test of integrability and is not invariant under the Galilean transformation [32].

Bulut et al. [30] discussed Equation (1) in 1D and 2D and found bright and dark soliton solutions via the extended sinh-Gordon equation method. Nishino et al. [33] solved Equation (1) in 1D only and introduced two categories of wave solutions like bright and dark soliton trains. Very recently, Raza and Javid [32] investigated the singular and dark solitons for the 2D-CNLS equation by two different approaches, namely the extended direct algebraic and trial equation methods. To the best of our knowledge, no studies have found optical wave solutions for (1) via the extended Fan sub-equation method.

The paper is organized as follows. Different solutions for the 2D-CNLS equation are evaluated in section 2. The physical interpretation of the solutions is discussed in section 3. The main deductions are presented in section 4.

2. Mathematical Analysis

In this section, we use the PFS-E technique to find more forms of exact solutions for Equation (1) by considering a more general transformation stated in [34, 35]. The PFS-E method includes an algebraic strategy to find different analytical solutions for NLPDEs that can be expressed as a polynomial in the variable that satisfies the general Riccati equation. The most significant achievement of this approach is that it offers all the solutions that can be found by the use of other methods such as processes using the Riccati equation, an elliptic equation of the first kind, an auxiliary ordinary equation, or the generalized Riccati equation as mapping equation.

Let the wave profile be defined as

$\begin{array}{ll}\Phi (x,y,t)=e^{i\psi }\Omega (\xi ),& (2)\end{array}$

while the amplitude

$\begin{array}{ll}\xi ={\alpha }_{1}x+{\beta }_{1}y-\lambda t,& (3)\end{array}$

and

$\begin{array}{ll}\psi ={\alpha }_{0}x+{\beta }_{0}y+{\lambda }_{0}t+{\eta }_0.& (4)\end{array}$

Inserting (2) into (1) and separating its real and imaginary parts, we get

$\begin{array}{ll}{\delta }_1\Omega -{\delta }_2{\Omega }^3-{\delta }_3{\Omega }^{″}=0,& (5)\end{array}$

where

$\begin{array}{l}{\delta }_1={\mu }_1\left({\alpha }_0^2+{\beta }_0^2\right)+{\lambda }_0,\\ {\delta }_2=2\left({\alpha }_0{\mu }_2+{\beta }_0{\mu }_3\right),\\ {\delta }_3={\mu }_1\left({\alpha }_1^2+{\beta }_1^2\right),& (6)\end{array}$

and

$\begin{array}{ll}(2{\mu }_1({\alpha }_0{\alpha }_1+{\beta }_0{\beta }_1)-\lambda )\frac{\partial \Omega }{\partial \xi }=0.& (7)\end{array}$

From (7), we have

$\begin{array}{ll}\lambda =2{\mu }_1({\alpha }_0{\alpha }_1+{\beta }_0{\beta }_1).& (8)\end{array}$

From the homogeneous balance condition on (5), the general solution can be written as

$\begin{array}{ll}\Omega =a_0+a_1\varphi (\xi ),& (9)\end{array}$

where ϕ is given by the following auxiliary equation,

$\begin{array}{ll}(\frac{d\varphi (\xi )}{d\xi }{)}^2={\zeta }_0+{\zeta }_1\varphi (\xi )+{\zeta }_2{\varphi }^2(\xi )+{\zeta }_3{\varphi }^3(\xi )+{\zeta }_4{\varphi }^4(\xi ),& (10)\end{array}$

where ζ_i(i = 0, 1, 2, 3, 4) are free parameters.

Plugging (9) and (10) into (5) and setting the coefficients of ϕ^j, j = 0, 1, ⋯ , 4 identical zero, we get

$\begin{array}{l}{a}_0^3(-{\delta }_2)+a_0{\delta }_1-\frac{1}{2}{a}_1{\delta }_3{\zeta }_1=0,\\ -3a_1{a}_0^2{\delta }_2+a_1{\delta }_1-a_1{\delta }_3{\zeta }_2=0,\\ -3a_0{a}_1^2{\delta }_2-\frac{3}{2}{a}_1{\delta }_3{\zeta }_3=0,\\ -a_1^3{\delta }_2-2a_1{\delta }_3{\zeta }_4=0.& (11)\end{array}$

Here, suitable values are selected for ζ_i, (i = 0, 1, 2, 3, 4).

$\begin{array}{l}{\zeta }_0={\zeta }_0,\\ {\zeta }_1=-\frac{2\left(a_0^3{\delta }_1+3a_0{\delta }_3\right)}{3a_1{\delta }_2},\\ {\zeta }_2=-\frac{a_0^2{\delta }_1+{\delta }_3}{{\delta }_2},\\ {\zeta }_3=-\frac{2a_0{a}_1{\delta }_1}{3{\delta }_2},\\ {\zeta }_4=-\frac{a_1^2{\delta }_1}{6{\delta }_2},& (12)\end{array}$

which give

$\begin{array}{l}{a}_0=\frac{\sqrt{{\delta }_1-{\delta }_3{\zeta }_2}}{\sqrt{3}\sqrt{{\delta }_2}},\\ a_1=\frac{\sqrt{2}\sqrt{-{\delta }_3}\sqrt{{\zeta }_4}}{\sqrt{{\delta }_2}}.& (13)\end{array}$

Different cases [34, 35] can be introduced to obtain the following solutions.

Case I.

If ${\zeta }_0={\vartheta }_3^2,{\zeta }_1=2{\vartheta }_1{\vartheta }_3,{\zeta }_2=2{\vartheta }_2{\vartheta }_3+{\vartheta }_1^2,{\zeta }_3=2{\vartheta }_1{\vartheta }_2,{\zeta }_4={\vartheta }_2^2$, we get the solution of (1) in the form ${\Phi }_{\eta }^I,(\eta =1,3,5,10,13,20,24).$ A variety of significant solitons are obtained below.

Type I: when ${\vartheta }_1^2-4{\vartheta }_2{\vartheta }_3>0$, ϑ₁ϑ₂ ≠ 0, ϑ₂ϑ₃ ≠ 0. A set of dark optical solitons is acquired as

$\begin{array}{l}{\Phi }_1^I(\xi )=[a_0\\ +a_1(-\frac{\sqrt{{\vartheta }_1^2-4{\vartheta }_2{\vartheta }_3}tanh\left(\frac{1}{2}\xi \sqrt{{\vartheta }_1^2-4{\vartheta }_2{\vartheta }_3}\right)+{\vartheta }_1}{2{\vartheta }_2})]\times e^{i\psi }.& (14)\end{array}$

A variety of bright-dark optical soliton is gained as

$\begin{array}{l}{\Phi }_3^I(\xi )=[a_0-\frac{a_1}{2{\vartheta }_2}(\sqrt{{\vartheta }_1^2-4{\vartheta }_2{\vartheta }_3}\\ (i\text{sech}\left(\xi \sqrt{{\vartheta }_1^2-4{\vartheta }_2{\vartheta }_3}\right)\\ +\tanh \left(\xi \sqrt{{\vartheta }_1^2-4{\vartheta }_2{\vartheta }_3}\right))+{\vartheta }_1)]\times e^{i\psi }.& (15)\end{array}$

A set of singular dark optical solitons is obtained as

$\begin{array}{l}{\Phi }_5^I\left(\xi \right)=[a_0-\frac{a_1}{2{\vartheta }_2}(\sqrt{{\vartheta }_1^2-4{\vartheta }_2{\vartheta }_3}\\ (\tanh \left(\frac{1}{4}\xi \sqrt{{\vartheta }_1^2-4{\vartheta }_2{\vartheta }_3}\right)\\ +\coth \left(\frac{1}{4}\xi \sqrt{{\vartheta }_1^2-4{\vartheta }_2{\vartheta }_3}\right))+{\vartheta }_1)]\times e^{i\psi }.& (16)\end{array}$

The family of solitons is obtained as

$\begin{array}{l}{\Phi }_{10}^I\left(\xi \right)=[a_0+a_1(2\cosh \left(\xi \sqrt{{\vartheta }_1^2-4{\vartheta }_2{\vartheta }_3}\right)\\ (\sqrt{{\vartheta }_1^2-4{\vartheta }_2{\vartheta }_3}\sinh \left(\xi \sqrt{{\vartheta }_1^2-4{\vartheta }_2{\vartheta }_3}\right)\\ -({\vartheta }_1\cosh \left(\xi \sqrt{{\vartheta }_1^2-4{\vartheta }_2{\vartheta }_3}\right)\\ {\pm i\sqrt{{\vartheta }_1^2-4{\vartheta }_2{\vartheta }_3}))}^{-1})]\times e^{i\psi }.& (17)\end{array}$

Type II: when ${\vartheta }_1^2-4{\vartheta }_2{\vartheta }_3<0$, ϑ₁ϑ₂ ≠ 0, ϑ₂ϑ₃ ≠ 0. The following collections of periodic solitons are given by

$\begin{array}{l}{\Phi }_{13}^I\left(\xi \right)=[a_0+a_1(\\ -\frac{\sqrt{4{\vartheta }_2{\vartheta }_3-{\vartheta }_1^2}\mathrm{ tan}\left(\frac{1}{2}\xi \sqrt{4{\vartheta }_2{\vartheta }_3-{\vartheta }_1^2}\right)-{\vartheta }_1}{2{\vartheta }_2})]\times e^{i\psi },& (18)\end{array}$

$\begin{array}{l}{\Phi }_{20}^I(\xi )=[a_0+a_1(-\\ \frac{2{\vartheta }_3\cos \left(\frac{1}{2}\xi \sqrt{4{\vartheta }_2{\vartheta }_3-{\vartheta }_1^2}\right)}{\sqrt{4{\vartheta }_2{\vartheta }_3-{\vartheta }_1^2}\sin \left(\frac{1}{2}\xi \sqrt{4{\vartheta }_2{\vartheta }_3-{\vartheta }_1^2}\right)+{\vartheta }_1\cos \left(\frac{1}{2}\xi \sqrt{4{\vartheta }_2{\vartheta }_3-{\vartheta }_1^2}\right)})]\times e^{i\psi },& (19)\end{array}$

$\begin{array}{l}{\Phi }_{24}^I(\xi )=[a_0+a_1((4r\sin \left(\frac{1}{4}\xi \sqrt{4{\vartheta }_2{\vartheta }_3-{\vartheta }_1^2}\right)\\ \cos \left(\frac{1}{4}\xi \sqrt{4{\vartheta }_2{\vartheta }_3-{\vartheta }_1^2}\right))\\ (2\sqrt{4{\vartheta }_2{\vartheta }_3-{\vartheta }_1^2}{\cos }^2\left(\frac{1}{4}\xi \sqrt{4{\vartheta }_2{\vartheta }_3-{\vartheta }_1^2}\right)\\ -2{\vartheta }_1\sin \left(\frac{1}{4}\xi \sqrt{4{\vartheta }_2{\vartheta }_3-{\vartheta }_1^2}\right)\\ {\cos \left(\frac{1}{4}\xi \sqrt{4{\vartheta }_2{\vartheta }_3-{\vartheta }_1^2}\right)-\sqrt{4{\vartheta }_2{\vartheta }_3-{\vartheta }_1^2})}^{-1})]\times e^{i\psi }.& (20)\end{array}$

Case II.

If ${\zeta }_0={\vartheta }_3^2,{\zeta }_1=2{\vartheta }_1{\vartheta }_3,{\zeta }_2=0,{\zeta }_3=2{\vartheta }_1{\vartheta }_2,{\zeta }_4={\vartheta }_2^2$, we get the solution of (1) in the form ${\Phi }_{\eta }^{II},(\eta =1,5).$ A collection of dark optical solitons is given by

$\begin{array}{l}{\Phi }_1^{II}(\xi )=[a_0+a_1(-\\ \frac{\sqrt{-6{\vartheta }_2{\vartheta }_3}\mathrm{ tanh}\left(\frac{1}{2}\xi \sqrt{-6{\vartheta }_2{\vartheta }_3}\right)+\sqrt{-2{\vartheta }_2{\vartheta }_3}}{2{\vartheta }_2})]\times e^{i\psi }.& (21)\end{array}$

Also, a different shape of singular dark optical soliton is acquired

$\begin{array}{l}{\Phi }_5^{II}(\xi )=[a_0+a_1(-\\ \frac{\sqrt{-6qr}\left(\tanh \left(\frac{1}{4}\xi \sqrt{-6qr}\right)+\coth \left(\frac{1}{4}\xi \sqrt{-6qr}\right)\right)+2\sqrt{-2qr}}{4q})]\times e^{i\psi },& (22)\end{array}$

Case III.

If ζ₀ = ζ₁ = 0, we get the solution of (1) in the form ${\Phi }_{\eta }^{III},(\eta =1,2,3,4,6,8,9)$.

Type I: ${\zeta }_2=1,{\zeta }_3=\frac{-2{\lambda }_3}{{\lambda }_1},{\zeta }_4=\frac{{\lambda }_3^2-{\lambda }_2^2}{{\lambda }_1^2}$, where λ₁, λ₂, λ₃ are arbitrary constants.

$\begin{array}{ll}{\Phi }_1^{III}(\xi )=\left[a_0+a_1\left(\frac{{\lambda }_1\text{sech}(\xi )}{{\lambda }_2\text{sech}(\xi )+{\lambda }_3}\right)\right]\times e^{i\psi }.& (23)\end{array}$

Type II: ${\zeta }_2=1,{\zeta }_3=\frac{-2{\lambda }_3}{{\lambda }_1},{\zeta }_4=\frac{{\lambda }_3^2+{\lambda }_2^2}{{\lambda }_1^2}$, where λ₁, λ₂, λ₃ are arbitrary constants.

$\begin{array}{ll}{\Phi }_2^{III}(\xi )=\left[a_0+a_1\left(\frac{{\lambda }_1\text{csch}(\xi )}{{\lambda }_2\text{csch}(\xi )+{\lambda }_3}\right)\right]\times e^{i\psi }.& (24)\end{array}$

In particular, if we take λ₂ = 0 in the above Equations (23), (24), we get

$\begin{array}{ll}{\Phi }_1^{III}(\xi )=\left[a_0+a_1\left(\frac{{\lambda }_1\text{sech}(\xi )}{{\lambda }_3}\right)\right]\times e^{i\psi }.& (25)\end{array}$

$\begin{array}{ll}{\Phi }_2^{III}(\xi )=\left[a_0+a_1\left(\frac{{\lambda }_1\text{csch}(\xi )}{{\lambda }_3}\right)\right]\times e^{i\psi }.& (26)\end{array}$

Type III: ${\zeta }_2=4,{\zeta }_3=-\frac{4(2{\lambda }_2+{\lambda }_4)}{{\lambda }_1},{\zeta }_4=\frac{4{\lambda }_2^2+4{\lambda }_4{\lambda }_2+{\lambda }_3^2}{{\lambda }_1^2}$, where λ₁, λ₂, λ₃, λ₄ are arbitrary constants.

$\begin{array}{ll}{\Phi }_3^{III}(\xi )=\left[a_0+a_1\left(\frac{{\lambda }_1{\text{sech}}^2(\xi )}{{\lambda }_2\tanh (\xi )+{\lambda }_3+{\lambda }_4{\text{sech}}^2(\xi )}\right)\right]\times e^{i\psi }.& (27)\end{array}$

Type IV: ${\zeta }_2=4,{\zeta }_3=\frac{4({\lambda }_4-2{\lambda }_2)}{{\lambda }_1},{\zeta }_4=\frac{4{\lambda }_2^2-4{\lambda }_4{\lambda }_2+{\lambda }_3^2}{{\lambda }_1^2}$, where λ₁, λ₂, λ₃, λ₄ are arbitrary constants.

$\begin{array}{ll}{\Phi }_4^{III}(\xi )=\left[a_0+a_1\left(\frac{{\lambda }_1{\text{csch}}^2(\xi )}{{\lambda }_2\coth (\xi )+{\lambda }_3+{\lambda }_4{\text{csch}}^2(\xi )}\right)\right]\times e^{i\psi }.& (28)\end{array}$

In particular, if we consider λ₂ = λ₄, we have another solution as

$\begin{array}{ll}{\Phi }_4^{III}(\xi )=\left[a_0+a_1\left(\frac{{\lambda }_1{\text{csch}}^2(\xi )}{{\lambda }_2\coth (\xi )+{\lambda }_3+{\lambda }_2{\text{csch}}^2(\xi )}\right)\right]\times e^{i\psi }.& (29)\end{array}$

Type V: ${\zeta }_2=-1,{\zeta }_3=\frac{2{\lambda }_3}{{\lambda }_1},{\zeta }_4=\frac{{\lambda }_3^2-{\lambda }_2^2}{{\lambda }_1^2}$, where λ₁, λ₂, λ₃ are arbitrary constants.

$\begin{array}{l}{\Phi }_6^{III}(\xi )=[a_0+a_1(-\\ \frac{{\lambda }_1(\sinh ({\lambda }_1\xi )+\cosh ({\lambda }_1\xi ))(\sinh ({\lambda }_1\xi )+\cosh ({\lambda }_1\xi )+{\lambda }_2)}{{\lambda }_3})]\times e^{i\psi }.& (30)\end{array}$

Type VI: ${\zeta }_2=4,{\zeta }_3=\frac{-2{\lambda }_3}{{\lambda }_1},{\zeta }_4=\frac{{\lambda }_3^2-{\lambda }_2^2}{{\lambda }_1^2}$, where λ₁, λ₂, λ₃ are arbitrary constants.

$\begin{array}{ll}{\Phi }_8^{III}(\xi )=\left[a_0+a_1\left(\frac{{\lambda }_1\csc (\xi )}{{\lambda }_2\csc (\xi )+{\lambda }_3}\right)\right]\times e^{i\psi }.& (31)\end{array}$

Type VII: ${\zeta }_2=-4,{\zeta }_3=\frac{4(2{\lambda }_2+{\lambda }_4)}{{\lambda }_1},{\zeta }_4=-\frac{4{\lambda }_2^2+4{\lambda }_4{\lambda }_2-{\lambda }_3^2}{{\lambda }_1^2}$, where λ₁, λ₂, λ₃, λ₄ are arbitrary constants.

$\begin{array}{ll}{\Phi }_9^{III}(\xi )=\left[a_0+a_1\left(\frac{{\lambda }_1{\sec }^2(\xi )}{{\lambda }_2\tan (\xi )+{\lambda }_3+{\lambda }_4{\sec }^2(\xi )}\right)\right]\times e^{i\psi }.& (32)\end{array}$

Case IV.

If ζ₁ = ζ₃ = 0, we get the solution of (1) in the form ${\Phi }_{\eta }^{IV},(\eta =3,13)$.

For ${\zeta }_0=\frac{1}{4},{\zeta }_2=\frac{1-2m^2}{2},{\zeta }_4=\frac{1}{4}$, the solution of (1) of the form

$\begin{array}{ll}{\Phi }_3^{IV}(\xi )=\left[a_0+a_1(cn\xi )\right]\times e^{i\psi },& (33)\end{array}$

leads to the bright optical soliton when m → 1,

$\begin{array}{ll}{\Phi }_3^{IV}(\xi )=[a_0+a_1\text{sech}(\xi )]\times e^{i\psi },& (34)\end{array}$

and the singular periodic solutions when m → 0,

$\begin{array}{ll}{\Phi }_3^{IV}(\xi )=\left[a_0+a_1\cos (\xi )\right]\times e^{i\psi },& (35)\end{array}$

For ${\zeta }_0=\frac{1}{4},{\zeta }_2=\frac{1-2m^2}{2},{\zeta }_4=\frac{1}{4}$, the solution of (1) of the form

$\begin{array}{ll}{\Phi }_{13}^{IV}(\xi )=\left[a_0+a_1(ns\xi \pm cs\xi )\right]\times e^{i\psi },& (36)\end{array}$

leads to a collection of singular dark solutions when m → 1,

$\begin{array}{ll}{\Phi }_{13}^{IV}(\xi )=\left[a_0+a_1(\coth (\xi )+\text{csch}(\xi ))\right]\times e^{i\psi }, & (37)\end{array}$

and singular periodic solutions when m → 0,

$\begin{array}{ll}{\Phi }_{13}^{IV}(\xi )=\left[a_0+a_1(\cot (\xi )+\text{csc}(\xi ))\right]\times e^{i\psi }.& (38)\end{array}$

3. Results and Discussion

In this part, the physical aspects of the solutions obtained are discussed by means of graphical 3D representations. Figures 1–4 show different categories of background for soliton solutions classified into dark or singular soliton solutions.

FIGURE 1

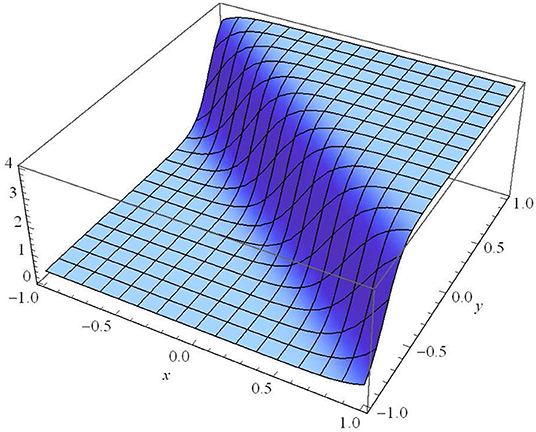
Figure 1. $|\Phi (x,y,t){|}_1^I:$ ϑ₁=1, ϑ₂ = −1, ϑ₃ = 1, μ₁ = 1, μ₂ = 1, μ₃ = 1, α₀ = 1, β₀ = 2, λ₀ = 3, α₁ = 4, β₁ = 5, λ = 6, η₀ = 1, t = 0.01.

Figure 1 illustrates $|\Phi (x,y,t){|}_1^I$ established in Case I (Type I) for ϑ₁ = 1, ϑ₂ = −1, ϑ₃ = 1, μ₁ = 1, μ₂ = 1, μ₃ = 1, α₀ = 1, β₀ = 2, λ₀ = 3, α₁ = 4, β₁ = 5, λ = 6, η₀ = 1, t = 0.01.

Moreover, Figure 2 illustrates $|\Phi (x,y,t){|}_5^{II}$ found in Case II for ϑ₁ = 1, ϑ₂ = −1, ϑ₃ = 1, μ₁ = 1, μ₂ = 1, μ₃ = 1, α₀ = 1, β₀ = 2, λ₀ = 3, α₁ = 4, β₁ = 5, λ = 6, η₀ = 1, t = 0.1.

FIGURE 2

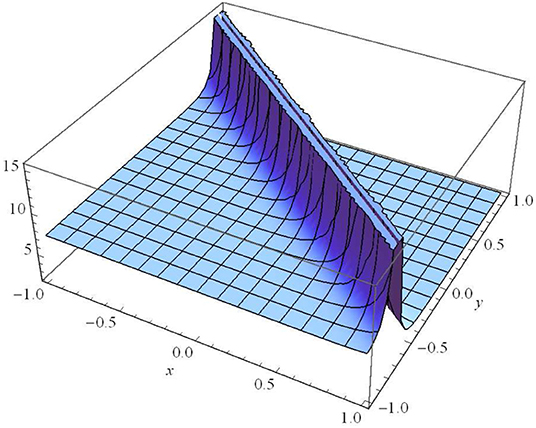
Figure 2. $|\Phi (x,y,t){|}_5^{II}:$ ϑ₁=1, ϑ₂ = −1, ϑ₃ = 1, μ₁ = 1, μ₂ = 1, μ₃ = 1, α₀ = 1, β₀ = 2, λ₀ = 3, α₁ = 4, β₁ = 5, λ = 6, η₀ = 1, t = 0.1.

Similarly, Figure 3 illustrates $|\Phi (x,y,t){|}_1^{III}$ found in Case III (Type I) for λ₁ = 1, λ₂ = 2, λ₃ = 3, μ₁ = 1, μ₂ = 1, μ₃ = 1, α₀ = 1, β₀ = 2, λ₀ = 3, α₁ = 4, β₁ = 5, λ = 6, η₀ = 1, t = 1. Similarly, Figure 4 expresses $|\Phi (x,y,t){|}_{13}^{IV}$ observed in Case IV (m → 1) for μ₁=1, μ₂=1, μ₃ = 2, α₀ = 1, β₀ = 2, λ₀ = 3, α₁ = 0.1, β₁ = 1, λ = 0.5, η₀ = 1, t = 0.1.

FIGURE 3

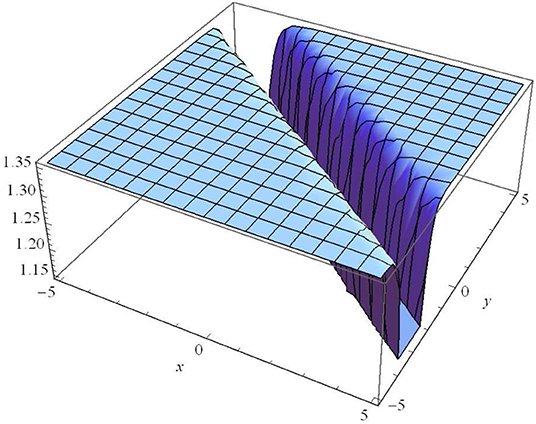
Figure 3. $|\Phi (x,y,t){|}_1^{III}:$ λ₁ = 1, λ₂ = 2, λ₃ = 3, μ₁ = 1, μ₂ = 1, μ₃ = 1, α₀ = 1, β₀ = 2, λ₀ = 3, α₁ = 4, β₁=5, λ = 6, η₀ = 1, t = 1.

FIGURE 4

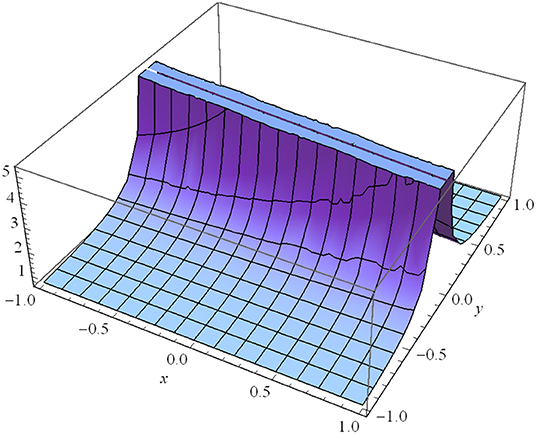
Figure 4. $|\Phi (x,y,t){|}_{13}^{IV}$ for m → 1: μ₁ = 1, μ₂ = 1, μ₃ = 2, α₀ = 1, β₀ = 2, λ₀ = 3, α₁ = 0.1, β₁ = 1, λ = 0.5, η₀ = 1, t = 0.1.

Figure 1 represents the absolute value of the complex wave solution given by Equation (14). We observe that this solution is a dark (or kink) soliton wave propagating along the y-axis. The kink wave is an essential aspect of numerous physical phenomena containing self-reinforcing, impulsive systems, and reaction-diffusion-advection. It is clear that there is a transmission of the dark soliton with invariant amplitude (without any gain or loss) in the homogeneous medium of motion. Due to the homogeneous (constant) coefficients of Equation (1), we cannot provide a possible way to control the propagation of the dark solitons in this medium. Figures 2–4 represent the absolute value of the complex wave solutions given by Equations (22), (23), and (37), respectively. We observe that these solutions are singular solitons that can be linked to a solitary wave when its center becomes an imaginary position. Furthermore, It is clear that their intensity gets Stronger, and consequently, they are not stable. These solutions have a cusp, which may lead to the formation of Rogue waves.

4. Conclusions

Herein, a large set of new analytical solutions with different wave structures of the 2D-CNLS equation has been reproduced with the aid of the PFS-E technique. As a positive result, a wide variety of unprecedented exact solutions were gained in an easy manner. Our study presents whether the suggested approach is trustworthy in treatment NLPDEs to promote a variety of exact solutions. Finally, we have plotted some 3D graphs of these solutions and have shown that these graphs can be controlled by adjusting the parameters. According to our knowledge, the obtained solutions are likely to provide a useful supplement to the existing literature on nonlinear optics.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Biswas A, Konar S. Introduction to Non-Kerr Law Optical Solitons. Chapman and Hall; CRC Press (2006).

Google Scholar

2. Zhou Q, Mirzazadeh M, Ekici M, Sonmezoglu A. Analytical study of solitons in non-Kerr nonlinear negative-index materials. Nonlinear Dyn. (2016) 86:623–38. doi: 10.1007/s11071-016-2911-1

CrossRef Full Text | Google Scholar

3. Ding Y, Osman MS, Wazwaz AM. Abundant complex wave solutions for the nonautonomous Fokas-Lenells equation in presence of perturbation terms. Optik. (2019) 181:503–13. doi: 10.1016/j.ijleo.2018.12.064

CrossRef Full Text | Google Scholar

4. Liu JG, Osman MS, Wazwaz AM. A variety of nonautonomous complex wave solutions for the (2+ 1)-dimensional nonlinear Schrödinger equation with variable coefficients in nonlinear optical fibers. Optik. (2019) 180:917–23. doi: 10.1016/j.ijleo.2018.12.002

CrossRef Full Text | Google Scholar

5. Osman MS. New analytical study of water waves described by coupled fractional variant Boussinesq equation in fluid dynamics. Pramana. (2019) 93:26. doi: 10.1007/s12043-019-1785-4

CrossRef Full Text | Google Scholar

6. Foursa D, Emplit P. Experimental investigation of dark soliton amplification in an optical fibre by stimulated Raman scattering. Electron Lett. (1996) 32:919–21. doi: 10.1049/el:19960614

CrossRef Full Text | Google Scholar

7. Kivshar YS. Nonlinear dynamics near the zero-dispersion point in optical fibers. Phys Rev A. (1991) 43:1677. doi: 10.1103/PhysRevA.43.1677

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Osman MS, Baleanu D, Adem AR, Hosseini K, Mirzazadeh M, Eslami M. Double-wave solutions and Lie symmetry analysis to the (2+ 1)-dimensional coupled Burgers equations. Chin J Phys. (2020) 63:122–9. doi: 10.1016/j.cjph.2019.11.005

CrossRef Full Text | Google Scholar

9. Osman MS, Liu JG, Hosseini K, Yusuf A. Different wave structures and stability analysis for the generalized (2+ 1)-dimensional Camassa-Holm-Kadomtsev-Petviashvili equation. Phys Scr. (2019) 95:035229. doi: 10.1088/1402-4896/ab52c1

CrossRef Full Text | Google Scholar

10. Lu D, Osman MS, Khater MMA, Attia RAM, Baleanu D. Analytical and numerical simulations for the kinetics of phase separation in iron [FeCrX (X = Mo, Cu)] based on ternary alloys. Phys A. (2020) 537:122634. doi: 10.1016/j.physa.2019.122634

CrossRef Full Text | Google Scholar

11. Lu D, Tariq KU, Osman MS, Baleanu D, Younis M, Khater MMA. New analytical wave structures for the (3+ 1)-dimensional Kadomtsev-Petviashvili and the generalized Boussinesq models and their applications. Results Phys. (2019) 14:102491. doi: 10.1016/j.rinp.2019.102491

CrossRef Full Text | Google Scholar

12. Hirota R. Exact solution of the Kortewegde Vries equation for multiple collisions of solitons. Phys Rev Lett. (1971) 27:1192. doi: 10.1103/PhysRevLett.27.1192

CrossRef Full Text | Google Scholar

13. Roy R, Akbar MA, Wazwaz AM. Exact wave solutions for the nonlinear time fractional Sharma-Tasso-Olver equation and the fractional Klein-Gordon equation in mathematical physics. Opt Quant Electron. (2018) 50:25. doi: 10.1007/s11082-017-1296-9

CrossRef Full Text | Google Scholar

14. Osman MS. One-soliton shaping and inelastic collision between double solitons in the fifth-order variable-coefficient Sawada-Kotera equation. Nonlinear Dyn. (2019) 96:1491–6. doi: 10.1007/s11071-019-04866-1

CrossRef Full Text | Google Scholar

15. Javid A, Raza N, Osman MS. Multi-solitons of thermophoretic motion equation depicting the wrinkle propagation in substrate-supported graphene sheets. Commun Theor Phys. (2019) 71:362. doi: 10.1088/0253-6102/71/4/362

CrossRef Full Text | Google Scholar

16. Osman MS, Ghanbari B, Machado JAT. New complex waves in nonlinear optics based on the complex Ginzburg-Landau equation with Kerr law nonlinearity. Eur Phys J Plus. (2019) 134:20. doi: 10.1140/epjp/i2019-12442-4

CrossRef Full Text | Google Scholar

17. Kumar D, Kaplan M. Application of the modified Kudryashov method to the generalized Schrödinger-Boussinesq equations. Opt Quant Electron. (2018) 50:329. doi: 10.1007/s11082-018-1595-9

CrossRef Full Text | Google Scholar

18. Osman MS, Lu D, Khater MM. A study of optical wave propagation in the nonautonomous Schrödinger-Hirota equation with power-law nonlinearity. Results Phys. (2019) 13:102157. doi: 10.1016/j.rinp.2019.102157

CrossRef Full Text | Google Scholar

19. Kaplan M. Two different systematic techniques to find analytical solutions of the (2+ 1)-dimensional Boiti-Leon-Manna-Pempinelli equation. Chinese J Phys. (2018) 56:2523–30. doi: 10.1016/j.cjph.2018.06.005

CrossRef Full Text | Google Scholar

20. Osman MS, Ghanbari B. New optical solitary wave solutions of Fokas-Lenells equation in presence of perturbation terms by a novel approach. Optik. (2018) 175:328–33. doi: 10.1016/j.ijleo.2018.08.007

CrossRef Full Text | Google Scholar

21. Osman MS, Machado JAT. The dynamical behavior of mixed-type soliton solutions described by (2+ 1)-dimensional Bogoyavlensky-Konopelchenko equation with variable coefficients. J Electromagnet Wave. (2018) 32:1457–64. doi: 10.1080/09205071.2018.1445039

CrossRef Full Text | Google Scholar

22. Rezazadeh H, Osman MS, Eslami M, Mirzazadeh M, Zhou Q, Badri SA, et al. Hyperbolic rational solutions to a variety of conformable fractional Boussinesq-Like equations. Nonlinear Eng. (2019) 8:224–30. doi: 10.1515/nleng-2018-0033

CrossRef Full Text | Google Scholar

23. Osman MS. Multi-soliton rational solutions for quantum Zakharov-Kuznetsov equation in quantum magnetoplasmas. Waves Random Complex. (2016) 26:434–43. doi: 10.1080/17455030.2016.1166288

CrossRef Full Text | Google Scholar

24. Raza N, Zubair A. Bright, dark and dark-singular soliton solutions of nonlinear Schrödinger's equation with spatio-temporal dispersion. J Mod Opt. (2018) 65:1975–82. doi: 10.1080/09500340.2018.1480066

CrossRef Full Text | Google Scholar

25. Osman MS. Multi-soliton rational solutions for some nonlinear evolution equations. Open Phys. (2016) 14:26–36. doi: 10.1515/phys-2015-0056

CrossRef Full Text | Google Scholar

26. Osman MS, Rezazadeh H, Eslami M, Neirameh A, Mirzazadeh M. Analytical study of solitons to benjamin-bona-mahony-peregrine equation with power law nonlinearity by using three methods. Univ Politeh Buch Ser A. (2018) 80:267–78. Available online at: https://www.scientificbulletin.upb.ro/rev_docs_arhiva/fullf37_570579.pdf

Google Scholar

27. Zhang S, Xia T. A further improved extended Fan sub-equation method and its application to the (3+ 1)-dimensional Kadomstev-Petviashvili equation. Phys Lett A. (2006) 356:119–23. doi: 10.1016/j.physleta.2006.03.027

CrossRef Full Text | Google Scholar

28. Cheemaa N, Younis M. New and more general traveling wave solutions for nonlinear Schrödinger equation. Waves Random Complex. (2016) 26:30–41. doi: 10.1080/17455030.2015.1099761

CrossRef Full Text | Google Scholar

29. Eslami M. Trial solution technique to chiral nonlinear Schrodinger's equation in (1 + 2)-dimensions. Nonlinear Dyn. (2016) 85:813–6. doi: 10.1007/s11071-016-2724-2

CrossRef Full Text | Google Scholar

30. Bulut H, Sulaiman TA, Demirdag B. Dynamics of soliton solutions in the chiral nonlinear Schrödinger equations. Nonlinear Dyn. (2018) 91:1985–91. doi: 10.1007/s11071-017-3997-9

CrossRef Full Text | Google Scholar

31. Vyas VM, Patel P, Panigrahi PK, Kumar CN, Greiner W. Chirped chiral solitons in the nonlinear Schrödinger equation with self-steepening and self-frequency shift. Phys Rev A. (2008) 78:021803. doi: 10.1103/PhysRevA.78.021803

CrossRef Full Text | Google Scholar

32. Raza N, Javid A. Optical dark and dark-singular soliton solutions of (1+ 2)-dimensional chiral nonlinear Schrodinger's equation. Waves Random Complex. (2019) 29:496–508. doi: 10.1080/17455030.2018.1451009

CrossRef Full Text | Google Scholar

33. Nishino A, Umeno Y, Wadati M. Chiral nonlinear Schrödinger equation. Chaos Soliton Fract. (1998) 9:1063–9. doi: 10.1016/S0960-0779(97)00184-7

CrossRef Full Text | Google Scholar

34. Yomba E. The extended fan sub-equation method and its application to the (2+1)-dimensional dispersive long wave and whitham-Broer-Kaup equations. Chinese J Phys. (2005) 43:789–805. Available online at: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.178.5618&rep=rep1&type=pdf

Google Scholar

35. Yomba E. The modified extended Fan sub-equation method and its application to the (2+ 1)-dimensional Broer-Kaup-Kupershmidt equation. Chaos Soliton Fract. (2006) 27:187–96. doi: 10.1016/j.chaos.2005.03.021

CrossRef Full Text | Google Scholar