Computing the Mixed Metric Dimension of a Generalized Petersen Graph P(n, 2)

Let Γ = (V, E) be a connected graph. A vertex i ∈ V recognizes two elements (vertices or edges) j, k ∈ E ∩ V, if d_Γ(i, j) ≠ d_Γ(i, k). A set S of vertices in a connected graph Γ is a mixed metric generator for Γ if every two distinct elements (vertices or edges) of Γ are recognized by some vertex of S. The smallest cardinality of a mixed metric generator for Γ is called the mixed metric dimension and is denoted by β_m. In this paper, the mixed metric dimension of a generalized Petersen graph P(n, 2) is calculated. We established that a generalized Petersen graph P(n, 2) has a mixed metric dimension equivalent to 4 for n ≡ 0, 2(mod4), and, for n ≡ 1, 3(mod4), the mixed metric dimension is 5. We thus determine that each graph of the family of a generalized Petersen graph P(n, 2) has a constant mixed metric dimension.

2010 Mathematics Subject Classification: 05C12, 05C90

1. Introduction

The aim of robot navigation functionality is to attain the coveted position promptly whenever it is desired. Let us imagine that robot navigation in a sensor network that can obtain the distances to a collection of landmarks. A robot's position is solely resolved by determining the subset of nodes in the sensor network. It can be achieved by the concept of landmarks in the graphs introduced in Khuller et al. [1]; this idea was later named the metric dimension. All the graphs considered here have no loops and are simple, measurable, and undirected.

Let Γ = (V, E) be the graph of the distance d_Γ(a, b) (or d(a, b)) among the vertices a, b ∈ V(Γ) the minimum length of paths between them. For a vertex a ∈ V, distinguish two vertices in a graph, say b and c, if the condition d_Γ(a, b) ≠ d_Γ(a, c) holds. A set R ⊂ V(Γ) is the metric generator if some chosen vertices of the set R recognizes a pair of distinguished vertices. The metric basis with the least number of elements is called the metric generator, and the cardinality of its metric basis is termed the metric dimension. The notation employed here is β(Γ). The fundamental concept of the metric dimension was instated by Slater [2], and the notation of the metric dimension was initiated by Haray and Melter [3]. This concept was later studied by many researchers with unique modifications; for reference, see [4–8]. Some of the recent results on metric dimension and its further variations are studied in Shao et al. [9] and Raza et al. [10–13].

Lemma 1. Suppose R is the distinguishing set of Γ and the vertices a, b ∈ V(Γ). If d_Γ(a, c) ≠ d_Γ(a, c), for all vertices c ∈ V(Γ)\{a, b}, then {a, b}⋂R ≠ ∅.

Analogous to this definition, Kelenc et al. [14] introduced the concept of edge metric dimension, and this was further studied in Zubrilina [15], Peterin and Yero [16], and Zhu et al. [17]. This distance between an edge e = ab and a vertex c is given as follows

$\begin{array}{l}d(e,c)=min\{d(a,c),d(b,c)\}\end{array}$

A vertex c ∈ V(Γ) distinguishes two edges of a graph e₁, e₂ ∈ E(Γ) if d_Γ(e₁, u) ≠ d_Γ(e₂, u). The set R_e ⊂ V is termed as the edge metric generator if some distinct edges of Γ are distinguished by the vertex set R_e. The cardinality of an edge metric generator is called an edge metric dimension, and it is depicted as β_e(Γ). Having defined the notion of an edge metric generator, which distinctly recognizes every edge in a graph, a common assumption would be that any edge metric generator R_e would be a metric dimension as well. This assumption is far from reality, as indicated in Kelenc et al. [14], but there are several families of graphs where this occurs, that is, β(Γ) = β_e(Γ). Some other distance related parameters are studied in Liu et al. [18–22].

In this paper, our focus is on mixed metric dimension, which is a mixed version of metric and edge metric dimension. A set R_m of vertices of a graph Γ is known as a mixed metric generator if any two distinct elements (vertices or edges) of a graph are recognized by some the vertex set of R_m. The least cardinality of a mixed metric generator for a graph is termed as a mixed metric dimension, denoted as β_m(Γ). The idea is recently brought forward by Kelenc et al. [23].

Lemma 2. Let for some vertex a ∈ V(Γ), and let R_m = V(Γ)\a, and if there is an element b ∈ N(a), also for some c ∈ R_m, d_Γ(ab, c) ≠ d_Γ(b, c), then R_m is the mixed metric generator for the graph Γ.

The notion of a mixed metric dimension clearly indicates that a mixed metric generator is also a standard metric generator and an edge metric generator, The following relationship is given in [23],

$\begin{array}{l}{\beta }_m(\Gamma )\text{max}\ge \{\beta (\Gamma ),{\beta }_e(\Gamma )\}\end{array}$

The following remark shows the structure of mixed metric dimension:

Remark 1: [23] Suppose for some graph Γ we have 2 ≤ β_m ≤ n. Recently, this concept has attracted some attention, and it has been studied by Raza et al. [24]. The authors discussed the mixed metric dimension among the prism graphs, which are commonly known as generalizes Petersen graphs P(n, 1), and two families of convex polytopes A_n, R_n, further presenting the problem of finding β_m(P(n, 2)).

Some of the results regarding metric and edge metric dimension are given:

Remark 2: [14] For n ≥ 2, the metric and edge metric dimension are, $\beta ({{P}}_n)={\beta }_e({{P}}_n)=1$; for cycle graph, $\beta ({{C}}_n)={\beta }_e({{C}}_n)=2$; for complete graph, $\beta ({{K}}_n)={\beta }_e({{K}}_n)=n-1$; and for any complete bipartite graph $({{K}}_{r,t})$ different from $({{K}}_{1,1})$, $\beta ({{K}}_{r,t})={\beta }_e({{K}}_{r,t})=r+t-2$.

1.1. Known Results

Next, we present some already known results for β_m,

Proposition 1: [23] For a path graph $({{P}}_n)$ order n ≥ 4, we have ${\beta }_m({{P}}_n)=2$.

Proposition 2: [23] Let us consider any two positive integers: e, f

$\begin{array}{l}{\beta }_m(K_{e,f})=\{\begin{array}{cc}e+f-1,& \text{if }e=2\text{ or }f=2;\\ e+f-2,& \text{otherwise}.\hfill \end{array}\end{array}$

Proposition 3: [23] For a grid graphs, P_m□P_n, with m ≥ n ≥ 2, β_m = 3.

Proposition 4: [23] Let us assume cycle graph $({{C}}_n)$ of order n ≥ 4, then β_m(C_n) = 3.

Lemma 3. [24]The mixed metric generator R_m must contain vertices from both the outer and inner cycle for the prism graph D_n.

Proof: For P(n, 1), this holds, and, by the same intuition, this must be true for P(n, 2). The mixed metric resolving set comprises of vertices from both the cycles, which contain vertices of outer and inner cycle, respectively. □

2. Main Result

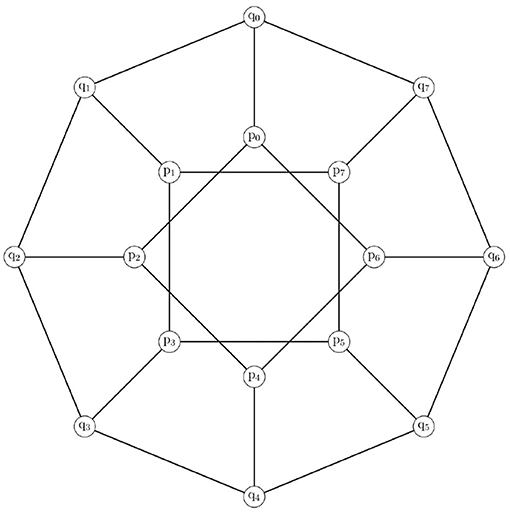
The generalized Petersen graphs is introduced by Watkins [25]. The P(n, ℓ), where n ≥ 3 and $1\le \ell \le \lfloor \frac{n-1}{2}\rfloor$ (see Figure 2), which is the cubic graph consists of vertices and edges, is shown below.

$\begin{array}{l}{V}(P(n,\ell ))=\left\{{\text{q}}_0,{\text{q}}_1,\dots ,{\text{q}}_{n-1},{\text{p}}_0,{\text{p}}_1,\dots ,{\text{p}}_{n-1}\right\}\end{array}$

$\begin{array}{l}\epsilon (P(n,\ell ))=\left\{{\text{q}}_i{\text{q}}_{i+1},{\text{p}}_i{\text{p}}_{i+\ell },{\text{q}}_i{\text{q}}_i|i=0,1,\dots ,n-1\right\}\end{array}$

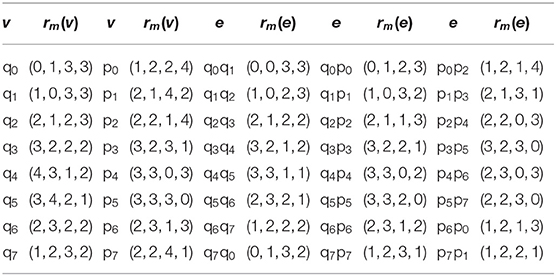
Example: We used the graph of P(n, 8), as can be seen in Figure 1. The mixed metric generator for P(n, 8) is β_m = {q₀, q₁, p₄, p₅}, and it can been seen from Table 1 that all the representation of vertices and edges are distinct.

FIGURE 1

Figure 1. The generalized Petersen graph P(8, 2).

FIGURE 2

Figure 2. (A) The generalized Petersen graph P(5, 2), (B) The generalized Petersen graph P(6, 2).

TABLE 1

Table 1. Codes for P(n, 8).

The graph of the generalized Petersen graph comprises of three types of edges, external edges, internal edges, and spokes between q_i and q_i+1, p_i and p_i+m, and q_i and p_i, respectively. The vertices q_i and p_i (0 ≤ i ≤ n − 1) are termed as external and internal vertices, respectively.

The prism graph D_n is known as P(n, 1) for m = 1. Some of the already known results are given as

Theorem 1. [26] The metric dimension of ${{D}}_n$, for n ≥ 4:

$\begin{array}{l}\beta ({{D}}_n)=\{\begin{array}{cc}2,& nisodd;\\ 3,& niseven.\end{array}\end{array}$

Theorem 2. [27] When, n ≥ 4, ${\beta }_e({{D}}_n)=3$.

Theorem 3. [24] For n ≥ 5,

$\begin{array}{l}{\beta }_m(P(n,1))=\{\begin{array}{cc}3,& niseven;\\ 4,& nisodd.\end{array}\end{array}$

The known results for P(n, 2) concerning metric and an edge metric dimension are

Theorem 4. [28] For n ≥ 5, the metric dimension is β(P(n, 2)) = 3.

Theorem 5. [27] For n ≥ 5, β_e(P(n, 2)) = 3.

It is quite natural to investigate the mixed metric dimension of P(n, 2). Now, we will find mixed the metric dimension of (P(n, 2)), and for this the following lemmas are presented.

Lemma 4. Case 1: If n ≡ 0(mod)4, then β_m(P(n, 2)) ≤ 4.

Proof: The proof is n = 4r, r ≥ 4, where r ∈ ℤ⁺. The distinguishing vertices that will distinguish the whole vertices and edges of the graph are R_m = {q₀, q₁, p_2r, p_2r+1}. The following representations are presented with respect to R_m.

Representation of external vertices:

$C_{R_m}({\text{q}}_{2s})=\{\begin{array}{ll}(2s,1,r-s+1,r+1),\hfill & 0\le s\le 1;\hfill \\ (2s,s+1,r-s+1,r),\hfill & s=2;\hfill \\ (s+2,s+2,r-s+1,r-s+2),\hfill & 3\le s\le r;\hfill \\ (2r-s+2,2r-s+3,s-r+1,\hfill & r+1\le s\le 2r-2;\hfill \\ s-r+1),\hfill & \hfill \\ (2,3,s-r+1,s-r+1),\hfill & s=2r-1.\hfill \end{array}$

and,

$C_{R_m}({\text{q}}_{2s+1})=\{\begin{array}{ll}(2s+1,2s,s-r+1,r-s+1),\hfill & 0\le s\le 2;\hfill \\ (s+3,s+2,2,r-s+1),\hfill & 3\le s\le r-1;\hfill \\ (r+2,r+2,2,1),\hfill & s=r;\hfill \\ (2r-s+2,2r-s+2,\hfill & r+1\le s\le 2r-3;\hfill \\ s-r+2,s-r+1),\hfill & \hfill \\ (3,4,s-r+2,r-s+1),\hfill & s=2r-2;\hfill \\ (1,2,s-r+2,s-r+1),\hfill & s=2r-1.\hfill \end{array}$

Representation of internal vertices:

$C_{R_m}({\text{p}}_{2s})=\{\begin{array}{ll}(s+1,2,r-s,r+2),\hfill & 0\le s\le 1;\hfill \\ (s+1,s+1,r-s,r-s+3),\hfill & 2\le s\le r;\hfill \\ (2r-s+1,2r-s+2,\hfill & r+1\le s\le 2r-1.\hfill \\ s-r,s-r+2),\hfill & \hfill \end{array}$

and,

$C_{R_m}({\text{p}}_{2s+1})=\{\begin{array}{ll}(s+2,s+1,r-s+2,r-s),\hfill & 0\le s\le r-1;\hfill \\ (2r-s+1,r,s-r+3,s-r),\hfill & r\le s\le r+1;\hfill \\ (2r-s+1,2r-s+1,\hfill & r+2\le s\le 2r-1.\hfill \\ s-r+3,s-r),\hfill & \hfill \end{array}$

Representation of external edges:

$C_{R_m}({\text{q}}_{2s}{\text{q}}_{2s+1})=\{\begin{array}{ll}(2s,s,r-s+1,r-s+1),\hfill & 0\le s\le 1;\hfill \\ (2s,s+1,r-s+1,\hfill & s=2;\hfill \\ r-s+1),\hfill & \hfill \\ (s+2,s+2,r-s+1,\hfill & 3\le s\le r;\hfill \\ r-s+1),\hfill & \hfill \\ (2r-s+2,2r-s+2,\hfill & r+1\le s\le 2r-3;\hfill \\ s-r+1,s-r+1),\hfill & \hfill \\ (3,4,s-r+1,s-r+1),\hfill & s=2r-2;\hfill \\ (1,2,s-r+1,s-r+1),\hfill & s=2r-1.\hfill \end{array}$

and,

$C_{R_m}({\text{q}}_{2s+1}{\text{q}}_{2s+2})=\{\begin{array}{ll}(2s+1,2s,r-s,r-s+1),\hfill & 0\le s\le 2;\hfill \\ (s+3,s+2,r-s,r-s+1),\hfill & 3\le s\le r-1;\hfill \\ (2r-s+1,2r-s+2,\hfill & r\le s\le 2r-3;\hfill \\ s-r+2,s-r+1),\hfill & \hfill \\ (2,3,s-r+2,s-r+1),\hfill & s=2r-2;\hfill \\ (0,1,s-r+2,s-r+1),\hfill & s=2r-1.\hfill \end{array}$

Representation of external and internal edges:

$C_{R_m}({\text{q}}_{2s}{\text{p}}_{2s})=\{\begin{array}{ll}(2s,1,r-s,r+1),\hfill & 0\le s\le 1;\hfill \\ (s+1,s+1,r-s,r-s+2),\hfill & 2\le s\le r;\hfill \\ (2r-s+1,2r-s+2,s-r,\hfill & r+1\le s\le 2r-1.\hfill \\ s-r+1),\hfill & \hfill \end{array}$

and,

$C_{R_m}({\text{q}}_{2s+1}{\text{q}}_{2s+1})=\{\begin{array}{ll}(2s+1,2s,r-s+1,r-s),\hfill & 0\le s\le 1;\hfill \\ (s+2,s+1,r-s+1,r-s),\hfill & 2\le s\le r-1;\hfill \\ (r+1,r+1,2,0),\hfill & s=r;\hfill \\ (2r-s+1,2r-s+1,\hfill & r+1\le s\le 2r-2;\hfill \\ s-r+2,s-r),\hfill & \hfill \\ (1,2,s-r+2,s-r),\hfill & s=2r-1.\hfill \end{array}$

Representation of internal edges:

$C_{R_m}({\text{p}}_{2s}{\text{p}}_{2s+2})=\{\begin{array}{ll}(1,2,r-s-1,r-s+2),\hfill & s=0;\hfill \\ (s+1,s+1,r-s-1,\hfill & 1\le s\le r-1;\hfill \\ r-s+2),\hfill & \hfill \\ (2r-s,r,s-r,3),\hfill & r\le s\le r+1;\hfill \\ (2r-s,2r-s+1,s-r,\hfill & r+2\le s\le 2r-1.\hfill \\ s-r+2),\hfill & \hfill \end{array}$

and,

$C_{R_m}({\text{p}}_{2s+1}{\text{p}}_{2s+3})=\{\begin{array}{ll}(2,1,r-s+1,r-s-1),\hfill & s=0;\hfill \\ (s+2,s+1,r-s+1,\hfill & 1\le s\le r-3;\hfill \\ r-s-1),\hfill & \hfill \\ (s+2,s+1,3,r-s-1),\hfill & r-2\le s\le r-1;\hfill \\ (2r-s,2r-s,s-r+3,\hfill & r\le s\le 2r-2;\hfill \\ s-r),\hfill & \hfill \\ (2,1,s-r+3,s-r),\hfill & s=2r-1.\hfill \end{array}$

□

Case 2: For n ≡ 2(mod)4, we have β_m(P(n, 2) ≤ 4

Proof: Now we can see n = 4r + 2, r ≥ 4, where r ∈ ℤ⁺. The set of vertices that will distinguish the whole vertices and edges of the graph are R_m = {q₀, q₁, p_2r+1, p_2r+2}. The following representations are presented with respect to R_m.

Representation of external vertices:

$C_{R_m}({\text{q}}_{2s})=\{\begin{array}{ll}(2s,2-s,r-s+2,r+1),\hfill & 0\le s\le 1;\hfill \\ (2s,3,r-s+2,r-s+2),\hfill & s=2;\hfill \\ (s+2,s+2,r-s+2,r-s+2),\hfill & 3\le s\le r;\hfill \\ (2r-s+3,2r-s+4,\hfill & r+1\le s\le 2r-1;\hfill \\ s-r+1,s-r),\hfill & \hfill \\ (2,3,s-r+1,s-r),\hfill & s=2r.\hfill \end{array}$

and,

$C_{R_m}({\text{q}}_{2s+1})=\{\begin{array}{ll}(2s+1,2s,s-r+1,r-s+2),\hfill & 0\le s\le 2;\hfill \\ (s+3,s+2,r-s+1,r-s+1),\hfill & 3\le s\le r;\hfill \\ (2r-s+3,2r-s+4,\hfill & r+1\le s\le 2r-2;\hfill \\ s-r+1,s-r+1),\hfill & \hfill \\ (3,5,s-r+1,s-r+1),\hfill & s=2r-1;\hfill \\ (1,3,s-r+1,s-r+1),\hfill & s=2r.\hfill \end{array}$

Representation of internal vertices:

$C_{R_m}({\text{p}}_{2s})=\{\begin{array}{ll}(s+1,2,r-s+3,r),\hfill & 0\le s\le 1;\hfill \\ (s+1,r+1,r-s+3,r-s+1),\hfill & 2\le s\le r;\hfill \\ (2r-s+2,2r-s+3,\hfill & r+1\le s\le 2r.\hfill \\ s-r+2,s-r-1),\hfill & \hfill \end{array}$

and,

$C_{R_m}({\text{p}}_{2s+1})=\{\begin{array}{ll}(s+2,s+1,r-s,r-s+3),\hfill & 0\le s\le r;\hfill \\ (2r-s+2,2r-s+3,\hfill & r+1\le s\le 2r.\hfill \\ s-r,s-r+2),\hfill & \hfill \end{array}$

Representation of external edges:

$C_{R_m}({\text{q}}_{2s}{\text{q}}_{2s+1})=\{\begin{array}{ll}(2s,s,r-s+1,r+1),\hfill & 0\le s\le 1;\hfill \\ (2s,s+1,r-s+1,r-s+2),\hfill & s=2;\hfill \\ (s+2,s+2,r-s+1,\hfill & 3\le s\le r;\hfill \\ r-s+2),\hfill & \hfill \\ (2r-s+3,2r-s+3,\hfill & r+1\le s\le 2r-2;\hfill \\ s-r+1,s-r),\hfill & \hfill \\ (3,4,s-r+1,s-r),\hfill & s=2r-1;\hfill \\ (1,2,s-r+1,s-r),\hfill & s=2r.\hfill \end{array}$

and,

$C_{R_m}({\text{q}}_{2s+1}{\text{q}}_{2s+2})=\{\begin{array}{ll}(2s+1,2s,r-s+1,r-s+1),\hfill & 0\le s\le 2;\hfill \\ (s+3,s+2,r-s+1,r-s+1),\hfill & 3\le s\le r-1;\hfill \\ (2r-s+2,r+2,s-r+1,\hfill & r\le s\le r+1;\hfill \\ s-r+1),\hfill & \hfill \\ (2r-s+2,2r-s+3,s-r+1,\hfill & r+2\le s\le 2r-2;\hfill \\ s-r+1),\hfill & \hfill \\ (2,3,s-r+1,s-r+1),\hfill & s=2r-1;\hfill \\ (0,1,s-r+1,s-r+1),\hfill & s=2r.\hfill \end{array}$

Representation of external and internal edges:

$C_{R_m}({\text{q}}_{2s}{\text{p}}_{2s})=\{\begin{array}{ll}(2s,1,r-s+2,r),\hfill & 0\le s\le 1;\hfill \\ (s+1,s+1,r-s+2,r-s+1),\hfill & 2\le s\le r;\hfill \\ (2r-s+2,2r-s+3,\hfill & r+1\le s\le 2r.\hfill \\ s-r+1,s-r-1),\hfill & \hfill \end{array}$

and,

$C_{R_m}({\text{q}}_{2s+1}{\text{q}}_{2s+1})=\{\begin{array}{ll}(2s+1,2s,r-s,r-s+2),\hfill & 0\le s\le 1;\hfill \\ (s+2,s+1,r-s,r-s+2),\hfill & 2\le s\le r;\hfill \\ (2r-s+2,2r-s+2,\hfill & r+1\le s\le 2r-1;\hfill \\ s-r,s-r+1),\hfill & \hfill \\ (1,2,s-r,s-r+1),\hfill & s=2r.\hfill \end{array}$

Representation of internal edges:

$C_{R_m}({\text{p}}_{2s}{\text{p}}_{2s+2})=\{\begin{array}{ll}(s+1,2,r-s+2,r-s),\hfill & 0\le s\le 1;\hfill \\ (s+1,s+1,r-s+2,r-s),\hfill & 2\le s\le r-1;\hfill \\ (2r-s+1,r+1,3,0),\hfill & r\le s\le r+1;\hfill \\ (2r-s+1,2r-s+2,\hfill & r+2\le s\le 2r.\hfill \\ s-r+2,s-r-1),\hfill & \hfill \end{array}$

and,

$C_{R_m}({\text{p}}_{2s+1}{\text{p}}_{2s+3})=\{\begin{array}{ll}(s+2,s+1,r-s-1,\hfill & 0\le s\le r-1;\hfill \\ r-s+2),\hfill & \hfill \\ (2r-s+1,2r-s+1,\hfill & r\le s\le r+1;\hfill \\ s-r,3),\hfill & \hfill \\ (2r-s+1,2r-s+1,\hfill & r+2\le s\le 2r-1;\hfill \\ s-r,s-r+2),\hfill & \hfill \\ (2,1,s-r,s-r+2),\hfill & s=2r.\hfill \end{array}$

□

Now from lemma3, the resolving set R_m contains vertices from external and internal cycles; that is, the resolving set cannot comprise either external or internal vertices.

Lemma 5. When n ≡ 0, 2(mod4), then β_m(P(n, 2)) ≥ 4.

Proof: Suppose that β_m(P(n, 2)) = 3, the following contradictions arises:

Case 1: This is when the two fixed vertices are in the external cycle, {q₀, q₁}, and the other vertex lie in internal cycle p_ℓ, that is, R_m = {q₀, q₁, p_ℓ}.

(i) If 0 ≤ ℓ ≤ 1 then, r_m{q₀|q₀, q₁, p_ℓ} = r_m{q₀q_n−1|q₀, q₁, p_ℓ} = (0, 1, ℓ + 1).

(ii) If ℓ = 2, 4, …, 2r, then r_m{q₀|q₀, q₁, p_ℓ} = r_m{q₀q_n−1|q₀, q₁, p_ℓ}.

(iii) If ℓ = 3, 5, …, 2r−1, then r_m{q₀|q₀, q₁, p_ℓ} = r_m{q₀q_n−1|q₀, q₁, p_ℓ}.

Case 2: When internal cycle contains two fixed vertices that is {p₀, p₁}, and the other vertex lie in external cycle q_ℓ. That is R_m = {p₀, p₁, q_ℓ}.

(i) If 0 ≤ ℓ ≤ 3, then r_m{q₀|p₀, p₁, q_ℓ} = r_m{q₀q_n−1|p₀, p₁, q_ℓ} = (1, 2, ℓ).

(ii) If ℓ = 4, 6, …, 2r, then r_m{q₀|p₀, p₁, q_ℓ} = r_m{q₀q_n−1|p₀, p₁, q_ℓ}.

(iii)If ℓ = 5, then r_m{q₀|p₀, p₁, q_ℓ} = r_m{q₀q_n−1|p₀, p₁, q_ℓ} = (1, 2, ℓ).

(iv) If ℓ = 7, 9, …, 4r − 1, then r_m{q₁|p₀, p₁, q_ℓ} = r_m{q₁q₂|p₀, p₁, q_ℓ}.

Similarly, other contradictions can be assumed; all the cases mentioned above suggest that β_m(P(n, 2)) ≥ 4, which clearly indicates that β_m(P(n, 2)) = 4 for n ≡ 0(mod4). Similar kind of contradictions can be proved for n ≡ 2(mod4). □

Remark 3: From the above cases, it can be deduced that if the mixed metric generator R_m for P(n, 2) contains two vertices of one cycle, then R_m contain at least two vertices of another cycle.

Lemma 6. β_m(P(n, 2) ≤ 5, for n ≡ 1(mod)4

Proof: Case 1: Now we can write, if n = 4r + 1, r ≥ 4, where r ∈ ℤ⁺. The set of vertices that will distinguish the whole vertices and the edges of the graph are R_m = {q₀, q₁, p₁, p_2r+1, p_2r+2}. The following representations are presented with respect to R_m.

Representation of external vertices:

$C_{R_m}({\text{q}}_{2s})=\{\begin{array}{ll}(2s,2-2s,2,r+1,r+1),\hfill & 0\le s\le 1;\hfill \\ (2s,s,s+1,r-s+2,r-s+2),\hfill & s=2;\hfill \\ (r+2,r+2,r+1,2,1),\hfill & s=r+1;\hfill \\ (2r-s+3,2r-s+4,\hfill & r+2\le s\le 2r-2;\hfill \\ 2r-s+2,s-r+1,s-r),\hfill & \hfill \\ (3,5,3,s-r+1,s-r),\hfill & s=2r-1;\hfill \\ (1,3,2,s-r+1,s-r),\hfill & s=2r.\hfill \end{array}$

and,

$C_{R_m}({\text{q}}_{2s+1})=\{\begin{array}{ll}(2s+1,1,s+1,r-s+1,r+1),\hfill & 0\le s\le 1;\hfill \\ (2s+1,s+1,s+1,r-s+1,\hfill & s=2;\hfill \\ r-s+2),\hfill & \hfill \\ (s+3,s+2,s+1,r-s+1,\hfill & 3\le s\le r-1;\hfill \\ r-s+2),\hfill & \hfill \\ (2r-s+2,r+2,r+1,s-r+1,2),\hfill & r\le s\le r+1;\hfill \\ (2r-s+2,2r-s+3,2r-s+2,\hfill & r+2\le s\le 2r-2;\hfill \\ s-r+1,s-r+1),\hfill & \hfill \\ (2,4,3,s-r+1,s-r+1),\hfill & s=2r-1.\hfill \end{array}$

Representation of internal vertices:

$C_{R_m}({\text{p}}_{2s})=\{\begin{array}{ll}(s+1,2-s,3,r+s,r-s+1),\hfill & 0\le s\le 1;\hfill \\ (s+1,s+1,s+2,r-s+3,\hfill & 2\le s\le r-1;\hfill \\ r-s+1),\hfill & \hfill \\ (r+1,s,2r-s+1,3,r-s+1),\hfill & r\le s\le r+1;\hfill \\ (2r-s+2,2r-s+3,2r-s+1,\hfill & r+2\le s\le 2r-1;\hfill \\ s-r+2,s-r-1),\hfill & \hfill \\ (2,3,1,s-r+1,s-r-1),\hfill & s=2r.\hfill \end{array}$

and,

$C_{R_m}({\text{p}}_{2s+1})=\{\begin{array}{ll}(s+2,2-s,s,r-s,r+s),\hfill & 0\le s\le 1;\hfill \\ (s+2,s+1,s,r-s,r-s+3),\hfill & 2\le s\le r-1;\hfill \\ (2r-s+1,r+2,s,s-r,3),\hfill & r\le s\le r+1;\hfill \\ (2r-s+1,2r-s+2,\hfill & r+2\le s\le 2r-1.\hfill \\ 2r-s+3,s-r,s-r+2),\hfill & \hfill \end{array}$

Representation of external edges:

$C_{R_m}({\text{q}}_{2s}{\text{q}}_{2s+1})=\{\begin{array}{ll}(2s,1-s,s+1,r-s+1,r+1),\hfill & 0\le s\le 1;\hfill \\ (2s,s,s+1,r-s+1,r-s+2),\hfill & s=2;\hfill \\ (s+2,s+1,s+1,r-s+1,\hfill & 3\le s\le r;\hfill \\ r-s+2),\hfill & \hfill \\ (2r-s+2,2r-s+3,\hfill & r+1\le s\le 2r-2;\hfill \\ 2r-s+2,s-r+1,s-r),\hfill & \hfill \\ (2,4,3,s-r+1,s-r),\hfill & s=2r-1;\hfill \\ (0,2,2,s-r+1,s-r),\hfill & s=2r.\hfill \end{array}$

and,

$C_{R_m}({\text{q}}_{2s+1}{\text{q}}_{2s+2})=\{\begin{array}{ll}(2s+1,s,s+1,r-s+1,\hfill & 0\le s\le 1;\hfill \\ ar-s+1),\hfill & \hfill \\ (2s+1,s+1,s+1,r-s+1,\hfill & s=2;\hfill \\ r-s+1),\hfill & \hfill \\ (2r-s+1,s+2,s+1,\hfill & 3\le s\le r-1;\hfill \\ r-s+1,r-s+1),\hfill & \hfill \\ (2r-s+2,r+1,2r-s+1,\hfill & r\le s\le 2r-4;\hfill \\ s-r+1,s-r+1),\hfill & \hfill \\ (5,6,4,s-r+1,s-r+1),\hfill & s=2r-3;\hfill \\ (3,5,3,s-r+1,s-r+1),\hfill & s=2r-2;\hfill \\ (1,2,3,s-r+1,s-r+1),\hfill & s=2r-1.\hfill \end{array}$

Representation of external and internal edges:

$C_{R_m}({\text{q}}_{2s}{\text{p}}_{2s})=\{\begin{array}{ll}(2s,2-s,2,r+s,r-s+1),\hfill & 0\le s\le 1;\hfill \\ (s+1,s,s+1,r-s+2,\hfill & 2\le s\le r;\hfill \\ r-s+1),\hfill & \hfill \\ (2r-s+2,r+1,2r-s+1,\hfill & r+3\le s\le 2r-1;\hfill \\ s-r+1,s-r-1),\hfill & \hfill \\ (1,3,1,s-r+1,s-r-1),\hfill & s=2r.\hfill \end{array}$

and,

$C_{R_m}({\text{q}}_{2s+1}{\text{p}}_{2s+1})=\{\begin{array}{ll}(2s+1,1,s,r-s,r+s),\hfill & 0\le s\le 1;\hfill \\ (s+2,s+1,s,r-s,r-s+2),\hfill & 2\le s\le r-1;\hfill \\ (r+1,r+1,2r-s,0,2),\hfill & s=r;\hfill \\ (2r-s+1,2r-s+2,\hfill & r+1\le s\le 2r-1.\hfill \\ 2r-s+2,s-r,s-r+1),\hfill & \hfill \end{array}$

Representation of internal edges:

$C_{R_m}({\text{p}}_{2s}{\text{p}}_{2s+2})=\{\begin{array}{ll}(s+1,1,3,r+s,r-s),\hfill & 0\le s\le 1;\hfill \\ (s+1,s,s+2,r-s+2,r-s),\hfill & 2\le s\le r-1;\hfill \\ (2r-s+1,s,2r-s,3,0),\hfill & r\le s\le r+1;\hfill \\ (2r-s+1,2r-s+2,2r-s,\hfill & r+2\le s\le 2r-1;\hfill \\ s-r+2,s-r-1),\hfill & \hfill \\ (2,2,0,s-r,s-r-1),\hfill & s=2r.\hfill \end{array}$

and,

$C_{R_m}({\text{p}}_{2s+1}{\text{p}}_{2s+3})=\{\begin{array}{ll}(s+2,2,s,r-s-1,r+s),\hfill & 0\le s\le 1;\hfill \\ (s+2,s+1,s,r-s-1,\hfill & 2\le s\le r-1;\hfill \\ r-s+2),\hfill & \hfill \\ (2r-s,2r-s+1,s,r-s,3),\hfill & r\le s\le r+1;\hfill \\ (2r-s,2r-s+1,2r-s+2,\hfill & r+2\le s\le 2r-1.\hfill \\ s-r,s-r+2),\hfill & \hfill \end{array}$

□

Proof: Case 2: Now we can write, if n = 4r + 3, r ≥ 4, where r ∈ ℤ⁺. The set of vertices which will distinguish the whole vertices, and edges of graph are R_m = {q₀, q₁, p₁, p_2r+3, p_2r+4}. The following representations are presented with respect to R_m.

Representation of external vertices:

$C_{R_m}({\text{q}}_{2s})=\{\begin{array}{ll}(2s,2-2s,2,r+s+1,r+s+1),\hfill & 0\le s\le 1;\hfill \\ (s+2,2s-2,s+1,r-s+3,\hfill & 2\le s\le 3;\hfill \\ r-s+3),\hfill & \hfill \\ (s+2,s+1,s+1,r-s+3,r-s+3),\hfill & 4\le s\le r+1;\hfill \\ (2r-s+4,2r-s+5,2r-s+3,\hfill & r+2\le s\le 2r-1;\hfill \\ s-r,s-r-1),\hfill & \hfill \\ (3,5,3,s-r,s-r-1),\hfill & s=2r;\hfill \\ (1,3,2,s-r,s-r-1),\hfill & s=2r+1.\hfill \end{array}$

and,

$C_{R_m}({\text{q}}_{2s+1})=\{\begin{array}{ll}(2s+1,1,s+1,r-s+2,\hfill & 0\le s\le 1;\hfill \\ r+s+1),\hfill & \hfill \\ (s+3,2s-1,s+1,r-s+2,\hfill & 2\le s\le 3;\hfill \\ r-s+3),\hfill & \hfill \\ (s+3,s+2,s+1,r-s+2,\hfill & 4\le s\le r;\hfill \\ r-s+3),\hfill & \hfill \\ (2r-s+3,2r-s+4,\hfill & r+1\le s\le r+2;\hfill \\ 2r-s+3,s-r,2),\hfill & \hfill \\ (2r-s+3,2r-s+4,\hfill & r+3\le s\le 2r-1;\hfill \\ 2r-s+3,s-r,s-r),\hfill & \hfill \\ (2,4,3,s-r,s-r),\hfill & s=2r.\hfill \end{array}$

Representation of internal vertices:

$C_{R_m}({\text{p}}_{2s})=\{\begin{array}{ll}(s+1,2-s,3,r+s,r-s+2),\hfill & 0\le s\le 1;\hfill \\ (s+1,s,s+2,r-s+4,r-s+2),\hfill & 2\le s\le r;\hfill \\ (2r-s+3,s,2r-s+1,3,r-s+1),\hfill & r+1\le s\le r+2;\hfill \\ (2r-s+3,2r-s+4,2r-s+2,\hfill & r+3\le s\le 2r+1.\hfill \\ s-r+1,s-r-2),\hfill & \hfill \end{array}$

and,

$C_{R_m}({\text{p}}_{2s+1})=\{\begin{array}{ll}(s+2,2,s,r-s+1,r+s),\hfill & 0\le s\le 1;\hfill \\ (s+2,s+1,s,r-s+1,r-s+4),\hfill & 2\le s\le r;\hfill \\ (2r-s+1,2r-s+3,2r-s+5,\hfill & r+1\le s\le r+2;\hfill \\ s-r-1,3),\hfill & \hfill \\ (2r-s+2,2r-s+3,2r-s+4,\hfill & r+3\le s\le 2r.\hfill \\ s-r-1,s-r+1),\hfill & \hfill \end{array}$

Representation of external edges:

$C_{R_m}({\text{q}}_{2s}{\text{q}}_{2s+1})=\{\begin{array}{ll}(2s,1-s,s+1,r+1,r+s+1),\hfill & 0\le s\le 1;\hfill \\ (2s,s,s+1,r-s+2,r-s+3),\hfill & s=2;\hfill \\ (s+2,s+1,s+1,r-s+2,\hfill & 3\le s\le r;\hfill \\ r-s+3),\hfill & \hfill \\ (2r-s+3,r+2,2r-s+3,\hfill & r+1\le s\le r+2;\hfill \\ s-r,s-r+3),\hfill & \hfill \\ (2r-s+3,2r-s+4,2r-s+3,\hfill & r+3\le s\le 2r-1;\hfill \\ s-r,s-r-1),\hfill & \hfill \\ (2,4,3,s-r,s-r-1),\hfill & s=2r;\hfill \\ (0,2,2,s-r,s-r-1),\hfill & s=2r+1.\hfill \end{array}$

and,

$C_{R_m}({\text{q}}_{2s+1}{\text{q}}_{2s+2})=\{\begin{array}{ll}(2s+1,s,s+1,r-s+2,r+1),\hfill & 0\le s\le 1;\hfill \\ (s+3,2s-1,s+1,r-s+2,\hfill & 2\le s\le 3;\hfill \\ r-s+2),\hfill & \hfill \\ (s+3,s+2,s+1,r-s+2,\hfill & 4\le s\le r;\hfill \\ r-s+2),\hfill & \hfill \\ (2r-s+3,2r-s+4,\hfill & r+1\le s\le 2r-2;\hfill \\ 2r-s+2,s-r,s-r),\hfill & \hfill \\ (3,5,3,s-r,s-r),\hfill & s=2r-1;\hfill \\ (1,3,2,s-r,s-r),\hfill & s=2r.\hfill \end{array}$

Representation of external and internal edges:

$C_{R_m}({\text{q}}_{2s}{\text{p}}_{2s})=\{\begin{array}{ll}(2s,2-s,2,r+s,r+1),\hfill & 0\le s\le 1;\hfill \\ (s+1,s,s+1,r-s+3,\hfill & 2\le s\le r;\hfill \\ r-s+2),\hfill & \hfill \\ (2r-s+3,s,2r-s+2,2,\hfill & r+1\le s\le r+2;\hfill \\ r-s+2),\hfill & \hfill \\ (2r-s+3,2r-s+4,2r-s+2,\hfill & r+3\le s\le 2r;\hfill \\ s-r,s-r-2),\hfill & \hfill \\ (1,3,1,s-r,s-r-2),\hfill & s=2r+1.\hfill \end{array}$

and,

$C_{R_m}({\text{q}}_{2s+1}{\text{p}}_{2s+1})=\{\begin{array}{ll}(2s+1,1,s,r-s+1,r+s),\hfill & 0\le s\le 1;\hfill \\ (s+2,s+1,s,r-s+1,\hfill & 2\le s\le r;\hfill \\ r-s+3),\hfill & \hfill \\ (2r-s+2,2r-s+3,r+1,\hfill & s=r+1;\hfill \\ s-r-1,2),\hfill & \hfill \\ (2r-s+2,2r-s+3,2r\hfill & r+2\le s\le 2r+1.\hfill \\ -s+3,\hfill & \hfill \\ s-r-2,s-r-1),\hfill & \hfill \end{array}$

Representation of internal edges:

$C_{R_m}({\text{p}}_{2s}{\text{p}}_{2s+2})=\{\begin{array}{ll}(s+1,1,3,r+s,r-s+1),\hfill & 0\le s\le 1;\hfill \\ (s+1,s,s+2,r-s+3,r-s+1),\hfill & 2\le s\le r-1;\hfill \\ (r+1,s,2r-s+1,3,1),\hfill & r\le s\le r+1;\hfill \\ (2r-s+1,2r-s+3,2r-s+1,\hfill & r+2\le s\le 2r;\hfill \\ s-r+1,s-r-2),\hfill & \hfill \\ (2,2,0,s-r,s-r-2),\hfill & s=2r+1.\hfill \end{array}$

and,

$C_{R_m}({\text{p}}_{2s+1}{\text{p}}_{2s+3})=\{\begin{array}{ll}(s+2,2,s,r-s,r+s),\hfill & 0\le s\le 1;\hfill \\ (s+2,s+1,s,r-s,r-s+4),\hfill & 2\le s\le r-1;\hfill \\ (2r-s+1,r+1,s,0,3),\hfill & r\le s\le r+1;\hfill \\ (2r-s+1,2r-s+2,2r-s+3,\hfill & r+2\le s\le 2r.\hfill \\ s-r-1,s-r+1),\hfill & \hfill \end{array}$

□

Now, from lemma3, the resolving set R_m must contain vertices from both the external and internal cycles of graph.

Lemma 7. Suppose n ≡ 1, 3(mod4), then β_m ≥ 5.

Proof: Suppose that β_m = 4. If so, the following contradictions are assumed.

Case 1: When the external cycle contain three fixed vertices, {q₀, q₁, q₂}, and other vertex lie in the internal cycle p_ℓ.

(i) If ℓ = 0, 2, 4, …, 2r, then r_m{q₀|q₀, q₁, q₂, p_ℓ} = r_m{q₀q_n−1|q₀, q₁, q₂, p_ℓ} = (0, 1, 2, ℓ + 1).

(ii) If ℓ = 1, 3, 5, …, 4r − 1, then r_m{q₀|q₀, q₁, q₂, p_ℓ} = r_m{q₀q_n−1|q₀, q₁, q₂, p_ℓ}.

Case 2: When {p₀, p₁, p₂} lie in the internal cycle and the other vertex lie in the external cycle q_ℓ.

(i) If ℓ = 0, 2, 4, …, 2r, then r_m{q₀|p₀, p₁, p₂, q_ℓ} = r_m{q₀q_n−1|p₀, p₁, p₂, q_ℓ}.

(ii) If ℓ = 1, 3, 5, …, 2r + 3, then r_m{q₀|p₀, p₁, p₂, q_ℓ} = r_m{q₀q_n−1|p₀, p₁, p₂, q_ℓ}.

We already proved that for n ≡ 1, 3(mod4), and the mixed metric dimension is β_m ≤ 5. From Remark2, we consider the following cases where the external and internal cycles comprise two vertices each.

Case 3: When two external vertices are fixed {q₀, q₁}, and the internal vertices are {p₀, p_ℓ}.

(i) If ℓ = 0, 2, 4, …, 2r, then r_m{q₀|q₀, q₁, p₀, p_ℓ} = r_m{q₀q_n−1|q₀, q₁, p₀, p_ℓ}.

(ii) If ℓ = 1, 3, 5, …, 4r − 1, then r_m{q₀|q₀, q₁, p₀, p_ℓ} = r_m{q₀q_n−1|q₀, q₁, p₀, p_ℓ}.

Because of the symmetry, other possible cases can also be derived. From all the above cases, therefore, it is proven that, for n ≡ 1, 3(mod4), the mixed metric dimension is β_m ≥ 5. We can therefore say β_m = 5 when n ≡ 1, 3(mod4). □

Theorem 6. For n ≥ 7, we have a mixed metric dimension

$\begin{array}{l}{\beta }_m(P(n,2))=\{\begin{array}{cc}4,\hfill & n\equiv 0,2(mod4);\hfill \\ 5,\hfill & n\equiv 1,3(mod4).\hfill \end{array}\hfill \end{array}$

Proof:Case 1: When n ≡ 0, 2(mod4).

From lemma 4,5, we have β_mP(n, 2) = 4.

Case 1: When n ≡ 1, 3(mod4).

From lemma 6,7, we have β_mP(n, 2) = 5. □

For the remainder of the cases, when n ≤ 15, the mixed metric dimension β_m(P(n, 2)) is calculated through the total enumeration method, shown in Table 2, along with the mixed metric basis.

TABLE 2

Table 2. Mixed Metric generator β_m for P(n, 2).

3. Conclusion and Further Research

The recently introduced mixed metric dimension is calculated for P(n, 2). It has been shown that P(n, 2) has mixed metric dimension equal to 4 for n ≡ 0, 2(mod4), and, for n ≡ 1, 3(mod4), the mixed metric dimension is 5. This shows that each graph of the family of generalized Petersen P(n, 2) has constant mixed metric dimension.

Theorem 7. [29] For the graph of P(n, 3),

$\begin{array}{l}\beta (P(n,3))=\{\begin{array}{cc}4,\hfill & whenn\equiv 0(mod6);\hfill \\ 3,\hfill & whenn\equiv 1,(mod6).\hfill \end{array}\hfill \end{array}$

and,

$\begin{array}{l}\beta (P(n,3))\le \{\begin{array}{cc}5,\hfill & whenn\equiv 2(mod6);\hfill \\ 4,\hfill & whenn\equiv 3,4,5(mod6).\hfill \end{array}\hfill \end{array}$

Theorem 8. [30] For n ≥ 17, we have,

$\begin{array}{l}\beta (P(n,4))\le \{\begin{array}{cc}3,\hfill & whenn\equiv 0(mod4);\hfill \\ 4,\hfill & whenn\equiv 1,2,3(mod4).\hfill \end{array}\hfill \end{array}$

Theorem 9. [31] The metric dimension of graph of P(2n, n) is

$\begin{array}{l}\beta (P(2n,n))=\{\begin{array}{cc}3,\hfill & whenniseven;\hfill \\ 4,\hfill & otherwise.\hfill \end{array}\hfill \end{array}$

The standard metric dimension is examined for these as well as other known classes of generalized Petersen graphs; the mixed metric dimension for these as well as other graphs would therefore be intriguing to investigate. If the other variants of dimension are identified, a comparative study can be carried out; this could evaluate the relationship between β(Γ), β_e(Γ), and β_m(Γ) in the different families of graphs.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary materials, further inquiries can be directed to the corresponding author/s.

Author Contributions

The main idea was presented by HR. YJ read and approved the final manuscript.

Funding

The work of HR was supported by Post-Doctoral fund of University of Shanghai for Science and Technology under the grant no. 5B19303001. The work of YJ was supported by the National Science Foundation of China under grant no. 71571055.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to express our sincere gratitude to the referees for a very careful reading of this paper and for all their insightful comments/criticism, which have led to a number of significant improvements to this paper.

References

1. Khuller S, Raghavachari B, Rosenfeld A. Landmarks in graphs. Discrete Appl Math. (1996) 70:217–29. doi: 10.1016/0166-218X(95)00106-2

CrossRef Full Text | Google Scholar

2. Slater PJ, Leaves of trees. Congr Numer. (1975) 14:549–59.

3. Harary F, Melter RA. On the metric dimension of a graph. Ars Comb. (1976) 2:191–5.

4. Chartrand G, Saenpholphat V, Zhang P. The independent resolving number of a graph. Math Bohem. (2003) 128:379–93. Available online at: http://dml.cz/dmlcz/134003

Google Scholar

5. Okamoto F, Phinezy B, Zhang P. The local metric dimension of a graph. Math Bohem. (2010) 135:239–55. Available online at: http://dml.cz/dmlcz/140702

Google Scholar

6. Sebǒ A, Tannier E. On metric generators of graph. Math Oper Res. (2004) 29:383–93. doi: 10.1287/moor.1030.0070

CrossRef Full Text | Google Scholar

7. Oellermann OR, Peters-Fransen J. The strong metric dimension of graphs and digraphs. Discrete Appl Math. (2007) 155:356–64. doi: 10.1016/j.dam.2006.06.009

CrossRef Full Text | Google Scholar

8. Trujillo-Rasua R, Yero IG. k-Metric antidimension: a privacy measure for social graphs. Inform Sci. (2016) 328:403–17. doi: 10.1016/j.ins.2015.08.048

CrossRef Full Text | Google Scholar

9. Shao Z, Wu P, Zhu E, Chen L. On metric dimension in some hex derived networks. Sensors. (2019) 19:94. doi: 10.3390/s19010094

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Raza H, Hayat S, Imran M, Pan XF. Fault-tolerant resolvability and extremal structures of graphs. Mathematics. (2019) 7:78. doi: 10.3390/math7010078

CrossRef Full Text | Google Scholar

11. Raza H, Hayat S, Pan XF. Binary locating-dominating sets in rotationally-symmetric convex polytopes. Symmetry. (2018) 10:727. doi: 10.3390/sym10120727

CrossRef Full Text | Google Scholar

12. Raza H, Hayat S, Pan XF. On the fault-tolerant metric dimension of certain interconnection networks. J Appl Math Comput. (2019) 60:517–35. doi: 10.1007/s12190-018-01225-y

CrossRef Full Text | Google Scholar

13. Raza H, Hayat S, Pan XF. On the fault-tolerant metric dimension of convex polytopes. Appl Math Comput. (2018) 339:172–85. doi: 10.1016/j.amc.2018.07.010

CrossRef Full Text | Google Scholar

14. Kelenc A, Tratnik N, Yero IG. Uniquely identifying the edges of a graph: the edge metric dimension. Discrete Appl Math. (2018) 251:204–20. doi: 10.1016/j.dam.2018.05.052

CrossRef Full Text | Google Scholar

15. Zubrilina N. On the edge dimension of a graph. Discrete Math. (2018) 341:2083–8. doi: 10.1016/j.disc.2018.04.010

CrossRef Full Text | Google Scholar

16. Peterin I, Yero IG. Edge metric dimension of some graph operations. Bull Malay Math Sci Soc. (2019) 43:2465–77. doi: 10.1007/s40840-019-00816-7

CrossRef Full Text | Google Scholar

17. Zhu E, Taranenko A, Shao Z, Xu J. On graphs with the maximum edge metric dimension. Discrete Appl Math. (2019) 257:317–24. doi: 10.1016/j.dam.2018.08.031

CrossRef Full Text | Google Scholar

18. Liu JB, Wang C, Wang S, Wei B. Zagreb indices and multiplicative Zagreb indices of Eulerian graphs. Bull Malay Math Sci Soc. (2019) 42:67–78. doi: 10.1007/s40840-017-0463-2

CrossRef Full Text | Google Scholar

19. Liu JB, Zhao J, Zhu Z. On the number of spanning trees and normalized Laplacian of linear octagonal quadrilateral networks. Int J Quantum Chem. (2019) 119:e25971. doi: 10.1002/qua.25971

CrossRef Full Text | Google Scholar

20. Liu JB, Zhao J, Min J, Cao J. The hosoya index of graphs formed by a fractal graph. Fractals. (2019) 27:1950135–875. doi: 10.1142/S0218348X19501354

CrossRef Full Text | Google Scholar

21. Liu JB, Zhao J, Cai ZQ. On the generalized adjacency, Laplacian and signless Laplacian spectra of the weighted edge corona networks. Phys A Stat Mech Appl. (2020) 540:123073. doi: 10.1016/j.physa.2019.123073

CrossRef Full Text | Google Scholar

22. Liu JB, Shi ZY, Pan YH, Cao J, Abdel-Aty M, Al-Juboori U. Computing the Laplacian spectrum of linear octagonal-quadrilateral networks and its applications. Polycycl Aromat Compd. (2020). doi: 10.1080/10406638.2020.1748666. [Epub ahead of print].

CrossRef Full Text | Google Scholar

23. Kelenc A, Kuziak D, Taranenko A, Yero IG. Mixed metric dimension of graphs. Appl Math Comput. (2017) 314:429–38. doi: 10.1016/j.amc.2017.07.027

CrossRef Full Text | Google Scholar

24. Raza H, Liu JB, Qu S. On mixed metric dimension of rotationally symmetric graphs. IEEE Access. (2019) 8:11560–9. doi: 10.1109/ACCESS.2019.2961191

CrossRef Full Text | Google Scholar

25. Watkins ME. A theorem on Tait colorings with an application to the generalized Petersen graphs. J Combinat Theory. (1969) 6:152–64. doi: 10.1016/S0021-9800(69)80116-X

CrossRef Full Text | Google Scholar

26. Cáceres J, Hernando C, Mora M, Pelayo IM, Puertas ML, Seara C, Wood DR. On the metric dimension of cartesian products of graphs. SIAM J Discrete Math. (2007) 21:423–41. doi: 10.1137/050641867

CrossRef Full Text | Google Scholar

27. Filipović V, Kartelj A, Kratica J. Edge metric dimension of some generalized petersen graphs. Results Math. (2019) 74:182. doi: 10.1007/s00025-019-1105-9

CrossRef Full Text | Google Scholar

28. Javaid I, Rahim MT, Ali K. Families of regular graphs with constant metric dimension. Utilitas Math. (2008) 75:21–34.

Google Scholar

29. Imran M, Baig AQ, Shafiq MK, Tomescu I. On metric dimension of generalized petersen graphs P (n, 3). Ars Comb. (2014) 117:113–30.

30. Naz S, Salman M, Ali U, Javaid I, Bokhary SA. On the constant metric dimension of generalized Petersen graphs P (n, 4). Acta Math Sin. (2014) 30:1145–60. doi: 10.1007/s10114-014-2372-8

CrossRef Full Text | Google Scholar

31. Imran M, Siddiqui MK, Naeem R. On the metric dimension of generalized petersen multigraphs. IEEE Access. (2018) 6:74328–38. doi: 10.1109/ACCESS.2018.2883556

CrossRef Full Text | Google Scholar