- 1Department of Engineering Science, Kermanshah University of Technology, Kermanshah, Iran
- 2Department of Mathematics, Faculty of Engineering and Natural Sciences, Bahçeşehir University, Istanbul, Turkey
- 3Department of Mathematics, College of Arts and Sciences, Prince Sattam Bin Abdulaziz University, Wadi Aldawaser, Saudi Arabia
Chaotic systems are dynamical systems that are highly sensitive to initial conditions. Such systems are used to model many real-world phenomena in science and engineering. The main purpose of this paper is to present several efficient numerical treatments for chaotic systems involving fractal-fractional operators. Several numerical examples test the performance of the proposed methods. Simulations with different values of the fractional and fractal parameters are also conducted. It is demonstrated that the fractal-fractional derivative enables one to capture all the useful information from the history of the phenomena under consideration. The numerical schemes can also be implemented for other chaotic systems with fractal-fractional operators.
1. Introduction
In recent decades numerical methods have been recognized as powerful mathematical techniques for solving nonlinear equations that model real-world problems [1–5]. Numerical techniques have been used to solve different classes of differential equations, including those of arbitrary order. Due to the outstanding contribution of nonlinear models to human understanding of many phenomena and the prediction of the future behavior of systems, many researchers are devoting their attention to developing new and reliable numerical techniques that could be applied to more complex cases. Chaotic behaviors are among the natural phenomena that have attracted the attention of many researchers, who aim to replicate and predict those behaviors. To achieve this, differential operators are often used as mathematical tools to construct the underlying models. Recently a new class of differential operators was introduced, which are convolutions of fractal derivatives and fractional kernels with different forms such as power law, exponential decay and the Mittag-Leffler function [6]. These differential operators are able to represent complexities that cannot be described with classical fractional differentiation and integration. One of the strengths of these operators is their two orders, where one is considered a fractional order and the other is the fractal dimension [7–9]. With these efficient operators, a new class of nonlinear differential and integral equations can be constructed, and existing chaotic models can be extended. Nevertheless, to verify the effectiveness of such fractal-fractional operators in modeling chaotic attractors, one needs to solve the models numerically as their exact solutions cannot be easily obtained by existing analytical methods. So far, a few numerical methods have been used to discretize such models, and some numerical results for chaotic attractors have been obtained. A different numerical scheme was suggested very recently [10–27] and was found to be efficient for solving nonlinear differential equations. Some articles have examined the analysis of errors and the determination of error bands in the context of the possible deficit differential equations [28–30]. Since the operators defined in this paper are novel in the field, the numerical methods associated with them are also very limited. One of the main motivations for this article was to introduce methods for solving fractal-fractional problems that have not been considered before. By using the proposed methods, approximate solutions to these problems can be determined more easily and with higher accuracy. In addition, the methods can be applied to real-world problems. In this work, we present applications of such numerical schemes in solving chaotic models that involve the new class of differential operators. We consider some well-known chaotic models with fractal-fractional differential operators, so that we can compare our results with those in the literature. The article is organized as follows. In section 2, we give a brief overview of some basic definitions of fractional differential calculus. Two efficient and effective numerical methods for determining approximate solutions to fractal-fractional problems are presented in section 3. The first is for the Caputo derivative and the second is for the Atangana-Baleanu-Caputo derivative. The kernels used in these two definitions are singular and non-singular, respectively. Several numerical simulations for chaotic systems are described in section 4. The results obtained are accurate, interesting, and meaningful. Finally, we present our overall conclusions.
2. Preliminary Definitions
In this section, we give a brief review of some existing definitions of fractal-fractional operators. These operators result from the combination of two important concepts: fractional differentiation and fractal derivatives. Most of the definitions given here are taken from Atangana [6] and Atangana and Qureshi [31].
Definition 1. If g(t) is a differentiable function on a finite open interval, then we define the fractal-fractional derivative of g(t) in the Caputo sense as
where
Definition 2. If g(t) is a differentiable function on a finite open interval, then we define the fractal-fractional derivative of g(t) in the Caputo-Fabrizio sense as
provided K(0) = K(1) = 1.
Definition 3. If g(t) is a differentiable function on a finite open interval, then we define the fractal-fractional derivative of g(t) in the Atangana-Baleanu sense as
where Eρ(.) is the Mittag-Leffler function, defined by
This function is an essential function in the modeling of physical processes using fractional calculus concepts. We know that Equation (5) reduces to the exponential function ex if one takes ρ = 1. Also, AB(·) is a function used for normalization, and it satisfies the property AB(0) = AB(1) = 1. One of the most popular definitions of AB(·) is
Definition 4. If g(t) is a differentiable function on a finite open interval, then we define the fractal-fractional integral of g(t) in the Caputo sense [31] as
Definition 5. If g(t) is a differentiable function on a finite open interval, then we define the fractal-fractional integral of g(t) in the Caputo-Fabrizio sense [31] as
Definition 6. If g(t) is a differentiable function on a finite open interval, then we define the fractal-fractional integral of g(t) in the Atangana-Baleanu sense [31] as
3. The Proposed Numerical Methods
In what follows, the main aim is to construct two equations involving fractal-fractional derivatives,
with the initial condition ξ(0) = ξ0.
3.1. The Caputo Fractal-Fractional Derivative
From the results in Atangana and Qureshi [31], Equation (9) reduces to the following Caputo fractional representation:
Now, taking into account the fundamental theorem of calculus, one gets
Then, inserting t = tn = t0 + nΔt into (17) leads to the following expression:
where is the time step for the discretization points.
Next, taking the linear Lagrange interpolation into account for the function of f(ω) = ωτ−1ℕ(ω, ξ(ω)), we obtain
where ξi = ξ(ti). At this point, the result obtained in formula (13) can be used in relation (12). This substitution results in the following relationship:
where
3.2. The Atangana-Baleanu Fractal-Fractional Derivative
In this case we can convert Equation (9) to the following Atangana-Baleanu fractional form [31]:
Upon applying the integral operator to both sides of Equation (16), the following Volterra integral equation is constructed:
Taking t = tn = t0 + nΔt in (17), we have
Now, substituting (13) into (18), we get the following implicit Atangana-Baleanu-Caputo scheme:
where ξn and dj are the coefficients defined in (15). A closer look at relations (14) and (19) shows that these expressions are implicit equations for determining yn. The Newton iteration method is one of the most popular and efficient techniques for solving such problems. In this article, as in Garrappa [32], Ghanbari and Kumar [33], and Ghanbari et al. [34], we will use the Newton method to solve these equations. By solving these equations, approximate solutions to the original problem will be determined.
4. Numerical Simulations for Some Chaotic Systems
In this section, to show the validity of the proposed numerical technique, three chaotic systems involving Atangana-Baleanu-Caputo fractional derivatives are considered.
Example 1. Consider the following modified cyclically symmetric Thomas attractor given by [35]
Now we take into account the iterative methods given by (14) and (19) to solve (20). Taking (14) into account, we get the iterative structure
Moreover, from (19) we get
In Figures 1–4 we plot the results of numerical simulations using the two iterative schemes (21) and (22) with = 0.2. For the numerical implementations we took (x0, y0, z0) = (0, 3, 11) as the initial condition. The results of the iterative scheme (21) are plotted in Figures 5–8. In each figure we have taken a fixed value of τ and different values of ρ. In these experiments we set Δt = 10−3 and T = 800.
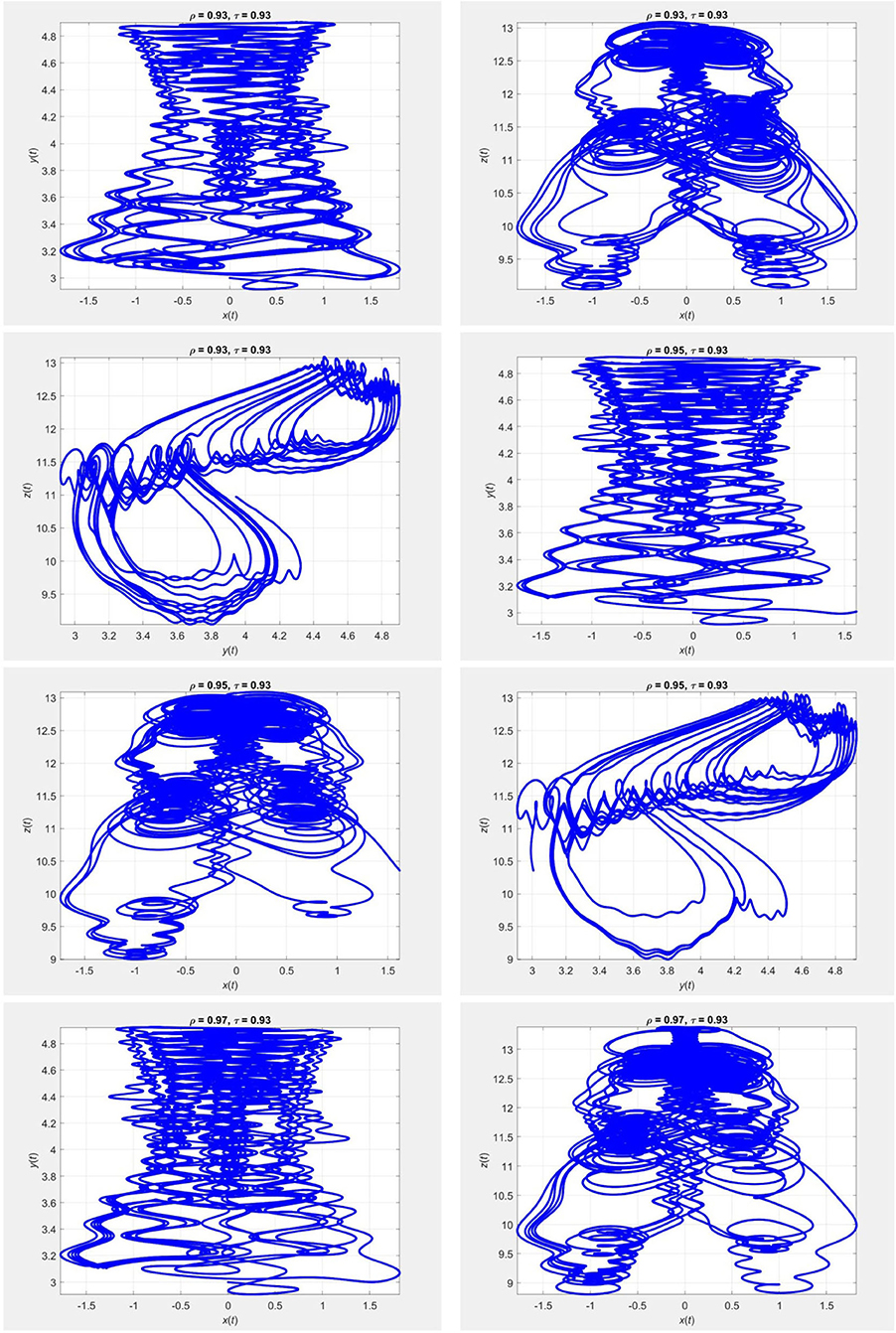
Figure 1. Evolution of the chaotic system (20) for τ = 0.93 and different values of ρ, using the iterative scheme (21).
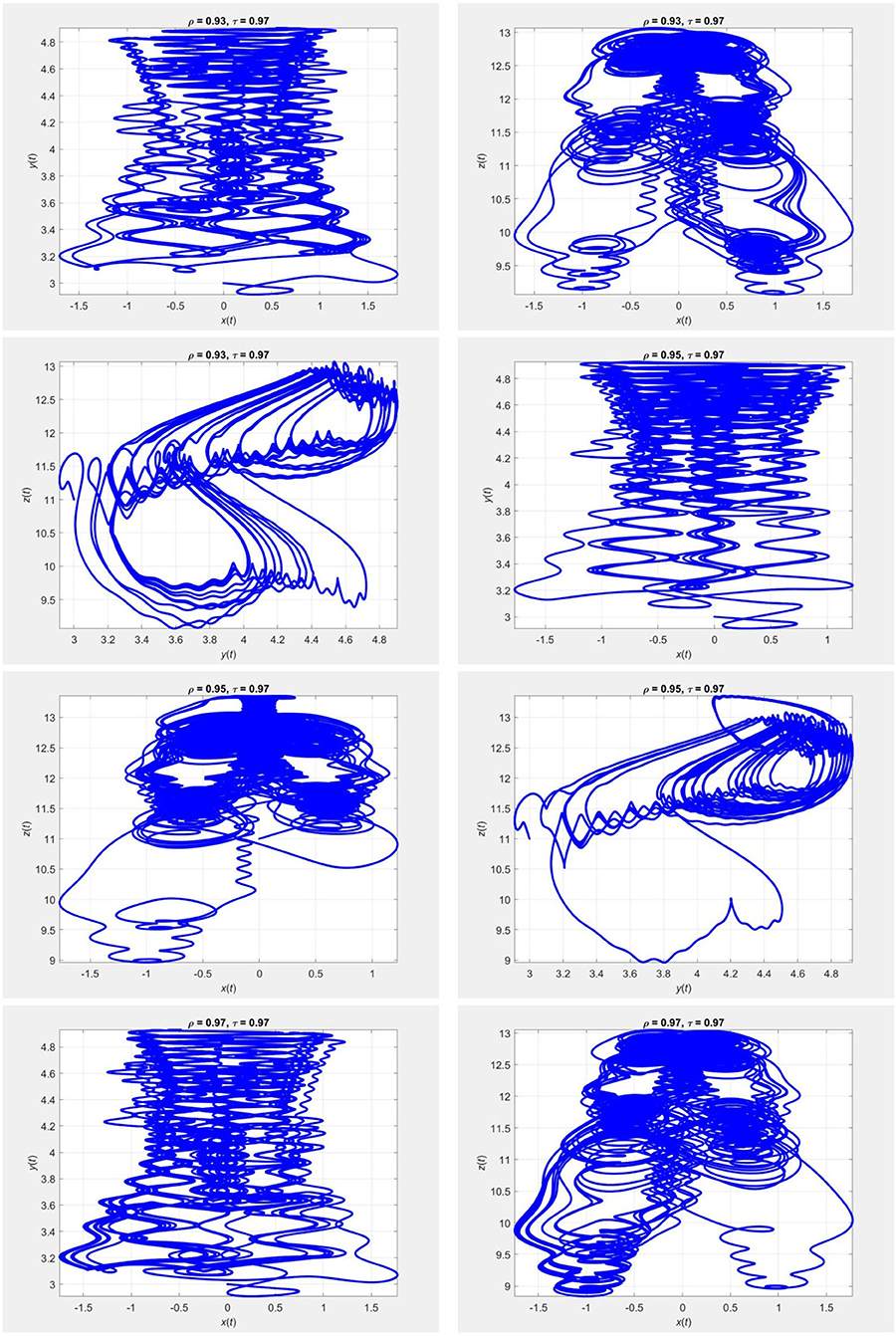
Figure 2. Evolution of the chaotic system (20) for τ = 0.97 and different values of ρ, using the iterative scheme (21).
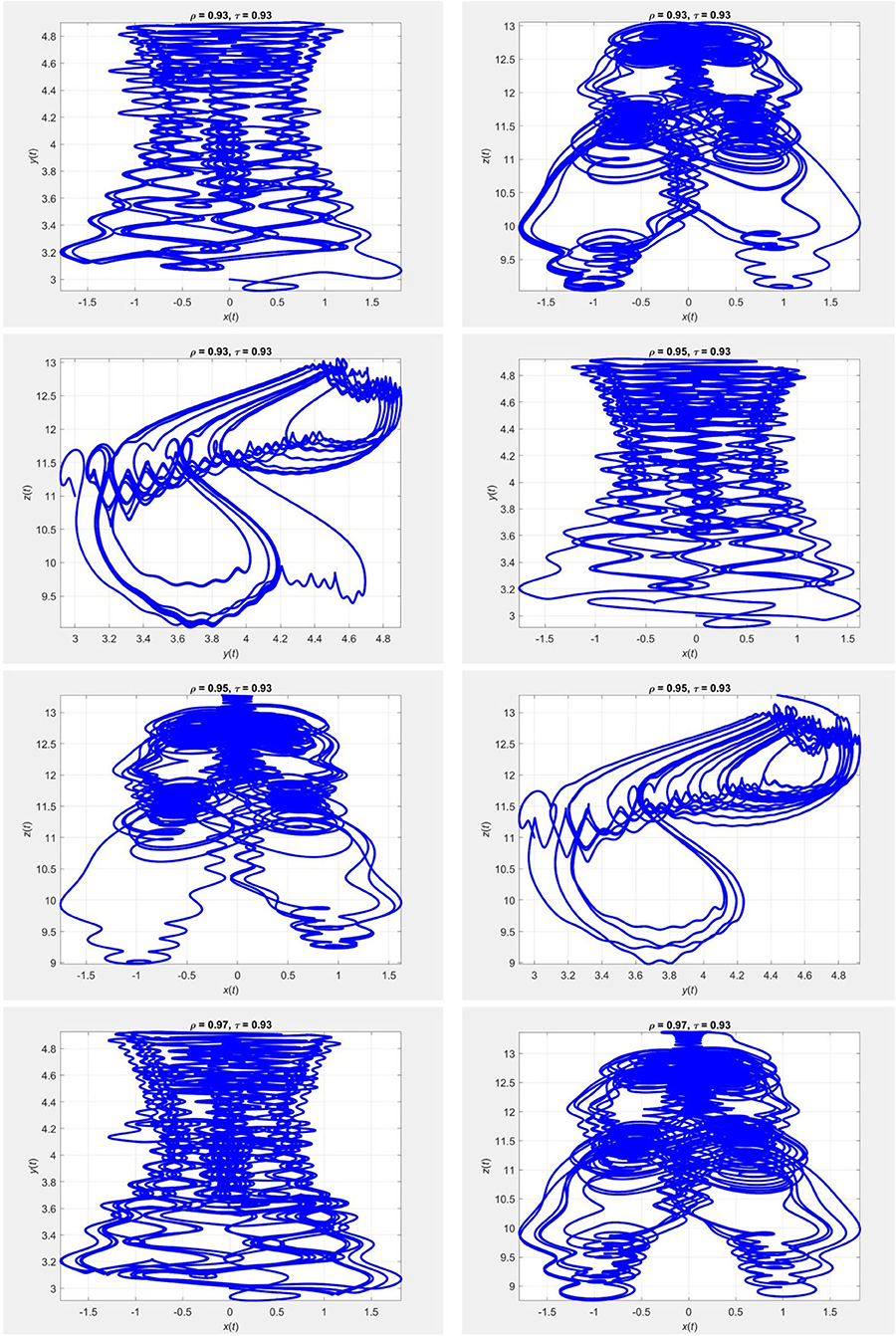
Figure 3. Evolution of the chaotic system (20) for τ = 0.93 and different values of ρ, using the iterative scheme (22).
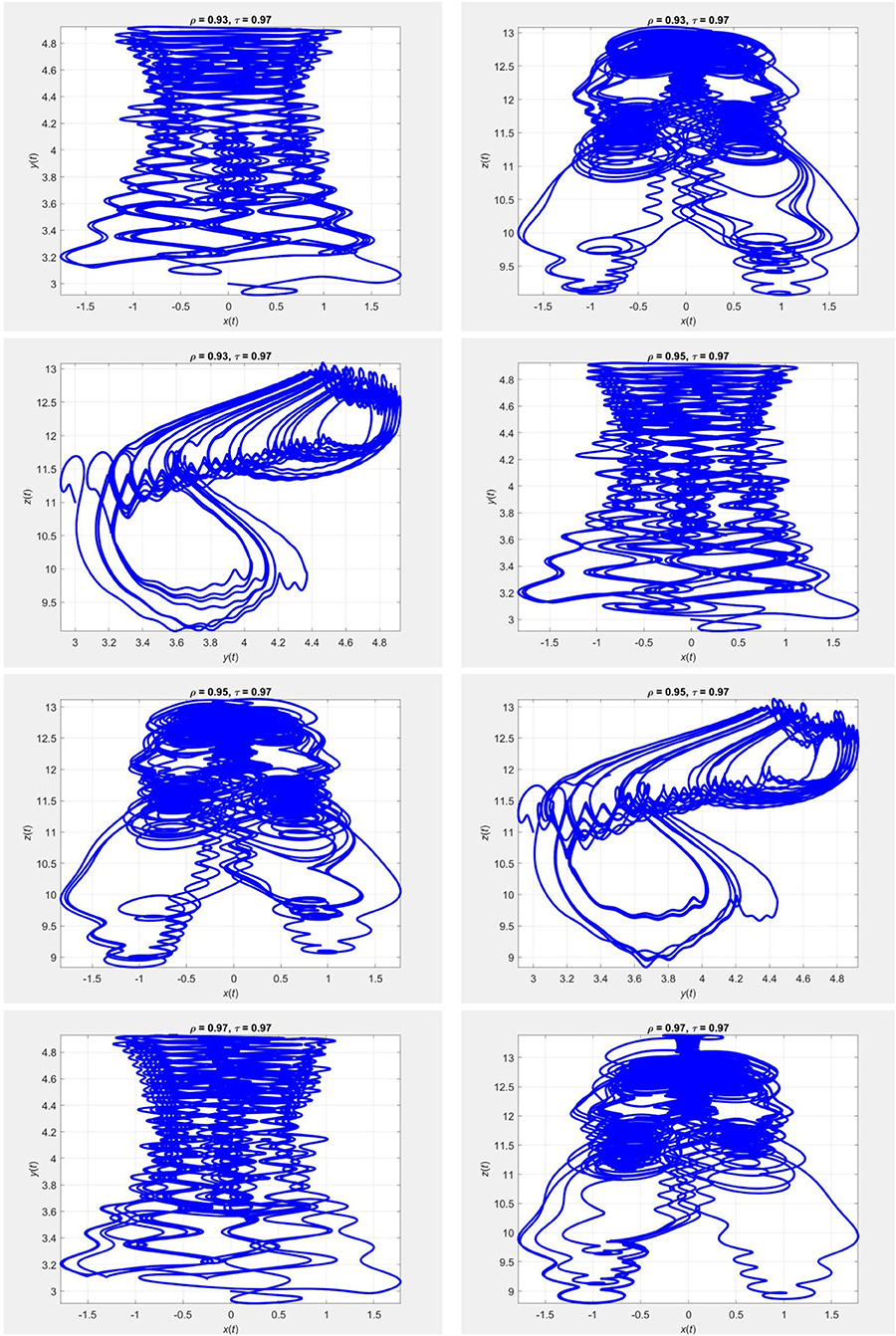
Figure 4. Evolution of the chaotic system (20) for τ = 0.97 and different values of ρ, using the iterative scheme (22).
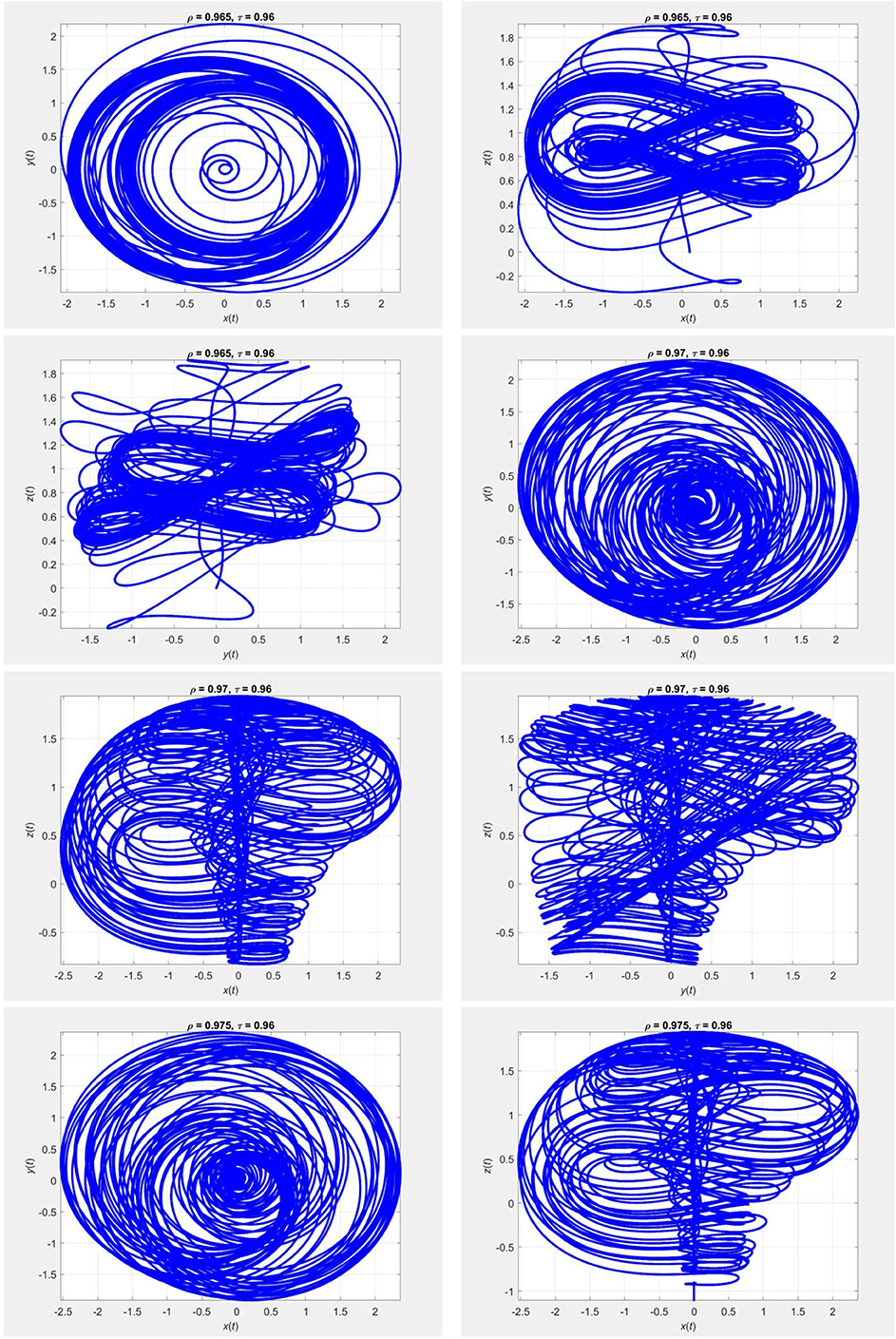
Figure 5. Evolution of the chaotic system (23) for τ = 0.96 and different values of ρ, using the iterative scheme (24).
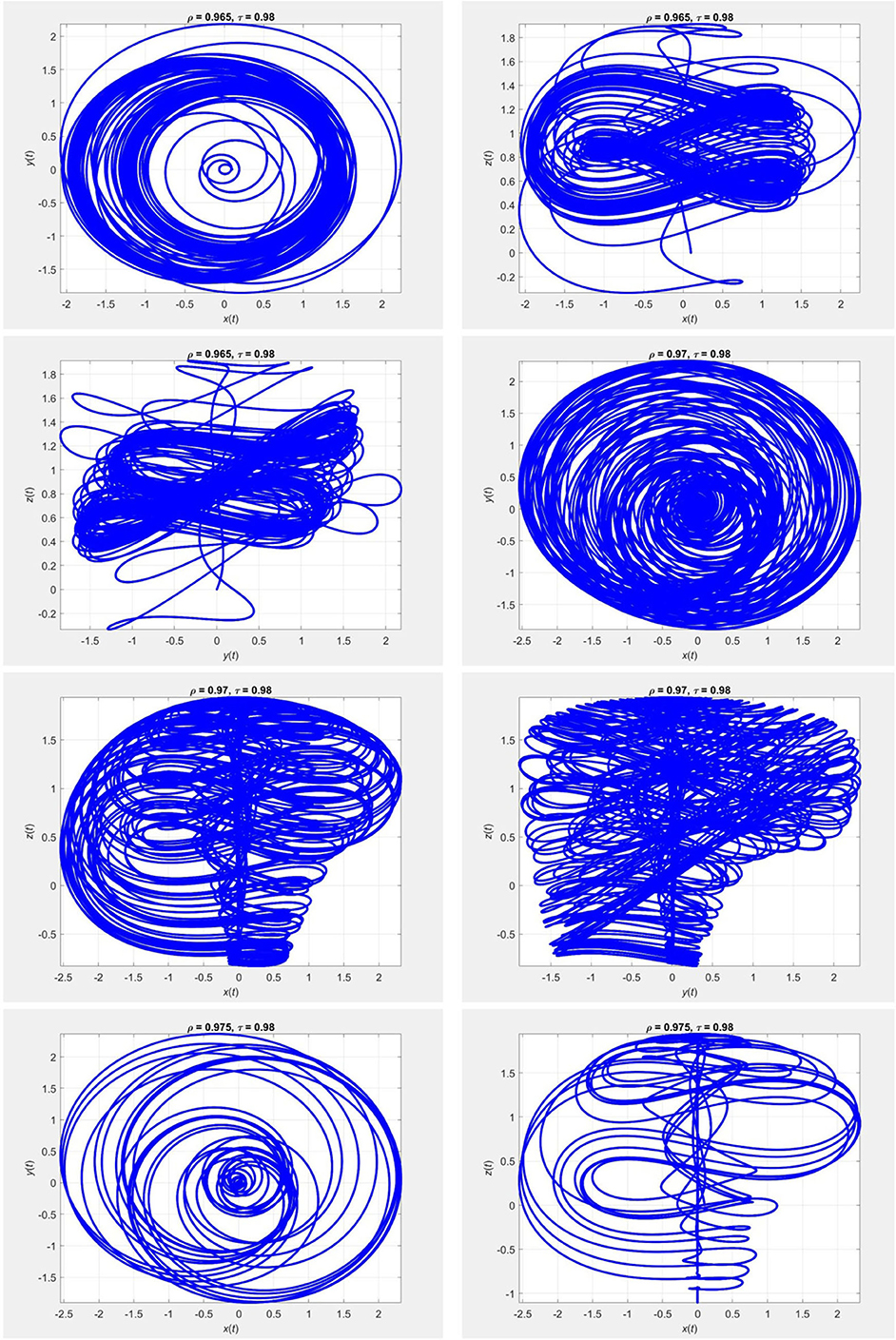
Figure 6. Evolution of the chaotic system (23) for τ = 0.98 and different values of ρ, using the iterative scheme (24).

Figure 7. Evolution of the chaotic system (23) for τ = 0.96 and different values of ρ, using the iterative scheme (25).
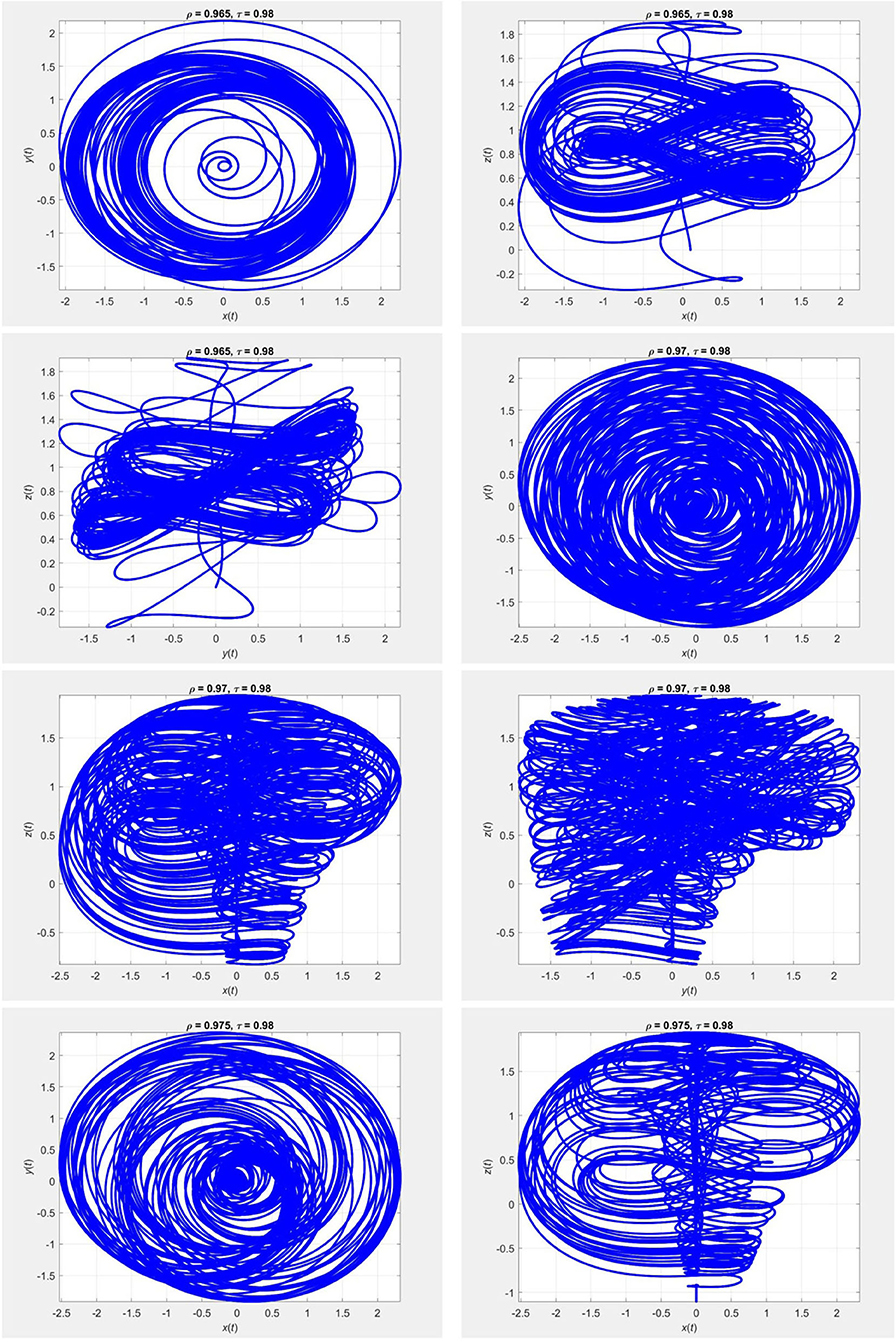
Figure 8. Evolution of the chaotic system (23) for τ = 0.98 and different values of ρ, using the iterative scheme (25).
Example 2. In this example we consider the chaotic system
To solve this chaotic system, we use the following iterative scheme obtained from (14):
Using (19) one gets
The approximate solutions obtained from (24) are plotted in Figures 5, 6, and those obtained from (25) are plotted in Figures 7, 8. The parameter values used in the model are = 0.95, = 0.7, = 0.6, = 3.5, and = 0.1. We used the initial guess (x0, y0, z0) = (0.1, 0, 0) for different fractional orders of ρ and τ.
Example 3. Consider the chaotic system given by [31]
For this system, from (14) we obtain the following iterative scheme:
Moreover, from (19), the approximate solution is obtained as
Figures 9–12 show the portraits corresponding to the chaotic system in (26) obtained using (27) and (28). The parameters for the model are = 50, = 2, = 30, 1 = 1, and 2 = 20. We used the initial guess (x0, y0, z0) = (2, 1, 1) for different fractional orders of ρ.
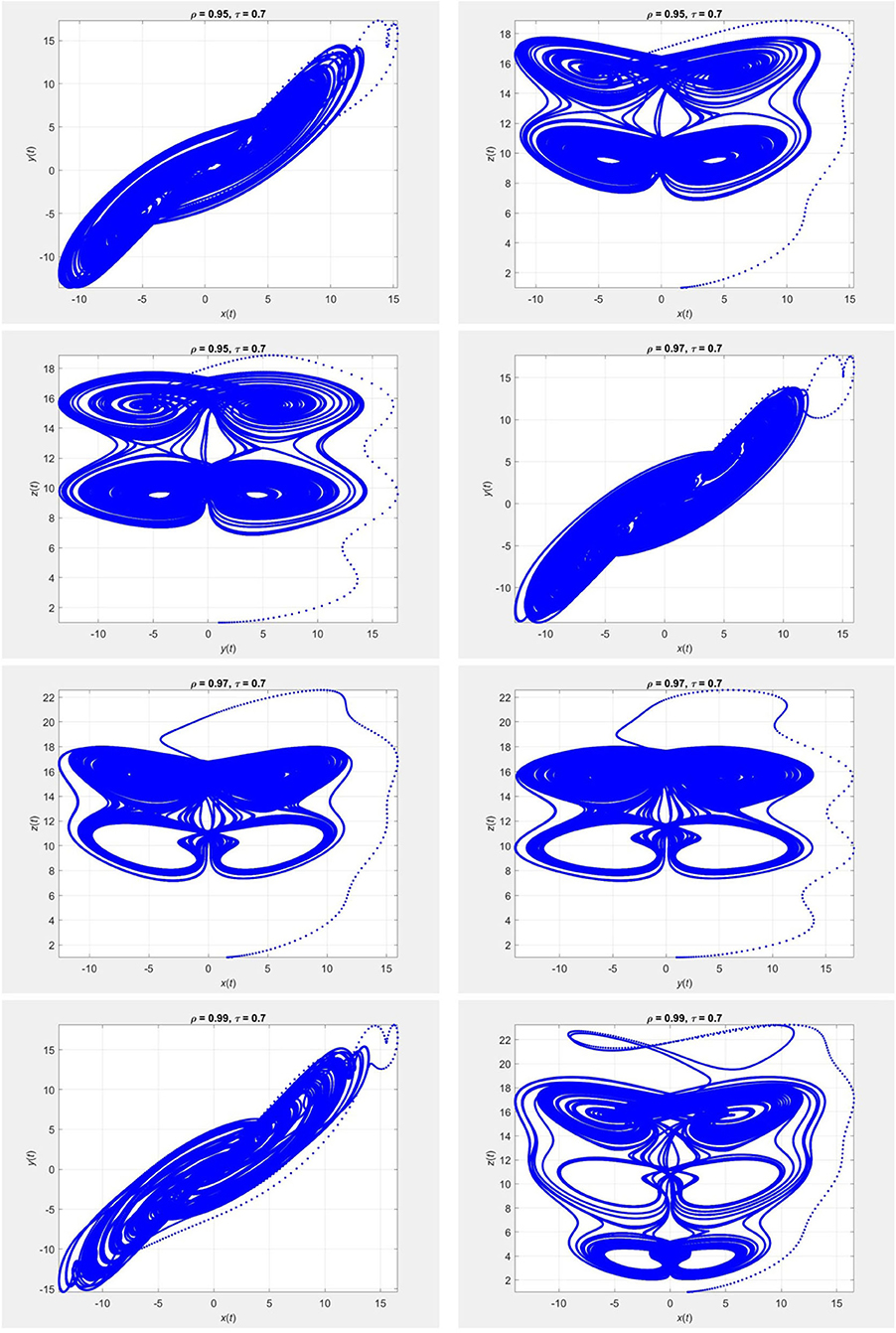
Figure 9. Evolution of the chaotic system (26) for τ = 0.7 and different values of ρ, using the iterative scheme (27).
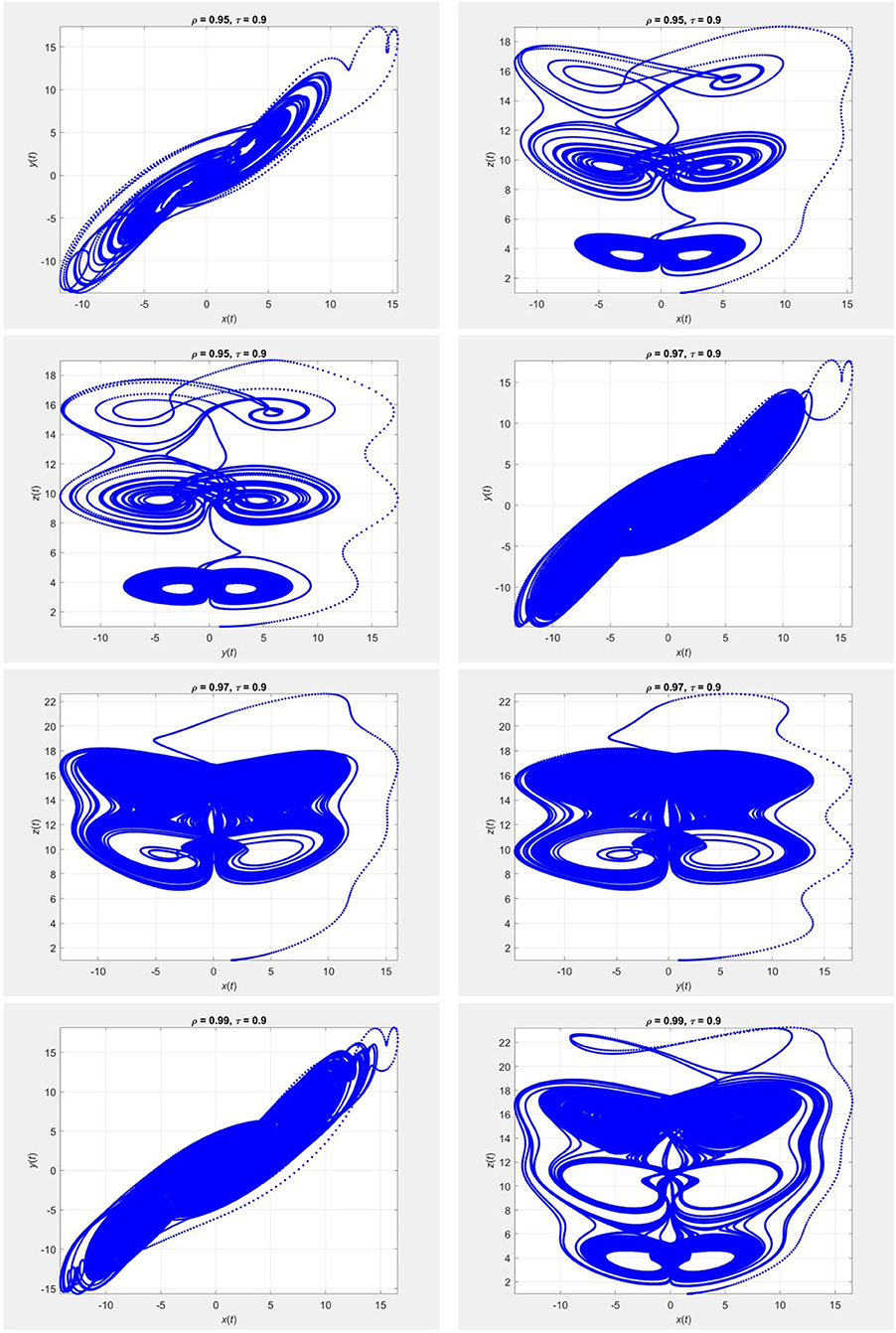
Figure 10. Evolution of the chaotic system (26) for τ = 0.9 and different values of ρ, using the iterative scheme (27).
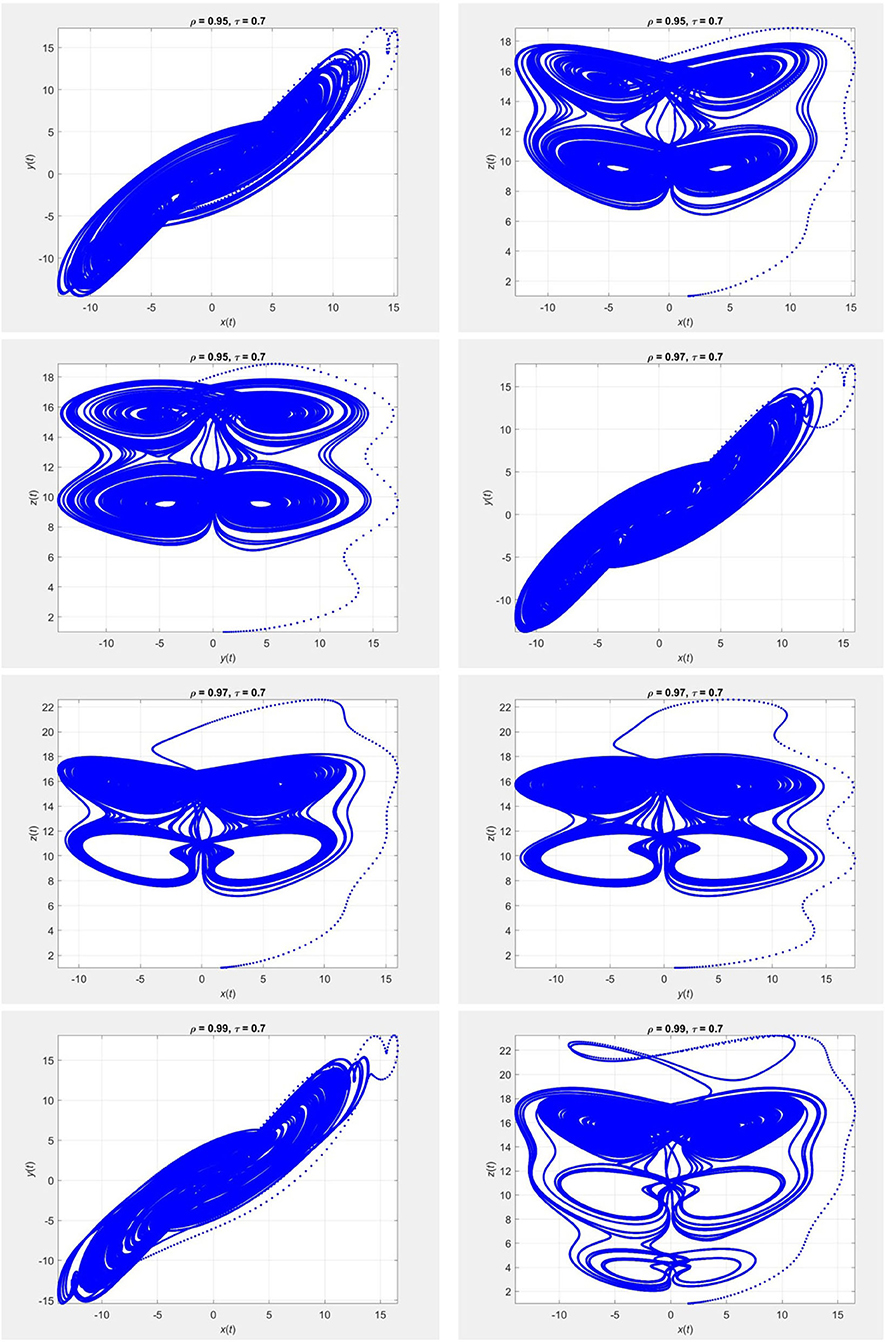
Figure 11. Evolution of the chaotic system (26) for τ = 0.7 and different values of ρ, using the iterative scheme (28).
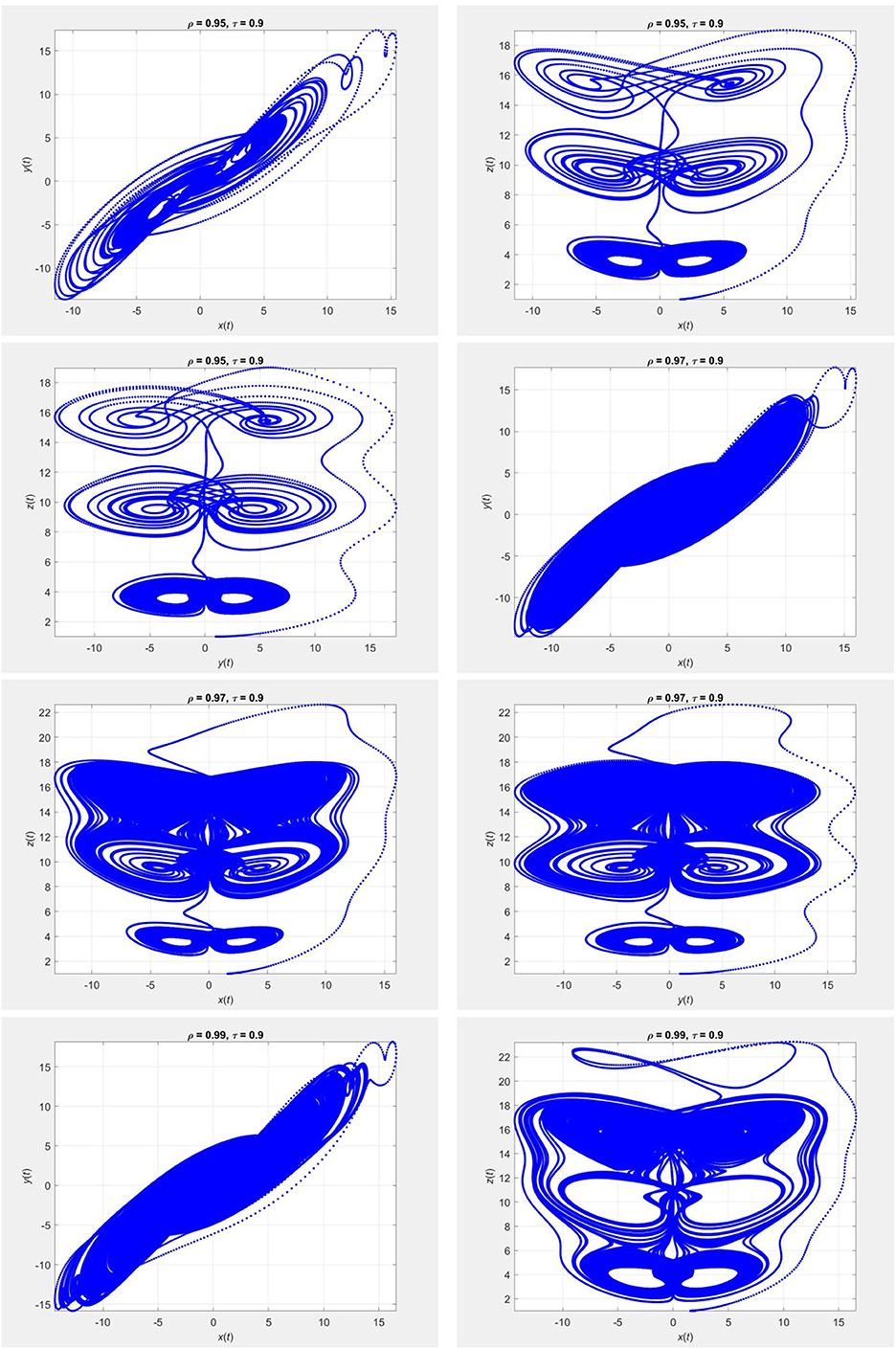
Figure 12. Evolution of the chaotic system (26) for τ = 0.9 and different values of ρ, using the iterative scheme (28).
5. Conclusion
Although many numerical methods are available, the development of new efficient numerical schemes has always been one of the most important concerns in applied mathematics and engineering. A foremost reason for the widespread interest in new numerical methods is that they may reveal new facts about real-world phenomena. This paper has presented some efficient approximate methods for solving chaotic systems that use new definitions for the derivative, called fractal-fractional derivatives. The concept of memory is one of the most important features of these types of derivatives. With this valuable feature, the evolution of the phenomena modeled by such systems can be more accurately predicted. The proposed new techniques have been tested by using them to solve several important practical problems. Application of the methods to these problems revealed very interesting behaviors of the systems that have meaningful interpretations. The numerical methods presented in this article have the potential to be used for solving similar models. Since any new numerical method should be validated in terms of convergence, stability and consistency of solutions, these are important research directions left to future work.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation, to any qualified researcher.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Kilbas AAA, Srivastava HM, Trujillo JJ. Theory and Applications of Fractional Differential Equations. Vol. 204. Amsterdam; Boston, MA: Elsevier Science Limited (2006).
2. Caputo M, Fabrizio M. A new definition of fractional derivative without singular kernel. Progr Fract Differ Appl. (2015) 1:1–13. doi: 10.18576/pfda/020101
3. Atangana A, Baleanu D. New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model. arXiv preprint arXiv:160203408. (2016). doi: 10.2298/TSCI160111018A
4. Gao W, Ghanbari B, Baskonus HM. New numerical simulations for some real world problems with Atangana-Baleanu fractional derivative. Chaos Solit Fract. (2019) 128:34–43. doi: 10.1016/j.chaos.2019.07.037
5. Ghanbari B, Gómez-Aguilar J. Modeling the dynamics of nutrient-phytoplankton-zooplankton system with variable-order fractional derivatives. Chaos Solit Fract. (2018) 116:114–20. doi: 10.1016/j.chaos.2018.09.026
6. Atangana A. Fractal-fractional differentiation and integration: connecting fractal calculus and fractional calculus to predict complex system. Chaos Solit Fract. (2017) 102:396–406. doi: 10.1016/j.chaos.2017.04.027
7. Losada J, Nieto JJ. Properties of a new fractional derivative without singular kernel. Progr Fract Differ Appl. (2015) 1:87–92.
8. Chen W, Sun H, Zhang X, Korošak D. Anomalous diffusion modeling by fractal and fractional derivatives. Comput Math Appl. (2010) 59:1754–8. doi: 10.1016/j.camwa.2009.08.020
9. Kanno R. Representation of random walk in fractal space-time. Phys A. (1998) 248:165–75. doi: 10.1016/S0378-4371(97)00422-6
10. Singh J, Kumar D, Baleanu D, Rathore S. An efficient numerical algorithm for the fractional Drinfeld-Sokolov-Wilson equation. Appl Math Comput. (2018) 335:12–24. doi: 10.1016/j.amc.2018.04.025
11. Qureshi S, Yusuf A, Shaikh AA, Inc M, Baleanu D. Fractional modeling of blood ethanol concentration system with real data application. Chaos. (2019) 29:013143. doi: 10.1063/1.5082907
12. Gill V, Singh J, Singh Y. Analytical solution of generalized space-time fractional advection-dispersion equation via coupling of Sumudu and Fourier transforms. Front Phys. (2019) 6:151. doi: 10.3389/fphy.2018.00151
13. Qureshi S, Atangana A, Shaikh AA. Strange chaotic attractors under fractal-fractional operators using newly proposed numerical methods. Eur Phys J Plus. (2019) 134:523. doi: 10.1140/epjp/i2019-13003-7
14. Kumar S, Kumar R, Singh J, Nisar K, Kumar D. An efficient numerical scheme for fractional model of HIV-1 infection of CD4+ T-cells with the effect of antiviral drug therapy. Alexandria Eng J. (2020). doi: 10.1016/j.aej.2019.12.046. [Epub ahead of print].
15. Berhe HW, Qureshi S, Shaikh AA. Deterministic modeling of dysentery diarrhea epidemic under fractional Caputo differential operator via real statistical analysis. Chaos Solit Fract. (2020) 131:109536. doi: 10.1016/j.chaos.2019.109536
16. Singh J. A new analysis for fractional rumor spreading dynamical model in a social network with Mittag-Leffler law. Chaos. (2019) 29:013137. doi: 10.1063/1.5080691
17. Qureshi S, Rangaig NA, Baleanu D. New numerical aspects of Caputo-Fabrizio fractional derivative operator. Mathematics. (2019) 7:374. doi: 10.3390/math7040374
18. Srivastava H, Kumar D, Singh J. An efficient analytical technique for fractional model of vibration equation. Appl Math Model. (2017) 45:192–204. doi: 10.1016/j.apm.2016.12.008
19. Qureshi S. Effects of vaccination on measles dynamics under fractional conformable derivative with Liouville-Caputo operator. Eur Phys J Plus. (2020) 135:63. doi: 10.1140/epjp/s13360-020-00133-0
20. Solís-Pérez J, Gómez-Aguilar J, Atangana A. Novel numerical method for solving variable-order fractional differential equations with power, exponential and Mittag-Leffler laws. Chaos Solit Fract. (2018) 114:175–85. doi: 10.1016/j.chaos.2018.06.032
21. Owolabi KM. Computational study of noninteger order system of predation. Chaos. (2019) 29:013120. doi: 10.1063/1.5079616
22. Yavuz M, Bonyah E. New approaches to the fractional dynamics of schistosomiasis disease model. Phys A. (2019) 525:373–93. doi: 10.1016/j.physa.2019.03.069
23. Jajarmi A, Ghanbari B, Baleanu D. A new and efficient numerical method for the fractional modeling and optimal control of diabetes and tuberculosis co-existence. Chaos. (2019) 29:093111. doi: 10.1063/1.5112177
24. Ghanbari B, Gómez-Aguilar J. Analysis of two avian influenza epidemic models involving fractal-fractional derivatives with power and Mittag-Leffler memories. Chaos. (2019) 29:123113. doi: 10.1063/1.5117285
25. Ganji R, Jafari H, Baleanu D. A new approach for solving multi variable orders differential equations with Mittag-Leffler kernel. Chaos Solit Fract. (2020) 130:109405. doi: 10.1016/j.chaos.2019.109405
26. Kadkhoda N, Jafari H. An analytical approach to obtain exact solutions of some space-time conformable fractional differential equations. Adv Differ Equat. (2019) 2019:428. doi: 10.1186/s13662-019-2349-0
27. Jafari H, Babaei A, Banihashemi S. A novel approach for solving an inverse reaction-diffusion-convection problem. J Optim Theory Appl. (2019) 183:688–704. doi: 10.1007/s10957-019-01576-x
28. Liu B, Hill DJ, Chen G. Synchronization errors and uniform synchronization with an error bound for chaotic systems. Int J Bifur Chaos. (2008) 18:3341–54. doi: 10.1142/S021812740802241X
29. Sorrentino F, Barlev G, Cohen AB, Ott E. The stability of adaptive synchronization of chaotic systems. Chaos. (2010) 20:013103. doi: 10.1063/1.3279646
30. Kazemi BF, Jafari H. Error estimate of the MQ-RBF collocation method for fractional differential equations with Caputo-Fabrizio derivative. Math Sci. (2017) 11:297–305. doi: 10.1007/s40096-017-0232-2
31. Atangana A, Qureshi S. Modeling attractors of chaotic dynamical systems with fractal-fractional operators. Chaos Solit Fract. (2019) 123:320–337. doi: 10.1016/j.chaos.2019.04.020
32. Garrappa R. Numerical solution of fractional differential equations: a survey and a software tutorial. Mathematics. (2018) 6:16. doi: 10.3390/math6020016
33. Ghanbari B, Kumar D. Numerical solution of predator-prey model with Beddington-DeAngelis functional response and fractional derivatives with Mittag-Leffler kernel. Chaos. (2019) 29:063103. doi: 10.1063/1.5094546
34. Ghanbari B, Kumar S, Kumar R. A study of behaviour for immune and tumor cells in immunogenetic tumour model with non-singular fractional derivative. Chaos Solit Fract. (2020) 133:109619. doi: 10.1016/j.chaos.2020.109619
Keywords: chaotic attractors, computational efficiency, fractal-fractional operators, thomas attractor, Newton's method, product integration rule
Citation: Ghanbari B and Nisar KS (2020) Some Effective Numerical Techniques for Chaotic Systems Involving Fractal-Fractional Derivatives With Different Laws. Front. Phys. 8:192. doi: 10.3389/fphy.2020.00192
Received: 19 March 2020; Accepted: 30 April 2020;
Published: 10 June 2020.
Edited by:
Jordan Yankov Hristov, University of Chemical Technology and Metallurgy, BulgariaReviewed by:
Sania Qureshi, Mehran University of Engineering and Technology, PakistanHossein Jaferi, University of South Africa, South Africa
Copyright © 2020 Ghanbari and Nisar. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kottakkaran Sooppy Nisar, bi5zb29wcHlAcHNhdS5lZHUuc2E=; a3NuaXNhcjFAZ21haWwuY29t
 Behzad Ghanbari
Behzad Ghanbari Kottakkaran Sooppy Nisar
Kottakkaran Sooppy Nisar