On Characterizing the Quantum Geometry Underlying Asymptotic Safety

The asymptotic safety program builds on a high-energy completion of gravity based on the Reuter fixed point, a non-trivial fixed point of the gravitational renormalization group flow. At this fixed point the canonical mass-dimension of coupling constants is balanced by anomalous dimensions induced by quantum fluctuations such that the theory enjoys quantum scale invariance in the ultraviolet. The crucial role played by the quantum fluctuations suggests that the geometry associated with the fixed point exhibits non-manifold like properties. In this work, we continue the characterization of this geometry employing the composite operator formalism based on the effective average action. Explicitly, we give a relation between the anomalous dimensions of geometric operators on a background d-sphere and the stability matrix encoding the linearized renormalization group flow in the vicinity of the fixed point. The eigenvalue spectrum of the stability matrix is analyzed in detail and we identify a “perturbative regime” where the spectral properties are governed by canonical power counting. Our results recover the feature that quantum gravity fluctuations turn the (classically marginal) R²-operator into a relevant one. Moreover, we find strong indications that higher-order curvature terms present in the two-point function play a crucial role in guaranteeing the predictive power of the Reuter fixed point.

1. Introduction

General relativity taught us to think of gravity in terms of geometric properties of spacetime. The motion of freely falling particles is determined by the spacetime metric g_μν which, in turn, is determined dynamically from Einstein's equations. It is then an intriguing question what replaces the concept of a spacetime manifold once gravity is promoted to a quantum theory. Typically, the resulting geometric structure is referred to as “quantum geometry” where the precise meaning of the term varies among different quantum gravity programs.

An approach toward a unified picture of the quantum gravity landscape could then build on identifying distinguished properties which characterize the underlying quantum geometry and lend themselves to a comparison between different programs. While this line of research is still in its infancy, a first step in this direction, building on the concept of generalized dimensions, has been very fruitful. In particular, the spectral dimension d_s, measuring the return probability of a diffusing particle in the quantum geometry, has been computed in a wide range of programs including Causal Dynamical Triangulations [1], Asymptotic Safety [2–5], Loop Quantum Gravity [6], string theory [7], causal set theory [8–10], the Wheeler-DeWitt equation [11], non-commutative geometry [12–14], and Hořava-Lifshitz gravity [15] [see [16, 17] for reviews]. A striking insight originating from this comparison is that, at microscopic distances, d_s = 2 rather universally. The interpretation of d_s as the dimension of a theories momentum space, forwarded in Amelino-Camelia et al. [18], then suggests that the dimensional reduction of the momentum space may be a universal feature of any viable theory of quantum gravity.

Following the suggestion [19]¹, a refined picture of quantum geometry could use the (anomalous) scaling dimension associated with geometric operators, comprising, e.g., spacetime volumes, integrated spacetime curvatures, and geodesic distances. Within the asymptotic safety program [22, 23], also reviewed in Percacci [24], Litim [25], Reuter and Saueressig [26], Ashtekar et al. [27], and Eichhorn [28], these quantities have been studied based on the composite operator formalism [19, 29–32]. This formalism allows to determine the anomalous scaling dimension of geometric operators based on an approximation of the quantum-corrected graviton propagator². For the Reuter fixed point in four dimensions the quantum corrections to the scaling of four-volumes $V_{d=4}~L^{4-{\gamma }_0}$ were determined in Pagani and Reuter [19]. The result γ₀ = 3.986 lent itself to the interpretation that “spacetime could be much more empty than expected.” Recently, Houthoff et al. [32] generalized this computation by determining the anomalous scaling dimensions associated with an infinite class of geometric operators

$\begin{array}{ll}{{O}}_n\equiv {\displaystyle \int }{d}^{d}x\sqrt{g}{R}^n,n=0,1,2,\cdots \in \mathbb{N}& (1)\end{array}$

where R denotes the Ricci scalar constructed from g_μν. While it was possible to extract analytic expressions for all γ_n, it also became apparent that the single-operator approximation underlying the computation comes with systematic uncertainties. In parallel, the anomalous scaling properties of subvolumes and geodesic distances resulting from the renormalization group fixed points underlying Stelle gravity and Weyl gravity have recently been computed in Becker et al. [31]. In combination, the results show that the scaling of geometric quantities carries information about the renormalization group fixed point providing the high-energy completion of the theory.

The purpose of present work is two-fold: Firstly, we extend the analysis [32] beyond the single-operator approximation and compute the complete matrix of anomalous dimensions associated with the class (1). This information allows to access the spectrum of the scaling matrix. We expect that the data linked to the scaling dimensions of the geometrical operators gives a refined characterization of the quantum spacetime underlying the Reuter fixed point. Our results are closely related but complementary to the ones obtained from solving the Wetterich equation [34–37] for effective average actions of f(R)-type [38–60]. The comparison between the two complementary computations indicates that one indeed needs to go beyond the single-operator approximation in order to reconcile the results. Secondly, our work gives information on the gauge-dependence of the anomalous dimensions associated with the operators (1). In this light, the value γ₀ = 3.986 found in Pagani and Reuter [19] may be rather extreme and quantum corrections to the scaling of volumes could be less drastic.

The rest of this work is organized as follows. Section 2 introduces the composite operator formalism and the propagators entering in our computation. The generating functional determining the matrix of anomalous dimensions is computed in section 3. The link to the stability matrix governing the gravitational renormalization group flow in the vicinity of the Reuter fixed point is made in section 4.1 and the spectral properties of the matrix are analyzed in section 4.2. Section 5 contains our concluding remarks and comments on the possibility of developing a geometric picture of Asymptotic Safety from random geometry. The technical details underlying our computation have been relegated to three appendices: Appendix A reviews the technical background for evaluating operator traces using the early-time expansion of the heat-kernel, Appendix B derives the beta functions governing the renormalization group flow of gravity in the Einstein-Hilbert truncation employing geometric gauge [61, 62], and Appendix C lists the two-point functions entering into the computation.

2. Computational Framework and Setup

Functional renormalization group methods provide a powerful tool for investigating the appearance of quantum scale invariance and its phenomenological consequences [63]. In particular, the Wetterich equation [34–37],

$\begin{array}{ll}k{\partial }_k{\Gamma }_k=\frac{1}{2}\text{Tr}\left[{\left({\Gamma }_k^{(2)}+{{R}}_k\right)}^{-1}k{\partial }_k{{R}}_k\right],& (2)\end{array}$

plays a key role in studying the renormalization group (RG) flow of gravity and gravity-matter systems based on explicit computations. It realizes the idea of Wilson's modern viewpoint on renormalization in the sense that it captures the RG flow of a theory generated by integrating out quantum fluctuations shell-by-shell in momentum space. Concretely, Equation (2) encodes the change of the effective average action Γ_k when integrating out quantum fluctuations with momentum p close to the coarse graining scale k. The flow of Γ_k is then sourced by the right-hand side where ${\Gamma }_k^{(2)}$ denotes the second variation of Γ_k with respect to the fluctuation fields, the regulator ${{R}}_k$ provides a k-dependent mass term for quantum fluctuations with momentum p² ≲ k², and Tr includes a sum over all fluctuation fields and an integral over loop-momenta. Lowering k “unsuppresses” further fluctuations which are then integrated out and change the value of the effective couplings contained in Γ_k. For later convenience, we then also introduce the “RG-time” t ≡ ln(k/k₀) with k₀ an arbitrary reference scale.

In practice, the Wetterich equation allows to extract non-perturbative information about a theories RG flow by restricting Γ_k to a subset of all possible interaction monomials and subsequently solving Equation (2) on this subspace. For gravity and gravity-matter systems such computations get technically involved rather quickly. Thus, it is interesting to have an alternative equation for studying the scaling properties of sets of operators ${{O}}_n$, n = 1, ⋯ , N, which are not included in Γ_k. Within the effective average action framework such an equation is provided by the composite operator equation [19, 64–66]. As a starting point, the operators ${{O}}_n$ are promoted to scale-dependent quantities by multiplying with a k-dependent matrix Z_nm(k)

$\begin{array}{ll}{{O}}_n(k)\equiv {\displaystyle \sum _m^N}{Z}_{nm}(k){{O}}_m.& (3)\end{array}$

The analogy of Z_nm to a wave-function renormalization then suggests to introduce the matrix of anomalous dimensions γ whose components are given by

$\begin{array}{ll}{\gamma }_{nm}\equiv {(Z^{-1}{\partial }_{t}Z)}_{nm}.& (4)\end{array}$

Following the derivation [19], the γ_nm can be computed from the composite operator equation

$\begin{array}{l}{\displaystyle \sum _{m=1}^N}{\gamma }_{nm}{{O}}_m=\\ -\frac{1}{2}\text{Tr}\left[{\left({\Gamma }_k^{(2)}+{{R}}_k\right)}^{-1}{{O}}_n^{(2)}{\left({\Gamma }_k^{(2)}+{{R}}_k\right)}^{-1}{\partial }_t{{R}}_k\right],& (5)\end{array}$

where ${{O}}_n^{(2)}$ denotes the second functional derivative of ${{O}}_n$ with respect to the fluctuation fields. For the geometric operators (1) the evaluation of γ has so far focused on the diagonal matrix elements γ_nn [c.f.[19, 32]]. The goal of the present work is to extend this analysis and, for the first time, study the eigenvalues of γ_ij associated with the operators (1).

3. Computing the Matrix of Anomalous Dimensions

The computation of γ_nm requires two inputs. First, one needs to specify the set of operators ${{O}}_n$. In the present work, these will be given by the geometric operators (1). Secondly, one needs to specify the gravitational propagators ${\Gamma }_k^{(2)}$. These will be derived from Γ_k approximated by the Euclidean Einstein-Hilbert (EH) action

$\begin{array}{ll}{\Gamma }_k^{\text{EH}}\left[g\right]=\frac{1}{16\pi G_k}{\displaystyle \int }{d}^{d}x\sqrt{g}(2{\Lambda }_k-R)& (6)\end{array}$

supplemented by a suitable choice for the gauge-fixing action (54). In practice, we obtain ${\Gamma }_k^{(2)}$ from the background field method, performing a linear split of the spacetime metric g_μν into a background metric ḡ_μν and fluctuations h_μν:

$\begin{array}{ll}{g}_{\mu \nu }={\overline{g}}_{\mu \nu }+h_{\mu \nu }.& (7)\end{array}$

In order to simplify the subsequent computation, we then chose the background metric as the metric on the d-sphere, so that the background curvature satisfies

$\begin{array}{l}{\bar{R}}_{\mu \nu \rho \sigma }=\frac{\bar{R}}{d(d-1)}\left[{\overline{g}}_{\mu \rho }{\overline{g}}_{\nu \sigma }-{\overline{g}}_{\mu \sigma }{\overline{g}}_{\nu \rho }\right],{\bar{R}}_{\mu \nu }=\frac{\bar{R}}{d}{\overline{g}}_{\mu \nu },\\ {\bar{D}}_{\mu }\bar{R}=0.& (8)\end{array}$

Moreover, we carry out a transverse-traceless (TT) decomposition of the metric fluctuations [67]

$\begin{array}{ll}{h}_{\mu \nu }=h_{\mu \nu }^{\text{T}}+{\bar{D}}_{\mu }{\xi }_{\nu }+{\bar{D}}_{\nu }{\xi }_{\mu }+\left({\bar{D}}_{\mu }{\bar{D}}_{\nu }-\frac{1}{d}{\overline{g}}_{\mu \nu }{\bar{D}}^2\right)\sigma +\frac{1}{d}{\overline{g}}_{\mu \nu }h,& (9)\end{array}$

where the component fields are subject to the differential constraints

$\begin{array}{ll}{\overline{g}}^{\mu \nu }{h}_{\mu \nu }^{\text{T}}=0,{\bar{D}}^{\mu }{h}_{\mu \nu }^{\text{T}}=0,{\bar{D}}_{\mu }{\xi }^{\mu }=0,{\overline{g}}^{\mu \nu }{h}_{\mu \nu }=h.& (10)\end{array}$

The Jacobians associated with the decomposition (9) are taken into account by a subsequent field redefinition

$\begin{array}{ll}\sqrt{2}{\left[\Delta -\frac{1}{d}\bar{R}\right]}^{1/2}{\xi }_{\mu }\mapsto {\xi }_{\mu },{\left[\frac{d-1}{d}{\Delta }^2-\frac{1}{d}\bar{R}\Delta \right]}^{1/2}\sigma \mapsto \sigma ,& (11)\end{array}$

and it is understood that in the sequel all propagators and the matrix elements ${{O}}_i^{(2)}$ are the ones associated with the rescaled fields. In combination with the background (8), this decomposition ensures that the differential operators appearing within the trace combine into Laplacians $\Delta \equiv -{\overline{g}}^{\mu \nu }{\bar{D}}_{\mu }{\bar{D}}_{\nu }$ constructed from the background metric [61].

We then specify the gauge-fixing introduced in Equation (54) to geometric gauge, setting ρ = 0 and subsequently evoking the Landau limit α → 0. Substituting the general form of the matrix elements listed in Table 2 into the right-hand side of (5) and tracing the α-dependence one finds that the contributions of the transverse vector fluctuations ξ_μ and the scalar σ drop out from the composite operator equation. As a consequence, the anomalous dimensions are only sourced by the transverse-traceless and conformal fluctuations. The relevant matrix elements are then readily taken from Table 2. They read

$\begin{array}{l}{{{O}}_n^{(2)}|}_{h^{\text{T}}{h}^{\text{T}}}=-\frac{1}{2}{\overline{R}}^{n-1}\left[n\Delta -\left(\frac{2n(d-2)}{d(d-1)}-1\right)\overline{R}\right],\\ {{{O}}_n^{(2)}|}_{hh}=\frac{n(n-1){(d-1)}^2}{d^2}{\overline{R}}^{n-2}{\Delta }^2\\ +\frac{n(d^2-(4n-1)(d-1)-1)}{2d^2}{\overline{R}}^{n-1}\Delta \\ +\left(\frac{d-2}{4d}-\frac{n(d-n-1)}{d^2}\right){\overline{R}}^n,& (12)\end{array}$

together with

$\begin{array}{l}{\Gamma }_k^{(2)}{|}_{h^{\text{T}}{h}^{\text{T}}}=\frac{1}{32\pi G_k}\left[\Delta -2{\Lambda }_k+C_T\overline{R}\right],\\ {\Gamma }_k^{(2)}{|}_{hh}=-\frac{(d-1)(d-2)}{32\pi G_k{d}^2}\left[\Delta -\frac{d}{d-1}{\Lambda }_k+C_S\overline{R}\right],& (13)\end{array}$

where

$\begin{array}{ll}{C}_T\equiv \frac{d^2-3d+4}{d(d-1)},C_S\equiv \frac{d-4}{2(d-1)}.& (14)\end{array}$

Finally, the matrix entries for the regulator ${{R}}_k$ are obtained from the substitution rule (59), which corresponds to a Type I regularization scheme in the nomenclature introduced in [40]

$\begin{array}{ll}{{R}}_k{|}_{h^{\text{T}}{h}^{\text{T}}}=\frac{1}{32\pi G_k}{R}_k,{{R}}_k{|}_{hh}=-\frac{(d-1)(d-2)}{32\pi G_k{d}^2}{R}_k.& (15)\end{array}$

Here $R_k(\Delta )=k^{2}r(\Delta /k^2)$ is a scalar regulator function which later on will be specified to the Litim regulator (51).

Substituting the expressions (12)–(15) into the composite operator Equation (5) then yields

$\begin{array}{ll}{\displaystyle \sum _{m=0}^N}{\gamma }_{nm}{{O}}_m=-\frac{1}{2}({\text{Tr}}_T\left[W_T(n;\Delta )\right]+{\text{Tr}}_S\left[W_S(n;\Delta )\right]),& (16)\end{array}$

where the subscripts T and S indicate that the trace is over transverse-traceless (T) and scalar (S) fluctuations, respectively. The explicit form of the operator-valued functions W_T and W_S is

$\begin{array}{l}{W}_T(n;\Delta )\equiv 16\pi G_k{\left[P_k-2{\Lambda }_k+C_{\text{T}}\overline{R}\right]}^{-2}{\overline{R}}^{n-1}\\ \left[-n\Delta +\left(\frac{2n(d-2)}{d(d-1)}-1\right)\overline{R}\right]\left({\partial }_t{R}_k-{\eta }_N{R}_k\right),\\ W_S(n;\Delta )\equiv -\frac{16\pi G_k}{(d-2)}{\left[P_k-\frac{d}{d-1}{\Lambda }_k+C_S\overline{R}\right]}^{-2}{\overline{R}}^{n-2}\\ \text{ [}2n(n-1)(d-1){\Delta }^2+n(d+2-4n)\overline{R}\Delta \\ +\frac{d^2-2d(2n+1)+4n(n+1)}{2(d-1)}{\overline{R}}^2]\left({\partial }_t{R}_k-{\eta }_N{R}_k\right).& (17)\end{array}$

Equation (16) should then be read as a series expansion in $\bar{R}$ at the origin where the matrix entries γ_nm are obtained by matching powers of $\bar{R}$ on the left- and right-hand side. We then define the infinite family of generating functionals, ${\Gamma }_n(\bar{R})$ with n ≥ 0 ∈ ℕ, via

$\begin{array}{ll}{\displaystyle \int d^d}x\sqrt{\overline{g}}{\Gamma }_n(\overline{R})\equiv -\frac{1}{2}({\text{Tr}}_T\left[W_T(n;\Delta )\right]+{\text{Tr}}_S\left[W_S(n;\Delta )\right]).& (18)\end{array}$

The structure of the traces appearing in the definition (18) ensures that ${\Gamma }_n(\bar{R})$ is regular at $\bar{R}=0$ and can be expressed as a Taylor series expansion. Equating the left-hand sides of Equations (16) and (18) one then has

$\begin{array}{ll}{\gamma }_{nm}=\frac{1}{2\pi i}{{\displaystyle \oint }}_C{\bar{R}}^{-(m+1)}{\Gamma }_n(\bar{R}),n,m\ge 0,& (19)\end{array}$

where C is an infinitesimal curve encircling the origin with counterclockwise orientation.

Before delving into the explicit evaluation of the traces, the following structural remark is in order. Inspecting (17), one observes that the right-hand side associated with the nth row starts at order ${\bar{R}}^{n-2}$ since ${{O}}_n^{(2)}$ will always contribute at least n−2 powers of the background curvature. This entails that the matrix of anomalous dimensions has the following triangular form

$\begin{array}{ll}\gamma =\left[\begin{array}{llllllll}{\gamma }_{00}\hfill & {\gamma }_{01}\hfill & {\gamma }_{02}\hfill & {\gamma }_{03}\hfill & {\gamma }_{04}\hfill & {\gamma }_{05}\hfill & {\gamma }_{06}\hfill & \cdots \hfill \\ {\gamma }_{10}\hfill & {\gamma }_{11}\hfill & {\gamma }_{12}\hfill & {\gamma }_{13}\hfill & {\gamma }_{14}\hfill & {\gamma }_{15}\hfill & {\gamma }_{16}\hfill & \cdots \hfill \\ {\gamma }_{20}\hfill & {\gamma }_{21}\hfill & {\gamma }_{22}\hfill & {\gamma }_{23}\hfill & {\gamma }_{24}\hfill & {\gamma }_{25}\hfill & {\gamma }_{26}\hfill & \cdots \hfill \\ 0\hfill & {\gamma }_{31}\hfill & {\gamma }_{32}\hfill & {\gamma }_{33}\hfill & {\gamma }_{34}\hfill & {\gamma }_{35}\hfill & {\gamma }_{36}\hfill & \cdots \hfill \\ 0\hfill & 0\hfill & {\gamma }_{42}\hfill & {\gamma }_{43}\hfill & {\gamma }_{44}\hfill & {\gamma }_{45}\hfill & {\gamma }_{46}\hfill & \cdots \hfill \\ 0\hfill & 0\hfill & 0\hfill & {\gamma }_{53}\hfill & {\gamma }_{54}\hfill & {\gamma }_{55}\hfill & {\gamma }_{56}\hfill & \cdots \hfill \end{array}\right].& (20)\end{array}$

This structure originates solely from the properties of the operators ${{O}}_n$ and is independent of the gauge choice or regularization procedure.

The explicit values of the matrix entries (16) are readily computed employing the heat-kernel techniques reviewed in Appendix A. In practice, we will truncated the heat-kernel expansion at order R², setting the coefficients a_n, n ≥ 3 to zero. This is in the spirit of the “paramagnetic approximation” suggested in [68], that the curvature terms relevant for asymptotic safety originate from the curvature terms contained in the propagators. For the matrix entries γ_nm this entails that all entries on the diagonal and below (marked in black) are computed exactly while contributions to the terms above the diagonal (marked in blue) will receive additional contributions from higher-orders in the heat-kernel. In particular all entries γ_nm with m ≥ n + 3 are generated solely from expanding the curvature terms proportional to C_T and C_S in the transverse-traceless and scalar propagators.

Evaluating (16) based on these approximations then results in an infinite family of generating functionals ${\Gamma }_n(\bar{R}),n\ge 0\in \mathbb{N}$:

$\begin{array}{l}{\Gamma }_n(\overline{R})=\frac{16\pi g}{{(4\pi )}^{d/2}}[c_1^T{q}_{d/2+1}^2(W_T^{\overline{R}}){\left(\frac{\overline{R}}{k^2}\right)}^{-1}+c_2^T{q}_{d/2}^2(W_T^{\overline{R}})\\ +c_3^T{q}_{d/2-1}^2(W_T^{\overline{R}})\left(\frac{\overline{R}}{k^2}\right)+c_4^T{q}_{d/2-2}^2(W_T^{\overline{R}}){\left(\frac{\overline{R}}{k^2}\right)}^2\\ +c_1^S{q}_{d/2+2}^2(W_T^{\overline{R}}){\left(\frac{\overline{R}}{k^2}\right)}^{-2}+c_2^S{q}_{d/2+1}^2(W_T^{\overline{R}}){\left(\frac{\overline{R}}{k^2}\right)}^{-1}\\ +c_3^S{q}_{d/2}^2(W_T^{\overline{R}})+c_4^S{q}_{d/2-1}^2(W_T^{\overline{R}})\left(\frac{\overline{R}}{k^2}\right)\\ +c_5^S{q}_{d/2-2}^2(W_T^{\overline{R}}){\left(\frac{\overline{R}}{k^2}\right)}^2].& (21)\end{array}$

Here we introduced the dimensionless couplings

$\begin{array}{ll}{g}_k=k^{d-2}{G}_k,{\lambda }_k={\Lambda }_k{k}^{-2},& (22)\end{array}$

and the anomalous dimension of Newton's coupling ${\eta }_N\equiv {(G_k)}^{-1}{\partial }_t{G}_k$. The threshold functions $q_n^p(w)$ are defined in Equation (46) and their arguments in the transverse-traceless and scalar sector are

$\begin{array}{l}{w}_T=-2\lambda ,w_S\equiv -\frac{d}{d-1}\lambda ,\\ \begin{array}{l}{w}_T^{\bar{R}}=w_T+C_T\bar{R}/k^2,w_S^{\bar{R}}\equiv w_S+C_S\bar{R}/k^2.\end{array}& (23)\end{array}$

The coefficients $c_k^i$ depend on d and n. In the tensor sector they are given by

$\begin{array}{l}{c}_1^T=\frac{1}{2}nd{a}_0^T,\\ c_2^T=\frac{1}{2}n(d-2)a_1^T-\left(\frac{2n(d-2)}{d(d-1)}-1\right)a_0^T,\\ c_3^T=\frac{1}{2}n(d-4)a_2^T-\left(\frac{2n(d-2)}{d(d-1)}-1\right)a_1^T,\\ c_4^T=-\left(\frac{2n(d-2)}{d(d-1)}-1\right)a_2^T.& (24)\end{array}$

Their counterparts in the scalar sector read

$\begin{array}{l}{c}_1^S=\frac{n(n-1)(d-1)d(d+2)}{2(d-2)}{a}_0^S,\\ c_2^S=\frac{1}{2}n(n-1)d(d-1)a_1^S+\frac{nd(d+2-4n)}{2(d-2)}{a}_0^S,\\ c_3^S=\frac{1}{2}n(n-1)(d-1)(d-4)a_2^S+\frac{1}{2}n(d+2-4n)a_1^S\\ +\frac{d^2-2d(2n+1)+4n(n+1)}{2(d-1)(d-2)}{a}_0^S,\\ c_4^S=\frac{n(d-4)(d+2-4n)}{2(d-2)}{a}_2^S+\frac{d^2-2d(2n+1)+4n(n+1)}{2(d-1)(d-2)}{a}_1^S,\\ c_5^S=\frac{d^2-2d(2n+1)+4n(n+1)}{2(d-1)(d-2)}{a}_2^S.& (25)\end{array}$

Finally, the $a_n^i$ are the heat-kernel coefficients listed in Table 1.

TABLE 1

Table 1. Heat-kernel coefficients $a_n^i$ for scalars (S), transverse vectors (TV), and transverse-traceless symmetric tensors (T) on a background d-sphere [69].

Evaluating (19) for the explicit generating functional (21) then yields the entries of the matrix γ. For instance, the two lines of entries below the diagonal, γ_n,n−2, n ≥ 2, and γ_n,n−1, n ≥ 1, obtained in this way are

$\begin{array}{l}{\gamma }_{n,n-2}=\frac{16\pi g}{{(4\pi )}^{d/2}}\frac{n(n-1)(d-1)d(d+2)}{2(d-2)}{k}^4{q}_{d/2+2}^2(W_s),\hfill \\ {\gamma }_{n,n-1}=\frac{16\pi g}{{(4\pi )}^{d/2}}n d k^2[\frac{1}{4}(d-2)(d+1)q_{d/2+1}^2(W_T)\hfill \\ +\frac{1}{12}(n-1)(d-1)q_{d/2+1}^2(W_s)\hfill \\ +\frac{d+2-4n}{2(d-2)}{q}_{d/2+1}^2(W_s)\hfill \\ -\frac{(n-1)(d-4)(d+2)}{2(d-2)}{q}_{d/2+2}^3(W_s)].\hfill & (26)\end{array}$

Equation (21) together with the relation (19) constitutes the main result of this work. They give completely analytic expressions for all entries of the anomalous dimension matrix γ.

At this stage, a few remarks are in order.

(1) The entries of the anomalous dimension matrix carry a specific k-dependence: ${\gamma }_{nm}\propto {(k^2)}^{n-m}$. This can be understood by noticing that the matrix γ acts on operators ${{O}}_m$ with different canonical mass dimensions. The k-dependence then guarantees that the eigenvalues of γ are independent of k.

(2) The entries γ_n,n−2 are solely generated from the scalar contributions, i.e., the transverse-traceless fluctuations do not enter into these matrix elements. Technically, this feature is associated with the Hessians ${{O}}_n^{(2)}$ (cf. Table 2): the matrix elements in the scalar sector start at ${\bar{R}}^{n-2}$ while the transverse-traceless sector starts at ${\bar{R}}^{n-1}$.

(3) Notably, d = 4 is special. In this case the entries above the diagonal, γ_nm with m ≥ n + 3 are generated from the transverse-traceless sector only. All contributions from the scalar sector are proportional to at least one power of C_S and thus vanish if d = 4.

(4) The matrix γ is a function of the (dimensionless) couplings entering the Einstein-Hilbert action. Thus γ assigns a set of anomalous dimensions to every point in the g-λ–plane. Since γ is proportional to g, the magnitude of the anomalous dimensions becomes small if g ≪ 1. In particular, γ vanishes at the Gaussian fixed point g_∗ = λ_∗ = 0 where one recovers the classical scaling of the geometric operators.

TABLE 2

Table 2. Components of the Hessians entering the right-hand side of the composite operator equation (5) and the Wetterich equation evaluated for the Einstein-Hilbert truncation.

4. Scaling Analysis for the Reuter Fixed Point

Starting from the general result (19), we now proceed and discuss its implications for the quantum geometry associated with Asymptotic Safety.

4.1. Relating the Scaling of Geometric Operators and the RG Flow

By construction, the matrix γ assigns anomalous scaling dimensions to any point in the g-λ plane. In order to characterize the quantum geometry related to Asymptotic Safety, we study the properties of this matrix at the Reuter fixed point found in Appendix B [cf. Equation (64)]

$\begin{array}{l}d=3:g_{*}=0.198,{\lambda }_{*}=0.042,{\lambda }_{*}{g}_{*}^2=1.65\times {10}^{-3},\\ d=4:g_{*}=0.911,{\lambda }_{*}=0.160,{\lambda }_{*}{g}_{*}=\mathrm{0.146.}& (27)\end{array}$

From the definition of the beta function ∂_tu_n = β_un(u_i) and the fact that at a fixed point ${\beta }_{u_n}(u_i^{*})=0$, it follows that the properties of the RG flow in the vicinity of the fixed point are encoded in the stability matrix B = [B_nm],

$\begin{array}{ll}{\partial }_t{u}_n(k)={\displaystyle \sum _m}{B}_{nm}(u_m(k)-u_m^{*}),B_{nm}\equiv {\frac{\partial {\beta }_{u_m}}{\partial u_n}|}_{u=u^{*}}.& (28)\end{array}$

Let us denote the eigenvalues of B by λ_n so that spec(B) = {λ_n}. Equation (28) then entails that eigendirections corresponding to eigenvalues with a negative (positive) real part attract (repel) the RG flow when k is increased, i.e., they correspond to UV-relevant (UV-irrelevant) directions. The number of UV-relevant directions then gives the number of free parameters which are not fixed by the asymptotic safety condition: along these directions the RG flow automatically approaches the Reuter fixed point as k → ∞.

Formally, one can then derive a relation between γ and the stability matrix B [32, 70],

$\begin{array}{ll}{B}_{nm}=-d_n{\delta }_{nm}+{\gamma }_{nm},& (29)\end{array}$

where d_n = d − 2n is the canonical scaling dimension of the operator ${{O}}_n$. This relation is remarkable in the following sense: The construction of the (approximate) fixed point solution (27) is based on the two operators ${{O}}_0$ and ${{O}}_1$, comprising the Einstein-Hilbert truncation. The relation (29) then shows that the matrix of anomalous dimensions carries information about the stability properties of the Reuter fixed point beyond the set of operators which are considered when solving the Wetterich equation to locate the fixed point. We illustrate this idea by studying the spectrum of B_nm obtained at the fixed points (27). Before embarking on this discussion, the following cautious remark is in order though. While the composite operator formalism may allow to obtain information on the stability properties of a fixed point beyond the approximation used for the propagators, it is also conceivable that the formalism becomes unreliable for eigenvalues λ_n with n ≥ N_max³. Heuristically, this is suggested by the following argument: when studying fixed point solutions in the f(R)-approximation the propagators include powers of $\bar{R}$ beyond the linear terms captured by the Einstein-Hilbert action. These terms give rise to additional contributions in the generating functional (19) which may become increasingly important in assessing the spectrum of B for eigenvalues with increasing numbers of n. This picture is also suggested by our results in section 4.2⁴.

This said, we now investigate the properties of the stability matrix (29). Here we will resort to the following frameworks:

I The spectrum of B generated by the full generating functional (21) including the contribution of zero-modes in the heat-kernel for d = 4.

II In the conformally reduced approximation [71]. In this case, the contribution of the tensor fluctuations is set to zero by hand, so that γ contains the contribution from the scalar trace in (16) only.

The latter choice is motivated by the observation that this framework gives rise to the spec(B) which is the most robust under increasing the size of the matrix B. Clearly, one could easily envision other approximations which could be applied to the general result (21). Examples include the exclusion of the zero-mode terms appearing in d = 4 or the “sparse approximation” where only two lines above and below the diagonal are non-trivial, i.e., the entries in the upper-triangular sector which are solely created by expanding the curvature terms contained in the gravitational propagators are eliminated. In order to understand the working (and limitations) of the conformal operator formalism, the frameworks I and II are sufficient though. We checked by explicit computations that the exclusion of zero-modes or evaluating the spectrum of B in the sparse approximation leads to the same qualitative picture.

4.2. Spectral Properties of the Stability Matrix

We first give the diagonal entries γ_nn within framework I. This corresponds to the “single-operator approximation” of the composite operator formalism employed in Pagani and Reuter [19], and Houthoff et al. [32]. At the fixed points (27) one finds

$\begin{array}{l}d=3:{\gamma }_{nn}^{*}=0.653-0.872n-0.029n^2,\\ d=4:{\gamma }_{nn}^{*}=2.299-3.765n.& (30)\end{array}$

These relations exhibit two remarkable features. Firstly, the structure of ${{O}}_n^{(2)}$ (cf. Table 2) entails that the entries of γ are second order polynomials in n. It is then remarkable that the diagonal entries essentially follow a linear scaling law up to n ≈ 30 (d = 3) or even exactly (d = 4). Secondly, Equation (30) entails that the diagonal entries of the stability matrix B are always negative. Thus the single-operator approximation predicts that all eigendirections of the Reuter fixed point in the f(R)-space are UV-attractive. It was noted in Houthoff et al. [32] that this is actually in tension with results obtained from solving the Wetterich equation on the same space. On this basis, it is expected that the off-diagonal entries in γ play a crucial role in determining the spectrum of B.

We now discuss the properties of the stability matrix evaluated at the Reuter fixed points (27) generated from the functional (21). In practice, we truncate B to square-matrices of size N choosing N = 100 if not stated otherwise. The eigenvalues λ_n ∈ spec(B) satisfying

$\begin{array}{ll}\text{B}{V}_n={\lambda }_n{V}_n,n=1,\cdots ,N,& (31)\end{array}$

with V_n denoting the right-eigenvectors of B, are readily found numerically. Since B is not symmetric there is no a priori reason that the λ_n are real or that the left- and right-eigenvectors of B agree.

The structure of B then entails that there is always one eigenvalue which is independent of the matrix size. For framework I its value is given by

$\begin{array}{l}d=3:{\lambda }_1^{\text{I}}=-2.347,\\ d=4:{\lambda }_1^{\text{I}}=-\mathrm{1.701.}& (32)\end{array}$

The eigenvector V₁ associated with these eigenvalues is aligned with the volume operator ${{O}}_0$ entailing that $V=\int d^{d}x\sqrt{g}$ is actually an eigenoperator of Equation (16). In the conformally reduced approximation (framework II) in d = 3, the independence of λ_n on the matrix size N extends to a second eigenvalue

$\begin{array}{ll}d=3:{\lambda }_1^{\text{II}}=-2.828,{\lambda }_2^{\text{II}}=-\mathrm{0.967.}& (33)\end{array}$

The normalized eigenvector associated with ${\lambda }_1^{\text{II}}$ is again given by the volume operator ${{O}}_0$ while the one associated with ${\lambda }_2^{\text{II}}$ is almost aligned with ${{O}}_1$, i.e., $V_2={(0.07,0.995,\cdots )}^{\text{T}}$ for N = 5.

The properties of spec(B) beyond these universal eigenvalues obtained from the framework I in d = 4 and d = 3 as well as in the conformally reduced approximation in d = 3 (framework II) are shown in Figures 1–3, respectively. The left diagrams show the real part, Re(λ_n) of the stability matrices of size N = 25 (left line, green dots), N = 50 (middle line, orange dots), and N = 100 (right line, blue dots). The lines clearly illustrate that increasing N adds additional eigenvalues coming with both increasingly positive and increasingly negative real parts. This feature is shared by all frameworks discussed above. The middle diagrams illustrate the location of spec(B) for N = 100 in the complex plane. While the patterns are quite distinct, they share the existence of nodes where complex eigenvalues are created which then move out into the complex plane along distinguished lines. The right diagrams trace the first two negative eigenvalues as a function of the matrix size N. In all cases, the structure of B implies that the first eigenvalue is independent of N while the other parts of the spectrum exhibit an N-dependence. As illustrated in Figures 1, 2, the eigenvalues λ_n, n ≥ 2 follow intriguing periodicity patterns. The average over the second and third eigenvalues found in the matrices of size up to N = 100 (for ${\bar{\lambda }}_2$) and N = 20 (for ${\bar{\lambda }}_3$, excluding values where a complex eigenvalue has appeared in the interval spanned by λ₁ and λ₃) are⁵

$\begin{array}{l}d=3:{\lambda }_2^{\text{I}}=-2.35\pm 0.08{\lambda }_3^{\text{I}}=-0.61\pm 0.40\\ d=4:{\lambda }_2^{\text{I}}=-2.86\pm 0.61{\lambda }_3^{\text{I}}=-6.36\pm 2.04& (34)\end{array}$

Carefully analyzing the N-dependence of spec(B) reveals that there is a close relation between the distribution of eigenvalues in the complex plane (middle diagrams) and the oscillations of λ₂ visible in the left diagrams: the oscillations are linked to the appearance of new complex pairs of eigenvalues. Focusing on the four-dimensional case where this feature is most prominent, one finds that singling out the values of λ₂ just before the occurrence of the new pair of complex eigenvalues in spec(B) essentially selects the λ₂(N) constituting the maxima in the oscillations. The resulting subset of eigenvalues is displayed in the inset shown in Figure 1 and is significantly more stable than the full set. The statistical analysis shows that in this case

$\begin{array}{ll}d=4:{\bar{\lambda }}_2^{\text{I},\text{subset}}=-2.61\pm 0.39,& (35)\end{array}$

so that the fluctuations are reduced by a factor two as compared to the full set 34.

FIGURE 1

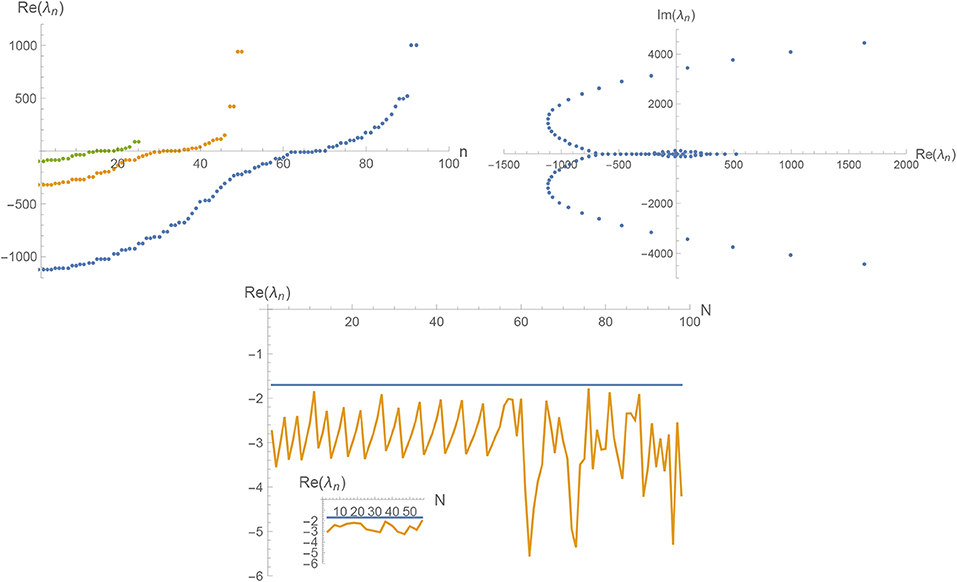
Figure 1. Spec(B) in d = 4 dimensions obtained within framework I. The top-left diagram displays the real parts Re(λ_n) of the eigenvalues found for the stability matrices of sizes N = 25 (left line, green dots), N = 50 (middle line, orange dots), and N = 100 (right line, blue dots). The top-right diagram shows the location of the eigenvalues λ_n (N = 100) in the complex plane. The bottom diagram traces the value of the first two relevant eigenvalues as a function of the matrix size N.

FIGURE 2

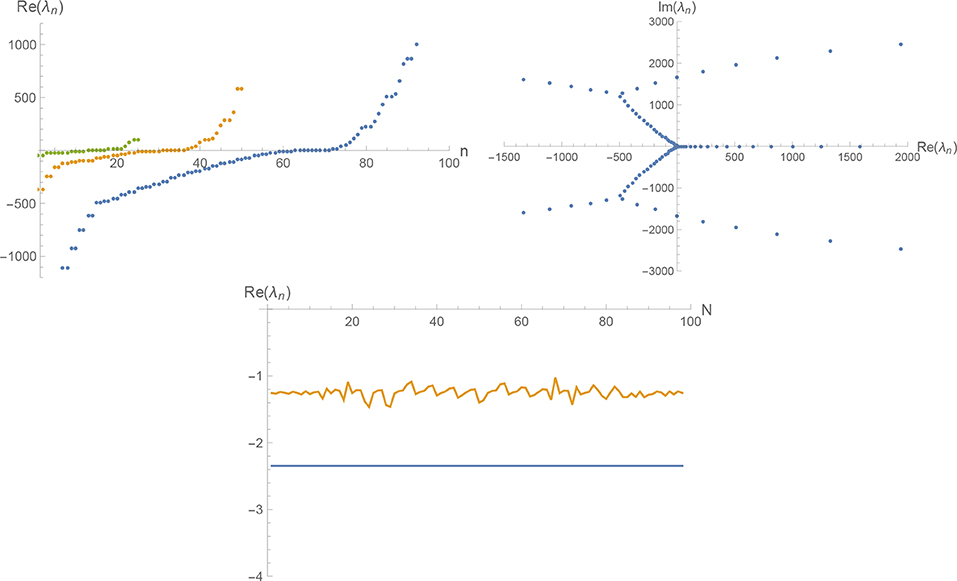
Figure 2. Spec(B) in d = 3 dimensions obtained within framework I. The top-left diagram displays the real parts Re(λ_n) of the eigenvalues found for the stability matrices of sizes N = 25 (left line, green dots), N = 50 (middle line, orange dots), and N = 100 (right line, blue dots). The top-right diagram shows the location of the eigenvalues λ_n (N = 100) in the complex plane. The bottom diagram traces the value of the first two relevant eigenvalues as a function of the matrix size N.

FIGURE 3

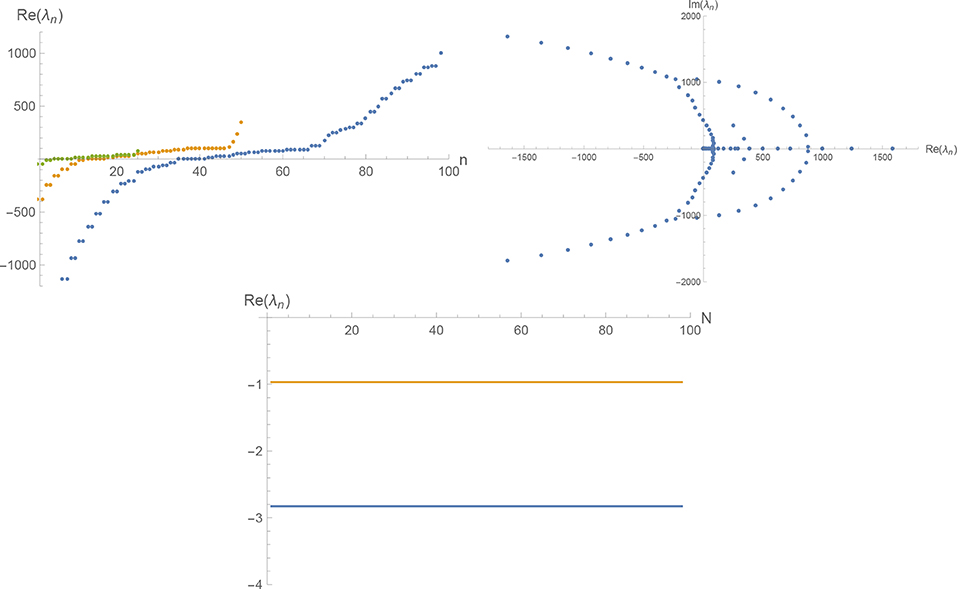
Figure 3. Spec(B) in d = 3 dimensions obtained within framework II. The top-left diagram displays the real parts Re(λ_n) of the eigenvalues found for the stability matrices of sizes N = 25 (left line, green dots), N = 50 (middle line, orange dots), and N = 100 (right line, blue dots). The top-right diagram shows the location of the eigenvalues λ_n (N = 100) in the complex plane. The bottom diagram establishes that the first two relevant eigenvalues are independent of the matrix size N.

At this stage, it is interesting to compare the averages 34 to the eigenvalue spectrum obtained from the smallest non-trivial stability matrix B with size N = 3:

$\begin{array}{l}d=3:{\lambda }_2^{\text{I}}=-2.35,{\lambda }_2^{\text{I}}=-1.26,{\lambda }_3^{\text{I}}=-0.20,\\ d=4:{\lambda }_2^{\text{I}}=-1.70,{\lambda }_2^{\text{I}}=-2.74,{\lambda }_3^{\text{I}}=-\mathrm{5.95.}& (36)\end{array}$

Thus we conclude that small values of N already give a good estimate of the (averaged) spectrum of B.

We close this section with a general remark on the structure of spec(B). The stability matrix is not tied to the Reuter fixed point but well-defined on the entire g-λ–plane: the generating functional (21) assigns an infinite tower of eigenvalues to each point in this plane. At the Gaussian fixed point, (λ_∗, g_∗) = (0, 0), γ = 0 and spec(B) follows from classical power counting. The strength of the quantum corrections to spec(B) is then controlled by the values of g and λ. In particular, there is a region in the vicinity of the Gaussian fixed point where these corrections are small. This motivates defining “perturbative domains” ${P}$ by the condition that spec(B) is dominated by its classical part. Concretely, we define

$\begin{array}{l}d=3:\{\begin{array}{c}{{P}}_2=\{(\lambda ,g)|\text{spec}(\text{B})\text{ has 2 UV-relevant eigenvalues}\}\\ {{P}}_3=\{(\lambda ,g)|\text{spec}(\text{B})\text{ has 3 UV-relevant eigenvalues}\}\end{array}\\ d=4:{{P}}_3=\{(\lambda ,g)|\text{spec}(\text{B})\text{has 3 UV-relevant eigenvalues}\}.& (37)\end{array}$

Loosely speaking, the definitions of these domains corresponds to imposing that the quantum corrections are not strong enough to turn more than one classically UV-marginal (d = 4) or UV-irrelevant (d = 3) eigendirection into a relevant one.

Figure 4 illustrates the shape of the domains ${P}$ obtained from the spectrum of the stability matrices with N = 10 (framework I) in d = 3 (left panel) and d = 4 (right panel). In d = 3 the regions ${{P}}_2$ and ${{P}}_3$ are shaded in blue and orange, respectively while in d = 4 ${{P}}_3$ is shaded blue. At the boundary of these regions a new complex pair of eigenvalues with negative real part appears in the spectrum which then violates the definitions (37). Within the present computation the Reuter fixed points (27) are located outside of ${{P}}_3$ which is consistent with the eigenvalue spectra shown in Figures 1, 2.

FIGURE 4

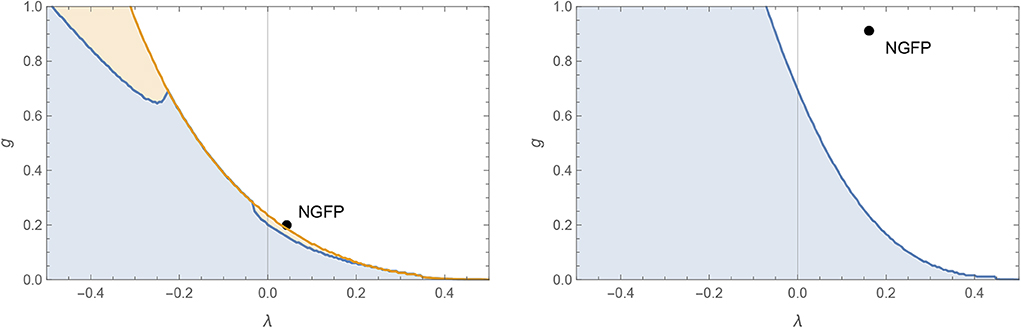
Figure 4. Spectral analysis for the matrices B of size N = 10 as a function of g and λ in d = 3 (left) and d = 4 (right). In the shaded region spec(B) is dominated by its classical part. In d = 3 the blue and orange regions support two and three negative eigenvalues, respectively, while in d = 4 the blue region supports three negative eigenvalues. The boundary to the white region is set by the appearance of a new, complex pair of eigenvalues coming with a negative real part. The Reuter fixed points (27) are marked by the black dots and are located outside the shaded regions.

The boundary of the domains ${{P}}_3$ is very well-described by the parametric curves

$\begin{array}{ll}b=\frac{g}{{(1-2\lambda )}^p}& (38)\end{array}$

with the best-fit parameters

$\begin{array}{ll}\begin{array}{c}d=3:b=0.24,p=2.94,\\ d=4:b=0.69,p=2.77.\end{array}& (39)\end{array}$

Following the ideas [72, 73], advocated in the context of gravity-matter systems, it is suggestive to interpret the right-hand side of (38) as the “effective strength of the gravitational fluctuations”. The values B then correspond to the critical value of the effective gravitational coupling g_eff which separates perturbative from non-perturbative behavior. Comparing the eigenvalue distributions for the Reuter fixed points shown in Figures 1–3 to a typical spectrum obtained in the perturbative region (cf. Figure 5), it is clear that this phase transition is easily visible in the scaling properties of the operators ${{O}}_n$.

FIGURE 5

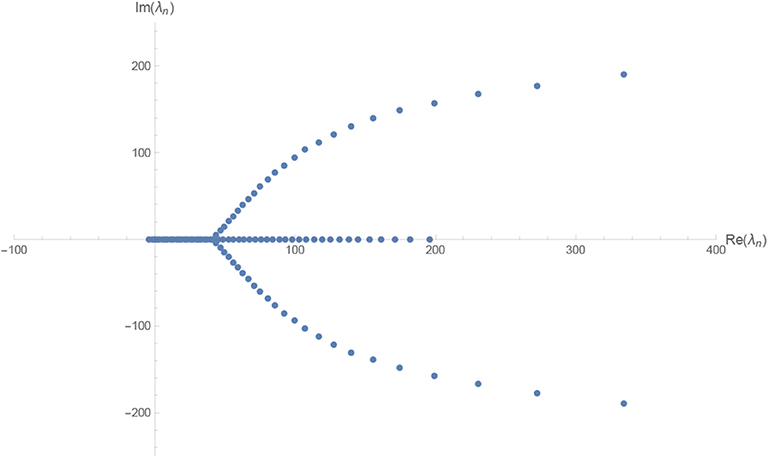
Figure 5. Spectral analysis for the matrix B of size N = 100 evaluated at a generic point in the perturbative region, (λ, g) = (0, 0.1), in d = 4. As its characteristic features, the eigenvalue spectrum is bounded from below and is controlled by the classical scaling dimensions d_n.

5. Conclusions and Outlook

In this work, we applied to composite operator formalism to construct a completely analytic expression for the matrix γ encoding the anomalous scaling dimensions of the geometrical operators ${{O}}_n\equiv \int d^{d}x\sqrt{g}{R}^n$, n ∈ ℕ, on a background sphere. Our work constitutes the first instance where the composite operator formalism for gravity is extended beyond the single-operator approximation. Within the geometric gauge adopted in our work, the anomalous dimensions originate from the transverse-traceless and trace mode of the gravitational fluctuations. The gauge-modes, corresponding to the vector sector of the transverse-traceless decomposition, decouple. Our derivation made two assumptions: firstly, we assumed that the propagators of the fluctuation fields can be approximated by the (gauge-fixed) Einstein-Hilbert action. Secondly, we assumed that terms appearing in the early-time expansion of the heat-kernel beyond the R²-level can be neglected. On this basis, we derived the generating functional (21) from which the matrix of anomalous dimensions (20) can be generated efficiently.

As illustrated in section 4 the stability matrix B resulting from the composite operator formalism allows to study the stability properties of the Reuter fixed point. This novel type of analysis provided the following structural insights on Asymptotic Safety:

(1) The composite operator approach suggests that in d = 4 quantum fluctuations turn the classically marginal R²-operator into a UV-relevant one. Similarly, the analysis in d = 3 dimensions predicts that the classically irrelevant R²-coupling becomes UV-relevant.

(2) The eigenvectors of B do not coincide with the geometric operators ${{O}}_n$. In general they are given by linear combinations containing an infinite number of terms.

(3) The non-diagonal terms γ_nm, n ≠ m play a crucial role in determining the spectrum of B. Within the assumptions made in our derivation one furthermore finds that increasing the size of B creates complex pairs of eigenvalues which wander through the complex plain and lead to new (most likely spurious) UV-relevant directions.

The analysis of the spectrum of the stability matrix as a function of the dimensionless Newton coupling g and cosmological constant λ reveals the existence of a domain where the eigenvalues are dominated by classical power counting. The resulting spectrum is then similar to the one encountered when solving the Wetterich equation in the polynomial f(R)-approximation which determined the eigenvalues of the stability matrix for N = 6 [38, 39], N = 8 [40], N = 35 [44, 47], and lately also N = 71 [58]. In particular, Falls et al. [58] reported that for large values of n the real parts of the eigenvalues λ_n follow an almost Gaussian behavior

$\begin{array}{ll}{\lambda }_n^{f(R)}\approx an-b,a=2.042\pm 0.002,b=2.91\pm 0.05.& (40)\end{array}$

where a and b are the best-fit values. As indicated in Figure 4, the present computation places the Reuter fixed point outside of this scaling domain, i.e., for sufficiently large matrices one obtains new eigenvalues coming with both positive and negative real parts. This makes it conceivable that the higher-order curvature terms appearing in the propagators of the f(R)-approximation play a crucial role in extending the domain such that it includes the fixed point, thereby guaranteeing its predictive power.

Putting our results into a broader context, we note that, by now, several classes of consistency tests related to the viability of an RG fixed point for the asymptotic safety program have been put forward. These include, e.g., the stability of the eigenvalue spectrum of B when increasing the set of operators included in Γ_k [38–40, 58], the concept of “apparent convergence” [74], “effective universality” in gravity-matter systems [75], or the “almost perturbative” nature of the fixed point [76]. Our results then provide key insights on how convergence of fixed point properties could organize itself outside the almost perturbative domain.

Arguably, the most intriguing result of our work is the spectral analysis of the stability matrix showing the distributions of its eigenvalues in the complex plane, c.f. the top-right diagrams of Figures 1–3, 5. The resulting patterns are reminiscent of the Lee-Yang theory for phase transitions [77]. This suggests two immediate applications. First, the status of Asymptotic Safety makes it conceivable that there are actually an infinite number of Reuter-type fixed points arising from gravity and gravity-matter systems. Understanding the characteristic features of their eigenvalue distributions in terms of nodal points creating complex eigenvalues may then constitute a powerful tool for classifying these fixed points and giving a precise definition to the notion of “gravity-dominated” renormalization group fixed points in gravity-matter systems. Secondly, tracing the eigenvalues λ_n along their Lee-Yang type orbits in the complex plane could provide a novel tool for testing the convergence of the eigenvalue distribution of B beyond the realm of a weak effective gravitational coupling (38) where the spectrum is governed by classical power counting. Clearly, it would be interesting to follow up on these points in the future.

As a by-product our analysis also computed the diagonal entries of the anomalous dimension matrix in geometric gauge [cf. Equation (30)]. It is instructive to compare this result to the value of the diagonal entries obtained in harmonic gauge [19, 32]

$\begin{array}{l}d=3:{\gamma }_{nn}^{*}=1.591-1.505n-0.118n^2,\\ d=4:{\gamma }_{nn}^{*}=3.987-4.733n-0.095n^2.& (41)\end{array}$

This identifies two features which are robust under a change of gauge-fixing: in both cases, the values of γ_nn up to $n\simeq {O}(10)$ follows a linear scaling law: in all cases the coefficients multiplying the quadratic terms are small or even vanishing when adopting geometric gauge in four dimensions. Secondly, the entries in the stability matrix B_nn are negative definite for all values n. At the same time, this comparison gives a first idea of the accuracy to which the composite operator formalism in the single-operator approximation is capable to determine the anomalous scaling dimension of the geometric operators: most likely, the results have the status of order-of-magnitude estimates: they should not be interpreted as “precision results” which one should try and reproduce to the given accuracy. Conceptually, it would be interesting to understand (and eliminate) the gauge-dependence of the result. Most likely, this will require imposing on-shell conditions to the master Equation (5) following, e.g., the ideas outlined in Benedetti [78] and Falls [79]. Along a different line, it would be interesting to extend the results for the single-operator approximation obtained in the present work to the case where the gravitational propagators include all terms up to order R⁴ in the curvature expansion. This computation would be “complete” in the sense that it includes all terms which contribute to the ${\gamma }_{nn}^{*}$ and therefore constitutes the “best” result attainable in the composite operator framework. We leave these points to future work though.

As one of its most intricate features, the composite operator formalism employed in this work could act as a connector between Asymptotic Safety [22, 23] and more geometric approaches to quantum gravity based on causal dynamical triangulations [80, 81] or random geometry. In d = 2 dimensions, a natural benchmark would involve a quantitative comparison of scaling properties associated with the geodesic length recently considered in Pagani and Reuter [19], Becker and Pagani[29, 30], Becker et al. [31], and Houthoff et al. [32] and exact computations for random discrete surfaces in the absence of matter fields [21, 82] as well as rigorous and numerical bounds arising from Liouville Gravity in the presence of matter [83, 84]. On the renormalization group side this will involve taking limits akin to Nink and Reuter [85]. Conversely, it is interesting to generalize the two-dimensional constructions to higher dimensions. The connection between the stability matrix B and the anomalous scaling dimension γ of geometric operators may then be an interesting link allowing to probe Asymptotic Safety based on geometric constructions of a quantum spacetime.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

The work of FS was supported by the Netherlands Organization for Scientific Research (NWO) within the Foundation for Fundamental Research on Matter (FOM) grant 13VP12. AK was supported by the Foundation for Theoretical Physics Development Basis and by the RFBR grant No. 20-02-00297.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

FS thanks T. Budd, L. Lionni, and M. Reuter for inspiring discussions. Furthermore, we are grateful to W. Houthoff for participating in the earlier parts of the program.

Footnotes

1. ^For related ideas advocated in the context of two-dimensional gravity (see [20, 21]).

2. ^Recently, the formalism has been generalized to the computation of operator product expansions [33].

3. ^Most conservatively, one may expect that the composite operator formalism allows a qualitatively reliable determination of the stability properties of operators containing two additional spacetime-derivatives on top of the terms included in the propagators. This picture is readily confirmed by comparing the spectrum of B obtained from the composite operator equation with the solution of the Wetterich equation for actions of f(R)-type.

4. ^A second effect which could lead to a stabilization of the spectrum of B at the Reuter fixed points could come from improving the truncation of the early-time expansion of the heat-kernel. There are two reasons to expect that these contributions will not play a relevant role though. Firstly, f(R)-type solutions of the Wetterich equation [38–40, 58], where the spectrum of B has been shown to be stable under the inclusion of further operators, essentially use the same truncation of the heat-kernel. Secondly, the structure of the heat-kernel expansion shows that the higher-order terms are highly suppressed compared to the ones included in our computation [40].

5. ^Our errors are purely statistical, giving the standard deviation based on the data set of eigenvalues. An estimate of the systematic errors is highly non-trivial and will not be attempted in this work.

References

1. Ambjørn J, Jurkiewicz J, Loll R. Spectral dimension of the universe. Phys Rev Lett. (2005) 95:171301. doi: 10.1103/PhysRevLett.95.171301

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Lauscher O, Reuter M. Fractal spacetime structure in asymptotically safe gravity. J High Energy Phys. (2005) 10:050. doi: 10.1088/1126-6708/2005/10/050

CrossRef Full Text | Google Scholar

3. Reuter M, Saueressig F. Fractal space-times under the microscope: a Renormalization Group view on Monte Carlo data. J High Energy Phys. (2011) 12:012. doi: 10.1007/JHEP12(2011)012

CrossRef Full Text | Google Scholar

4. Rechenberger S, Saueressig F. The R² phase-diagram of QEG and its spectral dimension. Phys Rev D. (2012) 86:024018. doi: 10.1103/PhysRevD.86.024018

CrossRef Full Text | Google Scholar

5. Calcagni G, Eichhorn A, Saueressig F. Probing the quantum nature of spacetime by diffusion. Phys Rev D. (2013) 87:124028. doi: 10.1103/PhysRevD.87.124028

CrossRef Full Text | Google Scholar

6. Modesto L. Fractal structure of loop quantum gravity. Class Quant Grav. (2009) 26:242002. doi: 10.1088/0264-9381/26/24/242002

CrossRef Full Text | Google Scholar

7. Atick JJ, Witten E. The hagedorn transition and the number of degrees of freedom of string theory. Nucl Phys B. (1988) 310:291–334. doi: 10.1016/0550-3213(88)90151-4

CrossRef Full Text | Google Scholar

8. Eichhorn A, Mizera S. Spectral dimension in causal set quantum gravity. Class Quant Grav. (2014) 31:125007. doi: 10.1088/0264-9381/31/12/125007

CrossRef Full Text | Google Scholar

9. Carlip S. Dimensional reduction in causal set gravity. Class Quant Grav. (2015) 32:232001. doi: 10.1088/0264-9381/32/23/232001

CrossRef Full Text | Google Scholar

10. Eichhorn A, Surya S, Versteegen F. Spectral dimension on spatial hypersurfaces in causal set quantum gravity. Class Quant Grav. (2019) 36:235013. doi: 10.1088/1361-6382/ab47cd

CrossRef Full Text | Google Scholar

11. Carlip S. Spontaneous dimensional reduction in short-distance quantum gravity? AIP Conf Proc. (2009) 1196:72. doi: 10.1063/1.3284402

CrossRef Full Text | Google Scholar

12. Nozari K, Hosseinzadeh V, Gorji MA. High temperature dimensional reduction in Snyder space. Phys Lett B. (2015) 750:218–24. doi: 10.1016/j.physletb.2015.09.014

CrossRef Full Text | Google Scholar

13. Kurkov MA, Lizzi F, Vassilevich D. High energy bosons do not propagate. Phys Lett B. (2014) 731:311–5. doi: 10.1016/j.physletb.2014.02.053

CrossRef Full Text | Google Scholar

14. Alkofer N, Saueressig F, Zanusso O. Spectral dimensions from the spectral action. Phys Rev D. (2015) 91:025025. doi: 10.1103/PhysRevD.91.025025

CrossRef Full Text | Google Scholar

15. Hořava P. Spectral dimension of the universe in quantum gravity at a lifshitz point. Phys Rev Lett. (2009) 102:161301. doi: 10.1103/PhysRevLett.102.161301

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Carlip S. Dimension and dimensional reduction in quantum gravity. Class Quant Grav. (2017) 34:193001. doi: 10.1088/1361-6382/aa8535

CrossRef Full Text | Google Scholar

17. Carlip S. Dimension and dimensional reduction in quantum gravity. Universe. (2019) 5:83. doi: 10.3390/universe5030083

CrossRef Full Text | Google Scholar

18. Amelino-Camelia G, Arzano M, Gubitosi G, Magueijo J. Dimensional reduction in momentum space and scale-invariant cosmological fluctuations. Phys Rev D. (2013) 88:103524. doi: 10.1103/PhysRevD.88.103524

CrossRef Full Text | Google Scholar

19. Pagani C, Reuter M. Composite operators in asymptotic safety. Phys Rev D. (2017) 95:066002. doi: 10.1103/PhysRevD.95.066002

CrossRef Full Text | Google Scholar

20. Knizhnik VG, Polyakov AM, Zamolodchikov AB. Fractal structure of 2D quantum gravity. Mod Phys Lett. (1988) A3:819–26. doi: 10.1142/S0217732388000982

CrossRef Full Text | Google Scholar

21. Ambjørn J, Watabiki Y. Scaling in quantum gravity. Nucl Phys B. (1995) 445:129–44. doi: 10.1016/0550-3213(95)00154-K

CrossRef Full Text | Google Scholar

22. Percacci R. An Introduction to Covariant Quantum Gravity and Asymptotic Safety, 100 Years of General Relativity. Vol. 3. Singapore: World Scientific (2017).

Google Scholar

23. Reuter M, Saueressig F. Quantum Gravity and the Functional Renormalization Group. Cambridge, UK: Cambridge University Press (2019).

Google Scholar

24. Percacci R. A short introduction to asymptotic safety. In: Time and Matter: Proceedings, 3rd International Conference, TAM2010. Budva (2011). p. 123.

Google Scholar

25. Litim DF. Renormalisation group and the Planck scale. Philos Trans R Soc Lond A. (2011) 369:2759. doi: 10.1098/rsta.2011.0103

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Reuter M, Saueressig F. Quantum Einstein gravity. New J Phys. (2012) 14:055022. doi: 10.1088/1367-2630/14/5/055022

CrossRef Full Text | Google Scholar

27. Ashtekar A, Reuter M, Rovelli C. From general relativity to quantum gravity. In: General Relativity and Gravitation: A Centennial Survey. Cambridge, UK: Cambridge University Press (2015)

PubMed Abstract | Google Scholar

28. Eichhorn A. An asymptotically safe guide to quantum gravity and matter. Front Astron Space Sci. (2019) 5:47. doi: 10.3389/fspas.2018.00047

CrossRef Full Text | Google Scholar

29. Becker M, Pagani C. Geometric operators in the asymptotic safety scenario for quantum gravity. Phys Rev D. (2019) 99:066002. doi: 10.1103/PhysRevD.99.066002

CrossRef Full Text | Google Scholar

30. Becker M, Pagani C. Geometric operators in the Einstein-Hilbert truncation. Universe. (2019) 5:75. doi: 10.3390/universe5030075

CrossRef Full Text | Google Scholar

31. Becker M, Pagani C, Zanusso O. Fractal geometry of higher derivative gravity. Phys Rev Lett. (2020) 124:15. doi: 10.1103/PhysRevLett.124.151302

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Houthoff W, Kurov A, Saueressig F. On the scaling of composite operators in Asymptotic Safety. J High Energy Phys. (2020) 04:99. doi: 10.1007/JHEP04(2020)099

CrossRef Full Text | Google Scholar

33. Pagani C, Sonoda H. Operator product expansion coefficients in the exact renormalization group formalism. Phys Rev D. (2020) 101:10. doi: 10.1103/PhysRevD.101.105007

CrossRef Full Text | Google Scholar

34. Wetterich C. Exact evolution equation for the effective potential. Phys Lett B. (1993) 301:90. doi: 10.1016/0370-2693(93)90726-X

CrossRef Full Text | Google Scholar

35. Morris TR. The Exact renormalization group and approximate solutions. Int J Mod Phys. (1994) A9:2411–50. doi: 10.1142/S0217751X94000972

CrossRef Full Text | Google Scholar

36. Reuter M, Wetterich C. Effective average action for gauge theories and exact evolution equations. Nucl Phys B. (1994) 417:181–214. doi: 10.1016/0550-3213(94)90543-6

CrossRef Full Text | Google Scholar

37. Reuter M. Nonperturbative evolution equation for quantum gravity. Phys Rev D. (1998) 57:971–85. doi: 10.1103/PhysRevD.57.971

CrossRef Full Text | Google Scholar

38. Codello A, Percacci R, Rahmede C. Ultraviolet properties of f(R)-gravity. Int J Mod Phys A. (2008) 23:143–50. doi: 10.1142/S0217751X08038135

CrossRef Full Text | Google Scholar

39. Machado PF, Saueressig F. On the renormalization group flow of f(R)-gravity. Phys Rev D. (2008) 77:124045. doi: 10.1103/PhysRevD.77.124045

CrossRef Full Text | Google Scholar

40. Codello A, Percacci R, Rahmede C. Investigating the ultraviolet properties of gravity with a Wilsonian renormalization group equation. Ann Phys. (2009) 324:414–69. doi: 10.1016/j.aop.2008.08.008

CrossRef Full Text | Google Scholar

41. Benedetti D, Caravelli F. The Local potential approximation in quantum gravity. J High Energy Phys. (2012) 1206:017. doi: 10.1007/JHEP06(2012)017

CrossRef Full Text | Google Scholar

42. Demmel M, Saueressig F, Zanusso O. Fixed-functionals of three-dimensional quantum Einstein gravity. J High Energy Phys. (2012) 11:131. doi: 10.1007/JHEP11(2012)131

CrossRef Full Text | Google Scholar

43. Demmel M, Saueressig F, Zanusso O. Fixed functionals in asymptotically safe gravity. In: Proceedings, 13th Marcel Grossmann Meeting on Recent Developments in Theoretical and Experimental General Relativity, Astrophysics, and Relativistic Field Theories (MG13) (Singapore) (2015).

Google Scholar

44. Falls K, Litim D, Nikolakopoulos K, Rahmede C. A bootstrap towards asymptotic safety. arXiv [Preprint]. arXiv:1301.4191 (2013).

Google Scholar

45. Demmel M, Saueressig F, Zanusso O. RG flows of Quantum Einstein Gravity on maximally symmetric spaces. J High Energy Phys. (2014) 06:026. doi: 10.1007/JHEP06(2014)026

CrossRef Full Text | Google Scholar

46. Demmel M, Saueressig F, Zanusso O. RG flows of Quantum Einstein Gravity in the linear-geometric approximation. Ann Phys. (2015) 359:141–65. doi: 10.1016/j.aop.2015.04.018

CrossRef Full Text | Google Scholar

47. Falls K, Litim DF, Nikolakopoulos K, Rahmede C. Further evidence for asymptotic safety of quantum gravity. Phys Rev D. (2016) 93:104022. doi: 10.1103/PhysRevD.93.104022

CrossRef Full Text | Google Scholar

48. Demmel M, Saueressig F, Zanusso O. A proper fixed functional for four-dimensional Quantum Einstein Gravity. J High Energy Phys. (2015) 08:113. doi: 10.1007/JHEP08(2015)113

CrossRef Full Text | Google Scholar

49. Dietz JA, Morris TR. Asymptotic safety in the f(R) approximation. J High Energy Phys. (2013) 1301:108. doi: 10.1007/JHEP01(2013)108

CrossRef Full Text | Google Scholar

50. Dietz JA, Morris TR. Redundant operators in the exact renormalisation group and in the f(R) approximation to asymptotic safety. J High Energy Phys. (2013) 07:064. doi: 10.1007/JHEP07(2013)064

CrossRef Full Text | Google Scholar

51. Dietz JA, Morris TR, Slade ZH. Fixed point structure of the conformal factor field in quantum gravity. Phys Rev D. (2016) 94:124014. doi: 10.1103/PhysRevD.94.124014

CrossRef Full Text | Google Scholar

52. Dietz JA, Morris TR. Background independent exact renormalization group for conformally reduced gravity. J High Energy Phys. (2015) 04:118. doi: 10.1007/JHEP04(2015)118

CrossRef Full Text | Google Scholar

53. Ohta N, Percacci R, Vacca GP. Flow equation for f(R) gravity and some of its exact solutions. Phys Rev D. (2015) 92:061501. doi: 10.1103/PhysRevD.92.061501

CrossRef Full Text | Google Scholar

54. Ohta N, Percacci R, Vacca GP. Renormalization Group Equation and scaling solutions for f(R) gravity in exponential parametrization. Eur Phys J C. (2016) 76:46. doi: 10.1140/epjc/s10052-016-3895-1

CrossRef Full Text | Google Scholar

55. Alkofer N, Saueressig F. Asymptotically safe f(R)-gravity coupled to matter I: the polynomial case. Ann Phys. (2018) 396:173–201. doi: 10.1016/j.aop.2018.07.017

CrossRef Full Text | Google Scholar

56. De Brito GP, Ohta N, Pereira AD, Tomaz AA, Yamada M. Asymptotic safety and field parametrization dependence in the f(R) truncation. Phys Rev D. (2018) 98:026027. doi: 10.1103/PhysRevD.98.026027

CrossRef Full Text | Google Scholar

57. Ohta N, Percacci R, Pereira AD. $f(R,R_{\mu \nu }^2)$ at one loop. Phys Rev D. (2018) 97:104039. doi: 10.1103/PhysRevD.97.104039

CrossRef Full Text | Google Scholar

58. Falls KG, Litim DF, Schröder J. Aspects of asymptotic safety for quantum gravity. Phys Rev D. (2019) 99:126015. doi: 10.1103/PhysRevD.99.126015

CrossRef Full Text | Google Scholar

59. Alkofer N. Asymptotically safe f(R)-gravity coupled to matter II: global solutions. Phys Lett B. (2019) 789:480. doi: 10.1016/j.physletb.2018.12.061

CrossRef Full Text | Google Scholar

60. Bürger B, Pawlowski JM, Reichert M, Schaefer BJ. Curvature dependence of quantum gravity with scalars. arXiv [Preprint]. arXiv:1912.01624 (2019).

Google Scholar

61. Benedetti D, Groh K, Machado PF, Saueressig F. The universal RG machine. J High Energy Phys. (2011) 1106:079. doi: 10.1007/JHEP06(2011)079

CrossRef Full Text | Google Scholar

62. Gies H, Knorr B, Lippoldt S. Generalized parametrization dependence in quantum gravity. Phys Rev. (2015) D92:084020. doi: 10.1103/PhysRevD.92.084020

CrossRef Full Text | Google Scholar

63. Wetterich C. Quantum scale symmetry. arXiv [Preprint]. arXiv:1901.04741. (2019).

Google Scholar

64. Ellwanger U. Flow equations and BRS invariance for Yang-Mills theories. Phys Lett B. (1994) 335:364. doi: 10.1016/0370-2693(94)90365-4

CrossRef Full Text | Google Scholar

65. D'Attanasio M, Morris TR. Gauge invariance, the quantum action principle, and the renormalization group. Phys Lett B. (1996) 378:213–21. doi: 10.1016/0370-2693(96)00411-X

CrossRef Full Text | Google Scholar

66. Litim DF, Pawlowski JM. Flow equations for Yang-Mills theories in general axial gauges. Phys Lett B. (1998) 435:181–8. doi: 10.1016/S0370-2693(98)00761-8

CrossRef Full Text | Google Scholar

67. York JW Jr. Conformally invariant orthogonal decomposition of symmetric tensors on Riemannian manifolds and the initial value problem of general relativity. J Math Phys. (1973) 14:456. doi: 10.1063/1.1666338

CrossRef Full Text | Google Scholar

68. Nink A, Reuter M. On the physical mechanism underlying Asymptotic Safety. J High Energy Phys. (2013) 01:062. doi: 10.1007/JHEP01(2013)062

CrossRef Full Text | Google Scholar

69. Lauscher O, Reuter M. Ultraviolet fixed point and generalized flow equation of quantum gravity. Phys Rev D. (2002) 65:025013. doi: 10.1103/PhysRevD.65.025013

CrossRef Full Text | Google Scholar

70. Pagani C. Note on scaling arguments in the effective average action formalism. Phys Rev D. (2016) 94:045001. doi: 10.1103/PhysRevD.94.045001

CrossRef Full Text | Google Scholar

71. Reuter M, Weyer H. Background independence and asymptotic safety in conformally reduced gravity. Phys Rev D. (2009) 79:105005. doi: 10.1103/PhysRevD.79.105005

CrossRef Full Text | Google Scholar

72. Eichhorn A, Held A. Viability of quantum-gravity induced ultraviolet completions for matter. Phys Rev D. (2017) D96:086025. doi: 10.1103/PhysRevD.96.086025

CrossRef Full Text | Google Scholar

73. Eichhorn A, Lippoldt S, Schiffer M. Zooming in on fermions and quantum gravity. Phys Rev D. (2019) 99:086002. doi: 10.1103/PhysRevD.99.086002

CrossRef Full Text | Google Scholar

74. Denz T, Pawlowski JM, Reichert M. Towards apparent convergence in asymptotically safe quantum gravity. Eur Phys J. (2018) C78:336. doi: 10.1140/epjc/s10052-018-5806-0

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Eichhorn A, Labus P, Pawlowski JM, Reichert M. Effective universality in quantum gravity. Sci Post Phys. (2018) 5:031. doi: 10.21468/SciPostPhys.5.4.031

CrossRef Full Text | Google Scholar

76. Eichhorn A, Lippoldt S, Pawlowski JM, Reichert M, Schiffer M. How perturbative is quantum gravity. Phys Lett B. (2019) 792:310–4. doi: 10.1016/j.physletb.2019.01.071

CrossRef Full Text | Google Scholar

77. Blythe R, Evans M. The Lee-Yang theory of equilibrium and nonequilibrium phase transitions. Braz J Phys. (2003) 33:464. doi: 10.1590/s0103-97332003000300008

CrossRef Full Text | Google Scholar

78. Benedetti D. Asymptotic safety goes on shell. New J Phys. (2012) 14:015005. doi: 10.1088/1367-2630/14/1/015005

CrossRef Full Text | Google Scholar

79. Falls K. On the renormalisation of Newton's constant. Phys Rev D. (2015) 92:124057. doi: 10.1103/PhysRevD.92.124057

CrossRef Full Text | Google Scholar

80. Ambjørn J, Goerlich A, Jurkiewicz J, Loll R. Nonperturbative quantum gravity. Phys Rept. (2012) 519:127–210. doi: 10.1016/j.physrep.2012.03.007

CrossRef Full Text | Google Scholar

81. Loll R. Quantum gravity from causal dynamical triangulations: a review. Class Quant Grav. (2020) 37:013002.

Google Scholar

82. Le Gall JF. The topological structure of scaling limits of large planar maps. Invent Math. (2007) 169:621–70. doi: 10.1007/s00222-007-0059-9

CrossRef Full Text | Google Scholar

83. Ding J, Gwynne E. The fractal dimension of Liouville quantum gravity: universality, monotonicity, and bounds. Commun Math Phys. (2019) 374:1877–934. doi: 10.1007/s00220-019-03487-4

CrossRef Full Text | Google Scholar

84. Barkley J, Budd T. Precision measurements of Hausdorff dimensions in two-dimensional quantum gravity. Class Quant Grav. (2019) 36:244001. doi: 10.1088/1361-6382/ab4f21

CrossRef Full Text | Google Scholar

85. Nink A, Reuter M. The unitary conformal field theory behind 2D Asymptotic Safety. J High Energy Phys. (2016) 02:167. doi: 10.1007/JHEP02(2016)167

CrossRef Full Text | Google Scholar

86. Lauscher O, Reuter M. Towards nonperturbative renormalizability of quantum Einstein gravity. Int J Mod Phys. (2002) A17:993. doi: 10.1142/S0217751X02010418

CrossRef Full Text | Google Scholar

87. Vassilevich DV. Heat kernel expansion: user's manual. Phys Rept. (2003) 388:279. doi: 10.1016/j.physrep.2003.09.002

CrossRef Full Text | Google Scholar

88. Brizuela D, Martin-Garcia JM, Mena Marugan GA. xPert: Computer algebra for metric perturbation theory. Gen Rel Grav. (2009) 41:2415. doi: 10.1007/s10714-009-0773-2

CrossRef Full Text | Google Scholar

89. Litim DF. Optimized renormalization group flows. Phys Rev D. (2001) 64:105007. doi: 10.1103/PhysRevD.64.105007

CrossRef Full Text | Google Scholar

90. Litim DF. Optimization of the exact renormalization group. Phys Lett B. (2000) 486:92. doi: 10.1016/S0370-2693(00)00748-6

CrossRef Full Text | Google Scholar

Appendices

A. Heat-kernel, Mellin Transforms, and Threshold Functions

The calculation of γ requires the evaluation of the operator traces appearing on the right-hand side of the composite operator equation (5). This computation can be done effectively by applying the early-time heat-kernel expansion for minimal second-order differential operators $\Delta \equiv -{\overline{g}}^{\mu \nu }{\bar{D}}_{\mu }{\bar{D}}_{\nu }$. Following the ideas advocated in Lauscher and Reuter [69] and Benedetti et al. [61], we carry out a transverse-traceless decomposition of the fluctuation fields. Paired with a maximally symmetric background geometry, this decomposition ensures that all differential operators in the trace arguments organize themselves into Laplacians Δ.

These traces can then be evaluated using the Seeley-deWitt expansion of the heat-kernel on the d-sphere S^d:

$\begin{array}{l}{\text{Tr}}_i\left[e^{-s\Delta }\right]{|}_{S^d}\\ \begin{array}{c}\simeq \frac{1}{{(4\pi s)}^{d/2}}{\displaystyle \int }{d}^{d}x\sqrt{\overline{g}}\left[a_0^i+a_1^{i}s\bar{R}+a_2^i{s}^2{\bar{R}}^2+\dots \right].\end{array}& (42)\end{array}$

Here i = {S, TV, T} labels the type of field on which the Laplacian acts and the dots represent higher-order curvature terms. The relevant coefficients $a_n^i$ have been computed in Lauscher and Reuter [69] and are listed in Table 1. Their derivation manifestly uses the identities (8) in order to simplify the heat-kernel expansion on a general manifold [87].

The expansion (42) is readily generalized to functions of the Laplacian. Introducing the Q-functionals

$\begin{array}{ll}{Q}_n\left[W\right]\equiv \frac{1}{\Gamma (n)}{\displaystyle {\int }_0^{\infty }}dz{z}^{n-1}W(z),n>0,Q_0\left[W\right]=W(0),& (43)\end{array}$

one has [40]

$\begin{array}{l}{\text{Tr}}_i\left[W(\Delta )\right]=\frac{1}{{(4\pi )}^{d/2}}{\displaystyle \int d^d}x\sqrt{\overline{g}}[a_0^i{Q}_{d/2}[W]\\ +a_1^i{Q}_{d/2-1}[W]\overline{R}+a_2^i{Q}_{d/2-2}[W]{\overline{R}}^2+\dots ].& (44)\end{array}$

In order to write γ and the beta functions of the Einstein-Hilbert truncation in a compact form, it is convenient to express the Q-functionals in terms of the dimensionless threshold functions [37]

$\begin{array}{ll}\begin{array}{c}{\Phi }_n^p(w)\equiv \frac{1}{\Gamma (n)}{\displaystyle {\int }_0^{\infty }}dz{z}^{n-1}\frac{r(z)-z{r}^{\prime }(z)}{{\left[z+r(z)+w\right]}^p},\\ {\tilde{\Phi }}_n^p(w)\equiv \frac{1}{\Gamma (n)}{\displaystyle {\int }_0^{\infty }}dz{z}^{n-1}\frac{r(z)}{{\left[z+r(z)+w\right]}^p}.\end{array}& (45)\end{array}$

Here r(z) is the dimensionless profile function associated with the scalar regulator $R_k(z)=k^{2}r(z)$ introduced in Equation (50) and the prime denotes a derivative with respect to the argument. For later convenience we also define the combination

$\begin{array}{ll}{q}_n^p(w)\equiv {\Phi }_n^p(w)-\frac{1}{2}{\eta }_N{\tilde{\Phi }}_n^p(w).& (46)\end{array}$

The arguments of the traces appearing in γ, Equation (16), and the Einstein-Hilbert truncation studied in Appendix 10 have a canoncial form. Defining P_k ≡ z + R_k(z), the identity

$\begin{array}{l}{Q}_n\left[z^q{(P_k+w{k}^2)}^{-p}{G}_k{\partial }_t(G_k^{-1}{R}_k)\right]\\ \begin{array}{l}=2\frac{\Gamma (n+q)}{\Gamma (n)}{(k^2)}^{n+q+1-p}{q}_{n+q}^p(w)\end{array}& (47)\end{array}$

allows to convert the corresponding Q-functionals into the dimensionless threshold functions. For q = 0 this reduces to

$\begin{array}{l}{Q}_n\left[{(P_k+w{k}^2)}^{-p}{\partial }_t{R}_k\right]=2{(k^2)}^{n+1-p}{\Phi }_n^p(w),\\ Q_n\left[{(P_k+w{k}^2)}^{-p}{G}_k{\partial }_t(G_k^{-1}{R}_k)\right]=2{(k^2)}^{n+1-p}{q}_n^p(w).& (48)\end{array}$

Notably, the second set of identities suffices to derive the beta functions of the Einstein-Hilbert truncation while the evaluation of γ requires the generalization (47).

For maximally symmetric backgrounds the background curvature $\bar{R}$ is covariantly constant. As a consequence, it has the status of a parameter and can be included in the argument of the threshold functions. Expansions in powers of $\bar{R}$ can then be constructed from the recursion relations

$\begin{array}{ll}\frac{d}{dw}{\Phi }_n^p(w)=-p{\Phi }_n^{p+1}(w),\frac{d}{dw}{q}_n^p(w)=-p{q}_n^{p+1}(w).& (49)\end{array}$

Throughout the work, we specify the (scalar) regulator

$\begin{array}{ll}{R}_k(\Delta )=k^{2}r(\Delta /k^2),& (50)\end{array}$

to the Litim regulator [89, 90]. In this case the dimensionless profile function r(z) is given by

$\begin{array}{ll}r(z)=(1-z)\Theta (1-z),& (51)\end{array}$

with Θ(x) the unit-step function. For this choice the integrals (45) can be carried out analytically, yielding

$\begin{array}{l}{\Phi }_n^{p,\text{Litim}}(w)=\frac{1}{\Gamma (n+1)}\frac{1}{{(1+w)}^p},\\ \begin{array}{l}{\tilde{\Phi }}_n^{p,\text{Litim}}(w)=\frac{1}{\Gamma (n+2)}\frac{1}{{(1+w)}^p}.\end{array}& (52)\end{array}$

B. The Einstein-Hilbert Truncation in General Gauge

Structurally, the composite operator equation provides a map from the couplings contained in the Hessian ${\Gamma }_k^{(2)}$ to the matrix of anomalous dimensions γ. This map is independent of the RG flow entailed by the Wetterich equation. In order to characterize the geometry associated with the Reuter fixed point, the map has to be evaluated at the location of the fixed point. This appendix then studies the flow of Γ_k in the Einstein-Hilbert truncation supplemented by a general gauge-fixing term. The key result is the position of the Reuter fixed point, Equation (27), which underlies the spectral analysis of section 4. Our analysis essentially follows [61, 62, 86], to which we refer for further details.

The Einstein-Hilbert truncation approximates the effective average action Γ_k[h; ḡ] by the Einstein-Hilbert action ${\Gamma }_k^{\text{EH}}\left[g\right]=\frac{1}{16\pi G_k}\int d^{d}x\sqrt{g}(2{\Lambda }_k-R)$ supplemented by a gauge-fixing functional ${\Gamma }_k^{\text{gf}}\left[h;\overline{g}\right]$ and the corresponding ghost action $S^{\text{ghost}}\left[h,\bar{C},C;\overline{g}\right]$

$\begin{array}{ll}{\Gamma }_k\left[h;\overline{g}\right]\simeq {\Gamma }_k^{\text{EH}}\left[g\right]+{\Gamma }_k^{\text{gf}}\left[h;\overline{g}\right]+S^{\text{ghost}}\left[h,\bar{C},C;\overline{g}\right].& (53)\end{array}$

This ansatz contains two scale-dependent couplings, Newton's coupling G_k and the cosmological constant Λ_k. In the present analysis, we work with a generic gauge-fixing term

$\begin{array}{l}{\Gamma }_k^{\text{gf}}\left[h;\overline{g}\right]=\frac{1}{32\pi G_k\alpha }{\displaystyle \int }{d}^{d}x\sqrt{\overline{g}}{\overline{g}}^{\mu \nu }{F}_{\mu }{F}_{\nu },\\ \begin{array}{l}{F}_{\mu }\equiv {\bar{D}}^{\nu }{h}_{\mu \nu }-\frac{1+\rho }{d}{\bar{D}}_{\mu }h,\end{array}& (54)\end{array}$

where α and ρ are free, dimensionless parameters. The harmonic gauge used in Pagani [70] and Houthoff et al. [32] corresponds to α = 1, ρ = d/2−1 while the present computation significantly simplifies when adopting geometric gauge, setting ρ = 0 before evoking the Landau limit α → 0. The ghost action associated with (54) is

$\begin{array}{l}{S}^{ghost}[h,\overline{C},C;\overline{g}]=\hfill \\ -{{\displaystyle \int }}^{\text{}}{d}^{d}x\sqrt{\overline{g}}{\overline{C}}_{\mu }[{\overline{D}}^{\rho }{\delta }_{\nu }^{\mu }{D}_{\rho }+{\overline{D}}^{\rho }{g}_{\rho \nu }{D}^{\mu }\hfill \\ -\frac{2(1+\rho )}{d}{\overline{D}}_{\mu }{\overline{g}}^{\sigma \rho }{g}_{\rho \nu }{D}_{\sigma }]C^{\nu }\hfill & (55)\end{array}$

Following the strategy employed in the gravitational sector, c.f. Equation (9), the fields ${\bar{C}}_{\mu }$, C^μ are decomposed into their transverse and longitudinal parts

$\begin{array}{ll}{C}^{\mu }=C^{\text{T}\mu }+{\bar{D}}^{\mu }\eta ,{\bar{D}}_{\mu }{C}^{\text{T}\mu }=0,& (56)\end{array}$

followed by a rescaling

$\begin{array}{ll}{\Delta }^{1/2}\eta \mapsto \eta .& (57)\end{array}$

The part of the ghost action quadratic in the fluctuation fields then becomes

$\begin{array}{l}{S}^{\text{ghost},\text{quad}}={\displaystyle \int d^d}x\sqrt{\overline{g}}\{{\overline{C}}_{\mu }^{\text{T}}\left[\Delta -\frac{1}{d}\overline{R}\right]C^{\text{T}\mu }\\ +2\overline{\eta }\left[\frac{d-1-\beta }{d}\Delta -\frac{1}{d}\overline{R}\right]\eta \}.& (58)\end{array}$

We now proceed by constructing the non-zero entries of the Hessian ${\Gamma }_k^{(2)}$. These are obtained by expanding Γ_k to second order in the fluctuation fields, substituting the transverse traceless decomposition (9) and (56), and implementing the field redefinitions (11) and (57). Subsequently taking two functional variations with respect to the fluctuation fields then leads to the matrix elements listed in the middle block of Table 2.

The final ingredient entering the right-hand side of the Wetterich equation is the regulator ${{R}}_k$. We generate this matrix from the substitution rule

$\begin{array}{ll}\Delta \mapsto P_k\equiv \Delta +R_k(\Delta ),& (59)\end{array}$

dressing each Laplacian by a scalar regulator R_k(Δ). The latter then provides a mass for fluctuation modes with momentum p² ≲ k². In the nomenclature introduced in Codello et al. [40] this corresponds to choosing a type I regulator. The non-zero entries of ${{R}}_k$ generated in this way are listed in the bottom block of Table 2.

We now have all the ingredients to compute the beta functions resulting from the Wetterich equation projected onto the Einstein-Hilbert action. Adopting the geometric gauge ρ = 0, α → 0 used in the main section, all traces appearing in the equation simplify to the Q-functionals evaluated in Equation (48). Defining

$\begin{array}{ll}{\partial }_t{g}_k={\beta }_g(g_{,}{\lambda }_k;d)\equiv (d-2+{\eta }_N)g_k,{\partial }_t{\lambda }_k\equiv {\beta }_{\lambda }(g_{,}{\lambda }_k;d)& (60)\end{array}$

where the anomalous dimension of Newton's coupling is parameterized by Reuter [37]

$\begin{array}{ll}{\eta }_N(g,\lambda )=\frac{g{B}_1(\lambda )}{1-g{B}_2(\lambda )},& (61)\end{array}$

the explicit computation yields

$\begin{array}{l}{\beta }_{\lambda }=({\eta }_N-2)\lambda +\frac{g}{{(4\pi )}^{d/2-1}}[(d-2)(d+1)q_{d/2}^1(W_T)\\ +2q_{d/2}^1(W_s)+2d{q}_{d/2}^1(0)-4d{\Phi }_{d/2}^1(0)].& (62)\end{array}$

and

$\begin{array}{l}{B}_1=\frac{1}{{(4\pi )}^{d/2-1}}[\frac{(d+1)(d+2)(d-5)}{3(d-1)}{\Phi }_{d/2-1}^1(W_T)\\ -\frac{2(d-2)(d+1)(d^2-3d+4)}{d(d-1)}{\Phi }_{d/2}^2(W_T)\\ +\frac{2}{3}{\Phi }_{d/2-1}^1(W_s)-\frac{2(d-4)}{d-1}{\Phi }_{d/2}^2(W_s)\\ -\frac{4(d^2-d+1)}{d(d-1)}{\Phi }_{d/2}^2(0)-\frac{2(d^2-6)}{3d}{\Phi }_{d/2-1}^1(0)],\\ B_2=-\frac{1}{2{(4\pi )}^{d/2-1}}[\frac{(d+1)(d+2)(d-5)}{3(d-1)}{\tilde{\Phi }}_{d/2-1}^1(W_T)\\ -\frac{2(d-2)(d+1)(d^2-3d+4)}{d(d-1)}{\tilde{\Phi }}_{d/2}^2(W_T)\\ +\frac{2}{3}{\tilde{\Phi }}_{d/2-1}^1(W_s)-\frac{2(d-4)}{d-1}{\tilde{\Phi }}_{d/2}^2(W_s)\\ +\frac{4(d^2-d+1)}{d(d-1)}{\tilde{\Phi }}_{d/2}^2(0)+\frac{2(d^2-6)}{3d}{\tilde{\Phi }}_{d/2-1}^1(0)].& (63)\end{array}$

Here the threshold functions ${\Phi }_n^p$, ${\tilde{\Phi }}_n^p$ and $q_n^p(w)$ are defined in Equations (45) and (46) and their arguments w_T and w_S have been introduced in (23).

It is now straightforward to localize the Reuter fixed point by determining the roots of the beta functions (60) numerically. For the Litim regulator (51) this yields

$\begin{array}{ll}\begin{array}{c}\text{Reuter fixed point:\hspace{1em}}d=3:g_{*}=0.198,{\lambda }_{*}=0.042,\\ \text{Reuter fixed point:\hspace{1em}}d=4:g_{*}=0.911,{\lambda }_{*}=0.160.\\ \end{array}& (64)\end{array}$

Analyzing the stability properties of the RG flow in its vicinity, it is found that the fixed point constitutes a UV attractor, with the eigenvalues of the stability matrix given by

$\begin{array}{ll}\begin{array}{c}\text{Reuter fixed point:\hspace{1em}}d=3:{\lambda }_{1,2}^{\text{EH}}=-1.658\pm 0.546i,\\ \text{Reuter fixed point:\hspace{1em}}d=4:{\lambda }_{1,2}^{\text{EH}}=-2.132\pm 2.697i.\\ \end{array}& (65)\end{array}$

These results agree with the ones found in Benedetti et al. [61] at the 10% level. The difference can be traced back to the two distinct regularization procedures employed in the computations, so that the findings are in qualitative agreement. This completes our analysis of the Einstein-Hilbert truncation underlying the scaling analysis in the main part of this work.

C. Matrix-elements of Geometric Operators

The expansions of ${{O}}_n$ and Γ_k in the fluctuation fields are readily computed using the xPert extension [88] of xAct. For completeness, the relevant expressions are listed in Table 2. The d-dependent coefficients C_i multiplying the curvature terms in ${\Gamma }_k^{(2)}$ are

$\begin{array}{l}{C}_T=\frac{d^2-3d+4}{d(d-1)},C_V=\frac{d-2}{d},C_S=\frac{d-4}{2(d-1)},\\ \begin{array}{l}{C}_{\sigma }=-(d-2).\end{array}& (66)\end{array}$