A Constitutive Model for Cemented Tailings Backfill Under Uniaxial Compression

Constitutive model is the foundation describing the mechanical properties of materials. Cemented tailings backfill (CTB) plays an important role in goaf filling. However, a universally applicable constitutive model for CTB has not been proposed yet. In this paper, a two-stage constitutive model of CTB under uniaxial compression was established, based on the Weibull distribution density function, the strain equivalence principle and the damage mechanics theory. Eight groups of CTB samples with a diameter of 50 mm and a height of 100 mm prepared with different solid contents (70–78 wt%) and cement-sand ratios (1/4–1/10) were subjected to uniaxial compression tests to verify the validity of the theoretical model. The compared results showed that the predictions of the proposed constitutive model agreed well with the experimental results. The following conclusions were also obtained: (i) Solid content and cement-sand ratio had a significant effect on the basic mechanical parameters of the CTB samples, especially at the peak stress; (ii) The constitutive model of CTB was similar to that of the ordinary cement mortar M5, but with obvious residual stress; (iii) The failure mode of the CTB specimens under uniaxial compression was mainly tensile failure. The results presented in this paper contribute to a better understanding of the uniaxial compression characteristics of CTB and lay an important foundation for future research.

Highlights

- A constitutive model for CTB under uniaxial compression was established.

- Influences of solid content and cement-sand ratio were analyzed.

- The failure mode of CTB specimens under uniaxial compression was mainly tensile failure.

Introduction

As one of the most commonly used filling aggregates for goaf filling, cemented tailings backfill (CTB) plays an important role in the safe, green, and efficient mining of metals [1]. CTB can effectively solve the problems related to deep rock pressure control and surface subsidence above the goaf, and can also avoid the environmental pollution caused by the accumulation of tailings [2–4]. Typically, CTB consists of dewatered tailings, a hydraulic binder and mixing water [5, 6]. Since its first use for the Bad Ground Mine (Germany) in the late 1970s, CTB has been widely used in many metal mines worldwide [7–12].

Many factors affect the mechanical properties of CTB samples, such as the filling parameters (filling times, filling interval times, and filling surface angles) [13–15], curing conditions [16–19], binding materials, admixtures (superplasticizers, organosilanes, and limestone powders) [20–23], solid contents, and cement-sand ratios [24–26], which have been considered in previous studies. Meanwhile, the strength properties of CTB under a frozen state and with different fiber reinforcements [27–31] have been analyzed. Moreover, numerous experimental studies have been carried out, especially uniaxial compression tests, which provide the most important parameters for underground mine backfill design [32–35].

The abovementioned research mainly focused on the strength properties of CTB. However, the constitutive model of CTB, which is very important for assessing and predicting its mechanical properties, has not been adequately addressed.

Only a few studies have been performed to investigate the constitutive relation of CTB in the literature. For example, several multiphysics models have been presented to describe and predict the temperature-time behavior [36] and the thermo-hydro-mechanical-chemical behavior of CTB [37, 38]. Evolutive elasto-plastic models based on the D–P yield criterion [39] have been developed to capture the mechanical behavior of CTB. Moreover, intelligent constitutive models have been proposed, based on boosted regression trees (BRT), particle swarm optimization (PSO), random forest (RF), firefly algorithm (FA), machine learning (ML) algorithm, genetic algorithm (GA), and genetic programming (GP), to predict the uniaxial compressive strength of CTB [40–42].

However, the existing studies on constitutive models have mainly focused on experimental data and give stress-strain relationships for a specific situation, but no universally applicable constitutive model has been proposed.

When the tailing cement filling method is used to mine underground mineral resources, before the end of ore mining at the middle level, CTB often acts as a pillar to support the surrounding rocks. At this point, the CTB pillar is under uniaxial compression and its stability plays an important role in stope safety [43, 44]. Therefore, the study on the mechanical properties of CTB under uniaxial compression has a great significance to ensure construction safety of ore mining used the tailing cement filling method.

In this paper, we propose a universally applicable constitutive model to accurately describe and predict the mechanical behavior of CTB under uniaxial loading conditions. Meanwhile, the influences of solid content and cement-sand ratio are analyzed.

Damage Variable

It is assumed that the correlated variables of the CTB element follow the Weibull distribution [45, 46], and the probability density function can be expressed as [47]:

$\begin{array}{ll}P(F)=\frac{m}{F_0}{(\frac{F}{F_0})}^{m-1}\text{ exp}[-{(\frac{F}{F_0})}^m],& (1)\end{array}$

where F is a random variable, and m>0 and F₀ >0 are the shape parameter and the scaling parameter, respectively.

The damage variable D under a certain load is defined as follows [48]:

$\begin{array}{ll}D=\frac{N_t}{N},& (2)\end{array}$

where N_t is the number of broken elements, and N is the total number of elements.

In an interval of [F, F + dF], the number of broken elements is NP(F)dF. When the external force is equal to F, the number of broken elements can be described as:

$\begin{array}{ll}{N}_t(F)={\displaystyle \underset{0}{\overset{F}{\int }}}NP(F)dF=N\left\{1-\text{exp}[-{(\frac{F}{F_0})}^m]\right\}.& (3)\end{array}$

Substituting Equation (3) into Equation (2) gives:

$\begin{array}{ll}D=\frac{N_t}{N}=1-\text{exp}[-{(\frac{F}{F_0})}^m].& (4)\end{array}$

Equation (4) is established using the general theory of continuous damage and statistics. The random variable F can be replaced by other physical quantities to establish different damage models. The axial linear strain ε is defined as the random variable in this paper. Then, Equation (4) can be rewritten as:

$\begin{array}{ll}D=1-\text{exp}[-{(\frac{\epsilon }{F_0})}^m].& (5)\end{array}$

Constitutive Model

According to the strain equivalence principle proposed by Lemaitre [49], the constitutive relation of damaged materials can be derived from undamaged materials, but the nominal stress is replaced by the effective stress of the damaged materials under uniaxial stress. Then, the constitutive relation can be defined [50]:

$\begin{array}{ll}\sigma =E\epsilon (1-D).& (6)\end{array}$

Substituting Equation (5) into Equation (6) gives:

$\begin{array}{ll}\sigma =E\epsilon \text{ exp}[-{(\frac{\epsilon }{F_0})}^m].& (7)\end{array}$

Considering the effect of the residual stress, Equation (7) is redefined as a two-stage function:

$\begin{array}{ll}\sigma =\{\begin{array}{c}E\epsilon \text{ exp}[-{(\frac{\epsilon }{F_0})}^m],\epsilon <{\epsilon }_m\hfill \\ E{\epsilon }_m\text{ exp}[-{(\frac{{\epsilon }_m}{F_0})}^m],\epsilon \ge {\epsilon }_m\hfill \end{array}.\hfill & (8)\end{array}$

In this paper, the elastic modulus E of the CTB is defined as follows, considering the influence of solid content and cement-sand ratio.

$\begin{array}{ll}E=E(x_1,x_2),& (9)\end{array}$

where x₁ is the solid content, and x₂ is the cement-sand ratio.

Then, Equation (8) can be rewritten as:

$\begin{array}{ll}\sigma =\{\begin{array}{c}E(x_1,x_2)\epsilon \text{ exp}[-{(\frac{\epsilon }{F_0})}^m],\epsilon <{\epsilon }_m\hfill \\ E(x_1,x_2){\epsilon }_m\text{ exp}[-{(\frac{{\epsilon }_m}{F_0})}^m],\epsilon \ge {\epsilon }_m\hfill \end{array}.\hfill & (10)\end{array}$

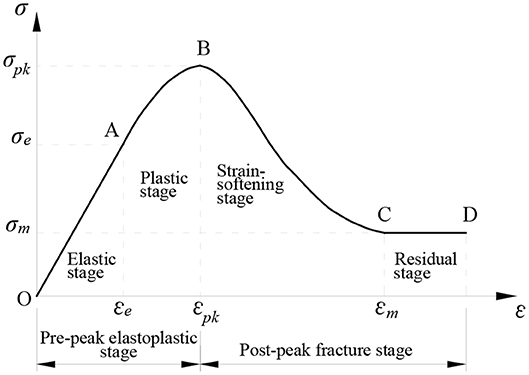
The corresponding constitutive model is shown in Figure 1, where σ_e, σ_pk, and σ_m represent the elastic stress, the peak stress, and the residual stress, and the corresponding strains ε_e, ε_pk, and ε_m are the elastic strain, the peak strain, and the starting strain of the residual stage, respectively.

FIGURE 1

Figure 1. Two-stage constitute model for CTB.

Determination of Model Parameters

To determine the unknown parameters m and F₀ in the first formula of Equation (10), the following boundary conditions are given:

(i) σ = σ_pk, ε = ε_pk, (ii) ε = ε_pk, dσ/dε = 0.

Based on the given boundary conditions (i), the following equation can be obtained:

$\begin{array}{ll}E(x_1,x_2){\epsilon }_{pk}\text{ exp}[-{(\frac{{\epsilon }_{pk}}{F_0})}^m]={\sigma }_{pk}.& (11)\end{array}$

Then, according to the boundary conditions (ii), the following equation can be obtained:

$\begin{array}{ll}\frac{d\sigma }{d\epsilon }=E(x_1,x_2)[1-m{(\frac{\epsilon }{F_0})}^m]\text{ exp}[-{(\frac{\epsilon }{F_0})}^m],& (12)\end{array}$

$\begin{array}{ll}E(x_1,x_2)[1-m{(\frac{{\epsilon }_{pk}}{F_0})}^m]\text{ exp}[-{(\frac{{\epsilon }_{pk}}{F_0})}^m]=0,& (13)\end{array}$

where E(x₁, x₂) and $\text{exp}[-{(\frac{{\epsilon }_{pk}}{F_0})}^m]$ cannot be equal to zero, then Equation (13) can be simplified as:

$\begin{array}{ll}1-m{(\frac{{\epsilon }_{pk}}{F_0})}^m=0.& (14)\end{array}$

Equation (11) and Equation (14) are solved simultaneously, and then the unknown parameters m and F₀ can be obtained:

$\begin{array}{ll}m=-\frac{1}{\text{ln }\{\raisebox{1ex}{${\sigma }_{pk}$}\!\left/ \!\raisebox{-1ex}{$\left[E(x_1,x_2){\epsilon }_{pk}\right]$}\right.\}},& (15)\end{array}$

$\begin{array}{ll}{F}_0=\frac{{\epsilon }_{pk}}{\sqrt[m]{1/m}}.& (16)\end{array}$

Substituting Equation (15) and Equation (16) into Equation (10) gives:

$\begin{array}{ll}\sigma =\{\begin{array}{c}E(x_1,x_2)\epsilon \text{ exp}[-{(\frac{\epsilon \sqrt[m]{1/m}}{{\epsilon }_{pk}})}^m],\epsilon <{\epsilon }_m\hfill \\ E(x_1,x_2){\epsilon }_m\text{ exp}[-{(\frac{{\epsilon }_m\sqrt[m]{1/m}}{{\epsilon }_{pk}})}^m],\epsilon \ge {\epsilon }_m\hfill \end{array}\hfill & (17)\end{array}$

Uniaxial Compression Tests

Characteristics of the Tailings

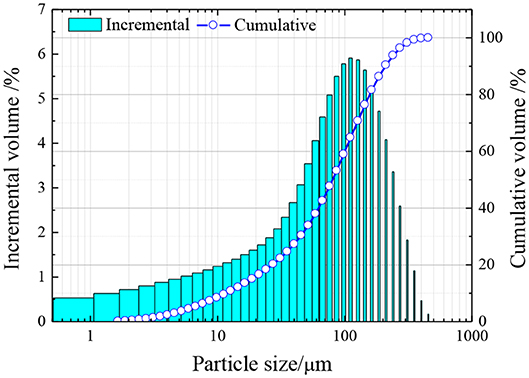
The tailings used in this paper are from a copper mine located in northwest China, and the particle size distribution is shown in Figure 2. The average particle size d₅₀ is 80.41 μm, the uniformity coefficient C_u is 8.57, and the curvature coefficient C_c is 1.71. As shown in Figure 2, the particle grading curve is smooth and continuous, and Fits grade is mild. Therefore, the tailings selected here have good gradation, compaction, and mechanical properties.

FIGURE 2

Figure 2. Particle size distribution of the used tailings.

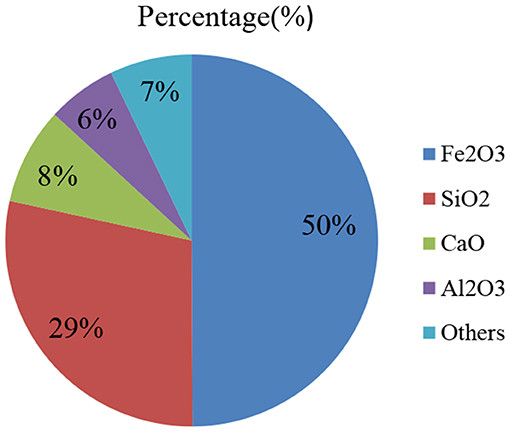
The chemical compositions of the tailings used in this paper are shown in Figure 3, which indicates that the main chemical compositions of the tailings are Fe₂O₃ and S_iO₂, accounting for 79% of the total solid weight. The content of CaO is less than 10%, which shows that the used tailings are low-calcium tailings.

FIGURE 3

Figure 3. Chemical components of the used tailings.

Specimen Preparation and Experimental Equipment

CTB is composed of gelling agents, aggregates and water. The gelling agent used in this experiment is ordinary Portland cement P.O42.5, the aggregates are the tailings mentioned above and the water is ordinary city tap water from Xi'an in China's Shaanxi Province. Eight groups of CTB cylinder specimens with dimensions of 50 and 100 mm in diameter and height, respectively, were made to perform uniaxial compression tests. Three specimens were in each group, and a total of 24 specimens, contained five groups with a constant cement-sand ratio of 1/4 and solid contents of 70, 72, 74, 76, and 78 wt% and three groups with a constant solid content of 76 wt% and cement-sand ratios of 1/6, 1/8, and 1/10. The curing environment was set at a constant temperature of 20°C with a relative humidity of 95%, and the curing period was 28 days. Then, the average value of each group was taken as the final result for the relevant quantities.

The experimental equipment is LRT-300 electric-fluid servo triaxial compression machine (see Figure 4) and the sample is loaded as Figure 5. The loading process was controlled by displacement at the rate of 1 × 10⁻⁵ m/s.

FIGURE 4

Figure 4. LRT-300 electric-fluid servo triaxial compr-ession machine.

FIGURE 5

Figure 5. Experimental process.

Model Parameters

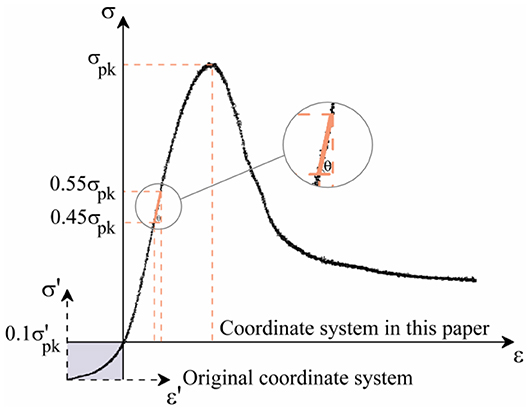
Through experimental investigation, it is found that at the initial stage of loading, when the stress is less than 10% of the peak value, the CTB has a compaction phase, especially for the low strength specimens [51]. At this stage, the stress-strain curve is concave, and the initial cracks are closed under axial pressure. For convenience in application, the constitutive model is simplified into two stages in the theoretical part of this paper, without considering the initial compaction stage. Therefore, the initial compaction stage of the material is ignored in this paper, assuming that the material starts directly from the elastic stage after loading, as shown in Figure 6. σ'-ε' and σ'_pk represent the original coordinate system and the true peak stress, and σ-ε and σ_pk represent the coordinate system selected in this paper and the corresponding peak stress, respectively.

FIGURE 6

Figure 6. Initial compaction stage and value of elastic modulus defined in this paper.

The elastic modulus E is defined as the tangent of the secants corresponding to 45–55% of the peak stress [52]. The average stress-strain curve of the specimens with a cement-sand ratio of 1/4 and a solid content of 76 wt% was taken as an example to show the value of the elastic modulus E defined in this paper (see Figure 6).

Table 1 lists the values of σ_pk and the model parameters involved in the constitutive model of Equation (17). Meanwhile, the first stages of the corresponding constitutive models are given. The average stress-strain curve of the three CTB cylinder specimens for each group was obtained. Then, the variables of E, σ_pk, ε_pk, and ε_m in Table 1 were gained from the average stress-strain curves. The value of E was defined as Figure 6, σ_pk and ε_pk are the peak stress and strain of the average curves, ε_m is the starting strain of the residual stage, and m was calculated according to Equation (15).

TABLE 1

Table 1. Model parameters and constitutive models.

Results and Discussion

Effects of Solid Content and Cement-Sand Ratio

Different solid contents (70, 72, 74, 76, and 78 wt%) and cement-sand ratios (1/4, 1/6, 1/8, and 1/10) were considered in the tests to analyze the effects of solid content and cement-sand ratio on the mechanical properties of CTB. The change in the mean stress-strain curves and the basic mechanical variables with solid contents and cement-sand ratios are shown in Figures 7, 8. The values of all the relevant variables in each group are the mean values of the three specimens.

FIGURE 7

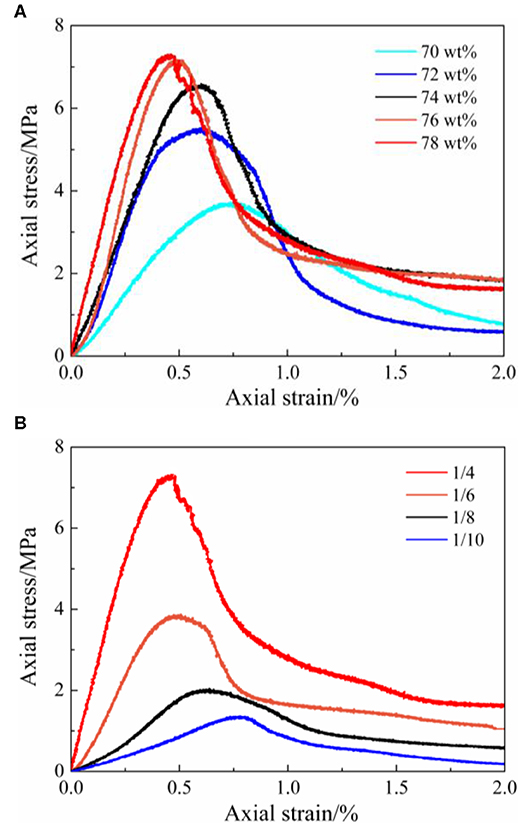
Figure 7. Stress-strain curves for different solid contents and cement-sand ratios: (A) solid contents, (B) cement-sand ratios.

FIGURE 8

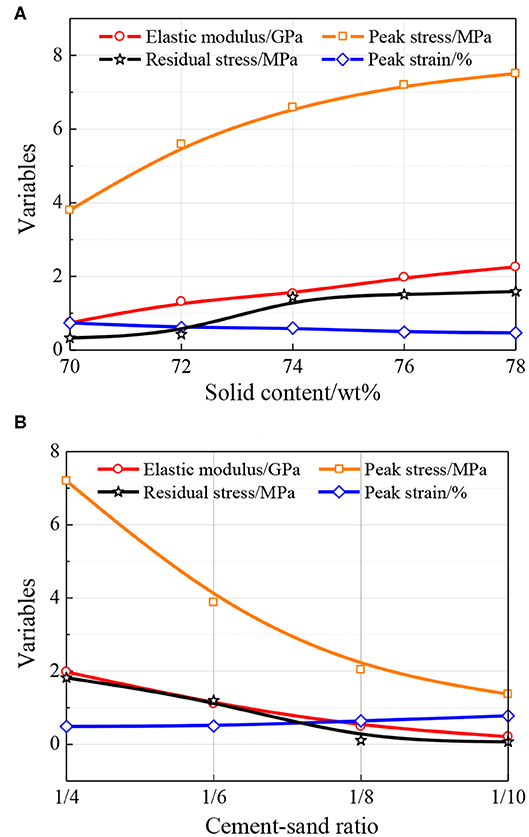
Figure 8. Basic mechanical variables for different solid contents and cement-sand ratios: (A) solid contents, (B) cement-sand ratios.

It can be seen from Figure 7 that the solid content gradually increases from 70 to 78 wt% or the cement-sand ratio gradually increases from 1/10 to 1/4, the peak points of the stress-strain curves rise and shift to the left relative to the axis, which indicates that the strength (σ_pk and σ_m), the elastic modulus E and the energy dissipation capacity of the CTB specimens increases, while ε_pk decreases. Meanwhile, with the increase of the solid content or the cement-sand ratio, the descending part of the curves gradually steepens, which indicates that the ductility decreases and the friability increases.

From Figure 8A, it can be observed that when the solid content ranges from 70 to 78 wt%, the corresponding value of E varies between 0.5 and 2.0 GPa, σ_pk varies between 4.0 and 7.5 MPa, ε_pk varies between 0.5 and 0.8% and σ_m varies between 0.5 and 1.5 MPa. Then, if the initial compaction stage is considered, the value range of σ_pk is from 4.5 to 8.5 MPa and the value range of σ_m is from 1.0 to 2.5 MPa.

From Figure 8B, it can be observed that when the cement-sand ratio ranges from 1/4 to 1/10, the corresponding value of E varies between 0.5 and 2.0 GPa, σ_pk varies between 1.5 and 7.5 MPa, ε_pk varies between 0.5 and 0.8% and σ_m varies between 1.0 and 2.0 MPa. Then, if the initial compaction stage is considered, the value range of σ_pk is from 2.0 to 8.5 MPa, and the value range of σ_m is form 0.3 to 3.0 MPa.

As shown in Figure 8, the influence of the solid content and cement-sand ratio on σ_pk is more obvious than that of the other quantities (E, ε_pk and σ_m), and the variation gradients of E and σ_m increase with the increase of solid content and cement-sand ratio are approximately equal. From Figures 7, 8, it can be seen that the increasing gradient of σ_pk gradually decreases with the increase of solid content but increases with the increase of cement-sand ratio.

Verification and Comparison of the Constitutive Model

To verify the validity of the constitutive model of CTB established in this paper, the experimental results are compared with those calculated using the theoretical model. The calculated and experimental results are in good agreement, especially in the pre-peak region (see Figure 9). Therefore, the proposed constitutive model can be used to describe the mechanical properties of CTB under uniaxial compression.

FIGURE 9

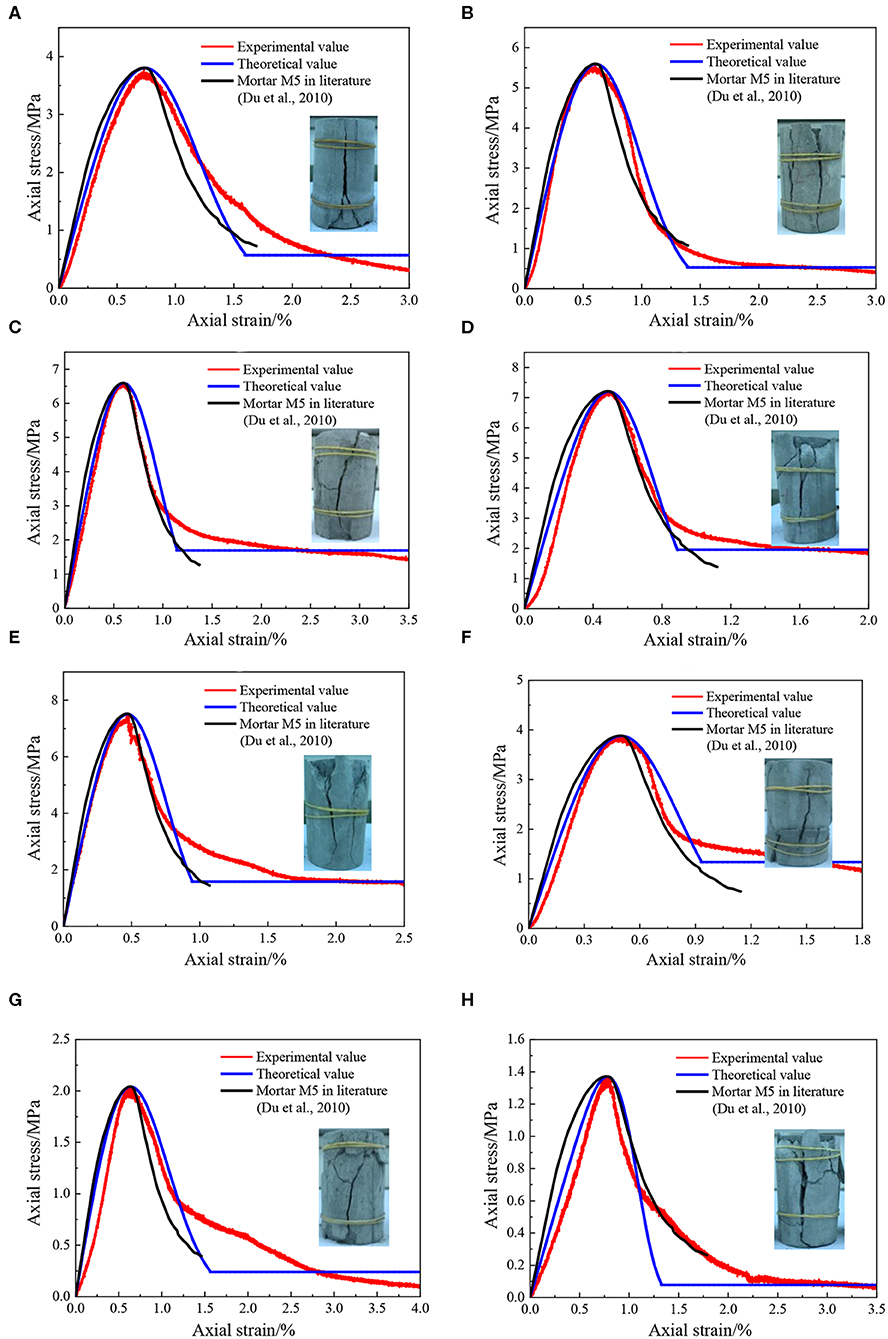
Figure 9. Comparison of theoretical and experimental results for stress-strain curves (cement-sand ratio = C/S, solid content = SC): (A) C/S = 1/4 and SC = 70 wt%, (B) C/S = 1/4 and SC = 72 wt%, (C) C/S = 1/4 and SC = 74 wt%, (D) C/S = 1/4 and SC = 76 wt%, (E) C/S = 1/4 and SC = 78 wt%, (F) C/S = 1/6 and SC = 76 wt%, (G) C/S = 1/8 and SC = 76 wt%, (H) C/S = 1/10 and SC = 76 wt%.

Ordinary cement mortar is also composed of gelling agents, aggregates and water, which is similar to the composition of CTB except that the aggregates are river sand and not tailings. To compare and illustrate the performance difference between the two materials under uniaxial compression, the peak point of the stress-strain curves for ordinary cement mortar M5 in reference [53] was scaled by the average peak value of each group of specimens in this paper. Then, the uniaxial compression stress-strain curves of the CTB and ordinary cement mortar M5 are compared in Figure 9. It can be seen that before the residual stress, the curves of the two materials are similar in shape. However, the CTB exhibits obvious residual stress, but the ordinary cement mortar M5 does not. Furthermore, the ordinary cement mortar M5 is slightly stronger than CTB at the pre-failure stage, but slightly weaker at the post-failure stage.

Meanwhile, it can also be seen from Figure 9 that under uniaxial compression, the CTB cylinder specimens are subjected to axial compression and transverse tension. The major failure mode is columnar splitting failure caused by tensile stress.

Limitations and Future Work

The results of the two-stage constitutive model for CTB proposed in this paper is in good agreement with the experimental results and can be used to predict the constitutive relation of CTB under uniaxial compression. The constitute model provided here is generally applicable, but the model parameters need to be specifically determined by testing the tailings from different sources.

Meanwhile, the long-term stress state of the CTB is constrained in three directions rather than in one direction. Therefore, our future work will investigate the mechanical properties of CTB under triaxial compression by triaxial compression tests and provide a simple and universally applicable triaxial compression constitutive model.

Conclusions

In this paper, the constitutive model for low-calcium copper mine tailings under uniaxial compression has been studied. The validity of the proposed two-stage constitutive model for CTB was verified by a comparison with the test results. Meanwhile, the effects of solid content and cement-sand ratio on the mechanical properties of CTB were also analyzed. The results are described as follows:

i) With the increase of solid content or cement-sand ratio, the strength (σ_pk and σ_m), E and energy dissipation capacity of the CTB increased, but ε_pk and the ductility decreased. The influence on σ_pk is more obvious than that on the other quantities (E, ε_pk and σ_m).

ii) Regardless of the initial compaction stage, for CTB specimens with solid contents of 70–78 wt% and cement-sand ratios of 1/4–1/10, the corresponding value of E remained between 0.5 and 2.0 GPa, σ_pk remained between 1.5 and 7.5 MPa, ε_pk remained between 0.5 and 0.8% and σ_m remained between 0.5 and 2.0 MPa. Then, if the initial compaction stage was considered, σ_pk ranged from 2.0 to 8.5 MPa and σ_m ranged from 0.3 to 3.0 MPa.

iii) The stress-strain curve of CTB is similar to that of ordinary cement mortar M5 but exhibits obvious residual stress. The failure mode of the CTB samples under uniaxial compression is mainly columnar splitting failure caused by tensile stress.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation, to any qualified researcher.

Author Contributions

BT and KC: writing-original draft preparation. LL: conceptualization. BZ: methodology. YZ: data curation. KS: validation. QY: supervision. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the National Natural Science Foundation of China (Nos. 51674188, 51874229, 51504182, 51974225, 51904224, 51904225, and 51704229), Shaanxi Innovative Talents Cultivate Program-New-star Plan of Science and Technology (No. 2018KJXX-083), Natural Science Basic Research Plan of Shaanxi Province of China (Nos. 2018JM5161, 2018JQ5183, 2015JQ5187, and 2019JM-074), Scientific Research Program funded by the Shaanxi Provincial Education Department (Nos. 2019JQ-354, 15JK1466, and 19JK0543), China Postdoctoral Science Foundation (No. 2015M582685), Open Project of State Key Laboratory of Green Building in Western China (No. LSKF201915), and Outstanding Youth Science Fund of Xi'an University of Science and Technology (No. 2018YQ2-01).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors are grateful for the support provided by College of Science and Energy School, Xi'an University of Science and Technology, Xi'an, 710054, China.

References

1. Dong L, Sun D, Shu W, Li X. Exploration: safe and clean mining on Earth and asteroids. J Clean Prod. (2020) 257:120899. doi: 10.1016/j.jclepro.2020.120899

CrossRef Full Text | Google Scholar

2. Sun X, Wang W. Theoretical research on high water material replacement mining the strip coal pillar above confined aquifer. J China Coal Soc. (2011) 36:909–13. doi: 10.13225/j.cnki.jccs.2011.06.018

CrossRef Full Text | Google Scholar

3. Zhang Q, Zhang J, Huang Y, Ju F. Backfilling technology and strata behaviors in fully mechanized coal mining working face. Int J Mining Sci. Technol. (2012) 22:151–7. doi: 10.1016/j.ijmst.2011.08.003

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Yilmaz E, Belem T, Bussiere B, Mbonimpa M, Benzaazoua M. Curing time effect on consolidation behaviour of cemented paste backfill containing different cement types and contents. Constr Build Mater. (2015) 75:99–111. doi: 10.1016/j.conbuildmat.2014.11.008

CrossRef Full Text | Google Scholar

5. Belem T, Benzaazoua M. Design and application of underground mine paste backfill technology. Geotech Geol Eng. (2007) 26:147–74. doi: 10.1007/s10706-007-9154-3

CrossRef Full Text | Google Scholar

6. Qi C, Chen Q, Fourie A, Zhang Q. An intelligent modelling framework for mechanical properties of cemented paste backfill. Miner Eng. (2018) 123:16–27. doi: 10.1016/j.mineng.2018.04.010

CrossRef Full Text | Google Scholar

7. Kesimal A, Yilmaz E, Ercikdi B, Alp I, Deveci H. Effect of properties of tailings and binder on the short-and long-term strength and stability of cemented paste backfill. Mater Lett. (2005) 59:3703–9. doi: 10.1016/j.matlet.2005.06.042

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Ercikdi B, Cihangir F, Kesimal A, Deveci H, Alp I. Utilization of water-reducing admixtures in cemented paste backfill of sulphide-rich mill tailings. J Hazard Mater. (2010) 179:940–6. doi: 10.1016/j.jhazmat.2010.03.096

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Cihangir F, Ercikdi B, Kesimal A, Deveci H, Erdemir F. Paste backfill of high-sulphide mill tailings using alkali-activated blast furnace slag: effect of activator nature, concentration and slag properties. Miner Eng. (2015) 83:117–27. doi: 10.1016/j.mineng.2015.08.022

CrossRef Full Text | Google Scholar

10. Chen Q, Zhang Q, Qi C, Fourie A, Xiao C. Recycling phosphogypsum and construction demolition waste for cemented paste backfill and its environmental impact. J Clean Prod. (2018) 186:418–29. doi: 10.1016/j.jclepro.2018.03.131

CrossRef Full Text | Google Scholar

11. Liu L, Fang Z, Qi C, Zhang B, Guo L, Song K. Experimental investigation on the relationship between pore characteristics and unconfined compressive strength of cemented paste backfill. Constr Build Mater. (2018) 179:254–64. doi: 10.1016/j.conbuildmat.2018.05.224

CrossRef Full Text | Google Scholar

12. Lu H, Qi C, Chen Q, Chen Q, Gan D, Xue Z, et al. A new procedure for recycling waste tailings as cemented paste backfill to underground stopes and open pits. J Clean Prod. (2018) 188:601–12. doi: 10.1016/j.jclepro.2018.04.041

CrossRef Full Text | Google Scholar

13. Cao S, Song W. Effect of filling interval time on long-term mechanical strength of layered cemented tailing backfill. Adv Mater Sci Eng. (2016) 2016:1–7. doi: 10.1155/2016/9507852

CrossRef Full Text | Google Scholar

14. Cao S, Song W. Effect of filling interval time on the mechanical strength and ultrasonic properties of cemented coarse tailing backfill. Int J Miner Process. (2017) 166:62–8. doi: 10.1016/j.minpro.2017.07.005

CrossRef Full Text | Google Scholar

15. Cao S, Song W, Yilmaz E. Influence of structural factors on uniaxial compressive strength of cemented tailings backfill. Constr Build Mater. (2018) 174:190–201. doi: 10.1016/j.conbuildmat.2018.04.126

CrossRef Full Text | Google Scholar

16. Jiang H, Fall M. Yield stress and strength of saline cemented tailings in sub-zero environments: Portland cement paste backfill. Int J Min Process. (2017) 160:68–75. doi: 10.1016/j.minpro.2017.01.010

CrossRef Full Text | Google Scholar

17. Yin S, Shao Y, Wu A, Wang Y, Chen X. Expansion and strength properties of cemented backfill using sulphidic mill tailings. Constr Build Mater. (2018) 165:138–48. doi: 10.1016/j.conbuildmat.2018.01.005

CrossRef Full Text | Google Scholar

18. Zheng J, Guo L, Sun X, Li W, Jia Q. Study on the strength development of cemented backfill body from lead-zinc mine tailings with sulphide. Adv Mater Sci Eng. (2018) 2018:1–8. doi: 10.1155/2018/7278014

CrossRef Full Text | Google Scholar

19. Xu W, Li Q, Zhang Y. Influence of temperature on compressive strength, microstructure properties and failure pattern of fiber-reinforced cemented tailings backfill. Constr Build Mater. (2019) 222:776–85. doi: 10.1016/j.conbuildmat.2019.06.203

CrossRef Full Text | Google Scholar

20. Zheng J, Zhu Y, Zhao Z. Utilization of limestone powder and water-reducing admixture in cemented paste backfill of coarse copper mine tailings. Constr Build Mater. (2016) 124:31–6. doi: 10.1016/j.conbuildmat.2016.07.055

CrossRef Full Text | Google Scholar

21. Hou C, Zhu W, Yan B, Guan K, Du J. Influence of binder content on temperature and internal strain evolution of early age cemented tailings backfill. Constr Build Mater. (2018) 189:585–93. doi: 10.1016/j.conbuildmat.2018.09.032

CrossRef Full Text | Google Scholar

22. Mangane M, Argane R, Trauchessec R, Lecomte A, Benzaazoua M. Influence of superplasticizers on mechanical properties and workability of cemented paste backfill. Miner Eng. (2018) 116:3–14. doi: 10.1016/j.mineng.2017.11.006

CrossRef Full Text | Google Scholar

23. Zheng J, Sun X, Guo L, Zhang S, Chen J. Strength and hydration products of cemented paste backfill from sulphide-rich tailings using reactive MgO-activated slag as a binder. Constr Build Mater. (2019) 203:111–9. doi: 10.1016/j.conbuildmat.2019.01.047

CrossRef Full Text | Google Scholar

24. Xu W, Cao P, Tian M. Strength development and microstructure evolution of cemented tailings backfill containing different binder types and contents. Minerals. 8:167. doi: 10.3390/min8040167

CrossRef Full Text | Google Scholar

25. Liu L, Xin J, Feng Y, Zhang B, Song K. Effect of the cement-tailing ratio on the hydration products and microstructure characteristics of cemented paste backfill. Arab J Sci Eng. (2019) 44:6547–56. doi: 10.1007/s13369-019-03954-z

CrossRef Full Text | Google Scholar

26. Xu W, Cao Y, Liu B. Strength efficiency evaluation of cemented tailings backfill with different stratified structures. Eng Struct. (2019) 180:18–28. doi: 10.1016/j.engstruct.2018.11.030

CrossRef Full Text | Google Scholar

27. Jiang H, Fall M, Cui L. Freezing behaviour of cemented paste backfill material in column experiments. Constr Build Mater. (2017) 147:837–46. doi: 10.1016/j.conbuildmat.2017.05.002

CrossRef Full Text | Google Scholar

28. Yi X, Ma G, Fourie A. Compressive behaviour of fibre-reinforced cemented paste backfill. Geotext Geomembr. (2015) 43:207–15. doi: 10.1016/j.geotexmem.2015.03.003

CrossRef Full Text | Google Scholar

29. Chen X, Shi X, Zhou J, Chen Q, Li E, Du X. Compressive behavior and microstructural properties of tailings polypropylene fibre-reinforced cemented paste backfill. Constr Build Mater. (2018) 190:211–21. doi: 10.1016/j.conbuildmat.2018.09.092

CrossRef Full Text | Google Scholar

30. Cao S, Yilmaz E, Song W. Fiber type effect on strength, toughness and microstructure of early age cemented tailings backfill. Constr Build Mater. (2019) 223:44–54. doi: 10.1016/j.conbuildmat.2019.06.221

CrossRef Full Text | Google Scholar

31. Xue G, Yilmaz E, Song W, Yilmaz E. Influence of fiber reinforcement on mechanical behavior and microstructural properties of cemented tailings backfill. Constr Build Mater. (2019) 213:275–85. doi: 10.1016/j.conbuildmat.2019.04.080

CrossRef Full Text | Google Scholar

32. Wang M, Liu L, Wang S, Lv B, Zhang B, Zhang X, et al. Numerical investigation of heat transfer and phase change characteristics of cold load and storage functional CPB in deep mine. Front Earth Sci. (2020) 8:31. doi: 10.3389/feart.2020.00031

CrossRef Full Text | Google Scholar

33. Hu J, Ren Q, Jiang Q, Gao R, Zhang L, Luo Z. Strength characteristics and the reaction mechanism of stone powder cement tailings backfill. Adv Mater Sci Eng. (2018) 2018:1–14. doi: 10.1155/2018/8651239

CrossRef Full Text | Google Scholar

34. Cao S, Yilmaz E, Song W, Yilmaz E, Xue G. Loading rate effect on uniaxial compressive strength behavior and acoustic emission properties of cemented tailings backfill. Constr Build Mater. (2019) 213:313–24. doi: 10.1016/j.conbuildmat.2019.04.082

CrossRef Full Text | Google Scholar

35. Sun Q, Cai C, Zhang S, Tian S, Li B, Xia Y, et al. Study of localized deformation in geopolymer cemented coal gangue-fly ash backfill based on the digital speckle correlation method. Constr Build Mater. (2019) 215:321–31. doi: 10.1016/j.conbuildmat.2019.04.208

CrossRef Full Text | Google Scholar

36. Wang Y, Wu A, Wang H, Wang Y, Cui L, Jin F, et al. Damage constitutive model of cemented tailing paste under initial temperature effect. Chinese J Eng. (2017) 39:31–8. doi: 10.13374/j.issn2095-9389.2017.01.004

CrossRef Full Text | Google Scholar

37. Cui L, Fall M. A coupled thermo–hydro-mechanical–chemical model for underground cemented tailings backfill. Tunnel Undergr Space Technol. (2015) 50:396–414. doi: 10.1016/j.tust.2015.08.014

CrossRef Full Text | Google Scholar

38. Wu D, Deng T, Zhao R. A coupled THMC modeling application of cemented coal gangue-fly ash backfill. Constr Build Mater. (2018) 158:326–36. doi: 10.1016/j.conbuildmat.2017.10.009

CrossRef Full Text | Google Scholar

39. Cui L, Fall M. An evolutive elasto-plastic model for cemented paste backfill. Comput Geotech. (2016) 71:19–29. doi: 10.1016/j.compgeo.2015.08.013

CrossRef Full Text | Google Scholar

40. Qi C, Fourie A, Chen Q, Zhang Q. A strength prediction model using artificial intelligence for recycling waste tailings as cemented paste backfill. J Clean Prod. (2018) 183:566–78. doi: 10.1016/j.jclepro.2018.02.154

CrossRef Full Text | Google Scholar

41. Qi C, Chen Q, Fourie A, Tang X, Zhang Q, Dong X, et al. Constitutive modelling of cemented paste backfill: a data-mining approach. Constr Build Mater. (2019) 197:262–70. doi: 10.1016/j.conbuildmat.2018.11.142

CrossRef Full Text | Google Scholar

42. Qi C, Tang X, Dong X, Chen Q, Fourie A, Liu E. Towards Intelligent Mining for Backfill: a genetic programming-based method for strength forecasting of cemented paste backfill. Miner Eng. (2019) 133:69–79. doi: 10.1016/j.mineng.2019.01.004

CrossRef Full Text | Google Scholar

43. Wu E. Specific energy characteristics of cemented tailings backfill of damage and fracture under uniaxial compression (Master). Wuhan: Wuhan University of Science and Technology (2018).

Google Scholar

44. Dong L, Tong X, Li X, Zhou J, Wang S, Liu B. Some developments and new insights of environmental problems and deep mining strategy for cleaner production in mines. J Clean Prod. (2019) 210:1562–78. doi: 10.1016/j.jclepro.2018.10.291

CrossRef Full Text | Google Scholar

45. Wang J, Song W, Tan Y, Fu J, Cao S. Damage constitutive model and strength criterion of horizontal stratified cemented backfill. Rock Soil Mech. (2019) 40:1731–9. doi: 10.16285/j.rsm.2018.0017

CrossRef Full Text | Google Scholar

46. Ahmad A, Ghazal M. Exponentiated additive Weibull distribution. Reliabil Eng Syst Saf. (2020) 193:106663. doi: 10.1016/j.ress.2019.106663

CrossRef Full Text | Google Scholar

47. Zhang H, Yuan C, Yang G, Wu LY, Peng C, Ye W, Shen Y, Moayedi H. A novel constitutive modelling approach measured under simulated freeze–thaw cycles for the rock failure. Eng. Comput. (2019) 35:1–14. doi: 10.1007/s00366-019-00856-4

CrossRef Full Text | Google Scholar

48. Dong L, Sun D, Li X, Ma J, Zhang L, Tong X. Interval non-probabilistic reliability of surrounding jointed rockmass considering microseismic loads in mining tunnels. Tunnel Undergr Space Technol. (2018) 81:326–35. doi: 10.1016/j.tust.2018.06.034

CrossRef Full Text | Google Scholar

49. Lemaitre J. A continuous damage mechanics model for ductile fracture. J Eng Mater Technol. (1985) 107:83–9. doi: 10.1115/1.3225775

CrossRef Full Text | Google Scholar

50. Dong L, Shu W, Li X, Zhang J. Quantitative evaluation and case studies of cleaner mining with multiple indexes considering uncertainty factors for phosphorus mines. J Clean Prod. (2018) 183:319–34. doi: 10.1016/j.jclepro.2018.02.105

CrossRef Full Text | Google Scholar

51. Cheng A, Zhang Y, Dai S, Dong F, Zeng W, Li D. Space-time evolution of acoustic emission parameters of cemented backfill and its fracture prediction under uniaxial compression. Rock Soil Mech. (2019) 40:2965–74. doi: 10.16285/j.rsm.2018.1940

CrossRef Full Text | Google Scholar

52. Wang X, Kang H, Gao F, Zhao K. DEM simulation of mechanical behavior of jointed coal in large scale under uniaxial compression. J China Coal Soc. (2018) 43:3088–97. doi: 10.13225/j.cnki.jccs.2018.0834

CrossRef Full Text | Google Scholar

53. Du X, Wang Y, Lu D. Study on static and dynamic stress strain relationship of cement mortar material. China Civil Eng J. (2010) 43S:119–26. doi: 10.15951/j.tmgcxb.2010.s2.033

CrossRef Full Text | Google Scholar