- 1Department of Applied Mathematics, Huainan Normal University, Huainan, China
- 2School of Mathematics and Physics, Guangxi University for Nationalities, Nanning, China
- 3Department of Mathematics, Deyang High School, Chengdu Normal University, Deyang, China
This paper discusses the synchronization problem for a class of unknown fractional-order chaotic systems (FOCSs) with indeterminate external disturbances and non-symmetrical control gain. A paralleled adaptive fuzzy synchronization controller is constructed in which indeterminate non-linear functions are approximated by the fuzzy logic systems depending on fractional-order Lyapunov stability criteria and the fractional-order parameter adaptive law is designed to regulate corresponding parameters of the fuzzy systems. The proposed method guarantees the boundedness of all of the signals in the closed-loop system, and at the same time, it ensures the convergence of the synchronization error between the master and slave FOCSs. Finally, the feasibility is demonstrated by simulation studies.
1. Introduction
The fractional calculus appeared in the same era as the classical integer-order calculus, but due to the facts that the fractional-order calculus lacks actual background and its theory is complex, the fractional calculus has rarely been investigated by scholars. Recently, it has been shown that fractional calculus not only provides new mathematical methods for practical systems but also is especially well-suited for describing some dynamical behaviors of physical systems [1–5]. Consequently, the fractional-order calculus has been employed to describe phonology and thermal systems, signal processing and system identification [6, 7], control and robotics [8–11], and many other real-world systems. Since the fractional-order calculus has memory ability, in the description of complex dynamic systems, a model built depending on fractional-order calculus is more accurate than an integer-order one. The study for the fractional-order chaotic system (FOCS) has thus slowly become a hot research topic.
It is well-known that chaotic systems (integer-order or fractional-order) are sensitive to initial state values, i.e., the stability of systems will change obviously with small changes in initial values; thus, the synchronization control of FOCSs is challenging work. Some methods, such as PD control [12], PID control [13–15], adaptive fuzzy backstepping control [16–20], sliding mode control [21–25], and Lyapunov direct [26–28] and adaptive neural network control [29–32] have been used to control or synchronize fractional chaotic systems. Chen et al. [21] investigated the adaptive synchronization of FOCSs, where different structures of the master and slave FOCSs and the existence of external disturbances are ignored. In Wang et al. [33], the synchronization of FOCSs accompanied by external disturbances was studied. To handle the unmatched disturbances, in He et al. [30], a robust synchronization method with non-linear input was proposed, but its control cost was very high. It should be mentioned that, in the above literature, the stability analysis of the synchronization of FOCSs still uses the ideal of linear systems. Generally speaking, the synchronization of FOCS systems with some unknown factors and external disturbances needs to be further researched.
Motivated by the above discussion, this paper aims to design a synchronization controller for a master and slave fractional-order chaotic system (FOCS) subject to different structures and external disturbances. The control gain matrix is assumed to be unknown. Fuzzy logic systems are used to approximate the unknown non-linear functions. Fractional-order parameter adaptive laws are designed to update the fuzzy parameters. The main contributions of this work are summarized as follows. (1) The non-symmetrical control gain matrix and external disturbances in FOCSs are considered. Besides, unlike some prior works, such as Liu et al. [16] and Pan et al. [31], the sequence-leading minor in the control gain matrix is not assumed to be zero. (2) Based on the Lyapunov stability theorem, fractional-order fuzzy parameter adaptive laws are designed.
2. Preliminaries
The ν-th fractional-order integral is defined as:
where Γ(·) function can be defined as
The ν-th Caputo's derivative can be defined as:
clearly, where n is an integer satisfying n − 1 ≤ ν < n.
The Laplace transform of Caputo's fractional-order derivative (3) can be expressed by Li et al. [2]
When 0 < ν < 1,
For simplicity, we suppose that ν ∈ (0, 1) in the rest of this paper. The following conclusions will be given in advance.
Definition 1. Pudlubny [3] The Mittag-Leffler function can be given by
where ν, ξ > 0, and z ∈ C, the Laplace transform of which is
Lemma 1. Pudlubny [3] If m(k) ∈ C1[0, T](T > 0) (the symbol C1 means that a function has a continuous derivative), the following equation satisfies:
Lemma 2. (Lyapunov's second fractional-order method [34]) Suppose that e(k) = 0 is an equilibrium point of the following FOCS:
where e(k) ∈ Rn is a system variable, and h(e(k)) ∈ Rn is a non-linear function that has a Lipschitz local condition. If there exists a Lyapunov function V(k, e(k)) and positive parameters a1, a2, a3 such that
then system (9) is asymptotically stable.
Lemma 3. Aguila-Camacho et al. [35] Suppose that e(k) ∈ Rn is a continuous and derivable function, then
Lemma 4. Costa et al. [36] and Liu et al. [37] Let matrix G ∈ Rn×n be the non-zero sequence-leading minor, then G can be factorized as G = G1AgTg, where is a positive matrix, is a diagonal matrix whose diagonal line is +1 or −1 (signal of each of its elements is determined by corresponding the sequence-leading minor signal of G), and is a upper triangular matrix.
3. Problem Description
3.1. System Dynamics
Suppose that the slave and respond FOCSs are separately defined as
where and are separately system measurable state variables of the drive system and respond system, h, p : Rn → Rn are uncertain non-linear continuous functions, G ∈ Rn×n is an unknown constant matrix, D(k) ∈ Rn×n is an indeterminate external disturbance, and u(k) ∈ Rn is the control input.
3.2. Introduction of a Fuzzy System
A fuzzy logic system includes the knowledge base, fuzzier, fuzzy inference engine based on the fuzzy rules and defuzzier [38–41]. The form of the j-th fuzzy rule is
: If x1 is , x2 is , ⋯ , xn is , then ĥ(x(k)) is Cj (j = 1, 2, ⋯ , N),
where and ĥ(x(k)) ∈ ℝ are respectively the input and the output of fuzzy logic systems. The output is
where θj(k) is a value where the fuzzy membership function is maximum. Generally, we can consider that , and the fuzzy basic function is Let φ(x(k)) = [φ1(x(k)), φ2(x(k)), ⋯ , φN(x(k))]T, θ(k) = [θ1(k), θ2(k, ⋯ , θN(k)]T then the output of fuzzy logic systems is written as
Theorem 1. Suppose that p(x) is a continuous function defined on compact set Ω. For any constants ε > 0, there exists a fuzzy logic system approximating function ĥ(x) forming (16) such that
where is an estimator of optimal vector θ*.
3.3. Control Objective
The synchronization error can be defined as e(k) = y(k) − x(k). Our control objective is to design an adaptive controller such that the synchronization error tends to zero asymptotically (i.e., ).
4. Controller Design and Stability Analysis
Assumption 1. The control gain matric G has a non-zero sequence-leading minor whose signal is known.
Remark 1. Assumption 1 is not strict. In fact, the gain matrix of some actual systems (such as a visual servo and vehicle thermal management system [42]) is non-symmetrical. According to Lemma 4, one can factorize G as G = G1AT, where G1 is an unknown positive definite matrix, A is a known matrix whose diagonal line is +1 or -1, AA = In×n (In×n is a n-order unitary matrix), and T is an uncertain upper triangle matrix.
Assumption 2. The product of the external disturbance D(k) and the positive definite matrix is a function that is bounded, i.e., there exists an uncertain constant Mi > 0 so that
Remark 2. Assumption 2 is not restrictive, and it is used in some similar literature, for example, in Liu et al. [9], Rahmani et al. [10], and Ferdaus et al. [11]. In fact, most commonly used disturbances satisfy Assumption 2.
The dynamic equation of synchronization error is expressed as
Let , then
Denote γ(z(k)) = γ(x(k), y(k), u(k)) = Qp(y(k)) − Qh(x(k)) + (AT − A)u(k) = [γ1(z(k)), γ2(z(k)), ⋯ , γn(z(k))]T as an indeterminate non-linear function; then, Equation (20) is expressed as
The indeterminate function γ(z(k)) can be approximated by the fuzzy logic system (16) as
Assume that the errors of the optimal parameter and the optimal estimated errors be respectively
From Boulkroune et al. [42] and Tong et al. [43] and Theorem 1, we assume that ( is an uncertain constant). If we denote ε(z(k)) = [ε1(z(k)), ε2(z(k)), ⋯ , εn(z(k))]T and , the estimated error of the indeterminate non-linear function can be written as
From the above discussion, the controller u(k) can be designed as
where L= diag are parameters that need to be designed, , are estimated values of uncertain constants , and , are estimated values of unknown constants Mi. For the sake of achieving the synchronization objective, this paper designs the following fractional-order parameter adaptive laws:
where λi, ξi, μi > 0, i = 1, 2, ⋯ , n are designed parameters.
To facilitate the coming stability analysis, let us display some results in advance.
Lemma 5. Suppose that then we have e(k) ≤ e(0) on [0, +∞). On the contrary, implies that e(k) ≥ e(0) on [0, +∞).
Proof. We only verify the first condition (the second condition is the same). Because there exists a non-negative function satisfying
Taking the Laplace transform on both sides of equation (31), we get sνE(s)−sν−1e(0)+F(s) = 0, where E(s) and F(s) are separately the Laplace transform of e(k) and h(k). It is simplified to
Taking the inverse Laplace transform on both sides of equation (32), we obtain
By the fractional-order integral (1), we have [D−νh](k) ≥ 0. Further, we have e(k) ≤ e(0) on [0, +∞).
Remark 3. Lemma 5 shows the difference between a fractional-order derivative and an integer-order derivative, but it cannot be described as: if , then e(k) is monotonically decreasing on the interval [0, +∞); if then e(k) is monotonically increasing on the interval [0, +∞). To explain this, a counterexample is given as follows.
Example 1. Consider that x(0) ≥ 0 is an initial value of the differential equation: where 0 < μ < 1, 0 < ν < 1, and k > 0. Obviously, h(k, x) ≥ 0, and the solution of the differential equation is It is clear that when 0 < μ ≤ 1 − ν. Therefore, x(k) is not monotonically increasing, defined on k ∈ [0, +∞).
Lemma 6. Suppose that e(k) ∈ Rn be a continuous one-order derivative, then
where Q is an arbitrary n-order positive definite matrix.
Proof. Since Q is a positive definite matrix, there exists an n-order non-singular symmetric matrix B = BT so that Q = BTB. From Lemmas 1, 2, and 3, we obtain
Lemma 7. Suppose that , where x(k) and y(k) ∈ Rn are continuous one-order derivatives. If there exists a constant q > 0 satisfying the following inequality
then ‖x(k)‖ and ‖y(k)‖ are both bounded, and x(k) tends to zero asymptotically, where ‖·‖ represents the Euclidian norm.
Proof. According to inequality (36), the following inequality holds:
From Lemma 5, we know that V(k) ≤ V(0)(∀t ≥ 0) when V(k) defines on [0, ∞). So, and Thereby, ‖x(k)‖ and ‖y(k)‖ are bounded.
Taking the ν-th integral on both sides of inequality , we have
From the structure of V(k), we have xT(k)x(k) ≤ 2V(k), and furthermore,
It follows from (39) that there exists a non-negative function M(k) such that
Taking the Laplace transform on (40), we obtain:
where X(s) and M(s) are respectively the Laplace transforms of x(k) and M(k). Taking the inverse Laplace transform on both sides of equation (41), the solution is
where * is the convolution. Since k−1 and are both non-negative functions, . From Li et al. [2], we know that x(k) is M-L stable and x(k) tends to zero asymptotically, i.e., .
Lemma 8. Suppose that , where z(k), d(k) ∈ Rn and are both positive definite matrixes. If there exists a positive definite matrix Q3 and a constant q0 > 0 satisfying
then ‖z(k)‖ and ‖d(k)‖ are bounded, and z(k) tends to zero asymptotically (i.e., = 0).
The main results of the paper are given as follows.
Theorem 2. Under Assumption 1 and Assumption 2, the synchronization between the drive system (13) and the respond system (14) can be achieved on the work of the adaptive fuzzy controller (26) and fractional-order adaptive laws (27), (28), and (29). In addition, all the signals of the closed-loop system are bounded.
Proof. Since A = In×n, substituting the controller (26) into the error dynamic equation (21) gives
It is simplified as
Let and . Multiplying both sides of equation (45) by eT(k) yields
Then, we have
Because the ν-order Caputo derivative of a constant is zero, we have , , and i = 1, 2, ⋯ , n. By Lemma 3 and Lemma 6, taking the ν-order derivative of V(k) in equality (47) yields
Substituting (27), (28), and (29) into (48) gives
where l0 = min{l1, l2, ⋯ , ln} and λmax is a maximal eigenvalue in positive definite matrix Q. From Lemma 8 and inequality (49), we know that the synchronization error satisfies and if , , and are bounded, then , , and are both bounded. Since system (13) is a chaotic system, we know that x(k) is also bounded. Thus, e(k) is also bounded, which implies that y(k) is bounded, too. Consequently, by using (26), we get that u(k) is bounded. Thereby, all the signals in the closed-loop system are bounded.
Remark 4. For respond system (14), when G = E, the synchronization between the uncertain FOCSs was solved in Liu et al. [44]. However, this solution cannot solve the synchronization question for systems with uncertain non-symmetrical control gain; when D(k) = 0, Ha et al. [45] researched the synchronization of FOCSs with indeterminate non-symmetrical control gain but also did not solve the synchronization question of systems with unknown disturbances. In contrast, by considering the above two conditions, this paper addresses the synchronization question for systems with uncertain non-symmetrical control gain and unknown disturbances.
5. Numerical Simulation
In the simulation, the effectiveness of the controller is tested by researching the synchronization between the fractional-order Newton-Leipnik system [46, 47] and the fractional-order Lü system [48, 49].
The fractional-order Newton-Leipnik system is given as follows.
The fractional-order Lü system can be written as:
The gain matrix G (which is non-symmetric) and its factorization (by Lemma 4) are as follows.
where parameters a and b are separately a = −0.2 and b = 0.9. The external disturbance is
It is easy to gather that the following inequality holds:
The initial values of the drive system and respond system can be respectively x(0) = [−0.3, 1, −0.4]T and y(0) = [2, −2, 3]T. When u(k) ≡ 0, D(k) = 0 and μ = 0.95, the above two systems exhibit chaotic phenomena.
In the numerical simulation, the input variables of the fuzzy system are x(k), y(k), and u(k). For inducing calculation of the fuzzy logic system, we will replace x(k) and y(k) by e(k). For e1(k), e2(k), and e3(k), we can select five Gaussian membership functions whose mathematical expectations are respectively −4, −2, 0, 2, and 4 and whose parameters are ([1.2],[-4, -2, 0, 2, 4]), uniformly distributed in the interval [−4, 4] for each input. Therefore, the number of the rules that are produced by the fuzzy logic system approximating function is 53 = 125. In order to better test the effectiveness of the controller, we can chose adjustable parameters, which are represented by θ1(0), θ2(0), and θ3(0), as random vectors in 125 dimensions.
The other parameters of the controller are defined as li = 5, λi = 500, ξi = 0.5, and μi = 0.5, and the estimated values of the fuzzy logic system approximating error are and . Estimators of the product between the uncertain external disturbance and unknown constant matrix are , and . For the sake of better showing the simulation results, the initial value of the respond system is chosen as y(0) = [0.2, −2, 0.3]T, which is compared to y(0) = [2, −2, 3]T. The simulation results are shown separately in Figures 1–4, detailed explanations of which follow.
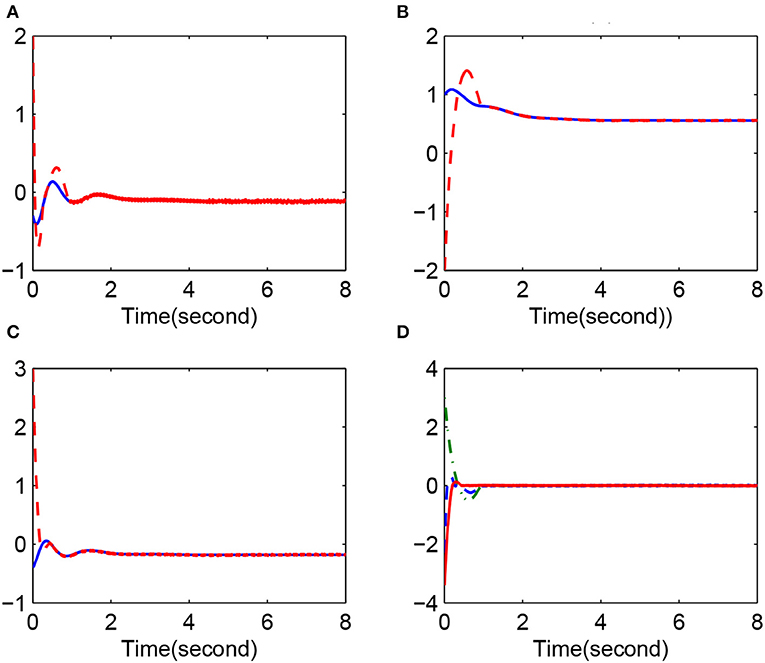
Case 1, in Figure 1, synchronization result: x(0) = [−0.3, 1, −0.4]T and y(0) = [2, −2, 3]T. (Figure 1A) x1(k) (solid line) and y1(k) (dotted line); (Figure 1B) x2(k) (solid line) and y2(k) (dotted line); (Figure 1C) x3(k) (solid line) and y3(k) (dotted line); (Figure 1D) synchronization error e1(k) (dotted line), e2(k) (dashed line), and e3(k) (solid line).
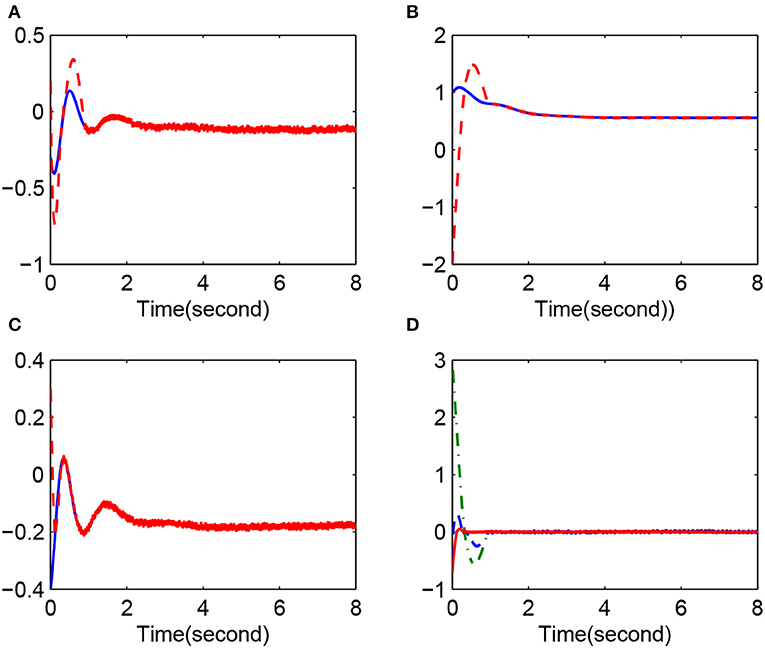
Case 2, in Figure 2, synchronization result: x(0) = [−0.3, 1, −0.4]T and y(0) = [0.2, −2, 0.3]T. (Figure 2A) x1(k) (solid line) and y1(k) (dotted line); (Figure 2B) x2(k) (solid line) and y2(k) (dotted line); (Figure 2C) x3(k) (solid line) and y3(k) (dotted line); (Figure 2D) synchronization error e1(k) (dotted line), e2(k) (dashed line), and e3(k) (solid line).
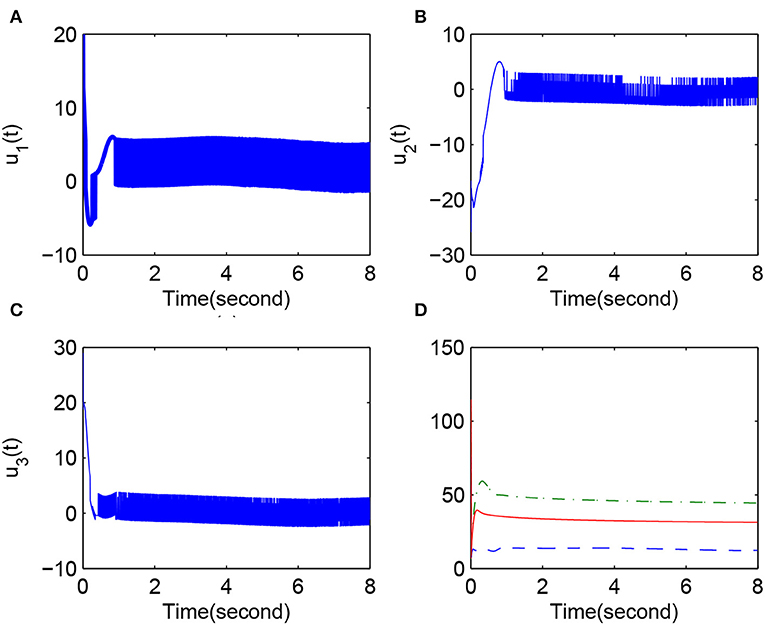
Case 3, in Figure 3, control variables and fuzzy logic system parameters: x(0) = [−0.3, 1, −0.4]T and y(0) = [2, −2, 3]T. (Figure 3A) u1(t); (Figure 3B) u2(k); (Figure 3C) u3(k); (Figure 3D) ‖θ1(k)‖ (dotted line), ‖θ2(k)‖ (dashed line), and ‖θ3(k)‖ (solid line).
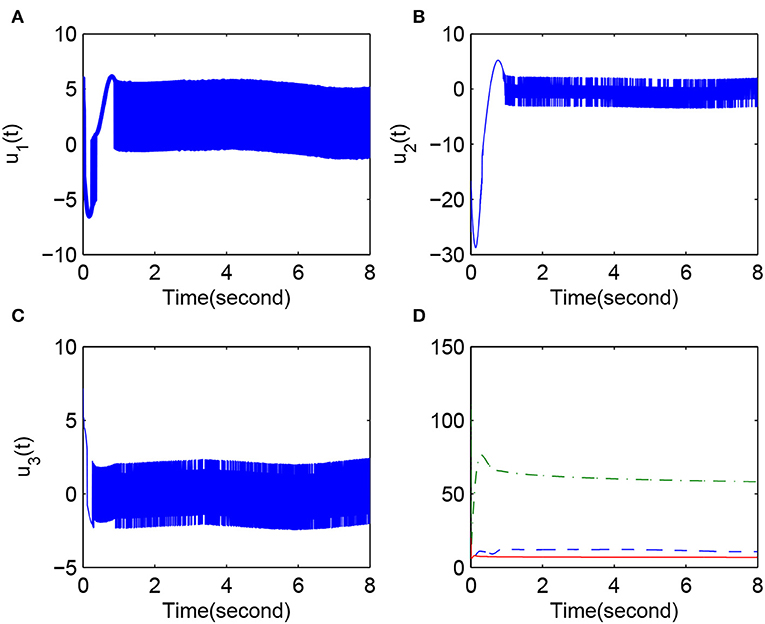
Case 4, in Figure 4, control variables and fuzzy logic system parameters: x(0) = [−0.3, 1, −0.4]T and y(0) = [0.2, −2, 0.3]T. (Figure 4A) u1(k); (Figure 4B) u2(k); (Figure 4C) u3(k); (Figure 4D) ‖θ1(k)‖ (dotted line), ‖θ2(k)‖ (dashed line), and ‖θ3(k)‖ (solid line).
The simulation results clearly show that the convergence rate of synchronization error is fast when li is reasonable. Figures 1, 4 give the error change trend that the error is large at first and then gets smaller and smaller after a time, finally tending to zero asymptotically. Furthermore, from case 1 and case 2, we know that a minimal change in initial values can have obvious effects on the error but cannot affect the eventual convergence of error. This implies that the fuzzy system proposed in this paper has good approximation performance. Figures 3, 4 display the changing situation of control variables and fuzzy logic system parameters, and it conforms to our expectations. In addition, from the above simulation results, we can see a chattering phenomenon because a discontinuous sign function is used in the synchronization controller.
6. Conclusion
In this paper, a robust adaptive fuzzy controller for indeterminate FOCSs with uncertain external disturbances and non-symmetrical control gain is proposed. The proposed method has good ability on the condition that each sequence-leading minor of the uncertain non-symmetrical gain matrix is non-zero, and the upper bound of the product of the positive definite matrix factorized by gain matrix and external disturbance is known. The stability of the closed-loop system is successfully discussed by using a fractional-order Lyapunov method and quadratic Lyapunov functions.
Data Availability Statement
All datasets generated for this study are included in the article/supplementary material.
Author Contributions
JX and XZ contributed the conception and design of the study. XQ and NL organized the literature. JX performed the design of figures and wrote the first draft of the manuscript. All authors contributed to manuscript revision and read and approved the submitted version.
Funding
This work was supported by the Basic Ability Promotion Project for Young and Middle-aged Teachers of Guangxi Colleges and Universities (2020KY04022), the Xiangsihu Young Scholars Innovative Research Teamof Guangxi University for Nationalities (2019RSCXSHQN02), and the Key Natural Science Research Projects in Anhui Universities (KJ2019A0696).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Liu H, Pan Y, Cao J. Composite learning adaptive dynamic surface control of fractional-order nonlinear systems. IEEE Trans Cybernet. (2019). doi: 10.1109/TCYB20192938754. [Epub ahead of print].
2. Li Y, Chen Y, Podlubny I. Mittag–Leffler stability of fractional order nonlinear dynamic systems. Automatica. (2009) 45:1965–9. doi: 10.1016/j.automatica.2009.04.003
4. Liu H, Wang H, Cao J, Alsaedi A, Hayat T. Composite learning adaptive sliding mode control of fractional-order nonlinear systems with actuator faults. J Franklin Inst. (2019) 356: 9580–99. doi: 10.1016/jjfranklin201902042
5. Qin X, Li S, Liu H. Adaptive fuzzy synchronization of uncertain fractional-order chaotic systems with different structures and time-delays. Adv Diff Equat. (2019) 2019:174. doi: 10.1186/s13662-019-2117-1
6. Shah SM, Samar R, Khan NM, Raja MAZ. Fractional-order adaptive signal processing strategies for active noise control systems. Nonlinear Dyn. (2016) 85:1363–76. doi: 10.1007/s11071-016-2765-6
7. Dabiri A, Nazari M, Butcher EA. The spectral parameter estimation method for parameter identification of linear fractional order systems. In: American Control Conference (ACC). Boston, MA: IEEE (2016). p. 2772–7.
8. Wang Y, Gu L, Xu Y, Cao X. Practical tracking control of robot manipulators with continuous fractional-order nonsingular terminal sliding mode. IEEE Trans Indus Electron. (2016) 63:6194–204. doi: 10.1109/TIE.2016.2569454
9. Liu H, Pan Y, Cao J, Zhou Y, Wang H. Positivity and stability analysis for fractional-order delayed systems: A T-S fuzzy model approach. IEEE Trans Fuzzy Syst. (2020). doi: 10.1109/TFUZZ20202966420. [Epub ahead of print].
10. Rahmani M, Ghanbari A, Ettefagh MM. Robust adaptive control of a bio-inspired robot manipulator using bat algorithm. Expert Syst. Appl. (2016) 56:164–76. doi: 10.1016/j.eswa.2016.03.006
11. Ferdaus M, Pratama M, Anavatti SG, Garratt MA, Pan Y. Generic evolving self-organizing neuro-fuzzy control of bio-inspired unmanned aerial vehicles. arXiv [Preprint]. arXiv:180200635 (2018). doi: 10.1109/TFUZZ.2019.2917808
12. Pan Y, Er MJ, Sun T, Xu B, Yu H. Adaptive fuzzy PD control with stable H∞ tracking guarantee. Neurocomputing. (2017) 237:71–8. doi: 10.1016/j.neucom.2016.08.091
13. Xu Y, Zhou J, Xue X, Fu W, Zhu W, Li C. An adaptively fast fuzzy fractional order PID control for pumped storage hydro unit using improved gravitational search algorithm. Energy Convers Manage. (2016) 111:67–78. doi: 10.1016/j.enconman.2015.12.049
14. Pinsker JE, Lee JB, Dassau E, Seborg DE, Bradley PK, Gondhalekar R, et al. Randomized crossover comparison of personalized MPC and PID control algorithms for the artificial pancreas. Diabetes Care. (2016) 39:1135–42. doi: 10.2337/dc15-2344
15. Ma D, Chen J, Liu A, Chen J, Niculescu SI. Explicit bounds for guaranteed stabilization by PID control of second-order unstable delay systems. Automatica. (2019) 100:407–11. doi: 10.1016/j.automatica.2018.11.053
16. Liu H, Pan Y, Li S, Chen Y. Adaptive fuzzy backstepping control of fractional-order nonlinear systems. IEEE Trans Syst Man Cybernet Syst. (2017) 47:2209–17. doi: 10.1109/TSMC.2016.2640950
17. Chang W, Li Y, Tong S. Adaptive fuzzy backstepping tracking control for flexible robotic manipulator. IEEE CAA J Autom Sin. (2018). doi: 10.1109/JAS.2017.7510886. [Epub ahead of print].
18. Liu YJ, Gao Y, Tong S, Li Y. Fuzzy approximation-based adaptive backstepping optimal control for a class of nonlinear discrete-time systems with dead-zone. IEEE Trans Fuzzy Syst. (2016) 24:16–28. doi: 10.1109/TFUZZ.2015.2418000
19. Li H, Wang L, Du H, Boulkroune A. Adaptive fuzzy backstepping tracking control for strict-feedback systems with input delay. IEEE Trans Fuzzy Syst. (2017) 25:642–52. doi: 10.1109/TFUZZ.2016.2567457
20. Xu D, Huang J, Su X, Shi P. Adaptive command-filtered fuzzy backstepping control for linear induction motor with unknown end effect. Inform Sci. (2019) 477:118–31. doi: 10.1016/j.ins.2018.10.032
21. Chen DY, Zhao WL, Ma XY, Zhang RF. No-chattering sliding mode control chaos in Hindmarsh–Rose neurons with uncertain parameters. Comput Math Appl. (2011) 61:3161–71. doi: 10.1016/j.camwa.2011.04.010
22. Farhat M, Barambones O, Sbita L. A new maximum power point method based on a sliding mode approach for solar energy harvesting. Appl Energy. (2017) 185:1185–98. doi: 10.1016/j.apenergy.2016.03.055
23. Zhou Q, Yao D, Wang J, Wu C. Robust control of uncertain semi-Markovian jump systems using sliding mode control method. Appl Math Comput. (2016) 286:72–87. doi: 10.1016/j.amc.2016.03.013
24. Li H, Wang J, Shi P. Output-feedback based sliding mode control for fuzzy systems with actuator saturation. IEEE Trans Fuzzy Syst. (2016) 24:1282–93. doi: 10.1109/TFUZZ.2015.2513085
25. Jiang B, Karimi HR, Kao Y, Gao C. Reduced-order adaptive sliding mode control for nonlinear switching semi-Markovian jump delayed systems. Inform Sci. (2019) 477:334–48. doi: 10.1016/j.ins.2018.10.054
26. Guo Y, Ma B. Extension of Lyapunov direct method about the fractional nonautonomous systems with order lying in (1, 2). Nonlinear Dyn. (2016) 84:1353–61. doi: 10.1007/s11071-015-2573-4
27. Dang QA, Hoang MT. Lyapunov direct method for investigating stability of nonstandard finite difference schemes for metapopulation models. J Diff Equat Appl. (2018) 24:15–47. doi: 10.1080/10236198.2017.1391235
28. Tuan HT, Trinh H. Stability of fractional-order nonlinear systems by Lyapunov direct method. IET Control Theory Appl. (2017) 12:2417–22. doi: 10.1049/iet-cta.2018.5233
29. Wang H, Shi P, Li H, Zhou Q. Adaptive neural tracking control for a class of nonlinear systems with dynamic uncertainties. IEEE Trans Cybernet. (2017) 47:3075–87. doi: 10.1109/TCYB.2016.2607166
30. He W, Chen Y, Yin Z. Adaptive neural network control of an uncertain robot with full-state constraints. IEEE Trans Cybernet. (2016) 46:620–9. doi: 10.1109/TCYB.2015.2411285
31. Pan Y, Liu Y, Xu B, Yu H. Hybrid feedback feedforward: an efficient design of adaptive neural network control. Neural Netw. (2016) 76:122–34. doi: 10.1016/j.neunet.2015.12.009
32. Li G, Sun C. Adaptive neural network backstepping control of fractional-order Chua–Hartley chaotic system. Adv Diff Equat. (2019) 2019:148. doi: 10.1186/s13662-019-2099-z
33. Wang H, Liu YJ, Tong S. Adaptive control of a class of switched nonlinear discrete-time systems with unknown parameter. Neurocomputing. (2016) 214:1–6. doi: 10.1016/j.neucom.2016.03.072
34. Zhou P, Ding R, Cao YX. Multi drive-one response synchronization for fractional-order chaotic systems. Nonlinear Dyn. (2012) 70:1263–71. doi: 10.1007/s11071-012-0531-y
35. Aguila-Camacho N, Duarte-Mermoud MA, Gallegos JA. Lyapunov functions for fractional order systems. Commun Nonlinear Sci Numer Simul. (2014) 19:2951–7. doi: 10.1016/j.cnsns.2014.01.022
36. Costa RR, Hsu L, Imai AK, Kokotović P. Lyapunov-based adaptive control of MIMO systems. Automatica. (2003) 39:1251–7. doi: 10.1016/S0005-1098(03)00085-2
37. Liu H, Pan Y, Cao J, Wang H, Zhou Y. Adaptive neural network backstepping control of fractionial-order nonlinear systems with actuator faults. IEEE Trans Neural Netw Learn Syst. (2020). doi: 10.1109/TNNLS20202964044. [Epub ahead of print].
38. Li Y, Sui S, Tong S. Adaptive fuzzy control design for stochastic nonlinear switched systems with arbitrary switchings and unmodeled dynamics. IEEE Trans Cybernet. (2017) 47:403–14. doi: 10.1109/TCYB.2016.2518300
39. Li Y, Tong S. Adaptive fuzzy output-feedback stabilization control for a class of switched nonstrict-feedback nonlinear systems. IEEE Trans Cybernet. (2017) 47:1007–16. doi: 10.1109/TCYB.2016.2536628
40. Liu Y, Park JH, Guo BZ, Shu Y. Further results on stabilization of chaotic systems based on fuzzy memory sampled-data control. IEEE Trans Fuzzy Syst. (2018) 26:1040–5. doi: 10.1109/TFUZZ.2017.2686364
41. Liu YJ, Gong M, Tong S, Chen CP, Li DJ. Adaptive fuzzy output feedback control for a class of nonlinear systems with full state constraints. IEEE Trans Fuzzy Syst. (2018) 26:2607–17. doi: 10.1109/TFUZZ.2018.2798577
42. Boulkroune A, Tadjine M, M'Saad M, Farza M. Fuzzy adaptive controller for MIMO nonlinear systems with known and unknown control direction. Fuzzy Sets Syst. (2010) 161:797–820. doi: 10.1016/j.fss.2009.04.011
43. Tong S, Tang J, Wang T. Fuzzy adaptive control of multivariable nonlinear systems1. Fuzzy Sets Systems. (2000) 111:153–67. doi: 10.1016/S0165-0114(98)00052-9
44. Liu H, Li S, Li G, Wang H. Adaptive controller design for a class of uncertain fractional-order nonlinear systems: an adaptive fuzzy approach. Int J Fuzzy Syst. (2018) 20:366–79. doi: 10.1007/s40815-017-0371-5
45. Ha S, Liu H, Li S, Liu A. Backstepping-based adaptive fuzzy synchronization control for a class of fractional-order chaotic systems with input saturation. Int J Fuzzy Syst. (2019) 21:1571–84. doi: 10.1007/s40815-019-00663-5
46. Sheu LJ, Chen HK, Chen JH, Tam LM, Chen WC, Lin KT, et al. Chaos in the Newton–Leipnik system with fractional order. Chaos Solitons Fract. (2008) 36:98–103. doi: 10.1016/j.chaos.2006.06.013
47. Dar MR, Kant NA, Khanday FA. Electronic implementation of fractional-order newton–leipnik chaotic system with application to communication. J Comput Nonlinear Dyn. (2017) 12:054502. doi: 10.1115/1.4036547
48. Lu J, Chen G, Yu X, Leung H. Design and analysis of multiscroll chaotic attractors from saturated function series. IEEE Trans Circuits Syst I Regul Pap. (2004) 51:2476–90. doi: 10.1109/TCSI.2004.838151
Keywords: adaptive fuzzy control, fractional-order chaotic system, fractional-order adaptation, chaos synchronization, fuzzy logic system
Citation: Xu J, Li N, Zhang X and Qin X (2020) Fuzzy Synchronization Control for Fractional-Order Chaotic Systems With Different Structures. Front. Phys. 8:155. doi: 10.3389/fphy.2020.00155
Received: 31 March 2020; Accepted: 15 April 2020;
Published: 21 May 2020.
Edited by:
Shaohui Wang, Louisiana College, United StatesCopyright © 2020 Xu, Li, Zhang and Qin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiulan Zhang, eGx6aGFuZ0BneHVuLmVkdS5jbg==
 Jin Xu
Jin Xu Ning Li1
Ning Li1 Xiulan Zhang
Xiulan Zhang