Anomalous Subdiffusion in Living Cells: Bridging the Gap Between Experiments and Realistic Models Through Collaborative Challenges

The life of a cell is governed by highly dynamical microscopic processes. Two notable examples are the diffusion of membrane receptors and the kinetics of transcription factors governing the rates of gene expression. Different fluorescence imaging techniques have emerged to study molecular dynamics. Among them, fluorescence correlation spectroscopy (FCS) and single-particle tracking (SPT) have proven to be instrumental to our understanding of cell dynamics and function. The analysis of SPT and FCS is an ongoing effort, and despite decades of work, much progress remains to be done. In this paper, we give a quick overview of the existing techniques used to analyze anomalous diffusion in cells and propose a collaborative challenge to foster the development of state-of-the-art analysis algorithms. We propose to provide labeled (training) and unlabeled (evaluation) simulated data to competitors all over the world in an open and fair challenge. The goal is to offer unified data benchmarks based on biologically-relevant metrics in order to compare the diffusion analysis software available for the community.

1. Introduction

The life of a cell is governed by highly dynamical microscopic processes occurring at different space and time scales from single macromolecules up to organelles. Optical microscopy provided four decades ago the first measurements of biomolecule motion in cells. First by fluorescence recovery after photobleaching (FRAP) [1] and fluorescence correlation spectroscopy (FCS) [2], and more recently with the help of single particle tracking (SPT) [3, 4]. Several factors have colluded to popularize these techniques in many biophysics and biology labs: (i) the development of highly sensitive detectors, (ii) the emergence of genetically encoded fluorescent protein labeling in the late 90s [5–7], and (iii) the advent in the years 2000–2010 of far-field super-resolution microscopy [8–12]. All these technological efforts have granted us access to the monitoring of molecular motion in cells with unprecedented spatial (down to single molecule) and temporal resolution [13, 14]. The adoption of these techniques has been paramount in the advancement of the understanding of cell organization and dynamics [15–17].

While acquiring sufficient experimental data sets used to be a limiting factor, these technological advances combined with data acquisition parallelization provide nowadays huge amounts of data available for analysis of molecular motion inside the cell. In turn, the richness of this data has unraveled an unforeseen complexity and diversity of mechanisms for biomolecule motion in cells. Therefore, many efforts are devoted to analyze data provided by FCS or SPT with direct or inference approaches.

However, choosing the appropriate algorithms to analyse the complexity of the observed phenomena is still an important challenge. Indeed, the richness of experimental data often makes it difficult to determine which are the physical models to be considered and which are the relevant biophysical parameters to be estimated from them. We review and address this issue in this perspective.

We will first briefly review key anomalous diffusion models relevant to cell biology and summarily describe some of the existing techniques to either infer model parameters or to perform model selection. We will discuss the relevance of numerical simulations and the importance of designing realistic data sets closely mimicking the results obtained in experiments on biological samples. We will also highlight the often overlooked limitations in current acquisition methods and emphasize the role of experimental noise and biases of the aforementioned techniques. Finally, we will present and advocate in favor of the development of comprehensive sets of simulated data and metrics, allowing the community to objectively evaluate existing and new analysis tools. Our hope is that this work will instigate an open discussion about the limitations and challenges of analysing and modeling diffusion of molecules in the complex environment of the cell.

2. Brownian vs. Anomalous Diffusion

Maybe one of the best-known result of the theory of Brownian diffusion is that the mean squared displacement (MSD) of a random walker scales linearly with time, and is proportional to the diffusion coefficient of the fluid in which diffusion takes place. With x(t) being the position of the random walker at time t (in one dimension), this means that the MSD 〈x(t)²〉 = 2Dt, where 〈·〉 denotes ensemble averaging and x(0) = 0. However, Brownian diffusion does not explain the physics of disordered systems. Interestingly, an ubiquitous observation in cell biology is that the diffusive motion of macromolecules and organelles is anomalous, i.e., the MSD change with time is typically characterized by a sublinear increase. In most instances, this sublinear increase of the MSD with time can be fitted to a power-law relation 〈x(t)²〉 ∝ t^α with exponent α < 1, which justifies the vocable of “subdiffusion.” Subdiffusion is usually attributed to cellular crowding, spatial heterogeneity or molecular interactions. Another possibility of anomalous diffusion is superdiffusion, with 1 < α < 2. Indeed a lot of processes in biology exhibit active transport or combinations of active and random motions.

Anomalous diffusion in cells is therefore a very active area of research involving biophysics, cell biology, statistical physics and mathematical modeling.

When confronted to a set of data retrieved from FCS or SPT experiments, the first question that one needs to answer is whether the measured subdiffusion is indeed a manifestation of an anomalous process. Often, a combination of several normal diffusion mechanisms or experimental artifacts gives rise to an apparent diffusion. If an anomalous subdiffusion—characterized by a power law scaling of the MSD with time—can be identified, establishing the physical model behind the diffusion process can shed light on the molecular mechanisms driving the motion of the molecule of interest.

Below, we will first focus on three classical models for anomalous subdiffusion and their common biological interpretation, namely the continuous-time random walk (CTRW) model, the fractional Brownian motion (fBm) model, and random walks on fractal and disordered systems (for a review, see e.g., [18]), then we will briefly describe different models covering super-diffusion processes that can be encountered in cells, such as run and tumble model, Lévy flights and super-diffusive fBm.

The continuous-time random walk model is a generalization of a random walk in which the diffusing particle waits for a random time between jumps. More generally, when the distribution ϕ(τ) of waiting times τ is long-tailed and cannot be averaged (with e.g., ϕ(τ) ∝ τ^−(1+α) and 0 < α < 1), the ensemble-averaged MSD shows anomalous scaling with a power law. A straightforward interpretation of a CTRW in the context of molecular biology is assimilating the waiting times to interactions of the molecule with an immobile substrate (at the relevant temporal and spatial scales). It is important to note that an interaction with a characteristic residence time does not fulfill the conditions of the model. Interestingly, however, the waiting-time distribution of non-specific interactions, abundant in the cell, might be non-averageable and thus CTRW a good microscopic model for one type of anomalous subdiffusion in the cell. It has been proposed to govern the cytosolic diffusion of nanosized objects in mammalian cells [19] and it has also been used to explain the lateral motion of potassium channels in the plasma membrane of cells [20].

The fractional Brownian motion model is a different generalization of Brownian diffusion in which the jumps between lag times follow a normal distribution but respect a correlation function given by 〈x(t)x(s)〉 = 1/2(t^2H + s^2H − (t − s)^2H) for t > s > 0. A fBm process is thus characterized by the Hurst index H, ranging between 0 and 1. The value of H determines the type of jump dependence in the fBm process, such that H > 1/2 indicates a positive correlation between the increments, Brownian motion is achieved for H = 1/2, and the increments are negatively correlated when H < 1/2. The MSD of a fBm is given by 〈x(t)²〉 ∝ t^2H, which, again, encompasses Brownian diffusion for H = 1/2 and yields subdiffusion for H < 1/2 or superdiffusion for H > 1/2 (see below). The fBm model describes faithfully the diffusion of particles in a viscoelastic fluid [21], and it has been often argued that molecular crowding in the cell gives rise to microviscosity and therefore to anomalous diffusion. It was proposed as the model of telomere diffusion in nucleus [22, 23].

Another possible model for anomalous diffusion in the cell is that of random walks in fractal media and disordered systems. Fractals are self-similar mathematical objects built upon the repetition of simple rules and characterized by a non-integer number: the fractal dimension. Although still under debate, some authors have proposed that chromatin organization follows, as a first order approximation, a fractal structure, and estimates of its fractal dimension have been proposed [24]. Random walks on fractals are subdiffusive due to the spatial correlation of displacements, and the power law scaling factor of the MSD with time is given by 2/d_w, where d_w is the dimension of the walk that is specific to the fractal. Although the pertinence of a fractal network model to describe molecular diffusion is still up to debate, it is justified to attempt to integrate the multiscale characteristics of the cell organization to such fractal model.

Amongst the existing superdiffusive motion in cells is the run-and-tumble process, which consists of alternating phases of fast active and slow passive motion leading to transient anomalous diffusion [25]. Initially observed for bacteria motion it has recently been used to describe molecular motions in cells, such as the motion of motors along cytoskeletal filaments. Motor proteins perform a number of steps (run) until they randomly unbind from the filaments and diffuse in the crowded cytoplasm (tumble) before rebinding [26]. The same could also stand for transcription factors in the nucleus searching for their initiation codon, alternating successively diffusion and 1D sliding along the DNA. Superdiffusive fBm which is characterized by an Hurst index H > 1/2 has been described as the intracellular motion of particles in the super-crowded cytoplasm of a amibae [27]. Finally, Lévy flights, has previously been proposed for intracellular actin-based transport mediated by molecular motors [28] and recently in the case of a membrane targeting C2 protein [29].

Note that by no means the above described models exhaustively cover the range of models that are known to exhibit anomalous diffusion (see e.g., [30–32]). However, the CTRW, fBM, and random walks in a fractal models have been extensively studied; more importantly, they have the potential to map parameters of the model to relevant biological and biophysical features. Therefore, we will limit our discussion to the aforementioned cases, and how they can be used to analyse and interpret experimental data obtained by FCS and SPT.

3. Which Methods to Correctly Analyse Diffusive Process?

3.1. Fluorescence Correlation Spectroscopy

The principle of FCS consists in measuring the temporal variations of molecular concentration at a given position within the volume of a biological sample. This is achieved by monitoring the temporal fluctuations of fluorescence signal emitted by the molecules present in the observation volume, which is excited with a focused laser. The underlying assumption of FCS is that the system is in a dynamic equilibrium and therefore the signal fluctuation can be correlated to the diffusion of molecules within the observation volume. While the amplitude of the fluctuations relates to the number of molecules in the observation volume, the decay of their autocorrelation in time depends on their mobility.

A typical FCS set-up consists of an illumination laser and a confocal microscope with a fast single-channel single-photon detector. The laser beam illuminates the detection volume with, usually, a Gaussian intensity profile and excites the fluorophores in the focal volume. The emitted fluorescent light is collected by the detector and it depends on the fluctuations of the local concentration of the labeled molecules.

Parameters, such as the average number of molecules (N) and their mean residence time (τ_d) in the confocal volume (surface) can be obtained either directly from this fluorescence intensity fluctuation measurement or indirectly by a temporal auto-correlation of this fluctuation. The second method is the most popular approach for FCS data analysis (see Figure 1). The main drawback of standard FCS is the lack in directly monitoring possible spatial and/or temporal heterogeneities that will give rise to deviation from pure Brownian motion. Several approaches have been proposed to overcome this issue including spot variation FCS (sv-FCS) [14, 33], line scanning FCS and STED-FCS [34, 35], as well as imaging approaches, such as (spatio)-temporal imaging correlation spectroscopy [(S)TICS], raster imaging correlation spectroscopy (RICS) [36] or more recently whole plane Imaging FCS (Im-FCS) [37]. With the development of commercial microscopes coupled to FCS capabilities, this technique and its derivatives are now becoming more and more popular in biology labs.

FIGURE 1

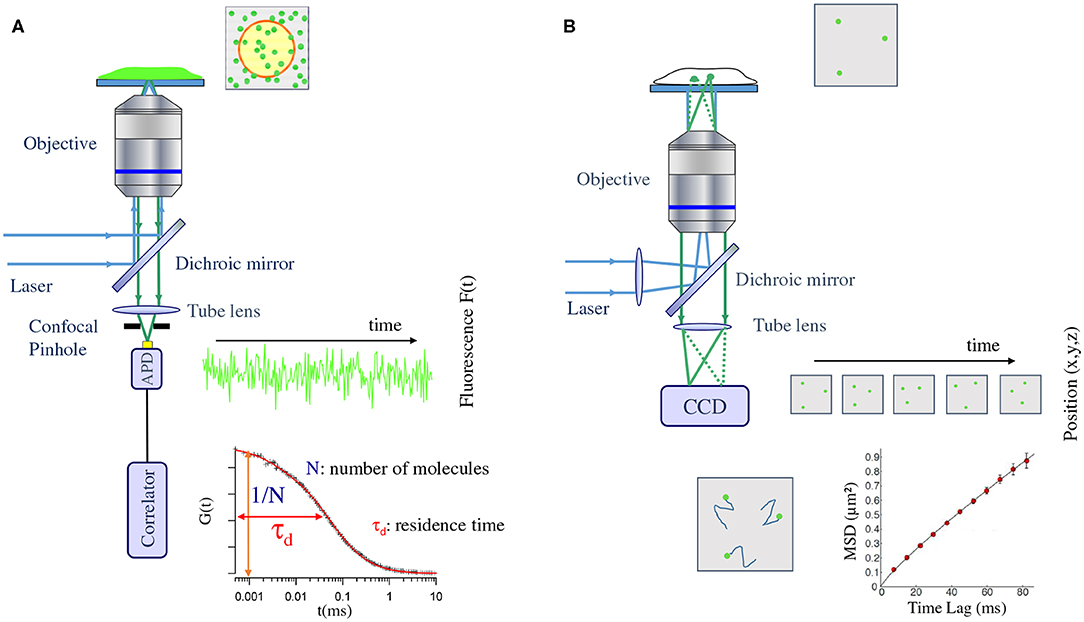
Figure 1. Schematic view of the typical setup used in fluorescence correlation spectroscopy (A) and single/multiple particle tracking (B) experiments. (A) A laser is focused on the fluorescently labeled sample by the objective of a microscope. The fluorescence is then collected by the objective and focused in a confocal way (using a pinhole) on a single photon counting detector (avalanche photodiode, APD). This detector records the fluctuation of fluorescence emission within the confocal volume of the sample. A direct link to an electronic correlator authorize on line generation of the autocorrelogram. (B) A laser is focused at the back focal plane of a microscope objective in order to obtain a full field illumination of the sample. The fluorescence emitted by each single particle present in the illumination field is then directly imaged on a sensitive camera (Charge Coupled Device, CCD). A movie is obtained and the post processing of this movie allow tracking of the individual emitter and latter on, generation of Mean Square Displacement (MSD) as a function of lag time curves.

A large range of dynamic processes leading to concentration fluctuations (i.e., diffusion, flow, chemical reactions and different combinations of these) has been investigated to generate corresponding analytical expressions of the temporal autocorrelation curve G(t) in the case of Gaussian (laser confocal) illumination/detection geometry (for a review, see [38] and references therein). For instance, in the case of a Brownian motion in 2D, $G(t)=1/\left\{\bar{N}(1+4Dt/w^2)\right\}$ where w is the size of the beam waist and $\bar{N}$ is the average number of molecules in the observation volume. The main approach to diffusive process identification and quantification in FCS consists in non linear least square fitting of experimental autocorrelation curves using above described analytical expressions and discriminate amongst these models which suits the best using various statistical test. Although it can deliver quantitative values of the parameters of the statistically chosen model of motion, it could be strongly biased, in particular for complex motions. A Bayesian approach to single spot FCS correlogram analysis has been proposed to discriminate between different models without bias [39, 40].

Another way to discriminate between different types of motion is to explore space and time with FCS using svFCS for example. svFCS offers the opportunity to generate so-called “diffusion-laws” by plotting changes in the residence time (τ_d) as a function of the surface (i.e., laser waist) explored w². This has enabled to directly identify deviations from pure Brownian motion in the plasma membrane of cells [41] or anomalous diffusion occurring, either during first order lipid phase transition [42] or in non-homogeneous fluids, gels and crowded solutions [43, 44]. It has been recently extended to the line-scanning STED-FCS [45] and to Im-FCS [46].

3.2. Single/Multiple Particle(s) Tracking

While the concentration of the subset of fluorescent molecules within a confocal volume in FCS experiments is close to the single-molecule regime, the measurement gauges the average motion of the ensemble of molecules diffusing in and out the observation spot. Conversely, SPT is by construction a single-molecule approach, monitoring thus the motion of individual molecules. One of the strengths of SPT is the potential to capture rare events or behaviors that would otherwise be buried within an average.

The principle of SPT experiments is simple, it consists in retrieving the changes in position of individual molecules within the sample of interest, i.e., the time series of two-dimensional or three-dimensional coordinates of the molecule location. This is achieved in two stages: firstly by estimating the centroid of the measured point spread function (PSF) of each detected individual emitter, and secondly by linking the trajectory of the same molecule between consecutive images. Importantly, the accuracy at which one is able to pinpoint the molecule position depends only on the signal-to-noise ratio of the measured PSF, obtaining sub-wavelength accuracy typically in the order of ~10 nm.

The basic SPT experimental setup consists of an excitation laser, a high NA objective, a set of dichroic and filters to separate the excitation and emission wavelengths, a tube lens, and a highly sensitive camera capable of detecting single fluorophores (see Figure 1). The laser is focused on the back focal plane of the objective to obtain a wide-field illumination configuration, which can be adjusted to total internal reflection (TIRF) or highly inclined illumination (HILO) [47] to increase the SNR when studying molecular dynamics in cellular membranes or at the interior of cells, respectively. The fluorescence light is collected by the same objective, and an image of the single emitters is formed on the camera plane via the tube lens [13, 48].

The amount of retrieved information about the biological system from an SPT assay depends on the nature of the experiment. The study of a slowly diffusing transmembrane protein will yield much longer traces than a fast diffusing transcription factor in the nucleus. In the latter case, the traces will be limited to the number of images in which the tracked particle remains within the depth of focus around the image plane, unlike the former case where photobleaching is the limiting factor.

The classical analysis of a set of trajectories consists in computing the dependence of the MSD (time-average or ensemble-average) over time from the distribution of jumps at increasing lag times defined by the camera acquisition, typically in the order of tens of ms. However, as we will see in the following section, different approaches and estimators have been proposed in order to analyze and interpret SPT data to its full extent. In comparison to FCS, the analysis of SPT has been intensively investigated, and one can distinguish several families of techniques (see also for reviews: [24, 49, 50]). In the field of stochastic processes, the inference of a diffusion coefficient from a sampled process is a common problem (see for instance [51, 52]). However, this theory cannot be applied when moving to experimental trajectories, and other approaches have been proposed.

3.2.1. MSD-Based Techniques

A first family of SPT analysis algorithms tries to perform robust MSD inference. The use of MSD to study diffusion was introduced by Einstein in 1906, and was revived in biology by [53]. MSD analysis can either be performed by inferring a diffusion coefficient from a single trajectory (a setting studied in [54]) or by pooling various trajectories [55], and many refinements and estimators based on the MSD have been proposed [56, 57].

When inferring kinetic parameters from a series of single trajectories, one faces the issue that for common trajectory lengths obtained in nuclear SPT (length of << 20 points per track) and common localization error, inaccuracy might reach 100% [54, 58]. As such, any approach that uses MSD on short trajectories should be evaluated with great care. For longer trajectories (such as diffusion in a membrane), approaches have been proposed that can segment trajectories based on the type of motion [59].

3.2.2. Hidden Markov Models (HMMs)

A second family of SPT analysis algorithms derives from Markov models and Hidden Markov Models. Most of them were derived to perform trajectory segment classification, the hidden variable inferred being the state of diffusion, or the current diffusion coefficient. For instance, Monnier et al. [60] introduces the HMM-Bayes technique to infer whether a trajectory segment is in one (or several) diffusive or active transport states. Moreover, Slator et al. [61] implemented the inference of localization noise to infer switches in diffusion coefficient within one trajectory. A similar approach was used to detect confinement [62].

These methods often rely on a fixed number of states, which comes from significant mathematical limitations. Some of these limitations were overcome using so-called variational Bayesian inference [63]. The prototypical algorithm performing variational Bayesian inference on a HMM is vbSPT [64]. This algorithm can estimate the number of diffusive states and progressively consolidate increasing information about these states as trajectories are analyzed. The algorithm was further refined to incorporate the estimate of localization error [65].

3.2.3. Inferring Maps of Diffusion Coefficients

A third family of SPT analysis algorithms not only infers the diffusion coefficient over the population of diffusing molecules, but also a spatial map of diffusivity [66, 67]. This approach has been pioneered in membranes, where a high density of tracks can easily be obtained. An extension of this approach using an overdamped Langevin equation of the single molecule motion has shed new lights on HIV-1 assembly within living cells [68]. These promising techniques have not been tested beyond membrane molecules, but the high diffusion coefficients of freely diffusing cellular proteins might render such a map difficult to establish. Moreover, unlike in membranes, proteins can reside at the same location with different diffusion coefficients, depending on whether they are interacting with a given structure or not.

3.2.4. Inferring Anomalous Diffusion

Many approaches have been proposed to infer anomalous diffusion in cells; some of them are reviewed in Guigas and Weiss [69]. A direct technique can be used by fitting the MSD with a power law to estimate the anomalous diffusion coefficient α. However, alternative techniques have been proposed, many of them focused on the inference of model-specific parameters, or on techniques to distinguish between types of anomalous diffusion.

Several methods have been proposed to infer diffusion parameters for several anomalous diffusion models. For the case of diffusion in disordered (fractal) media, Shkilev [70] proposes estimators that can be applied to SPT, FCS and FRAP. For the case of fractional Brownian motion, techniques to infer both the anomalous diffusion coefficient (α) and the generalized diffusion coefficient (D_α) have been proposed. The former approach [71] takes into account noise (localization error) and drift, and uses Bayesian inference. The latter [72] relies on squared displacements and uses least squares to estimate D_α.

Conversely, instead of trying to estimate the parameters of a known model, a key question is to distinguish between various anomalous diffusion models. A prototypical approach [73] used Bayesian inference to distinguish between Brownian, anomalous, confined and directed diffusion, and uses the propagators associated with each different diffusion model. However, Hellmann et al. [74] found using simulations that it is very hard to distinguish between fBm and diffusion on a fractal when localization noise is present, both in SPT and FCS. The authors used a combination of techniques for the inference, including MSD and p-variation techniques. In Burnecki et al. [23], the authors propose a series of tests to “unambiguously” identify fBm, by progressively proving that several other models are wrong. Other tests were proposed to distinguish fBm from a CTRW using a test based on p-variations [75]. The p-variations are the finite sum of the p-th powers of the increments of the trajectory. Finally, approaches inferring the mean first passage time of a particle were used to distinguish between CTRW and diffusion in fractals [76, 77].

Many other families of techniques to identify types of diffusion have been proposed. Some relied on maximum likelihood estimates [78], auto-correlation functions [79] or on more exotic estimators [80]. Another line of progress was made in the type of models being simulated. For instance, Amitai [81] introduced a model in which TFs can bind and rebind in a dense chromatin mesh. This model was successively fitted to explain anomalous diffusion of CTCF dynamics [82].

Finally, we note that many models were developed to infer trapping potential in membranes ([83, 84] for instance). We do not review them here since their application seems limited to membranes.

3.3. Strengths and Limitations of the Two Techniques

A strong limitation is that the experimental context, either in FCS or in SPT, may lead to spurious determination of anomalous diffusion. In other words, specific experimental parameters (low statistics, location noise, spatial confinement, etc.) and/or inappropriate analysis of the data can lead to incorrectly conclude that the diffusion exponent α≠1. Those artifacts concern both SPT [85] and FCS [43]. This is for instance the case if α is determined by a fit of the MSD or the autocorrelation with time and the statistical power is low (low sampling of the time points or short trajectories in SPT, low signal/noise at small or large times in FCS). To avoid such caveats, model selection must use more elaborate approaches to unambiguously demonstrate and characterize an underlying complex diffusion process.

So far, most of the inference tools available in the literature only partially account for the biases detailed above, and are usually limited in terms of the anomalous diffusion models they consider. For instance, in Hansen et al. [58], the authors showed that an algorithm not taking into account localization error was likely to improperly estimate diffusion coefficients. Similarly, the fact that the observed proteins diffuse in a confined volume leads to a sublinear MSD, a phenomenon that has been widely documented and that needs to be taken into account to properly distinguish between genuine anomalous diffusion and mere confinement effect. Similarly, tracking errors (misconnections between tracks) can also look like anomalous diffusion.

Some of these biases can be minimized at the acquisition step (for instance by using fast frame rates and low labeling density [58]), other need to be explicitly taken into account in the model. As of today, most inference algorithms available have not been benchmarked against realistic imaging conditions. Furthermore, a general realistic inference algorithm is still missing.

4. Conclusion: The Need for Controlled Benchmarks

Confronted with the variety of approaches described above, one would like to know the performance of each approach on typical representative datasets. For the comparison to be fair, this demands two main ingredients: (i) the existence of a reference dataset, or benchmark—possibly one reference dataset for each main classes of experimental methods and (ii) a fair, objective, transparent and open comparison process, with datasets, comparison procedures and performance results that are clearly stated and publicly available. Several fields in computer science have been using open community competitions to organize the process and produce open benchmarks for the community. Computer vision, applied machine learning or time series forecasting, among many others, have a long tradition of leveraging these competitions. The strategy has been widely successful because it parallelizes research along a vast community of high-skilled researchers. Internet platforms or services are even available to that purpose, including, among many others, Kaggle (www.kaggle.com) or DrivenData (www.drivendata.org). This increases further the size of the competing community, and the richness of the proposals. In fact, in addition to providing reference datasets and benchmarks, open competitive challenges can also foster the emergence of radically new approaches to the open problem at hand. Many of these competitive challenges are concerned with biomedical applications (for instance, http://dreamchallenges.org or https://grand-challenge.org), including several revolving around microscopy (see e.g., https://cremi.org). Recently, a series of consecutive community competitions for single-molecule imaging have involved dozens of labs and focused on tracking algorithms [86], and 2D and 3D localization for super-resolution [87]. Finally, another challenge has also been set up recently to infer the anomalous diffusion exponent from particle trajectories (http://www.andi-challenge.org/) [88].

In practice, an important feature of competitive challenges is to provide labeled data examples that the participants will be able to use as a training set. Indeed according to standard machine learning practice, this training dataset must be distinct from the test set, that includes the data used to estimate the performance of the algorithm. The organizers therefore usually publish two datasets (training dataset and test), of which only the training dataset comes with the label of each examples—only the organizers know the true label of the test dataset. After training, the results of the challenge is based on some quantification of the performance of the participant tools on the test set, although performance on the learning set can also be communicated as a way to judge overtraining/generalization capacities. In many cases however, it is not possible to provide the “true” label of experimental data, because such a gold standard does not exist. In this case, computer simulations can be used to generate synthetic data, as long as these simulations are realistic enough that the performance of the algorithms is not different than their performance on real experimental measurements. In the recent challenges on super-resolution, training and test data were a combination of computer-generated data and experimental data. Computer-generated data gives a clear access to ground truth whereas experimental data incorporate uncharacterized biases that can affect the inference process.

Here we propose to organize an international open collaborative challenge for the quantification and analysis of molecule movements in living cells via SPT and FCS. To date, the generation of realistic computer-simulated data has been hampered by the number of experimental biases to be taken into account, and by the diversity of the diffusion models, in particular for anomalous diffusion. For the challenge, we will generate both SPT and FCS data from the same set of simulated trajectories and in different modalities (2D in membranes and 3D in the nucleus) using a dedicated open source simulation software, simSPT (https://gitlab.com/tjian-darzacq-lab/simSPT), that is freely available to the participants to generate their own additional training sets if needed.

The challenge will be organized around various sub-challenges that represent the main classes of experimental situations (high-density short trajectories in membranes, less dense long trajectories in membranes, very short trajectories in the nucleus) and the main types of Brownian and anomalous diffusion (Brownian motion, fractional Brownian motion, continuous-time random walks and diffusion on fractals), and mixtures thereof. In the long run, we will also propose sub-challenges where the molecule dynamics depends on the location, to emulate localized spatial heterogeneity in the dynamics (local potentials, position-dependent diffusion coefficients). Moreover, we will progressively propose two challenge categories. In parameter inference challenges, the models used to generate the trajectories (Brownian motion, anomalous diffusion, …) will be given and the task will be to infer as precisely as possible the value of the parameters used for the generation. In model selection challenges, the goal will be to infer what model was used to generate the data given a known limited list of models.

Finally, we are aware that it may well be that no generic tool is able to solve all the sub-challenges evoked above. We are also aware that the difficulty of each sub-challenges can be quite variable. We therefore propose to start with the simple challenges and work in collaboration with the community involved in the analysis of molecular dynamics in living cells, to progressively climb the steps toward the more difficult sub-challenges. In this strategy, maintaining an open communication channel between the organizers and the participants is paramount. To this aim, we propose to start with a mailing list that will be used to support this communication. Every interested individual is therefore welcome to subscribe to the mailing list of the challenge by visiting https://listes.services.cnrs.fr/wws/info/diffusion.challenge. Once registered in the mailing list through this website, participants will be able to exchange with themselves and the organizers and they will receive the instructions to access the datasets of the challenge.

Author Contributions

MW, II, CF, and HB developed these perspectives and wrote the manuscript.

Funding

This work was partly funded by the CNRS-supported GDR ImaBio, http://imabio-cnrs.fr.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Axelrod D, Koppel DE, Schlessinger J, Elson E, Webb WW. Mobility measurement by analysis of fluorescence photobleaching recovery kinetics. Biophys J. (1976) 16:1055–69. doi: 10.1016/S0006-3495(76)85755-4

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Magde D, Webb W, Elson E. Thermodynamic fluctuations in a reacting system–measurement by fluorescence correlation spectroscopy. Phys Rev Lett. (1972) 29:705. doi: 10.1103/PhysRevLett.29.705

CrossRef Full Text | Google Scholar

3. Geerts H, De Brabander M, Nuydens R, Geuens S, Moeremans M, De Mey J, et al. Nanovid tracking: a new automatic method for the study of mobility in living cells based on colloidal gold and video microscopy. Biophys J. (1987) 52:775–82. doi: 10.1016/S0006-3495(87)83271-X

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Geerts H, de Brabander M, Nuydens R. Nanovid microscopy. Nature. (1991) 351:765–6. doi: 10.1038/351765a0

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Heim R, Prasher DC, Tsien RY. Wavelength mutations and posttranslational autoxidation of green fluorescent protein. Proc Natl Acad Sci USA. (1994) 91:12501–4. doi: 10.1073/pnas.91.26.12501

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Heim R, Tsien RY. Engineering green fluorescent protein for improved brightness, longer wavelengths and fluorescence resonance energy transfer. Curr Biol. (1996) 6:178–82. doi: 10.1016/S0960-9822(02)00450-5

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Matz MV, Fradkov AF, Labas YA, Savitsky AP, Zaraisky AG, Markelov ML, et al. Fluorescent proteins from nonbioluminescent Anthozoa species. Nat Biotechnol. (1999) 17:969–73. doi: 10.1038/13657

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Hell SW, Wichmann J. Breaking the diffraction resolution limit by stimulated emission: stimulated-emission-depletion fluorescence microscopy. Opt Lett. (1994) 19:780–2. doi: 10.1364/OL.19.000780

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Betzig E, Patterson GH, Sougrat R, Lindwasser OW, Olenych S, Bonifacino JS, et al. Imaging intracellular fluorescent proteins at nanometer resolution. Science. (2006) 313:1642–5. doi: 10.1126/science.1127344

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Hess ST, Girirajan TP, Mason MD. Ultra-high resolution imaging by fluorescence photoactivation localization microscopy. Biophys J. (2006) 91:02222. doi: 10.1529/biophysj.106.091116

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Klar TA, Jakobs S, Dyba M, Egner A, Hell SW. Fluorescence microscopy with diffraction resolution barrier broken by stimulated emission. Proc Natl Acad Sci USA. (2000) 97:8206–10. doi: 10.1073/pnas.97.15.8206

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Rust MJ, Bates M, Zhuang X. Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (STORM). Nat Methods. (2006) 3:793–5. doi: 10.1038/nmeth929

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Manley S, Gillette JM, Patterson GH, Shroff H, Hess HF, Betzig E, et al. High-density mapping of single-molecule trajectories with photoactivated localization microscopy. Nat Methods. (2008) 5:155–7. doi: 10.1038/nmeth.1176

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Eggeling C, Ringemann C, Medda R, Schwarzmann G, Sandhoff K, Polyakova S, et al. Direct observation of the nanoscale dynamics of membrane lipids in a living cell. Nature. (2009) 457:1159–62. doi: 10.1038/nature07596

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Sarkar P, Chattopadhyay A. Exploring membrane organization at varying spatiotemporal resolutions utilizing fluorescence-based approaches: implications in membrane biology. Phys Chem Chem Phys. (2019) 21:11554–63. doi: 10.1039/C9CP02087J

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Liu H, Ye Z, Wang X, Wei L, Xiao L. Molecular and living cell dynamic assays with optical microscopy imaging techniques. Analyst. (2019) 144:859–71. doi: 10.1039/C8AN01420E

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Priest DG, Solano A, Lou J, Hinde E. Fluorescence fluctuation spectroscopy: an invaluable microscopy tool for uncovering the biophysical rules for navigating the nuclear landscape. Biochem Soc Trans. (2019) 47:1117–29. doi: 10.1042/BST20180604

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Hoefling F, Franosch T. Anomalous transport in the crowded world of biological cells. Rep Prog Phys. (2013) 76:046602. doi: 10.1088/0034-4885/76/4/046602

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Etoc F, Balloul E, Vicario C, Normanno D, Lie D, Sittner A, et al. Non-specific interactions govern cytosolic diffusion of nanosized objects in mammalian cells. Nat Mater. (2018) 17:740–6. doi: 10.1038/s41563-018-0120-7

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Weigel AV, Simon B, Tamkun MM, Krapf D. Ergodic and nonergodic processes coexist in the plasma membrane as observed by single-molecule tracking. Proc Natl Acad Sci USA. (2011) 108:6438–43. doi: 10.1073/pnas.1016325108

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Ernst D, Hellmann M, Köhler J, Weiss M. Fractional brownian motion in crowded fluids. Soft Matter. (2012) 8:4886–9. doi: 10.1039/c2sm25220a

CrossRef Full Text | Google Scholar

22. Kepten E, Bronshtein I, Garini Y. Ergodicity convergence test suggests telomere motion obeys fractional dynamics. Phys Rev E. (2011) 83:041919. doi: 10.1103/PhysRevE.83.041919

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Burnecki K, Kepten E, Janczura J, Bronshtein I, Garini Y, Weron A. Universal algorithm for identification of fractional brownian motion. A case of telomere subdiffusion. Biophys J. (2012) 103:1839–47. doi: 10.1016/j.bpj.2012.09.040

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Rcamier V, Izeddin I, Bosanac L, Dahan M, Proux F, Darzacq X. Single cell correlation fractal dimension of chromatin: a framework to interpret 3D single molecule super-resolution. Nucleus. (2014) 5:75–84. doi: 10.4161/nucl.28227

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Shaebani MR, Rieger H. Transient anomalous diffusion in run-and-tumble dynamics. Front Phys. (2019) 7:120. doi: 10.3389/fphy.2019.00120

CrossRef Full Text | Google Scholar

26. Hafner AE, Santen L, Rieger H, Shaebani MR. Run-and-pause dynamics of cytoskeletal motor proteins. Sci Rep. (2016) 6:37162. doi: 10.1038/srep37162

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Reverey JF, Jeon JH, Bao H, Leippe M, Metzler R, Selhuber-Unkel C. Superdiffusion dominates intracellular particle motion in the supercrowded cytoplasm of pathogenic Acanthamoeba castellanii. Sci Rep. (2015) 5:11690. doi: 10.1038/srep11690

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Bruno L, Levi V, Brunstein M, Despósito MA. Transition to superdiffusive behavior in intracellular actin-based transport mediated by molecular motors. Phys Rev E. (2009) 80:011912. doi: 10.1103/PhysRevE.80.011912

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Campagnola G, Nepal K, Schroder BW, Peersen OB, Krapf D. Superdiffusive motion of membrane-targeting C2 domains. Sci Rep. (2015) 5:17721. doi: 10.1038/srep17721

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Metzler R, Jeon JH, Cherstvy AG, Barkai E. Anomalous diffusion models and their properties: non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys Chem Chem Phys. (2014) 16:24128–64. doi: 10.1039/C4CP03465A

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Pavlos GP, Karakatsanis LP, Xenakis MN, Pavlos EG, Iliopoulos AC, Sarafopoulos DV. Universality of non-extensive Tsallis statistics and time series analysis: theory and applications. Phys A Stat Mech Appl. (2014) 395:58–95. doi: 10.1016/j.physa.2013.08.026

CrossRef Full Text | Google Scholar

32. Lenzi EK, Ribeiro HV, Tateishi AA, Zola RS, Evangelista LR. Anomalous diffusion and transport in heterogeneous systems separated by a membrane. Proc R Soc A Math Phys Eng Sci. (2016) 472:20160502. doi: 10.1098/rspa.2016.0502

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Wawrezinieck L, Rigneault H, Marguet D, Lenne PF. Fluorescence correlation spectroscopy diffusion laws to probe the submicron cell membrane organization. Biophys J. (2005) 89:4029–42. doi: 10.1529/biophysj.105.067959

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Petrek Z, Schwille P. Precise measurement of diffusion coefficients using scanning fluorescence correlation spectroscopy. Biophys J. (2008) 94:1437–48. doi: 10.1529/biophysj.107.108811

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Honigmann A, Mueller V, Ta H, Schoenle A, Sezgin E, Hell SW, et al. Scanning STED-FCS reveals spatiotemporal heterogeneity of lipid interaction in the plasma membrane of living cells. Nat Commun. (2014) 5:5412. doi: 10.1038/ncomms6412

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Digman MA, Brown CM, Sengupta P, Wiseman PW, Horwitz AR, Gratton E. Measuring fast dynamics in solutions and cells with a laser scanning microscope. Biophys J. (2005) 89:1317–27. doi: 10.1529/biophysj.105.062836

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Kannan B, Har JY, Liu P, Maruyama I, Ding JL, Wohland T. Electron multiplying charge-coupled device camera based fluorescence correlation spectroscopy. Anal Chem. (2006) 78:3444–51. doi: 10.1021/ac0600959

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Elson E. Fluorescence correlation spectroscopy: past, present, future. Biophys J. (2011) 101:2855–70. doi: 10.1016/j.bpj.2011.11.012

PubMed Abstract | CrossRef Full Text | Google Scholar

39. He J, Guo SM, Bathe M. Bayesian approach to the analysis of fluorescence correlation spectroscopy data I: theory. Anal Chem. (2012) 84:3871–9. doi: 10.1021/ac2034369

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Guo SM, He J, Monnier N, Sun G, Wohland T, Bathe M. Bayesian approach to the analysis of fluorescence correlation spectroscopy data II: application to simulated and in vitro data. Anal Chem. (2012) 84:3880–8. doi: 10.1021/ac2034375

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Lenne PF, Wawrezinieck L, Conchonaud F, Wurtz O, Boned A, Guo XJ, et al. Dynamic molecular confinement in the plasma membrane by microdomains and the cytoskeleton meshwork. EMBO J. (2006) 25:3245–56. doi: 10.1038/sj.emboj.7601214

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Favard C, Wenger J, Lenne PF, Rigneault H. FCS diffusion laws in two-phase lipid membranes: determination of domain mean size by experiments and Monte Carlo simulations. Biophys J. (2011) 100:1242–51. doi: 10.1016/j.bpj.2010.12.3738

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Banks DS, Tressler C, Peters RD, Hfling F, Fradin C. Characterizing anomalous diffusion in crowded polymer solutions and gels over five decades in time with variable-lengthscale fluorescence correlation spectroscopy. Soft Matter. (2016) 12:4190–203. doi: 10.1039/C5SM01213A

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Masuda A, Ushida K, Okamoto T. Direct observation of spatiotemporal dependence of anomalous diffusion in inhomogeneous fluid by sampling-volume-controlled fluorescence correlation spectroscopy. Phys Rev E. (2005) 72:060101. doi: 10.1103/PhysRevE.72.060101

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Schneider F, Waithe D, Galiani S, Bernardino de la Serna J, Sezgin E, Eggeling C. Nanoscale spatiotemporal diffusion modes measured by simultaneous confocal and stimulated emission depletion nanoscopy imaging. Nano Lett. (2018) 18:4233–40. doi: 10.1021/acs.nanolett.8b01190

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Veerapathiran S, Wohland T. The imaging FCS diffusion law in the presence of multiple diffusive modes. Methods. (2018) 140–141:140–50. doi: 10.1016/j.ymeth.2017.11.016

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Tokunaga M, Imamoto N, Sakata-Sogawa K. Highly inclined thin illumination enables clear single-molecule imaging in cells. Nat Methods. (2008) 5:159–61. doi: 10.1038/nmeth1171

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Izeddin I, Récamier V, Bosanac L, Cissé II, Boudarene L, Dugast-Darzacq C, et al. Single-molecule tracking in live cells reveals distinct target-search strategies of transcription factors in the nucleus. eLife. (2014) 3:e02230. doi: 10.7554/eLife.02230

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Metzler R, Tejedor V, Jeon JH, He Y, Deng WH, Burov S, et al. Analysis of single particle trajectories: from normal to anomalous diffusion. Acta Phys Pol B. (2009) 40:1315. Available online at: https://www.actaphys.uj.edu.pl/R/40/5/1315/pdf

Google Scholar

50. Ernst D, Köhler J, Weiss M. Probing the type of anomalous diffusion with single-particle tracking. Phys Chem Chem Phys. (2014) 16:7686–91. doi: 10.1039/C4CP00292J

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Florens-Zmirou D. On estimating the diffusion coefficient from discrete observations. J Appl Probab. (1993) 30:790. doi: 10.1017/S0021900200044570

CrossRef Full Text | Google Scholar

52. Hoffmann M. On estimating the diffusion coefficient: parametric versus nonparametric. Ann l'IHP Probab Stat. (2001) 37:339–72. doi: 10.1016/S0246-0203(00)01070-0

CrossRef Full Text | Google Scholar

53. Qian H, Sheetz MP, Elson EL. Single particle tracking. Analysis of diffusion and flow in two-dimensional systems. Biophys J. (1991) 60:910–21. doi: 10.1016/S0006-3495(91)82125-7

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Michalet X, Berglund AJ. Optimal diffusion coefficient estimation in single-particle tracking. Phys Rev E. (2012) 85:061916. doi: 10.1103/PhysRevE.85.061916

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Liu Z, Legant WR, Chen BC, Li L, Grimm JB, Lavis LD, et al. 3D imaging of Sox2 enhancer clusters in embryonic stem cells. eLife. (2014) 3:e04236. doi: 10.7554/eLife.04236

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Michalet X. Mean square displacement analysis of single-particle trajectories with localization error: Brownian motion in an isotropic medium. Phys Rev E. (2010) 82:041914. doi: 10.1103/PhysRevE.82.041914

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Boyer D, Dean DS, Mejía-Monasterio C, Oshanin G. Optimal estimates of the diffusion coefficient of a single brownian trajectory. Phys Rev E. (2012) 85:031136. doi: 10.1103/PhysRevE.85.031136

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Hansen AS, Woringer M, Grimm JB, Lavis LD, Tjian R, Darzacq X. Robust model-based analysis of single-particle tracking experiments with spot-on. eLife. (2018) 7:e33125. doi: 10.7554/eLife.33125

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Monnier N, Guo SM, Mori M, He J, Lénárt P, Bathe M. Bayesian approach to MSD-based analysis of particle motion in live cells. Biophys J. (2012) 103:616–26. doi: 10.1016/j.bpj.2012.06.029

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Monnier N, Barry Z, Park HY, Su KC, Katz Z, English BP, et al. Inferring transient particle transport dynamics in live cells. Nat Methods. (2015) 12:838–40. doi: 10.1038/nmeth.3483

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Slator PJ, Cairo CW, Burroughs NJ. Detection of diffusion heterogeneity in single particle tracking trajectories using a hidden Markov model with measurement noise propagation. PLoS ONE. (2015) 10:e0140759. doi: 10.1371/journal.pone.0140759

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Slator PJ, Burroughs N. A hidden Markov model for detecting confinement in single particle tracking trajectories. bioRXiv. (2018) 275107. doi: 10.1101/275107

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Blei DM, Kucukelbir A, McAuliffe JD. Variational inference: a review for statisticians. arXiv. (2016) 112:859–77. doi: 10.1080/01621459.2017.1285773

CrossRef Full Text | Google Scholar

64. Persson F, Lindn M, Unoson C, Elf J. Extracting intracellular diffusive states and transition rates from single-molecule tracking data. Nat Methods. (2013) 10:265–9. doi: 10.1038/nmeth.2367

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Lindén M, Elf J. Variational algorithms for analyzing noisy multistate diffusion trajectories. Biophys J. (2018) 115:276–82. doi: 10.1016/j.bpj.2018.05.027

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Masson JB, Casanova D, Türkcan S, Voisinne G, Popoff MR, Vergassola M, et al. Inferring maps of forces inside cell membrane microdomains. Phys Rev Lett. (2009) 102:048103. doi: 10.1103/PhysRevLett.102.048103

PubMed Abstract | CrossRef Full Text | Google Scholar

67. El Beheiry M, Dahan M, Masson JB. InferenceMAP: mapping of single-molecule dynamics with Bayesian inference. Nat Methods. (2015) 12:594–5. doi: 10.1038/nmeth.3441

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Floderer C, Masson JB, Boilley E, Georgeault S, Merida P, El Beheiry M, et al. Single molecule localisation microscopy reveals how HIV-1 Gag proteins sense membrane virus assembly sites in living host CD4 T cells. Sci Rep. (2018) 8:16283. doi: 10.1038/s41598-018-34536-y

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Guigas G, Weiss M. Sampling the cell with anomalous diffusion—the discovery of slowness. Biophys J. (2008) 94:90–4. doi: 10.1529/biophysj.107.117044

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Shkilev VP. A kinetic model for fluorescence microscopy experiments in disordered media that contains binding sites and obstacles. Phys Rev E. (2018) 98:032140. doi: 10.1103/PhysRevE.98.032140

CrossRef Full Text | Google Scholar

71. Krog J, Jacobsen LH, Lund FW, Wstner D, Lomholt MA. Bayesian model selection with fractional Brownian motion. J Stat Mech Theory Exp. (2018) 2018:093501. doi: 10.1088/1742-5468/aadb0e

CrossRef Full Text | Google Scholar

72. Boyer D, Dean DS, Mejia-Monasterio C, Oshanin G. On ergodic least-squares estimators of the generalized diffusion coefficient for fractional Brownian motion. Biophys J. (2013) 87:030103. doi: 10.1103/PhysRevE.87.030103

CrossRef Full Text | Google Scholar

73. Robson A, Burrage K, Leake MC. Inferring diffusion in single live cells at the single-molecule level. Philos Trans R Soc B Biol Sci. (2012) 368:20120029. doi: 10.1098/rstb.2012.0029

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Hellmann M, Klafter J, Heermann DW, Weiss M. Challenges in determining anomalous diffusion in crowded fluids. J Phys Condens Matter. (2011) 23:234113. doi: 10.1088/0953-8984/23/23/234113

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Magdziarz M, Weron A, Burnecki K, Klafter J. Fractional Brownian motion versus the continuous-time random walk: a simple test for subdiffusive dynamics. Phys Rev Lett. (2009) 103:180602. doi: 10.1103/PhysRevLett.103.180602

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Condamin S, Bénichou O, Tejedor V, Voituriez R, Klafter J. First-passage times in complex scale-invariant media. Nature. (2007) 450:77–80. doi: 10.1038/nature06201

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Condamin S, Tejedor V, Voituriez R, Benichou O, Klafter J. Probing microscopic origins of confined subdiffusion by first-passage observables. Proc Natl Acad Sci USA. (2008) 105:5675–80. doi: 10.1073/pnas.0712158105

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Thapa S, Lomholt MA, Krog J, Cherstvy AG, Metzler R. Bayesian analysis of single-particle tracking data using the nested-sampling algorithm: maximum-likelihood model selection applied to stochastic-diffusivity data. Phys Chem Chem Phys. (2018) 20:29018–37. doi: 10.1039/C8CP04043E

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Weber SC, Thompson MA, Moerner WE, Spakowitz AJ, Theriot JA. Analytical tools to distinguish the effects of localization error, confinement, and medium elasticity on the velocity autocorrelation function. Biophys J. (2012) 102:2443–50. doi: 10.1016/j.bpj.2012.03.062

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Vestergaard CL, Blainey PC, Flyvbjerg H. Optimal estimation of diffusion coefficients from single-particle trajectories. Phys Rev E. (2014) 89:022726. doi: 10.1103/PhysRevE.89.022726

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Amitai A. Chromatin configuration affects the dynamics and distribution of a transiently interacting protein. Biophys J. (2019) 114:766–71. doi: 10.1016/j.bpj.2017.12.037

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Hansen AS, Amitai A, Cattoglio C, Tjian R, Darzacq X. Guided nuclear exploration increases CTCF target search efficiency. bioRXiv. (2018) 495457. doi: 10.1101/495457

PubMed Abstract | CrossRef Full Text

83. Türkcan S, Alexandrou A, Masson JB. A Bayesian inference scheme to extract diffusivity and potential fields from confined single-molecule trajectories. Biophys J. (2012) 102:2288–98. doi: 10.1016/j.bpj.2012.01.063

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Masson JB, Dionne P, Salvatico C, Renner M, Specht CG, Triller A, et al. Mapping the energy and diffusion landscapes of membrane proteins at the cell surface using high-density single-molecule imaging and Bayesian inference: application to the multiscale dynamics of glycine receptors in the neuronal membrane. Biophys J. (2014) 106:74–83. doi: 10.1016/j.bpj.2013.10.027

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Martin DS, Forstner MB, Ks JA. Apparent subdiffusion inherent to single particle tracking. Biophys J. (2002) 83:2109–17. doi: 10.1016/S0006-3495(02)73971-4

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Chenouard N, Smal I, de Chaumont F, Maka M, Sbalzarini IF, Gong Y, et al. Objective comparison of particle tracking methods. Nat Methods. (2014) 11:281–9. doi: 10.1038/nmeth.2808

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Sage D, Pham Ta, Babcock H, Lukes T, Pengo T, Chao J, et al. Super-resolution fight club: assessment of 2D & 3D single-molecule localization microscopy software. Nat Methods. (2019) 16:387–95. doi: 10.1101/362517

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Muñoz-Gil G, Volpe G, Garcia-March MA, Metzler R, Lewenstein M, Manzo C. AnDi: the anomalous diffusion challenge. arXiv. (2020) ArXiv:2003.12036.

Google Scholar