Super-Resolution Structured Illumination Microscopy Reconstruction Using a Least-Squares Solver

Super-resolution microscopy enables images to be obtained at a resolution higher than that imposed by the diffraction limit of light. Structured illumination microscopy (SIM) is among the fastest super-resolution microscopy techniques currently in use, and it has gained popularity in the field of cytobiology research owing to its low photo-toxicity and widefield modality. In typical SIM, a fluorescent sample is excited by sinusoidal patterns by employing a linear strategy to reconstruct super-resolution images. However, this strategy fails in cases where non-sinusoidal illumination patterns are used. In this study, we propose the least-squares SIM (LSQ-SIM) approach, which is an efficient super-resolution reconstruction algorithm in the framework of least-squares regression that can process raw SIM data under both sinusoidal and non-sinusoidal illuminations. The results obtained in this study indicate the potential of LSQ-SIM for use in structured illumination microscopy and its various application fields.

Introduction

The resolution of a fluorescence microscope is limited by the optical diffraction effect, which can be described by Abbe's Equation [1]. Several super-resolution fluorescence microscopy techniques have been previously developed, such as stochastic optical reconstruction microscopy (STORM) [2], stimulated emission depletion fluorescence microscopy (STED) [3], and structured illumination microscopy (SIM) [4]. SIM features low photo-toxicity and a relatively high imaging speed, and has been widely applied in the field of biological sciences to study cellular and subcellular dynamics and mechanisms [5, 6]. SIM employs sinusoidal illumination patterns with different directions and initial phases to downshift the high-frequency component of the fluorescence signals of a specimen into the scope of the optical transfer function (OTF), which is otherwise filtered in conventional microscopic optics, leading to resolution loss. The high- and low-frequency components are then unmixed using the solution of a set of linear equations and shifted to their correct positions in the reciprocal domain. With this expanded spectrum, the resulting resolution is almost twice that of widefield fluorescence microscopy. The resolution enhancement provided by SIM can be further improved if the nonlinear characteristics of fluorescent labels are utilized, such as saturation [7] and photo-switching [8, 9], depending on the strength of the high-frequency signal and level of noise corruption in the system.

In super-resolution reconstruction of SIM data, the parameters of sinusoidal illumination patterns (e.g., the frequency vectors and initial phases) must be precisely known. However, this knowledge is difficult and even impossible to obtain if the illumination patterns are distorted due to aberrations caused by the observed specimen, especially in the case of thick biological tissue [10]. Mudry et al. [11] developed a structured illumination microscopy approach using unknown speckle illumination (referred to as blind SIM), in which both the object and speckle patterns are estimated by conjugate gradient descent. With the grain size of speckle being close to the diffraction limit, the resolution of blind SIM is comparable to that of classical structured illumination microscopy [11]. In addition to speckle, multi-foci has also been applied as structured illumination to realize a doubling in resolution and optical sectioning with an extra digital pinhole [12]. Unfortunately, the reconstruction algorithm of original structured illumination microscopy is unable to process the raw data from these novel SIM techniques. Various reconstruction methods have been invented to deal with SIM data under non-sinusoidal illumination, though these approaches are both iterative and time consuming [13–15].

In this paper, we propose a highly efficient reconstruction method for use with SIM images under general structured illumination (sinusoidal and non-sinusoidal). As reported in the previous literature, the reconstruction of an object is formulated in terms of an optimization problem [11]. This optimization problem lacks an analytical solution owing to the convolution operator in the SIM imaging model, which is also ill-conditioned. We introduce a pre-deconvolution step for simplification, so a direct solution to this problem is available that can be instantly calculated through least-squares fitting. Furthermore, our method is conducted mainly in the spatial domain, which makes it faster because it requires fewer computationally intensive Fourier transformation operations.

In section Method, we present the SIM imaging forward model that we exploit in the least-squares algorithmic framework for super-resolution reconstruction of objects. The principles of our method are demonstrated and reconstruction results obtained using simulated data are shown. Section Results and Discussion describes the validation of our approach using open-access SIM data under sinusoidal and non-sinusoidal illumination.

Method

In two-dimensional (2D) SIM, the relation of an object f illuminated by an excitation pattern p and a captured image g can be described by:

$\begin{array}{ll}\text{g}=(\text{f}\times \text{p})\otimes \text{p}\text{s}\text{f},& (1)\end{array}$

where ⊗ denotes the 2D convolution operator, and psf the point spread function. For convenience, the magnification is assumed to equal 1 here, without loss of generality. In the frequency domain, Equation (1) becomes:

$\begin{array}{ll}\text{G}=(\text{F}\otimes \text{P})\times \text{O}\text{T}\text{F},& (2)\end{array}$

where OTF denotes the optical transfer function, and G, F, and P are the 2D Fourier transformations of g, f, and p, respectively. As the OTF is band-limited, spectrum information at frequencies higher than the cutoff frequency is filtered and unrecoverable after imaging if the illumination pattern is uniform, as in the case of widefield microscopy, which leads to resolution degradation. Through pulse function decomposition, Equation (2) becomes:

$\begin{array}{ll}\text{G}({\text{k}}_{\text{x}},{\text{k}}_{\text{y}})={\displaystyle \int \int }\text{P}(\text{u},\text{v})\text{F}({\text{k}}_{\text{x}}-\text{u},{\text{k}}_{\text{y}}-\text{v})\text{OTF}({\text{k}}_{\text{x}},{\text{k}}_{\text{y}})\text{dudv}& (3)\end{array}$

where k_x and k_y denote frequency coordinates corresponding to spatial coordinates x and y, respectively, and u and v are integration variables. This implies that a high-frequency component is coded into the frequency domain within the range of the OTF weighted by the spectrum of the illumination pattern. As a specific case of SIM, the integration in Equation (3) is replaced with a discrete summation of the spectrum of the object filtered by the OTF and its shifted copies. It can be seen that the essence of super-resolution SIM consists of accessible high-frequency information resulting from structured illumination. SIM illumination patterns are usually generated through the same objective in the detection path, which restricts their spatial frequency below its cutoff frequency, so the resolution improvement is at most 2-fold. The resolution enhancement of SIM can be further extended if certain nonlinear processes of fluorescence dyes are applied to effectively excite higher-order harmonics [7–9].

The task of reconstructing an object from SIM data can be viewed as an optimization problem, for which the cost function to be minimized is

$\begin{array}{ll}{L}_1(f)={\displaystyle \sum _{i=1}^N{\Vert g_i-(f\times p_i)\otimes psf\Vert }_2^2},& (4)\end{array}$

where N is the total number of illumination patterns. There is no direct solution to this optimization problem as a result of the convolution operator. Considering the band-limiting nature of the point spread function, minimization of L₁(f) is equivalent to that of

$\begin{array}{ll}{L}_2(f)={\displaystyle \sum _{i=1}^N{\Vert deconwnr(g_i)-S_{cutoff}(f\times p_i)\Vert }_2^2},& (5)\end{array}$

where deconwnr denotes the Wiener deconvolution and S_cut−off is a frequency-bound constraint function that sets spectrum values outside the cutoff bound of OTF to zero. The analytical solution for the minimization of L₂(f) is then described by Tian et al. [16]

$\begin{array}{ll}{f}_{lsq}=\frac{{\displaystyle \sum _{i=1}^{N}deconwnr(g_i)\times p_i}}{{\displaystyle \sum _{i=1}^N{p}_i^2}},& (6)\end{array}$

which is also a least-squares estimation. To avoid division by zero, a small positive constant acting as the Tikhonov regularization is added to the denominator in Equation (6) when applied to the SIM data. We find that Wiener deconvolution causes obvious artifacts and noise amplification, especially when the sample is bead-like, which leads to significant corruption of the reconstruction results. This issue can be solved by simply replacing the Wiener deconvolution through using Richardson-Lucy deconvolution in this pre-deconvolution step. We also implement high-frequency elevation for each illumination pattern before applying Equation (6), and deconvolve f_lsq after high-frequency emphasis with an point spread function that corresponds to a doubled numerical aperture, to strengthen the contrast of the final reconstruction result. With high-frequency elevation for illumination patterns, the weight of low frequency components in final reconstruction can be reduced so out-of-focus background is suppressed, which benefits thick biological tissue imaging. A block diagram describing our approach is shown in Figure 1.

FIGURE 1

Figure 1. Block diagram showing the proposed LSQ-SIM algorithm.

We use a simulated Siemens Star target [o(r,θ)=1+cos32θ in polar coordinates] to test our method. The numerical aperture for simulation is set to 0.7 and five types of two-dimensional illumination patterns are used: sinusoidal fringes, quadratic lattice, hexagonal lattice, multi-spots, and pseudo-random speckles. In 2D SIM, sinusoidal fringes are usually generated through the interference of two coherent beams or projection of the light field on a digital micromirror device (DMD) [17, 18]. The quadratic lattice, which contains two more peaks in the reciprocal domain compared to the sinusoidal fringe, is produced with two pairs of coherent orthogonal beams. The hexagonal lattice is generated in a similar manner, with three pairs of light beams with a high degree of coherence [19]. Due to increased sparsity, the quadratic and hexagonal lattices bear higher modulation depth than sinusoidal fringes in a thick sample, which can yield better reconstruction results.

Multi-spots and pseudo-random speckle have also been used to achieve super-resolution SIM, both of which can be created with the economical DMD [20, 21]. Due to the flexibility of DMD, which is digitally controlled, the properties of illumination patterns, such as quantity and sparsity, can be appropriately designed. In our simulation, the multi-spots pattern scans the target uniformly and the speckle patterns are generated using a pseudo-random algorithm, as such, the sum of SIM images forms a complete widefield frame of the target, which promotes unbiased reconstruction [22]. Note that the speckle illumination applied in blind SIM [11] is produced by placing a mechanically driven optical diffuser in the excitation path, which leads to a high required number of captured images to obtain an unbiased reconstruction.

Figure 2 shows the simulation results for these different types of structured illumination. The outer blue dashed circle indicates the resolution that is limited by optical diffraction, and the inner one indicates resolution doubling. The area inside the outer circle is still blurred after pure deconvolution. In the case of the reconstructions obtained using our method (Figures 2D–H), the details between the two circles of the target are clearly distinguishable, with some slight ambiguity close to the inner circle, which suggests that a nearly 2-fold resolution enhancement is achieved. It is noteworthy that the resolution enhancement of image reconstruction in the case of pseudo-random speckle illumination is slightly weaker than those of the other examples, which may result from the irregularity of the speckle.

FIGURE 2

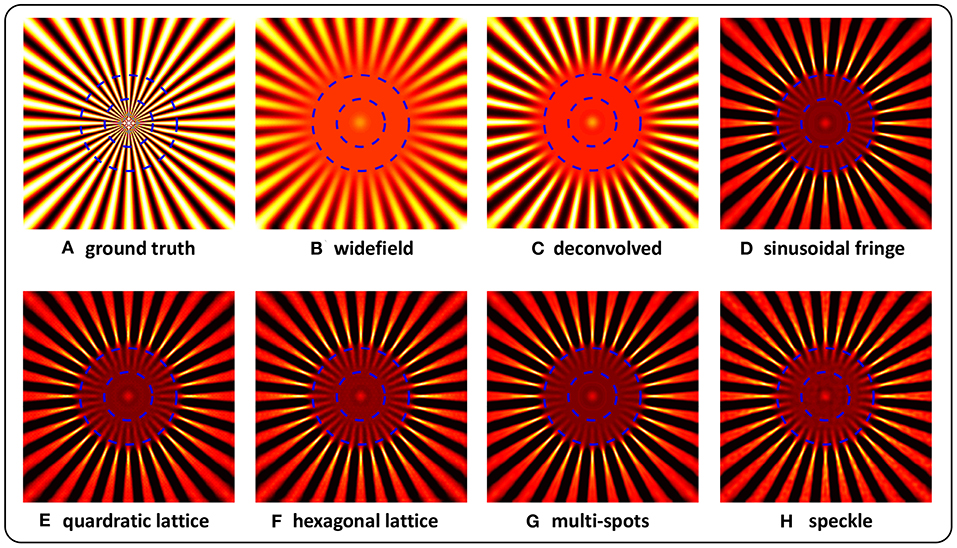
Figure 2. Reconstructions of simulated Siemens Star targets imaged under structured illuminations of sinusoidal fringe (D), quadratic lattice (E), hexagonal lattice (F), multi-spots (G), and speckle (H). The ground truth (A), together with widefield (B), and deconvolved (C) images is also shown. The outer blue dashed circle indicates the resolution limited by optical diffraction, and the inner circle denotes resolution doubling.

To assess the performance of our method, contrasts at different circular spatial periods are calculated, as shown in Figure 3. For the widefield and deconvolved images, the contrast falls close to zero at a spatial period of λ/2NA, in accordance with the theoretical diffraction limit. In the case of reconstructions obtained using the proposed LSQ-SIM method, the contrast remains comparatively high, at spatial periods ranging between 0.5 and 1 times λ/2NA, which verifies the resolution improvement. As shown in Figure 3, the reconstructions of lattice-illuminated images present much higher contrasts within the middle of the super-resolution region compared with the other reconstructions, which reveals the superiority of lattice-structured illumination.

FIGURE 3

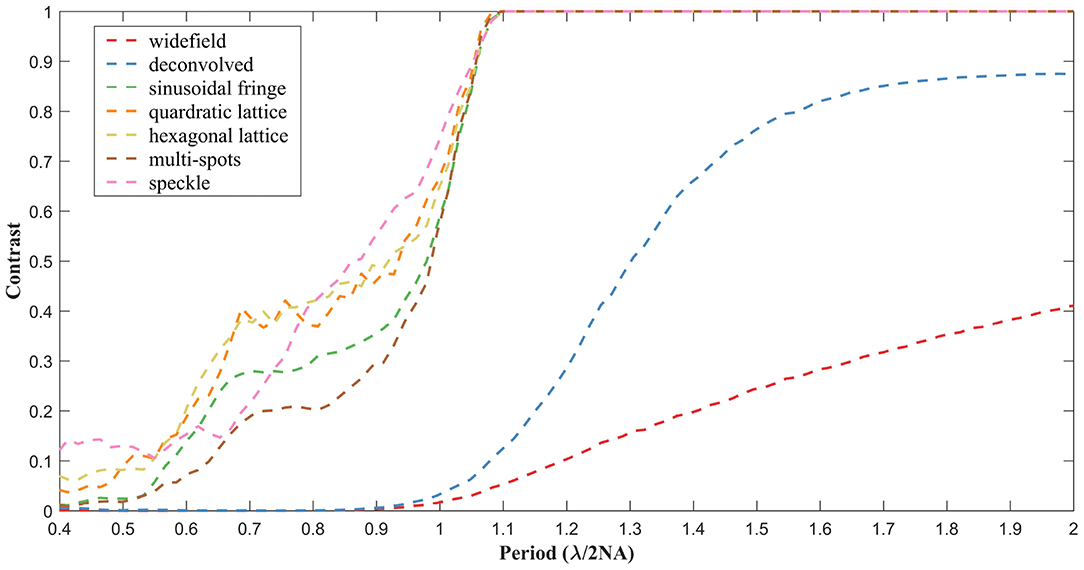
Figure 3. Contrast degradation curves of the reconstructed simulated target under different types of structured illumination.

Results and Discussion

We validate our LSQ-SIM reconstruction algorithm on two open-accessible experimental data sets (Laser Analytics Group), and compare it with joint Richardson-Lucy deconvolution, an iterative method that has been used to successfully reconstruct SIM images by sinusoidal and multi-focal excitation (jRL-SIM) [13, 23]. The jRL-SIM approach originates from the Richardson-Lucy (RL) deconvolution used in image restoration, the idea of which is to get an estimation of the object to maximize the likelihood of the observation under the Poisson noise model by multiplicative iteration [24, 25]. In RL deconvolution, the blurring convolution kernel (e.g., the point spread function) is regarded as a linear operator. While in jRL-SIM, this convolution operator is modified to be a mixed operator that combines convolution and structured excitation operations. As a result of this iteration approach, jRL-SIM is particularly time consuming for large numbers of raw SIM images.

All the reconstructions described in this study were conducted on a personal computer equipped with a 2.9 GHz i5-9400 CPU. The first data set contains SIM images of fluorescent beads (Tetraspeck, Thermo Fisher Scientific) with a nominal diameter of 100 nm by sinusoidal excitation at the wavelength of 488 nm [23]. The widefield image is acquired by summing all the raw images on which deconvolution is subsequently implemented. The number of iterations for jRL-SIM reconstruction is chosen to be 30 to guarantee sufficient convergence and prevent intolerable artifacts and noise amplification. At the pre-deconvolution step of our LSQ-SIM reconstruction, we use iterative RL deconvolution rather than instant Wiener deconvolution because we find that Wiener deconvolution leads to obvious ringing artifacts that severely corrupt the reconstruction result. Figure 4 shows a comparison of jRL-SIM and LSQ-SIM reconstructions for fluorescent beads. In the widefield image, fluorescent beads that are lying in proximity cannot be discriminated (pure deconvolution also fails to distinguish these) although the contrast is boosted. Both the jRL-SIM and LSQ-SIM reconstruction methods successfully resolve these neighboring beads, while the latter partially presents a slightly higher contrast, according to the intensity profile shown in Figure 4.

FIGURE 4

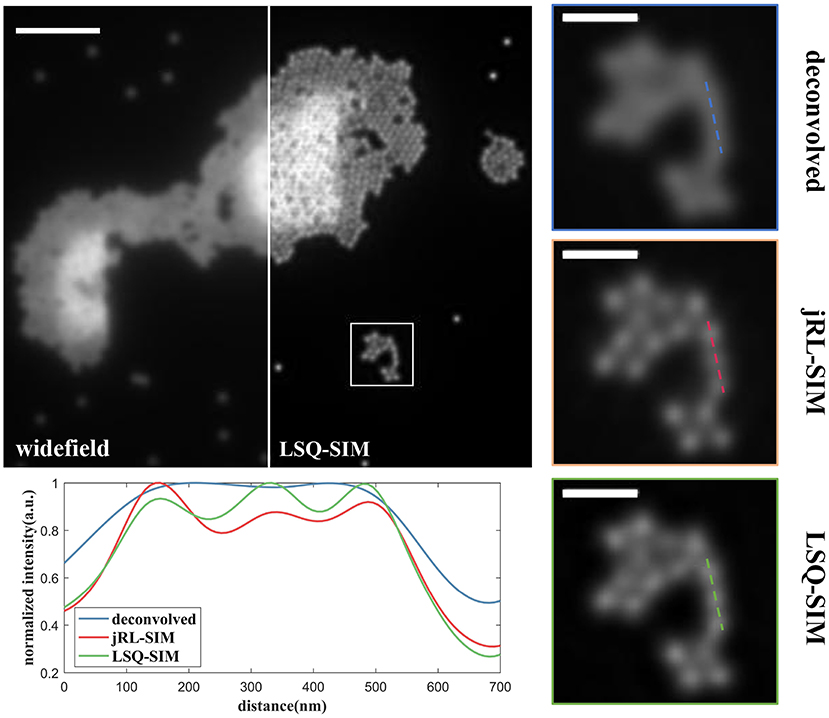
Figure 4. Comparison of reconstructions of fluorescent beads under sinusoidal illumination using the jRL-SIM and LSQ-SIM methods. Scale bar: 2 μm for full-frame image and 0.5 μm for the zoomed region.

To further compare the resolution improvement provided by the proposed LSQ-SIM method and jRL-SIM, we study their capacity to compress the full width at half maximum (FWHM) of a sub-diffraction object [18]. The intensity profiles of a single bead are plotted in Figure 5. The FWHM value for the single bead in the widefield image is approximately 250 nm, whereas the FWHMs for jRL-SIM and LSQ-SIM reconstructions were ~120 nm and ~140 nm, respectively. Although the FWHM confinement of LSQ-SIM is a little lower than that of jRL-SIM, a reduction of the FWHM by nearly one half is still realized.

FIGURE 5

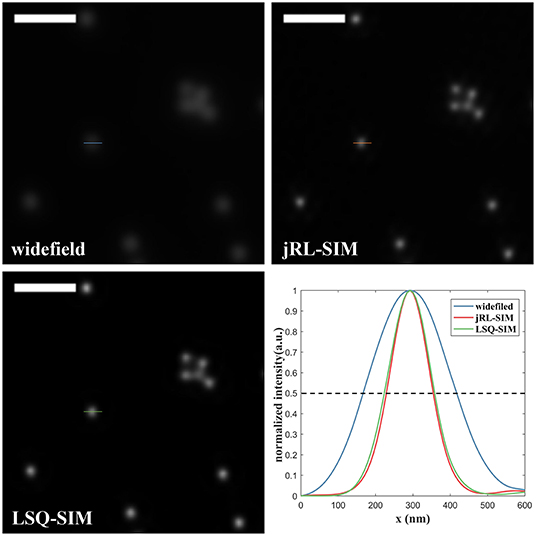
Figure 5. Comparison of the intensity profile of a single fluorescent bead reconstructed using jRL-SIM and LSQ-SIM. Scale bar: 1 μm.

The efficacy of the proposed LSQ-SIM method is also assessed using a data set consisting of sample images from multi-focal SIM (MSIM). The target sample is a microtubule structure labeled by Alexa Fluor 488 in a fixed cell imaged under a 60 × TIRF objective with NA1.45 [12]. The reconstruction results of jRL-SIM and LSQ-SIM are shown in Figure 6. For the pre-deconvolution step in LSQ-SIM reconstruction, an easily performed quasi-Wiener deconvolution is applied by replacing the signal-to-noise (SNR) regularization term in the standard Wiener deconvolution with a small positive constant (referred to as Tikhonov regularization). We find that the proposed LSQ-SIM method provides sample reconstruction that is similar to that of jRL-SIM, with a clearer background but without the post-deconvolution procedure mentioned earlier in this section, revealing two closely nestling branches that are nevertheless obscured in the deconvolved widefield images. Employing the post-deconvolution process described above in LSQ-SIM reconstruction provides clear resolution enhancement, as well as significant contrast improvement.

FIGURE 6

Figure 6. Reconstruction results of the microtubule sample, obtained using widefield, jRL-SIM, and proposed LSQ-SIM methods without and with post-deconvolution. Scale bar: 1.5 μm.

The frequency spectra of jRL-SIM and LSQ-SIM reconstructions are also compared, as shown in Figure 7. The inner red dashed circle indicates the experimentally calibrated widefield cut-off at a spatial frequency of 1/280 nm⁻¹, while the outer circle indicates a cutoff of 1/145 nm⁻¹. The spectrum of jRL-SIM reconstruction is expanded and almost fills the area bounded by the outer circle, which is consistent with the result of the previous study [12]. Without post-deconvolution, the spectrum expansion of LSQ-SIM reconstruction is slightly weaker than that of jRL-SIM, which is compensated for by the proposed post-deconvolution method.

FIGURE 7

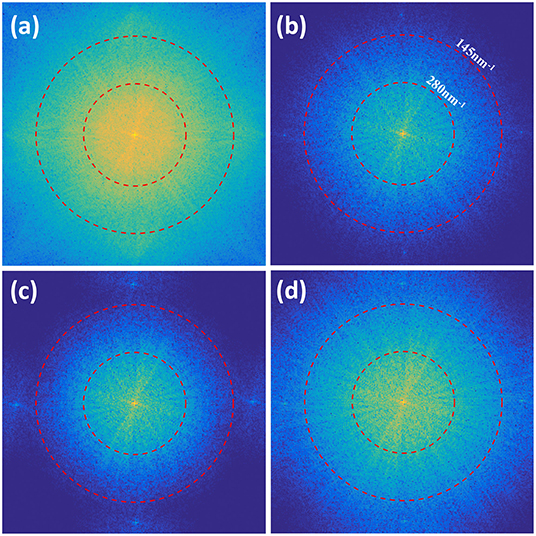
Figure 7. Comparison of frequency spectral of the reconstructions of the microtubule sample. The spectra of the deconvolved image (a), jRL-SIM reconstruction (b), and LSQ-SIM reconstruction without (c) and with (d) post-deconvolution are displayed.

With regards to computation time, the jRL-SIM reconstruction of fluorescent beads requires 48.1 s in contrast to the 16.7 s required by the proposed LSQ-SIM method, which is nearly three times faster. For the reconstruction of the microtubule sample, jRL-SIM requires 14.2 s to reconstruct a super-resolution image, while the proposed LSQ-SIM method requires 0.69 and 0.71 s with and without post-deconvolution, respectively. The speed improvement obtained by the LSQ-SIM algorithm is dramatically increased to over 25 times because of the fast quasi-Wiener deconvolution utilized at the pre-deconvolution step of microtubule reconstruction.

Conclusion

We propose a novel super-resolution image reconstruction algorithm in the least-squares regression framework to efficiently process SIM data under both sinusoidal and non-sinusoidal structured illumination. Our method is conducted mainly in the spatial domain, which greatly reduces the computation time required for an individual reconstruction. The super-resolution capability of the proposed LSQ-SIM approach is verified both in silico and in vitro. The performance of our method is assessed on two open-access experimental data sets, giving results that are comparable to those of the jRL-SIM method. Our findings indicate that the proposed LSQ-SIM method has the potential for use in biological applications.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

JL contributed to conception of this work, accomplished the simulation, performed the analysis of results, and wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This research was funded by the National Natural Science Foundation of China (61827825 and 61735017), Fundamental Research Funds for the Central Universities (2019XZZX003-06), and Zhejiang Lab (2018EB0ZX01 and 2020MC0AE01).

Conflict of Interest

JW was employed by the company Texas Instruments Semiconductor Technologies (Shanghai) Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Abbe E. Beitirage zur theorie des mikroskops und der mikroskopischen Wahrnehmung. Arch Mikroskopische Anat. (1873) 9:413–8. doi: 10.1007/BF02956173

CrossRef Full Text | Google Scholar

2. Rust MJ, Bates M, Zhuang X. Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (STORM). Nat Methods. (2006) 3:793–5. doi: 10.1007/978-3-642-02597-6_20

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Hell SW, Wichmann J. Breaking the diffraction resolution limit by stimulated emission: stimulated-emission-depletion-fluorescence microscopy. Opt Lett. (1994) 19:780–92. doi: 10.1364/OL.19.000780

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Gustafsson MG. Surpassing the lateral resolution limit by a factor of two using structured illumination microscopy. J Microsc. (2010) 198:82–7. doi: 10.1046/j.1365-2818.2000.00710.x

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Guo Y, Li D, Zhang S, Yang Y, Liu JJ, Wang X. Visualizing intracellular organelle and cytoskeletal interactions at nanoscale resolution on millisecond timescales. Cell. (2018) 175:1–13. doi: 10.1016/j.cell.2018.09.057

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Huang X, Fan J, Li L, Liu H, Chen L. Fast, long-term, super-resolution imaging with hessian structured illumination microscopy. Nat Biotechnol. (2018) 36:451–9. doi: 10.1038/nbt.4115

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Gustafsson GLM. Nonlinear structured-illumination microscopy: wide-feld fuorescence imaging with theoretically unlimited resolution. Proc Natl Acad Sci USA. (2005) 102:13081–6. doi: 10.1073/pnas.0406877102

CrossRef Full Text | Google Scholar

8. Li D, Shao L, Chen BC, Zhang X, Zhang M, Moses B. Extended-resolution structured illumination imaging of endocytic and cytoskeletal dynamics. Science. (2015) 349:aab3500. doi: 10.1126/science.aab3500

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Rego EH, Shao L, Macklin JJ, Winoto L, Gustafsson MGL. Nonlinear structured-illumination microscopy with a photoswitchable protein reveals cellular structures at 50-nm resolution. Proc Natl Acad Sci USA. (2011) 109:E135–43. doi: 10.1073/pnas.1107547108

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Aurélie J, Tolstik E, Feldmann P, Wicker K, Sentenac A, Heintzmann R. Optical sectioning and high resolution in single-slice structured illumination microscopy by thick slice blind-sim reconstruction. PLOS ONE. (2015) 10:e0132174. doi: 10.1371/journal.pone.0132174

CrossRef Full Text | Google Scholar

11. Mudry E, Belkebir K, Girard J, Savatier E, Moal C, Nicoletti C. Structured illumination microscopy using unknown speckle patterns. Nat Photon. (2012) 6:312–5. doi: 10.1038/nphoton.2012.83

CrossRef Full Text | Google Scholar

12. York AG, Parekh SH, Nogare DD, Fischer RS, Temprine K, Mione M. Resolution doubling in live, multicellular organisms via multifocal structured illumination microscopy. Nat Methods. (2012) 9:749–54. doi: 10.1038/nmeth.2025

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Ströhl F, Kaminski CF. A joint richardson—lucy deconvolution algorithm for the reconstruction of multifocal structured illumination microscopy data. Methods Appl Fluoresc. (2015) 3:014002. doi: 10.1088/2050-6120/3/1/014002

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Dong S, Nanda P, Shiradkar R, Guo K, Zheng G. High-resolution fluorescence imaging via pattern-illuminated fourier ptychography. Opt Exp. (2014) 22:20856–70. doi: 10.1364/OE.22.020856

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Chakrova N, Rieger B, Stallinga S. Deconvolution methods for structured illumination microscopy. J Opt Soc Am A. (2016) 33:B12. doi: 10.1364/JOSAA.33.000B12

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Tian L, Li X, Ramchandran K, Waller L. Multiplexed coded illumination for fourier ptychography with an led array microscope. Biomed Opt Exp. (2014) 5:2376–89. doi: 10.1364/BOE.5.002376

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Florian S, Kaminski CF. Frontiers in structured illumination microscopy. Optica. (2016) 3:667–77. doi: 10.1364/optica.3.000667

CrossRef Full Text | Google Scholar

18. Dan D, Lei M, Yao B, Wang W, Winterhalder M, Zumbusch A, et al. DMD-based LED-illumination super-resolution and optical sectioning microscopy. Sci Rep. (2013) 3:1116. doi: 10.1038/srep01116

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Ingerman EA, London RA, Heintzmann R, Gustafsson MGL. Signal, noise and resolution in linear and nonlinear structured-illumination microscopy. J Microscopc. (2018) 273:3–25. doi: 10.1111/jmi.12753

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Yeh LH, Tian L, Waller L. Structured illumination microscopy with unknown patterns and a statistical prior. Biomed Opt Exp. (2016) 8:695–711. doi: 10.1364/BOE.8.000695

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Chakrova N, Heintzmann R, Rieger B, Stallinga S. Studying different illumination patterns for resolution improvement in fluorescence microscopy. Opt Exp. (2015) 23:31367–83. doi: 10.1364/OE.23.031367

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Dong S, Liao J, Guo K, Bian L, Suo J, Zheng G. Resolution doubling with a reduced number of image acquisitions. Biomed Opt Exp. (2015) 6:2946–52. doi: 10.1364/BOE.6.002946

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Ströhl F, Kaminski C. Speed limits of structured illumination microscopy. Opt Lett. (2017) 42:2511–4. doi: 10.1364/OL.42.002511

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Richardson WH. Bayesian-based iterative method of image restoration. J Opt Soc Am. (1972) 62:55–9. doi: 10.1364/JOSA.62.000055

CrossRef Full Text | Google Scholar

25. Lucy LB. An iterative technique for the rectification of observed distributions. J Astron. (1974) 79:745–54. doi: 10.1086/111605

CrossRef Full Text | Google Scholar